Enhancing Oscillation Damping in an Interconnected Power System with Integrated Wind Farms Using Unified Power Flow Controller
Abstract
1. Introduction
1.1. Motivation
1.2. Literature Review
1.3. Contributions
- A power oscillation damping controller (PODC) is designed and used with UPFC for damping oscillations in an interconnected power system.
- The continuous load fluctuation profile is employed for oscillation characteristics analysis.
- Typical impacting factors such as tie-line power, DFIG output, and load disturbances, as well as the damping controller of UPFC, are considered as part of a small signal stability analysis of an interconnected power system.
- Eigenvalue analysis and dynamic time-domain simulations are carried out to examine the capability of UPFC on improving inter-area oscillation mode and enhancing oscillation damping of an interconnected power system with wind farm integrated.
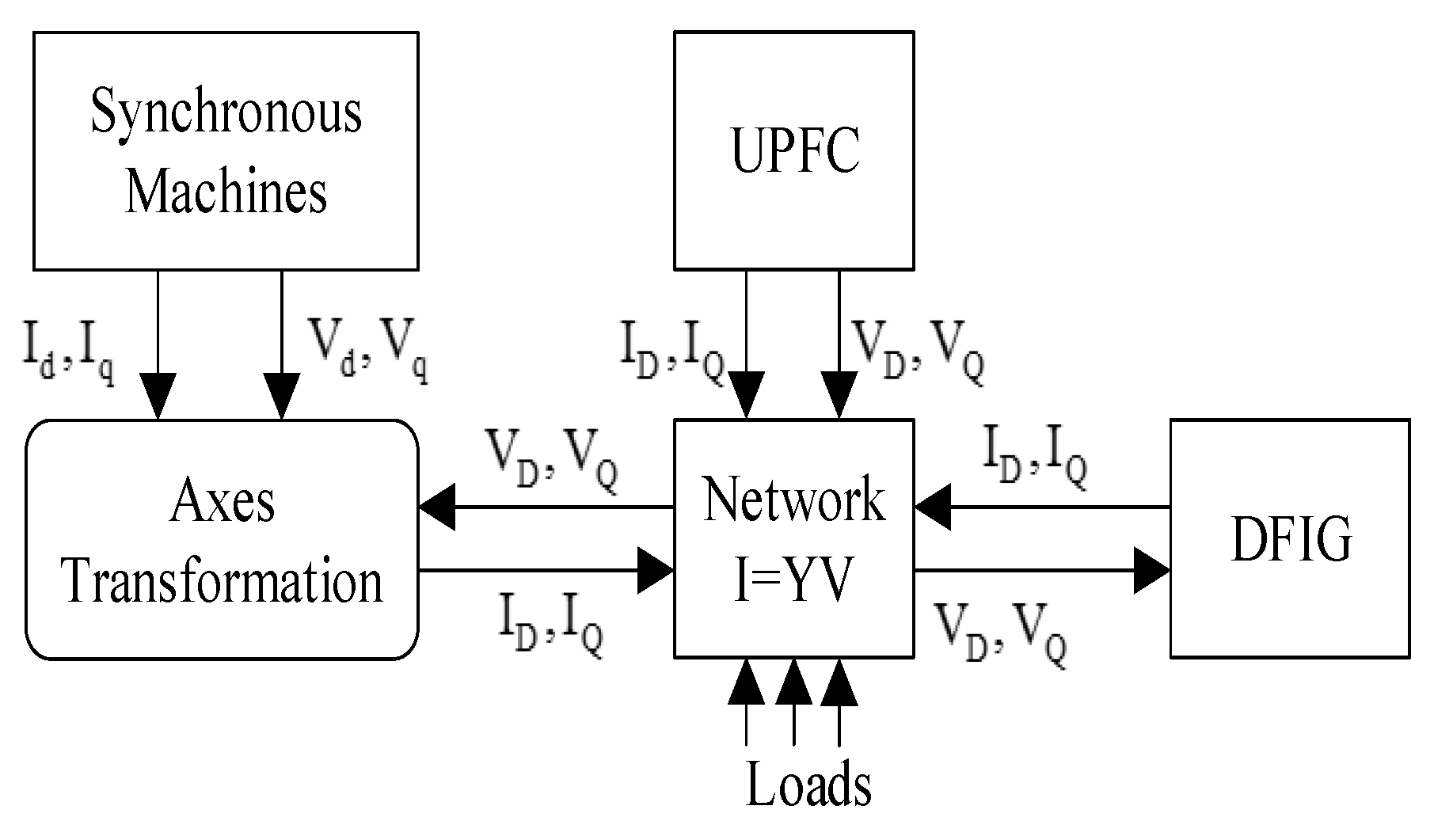
2. System Configuration and Models
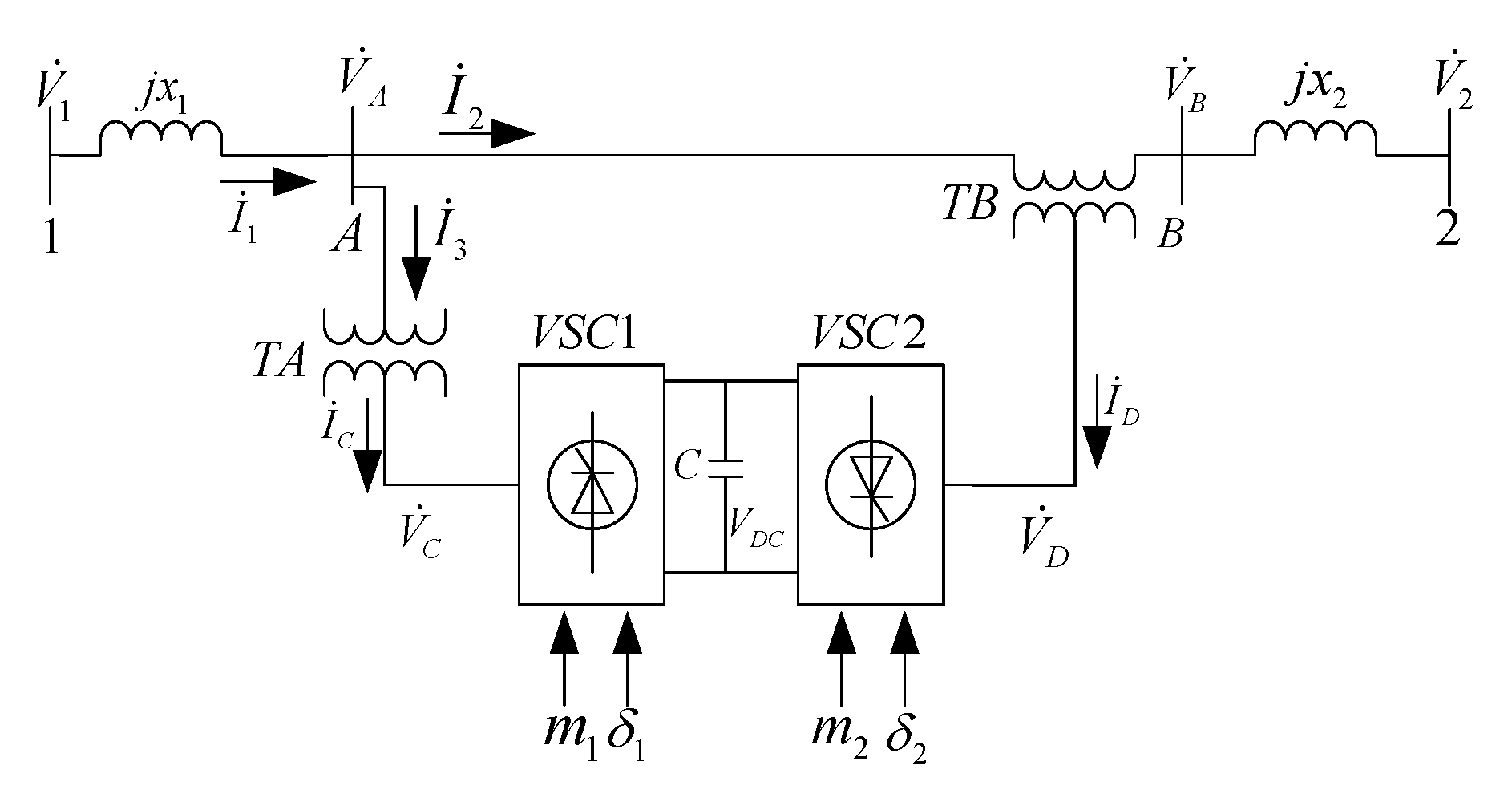
2.1. Modelling of UPFC
2.2. Modeling of DFIG
3. Fundamentals of Small Signal Stability Analysis
4. Oscillation Damping Analysis of a Power System Using UPFC with Compensated Wind Farms
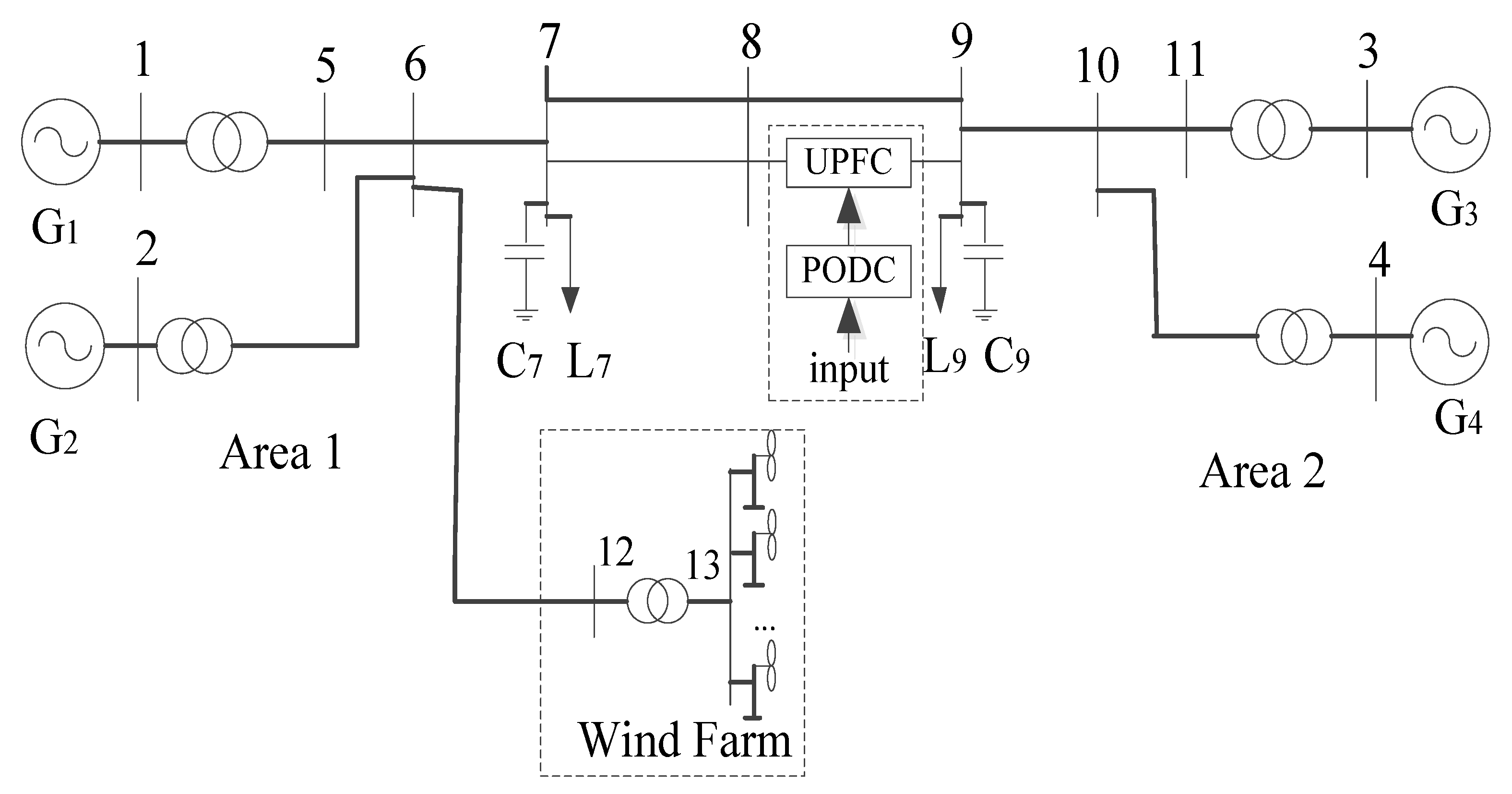
4.1. Test System
4.2. Oscillation Damping Analysis in a Compensated Wind Farm
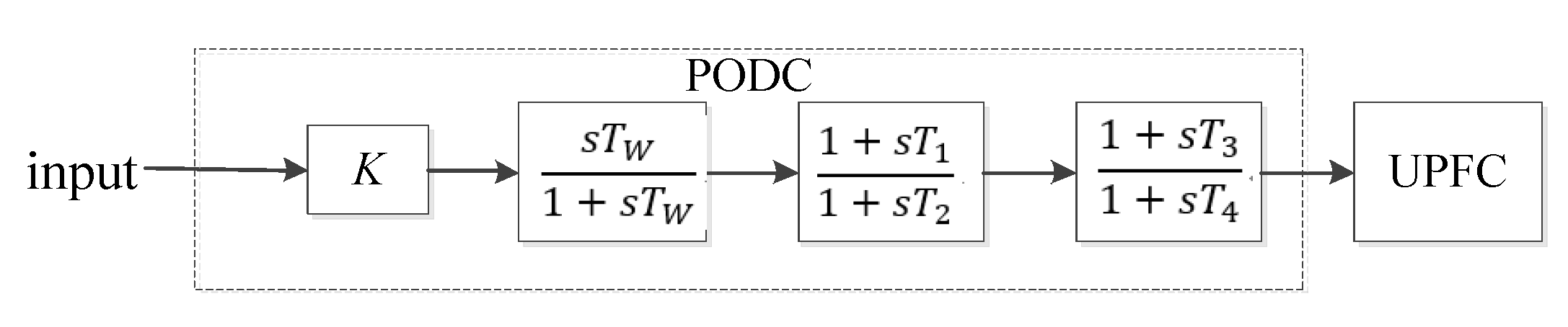
5. Power Oscillation Damping Controller of UPFC
6. Sensitivity Analysis
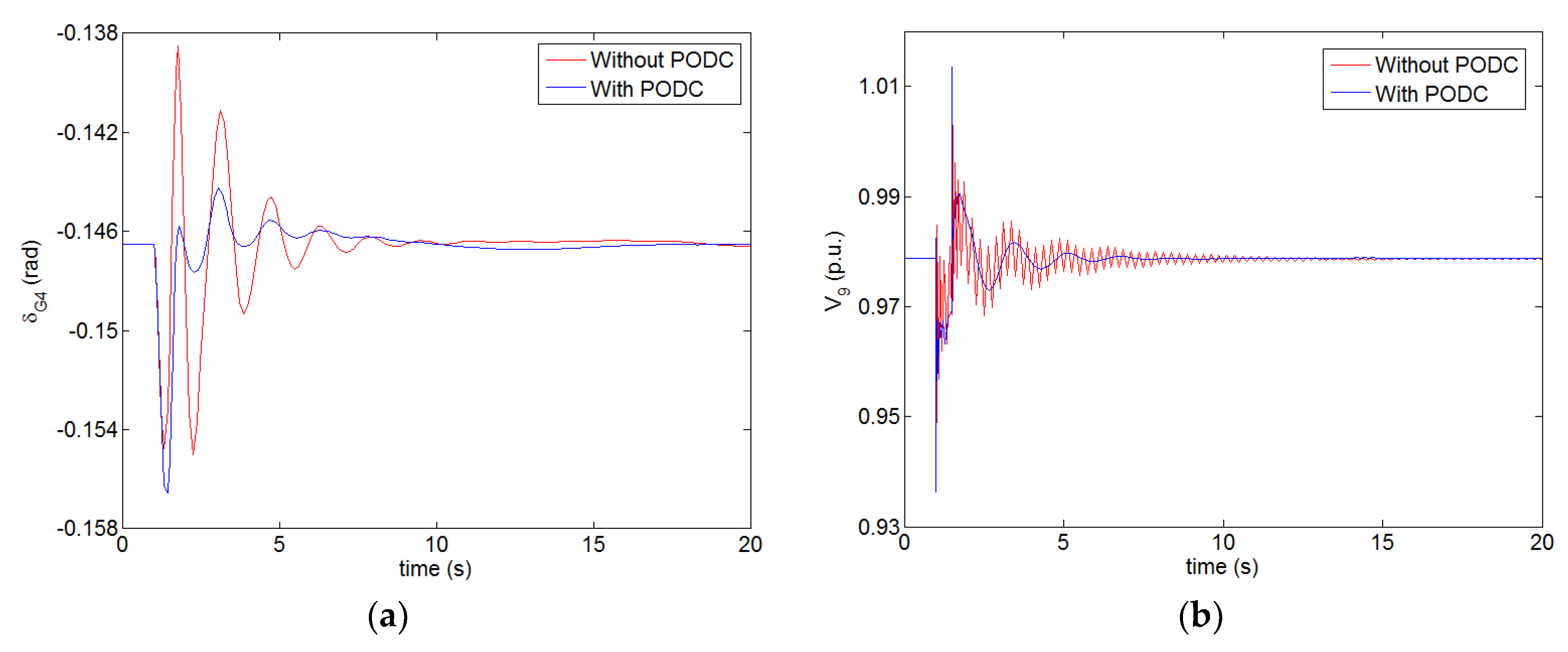
6.1. Disturbance of Tie-Line Power Change
- Without UPFC: Basic case
- With both UPFC and PODC: Corresponding to the scenario described in Section 5
6.2. Disturbance of Transmission Line Outage
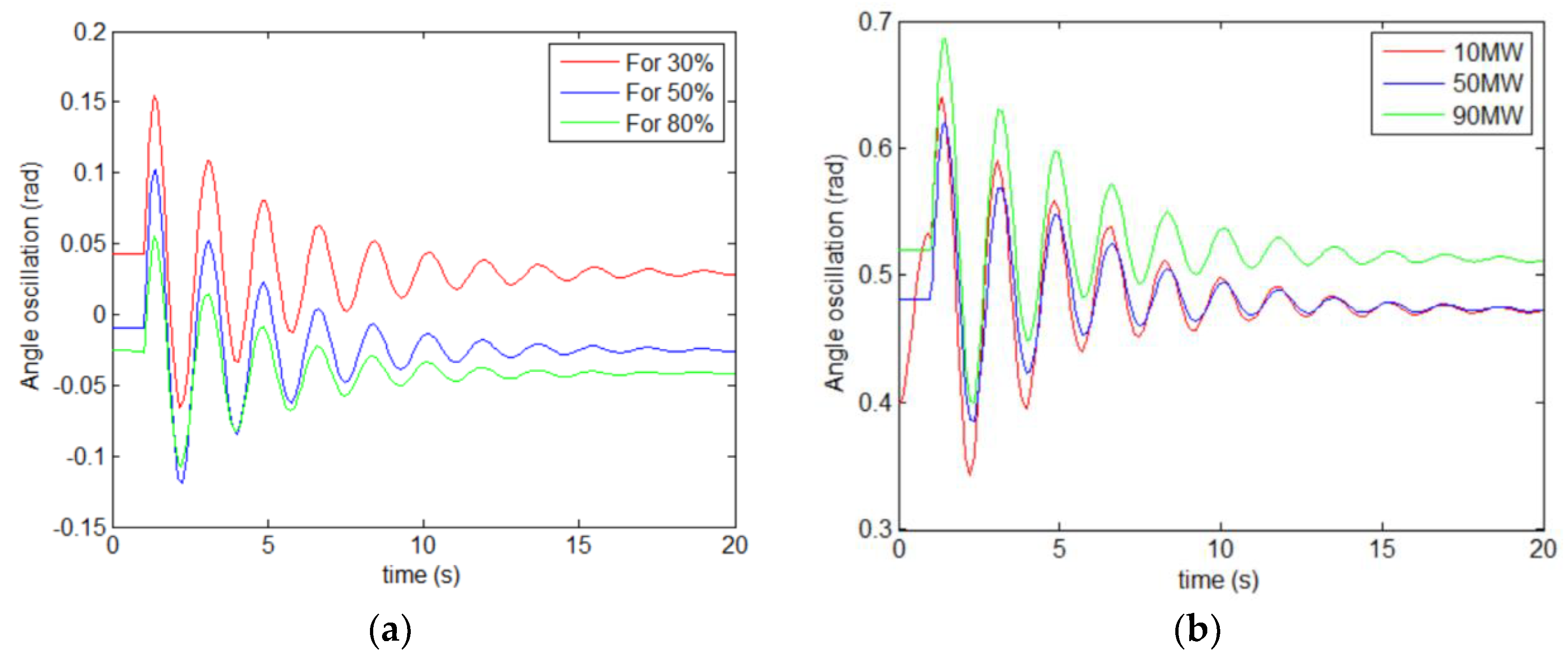
6.3. Oscillation Modes with Different Levels of Wind Penetration
6.4. System Robustness Analysis
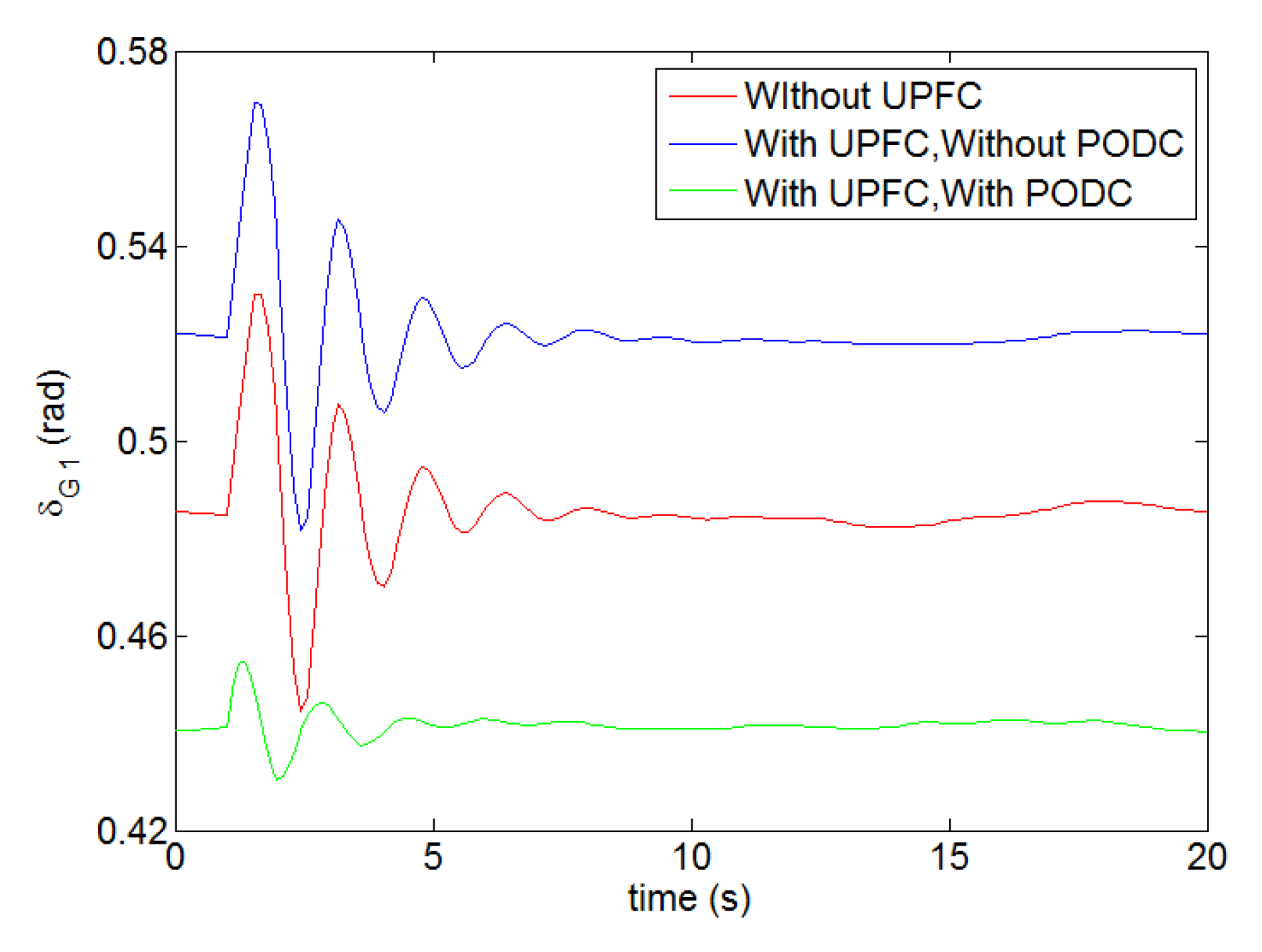
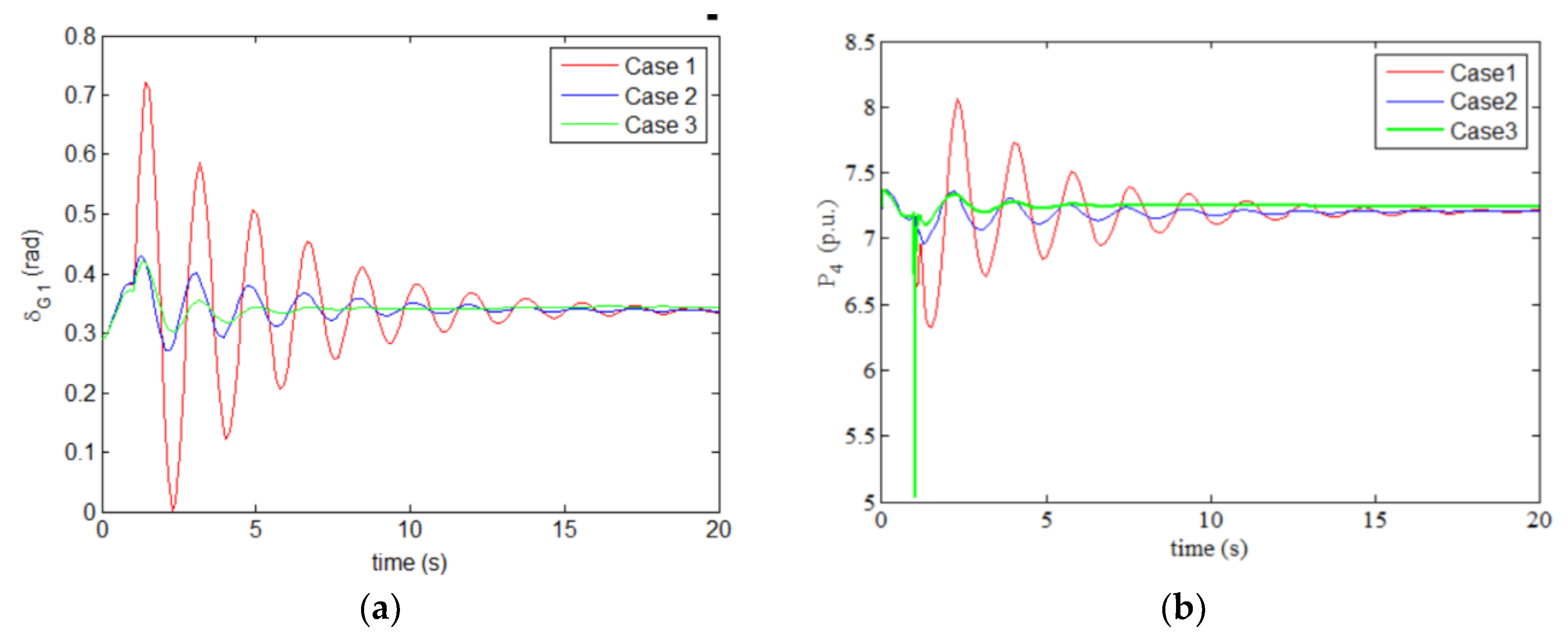
- Case 1: Both the UPFC and PODC were not equipped. The power output of the wind farm was 30 MW, and the tie-line power from region 1 to region 2 was 430 MW;
- Case 2: The UPFC was equipped and the PODC was not. The power output of the wind farm and the tie-line power from region 1 to region 2 were the same with those in Case 1;
- Case 3: Both the UPFC and PODC were equipped. The power output of the wind farm was 50 MW, and the tie-line power from region 1 to region 2 was 449 MW.
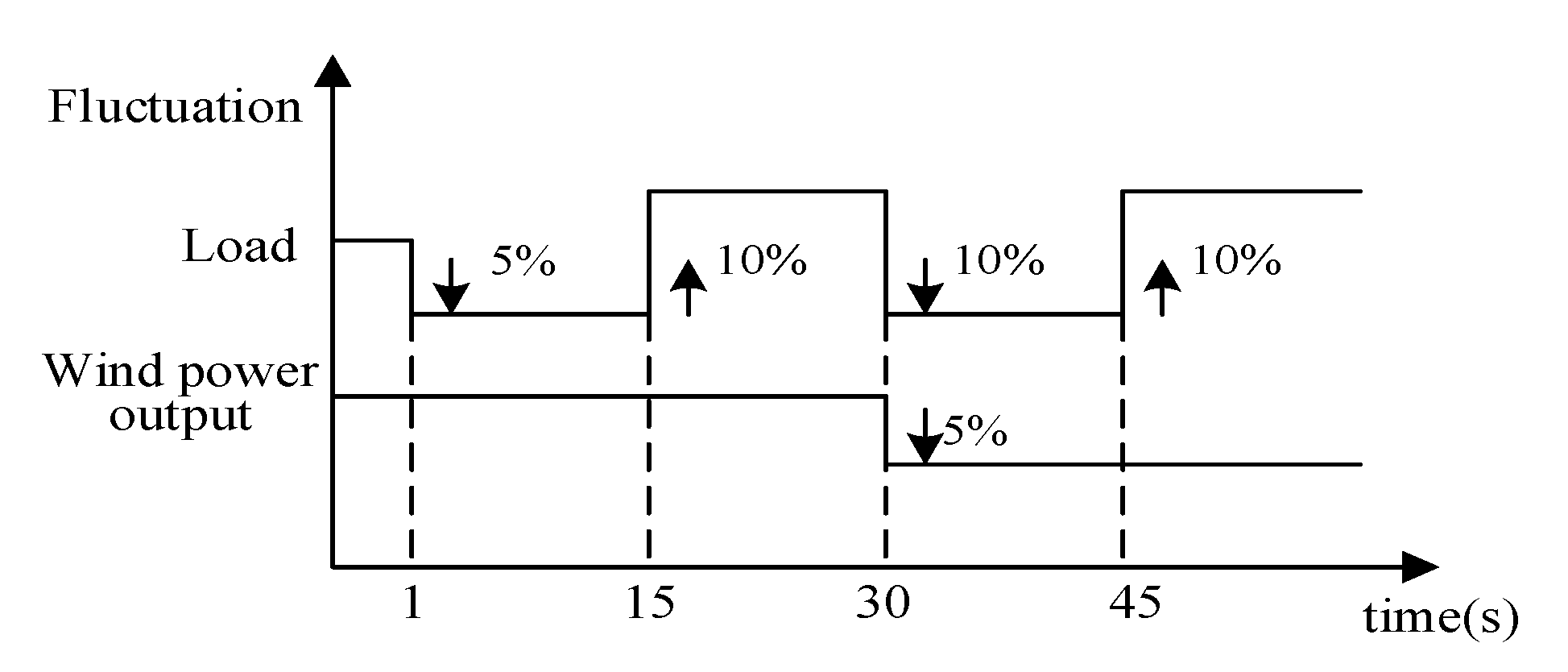
6.5. Variations of Load and Wind Power Output
7. Applications in a Larger Sample Power System
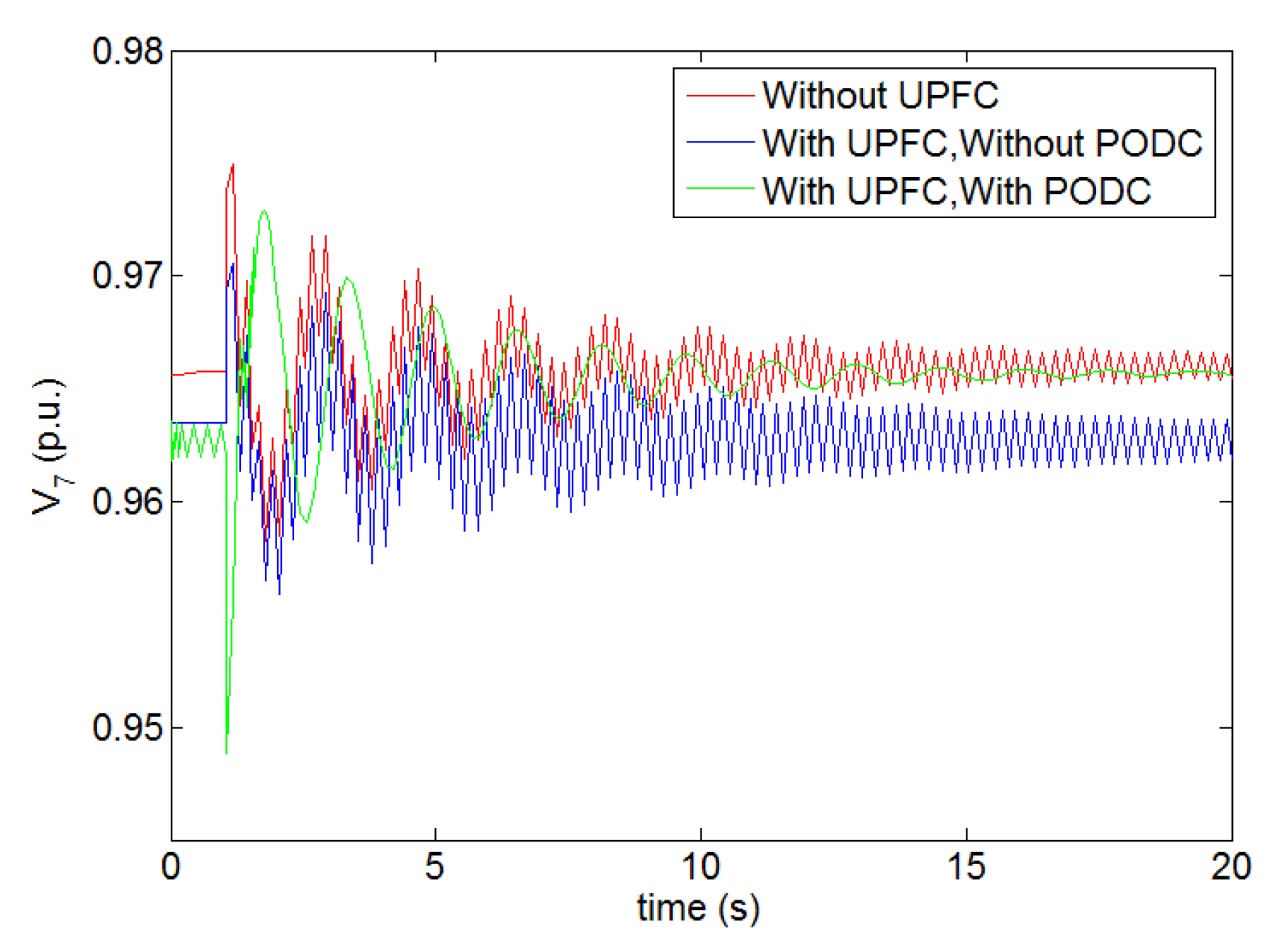
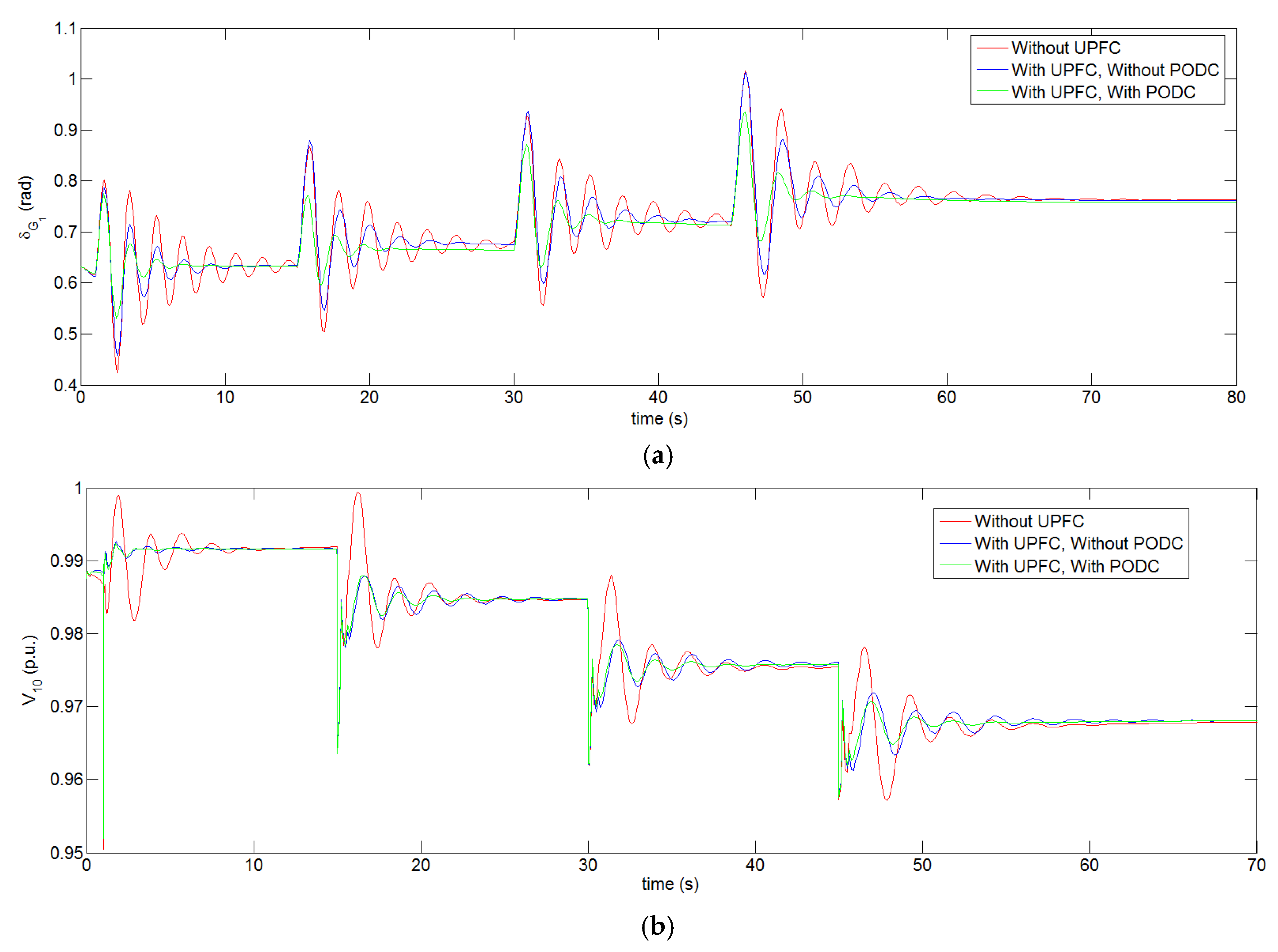
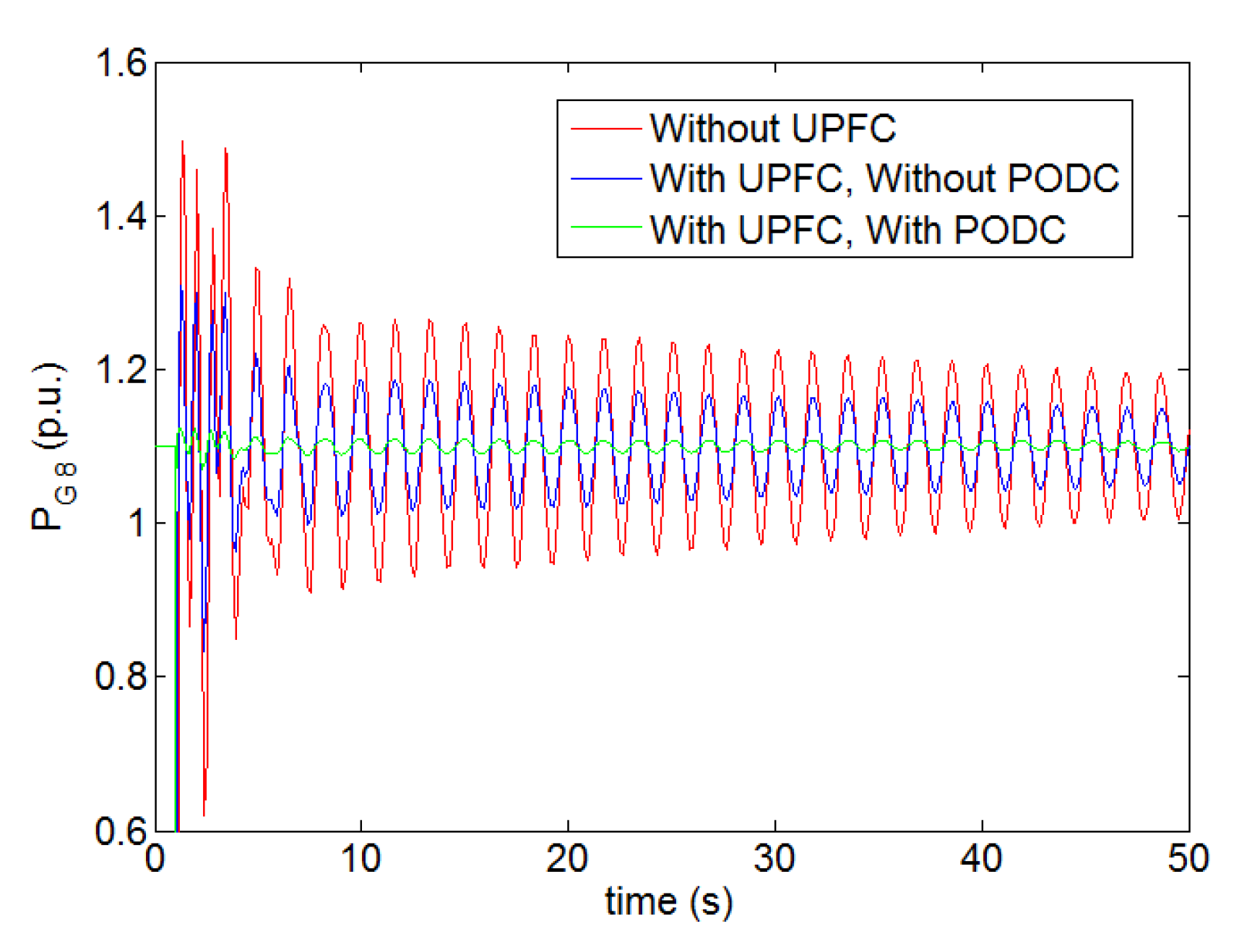
- Case 1. Without UPFC. This represents the basic case. The total active power output of the wind farm was around 50 MW, and the tie-line power from region 1 to 2 through the tie-line 6–7 was 265 MW;
- Case 2. With UPFC, Without PODC. This case corresponded to the one in Section 4, and the other operating conditions were the same as Case 1;
- Case 3. Withboth UPFCand PODC. This case corresponded to the one in Section 5, and the other operating conditions were the same as Case 1.
8. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| A. Acronym | |
| UPFC | Unified power flow controller |
| PODC | Power oscillation damping controller |
| DFIG | Doubly-fed induction generators |
| GWEC | Global Wind Energy Council |
| FACTS | Flexible AC transmission system |
| VSC1 | Static synchronous shunt compensator |
| VCS2 | Static synchronous series compensator |
| TA | Parallel transformer |
| TB | Series transformer |
| DC | Direct current |
| PSS | Power system stabilizer |
| PI | Proportional integral |
| AC | Alternating current |
| DAE | Differential algebraic equation |
| B. Parameters | |
| d-q axis component of connecting point voltage VA | |
| d-q axis component of connecting point voltage VB | |
| Reactance of transformer TA | |
| d-q axis component of current I3 | |
| Reactance of transformer TB | |
| d-q axis component of current I2 | |
| Amplitude modulation ratio/phase angle of VSC1 | |
| Amplitude modulation ratio/phase angle of VSC2 | |
| C | DC capacitor |
| Voltage across DC capacitor | |
| Current/voltage of the parallel side converter | |
| Current/voltage of the series side converter | |
| The conjugate value of | |
| Equivalent reactance of the parallel/series sides | |
| Output of the wind wheel | |
| Wind energy utilization factor | |
| The wind turbine generators blade radius | |
| Swept area of the wind wheel | |
| Density of air | |
| V | Wind speed |
| Tip speed ratio | |
| Maximum wind energy utilization factor | |
| Speeds of generator/reference/wind turbine | |
| Inertia constants of the turbine/the generator | |
| Shaft twist angle | |
| Damping coefficient of wind turbine | |
| Torque of electromagnetic/shaft/mechanical | |
| Shaft stiffness coefficient | |
| Damping coefficient | |
| Mutual inductance | |
| d-q axis stator currents | |
| d-q axis rotor currents | |
| Stator/rotor self-inductance/the mutual inductance | |
| Rotor resistance/slip/stator reactance/stator transient reactance | |
| Rotor circuit time | |
| Voltages behind the transient reactance of d-q axis | |
| Stator voltages/rotor voltages of d-q axis | |
| Vectors of the state variables and the algebraic variables | |
| A | State matrix |
| Eigenvalue of state matrix | |
| Real part of eigenvalue | |
| Imaginary part of eigenvalue | |
| Participation factor of the i-th state variable to the j-th eigenvalue | |
| Right eigenvector | |
| Left eigenvector | |
| Gain | |
| Washout circuit | |
| Oscillation frequency | |
| Three-phase short-circuit grounding fault time | |
| Three-phase short-circuit grounding fault clearing time | |
| C. Variables | |
| Eigenvalues of mode i | |
| Damping ratio | |
| Damping ratio of mode i | |
| voltage of bus i | |
| Power angle of Gi |
References
- Ackermann, T. Wind Power in Power Systems; John Wiley & Sons Press: Hoboken, NJ, USA, 2005. [Google Scholar]
- Edrah, M.; Lo, K.L.; Anaya-Lara, O. Reactive power control of DFIG wind turbines for power oscillation damping under a wide range of operating conditions. IET Gener. Transm Distrib. 2016, 10, 3777–3785. [Google Scholar] [CrossRef]
- GWEC. Global Wind Reports 2016. Available online: http://gwec.net/publications/global-wind-report-2 /global-wind-report-2016/ (accessed on 5 May 2017).
- Kundur, P. Power System Stability and Control; McGraw-Hill Press: New York, NY, USA, 1994. [Google Scholar]
- Klein, M.; Rogers, G.J.; Kundur, P. A fundamental study of interarea oscillations in power systems. IEEE Trans. Power Syst. 1991, 6, 914–921. [Google Scholar] [CrossRef]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability. 2003. Available online: https://ieeexplore.ieee.org/book/5264012?bknumber=5264012 (accessed on 15 November 2018).
- Slootweg, J.G.; Klind, W.L. The impact of large scale wind power generation on power system oscillations. Electr. Power Syst. Res. 2003, 67, 9–20. [Google Scholar] [CrossRef]
- Singh, M.; Allen, A.J.; Muljadi, E.; Gevorgian, V.; Zhang, Y.C.; Santoso, S. Interarea oscillation damping controls for wind power plants. IEEE Trans. Sustain. Energy 2015, 6, 967–975. [Google Scholar] [CrossRef]
- He, P.; Wen, F.S.; Ledwich, G.; Xue, Y.S. An investigation on interarea mode oscillations of interconnecte-dpower systems with integrated wind farms. Int J. Electr. Power Energy Syst. 2016, 78, 145–157. [Google Scholar] [CrossRef]
- Lin, Z.; Wen, F.S.; Ding, Y.; Xue, Y.S. Wide-area coherency identification of generators in interconnected power systems with renewables. IET Gener. Transm. Distrib. 2017, 11, 4444–4455. [Google Scholar] [CrossRef]
- Ma, J.; Qiu, Y.; Li, Y.N.; Thorp, J.S. Stability analysis of power system with multiple operating conditions considering the stochastic characteristic of wind speed. IET Gener. Transm Distrib. 2016, 10, 1056–1066. [Google Scholar] [CrossRef]
- Yang, Y.D.; Zhao, J.X.; Liu, H.; Qin, Z.J.; Deng, J.; Qi, J.J. A matrix-perturbation-theory-based optimal strategy for small-signal stability analysis of large-scale power grid. Protect. Control Mod. Power Syst. 2018, 3, 353–363. [Google Scholar] [CrossRef]
- Lin, Z.; Wen, F.S.; Ding, Y.; Xue, Y.S.; Liu, S.Y.; Zhao, Y.X.; Yi, S.M. WAMS-based coherency detection for situational awareness of power systems with high penetration levels of renewable generation. IEEE Trans. Power Syst. 2018, 33, 5410–5426. [Google Scholar] [CrossRef]
- Eremia, M.; Liu, C.C.; Edris, A.A. Advanced Solutions in Power Systems: HVDC, FACTS, and Artificial Intelligence. 2016. Available online: https://onlinelibrary.wiley.com/doi/book/10.1002/9781119175391 (accessed on 30 September 2016).
- Bhushan, R.; Chatterjee, K. Effects of parameter variation in DFIG-based grid connected system with a FACTS device for small-signal stability analysis. IET Gener. Transm. Distrib. 2017, 11, 2762–2777. [Google Scholar] [CrossRef]
- Yang, S.T.; Liu, Y.; Wang, X.R.; Gunasekaran, D.; Karki, U.; Peng, F.Z. Modulation and control of transformer-less UPFC. IEEE Trans. Power Electron. 2016, 31, 1050–1063. [Google Scholar] [CrossRef]
- Arun Kumar, K.; Singh, S.P. Congestion mitigation using UPFC. IET Gener. Transm. Distrib. 2016, 10, 2433–2442. [Google Scholar]
- Song, P.; Xu, Z.; Dong, H. UPFC-based line overload control for power system security enhancement. IET Gener. Transm. Distrib. 2017, 11, 3310–3317. [Google Scholar] [CrossRef]
- Jelavić, M.; Perić, N.; Petrović, I. Damping of wind turbine tower oscillations through rotor speed control. In Proceedings of the Ecologic Vehicles and Renewable Energies International Exhibition and Conference (EVER), Monte Carlo, Monako, 29 March–1 April 2007; pp. 1–10. [Google Scholar]
- Wang, L.; Li, H.W.; Wu, C.T. Stability analysis of an integrated offshore wind and seashore wave farm fed to a power grid using a unified power flow controller. IEEE Trans. Power Syst. 2013, 28, 2211–2221. [Google Scholar] [CrossRef]
- Golshannavaz, S.; Aminifar, F.; Nazarpour, D. Application of UPFC to enhancing oscillatory response of seriescompensated wind farm integrations. IEEE Trans. Smart Grid 2014, 5, 1961–1968. [Google Scholar] [CrossRef]
- Zuo, J.; Li, Y.; Shi, D.; Duan, X. Simultaneous robust coordinated damping control of power system stabilizers (PSSs), static Var compensator (SVC) and doubly-fed induction generator power oscillation dampers (DFIG PODs) in multimachine power systems. Energies 2017, 10, 565. [Google Scholar]
- Mohanty, A.; Patra, S.; Ray, P.K. Robust fuzzy-sliding mode based UPFC controller for transient stability analysis in autonomous wind-diesel-PV hybrid system. IET Gener. Transm. Distrib. 2016, 10, 1248–1257. [Google Scholar] [CrossRef]
- Shotorbani, A.M.; Ajami, A.; Aghababa, M.P.; Hosseini, S.H. Direct lyapunov theory-based method for power oscillation damping by robust finite-time control of unified power flow controlle. IET Gener. Transm. Distrib. 2013, 7, 691–699. [Google Scholar] [CrossRef]
- Malhotra, U.; Gokaraju, R. An add-on self-tuning control system for a UPFC application. IEEE Trans. Ind. Electron. 2014, 61, 2378–2388. [Google Scholar] [CrossRef]
- Dash, P.K.; Patnaik, R.K.; Mishra, S.P. Adaptive fractional integral terminal sliding mode power control of UPFC in DFIG wind farm penetrated multimachine power system. Protect. Control Mod. Power Syst. 2018, 3, 79–92. [Google Scholar] [CrossRef]
- Miao, Z.; Fan, L.; Osborn, D.; Yuvarajan, S. Control of DFIG-based wind generation to improve interarea oscillation damping. IEEE Trans. Energy Convers. 2009, 24, 415–422. [Google Scholar] [CrossRef]
- Tan, A.; Lin, X.; Sun, J.; Lyu, R.; Li, Z.; Peng, L.; Khalid, M.S. A novel DFIG damping control for power system with high wind power penetration. Energies 2016, 9, 521. [Google Scholar] [CrossRef]
- Pena, R.; Clare, J.C.; Asher, G.M. Doubly fed induction generator using back-to-back PWM converters and its application to variable speed wind-energy generation. IEE Proc.-Electr. Power Appl. 1996, 143, 231–241. [Google Scholar] [CrossRef]
- Bourdoulis, M.K.; Alexandridis, A.T. Direct power control of DFIG wind systems based on nonlinear modeling and analysis. IEEE J. Emerg. Sel. Top. Power Electron. 2014, 2, 764–775. [Google Scholar] [CrossRef]
- Wang, K.W. Robust PSS Design Based on Probabilistic Approach; The Hong Kong Polytechnic University: Hong Kong, China, 2000. [Google Scholar]
- Milano, F. An open source power system analysis toolbox. IEEE Trans. Power Syst. 2005, 20, 1199–1206. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Power | 30 MW | Rotor Resistance | 0.005 p.u. |
| Frequency | 60 Hz | Rotor Reactance | 0.156 p.u |
| Blade Length | 75 m | Magnetization Reactance | 3.5 p.u. |
| Stator Resistance | 0.00706 p.u | Inertia constant | 3 kWs/kVA |
| Stator Reactance | 0.171 p.u | Gear Box Ratio | 1/89 |
| Without UPFC | With UPFC | |||||||
|---|---|---|---|---|---|---|---|---|
| No. | λ | ξ (%) | f (Hz) | λ | ξ (%) | f (Hz) | Dominant Machines | |
| Without DFIG | 1 | −3.0984 ± j8.8672 | 32.99 | 1.4949 | −3.1008 ± j8.8665 | 33.01 | 1.4950 | G3, G4 |
| 2 | −1.9635 ± j7.5341 | 25.85 | 1.2391 | −1.9722 ± j7.5289 | 25.34 | 1.2387 | G1, G2 | |
| 3 | −0.6609 ± j4.0114 | 16.26 | 0.6470 | −0.6563 ± j3.9845 | 16.25 | 0.6427 | G1, G4 | |
| With DFIG | 1 | −3.1005 ± j8.8664 | 33.01 | 1.4949 | −3.1029 ± j8.8658 | 33.03 | 1.4950 | G3, G4 |
| 2 | −2.0195 ± j7.5357 | 25.89 | 1.2417 | −2.0267 ± j7.5306 | 25.99 | 1.2412 | G1, G2 | |
| 3 | −0.6634 ± j4.0267 | 16.26 | 0.6495 | −0.6589 ± j4.0005 | 16.25 | 0.6453 | G1, G4 | |
| 4 | −0.6092 ± j0.7568 | 62.71 | 0.1546 | −0.6238 ± j0.7470 | 64.10 | 0.1549 | ALL | |
| Parameter | K | Tw | Tl | T2 | T3 | T4 |
|---|---|---|---|---|---|---|
| Value | 0.1 p.u. | 10 s | 0.35 s | 0.2 s | 0.5 s | 0.3 s |
| No. | Tie-Line Power/MW | Without UPFC | With UPFC, Without PODC | With Both UPFC and PODC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| λ | ξ (%) | f (Hz) | λ | ξ (%) | f (Hz) | λ | ξ (%) | f (Hz) | ||
| Interarea mode 1 | 46 | −0.5790 ± j3.9564 | 14.48 | 0.6364 | −0.6054 ± j4.0426 | 14.81 | 0.6506 | −1.7012 ± j4.3688 | 36.28 | 0.7462 |
| 143 | −0.5720 ± j4.0201 | 14.09 | 0.6463 | −0.5730 ± j4.0296 | 14.08 | 0.6478 | −1.0519 ± j3.7497 | 27.01 | 0.6198 | |
| 239 | −0.6687 ± j4.0328 | 16.36 | 0.6506 | −0.6670 ± j4.0394 | 16.29 | 0.6516 | −1.0583 ± j3.5303 | 28.72 | 0.5866 | |
| 335 | −0.6656 ± j4.0418 | 16.25 | 0.6519 | −0.6618 ± j4.0417 | 16.16 | 0.6518 | −1.0247 ± j3.4482 | 28.49 | 0.5725 | |
| 430 | −0.6634 ± j4.0267 | 16.26 | 0.6495 | −0.6581 ± j4.0144 | 16.18 | 0.6474 | −1.0090 ± j3.3843 | 28.57 | 0.5621 | |
| Interarea mode 2 | 46 | −0.4905 ± j0.4320 | 75.04 | 0.1040 | −0.5010 ± j0.4253 | 76.24 | 0.1046 | −0.4693 ± j0.4629 | 71.19 | 0.1049 |
| 143 | −0.5090 ± j0.5055 | 70.95 | 0.1142 | −0.5173 ± j0.4968 | 72.13 | 0.1142 | −0.5088 ± j0.5438 | 68.32 | 0.1185 | |
| 239 | −0.6026 ± j0.6578 | 67.55 | 0.1420 | −0.6105 ± j0.6463 | 68.67 | 0.1415 | −0.5887 ± j0.6787 | 65.52 | 0.1430 | |
| 335 | −0.6073 ± j0.7070 | 65.16 | 0.1483 | −0.6153 ± j0.6941 | 66.34 | 0.1476 | −0.6024 ± j0.7317 | 63.56 | 0.1508 | |
| 430 | −0.6092 ± j0.7568 | 62.71 | 0.1546 | −0.6178 ± j0.7419 | 63.99 | 0.1537 | −0.6119 ± j0.7854 | 61.46 | 0.1585 | |
| No. | Wind Power Output/MW | Without UPFC | With UPFC, Without PODC | With Both UPFC and PODC | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| λ | ξ (%) | f (Hz) | λ | ξ (%) | f (Hz) | Λ | ξ (%) | f (Hz) | ||
| Interarea mode 1 | 0 | −0.6609 ± j4.0114 | 16.26 | 0.6470 | −0.6563 ± j3.9845 | 16.25 | 0.6427 | −0.9429 ± j3.4921 | 26.07 | 0.5757 |
| 10 | −0.6605 ± j4.0293 | 16.18 | 0.6498 | −0.6560 ± j4.0031 | 16.17 | 0.6456 | −0.9358 ± j3.5055 | 25.79 | 0.5775 | |
| 30 | −0.6634 ± j4.0267 | 16.26 | 0.6495 | −0.6589 ± j4.0005 | 16.25 | 0.6453 | −0.9350 ± j3.5047 | 25.78 | 0.5773 | |
| 70 | −0.6700 ± j4.0228 | 16.43 | 0.6491 | −0.6654 ± j3.9969 | 16.42 | 0.6449 | −0.9328 ± j3.5044 | 25.72 | 0.5772 | |
| Interarea mode 2 | 0 | −0.5455 ± j0.5501 | 70.41 | 0.1233 | −0.5602 ± j0.5390 | 72.06 | 0.1237 | −0.5406 ± j0.5398 | 70.76 | 0.1216 |
| 10 | −0.6120 ± j0.7220 | 64.66 | 0.1506 | −0.6273 ± j0.7155 | 65.92 | 0.1515 | −0.6231 ± j0.7446 | 64.18 | 0.1545 | |
| 30 | −0.6092 ± j0.7568 | 62.71 | 0.1546 | −0.6238 ± j0.7470 | 64.10 | 0.1549 | −0.6198 ± j0.7815 | 62.14 | 0.1588 | |
| 70 | −0.5967 ± j0.8511 | 57.41 | 0.1654 | −0.6106 ± j0.8378 | 58.90 | 0.1650 | −0.6089 ± j0.8868 | 56.60 | 0.1712 | |
| No. | Without UPFC | With UPFC, Without PODC | With Both UPFC and PODC | Dominant Generators | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| λ | ξ (%) | f (Hz) | Λ | ξ (%) | f (Hz) | λ | ξ (%) | f (Hz) | ||
| 1 | −0.9215 ± j10.6661 | 8.61 | 1.7038 | −0.9289 ± j10.6302 | 8.71 | 1.6983 | −0.9490 ± j10.6779 | 8.85 | 1.7061 | G1, G7 |
| 2 | −0.53111 ± j9.2646 | 5.72 | 1.4769 | −0.5421 ± j9.2667 | 5.84 | 1.4774 | −0.4303 ± j8.8692 | 4.85 | 1.4132 | G1, G2, G7 |
| 3 | −0.6954 ± j7.5278 | 9.20 | 1.2032 | −0.7014 ± j7.5461 | 9.25 | 1.2062 | −0.7366 ± j7.5910 | 9.66 | 1.2137 | G5, G6 |
| 4 | −0.4685 ± j6.4509 | 7.24 | 1.0294 | −0.4792 ± j6.4622 | 7.40 | 1.0313 | −0.5226 ± j6.5064 | 8.01 | 1.0389 | G1, G5, G6 |
| 5 | −0.00354 ± j3.7425 | 0.0946 | 0.5956 | −0.00201 ± j3.5011 | 0.0574 | 0.5572 | −0.0412 ± j 3.5926 | 1.15 | 0.5718 | G1, G5, DFIG |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, P.; Arefifar, S.A.; Li, C.; Wen, F.; Ji, Y.; Tao, Y. Enhancing Oscillation Damping in an Interconnected Power System with Integrated Wind Farms Using Unified Power Flow Controller. Energies 2019, 12, 322. https://doi.org/10.3390/en12020322
He P, Arefifar SA, Li C, Wen F, Ji Y, Tao Y. Enhancing Oscillation Damping in an Interconnected Power System with Integrated Wind Farms Using Unified Power Flow Controller. Energies. 2019; 12(2):322. https://doi.org/10.3390/en12020322
Chicago/Turabian StyleHe, Ping, Seyed Ali Arefifar, Congshan Li, Fushuan Wen, Yuqi Ji, and Yukun Tao. 2019. "Enhancing Oscillation Damping in an Interconnected Power System with Integrated Wind Farms Using Unified Power Flow Controller" Energies 12, no. 2: 322. https://doi.org/10.3390/en12020322
APA StyleHe, P., Arefifar, S. A., Li, C., Wen, F., Ji, Y., & Tao, Y. (2019). Enhancing Oscillation Damping in an Interconnected Power System with Integrated Wind Farms Using Unified Power Flow Controller. Energies, 12(2), 322. https://doi.org/10.3390/en12020322





