A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction
Abstract
1. Introduction
2. Motivations behind Wind Data Prediction
3. Conventional Models for Wind Data Prediction
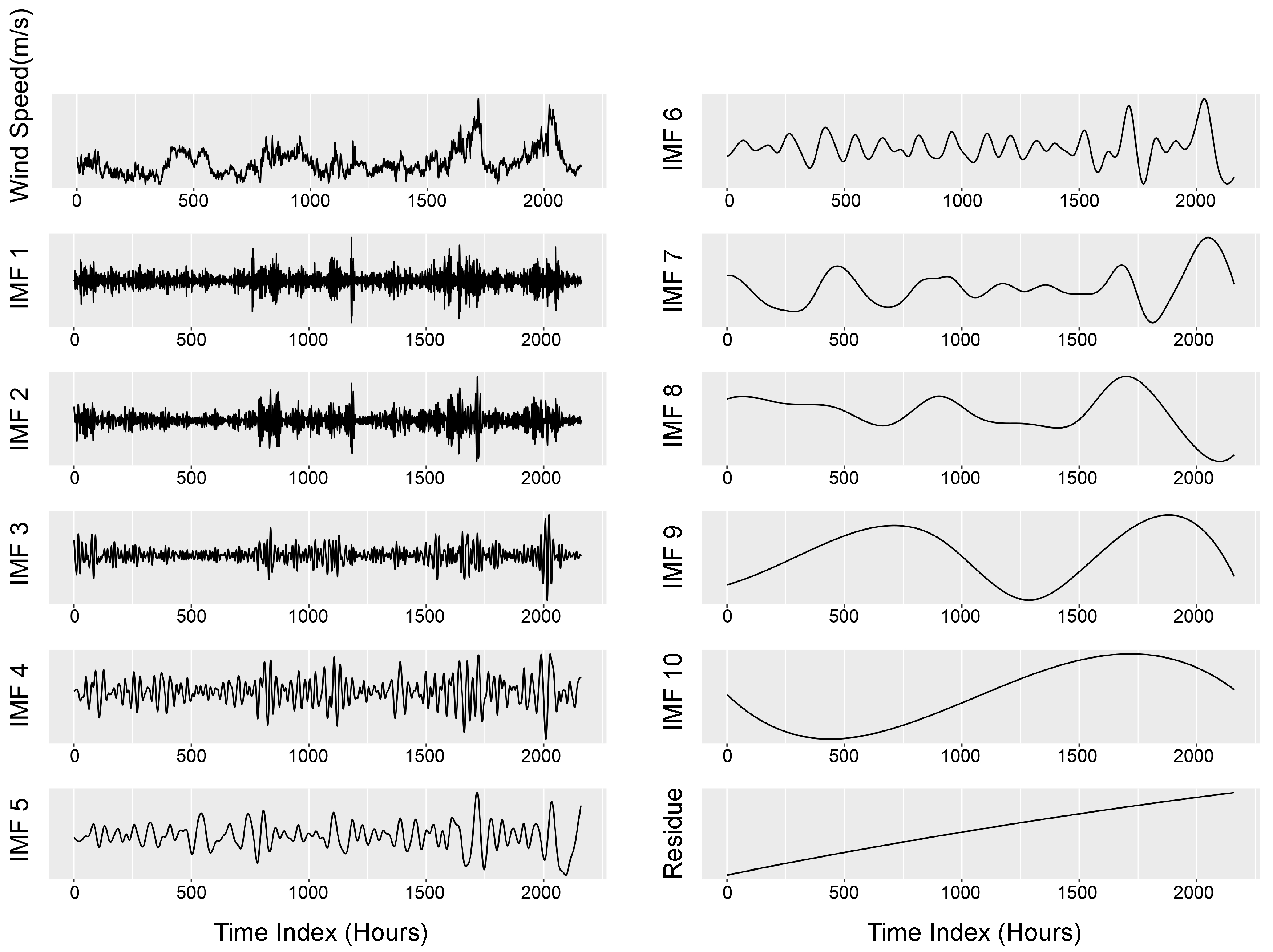
4. Empirical Mode Decomposition
- (1)
- the mean of lower and upper envelopes tends to zero, and
- (2)
- the number of extrema and zero crossing differs at most by one.
5. Improvements in EMD
6. Motivations for Proceeding with EMD
- Apart from unique signal decomposition, IMFs (generated with EMD) have good local characteristics in both time as well as frequency domains [27].
- The working principle of EMD is empirical without any mathematical/statistical calculations and hence is very easy to understand [28].
- EMD is empirical, intuitive, direct and analyzes multi-component signals with predetermined basis functions [13].
- EMD can handle complex valued time series very efficiently [54].
- EMD decreases the instability of wind data and hence minimizes the difficulties in high precision predictions [48].
- After addition of all IMFs, the coupling of characteristics information gets reduced and hence original signal gets reconstructed more accurately [26].
7. Intrinsic Mode Functions
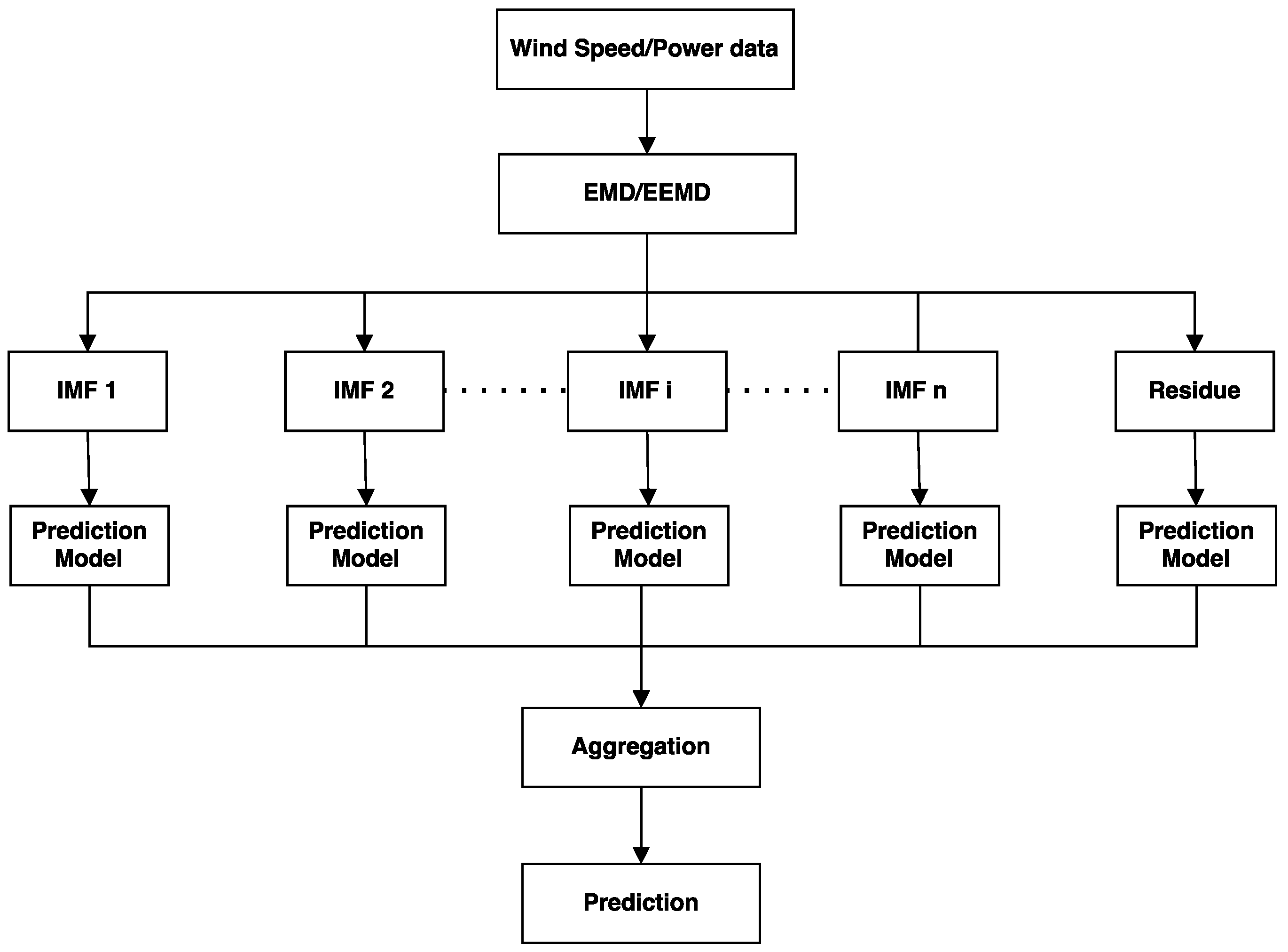
8. Review on EMD/EEMD Based Ensemble Methods for Wind Data Prediction
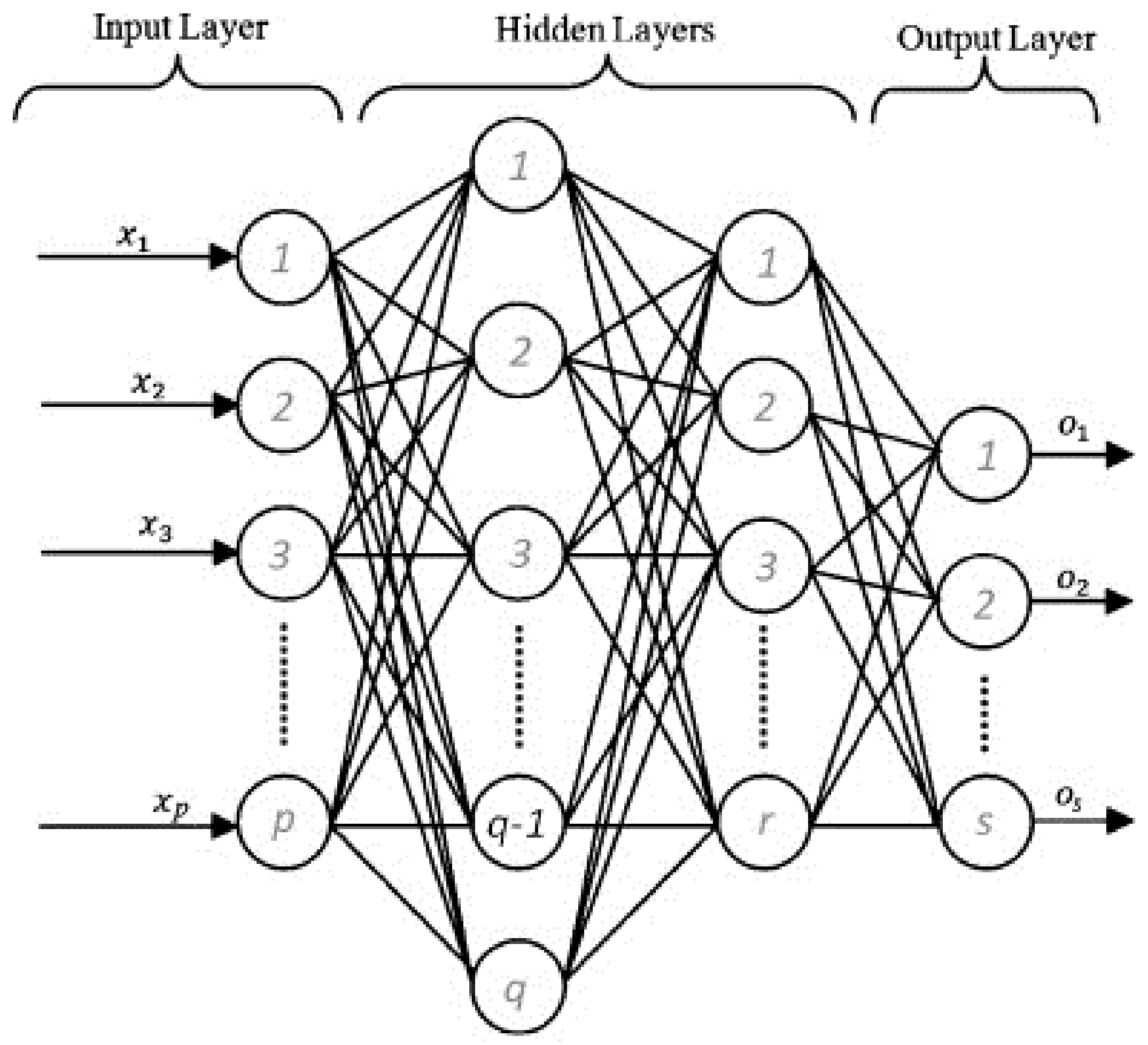
8.1. Artificial Neural Networks
8.1.1. EMD-BPNN Models
8.1.2. EEMD-BPNN Model
8.1.3. EMD-GABP Model
8.1.4. EEMD-GABP Model
8.1.5. EMD-ENN Model
8.1.6. EEMD-ENN Model
8.1.7. EMD-RBFNN Model
8.1.8. EEMD-FNN Model
8.1.9. EEMD-WNN Model
8.1.10. EMD-LMNN Model
8.1.11. EEMD-MLP Models
8.1.12. EEMD-ELM Models
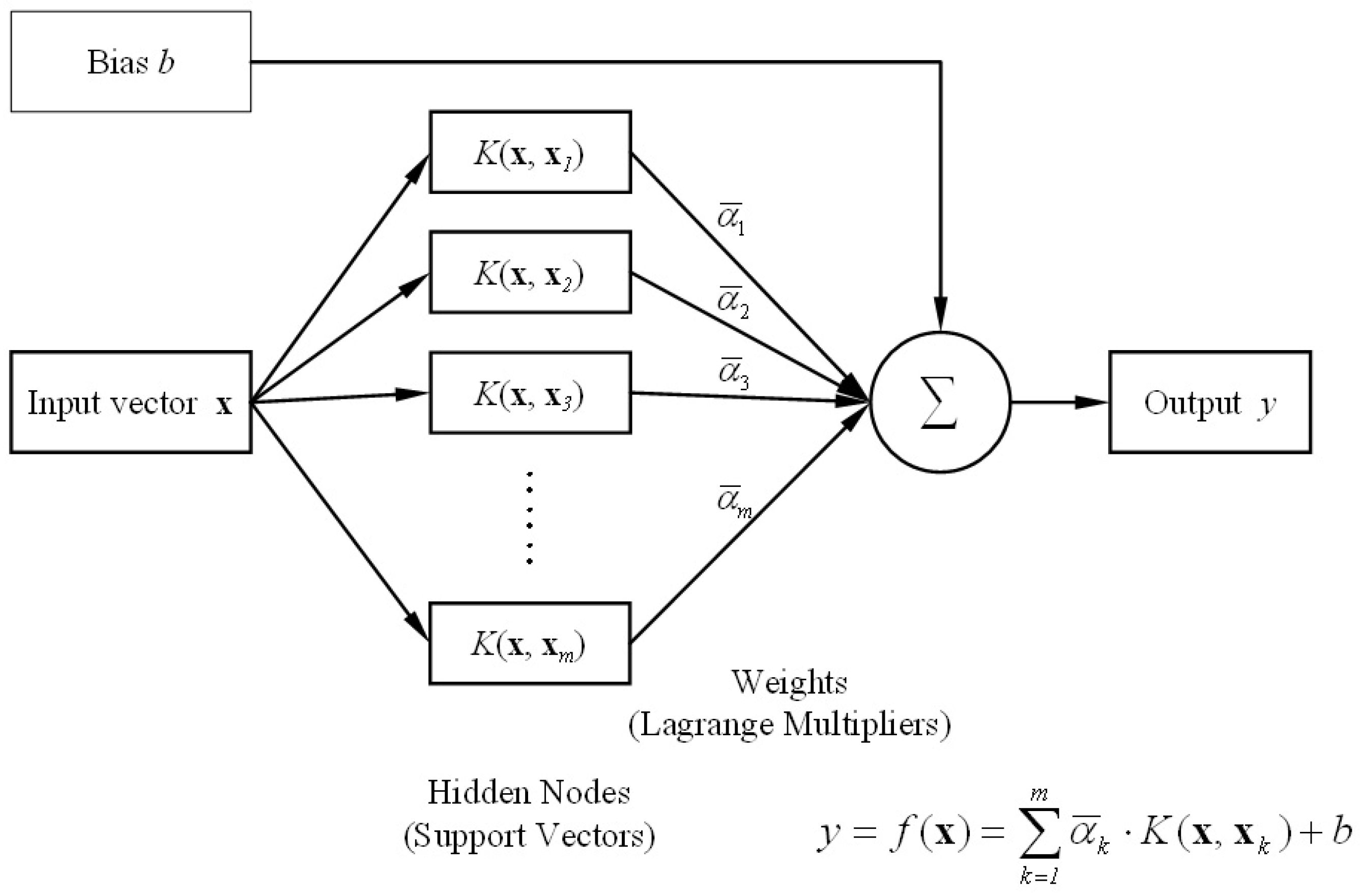
8.2. Support Vector Machines and Least Square SVM
8.2.1. EMD-SVM Models
8.2.2. EEMD-SVM Models
8.2.3. EMD-LSSVM Models
8.2.4. EEMD-LSSVM Models
8.2.5. EMD-RVM Models
8.2.6. EEMD-RVM Models
8.3. Statistical Models
8.3.1. EMD-Autoregression Models
8.3.2. EEMD-Autoregression Model
- The hybridization of EMD/EEMD with an autoregression model improved the prediction accuracy as compared to simple autoregression models for wind data sets.
- In most of the models (reviewed in this section), the autoregression methods were combined with other methods such as ANN and LSSVM and were found to be more suitable for low-frequency components, while the other methods were kept restricted for IMFs with higher frequency components.
8.3.3. EMD-kNN Model
8.3.4. EEMD-PSF Model
8.4. Chaotic Theory Treatments
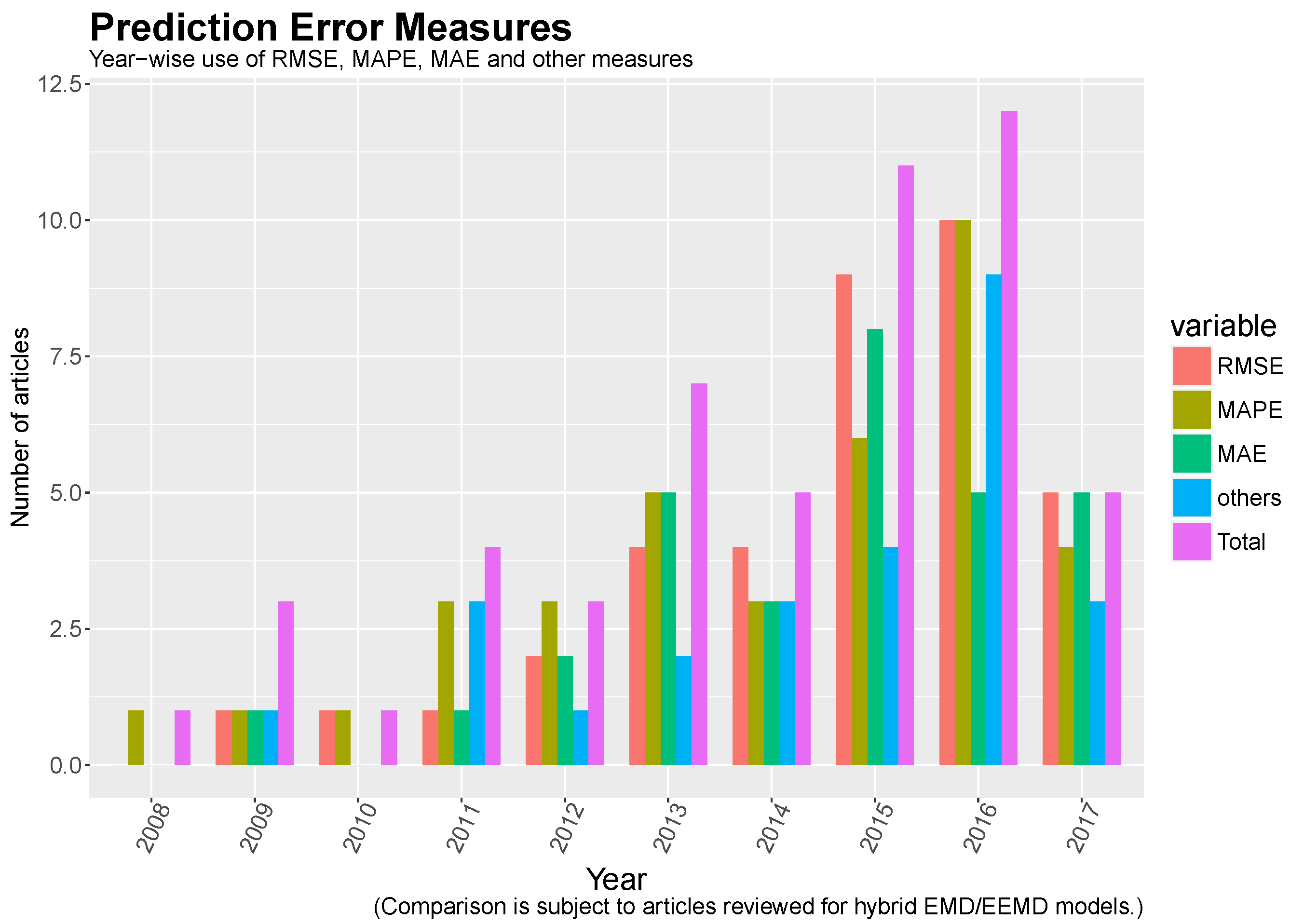
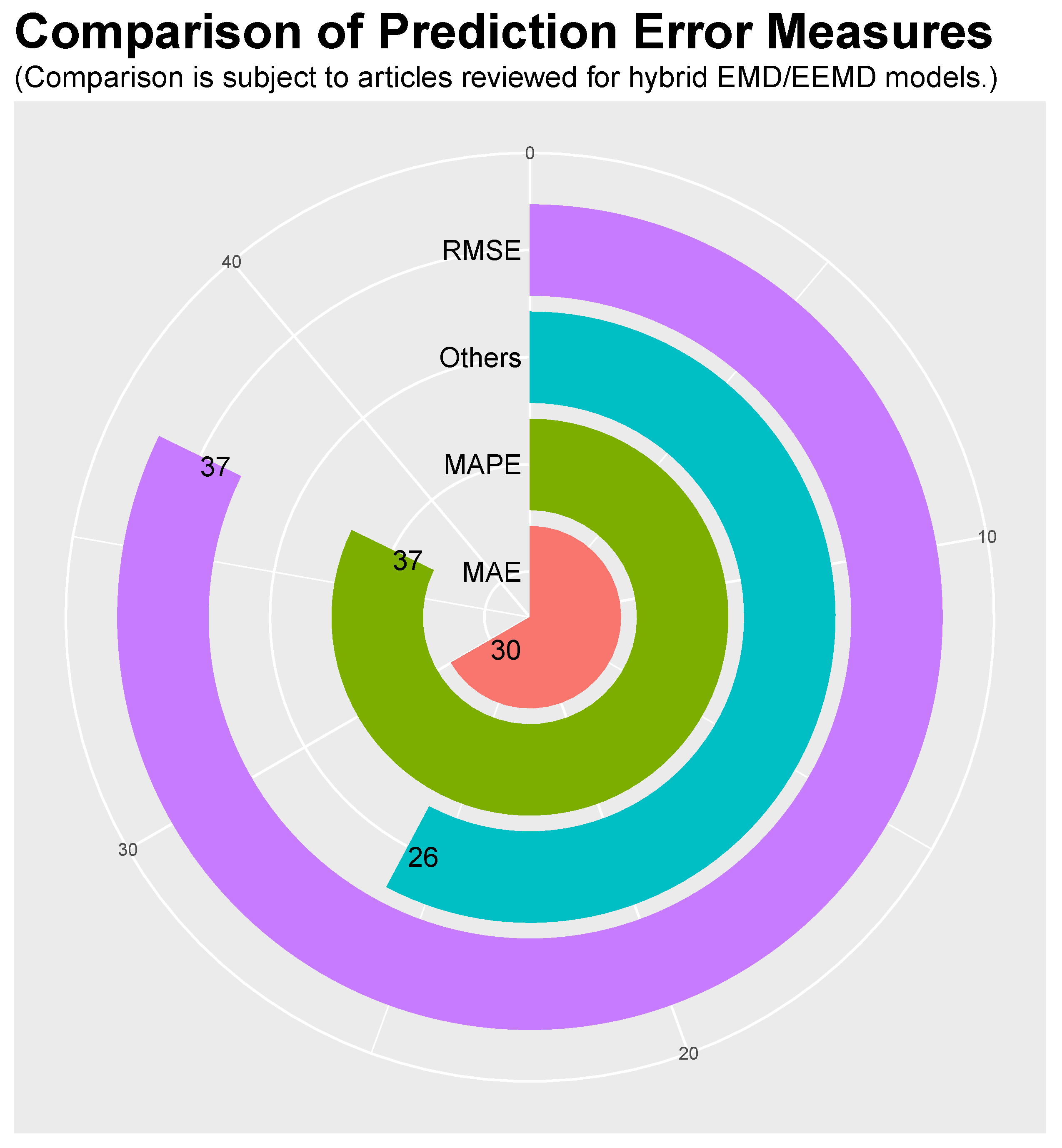
9. Measures to Estimate Prediction Errors
10. Discussion
11. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| ANFIS | Adaptive Neural Network based Fuzzy Interface System |
| ANN | Artificial Neural Networks |
| AR | Autoregression |
| ARIMA | Autoregressive Integrated Moving Average |
| ARMA | Autoregressive Moving Average |
| BA | Bat Algorithm |
| BPNN | Back-Propagation Neural Networks |
| CEEMD | Complete Ensemble Empirical Mode Decomposition |
| CEEMDAN | Complete Ensemble Empirical Mode Decomposition with Adaptive Noise |
| CS | Cuckoo Search |
| DSF | Decomposition Selection Forecasting |
| ELM | Extreme Learning Machine |
| EEMD | Ensemble Empirical Mode Decomposition |
| EMD | Empirical Mode Decomposition |
| ENN | Elman Neural Networks |
| ESN | Echo State Network |
| EWT | Empirical Wavelet Transform |
| FEEMD | Fast Ensemble Empirical Mode Decomposition |
| FNN | Feed-forward Neural Network |
| GABP | Genetic Algorithm Back-Propagation Neural Network |
| HS | Harmony Search |
| IMF | Intrinsic Mode Function |
| kNN | k - Nearest Neighbors |
| LFO | Local First Order |
| LMNN | Levenberg-Marquardt Neural Network |
| LSSVM | Least Squares Support Vector Machine |
| MA | Moving Average |
| MAE | Mean Absolute Error |
| MAPE | Mean Absolute Percentage Error |
| MEA | Mind Evolutionary Algorithm |
| MkRVR | Multiple-kernel Relevance Vector Regression |
| MLP | Multilayer Perceptron |
| MMLP | Mathematical Morphologybased Local Predictor |
| MTD | Mean Trend Detector |
| NWP | Numerical Weather Prediction |
| PACF | Partial Auto-correlation Function |
| PCA | Principle Component Analysis |
| PolyRVR | Polynomial kernel Multiple-kernel Relevance Vector Regression |
| PSF | Pattern Sequence based Forecasting |
| PSO | Particle Swarm Optimization |
| RARIMA | Recursive Autoregression of Integrated Moving Average |
| RBFNN | Radial Basis Function Network |
| RELM | Regularized Extreme Learning Machine |
| RMSE | Root Mean Square Error |
| RT | Runs Test |
| RVM | Relevance Vector Machine |
| SARIMA | Seasonal Autoregressive Integrated Moving Average |
| SD | Standard Deviation |
| SSA | Singular Spectrum Analysis |
| SVD | Singular Value Decomposition |
| SVM | Least Squares Support Vector Machine |
| SWEMD | Sliding Window Empirical Mode Decomposition |
| VMD | Variation Mode Decomposition |
| WD | Wavelet Decomposition |
| WNN | Weighted Neural Network |
| WPD | Wavelet Packet Decomposition |
| WT | Wavelet Transform |
References
- Yuan, X.; Chen, C.; Yuan, Y.; Huang, Y.; Tan, Q. Short-term wind power prediction based on LSSVM–GSA model. Energy Convers. Manag. 2015, 101, 393–401. [Google Scholar] [CrossRef]
- Zhu, X.; Genton, M.G. Short-Term Wind Speed Forecasting for Power System Operations. Int. Stat. Rev. 2012, 80, 2–23. [Google Scholar] [CrossRef]
- Erdem, E.; Shi, J. ARMA based approaches for forecasting the tuple of wind speed and direction. Appl. Energy 2011, 88, 1405–1414. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S.; Selvakumar, A.I.; Kumar, G.E.P. A comprehensive review on wind turbine power curve modeling techniques. Renew. Sustain. Energy Rev. 2014, 30, 452–460. [Google Scholar] [CrossRef]
- Carrillo, C.; Montaño, A.O.; Cidrás, J.; Díaz-Dorado, E. Review of power curve modelling for wind turbines. Renew. Sustain. Energy Rev. 2013, 21, 572–581. [Google Scholar] [CrossRef]
- Shi, J.; Qu, X.; Zeng, S. Short-term wind power generation forecasting: Direct versus indirect arima-based approaches. Int. J. Green Energy 2011, 8, 100–112. [Google Scholar] [CrossRef]
- Hong, Y.Y.; Yu, T.H.; Liu, C.Y. Hour-ahead wind speed and power forecasting using empirical mode decomposition. Energies 2013, 6, 6137–6152. [Google Scholar] [CrossRef]
- Liu, H.; Chen, C.; Tian, H.Q.; Li, Y.F. A hybrid model for wind speed prediction using empirical mode decomposition and artificial neural networks. Renew. Energy 2012, 48, 545–556. [Google Scholar] [CrossRef]
- Ren, Y.; Qiu, X.; Suganthan, P.N. Empirical mode decomposition based adaboost-backpropagation neural network method for wind speed forecasting. In Proceedings of the 2014 IEEE Symposium on Computational Intelligence in Ensemble Learning, Orlando, FL, USA, 9–12 December 2014; pp. 1–6. [Google Scholar]
- Guo, Z.; Zhao, W.; Lu, H.; Wang, J. Multi-step forecasting for wind speed using a modified EMD-based artificial neural network model. Renew. Energy 2012, 37, 241–249. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.; Srikanth, N. A comparative study of empirical mode decomposition-based short-term wind speed forecasting methods. IEEE Trans. Sustain. Energy 2015, 6, 236–244. [Google Scholar] [CrossRef]
- Zhang, W.; Qu, Z.; Zhang, K.; Mao, W.; Ma, Y.; Fan, X. A combined model based on CEEMDAN and modified flower pollination algorithm for wind speed forecasting. Energy Convers. Manag. 2017, 136, 439–451. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P.N.; Srikanth, N. A novel empirical mode decomposition with support vector regression for wind speed forecasting. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 1793–1798. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Wei, H.; Zhao, J.; Liu, T.; Zhu, T.; Zhang, K. Short-term wind speed forecasting using empirical mode decomposition and feature selection. Renew. Energy 2016, 96, 727–737. [Google Scholar] [CrossRef]
- Wang, C.; Wu, J.; Wang, J.; Hu, Z. Short-Term Wind Speed Forecasting Using the Data Processing Approach and the Support Vector Machine Model Optimized by the Improved Cuckoo Search Parameter Estimation Algorithm. Math. Probl. Eng. 2016, 2016, 4896854. [Google Scholar] [CrossRef]
- Zhang, W.; Liu, F.; Zheng, X.; Li, Y. A hybrid EMD-SVM based short-term wind power forecasting model. In Proceedings of the 2015 IEEE PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Brisbane, QLD, Australia, 15–18 November 2015; pp. 1–5. [Google Scholar]
- Han, Z.H.; Zhu, X.X. Training set of support vector regression extracted by empirical mode decomposition. In Proceedings of the 2011 IEEE Asia-Pacific Power and Energy Engineering Conference (APPEEC), Wuhan, China, 25–28 March 2011; pp. 1–4. [Google Scholar]
- Lin, Y.; Peng, L. Combined model based on EMD-SVM for short-term wind power prediction. Proc. Chin. Soc. Electr. Eng. 2011, 31, 102–108. [Google Scholar]
- Hu, J.; Wang, J.; Zeng, G. A hybrid forecasting approach applied to wind speed time series. Renew. Energy 2013, 60, 185–194. [Google Scholar] [CrossRef]
- Jia, S. A new method for the short-term wind speed forecasting. In Proceedings of the 4th International Conference on Electric Utility Deregulation and Restructuring and Power Technologies (DRPT), Weihai, China, 6–9 July 2011; pp. 1320–1324. [Google Scholar]
- Tatinati, S.; Veluvolu, K.C. A hybrid approach for short-term forecasting of wind speed. Sci. World J. 2013, 2013, 548370. [Google Scholar] [CrossRef] [PubMed]
- Hong, D.; Ji, T.; Zhang, L.; Li, M.; Wu, Q. An indirect short-term wind power forecast approach with multi-variable inputs. In Proceedings of the Innovative Smart Grid Technologies-Asia (ISGT-Asia), Melbourne, VIC, Australia, 28 November–1 December 2016; pp. 793–798. [Google Scholar]
- Liu, H.; Tian, H.Q.; Li, Y.F. An EMD-recursive ARIMA method to predict wind speed for railway strong wind warning system. J. Wind Eng. Ind. Aerodyn. 2015, 141, 27–38. [Google Scholar] [CrossRef]
- Liu, X.; Mi, Z.; Li, P.; Mei, H. Study on the multi-step forecasting for wind speed based on EMD. In Proceedings of the International Conference on Sustainable Power Generation and Supply, Nanjing, China, 6–7 April 2009; pp. 1–5. [Google Scholar]
- Liu, X.J.; Mi, Z.Q.; Bai, L.; Wu, T. A novel approach for wind speed forecasting based on EMD and time-series analysis. In Proceedings of the Asia-Pacific Power and Energy Engineering Conference, Wuhan, China, 27–31 March 2009; pp. 1–4. [Google Scholar]
- Li, R.; Wang, Y. Short-term wind speed forecasting for wind farm based on empirical mode decomposition. In Proceedings of the International Conference on Electrical Machines and Systems, Wuhan, China, 17–20 October 2008; pp. 2521–2525. [Google Scholar]
- Sun, C.; Yuan, Y.; Li, Q. A new method for wind speed forecasting based on empirical mode decomposition and improved persistence approach. In Proceedings of the Conference on Power & Energy (IPEC), Ho Chi Minh City, Vietnam, 12–14 December 2012; pp. 659–664. [Google Scholar]
- Zhang, J.; Wei, Y.; Tan, Z.F.; Ke, W.; Tian, W. A hybrid method for short-term wind speed forecasting. Sustainability 2017, 9, 596. [Google Scholar] [CrossRef]
- Drisya, G.; Kumar, K.S. Empirical mode decomposition and chaos based prediction model for wind speed oscillations. In Proceedings of the Conference on Recent Advances in Intelligent Computational Systems (RAICS), Trivandrum, India, 10–12 December 2015; pp. 306–311. [Google Scholar]
- An, X.; Jiang, D.; Zhao, M.; Liu, C. Short-term prediction of wind power using EMD and chaotic theory. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 1036–1042. [Google Scholar] [CrossRef]
- Zhang, X.Q.; Liang, J. Chaotic time series prediction model of wind power based on ensemble empirical mode decomposition-approximate entropy and reservoir. Acta Phys. Sin. 2013, 62, 50505. [Google Scholar]
- Wang, Y.; Wu, L.; Wang, S. Challenges in applying the empirical mode decomposition based hybrid algorithm for forecasting renewable wind/solar in practical cases. In Proceedings of the Power and Energy Society General Meeting (PESGM), Boston, MA, USA, 17–21 July 2016; pp. 1–5. [Google Scholar]
- Wang, Y.; Wang, S.; Zhang, N. A novel wind speed forecasting method based on ensemble empirical mode decomposition and GA-BP neural network. In Proceedings of the Power and Energy Society General Meeting (PES), Vancouver, BC, Canada, 21–25 July 2013; pp. 1–5. [Google Scholar]
- Wang, S.; Zhang, N.; Wu, L.; Wang, Y. Wind speed forecasting based on the hybrid ensemble empirical mode decomposition and GA-BP neural network method. Renew. Energy 2016, 94, 629–636. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, W.; Li, Y.; Wang, J.; Dang, Z. Forecasting wind speed using empirical mode decomposition and Elman neural network. Appl. Soft Comput. 2014, 23, 452–459. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Liang, X.F.; Li, Y.F. Wind speed forecasting approach using secondary decomposition algorithm and Elman neural networks. Appl. Energy 2015, 157, 183–194. [Google Scholar] [CrossRef]
- Yu, C.; Li, Y.; Zhang, M. Comparative study on three new hybrid models using Elman Neural Network and Empirical Mode Decomposition based technologies improved by Singular Spectrum Analysis for hour-ahead wind speed forecasting. Energy Convers. Manag. 2017, 147, 75–85. [Google Scholar] [CrossRef]
- Zheng, Z.W.; Chen, Y.Y.; Zhou, X.W.; Huo, M.M.; Zhao, B.; Guo, M. Short-term wind power forecasting using empirical mode decomposition and RBFNN. Int. J. Smart Grid Clean Energy 2013, 2, 192–199. [Google Scholar] [CrossRef]
- Sun, C.; Yuan, Y. Wind Speed Prediction Based on Empirical Mode Decomposition and Improved LS-SVM. In Proceedings of the 2nd IET Renewable Power Generation Conference (RPG 2013), Beijing, China, 9–11 September 2013. [Google Scholar]
- Jiang, Y.; Huang, G. Short-term wind speed prediction: Hybrid of ensemble empirical mode decomposition, feature selection and error correction. Energy Convers. Manag. 2017, 144, 340–350. [Google Scholar] [CrossRef]
- Wu, Q.; Peng, C. Wind power generation forecasting using least squares support vector machine combined with ensemble empirical mode decomposition, principal component analysis and a bat algorithm. Energies 2016, 9, 261. [Google Scholar] [CrossRef]
- Safari, N.; Chung, C.; Price, G. A Novel Multi-Step Short-Term Wind Power Prediction Framework Based on Chaotic Time Series Analysis and Singular Spectrum Analysis. IEEE Trans. Power Syst. 2017, 33, 590–601. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M.; Liang, Y. Wind speed forecasting based on FEEMD and LSSVM optimized by the bat algorithm. Energies 2015, 8, 6585–6607. [Google Scholar] [CrossRef]
- Wang, J.; Jiang, H.; Han, B.; Zhou, Q. An experimental investigation of FNN model for wind speed forecasting using EEMD and CS. Math. Probl. Eng. 2015, 2015, 464153. [Google Scholar] [CrossRef]
- Bokde, N.; Feijóo, A.; Kulat, K. Analysis of differencing and decomposition preprocessing methods for wind speed prediction. Appl. Soft Comput. 2018, 71, 926–938. [Google Scholar] [CrossRef]
- Zhang, K.; Qu, Z.; Wang, J.; Zhang, W.; Yang, F. A novel hybrid approach based on cuckoo search optimization algorithm for short-term wind speed forecasting. Environ. Prog. Sustain. Energy 2017, 36, 943–952. [Google Scholar] [CrossRef]
- Dokur, E.; Kurban, M.; Ceyhan, S. Hybrid model for short-term wind speed forecasting using empirical mode decomposition and artificial neural network. In Proceedings of the 9th International Conference on Electrical and Electronics Engineering (ELECO), Bursa, Turkey, 26–28 November 2015; pp. 420–423. [Google Scholar]
- Liu, H.; Tian, H.; Liang, X.; Li, Y. New wind speed forecasting approaches using fast ensemble empirical model decomposition, genetic algorithm, mind evolutionary algorithm and artificial neural networks. Renew. Energy 2015, 83, 1066–1075. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of new hybrid FEEMD-MLP, FEEMD-ANFIS, Wavelet Packet-MLP and Wavelet Packet-ANFIS for wind speed predictions. Energy Convers. Manag. 2015, 89, 1–11. [Google Scholar] [CrossRef]
- Bao, Y.; Wang, H.; Wang, B. Short-term wind power prediction using differential EMD and relevance vector machine. Neural Comput. Appl. 2014, 25, 283–289. [Google Scholar] [CrossRef]
- Fei, S.W. A hybrid model of EMD and multiple-kernel RVR algorithm for wind speed prediction. Int. J. Electr. Power Energy Syst. 2016, 78, 910–915. [Google Scholar] [CrossRef]
- Zang, H.; Liang, Z.; Guo, M.; Qian, Z.; Wei, Z.; Sun, G. Short-term wind speed forecasting based on an EEMD-CAPSO-RVM model. In Proceedings of the PES Asia-Pacific Power and Energy Engineering Conference (APPEEC), Xi’an, China, 25–28 October 2016; pp. 439–443. [Google Scholar]
- Zang, H.; Fan, L.; Guo, M.; Wei, Z.; Sun, G.; Zhang, L. Short-Term Wind Power Interval Forecasting Based on an EEMD-RT-RVM Model. Adv. Meteorol. 2016, 2016, 8760780. [Google Scholar] [CrossRef]
- Ren, Y.; Suganthan, P. Empirical mode decomposition-k nearest neighbor models for wind speed forecasting. J. Power Energy Eng. 2014, 2, 176–185. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Four wind speed multi-step forecasting models using extreme learning machines and signal decomposing algorithms. Energy Convers. Manag. 2015, 100, 16–22. [Google Scholar] [CrossRef]
- Sun, W.; Liu, M. Wind speed forecasting using FEEMD echo state networks with RELM in Hebei, China. Energy Convers. Manag. 2016, 114, 197–208. [Google Scholar] [CrossRef]
- Soman, S.S.; Zareipour, H.; Malik, O.; Mandal, P. A review of wind power and wind speed forecasting methods with different time horizons. In Proceedings of the North American Power Symposium (NAPS), Arlington, TX, USA, 26–28 September 2010; pp. 1–8. [Google Scholar]
- Liang, Z.; Liang, J.; Zhang, L.; Wang, C.; Yun, Z.; Zhang, X. Analysis of multi-scale chaotic characteristics of wind power based on Hilbert–Huang transform and Hurst analysis. Appl. Energy 2015, 159, 51–61. [Google Scholar] [CrossRef]
- Wang, X.; Hui, L. One-month ahead prediction of wind speed and output power based on EMD and LSSVM. In Proceedings of the International Conference on Energy and Environment Technology, Guilin, China, 16–18 October 2009; Volume 3, pp. 439–442. [Google Scholar]
- Dejun, L.; Hui, L.; Zhonghua, M. One hour ahead prediction of wind speed based on data mining. In Proceedings of the 2nd International Conference on Advanced Computer Control (ICACC), Shenyang, China, 27–29 March 2010; Volume 5, pp. 199–203. [Google Scholar]
- Zhang, Y.; Wang, J. K-nearest neighbors and a kernel density estimator for GEFCom2014 probabilistic wind power forecasting. Int. J. Forecast. 2016, 32, 1074–1080. [Google Scholar] [CrossRef]
- Pinson, P.; Kariniotakis, G. Conditional prediction intervals of wind power generation. IEEE Trans. Power Syst. 2010, 25, 1845–1856. [Google Scholar] [CrossRef]
- Alexiadis, M.; Dokopoulos, P.; Sahsamanoglou, H.; Manousaridis, I. Short-term forecasting of wind speed and related electrical power. Sol. Energy 1998, 63, 61–68. [Google Scholar] [CrossRef]
- Damousis, I.G.; Alexiadis, M.C.; Theocharis, J.B.; Dokopoulos, P.S. A fuzzy model for wind speed prediction and power generation in wind parks using spatial correlation. IEEE Trans. Energy Convers. 2004, 19, 352–361. [Google Scholar] [CrossRef]
- Barbounis, T.; Theocharis, J. A locally recurrent fuzzy neural network with application to the wind speed prediction using spatial correlation. Neurocomputing 2007, 70, 1525–1542. [Google Scholar] [CrossRef]
- Al-Yahyai, S.; Charabi, Y.; Al-Badi, A.; Gastli, A. Nested ensemble NWP approach for wind energy assessment. Renew. Energy 2012, 37, 150–160. [Google Scholar] [CrossRef]
- Perrone, T.J.; Miller, R.G. Generalized exponential Markov and model output statistics: A comparative verification. Mon. Weather Rev. 1985, 113, 1524–1541. [Google Scholar] [CrossRef]
- Guo, Z.; Dong, Y.; Wang, J.; Lu, H. The forecasting procedure for long-term wind speed in the Zhangye area. Math. Probl. Eng. 2010, 2010, 684742. [Google Scholar] [CrossRef]
- Liu, H.; Tian, H.Q.; Li, Y.F. Comparison of two new ARIMA-ANN and ARIMA-Kalman hybrid methods for wind speed prediction. Appl. Energy 2012, 98, 415–424. [Google Scholar] [CrossRef]
- Bokde, N.; Asencio-Cortés, G.; Martínez-Álvarez, F.; Kulat, K. PSF: Introduction to R Package for Pattern Sequence Based Forecasting Algorithm. R J. 2017, 9, 324–333. [Google Scholar]
- Bokde, N.; Troncoso, A.; Asencio-Cortés, G.; Kulat, K.; Martínez-Álvarez, F. Pattern sequence similarity based techniques for wind speed forecasting. In Proceedings of the International Work-Conference on Time Series, Granada, Spain, 18–20 September 2017; Universidad de Granada: Granada, Spain, 2017. in press. [Google Scholar]
- Bokde, N.; Wakpanjar, A.; Kulat, K.; Feijóo, A. Robust performance of PSF method over outliers and random patterns in univariate time series forecasting. In Proceedings of the International Technology Congress, Pune, India, 28–29 December 2017. [Google Scholar]
- Louka, P.; Galanis, G.; Siebert, N.; Kariniotakis, G.; Katsafados, P.; Pytharoulis, I.; Kallos, G. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering. J. Wind Eng. Ind. Aerodyn. 2008, 96, 2348–2362. [Google Scholar] [CrossRef]
- Veluvolu, K.; Ang, W. Estimation and filtering of physiological tremor for real-time compensation in surgical robotics applications. Int. J. Med. Robot. Comput. Assist. Surg. 2010, 6, 334–342. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Wu, J.; Wang, J.; Zhao, W.; Shen, L. Performance analysis of four modified approaches for wind speed forecasting. Appl. Energy 2012, 99, 324–333. [Google Scholar] [CrossRef]
- Bilgili, M.; Sahin, B.; Yasar, A. Application of artificial neural networks for the wind speed prediction of target station using reference stations data. Renew. Energy 2007, 32, 2350–2360. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Halawani, T.O.; Rehman, S.; Hussain, A.A. Support vector machines for wind speed prediction. Renew. Energy 2004, 29, 939–947. [Google Scholar] [CrossRef]
- Fazelpour, F.; Tarashkar, N.; Rosen, M.A. Short-term wind speed forecasting using artificial neural networks for Tehran, Iran. Int. J. Energy Environ. Eng. 2016, 7, 377–390. [Google Scholar] [CrossRef]
- Rodriguez, C.P.; Anders, G.J. Energy price forecasting in the Ontario competitive power system market. IEEE Trans. Power Syst. 2004, 19, 366–374. [Google Scholar] [CrossRef]
- Lydia, M.; Kumar, S.S. A comprehensive overview on wind power forecasting. In Proceedings of the International Power Electronics Conference, Singapore, 27–29 October 2010; pp. 268–273. [Google Scholar]
- Ren, Y.; Suganthan, P.; Srikanth, N. Ensemble methods for wind and solar power forecasting—A state-of-the-art review. Renew. Sustain. Energy Rev. 2015, 50, 82–91. [Google Scholar] [CrossRef]
- Wu, Y.K.; Hong, J.S. A literature review of wind forecasting technology in the world. In Proceedings of the IEEE Lausanne Power Tech, Lausanne, Switzerland, 1–5 July 2007; pp. 504–509. [Google Scholar]
- Kani, S.P.; Ardehali, M. Very short-term wind speed prediction: A new artificial neural network–Markov chain model. Energy Convers. Manag. 2011, 52, 738–745. [Google Scholar] [CrossRef]
- Wang, J.; Hu, J. A robust combination approach for short-term wind speed forecasting and analysis–Combination of the ARIMA (Autoregressive Integrated Moving Average), ELM (Extreme Learning Machine), SVM (Support Vector Machine) and LSSVM (Least Square SVM) forecasts using a GPR (Gaussian Process Regression) model. Energy 2015, 93, 41–56. [Google Scholar]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble empirical mode decomposition: A noise-assisted data analysis method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Fei, S.W.; He, Y. Wind speed prediction using the hybrid model of wavelet decomposition and artificial bee colony algorithm-based relevance vector machine. Int. J. Electr. Power Energy Syst. 2015, 73, 625–631. [Google Scholar] [CrossRef]
- An, X.; Jiang, D.; Liu, C.; Zhao, M. Wind farm power prediction based on wavelet decomposition and chaotic time series. Expert Syst. Appl. 2011, 38, 11280–11285. [Google Scholar] [CrossRef]
- Katsigiannis, Y.; Tsikalakis, A.; Georgilakis, P.; Hatziargyriou, N. Improved wind power forecasting using a combined neuro-fuzzy and artificial neural network model. In Advances in Artificial Intelligence; Springer: Berlin, Germany, 2006; pp. 105–115. [Google Scholar]
- Okumus, I.; Dinler, A. Current status of wind energy forecasting and a hybrid method for hourly predictions. Energy Convers. Manag. 2016, 123, 362–371. [Google Scholar] [CrossRef]
- Wang, Y.H.; Yeh, C.H.; Young, H.W.V.; Hu, K.; Lo, M.T. On the computational complexity of the empirical mode decomposition algorithm. Phys. A: Stat. Mech. Appl. 2014, 400, 159–167. [Google Scholar] [CrossRef]
- Meignen, S.; Perrier, V. A new formulation for empirical mode decomposition based on constrained optimization. IEEE Signal Process. Lett. 2007, 14, 932–935. [Google Scholar] [CrossRef]
- Pustelnik, N.; Borgnat, P.; Flandrin, P. A multicomponent proximal algorithm for empirical mode decomposition. In Proceedings of the 20th European Signal Processing Conference (EUSIPCO), Bucharest, Romania, 27–31 August 2012; pp. 1880–1884. [Google Scholar]
- Hou, T.Y.; Shi, Z. Adaptive data analysis via sparse time-frequency representation. Adv. Adapt. Data Anal. 2011, 3, 1–28. [Google Scholar] [CrossRef]
- Feldman, M. Time-varying vibration decomposition and analysis based on the Hilbert transform. J. Sound Vib. 2006, 295, 518–530. [Google Scholar] [CrossRef]
- Blakely, C.D. A Fast Empirical Mode Decomposition Technique for Nonstationary Nonlinear Time Series; Elsevier Science: New York, NY, USA, 2005; Volume 3. [Google Scholar]
- Gilles, J. Empirical wavelet transform. IEEE Trans. Signal Process. 2013, 61, 3999–4010. [Google Scholar] [CrossRef]
- Huang, B.; Kunoth, A. An optimization based empirical mode decomposition scheme. J. Comput. Appl. Math. 2013, 240, 174–183. [Google Scholar] [CrossRef]
- Stepien, P. Sliding window empirical mode decomposition-its performance and quality. EPJ Nonlinear Biomed. Phys. 2014, 2, 14. [Google Scholar] [CrossRef]
- Yeh, J.R.; Shieh, J.S.; Huang, N.E. Complementary ensemble empirical mode decomposition: A novel noise enhanced data analysis method. Adv. Adapt. Data Anal. 2010, 2, 135–156. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A complete ensemble empirical mode decomposition with adaptive noise. In Proceedings of the International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Jun, W.; Lingyu, T.; Yuyan, L.; Peng, G. A weighted EMD-based prediction model based on TOPSIS and feed forward neural network for noised time series. Knowl. Based Syst. 2017, 132, 167–178. [Google Scholar] [CrossRef]
- Matsuoka, F.; Takeuchi, I.; Agata, H.; Kagami, H.; Shiono, H.; Kiyota, Y.; Honda, H.; Kato, R. Morphology-based prediction of osteogenic differentiation potential of human mesenchymal stem cells. PLoS ONE 2013, 8, e55082. [Google Scholar] [CrossRef]
- Kim, D.; Oh, H.S. EMD: A package for empirical mode decomposition and Hilbert spectrum. R J. 2009, 1, 40–46. [Google Scholar]
- Luukko, P.; Helske, J.; Räsänen, E. Introducing libeemd: A program package for performing the ensemble empirical mode decomposition. Comput. Stat. 2016, 31, 545–557. [Google Scholar] [CrossRef]
- Zimmerman, D.W. Teacher’s corner: A note on interpretation of the paired-samples t test. J. Educ. Behav. Stat. 1997, 22, 349–360. [Google Scholar] [CrossRef]
- Mohandes, M.A.; Rehman, S.; Halawani, T.O. A neural networks approach for wind speed prediction. Renew. Energy 1998, 13, 345–354. [Google Scholar] [CrossRef]
- Wijayasekara, D.; Manic, M.; Sabharwall, P.; Utgikar, V. Optimal artificial neural network architecture selection for performance prediction of compact heat exchanger with the EBaLM-OTR technique. Nucl. Eng. Des. 2011, 241, 2549–2557. [Google Scholar] [CrossRef]
- Duan, G.; Yu, Y. Problem-specific genetic algorithm for power transmission system planning. Electr. Power Syst. Res. 2002, 61, 41–50. [Google Scholar] [CrossRef]
- Broomhead, D.S.; Lowe, D. Radial Basis Functions, Multi-Variable Functional Interpolation and Adaptive Networks; Royal Signals and Radar Establishment Malvern: Malvern, UK, 1988. [Google Scholar]
- Alexandridis, A.K.; Zapranis, A.D. Wavelet neural networks: A practical guide. Neural Netw. 2013, 42, 1–27. [Google Scholar] [CrossRef] [PubMed]
- Liu, H. On the levenberg-marquardt training method for feed-forward neural networks. In Proceedings of the Sixth International Conference on Natural Computation (ICNC), Yantai, China, 10–12 August 2010; Volume 1, pp. 456–460. [Google Scholar]
- Mishra, P.; Mishra, S.; Nanda, J.; Sajith, K. Multilayer perceptron neural network (MLPNN) controller for automatic generation control of multiarea thermal system. In Proceedings of the North American Power Symposium (NAPS), Boston, MA, USA, 4–6 August 2011; pp. 1–7. [Google Scholar]
- Yeung, D.S.; Li, J.C.; Ng, W.W.; Chan, P.P. MLPNN training via a multiobjective optimization of training error and stochastic sensitivity. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 978–992. [Google Scholar] [CrossRef] [PubMed]
- Huang, G.B.; Zhu, Q.Y.; Siew, C.K. Extreme learning machine: A new learning scheme of feed-forward neural networks. In Proceedings of the International Joint Conference on Neural Networks, Budapest, Hungary, 25–29 July 2004; Volume 2, pp. 985–990. [Google Scholar]
- Salcedo-Sanz, S.; Pastor-Sánchez, A.; Prieto, L.; Blanco-Aguilera, A.; García-Herrera, R. Feature selection in wind speed prediction systems based on a hybrid coral reefs optimization–Extreme learning machine approach. Energy Convers. Manag. 2014, 87, 10–18. [Google Scholar] [CrossRef]
- Schapire, R.E. Explaining adaboost. In Empirical Inference; Springer: Berlin, Germany, 2013; pp. 37–52. [Google Scholar]
- Vautard, R.; Yiou, P.; Ghil, M. Singular-spectrum analysis: A toolkit for short, noisy chaotic signals. Phys. D Nonlinear Phenom. 1992, 58, 95–126. [Google Scholar] [CrossRef]
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBIC), Coimbatore, India, 9–11 December 2009; pp. 210–214. [Google Scholar]
- Drucker, H.; Burges, C.J.; Kaufman, L.; Smola, A.J.; Vapnik, V. Support vector regression machines. In Proceedings of the 9th International Conference on Neural Information Processing Systems, Denver, CL, USA, 3–5 December 1996. [Google Scholar]
- Chen, S.T.; Yu, P.S. Pruning of support vector networks on flood forecasting. J. Hydrol. 2007, 347, 67–78. [Google Scholar] [CrossRef]
- Suykens, J.A.; Van Gestel, T.; De Brabanter, J. Least Squares Support Vector Machines; World Scientific: Singapore, 2002. [Google Scholar]
- Ye, J.; Xiong, T. SVM versus least squares SVM. In Proceedings of the Eleventh International Conference on Artificial Intelligence and Statistics, San Juan, Puerto Rico, 21–24 March 2007; pp. 644–651. [Google Scholar]
- Box, G.; Jenkins, G. Some comments on a paper by Chatfield and Prothero and on a review by Kendall. J. R. Stat. Soc. Ser. A 1973, 136, 337–352. [Google Scholar] [CrossRef]
- Lall, U.; Sharma, A. A nearest neighbor bootstrap for resampling hydrologic time series. Water Resour. Res. 1996, 32, 679–693. [Google Scholar] [CrossRef]
- Alvarez, F.M.; Troncoso, A.; Riquelme, J.C.; Ruiz, J.S.A. Energy time series forecasting based on pattern sequence similarity. IEEE Trans. Knowl. Data Eng. 2011, 23, 1230–1243. [Google Scholar] [CrossRef]
- Wolf, A.; Swift, J.B.; Swinney, H.L.; Vastano, J.A. Determining Lyapunov exponents from a time series. Phys. D Nonlinear Phenom. 1985, 16, 285–317. [Google Scholar] [CrossRef]
- Kayacan, E.; Ulutas, B.; Kaynak, O. Grey system theory-based models in time series prediction. Expert Syst. Appl. 2010, 37, 1784–1789. [Google Scholar] [CrossRef]
- Lorenz, E.N. Deterministic nonperiodic flow. J. Atmos. Sci. 1963, 20, 130–141. [Google Scholar] [CrossRef]
- Lukoševičius, M. A practical guide to applying echo state networks. In Neural Networks: Tricks of the Trade; Springer: Berlin, Germany, 2012; pp. 659–686. [Google Scholar]
- Abbott, D. Applied Predictive Analytics: Principles and Techniques for the Professional Data Analyst; John Wiley & Sons: Hoboken, NJ, USA, 2014. [Google Scholar]

| Prediction Models | Artificial Intelligence Methods | Statistical Methods | Chaotic Methods | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| ANN | SVM/LSSVM | AR/ARMA/ARIMA | - | ||||||||
| Methods | EMD | EEMD | Methods | EMD | EEMD | Methods | EMD | EEMD | EMD | EEMD | |
| BPNN | Hong et al. [7] Liu et al. [8] Ren et al. [9] Guo et al. [10] | Ren et al. [11] Zhang et al. [12] | SVM | Ren et al. [13] Zhang et al. [14] Wang et al. [15] Zhang et al. [16] Han and Zhu [17] Lin and Peng [18] | Hu et al. [19] Ren et al. [11] Jia [20] | AR/ARMA/ARIMA | Tatinati and Veluvolu [21] Hong et al. [22] Liu et al. [23] Xingjie et al. [24] Liu et al. [25] Li and Wang [26] Sun et al. [27] | Zhang et al. [28] | Drisya and Kumar [29] | An et al. [30] Zhang Xue-Qing [31] | |
| GABP | Wang et al. [32] | Wang et al. [33] Wang et al. [34] | |||||||||
| ENN | Wang et al. [35] Liu et al. [36] | Yu et al. [37] Xingjie et al. [24] Zhang et al. [12] | |||||||||
| RBFNN | Zheng et al. [38] | Zhang et al. [12] | LSSVM | Sun and Yuan [39] Tatinati and Veluvolu [21] Liu et al. [23] Xingjie et al. [24] Liu et al. [25] Li and Wang [26] | Jiang and Huang [40] Wu and Peng [41] Safari et al. [42] Sun et al. [43] | ||||||
| FNN | - | Wang et al. [44] | PSF | Bokde et al. [45] | |||||||
| WNN | - | Zhang et al. [46] Zhang et al. [12] | |||||||||
| LMNN | Dokur et al. [47] Zhang et al. [14] | - | |||||||||
| MLP | - | Liu et al. [48] Liu et al. [49] | RVM | Bao et al. [50] Fei [51] | Zang et al. [52] Zang et al. [53] | k-NN | Ren and Suganthan [54] | - | |||
| ELM | - | Liu et al. [55] Sun and Liu [56] | |||||||||
| Motivations for Wind Data Prediction | Articles | ||
|---|---|---|---|
| 1 | Selection of land/place for wind farm establishment | Hu et al. [19] | |
| 2 | Power grid operations and energy generation | ||
| a. | Dispatch planning | Ren et al. [13], Sun and Yuan [39], Liu et al. [8], Dokur et al. [47], Liang et al. [58], Wu and Peng [41], Bao et al. [50], Wang et al. [44], Zhang et al. [46], Zhang et al. [12] | |
| b. | Unit commitment decisions | Ren et al. [13], Hong et al. [7], Hu et al. [19], Guo et al. [10], Wu and Peng [41], Ren et al. [11] | |
| c. | Wind farm regulations | Ren et al. [13], Guo et al. [10], Zhang et al. [46] | |
| d. | Maintenance and program scheduling | Dokur et al. [47], Xiaolan and Hui [59], Ren et al. [13], Guo et al. [10], Hu et al. [19] Liang et al. [58], Zang et al. [52], Xingjie et al. [24], Liu et al. [55], Bao et al. [50] Zhang et al. [46], An et al. [30], Dejun et al. [60] | |
| e. | Guarantee of wind energy integration with power system | Liu et al. [8], Hong et al. [22], Zang et al. [52], Bao et al. [50], Zhang et al. [46], Xiaolan and Hui [59] | |
| f. | Improvement in utilisation efficiency of wind power | Wang et al. [35], Tatinati and Veluvolu [21], Guo et al. [10], Yu et al. [37], Xiaolan and Hui [59] Ren and Suganthan [54], Wang et al. [33], Ren et al. [11], Wang et al. [44] | |
| g. | Reduction in intergration and operation costs. | Wang et al. [35], Sun and Yuan [39], Zang et al. [52], Ren et al. [11], Bao et al. [50], An et al. [30] | |
| h. | Sizing of energy storage capacity | Sun and Yuan [39], Sun et al. [27], Liu et al. [8], Dokur et al. [47], Xiaolan and Hui [59] | |
| 3 | Security | ||
| a. | Ensure security, safety and stability of power system | Sun and Yuan [39], Hong et al. [7], Tatinati and Veluvolu [21], Sun et al. [27], Liang et al. [58] Ren and Suganthan [54], Liu et al. [48], Yu et al. [37], Liu et al. [55], Liu et al. [49] Bao et al. [50], Wang et al. [44], An et al. [30], Xingjie et al. [24], Liu et al. [25] | |
| b. | Reduction of chances of wind power system collapse or breakdown | Liu et al. [48], Wang et al. [15], Liu et al. [36], Zhang et al. [46], Zhang et al. [12] | |
| 4 | Revenue Generation | ||
| a. | Maintenence of controllable demand-supply equillibrium | Ren and Suganthan [54] | |
| b. | Electricity bidding and trading | Dokur et al. [47], Wu and Peng [41], Wang et al. [15], Drisya and Kumar [29], Dejun et al. [60] Xingjie et al. [24], Xiaolan and Hui [59], Li and Wang [26] | |
| 5 | Other applications | ||
| a. | To avoid accident calamities caused by derailment of trains | Liu et al. [23] | |
| Language | Package | Publication/Manual/Website Link |
|---|---|---|
| R | EMD | Kim and Oh [105] |
| Rlibeemd | Luukko et al. [106] | |
| Python | PyEMD | https://pypi.python.org/pypi/EMD-signal |
| pyeemd | https://bitbucket.org/luukko/pyeemd.git | |
| Matlab | EMD | https://goo.gl/zp8BG2 |
| CEEMDAN | https://goo.gl/2Dp7d8 | |
| Scilab | EMD Toolbox | https://atoms.scilab.org/toolboxes/emd_toolbox/1.3 |
| Model | Liu et al. [8] (EMD-BPNN) | Ren et al. [9] (EMD-BPNN) | Hong et al. [7] (EMD-BPNN) | Mean | |||||
|---|---|---|---|---|---|---|---|---|---|
| Data | Speed | Speed | Speed (Spring) | Power (Spring) | - | ||||
| Step size | 1 | 2 | 3 | 1 | 3 | 5 | 1 | 1 | - |
| RMSE | 47.14 | 62.38 | 12.17 | 29.60 | 32.21 | 29.91 | 63.00 | 32.20 | 38.58 |
| MAE | 42.25 | 59.29 | 7.49 | - | - | - | 53.60 | 22.13 | 36.35 |
| MAPE | 42.01 | 55.75 | 29.75 | - | - | - | - | - | 42.50 |
| Other Methods under comparison | ARIMA, Persistence method | Various combination of BPNN, AdaBoost and Regression tree | ARIMA, Persistence method | - | |||||
| Model | Ren et al. [11] (EEMD-BPNN) | Wang et al. [33] Wang et al. [34] (EEMD-GABP) | ||
|---|---|---|---|---|
| Data | Speed | Speed | ||
| Step size | 1 | 3 | 5 | 1 |
| Comparative method | BPNN | GABP | ||
| RMSE | 16.66 | 5.39 | 6.10 | 62.17 |
| MAPE | - | - | - | 59.57 |
| Comparative method | EMD-BPNN | EMD-GABP | ||
| RMSE | 44.44 | 33.55 | 33.94 | 25.31 |
| MAPE | - | - | - | 25.95 |
| Other methods under comparison | Various combinations of BPNN, SVR with EMD, EEMD, CEEMD, CEEMDAN | WNN | ||
| Model | Wang et al. [35] (EMD-ENN) | Mean | |||
|---|---|---|---|---|---|
| Data | Speed | - | |||
| Season | Spring | Summer | Fall | Winter | - |
| RMSE | 4.12 | 16.07 | 46.34 | 16.66 | 20.79 |
| MAE | 13.5 | 9.85 | 33.92 | 16.48 | 18.43 |
| MAPE | 15.62 | 24.00 | 47.82 | 35.29 | 30.68 |
| Other methods under comparison | Presistance method, BPNN | ||||
| Model | Liu et al. [36] (EEMD-ENN) | Yu et al. [37] (EEMD-ENN) | Mean | ||||
|---|---|---|---|---|---|---|---|
| Data | Speed | Speed | - | ||||
| Step size | 1 | 2 | 3 | 1 | 2 | 3 | - |
| RMSE | 79.35 | 68.68 | 56.81 | 53.71 | 53.99 | 57.75 | 61.71 |
| MAE | 79.23 | 66.52 | 55.00 | 52.71 | 52.83 | 54.25 | 60.09 |
| MAPE | 78.95 | 63.57 | 50.82 | 50.35 | 52.12 | 65.20 | 52.66 |
| Other methods under comparison | MPL-NN, ARIMA | Persistance method, ARIMA | - | ||||
| Model | Zheng et al. [38] EMD-RBFNN | Wang et al. [44] EEMD-FNN | Zhang et al. [46] EEMD-WNN | Dokur et al. [47] EMD-LMNN | Zhang et al. [14] EMD-LMNN | Mean |
|---|---|---|---|---|---|---|
| Data | Power | Speed | Speed | Speed | Speed | - |
| Comparative Method | RBFNN | FNN | WNN | LMNN | LMNN | - |
| Step size | 1 | 1 | 1 | 1 | 1 | - |
| RMSE | 42.11 | 50.00 | 67.27 | 69.38 | 36.00 | 52.95 |
| MAE | 36.75 | 44.68 | 68.40 | 45.87 | 32.60 | 45.66 |
| MAPE | 40.48 | 40.73 | 66.59 | - | 28.76 | 44.14 |
| Other methods under comparison | - | - | BPNN, RBFNN | - | SVM | - |
| Model | Liu et al. [49] FEEMD-MLP | Liu et al. [48] FEEMD-MEA-MLP | Mean | ||||
|---|---|---|---|---|---|---|---|
| Data | Speed | Speed | - | ||||
| Step size | 1 | 2 | 3 | 1 | 2 | 3 | - |
| RMSE | 68.50 | 65.20 | 68.76 | 67.52 | 71.61 | 72.83 | 69.07 |
| MAE | 68.37 | 65.60 | 69.43 | 67.71 | 75.18 | 77.62 | 70.65 |
| MAPE | 67.26 | 66.01 | 69.39 | 68.69 | 77.40 | 80.32 | 71.51 |
| Other methods under comparison | ARIMA, ANFIS | FEEMD-GA-MLP | - | ||||
| Model | Liu et al. [55] | Sun and Liu [56] | Mean | |||
|---|---|---|---|---|---|---|
| Data | Speed | Speed | - | |||
| Step size | 1 | 2 | 3 | 1 | 1 | - |
| Location | - | - | - | 1 | 2 | - |
| Method | EMD-ELM | EMD-RELM | - | |||
| RMSE | 50.83 | 63.04 | 65.79 | - | - | 59.88 |
| MAE | 47.34 | 62.65 | 63.13 | 11.46 | 5.09 | 37.93 |
| MAPE | 48.02 | 63.79 | 64.13 | 43.30 | 38.07 | 51.46 |
| Method | FEEMD-ELM | FEEMD-RELM | - | |||
| RMSE | 70.94 | 69.39 | 71.16 | - | - | 70.49 |
| MAE | 71.46 | 70.17 | 70.75 | 37.75 | 21.32 | 54.29 |
| MAPE | 70.75 | 71.09 | 71.80 | 31.52 | 21.84 | 53.40 |
| Model | Han and Zhu [17] EMD-SVM | Lin and Peng [18] EMD-SVM | Zhang et al. [16] EMD-SVM | Zhang et al. [14] EMD-SVM | Wang et al. [15] EMD-SVM | Mean | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| Data | Speed | Power | Power | Speed | Speed | - | ||||
| Step Size | - | - | - | one step | One | Three | Five | - | ||
| Location | - | - | - | 1 | 2 | 3 | - | - | - | - |
| %RMSE | - | 20.76 | 55.84 | 36.29 | 40.44 | 11.95 | 36.22 | 35.55 | 34.64 | 33.96 |
| %MAE | 39.54 | - | - | 34.06 | 38.23 | 08.40 | - | - | - | 30.05 |
| %MAPE | - | 31.63 | - | 28.51 | 36.31 | 05.49 | - | - | - | 25.48 |
| Other methods under comparison | - | - | - | ANN, DFA-ANN, DFA-SVM, DSF-ANN, DSF-SVM | ANN, BPNN, ENN, WNN | - | ||||
| Model | Jia [20] EEMD-SVM | Hu et al. [19] EEMD-SVM | Ren et al. [11] EEMD-SVM | Mean | ||||
|---|---|---|---|---|---|---|---|---|
| Data | Speed | Speed | Speed | - | ||||
| Step Size | one | one | one | one | three | five | - | |
| Location | - | 1 | 2 | - | - | - | - | |
| SVM | RMSE | - | - | - | 18.87 | 35.48 | 37.75 | 30.7 |
| MAE | - | 51.61 | 17.30 | - | - | - | 34.45 | |
| MAPE | 11.79 | 53.85 | 13.66 | 17.60 | 37.86 | 31.78 | 27.75 | |
| EMD-SVM | RMSE | - | - | - | 16.89 | 18.48 | 12.57 | 15.98 |
| MAE | - | 21.05 | 20.37 | - | - | - | 20.71 | |
| MAPE | - | 27.45 | 19.49 | 21.11 | 22.04 | 19.36 | 21.89 | |
| Other methods under comparison | EMD-ARIMA, Persistence | ARIMA, SARIMA | Persistence | - | ||||
| Model | Hong et al. [22] | Liang et al. [58] | Dejun et al. [60] | Xiaolan and Hui [59] | Mean | ||||
|---|---|---|---|---|---|---|---|---|---|
| Methods | EMD-LSSVM, Polyregression | EMD-LSSVM | EMD-LSSVM-ELM | EMD-WT-LSSVM | EMD-LSSVM | - | |||
| Data | Power (indirect) | Power | Speed | Speed | - | ||||
| Step size | one | two | three | four | six | six | one | one | - |
| RMSE | 40.16 | 34.53 | 36.21 | 40.81 | 18.51 | 49.44 | 81.30 | 20.33 | 40.53 |
| MAE | 42.13 | 37.96 | 39.57 | 41.66 | 23.56 | 44.29 | - | - | 38.19 |
| MAPE | - | - | - | - | - | - | 72.34 | 27.66 | 50.00 |
| Other methods under comparison | MTD/MMLP, Persistence | ELM, EMD-ELM | - | EMD-RLS | - | ||||
| Model | Jiang and Huang [40] EEMD-LSSVM | Wu and Peng [41] EEMD-LSSVM | Safari et al. [42] EEMD-LSSVM | Mean | ||
|---|---|---|---|---|---|---|
| Data | Speed | Power | Power | - | ||
| Step size | one | one | six | Twelve | - | |
| LSSVM | RMSE | 13.93 | 45.25 | 47.79 | 49.68 | 39.16 |
| MAE | 13.26 | 54.36 | 47.13 | 11.55 | 31.57 | |
| MAPE | - | 41.64 | - | - | 41.64 | |
| EEMD-LSSVM | RMSE | 22.49 | 31.29 | 7.87 | 18.67 | 20.08 |
| MAE | 21.66 | 39.52 | 2.32 | 3.47 | 16.74 | |
| MAPE | - | 20.98 | - | - | 20.98 | |
| Other methods under comparison | - | ARIMA, BPNN, PCA, BA, PSO | Persistence, RBFNN | - | ||
| Model | Zang et al. [52] EEMD-RVM | Zang et al. [53] EEMD-RVM |
|---|---|---|
| Data | Speed | Power |
| RMSE | 16.33 | - |
| MAPE | 4.58 | 51.06 |
| Other methods under comparison | BPNN, SVM | ELM |
| Model | Liu et al. [23] EMD-ARMA | Liu et al. [25] EMD-ARMA | Li and Wang [26] EMD-ARMA | |||
|---|---|---|---|---|---|---|
| Data | Speed | Speed | Speed | |||
| Step size | 1 | 3 | 5 | 1 | 1 | |
| ARMA | RMSE | - | - | - | 39.45 | - |
| MAE | 50.40 | 64.15 | 75.41 | - | - | |
| MAPE | 50.00 | 63.81 | 75.76 | - | 16.49 | |
| Other methods under comparison | ARIMA, PRWM, BPNN | ARMA, Persistance | ARMA | |||
| Model | Zhang et al. [28] EEMD-ANFIS-SARIMA | Mean | ||||
|---|---|---|---|---|---|---|
| Location/Date | Site 1 28 February 2016 | Site 2 28 February 2016 | - | |||
| Prediction Horizon | 3 h | 24 h | 3 h | 24 h | - | |
| SARIMA | RMSE | 65.21 | 66.66 | 65.85 | 70.00 | 66.93 |
| MAE | 66.66 | 64.28 | 64.70 | 65.00 | 65.15 | |
| MAPE | 64.45 | 63.93 | 72.11 | 68.52 | 67.25 | |
| Model | Ren and Suganthan [54] EMD-kNN-M | ||||
|---|---|---|---|---|---|
| Data | Speed | ||||
| Comparative Methods | kNN | EMD-kNN-P | Mean | ||
| Step size | 1 | 3 | 1 | 3 | - |
| RMSE | 18.91 | 13.08 | 14.88 | 14.17 | 15.26 |
| MAPE | 18.15 | 04.01 | 18.85 | 11.72 | 13.18 |
| Other methods under comparison | Persistence model | ||||
| Model | Bokde et al. [45] EEMD-PSF | Mean | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Data | Speed | ||||||||||
| Comparative method | PSF | ARIMA | EMD-PSF | EMD-ARIMA | EEMD-ARIMA | - | |||||
| Step size | 12 | 24 | 12 | 24 | 12 | 24 | 12 | 24 | 12 | 24 | - |
| RMSE | 19.14 | 20.00 | 71.18 | 75.51 | 69.61 | 74.10 | 51.42 | 64.00 | 45.16 | 46.26 | 53.63 |
| MAE | 26.31 | 14.70 | 72.27 | 79.57 | 71.42 | 76.94 | 57.57 | 68.81 | 51.72 | 45.28 | 56.45 |
| MAPE | 25.83 | 25.78 | 70.50 | 71.04 | 69.42 | 67.36 | 55.37 | 42.57 | 49.87 | 42.57 | 52.02 |
| Articles | RMSE | MAPE | MAE |
|---|---|---|---|
| An et al. [30], Bao et al. [50], Wang et al. [44], Liu et al. [48], Sun et al. [43], Liu et al. [36], Liu et al. [55] Liu et al. [49], Zhang et al. [14], Wu and Peng [41], Zhang et al. [28], Zhang et al. [46], Zhang et al. [12], Yu et al. [37] | √ | √ | √ |
| Xiaolan and Hui [59], Dejun et al. [60], Lin and Peng [18], Sun et al. [27], Sun and Yuan [39], Wang et al. [33], Ren et al. [13], Wang et al. [32], Zang et al. [52], Wang et al. [15], Wang et al. [34], Zang et al. [52] | √ | √ | |
| Guo et al. [10], Liu et al. [8], Zheng et al. [38], Hu et al. [19], Tatinati and Veluvolu [21], Wang et al. [35], Sun and Liu [56] | √ | √ | |
| Hong et al. [7], Zhang Xue-Qing [31], Liang et al. [58], Hong et al. [22], Safari et al. [42], Jiang and Huang [40] | √ | √ | |
| Ren and Suganthan [54], Ren and Suganthan [54], Zhang et al. [16], Ren et al. [11], Drisya and Kumar [29] | √ | ||
| Li and Wang [26], Jia [20], Fei [51] | √ | ||
| Xingjie et al. [24], Dokur et al. [47] | √ |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bokde, N.; Feijóo, A.; Villanueva, D.; Kulat, K. A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction. Energies 2019, 12, 254. https://doi.org/10.3390/en12020254
Bokde N, Feijóo A, Villanueva D, Kulat K. A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction. Energies. 2019; 12(2):254. https://doi.org/10.3390/en12020254
Chicago/Turabian StyleBokde, Neeraj, Andrés Feijóo, Daniel Villanueva, and Kishore Kulat. 2019. "A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction" Energies 12, no. 2: 254. https://doi.org/10.3390/en12020254
APA StyleBokde, N., Feijóo, A., Villanueva, D., & Kulat, K. (2019). A Review on Hybrid Empirical Mode Decomposition Models for Wind Speed and Wind Power Prediction. Energies, 12(2), 254. https://doi.org/10.3390/en12020254








