Numerical Analysis of Roadway Rock-Burst Hazard under Superposed Dynamic and Static Loads
Abstract
1. Introduction
2. Model Description
2.1. General Engineering Geology Conditions
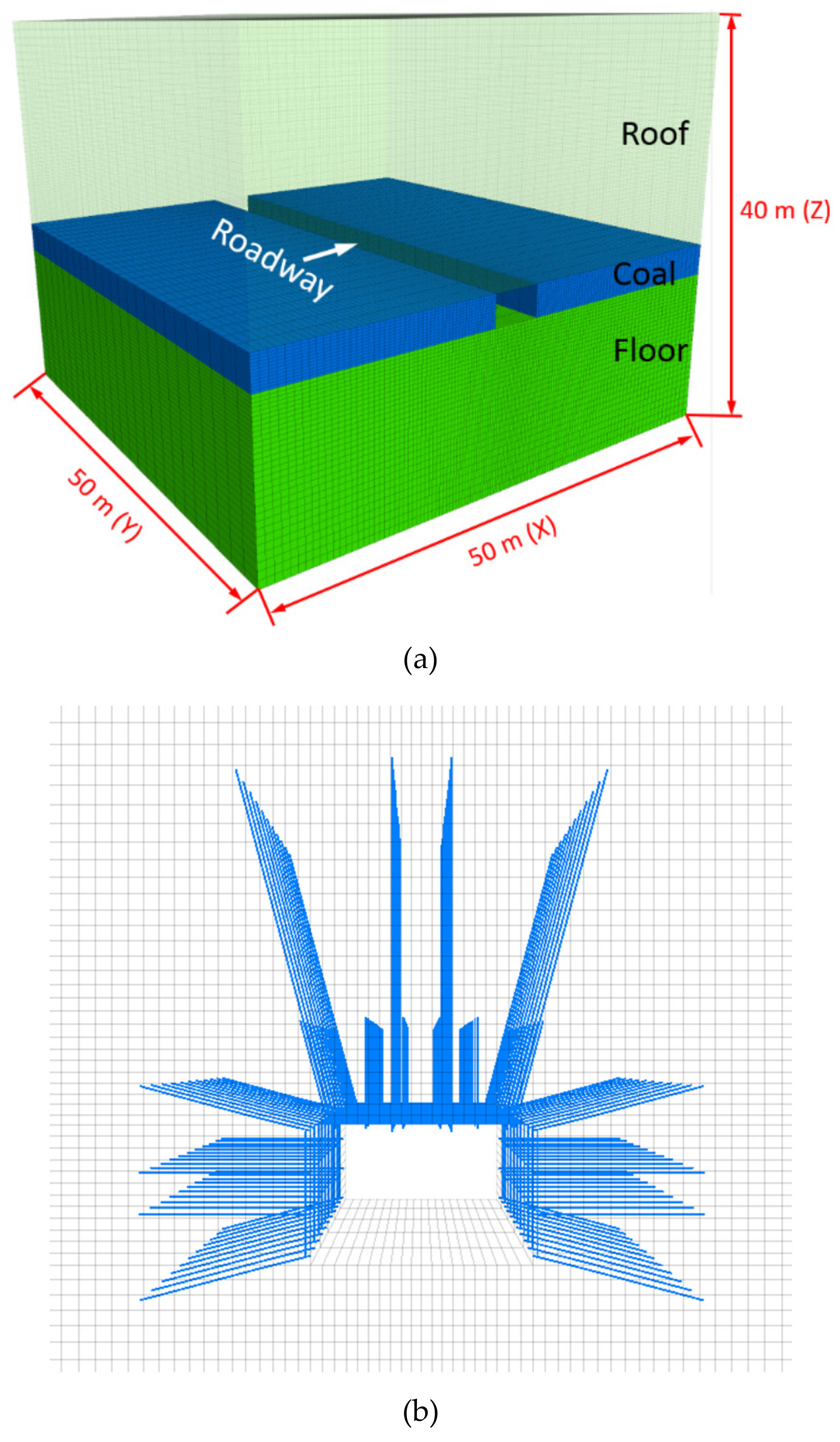
2.2. Development of Numerical Models
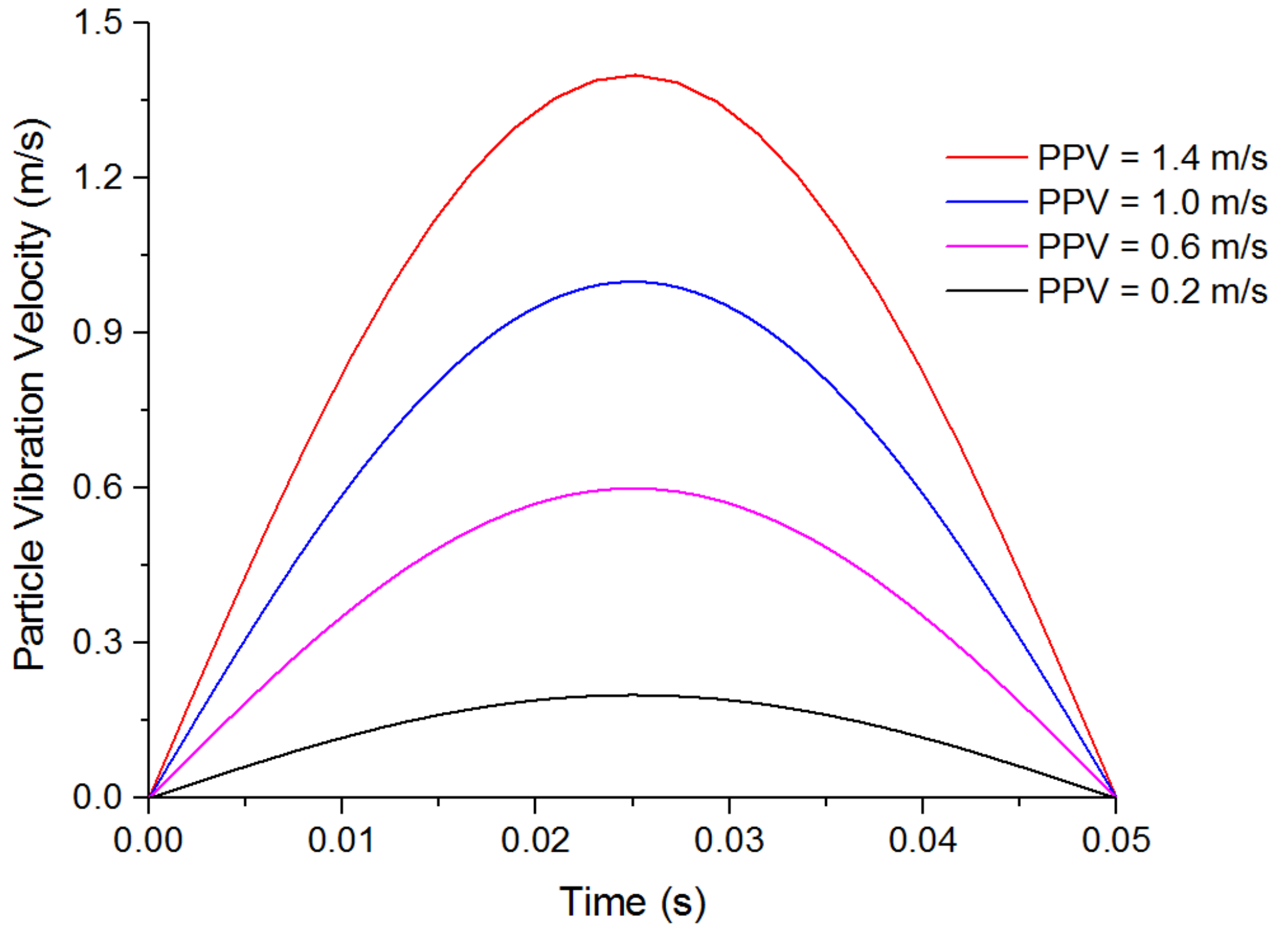
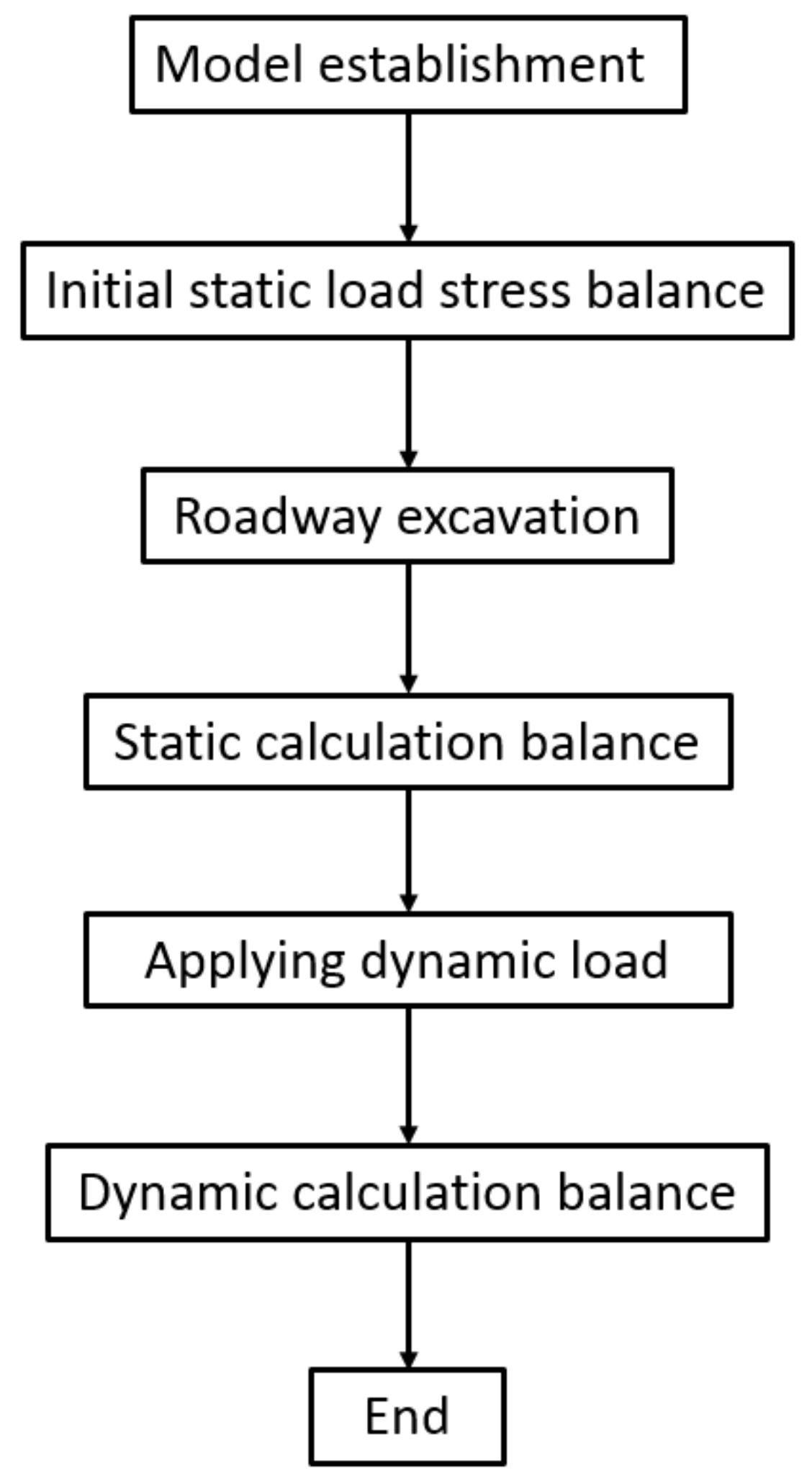
2.3. Simulation Methodology
3. Distribution Characteristics of the Deformation and Plastic Zone under Different Loads
3.1. Deformation of the Roadway under Different Superposed Dynamic and Static Loads
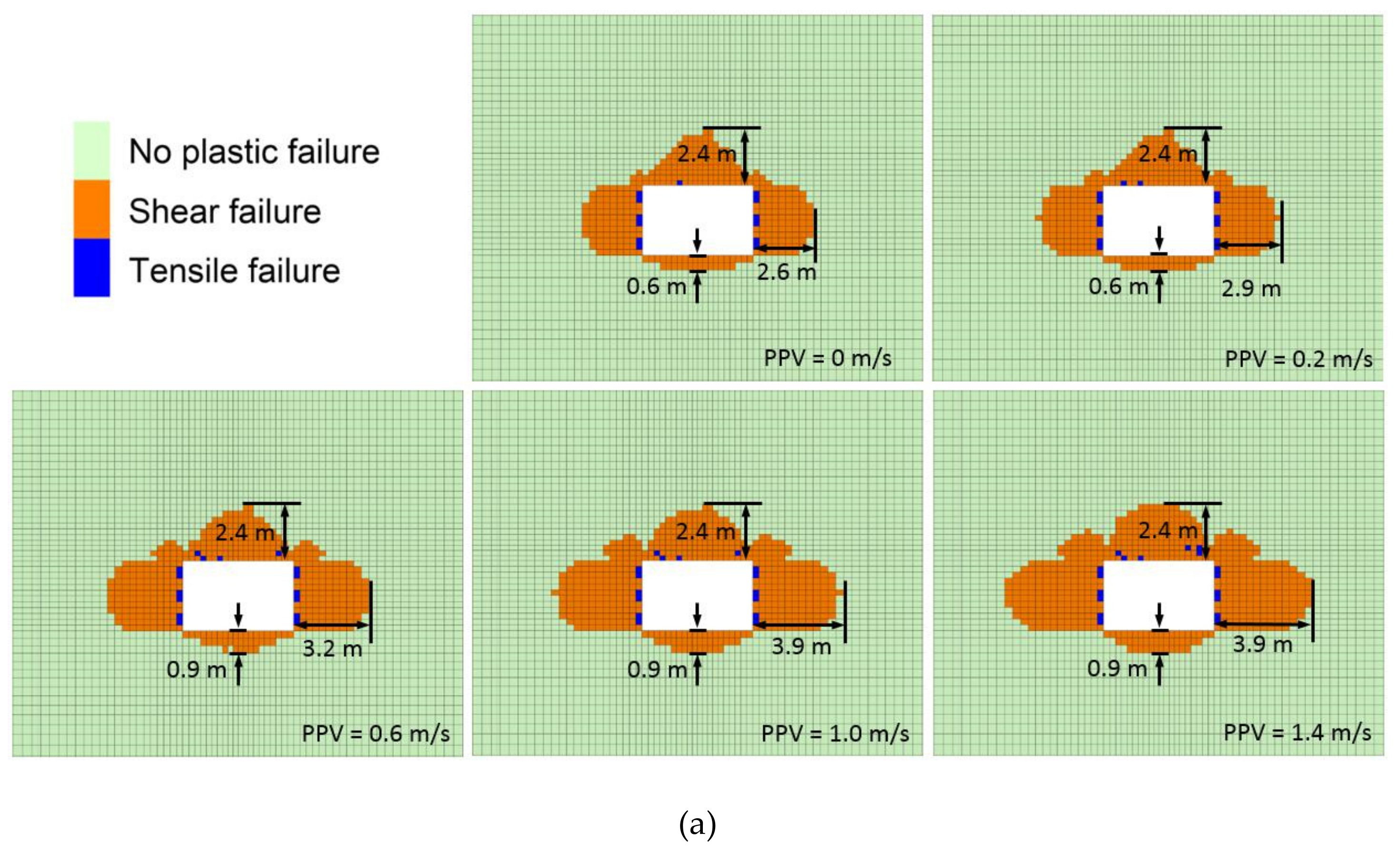
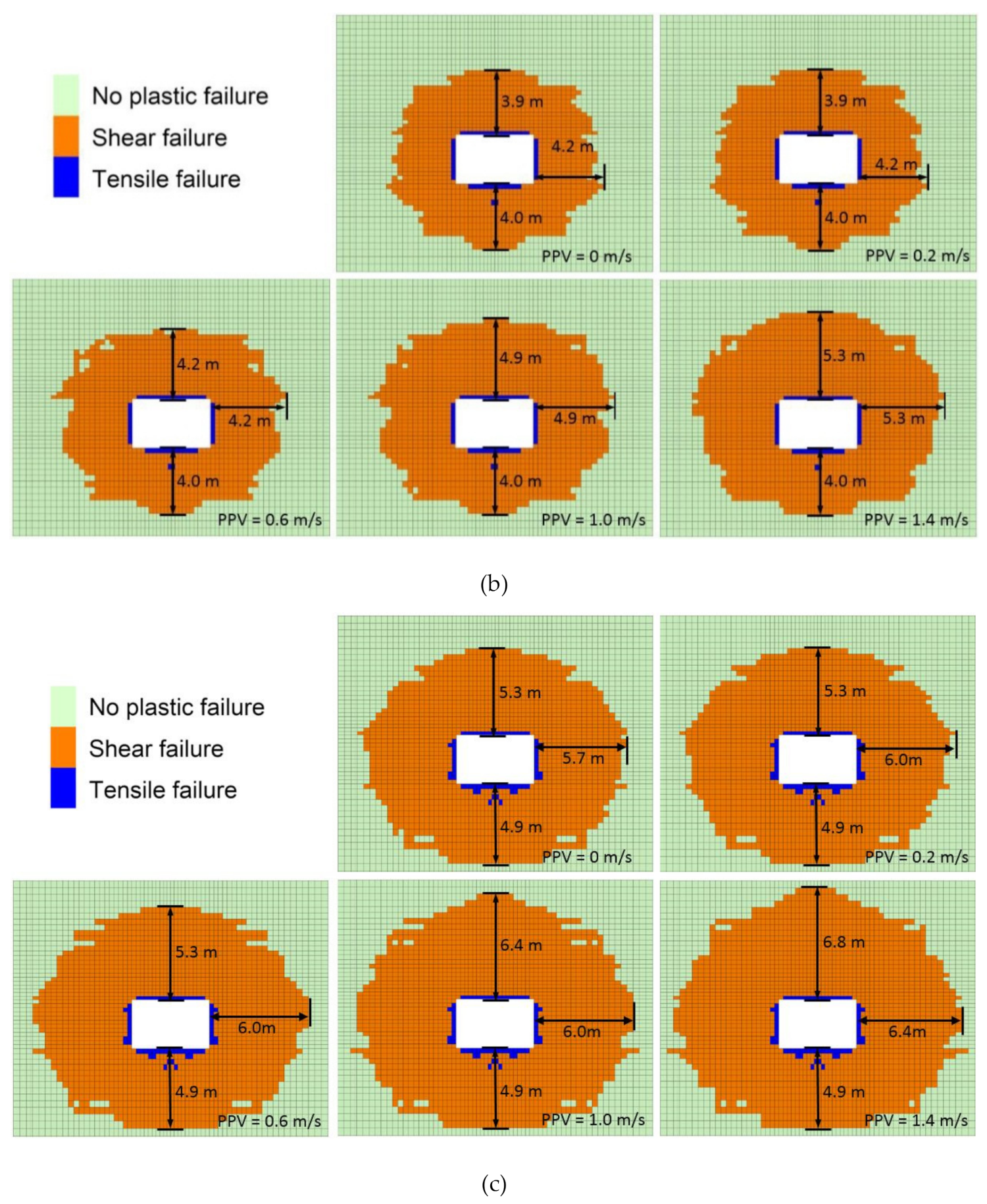
3.2. Distribution of the Plastic Zone of the Roadway under Different Superposed Dynamic and Static Loads
4. Rock-burst Risk Analysis under Different Superposed Dynamic and Static Loads
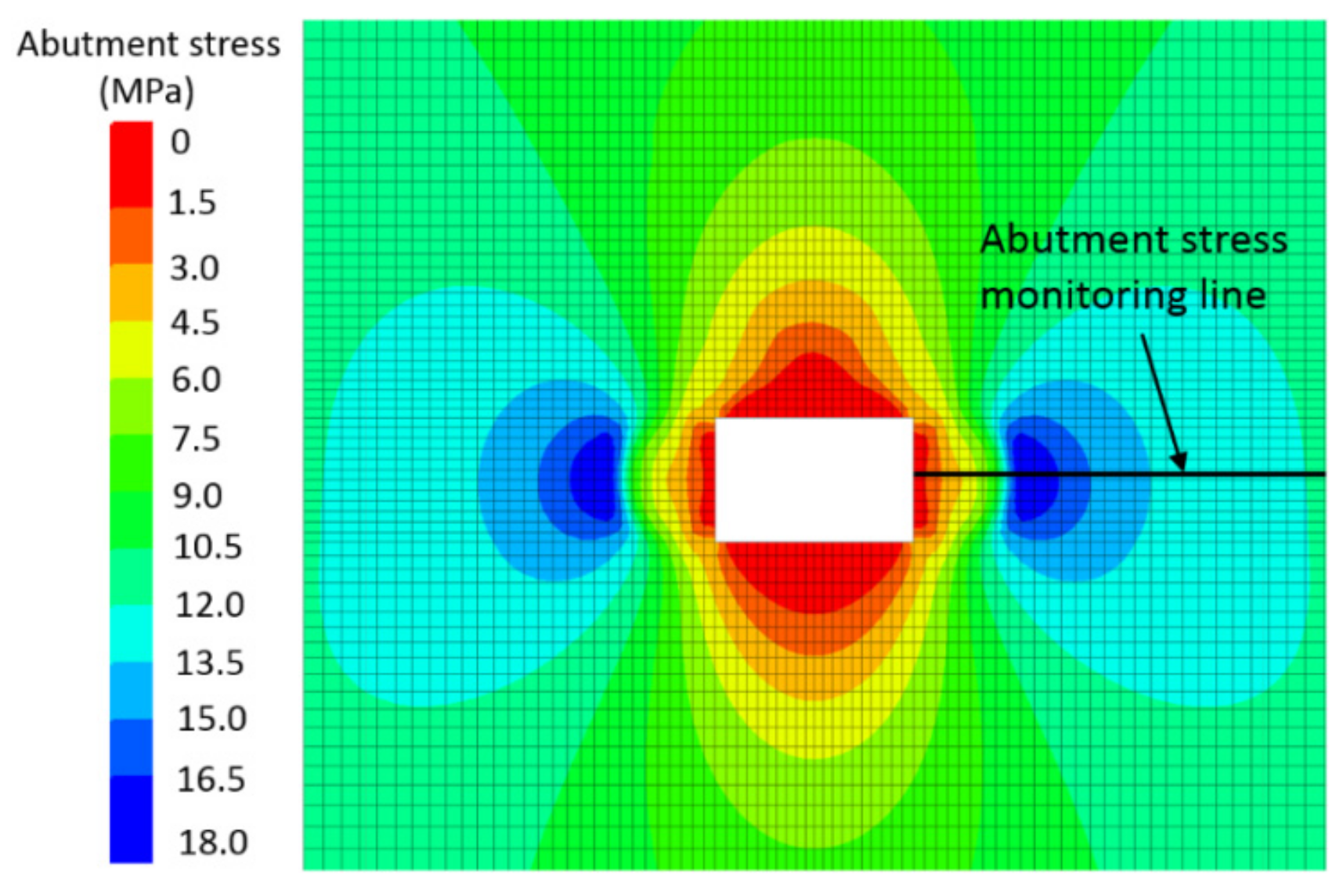
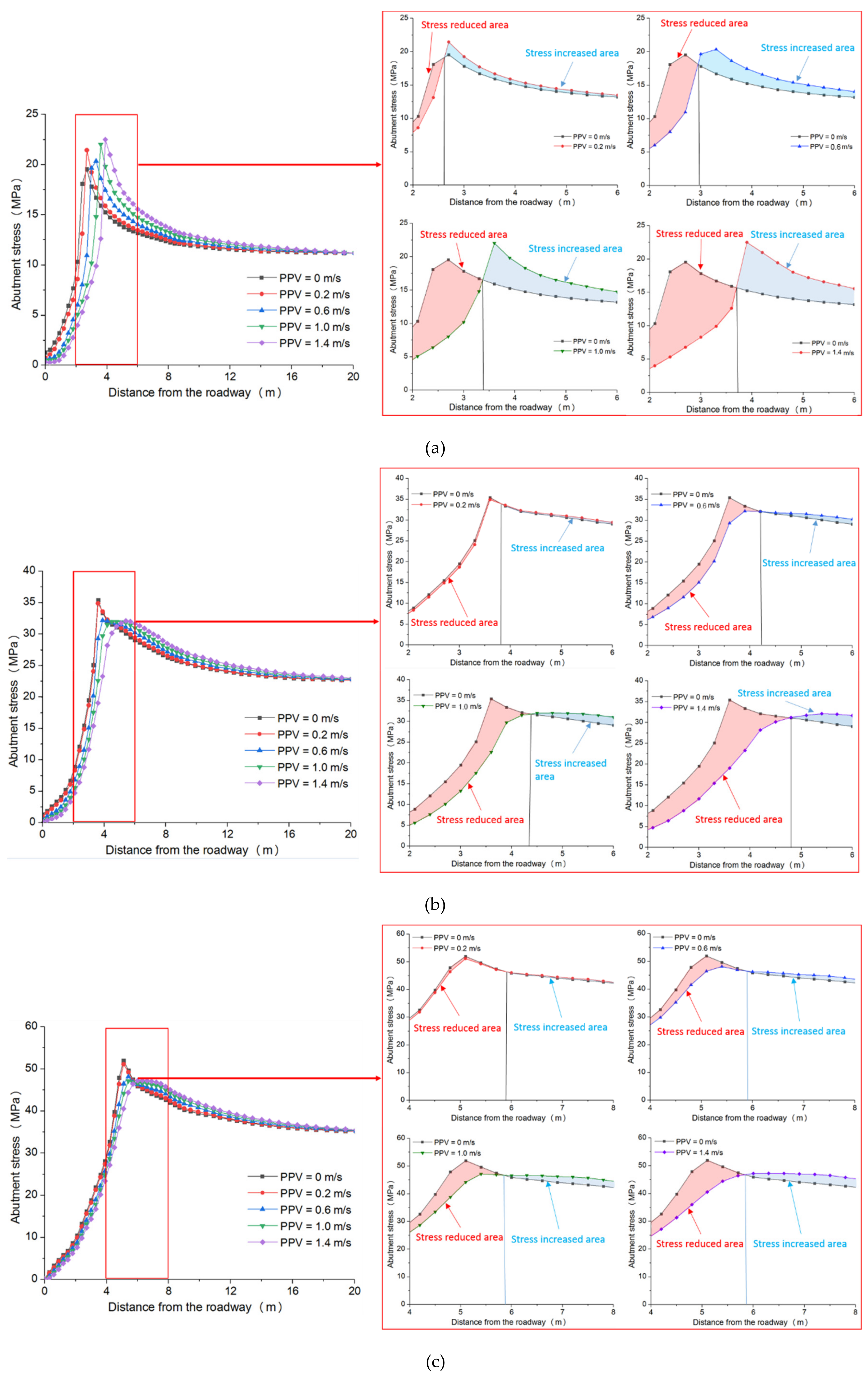
4.1. Variation in the Abutment Stress under Different Superposed Dynamic and Static Loads
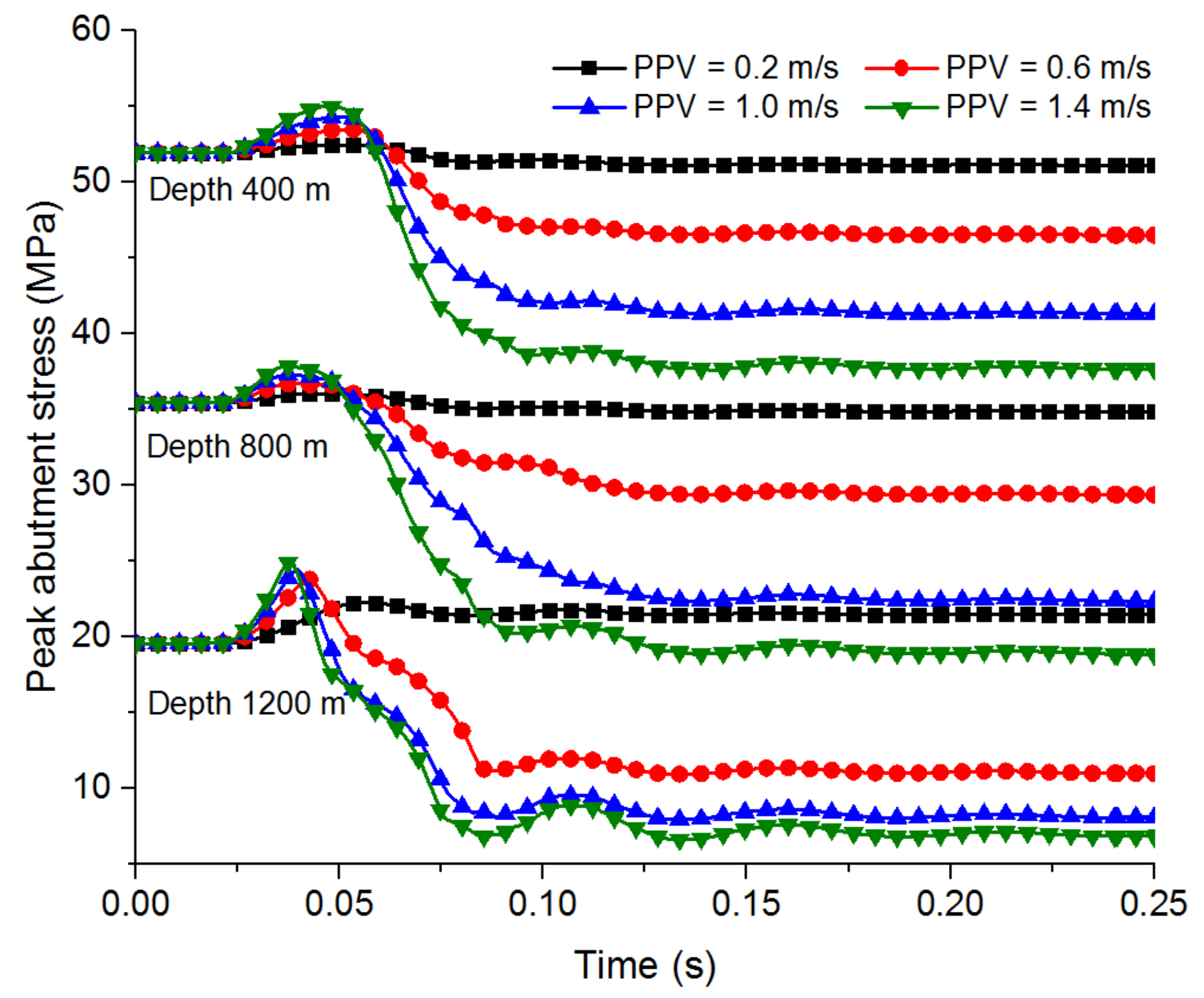
4.2. Variations in the Peak Abutment Stress and Elastic Energy Density under Different Superposed Dynamic and Static Loads
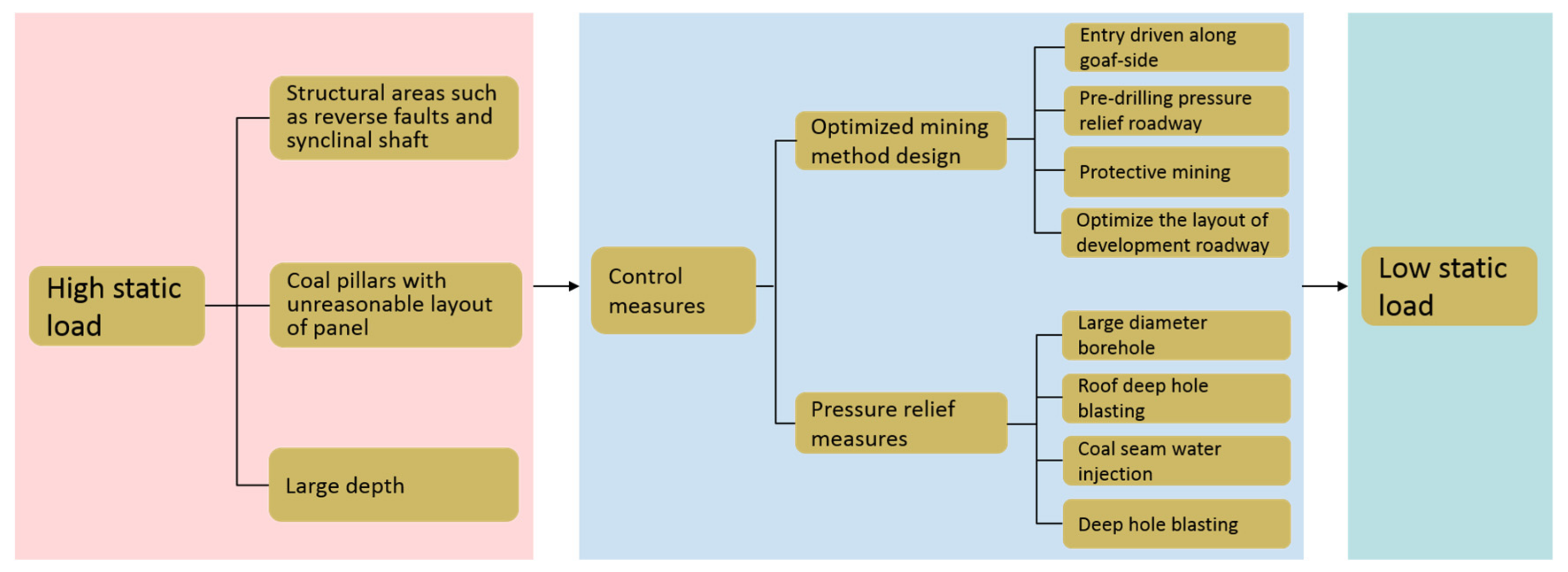
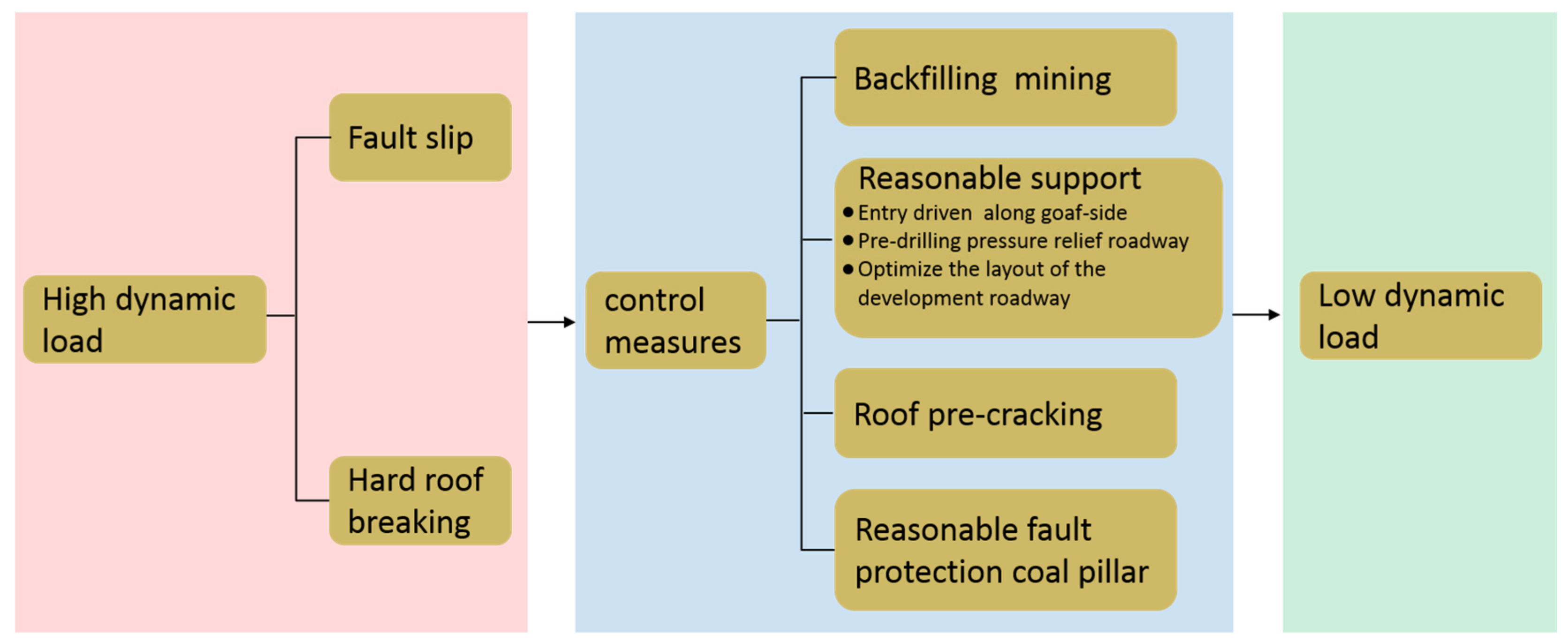
5. Discussion
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Whyatt, J.K.; Blake, W.; Williams, T.J.; White, B.G. 60 years of rockbursting in the Coeur D’ Alene District of northeastern Idaho, USA: lessons learned and remaining issues. In Proceedings of the 109th Annual Exhibit and Meeting, Society for Mining, Metallurgy, and Exploration, Phoenix, AZ, USA, 25–27 February 2002; pp. 1–10. [Google Scholar]
- Zhu, W.C.; Li, Z.H.; Zhu, L.; Tang, C.A. Numerical simulation on rockburst of underground opening triggered by dynamic disturbance. Tunn. Undergr. Space Technol. 2010, 25, 587–599. [Google Scholar] [CrossRef]
- Kong, P.; Jiang, L.; Shu, J.; Wang, L. Mining Stress Distribution and Fault-Slip Behavior: A Case Study of Fault-Influenced Longwall Coal Mining. Energies 2019, 12, 2494. [Google Scholar] [CrossRef]
- Wang, G.F.; Gong, S.Y.; Dou, L.M.; Cai, W.; Yuan, X.Y.; Fan, C.J. Rockburst mechanism and control in coal seam with both syncline and hard strata. Saf. Sci. 2019, 115, 320–328. [Google Scholar] [CrossRef]
- Wang, L.H.; Cao, A.Y.; Dou, L.M.; Guo, W.H.; Zhang, Z.Y.; Zhi, S.; Zhao, Y.X. Numerical simulation on failure effect of mining-induced dynamic loading and its influential factors. Saf. Sci. 2019, 113, 372–381. [Google Scholar] [CrossRef]
- Shepherd, J.; Rixon, L.K.; Griffiths, L. Outbursts and geological structures in coal mines: A review. Int. J. Rock Mech. Min. Sci. Géoméch. Abstr. 1981, 18, 267–283. [Google Scholar] [CrossRef]
- Li, Z.; Dou, L.; Cai, W.; Wang, G.; He, J.; Gong, S.; Ding, Y. Investigation and analysis of the rock burst mechanism induced within fault–pillars. Int. J. Rock Mech. Min. Sci. 2014, 70, 192–200. [Google Scholar] [CrossRef]
- Wang, Z.; Li, L. Study of Energy Release in Failure of Coal and Rock Near Fault on ANSYS. Geotech. Geol. Eng. 2019, 37, 2577–2589. [Google Scholar] [CrossRef]
- Chen, S.J.; Yin, D.W.; Jiang, N.; Wang, F.; Guo, W.J. Simulation study on effects of loading rate on uniaxial compression failure of composite rock-coal layer. Geomech. Eng. 2019, 17, 333–342. [Google Scholar]
- Li, Y.; Zhang, S.; Zhang, X. Classification and fractal characteristics of coal rock fragments under uniaxial cyclic loading conditions. Arab. J. Geosci. 2018, 11, 201. [Google Scholar] [CrossRef]
- Shen, W.L.; Bai, J.B.; Li, W.F.; Wang, X.Y. Prediction of relative displacement for entry roof with weak plane under the effect of mining abutment stress. Tunn. Undergr. Space Technol. 2018, 71, 309–317. [Google Scholar] [CrossRef]
- Jiang, L.; Wu, Q.S.; Wu, Q.L.; Wang, P.; Xue, Y.; Kong, P.; Gong, B. Fracture failure analysis of hard and thick key layer and its dynamic response characteristics. Eng. Fail. Anal. 2019, 98, 118–130. [Google Scholar] [CrossRef]
- Wang, J.; Ning, J.G.; Qiu, P.Q.; Yang, S.; Shang, H.F. Microseismic monitoring and its precursory parameter of hard roof collapse in longwall faces: A case study. Geomech. Eng. 2019, 17, 375–383. [Google Scholar]
- Sainoki, A.; Mitri, H.S. Simulating intense shock pulses due to asperities during fault-slip. J. Appl. Geophys. 2014, 103, 71–81. [Google Scholar] [CrossRef]
- Ortlepp, W.D.; Stacey, T.R. Rockburst mechanisms in tunnels and shafts. Tunn. Undergr. Space Technol. 1994, 9, 59–65. [Google Scholar] [CrossRef]
- Hossein, H.; Felix, H.; Catherine, A.; Stefan, B. Migration-based microseismic event location in the schlema-alberoda mining area. Int. J. Rock Mech. Min. 2018, 110, 161–167. [Google Scholar]
- Zhao, Y.X.; Jiang, Y.D.; Wang, T.; Gao, F.; Xie, S.T. Features of microseismic events and precursors of rock-burst in underground coal mining with hard roof. J. China Coal Soc. 2012, 37, 1960–1966. [Google Scholar]
- Li, Z.L.; Dou, L.M.; Cai, W.; Wang, G.F.; Ding, Y.L.; Kong, Y. Roadway stagger layout for effective control of gob-side rock-bursts in the longwall mining of a thick coal seam. Rock Mech. Rock Eng. 2016, 49, 621–629. [Google Scholar] [CrossRef]
- Cai, W. Fault Rockburst Induced by Static and Dynamic Loads Superposition and Its Monitoring and Warning. Ph.D. Thesis, China University of Mining and Technology, Xuzhou, China, 2015. [Google Scholar]
- Kong, P.; Jiang, L.; Shu, J.; Sainoki, A.; Wang, Q. Effect of Fracture Heterogeneity on Rock Mass Stability in a Highly Heterogeneous Underground Roadway. Rock Mech. Rock Eng. 2019, 1–18. [Google Scholar] [CrossRef]
- Jiang, L.S.; Kong, P.; Shu, J.M.; Fan, K. Numerical Analysis of Support Designs Based on a Case Study of a Longwall Entry. Rock Mech. Rock Eng. 2019, 1–12. [Google Scholar] [CrossRef]
- Shu, J.; Jiang, L.; Kong, P.; Wang, P.; Zhang, P. Numerical Modeling Approach on Mining-Induced Strata Structural Behavior by Considering the Fracture-Weakening Effect on Rock Mass. Appl. Sci. 2019, 9, 1832. [Google Scholar] [CrossRef]
- Oggeri, C.; Ova, G. Quality in tunnelling: ITA-AITES Working Group 16 Final report. Tunn. Undergr. Space Technol. Inc. Trenchless Technol. Res. 2004, 19, 239–272. [Google Scholar] [CrossRef]
- Jiang, L.; Sainoki, A.; Mitri, H.S.; Ma, N.; Liu, H.; Hao, Z. Influence of fracture-induced weakening on coal mine gateroad stability. Int. J. Rock Mech. Min. Sci. 2016, 88, 307–317. [Google Scholar] [CrossRef]
- Yan, S.; Bai, J.; Wang, X.; Huo, L. An innovative approach for gateroad layout in highly gassy longwall top coal caving. Int. J. Rock Mech. Min. Sci. 2013, 59, 33–41. [Google Scholar] [CrossRef]
- Zhang, G.; Wen, Z.; Liang, S.; Wu, Y.; Zhou, H. S Ground Response of a Gob-side Entry in a Longwall Panel Extracting 17m-thick Coal Seam: A case study. Rock Mech. Rock Eng. 2019. [Google Scholar] [CrossRef]
- Mutke, G.; Dubiński, J.; Lurka, A. New criteria to assess seismic and rock-burst hazard in coal mines. Arch. Min. Sci. 2015, 60, 743–760. [Google Scholar]
- Mutke, G.; Lurka, A.; Dubiński, J. Seismic monitoring and rock burst hazard assessment in Deep Polish Coal Mines–Case study of rock burst on April 16, 2008 in Wujek-Slask Coal Mine. In 7th International Symposium on Rockburst and Seismicity in Mines (RASiM 7): Controlling Seismic Hazard and Sustainable Development of Deep Mines, January, 2009; Tang, C.A., Ed.; Rinton Press: Paramus, NJ, USA, 2009; pp. 1413–1424. [Google Scholar]
- Wang, X.; Cai, M. Numerical modeling of seismic wave propagation and ground motion in underground mines. Tunn. Undergr. Space Technol. 2017, 68, 211–230. [Google Scholar] [CrossRef]
- Mortazavi, A.; Alavi, F.T. A numerical study of the behavior of fully grouted rockbolts under dynamic loading. Soil Dyn. Earthq. Eng. 2013, 54, 66–72. [Google Scholar] [CrossRef]
- He, J.; Dou, L.M.; Cai, W.; Li, Z.L.; Ding, Y.L. In Situ Test Study of Characteristics of Coal Mining Dynamic Load. Shock. Vib. 2015, 2015, 1–8. [Google Scholar] [CrossRef]
- Li, Y.C.; Sun, S.Y.; Tang, C.A. Analytical Prediction of the Shear Behaviour of Rock Joints with Quantified Waviness and Unevenness Through Wavelet Analysis. Rock Mech. Rock Eng. 2019, 1–13. [Google Scholar] [CrossRef]
- Wu, S.; Wu, Z.; Zhang, C. Rock burst prediction probability model based on case analysis. Tunn. Undergr. Space Technol. 2019, 93, 103069. [Google Scholar] [CrossRef]
- Itasca. FLAC3D-Fast Lagrangian Analysis of Continua; Itasca Consulting Group Inc.: Minneapolis, MN, USA, 2009. [Google Scholar]
- Sainoki, A.; Mitri, H.S. Influence of mining activities on the reactivation of a footwall fault. Arab. J. Geosci. 2017, 10, 99. [Google Scholar] [CrossRef]
- ABAQUS. ABAQUS Online Documentation: Ver 6.4-1; Dassault Systemes: Vélizy-Villacoublay, France, 2003. [Google Scholar]
- Wei, C.; Zhang, C.; Canbulat, I.; Cao, A.; Dou, L. Evaluation of current coal burst control techniques and development of a coal burst management framework. Tunn. Undergr. Space Technol. 2018, 81, 129–143. [Google Scholar] [CrossRef]
- Wu, Q.H.; Weng, L.; Zhao, Y.L.; Guo, B.H.; Luo, T. On the tensile mechanical characteristics of fine-grained granite after heating/cooling treatments with different cooling rates. Eng. Geol. 2019, 253, 94–110. [Google Scholar] [CrossRef]
- Zhang, Z.; Yu, X.; Wu, H.; Deng, M. Stability Control for Gob-Side Entry Retaining with Supercritical Retained Entry Width in Thick Coal Seam Longwall Mining. Energies 2019, 12, 1375. [Google Scholar] [CrossRef]
- Kaiser, P.K.; Cai, M. Design of rock support system under rockburst condition. J. Rock Mech. Geotech. Eng. 2012, 4, 215–227. [Google Scholar] [CrossRef]
- Fu, M.X.; Liu, S.W.; Jia, H.S.; He, D.Y. Experimental study of an orientation and resin-lifting device for improving the performance of resin-anchored roof bolts. Rock Mech. Rock Eng. 2019. [Google Scholar] [CrossRef]
- Wu, Q.H.; Li, X.B.; Weng, L.; Li, Q.; Zhu, Y.; Luo, R. Experimental investigation of the dynamic response of prestressed rockbolt by using an SHPB-based rockbolt test system. Tunn. Undergr. Space Technol. 2019, 93, 103088. [Google Scholar] [CrossRef]
- Wu, Y.; Hao, Y.; Tao, J.; Teng, Y.; Dong, X. Non-destructive testing on anchorage quality of hollow grouted rock bolt for application in tunneling, lessons learned from their uses in coal mines. Tunn. Undergr. Space Technol. 2019, 93, 103094. [Google Scholar] [CrossRef]


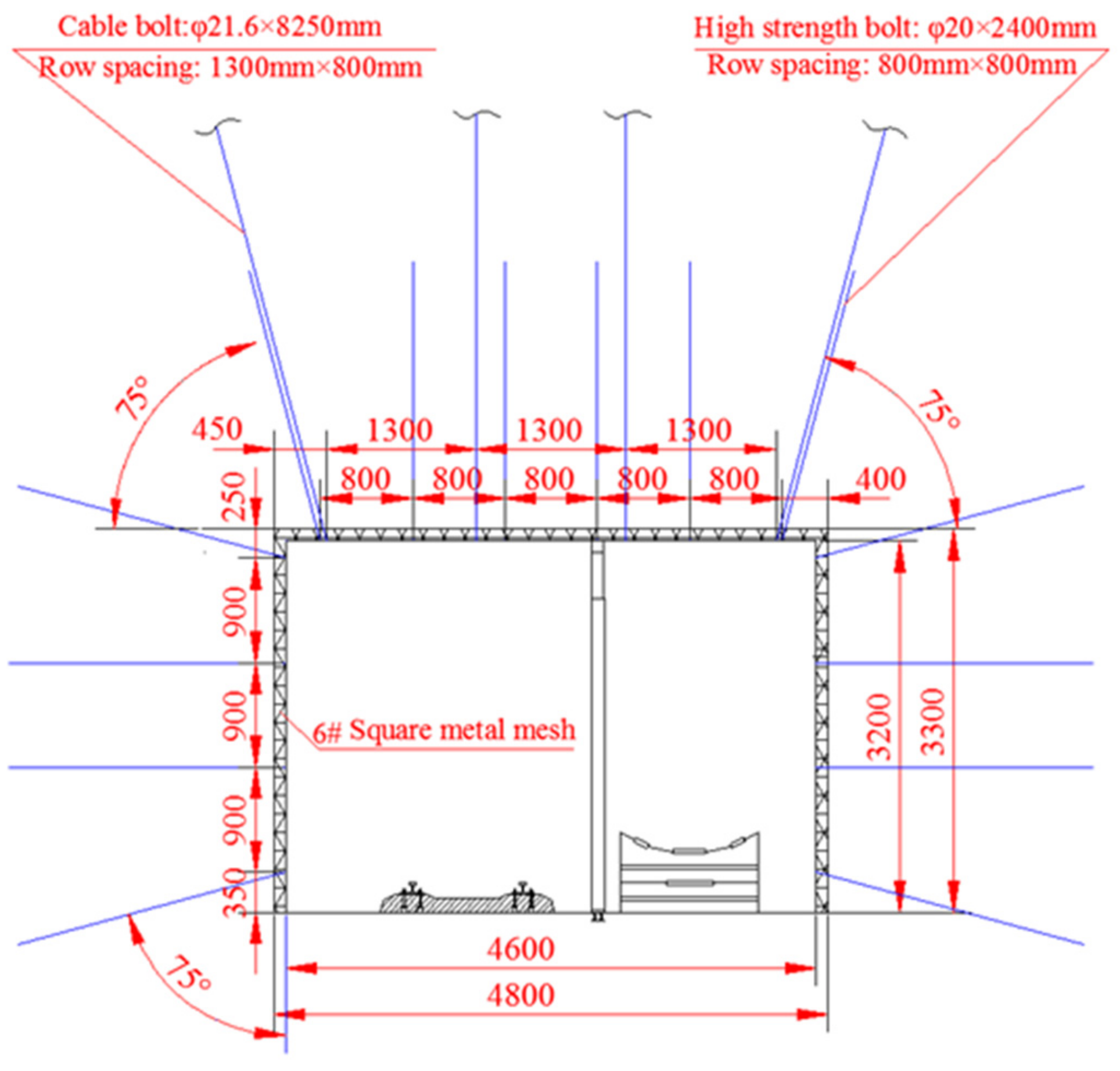


| Lithology | Ei (GPa) | υ | C (MPa) | σt (MPa) | φ (deg.) | cr (MPa) | εp (%) |
|---|---|---|---|---|---|---|---|
| Mudstone | 6.7 | 0.24 | 2.1 | 0.37 | 31 | 0.21 | 0.01 |
| Coal | 1.1 | 0.34 | 0.9 | 0.12 | 26 | 0.09 | 0.01 |
| Siltstone | 2.9 | 0.28 | 1.2 | 0.2 | 29 | 0.12 | 0.01 |
| Type | L (mm) | Lr (mm) | D (mm) | Ft (kN) |
|---|---|---|---|---|
| Rebar bolt Cable bolt | 2400 8250 | 1200 2400 | 20 21.6 | 225 510 |
| Hazard Level of Roadway | PPV | Depth of Roadway (D) |
|---|---|---|
| Lack of hazard | PPV ≤ 0.05 m/s | D ≤ 300 m |
| Low hazard | 0.05 < PPV ≤ 0.2m/s | 300 < D ≤ 5 00m |
| Medium hazard | 0.2 < PPV ≤ 0.4 m/s | 500 < D ≤ 700 m |
| High hazard | PPV > 0.4 m/s | D > 700 m |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kong, P.; Jiang, L.; Jiang, J.; Wu, Y.; Chen, L.; Ning, J. Numerical Analysis of Roadway Rock-Burst Hazard under Superposed Dynamic and Static Loads. Energies 2019, 12, 3761. https://doi.org/10.3390/en12193761
Kong P, Jiang L, Jiang J, Wu Y, Chen L, Ning J. Numerical Analysis of Roadway Rock-Burst Hazard under Superposed Dynamic and Static Loads. Energies. 2019; 12(19):3761. https://doi.org/10.3390/en12193761
Chicago/Turabian StyleKong, Peng, Lishuai Jiang, Jinquan Jiang, Yongning Wu, Lianjun Chen, and Jianguo Ning. 2019. "Numerical Analysis of Roadway Rock-Burst Hazard under Superposed Dynamic and Static Loads" Energies 12, no. 19: 3761. https://doi.org/10.3390/en12193761
APA StyleKong, P., Jiang, L., Jiang, J., Wu, Y., Chen, L., & Ning, J. (2019). Numerical Analysis of Roadway Rock-Burst Hazard under Superposed Dynamic and Static Loads. Energies, 12(19), 3761. https://doi.org/10.3390/en12193761






