Abstract
The phase shift full bridge (PSFB) is a widely known isolated DC-DC converter topology commonly used in medium to high power applications, and one of the best candidates for the front-end DC-DC converter in server power supplies. Since the server power supplies consume an enormous amount of power, the most critical issue is to achieve high efficiency. Several organizations promoting electrical energy efficiency, like the 80 PLUS, keep introducing higher efficiency certifications with growing requirements extending also to light loads. The design of a high efficiency PSFB converter is a complex problem with many degrees of freedom which requires of a sufficiently accurate modeling of the losses and of efficient design criteria. In this work a losses model of the converter is proposed as well as design guidelines for the efficiency optimization of PSFB converter. The model and the criteria are tested with the redesign of an existing reference PSFB converter of 1400 W for server applications, with wide input voltage range, nominal 400 V input and 12 V output; achieving 95.85% of efficiency at 50% of the load. A new optimized prototype of PSFB was built with the same specifications, achieving a peak efficiency of 96.68% at 50% of the load.
1. Introduction
As the number of devices connected to the Internet and the available services increase, the volume of data transferred and processed by server systems is growing exponentially. The amount of data centers is rising consequently. Therefore, the server power systems are under continuous development. Since the server power supplies consume massive amounts of power, the most critical matter is to achieve high efficiency []. To promote electrical energy efficiency of server systems several organizations have setup initiatives like climate-savers-computing-initiative (CSCI) [] and 80 PLUS [] which certifies individual power supplies corresponding to their performance level. CSCI and 80 PLUS keep introducing higher efficiency certifications such as Gold, Platinum, and Titanium with growing requirements extending also to light loads (Table 1). Noticeably, the required efficiency at 50% load condition for each certification is the highest and the most difficult to achieve, based on the redundant configuration of the server power system. The redundant structure is widely used in the server power supply applications because of the very high reliability demand characteristics of the application. A redundant structure means parallel power supplies sharing the total load and capable of taking over in case of a fault in one of the supplies [,]. Moreover, low power consumption of the server system in idle/sleep is becoming increasingly important. This is confirmed by efficiency requirements extending down to 10% load in 80 PLUS Titanium []. Meanwhile the power rating of the power supply unit (PSU) tends to increase to maximize the performance of the server system. A smaller volume requirement allows a greater processing power at a lower cost in the building infrastructure []. This leads to very high power density server PSU because the server system is required to reduce its mechanical size [].

Table 1.
Summary of efficiency requirements of 80 PLUS certification for redundant power supplies.
A server PSU is primarily composed of two stages: a back-end power factor correction (PFC) AC-DC stage powered by universal AC input (90~265 VAC rms) followed by a front-end DC-DC isolated step-down converter []. Among these parts, the front-end DC-DC converter stage has the biggest impact on the efficiency of the server power system because of its high conversion ratio of voltages and currents, and the required isolation transformer, which results in large power losses []. The output voltage typically ranges between 12 VDC to 48 VDC. In the literature many different topologies have been proposed for this application. The DC-DC stage can be a single switch isolated converter like a fly-back for low power applications (under 250 W), and half bridge converter or full bridge converter for higher power applications [,].
Half bridge LLC resonant converter is a popular isolated DC-DC topology. This is mostly due to its high efficiency and simple circuit structure, which helps to achieve high power density. However, the switching frequency (Fsw) span of the LLC is very wide, especially when a wide gain range of operation is required [,]. DC-DC converters with a wide gain range capability are common in many power conversion applications. Server power supplies have demanding requirements on continuity and reliability which includes hold-up time operation. During hold-up time the AC input of the back-end AC-DC converter is lost, while the DC-DC should maintain a stable output. During this time the intermediate storage capacitor continues to provide the energy while the DC bus voltage drops considerably. Therefore, the DC-DC converter needs to work normally with a wide input voltage range [].
The other most common alternative for high efficiency and high power density DC-DC converters in server PSU is the PSFB with synchronous rectifier (SR) MOSFETs, external resonant inductor and clamping diodes, shown in Figure 1. Its most remarkable characteristic is the wide zero-voltage-switching (ZVS) range from mid to full load [], nearly suppressing switching losses, which are especially high for high voltage (HV) devices in hard-switched converters []. Moreover, the constant switching frequency allows a simple control and EMI design [,]. One of the major advantages of PSFB over other resonant soft-switching topologies is the comparatively lower rms currents through the converter thanks to the output filter inductance. However, hold-up time regulation requirements means the PSFB converter cannot to be operated with its maximum effective duty in nominal conditions and causes a long freewheeling period []. The freewheeling period increases circulating currents and conduction losses [].
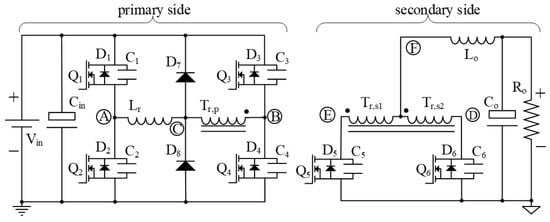
Figure 1.
Phase shift full bridge (PSFB) converter with center tapped rectification stage, external resonant inductance and clamping diodes.
The design of the DC-DC converter has many degrees of freedom which complicates the selection of the components values resulting in the best solution. Finding the design solution with the highest power density and/or efficiency and/or cost requires an optimization procedure based on comprehensive analytical models and equations considering the losses in the converter components [,]. With this procedure, the optimal design parameters could be determined. In [] a design process is presented to reach the point of highest efficiency ηmax and highest power density ρmax for a 5 kW PSFB DC-DC converter. The design process is based on an automatic optimization procedure which finds the optimal component values of the converter system. The space of solutions is limited by a curve in the η-ρ-plane, called the Pareto front, which presents the optimal points for varying weights of the efficiency and of the power density []. However, the automated process obscures the nature of the design parameters influence on the converter behavior, the design parameter interdependencies and limits the design engineer understanding of the converter.
In this work we present a complete losses model of the PSFB, which should prove useful for practicing engineers in their understanding on the origin of losses in the converter. The provided set of equations is based on a simplified model of the PSFB: all capacitances are linear; it does not include the clamping diodes; and it does not include the secondary side rectifiers’ capacitance. Furthermore, possible improvements in the calculation of losses will be discussed. Those and other additional considerations have been included by the authors in an extended set of equations, excluded from this document for clarity. The design criteria for a semi-automated design process presented in the following section has been performed on the authors’ extended version of the model. The losses model is tested, and the design criteria is demonstrated with the design of a PSFB DC-DC 1.4 kW 12 V output converter for server applications. The optimized PSFB design is compared to a reference converter with the same specifications. The rest of this paper is organized as follows: In Section 2 we propose a comprehensive losses model for the PSFB converter. The model is later used in Section 3 to analyze the influence of several of the design parameters in the converter performance. Section 3 also includes design guidelines or criteria for a semi-automated design procedure. In Section 4 the losses model and the design criteria have been applied to optimize a 1.4 kW PSFB DC-DC converter with 12 V output for server applications. Section 5 presents a summary of results comparing a previous reference design of PSFB with the new optimized prototype. Finally, Section 6 presents a summary of conclusions from this work.
2. Losses Model
A sufficiently detailed and accurate losses analysis model is necessary in order to perform efficiency optimization. The losses model and the design procedure should be a trade-off between accuracy and usability. Excessively precise and accurate estimations may lead to heavy computation requirements and long calculation times which makes the design process, iterative by nature, slow and tedious. Moreover, the complexity of the problem and the difficulty of estimating the real values of parameters in the circuit makes a precise estimation impractical. Ideally, the losses model is updated later on or corrected based on the results of the real hardware, giving more accurate results for each design iteration. The power losses analysis is discussed in this section to help understand where the losses are originated. There are three types of power losses for a switching power converter, as follows []: conduction losses, switching losses (including gate-driving power losses), and magnetic core losses.
The PSFB converter’s operation can be classified into discontinuous conduction mode (DCM), if the output filter inductor current ripple is higher than the average output or continuous conduction mode (CCM) otherwise. The circuit analysis in CCM is quite different from that in DCM because of the different operation modes []. In this work we will consider only the CCM working mode (the proposed losses model does not include DCM operation). The high-efficiency designs operate in CCM in all load ranges of interest. Moreover, the DCM control of the SRs could be challenging. Therefore, the PSFB converter is normally preferred not to operate in DCM [].
2.1. Conduction Losses
These losses are caused by the currents passing through the parasitic resistances in the circuit, such as on the resistance of the switches RDS(on), the transformer, and inductor winding resistance. These losses can be calculated with the equivalent resistance and the rms current value in the different components of the converter [].
2.1.1. Transformer Conduction Losses
The principles of operation of the PSFB converter have been already widely covered in the literature []. Briefly, the PSFB converter has three main working modes, which can be identified in Figure 2:
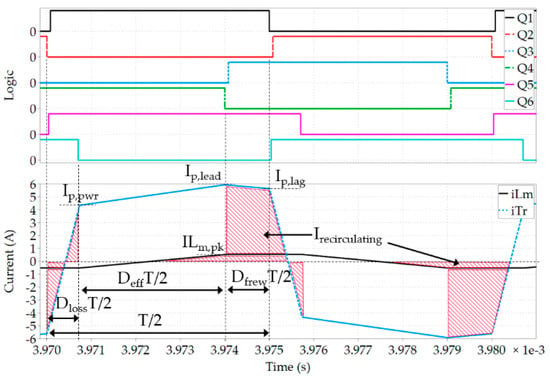
Figure 2.
Primary side current and PWM control signals of a simplified model of a PSFB converter.
- Effective duty (Deff). In this mode the primary side bulk voltage (Vin) is applied to the resonant inductance Lr and the primary side of the transformer. Power is being transferred from primary to secondary through the transformer (overlap of current and voltage of same sign).
- Duty losses (Dloss). Before the next power transfer the current has to reverse polarity on the primary side of the transformer. The current through the resonant inductance (Lr) and leakage of the transformer (Llkg) require a certain time to reach the reflected output current with reverse sign.
- Freewheeling duty (Dfrew). During the remaining time the current recirculates on the primary side without effective power transfer (there is no overlap of current and voltage on the primary side of the transformer) while it freewheels on the secondary side.
Figure 2 shows a simplified representation of the primary side current in a PSFB converter: all capacitances are linear; it does not include the clamping diodes; and it does not include the secondary side rectifiers’ capacitance. The enclosed area between iTr and iLm corresponds to the reflected secondary current during Deff, while power is being transferred from the primary to the secondary. The enclosed shaded areas correspond to currents recirculating on the primary side without effective power being delivered to the secondary side. From Figure 2 it can be inferred that two parameters have the most impact on the circulating currents: the effective duty (Deff) and the magnetizing current (iLm).
The current passing through the primary side of the transformer, excluding the effect of the magnetizing inductance, can be calculated with Equations (1)–(4). The secondary side reflected current could be calculated from Equations (1)–(4) by multiplying the turns ratio of transformer n.
The magnetizing current is proportional to the input voltage and inversely proportional to the magnetizing inductance. It can be calculated with Equations (5) and (6):
Taking into account the magnetizing current the resulting primary side current can be calculated with Equations (7)–(9):
The rms current of the primary side of the transformer and secondary side of the transformer can be calculated from the previous equations which result in Equations (10)–(12):
The conduction losses of the transformer can be estimated with the rms currents and Equation (13), where RTr,p stands for the primary side equivalent resistance of the transformer, Lr,ESR for the equivalent resistance of the resonant inductance, and RTr,s for the equivalent resistance of the secondary side of the transformer. Additionally, the contribution to conduction losses of the printed circuit board (PCB) could be added both in the primary and in the secondary of the converter, which have a noticeable impact in high output current converters.
The skin and proximity effects increase the equivalent resistance of the windings and should be included for an accurate estimation of the transformer conduction losses. The magnetic fields generated by the alternating currents through the windings reduce the effective conduction area of the conductor itself (skin) and of other surrounding conductors (proximity). The studies in [] show that the proximity effect dominates at high frequencies.
In the authors’ extended model, the AC resistance RAC of the primary and secondary windings of the transformer was estimated at different frequencies with finite element analysis (FEA) software []. The spectrum of the transformer’s primary and secondary currents was calculated from the previously analyzed waveforms. The total conduction losses was approximated by the sum of the rms current for each of the frequency components multiplied by the RAC at that frequency.
2.1.2. Primary Side HV MOSFETs
As suggested in [] the power losses of the leading and lagging legs, which is dependent on MOSFETs current and voltage waveforms, should be analyzed separately. Therefore, the key waveforms for the MOSFETs in both of the primary side full bridge legs are shown in Figure 3 and will be described analytically. The proposed loss model is precise enough and easily computable using datasheet parameters.
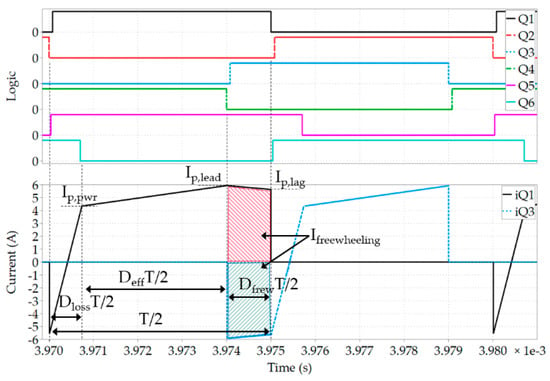
Figure 3.
Primary side HV MOSFETs current and PWM control signals of a simplified model of a PSFB converter.
The current waveform for the lagging leg (Q1, Q2 in Figure 1) can be calculated with Equation (14):
The current waveform for the leading leg (Q3, Q4 in Figure 1) can be calculated with Equation (15):
The rms currents of both legs are equal in this simplified model, calculated from the previous formulas and resulting in Equation (16):
The conduction losses of the HV switches can be estimated from their rms currents with Equation (17), where RDS(on) stands for the equivalent resistance of the MOSFETs. Note that the RDS(on) of MOSFETs increases with temperature and it is also influenced by the gate driving voltage. Most of the conduction losses, like in MOSFETs, increase with temperature. This should be taken into account in the computation of the equivalent resistance of the components.
In the authors’ extended model, the equivalent resistance of MOSFETs is estimated at the operating junction temperature TJ from their temperature coefficient, available in the manufacturer’s datasheet. Since the conduction losses are consequently updated, the temperature is recalculated until the solution of the equations converge. The process is also performed for other converter components: transformer windings, transformer core, secondary side rectifiers, PCB and output inductor windings. The iterative calculation can be easily automated in a computer (e.g., in a calculation sheet).
The estimations of components’ temperature require additional values for the thermal impedances, for example from junction to air for the HV and the low voltage (LV) MOSFETs. This was estimated with thermal simulation tools and thermal captures of the real hardware.
Additionally, the conduction losses of the HV MOSFETs body diode could be estimated accounting for the turn on delay of the switches, so-called dead times. Not included here for simplicity, since for a reasonably well-adjusted control of the dead times the body diode contribution is minor in silicon devices. Moreover, because of the strong non-linearity of the output capacitance in modern super-junction MOSFETs, the equivalent Coss in the depletion region is big, which enables relatively high tolerance for the turn on delay prior to the body diode conducts.
2.1.3. Secondary Side Rectifier LV MOSFETs
The Schottky barrier diode (SBD) or fast recovery diode (FRD) are commonly used as secondary side rectification devices in PSFB DC-DC converters because of their low cost and simplified control of the converter. However, the forward voltage drop of diodes cause relatively high conduction losses. By replacing the diode with an active switching element, the so called synchronous rectifier (SR), the losses can be notably reduced [].
The rectification stage may have different configurations: center tapped, current doubler or full bridge []. Although these alternatives have no major impact on the working principles of the converter, they do have a significant impact on the current and voltage stress over the rectification devices and their related conduction and switching losses. The blocking voltage of the secondary side devices is two times the transformer reflected secondary voltage for center tapped and current doubler, or one time the transformer reflected secondary voltage for full bridge. However, the effective RDS(on) is twice as big for full bridge rectification []. Therefore, current doubler and center tapped rectifiers are the most appropriate for low voltage and high current applications. In [] both configurations are analyzed and compared. The center tapped rectifier presents only one output inductor, which operates at double the switching frequency of the semiconductors, becoming an interesting alternative at low and medium current applications.
The current of the SRs (Q5, Q6 in Figure 1) is plotted in Figure 4 and can be calculated with Equations (18)–(21):
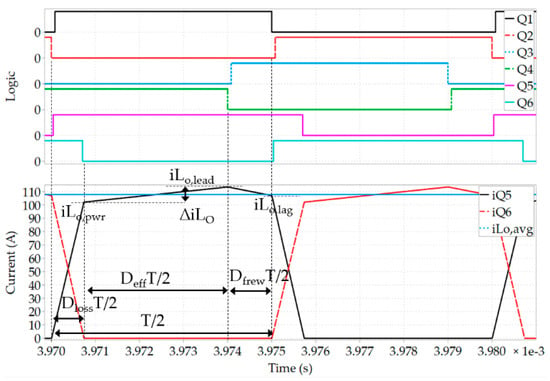
Figure 4.
Secondary side LV MOSFETs current and PWM control signals of a simplified model of a PSFB converter.
The rms currents of both legs are equal in this ideal case and can be calculated from the previous formulas as expressed by Equation (22):
Out of the rms currents the conduction losses of the secondary side rectifiers can be estimated with Equation (23) where RDS(on),SR stands for the equivalent resistance of the secondary side switches:
Additionally, the conduction losses of the body diode of the secondary side rectifiers could be estimated accounting for the unavoidable turn on and turn off delays of the switches. Not included here for simplicity, since for a good adjusted control of the SRs the body diode contribution is minor in silicon devices.
2.1.4. Input and Output Filter
The output filter includes the output choke Lo and the output capacitance of the converter Co. The input filter includes the bulk capacitance between the back-end AC-DC converter and the front-end DC-DC converter. In reality part of the current ripple through the input filter caused by the DC-DC stage is cancelled by the output current ripple of the AC-DC converter but, for simplicity, we will only consider the rms current of the DC-DC as a stand-alone converter.
The current of the output choke is plotted in Figure 5 and can be calculated with Equation (24):
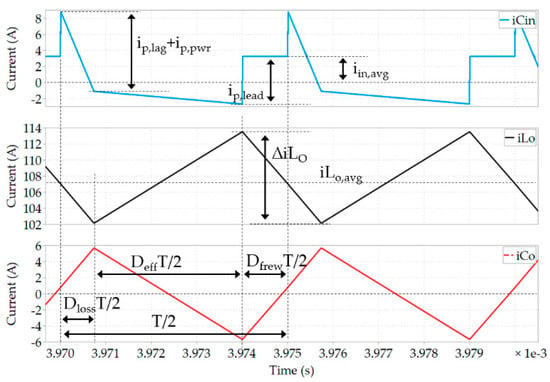
Figure 5.
Input capacitor, output choke and output capacitor currents of a simplified model of a PSFB converter.
The rms current through the output choke can be estimated with Equation (25):
The current of the output capacitor can be calculated with Equation (26):
The rms current through the output capacitor can be estimated with Equation (27):
The current through the input capacitor can be calculated with Equations (28) and (29):
The rms current through the input capacitor can be estimated with Equation (30):
The conduction losses of the input and output filter can be estimated with the rms currents and Equation (31) where Cin,ESR stands for the equivalent resistance of the input capacitor, Co,ESR stands for the equivalent resistance of the output capacitor, and Lo,ESR stands for the equivalent series resistance of the output choke:
2.2. Switching and Driving Losses
The voltage and current crossover during switching transitions results in switching power losses. Additionally, charging and discharging of the MOSFETs gate capacitance causes gate-driving power losses [].
2.2.1. Primary Side HV MOSFETs Switching and Driving Losses
If the primary side MOSFETs operate under zero voltage switching, then there is no overlap between voltage and current, and transitions could be considered near lossless. However, it is known that in modern super-junction devices the charging and discharging of the device output capacitance shows a hysteresis which is the source of additional power losses that should be considered [].
The minimum energy required to achieve ZVS transitions for the lagging and the leading leg can be estimated with Equations (32) and (33), with Cleading equal to the sum of capacitances C3 and C4, and Clagging equal to the sum of C1 and C2. The lumped capacitance of the transformer CTr constitutes an important contribution to the leading leg transition but it does not have an influence on the lagging leg.
An efficiency optimized PSFB design operates in full or nearly full ZVS in all load ranges. The ZVS is especially important at light and medium loads, where the switching losses become dominant [,]. During partial ZVS the capacitance of the switches is not fully discharged when the device turns on. For modern HV super-junction MOSFETs the remaining losses are not significative []. The use of an external resonant inductance (Lr) in the primary side of a PSFB, while increasing the component count, helps achieving ZVS in light to medium load conditions and thus increases the overall efficiency of the converter. Although it is possible to increase the leakage of the transformer for the same purpose, using an external resonant inductance on the primary side of the converter and placing clamping diodes between the transformer and Lr helps to reduce the secondary side rectifiers overshoot as well as reduce their switching/commutation-related losses [,]. The solution, previously reported in the literature, is analyzed in detail in [].
To achieve full ZVS, whenever there is enough energy available, a minimum dead time is also required for the transition of the drain voltage. The time it takes for the transition to happen depends on the transfer of energy from the inductances to the capacitances involved in the resonance. The output capacitance of modern MOSFETs is non-linear, and an accurate estimation of the transition times is not straightforward. A simple approximation can be estimated with Equation (34), where the capacitance is modeled by an equivalent time related fixed value of capacitance (Co(tr)) and the current from the inductances is considered also as a constant current source. Co(tr) is a parameter often provided by the manufacturer in the datasheet of the device.
However, if there is not enough energy to achieve full ZVS, the transition time could be better approximated by the resonance between the inductors and the capacitors (Equations (35) and (36)). Since the reflected value of Lo is relatively big the transition of the leading leg can be well approximated by the previous linear model in all working conditions of the converter. However, for the lagging leg, the dead time has to match one fourth of the resonance period to switch at the minimum possible voltage.
Assuming the dead time to be always optimum (with the devices switching at the minimum possible drain voltage), the switching losses can be estimated with Equation (37) where EOFF is a function of the current and voltage overlap during the turn off transition. In general, for modern super-junction MOSFETs EOFF is relatively small, but not zero.
If the energy is not enough to achieve the ZVS part or all the energy stored in the output capacitance is dissipated, then the switching losses become Equation (38) where EON is a function of the current and drain voltage overlap and the EOSS is the stored energy in the output capacitance of the switch, which is also a function of the drain voltage.
The switching losses could be calculated, measured or simulated and tabulated for different values of current and switching voltages. The switching losses are computationally costly to calculate accurately. Moreover, it is difficult to estimate the real layout parasitics which have a relatively big impact on the losses. Therefore, in the authors’ extended model, the switching losses were interpolated from a table extracted from experimental measurements and characterization.
The driving losses are a function of the driving voltage Vdrive and the switching frequency. The reader may note that the gate charge differs in soft switching (ZVS) (Equation (39)) and hard switching (Equation (40)). In ZVS, the Qgd is supplied by the power stage during the resonant transition prior to the charge of the switch input capacitance from the driver path.
2.2.2. Secondary Side LV MOSFETs Switching and Driving Losses
It was mathematically demonstrated in [,] that charging a capacitor inevitably causes energy losses. When charged through a resistive path the resistor dissipates energy equal to the one eventually stored (Equations (41)–(43)). The analysis shows that a capacitor can be charged with only a modest energy loss in a series RLC circuit only if the source is disconnected after ½ resonance cycle. Otherwise the remaining energy is dissipated during the dampening of the resonance and the energy loss becomes also equal to the stored. Their analysis is consistent with the formula for the estimation of switching losses in SRs in [].
When using clamping diodes on the primary side of the converter part of the energy of the resonance is recovered. During the charge of Qrr and Qoss of the secondary side rectification devices an equal energy is stored in the inductances along the charging path (Lr, Llkg). It follows that the larger Lr is in relation to Llkg, the more energy it stores comparatively. Due to the action of the primary side clamping diodes, the energy in Lr is actually recirculated on the primary side of the converter and does not contribute to the secondary side commutation resonance. Therefore, the switching losses calculated in Equations (41)–(43) are reduced down to the energy calculated in Equations (44)–(46) where Eclmp stands for the conduction losses of the clamping diodes which can be estimated from their average current (Equation (45)).
Qrr is not constant but depends on the average forward current of the diode, the conduction time, the temperature of the device and the slope of the current among other factors [,]. This was taken into consideration in the complete and more accurate model where Qrr is a linear fitting function of the average current and the slope (Equation (47)). The coefficients of the relation were extracted from experimental measurements and characterization of the devices.
Driving losses is a function of the driving voltage and the switching frequency (Equation (48)). Since the SRs are operated in ZVS, we can exclude the plateau charge (Qgd) from the driving losses. Notice that the driving voltage Vdrive is not necessarily equal to the driving voltage of the HV MOSFETs. Due to the higher gate charge of the LV MOSFETs in high current output converters, it is usually desirable to lower their driving voltage always in accordance to the device characteristics.
2.2.3. Core Losses
The empirical methods based on measurement results are one major group of core losses calculations. A widely used empirical method is the Steinmetz equation (Equation (47)) []. The frequency of the flux variation Fcore in Equation (49) is the switching frequency Fsw for the main transformer and the resonant inductance but two times the switching frequency for the output choke 2Fsw. Vcore is the volume of the core, Bpk is the peak magnetic flux density, and k, a and b are called the Steinmetz coefficients, which are material parameters generally found empirically from the materials B–H hysteresis curves. The coefficients for the Steinmetz equations are frequently given by the magnetic core manufacturers.
The temperature of the cores also influences the core losses, with some materials having an optimum operating temperature. The relation of core-losses to temperature is often found in the material datasheets. In the authors’ extended model, the core losses of the transformer are recalculated until the solution converges, also taking into account the transfer of heat from the windings.
The Steinmetz equation accuracy is frequently discussed. In [] an improved core-loss calculation is proposed. However, there is currently no agreement on a better estimation method. Moreover, manufacturers frequently provide the Steinmetz coefficients or only experimental data for pure sinusoidal excitation at several flux and frequency conditions. In the authors’ extended model, the core losses are interpolated from the manufacturer’s experimental data for the main frequency component of the flux.
2.3. Other Losses
2.3.1. Control Circuitry and Fan
The control circuitry in server PSU is generally powered by an auxiliary supply. The efficiency of the auxiliary bias (a converter itself) has to be taken into account in the power consumption of the control circuitry. Moreover, an internal PSU fan is also commonly supplied from the bias. Therefore, the efficiency of the bias has to be also considered in this case (Equation (50)).
Alternatively, the fan or the control circuitry could be supplied by the main converter itself. This is especially convenient in server PSU because their output voltage is commonly equal to the control and fan supplies (12 V). Since the efficiency of the main converter is normally higher than the small auxiliary converter, this technique slightly improves the overall efficiency of the system. In contrast to the reference converter in this document, in the optimized prototype the fan is supplied by the main converter.
2.3.2. Capacitors Leakage
In addition to the previously analyzed conduction losses for the input and output capacitors there is an additional contribution from their current leakage (Equation (51)). The values of current leakage can be often found in the manufacturer’s datasheet.
2.4. Overall Losses
The overall losses of the converter include all previously analyzed contributions that should be evaluated for each of the load points Po of interest (Equations (52) and (53)):
Since the distribution of losses is load dependent, some different losses mechanisms are dominant at different load points. More interestingly, reducing the conduction losses at full load often impacts negatively on the switching and core losses at light load and vice versa. Achieving the highest efficiency at mid load is the greatest challenge, because most of the losses’ contributions have a noticeable impact in that range. Therefore, a converter with the highest efficiency at mid load will have balanced light and full load efficiencies, so-called the flat efficiency curve.
3. Design Criteria
Following the Platinum 80 PLUS requirements, the objective for the proposed design was to achieve maximum efficiency at 50% of the load of the converter while having balanced light (20%) and full load (100%) performances. The volume is constrained by the standard PSU height (1 U). Additionally, the converter should have a reasonable bill of materials (BOM) and/or production cost.
In this section we analyze the impact on the converter’s efficiency of the most influential design parameters. In the analysis, the effects of the parameters are described sequentially, in the preferred order of design, and isolated from the other parameters’ effects. However, the design process is an iterative process and normally with more than one optimal solution. Due to the complex interrelations between the parameters, the possible alternative might be constrained by previous design choices. It is therefore convenient to explore the full space of solutions.
3.1. Clamping Diodes Position
The ZVS range of the converter can be extended by adding an external resonant inductance (Lr) to the leakage of the transformer. However, the additional inductance causes loss of effective duty cycle and limits the maximum power of the converter at the minimum required input voltage [,]. On the other hand, the secondary side overshoot induced during the commutation of the SRs can be effectively reduced by the usage of clamping diodes between the transformer and Lr, as is suggested in [].
When using clamping diodes on the primary side of the converter part of the energy of the resonance is recovered. During the charge of Qrr and Qoss of the secondary side rectification devices an equal energy is stored in the inductances along the charging path (Lr, Llkg). It follows that the larger Lr is in relation to Llkg, the more energy it stores comparatively. Due to the action of the primary side clamping diodes, the energy in Lr is actually recirculated on the primary side of the converter and does not contribute to the secondary side commutation resonance.
The position of the clamping diodes and the external resonant inductance Lr influences the current waveforms of the converter and on the overall efficiency of the system []. The clamping diodes in the leading position notably reduces the conduction losses along all the load range of the converter (Figure 6). However, the available energy for the ZVS transition of the leading leg is heavily reduced which has a major impact on the switching losses, in the reliability and the control of the converter: the non-linearity of the output capacitance of the HV super-junction MOSFETs makes it challenging to track the optimum dead time for the leading leg, which ultimately increases the switching losses.
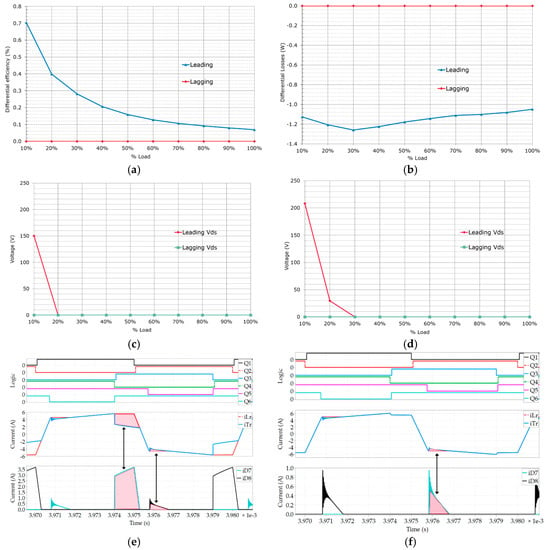
Figure 6.
Efficiency for different clamping diodes’ configuration and the effect on switching voltage of the primary side HV MOSFETs and the primary side circulating currents: (a) differential efficiencies; (b) differential losses; (c) leading and lagging leg switching voltages with the clamping diodes on the lagging leg position; (d) leading and lagging leg switching voltages with the clamping diodes on the leading leg position; (e) primary side and clamping diodes current with clamping diodes in the lagging leg; (f) primary side and clamping diodes current with clamping diodes in the leading leg.
In summary, the leading leg configuration of the clamping diodes is not recommended. In the new optimized design, the clamping diodes have been placed in the lagging leg position, as in Figure 1, whereas in the reference design the diodes were placed in the leading leg position.
3.2. Rectification Stage Configuration
Figure 7 shows a comparison between full bridge rectification and center tapped rectification configurations in low voltage server applications. Twice as many switches are required in full bridge configuration to achieve an equivalent RDS(on) because the current passes always through two devices along the rectification path. Although the figure of merit (FOM) of the lower voltage class MOSFETs is better, it is not near twice as better. Therefore, overall the switching and driving losses increase in the full bridge configuration. Moreover, the high number of rectification devices is not practical from power density and cost point of view.
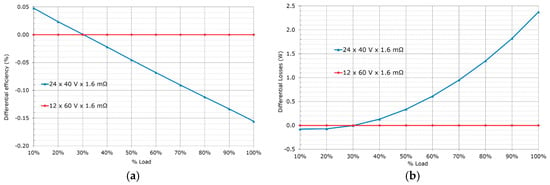
Figure 7.
Performance comparison for different rectification stage configuration of equivalent RDS(on). Full bridge rectification with 24 units of 40 V class devices in blue, and the center tapped with 12 units of 60 V class devices in red. (a) Differential efficiency; (b) differential losses.
3.3. Transformer Turns Ratio Selection
In the PSFB converter, like in other isolated topologies, the blocking voltage of the secondary side devices depends on the rectification stage configuration. However, unlike other resonant topologies, the secondary reflected voltage of the transformer does not depend on the output voltage Vo and it is always necessarily higher than it. The reflected voltage is proportional to the transformer turns ratio and the input voltage, as expressed in Equation (54) where VE and VD represent the amplitude of the output voltage of the rectification stage, and NP and NS represent the primary and secondary turns of the main transformer, respectively.
In the PSFB converter the output voltage of the rectification stage is a square wave of duty cycle Deff, with the amplitude of the transformer reflecting the voltage and average value Vo (Equation (55)). Deff is necessarily less than or equal to one and, in practical converters, commonly much smaller, as the transformer turns ratio n is constrained by the input and output voltage range requirements: the converter should be capable of regulation at the minimum specified input voltage Vin,min and maximum specified output voltage Vo,max.
Wide input voltage is required, for example, during hold-up time conditions [,,]. The power supply needs to maintain its output voltage during a time period of 20 ms (Thold) after the input AC line is lost. The resulting minimum input voltage at the end of Thold depends on the power supply intermediate storage capacity Cbulk, the nominal operating voltage, the maximum power of the DC-DC converter Po,max and its efficiency ηDCDC (Equation (56)). A simple solution to hold-up is to increase the amount of intermediate storage, however this increases the cost and reduces the power density.
The wide regulation requirement makes the PSFB converter not to be operated with its maximum duty in the nominal state. The turns ratio of the transformer is constrained by Vin,min and Vo,max. Additionally, because of the time it takes for the current through the transformer to reverse polarity, part of the otherwise available duty is lost (Dloss), which further constrains the maximum possible transformer turn ratio (Equations (57)–(61)). During the remaining duty, the so-called freewheeling (Dfrew), the primary current recirculates without transferring energy to the output of the converter.
On the other hand, the realizable transformer turns ratio is constrained by its mechanical construction: the available room for the windings, the wire size, and the amount of interleaving between primary and secondary windings. A planar construction reduces the transformer leakage which impacts the secondary side overshoot and consequently the required rectifier’s voltage class. The bigger transformer capacitance in planar construction does not have a big impact on the ZVS capability but does have an impact on the EMI performance. For isolated power converters, the inter-winding capacitance of the transformer is a critical coupling path for common mode (CM) noise. The (CM) noise model of PSFB converter is analyzed in detail in [,]. However, the capacitance can be adjusted with low dielectric constant isolation between primary and secondary windings. In both of the designs analyzed in this work the transformers have a planar or semi-planar construction:
- In the reference design the primary winding of the transformer is made of 44 turns built in PCB and distributed in three sections and the secondary winding of the transformer is made of four times two plus two turns (center tapped) interleaved with the primary in four sections.
- In the new design the primary winding of the transformer is made of two times twenty-one turns of Litz wire distributed in six sections and the secondary winding of the transformer is made of four times one plus one turns interleaved with the primary in eight sections.
Figure 8 shows a comparison among the reference design turns ratio (44:2:2), the new design turns ratio (21:1:1) and some possible similar variants (24:1:1 and 18:1:1). To fulfill the input wide range requirements of the converter Lr was adjusted consequently for each of the turn ratios. From the results in Figure 8 we can extract some conclusions:
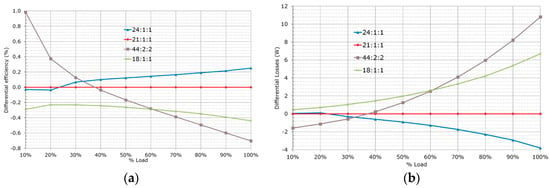
Figure 8.
Performance comparison for different transformer turns ratios. The value of Lr is adjusted to maintain the required input voltage range. The original reference converter had a turn ratio of 44:2:2. The optimized converter has a turn ratio of 21:1:1. (a) Differential efficiency of the converter with the different configurations; (b) differential power loss of the converter with the different configurations.
- More primary turns reduce the core losses of the transformers which helps to improve the light load efficiency. However, it also increases the conduction losses at mid and full load because of the extra winding length and the relatively reduced wire size.
- A larger turns ratio decreases the transformer secondary side reflected voltage, which reduces the freewheeling time and circulating currents. Potentially it could also enable a lower voltage class for the secondary side devices. However, it limits the maximum possible Lr which in turn limits the ZVS range of the lagging leg. This can be noticed by the comparison among the 24:1:1 and 21:1:1 variants, where the higher ratio performs worse at light load because of the extra switching losses.
In summary, primary side turns should be as high as possible without compromising conduction losses and turns ratio high enough to fit the best possible SRs’ voltage class. Additionally, increasing the primary winding number of turns also helps to implement a bigger magnetizing inductance Lm. Increasing the magnetizing inductance helps reduce the primary side circulating currents, reduce conduction losses and improve overall efficiency (Figure 9).
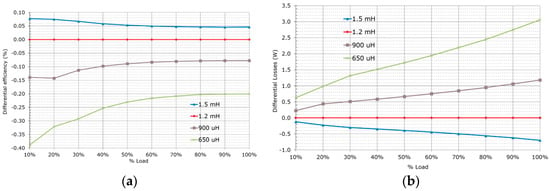
Figure 9.
Performance comparison for different magnetizing inductances: (a) differential efficiency; (b) differential losses.
On the other hand, a compromise in Lm value is required since reducing the magnetizing inductance increases the available energy for the ZVS transition of the primary side HV switches. As shown in Figure 10, this enables full ZVS for the lagging leg at very light loads.
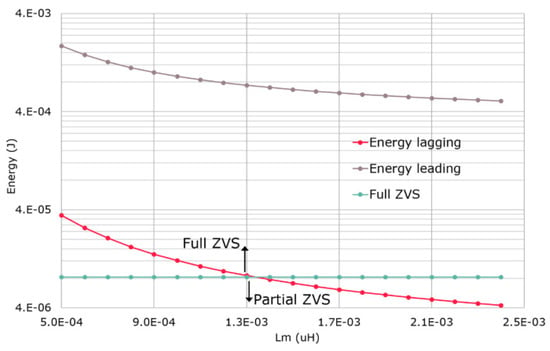
Figure 10.
Available energy for the zero-voltage-switiching (ZVS) transitions depending on the value of the magnetizing inductance with the converter operating at 10% of the load.
3.4. External Resonant Inductance and Leakage.
Figure 11 shows the impact of increasing and decreasing the external resonant inductance with the reference being the nominal Lr value of the optimized prototype. The inductance is modified by changing the gap size between the ferrite cores but keeping the same amount of turns. A larger resonant inductance decreases the conduction losses because the circulating currents are effectively reduced, however the hold-up time regulation cannot be fulfilled unless the transformer turns ratio or the amount of bulk capacitance is adjusted in consequence. Additionally, a larger Lr increases ZVS energy at light load, which potentially reduces switching losses or enables a lower HV MOSFETs RDS(on).
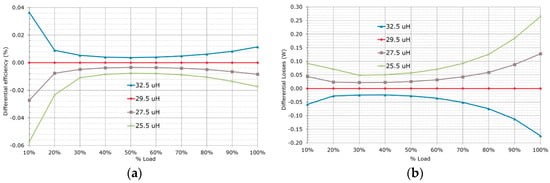
Figure 11.
Performance comparison for different external resonant inductances: (a) differential efficiency; (b) differential losses.
4. Output Filter Inductor
The output filter inductor selection is constrained by the output current ripple and the maximum output voltage ripple requirements. The output current ripple can be calculated with Equation (62), which has an impact on the rms losses in the output capacitors (Equation (63)). The maximum output voltage ripple is also a function of the total amount of output capacitance and its parasitic equivalent resistance (Equations (64)–(66)). Moreover, a small value of inductance at the output makes the secondary side rectifiers operate in DCM at light loads. When operating with SRs this can introduce additional complexity and reliability issues [].
A side effect of the Lo value is the available energy for the ZVS transitions on the primary side of the converter. In the simplified model, not considering the effect of the clamping diodes, because Ip,lead increases and Ip,lag decreases for bigger output current ripples, the ZVS range of the lagging leg is extended for larger values of Lo. However, because of the effect of the clamping diodes in the lagging position, both Ip,lead and Ip,lag increase for larger output current ripples, and the ZVS range of the lagging leg can be further extended with smaller values of Lo (Figure 12).
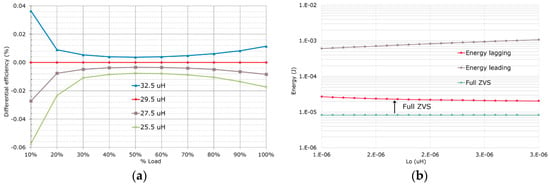
Figure 12.
Available energy for the ZVS transitions depending on the value of the output inductor Lo at 10% of the load. (a) Simplified model without clamping diodes; (b) with primary side clamping diodes in the lagging leg.
In the realization of Lo a low permeability core is preferred because it maintains a more stable value of inductance along the load and the core losses are normally lower. For a given core geometry and core material the core losses and copper losses can be balanced adjusting the number of turns and the number of parallel wires. However, the available winding room in the core limits the possible combinations. In Figure 13 we compare the effect of only changing the number of turns in the output choke of the optimized prototype design: 1.88 µH corresponds to five turns of five parallel wires of the prototype; 2.70 µH corresponds to six turns and five parallel wires; 1.20 µH corresponds to four turns and five wires; and 3.68 µH to seven turns and five wires. For the estimation of losses in Figure 13 the number of wires or their diameter has not been adjusted, but the impact on the conduction losses is already visible because of the variations in winding length.
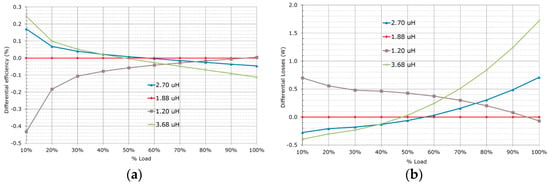
Figure 13.
Performance comparison for different numbers of turns of the output inductor: (a) differential efficiency; (b) differential losses.
4.1. Primary Dide HV MOSFETs and Secondary Side SRs LV MOSFETs
The balance of switching losses and conduction losses for the different RDS(on) allows the balance of the efficiency curve. The possible values are limited to the available portfolio of the selected MOSFET technology. Unfortunately, there have been reports of failures of the primary HV MOSFETs during load jumps, light-load operation and start-up of the converter. The failure modes are linked to the incomplete clearance of the reverse recovery charge of the intrinsic body diode followed by the turn-on of the opposite half bridge device, the so called hard-commutation. The remaining charge creates a large current at turn-on which may cause the failure of the MOSFET. To overcome this problem the use of MOSFETs with reduced Qrr and a rugged body diode has been suggested in []. Therefore, the most recommendable choice for the primary side HV MOSFETs is CoolMOS™ CFD7.
The available RDS(on) also depends on the package selection (the package itself contributes to the equivalent resistance). In the optimized prototype all semiconductors are surface mount devices (SMD). The selected RDS(on) for the final design is 140 mΩ. The resulting efficiency for a few of the available RDS(on) is compared in Figure 14. Due to the large availability of ZVS energy of the converter, 115 mΩ is performing nearly better in all load ranges. The final selection of RDS(on) is a matter of cost.
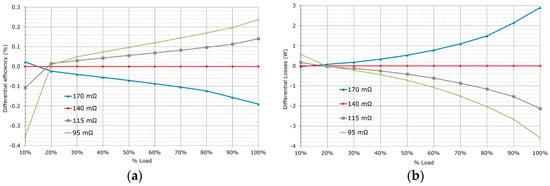
Figure 14.
Efficiency for different HV MOSFETs RDS(on): (a) differential efficiencies; (b) differential losses.
4.2. Secondary Side SRs LV MOSFETs
The voltage class selection of the SRs is key for the final performance of the system. The voltage class influences heavily on the MOSFET characteristics, frequently benchmarked by their figure of merit (FOM) []. A summary of the characteristics of two devices with similar RDS(on) in Table 2 shows the influence of the blocking voltage in their characteristic charges and forward voltage drop, which ultimately affects the switching and conduction losses. A lower voltage class is enabled by a proper design of the transformer turns ratio, a reduction in the leakage combined with a big external resonant inductance and clamping diodes []. Any additional overshoot above the nominal blocking voltage would require further increasing the maximum limits of the blocking voltage capabilities of the rectification devices; or alternatively to use clamping or snubbering mechanisms that bring additional power losses, complexity and costs [,]. Furthermore, it is a common practice in the design of switched mode power supplies (SMPS), to limit the maximum stress on the components (voltage, current, temperature) to a rated percentage of their safe maximum limits under any normal working conditions of the converter []. The rating percentage depends on the application, lifetime and reliability requirements, but 80% is a common choice. For semiconductor devices the commonly rated parameters are the maximum drain voltage and the working temperature.

Table 2.
Si LV MOSFETs.
Figure 15 shows the impact of the selection of voltage class between the former reference design, with 80 V MOSFETs, and the selection of the optimized prototype design, with 60 V devices. The losses both at light load and full load are higher, which indicates an increase in both the switching and conduction losses that cannot be balanced by RDS(on) or paralleled devices. Like for the HV MOSFETs, the selection of the SRs RDS(on) can balance the efficiency between light and full load by modifying the distribution of switching to conduction losses.
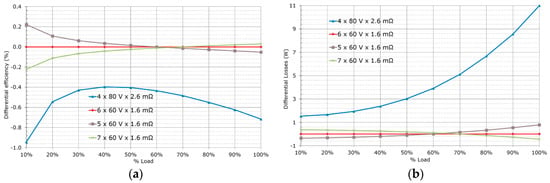
Figure 15.
Efficiency for different LV MOSFETs voltage class and number of devices: (a) differential efficiencies; (b) differential losses.
The number of paralleled devices adds another degree of freedom, at the expense of the extra cost and PCB area. Figure 15 compares the efficiency of different numbers of rectification devices, which effectively decrease the equivalent resistance of the rectification stage.
The Si-MOSFETs have been widely used to improve power density and efficiency. However, the SiC MOSFET and the GaN HEMT are promising alternatives to achieve high efficiency and high switching frequency. The advantages of wide band gap (WBG) devices are lower parasitic capacitances, lower equivalent RDS(on), zero reverse recovery charge and higher operating temperature capabilities. In [] the efficiency of 2 kW PSFB designs based on Si and SiC MOSFETs is measured and compared. In [] the efficiency improvement in a 500 W PSFB converter with GaN HEMT SRs is verified experimentally.
4.3. Input and Output Capacitance
The previous analysis demonstrates the influence of the input and output capacitances in the hold-up time operation and the output voltage ripple. However, the capacitors occupy a large volume and are costly, which will ultimately constraint their selection. Although the leakage current of the capacitors adds some losses, these losses are relatively small and in general can be dismissed.
4.4. Switching Frequency Selection. Balance of Losses
The switching frequency is a key parameter to be optimized for the converter. A specific frequency achieves its maximum efficiency only under a given set of operating conditions. In [] a variable switching frequency control method has been adopted in a PSFB DC-DC converter to improve the efficiency. This method implies wide variations in switching frequency, which makes it difficult to design, filter and control circuits, so these techniques are hard to implement in the PSFB converter.
For the two designs in this document the switching frequency was selected to be in the range of 100 kHz and all the other design variables chosen consequently. The transformer construction and the magnetics volume have the major impact in the resulting range of optimum switching frequencies for the converter, and/or vice versa. Figure 16 plots the efficiency patterns of the optimized prototype for different switching frequencies. For the point of load of interest (50%) the estimated peak efficiency is reached around the target switching frequency.
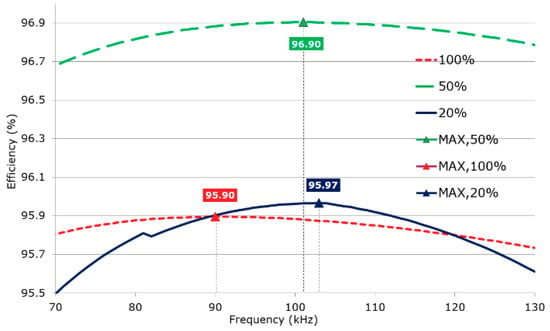
Figure 16.
Efficiency plot of the system as a function of the switching frequency. Not including fan. Keeping the wide input design maintaining a minimum freewheeling time (Lr is updated for each frequency in consequence).
Figure 16 compares the overall system efficiency along the load range only modifying the switching frequency in the optimized prototype design, which was designed for peak efficiency at 50% of the load at 100 kHz Fsw. In the estimation of efficiencies Lr was also modified to account for the different freewheeling times available when the switching frequency changes. As depicted on Figure 17 the efficiency at 100% of the load peaks at 90 kHz Fsw, like previously reported in Figure 16.
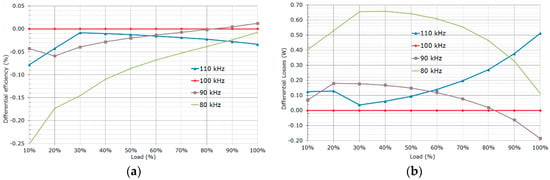
Figure 17.
Performance comparison for different switching frequencies: (a) differential efficiencies; (b) differential losses.
4.5. Thermal Management.
Although the fan consumption is normally not taken into account while measuring efficiency for the 80 PLUS certification, the temperature of the converter has a major impact on the performance. Most of the losses contributions have a positive coefficient in relation to the temperature: the RDS(on) of MOSFETs increases with temperature, as does the resistance of the metallic conductors. However, some of the losses have a negative temperature coefficient: the forward voltage drop of diodes decreases with temperature; and the core losses of some magnetic materials has a minimum at a relatively high temperature. Controlling the temperature, or the fan speed, could impact notably the efficiency along the load ranges.
4.6. Input and Output Voltage
Whereas the output voltage depends on the application and it is usually fixed to a certain value, the nominal input voltage can be adjusted taking into account the previously discussed hold-up time requirements. Moreover, other system restrictions apply: the bulk voltage has to be higher than the maximum VAC peak voltage for the PFC functionality to work (the front end is most commonly a boost converter). For the PSFB DC-DC converter the efficiency is higher for lower input voltages mostly because of the reduction in switching, core losses and magnetizing currents. For the results in Figure 18 and Figure 19 the converter design was fixed only varying the input voltage operating point and the output voltage operating point, consequently the freewheeling time and the circulating currents are also reduced.
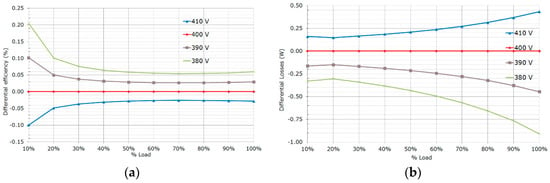
Figure 18.
Performance comparison for different nominal input voltages: (a) differential efficiency; (b) differential losses.
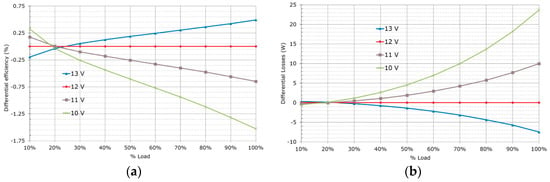
Figure 19.
Performance comparison for different nominal output voltages: (a) differential efficiency; (b) differential losses.
Increasing the output voltage operation point has a similar effect to reducing the input voltage, freewheeling time and the circulating currents. However, this is usually fixed by the application requirements. In the intended application, in server power supplies are typically 12 V.
5. Comparison of Two PSFB Converter Designs
In this section two different designs of DC-DC PSFB converters for server applications are compared. Both converters have a maximum power of 1.4 kW, the same input voltage range, nominal input voltage 400 V and 12 V output voltage. The first design serves as a reference with state-of-the-art performance levels. The second converter has been designed with the provided loss model and design criteria. The new design improves the performance of the reference design in all working conditions while also achieving a higher power density.
5.1. Summary of Specifications
For a fair comparison, both converters have the same basic requirements, summarized in Table 3, targeting the front-end DC-DC converter of a full PSU for server applications. The nominal operating voltage is 400 V, while the converters should be capable of regulation at full load down to 360 V required during hold-up time. The nominal output voltage is 12 V. During dynamic load jumps the overshoot and undershoot should fall within less than ±5% of the nominal output voltage. The load jumps are defined from 5% to 50% of the load and from 50% of the load up to 100% of the load with a di/dt of 1 A/µs.

Table 3.
Summary of converter design specifications.
5.2. Summary of Design Data
Both designs use the same HV MOSFETs technology, 600 V CoolMOS™ CFD7 from Infineon Technologies AG. The reference design mounts through-hole devices, which are capable of higher power dissipation. The optimized design mounts all semiconductor switches in the SMD. Although the power dissipation could be more challenging, an SMD solution easily achieves a higher power density with less building complexity. In the new design the RDS(on) of the HV MOSFETs is slightly reduced (Table 4 and Table 5) taking advantage of the higher amount of energy available for the ZVS transitions at light loads.

Table 4.
Primary side HV MOSFETs and synchronous rectifiers (SRs) MOSFETs in reference design.

Table 5.
Primary side HV MOSFETs and SRs MOSFETs in optimized design.
The voltage class of the secondary side rectifier MOSFETs has been improved from 80 V in the reference design down to 60 V in the new optimized design. The improved transformer construction (less leakage), improved PCB layout, bigger value of external resonant inductance together with novel control techniques ensure that the drain voltage overshoot remains well within the rated limits in all working conditions of the new converter. The better figure of merit of the 60 V technology enables the usage of lower RDS(on) and a higher number of devices without sacrificing light or medium load efficiency thanks to the comparative reduction in switching and driving losses.
The transformer turns ratio is very similar in both cases (44:2:2) and (21:1:1). The higher number of primary turns of the reference design reduces notably the core losses at light and medium loads, furthermore aided by the smaller core volume (Table 6 and Table 7). However, the high number of turns and the smaller room for the windings penalize heavily on the conduction losses at full load. The new design has a more balanced relation between core and conduction losses among light, medium and full loads. Moreover, the novel mechanical construction improves the coupling and reduces the leakage without excessive impact on the intra-winding and inter-winding capacitances thanks to the usage of an isolation with low dielectric constant.

Table 6.
Inductance values and their winding realization in reference design.

Table 7.
Inductance values and their winding realization in optimized design.
The nominal magnetizing inductance is equal in both designs, aiming to reduce the circulating currents. The external resonant inductance, however, is twice as big in the optimized design, which extends the full ZVS range for the lagging leg down to almost no load, whereas in the former reference design the lagging leg is partially hard switched up to near full load (further exacerbated by the clamping diodes position).
In the new design the output inductance value has been reduced using a core with lower permeability material but improved core losses (Table 8 and Table 9). The balance of core losses to conduction losses is also improved reducing the number of turns and increasing the wire diameter. Furthermore, the smaller output inductance provides additional energy for the lagging leg ZVS, as previously analyzed.

Table 8.
Magnetic core selection in reference design.

Table 9.
Magnetic core selection in optimized design.
The stacked magnetic structure integrated by the transformer and the external resonant inductance has a bigger core volume in the new design, which incurs in higher core losses and impacts in the light and medium load converter losses. On the other hand, there is more room for the windings which enables a larger conduction area and decreases the conduction losses at medium and full load.
6. Results
Two prototypes of PSFB converters, one of the reference design [] and one of the new optimized design [], were built and tested to compare their performance. Figure 20 shows a capture of both converters. While the reference design operates with an open frame, the new design operates within an enclosure, not shown in Figure 20 for clarity. Many of the building components among the two converters are the same and have no impact on the difference in performance: input capacitor (size and model), output capacitors (size and model, but not number), fan, auxiliary bias supply and controller. The overall dimensions of the reference designs are 150 mm × 70 mm × 44 mm, which results in a power density in the range of 3.03 W/cm3 (49.66 W/in3). The overall dimensions of the new design are 133 mm × 64.5 mm × 44 mm, which results in a power density in the range of 3.70 W/cm3 (60.78 W/in3).

Figure 20.
Prototypes of PSFB DC-DC converter for server applications: (a) original reference design; (b) optimized design.
6.1. Summary of Performance
Figure 21 shows the measure efficiency of the reference and the new design. The efficiency was notably improved in all load ranges. Table 10 is a summary of the requirements for the back-end PFC AC-DC converter, which may accompany the new PSFB design in a full PSU achieving one of the 80 PLUS certification levels (Table 1). This demonstrates the impact of the efficiency of the front-end DC-DC stage in the final efficiency of the system and/or the imposed constraints on the back-end stage by a poorly designed DC-DC. The efficiency levels for the AC-DC PFC stage listed in Table 10 for the 80 PLUS Platinum can be achieved with a classic continuous conduction mode (CCM) boost converter with passive diode bridge rectification. This confirms the suitability of the design for an 80 PLUS Platinum server PSU. However, the required PFC efficiency levels for the 80 PLUS Titanium listed in Table 10 are beyond the levels commonly achieved with classic topologies.
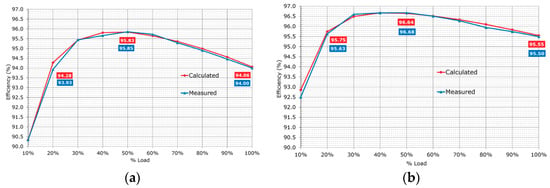
Figure 21.
Overall efficiency of the converters, including fan consumption. (a) Original reference design. (b) New optimized design.

Table 10.
Summary of efficiency requirements for back-end power factor correction (PFC) AC-DC stage.
The calculated efficiency was based on the losses model presented previously in this document which was further adjusted based on the measurements of efficiency and temperature of the different components in the converter. The losses model and its adjustment based on the measurements of the real hardware allows for estimation of the losses’ distribution of the two converters for the different load points. The estimated distribution of losses is summarized in Figure 22. From the estimations, in both designs the main losses contribution corresponds to the stacked magnetic structure integrated by the transformer and the external resonant inductance. Table 11 and Table 12 details the previous Figure 22 numerically.
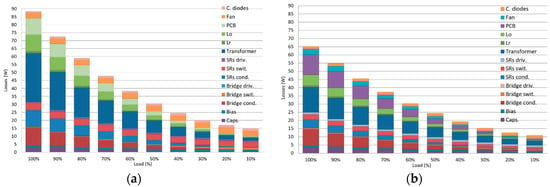
Figure 22.
Overall estimation of losses based on the loss model and the experimental results. (a) Reference design. (b) Optimized design.

Table 11.
Summary of the distribution of losses in the reference design.

Table 12.
Summary of the distribution of losses in the optimized design.
At full load, the difference in losses between the reference design and the new design is near 25 W. The extra losses make it much more difficult to cool down the converter. This is confirmed by the position of the fan in the reference design, directly blowing over the integrated magnetic structure and the SRs.
Table 13 details the difference between the component losses of the reference design and the improved design. Although in some of the losses contribution the losses actually have increased, the overall result is a general improvement in all points of the load. In Table 13 it can be observed that the main improvements come from the transformer conduction and the SRs (conduction and switching), the output inductor (conduction and core), Lr conduction, the fan and the HV bridge (conduction and switching).

Table 13.
Summary of difference of losses between the optimized and the reference designs.
6.2. Waveforms Reference Design
The steady state operation of the reference design was tested and summarized in the captures in this section.
The different energy available for the ZVS transitions of the leading and the lagging leg of the primary side bridge was already analyzed in the previous sections. Figure 23 shows captures of the leading leg drain and gate voltages at different loads. Whereas Figure 24 shows captures of the lagging leg drain and gate voltage also operating at different loads.
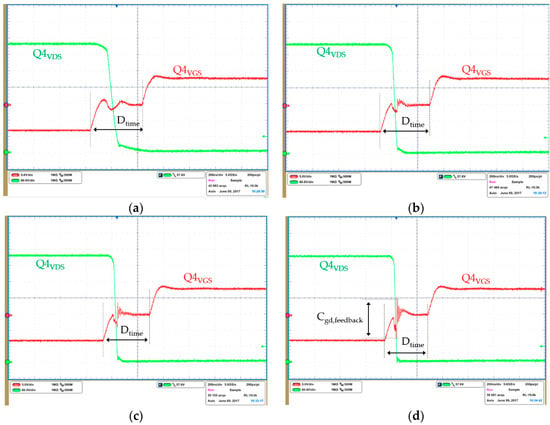
Figure 23.
Turn on switching waveforms of the low side switch of the leading leg at different loads (Io,avg). (a) 25 A; (b) 60 A; (c) 75 A; (d) 117 A.
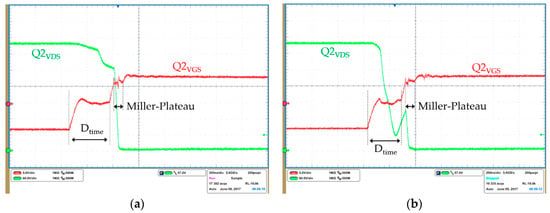
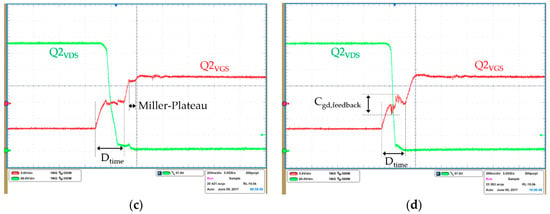
Figure 24.
Turn on switching waveforms of the low side switch of the lagging leg at different loads (Io,avg). (a) 25 A of load; (b) 60 A of load; (c) 75 A of load; (d) 117 A of load (100%).
The leading leg operates in full ZVS in all load ranges of the converter, which can be observed in the gate voltages in Figure 23, where the drain voltage is zero prior to the gate voltage rising and no Miller plateau can be observed. The full bridge is driven with an isolated pulse transformer which outputs ±Vdrive. Only during the dead time is the gate voltage zero. Certain Cgd feedback can be observed at higher loads where the dv/dt of the VDS transition increases because of the higher starting currents involved in the resonant transition.
The lagging leg achieves full ZVS only at full load (Figure 24). The main reasons for the lack of energy for the ZVS transitions are the small external resonant inductance and the position of the clamping diodes. The reference design mounts the clamping diodes in the leading leg. The clamping diodes in the leading leg reduces circulating currents and conduction losses all along the load range of the converter. However, it also reduces the current through Lr at the end of the freewheeling stage, which directly impacts the energy available for ZVS.
The lack of energy for the ZVS transitions of the leading leg increases the switching losses. Moreover, because of the non-linearity of the output capacitance of super-junction MOSFETs, the optimum dead time varies non-linearly with the load. The non-linear variation of the dead times makes it difficult to optimize the control with may further increase the switching losses. This is further aggravated by the variation of capacitances and inductances between the components in different converters.
Moreover, the fast dv/dt induced by the partial hard switching of the leading leg impacts on the secondary side overshoot at light loads. It can be observed in Figure 25 how the overshoot of the SRs is higher at the light load in the former converter, exceeding the 80% rating of the 80 V breakdown limit.
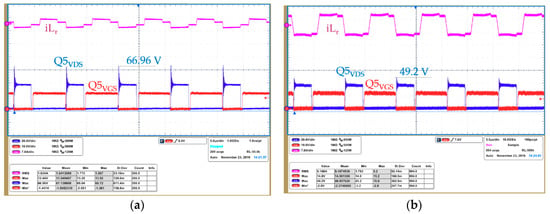
Figure 25.
SRs drain voltage overshoot: (a) Working at 140 W of output power (10% of load); (b) working at 1400 W of output power (full load).
These results corroborate the drawbacks of the clamping diodes on the leading leg position and support the recommendation of placing them in the lagging leg instead.
Figure 26 shows in more detail the secondary side overshoot of the SRs in steady state and the effect on the primary side current of the clamping diodes on the leading leg position.
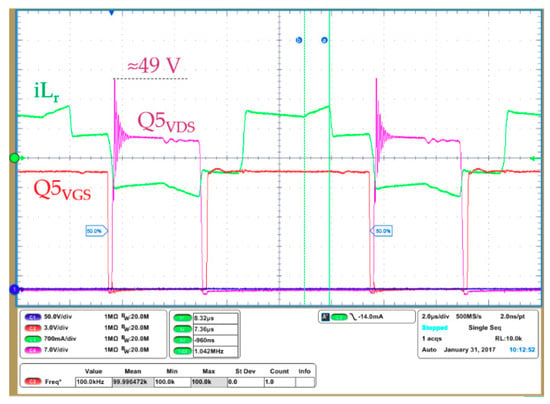
Figure 26.
Detail on the SRs overshoot and the primary side current with the clamping diodes on the leading leg position.
6.3. Waveforms of New Optimized Design
The leading leg of the new design achieves full ZVS above 20% of the load (Figure 27). Moreover, it achieves nearly full ZVS down to no load. The lagging leg, like in the reference design, also achieves full ZVS along all load ranges. However, the Cgd feedback effects on the gate voltage at full load are less noticeable thanks to the improved layout and driving scheme.
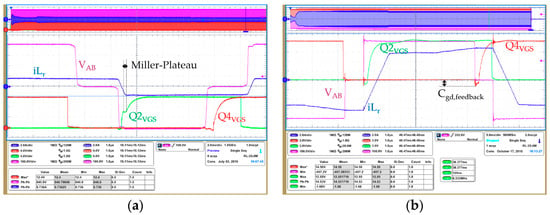
Figure 27.
Primary side HV MOSFETs ZVS: (a) ZVS at 20 A of load; (b) ZVS at full load.
The overshoot on the secondary side rectifiers is very much improved in the all load range, and well within the 80% rated limit of the 60 V breakdown voltage (Figure 28).
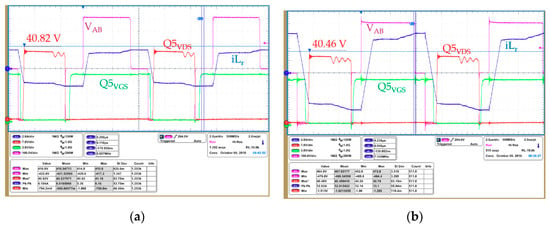
Figure 28.
SRs drain voltage overshoot: (a) Working at 140 W of output power (10% of load); (b) working at 1400 W of output power (full load).
Near no load, both the reference design and the optimized design, implement burst mode operation. The burst mode operation enables soft switching at no load operation. Figure 29 shows captures of the drain voltage overshoot on the primary side devices and the secondary side devices of the optimized converter. Also, in burst mode operation the drain and gate voltages remain well within their rated limits.
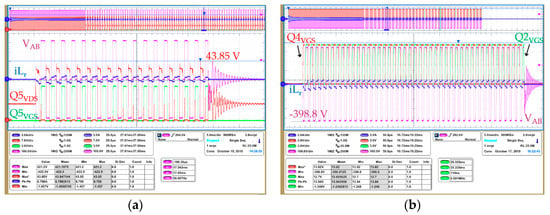
Figure 29.
SRs and HV bridge MOSFETs overshoot during burst: (a) SRs drain voltage overshoot; (b) HV bridge overshoot.
Load jumps are usually considered critic for the PSFB topology. Figure 30 shows a capture of dynamic load jumps where the reader can observe that the drain voltage of the primary and secondary switches is well within the limits.
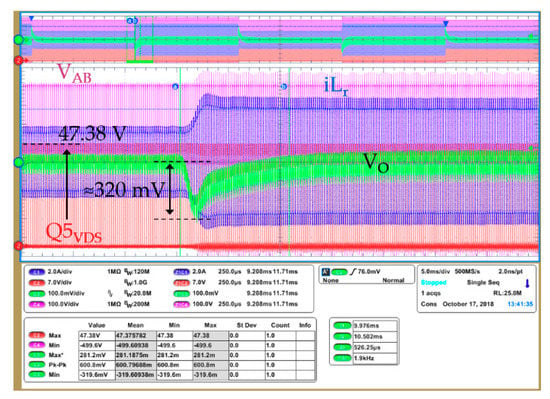
Figure 30.
SRs overshoot during load jump.
7. Conclusions
Since the server power supplies consume an enormous amount of power, the most critical issue is high efficiency. In order to implement a high efficiency and high power density server PSU, a PSFB converter with SRs MOSFETs, external resonant inductor and clamping diodes is the perfect topology for the DC-DC stage. Its main characteristic is the wide ZVS operation from mid to full load, nearly suppressing switching losses. Moreover, the constant switching frequency allows a simple control and EMI design. One of the major advantages of PSFB over other resonant soft-switching topologies is the comparatively lower rms currents through the converter thanks to the output filter inductance. However, hold-up time regulation requirements make PSFB converter not to be operated with its maximum effective duty in nominal conditions and causes a long freewheeling period.
The design of a high efficiency PSFB converter is a complex problem with many degrees of freedom which requires a sufficiently accurate modeling of the losses of the converter and of efficient design criteria. In this work a losses model of the converter has been proposed as well as design guidelines for the efficiency optimization of the PSFB converter. The losses model and the criteria have been tested with the redesign of an existing reference PSFB DC-DC converter for server applications that achieved 95.85% of efficiency at 50% of the load. The new converter was designed following the same specifications as the reference: 1400 W of maximum power; 400 V nominal input voltage; hold-up regulation down to 360 V input voltage; and 12 V output. The new optimized prototype of the PSFB converter was built and tested achieving a peak efficiency of 96.68% at 50% of the load, notably exceeding the performance of the reference converter in all load ranges and operating conditions.
The main differences between both designs are related to the magnetics construction, with an improved balance of core and conduction losses along the load range of the converter. Furthermore, the transformer turns ratio and the dimensioning of the external resonant inductance enabled lower RDS(on) in the primary side HV devices and lower voltage class (and consequently also lower RDS(on)) in the secondary side LV devices. Moreover, all semiconductors in the new optimized design are SMD, which together with the high efficiency at full load enables a power density in the range of 3.70 W/cm3 (60.78 W/in3).
In summary, the key of an efficient and reliable DC-DC PSFB converter in this power range and output voltage is in the magnetics design, more specifically the transformer and the external resonant inductance. This demonstrates that the PSFB converter is a relatively simple and efficient topology for DC-DC converter applications at the level of fully resonant topologies.
Author Contributions
Conceptualization, M.E., M.-A.K. and D.M.; supervision, N.R. and D.P.M.; validation, M.E.; writing—original draft, M.E.; writing—review, discussion and editing, M.-A.K., D.M., N.R. and D.P.M.
Funding
This research was financed by Infineon Technologies AG.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Emami, Z.; Nikpendar, M.; Shafiei, N.; Motahari, S.R. Leading and lagging legs power loss analysis in ZVS Phase-Shift Full Bridge converter. In Proceedings of the 2011 2nd Power Electronics, Drive Systems and Technologies Conference, Tehran, Iran, 16–17 February 2011; pp. 632–637. [Google Scholar] [CrossRef]
- Climate Savers Computing Initiative (CSCI). Available online: http://www.climatesaverscomputing.org (accessed on 28 August 2019).
- 80Plus Program. Available online: http://www.plugloadsolutions.com (accessed on 28 August 2019).
- Kim, D.; Kim, C.; Moon, G. A new control method in Phase-Shifted Full-bridge converter for reduced power consumption under light load conditions. In Proceedings of the IECON 2012—38th Annual Conference on IEEE Industrial Electronics Society, Montreal, QC, Canada, 25–28 October 2012; pp. 86–91. [Google Scholar] [CrossRef]
- Jeong, Y.; Kim, J.; Lim, C.; Kim, D.; Baek, J.; Moon, G. A strategic control scheme of phase-shift full bridge converter for improving light-load efficiency in server power system. In Proceedings of the 2015 9th International Conference on Power Electronics and ECCE Asia (ICPE-ECCE Asia), Seoul, Korea, 1–5 June 2015; pp. 488–494. [Google Scholar] [CrossRef]
- Kim, C. Optimal Dead-time Control Scheme for Extended ZVS Range and Burst-mode Operation of Phase-Shift Full-Bridge (PSFB) Converter at Very Light Load. IEEE Trans. Power Electron. 2019, 34, 10823–10832. [Google Scholar] [CrossRef]
- Kolar, J.W.; Drofenik, U.; Biela, J.; Heldwein, M.L.; Ertl, H.; Friedli, T.; Round, S. PWM Converter Power Density Barriers. In Proceedings of the 2007 Power Conversion Conference-Nagoya, Nagoya, Japan, 2–5 April 2007; pp. 9–29. [Google Scholar] [CrossRef]
- Kathiresan, R.; Parthiban, T.; Das, P.; Pahlevaninezhad, M. Analysis of a ZVS DC-DC full-bridge converter with natural hold-up time. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 1521–1527. [Google Scholar] [CrossRef]
- Badstuebner, U.; Biela, J.; Faessler, B.; Hoesli, D.; Kolar, J.W. An Optimized 5 kW, 147 W/in3 Telecom Phase-Shift DC-DC Converter with Magnetically Integrated Current Doubler. In Proceedings of the 2009 Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington, DC, USA, 15–19 February 2009; pp. 21–27. [Google Scholar] [CrossRef]
- Cao, Q.; Li, Z.; Wang, H. Wide Voltage Gain Range LLC DC/DC Topologies: State-of-the-Art. In Proceedings of the 2018 International Power Electronics Conference (ECCE Asia), Niigata, Japan, 20–24 May 2018; pp. 100–107. [Google Scholar]
- Yang, B.; Lee, F.C.; Zhang, A.J.; Huang, G. LLC resonant converter for front end DC/DC conversion. In Proceedings of the APEC. Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 10–14 March 2002; Volume 2, pp. 1108–1112. [Google Scholar] [CrossRef]
- Castro, I.; Roig, J.; Gelagaev, R.; Vlachakis, B.; Bauwens, F.; Lamar, D.G.; Driesen, J. Analytical Switching Loss Model for Superjunction MOSFET with Capacitive Nonlinearities and Displacement Currents for DC–DC Power Converters. IEEE Trans. Power Electron. 2016, 31, 2485–2495. [Google Scholar] [CrossRef]
- Badstuebner, U.; Biela, J.; Kolar, J.W. Design of an 99%-efficient, 5kW, phase-shift PWM DC-DC converter for telecom applications. In Proceedings of the 2010 Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; pp. 773–780. [Google Scholar] [CrossRef]
- Cho, I.; Cho, K.; Kim, J.; Moon, G. A New Phase-Shifted Full-Bridge Converter with Maximum Duty Operation for Server Power System. IEEE Trans. Power Electron. 2011, 26, 3491–3500. [Google Scholar] [CrossRef]
- Zhao, L.; Li, H.; Liu, Y.; Li, Z. High Efficiency Variable-Frequency Full-Bridge Converter with a Load Adaptive Control Method Based on the Loss Model. Energies 2015, 8, 2647–2673. [Google Scholar] [CrossRef]
- Yin, L.; Chen, Q.; Peng, B.; Wang, J.; Ruan, X. Key Issues of Clamping Diodes in DCM Phase-Shift Full-Bridge Converter. In Proceedings of the 2007 IEEE Power Electronics Specialists Conference, Orlando, FL, USA, 17–21 June 2007; pp. 1721–1725. [Google Scholar] [CrossRef]
- Ruan, X. Soft-Switching PWM Full-Bridge Converters, 1st ed.; John Wiley & Sons Singapore Pte. Ltd.: Singapore, 2014; pp. 1–66, 121–147, 181–198. [Google Scholar]
- Phung, A.; Meunier, G.; Chadebec, O.; Margueron, X.; Keradec, J. High-Frequency Proximity Losses Determination for Rectangular Cross-Section Conductors. IEEE Trans. Magn. 2007, 43, 1213–1216. [Google Scholar] [CrossRef]
- Finite Element Method Magnetics: HomePage. Available online: http://www.femm.info/wiki/HomePage (accessed on 10 September 2019).
- Krismer, F.; Biela, J.; Kolar, J.W. A comparative evaluation of isolated bi-directional DC/DC converters with wide input and output voltage range. In Proceedings of the Fourtieth IAS Annual Meeting. Conference Record of the 2005 Industry Applications Conference, Hong Kong, China, 2–6 October 2005; Volume 1, pp. 599–606. [Google Scholar] [CrossRef]
- Yoo, J.; Joo, D.; Kim, H.; Kim, J. Implementation of a phase shift full-bridge converter for LDC using GaN HEMT. In Proceedings of the 2017 20th International Conference on Electrical Machines and Systems (ICEMS), Sydney, NSW, Australia, 11–14 August 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Zeljkovic, S.; Reiter, T.; Gerling, D. Analysis of rectifier topologies for automotive HV to LV phase shift ZVT DC/DC converter. In Proceedings of the 2012 15th International Power Electronics and Motion Control Conference (EPE/PEMC), Novi Sad, Serbia, 4–6 September 2012; pp. DS1b.4-1–DS1b.4-7. [Google Scholar] [CrossRef]
- Alou, P.; Oliver, J.A.; Garcia, O.; Prieto, R.; Cobos, J.A. Comparison of current doubler rectifier and center tapped rectifier for low voltage applications. In Proceedings of the Twenty-First Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 19–23 March 2006. [Google Scholar] [CrossRef]
- Roig, J.; Bauwens, F. Origin of Anomalous Coss Hysteresis in Resonant Converters with Superjunction FETs. IEEE Trans. Electr. Devices 2015, 62, 3092–3094. [Google Scholar] [CrossRef]
- Badstuebner, U.; Biela, J.; Kolar, J.W. An optimized, 99% efficient, 5 kW, phase-shift PWM DC-DC converter for data centers and telecom applications. In Proceedings of the 2010 International Power Electronics Conference (ECCE ASIA), Sapporo, Japan, 21–24 June 2010; pp. 626–634. [Google Scholar] [CrossRef]
- Kasper, M.; Burkart, R.M.; Deboy, G.; Kolar, J.W. ZVS of Power MOSFETs Revisited. IEEE Trans. Power Electron. 2016, 31, 8063–8067. [Google Scholar] [CrossRef]
- Chen, Q.; Yin, L.; Wang, J.; Peng, B.; Wong, S.C.; Ruan, X.; Chen, X. Phase-shifted full-bridge PWM converter with clamping diodes and current transformer. In Proceedings of the 2008 IEEE Power Electronics Specialists Conference, Rhodes, Greece, 15–19 June 2008; pp. 2403–2409. [Google Scholar] [CrossRef]
- Ruan, X.; Liu, F. An Improved ZVS PWM Full-bridge Converter with Clamping Diodes. In Proceedings of the 2004 35th Annual IEEE Power Electronics Specialists Conference, Aachen, Germany, 20–25 June 2004; Volume 2, pp. 1476–1481. [Google Scholar] [CrossRef]
- Escudero, M.; Kutschak, M.; Meneses, D.; Rodriguez, N.; Morales, D.P. Synchronous rectifiers drain voltaje overshoot reduction in PSFB converters. IEEE Trans. Power Electron. 2019. manuscript submitted for publication. [Google Scholar]
- Paul, S.; Schlaffer, A.M.; Nossek, J.A. Optimal charging of capacitors. IEEE Trans. Circuits Syst. I: Fundam. Theory Appl. 2000, 47, 1009–1016. [Google Scholar] [CrossRef]
- Perrin, Y.; Galisultanov, A.; Fanet, H.; Pillonnet, G. Optimal Charging of Nonlinear Capacitors. IEEE Trans. Power Electron. 2019, 34, 5023–5026. [Google Scholar] [CrossRef]
- MOßlacher, C.; Guillemant, O.; Management, P. Multimarket. Improving Efficiency of Synchronous Rectification by Analysis of the Mosfet Power Loss Mechanism. In Proceedings of the International Exhibition & Conference for Power Electronics, Intelligent Motion, Power Quality (PCIM 2009), Nürnberg, Germany, 12–14 May 2009. [Google Scholar]
- Mao, H.; Abu-Qahouq, J.A.; Qiu, W.; Wen, Y.; Batarseh, I. Lossless snubber circuits for current doubler rectifiers to reduce reverse-recovery losses. In Proceedings of the 29th Annual Conference of the IEEE Industrial Electronics Society, Roanoke, VA, USA, 2–6 November 2003; Volume 3, pp. 2639–2644. [Google Scholar] [CrossRef]
- Muhlethaler, J.; Biela, J.; Kolar, J.W.; Ecklebe, A. Improved Core-Loss Calculation for Magnetic Components Employed in Power Electronic Systems. IEEE Trans. Power Electron. 2012, 27, 964–973. [Google Scholar] [CrossRef]
- Mao, S.; Popovic, J.; Ramabhadran, R.; Ferreira, J.A. Comparative study of half-bridge LCC and LLC resonant DC-DC converters for ultra-wide output power range applications. In Proceedings of the 2015 17th European Conference on Power Electronics and Applications (EPE’15 ECCE-Europe), Geneva, Switzerland, 8–10 September 2015; pp. 1–10. [Google Scholar] [CrossRef]
- Xie, L.; Ruan, X.; Ye, Z. Modeling of common-mode noise in phase-shift full-bridge converter. In Proceedings of the IECON 2016—42nd Annual Conference of the IEEE Industrial Electronics Society, Florence, Italy, 24–27 October 2016; pp. 1371–1375. [Google Scholar] [CrossRef]
- Makda, I.A.; Nymand, M. Common-mode noise analysis, modeling and filter design for a phase-shifted full-bridge forward converter. In Proceedings of the 2015 IEEE 11th International Conference on Power Electronics and Drive Systems, Sydney, NSW, Australia, 9–12 June 2015; pp. 1100–1105. [Google Scholar] [CrossRef]
- Deboy, G.; Hancock, J.; Purschel, M.; Wahl, U.; Willmeroth, A. Compensation devices solve failure mode of the phase shift ZVS bridge during light-load operation. In Proceedings of the APEC. Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 10–14 March 2002; Volume 2, pp. 988–993. [Google Scholar] [CrossRef]
- Wang, H.; Wang, F.; Zhang, J. Power Semiconductor Device Figure of Merit for High-Power-Density Converter Design Applications. IEEE Trans. Electron Devices 2008, 55, 466–470. [Google Scholar] [CrossRef]
- IPC. Performance Parameters for Power Conversion Devices; final draft; IPC—Association Connecting Electronics Industries: Bannockburn, Illinois, USA, 2007. [Google Scholar] [CrossRef]
- Haihong, Q.; Kefeng, X.; Xin, N.; Ziyue, Z.; Zhiyuan, Z.; Dafeng, F. Characteristics of SiC MOSFET and its application in a phase-shift full-bridge converter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; pp. 1639–1643. [Google Scholar] [CrossRef]
- Di Domenico, F.; Schmölzer, B.; Escudero, M.; Raghunath, S. 1400 W ZVS Phase Shift Full Bridge Evaluation Board. Available online: https://www.infineon.com/cms/de/product/evaluation-boards/eval_1k4w_zvs_fb_cfd7 (accessed on 10 September 2019).
- Kutschak, M.; Escudero, M. 1400 W 12 V Phase-Shift Full-Bridge with 600 V CoolMOS™ CFD7 and XMC™. Available online: https://www.infineon.com/cms/de/product/evaluation-boards/eval_1k4w_zvs_fb_smd (accessed on 10 September 2019).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).