1. Introduction
The integration of renewable energy sources is normally assisted by power electronic converters due to its ability for asynchronous connection and fully-AC voltage control. The high demand for renewable energies requires more and more inverters to be connected to the grid. The interaction between the grid-connected inverter and the grid may cause instabilities [
1]. The stability analysis for the grid-connected inverter is essential to ensure secure power transportation to the grid.
Two stability analysis methods can be applied according to the small-signal linearization technology. The state-space stability analysis [
2] is a mature and commonly-used method. However, a high order and a complex state matrix have to be built. Impedance stability analysis is achieved via the impedance ratio, which is determined via the equivalent impedance of the inverter and the grid impedance. The impedance ratio can also be drawn as the Bode plot for the frequency analysis. Both Norton-based [
3] and Thevenin-based [
4] equivalent impedances of the inverter can be derived in the impedance stability analysis.
For a three-phase inverter controlled via the dq frame, the impedance ratio is normally derived in the dq frame, which is a
matrix. Both eigenvalues of the impedance-ratio matrix are required for the stability analysis via the generalized Nyquist criterion (GNC) [
5]. The criterion is commonly used in the grid-connected inverter system to identify the negative impact on the stability, such as increasing the cut-off frequency of the phase-locked loop (PLL) [
6] and current control loop [
7], increasing power injection from the inverter and grid impedance [
8]. For a grid-connected current control inverter, only the q-axis is used for the PLL to synchronize the dq frame. Therefore, its impedance-ratio matrix is a coupled asymmetrical matrix, whose eigenvalues are difficult to derive. Couplings are normally ignored to simplify the eigenvalue derivation during the impedance stability analysis [
8,
9]. To achieving an accurate impedance stability analysis based on GNC, the impedance-ratio matrix is transferred into the stationary frame in order to decouple the matrix [
10]. However, it is found that couplings still exist because the impedance-ratio matrix is asymmetrical [
11].
The determinant, rather than both eigenvalues of the impedance-ratio matrix, which is derived simply for including couplings, was used for the three-phase rectifier’s stability analysis [
12,
13] in the 1990s. Recently, the impedance stability analysis based on the determinant was applied for the inverter system [
14,
15]. Only the determinant, rather than two eigenvalues, is figured as one pole map or one Nyquist plot for the stability analysis, which simplifies the analysis process. Another method for including couplings is to convert the multi-input and multi-output dq impedance into its sequence domain single-input and single-output equivalents [
16]. Then, the Nyquist criterion, rather than the generalized Nyquist criterion, can be applied.
In this paper, the coupling influence on the dq impedance stability analysis is studied. The question about whether ignoring couplings causes unacceptable analysis errors will be answered. Analysis errors are defined and quantified to assist the study of the coupling influence. The dq impedance stability analysis based on the determinant rather than eigenvalues is used to include the couplings easily and present the accurate analysis results. The mechanism by which the stability of the inverter system is determined only by the determinant of the impedance-ratio matrix will be unveiled. The dq impedance stability analysis results will be validated in the time-domain simulation. The state-space stability analysis will be used as the benchmark to validate the accuracy of the determinant-based impedance stability analysis.
This paper is organized as follows: In
Section 2, the dq impedance stability analysis is introduced. The equivalent dq impedance of the inverter is derived in
Section 3. The simulation verification and the coupling influence are shown in
Section 4.
2. dq Impedance Stability Analysis
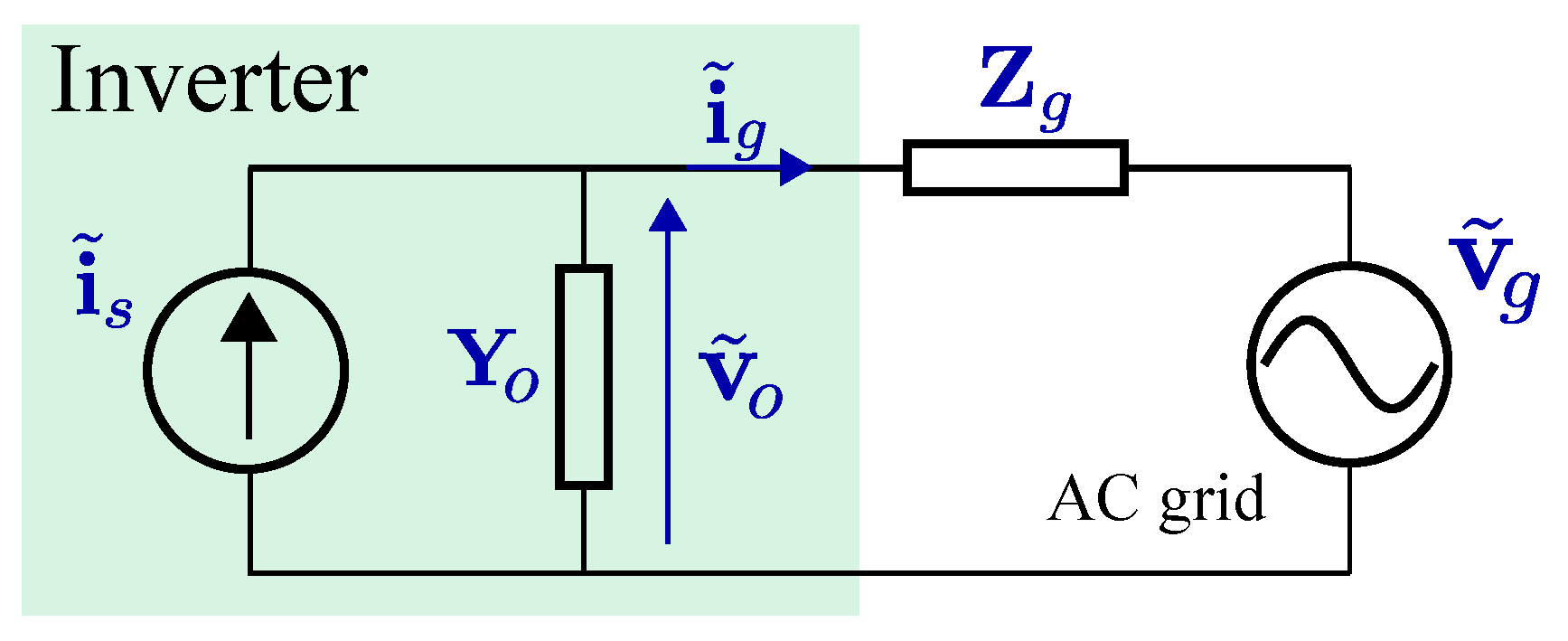
Grid-connected inverters are normally controlled in the dq frame as a current source. Therefore, its small-signal model is built according to the Norton law [
3], as shown in
Figure 1. A list of variables, which are shown in
Figure 1, is explained below:
: reference deviation of the control system
: output voltage deviation
: feeding current deviation from the inverter
: grid impedance
: grid voltage deviation
: equivalent inverter admittance
the bold variables stand for its d-q matrix such as .
The frequently-used notations are summarized below:
d,q: d-axis and q-axis parameters
dd, dq, qd, qq: the postion of each element in the matrix
rt: ratio matrix
u,l: upper and lower parameters
From the inverter side, the relation between
and
is derived as:
From the grid side, the relation between
and
is derived as:
Substituting
in (
2) with (
1) yields:
Rearranging (
3) for
yields:
where the impedance-ratio matrix is
.
It is reported [
3] that the system stability is determined by the impedance-ratio matrix
based on (
4).
2.1. dq Impedance Stability Analysis via Eigenvalues
Based on the generalized Nyquist criterion, both eigenvalues of the impedance-ratio matrix need to be drawn as Nyquist plots for the stability analysis [
8].
Each element of the impedance-ratio matrix is presented below:
where notation dd, dq, qd, and qqmeans the postion of each element in the matrix, rt means the ratio matrix, and
are couplings.
The eigenvalues
of the matrix are calculated as:
The transfer functions of the eigenvalues are found by rearranging the equation above:
It is difficult to do the square root of
in (
7), as each element of the impedance-ratio matrix is a complicated transfer function in the s domain. If the couplings
are ignored, eigenvalues are therefore simplified and calculated below based on (
7):
The ignoration removes the coupling influence on the system stability analysis. The stability analysis will be more accurate if the couplings are considered.
2.2. dq Impedance Stability Analysis via the Determinant
It was found that the determinant of the impedance-ratio matrix is the key factor that determines the system stability. Couplings of the impedance-ratio matrix are contained in the determinant; thus, their influences on the stability are all accounted for. The Nyquist plot or the pole map as the stability analysis tool can be drawn via the determinant to check the right-plane poles. The mechanism of the determinant as the key factor for the stability analysis is shown below.
The impedance-ratio matrix can be reconstructed as two parts: an adjacent matrix and a determinant as shown below:
The adjacent matrix is calculated based on (
5):
Each element of
and
is rewritten as the form such as
, where the numerator
stands for all its zeros and the denominator
stands for all its poles as shown below:
where
n and
m are the number of zeros and poles, respectively.
The equivalent admittance
of the inverter and the impedance
of the grid can be presented as below:
One element of
such as
will be calculated based on (
10), (
13), and (
14):
All poles of
can be derived from (
15):
The equivalent admittance
of the inverter has no right-plane poles ([
3]), neither the grid impedance
. Therefore, no right-plane poles exist in
,
,
, and
. It can be identified via (
16) that
has no right-plane poles. Following the same way, the other elements of
have no right-plane poles.
It can be concluded finally via the identification above and (
9) that the system stability is determined only by the determinant
of the impedance-ratio matrix. For the stability analysis, one Nyquist plot or one pole map can be used based on the determinant for the stability analysis by checking the right-plane poles.
3. Small Signal Impedance of a Current-Controlled Inverter
Before validating the accuracy of the determinant-based stability analysis,
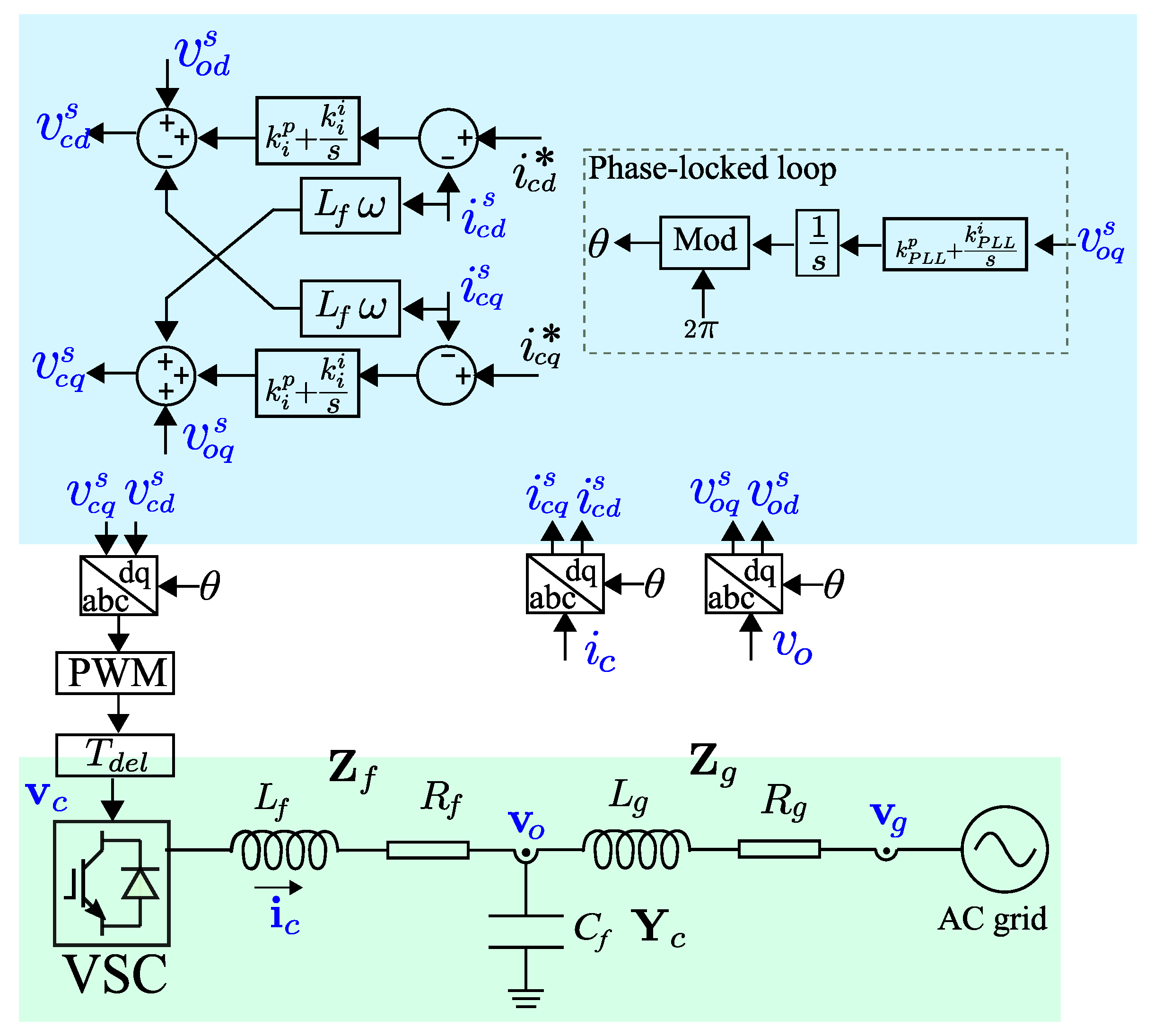
of the grid-connected inverter will be derived in this section. The grid-connected inverter is usually controlled in the dq frame as a current source, and the frame is synchronized via a PLL, as shown in
Figure 2. The abc-dq transformation in terms of the PLL is linearized first, and the impedance derivation is followed. The variables are shown in
Figure 2 and are listed and explained below to help define the equations.
: time delay from the control and pulse width modulation (PWM) dead time.
: synchronized phase from PLL.
: inverter voltage
: inverter current
: output voltage
: inverter voltage after abc-dq transform
: inverter current after abc-dq transform
: output voltage after abc-dq transform,
: PI controller for the current loop.
: PI controller for PLL.
: impedance of LC filter.
: admittance of LC filter.
3.1. Linearization of the abc-dq Transformation
It is convenient to derive the impedance of the inverter in the dq frame due to the applied dq control. The three-phase abc system is therefore presented as the dq form in the derivation. Theses dq-presented abc parameters ( ) are equal to their dq parameters ( ) after the abc-dq transformation at steady state, but are different when a synchronized phase error is applied at the transformation.
Their relations that take
as an example are summarized below via the small-signal modelling:
where
and
are the corresponding steady state values.
Equation (
17) can be linearized as below due to the small value of
,
and
are equal at steady state, and (
18) is therefore simplified as:
Following the same way, the relationship between
and
is derived:
Considering the dq-abc transformation for the dq-presented inverter voltage
, this yields:
3.2. Small-Signal Model of the Phase-Locked Loop
The synchronized-phase error as the output of the phase-locked loop is generated by its input
. Their relation is summarized as below according to the control diagram
Figure 2:
where
. Notation PLL stands for phase-locked loop; notation p and i are the proportion parameter and the integration parameter of the PI controller, respectively.
Substituting
in (
22) with (
19) yields:
Substituting
in (
19)–(
21) with (
23) yields:
Equations (
24)–(
26) present the fully-linearized relation between the dq parameters and the dq-presented abc parameters.
3.3. Inverter Admittance Derivation
After the linearization, the current control, LC filter, and grid impedance will be accounted for in the derivation for the final admittance of the inverter. The current control is presented below according to
Figure 2:
where
,
.
Substituting
,
in (
27) with (
24) and (
25) yields:
Substituting
in (
26) with (
28) and taking the time
including control delay and the dead time of PWM into account yields:
where
can be presented as the crossing voltage over
:
Substituting
in (
29) with (
30) and rearranging yield:
Rewriting (
31) yields:
where
,
Considering the influence of the capacitor of the LC filter yields:
Substituting
in (
32) with (
33) yields:
It is found based on (
1) that
is
, and
is
. Therefore,
has been derived based on the above equations, and the dq impedance stability analysis based on the determinant can be applied.
3.4. Comparison between Determinant-Based Impedance Stability Analysis and State-Space Stability Analysis
It is essential to validate the accuracy of the determinant-based impedance stability analysis. Therefore, the state-space stability analysis, as a benchmark of the stability analysis [
2], is used for the validation. The derivation for the state-space stability analysis is shown in the
Appendix A. The grid-connected current-controlled inverter system for the stability analysis is shown in
Figure 2, and its parameters are shown in
Table 1. The inductors and resistors of the AC transformer (
) and the transmission line (SCR) are noted as
and
in
Figure 2.
The pole map is used for the comparison between both stability analyses because it shows the pole position and pole locus in detail and simply. For the determinant-based impedance stability analysis, all the poles of the determinant based on (
9) are drawn in the pole map.
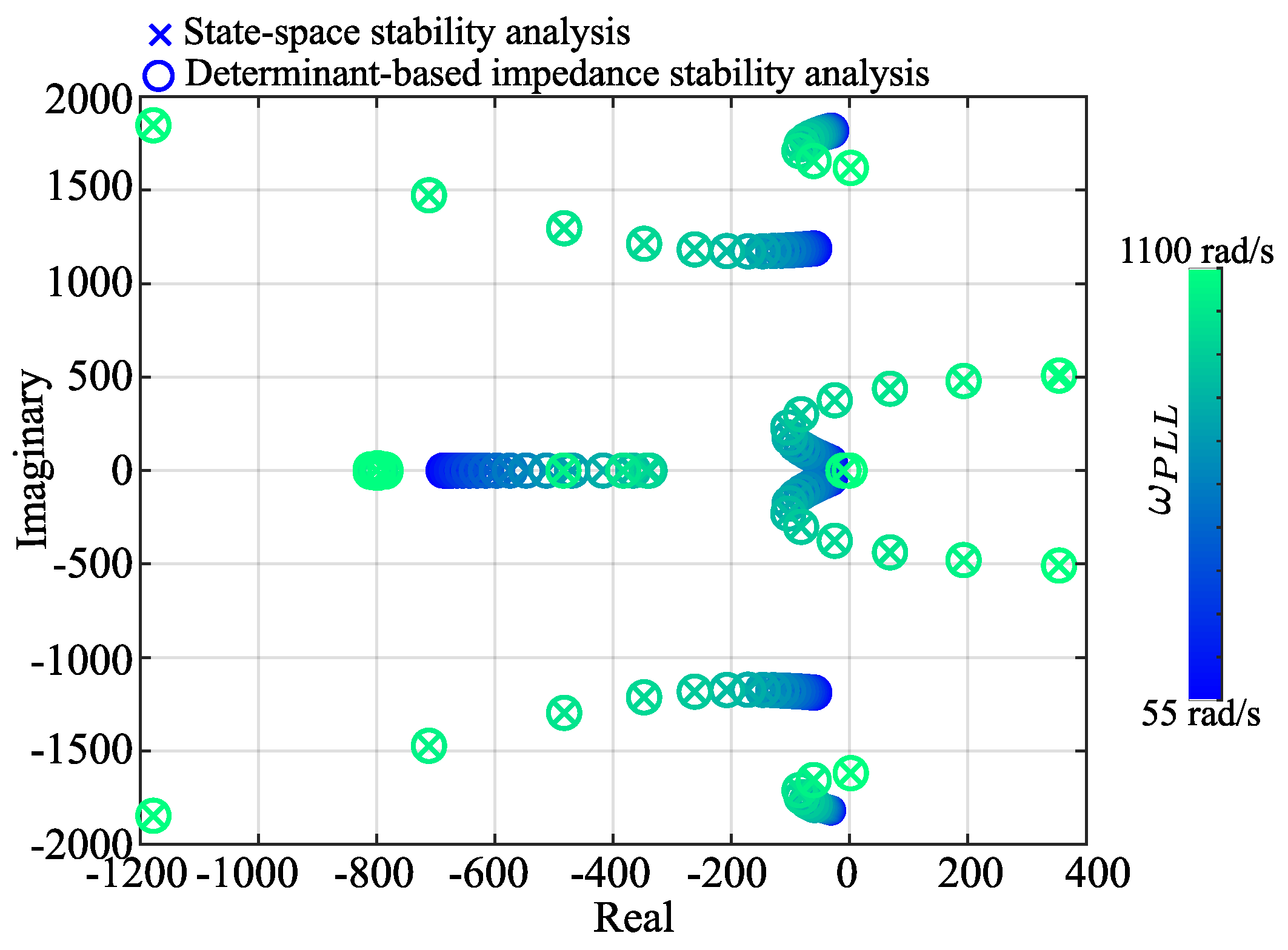
The pole locus of both stability analyses are drawn in
Figure 3 by changing the cut-off frequency of PLL (
) from 55 rad/s to 1100 rad/s. As shown in
Figure 3, the pole locus and each pole of both stability analyses are precisely matched. The same stability analysis result based on their pole locus is found, that increasing
leads the poles towards to the right-half plane and causes the low stability or instability of the inverter system. It is concluded that both stability analyses have the same accuracy.
4. Coupling Influence on the dq Impedance Stability Analysis
As mentioned in
Section 2, the couplings of the impedance-ratio matrix in the eigenvalue-based impedance stability analysis are difficult to include. If the couplings are ignored, the dq impedance stability analysis will lose accuracy. To consider the couplings, the determinant-based dq impedance stability analysis is used. Three cases below are presented to show the influence of the couplings on the stability analysis.
Ignoring couplings causes the error of the stability analysis via the time-domain simulation;
The influence of the couplings on the pole locus;
The error quantification for the coupling influence on the stability analysis.
The inverter system as shown in
Figure 2 is used for the stability analysis, and its parameters are shown in
Table 1. Time-domain simulation of the grid-connected current-controlled inverter system was built in MATLAB/Simulink. The pole map was used to show the stability analysis results.
4.1. Time-Domain Validation
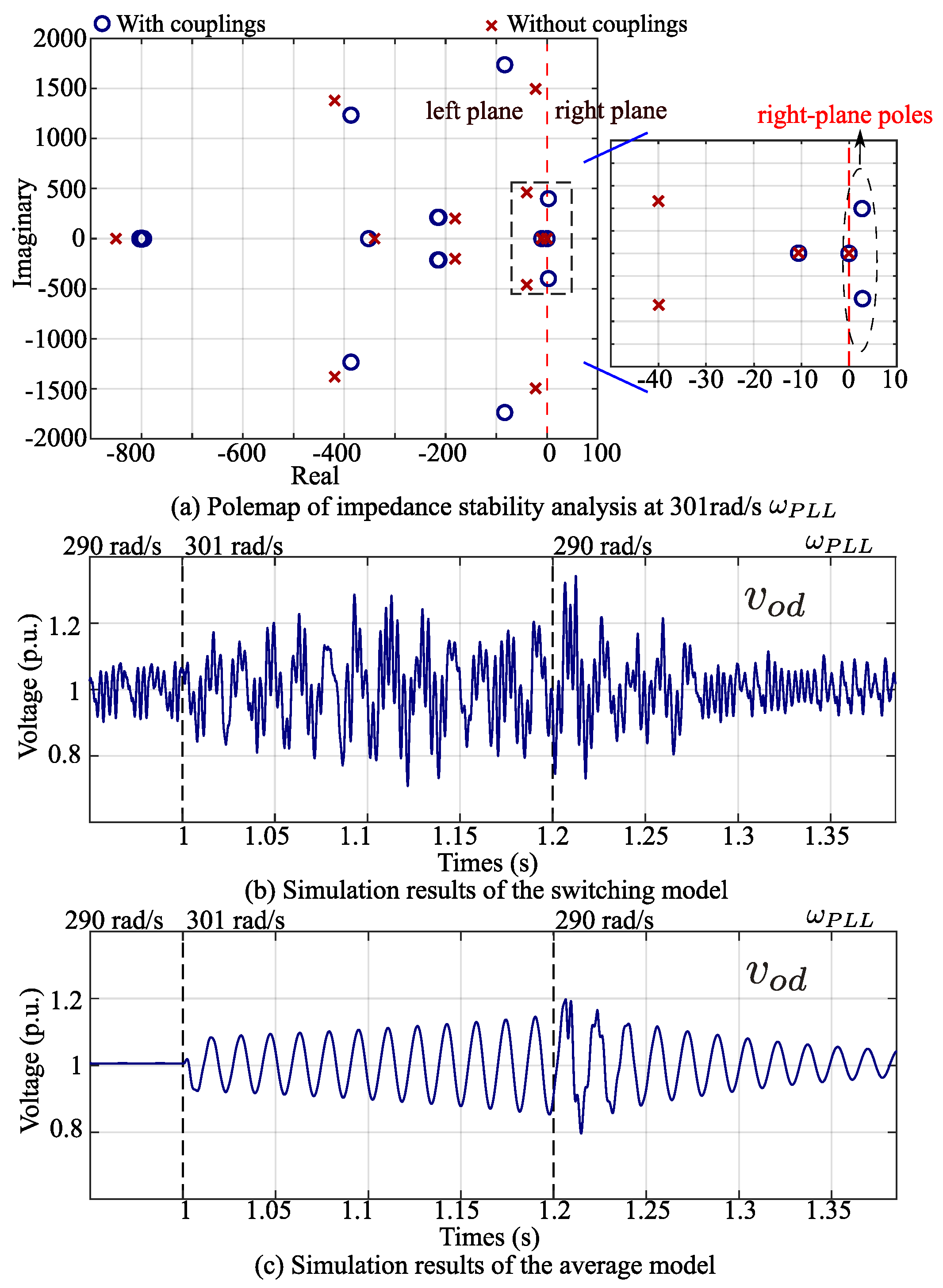
Based on the determinant-based dq impedance stability analysis, the analysis results with considering couplings or without considering couplings are shown as the pole map in
Figure 4a under the 301-rad/s cut-off frequency of the PLL. The right-plane poles appear when the couplings are considered. On the contrary, if the couplings were ignored, the analysis shows that the system was stable because all its poles still stayed in the left plane. The stability analysis results of both impedance stability analyses were mismatched.
The time-domain simulation of the grid-connected current-controlled inverter system was built in MATLAB/Simulink to validate the results from the stability analysis. The d-axis output voltage was used to show the system state. The average model of the two-level VSCs was also added to show clearly that the system was unstable or became stable gradually without the disturbances of the harmonics.
As shown in
Figure 4b,c, when the
was increased from 290 rad/s to 301 rad/s at 1 s,
started to oscillate, and its magnitude increased gradually. It shows that the system was unstable at a 301-rad/s PLL cut-off frequency. At 1.2 s, the system was back to the stable condition as
was changed back to 290 rad/s.
The time-domain simulation result at 301 rad/s
matched the analysis result with the couplings, as shown in
Figure 4a. Ignoring couplings failed to identify the instability. It proved that ignoring the couplings caused errors in the stability analysis.
4.2. Pole Locus Comparison
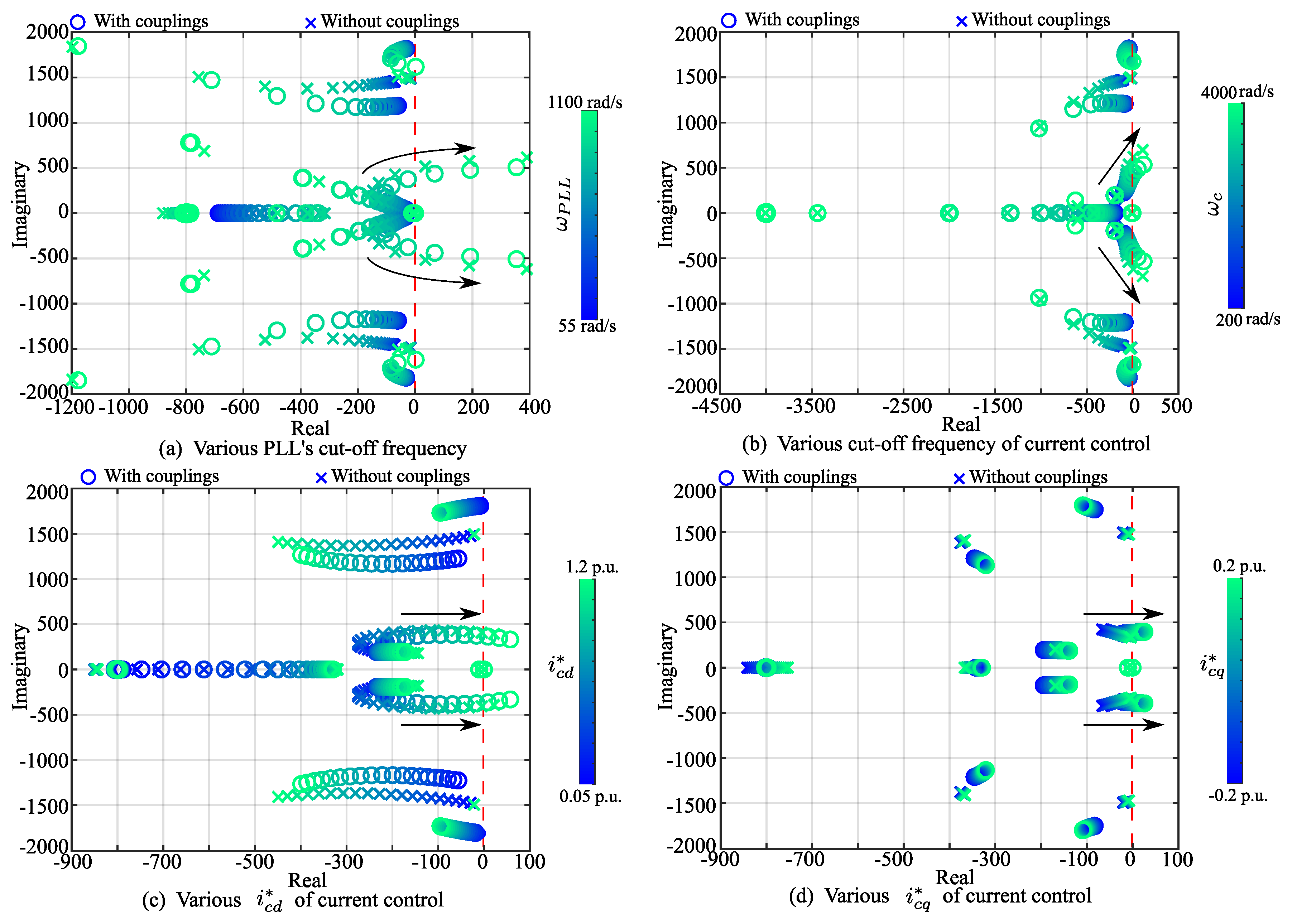
The coupling influence on the pole locus is drawn in this section. The influence of ignoring couplings on the pole locus is studied. Four pole locus are drawn via changing the parameters including
,
,
, and
, as shown in
Figure 5.
It is observed that the pole locus without considering the couplings was not precisely matched to the one with the couplings, as shown in
Figure 5a–d. The movements of both pole loci were the same, but there were errors between each pair of poles.
For the movement, each pair of pole loci with or without coupling are shown in
Figure 5a–d. The poles in the middle moved to the right-half plane when the parameters were increased significantly. Therefore, both impedance stability analyses can show that increasing
(
,
and
) reduced the system stability or even led to instability.
For the pole errors, it is observed that the error between each pair of poles always existed under the different values of the parameters, as shown in
Figure 5a–d. These errors led the analysis without couplings to lose accuracy for the stability analysis. Furthermore, ignoring couplings could fail to identify the instabilities, as shown in
Section 4.1.
4.3. Error Quantification for the Stability Analysis without Couplings
In this section, the error of the analysis without couplings is defined and shown. The cut-off frequency of the PLL, which is the basic control for the dq frame, was selected to determine the error, as shown below:
where
are the maximum PLL cut-off frequency to keep the system stable based on the analysis without couplings.
are the maximum PLL cut-off frequencies to keep the system stable based on the analysis with couplings.
and
were identified by increasing
and
until their right-plane poles appeared in the pole map, respectively. Various SCRs were also selected to show the errors. The stability analysis errors based on (
35) are therefore calculated and summarized in
Table 2.
The error from the eigenvalue-based impedance stability analysis was 12.7% when the inverter connected to a weak AC grid (SCR = 2). It was reduced when the grid became stronger (SRC = 15); the error was only 0.2%. This is because the weak AC grid enhanced the couplings, and therefore, caused the large error in the eigenvalue-based impedance stability analysis.
The output voltage
(magnitude) was changed in terms of the various SCRs. The same operation point, that
at 1 p.u., should be maintained.
was changed to achieve this in terms of various SCRs. The errors under the same magnitude of
are shown in
Table 3.
It is observed that even a strong grid was connected, and the error (11.53%) was almost same as that of a week grid under the same output voltage operation point. No matter which type of AC grid was connected, the error from the eigenvalue-based impedance stability analysis could be around 10%, as shown in
Table 3.
It was also found that
increased along with the increasing SCR, as shown in
Table 2 and
Table 3. When the inverter connects to a weak AC grid,
should be reduced within the limit of
in order to maintain the stable operation of the inverter system.
5. Conclusions
The coupling influence on the dq impedance stability analysis was studied. The results showed that ignoring the couplings of the impedance-ratio matrix brought significant errors up to 12.7% in the stability analysis, which may fail to identify the instabilities. The failure was validated in the time-domain simulation. Ignoring the couplings caused the wrong stability analysis results. A weak AC grid strengthened the couplings and caused the large errors. However, when the same output voltage magnitude of the inverter was maintained, the errors were around 10%, no matter whether a strong or a weak AC grid was connected. The couplings did not change the movement of the pole locus. In other words, the analysis without couplings could still identify whether the stability was increased or decreased because of the changing parameters. The dq impedance stability analysis based on the determinant of the impedance-ratio matrix can achieve accurate stability analysis simply, which had the same accuracy as the state-space stability analysis.
For the future work, an auxiliary control will be designed based on the dq impedance stability analysis in order to stabilize the grid-connected inverter. The coupling influence on the outer loop control that regulates the power can be further studied via the impedance stability analysis.