1. Introduction
Power transformers are one of the most important electric power devices in the electrical power distribution system. To provide reliable and continuous power delivery, it is crucial to monitor and analyze various parameters, that allow to indicate any abnormalities in operation of each transformer unit, i.e., partial discharges [
1,
2,
3,
4,
5], dissolved gas concentrations [
6,
7], vibrations [
8], general insulation condition [
6,
9], temperature [
10,
11,
12] and a number of others [
6]. In order to support a continuous rating of transformers, various on-line monitoring systems (OMS) have been willingly implemented so far. Those systems usually cooperate with technical assessment decision support systems (DSS) [
13,
14]. Artificial intelligent based algorithms, such as artificial neural networks, fuzzy logic, or machine learning, have been willingly and successfully applied in DSS for the last decade [
15,
16,
17,
18]. Apart from numerous other indicators, temperature is one of the fundamental parameters that deliver valuable information about potential abnormalities in apparatus operation: Typically, if temperature is higher than expected (or typical) it may be a symptom of some potential faults. Moreover, in the case of transformers, raised temperature is also expected to be a serious threat for the condition of the insulation system, as the aging process of the paper, as well as the oil, is mainly accelerated by the temperature. The degradation rate of the celluloses mainly depends on the temperature and moisture, it is assumed that average temperature rise of transformer by each 6 °C results in doubling its relative aging rate, in other words, its exploitation perspective is shortened twice [
19,
20]. There are various state-of-art papers where that issue has been investigated [
14,
21,
22]. The factors that most affect the transformer HS temperature are generally its load and ambient temperature. The currently used diagnostic criteria are based on the acceptable temperature rise of the HS and the top-oil: It is assumed that the average temperature of the windings should not be higher than 65 °C above the ambient temperature, and the HS temperature should not be higher than 78 °C from the ambient temperature, while the temperature of the top-oil should not be more than 60 °C above the ambient temperature [
23,
24].
A number of methods for rating the temperature of transformers have been proposed so far, and some of them are normalized, i.a., in [
25,
26]. Most of the methods are based on the thermodynamic model of the transformer, where the HS temperature is calculated on the grounds of the numerical model. Radakovic et al. presented in [
27] a new method that allows to estimate the temperatures of the active parts of the oil-filled transformers. The proposed method uses a detailed thermal-hydraulic model that utilizes a number of parameters that characterize the analyzed unit, including unit design, properties of the used materials, and temperatures in various points. As a result, the distribution of temperatures within the transformer tank with relatively good accuracy and resolution is yielded by the proposed method. In [
11] Tenbohlen et al. evaluated the thermal behavior of the transformer winding through the analysis of oil velocity in horizontal ducts of winding with direct oil cooling. Susa et al. in [
28] proposed a simple model for calculating the HS temperature, which uses the HS to ambient gradient as the main input parameter. Various additional parameters, such as changes of the oil viscosity, as well as winding losses due to temperature adjustments are investigated. The results have been verified on real-life units and compared to models proposed by IEEE C57.91 annex G. Feng et al. have noticed that the accuracy of modeling HS temperature significantly depends on the HS factor, that, in most cases, is not known and need to be estimated experimentally. In [
12], the method for effective HS factor calculation, based on the International Electrotechnical Commission (IEC) thermal model has been evaluated. Authors analyzed a number of scenarios including different aging mechanisms and various paper samples with different rates of polymerization. An interesting issue was also raised in [
29], where a new model for prediction of the oil temperature in distribution transformers was proposed. Authors included a solar radiation influence in their model and showed that solar radiation may increase the oil temperature by almost 4 °C at rated power and should not be omitted in calculations. Mikha-Beyranvand et al. in [
30] proposed a novel model for prediction of the temperature in transformers under unbalanced supply voltage. Authors noticed that conventional models are not optimized for such scenarios and evaluated their own solution based on the numerical simulations that considered selected galvanic parts of the transformer as heating sources with their thermal power related to losses of each part.
Some papers that deal with the dynamic thermal ratings (DTR) for other devices should also be mentioned here. In [
31] authors propose an adaptive model of soil for DTR of underground cables. Many papers deal with DTR for overhead power lines. Kim et al. in [
32] proposed a method for dynamic rating of the old transmission lines that allows to increase its ampacity rate without the necessity of modernization or adjusting voltage of the line. Greenwood et al. in [
33] compared DTR for overhead lines used in the USA and UK. In [
34] authors introduced methods for estimating probabilistic DTR dedicated for overhead lines that are based on the weather data. The methods may be used by a system operator within a selected risk policy with respect to the probability of a rating being exceeded.
As it has been presented above, most of the methods for thermal rating of transformers assume that the HS temperature is unknown. Such an attitude is redundant when temperature OMS is installed on the unit, the HS temperature is then directly measured (known). Furthermore, most of the research deals with relatively high load profiles (usually around 100% and above), where expected HS temperatures are in the range of the highest allowed values proposed by the contemporary load guides [
28,
35,
36]. Most of the current models are optimized for maximum loads, where the highest HS temperature is expected. Thus, the open issue is how (and if) to assess the temperature in low-loaded units, where expected HS temperatures are far below the commonly allowed values, and probably never reach them. Thus, it is possible that temperature is not proper but it is still below any of the allowed boundaries, and as a result, symptoms of a potential fault may be omitted? The aim of the paper is to propose the method for DTR of the low-loaded power transformers equipped with temperature OMS, where expected HS temperatures are relatively low. The proposed method has been already implemented in the DSS designed for the analyzed fleet.
2. Case Study
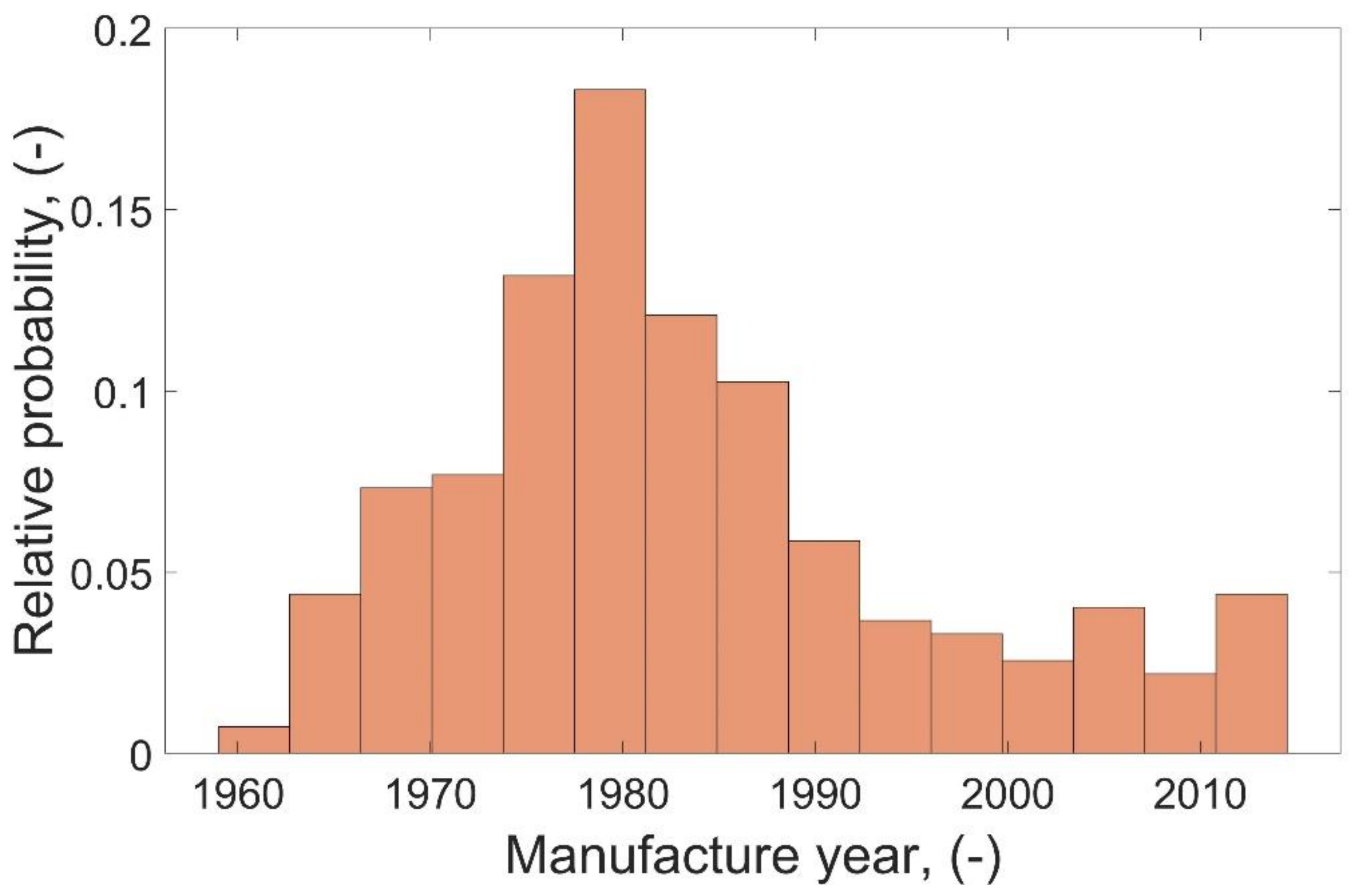
In this research, a characteristic population of mid-power HV/MV transformers is analyzed. The fleet consists of over 1500 units. The age structure of the population (
Figure 1) shows that approx. 60% of the units are older than 30 years. Typical rated voltage levels are 115/16.5 kV and rated power span is from 10 to 30 MVA. Depending on the rated power, typical load losses span between approx. 60 and 130 kW, while no-load losses span between approx. 10 and 25 kW. What is the most significant, typical relative load of the units during normal exploitation conditions usually is not higher than 40%. It is mostly because a common substation configuration is a parallel setup of the transformers and each unit is designed to temporally take the load from both transformers. All units are filled with mineral oil and generally equipped with oil-natural air-natural (ON-AN) or oil-natural air-forced (ON-AF) cooling systems. Three representative units were selected from the analyzed fleet for further investigation: 25 MVA 2-winding unit with one of the highest loads in the population, 115/16.5 kV, 108.7 kW of load losses and 10.8 kW of no-load losses and ON-AN cooling system (Tr1); 25 MVA 2-winding unit with an average load in the population, 115/16.5 kV, 126.4 kW of load losses and 16.7 kW of no-load losses and ON-AN cooling system (Tr2); 25 MVA 3-winding unit which represents an average load in population, 115/16.5/6.6 kV, 128.7 kW of load losses and 21.1 kW of no-load losses and ON-AF cooling system, working in an indoor substation (Tr3).
All of the selected units were equipped with fiber optic sensors for on-line temperature monitoring: One sensor per HS of each coil and one for core HS (as a result: 10 sensors in 3-winding units and 7 sensors in 2-winding units) and then data were stored within a two-year period (2016–2017) in 1 h steps for further analysis. Additionally, top oil temperature was registered as well as external ambient temperature and the relative load of each phase of the transformers, also in 1 h steps. In
Figure 2,
Figure 3 and
Figure 4 some representative temperature runs that illustrate the dependencies between load, ambient temperature, and HS temperatures in the selected units have been showed. Generally, a quite constant load may be noted regarding all units, with characteristic 24-hour fluctuations. Furthermore, significant, tight relation between HS temperatures and ambient temperature is also observed, more detailed correlation analysis of the HS temperatures of those units has been presented in [
10].
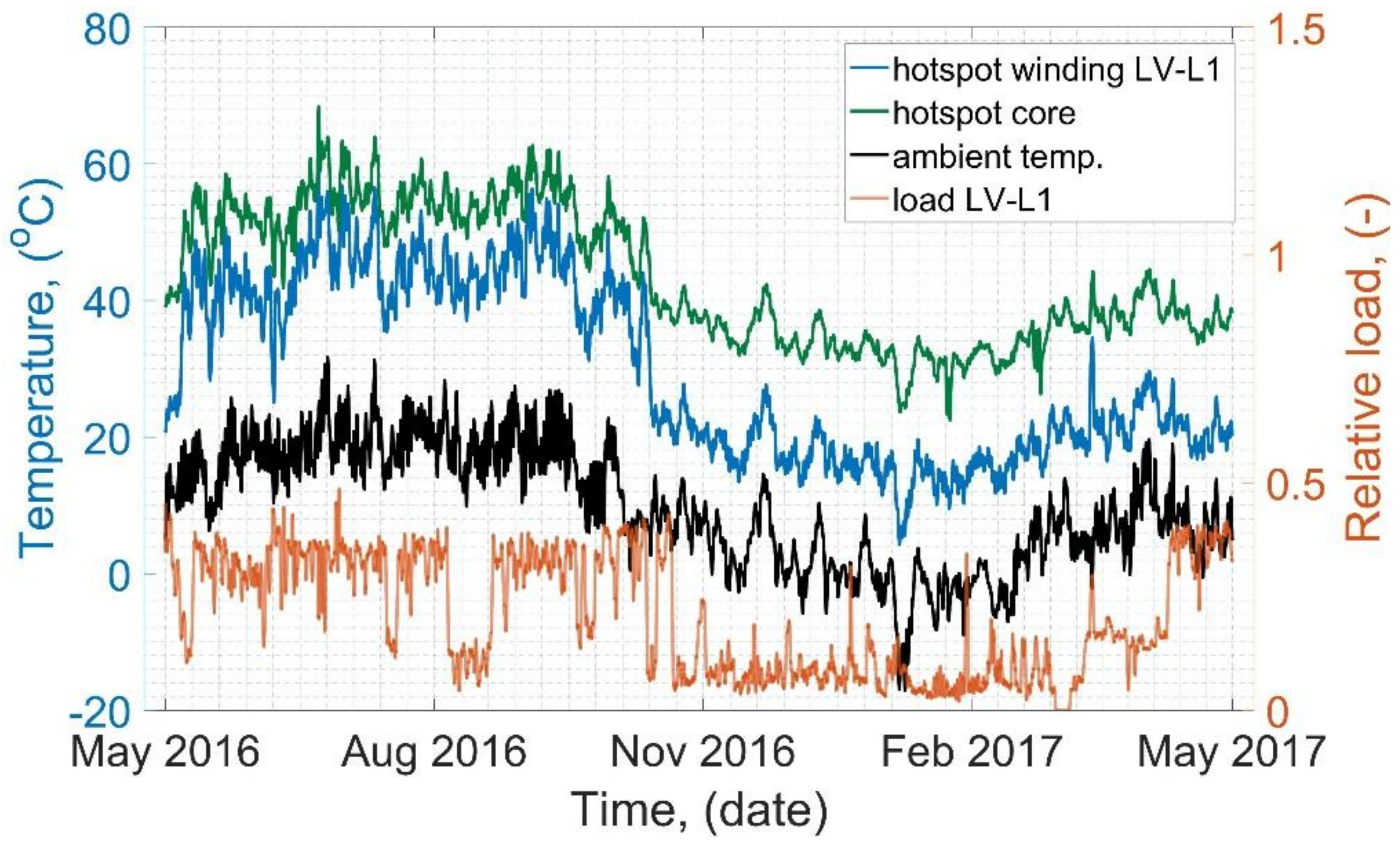
Moreover, representative runs of the temperature and load regarding the Tr3 are shown in
Figure 4. An interesting period may be observed between approx. November 2016 and February 2017, where the average load was around 10%. This is because the transformer works in a substation that powers the heating plant equipped with a gas turbine, thus in the winter period, when a high heat generation is needed, the turbine generates power that covers almost all electrical power needs of the plant.
3. Overview of the Proposed Method
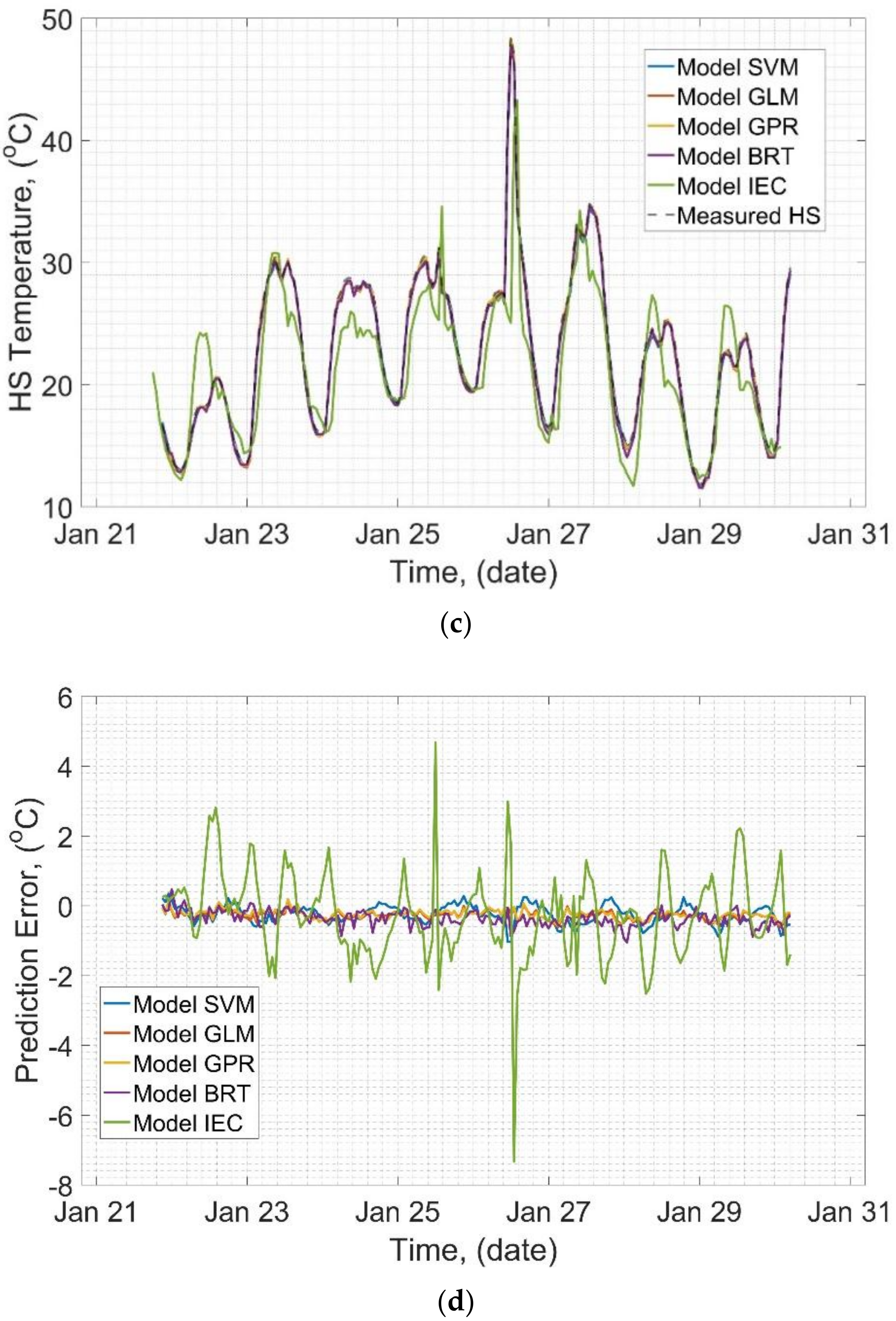
In general, the proposed method for interpreting the results of the temperature measurement of winding HS is based on modeling the expected temperature of each from measured HS and comparing the expected temperature of the modeled point with the value coming from a particular sensor (measured), relative temperature criterion. The idea is shown schematically in
Figure 5. Therefore, the assumption of the method is that rated transformer is equipped with the HS temperature OMS. The crucial issue is that, in the proposed method, temperature value being the model’s response is treated as a reference value, while the value coming from the actual measurement is validated by the reference one. Such “inversed” situation is possible due to almost perfect prediction accuracy of the applied model, which is discussed more-in-depth in
Section 4. On the grounds of the analysis of the historical data and specification of the particular unit (or population), some relative range that is to indicate if the HS measured temperature is normal or abnormal needs to be proposed. In the analyzed case, ±10% of the reference value is proposed as a boundary of the normal thermal state. It means that if the measured temperature
τn from the given sensor
n is different from the modeled value
Tn by not more than 10%, then the thermal state of the transformer will be considered as normal, and otherwise, as abnormal and requiring more detailed analysis (e.g., comparison to other diagnostic measurements by the external technical condition assessment system). According to the proposed approach, it is possible not only to identify overheating (temperature above expected) but also other anomalies related to the operation of the cooling system, as well as the temperature measurement system itself.
Machine learning algorithms have been used for modeling the HS temperatures, detailed analysis of the applied algorithms is introduced in
Section 4. Learning process of each of the models was the initial stage, for which historical data were used. At the learning process of the models, both the predictor values and the output values were known. The predictors were all of the measurement data (hotspot temperatures, load, ambient temperature, top oil temperature) aside from the one particular modeled temperature, which was the output value of the model. Hence, for the 2-winding transformer, six models were created: three for LV coils HS, three for HV coils HS, and for the 3-winding transformer three more models were applied for the MV coils HS, that is, there were nine of them.
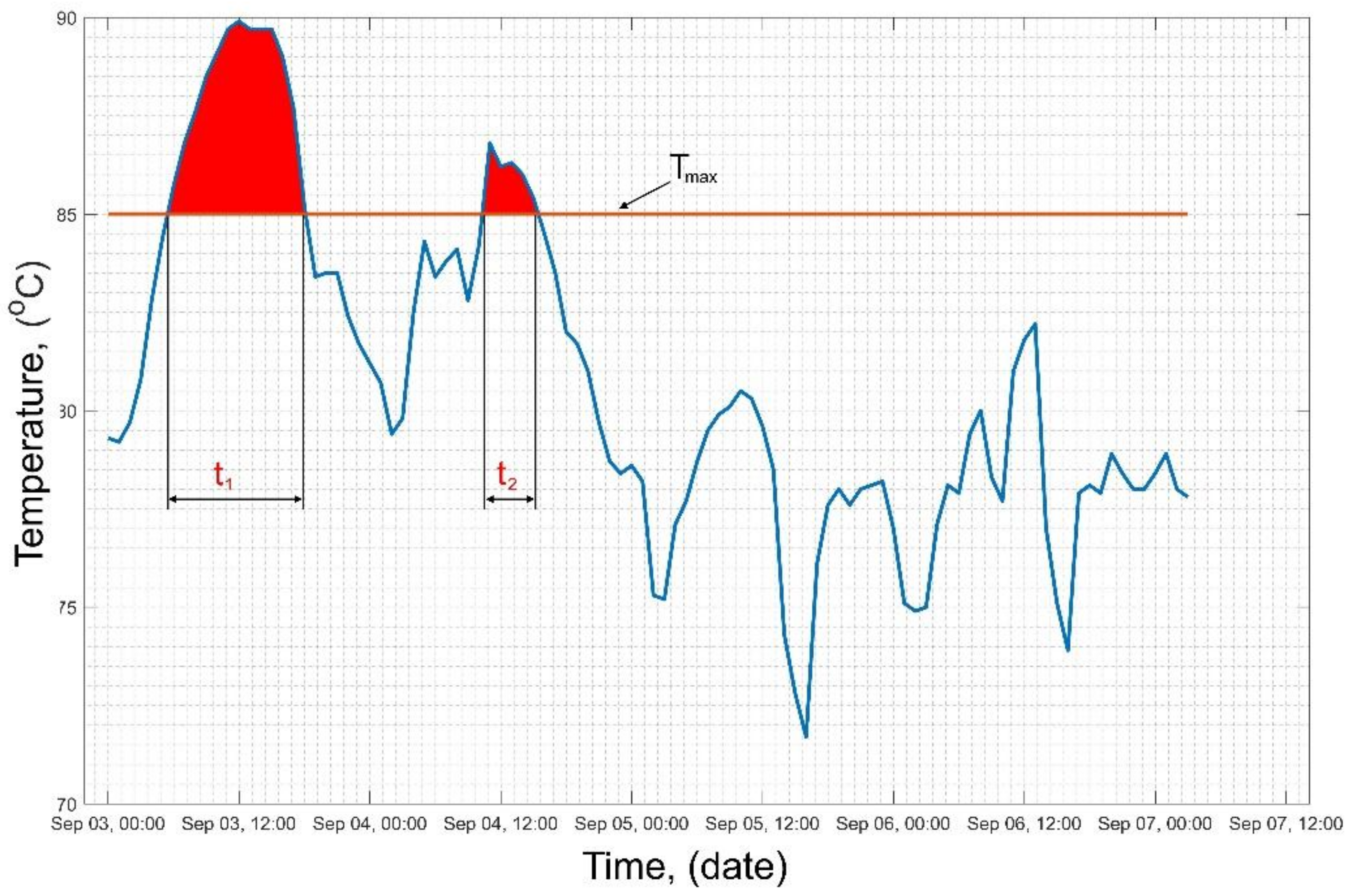
The proposed method does not constrict the conventional thermal rating based on the maximum allowed HS temperature (
Tmax), absolute temperature criterion. It is possible and highly recommended to apply them simultaneously. Thus, it is proposed to use the second criterion, the criterion of cumulative minimum time
t0 of the impact of
Tmax within a selected time interval
Δt (
Figure 6). Both
Tmax and
t0 should be specified with particular consideration of the working conditions of the analyzed unit or population of the transformers. In the analyzed case, proposed values are
Tmax = 85 °C,
t0 = 200 h and Δ
t = 1 year, chosen on the grounds of the historical data analysis and population load profile and age. The criterion of the minimum cumulative time
t0 allows to eliminate the situation in which the thermal state of a given unit would be considered as abnormal when a single, short-term exceeding of the temperature limit
Tmax appears. It also allows to store the whole historical data of the exceeded temperatures which may be recalled and analyzed at any time. According to this criterion, an absolute temperature
Tmax may also be freely replaced with temperature raise Δ
Tmax above the ambient, which is more often used according to the current load guides. The only thing that needs to be also adjusted in the algorithm is the allowed temperature raise limit (it should be fitted to the particular fleet on the grounds of the historical data analysis).
4. Applied Models
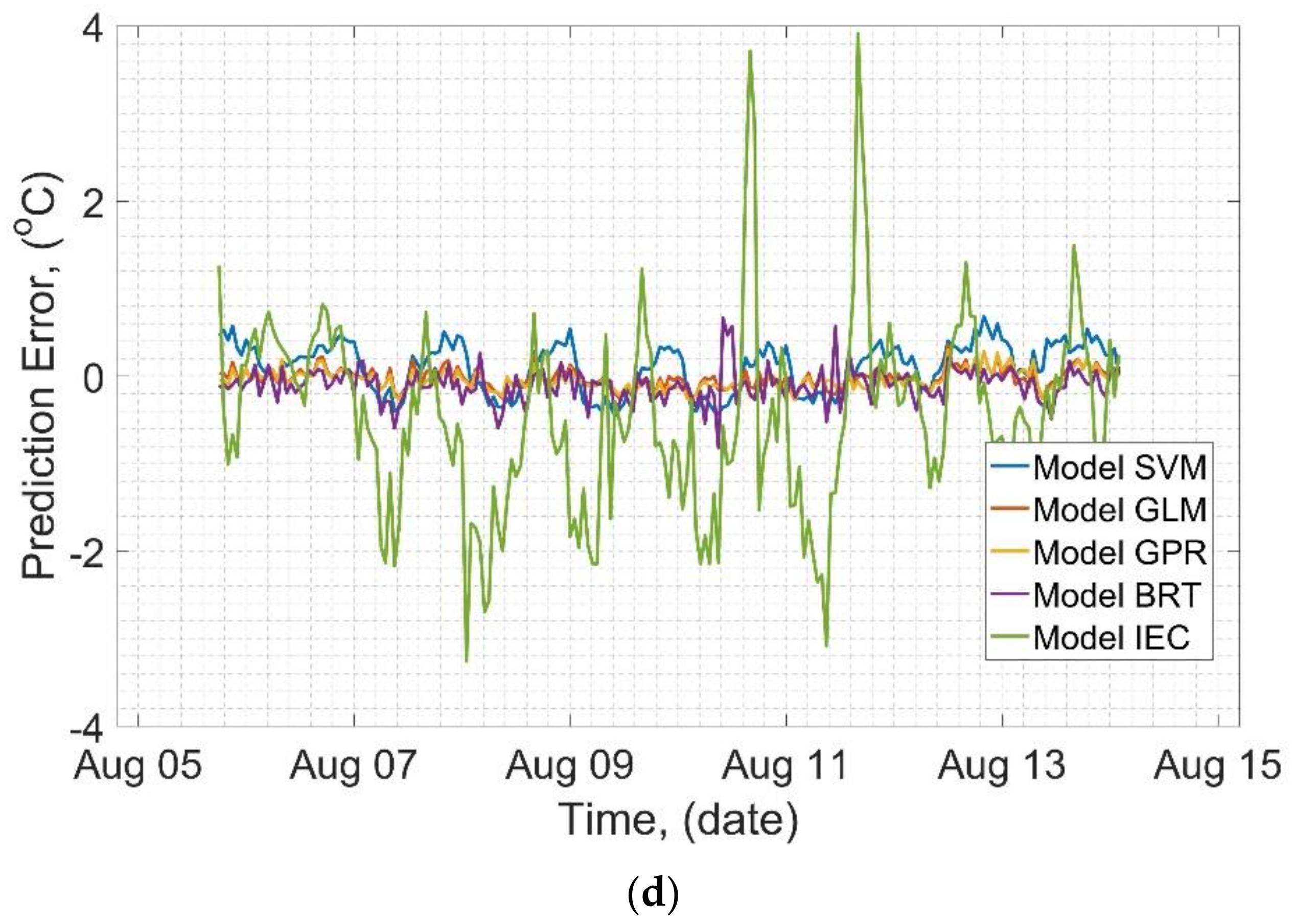
The analyzed problem was a typical nonlinear regression. In this section, results of application and testing of four different algorithms of ML for prediction of the HS temperatures are presented: Binary regression tree (BRT), generalized linear model (GLM), Gaussian process regression (GPR), and support vector machine (SVM). These are typical models that are freely available in almost every simulation software library, thus the presented experiments may be easily reproduced. The short descriptions of each algorithm are provided in the relevant sections, additionally, some key parameters of each model are described, and finally, exemplary results of the prediction of HS temperatures on the example of the selected real-life transformer are also presented. Moreover, the conventional model for HS estimation proposed by [
26] has also been evaluated and optimized for the selected unit.
4.1. Binary Regression Tree
One of the key aspects of the BRT is the procedure of splitting node
t. Weighed mean-square error (MSE) of the responses in node
t is calculated by BRT using (1)
where w
j is the weight of observation
j, and
T is the set of all observation indices in node
t. Pruning was applied only to the leaves and was based on the MSE. This procedure involves combining leaves from the same parent node whose MSE is not higher than the sum of MSE of its two leaves. In the presented case of the prediction process, a minimum number of branch node observations was set to 10. In order to achieve the best split predictor at particular nodes, a standard classification and regression trees (CART) algorithm was applied. Fold value in a cross-validation process was set to 10 [
37].
4.2. Generalized Linear Model
GLM solves a nonlinear problem using linear methods. It may be explained that the nonlinear problem is divided into some small linear problems that are solved using linear models. Some general properties of the linear models are: For every set of input values, the output comes from a normal distribution with the mean
μ, a vector of coefficients
b determines a linear combination
Xb of the input values
X, the model may be defined as
μ =
Xb. GLM uses a generalization procedure on those characteristics, and finally, they may be described as: For every set of input values, the output distribution may be one of the following: Normal, gamma, Poisson, binomial, or inverse Gaussian, with parameters such as a mean
μ, a coefficient vector
b that describes a linear combination
Xb of the input values
X, a link function
f that describes the model as
f(
μ) =
Xb. Regarding the GLM model in the presented research, the distribution of the output variable was set to normal. The next predefined parameter was a link function. This function, as mentioned above, shows the dependency
f(
μ) =
Xb between the mean output value
μ and the linear combination of input values
X∙
b. In that case, a canonical link function in the form presented below was selected:
f(
μ) =
μ, and its relevant inverse function:
μ =
Xb, [
38].
4.3. Gaussian Process Regression
GPR models are nonparametric kernel-based probabilistic models. GPR is based on the estimation of several parameters that describe the data: A covariance function
k(
xi,
xj|
θ) that is parameterized regarding the kernel parameters defined in vector
θ, noise variance
σ2, coefficient vector
β that contains fixed fundamental functions. Kernel parameters are defined as a vector that contains starting values regarding the standard deviation
σf of the input data and the relevant length scales
σl. A vector of unbounded starting parameter values
η0is created by GPR within the optimization process, on the grounds of the starting values regarding the noise standard deviation and the kernel parameters. GPR model analytically computes the explicit fundamental coefficients
β, using approximated values of
θ and
σ2. As a result,
β is not presented in the
η0 vector during the initialization of the numerical optimization by GPR. In the presented application, subset of data points approximation was set as a method for estimation of parameters for the GPR model. Explicit basis in the GPR model was set to constant, which is
H = 1 (
n-by-1 vector of ones, where
n is the number of observations). As
n is the number of samples, the expression
H,∙
β is supplemented to the model by the fundamental function, where
H is the fundamental matrix and
β is a
p-by-1 vector of fundamental coefficients. Starting value regarding the noise standard deviation σ of the GPR model was set to (2)
where
STD is a standard deviation of the response data
y. Quadratic exponential function was set as a kernel covariance function. The method for computing inter-point distances
DST (between
x and
y) to evaluate built-in kernel functions has been defined as (3)
The method used to make predictions from a GPR was set as an exact Gaussian process regression method. The maximum number of block coordinate descent method iterations was limited to 10
6. Dense, symmetric, and based on the first rank, quasi-Newton estimation to the Hessian was assigned as an optimizer to use for parameter estimation. Fold value in cross-validation was set to 10, as in other models [
39].
4.4. Support Vector Machine
The applied algorithm uses a low or moderate dimensional input data set to learn or cross-validate an SVM regression model. SVM allows to trace the input data applying kernel functions and uses sequential minimal optimization (SMO), iterative single data algorithm (ISDA), or L1 soft-margin minimization by using nonlinear computation for optimization. The applied SVM regression model used 10-fold cross-validation and was specified to standardize the predictors. For example, if G(xj,xk) is an element (j,k) of the Gram matrix, where xj and xk are p-dimensional vectors referring to the observations j and k in X, then training kernel may be specified as the linear kernel (4)
The algorithm centers and scales every column of the input data by using the weighted mean of each column and standard deviation, respectively. The model was trained using the standardized predictor matrix, but unstandardized data were stored in the model data
X. The maximal number of numerical optimization iterations was set to 10
6. The SMO was set as an optimization routine for the SVM model [
40].
4.5. IEC 60076-7 Model
The simple conventional model for calculating the expected HS temperature, proposed by [
26] and used in the current study is defined by Equation (5)
where:
THS is modeled HS temperature,
Tamb is temporary ambient temperature,
TOR is top of winding oil temperature rise when
K = 1,
K is temporary relative load,
R is the loss ratio of the unit,
h is the HS ratio,
g is the mean winding to top oil temperature gradient, while
x and
y are model parameters (the
x exponent is related to oil temperature rise due to total losses, and
y exponent is related to winding temperature rise due to load currents).
As one may notice, only two inputs of the model are time-dependent:
Tamb and
K, and they need to be measured. The rest of the inputs are constant and come either from the heat-run tests (
TOR,
g,
R), are defined experimentally, or are proposed by [
26] (
x,
y,
h). In this case, all of the parameters were personalized: It means that they come from the heat-run test of the particular unit (
TOR,
g,
R) and the rest of them (
x,
y,
h) were optimized for the minimum of the mean prediction error of the model. Moreover, all of the model input parameters were also distinguished between HV and LV windings for better prediction results. The applied simple objective function that was used for optimization is defined in (6)
where MPE =
f(
h,x,y) and is defined by Equation (7). Initial values of
H,
x and
y were assigned as 1.3, 0.8, and 1.3, respectively, according to [
26] recommendation for medium and large units with ON cooling system. The applied optimization method uses the Nelder–Mead simplex algorithm described in [
41].
Table 1 presents some selected final parameters of the IEC model applied for Tr1.
6. Conclusions
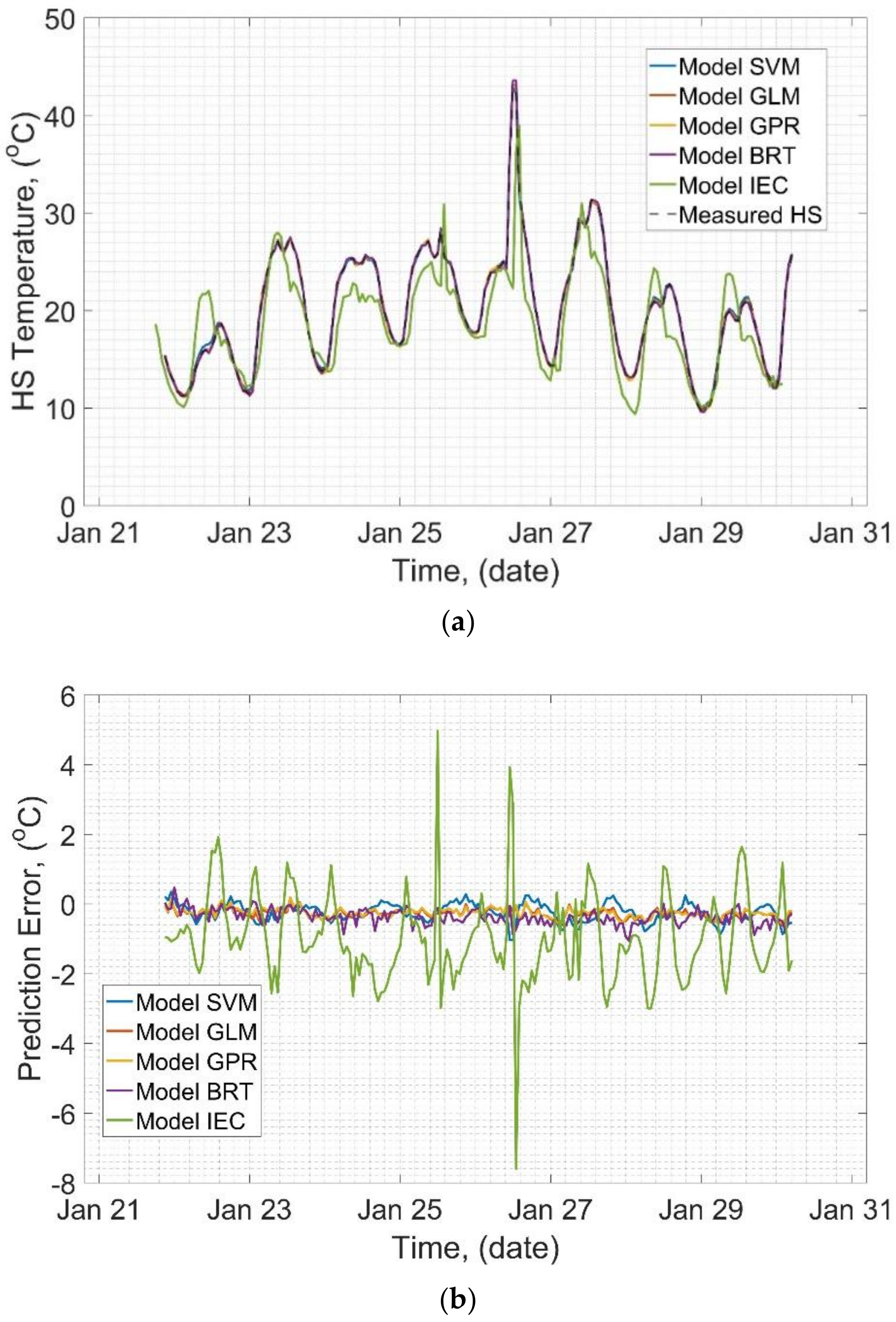
In this paper, a method for dynamic thermal rating of power transformers based on the ML algorithms has been proposed. The method is dedicated to low-loaded units equipped with temperature OMS and has been already implemented in the DSS designed for the analyzed fleet. An exemplary case study of the low-loaded transformer fleet has been investigated and used for simulations and verification of the announced method, on an example of a particular unit. Furthermore, four different ML models based on different algorithms have been trained on the historical data and tested on the prediction of the relevant HS temperatures. The achieved results have been compared to conventional IEC 60076-7 model, that was optimized for the analyzed unit. As a result, high accuracy of the applied ML models has been confirmed and GLM model has been selected as an optimal solution. The most significant contributions of the presented paper are, i.e.:
High accuracy of the HS temperature prediction using the proposed method has been confirmed,
All ML algorithms have yielded significantly higher accuracy than the IEC model, as IEC model is basically designed for full load profiles rather than low ones,
All of the ML-based models have not missed a temporary rise of the HS temperature due to rapid load raise, thus the utility of the method has been confirmed,
The method delivers personalized rating criteria for each transformer unit or group of units (if similar construction and working conditions),
It allows detection not only of the overheating but also of the cooling system failures or temperature OMS failures,
Easy to apply in DSS (condition assessment systems) as an additional indicator in the transformer condition rating process,
Supports an open architecture: It is possible to add some other predictors if they are crucial regarding the thermal condition of the particular unit or fleet (e.g., harmonic content, some information from the cooling system, pumps, other environmental data),
May be easily adopted for other apparatus than transformers, only the relevant learning data set as well as the predictor data set need to be provided,
Self-learning may be applied if needed (either automatic or manual): After the new data are added to the learning database (historical data), a learning process may be initialized, and a new model replaces the old one.
Some weaknesses of the proposed method should be mentioned as well. Temperature itself does not bring any crucial information about the overall technical condition of the apparatus. Thus, it should be used as one of the various parameters that are analyzed together in order to complete technical condition assessment of the transformer. Another crucial issue related to the proposed method is the quality of the learning data set, the method is very prone to the incomplete or invalid data used in the learning process. Therefore, before each learning process, data should be validated and rejected if some abnormalities are detected. Nevertheless, the proposed method gives an alternative solution for other contemporary thermal ratings and may be valuable complementation of the condition assessment process of the power transformers as well as other apparatus.