On Blockage Effects for a Tidal Turbine in Free Surface Proximity
Abstract
1. Introduction
2. Materials and Methods
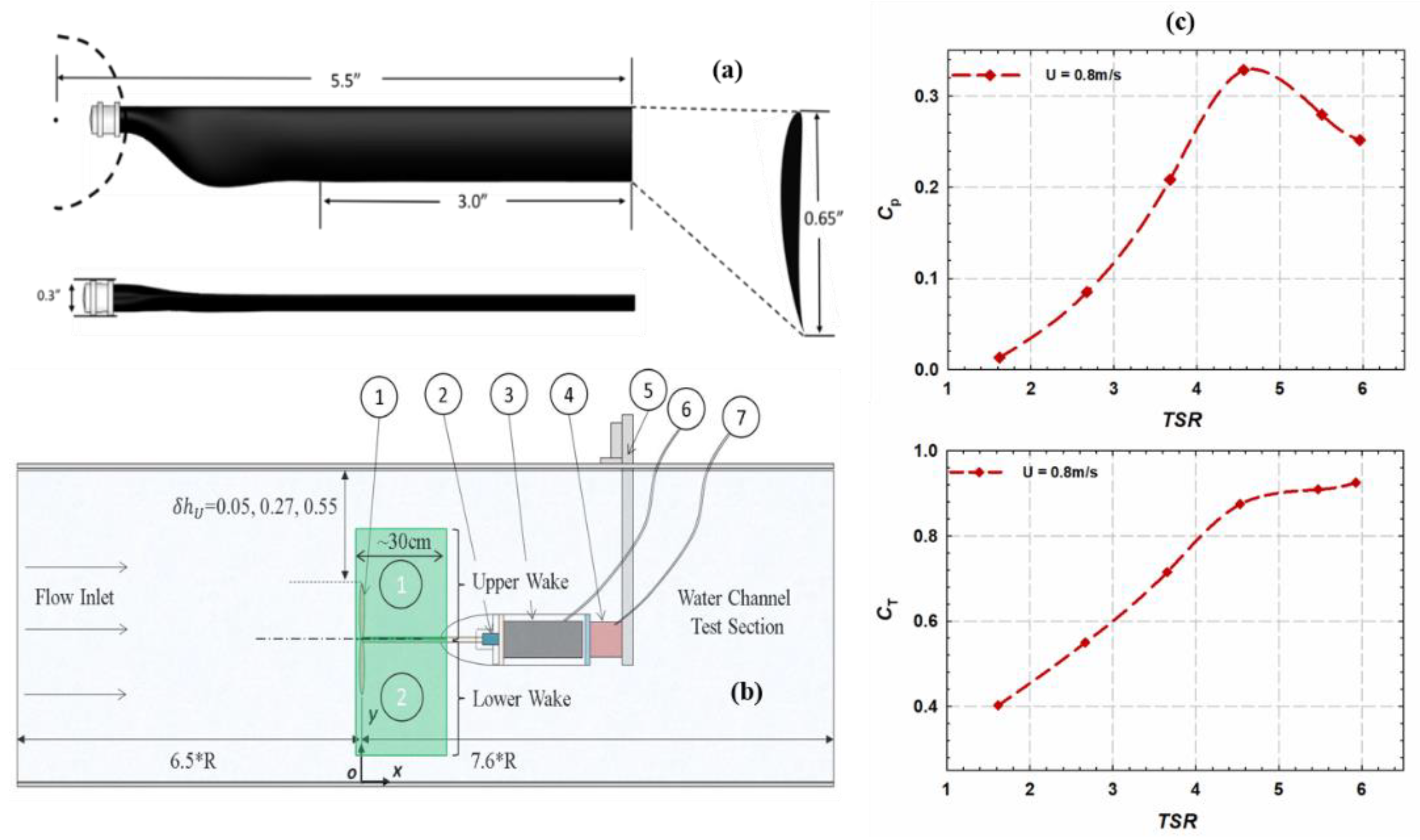
2.1. Flow Channel Conditions and Turbine Assembly
2.2. Stereoscopic-Particle Imaging Velocimetry (PIV) System
3. Results and Discussion
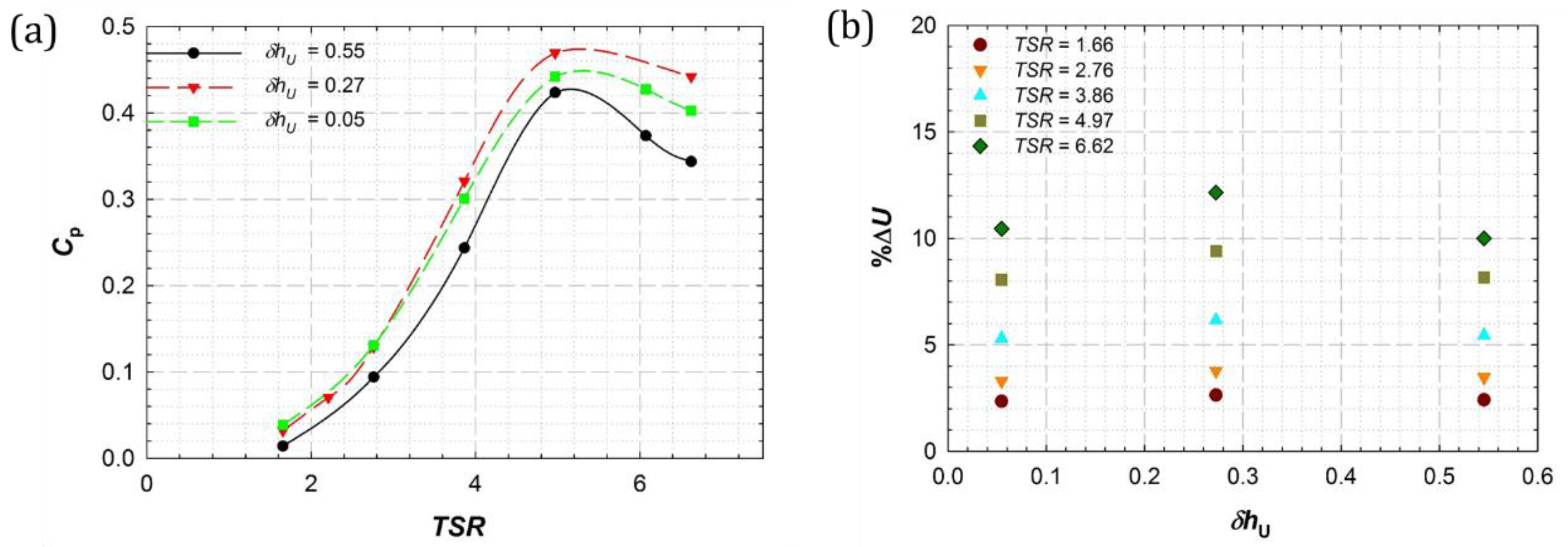
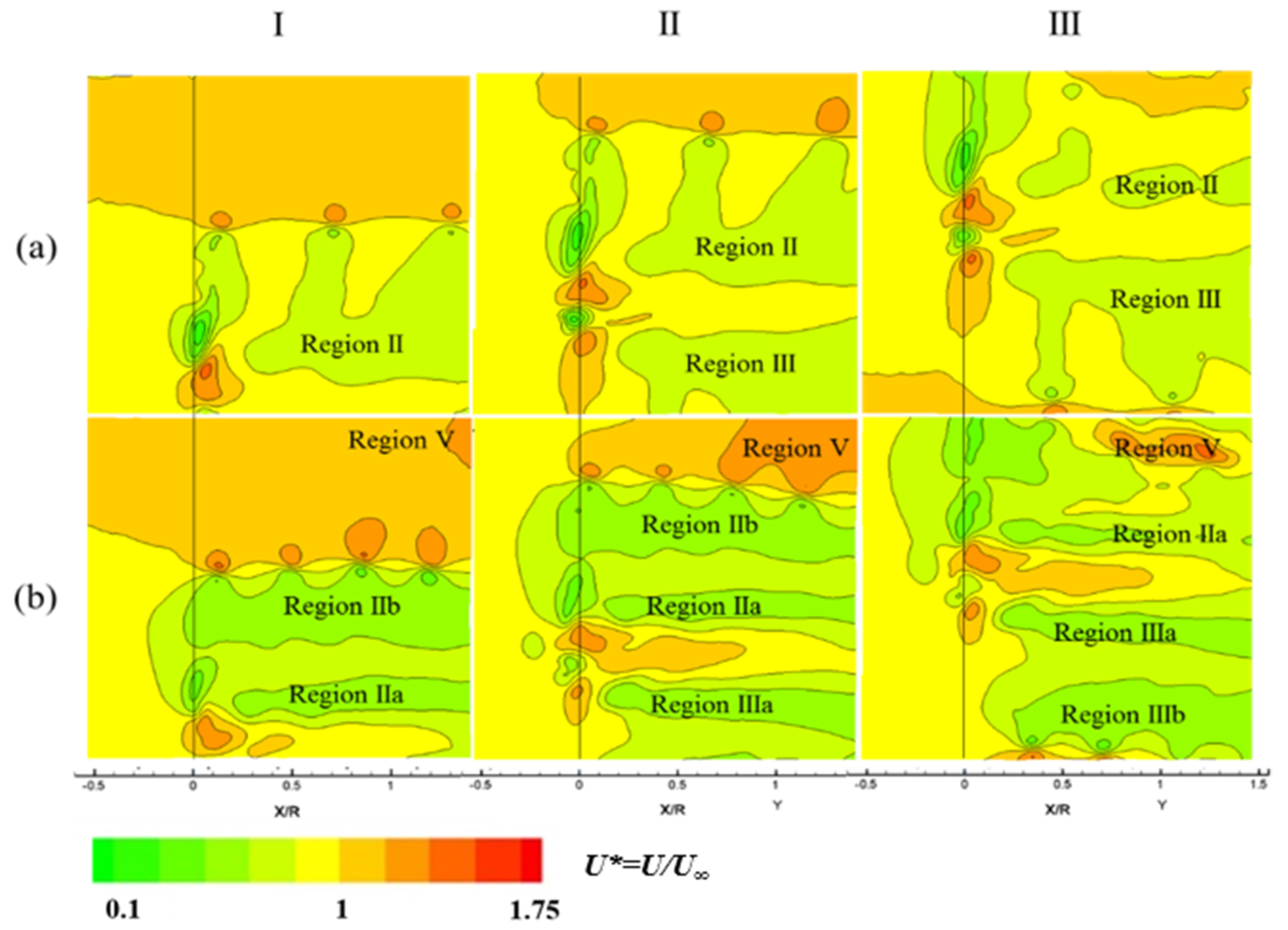
3.1. Effect of Free Surface Proximity on Blockage
3.2. Effect of Blockage and Free Surface Proximity on the Near-Wake Flow: Free-Run PIV
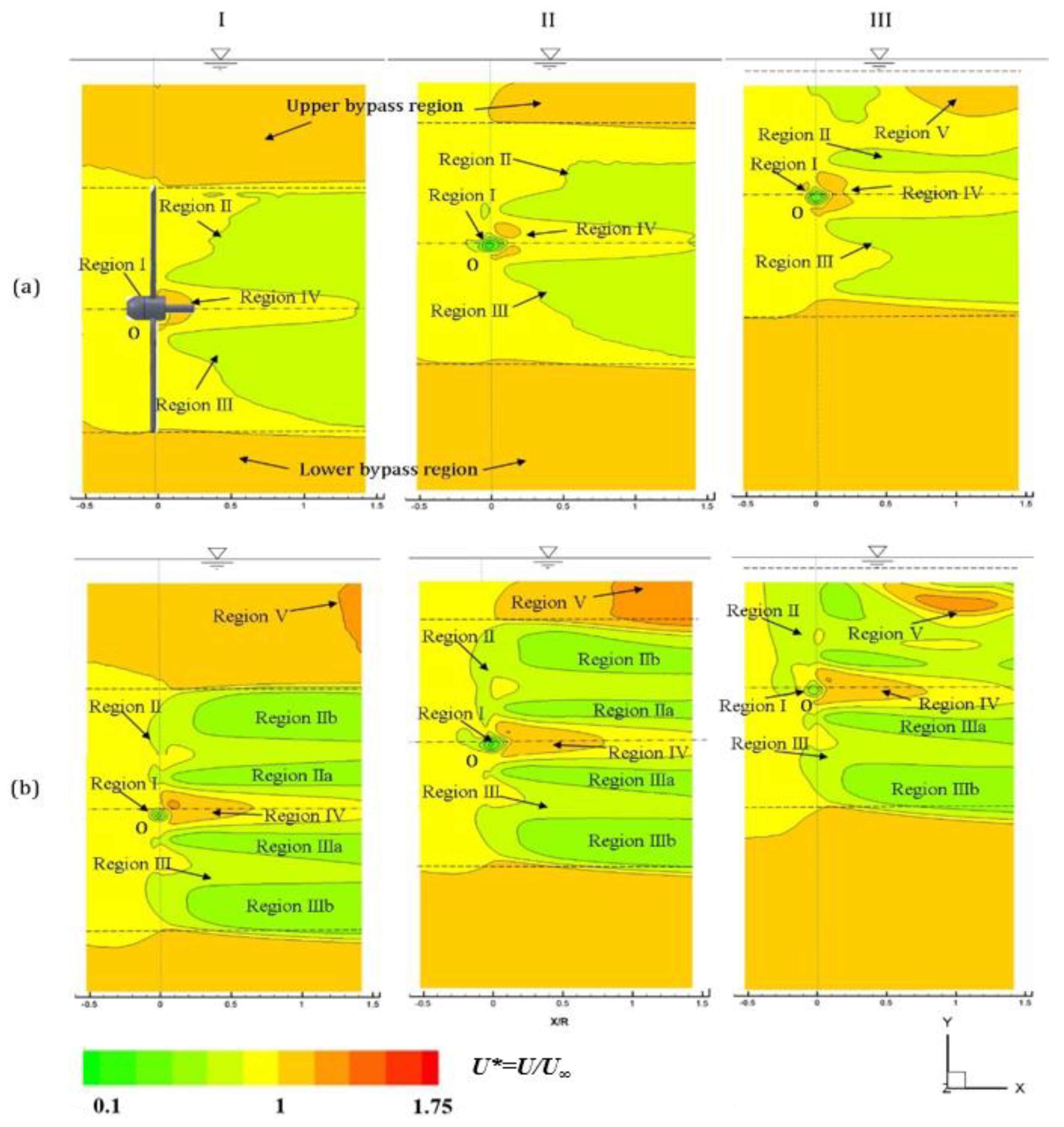
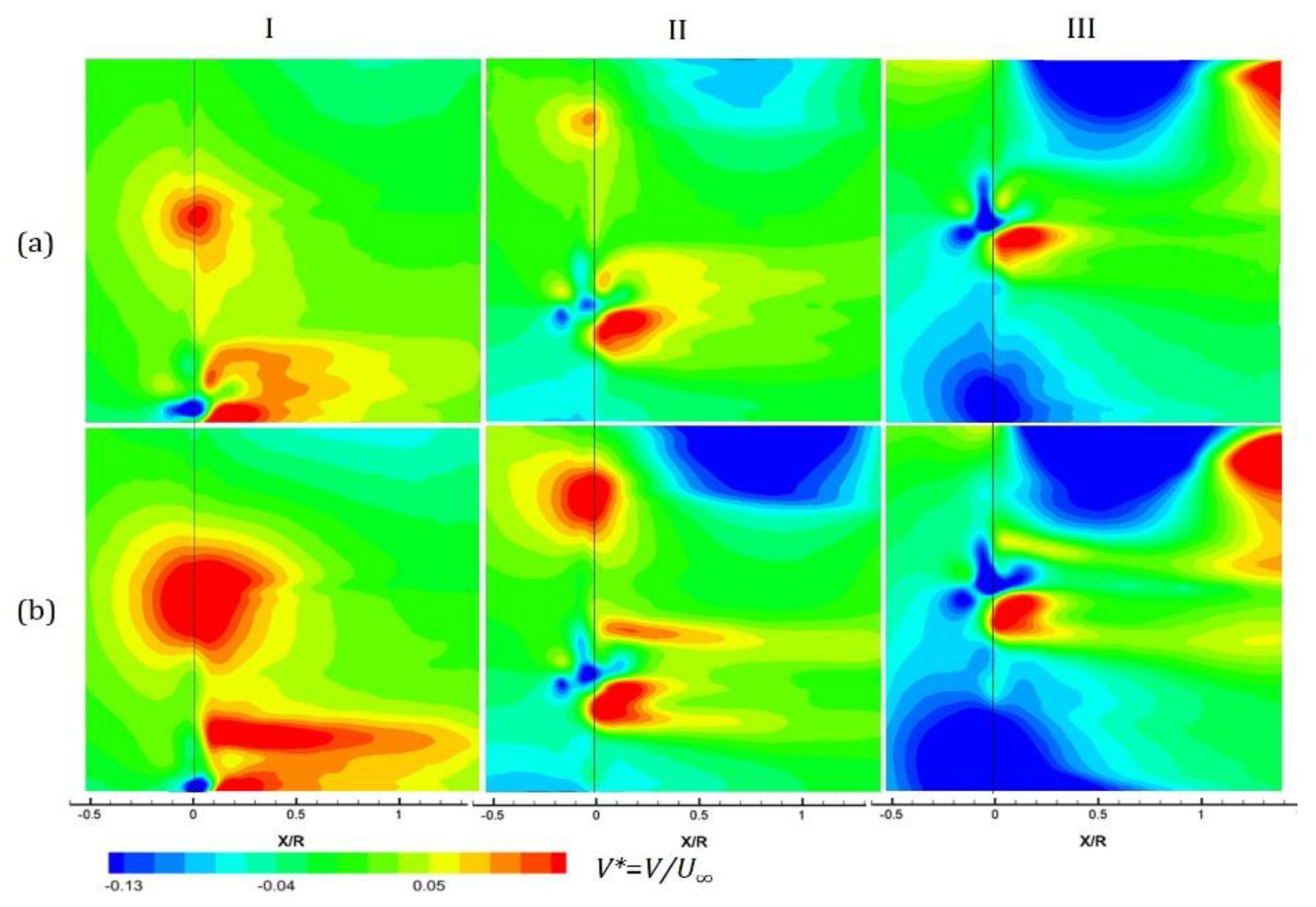
3.2.1. Contours of Stream-Wise Velocity
3.2.2. Contours of Vertical Velocity
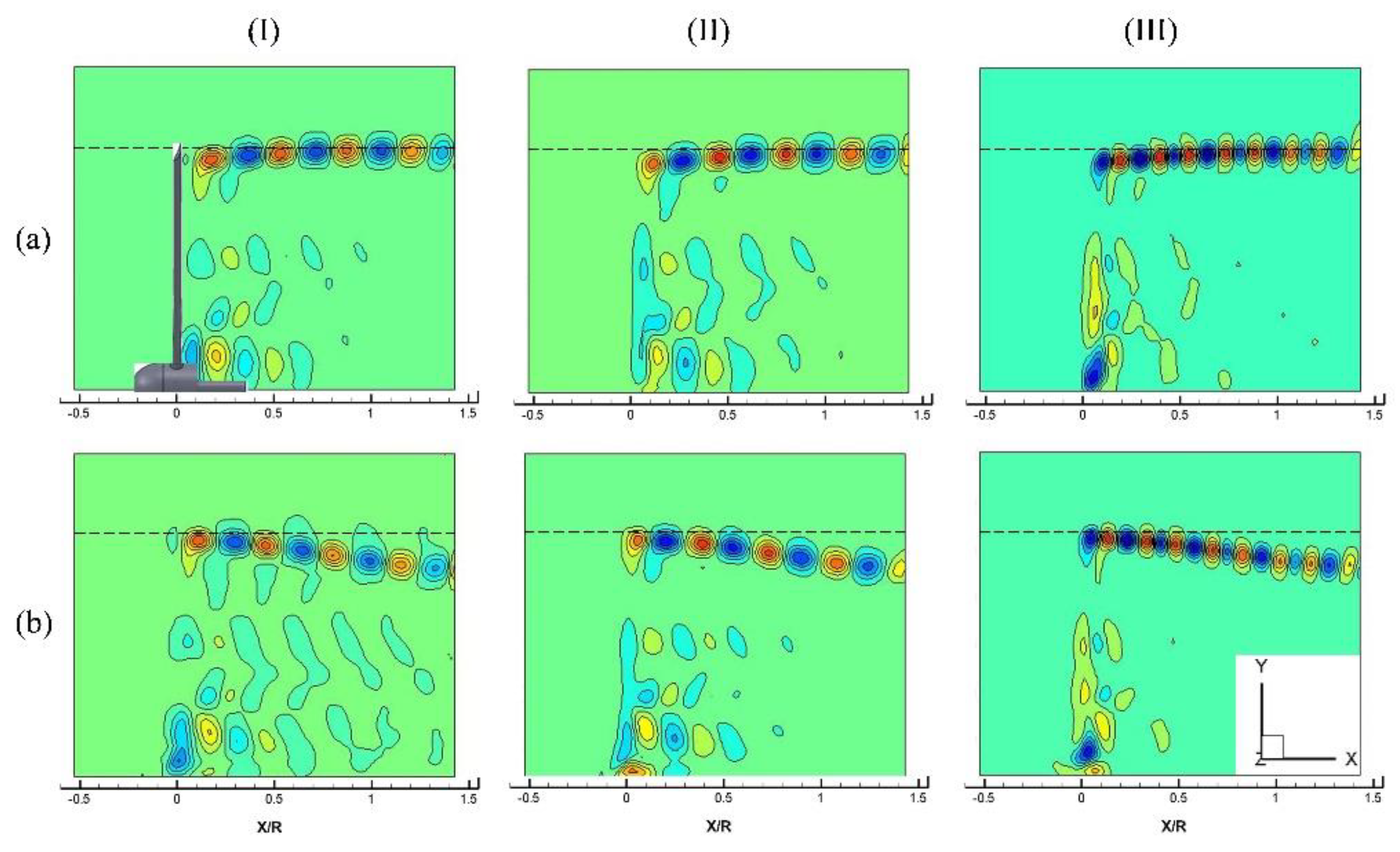
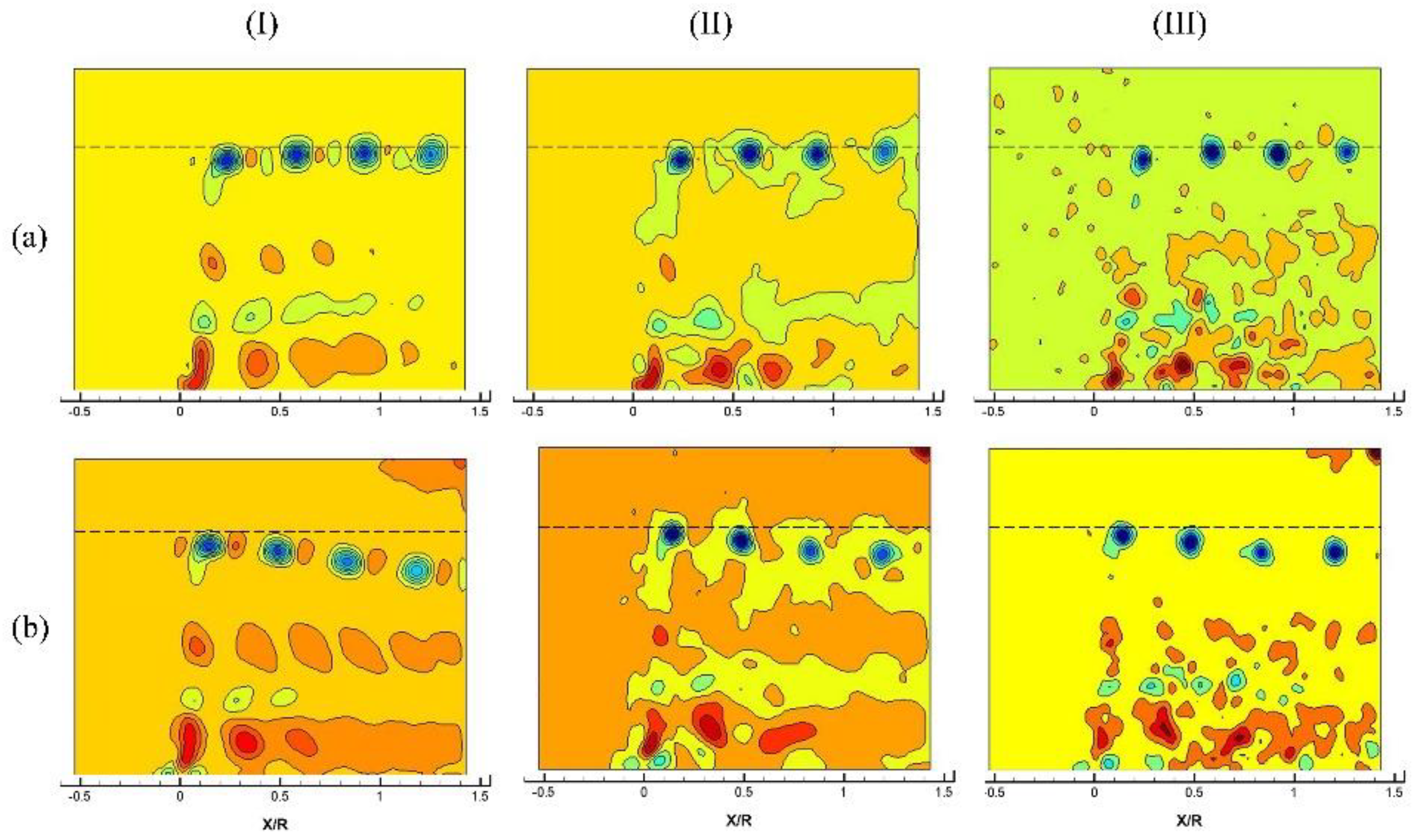
3.2.3. Proper Orthogonal Decomposition Analysis for Free-Run PIV Data
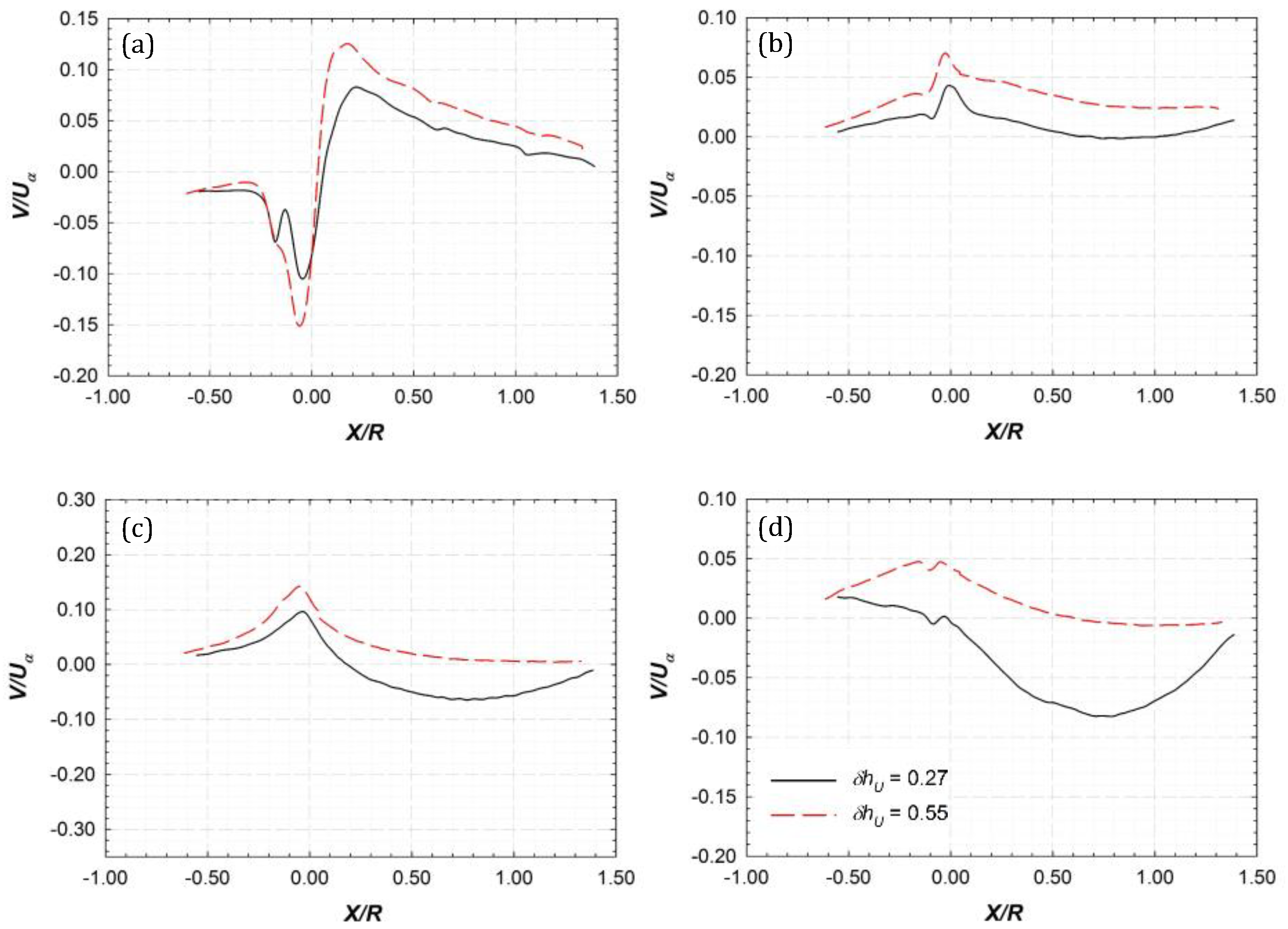
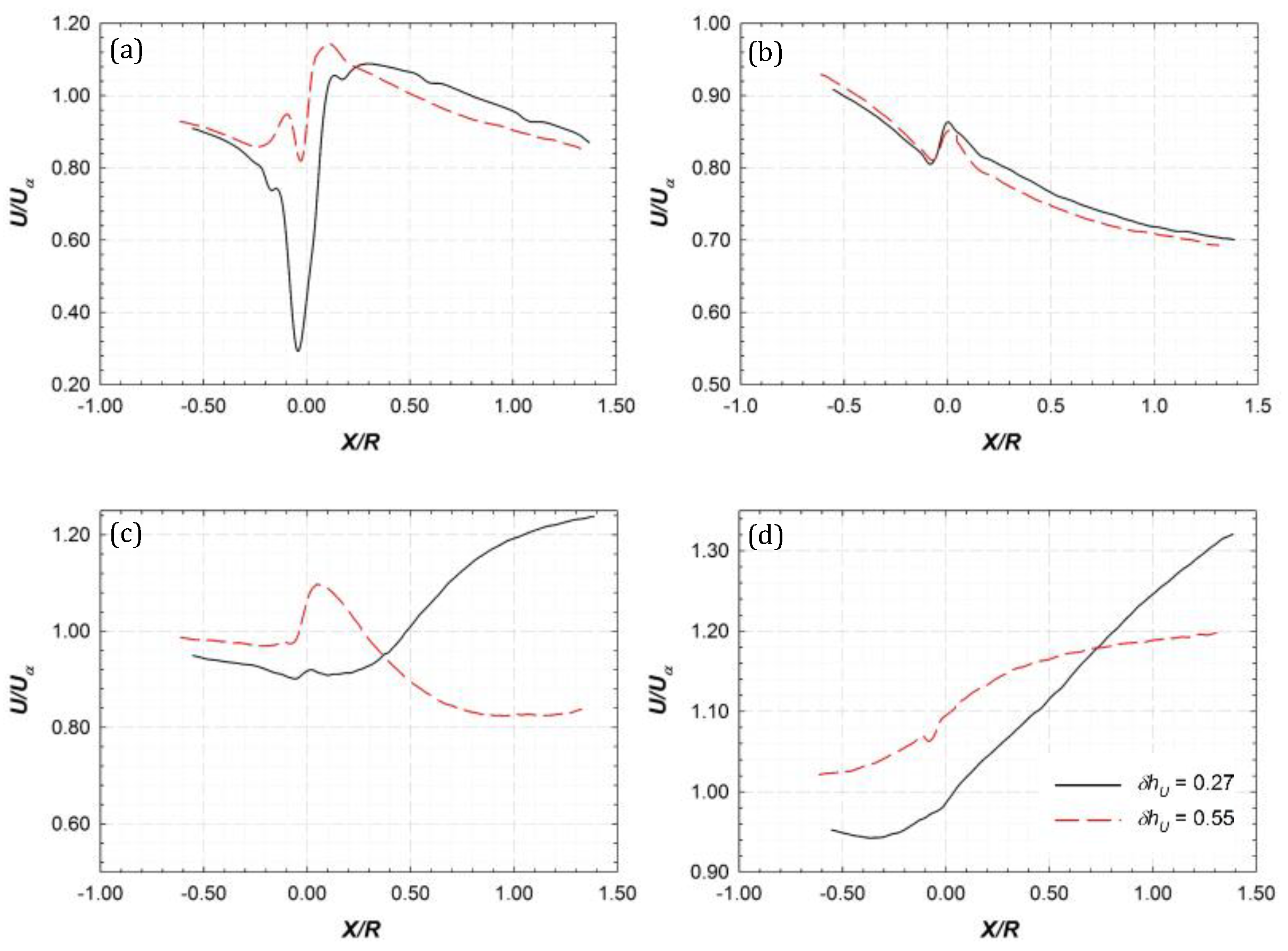
3.3. Variation of Flow Velocities Along Wake Propagation Direction (Along Constant Y)
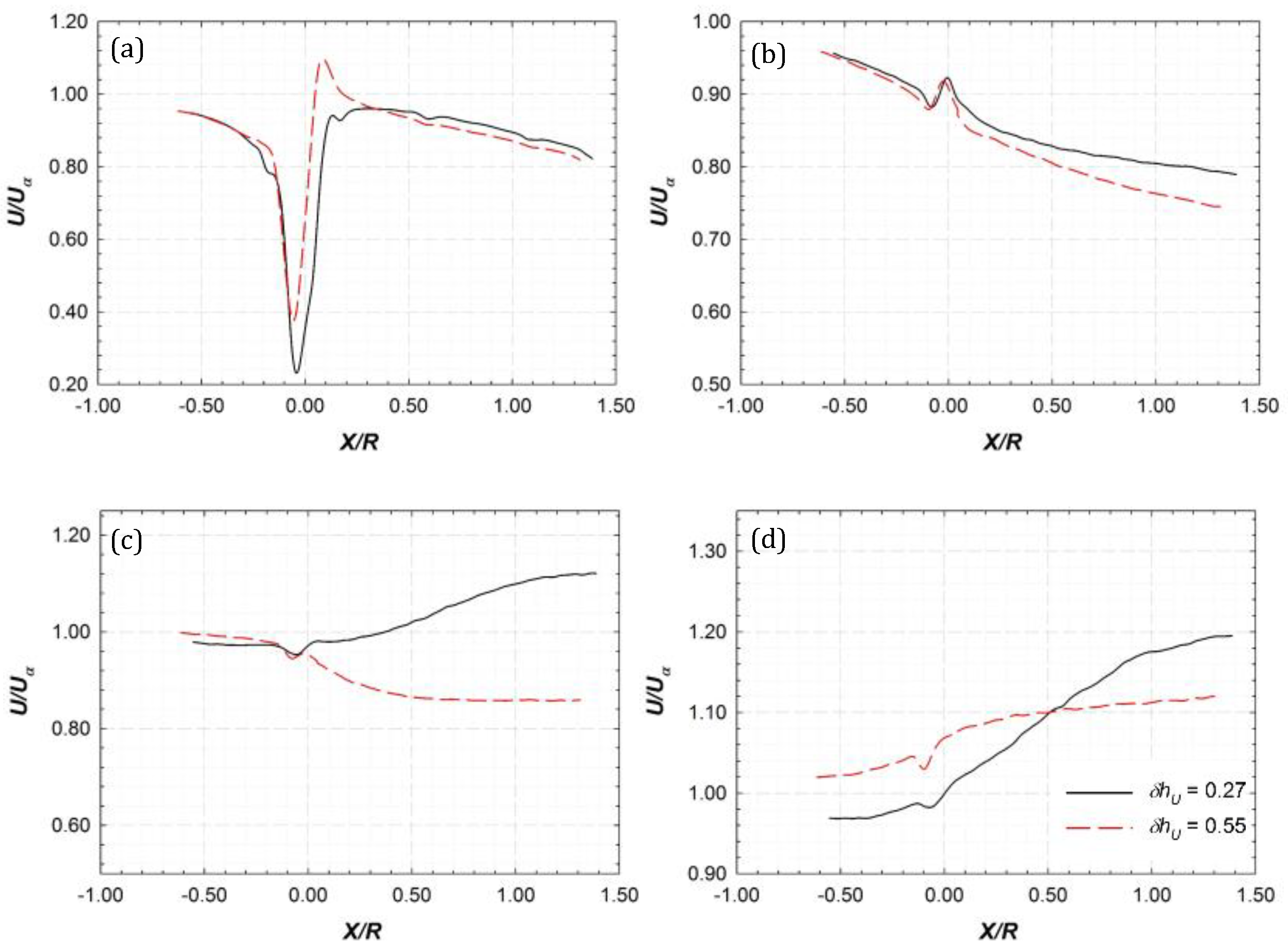
3.3.1. Profiles of Streamwise and Vertical Velocity
3.3.2. Effect of Rotational Speed on Velocity Profiles
3.3.3. Comparison of Flow in the Regions Above and Below the Turbine Axis
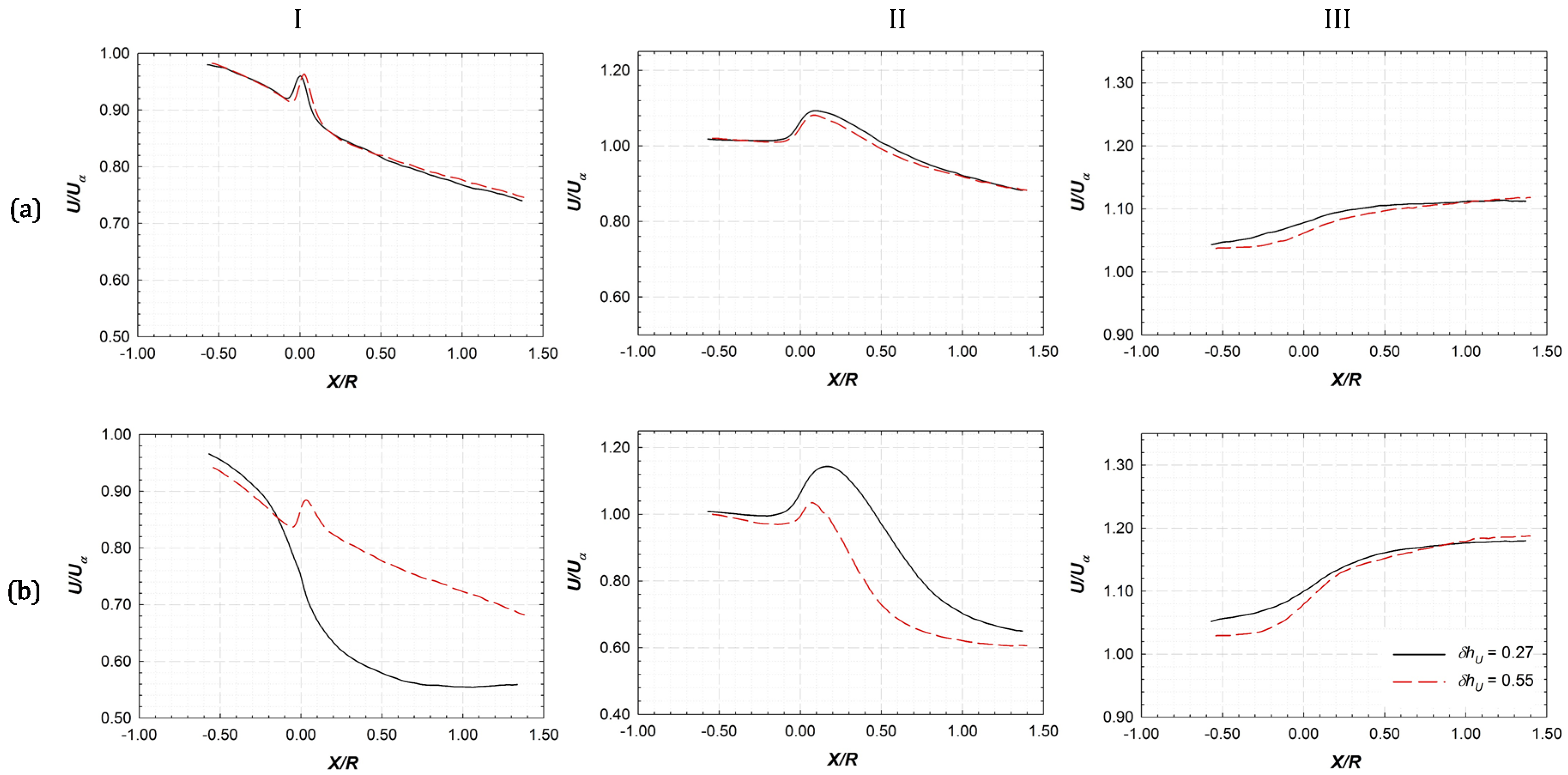
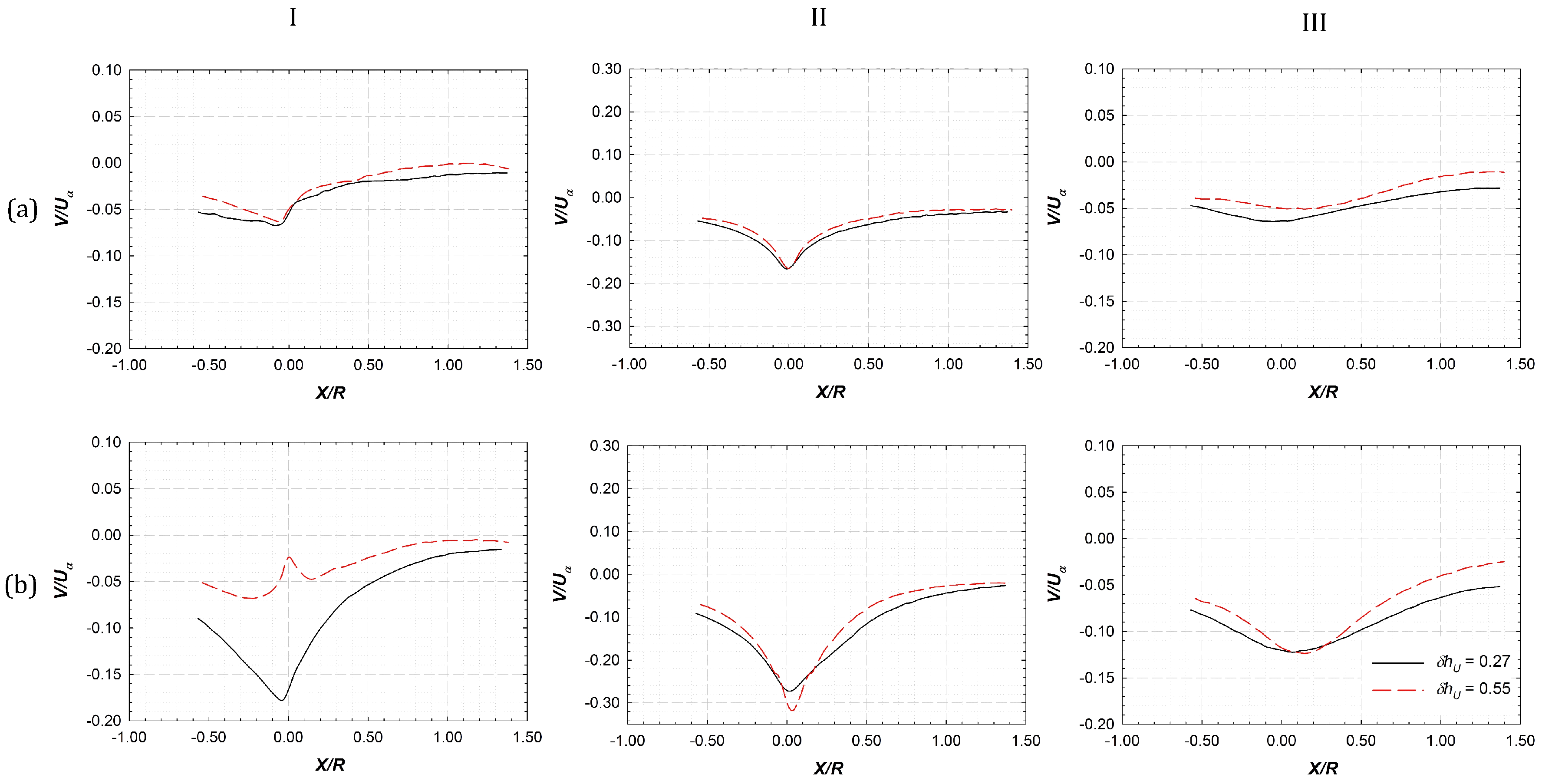
3.4. Phase-Averaged Statistics for Bypass and Wake Regions
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
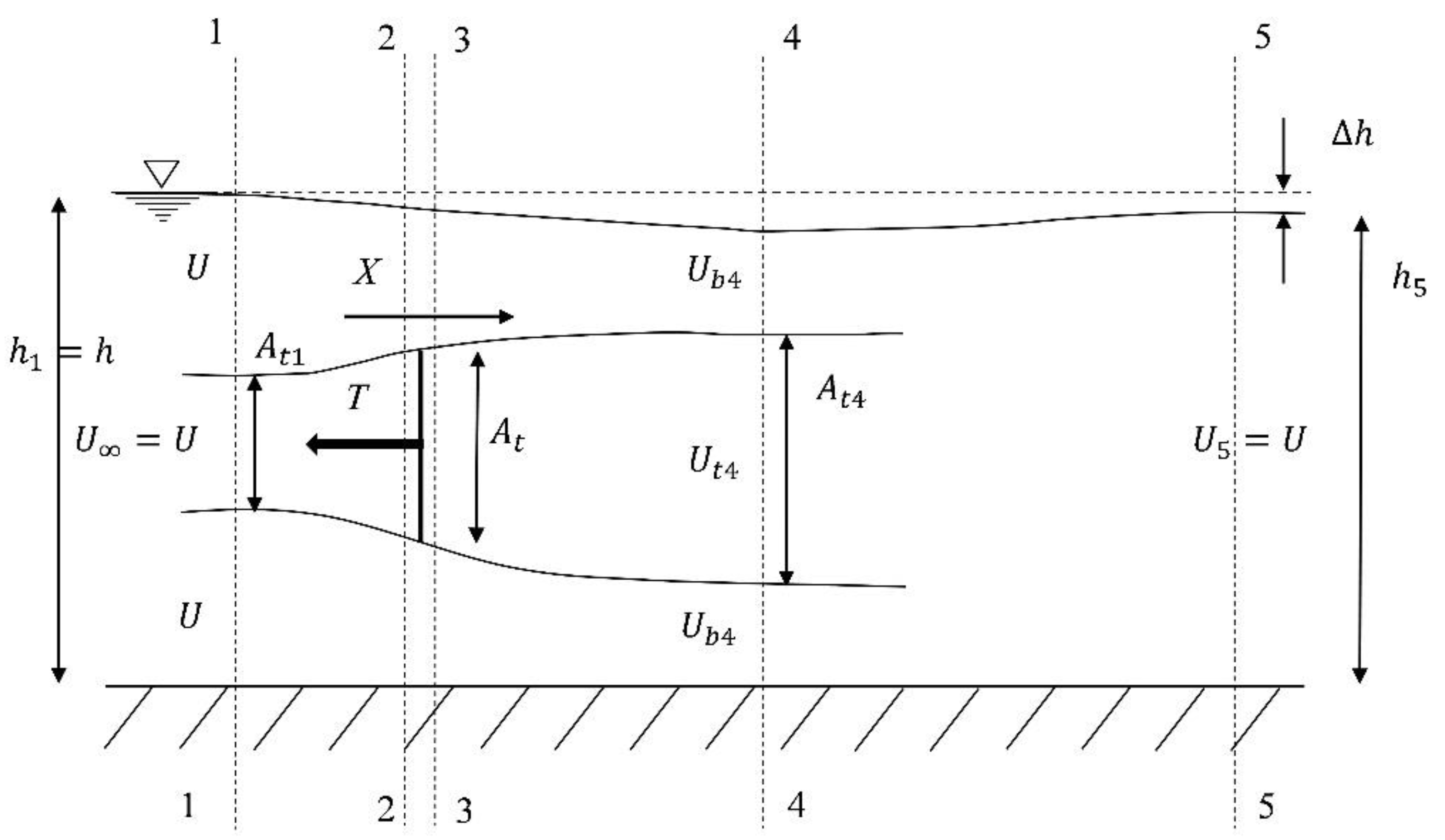
Appendix A. Blockage Correction for Experimental Data
References
- Neary, V.S. Reference Inflow Characterization for River Resource Reference Model (RM2); No. ORNL/TM-2011/360; Oak Ridge National Lab (ORNL): Oak Ridge, TN, USA, 2011.
- Goundar, J.N.; Ahmed, M.R. Marine current energy resource assessment and design of a marine current turbine for Fiji. Renew. Energy 2014, 65, 14–22. [Google Scholar] [CrossRef]
- Kolekar, N.; Banerjee, A. Performance characterization and placement of a marine hydrokinetic turbine in a tidal channel under boundary proximity and free surface effects. J. Appl. Energy 2015, 148, 121–133. [Google Scholar] [CrossRef]
- Guo, X.; Yang, J.; Gao, Z.; Moan, T.; Lu, H. The surface wave effects on the performance and the loading of a tidal turbine. Ocean Eng. 2018, 156, 120–134. [Google Scholar] [CrossRef]
- Maskell, E.C. A Theory of the Blockage Effects on Bluff Bodies and Stalled Wings in a Closed Wind Tunnel; Defense Technical Information Center: Ft. Belvoir, VA, USA, 1963.
- Gould, R.W.F. Wake Blockage Corrections in a Closed Wind Tunnel for One or Two Wall-mounted Models Subject to Separated Flow; HMSO: London, UK, 1969. [Google Scholar]
- Pope, A. Wind-Tunnel-Boundary Corrections, in Wind-tunnel Testing; John Wiley & Sons Inc.: Hoboken, NJ, USA, 1954; pp. 268–344. [Google Scholar]
- Chen, T.Y.; Liou, L.R. Blockage corrections in wind tunnel tests of small horizontal-axis wind turbines. Exp. Therm. Fluid Sci. 2011, 35, 565–569. [Google Scholar] [CrossRef]
- Medici, D.; Ivanell, S.; Dahlberg, J.Å.; Alfredsson, P.H. The upstream flow of a wind turbine: Blockage effect. Wind Energy 2011, 14, 691–697. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Molland, A.F.; Chaplin, J.R.; Batten, W.M.J. Power and thrust measurements of marine current turbines under various hydrodynamic flow conditions in a cavitation tunnel and a towing tank. Renew. Energy 2007, 32, 407–426. [Google Scholar] [CrossRef]
- Birjandi, A.H.; Bibeau, E.L.; Chatoorgoon, V.; Kumar, A. Power measurement of hydrokinetic turbines with free-surface and blockage effect. Ocean Eng. 2013, 69, 9–17. [Google Scholar] [CrossRef]
- Consul, C.A.; Willden, R.H.J.; McIntosh, S.C. Blockage effects on the hydrodynamic performance of a marine cross-flow turbine. Philos. Trans. R. Soc. A 2013, 371, 20120299. [Google Scholar] [CrossRef]
- Whelan, J.I.; Graham, J.M.R.; Peiro, J. A free-surface and blockage correction for tidal turbines. J. Fluid Mech. 2009, 624, 281–291. [Google Scholar] [CrossRef]
- Garrett, C.; Cummins, P. The efficiency of a turbine in a tidal channel. J. Fluid Mech. 2007, 588, 243–251. [Google Scholar] [CrossRef]
- McTavish, S.; Feszty, D.; Nitzsche, F. An experimental and computational assessment of blockage effects on wind turbine wake development. Wind Energy 2014, 17, 1515–1529. [Google Scholar] [CrossRef]
- Whale, J.; Anderson, C.G.; Bareiss, R.; Wagner, S. An experimental and numerical study of the vortex structure in the wake of a wind turbine. J. Wind Eng. Ind. Aerody. 2000, 84, 1–21. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Troolin, D.; Lee, S.-J.; Arndt, R.E.A.; Sotiropoulos, F. Three-dimensional flow visualization in the wake of a miniature axial-flow hydrokinetic turbine. Exp. Fluids 2013, 54, 1–12. [Google Scholar] [CrossRef]
- Chamorro, L.P.; Hill, C.; Morton, S.; Ellis, C.; Arndt, R.E.A.; Sotiropoulos, F. On the interaction between a turbulent open channel flow and an axial-flow turbine. J. Fluid Mech. 2013, 716, 658–670. [Google Scholar] [CrossRef]
- Lust, E.E.; Flack, K.A.; Luznik, L. Survey of the near wake of an axial-flow hydrokinetic turbine in quiescent conditions. Renew. Energy 2018, 129, 92–101. [Google Scholar] [CrossRef]
- Eriksen, P.E.; Krogstad, P.Å. An experimental study of the wake of a model wind turbine using phase-averaging. Int. J. Heat Fluid Flow 2017, 67, 52–62. [Google Scholar] [CrossRef]
- Aghsaee, P.; Markfort, C.D. Effects of flow depth variations on the wake recovery behind a horizontal-axis hydrokinetic in-stream turbine. Renew. Energy 2018, 125, 620–629. [Google Scholar] [CrossRef]
- Chen, Y.; Lin, B.; Sun, J.; Guo, J.; Wu, W. Hydrodynamic effects of the ratio of rotor diameter to water depth: An experimental study. Renew. Energy 2019, 136, 331–341. [Google Scholar] [CrossRef]
- Bahaj, A.S.; Myers, L.E.; Rawlinson-Smith, R.I.; Thomson, M. The Effect of Boundary Proximity upon the Wake Structure of Horizontal Axis Marine Current Turbines. J. Offshore Mech. Arct. Eng. 2011, 134, 021104. [Google Scholar] [CrossRef]
- Manar, F.; Medina, A.; Jones, A. Tip vortex structure and aerodynamic loading on rotating wings in confined spaces. Exp. Fluids 2014, 55, 1–18. [Google Scholar] [CrossRef]
- Vinod, A.; Banerjee, A. Performance and near-wake characterization of a tidal current turbine in elevated levels of free stream turbulence. Appl. Energy 2019, 254, 113639. [Google Scholar] [CrossRef]
- Vinod, A.; Lawrence, A.; Banerjee, A. Effects of Free Stream Turbulence on Tidal Turbines. Part II-Turbine Performance and Near Wake Characteristics. In Proceedings of the 12th European Wave and Tidal Energy Conference, Cork, Ireland, 27 August–1 September 2017. [Google Scholar]
- Kline, S.J.; McClintock, F.A. Describing Uncertainties in Single-Sample Experiments. Mech. Eng. 1953, 75, 3–8. [Google Scholar]
- INSIGHT4G Data Acquisition, Analysis, and Display Software Platform-Users Guide; TSI Inc.: Shoreview, MN, USA, 2011.
- Adrian, R.J.; Westerweel, J. Particle Image Velocimetry; Cambridge University Press: Cambridge, MA, USA, 2011. [Google Scholar]
- Manwell, J.F.; McGowan, J.G.; Rogers, A.L. Wind Energy Explained: Theory, Design and Application, 2nd ed.; John Wiley and Sons: New York, NY, USA, 2009. [Google Scholar]
- Van Kuik, G.A.M.; Sørensen, J.N.; Okulov, V.L. Rotor theories by Professor Joukowsky: Momentum theories. Prog. Aerosp. Sci. 2015, 73, 1–18. [Google Scholar] [CrossRef]
- Berkooz, G.; Holmes, P.; Lumley, J.L. The Proper Orthogonal Decomposition in the Analysis of Turbulent Flows. Ann. Rev. Fluid Mech. 1993, 25, 539–575. [Google Scholar] [CrossRef]
- Lumley, J.L. The structure of inhomogeneous turbulent flows. In Atmospheric Turbulence and Radio Propagation; Yaglom, A.M., Tatarski, V.I., Eds.; Nauka: Moscow, Russia, 1967; pp. 166–178. [Google Scholar]
- Lumley, J.L. Coherent Structures in Turbulence. Transition and Turbulence; Academic Press: New York, NY, USA, 1981; pp. 215–242. [Google Scholar]
- Myers, L.; Bahaj, A.S. Wake Studies of a 1/30th Scale Horizontal Axis Marine Current Turbine. Ocean Eng. 2007, 34, 758–762. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kolekar, N.; Vinod, A.; Banerjee, A. On Blockage Effects for a Tidal Turbine in Free Surface Proximity. Energies 2019, 12, 3325. https://doi.org/10.3390/en12173325
Kolekar N, Vinod A, Banerjee A. On Blockage Effects for a Tidal Turbine in Free Surface Proximity. Energies. 2019; 12(17):3325. https://doi.org/10.3390/en12173325
Chicago/Turabian StyleKolekar, Nitin, Ashwin Vinod, and Arindam Banerjee. 2019. "On Blockage Effects for a Tidal Turbine in Free Surface Proximity" Energies 12, no. 17: 3325. https://doi.org/10.3390/en12173325
APA StyleKolekar, N., Vinod, A., & Banerjee, A. (2019). On Blockage Effects for a Tidal Turbine in Free Surface Proximity. Energies, 12(17), 3325. https://doi.org/10.3390/en12173325




