Torque Ripple Mitigation of T-3L Inverter Fed Open-End Doubly-Salient Permanent-Magnet Motor Drives Using Current Hysteresis Control
Abstract
:1. Introduction
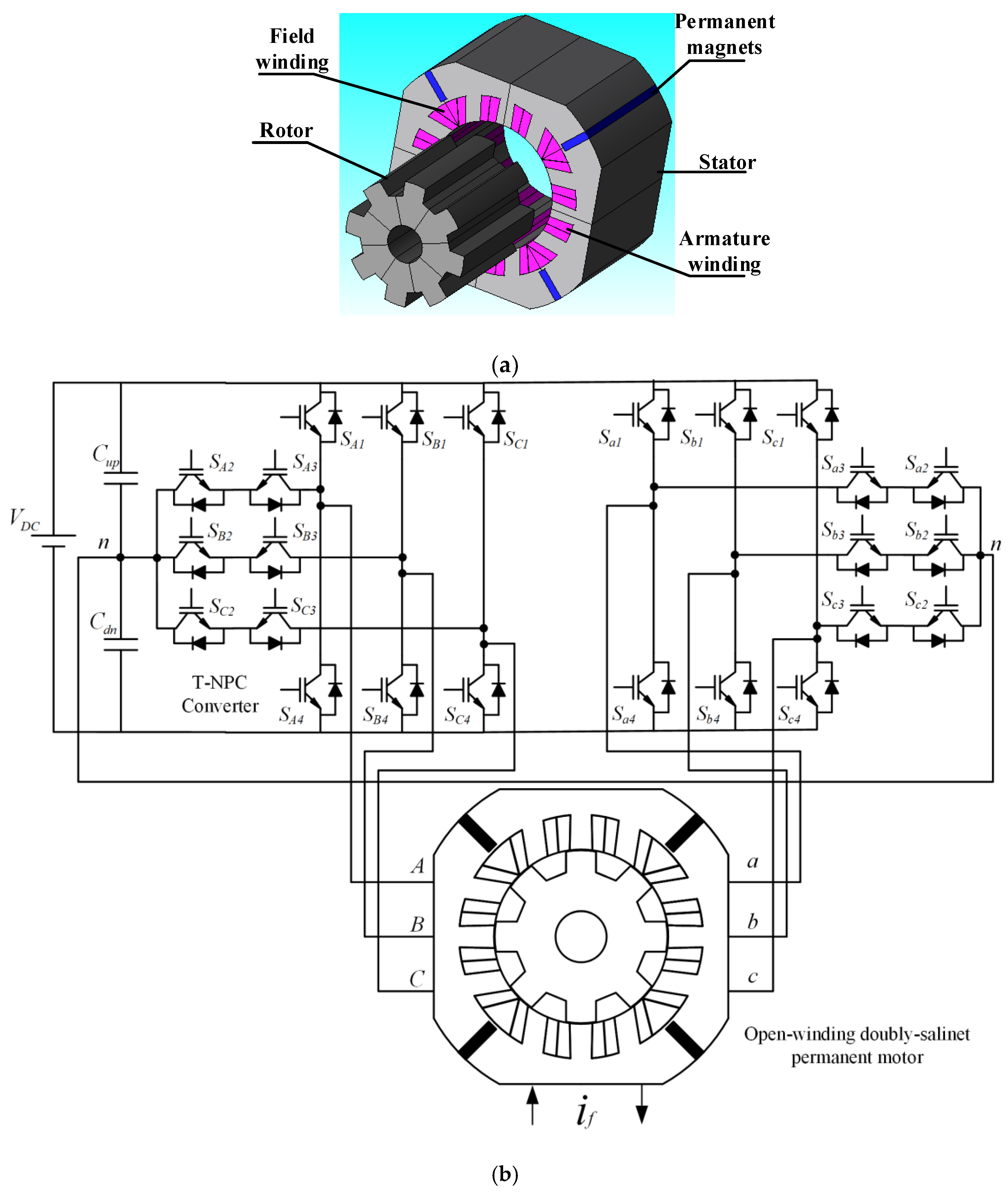
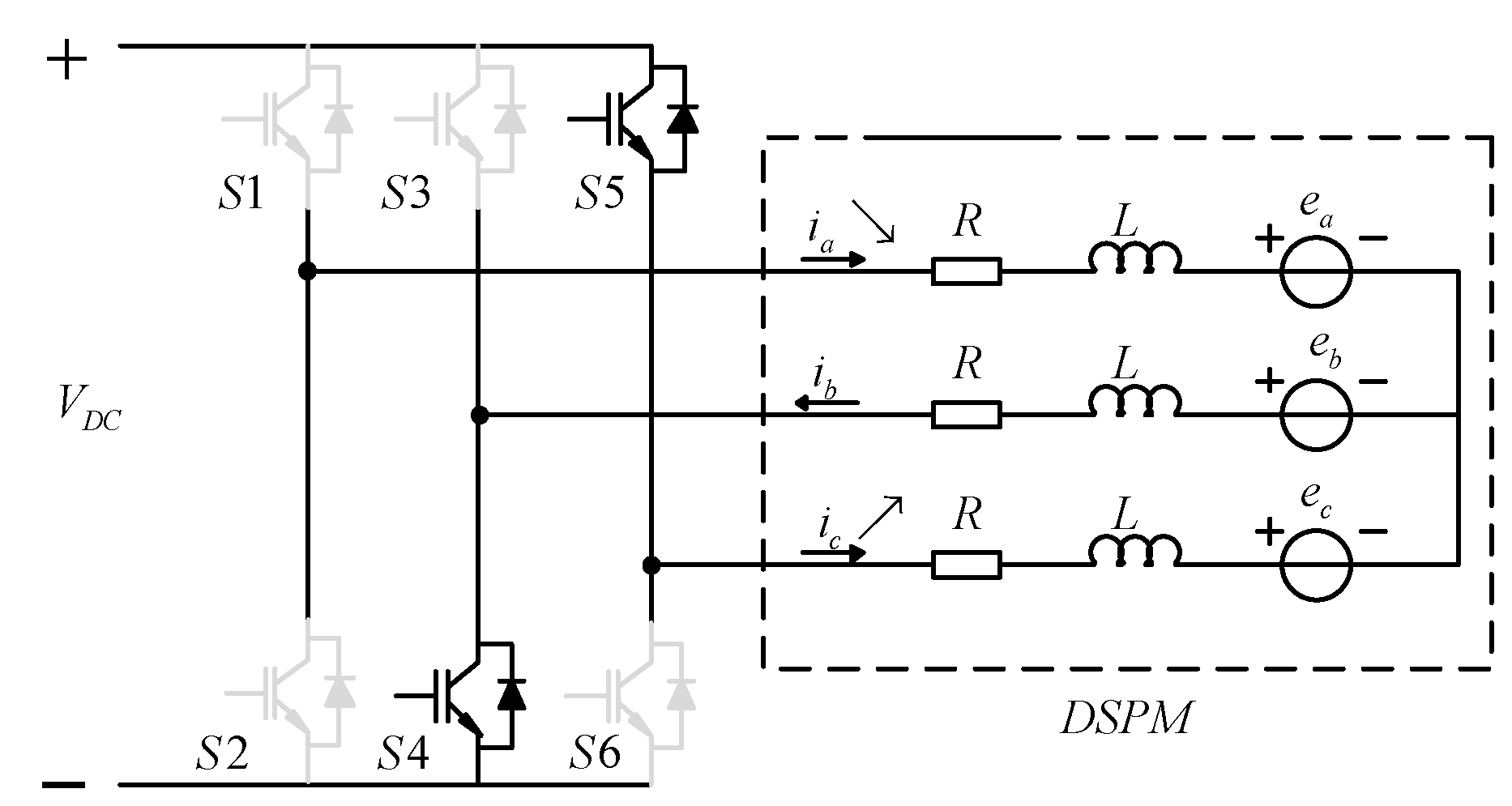
2. Configuration and Modeling
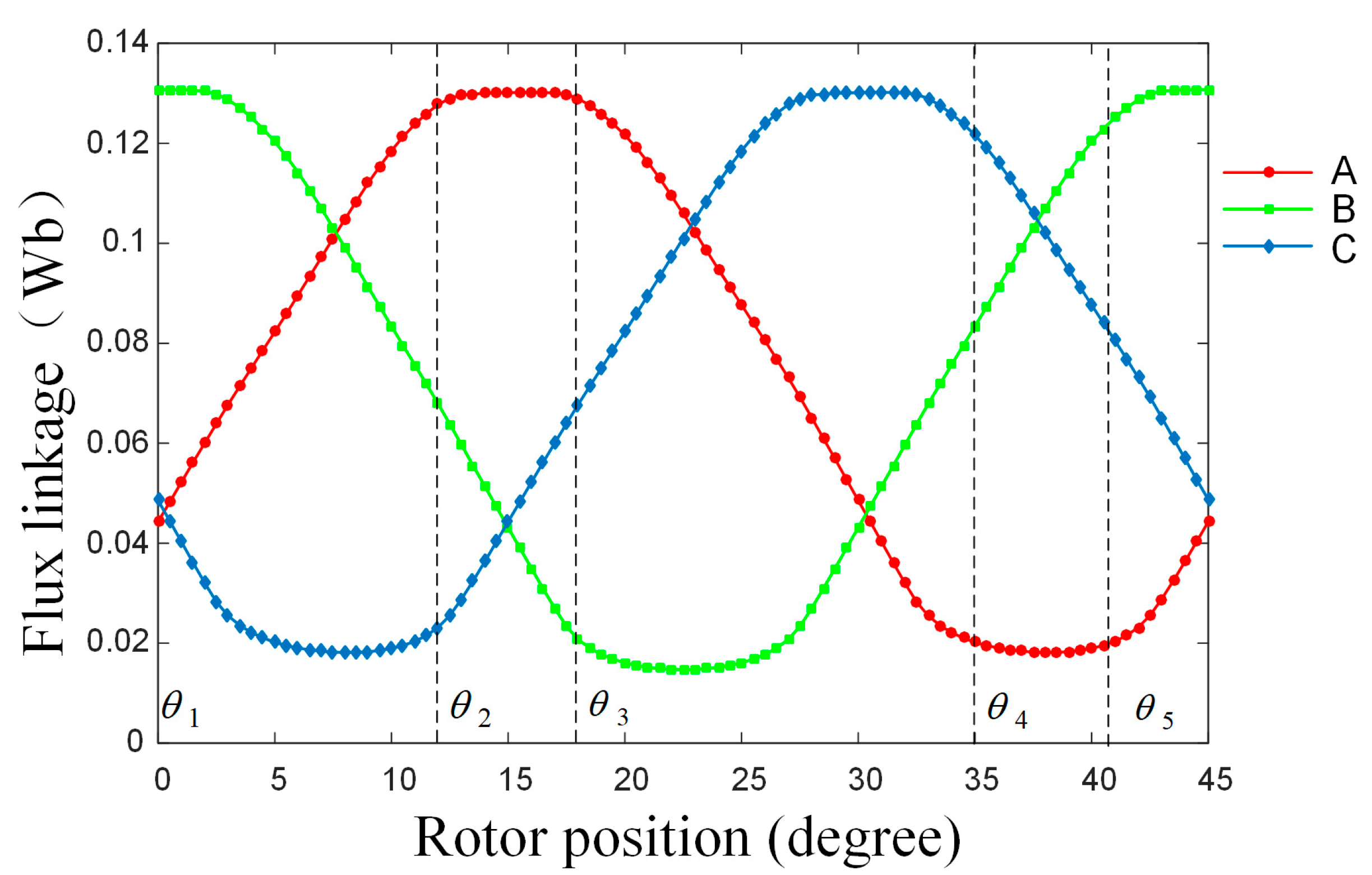
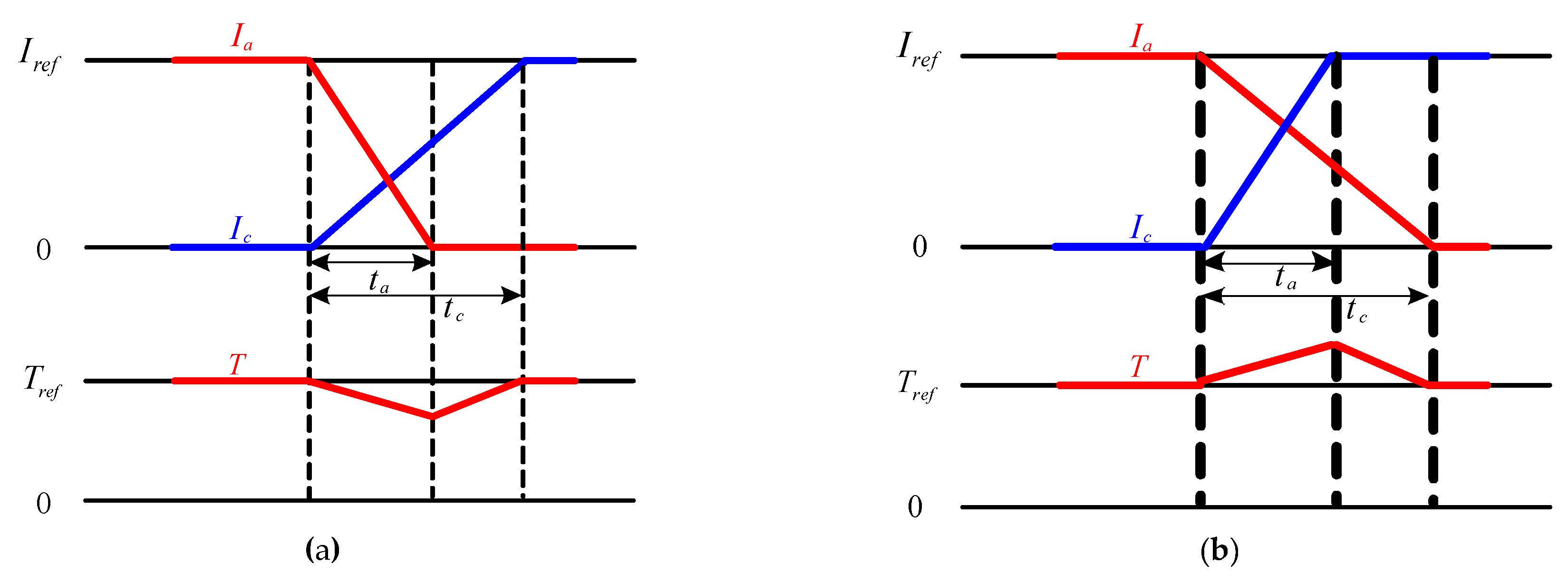
3. Current Reference Design for Torque Ripple Mitigation
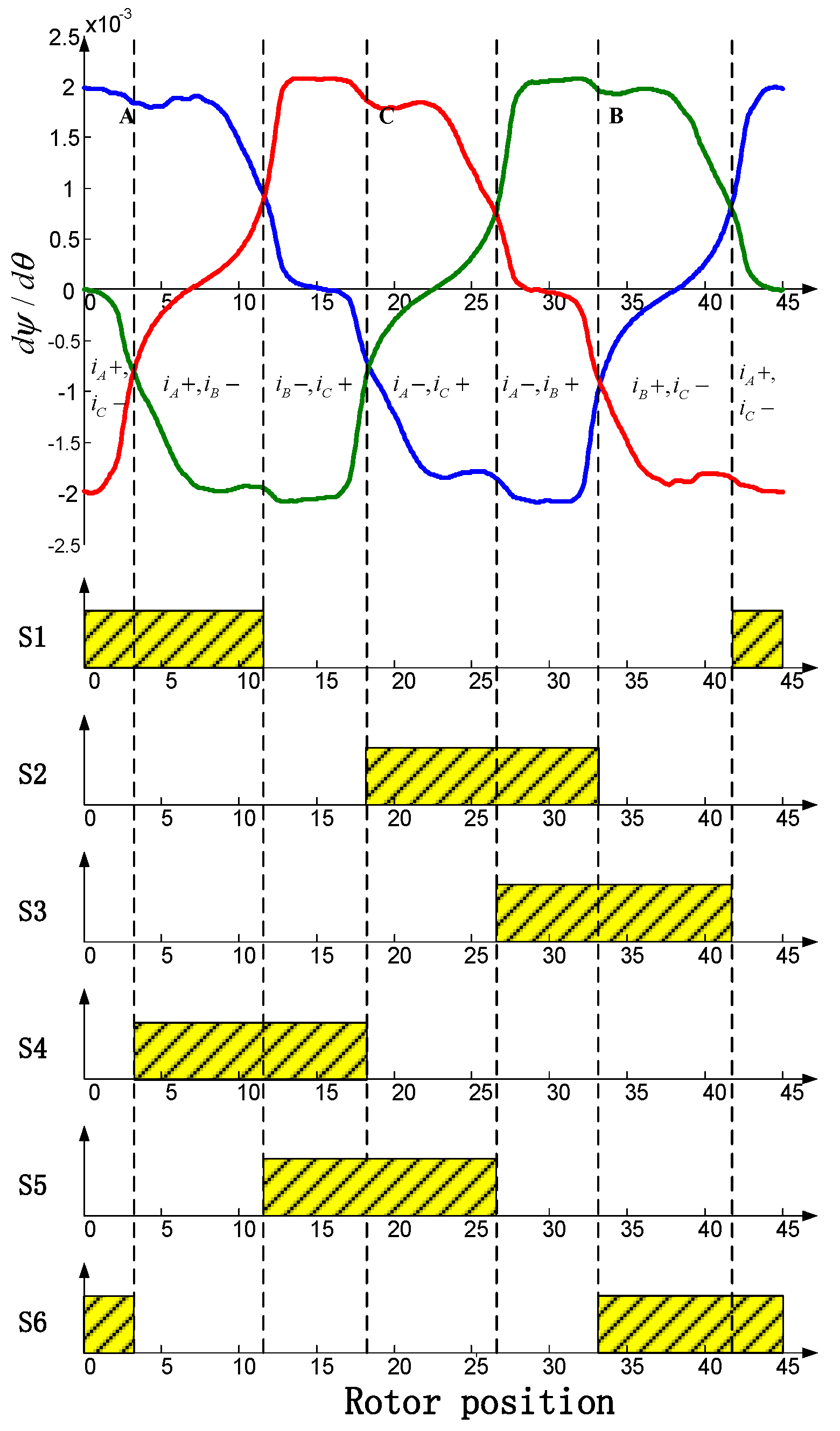
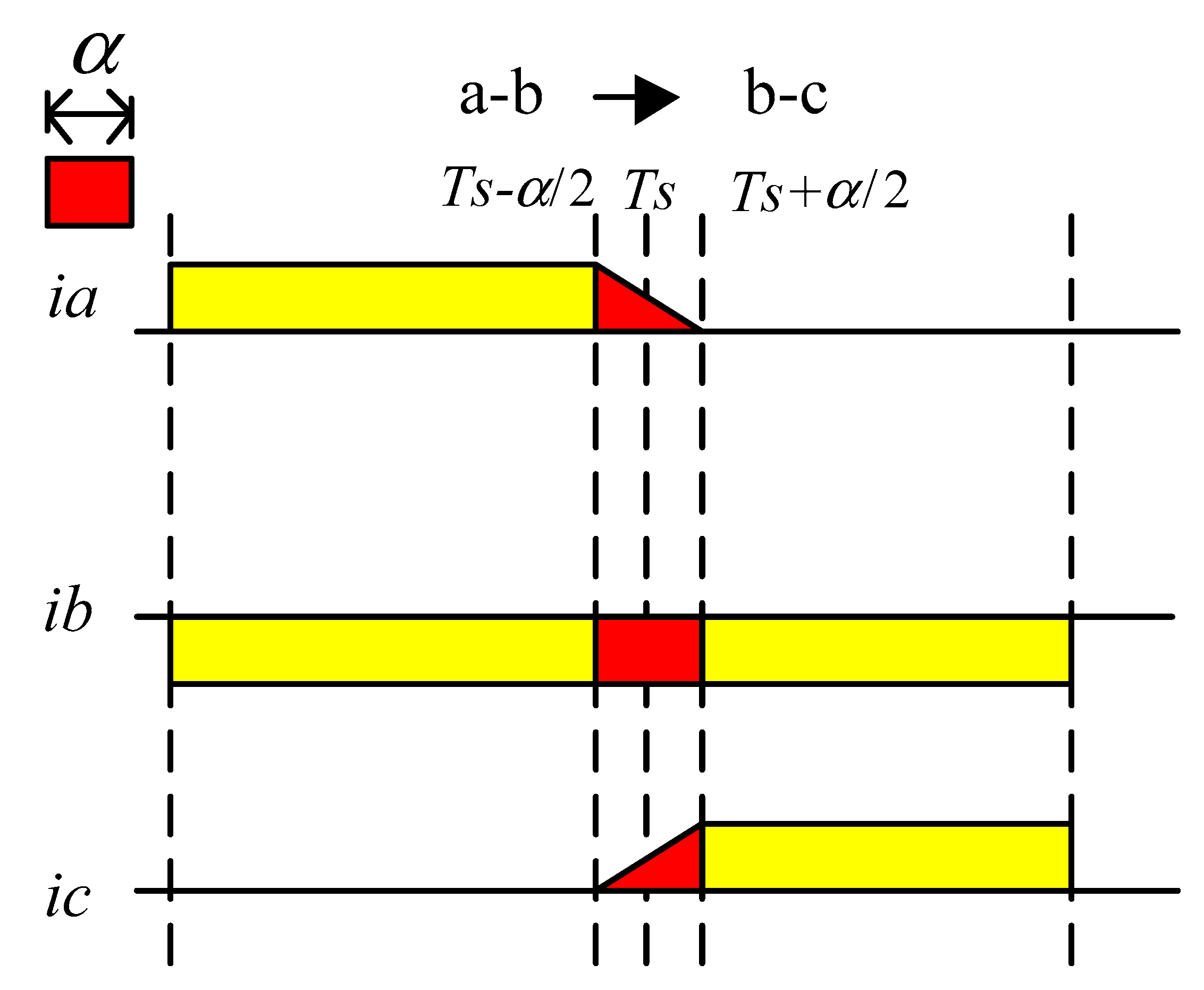
4. Phase Commutation Strategy for Torque Ripple Mitigation
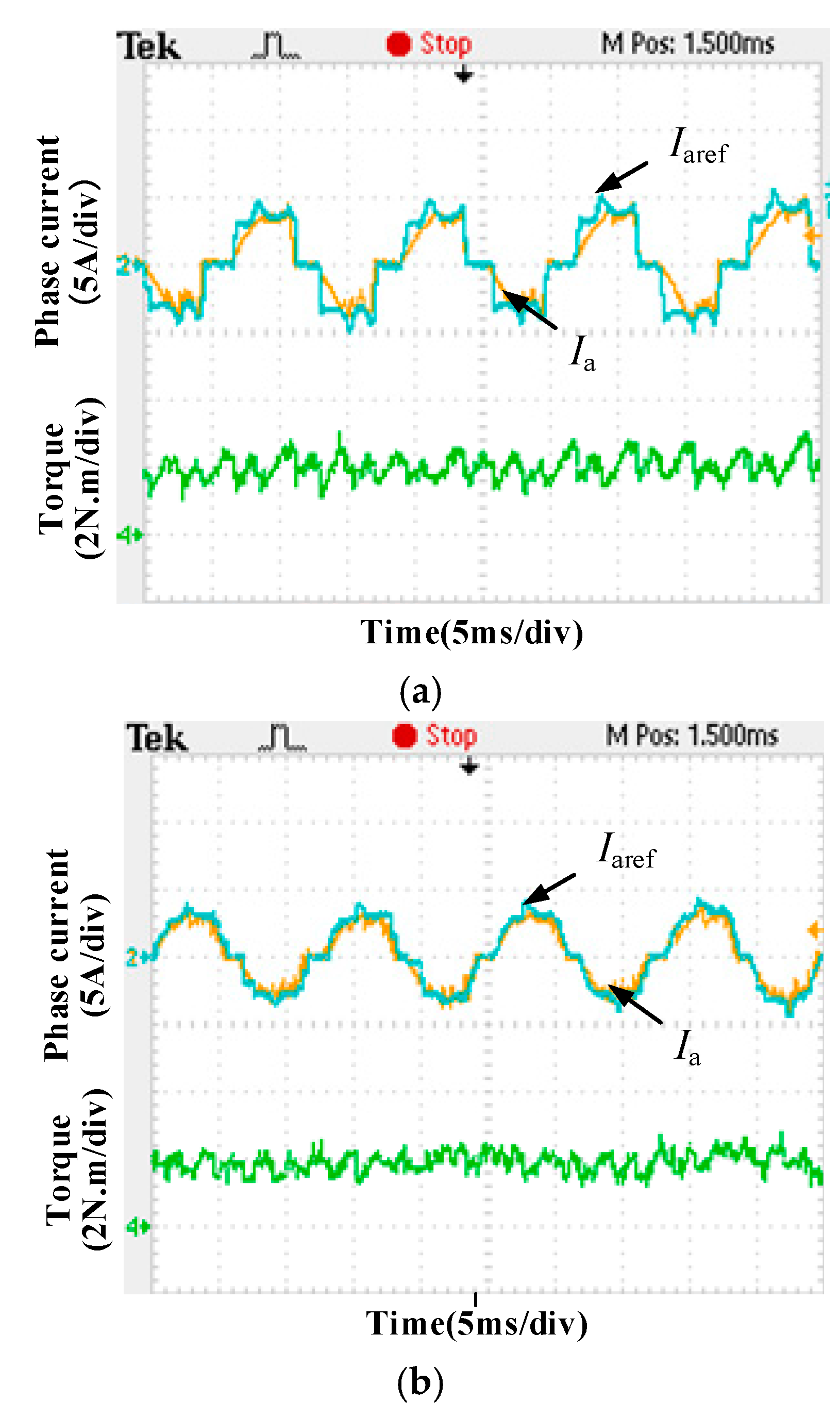
5. Current Tracking for Torque Ripple Mitigation
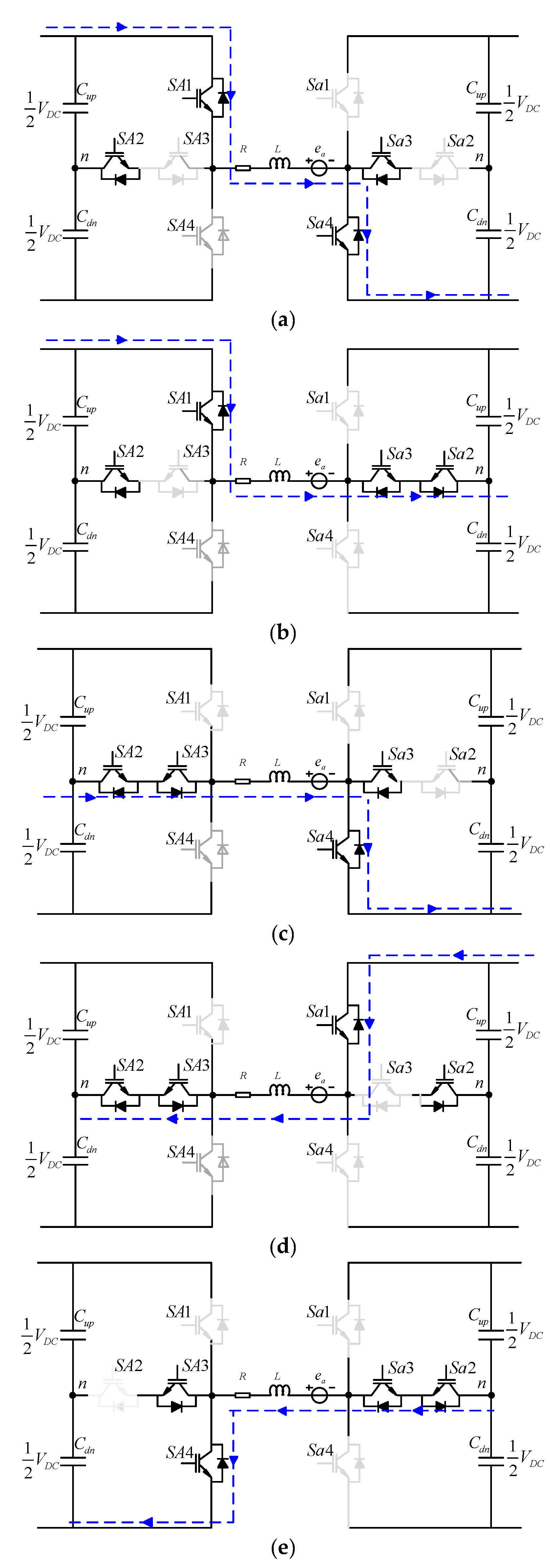
5.1. Hysteresis Current Control
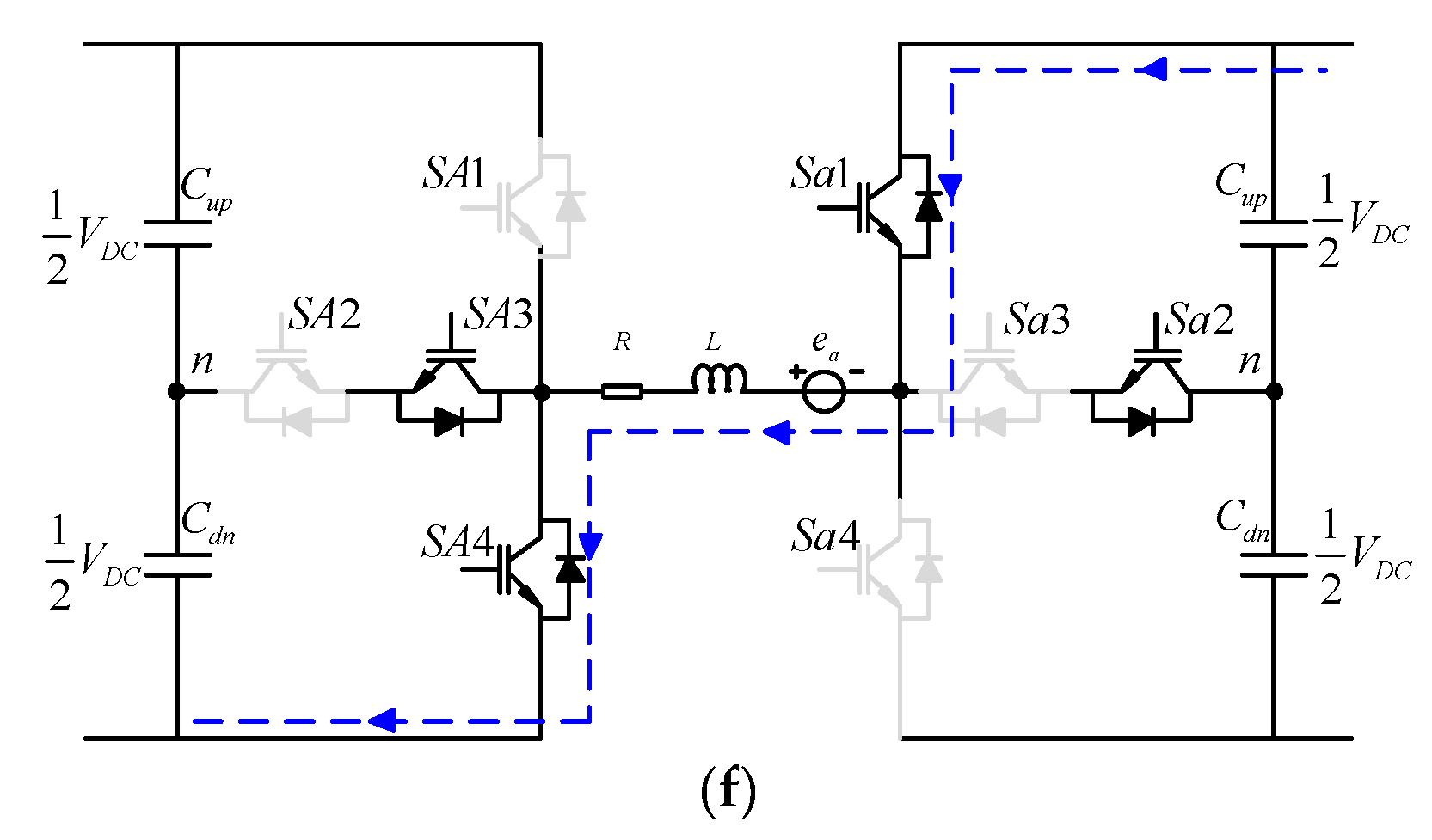
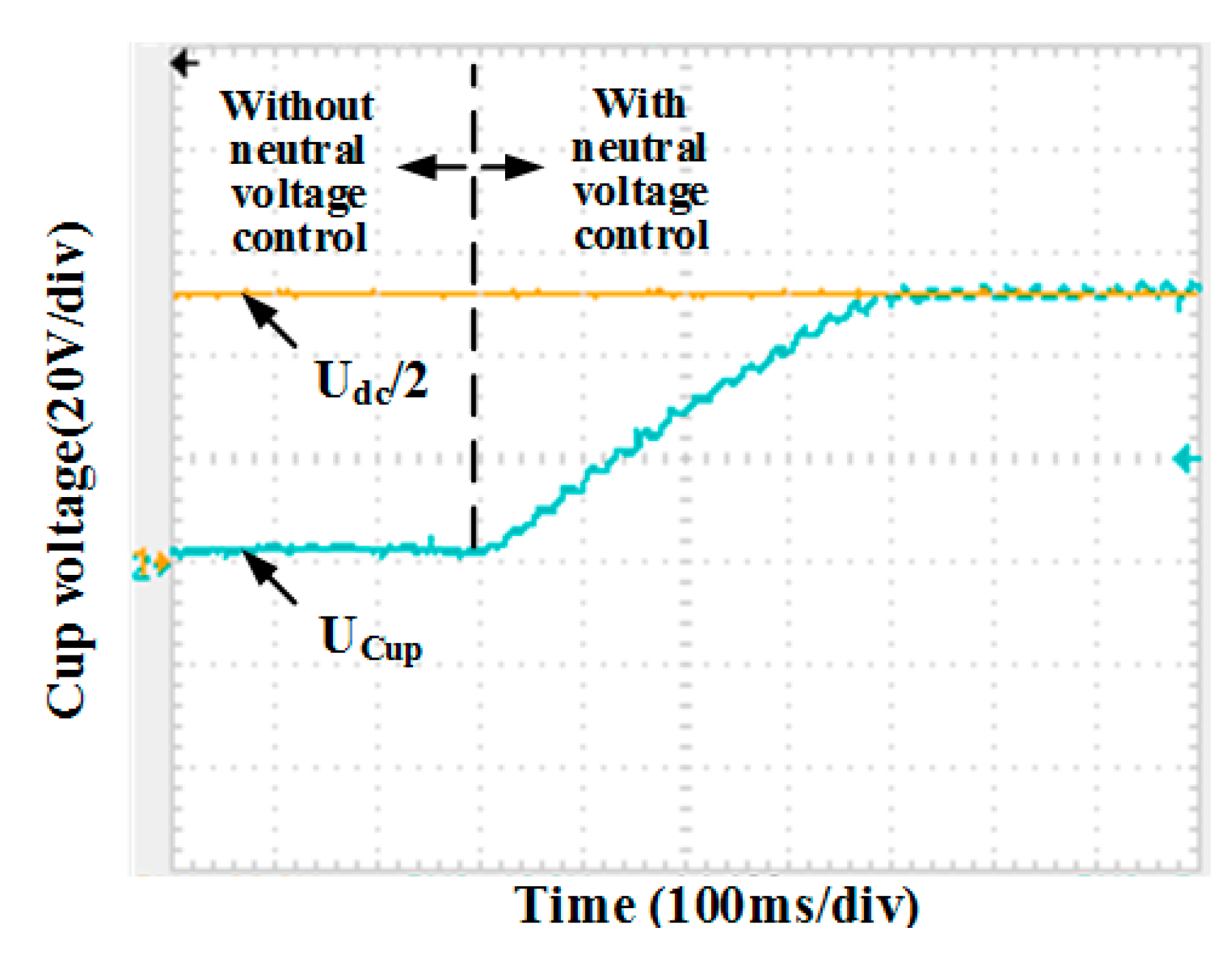
5.2. Control of Mid-Point Voltage in DC Link
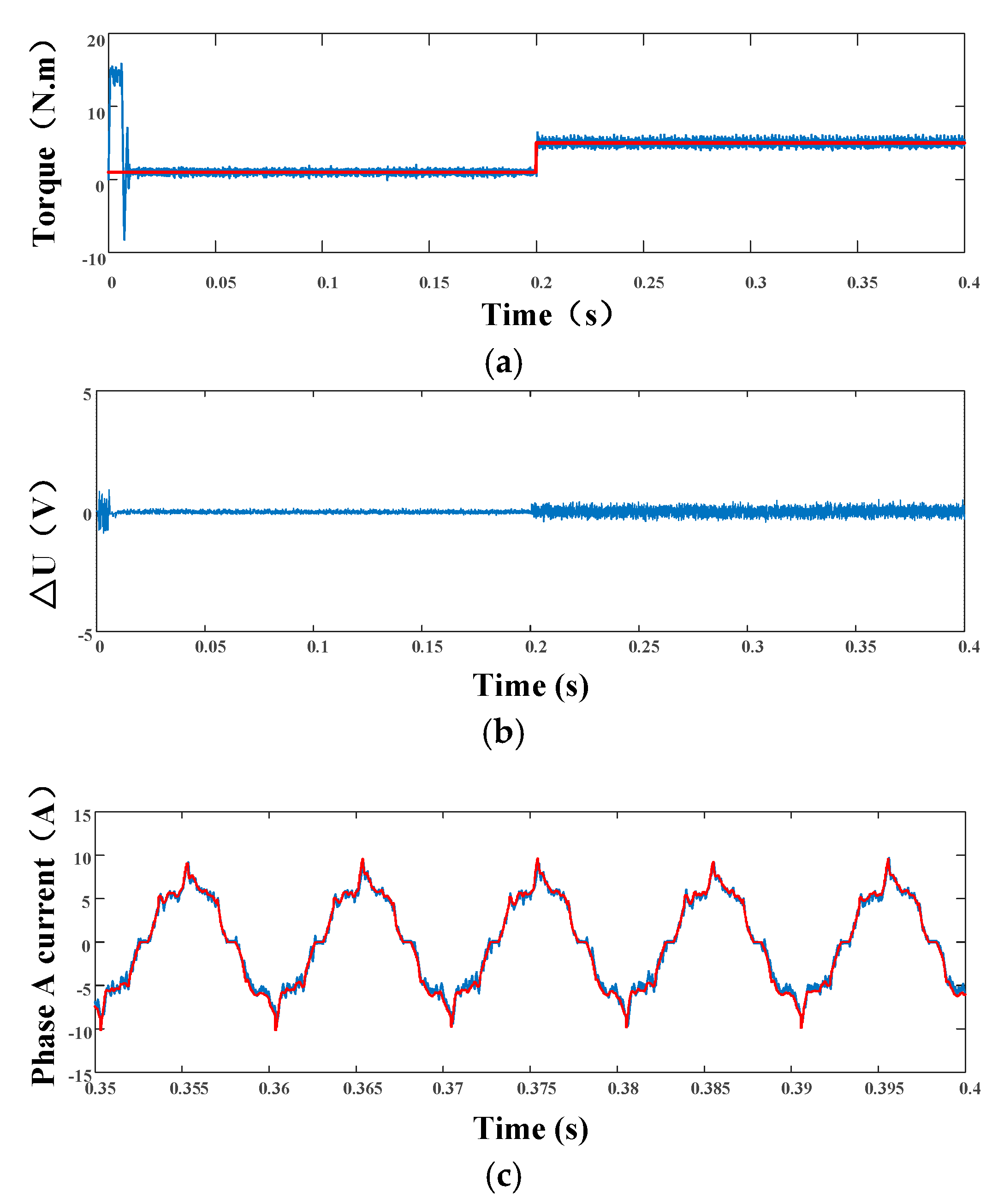
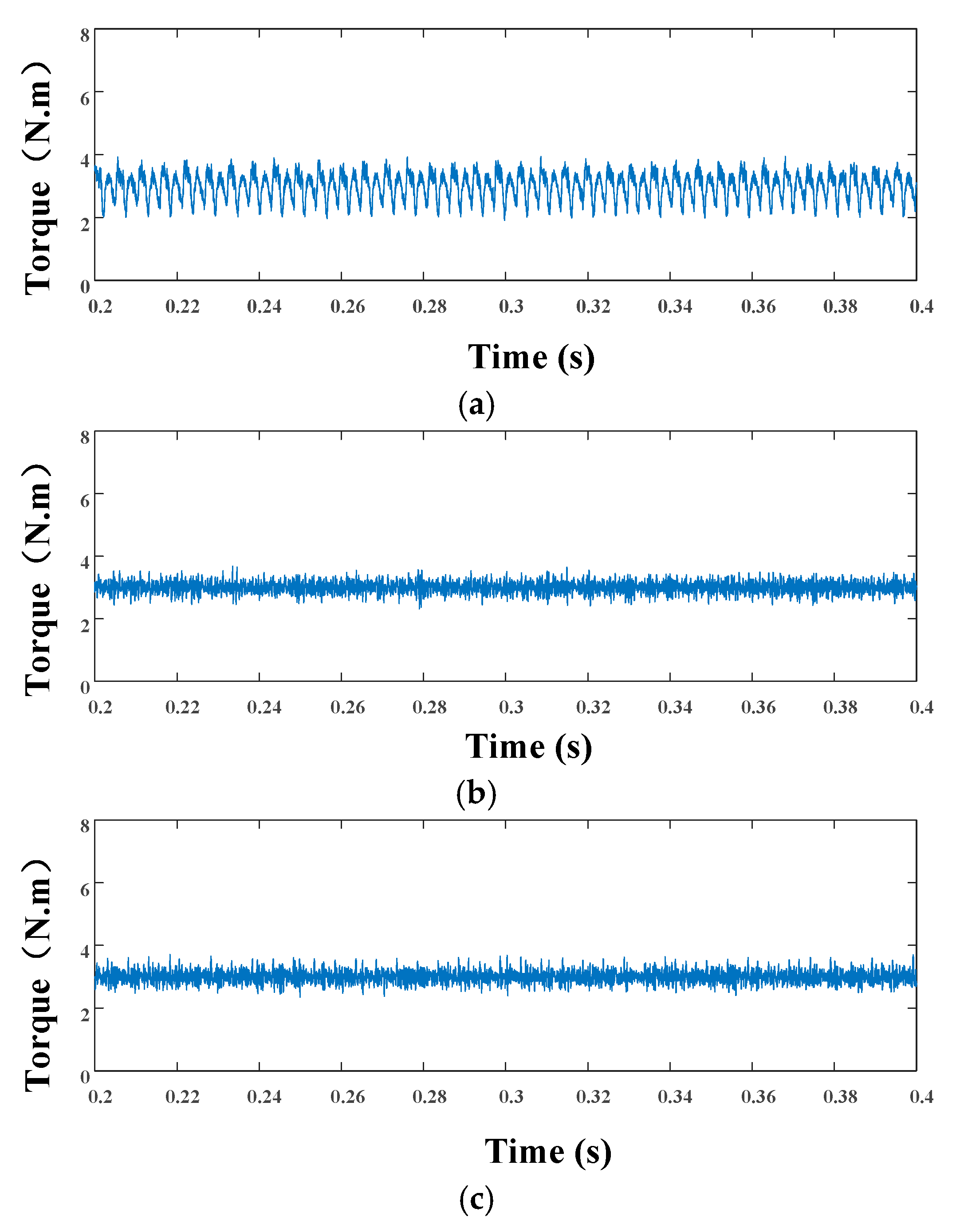
6. Simulation and Experimental Verification
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Afinowi, I.A.A.; Zhu, Z.Q.; Guan, Y.; Mipo, J.C.; Farah, P. Hybrid-Excited Doubly Salient Synchronous Machine with Permanent Magnets Between Adjacent Salient Stator Poles. IEEE Trans. Magn. 2015, 51, 1–9. [Google Scholar] [CrossRef]
- Chan, B.C.C. The State of the Art of Electric, Hybrid, and Fuel Cell Vehicles. Proc. IEEE 2007, 95, 704–718. [Google Scholar] [CrossRef]
- Cheng, M.; Hua, W.; Zhang, J.; Zhao, W. Overview of Stator-Permanent Magnet Brushless Machines. IEEE Trans. Ind. Electron. 2011, 58, 5087–5101. [Google Scholar] [CrossRef]
- Cheng, M.; Chau, K.T.; Chan, C.C.; Sun, Q. Control and operation of a new 8/6-pole doubly salient permanent-magnet motor drive. IEEE Trans. Ind. Appl. 2003, 39, 1363–1371. [Google Scholar] [CrossRef]
- Yuan, X.; Gao, Y.; Ehsani, M. Harmonic control of chopping frequency and shaft speed in SRM. In Proceedings of the 2008 IEEE Vehicle Power and Propulsion Conference, Harbin, China, 3–5 September 2008; pp. 1–5. [Google Scholar]
- Lu, J.X.; Ebihara, D.; Hamatsu, K.; Arima, H. A movable angle control strategy of switched reluctance motor with Hall-effect position sensor. In Proceedings of the IPEMC 2000 Third International Power Electronics and Motion Control Conference (IEEE Cat. No.00EX435), Beijing, China, 15–18 August 2000; Volume 3, pp. 1279–1284. [Google Scholar]
- Harkati, N.; Moreau, L.; Zaïm, M.E.; Charpentier, J.F. Torque-speed characteristic determination of an excited doubly salient machine (DSPM). In Proceedings of the 2014 International Conference on Electrical Sciences and Technologies in Maghreb (CISTEM), Tunis, Tunisia, 3–6 November 2014; pp. 1–6. [Google Scholar]
- Fan, H.; Chau, K.T.; Cao, L.; Jiang, C. Design and Analysis of a New Bipolar-Flux DSPM Linear Machine. IEEE Trans. Energy Convers. 2018, 33, 2081–2090. [Google Scholar] [CrossRef]
- Ji, Y.; Yang, Y.; Zhou, J.; Ding, H.; Guo, X.; Padmanaban, S. Control Strategies of Mitigating Dead-time Effect on Power Converters: An Overview. Electronics 2019, 8, 196. [Google Scholar] [CrossRef]
- Yu, C.; Chau, K.T. Dual-Mode Operation in DC-Excited Memory Motors Under Flux Regulation. IEEE Trans. Ind. Appl. 2011, 47, 2031–2041. [Google Scholar] [CrossRef]
- Sekhar, K.R.; Srinivas, S. Discontinuous Decoupled PWMs for Reduced Current Ripple in a Dual Two-Level Inverter Fed Open-End Winding Induction Motor Drive. IEEE Trans. Power Electron. 2013, 28, 2493–2502. [Google Scholar] [CrossRef]
- Gaeta, G.; Scelba, G.; Consoli, A. Modeling and Control of Three-Phase PMSMs Under Open-Phase Fault. IEEE Trans. Ind. Appl. 2013, 49, 74–83. [Google Scholar] [CrossRef]
- Yi, L.; Zhao, M. Doubly Salient Permanent Magnet Motor Development Review. In Proceedings of the 2013 Third International Conference on Instrumentation, Measurement, Computer, Communication and Control, Shenyang, China, 21–23 September 2013; pp. 1513–1516. [Google Scholar]
- Babu, A.S.; Rajagopal, K.R.E. Analysis of multiphase doubly salient permanent magnet motors. IEEE Trans. Magn. 2005, 41, 3955–3957. [Google Scholar] [CrossRef]
- Hua, W.; Ming, C. Inductance characteristics of 3-phase flux-switching permanent magnet machine with doubly-salient structure. In Proceedings of the 2006 CES/IEEE 5th International Power Electronics and Motion Control Conference, Shanghai, China, 14–16 August 2006; pp. 1–5. [Google Scholar]
- Guo, X.; Yang, Y.; He, R.; Wang, B.; Blaabjerg, F. Transformerless Z-source four-leg PV inverter with leakage current reduction. IEEE Trans. Power Electron. 2019, 34, 4343–4352. [Google Scholar] [CrossRef]
- Rodriguez, J.; Franquelo, L.G.; Kouro, S.; Leon, J.I.; Portillo, R.C.; Prats, M.A.M.; Perez, M.A. Multilevel converters: An enabling technology for high-power applications. Proc. IEEE 2009, 97, 1786–1817. [Google Scholar] [CrossRef]
- Guo, X.; Zhou, J.; He, R.; Jia, X.; Rojas, C.A. Leakage current attenuation of a three-phase cascaded inverter for transformerless grid-connected PV systems. IEEE Trans. Ind. Electron. 2018, 65, 676–686. [Google Scholar] [CrossRef]
- Lezana, P.; Pou, J.; Meynard, T.A.; Rodriguez, J.; Ceballos, S.; Richardeau, F. Survey on fault operation on multilevel inverters. IEEE Trans. Ind. Electron. 2010, 57, 2207–2218. [Google Scholar] [CrossRef]
- Guo, X.; Jia, X. Hardware-based cascaded topology and modulation strategy with leakage current reduction for transformerless PV systems. IEEE Trans. Ind. Electron. 2016, 62, 7823–7832. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Chen, J.; Cheng, M. Fault-Tolerant Control of NPC Three-Level Inverters-Fed Double-Stator-Winding PMSM Drives Based on Vector Space Decomposition. IEEE Trans. Ind. Electron. 2017, 64, 8446–8458. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, X.; Cao, J.; Cheng, M.; Hu, Y. Direct Torque Control of T-NPC Inverters-Fed Double-Stator-Winding PMSM Drives with SVM. IEEE Trans. Power Electron. 2018, 33, 1541–1553. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Chen, J.; Hu, Y. Decoupled Vector Space Decomposition Based Space Vector Modulation for Dual Three-Phase Three-Level Motor Drives. IEEE Trans. Power Electron. 2018, 33, 10683–10697. [Google Scholar] [CrossRef]
- Choi, U.; Blaabjerg, F. A novel active T-type three-level converter with open-circuit fault-tolerant control. In Proceedings of the 2015 IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015; pp. 4765–4772. [Google Scholar]



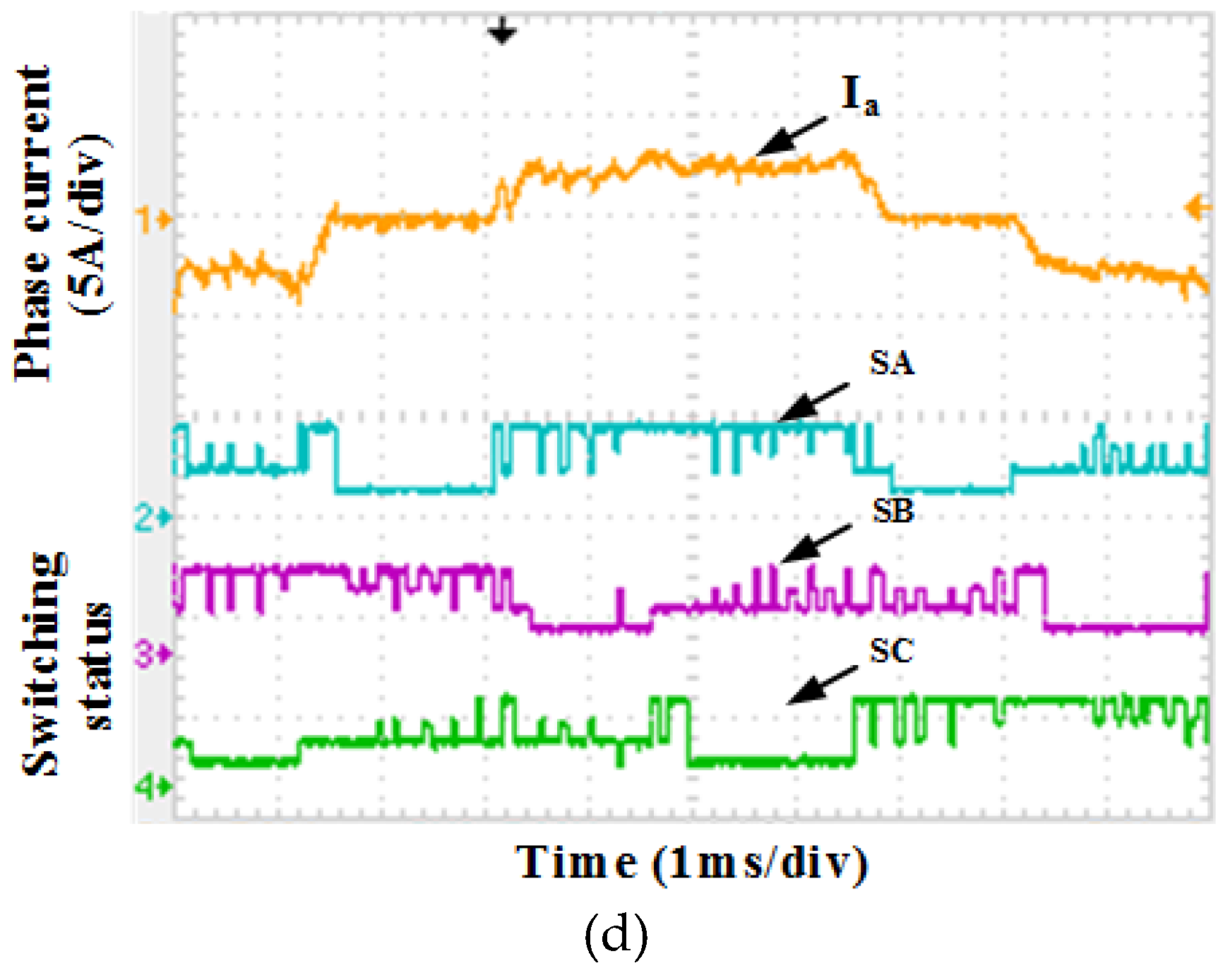
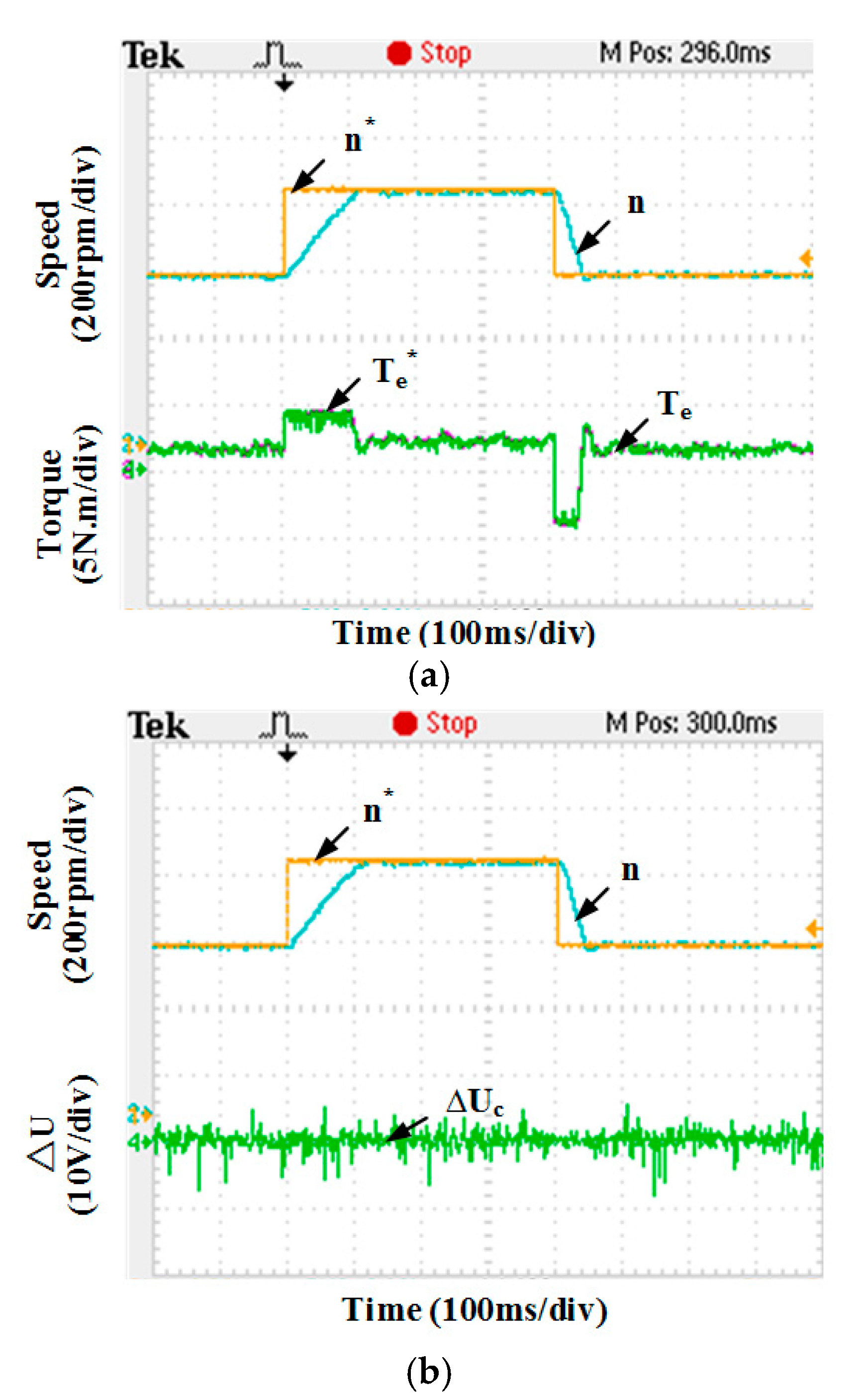
| Switching Status | SA1 | SA2 | SA3 | SA4 | Status Number |
|---|---|---|---|---|---|
| P | ON | ON | OFF | OFF | 4 |
| O | OFF | ON | ON | OFF | 3 |
| N | OFF | OFF | ON | ON | 2 |
| X | OFF | OFF | OFF | OFF | 1 |
| e(i) | (SA, Sa) |
|---|---|
| e(i) > BW1 | (4, 2) |
| BW2 < e(i) ≤ BW1 | (4, 3), (3, 2) |
| −BW2 ≤ e(i) ≤ BW2 | Maintain the last sample cycle’s switching state |
| −BW1 ≤ e(i) < −BW2 | (3, 4), (2, 3) |
| e(i) < −BW1 | (2, 4) |
| Current Direction | uCup < Vdc/2 | uCup < Vdc/2 | ||
|---|---|---|---|---|
I  | I  | I  | I  | |
| From A to a | (3, 2) | (3, 4) | (4, 3) | (2, 3) |
| From a to A | (2, 3) | (4, 3) | (3, 4) | (3, 2) |
| Items | Value |
|---|---|
| Pole pair number | 8 |
| Rated speed | 1000 rpm |
| Rated power | 750 W |
| DC-link voltage | 100 V |
| DC capacitors | 400 uF |
| Resistor value | 0.21 Ω |
| Sampling frequency | 20 kHz |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Pu, S.; Cao, J.; Yang, X.; Wang, Z. Torque Ripple Mitigation of T-3L Inverter Fed Open-End Doubly-Salient Permanent-Magnet Motor Drives Using Current Hysteresis Control. Energies 2019, 12, 3109. https://doi.org/10.3390/en12163109
Liu H, Pu S, Cao J, Yang X, Wang Z. Torque Ripple Mitigation of T-3L Inverter Fed Open-End Doubly-Salient Permanent-Magnet Motor Drives Using Current Hysteresis Control. Energies. 2019; 12(16):3109. https://doi.org/10.3390/en12163109
Chicago/Turabian StyleLiu, Hongliang, Shaoning Pu, Jiawei Cao, Xiaojie Yang, and Zheng Wang. 2019. "Torque Ripple Mitigation of T-3L Inverter Fed Open-End Doubly-Salient Permanent-Magnet Motor Drives Using Current Hysteresis Control" Energies 12, no. 16: 3109. https://doi.org/10.3390/en12163109
APA StyleLiu, H., Pu, S., Cao, J., Yang, X., & Wang, Z. (2019). Torque Ripple Mitigation of T-3L Inverter Fed Open-End Doubly-Salient Permanent-Magnet Motor Drives Using Current Hysteresis Control. Energies, 12(16), 3109. https://doi.org/10.3390/en12163109




