Figure 1.
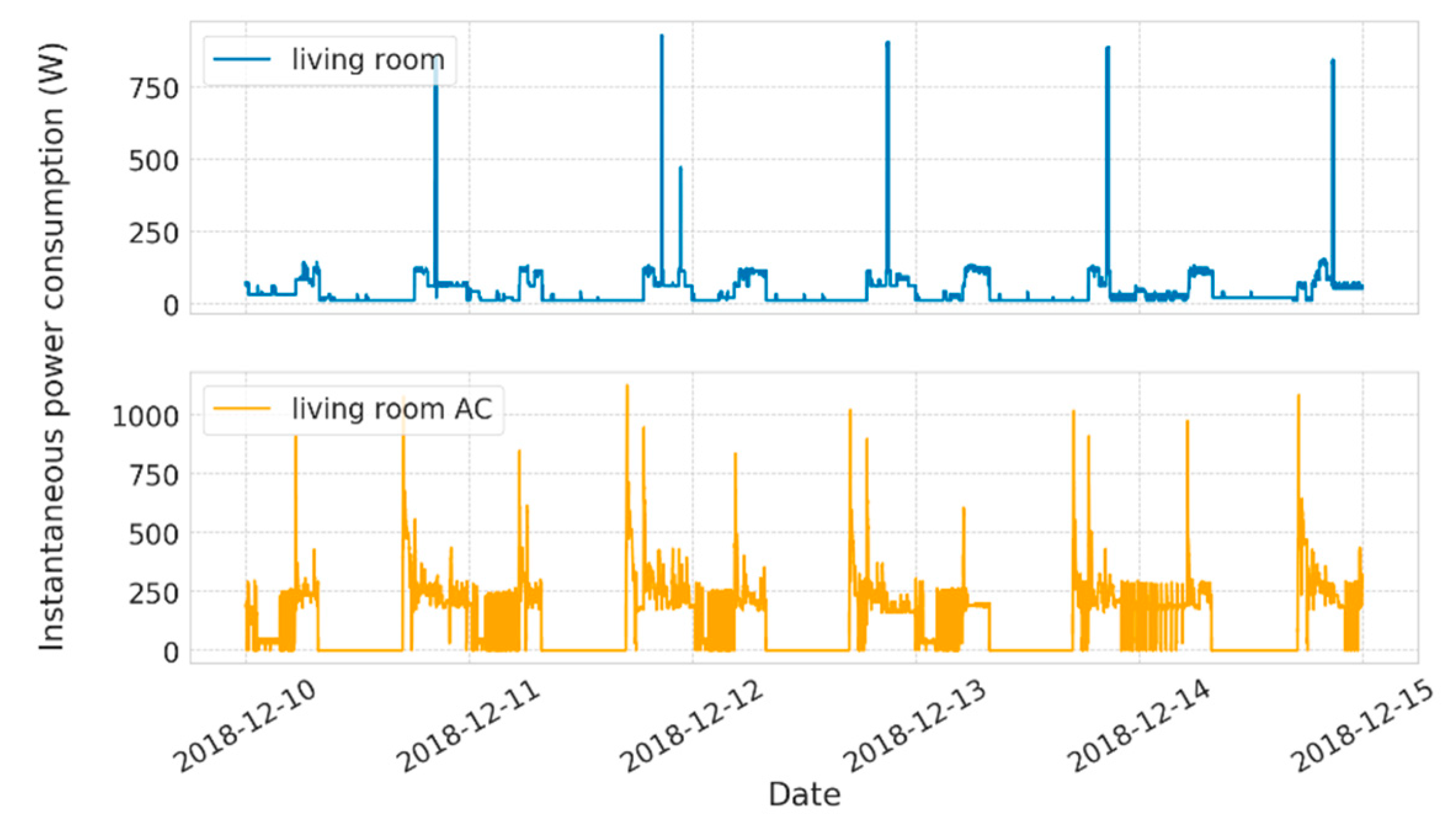
Power consumption of electric appliances in the living room (in blue) and the AC (in orange).
Figure 1.
Power consumption of electric appliances in the living room (in blue) and the AC (in orange).
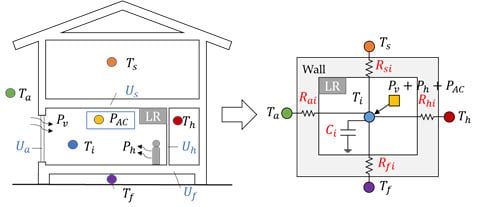
Figure 2.
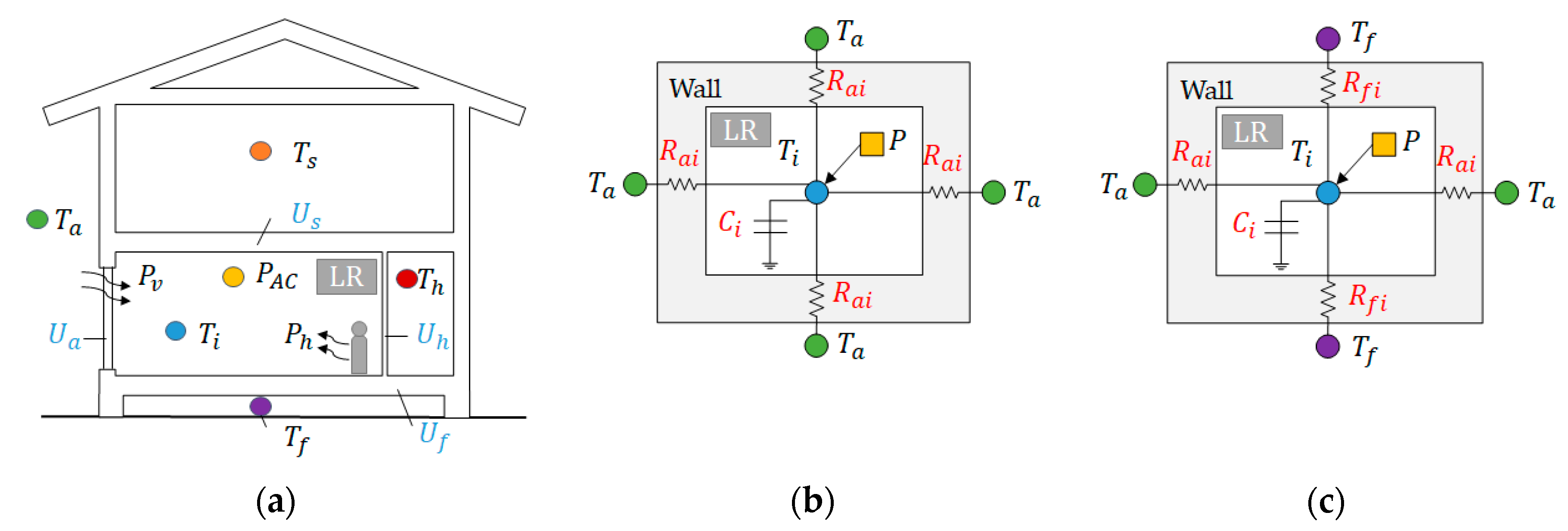
(a) Heat exchange for the living room (LR), (b) one-room model, (c) two-room model, where the measured inputs by sensors, ( are represented in circles, total heat supply to the living room () are in a square, unknown parameters of heat capacity () and thermal resistances () are in red texts, and heat transfer coefficients () derived from estimated parameters are in blue texts.
Figure 2.
(a) Heat exchange for the living room (LR), (b) one-room model, (c) two-room model, where the measured inputs by sensors, ( are represented in circles, total heat supply to the living room () are in a square, unknown parameters of heat capacity () and thermal resistances () are in red texts, and heat transfer coefficients () derived from estimated parameters are in blue texts.
Figure 3.
Methods for data selection and preprocessing: The y-axis in the left and right represent temperature in the living room () and outdoor () and power consumption of the AC (), respectively, the x-axis represents time. Data windows with the size of are generated periodically ( after the previous window) 2 h after the peak of .
Figure 3.
Methods for data selection and preprocessing: The y-axis in the left and right represent temperature in the living room () and outdoor () and power consumption of the AC (), respectively, the x-axis represents time. Data windows with the size of are generated periodically ( after the previous window) 2 h after the peak of .
Figure 4.
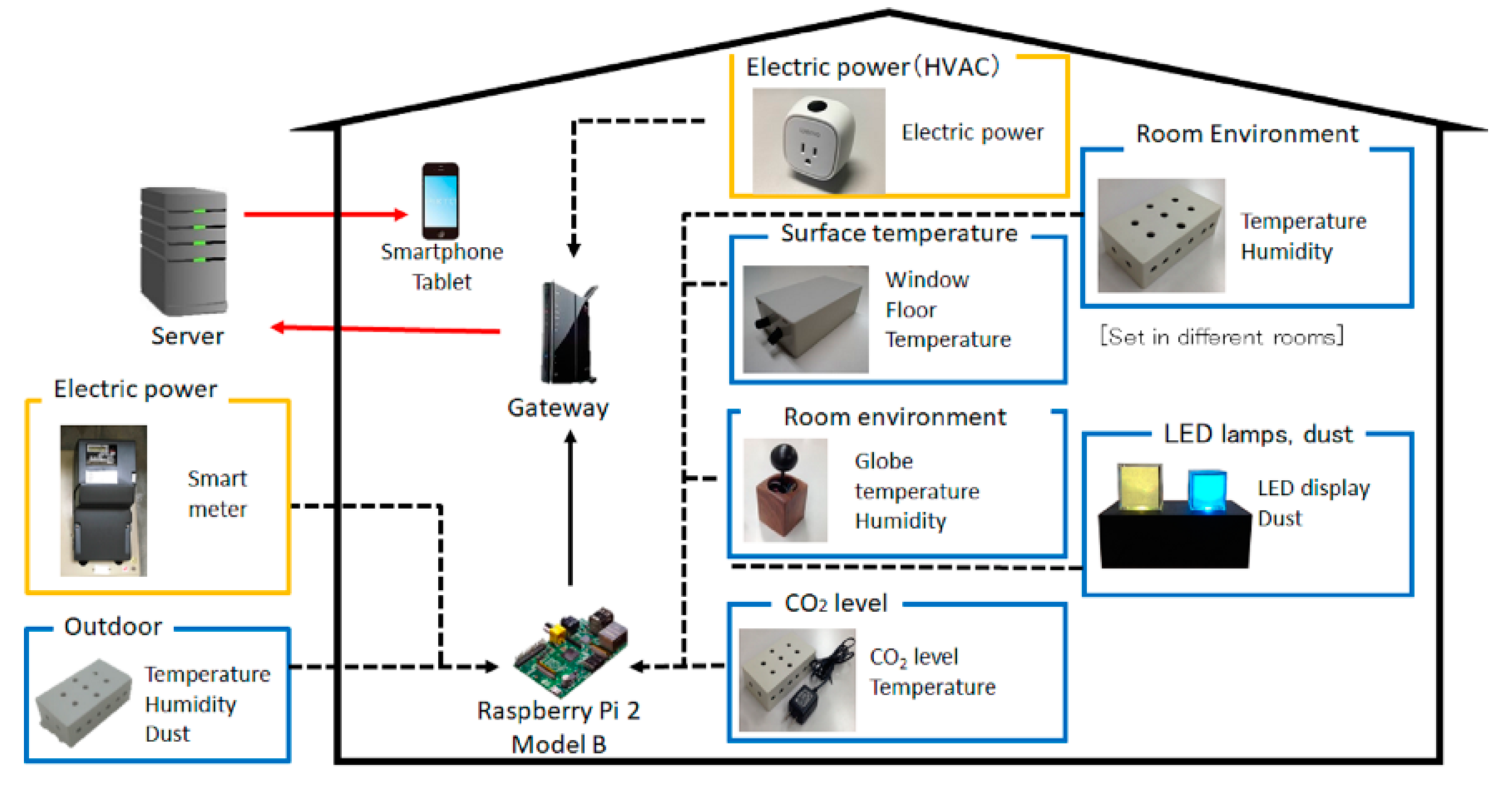
House energy management system (HEMS) installed in smart houses for the Urban Design Center Misono (UDCMi) project. Environmental and electric data are collected at the gateway and sent to the server for storage. Various home services using these data are provided for UDCMi.
Figure 4.
House energy management system (HEMS) installed in smart houses for the Urban Design Center Misono (UDCMi) project. Environmental and electric data are collected at the gateway and sent to the server for storage. Various home services using these data are provided for UDCMi.
Figure 5.
Installment of environmental sensors: (a) A thermometer in the room, (b) CO2 sensor, (c) a thermometer on the outside north-facing wall. Sensors are circled in red.
Figure 5.
Installment of environmental sensors: (a) A thermometer in the room, (b) CO2 sensor, (c) a thermometer on the outside north-facing wall. Sensors are circled in red.
Figure 6.
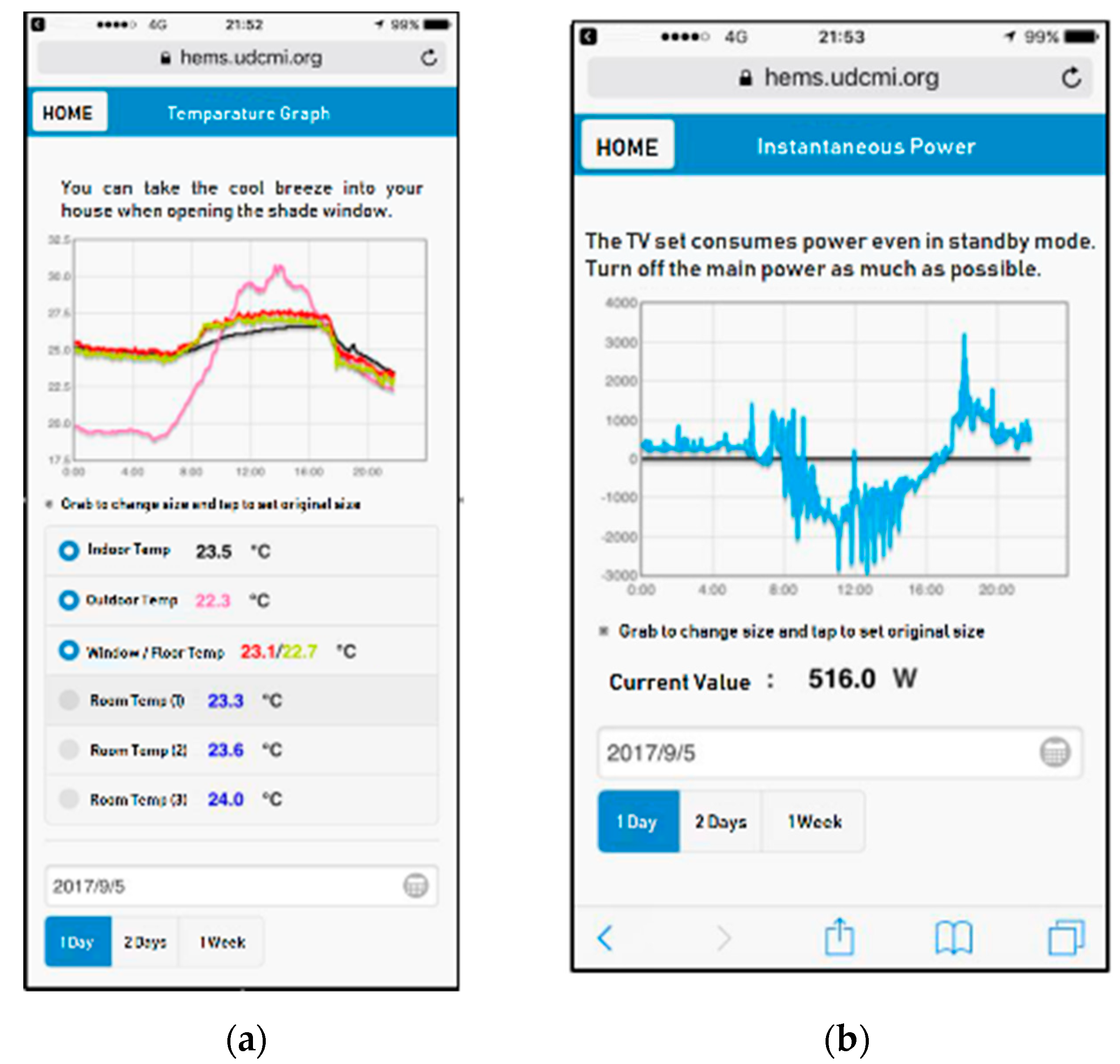
Screenshots of the smartphone application: (a) Room environment information (b) electricity usage information.
Figure 6.
Screenshots of the smartphone application: (a) Room environment information (b) electricity usage information.
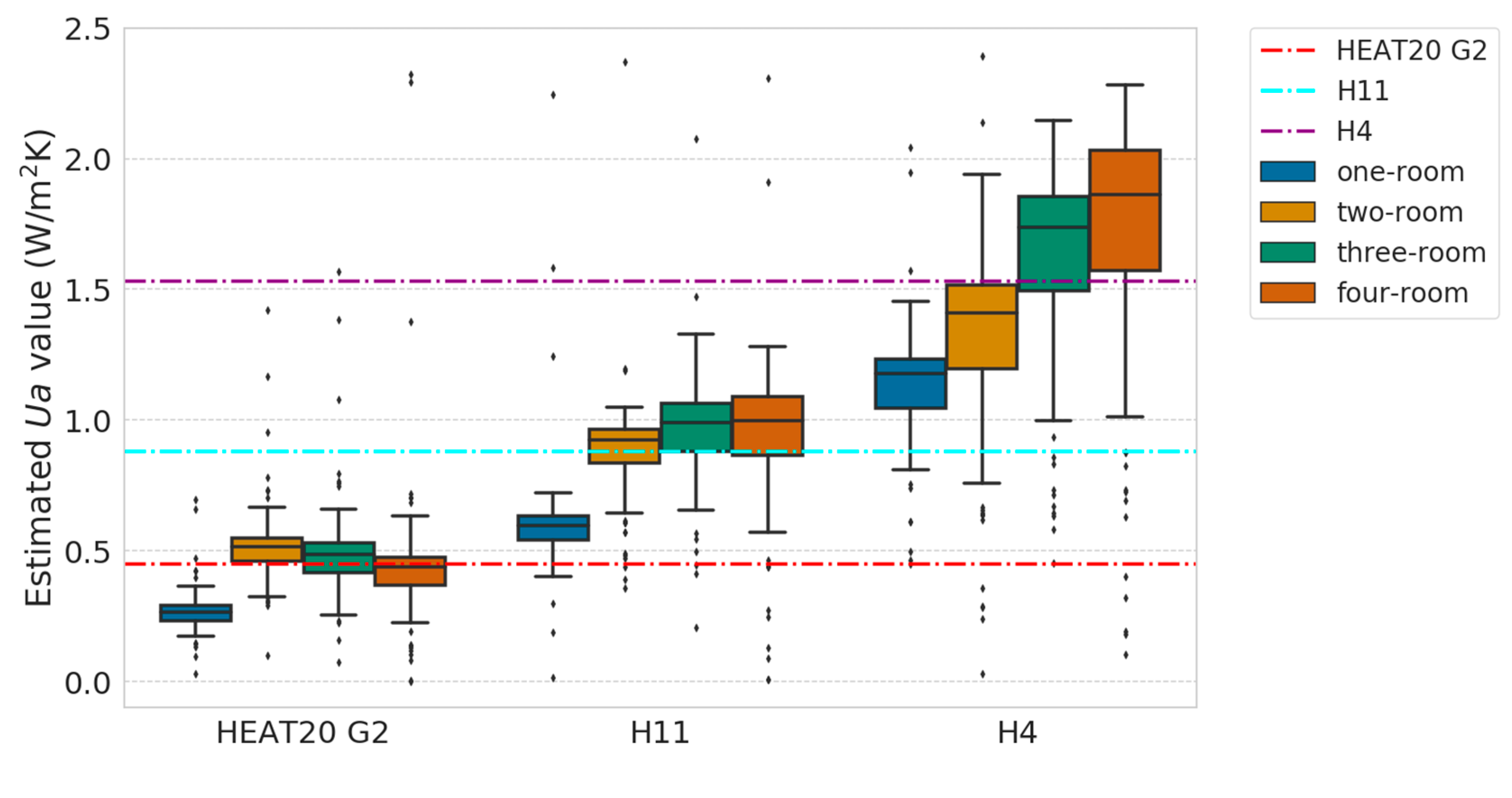
Figure 7.
Estimated Ua values for different simulation data (HEAT20 G2, H11, and H4) and models (one-, two-, three-, and four-room model). The dotted line represents literature Ua values for each standard. Boxplots represent the distribution of estimated results for the different models.
Figure 7.
Estimated Ua values for different simulation data (HEAT20 G2, H11, and H4) and models (one-, two-, three-, and four-room model). The dotted line represents literature Ua values for each standard. Boxplots represent the distribution of estimated results for the different models.
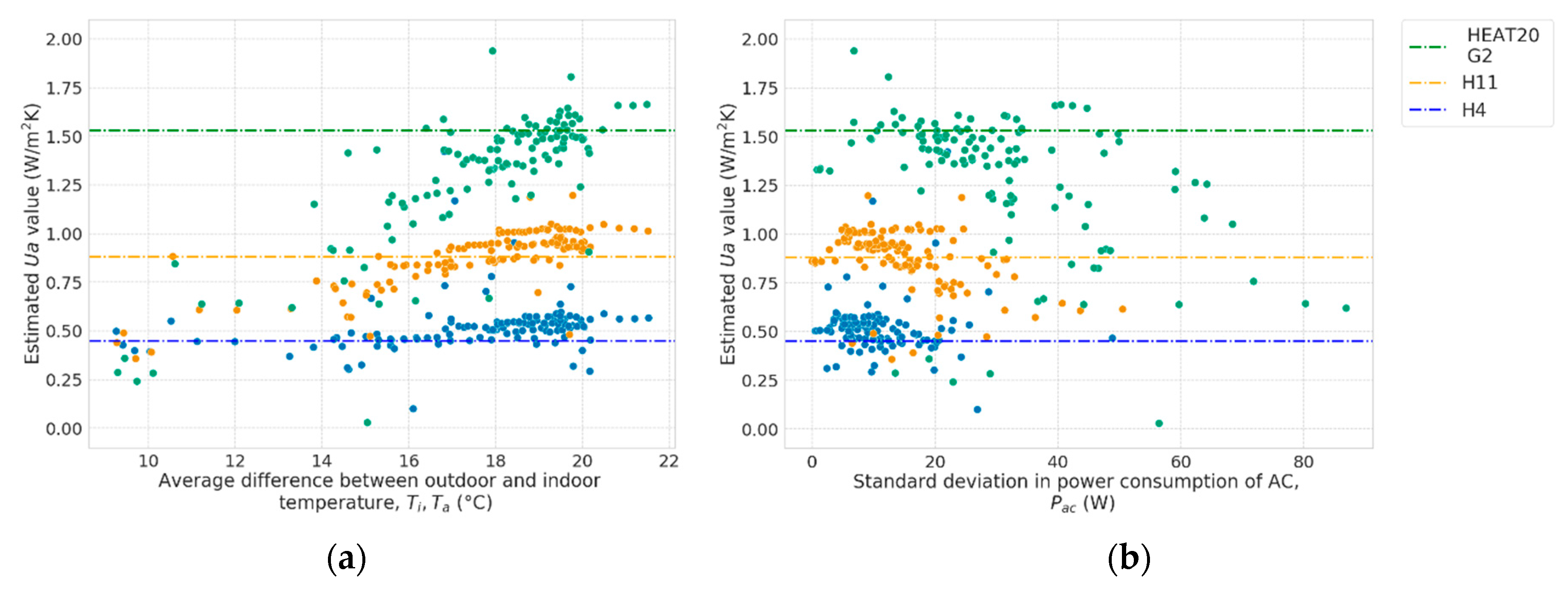
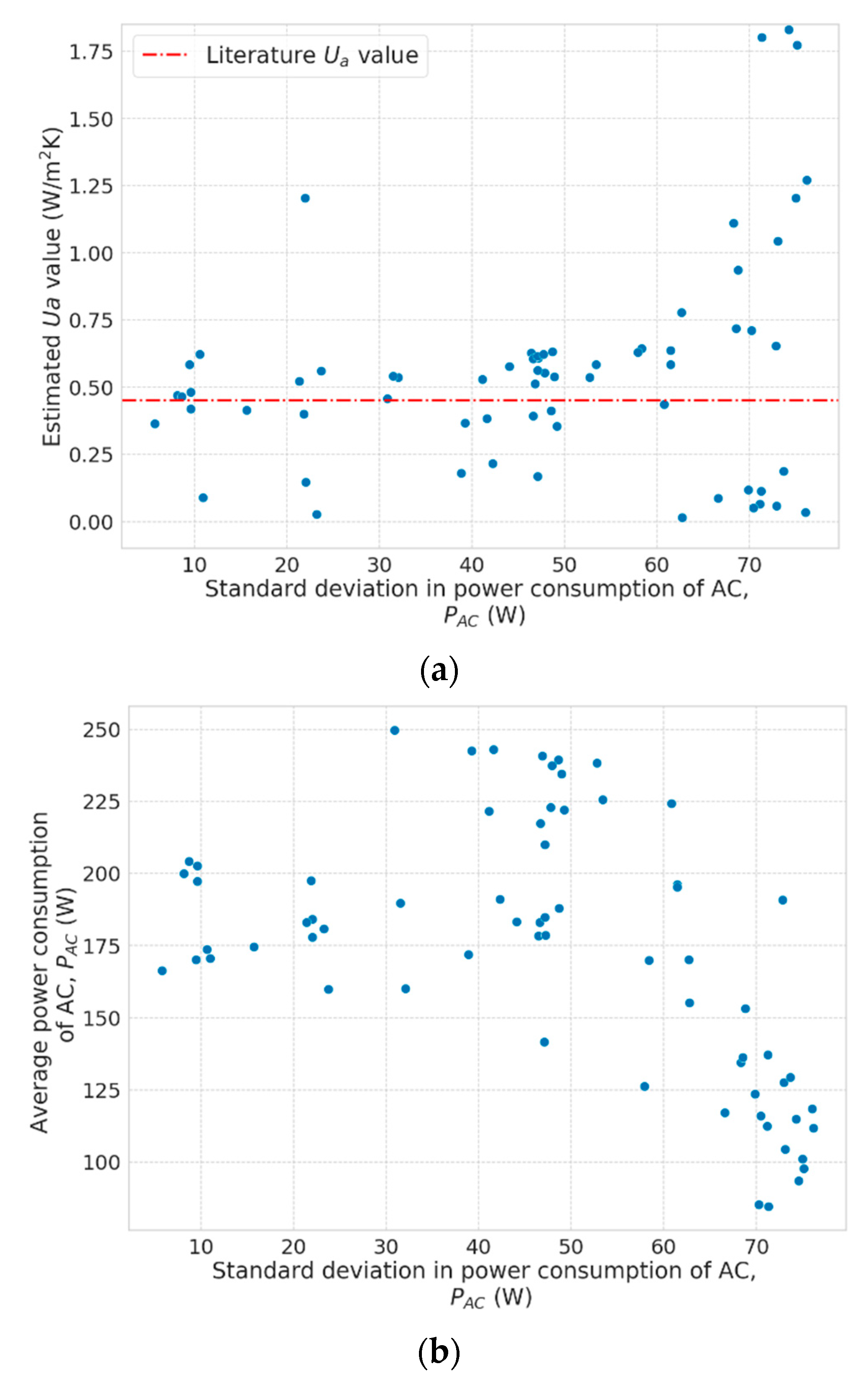
Figure 8.
Estimated Ua values and: (a) Average difference between outdoor and indoor temperature (), (b) standard deviation in power consumption of the ACs (). Dotted lines represent literature values for different standards (HEAT20 G2, H11, and H4).
Figure 8.
Estimated Ua values and: (a) Average difference between outdoor and indoor temperature (), (b) standard deviation in power consumption of the ACs (). Dotted lines represent literature values for different standards (HEAT20 G2, H11, and H4).
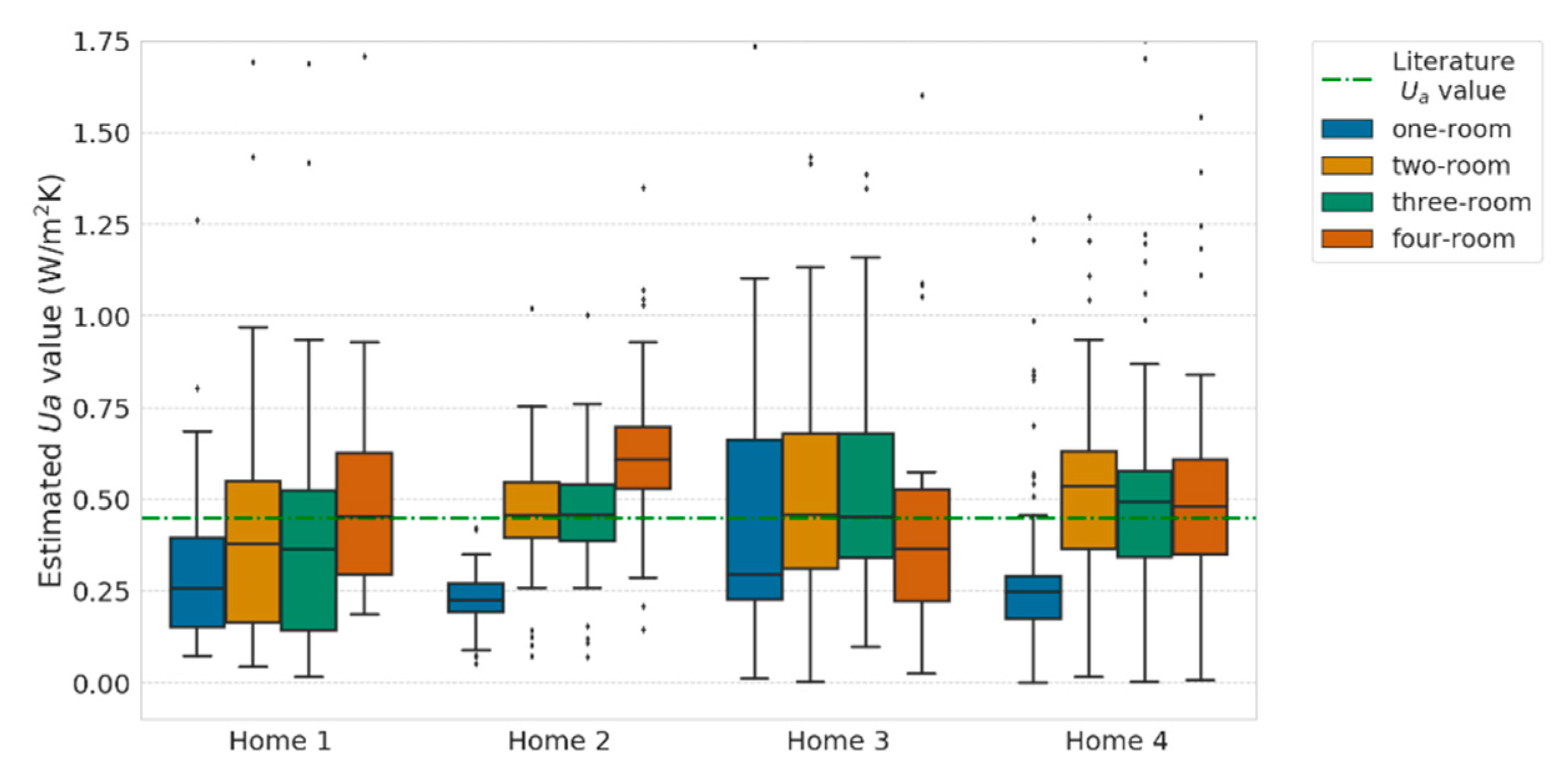
Figure 9.
Estimated Ua values for different experimental data (Home 1 to 4) and models (one-, two-, three- and four-room model). The dotted line represents the literature Ua value. Boxplots represent distribution of estimated results for the different models.
Figure 9.
Estimated Ua values for different experimental data (Home 1 to 4) and models (one-, two-, three- and four-room model). The dotted line represents the literature Ua value. Boxplots represent distribution of estimated results for the different models.
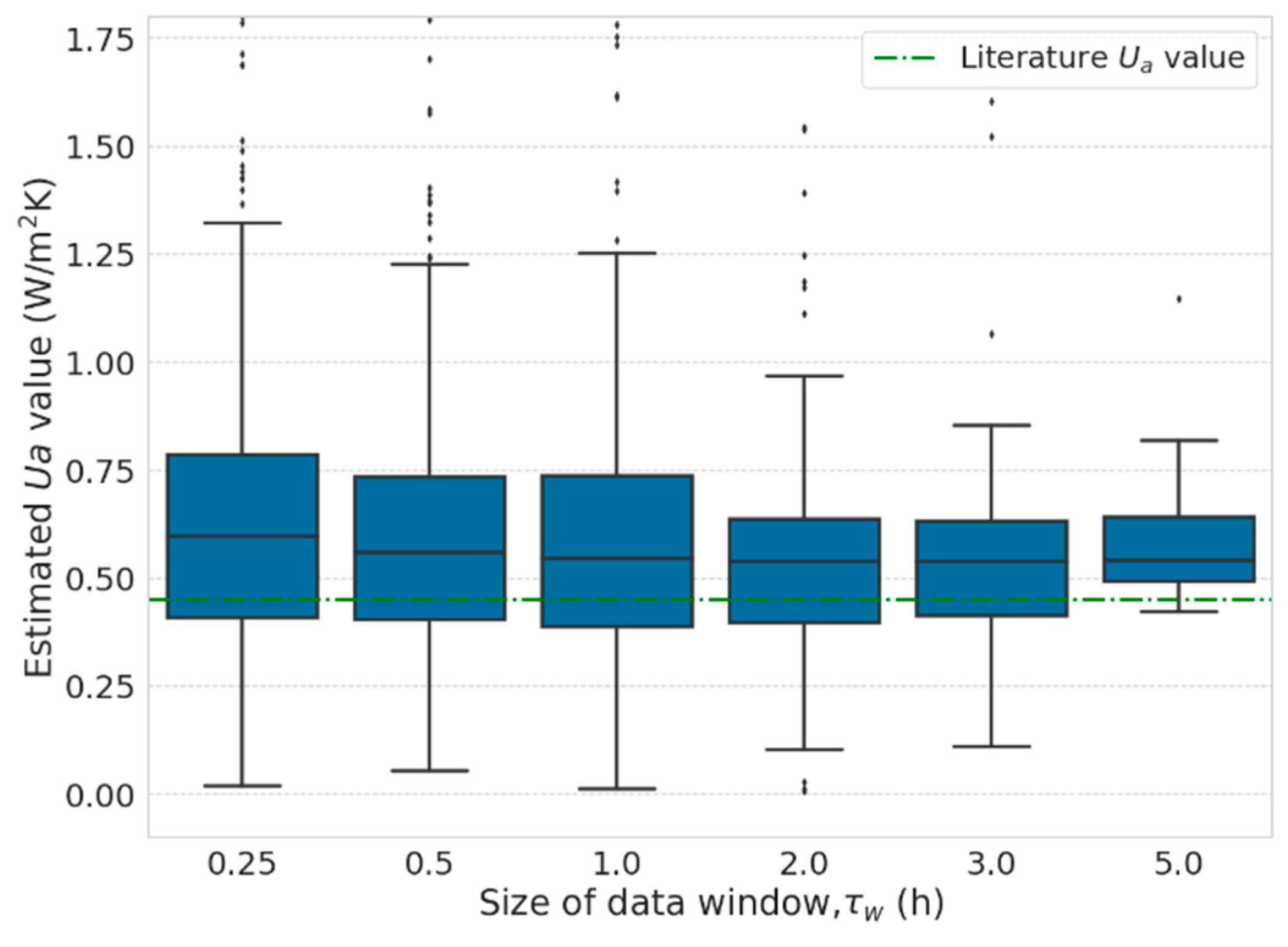
Figure 10.
Estimated Ua values for different size of data window for Home 4 using three-room model. The dotted line represents the literature Ua value. Boxplots represent the distribution of estimated results for the different size of data windows.
Figure 10.
Estimated Ua values for different size of data window for Home 4 using three-room model. The dotted line represents the literature Ua value. Boxplots represent the distribution of estimated results for the different size of data windows.
Figure 11.
Impacts of AC operation on estimation accuracy: (a) Estimated values and standard deviation of , (b) the relationship between average and standard deviation of .
Figure 11.
Impacts of AC operation on estimation accuracy: (a) Estimated values and standard deviation of , (b) the relationship between average and standard deviation of .
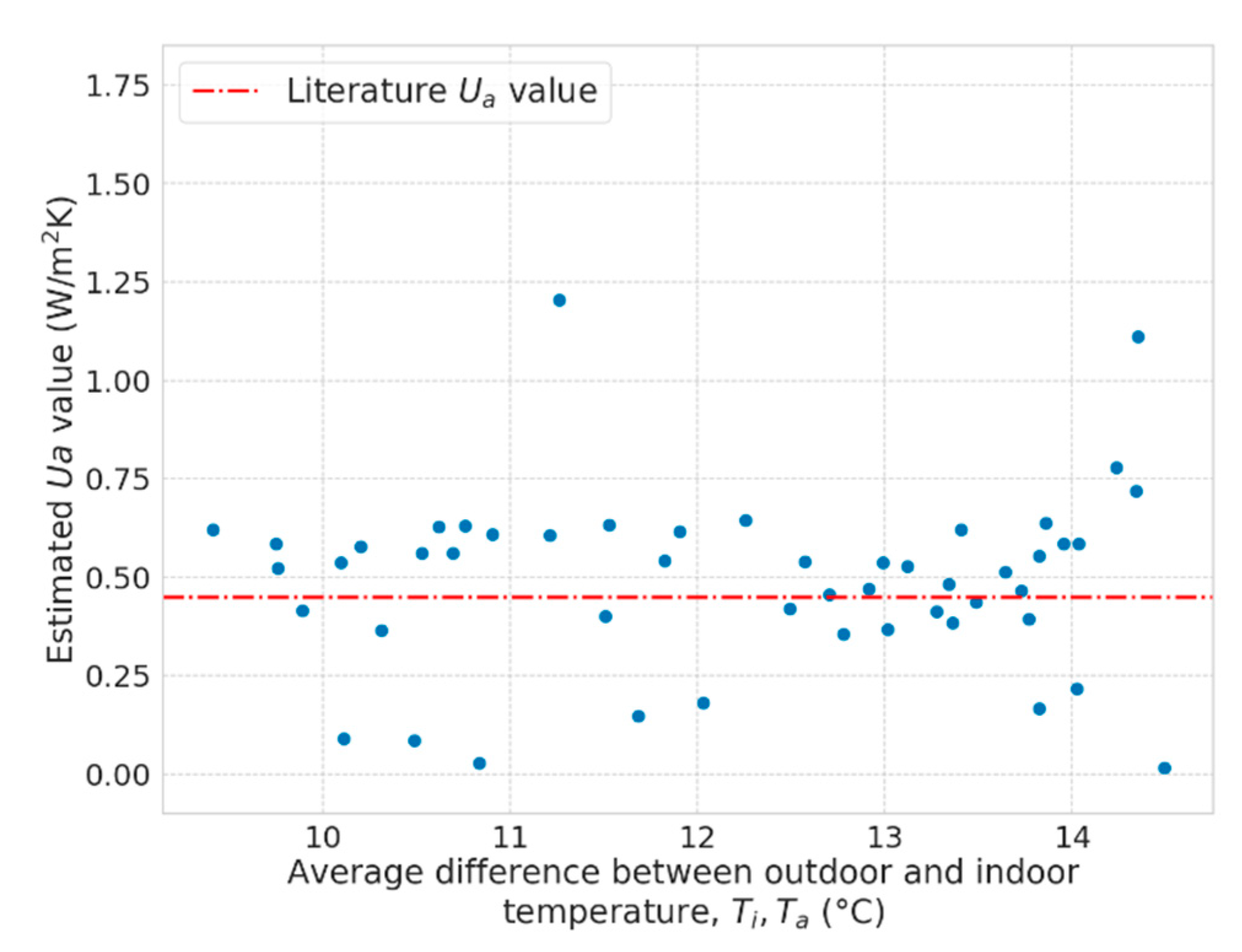
Figure 12.
Estimated Ua values and the average difference between outdoor and indoor temperature.
Figure 12.
Estimated Ua values and the average difference between outdoor and indoor temperature.
Table 1.
Summary of symbols.
Table 1.
Summary of symbols.
| Symbol | Description (unit) |
|---|
| Area of outer walls (m2) |
| Area of inner walls to adjacent room (m2) |
| Surface area of humans (m2) |
| Thermal capacity of room (J/K) |
| Resistance to thermal transfer through clothing (clo) |
| Thermal resistance between rooms and (K/W) |
| Total input power to the living room (W) |
| Power consumption of the AC (W) |
| Input power by the AC and ventilation (W) |
| Metabolic heat gain from occupants (W) |
| Ambient air temperature (°C) |
| Temperature of room (°C) |
| Surface temperature of skin (°C) |
| Surface temperature of clothing (°C) |
| Average transmission heat transfer coefficient of fabric of building (Ua value) (W/m2K) |
| Transmission heat transfer coefficient of walls to adjacent room (W/m2K) |
| Volume of exchanged air per unit time (m3/s) |
| Specific heat capacity of the air (J/kg) |
| Average residual (K) |
| Prediction error at time (K) |
| Density of the air (kg/m3) |
| Interval of data window (min) |
| Size of data window (min) |
Table 2.
Transmission heat transfer coefficients (W/m2K) for each part of walls for different standards.
Table 2.
Transmission heat transfer coefficients (W/m2K) for each part of walls for different standards.
| Standard | Outer Walls | Ceilings | Floors | Windows | Ua Value |
|---|
| HEAT20 G2 | 0.31 | 0.15 | 0.21 | 1.6 | 0.45 |
| H11 | 0.53 | 0.24 | 0.48 | 4.65 | 0.88 |
| H4 | 1.11 | 0.67 | 1.26 | 6.54 | 1.53 |
Table 3.
Summary of identified thermal performance parameters. The median of estimation results for Ua values () and heat capacity () for each standard (HEAT G2, H11, and H4) and models (one-, two-, three-, and four-room) are represented.
Table 3.
Summary of identified thermal performance parameters. The median of estimation results for Ua values () and heat capacity () for each standard (HEAT G2, H11, and H4) and models (one-, two-, three-, and four-room) are represented.
| Standard | Literature | One-Room | Two-Room | Three-Room | Four-Room |
|---|
| | Uavalue,( |
| HEAT20 G2 | 0.45 | 0.28 | 0.52 | 0.49 | 0.44 |
| H11 | 0.88 | 0.60 | 0.92 | 0.99 | 1.00 |
| H4 | 1.53 | 1.18 | 1.41 | 1.74 | 1.86 |
| | Heat capacity,( |
| HEAT20 G2 | 3.34 × 106 | 8.26 × 106 | 5.57 × 106 | 7.24 × 106 | 4.54 × 106 |
| H11 | 2.70 × 106 | 1.00 × 106 | 5.52 × 106 | 7.35 × 106 | 6.46 × 106 |
| H4 | 2.48× 106 | 1.34 × 107 | 9.56 × 106 | 1.17 × 107 | 1.11 × 107 |
Table 4.
Summary of average residuals () () for simulation data.
Table 4.
Summary of average residuals () () for simulation data.
| Standard | One-Room | Two-Room | Three-Room | Four-Room |
|---|
| HEAT20 G2 | 4.58 × 10−3 | 4.94 × 10−3 | 4.64 × 10−3 | 4.42 × 10−3 |
| H11 | 5.48 × 10−3 | 5.28 × 10−3 | 5.36 × 10−3 | 5.32 × 10−3 |
| H4 | 7.26 × 10−3 | 7.12 × 10−3 | 6.95 × 10−3 | 7.06 × 10−3 |
Table 5.
Summary of identified Ua values before and after retrofits. The median of estimation results for Ua values (W/m2 K) for different cases of retrofits (none, outer walls, all windows, living room windows only) is represented for three-room model.
Table 5.
Summary of identified Ua values before and after retrofits. The median of estimation results for Ua values (W/m2 K) for different cases of retrofits (none, outer walls, all windows, living room windows only) is represented for three-room model.
| Retrofitted Parts | Literature | Estimated |
|---|
| None (before retrofits) | 0.88 | 0.99 |
| Outer walls | 0.84 | 0.87 |
| All windows | 0.65 | 0.61 |
| Living room windows only | 0.78 | 0.65 |
Table 6.
Summary of thermal performance parameters for experimental data. The median of estimation results for Ua values (), and heat capacity () for each house (Home 1-4) and models (one-, two-, three-, and four-room).
Table 6.
Summary of thermal performance parameters for experimental data. The median of estimation results for Ua values (), and heat capacity () for each house (Home 1-4) and models (one-, two-, three-, and four-room).
| Home | One-Room | Two-Room | Three-Room | Four-Room |
|---|
| | Uavalue,() |
| 1 | 0.258 | 0.379 | 0.375 | 0.454 |
| 2 | 0.227 | 0.459 | 0.460 | 0.460 |
| 3 | 0.265 | 0.439 | 0.407 | 0.336 |
| 4 | 0.234 | 0.552 | 0.521 | 0.540 |
| | Heat capacity,() |
| 1 | 3.88 × 105 | 1.13 × 105 | 1.10 × 105 | 2.59 × 105 |
| 2 | 4.24 × 106 | 4.11 × 106 | 4.09 × 107 | 3.59 × 106 |
| 3 | 2.24 × 106 | 2.37 × 106 | 2.26 × 106 | 2.23 × 106 |
| 4 | 1.65 × 106 | 1.60 × 106 | 1.62 × 106 | 1.59 × 106 |
Table 7.
Summary of average residuals () () for experimental data.
Table 7.
Summary of average residuals () () for experimental data.
| Home | One-Room | Two-Room | Three-Room | Four-Room |
|---|
| 1 | 1.95 × 10−1 | 1.98 × 10−1 | 1.92 × 10−1 | 1.98 × 10−1 |
| 2 | 3.99 × 10−2 | 3.97 × 10−2 | 4.02 × 10−2 | 4.07 × 10−2 |
| 3 | 6.06 × 10−2 | 5.94 × 10−2 | 6.00 × 10−2 | 5.57 × 10−2 |
| 4 | 5.48 × 10−2 | 5.52 × 10−2 | 5.47 × 10−2 | 5.58 × 10−2 |
Table 8.
Summary of information on AC operation.
Table 8.
Summary of information on AC operation.
| Home | Average Operation Time of the AC (h) |
|---|
| 1 | 4.01 |
| 2 | 7.39 |
| 3 | 4.69 |
| 4 | 3.52 |