Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works
Abstract
:1. Introduction
2. Methodology
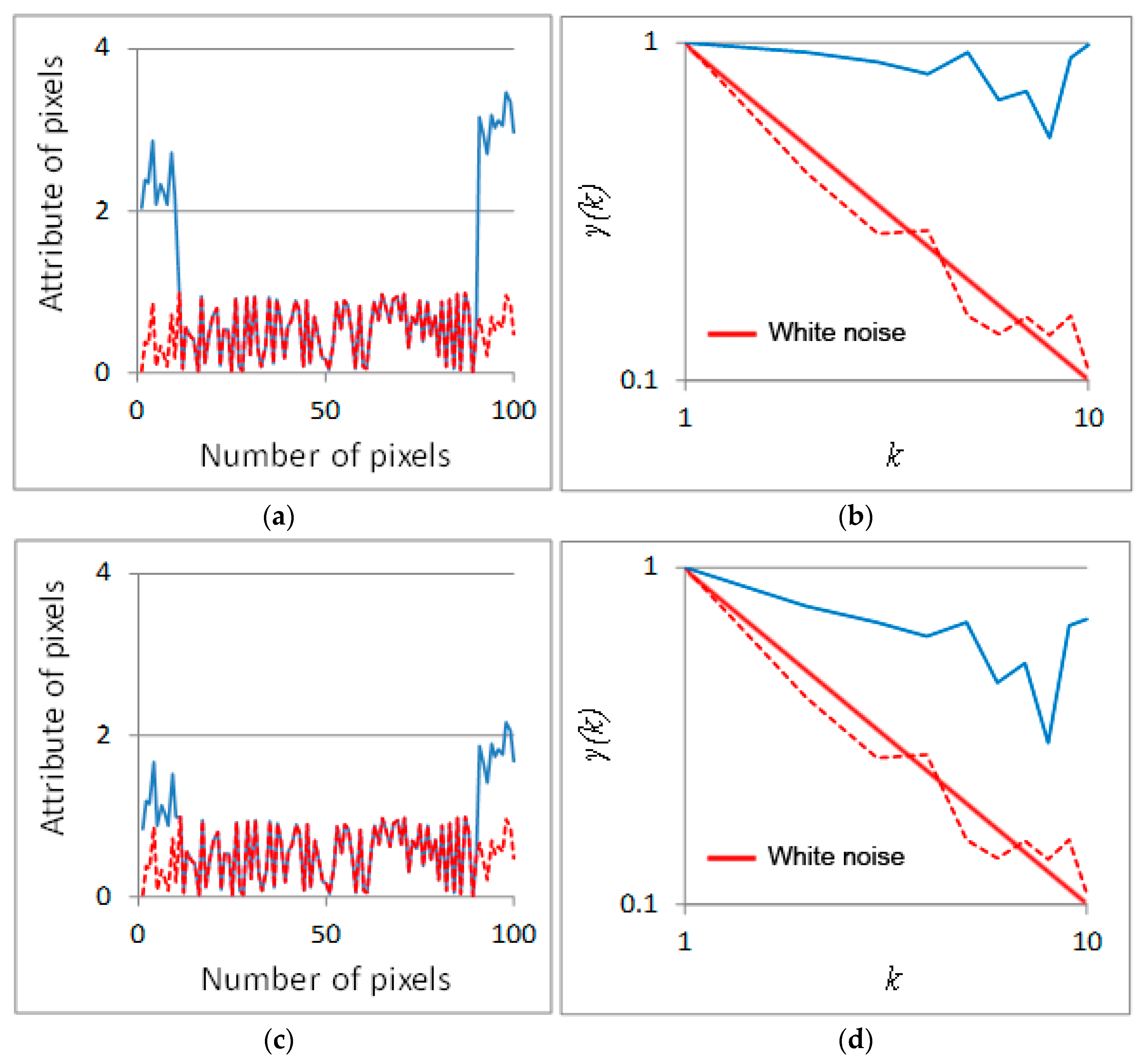
2.1. Stochastic Analysis in 2d
2.2. Illustration of Stochastic Analysis in 2d
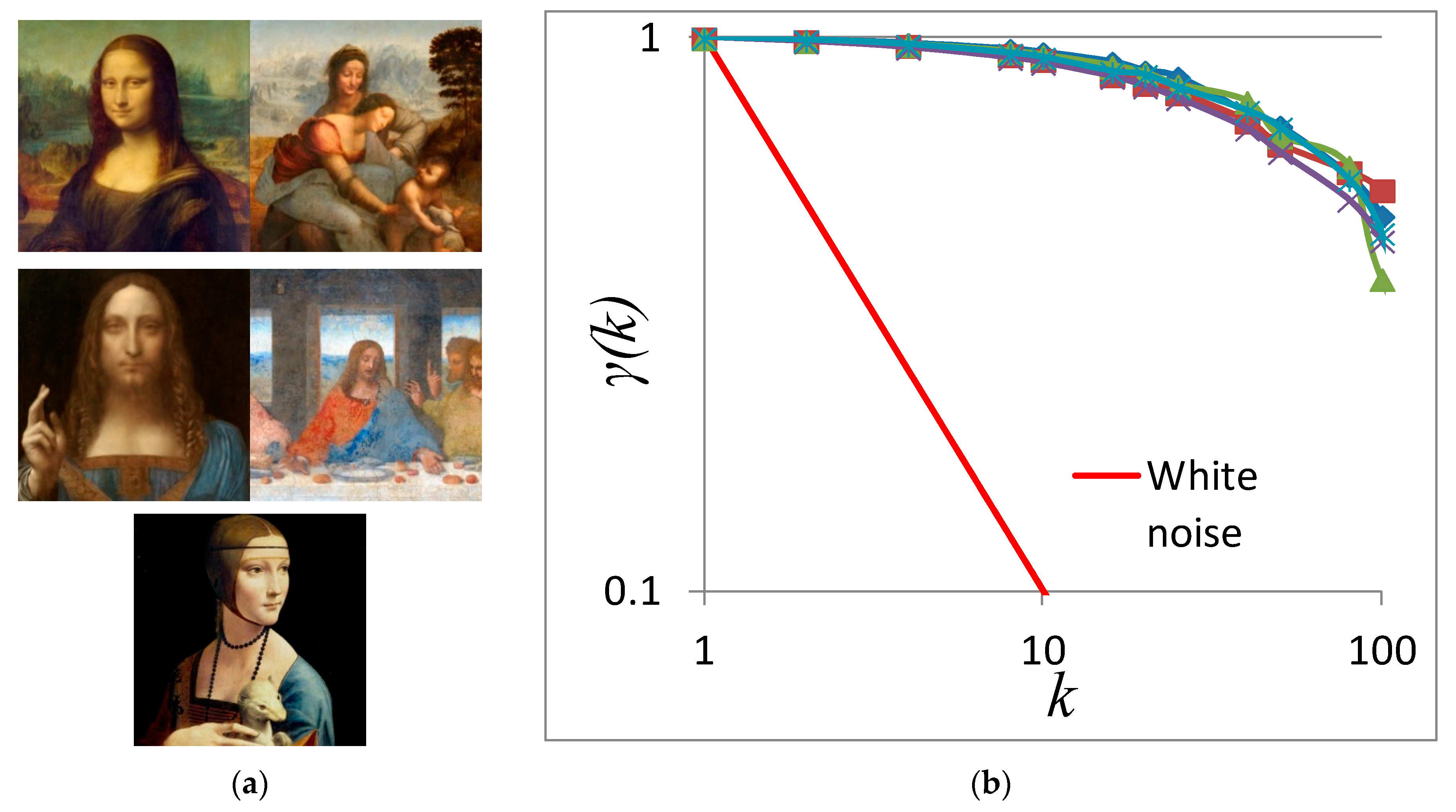
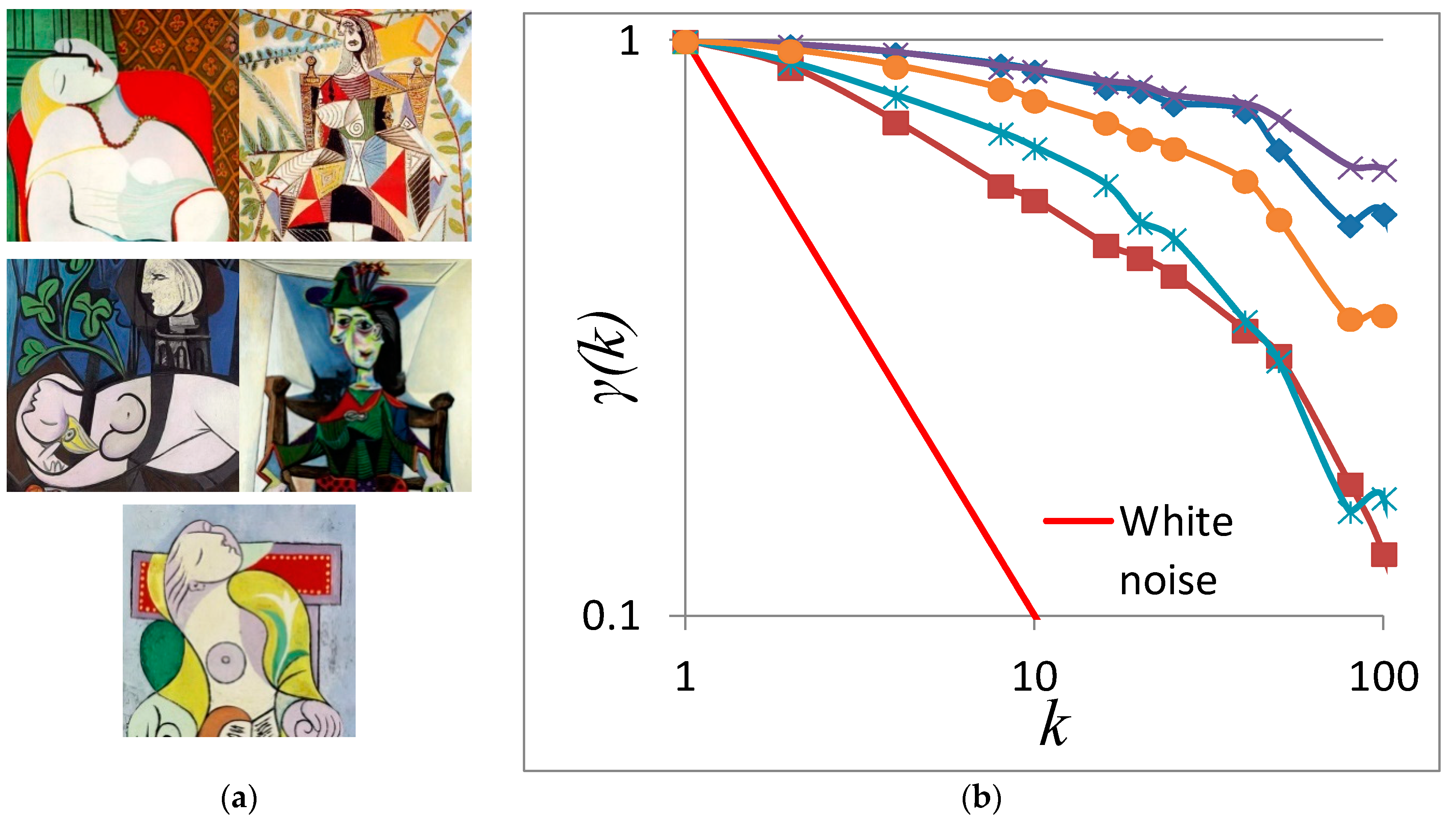
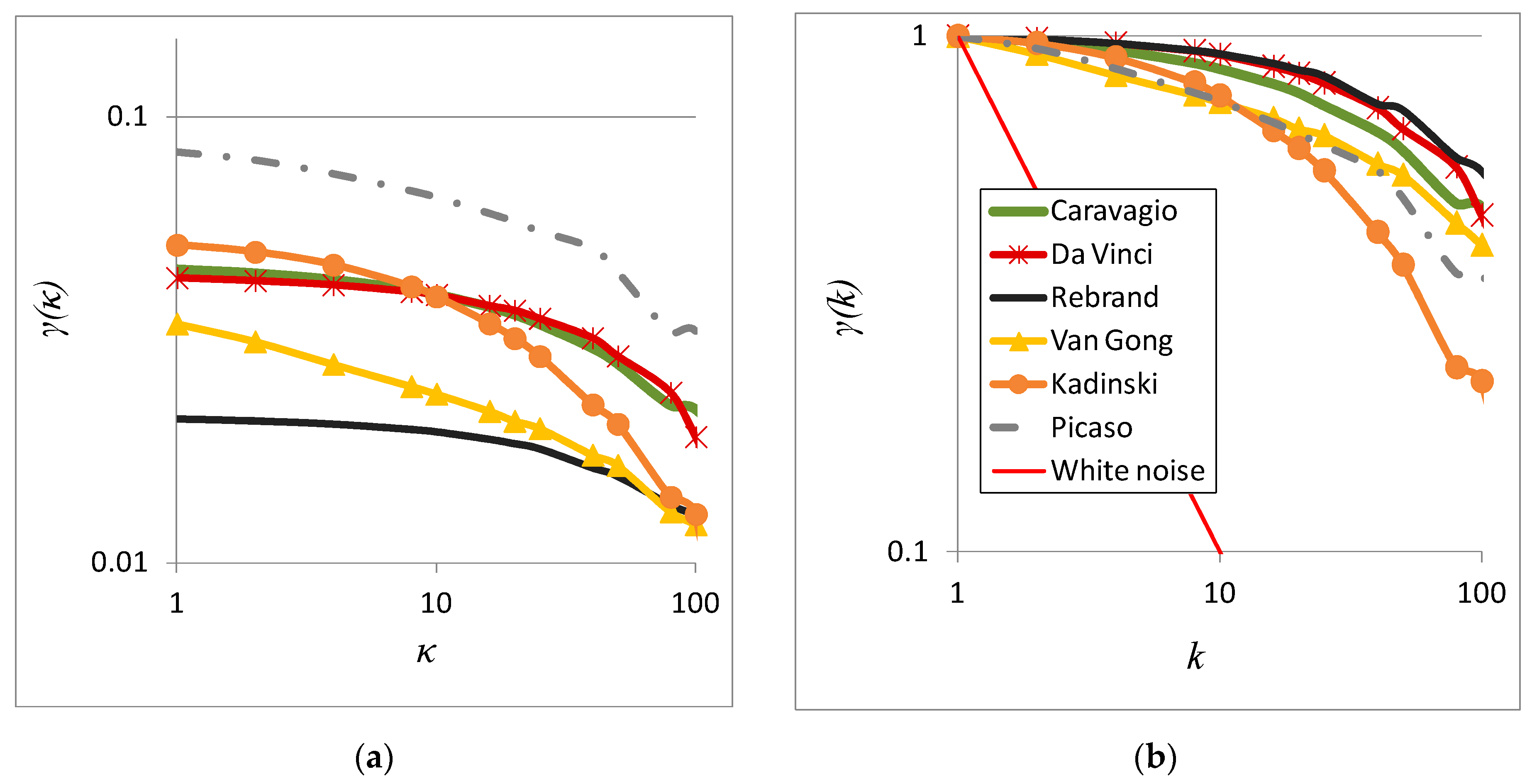
3. Benchmark Application in the Analysis of Art Paintings
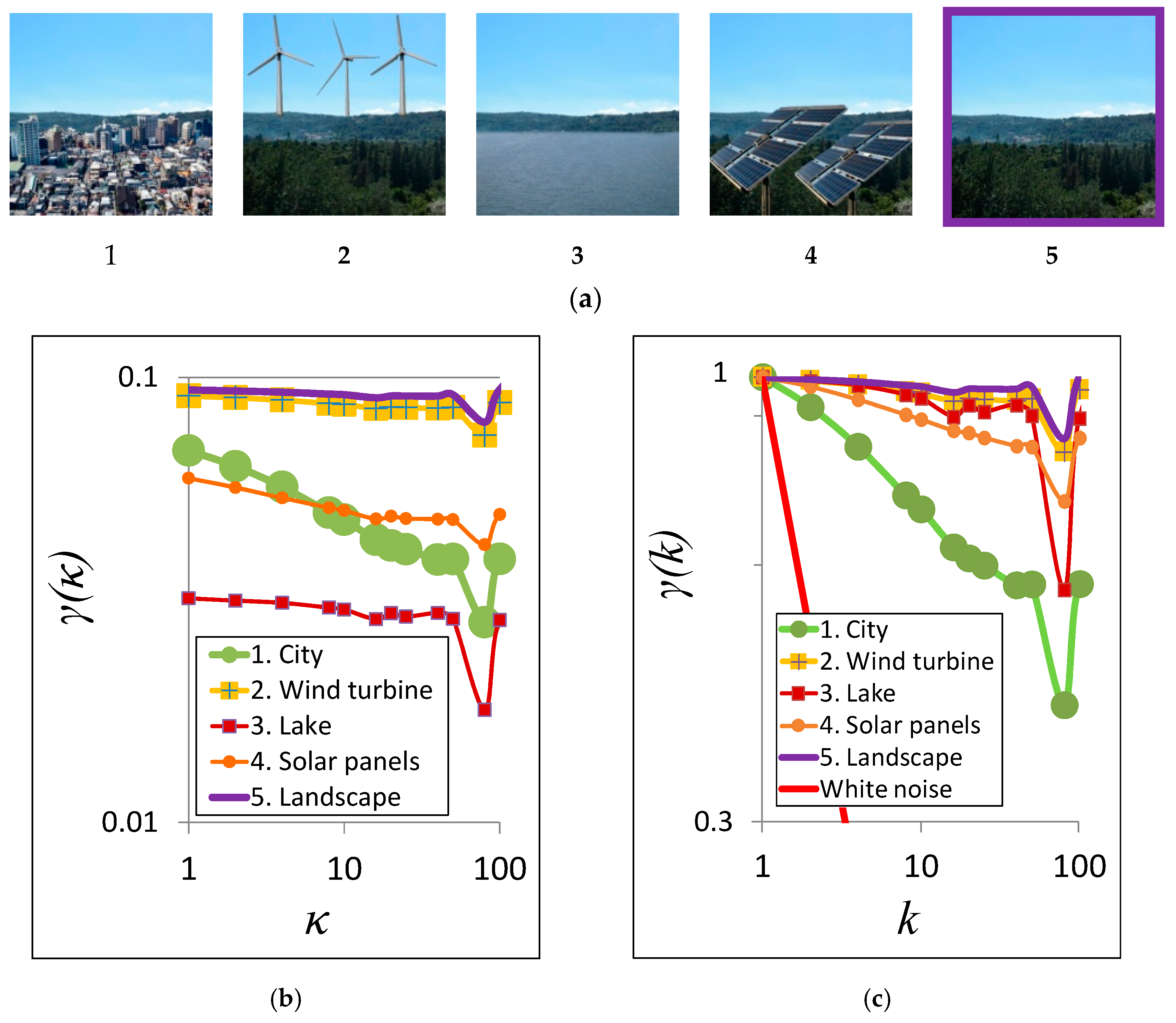
4. Application in Analysis of the Transformation of Landscape by RE Installations and Civil Works
4.1. Evaluating Future Scenarios of Landscape Transformations by Civil Works
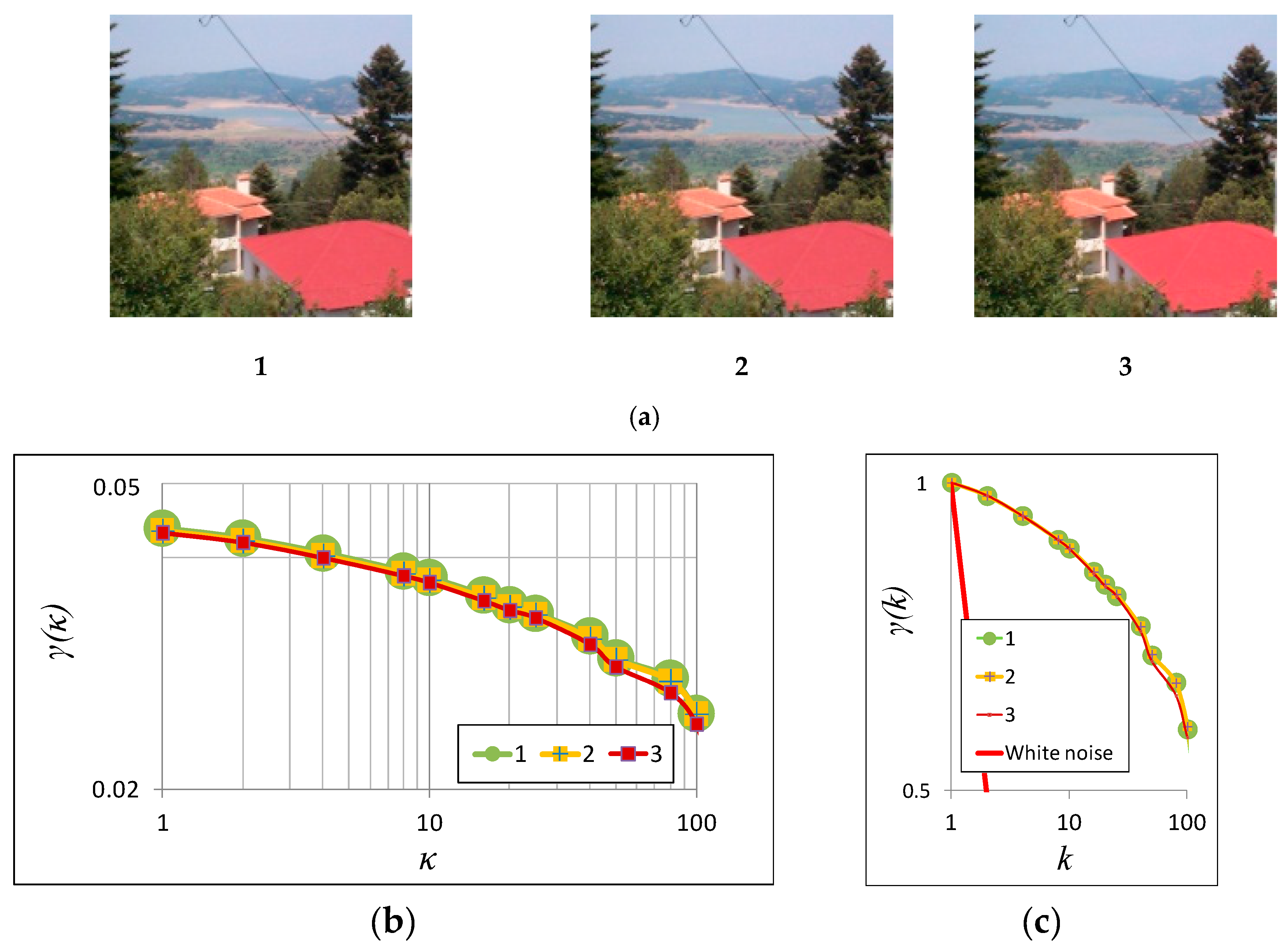
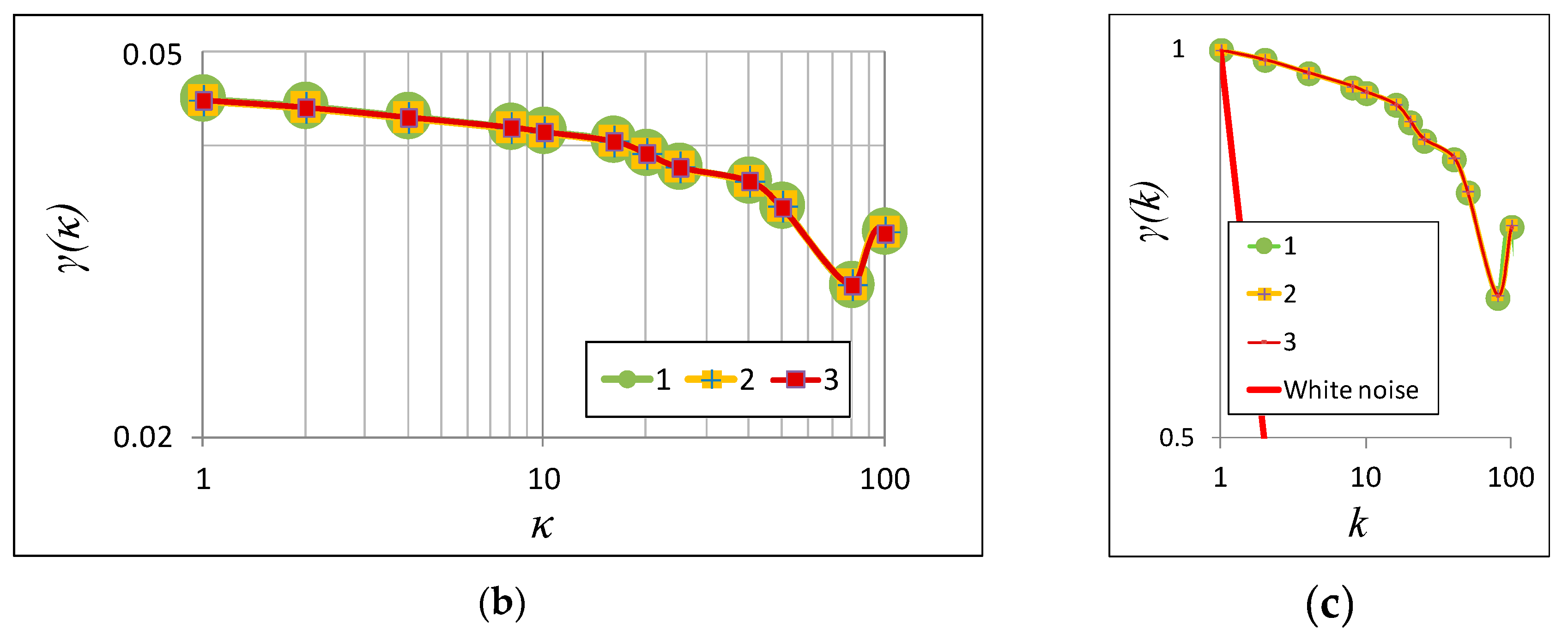
4.2. Landscape Analysis, the Case of Plastiras Lake
5. Discussion and Conclusions
- The evaluation of images with 2D-C can be useful in landscape aesthetics problems as the quantitative analysis can serve as a basis for objectivity in the evaluation of landscape changes.
- 2D-C can evaluate one image of the landscape by a specific view point in a specific time. Thus, we cannot have a holistic approach of the landscape. However, as methods of the landscape analysis seek a global approach identifying landscape with multicriteria analysis, 2D-C could serve as a new quantitative criterion.
- 2D-C provides only a relative score among the transformed images, while sources of uncertainty relating to objective segmentation of images need also to be further studied. Nevertheless, 2D-C can serve as a robust stochastic tool for comparisons, with promising results regarding the possible generalized application to image analysis.
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Rodrigues, M.; Montañés, C.; Fueyo, N. A method for the assessment of the visual impact caused by the large-scale deployment of renewable-energy facilities. Environ. Impact Assess. Rev. 2010, 30, 240–246. [Google Scholar] [CrossRef]
- Visibility and Influence of Landscape Appreciation by Wind Turbines. Environmental Data Compendium, Government of the Netherlands, 2012. Available online: https://www.clo.nl/en/indicators/en1408-visual-disturbance-of-landscape-perception (accessed on 17 July 2019).
- SNH. Visual Influence of Built Development Indicator—2013 Data Update—Technical Note; Scottish Natural Heritage: Inverness, UK, 2014. [Google Scholar]
- Renewable Energies and European Landscapes: Lessons from Southern European Cases; Frolova, M.; Prados, M.-J.; Nadaï, A. (Eds.) Springer: Berlin, Germany, 2015. [Google Scholar]
- Wolsink, M. Planning of renewables schemes: Deliberative and fair decision-making on landscape issues instead of reproachful accusations of non-cooperation. Energy Policy 2007, 35, 2692–2704. [Google Scholar] [CrossRef]
- Haaren, V.C.; Galler, C.; Ott, S. Landscape Planning. The Basis of Sustainable Landscape Development; German Federal Agency for Nature Conservation, Ed.; Gebr. Kling. Buchkunst Leipz. Gmbh: Bonn, Germany, 2008.
- Cosmopoulos, P. Greek Research (2018–2019) on Quality of Life, Energy Needs and Public Standpoints for Renewable Energy Sources; University of Thrake: Komotini, Greece, 2019; Available online: https://energypress.gr/news/ereyna-panepistimioy-thrakis-se-oli-tin-ellada-safis-strofi-tis-koinis-gnomis-yper-tis (accessed on 3 July 2019).
- Social Mobilizations for the Installation of Giant Wind Farms. Available online: http://epohi.gr/kinhtopoihseis-enantia-sta-aioloka-parka/ (accessed on 3 July 2019).
- Information and Decisions against the Installation of RE in Sitia (Crete Greece). Available online: https://radiolasithi.gr/enimerosi-ke-apofasis-enantia-stin-egkatastasi-ape-stin-sitia/ (accessed on 3 July 2019).
- Wind Turbines in Evritania. The Fight Now Begins. What Happened in the Informative Day (6 April 2014) in Karpenissi. Available online: https://www.evrytanika.gr/index.php?option=com_content&id=786006%3A-l-r-&Itemid=124 (accessed on 3 July 2019).
- Social Organization and Fight against Wind Turbines. Available online: https://www.larissanet.gr/2019/03/26/laiki-organosi-kai-pali-enantia-stis-anemogennitries/ (accessed on 3 July 2019).
- Samothrace Against Wind Turbines. Available online: https://edromos.gr/h-samothrakh-enantia-stis-anemogennhtries/ (accessed on 3 July 2019).
- Ong, S.; Campbell, C.; Denholm, P.; Margolis, R.; Heath, G. Land-Use Requirements for Solar Power Plants in the United States; National Renewable Energy Laboratory: Golden, CO, USA, 2013.
- Trainor, A.M.; McDonald, R.I.; Fargione, J. Energy Sprawl Is the Largest Driver of Land Use Change in United States. PLoS ONE 2016, 11. [Google Scholar] [CrossRef] [PubMed]
- Denholm, P.; Hand, M.; Jackson, M.; Ong, S. Land-Use Requirements of Modern Wind Power Plants in the United States; National Renewable Energy Laboratory: Golden, CO, USA, 2009.
- World Energy Council, Word Energy Resources Hydropower 2016. Available online: https://www.worldenergy.org/data/resources/resource/hydropower/ (accessed on 17 July 2019).
- Guidelines for Landscape and Visual Impact Assessment; Landscape Institute, I.E.M.A.; Routledge: London, UK, 2013.
- Stephanou, I. The Physiognomy of a Place: Characteristics of the Greek City; Notes for School of Architecture; National Technical University of Athens: Athens, Greece, 2000. [Google Scholar]
- Sören, S.; Dittrich, A.R.; Czechowski, D. Energy landscape visualization: Scientific quality and social responsibility of a powerful tool. Sustain. Energy Landsc. Des. Plan. Dev. 2012, 7, 133. [Google Scholar]
- Grêt-Regamey, A.; Wissen Hayek, U. Multicriteria decision analysis for the planning and design of sustainable energy landscapes. In Sustainable Energy Landscapes: Designing, Planning and Development; CRC Press: Boca Raton, FL, USA, 2012; pp. 111–132. Available online: https://www.research-collection.ethz.ch/handle/20.500.11850/57466 (accessed on 17 July 2019).
- Hurtado, J.P.; Fernández, J.; Parrondo, J.L.; Blanco, E. Spanish method of visual impact evaluation in wind farms. Renew. Sustain. Energy Rev. 2004, 8, 483–491. [Google Scholar] [CrossRef]
- Vissering, J.; Sinclair, M.; Margolis, A. A Visual Impact Assessment Process for Wind Energy Projects. Clean Energy States Alliance, 2011. Available online: https://www.cesa.org/assets/2011-Files/States-Advancing-Wind-2/CESA-Visual-Impacts-Methodology-May2011.pdf (accessed on 17 July 2019).
- Ruth, S.; Griffiths, S. The Visual Impact of Windfarms: Lessons from the UK Experience; Harwell Laboratory, Energy Technology Support Unit: Harwell, UK, 1994. [Google Scholar]
- Buchan, N. Visual Assessment of Windfarms: Best Practice; Scottish Natural Heritage Commissioned Report F01AA303A; University of Newcastle: Callaghan, Australia, 2002. [Google Scholar]
- Sullivan, R.G.; Kirchler, L.; Lahti, T.; Roché, S.; Beckman, K.; Cantwell, B.; Richmond, P. Wind turbine visibility and visual impact threshold distances in western landscapes. In Proceedings of the National Association of Environmental Professionals 37th Annual Conference, Portland, OR, USA, 18 June–2 July 2012. [Google Scholar]
- Swanwick, C. Landscape Character Assessment (LCA)—Guidance for England and Scotland; Countryside Agency and Scottish Natural Heritage: Johnstown, NY, USA, 2002. [Google Scholar]
- Scottish Natural Heritage Landscape, SNH’s Landscape Policy Framework, Policy Statement No. 05/01. 2005. Available online: https://www.nature.scot/sites/default/files/2017-06/A147583%20-%20policy%20statement%200501-%20Landscape%20Policy%20Framework.pdf (accessed on 17 July 2019).
- National Heritage Zones: A National Assessment of Scotland’s Landscapes. Available online: https://www.nature.scot/sites/default/files/2017-06/B464892%20-%20National%20Assessment%20of%20Scotland%27s%20landscapes%20%28from%20NHF%29.pdf (accessed on 17 July 2019).
- Handbook on Environmental Impact Assessment; Appendix 2, Landscape and Visual Impact Assessment; Scottish Natural Heritage: Scotland, UK, 2013; Available online: https://www.nature.scot/sites/default/files/Publication%202014%20-%20A%20handbook%20on%20environmental%20impact%20assessment.pdf (accessed on 17 July 2019).
- Fitting Landscapes—Securing More Sustainable Landscapes; Transport Scotland: Scotland, UK, 2014.
- Planning Advice Note 1/2013: Environmental Impact Assessment; Guidance to Replace PAN:58 and Containing Advice on the Integration of EIA Procedures into the Overall Development Management Process; Scottish Government: Scotland, UK, 2014.
- Zhang, H.; Fritts, J.E.; Goldman, S.A. An entropy-based objective evaluation method for image segmentation. In Proceedings of the SPIE 5307, Storage and Retrieval Methods and Applications for Multimedia 2004, San Jose, CA, USA, 18 December 2003. [Google Scholar] [CrossRef]
- Martin, D.; Fowlkes, C.; Tal, D.; Malik, J.A. Database of Human Segmented Natural Images and Its Application to Evaluating Algorithms and Measuring Ecological Statistics; ICCV: Vancouver, BC, Canada, 2001; pp. 416–423. [Google Scholar]
- Kohonen, T. Self-Organizing Maps, 2nd ed.; Springer: Heidelberg, Germany, 1997. [Google Scholar]
- Abdou, I.E.; Pratt, W.K. Quantitative design and evaluation of enhancement/thresholding edge detector. Proc. IEEE 1979, 67, 753–763. [Google Scholar] [CrossRef]
- Yasnoff, W.A.; Mui, J.K. Error Measure for scene segmentation. Pattern Recognit. 1977, 9, 217–231. [Google Scholar] [CrossRef]
- Sahoo, P.K.; Soltani, S.; Wong, A.K.C.; Chen, Y.C. Survey: A survey of thresholding techniques. Comput. Vis. Graph. Image Process. 1988, 41, 233–260. [Google Scholar] [CrossRef]
- Otsu, N. A threshold selection method from gray-level histograms. IEEE Trans. Syst. Man Cybern. 1979, 9, 62–66. [Google Scholar] [CrossRef]
- Martin, D.; Nazif, L.; Nazif, A. Dynamic Measurement of Computer Generated Image Segmentations. IEEE Trans. Pattern Anal. Mach. Intell. 1985, 7, 155–164. [Google Scholar]
- Pal, N.; Pal, S. A Review on Image Segmentation Techniques. Pattern Recognit. 1993, 26, 1277–1294. [Google Scholar] [CrossRef]
- Weszka, J.S.; Rosenfeld, A. Threshold evaluation techniques. IEEE Trans Syst. Man Cybernet 1978, 8, 622–629. [Google Scholar] [CrossRef]
- Koutsoyiannis, D. A random walk on water. Hydrol. Earth Syst. Sci. 2010, 14, 585–601. [Google Scholar] [CrossRef]
- Dimitriadis, P.; Koutsoyiannis, D.; Tzouka, K. Predictability in dice motion: How does it differ from hydro-meteorological processes? Hydrol. Sci. J. 2016, 61, 1611–1622. [Google Scholar] [CrossRef]
- Dimitriadis, P. Hurst-Kolmogorov Dynamics in Hydrometeorological Processes and in the Microscale of Turbulence. Ph.D. Thesis, Department of Water Resources and Environmental Engineering—National Technical University of Athens, Athens, Greece, 2017. [Google Scholar]
- Dimitriadis, P.; Tzouka, K.; Koutsoyiannis, D.; Tyralis, H.; Kalamioti, A.; Lerias, E.; Voudouris, P. Stochastic investigation of long-term persistence in two-dimensional images of rocks. Spat. Stat. 2019, 29, 177–191. [Google Scholar] [CrossRef]
- Koutsoyiannis, D.; Paschalis, A.; Theodoratos, N. Two-dimensional Hurst-Kolmogorov process and its application to rainfall fields. J. Hydrol. 2011, 398, 91–100. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; van Ness, J.W. Fractional Brownian Motions, Fractional Noises and Applications. SIAM Rev. 1968, 10, 422–437. [Google Scholar] [CrossRef]
- Sargentis, F.; Dimitriadis, P.; Iliopoulou, T.; Ioannidis, R.; Koutsoyiannis, D. Stochastic investigation of the Hurst-Kolmogorov behaviour in arts, European Geosciences Union General Assembly. In Geophysical Research Abstracts; Vienna, EGU2018-17740-1; European Geosciences Union: Munich, Germany, 2018; Volume 20. [Google Scholar]
- Ioannidis, R.; Dimitriadis, P.; Sargentis, G.-F.; Frangedaki, E.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic similarities between hydrometeorogical and art processes for optimizing architecture and landscape aesthetic parameters. In European Geosciences Union General Assembly 2019; Geophysical Research Abstracts, EGU2019-11403; European Geosciences Union: Munich, Germany, 2019; Volume 21. [Google Scholar]
- Panagiotakis, K.A. Research of tourist development of lake Megdoba. Report for the Hellenic Tourism Organization. 1967. [Google Scholar]
- Zaharatos, G.A. Program for the Touristic Development of the Plastira Lake (Megdova); KPOE: Athens, Greece, 1986. [Google Scholar]
- Life Program. Lake Plastira Area, A Pilot Sustainable Touristic Interference; ANKA City: Karditsa, Greece, 1994. [Google Scholar]
- Life Program. Lake Plastira Area, A Pilot Sustainable Touristic Interference 6; ANKA City: Karditsa, Greece, 1995. [Google Scholar]
- Sargentis, G.-F. The Aesthetic Element in Water, Hydraulics and Dams. Master’s Thesis, Department of Civil Engineer, NTUA, Athens, Greece, 1998. [Google Scholar]
- Sargentis, G.-F.; Hadjibiros, K.; Christofides, A. Plastiras Lake: The impact of water level on the aesthetic value of the landscape. In 9th International Conferenceon Environmental Science and Technology; Department of Environmental Studies, University of the Aegean: Mytilene, Greece, 2005. [Google Scholar]
- Sargentis, G.-F.; Hadjibiros, K.; Papagiannakis, I.; Papagiannakis, E. Plastiras Lake: influence of the relief on the revelation of the water presence, In 9th International Conference on Environmental Science and Technology, Rhodes Island; Department of Environmental Studies, University of the Aegean: Mytilene, Greece, 2005. [Google Scholar]
- Christofides, A.; Efstratiadis, A.; Koutsoyiannis, D.; Sargentis, G.-F.; Hadjibiros, K. Resolving conflicting objectives in the management of the Plastiras Lake: Can we quantify beauty? Hydrol. Earth Syst. Sci. 2005, 9, 507–515. [Google Scholar] [CrossRef]
- Beardsley, M.C. Aesthetics from Classical Greece to the Present: A Short History; University of Alabama Press: Tuscaloosa, AL, USA, 1975. [Google Scholar]
- Guyer, P. Kant and the Claims of Taste, 2nd ed.; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Donovan, F. Our Uncertain Future: Can Good Planning Create Sustainable Communities; University of Illinois: Champaign-Urbana, IL, USA, 2009. [Google Scholar]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sargentis, G.-F.; Dimitriadis, P.; Ioannidis, R.; Iliopoulou, T.; Koutsoyiannis, D. Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works. Energies 2019, 12, 2817. https://doi.org/10.3390/en12142817
Sargentis G-F, Dimitriadis P, Ioannidis R, Iliopoulou T, Koutsoyiannis D. Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works. Energies. 2019; 12(14):2817. https://doi.org/10.3390/en12142817
Chicago/Turabian StyleSargentis, G.-Fivos, Panayiotis Dimitriadis, Romanos Ioannidis, Theano Iliopoulou, and Demetris Koutsoyiannis. 2019. "Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works" Energies 12, no. 14: 2817. https://doi.org/10.3390/en12142817
APA StyleSargentis, G.-F., Dimitriadis, P., Ioannidis, R., Iliopoulou, T., & Koutsoyiannis, D. (2019). Stochastic Evaluation of Landscapes Transformed by Renewable Energy Installations and Civil Works. Energies, 12(14), 2817. https://doi.org/10.3390/en12142817








