Economic-Engineering Modelling of the Buildings Sector to Study the Transition towards Deep Decarbonisation in the EU
Abstract
1. Introduction
2. Approach
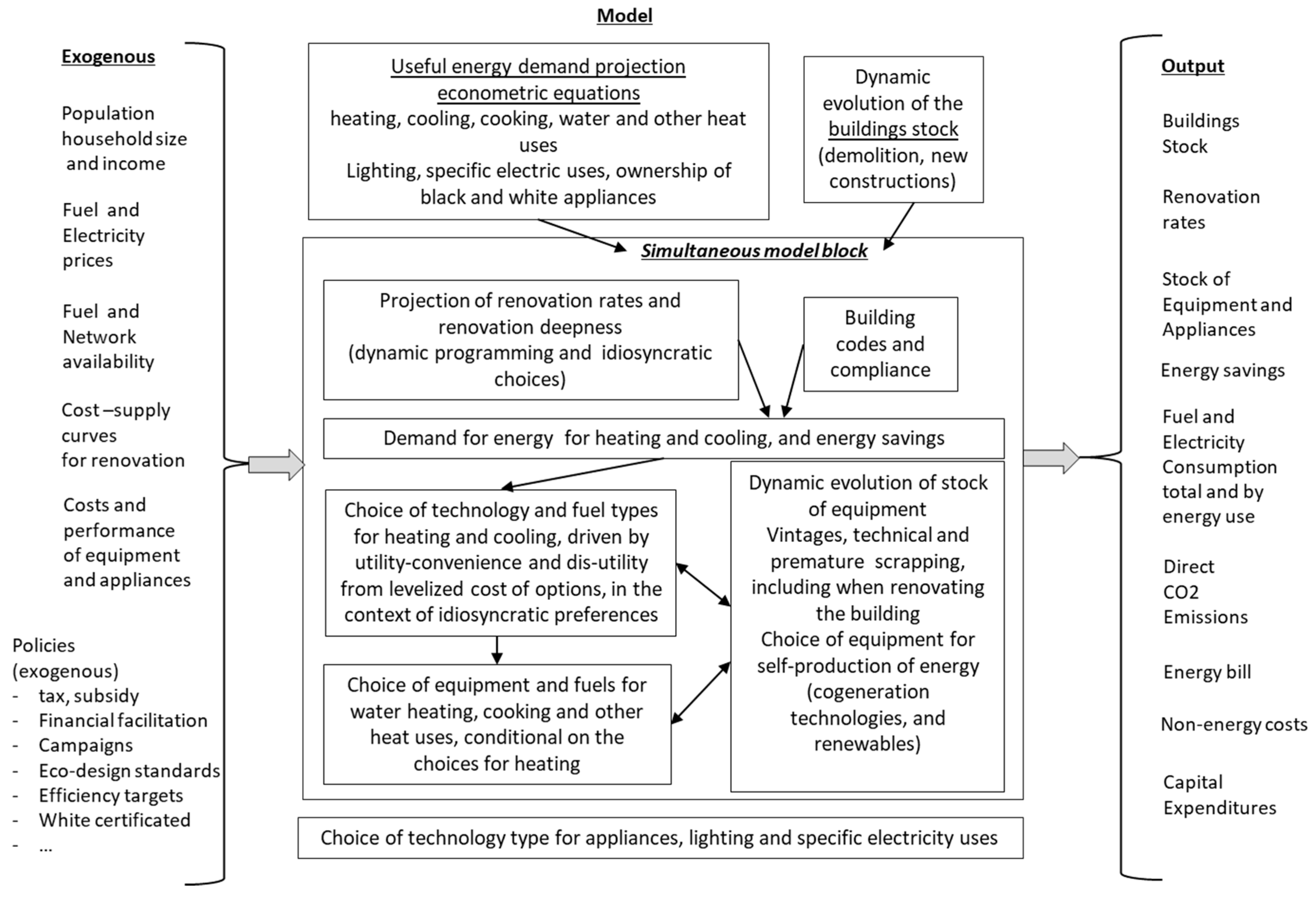
2.1. Rationale
2.2. The Mathematical Framework
2.3. The Dataset
- Types of buildings: single or multi-storey buildings.
- Age of construction: nine age bands covering the period 1920–2015. Historical data on the housing regarding demolition, new constructions and renovation draw on [9].
- Geographical regions: three stylised areas, namely urban, semi-urban and rural areas.
- Income classes: five income classes based on Eurostat statistics.
- Trade
- Commercial buildings
- Warehouses
- Cold Storage
- Market Services
- Private offices and other buildings in market services
- Hotels and restaurants
- Non-Market Services
- Public offices
- Hospitals and health institutions
- Schools and educational buildings
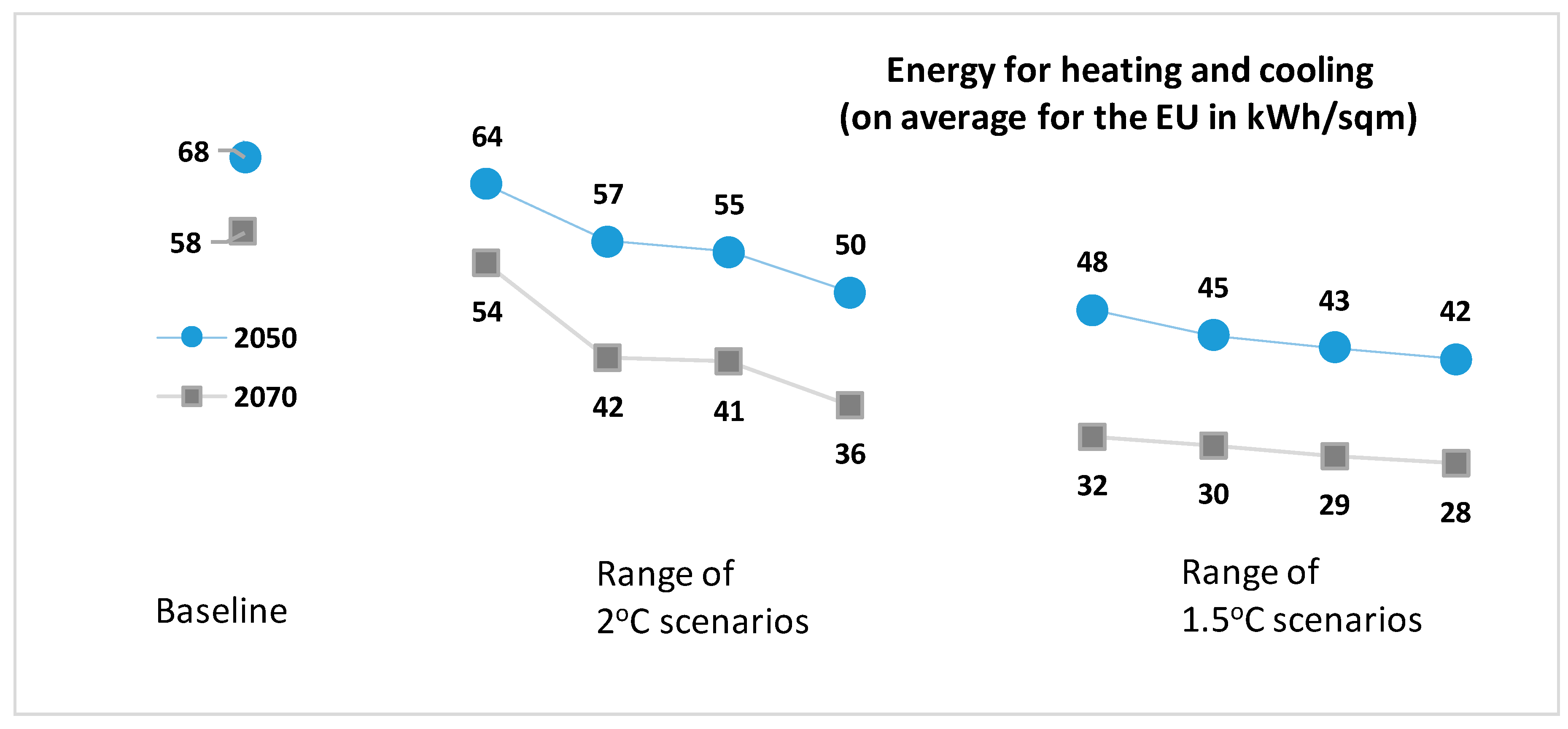
3. Illustrative Model Applications
- The Energy Performance of Buildings Directive (Directive (EU) 2018/844), which entered into force on 9 July 2018 [76], and according to which new buildings are assumed to be nearly zero-energy buildings as of 2020.
- The amended Energy Efficiency Directive (EED) [77].
- The revised Renewable Energy Directive [78].
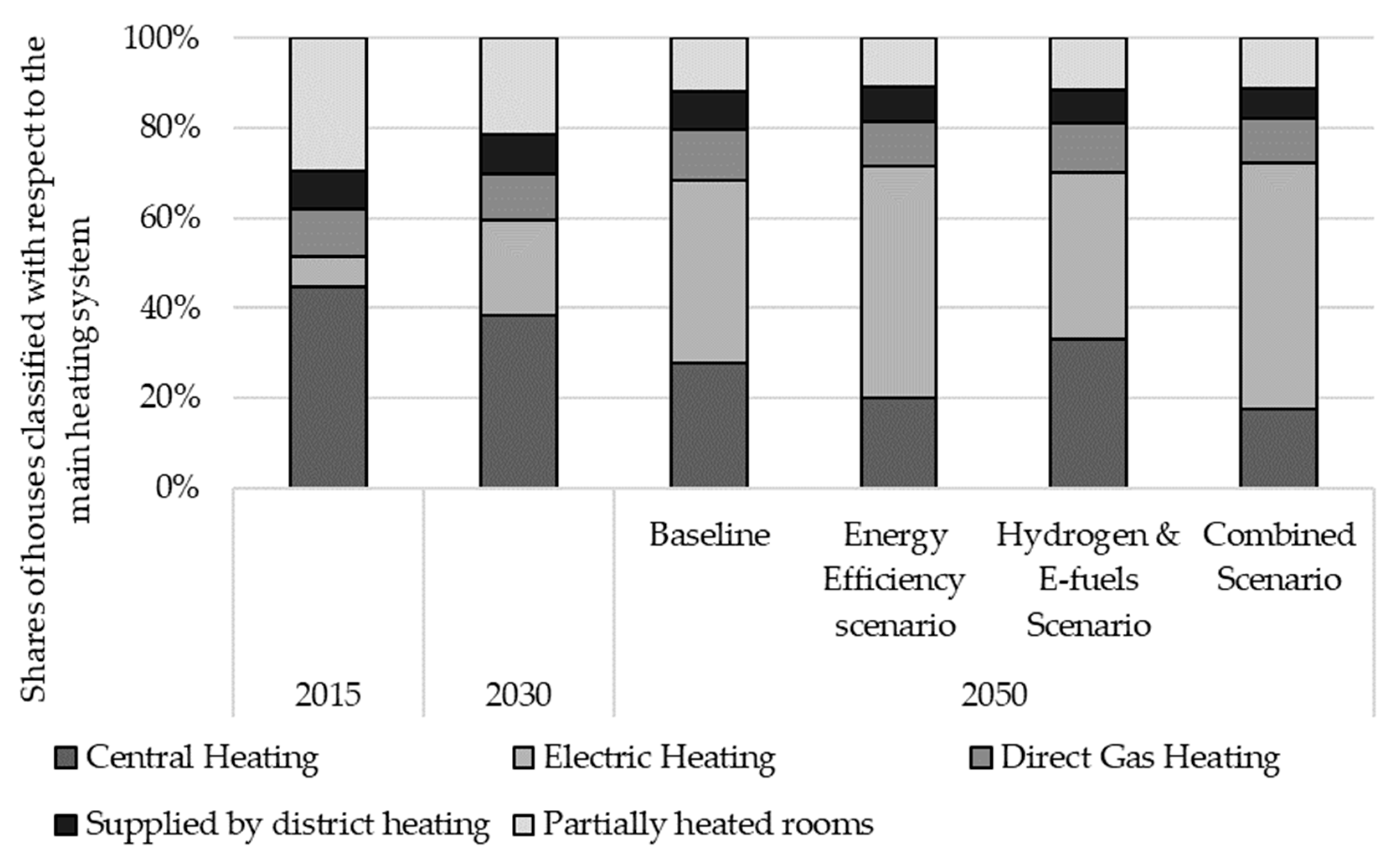
- The Energy-Efficiency scenario involves policies that deliver very ambitious energy savings in the buildings sector and at the same time, projects further electrification of heat. The scenario does not include the development of carbon-neutral hydrogen and hydrocarbons.
- The Hydrogen and E-fuels scenario focuses on the supply-side of the energy system and assumes the development of climate-neutral fuels that can replace natural gas in distribution systems. The scenario assumes that ambitious energy savings take place to avoid the excessive increase in the volume of electricity needed to produce hydrogen and e-fuels. However, energy efficiency ambition is lower than in the previous scenario.
- The Combined scenario assumes a more ambitious emissions reduction target for 2050 compared to the previous two scenarios, aiming at carbon-neutrality by 2050. To this end, the scenario assumes development of very ambitious energy savings together with carbon-neutral hydrogen and e-fuels.
4. Concluding Remarks
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Use | Type of Fuel | Technology |
| Space Heating | Diesel Oil | Conventional Boiler |
| Condensing Boiler | ||
| Natural Gas | Conventional Boiler | |
| Condensing Boiler | ||
| Micro-Cogeneration (CHP) Internal combustion engine | ||
| Micro-CHP CCGT (Combined Cycle Gas Turbine) | ||
| Micro-CHP Fuel Cell | ||
| Gas Heat Pump (air to water) | ||
| Autonomous Gas heater | ||
| Biomass | Wood Pellets Boiler | |
| Electricity | Air-Source Heat Pump (air to water) | |
| Water Source Heat pumps (water to water/air) | ||
| Ground-Source Heat Pump (brine to water/air) | ||
| Electrical space heater | ||
| Solar | Thermal Solar | |
| Steam | Distributed Heat | |
| Geothermal | Geothermal Ponds | |
| Solids | Stove for solid fuels | |
| LPG | Autonomous LPG heater | |
| Stove for liquid fuels | ||
| Space Cooling | Electricity | Air-Source Heat Pump (air to water) |
| Water Source Heat pumps (water to water/air) | ||
| Ground-Source Heat Pump (brine to water/air) | ||
| Split system air condition | ||
| Centralized cooling systems | ||
| Natural Gas | Gas Heat Pump (air) | |
| Absorption Chiller | ||
| Adsorption Chiller | ||
| Steam | District Cooling |
| Use | Type of Fuel | Technology |
| Water Heating | Diesel Oil | Conventional Boiler |
| Condensing Boiler | ||
| Natural Gas | Conventional Boiler | |
| Condensing Boiler | ||
| Micro-CHP Internal combustion engine | ||
| Micro-CHP CCGT | ||
| Micro-CHP Fuel Cell | ||
| Gas Heat Pump (air to water) | ||
| Autonomous Gas heater | ||
| Biomass | Wood Pellets Boiler | |
| Electricity | Air-Source Heat Pump (air to water) | |
| Water Source Heat pumps (water to water/air) | ||
| Ground-Source Heat Pump (brine to water/air) | ||
| Heat Pump Water Heater | ||
| Simple electrical water heater | ||
| Solar | Thermal Solar | |
| Steam | Distributed Heat | |
| Geothermal | Geothermal Ponds | |
| Solids | Stove for solid fuels | |
| LPG | Autonomous LPG heater | |
| Cooking | Natural Gas | Gas Cookers |
| Biomass | Solid/Biomass Cookers | |
| Electricity | Electric Cookers | |
| LPG | Liquid Cookers |
References
- Eurostat Energy Balances. Available online: https://ec.europa.eu/eurostat/web/energy/data/energy-balances (accessed on 28 May 2019).
- Fleiter, T.; Steinbach, J.; Ragwitz, M.; Dengler, J.; Köhler, B.; Reitze, F.; Tuille, F.; Hartner, M.; Kranzl, L.; Forthuber, S. Mapping and analyses of the current and future (2020–2030) heating/cooling fuel deployment (fossil/renewables). Work Package 2016, 1, 1–156. [Google Scholar]
- IEA. Energy Efficiency 2018; Market Report Series; IEA/OECD Publications: Paris, France, 2018. [Google Scholar]
- European Parliament. Directive 2010/31/EU of the European Parliament and of the Council of 19 May 2010 on the Energy Performance of Buildings. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32010L0031&from=EN (accessed on 28 May 2019).
- Hermelink, A.; Schimschar, S.; Boermans, T.; Pagliano, L.; Zangheri, P.; Armani, R.; Voss, K.; Musall, E. Towards Nearly Zero-Energy Buildings Definition of Common Principles under the EPBD—Final Report. In Proceedings of the 2013 European Council for an Energy Efficient Economy, Brussels, Belgium, 14 February 2013. [Google Scholar]
- Economidou, M. Energy performance requirements for buildings in Europe. REHVA J. 2012, March, 16–21. [Google Scholar]
- Jamieson, M.; Brajterman, O.; Verstraeten, Y.; Arbon, J.; Lonsdale, J.; Allington, M. International Energy Performance of Buildings Directive (EPBD) Compliance Study: Final Report, Study for the European Commission; Directorate-General for Energy Publications Office: Luxembourg, 2015; ISBN 978-92-79-54219-0. [Google Scholar]
- Economidou, M.; Atanasiu, B.; Despret, C.; Maio, J.; Nolte, I.; Rapf, O. Europe’s buildings under the microscope. A Country-by-Country Review of the Energy Performance of Buildings; Buildings Performance Institute Europe (BPIE): Bruxelles, Belgium, 2011; ISBN 9789491143014. [Google Scholar]
- Meijer, F.; Visscher, H. Jobs Creation Through Energy Renovation of the Housing Stock. Neujobs Working Paper D14.2. December 2012. Available online: http://conference.iza.org/conference_files/neujobs_2014/4.pdf (accessed on 16 July 2019).
- European Parliament. Regulation (EU) 2017/1369 of the European Parliament and of the Council-of 4 July 2017—Setting a Framework for Energy Labelling and Repealing Directive 2010/30/EU. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/PDF/?uri=CELEX:32017R1369&rid=1 (accessed on 28 May 2019).
- IEA. Achievements of Appliance Energy Efficiency Standards and Labelling Programs: A Global Assessment; IEA/OECD Publications: Paris, France, 2015. [Google Scholar]
- van Delft, Y.; de Kler, R. Matching Processes with Electrification Technologies; Final Report of the E-Match Project; ECN-E-17-008; ECN: Petten, The Netherlands, 2017. [Google Scholar]
- Brown, M.A. Market failures and barriers as a basis for clean energy policies. Energy Policy 2001, 29, 1197–1207. [Google Scholar] [CrossRef]
- Golove, W.H.; Eto, J.H. Market Barriers to Energy Efficiency: A Critical Reappraisal of the Rationale for Public Policies to Promote Energy Efficiency; Energy & Environment Division, Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1996; No. LBL-38059. [Google Scholar]
- Valentová, M. Barriers to Energy Efficiency—Focus on Transaction Costs. Acta Polytech. 2010, 50, 4. [Google Scholar]
- Hausman, J.A. Individual Discount Rates and the Purchase and Utilization of Energy-Using Durables. Bell J. Econ. 1979, 10, 33–54. [Google Scholar] [CrossRef]
- Howarth, R.B.; Sanstad, A.H. Discount Rates and Energy Efficiency. Contemp. Econ. Policy 1995, 13, 101–109. [Google Scholar] [CrossRef]
- Kavgic, M.; Mavrogianni, A.; Mumovic, D.; Summerfield, A.; Stevanovic, Z.; Djurovic-Petrovic, M. A review of bottom-up building stock models for energy consumption in the residential sector. Build. Environ. 2010, 45, 1683–1697. [Google Scholar] [CrossRef]
- Charlier, D.; Mosiño, A.; Pommeret, A. Energy-saving technology adoption under uncertainty in the residential sector. Annales d’Economie et Statistiques 2011, 103–104, 43–70. [Google Scholar] [CrossRef][Green Version]
- Bhattacharyya, S.C.; Timilsina, G.R. Energy Demand Models for Policy Formulation: A Comparative Study of Energy Demand Models; Development Research Group Environment and Energy Team, The World Bank: Washington, DC, USA, 2009. [Google Scholar]
- Clinch, J.P.; Healy, J.D.; King, C. Modelling improvements in domestic energy efficiency. Environ. Model. Softw. 2001, 16, 87–106. [Google Scholar] [CrossRef]
- Coffy, B.; Borgeson, S.; Selkowitz, S.; Apte, J.; Mathew, P.; Haves, P. Towards a very low-energy building stock: Modelling the US commercial building sector to support policy and innovation planning. Build. Res. Inf. 2009, 37, 610–624. [Google Scholar] [CrossRef]
- Bernard, J.T. An Integrated Total Energy Demand Model for the Province of Québec; Département D’économie, Université Laval: Sainte-Foy, QC, Canada, 1996. [Google Scholar]
- Dong, B.; Li, Z.; Rahman, S.M.; Vega, R. A hybrid model approach for forecasting future residential electricity consumption. Energy Build. 2016, 117, 341–351. [Google Scholar] [CrossRef]
- Weiss, M.; Patel, M.K.; Junginger, M.; Blok, K. Analyzing price and efficiency dynamics of large appliances with the experience curve approach. Energy Policy 2010, 38, 770–783. [Google Scholar] [CrossRef]
- Aydinalp, M.; Ugursal, V.I.; Fung, A.S. Modeling of the space and domestic hot-water heating energy-consumption in the residential sector using neural networks. Appl. Energy 2004, 79, 159–178. [Google Scholar] [CrossRef]
- Dinan, T.M.; Miranowski, J.A. Estimating the implicit price of energy efficiency improvements in the residential housing market: A hedonic approach. J. Urban Econ. 1989, 25, 52–67. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I. Modeling of end-use energy consumption in the residential sector: A review of modeling techniques. Renew. Sustain. Energy Rev. 2009, 13, 1819–1835. [Google Scholar] [CrossRef]
- Aydinalp, M.; Ugursal, V.I.; Fung, A.S. Modeling of the appliance, lighting, and space-cooling energy consumptions in the residential sector using neural networks. Appl. Energy 2002, 71, 87–110. [Google Scholar] [CrossRef]
- Daioglou, V.; Van Ruijven, B.J.; Van Vuuren, D.P. Model projections for household energy use in developing countries. Energy 2012, 37, 601–615. [Google Scholar] [CrossRef]
- Shorrock, L.D.; Dunster, J.E. The physically-based model BREHOMES and its use in deriving scenarios for the energy use and carbon dioxide emissions of the UK housing stock. Energy Policy 1997, 25, 1027–1037. [Google Scholar] [CrossRef]
- Anderson, B.R.; Chapman, P.F.; Cutland, N.G.; Dickson, C.M.; Henderson, G.; Henderson, J.H.; Iles, P.J.; Kosmina, L.; Shorrock, L.D. BREDEM-12 Model Description; Building Research Establishment: Watford, UK, 1996. [Google Scholar]
- Natarajan, S.; Levermore, G.J. Predicting future UK housing stock and carbon emissions. Energy Policy 2007, 35, 5719–5727. [Google Scholar] [CrossRef]
- Pout, C.H. N-DEEM: The national nondomestic buildings energy and emissions model. Environ. Plan. B Plan. Des. 2000, 27, 721–732. [Google Scholar] [CrossRef]
- Nemry, F.; Uihlein, A.; Colodel, C.M.; Wittstock, B.; Braune, A.; Wetzel, C.; Hasan, I.; Niemeier, S.; Frech, Y.; Kreissig, J.; et al. Environmental Improvement Potentials of Residential Buildings (IMPRO-Building); JRC Report; European Communities: Brussels, Belgium, 2008. [Google Scholar]
- Uihein, A.; Eder, P. Towards Additional Policies to Improve the Environmental Performance of Buildings; European Communities: Brussels, Belgium, 2009. [Google Scholar]
- Arpano, M.R.; Sassi, P. A multi-stage approach to low carbon housing renovations. In Proceedings of the 30th International Plea Conference, CEPT University, Ahmedabd, India, 16–18 December 2014. [Google Scholar]
- Skaran, A.M. Typologies and Energy Demand Modelling of the Norwegian Building Stock—Part 2, Project Work; Norwegian University of Science and Technology: Trondheim, Norway, 2013. [Google Scholar]
- Chateau, B.; Lapillonne, B. Long term energy demand forecasting: A new approach. Energy Policy 1978, 6, 140–157. [Google Scholar] [CrossRef]
- IAEA. Model for Analysis of Energy Demand, (MAED-2), Manual 18; International Atomic Energy Agency: Vienna, Austria, 2006. [Google Scholar]
- Tanatvanit, S.; Limmeechokchai, B.; Chungpaibulpatana, S. Sustainable energy development strategies: Implications of energy demand management and renewable energy in Thailand. Renew. Sustain. Energy Rev. 2003, 7, 367–395. [Google Scholar] [CrossRef]
- Swan, L.G.; Ugursal, V.I.; Beausoleil-Morrison, I. Hybrid residential end-use energy and greenhouse gas emissions model-development and verification for Canada. J. Build. Perform. Simul. 2013, 6, 1–23. [Google Scholar] [CrossRef]
- Swan, L.G. Residential Sector Energy and GHG Emissions Model for the Assessment of New Technologies. Ph.D. Thesis, Dalhousie University, Halifax, NS, Canada, 2010. [Google Scholar]
- Wills, A.D. On the Modelling and Analysis of Converting Existing Canadian Residential Communities to Net-Zero Energy. Ph.D. Thesis, Carleton University, Ottawa, ON, Canada, 2018. [Google Scholar]
- EIA, D. Residential Demand Module of the National Energy Modeling System Model Documentation Report; US Energy Information Administation: Washington, DC, USA, 2013. [Google Scholar]
- Bataille, C.G.F. Design and Application of a Technologically Explicit Hybrid Energy-Economy Policy Model with Micro and Macroeconomic Dynamics. Ph.D. Thesis, School of Resource and Environmental Management-Simon Fraser University, Burnaby, BC, Canada, 2005. [Google Scholar]
- Sadler, M. Home energy preferences & policy: Applying stated choice modeling to a hybrid energy economy model. Ph.D. Thesis, Environment School of Resource and Environmental Management, Burnaby, BC, Canada, 2003. [Google Scholar]
- Kannan, R.; Strachan, N. Modelling the UK residential energy sector under long-term decarbonisation scenarios: Comparison between energy systems and sectoral modelling approaches. Appl. Energy 2009, 86, 416–428. [Google Scholar] [CrossRef]
- Stecley, S.G.; Meade, D.S.; Lenox, C.S.; Hoffman, K.C.; Reid, D.H.; Schoener, B.C. Energy demand analytics using coupled technological and economic models. Energy J. 2011, 173–191. [Google Scholar] [CrossRef]
- Friege, J.; Chappin, E. Modelling decisions on energy-efficient renovations: A review. Renew. Sustain. Energy Rev. 2014, 39, 196–208. [Google Scholar] [CrossRef]
- Jakob, M. Modeling the choice of renovation modes of single-family home owners with respect to energy-efficiency. In Proceedings of the 15th EAERE Annual Conference, University of Macedonia, Thessaloniki, Greece, 30 June 2007; pp. 27–30. [Google Scholar]
- Friege, J.; Chappin, E. Simulating the influence of socio-spatial structures on energy-efficient renovations. In Proceedings of the Social Simulation Conference, Barcelona, Spain, 1–5 September 2014. [Google Scholar]
- Clinch, J.P.; Healy, J.D. Valuing improvements in comfort from domestic energy-efficiency retrofits using a trade-off simulation model. Energy Econ. 2003, 25, 565–583. [Google Scholar] [CrossRef]
- Ximenes, R.; Ferrao, P. Energy Demand Model to Support the Definition of Sustainable Energy Systems: Residential Sector. Master’s Thesis, Tecnico Lisboa, Portugal, 2015. [Google Scholar]
- Lutzenhiser, L.; Moezzi, M.; Hungerford, D.; Friedmann, R. Sticky points in modeling household energy consumption. In Proceedings of the 2010 ACEEE Summer Study on Energy Efficiency in Buildings, Pacific Grove, CA, USA, 15–20 August 2010. [Google Scholar]
- Train, K. Discrete Choice Methods with Simulation; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Loga, T.; Diefenbach, N. TABULA Calculation Method—Energy Use for Heating and Domestic Hot Water. TABULA Proj. 2013. Available online: http://episcope.eu/fileadmin/tabula/public/docs/report/TABULA_CommonCalculationMethod.pdf (accessed on 17 July 2019).
- Ameli, N.; Brandt, N. What impedes household investment in energy efficiency and renewable energy? Int. Rev. Environ. Resour. Econ. 2014, 8, 101–138. [Google Scholar] [CrossRef]
- Deaton, A.; Muellbauer, J. Economics and Consumer Behaviour; Cambridge University Press: Cambridge, UK, 1980; ISBN 0521296765. [Google Scholar]
- Jehle, G.A.; Reny, P.J. Advanced Microeconomic Theory, 3rd ed.; Financial Times, Prentice Hall: Harlow, UK, 2011; ISBN 978-0-273-73191-7. [Google Scholar]
- Chipman, J.S. Aggregation and Estimation in the Theory of Demand. Hist. Polit. Econ. 2006, 38, 106–129. [Google Scholar] [CrossRef]
- Rosen, H.S. Applied welfare economics with discrete choice models. Econometrica 1981, 49, 105–130. [Google Scholar]
- Claudy, M.; O’Driscoll, A. Beyond Economics: A Behavioural Approach to Energy Efficiency in Domestic Buildings. J. Sustain. Energy Dev. Policy 2008, 1, 27–40. [Google Scholar]
- Sanstad, A.H.; McMahon, J.E. Aspects of Consumers’ and Firms’ Energy Decision-Making: A Review and Recommendations for the National Energy Modelling System (NEMS); Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2008. [Google Scholar]
- Loga, T.; Stein, B.; Diefenbach, N. TABULA building typologies in 20 European countries—Making energy-related features of residential building stocks comparable. Energy Build. 2016, 132, 4–12. [Google Scholar] [CrossRef]
- Schimschar, S.; Grözinger, J.; Korte, H.; Boermans, T.; Lilova, V.; Bhar, R. Panorama of the European Non-Residential Construction Sector. ECOFYS, Report to European Copper Institute. 2011. Available online: http://leonardo-energy.pl/wp-content/uploads/2018/03/Europejski-sektor-budownictwa-niemieszkalnego.pdf (accessed on 17 July 2019).
- Fleiter, T.; Braungardt, S.; Sohaib, T.; Schlomann, B.; Eichhammer, W.; Elsland, R.; Kranzl, L.; Jakob, M. Assessing the impact of the EU Ecodesign Directive on a member state level monitoring. In Proceedings of the Summer study on Energy Efficiency (ECEEE 2015), Hyères, France, 1–6 June 2015. [Google Scholar]
- Eurostat. Average Number of Rooms Per Person by Degree of Urbanization. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=ilc_lvho04d&lang=en (accessed on 28 May 2019).
- Eurostat. Household Characteristics by Degree of Urbanisation. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=hbs_car_t315&lang=en (accessed on 28 May 2019).
- Eurostat. Living Conditions Cities and Greater Cities. Available online: http://appsso.eurostat.ec.europa.eu/nui/show.do?dataset=urb_clivcon&lang=en (accessed on 28 May 2019).
- Dol, K.; Haffner, M. Housing Statistics in the European Union 2010; Delft University of Technology: Delft, The Netherlands, 2010. [Google Scholar]
- Birchall, S.; Wallis, I.; Churcher, D.; Pezzutto, S.; Fedrizzi, R.; Causse, E. Survey on the Energy Needs and Architectural Features of the EU Building Stock; BSRIA: Bracknell, UK, 2014. [Google Scholar]
- Arran, J.; Slowe, J. 2050 Pathways for Domestic Heat Final Report; Delta Energy & Environment Ltd.: Edinburgh, UK, 2012. [Google Scholar]
- De Vita, A.; Kielichowska, I.; Mandatowa, P. Technology Pathways in Decarbonisation Scenarios, ASSET Project Report. July 2018. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/2018_06_27_technology_pathways_-_finalreportmain2.pdf (accessed on 28 May 2019).
- European Commission. Clean Energy for All Europeans Policy Package. November 2016. Available online: https://ec.europa.eu/energy/en/topics/energy-strategy-and-energy-union/clean-energy-all-europeans (accessed on 28 May 2019).
- European Parliament. Directive (EU) 2018/844 of the European Parliament and of the Council of 30 May 2018 Amending Directive 2010/31/EU on the Energy Performance of Buildings and Directive 2012/27/EU on Energy Efficiency. 30 May 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=uriserv%3AOJ.L_.2018.156.01.0075.01.ENG (accessed on 28 May 2019).
- European Parliament. Directive (EU) 2018/2002 of the European Parliament and of the Council of 11 December 2018 Amending Directive 2012/27/EU on Energy Efficiency. 11 December 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=uriserv%3AOJ.L_.2018.328.01.0210.01.ENG (accessed on 28 May 2019).
- European Parliament. Directive (EU) 2018/2001 of the European Parliament and of the Council of 11 December 2018 on the Promotion of the Use of Energy from Renewable Sources. 11 December 2018. Available online: https://eur-lex.europa.eu/legal-content/EN/TXT/?uri=uriserv:OJ.L_.2018.328.01.0082.01.ENG&toc=OJ:L:2018:328:TOC (accessed on 28 May 2019).
- Paltsev, S.; Capros, P. Cost Concepts for Climate Change Mitigation. Clim. Change Econ. 2013, 4, 1340003. [Google Scholar] [CrossRef]
| Nomenclature | |
|---|---|
| Sets | |
| Time (years) within a time horizon | |
| Building categories | |
| Discrete set of dynamic renovation strategies | |
| Discrete set of dynamic equipment strategies | |
| Parameters | |
| Macroeconomic factors | |
| Net annual cost (operating and capital costs, inclusive of investment for building insulation) for the useful energy demand | |
| Log-linear function for the steady-state relationship between the useful energy and the explanatory factors | |
| Upper bound of the logistic curve for useful energy demand | |
| Scale parameter of the logistic curve for useful energy demand | |
| Slope parameter of logistic curve for useful energy demand | |
| Exogenous rate of demolition of the buildings stock | |
| Annual growth rate of macroeconomic and demographic factors | |
| Pace at which dynamically tends to an optimal buildings stock | |
| Exogenous rhythm of transfer of population from building category to | |
| Maximum growth limit of transfer of population from to | |
| Discount rate reflecting the subjective cost of equity and the cost of debt | |
| Technology maturity factors | |
| Variables | |
| Econometrically estimated useful energy demand for the specific end-uses | |
| Stock of building | |
| Annual growth rate of buildings stock | |
| Annual growth rate of new buildings | |
| Transfer of population from to | |
| Annual growth rate of transfer of population from to | |
| Investment expenditures for renovation (i.e., investment costs, hidden costs and/or subsidies) | |
| Annual costs of renovation (i.e., variable fuel and non-fuel costs) | |
| Present value of cost streams to compare alternative renovation strategies | |
| Frequency of choice of equipment strategies per building category | |
| Investment expenditures for energy using equipment (i.e., investment costs, hidden costs and/or subsidies) | |
| Annual costs of energy using equipment (i.e., variable fuel and non-fuel costs, and fixed operation and maintenance costs) | |
| Present value of cost streams to compare alternative dynamic strategies of energy using equipment | |
| Frequency of choice of equipment strategies per building category | |
| Baseline Scenario, EU | 2015 | 2030 | 2050 |
|---|---|---|---|
| Residential sector | |||
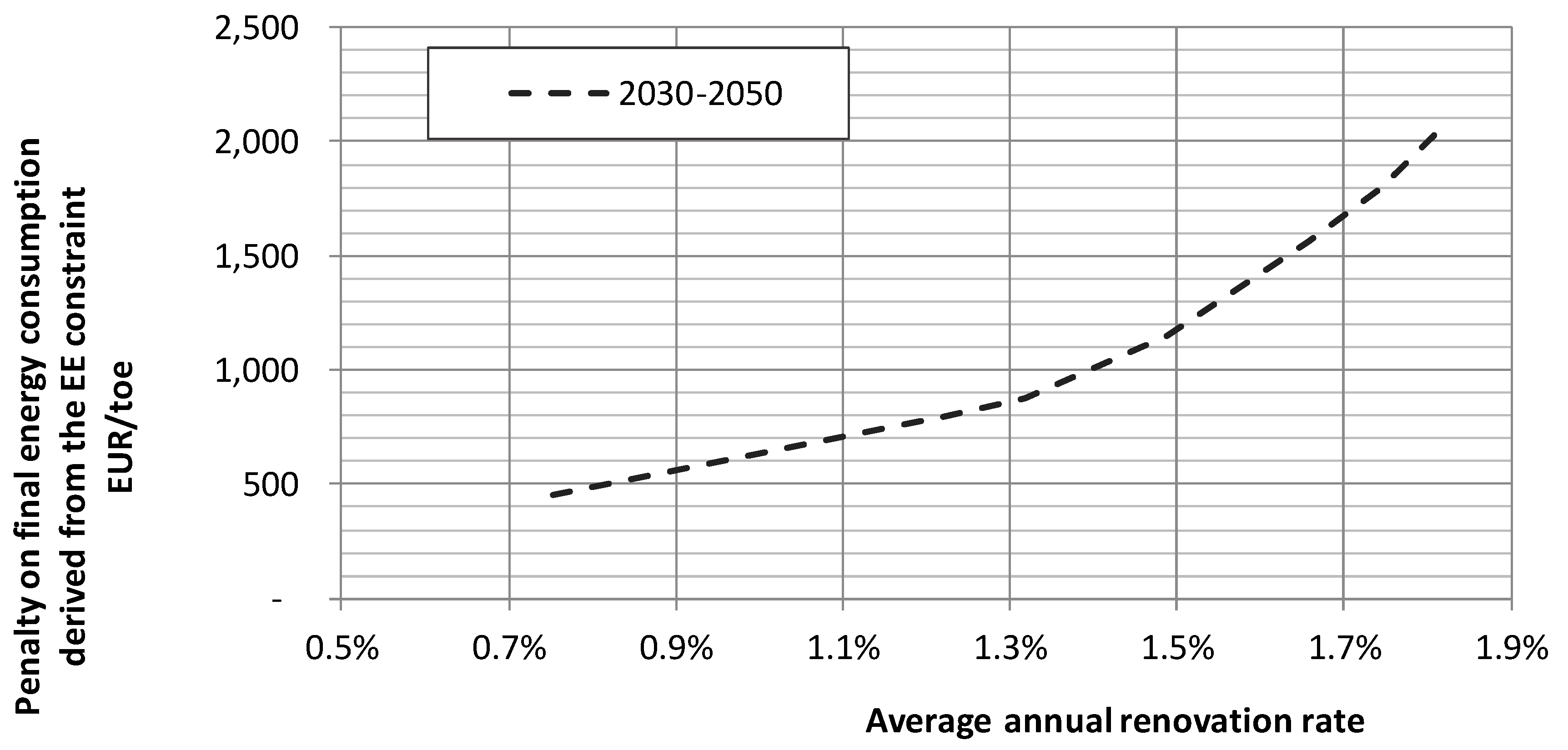
| Average renovation rate per year (%) | 0.84% | 2.04% | 1.00% |
| Energy deepness of renovation (%) | 12% | 66% | 34% |
| Final energy consumption (Mtoe) | 300 | 224 | 192 |
| of which solid and liquid fossil fuels | 48 | 6 | 1 |
| of which natural gas | 113 | 82 | 55 |
| of which renewables | 43 | 32 | 20 |
| of which district heating | 24 | 17 | 12 |
| of which electricity | 72 | 87 | 105 |
| Share of electricity in total consumption (%) | 24% | 39% | 55% |
| Annual rate of energy savings (%) | - | 1.9% | 0.8% |
| Direct CO2 emissions (MtCO2) | 423 | 214 | 130 |
| Annual rate of change of direct CO2 emissions | - | −3.7% | −2.5% |
| Services sector | |||
| Average renovation rate per year (%) | 0.46% | 1.98% | 0.62% |
| Average energy savings per year, due to renovation (%) | 16% | 60% | 23% |
| Final energy consumption (Mtoe) | 161 | 127 | 133 |
| of which solid and liquid fossil fuels | 20 | 2 | 0 |
| of which natural gas | 52 | 32 | 17 |
| of which renewables | 5 | 4 | 3 |
| of which district heating | 11 | 8 | 7 |
| of which electricity | 73 | 81 | 105 |
| Share of electricity in total consumption (%) | 45% | 64% | 79% |
| Annual rate of energy savings (%) | - | 1.6% | −0.2% |
| Direct CO2 emissions (MtCO2) | 184 | 82 | 40 |
| Annual rate of change of direct CO2 emissions | - | −5.2% | −3.5% |
| Year 2050 | Energy Efficiency Scenario | Hydrogen and E-Fuels Scenario | Combined Scenario |
|---|---|---|---|
| Residential sector | |||
| Average renovation rate per year (%) | 1.77% | 1.21% | 1.59% |
| Energy deepness of renovation (%) | 55% | 42% | 52% |
| Final energy consumption (Mtoe) | 137 | 183 | 142 |
| of which solid and liquid fossil fuels | 0 | 0 | 0 |
| of which natural gas | 30 | 57 | 29 |
| of which renewables | 13 | 18 | 14 |
| of which district heating | 9 | 11 | 8 |
| of which electricity | 84 | 97 | 90 |
| Share of electricity in total consumption (%) | 61% | 53% | 63% |
| Energy savings from Baseline (%) | 28% | 5% | 26% |
| Direct CO2 emissions (MtCO2) | 60 | 45 | 12 |
| Change of direct CO2emissions from Baseline | −54% | −65% | −91% |
| Services sector | |||
| Average renovation rate per year (%) | 1.35% | 0.92% | 1.18% |
| Average energy savings per year, due to renovation (%) | 48% | 37% | 45% |
| Final energy consumption (Mtoe) | 89 | 123 | 96 |
| of which solid and liquid fossil fuels | 0 | 0 | 0 |
| of which natural gas | 12 | 17 | 11 |
| of which renewables | 2 | 3 | 3 |
| of which district heating | 5 | 7 | 6 |
| of which electricity | 69 | 97 | 76 |
| Share of electricity in total consumption (%) | 78% | 78% | 79% |
| Energy savings from Baseline (%) | 33% | 7% | 28% |
| Direct CO2 emissions (MtCO2) | 23 | 13 | 4 |
| Change of direct CO2emissions from Baseline | −42% | −68% | −90% |
| Baseline Scenario, EU | 2011–2020 | 2021–2030 | 2031–2050 |
|---|---|---|---|
| Residential sector | |||
| Investment expenditure (Bn €) | 1161 | 1989 | 3988 |
| For the building shell | 201 | 479 | 641 |
| For equipment and appliances | 960 | 1510 | 3346 |
| Annuity capital payment (annual, on average, Bn €) | 204 | 347 | 461 |
| For the building shell | 10 | 53 | 101 |
| For equipment and appliances | 194 | 294 | 360 |
| Cost of purchasing energy products (annual, on average, Bn €) | 362 | 398 | 349 |
| Total cost of energy services (annual, on average, Bn €) | 566 | 745 | 811 |
| % change of operating expenditures (OPEX), from 2011–2020 | - | 10% | −4% |
| % change of capital expenditures (CAPEX), from 2011–2020 | - | 71% | 72% |
| Services sector | |||
| Investment expenditure (Bn €) | 384 | 607 | 1042 |
| For the building shell | 81 | 163 | 214 |
| For equipment and appliances | 303 | 444 | 828 |
| Annuity capital payment (annual, on average, Bn €) | 41 | 91 | 127 |
| For the building shell | 5 | 19 | 38 |
| For equipment and appliances | 36 | 73 | 89 |
| Cost of purchasing energy products (annual, on average, Bn €) | 188 | 213 | 216 |
| Total cost of energy services (annual, on average, Bn €) | 229 | 305 | 344 |
| % change of OPEX, from 2011–2020 | - | 14% | 15% |
| % change of CAPEX, from 2011–2020 | - | 58% | 36% |
| Average or Cumulative Values, in the Period 2031–2050 for the EU | Energy Efficiency Scenario | Hydrogen and E-Fuels Scenario | Combined Scenario |
|---|---|---|---|
| Residential sector | |||
| Investment Expenditures (Bn €) | 4703 | 3955 | 4520 |
| For the Building shell | 1045 | 692 | 890 |
| For Equipment and Appliances | 3658 | 3263 | 3629 |
| Annuity capital payment (annual, on average, Bn €) | 497 | 458 | 480 |
| For the Building shell | 118 | 103 | 111 |
| For Equipment and Appliances | 378 | 355 | 370 |
| Cost of purchasing energy products (annual, on average, Bn €) | 323 | 389 | 421 |
| Total cost of energy services (annual, on average, Bn €) | 820 | 846 | 902 |
| % change of OPEX, from the Baseline, in 2031–2050 | −7% | 11% | 21% |
| % change of CAPEX, from the Baseline, in 2031–2050 | 18% | −1% | 13% |
| Services sector | |||
| Investment Expenditures (Bn €) | 1227 | 1064 | 1226 |
| For the Building shell | 337 | 240 | 309 |
| For Equipment and Appliances | 890 | 824 | 917 |
| Annuity capital payment (annual, on average, Bn €) | 135 | 128 | 135 |
| For the Building shell | 43 | 39 | 43 |
| For Equipment and Appliances | 92 | 89 | 92 |
| Cost of purchasing energy products (annual, on average, Bn €) | 210 | 242 | 250 |
| Total cost of energy services (annual, on average, Bn €) | 345 | 369 | 385 |
| % change of OPEX, from the Baseline, in 2031–2050 | −3% | 12% | 15% |
| % change of CAPEX, from the Baseline, in 2031–2050 | 18% | 2% | 18% |
| Calculated Using Cumulative Figures in the Period 2031–2050, in the EU | Energy Efficiency Scenario | Hydrogen and E-fuels Scenario | Combined Scenario |
|---|---|---|---|
| Residential sector | |||
| % contribution of Energy intensity to Emissions reduction from Baseline | 73% | 4% | 21% |
| % contribution of Carbon intensity to Emissions reduction from Baseline | 27% | 96% | 79% |
| % change of cumulative energy consumption from the Baseline | −12% | −1% | −11% |
| % change of cumulative CO2 emissions from the Baseline | −16% | −28% | −42% |
| % change of cumulative total energy costs from the Baseline | 1% | 4% | 11% |
| Services sector | |||
| % contribution of Energy intensity to Emissions reduction from Baseline | 89% | 7% | 27% |
| % contribution of Carbon intensity to Emissions reduction from Baseline | 11% | 93% | 73% |
| % change of cumulative energy consumption from the Baseline | −11% | −2% | −13% |
| % change of cumulative CO2 emissions from the Baseline | −12% | −28% | −41% |
| % change of cumulative total energy costs from the Baseline | 0% | 7% | 12% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Fotiou, T.; de Vita, A.; Capros, P. Economic-Engineering Modelling of the Buildings Sector to Study the Transition towards Deep Decarbonisation in the EU. Energies 2019, 12, 2745. https://doi.org/10.3390/en12142745
Fotiou T, de Vita A, Capros P. Economic-Engineering Modelling of the Buildings Sector to Study the Transition towards Deep Decarbonisation in the EU. Energies. 2019; 12(14):2745. https://doi.org/10.3390/en12142745
Chicago/Turabian StyleFotiou, Theofano, Alessia de Vita, and Pantelis Capros. 2019. "Economic-Engineering Modelling of the Buildings Sector to Study the Transition towards Deep Decarbonisation in the EU" Energies 12, no. 14: 2745. https://doi.org/10.3390/en12142745
APA StyleFotiou, T., de Vita, A., & Capros, P. (2019). Economic-Engineering Modelling of the Buildings Sector to Study the Transition towards Deep Decarbonisation in the EU. Energies, 12(14), 2745. https://doi.org/10.3390/en12142745




