Aerodynamically Interacting Vertical-Axis Wind Turbines: Performance Enhancement and Three-Dimensional Flow
Abstract
1. Introduction
2. Experimental Methods
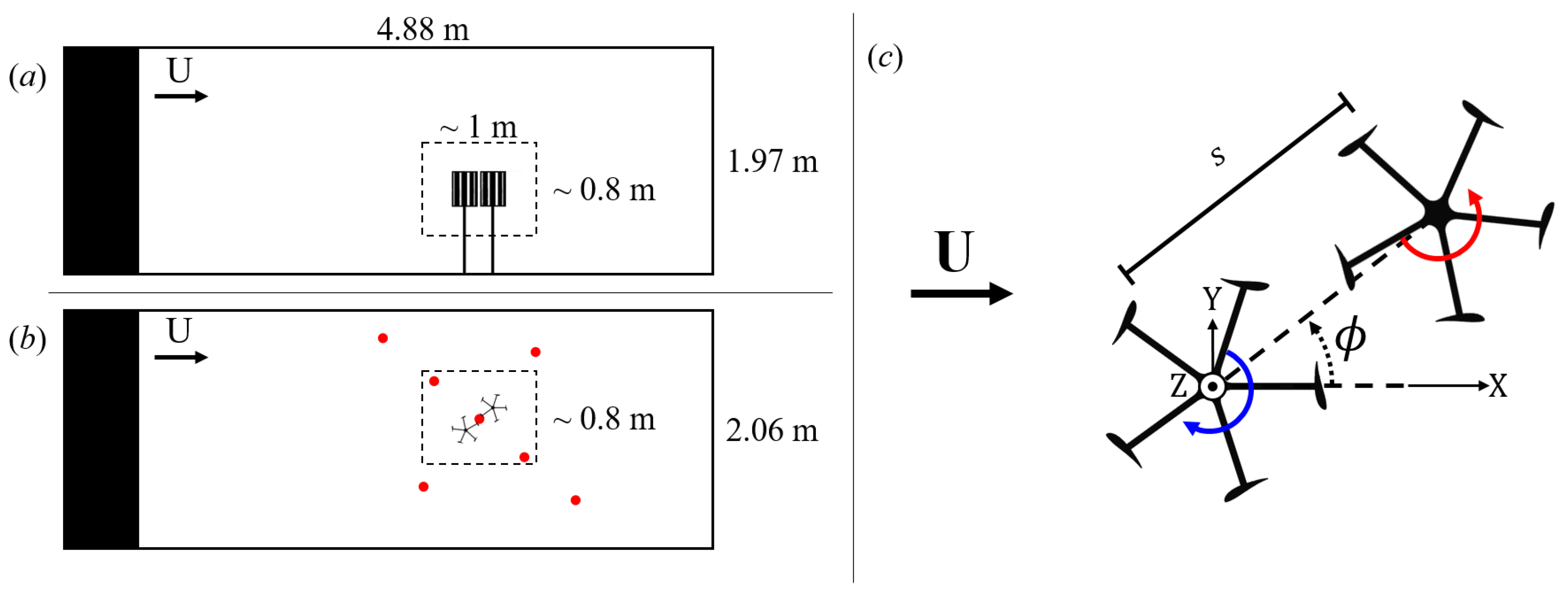
2.1. Facility and Wind Turbines
2.2. Performance Measurements
2.3. Flow Velocity Measurements
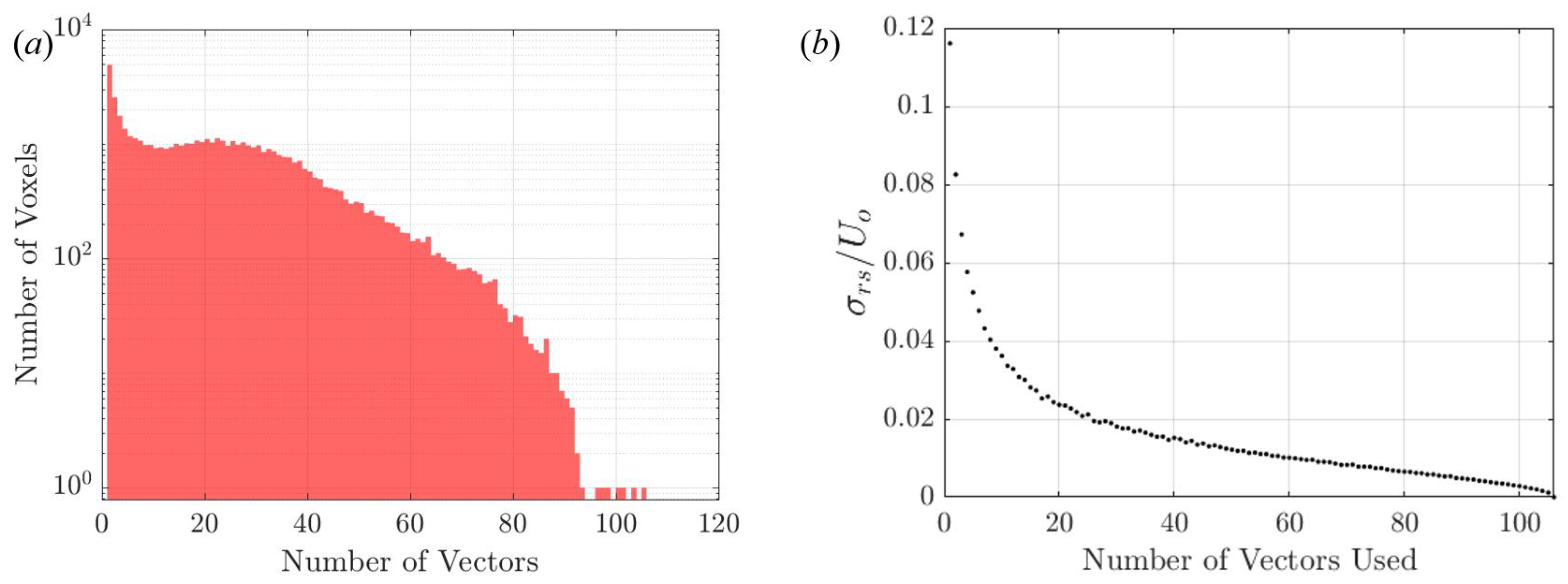
2.3.1. Tracking Technique and Data Collection
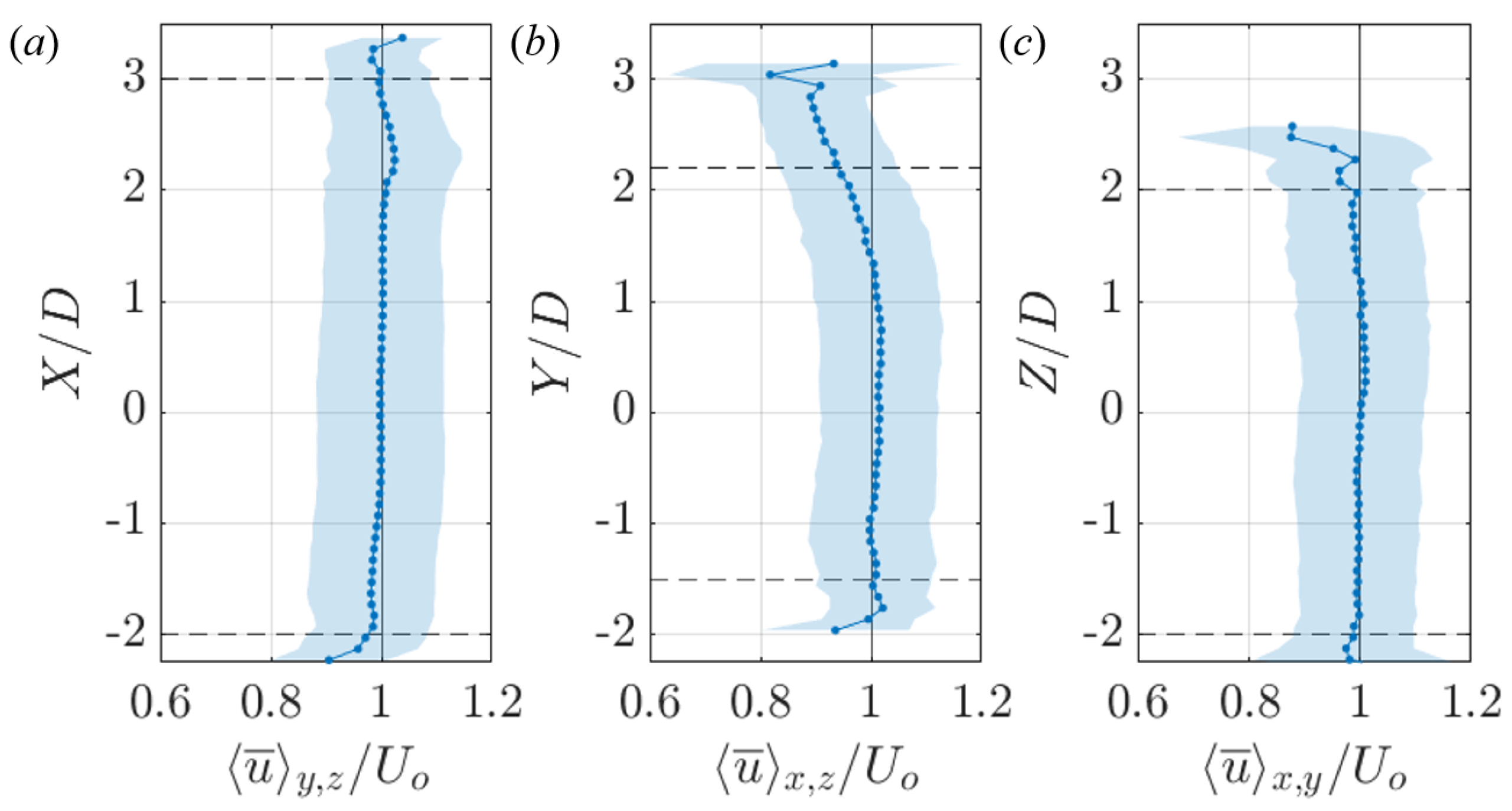
2.3.2. Characterization of Wind Tunnel
3. Results
3.1. Performance Adjustments in Paired Turbine Arrays
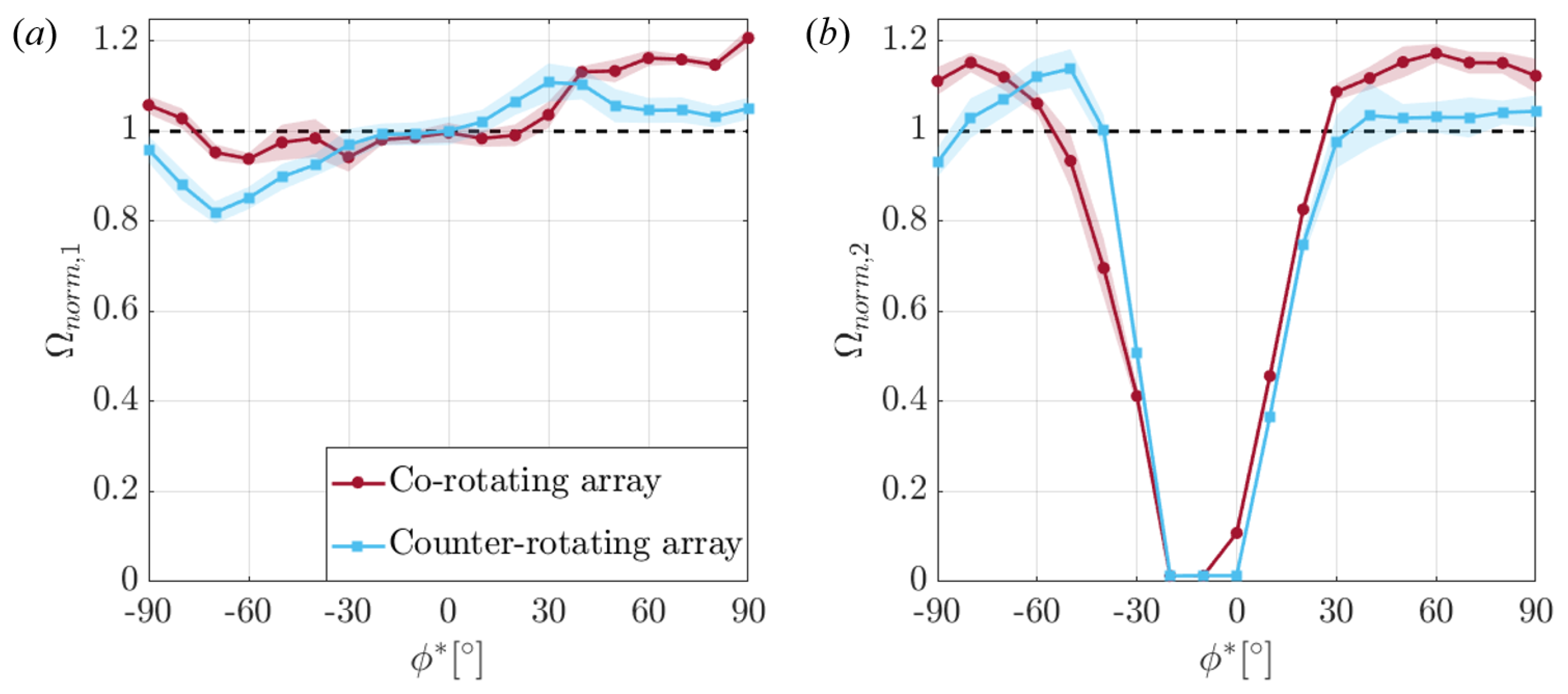
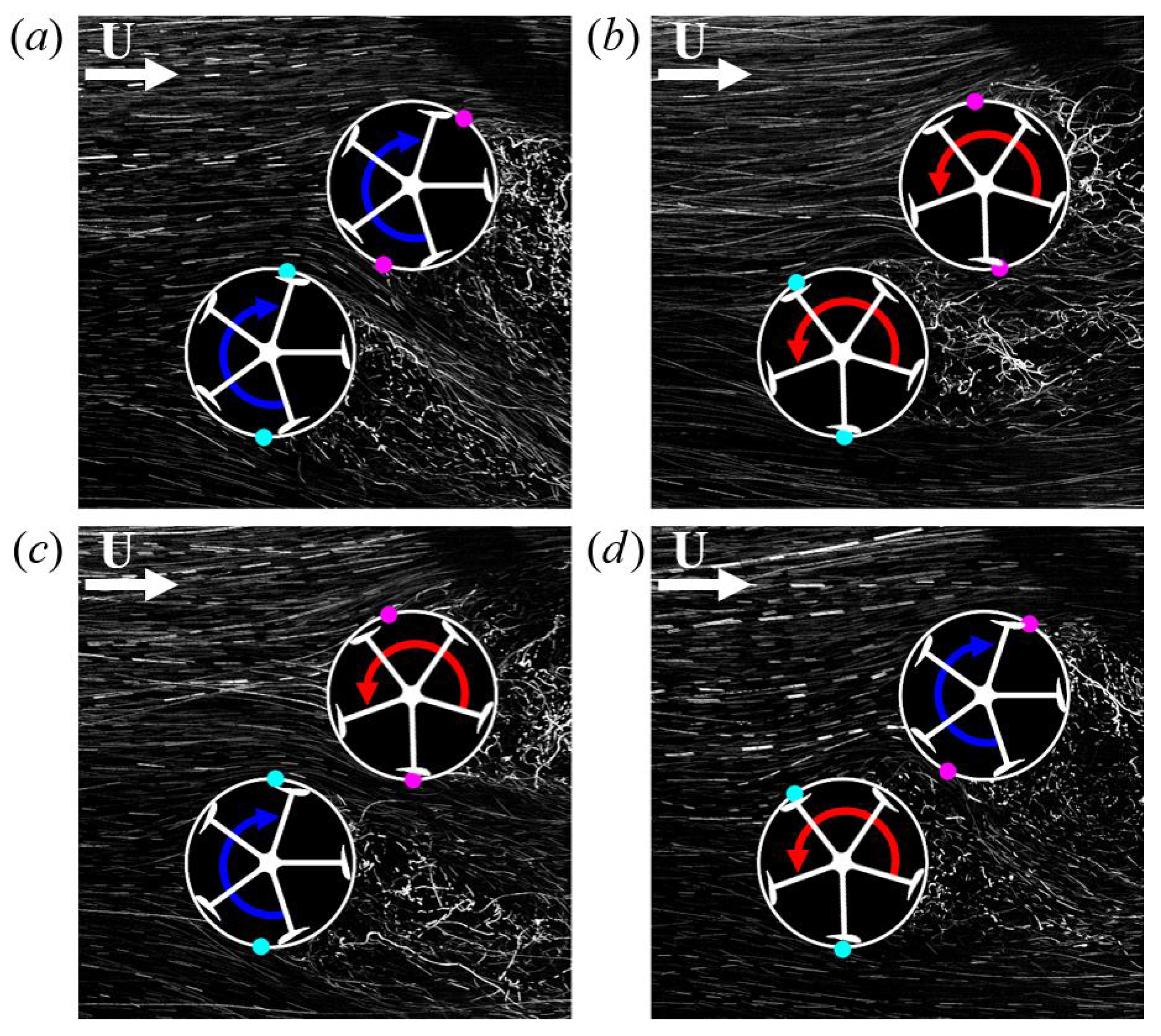
3.1.1. Performance Dependence on Relative Turbine Orientation
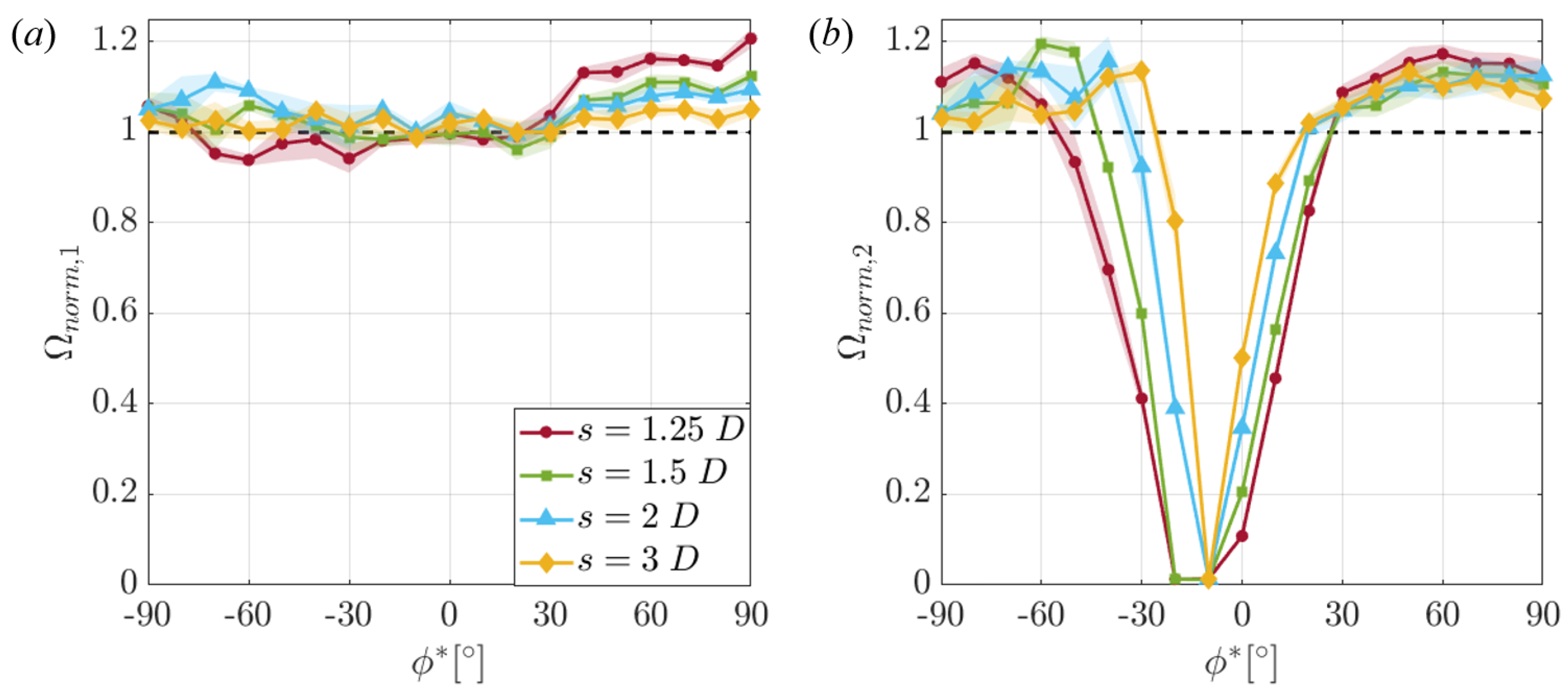
3.1.2. Performance Dependence on Turbine Spacing
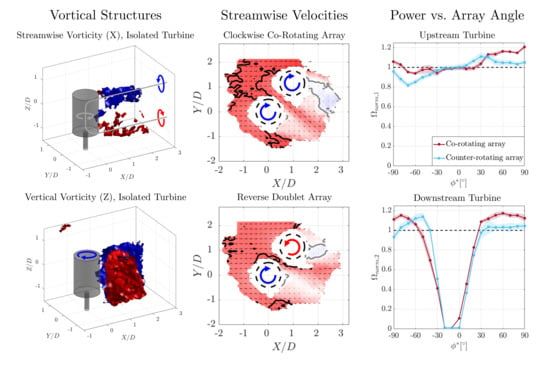
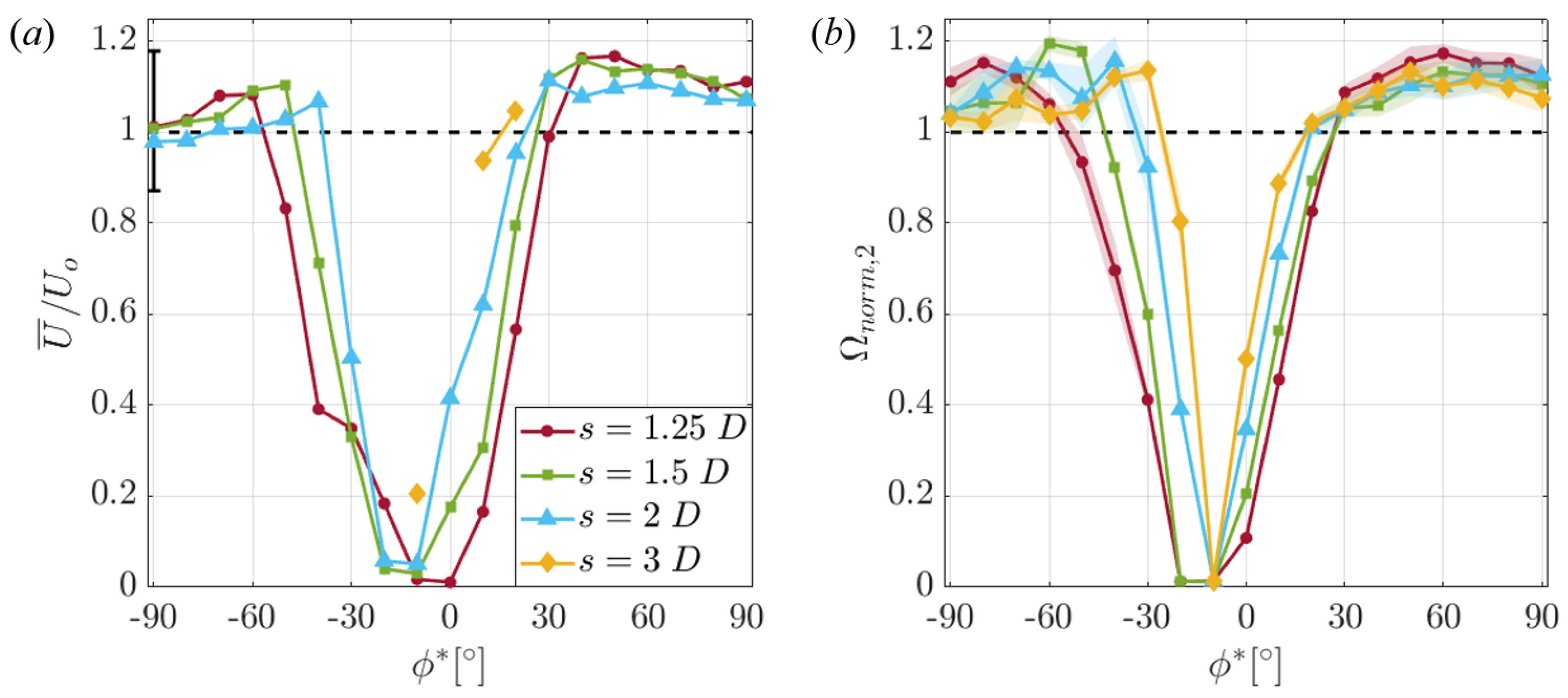
3.2. Flow Features of an Isolated Turbine
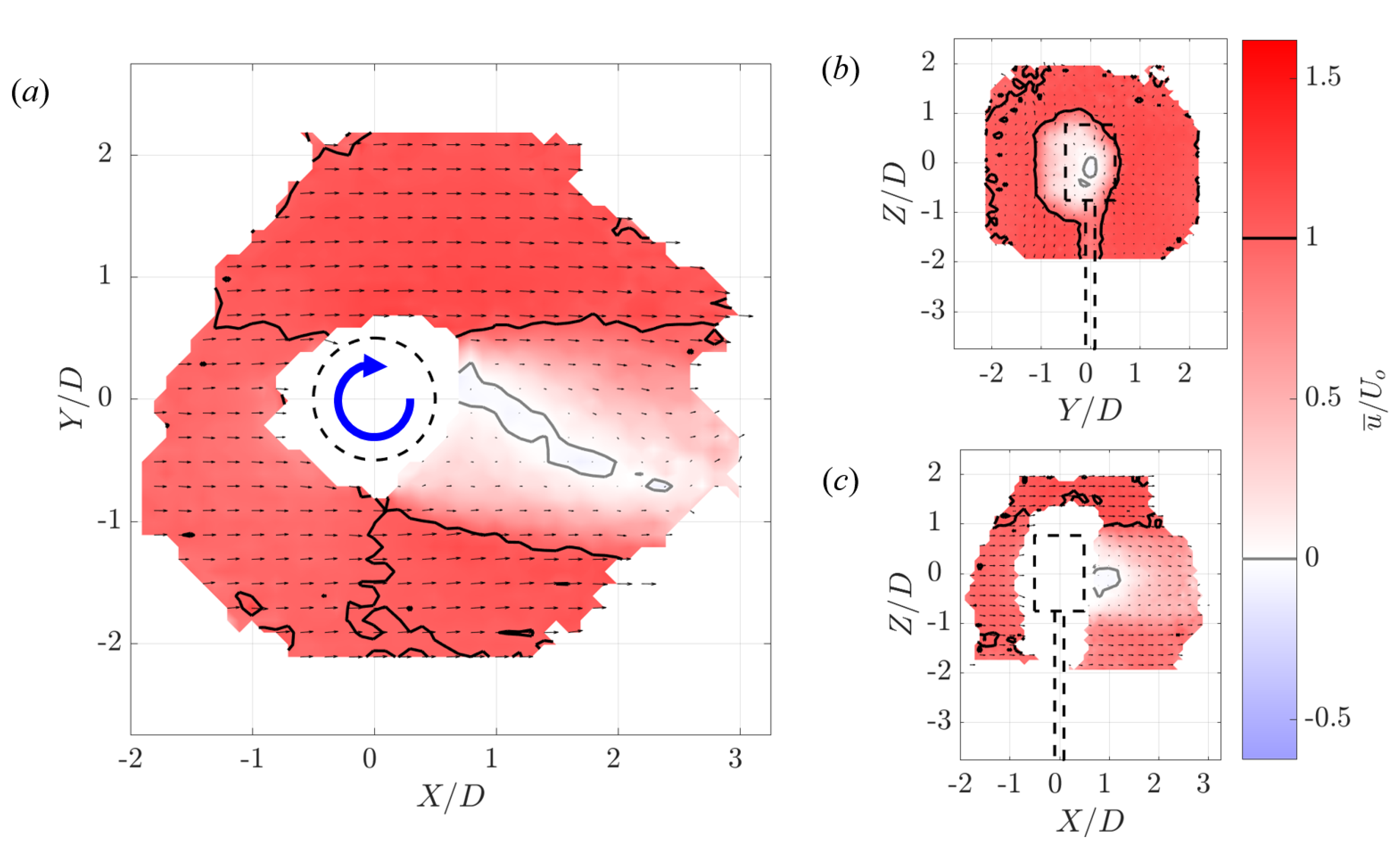
3.2.1. Velocity Field around an Isolated Turbine
3.2.2. Vortical Structures Downstream of an Isolated Turbine
3.3. Flow Features of a Pair Turbines
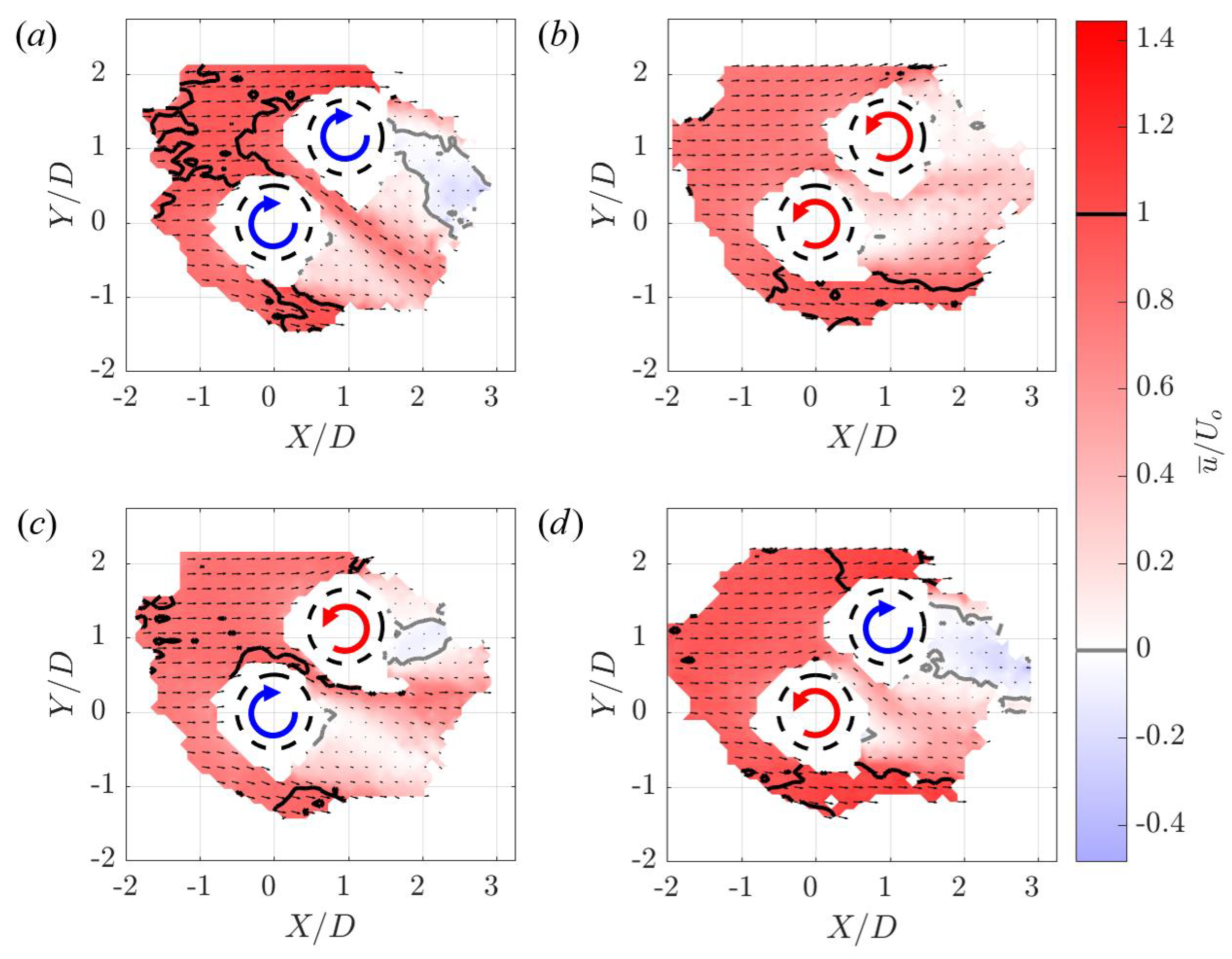
3.3.1. Velocity Fields around a Pair of Turbines
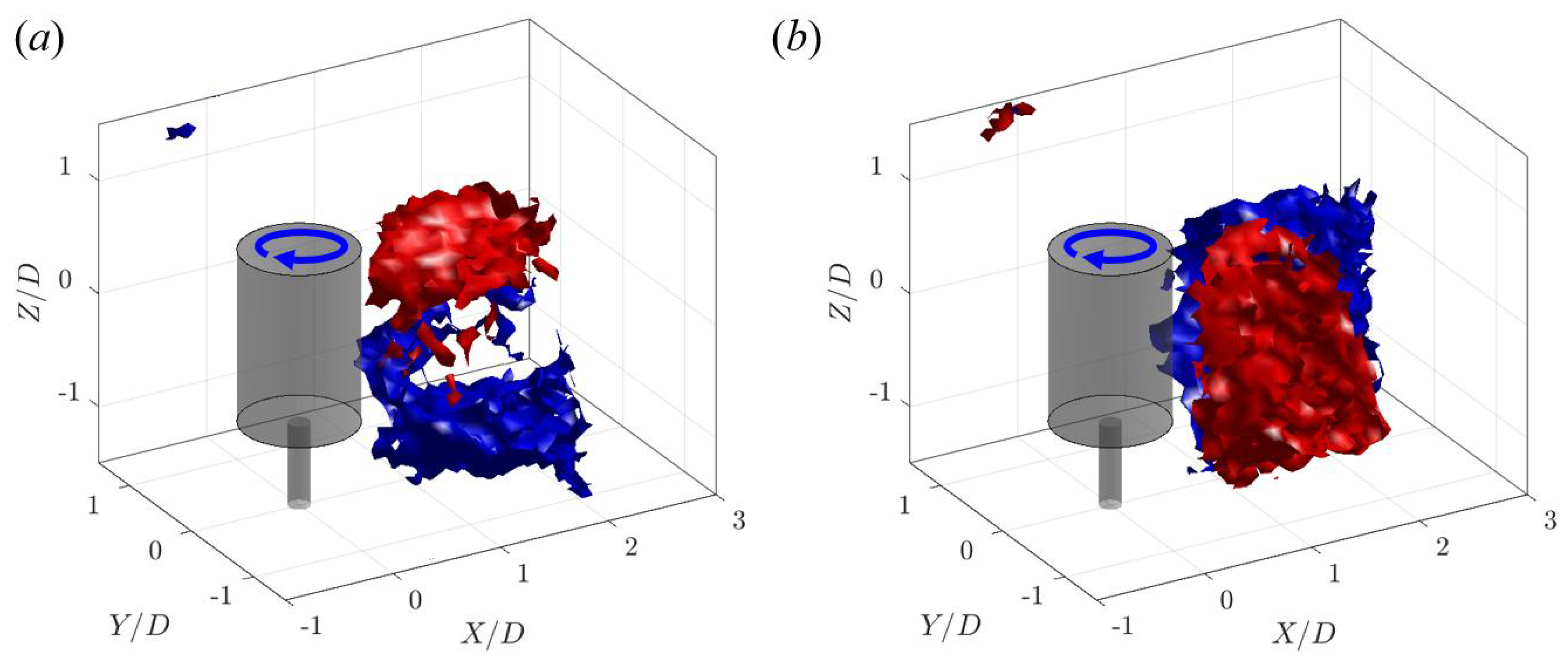
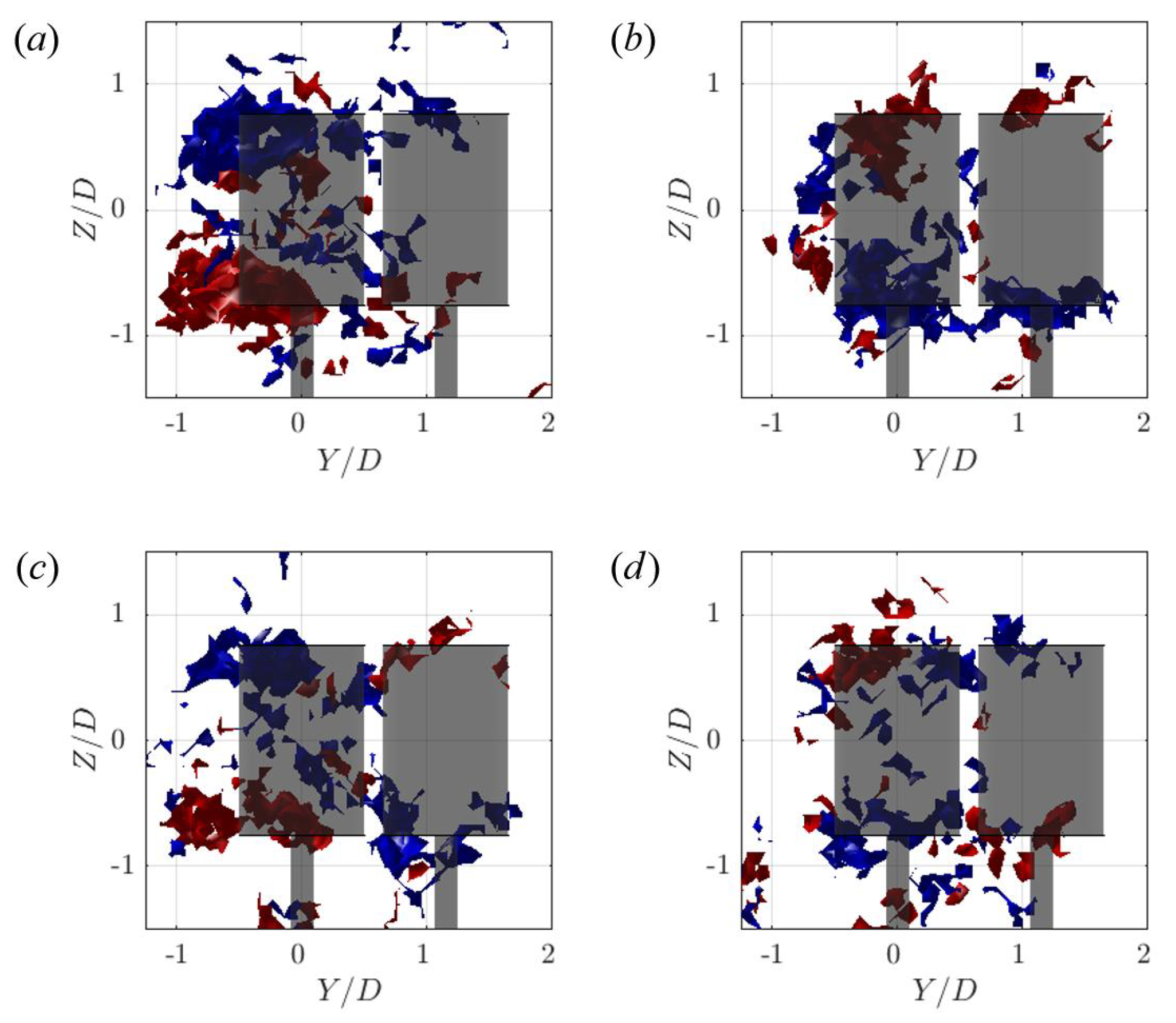
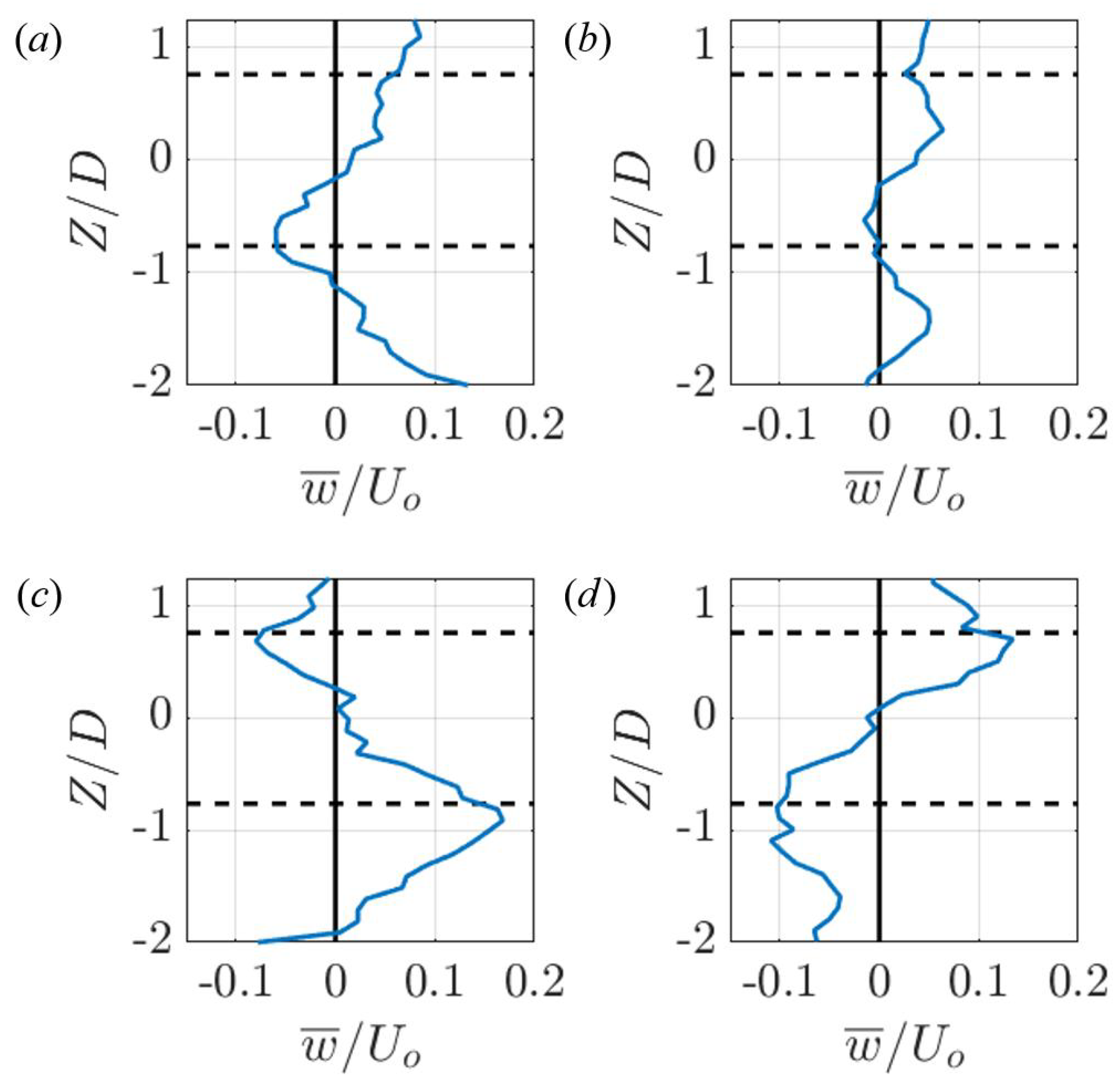
3.3.2. Vortical Structures Downstream of a Pair of Turbines
4. Discussion
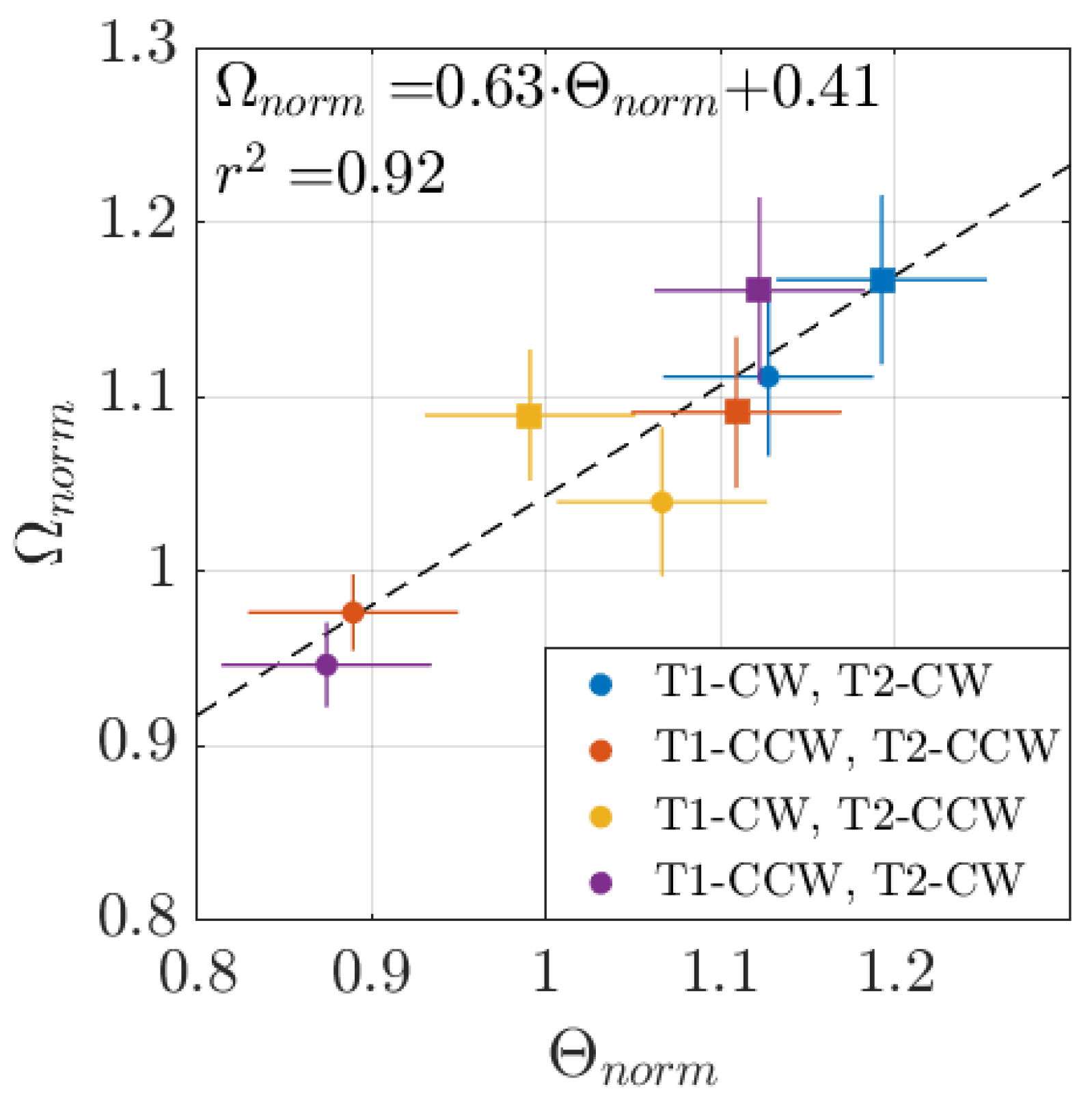
4.1. Relating Performance Variations and Flow Measurements
4.1.1. Downstream Turbine Performance
4.1.2. Upstream Turbine Performance
4.2. Implications for Wind Farm Performance
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Shigetomi, A.; Murai, Y.; Tasaka, Y.; Takeda, Y. Interactive flow field around two Savonius turbines. Renew. Energy 2011, 36, 536–545. [Google Scholar] [CrossRef]
- Kinzel, M.; Mulligan, Q.; Dabiri, J.O. Energy exchange in an array of vertical-axis wind turbines. J. Turbul. 2012, 13, 1–13. [Google Scholar] [CrossRef]
- Kinzel, M.; Araya, D.B.; Dabiri, J.O. Turbulence in vertical axis wind turbine canopies. Phys. Fluids 2015, 27, 115102. [Google Scholar] [CrossRef]
- Giorgetti, S.; Pellegrini, G.; Zanforlin, S. CFD investigation on the aerodynamic interferences between medium-solidity Darrieus Vertical Axis Wind Turbines. Energy Procedia 2015, 81, 227–239. [Google Scholar] [CrossRef]
- Shaheen, M.; Abdallah, S. Development of efficient vertical axis wind turbine clustered farms. Renew. Sustain. Energy Rev. 2016, 63, 237–244. [Google Scholar] [CrossRef]
- Bremseth, J.; Duraisamy, K. Computational analysis of vertical axis wind turbine arrays. Theor. Comput. Fluid Dyn. 2016, 30, 387–401. [Google Scholar] [CrossRef]
- Ahmadi-Baloutaki, M.; Carriveau, R.; Ting, D.S.K. A wind tunnel study on the aerodynamic interaction of vertical axis wind turbines in array configurations. Renew. Energy 2016, 96, 904–913. [Google Scholar] [CrossRef]
- Brownstein, I.; Kinzel, M.; Dabiri, J. Performance enhancement of downstream vertical-axis wind turbines. J. Renew. Sustain. Energy 2016, 8, 053306. [Google Scholar] [CrossRef]
- Dabiri, J.O. Potential order-of-magnitude enhancement of wind farm power density via counter-rotating vertical-axis wind turbine arrays. J. Renew. Sustain. Energy 2011, 3, 043104. [Google Scholar] [CrossRef]
- Dabiri, J.O.; Greer, J.R.; Koseff, J.R.; Moin, P.; Peng, J. A New Approach To Wind Energy: Opportunities And Challenges. AIP Conf. Proc. 2015, 1652, 51–57. [Google Scholar]
- MacKay, D.J. Sustainable Energy—Without the Hot Air; UIT: Tromsø, Norway, 2009. [Google Scholar]
- Tescione, G.; Ragni, D.; He, C.; Ferreira, C.J.S.; Van Bussel, G.J.W. Near wake flow analysis of a vertical axis wind turbine by stereoscopic particle image velocimetry. Renew. Energy 2014, 70, 47–61. [Google Scholar] [CrossRef]
- Rolin, V.; Porté-Agel, F. Wind-tunnel study of the wake behind a vertical axis wind turbine in a boundary layer flow using stereoscopic particle image velocimetry. J. Phys. Conf. Ser. 2015, 625, 012012. [Google Scholar] [CrossRef]
- Craig, A.E.; Dabiri, J.O.; Koseff, J.R. A Kinematic Description of the Key Flow Characteristics in an Array of Finite-Height Rotating Cylinders. J. Fluids Eng. 2016, 138, 070906. [Google Scholar] [CrossRef]
- Araya, D.B.; Colonius, T.; Dabiri, J.O. Transition to bluff-body dynamics in the wake of vertical-axis wind turbines. J. Fluid Mech. 2017, 813, 346–381. [Google Scholar] [CrossRef]
- Hezaveh, S.H.; Bou-Zeid, E. Mean kinetic energy replenishment mechanisms in vertical-axis wind turbine farms. Phys. Rev. Fluids 2018, 3, 094606. [Google Scholar] [CrossRef]
- Hau, E. Wind Turbines Fundamentals, Technologies, Application, Economics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Mittal, S.; Kumar, B. Flow past a rotating cylinder. J. Fluid Mech. 2003, 476, 303–334. [Google Scholar] [CrossRef]
- Feng, L.H.; Wang, J.J.; Pan, C. Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control. Phys. Fluids 2011, 23, 014106. [Google Scholar] [CrossRef]
- Calaf, M.; Meneveau, C.; Meyers, J. Large eddy simulation study of fully developed wind-turbine array boundary layers. Phys. Fluids 2010, 22, 015110. [Google Scholar] [CrossRef]
- De Tavernier, D.; Ferreira, C.; Li, A.; Paulsen, U.S.; Madsen, H.A. VAWT in double-rotor configuration: The effect on airfoil design. In Proceedings of the Wind Energy Symposium, Kissimmee, FL, USA, 8–12 January 2018. [Google Scholar]
- Rajagopalan, R.G.; Rickerlt, T.L.; Klimasj, P.C. Aerodynamic Interference of Vertical Axis Wind Turbines. J. Propuls. 1990, 6, 645–653. [Google Scholar] [CrossRef]
- Araya, D.B.; Craig, A.E.; Kinzel, M.; Dabiri, J.O. Low-order modeling of wind farm aerodynamics using leaky Rankine bodies. J. Renew. Sustain. Energy 2014, 6, 063118. [Google Scholar] [CrossRef]
- Zanforlin, S.; Burchi, F.; Bitossi, N. Hydrodynamic interactions between three closely-spaced Vertical Axis Tidal Turbines. Energy Procedia 2016, 101, 520–527. [Google Scholar] [CrossRef]
- Hezaveh, S.H.; Bou-Zeid, E.; Dabiri, J.O.; Kinzel, M.; Cortina, G.; Martinelli, L. Increasing the Power Production of Vertical-Axis Wind-Turbine-Farms using Synergistic Clustering. Bound. Layer Meteorol. 2018, 169, 275–296. [Google Scholar] [CrossRef]
- Brochier, G.; Fraunie, P.; Beguierj, C. Water Channel Experiments of Dynamic Stall on Darrieus Wind Turbine Blades. J. Propuls. 1986, 2. [Google Scholar] [CrossRef]
- Hofemann, C.; Ferreira, C.S.; Dixon, K.; Van Bussel, G.; Van Kuik, G.; Scarano, F. 3D Stereo PIV study of tip vortex evolution on a VAWT. In Proceedings of the European Wind Energy Conference, Brussels, Belgium, 31 March–3 April 2008. [Google Scholar]
- Ferreira, C.S.; van Kuik, G.; van Bussel, G.; Scarano, F. Visualization by PIV of dynamic stall on a vertical axis wind turbine. Exp. Fluids 2009, 46, 97–108. [Google Scholar] [CrossRef]
- Parker, C.M.; Araya, D.B.; Leftwich, M.C. Effect of chord-to-diameter ratio on vertical–axis wind turbine wake development. Exp. Fluids 2017, 58, 168. [Google Scholar] [CrossRef]
- Caridi, G.C.A.; Ragni, D.; Sciacchitano, A.; Scarano, F. HFSB-seeding for large-scale tomographic PIV in wind tunnels. Exp. Fluids 2016, 57, 190. [Google Scholar] [CrossRef][Green Version]
- Ryan, K.J.; Coletti, F.; Elkins, C.J.; Dabiri, J.O.; Eaton, J.K. Three–dimensional flow field around and downstream of a subscale model rotating vertical axis wind turbine. Exp. Fluids 2016, 57, 38. [Google Scholar] [CrossRef]
- Howell, R.; Qin, N.; Edwards, J.; Durrani, N. Wind tunnel and numerical study of a small vertical axis wind turbine. Renew. Energy 2009, 35, 412–422. [Google Scholar] [CrossRef]
- Bazilevs, Y.; Korobenko, A.; Deng, X.; Yan, J.; Kinzel, M.; Dabiri, J. Fluid-Structure Interaction Modeling of Vertical-Axis Wind Turbines. J. Appl. Mech. 2014, 81. [Google Scholar] [CrossRef]
- Shamsoddin, S.; Porté-Agel, F. Large Eddy Simulation of Vertical Axis Wind Turbine Wakes. Energies 2014, 7, 890–912. [Google Scholar] [CrossRef]
- Posa, A.; Balaras, E. Large Eddy Simulation of an isolated vertical axis wind turbine. J. Wind Eng. Ind. Aerodyn. 2018, 172, 139–151. [Google Scholar] [CrossRef]
- Miller, M.; Duvvuri, S.; Brownstein, I.; Lee, M.; Dabiri, J.; Hultmark, M. Vertical-axis wind turbine experiments at full dynamic similarity. J. Fluid Mech. 2018, 844, 707–720. [Google Scholar] [CrossRef]
- Han, D.; Heo, Y.G.; Choi, N.J.; Nam, S.H.; Choi, K.H.; Kim, K.C. Design, Fabrication, and Performance Test of a 100-W Helical-Blade Vertical-Axis Wind Turbine at Low Tip-Speed Ratio. Energies 2018, 11, 1517. [Google Scholar] [CrossRef]
- Delafin, P.; Nishino, T.; Wang, L.; Kolios, A. Effect of the number of blades and solidity on the performance of a vertical axis wind turbine. J. Phys. Conf. Ser. 2016, 753, 022033. [Google Scholar] [CrossRef]
- Eboibi, O.; Danao, L.A.M.; Howell, R.J. Experimental investigation of the influence of solidity on the performance and flow field aerodynamics of vertical axis wind turbines at low Reynolds numbers. Renew. Energy 2016, 92, 474–483. [Google Scholar] [CrossRef]
- Miller, M.A.; Duvvuri, S.; Kelly, W.D.; Hultmark, M. Rotor Solidity Effects on the Performance of Vertical-Axis Wind Turbines at High Reynolds Numbers; IOP Conference Series; IOP Publishing: Milan, Italy, 2018; Volume 1037. [Google Scholar]
- Rezaeiha, A.; Montazeri, H.; Blocken, B. Towards optimal aerodynamic design of vertical axis wind turbines: Impact of solidity and number of blades. Energy 2018, 165, 1129–1148. [Google Scholar] [CrossRef]
- Möllerström, E.; Gipe, P.; Beurskens, J.; Ottermo, F. A historical review of vertical axis wind turbines rated 100 kW and above. Renew. Sustain. Energy Rev. 2019, 105, 1–13. [Google Scholar] [CrossRef]
- Von Meier, A. Electric Power Systems; John Wiley & Sons: Hoboken, NJ, USA, 2006. [Google Scholar]
- Araya, D.B.; Dabiri, J.O. A comparison of wake measurements in motor-driven and flow-driven turbine experiments. Exp. Fluids 2015, 56, 150. [Google Scholar] [CrossRef]
- Widmann, A.; Tropea, C. Parameters influencing vortex growth and detachment on unsteady aerodynamic profiles. J. Fluid Mech. 2015, 773, 432–459. [Google Scholar] [CrossRef]
- Theriault, D.H.; Fuller, N.W.; Jackson, B.E.; Bluhm, E.; Evangelista, D.; Wu, Z.; Betke, M.; Hedrick, T.L. A protocol and calibration method for accurate multi-camera field videography. J. Exp. Biol. 2014, 217, 1843–1848. [Google Scholar] [CrossRef]
- Hartley, R.; Zisserman, A. Multiple View Geometry, 2nd ed.; Cambridge University Press: Cambridge, UK, 2003. [Google Scholar]
- Elsinga, G.E.; Westerweel, J.; Scarano, F.; Novara, M. On the velocity of ghost particles and the bias errors in Tomographic-PIV. Exp. Fluids 2010, 50, 825–838. [Google Scholar] [CrossRef]
- Ouellette, N.T.; Xu, H.; Bodenschatz, E. A quantitative study of three-dimensional Lagrangian particle tracking algorithms. Exp. Fluids 2006, 40, 301–313. [Google Scholar] [CrossRef]
- Xu, H. Tracking Lagrangian trajectories in position-velocity space. Meas. Sci. Technol. 2008, 19, 075105. [Google Scholar] [CrossRef]
- Efron, B. Bootstrap Methods: Another Look at the Jackknike. Ann. Stat. 1979, 7, 1–26. [Google Scholar] [CrossRef]
- Chan, A.S.; Dewey, P.A.; Jameson, A.; Liang, C.; Smits, A.J. Vortex suppression and drag reduction in the wake of counter-rotating cylinders. J. Fluid Mech. 2011, 679, 343–382. [Google Scholar] [CrossRef]
- Resagk, C.; Lobutova, E.; Rank, R.; Müller, D.; Putze, T.; Maas, H.G. Measurement of large-scale flow structures in air using a novel 3D particle tracking velocimetry technique. In Proceedings of the 3th International Symposium on Applications of Laser Techniques to Fluid Mechanics, Lisbon, Portugal, 26–29 June 2006. [Google Scholar]
- Biwole, P.H.; Yan, W.; Zhang, Y.; Roux, J.J. A complete 3D particle tracking algorithm and its applications to the indoor airflow study. Meas. Sci. Technol. 2009, 20, 115403. [Google Scholar] [CrossRef]
- Bosbach, J.; Kühn, M.; Wagner, C. Large scale particle image velocimetry with helium filled soap bubbles. Exp. Fluids 2009, 46, 539–547. [Google Scholar] [CrossRef]
- Kühn, M.; Ehrenfried, K.; Bosbach, J.; Wagner, C. Large–scale tomographic particle image velocimetry using helium-filled soap bubbles. Exp. Fluids 2011, 50, 929–948. [Google Scholar] [CrossRef]
- Kerho, M.F.; Bragg, M.B. Neutrally buoyant bubbles used as flow tracers in air. Exp. Fluids 1994, 16, 393–400. [Google Scholar] [CrossRef]
- Scarano, F.; Ghaemi, S.; Carlo, G.C.A.; Bosbach, J.; Dierksheide, U.; Sciacchitano, A. On the use of helium-filled soap bubbles for large-scale tomographic PIV in wind tunnel experiments. Exp. Fluids 2015, 56, 42. [Google Scholar] [CrossRef]
- Crowe, C.T.; Schwarzkopf, J.D.; Sommerfeld, M.; Tsuji, Y. Multiphase Flows with Droplets and Particles, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2012. [Google Scholar]
- Tropea, C.; Yarin, A.L.; Foss, J.F. Springer Handbook of Experimental Fluid Mechanics; Springer: Berlin, Germany, 2007. [Google Scholar]
- Zhu, H.Y.; Wang, C.Y.; Wang, H.P.; Wang, J.J. Tomographic PIV investigation on 3D wake structures for flow over a wall-mounted short cylinder. J. Fluid Mech. 2017, 831, 743–778. [Google Scholar] [CrossRef]
- Craig, A.E.; Dabiri, J.O.; Koseff, J.R. Low order physical models of vertical axis wind turbines. J. Renew. Sustain. Energy 2017, 9, 013306. [Google Scholar] [CrossRef]
- Kawamura, T.; Hiwada, M.; Hibino, T.; Mabuchi, I.; Kumada, M. Flow around a Finite Circular Cylinder on a Flat Plate. Bull. JSME 1984, 27, 2142–2151. [Google Scholar] [CrossRef]
- Fröhlich, J.; Rodi, W. LES of the flow around a circular cylinder of finite height. Int. J. Heat Fluid Flow 2004, 25, 537–548. [Google Scholar] [CrossRef]
- Pattenden, R.J.; Turnock, S.R.; Zhang, X. Measurements of the flow over a low-aspect-ratio cylinder mounted on a ground plane. Exp. Fluids 2005, 39, 10–21. [Google Scholar] [CrossRef]
- Zanforlin, S.; Nishino, T. Fluid dynamic mechanisms of enhanced power generation by closely spaced vertical axis wind turbines. Renew. Energy 2016, 99, 1213–1226. [Google Scholar] [CrossRef]


© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Brownstein, I.D.; Wei, N.J.; Dabiri, J.O. Aerodynamically Interacting Vertical-Axis Wind Turbines: Performance Enhancement and Three-Dimensional Flow. Energies 2019, 12, 2724. https://doi.org/10.3390/en12142724
Brownstein ID, Wei NJ, Dabiri JO. Aerodynamically Interacting Vertical-Axis Wind Turbines: Performance Enhancement and Three-Dimensional Flow. Energies. 2019; 12(14):2724. https://doi.org/10.3390/en12142724
Chicago/Turabian StyleBrownstein, Ian D., Nathaniel J. Wei, and John O. Dabiri. 2019. "Aerodynamically Interacting Vertical-Axis Wind Turbines: Performance Enhancement and Three-Dimensional Flow" Energies 12, no. 14: 2724. https://doi.org/10.3390/en12142724
APA StyleBrownstein, I. D., Wei, N. J., & Dabiri, J. O. (2019). Aerodynamically Interacting Vertical-Axis Wind Turbines: Performance Enhancement and Three-Dimensional Flow. Energies, 12(14), 2724. https://doi.org/10.3390/en12142724