Voltage Stability Index Calculation by Hybrid State Estimation Based on Multi Objective Optimal Phasor Measurement Unit Placement
Abstract
1. Introduction
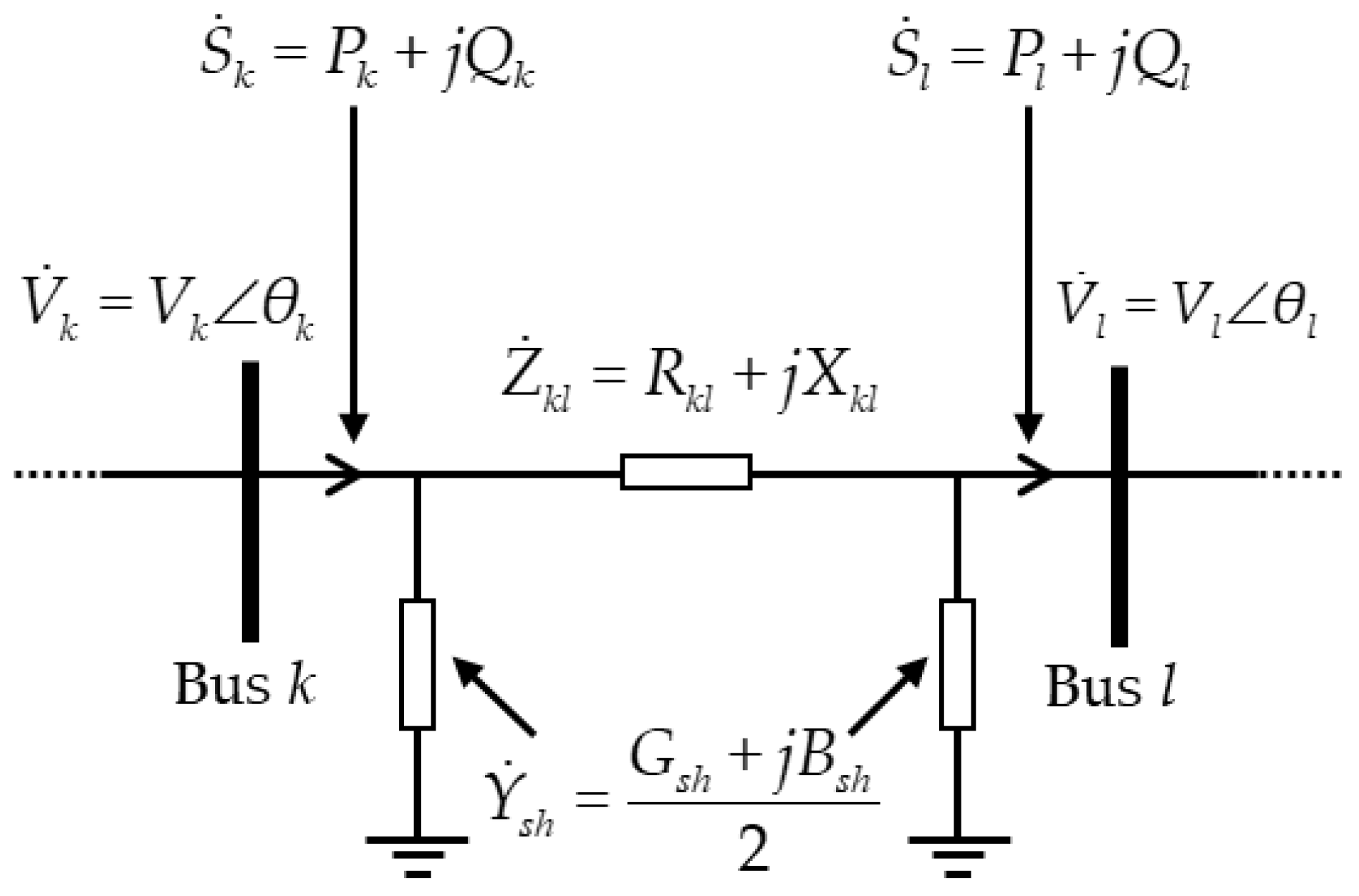
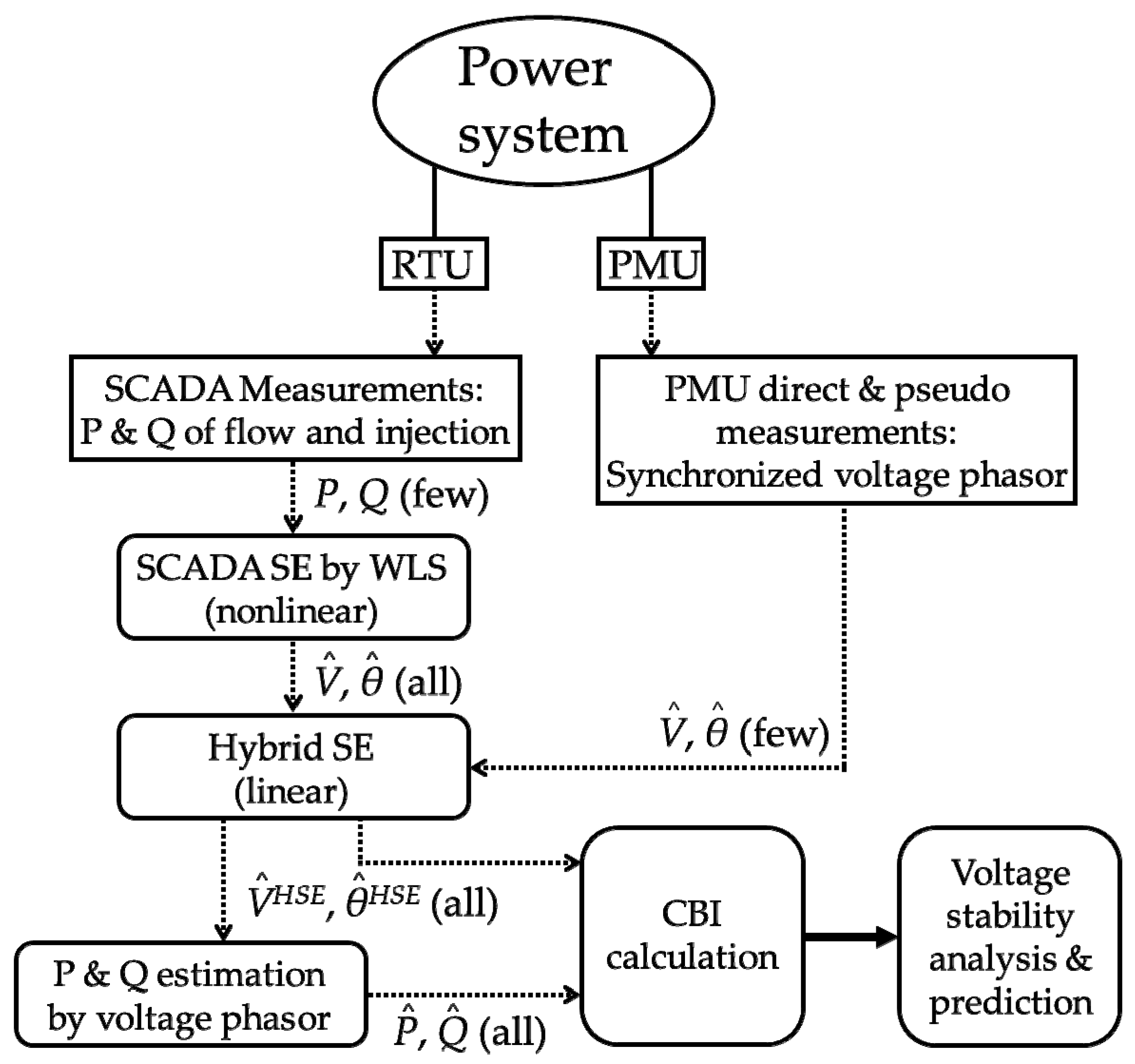
2. Power System State Estimation
2.1. Conventional State Estimation by Weighted Least Square
2.2. Hybrid State Estimation with Measurment Uncertainty Propagation of Phasor Measurement Unit (PMU) Measurements
3. Voltage Stability Index Calculation
- Sensitivity analysis by Jacobian
- Bus VSIs
- Line VSIs
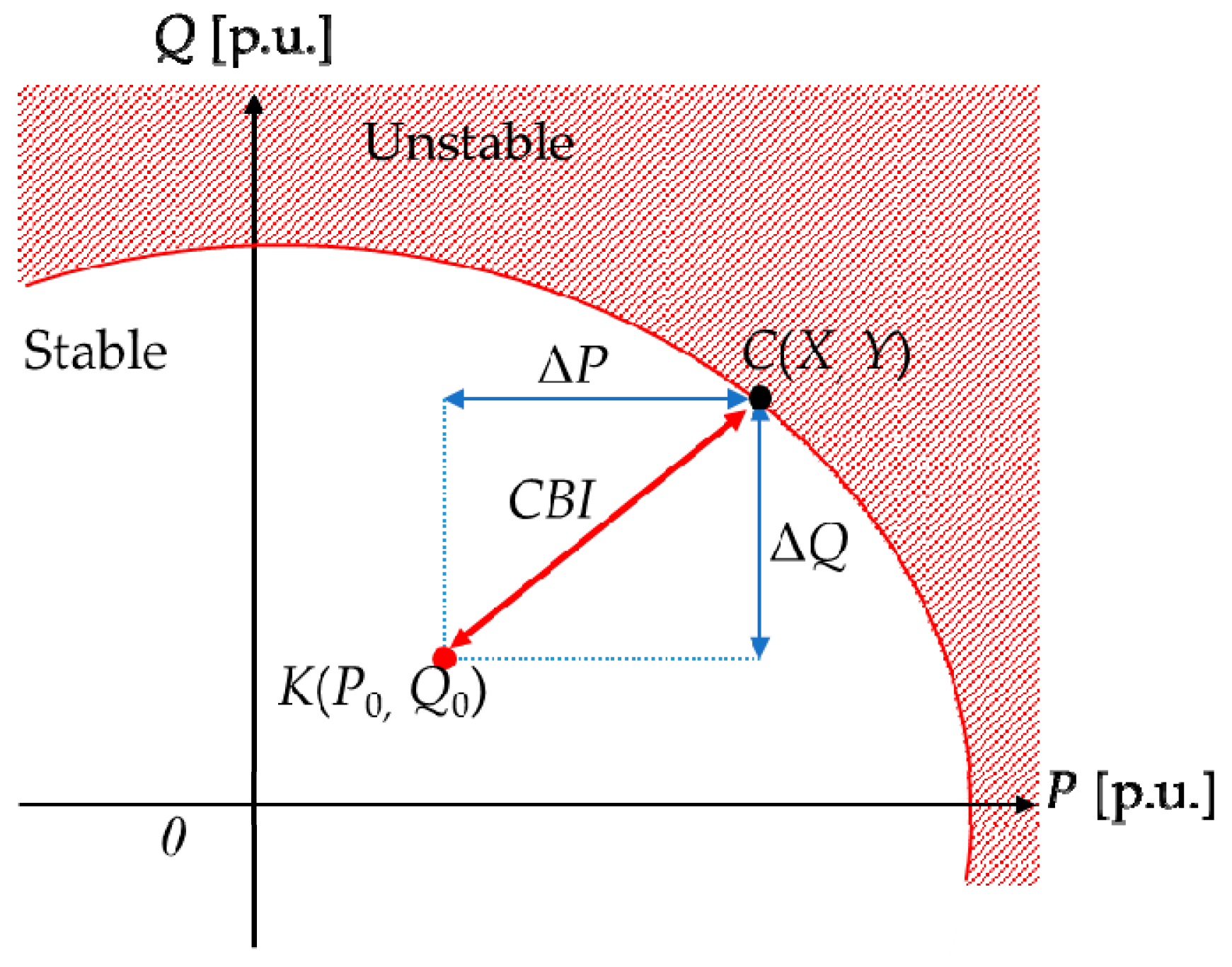
3.1. Critical Boundary Index
3.2. Active and Reactive Power Estimation by Obtained Bus Voltage Phasor
4. Multi Objective Optimal Phasor Measurement Unit (PMU) Placement
4.1. Formulation
4.2. Optimization Method
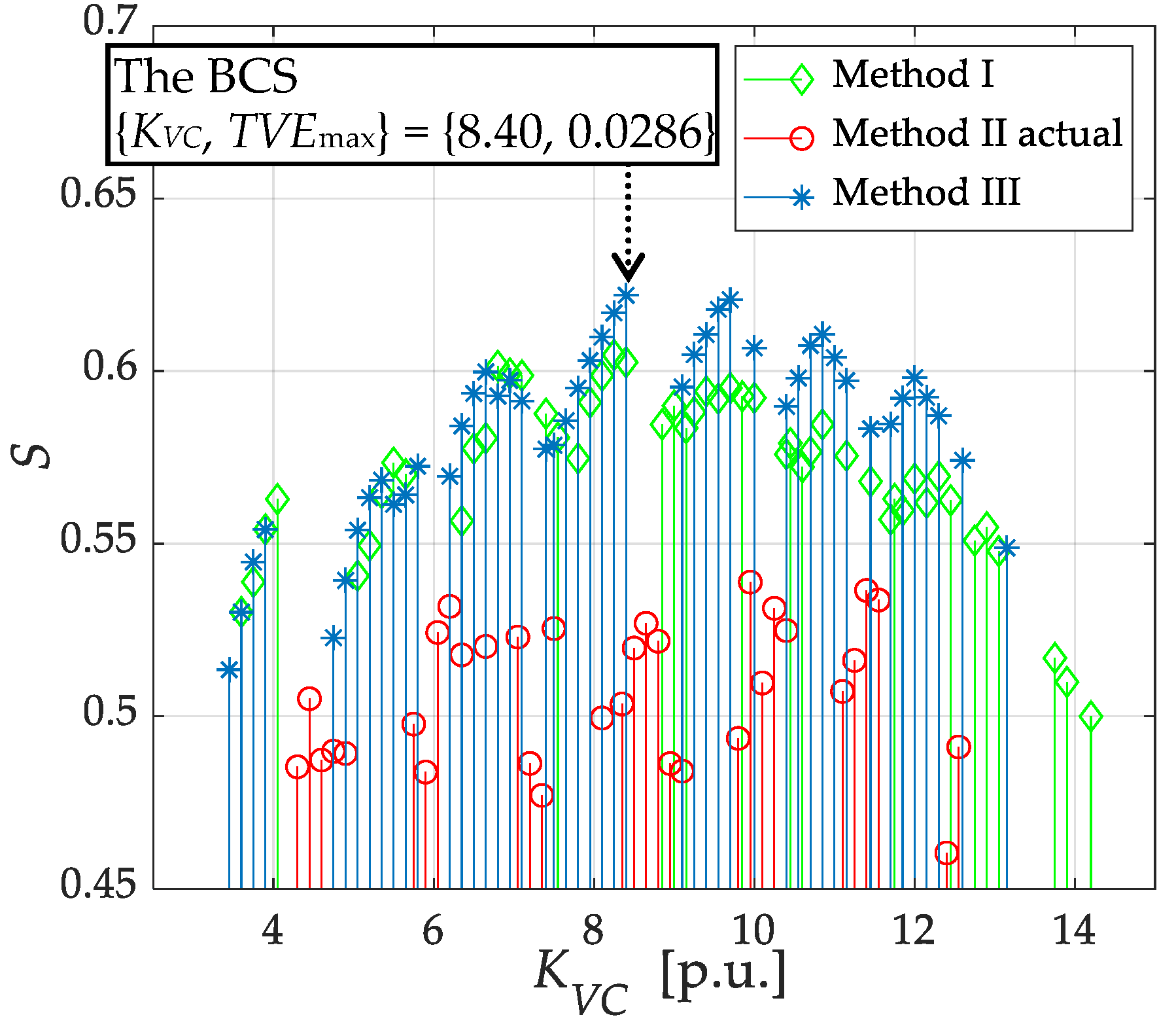
4.3. The Best Compromised Solution Selection
5. Numerical Simulation Results and Discussions
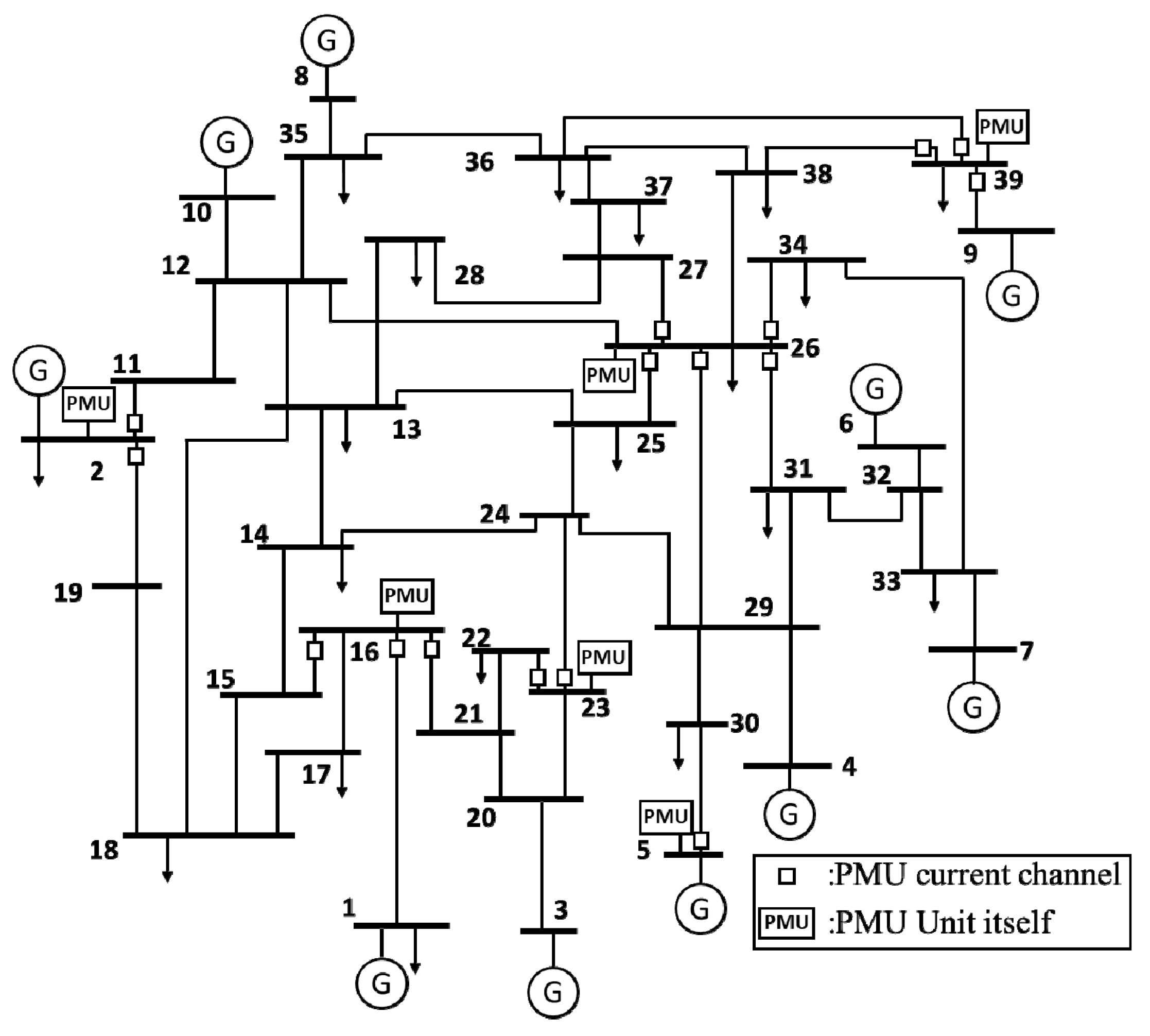
5.1. Configuration
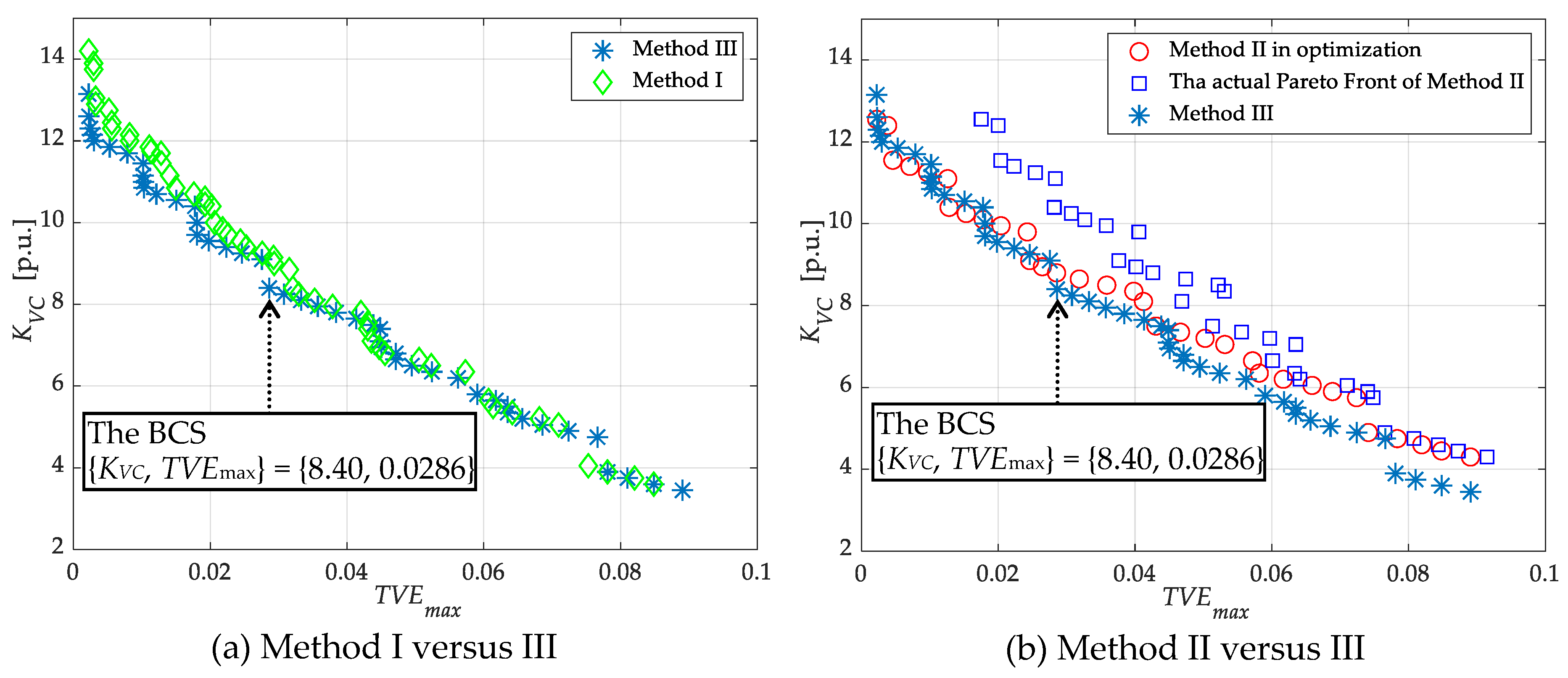
5.2. Pareto Optimal Solutions Obtained by Non-Dominated Sorting Genetic Algorithm II (NSGA-II)
- Method I: no consideration of the current channel selectivity. The current channel is placed at all lines incident to the PMU placed bus in calculation of KVC. The decision variable is only y.
- Method II: no consideration of measurement uncertainty propagation in PMU pseudo measurement. Measurement uncertainty in HSE is always constant given by Table 3 regardless of the use of pseudo measurement.
- Method III: with consideration of both the current channel selectivity and measurement uncertainty propagation in PMU pseudo measurements.
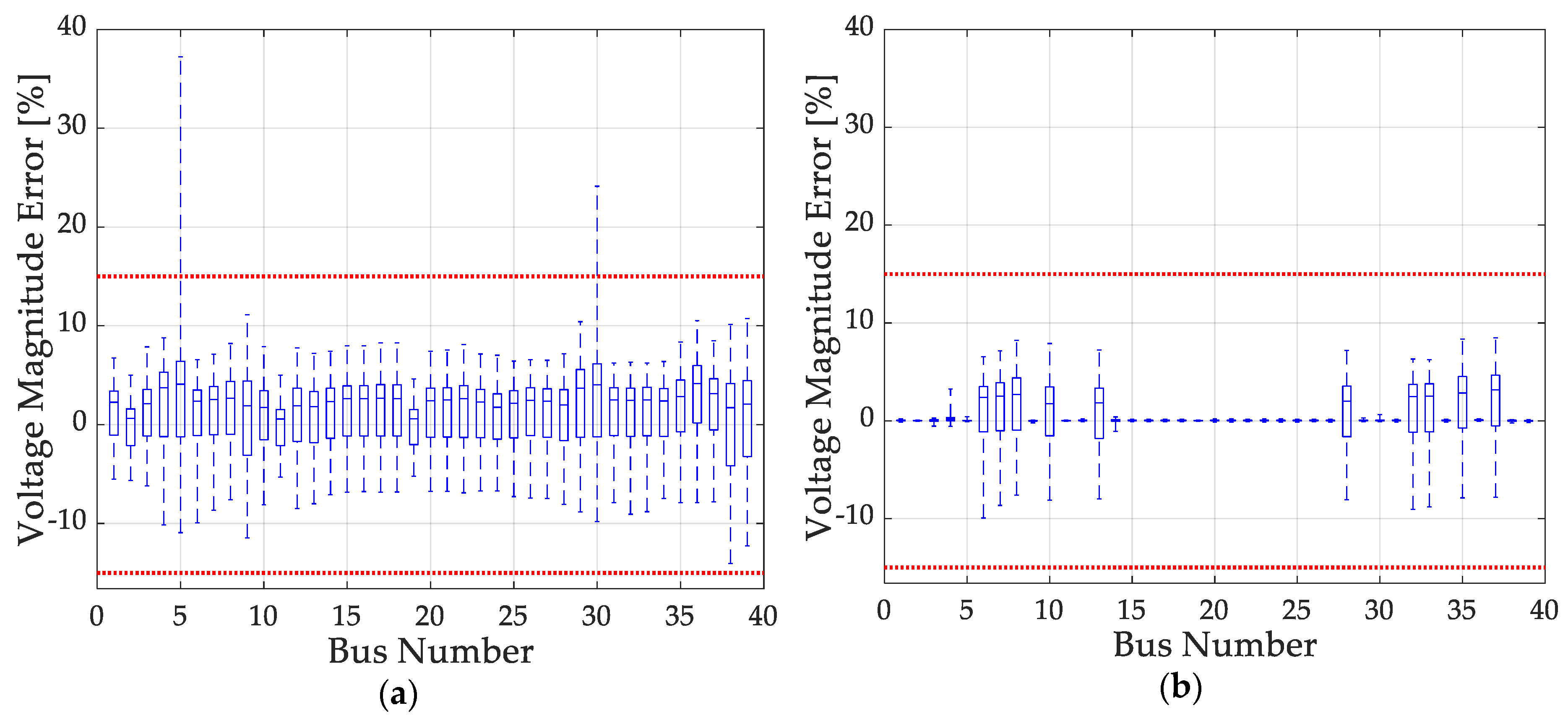
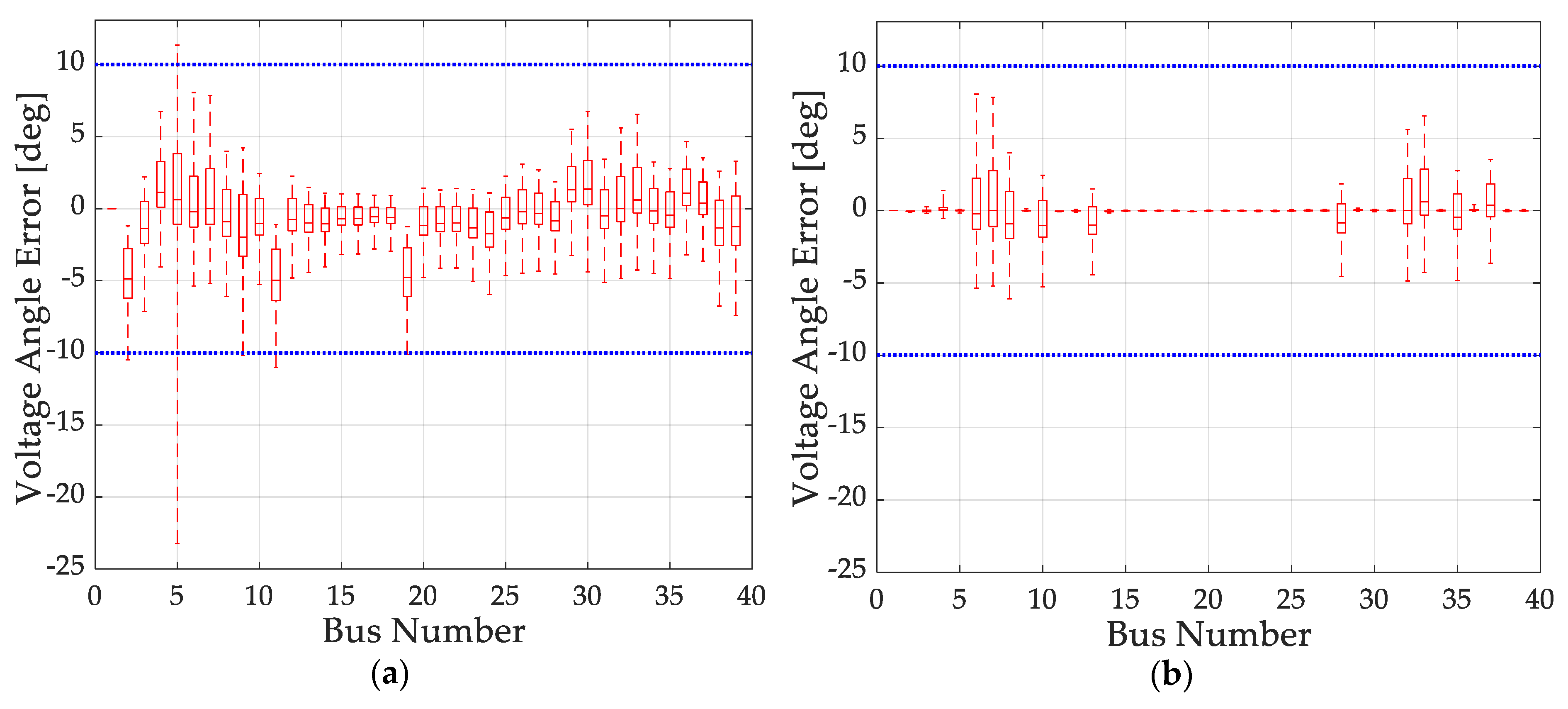
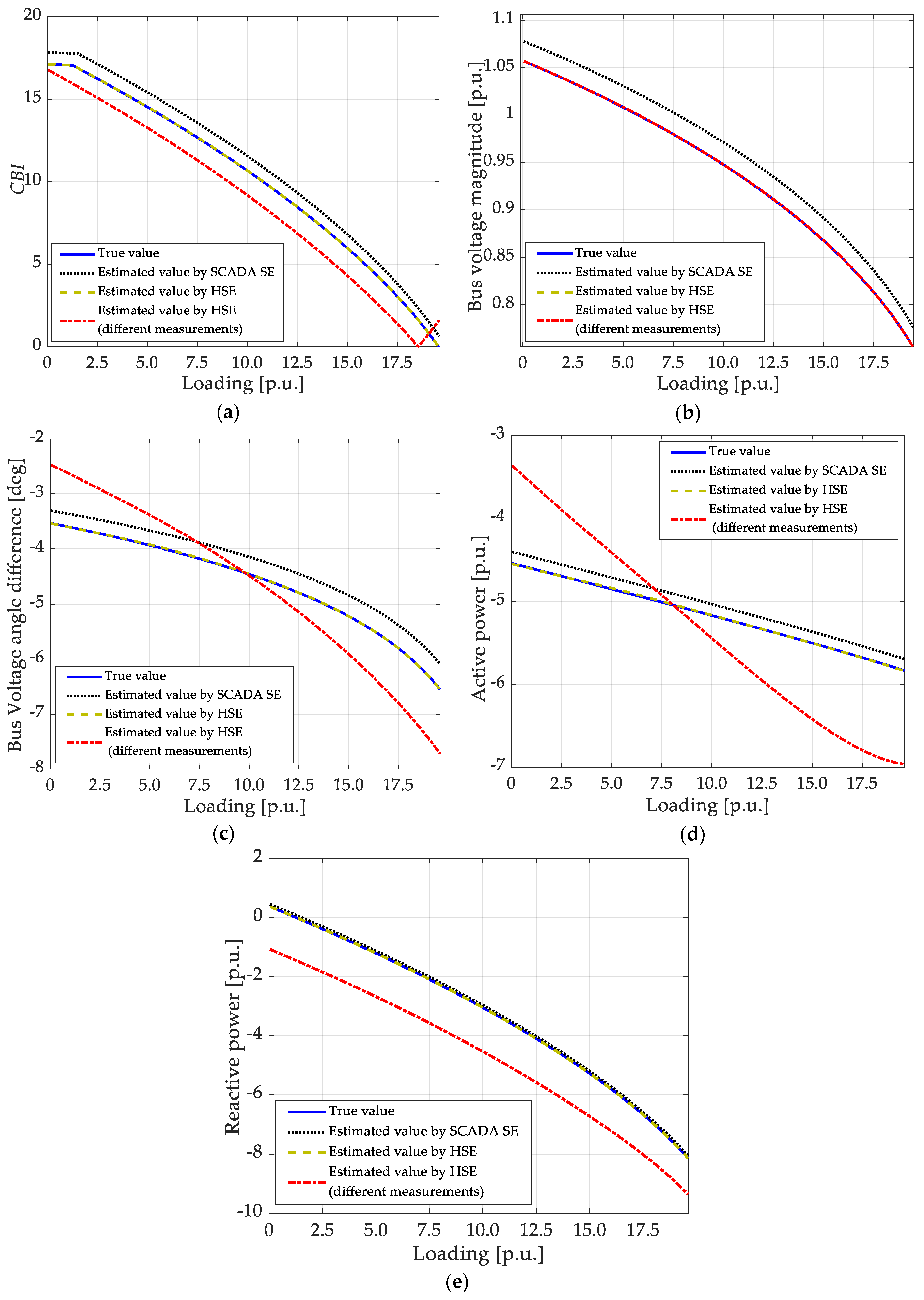
5.3. CBI Estimation Using Bus Voltage Phasor Obtained by the Hybrid State Estimation (HSE) Based on the PMU Placement
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ajjarapu, V. Chapter 1 Introduction, Chapter 4 Sensitivity Analysis for Voltage Stability. In Computational Technique for Voltage Stability Assessment and Control, 1st ed.; Pai, M.A., Stankovic, A., Eds.; Springer: New York, NY, USA, 2006. [Google Scholar]
- NERC. 1996 System Disturbances: Review of Selected Electric System Disturbances in North America. Available online: https://www.nerc.com/pa/rrm/ea/SystemDisturbanceReportDL/1996SystemDisturbance.pdf (accessed on 13 March 2019).
- Vargas, L.S.; Quintana, V.H.; Miranda, D.R. Voltage collapse scenario in the Chilean interconnected system. IEEE Trans. Power Syst. 1999, 14, 1415–1421. [Google Scholar] [CrossRef]
- Vournas, C. Technical Summary of the Athens and Southern Greece Blackout of July 12, 2004; National Technical University of Athens: Athens, Greece, 2004. [Google Scholar]
- Liu, S.; Deng, H.; Guo, S. Analyses and discussions of the blackout in Indian power grid. Energy Sci. Technol. 2013, 6, 61–66. [Google Scholar]
- Modarresi, J.; Gholipour, E.; Khodabakhshian, A. A comprehensive review of the voltage stability indices. Renew. Sustain. Energy Rev. 2016, 63, 1–12. [Google Scholar] [CrossRef]
- Makasa, K.J.; Venayagamoorthy, G.K. On-line voltage stability load index estimation based on PMU measurements. In Proceedings of the 2011 IEEE Power and Energy Society General Meeting, Detroit, MI, USA, 24–28 July 2011. [Google Scholar]
- Chouhan, D.; Jaiswal, V. A literature review on optimal placement of PMU and voltage stability. Indian J. Sci. Technol. 2016, 9, 1–7. [Google Scholar] [CrossRef][Green Version]
- Phadke, A.G.; Thorp, J.S.; Adamiak, M.G. A new measurement technique for tracking voltage phasors, local system frequency, and rate of change of frequency. IEEE Trans. Power Appar. Syst. 1983, 102, 1025–1038. [Google Scholar] [CrossRef]
- Phadke, A.G.; Thorp, J.S. Chapter 7 State estimation, Chapter 8 Control with phasor feedback, Chapter 9 Protection systems with phasor inputs. In Synchronized Phasor Measurements and Their Applications, 1st ed.; Pai, M.A., Stankovic, A., Eds.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Esmaili, M. Inclusive multi-objective PMU placement in power systems considering conventional measurements and contingencies. Int. Trans. Electr. Energy Syst. 2016, 26, 609–626. [Google Scholar] [CrossRef]
- Tran, V.; Zhang, H.; Nguyen, V. Optimal Placement of Phasor measurement unit for observation reliability enhancement. J. Electer. Eng. Technol. 2017, 12, 1921–1931. [Google Scholar] [CrossRef]
- Parimalam, L.; Rajeswari, R. Achieving effective power system observability in optimal PMUs placement using GA-EHBSA. Circuits Syst. 2016, 7, 2002–2013. [Google Scholar] [CrossRef][Green Version]
- Abiri, E.; Rashidi, F.; Niknam, T. An optimal PMU placement method for power system observability under various contingencies. Int. Trans. Electr. Energy Syst. 2015, 25, 589–606. [Google Scholar] [CrossRef]
- Baldwin, T.L.; Mili, L.; Boisen, M.B., Jr. Power system observability with minimal phasor measurement placement. IEEE Trans. Power Syst. 1993, 8, 705–715. [Google Scholar] [CrossRef]
- Jerin, J.; Bindu, S. Hybrid state estimation including PMU measurements. In Proceedings of the International Conference on Control, Communication & Computing, Trivandrum, India, 19–21 November 2015. [Google Scholar]
- Tang, J.; Liu, J.; Ponci, F.; Monti, A. Adaptive load shedding based on combined frequency and voltage stability assessment using synchrophasor measurements. IEEE Trans. Power Syst. 2013, 28, 2035–2047. [Google Scholar] [CrossRef]
- Matsukawa, Y.; Watanabe, M.; Mitani, Y.; Othman, M.L. Multi objective PMU placement optimization considering the placement cost including the current channel allocation and state estimation accuracy. IEEJ Trans. Power Energy 2019, 139, 84–90. [Google Scholar] [CrossRef]
- Matsukawa, Y.; Watanabe, M.; Mitani, Y.; Othman, M.L. Influence of measurement uncertainty propagation in current-channel-selectable multi objective optimal phasor measurement unit placement problem. In Proceedings of the IEEE Power and Energy Society Generation, Transmission and Distribution Grand International Conference and Exposition Asia 2019, Bangkok, Thailand, 19–23 March 2019. [Google Scholar]
- Furukakoi, M.; Adewuyi, O.B.; Danish, M.S.S.; Howlader, A.M.; Senjyu, T.; Funabashi, T. Critical Boundary Index (CBI) based on active and reactive power deviations. Int. J. Electr. Power Energy Syst. 2018, 100, 50–57. [Google Scholar] [CrossRef]
- Valverde, G.; Chakrabarti, S.; Kyriakudes, E.; Terzija, V. A constrained formulation for hybrid state estimation. IEEE Trans. Power Syst. 2011, 26, 1102–1109. [Google Scholar] [CrossRef]
- Deb, K.; Paratab, S.; Agarwal, S.; Meyarivan, T. A fast end elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Rakpenthai, C.; Uatrongjit, S. A new hybrid state estimation based on pseudo-voltage measurements. IEEJ Trans. Electr. Electron. Eng. 2015, 10, S19–S27. [Google Scholar] [CrossRef]
- ISO-IEC-OMIL-BIPM. Guide to the Expression of Uncertainty in Measurement; JCGM: Sèvres, France, 1992. [Google Scholar]
- Milosevic, B.; Begovic, M. Nondominated sorting genetic algorithm for optimal phasor measurement placement. IEEE Trans. Power Syst. 2003, 18, 69–75. [Google Scholar] [CrossRef]
- Jamuna, K.; Swarup, K.S. Multi-objective biogeography based optimization for optimal PMU placement. Appl. Soft Comput. 2012, 12, 1503–1510. [Google Scholar] [CrossRef]
- Peng, C.; Sun, H.; Guo, J. Multi-objective optimal PMU placement using a non-dominated sorting differential evolution algorithm. Int. J. Electr. Power Energy Syst. 2010, 32, 886–892. [Google Scholar] [CrossRef]
- Ghamsari-Yazdel, M.; Esmaili, M. Reliability-based probabilistic optimal joint placement of PMUs and flow measurements. Int. J. Electr. Power Energy Syst. 2016, 78, 857–863. [Google Scholar] [CrossRef]
- Knowles, J.D.; Corne, D.W. Approximating the nondominated front using the Pareto archived evolution strategy. Evol. Comput. 2000, 8, 149–172. [Google Scholar] [CrossRef] [PubMed]

| Parameter | Value |
|---|---|
| The number of buses | 39 |
| The number of lines | 52 |
| The number of load buses | 19 |
| The number of the current channel placement candidates | 104 |
| The length of decision variable in MOOPP | 143 |
| Parameter | Value/Method |
|---|---|
| The population size | 70 |
| Crossover rate | 0.95 |
| Mutation rate | 0.05 |
| The number of generations | 1000 |
| The crossover method | Uniform crossover |
| Class | Parameter | Value |
|---|---|---|
| MOOPP problem | A PMU and a voltage channel cost wV [28] | 1.0 (p.u.) |
| A current channel cost wC [28] | 0.15 (p.u.) | |
| Estimation error limit for voltage magnitude | 15 (%) | |
| Estimation error limit for voltage angle | 10 (deg) | |
| The number of power flow scenarios | 1000 | |
| Maximum measurement uncertainty [21] | SCADA injection | 2 (%) |
| SCADA flow | 2 (%) | |
| PMU voltage magnitude | 0.02 (%) | |
| PMU current magnitude | 0.03 (%) | |
| PMU phase angle | 0.01 (deg) |
| Method I | Method II | |
|---|---|---|
| Method III | 0.8125:0.1875 | 1:0 |
| Class | Value |
|---|---|
| PMU placement buses | 2, 5, 16, 23, 26, 39 |
| Current channel placement lines | 2-11, 2-19, 5-30, 16-1, 16-15, 16-21, 23-22, 23-24, 26-25, 26-27, 26-29, 26-31, 26-34, 39-9, 39-36, 39-38 |
| KVC | 8.40 |
| TVEmax | 0.0286 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Matsukawa, Y.; Watanabe, M.; Abdul Wahab, N.I.; Othman, M.L. Voltage Stability Index Calculation by Hybrid State Estimation Based on Multi Objective Optimal Phasor Measurement Unit Placement. Energies 2019, 12, 2688. https://doi.org/10.3390/en12142688
Matsukawa Y, Watanabe M, Abdul Wahab NI, Othman ML. Voltage Stability Index Calculation by Hybrid State Estimation Based on Multi Objective Optimal Phasor Measurement Unit Placement. Energies. 2019; 12(14):2688. https://doi.org/10.3390/en12142688
Chicago/Turabian StyleMatsukawa, Yoshiaki, Masayuki Watanabe, Noor Izzri Abdul Wahab, and Mohammad Lutfi Othman. 2019. "Voltage Stability Index Calculation by Hybrid State Estimation Based on Multi Objective Optimal Phasor Measurement Unit Placement" Energies 12, no. 14: 2688. https://doi.org/10.3390/en12142688
APA StyleMatsukawa, Y., Watanabe, M., Abdul Wahab, N. I., & Othman, M. L. (2019). Voltage Stability Index Calculation by Hybrid State Estimation Based on Multi Objective Optimal Phasor Measurement Unit Placement. Energies, 12(14), 2688. https://doi.org/10.3390/en12142688






