Harmonic Stability Analysis for Multi-Parallel Inverter-Based Grid-Connected Renewable Power System Using Global Admittance †
Abstract
:1. Introduction
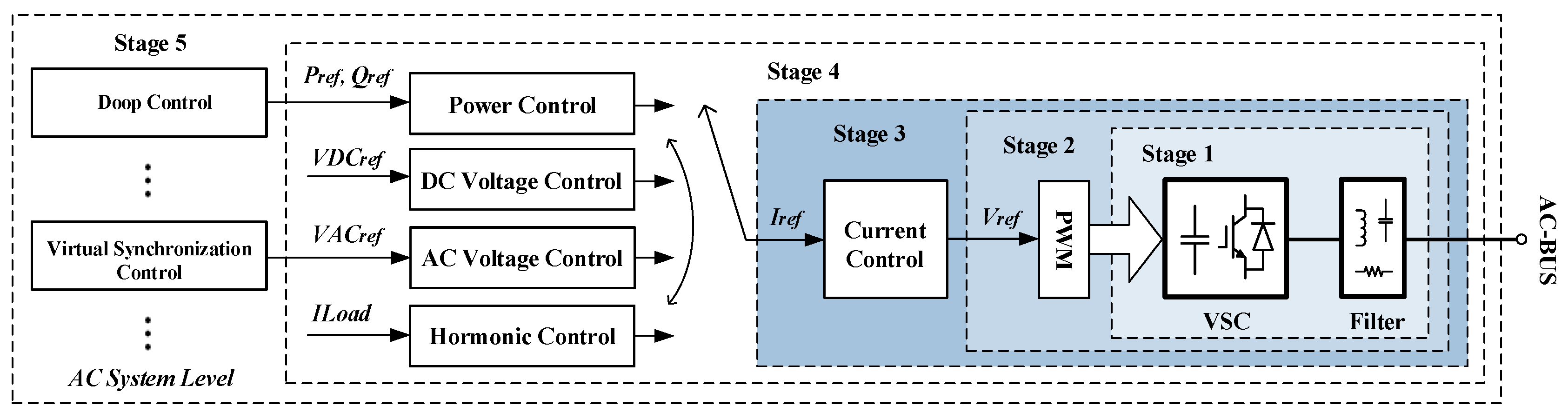
2. System Modeling
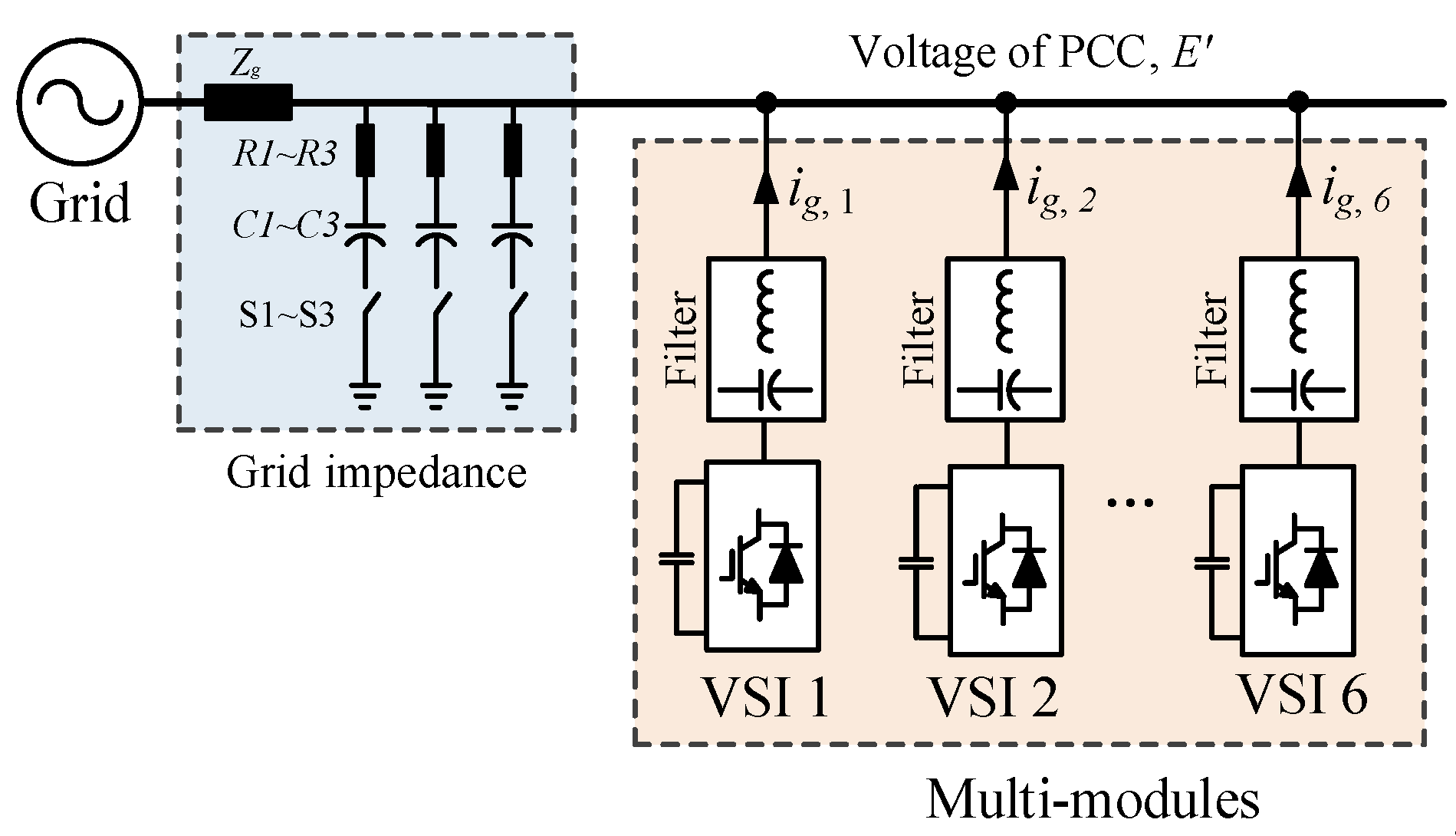
2.1. System Description
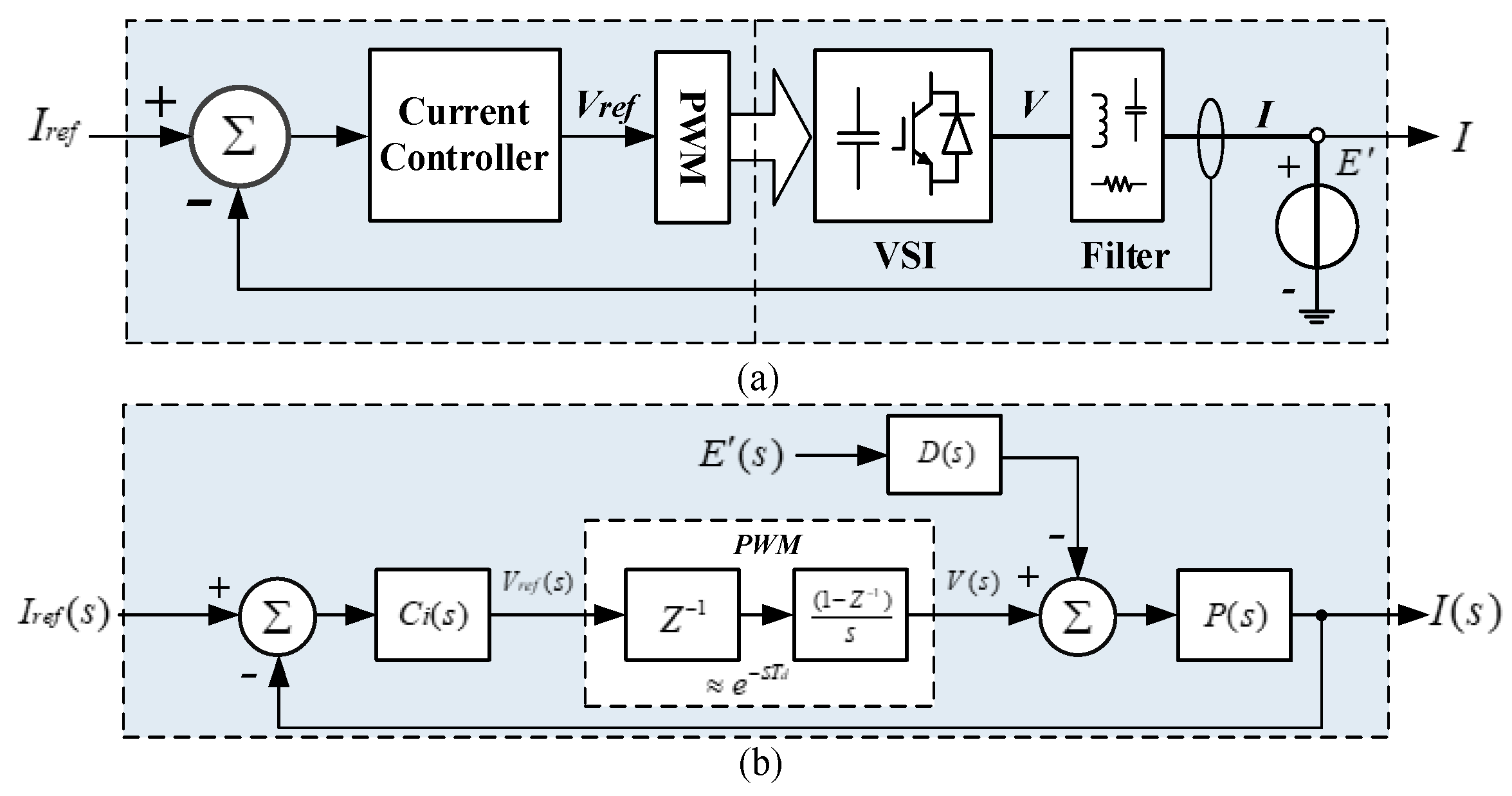
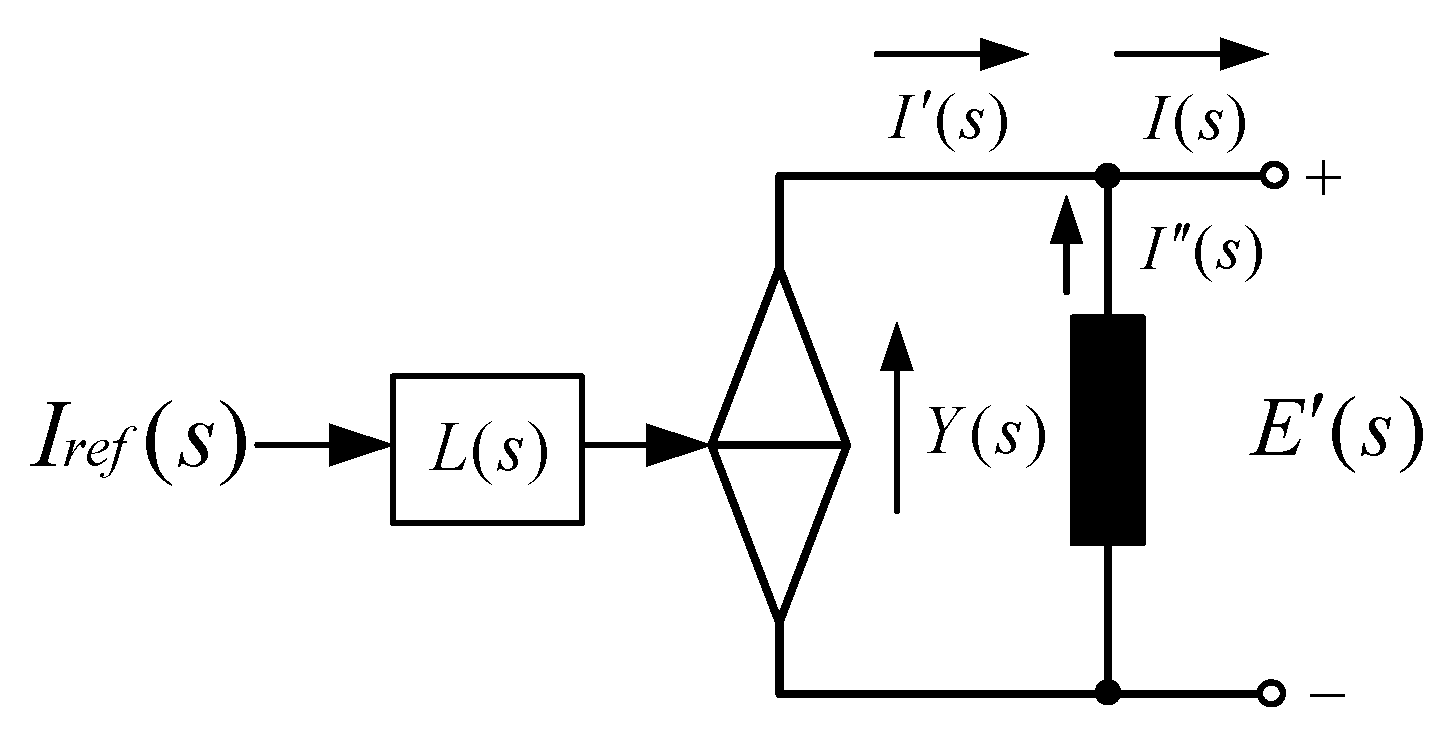
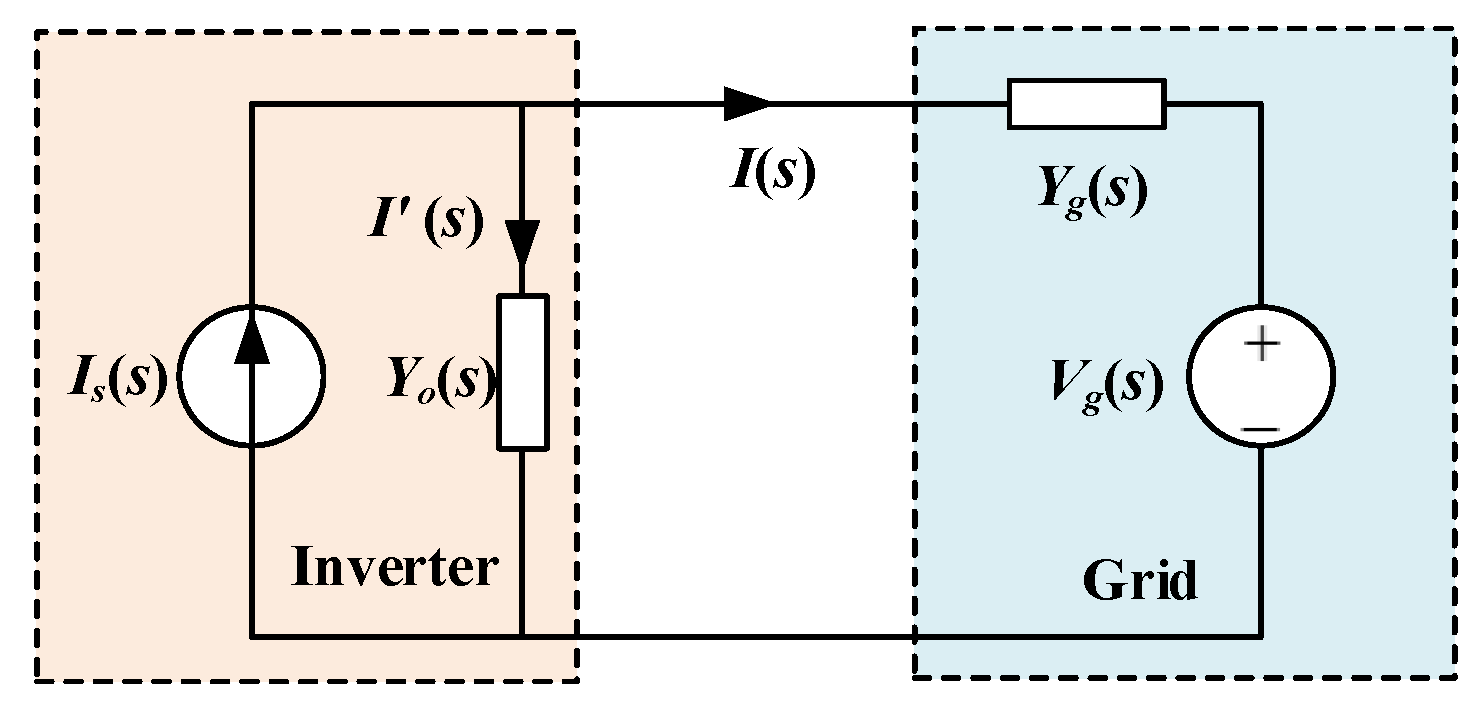
2.2. Admittance Modeling of a Single-Inverter System
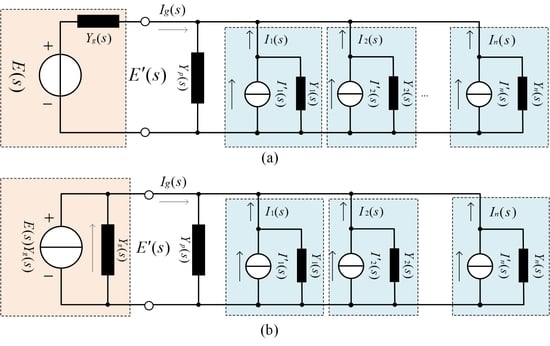
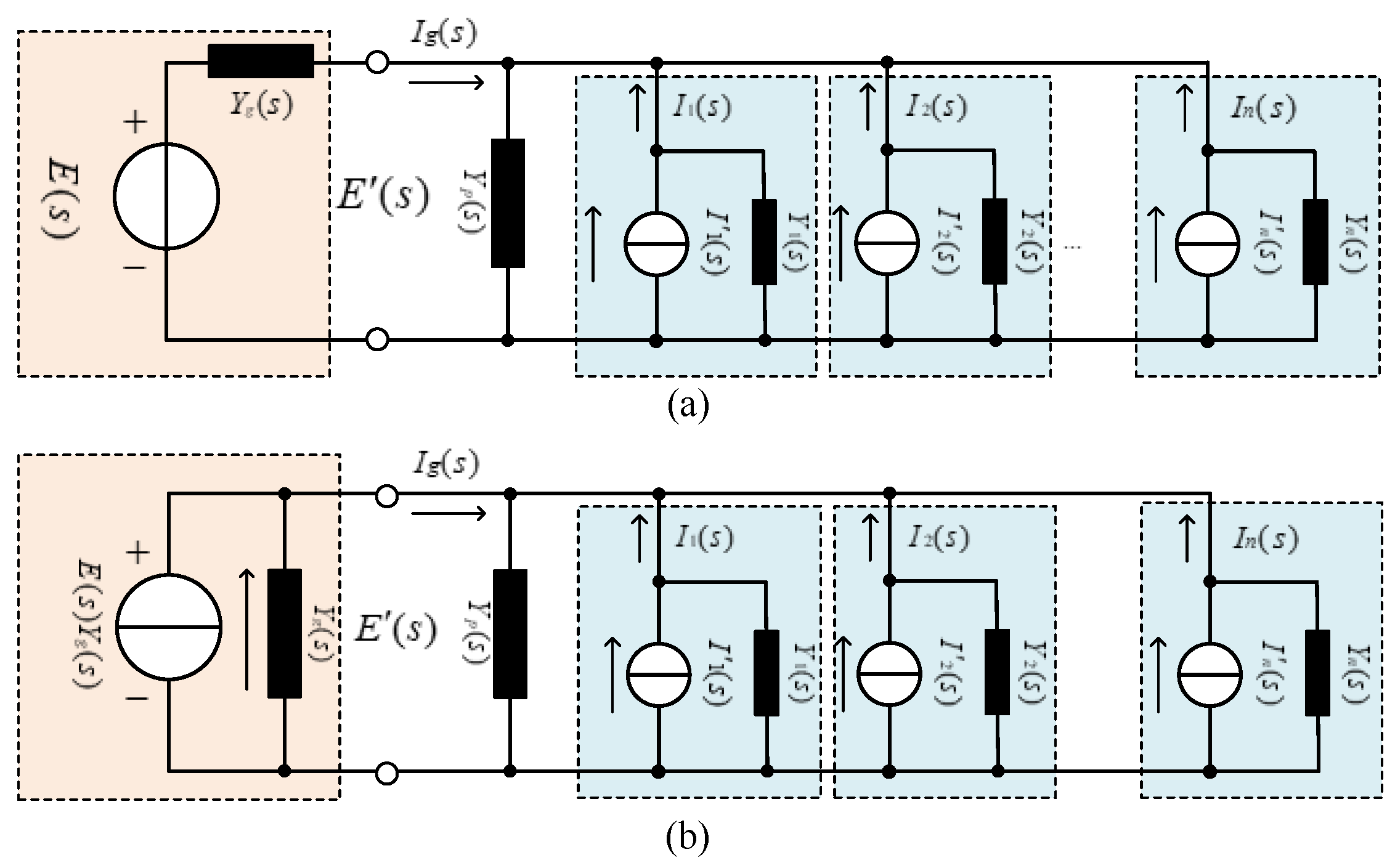
2.3. Admittance Modeling of the VSIs System
3. Traditional Impedance-Based Stability Criterion
3.1. Stability Criterion for a Single Grid-Connected Inverter System
3.2. Stability Criterion for a Multi-Parallel Grid-Connected Inverter System
3.3. Unified Impedance-Based Stability Criterion
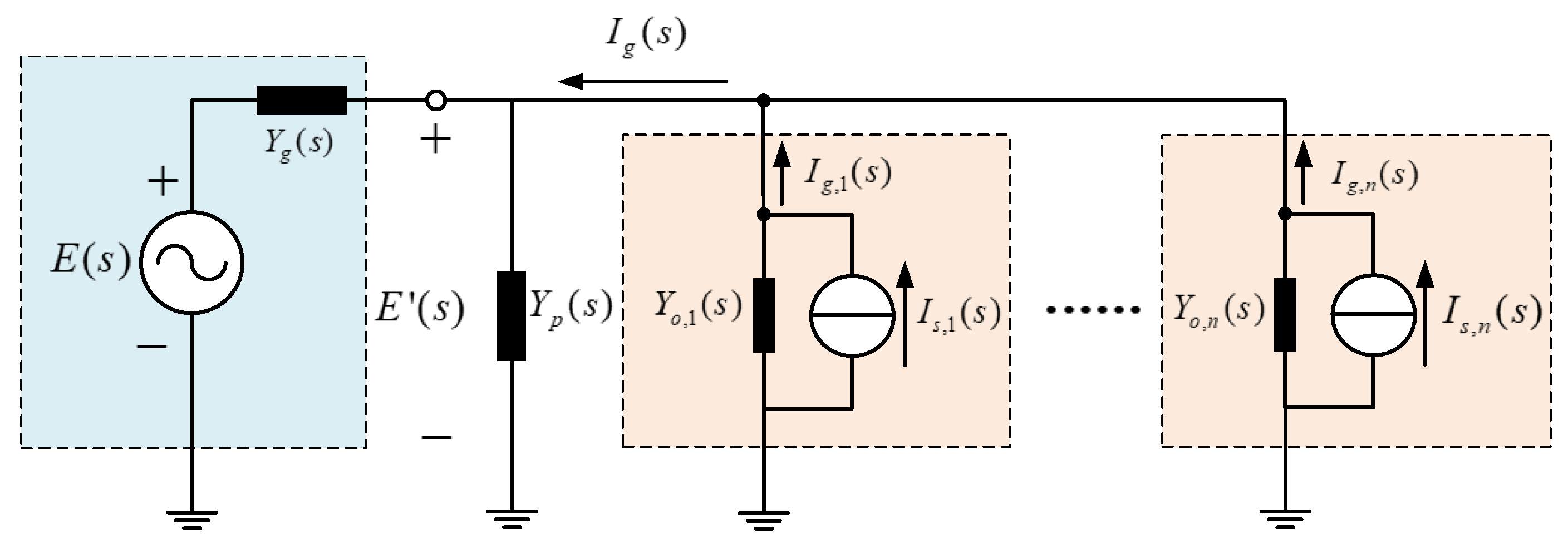
4. The Proposed Global Admittance-Based Stability Criterion
4.1. Description of the Basic Principle
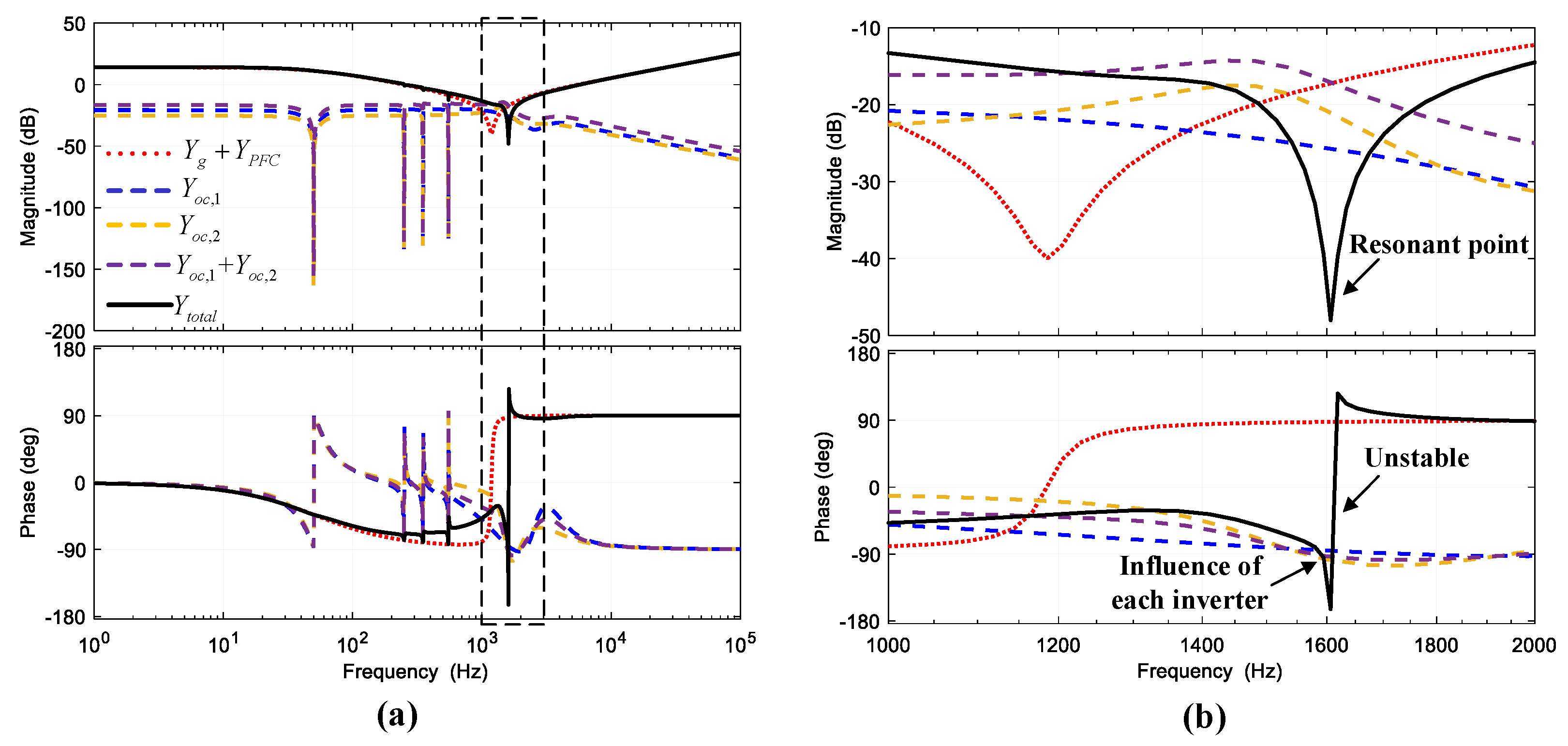
4.2. The Proposed Stability Criterion
4.3. Discussion of the Case in which the Parameters are Different
5. Simulation and Experimental Results
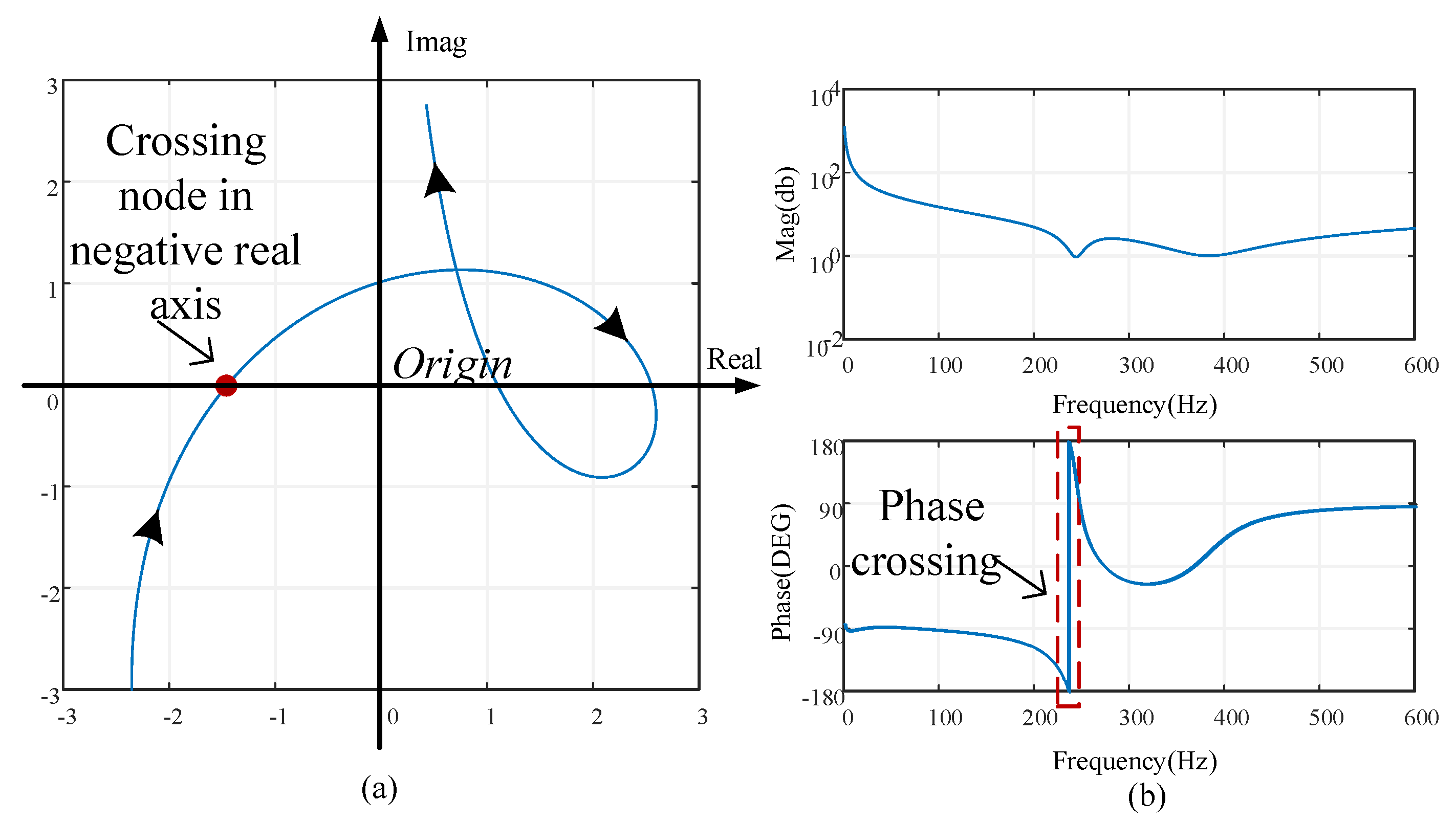
5.1. Simulation Verification
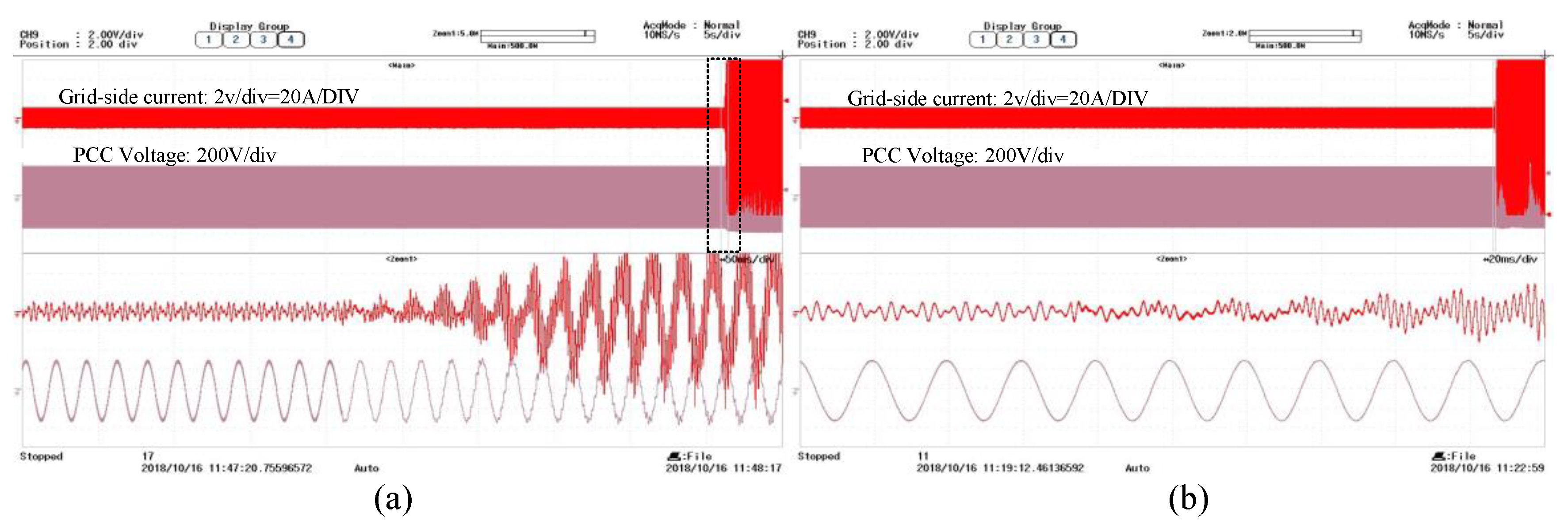
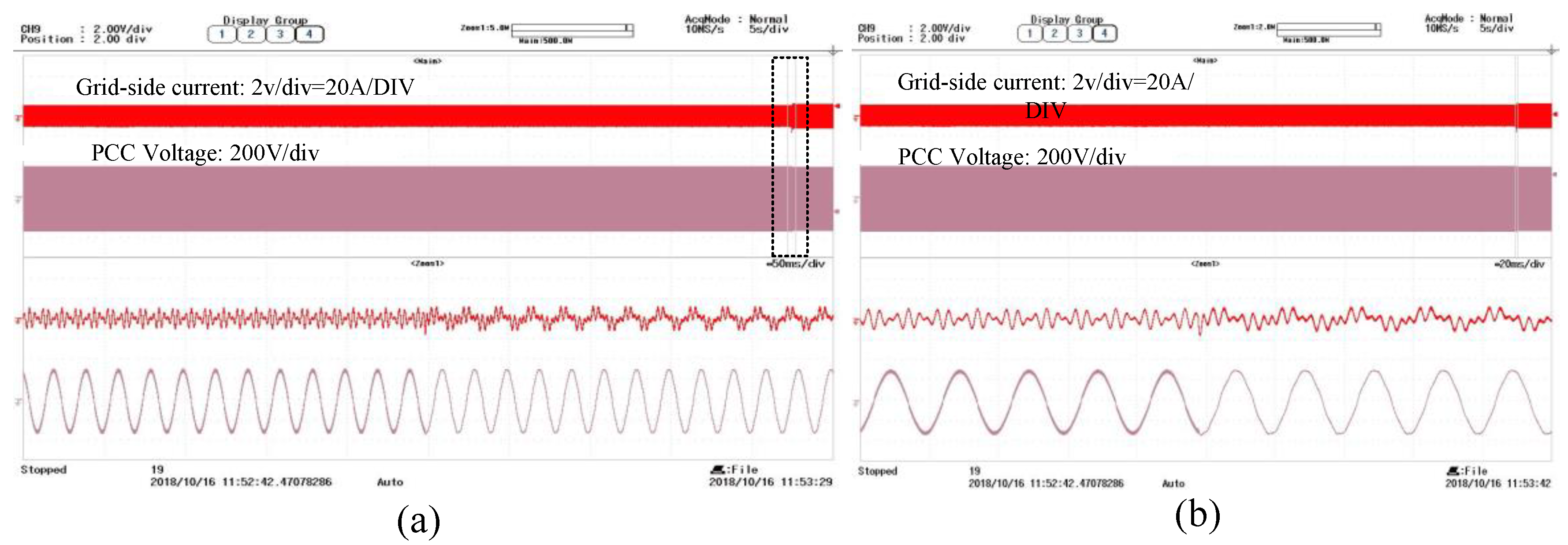
5.2. Experimental Verification
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Blaabjerg, F.; Chen, Z.; Kjaer, S.B. Power electronics as efficient interface in dispersed power generation systems. IEEE Trans. Power Electron. 2004, 19, 1184–1194. [Google Scholar] [CrossRef]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of Power Converters in AC Microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Liserre, M.; Teodorescu, R.; Blaabjerg, F. Stability of photovoltaic and wind turbine grid-connected inverters for a large set of grid impedance values. IEEE Trans. Power Electron. 2006, 21, 263–272. [Google Scholar] [CrossRef]
- Turner, R.; Walton, S.; Duke, R. Stability and Bandwidth Implications of Digitally Controlled Grid-Connected Parallel Inverters. IEEE Trans. Ind. Electron. 2010, 57, 3685–3694. [Google Scholar] [CrossRef]
- Wang, F.; Duarte, J.L.; Hendrix, M.A.M.; Ribeiro, P.F. Modeling and Analysis of Grid Harmonic Distortion Impact of Aggregated DG Inverters. IEEE Trans. Power Electron. 2011, 26, 786–797. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Chen, Z. Autonomous Control of Inverter-Interfaced Distributed Generation Units for Harmonic Current Filtering and Resonance Damping in an Islanded Microgrid. IEEE Trans. Ind. Appl. 2014, 50, 452–461. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, X.; Harnefors, L.; Gong, H.; Hasler, J.; Nee, H. SISO Transfer Functions for Stability Analysis of Grid-Connected Voltage-Source Converters. IEEE Trans. Ind. Appl. 2019, 55, 2931–2941. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Wu, W. Modeling and Analysis of Harmonic Stability in an AC Power-Electronics-Based Power System. IEEE Trans. Power Electron. 2014, 29, 6421–6432. [Google Scholar] [CrossRef]
- Turner, R.; Walton, S.; Duke, R. A case study on the application of the Nyquist stability criterion as applied to interconnected loads and sources on grids. IEEE Trans. Ind. Electron. 2013, 60, 2740–2749. [Google Scholar] [CrossRef]
- Cao, W.; Fan, D.; Liu, K.; Zhao, J.; Ruan, L.; Wu, X. Harmonic Stability Assessment based on Global Admittance for Multi-Paralleled Grid-Connected VSIs using Modified Nyquist Criterion. In Proceedings of the International Power Electronics Conference (IPEC-Niigata 2018 -ECCE Asia), Niigata, Japan, 20–24 May 2018. [Google Scholar]
- Wang, X.; Blaabjerg, F. Harmonic Stability in Power Electronic-Based Power Systems: Concept, Modeling, and Analysis. IEEE Trans. Smart Grid. 2019, 10, 2858–2870. [Google Scholar] [CrossRef]
- Hu, T. A Nonlinear-System Approach to Analysis and Design of Power-Electronic Converters with Saturation and Bilinear Terms. IEEE Trans. Power Electron. 2011, 26, 399–410. [Google Scholar] [CrossRef]
- Wu, H.; Pickert, V.; Giaouris, D.; Ji, B. Nonlinear Analysis and Control of Interleaved Boost Converter Using Real-Time Cycle to Cycle Variable Slope Compensation. IEEE Trans. Power Electron. 2017, 32, 7256–7270. [Google Scholar] [CrossRef]
- Amin, M.; Molinas, M. Small-Signal Stability Assessment of Power Electronics Based Power Systems: A Discussion of Impedance- and Eigenvalue-Based Methods. IEEE Trans. Ind. Appl. 2017, 53, 5014–5030. [Google Scholar] [CrossRef]
- Kalcon, G.O.; Adam, G.P.; Anaya-Lara, O.; Lo, S.; Uhlen, K. Small-Signal Stability Analysis of Multi-Terminal VSC-Based DC Transmission Systems. IEEE Trans. Power Syst. 2012, 27, 1818–1830. [Google Scholar] [CrossRef]
- Pinares, G.; Bongiorno, M. Modeling and Analysis of VSC-Based HVDC Systems for DC Network Stability Studies. IEEE Trans. Power Deliv. 2016, 31, 848–856. [Google Scholar] [CrossRef]
- Beerten, J.; D’Arco, S.; Suul, J.A. Identification and Small-Signal Analysis of Interaction Modes in VSC MTDC Systems. IEEE Trans. Power Deliv. 2016, 31, 888–897. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Middlebrook, R.D.D. Input filter consideration in design and application of switching regulators. In Proceedings of the IEEE Industry Applications Society Annual Meeting, Chicago, IL, USA, 11–14 October 1976. [Google Scholar]
- Cao, W.; Ma, Y.; Yang, L.; Wang, F.; Tolbert, L.M. D-Q Impedance Based Stability Analysis and Parameter Design of Three-Phase Inverter-Based AC Power Systems. IEEE Trans. Ind. Electron. 2017, 64, 6017–6028. [Google Scholar] [CrossRef]
- Cao, W.; Ma, Y.; Wang, F. Sequence-Impedance-Based Harmonic Stability Analysis and Controller Parameter Design of Three-Phase Inverter-Based Multibus AC Power Systems. IEEE Trans. Power Electron. 2017, 32, 7674–7693. [Google Scholar] [CrossRef]
- Cho, Y.; Hur, K.; Kang, Y.C.; Muljadi, E. Impedance-Based Stability Analysis in Grid Interconnection Impact Study Owing to the Increased Adoption of Converter-Interfaced Generators. Energies 2017, 10, 1355. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, J.; Bao, W.; Zhao, Y. Infinity-norm of impedance-based stability criterion for three-phase AC distributed power systems with constant power loads. IEEE Trans. Power Electron. 2015, 30, 3030–3043. [Google Scholar] [CrossRef]
- Vesti, S.; Suntio, T.; Oliver, J.A.; Prieto, R.; Cobos, J.A. Impedance-based stability and transient-performance assessment applying maximum peak criteria. IEEE Trans. Power Electron. 2013, 28, 2099–2104. [Google Scholar] [CrossRef]
- Suntio, T.; Messo, T.; Berg, M.; Alenius, H.; Reinikka, T.; Luhtala, R.; Zenger, K. Impedance-Based Interactions in Grid-Tied Three-Phase Inverters in Renewable Energy Applications. Energies 2019, 12, 464. [Google Scholar] [CrossRef]
- Sun, J. Impedance-based stability criterion for grid-connected inverters. IEEE Trans. Power Electron. 2011, 26, 3075–3078. [Google Scholar] [CrossRef]
- Liu, F.; Liu, J.; Zhang, H.; Xue, D. Stability issues of Z + Z type cascade system in hybrid energy storage system (HESS). IEEE Trans. Power Electron. 2014, 29, 5846–5859. [Google Scholar] [CrossRef]
- Wang, X.; Blaabjerg, F.; Liserre, M.; Chen, Z.; He, J.; Li, Y. An active damper for stabilizing power-electronics-based AC systems. IEEE Trans. Power Electron. 2014, 29, 3318–3329. [Google Scholar] [CrossRef]
- Ye, Q.; Mo, R.; Shi, Y.; Li, H. A unified Impedance-based Stability Criterion (UIBSC) for paralleled grid-tied inverters using global minor loop gain (GMLG). In Proceedings of the IEEE Energy Conversion Congress and Exposition (ECCE), Montreal, QC, Canada, 20–24 September 2015. [Google Scholar]
- Harnefors, L.; Wang, X.; Yepes, A.G.; Blaabjerg, F. Passivity-Based Stability Assessment of Grid-Connected VSCs-An Overview. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 116–125. [Google Scholar] [CrossRef]




| Method | Calculation Burden | Reflect the Instability-Causing Element | Ease of Stability-Oriented Redesign |
|---|---|---|---|
| MLG | massive | positive | direct |
| GMLG | small | negative | complicated |
| Parameters | Values | ||
|---|---|---|---|
| Inverter 1 | LCL-filter | Lf,1 | 1.3 mH |
| RLf,1 | 0.1 Ω | ||
| Cf,1 | 3 μF | ||
| Lg,1 | 1.5 mH | ||
| RLg,1 | 0.2 Ω | ||
| PR current controller | Kp,1 | 10.5 | |
| Ki,1 | 2000 | ||
| Ki,5 | 500 | ||
| Ki,7 | 500 | ||
| Ki,11 | 500 | ||
| Inverter 2 | LCL-filter | Lf,2 | 1.5 mH |
| RLf,2 | 0.1 Ω | ||
| Cf,2 | 4.7 μF | ||
| Lg,2 | 1.8 mH | ||
| RLg,2 | 0.2 Ω | ||
| PR current controller | Kp2 | 18 | |
| Ki,2 | 3000 | ||
| Ki,5 | 500 | ||
| Ki,7 | 500 | ||
| Ki,11 | 500 | ||
| DC-link voltage | Vdc | 700 V | |
| Grid | Ls | 0.6 mH | |
| Rs | 0.2 Ω | ||
| PFC device capacity | YPFC | 30 μF | |
| ωf (Hz) | Rd | Rd,1 | Rd,2 | Rd, p |
|---|---|---|---|---|
| 1600 | −0.0041 | 0.0038 | −0.0133 | 0.0054 |
| Case | Number of Inverters | Resonance Frequency | Rd | System Stability |
|---|---|---|---|---|
| I | 4 | 2000 Hz | 0.02 | stable |
| II | 6 | 2250 Hz | −0.1 | unstable |
| III | 8 | 2250 Hz | −0.6 | unstable |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, W.; Liu, K.; Wang, S.; Kang, H.; Fan, D.; Zhao, J. Harmonic Stability Analysis for Multi-Parallel Inverter-Based Grid-Connected Renewable Power System Using Global Admittance. Energies 2019, 12, 2687. https://doi.org/10.3390/en12142687
Cao W, Liu K, Wang S, Kang H, Fan D, Zhao J. Harmonic Stability Analysis for Multi-Parallel Inverter-Based Grid-Connected Renewable Power System Using Global Admittance. Energies. 2019; 12(14):2687. https://doi.org/10.3390/en12142687
Chicago/Turabian StyleCao, Wu, Kangli Liu, Shunyu Wang, Haotian Kang, Dongchen Fan, and Jianfeng Zhao. 2019. "Harmonic Stability Analysis for Multi-Parallel Inverter-Based Grid-Connected Renewable Power System Using Global Admittance" Energies 12, no. 14: 2687. https://doi.org/10.3390/en12142687
APA StyleCao, W., Liu, K., Wang, S., Kang, H., Fan, D., & Zhao, J. (2019). Harmonic Stability Analysis for Multi-Parallel Inverter-Based Grid-Connected Renewable Power System Using Global Admittance. Energies, 12(14), 2687. https://doi.org/10.3390/en12142687