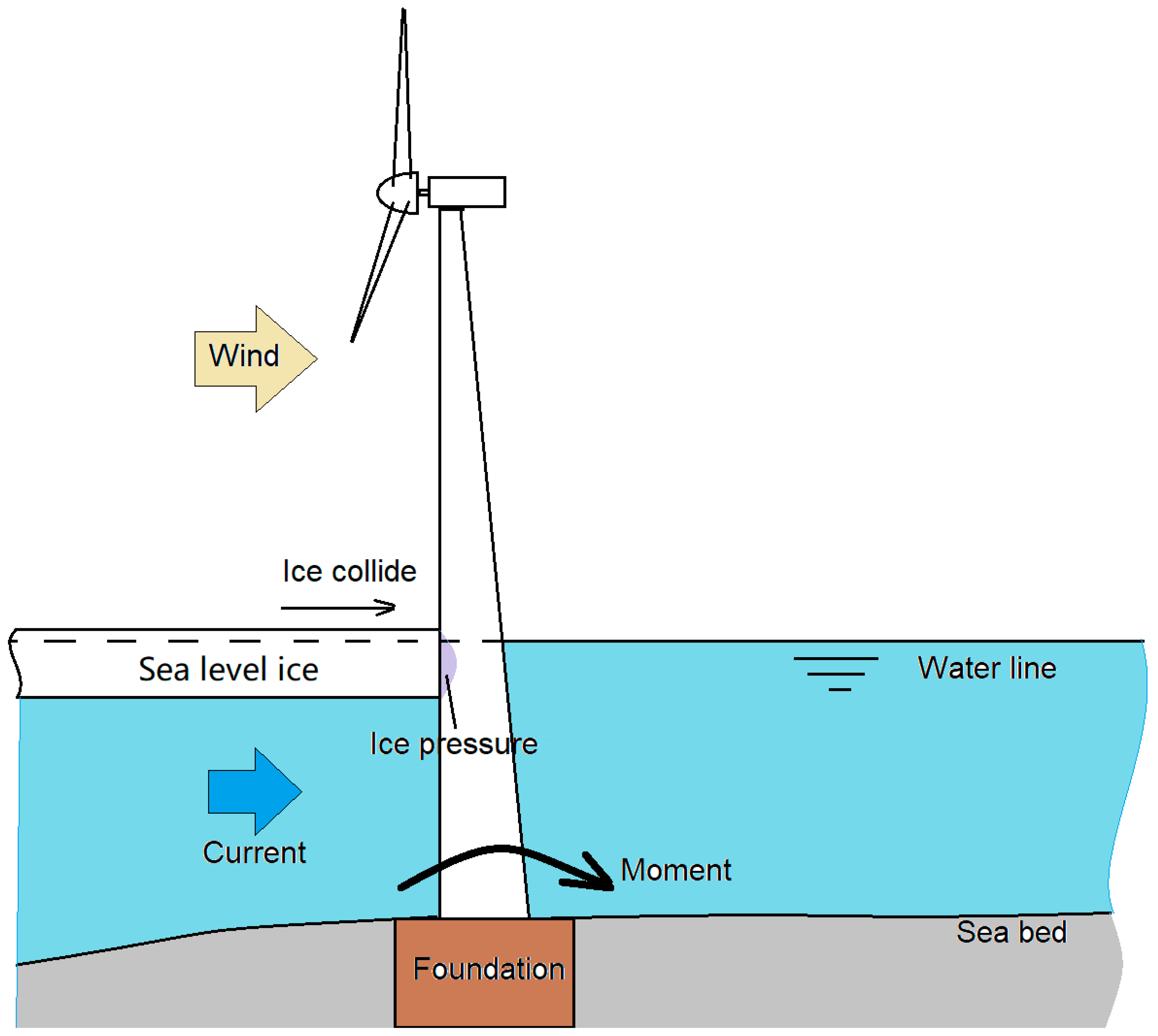
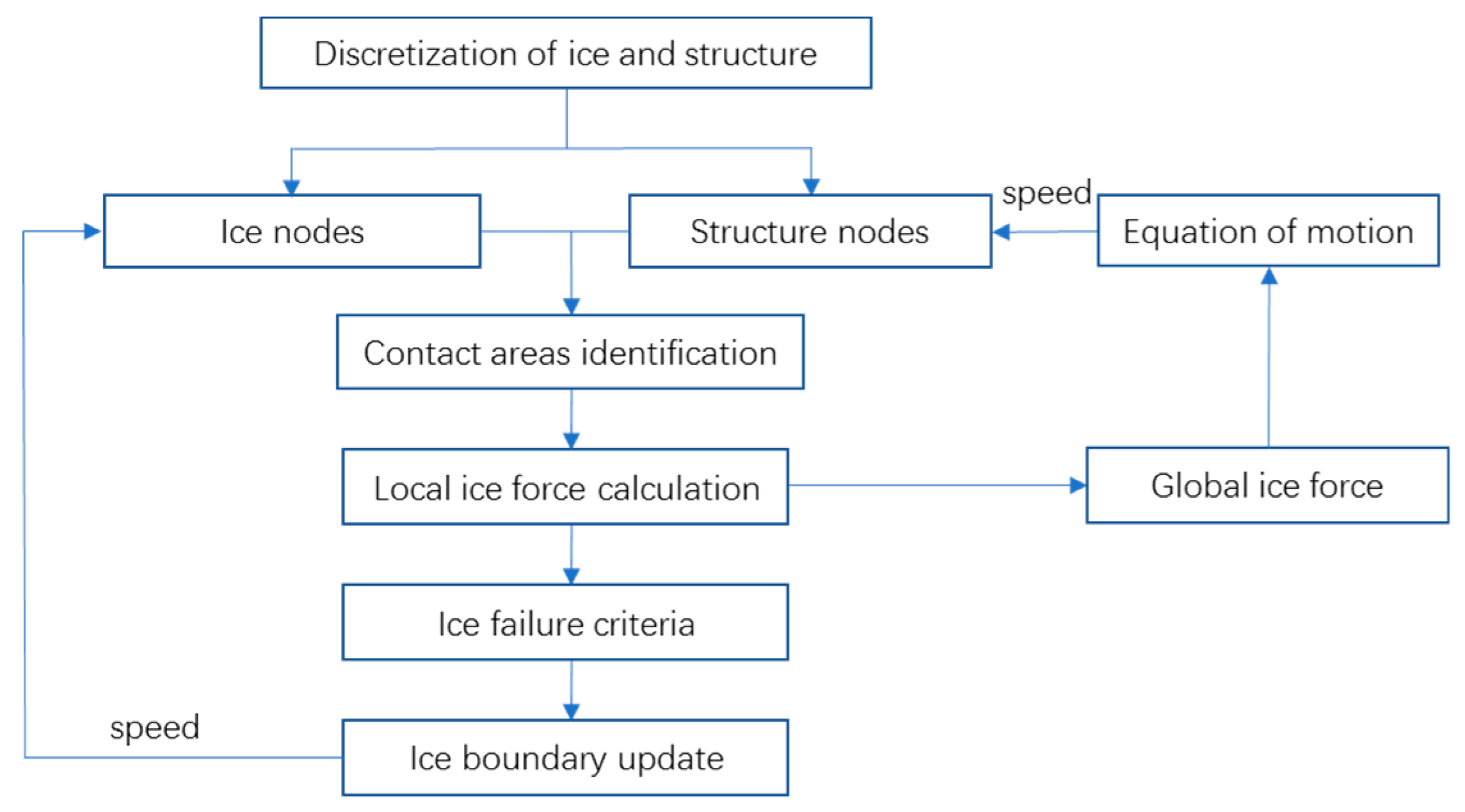
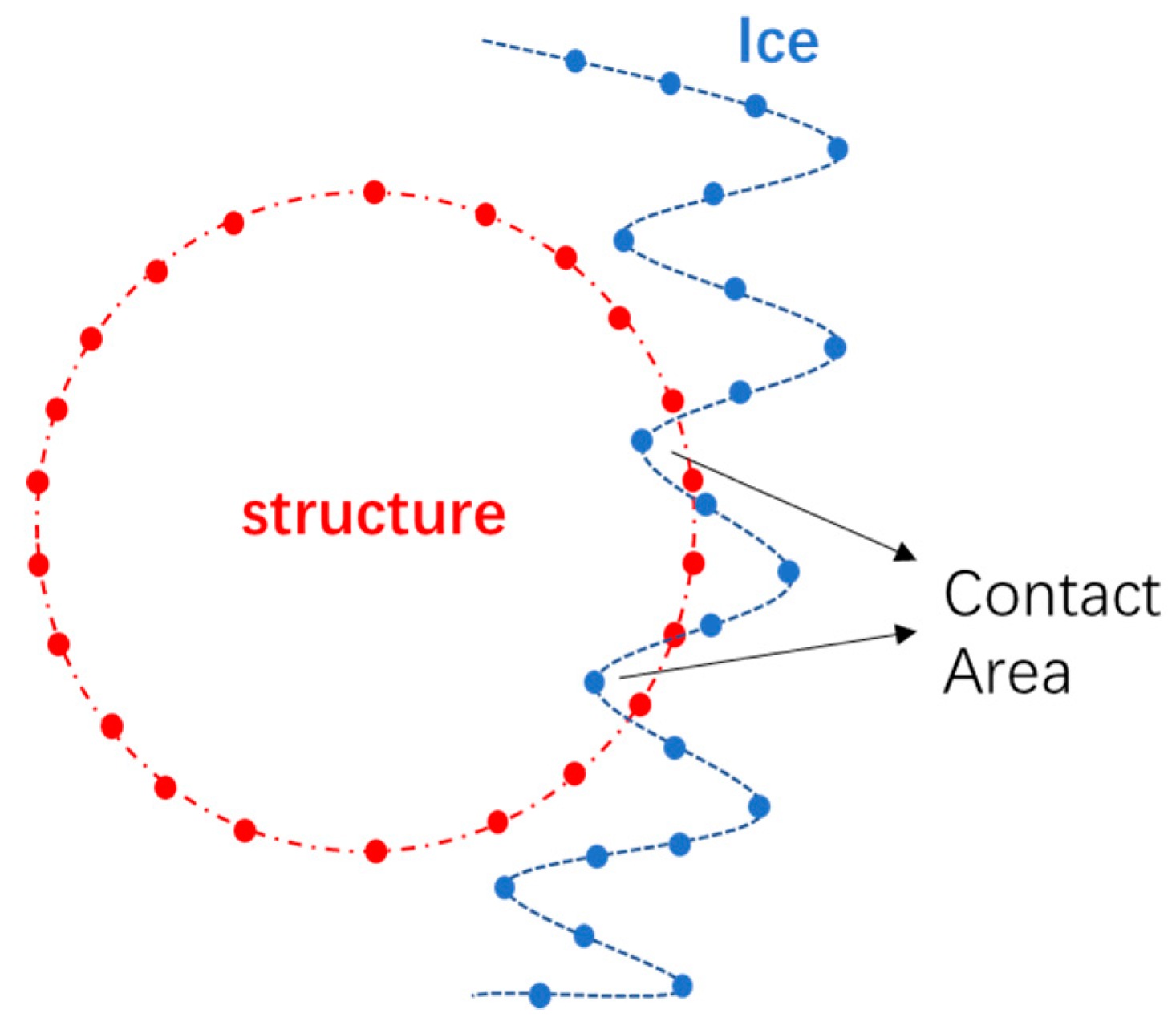
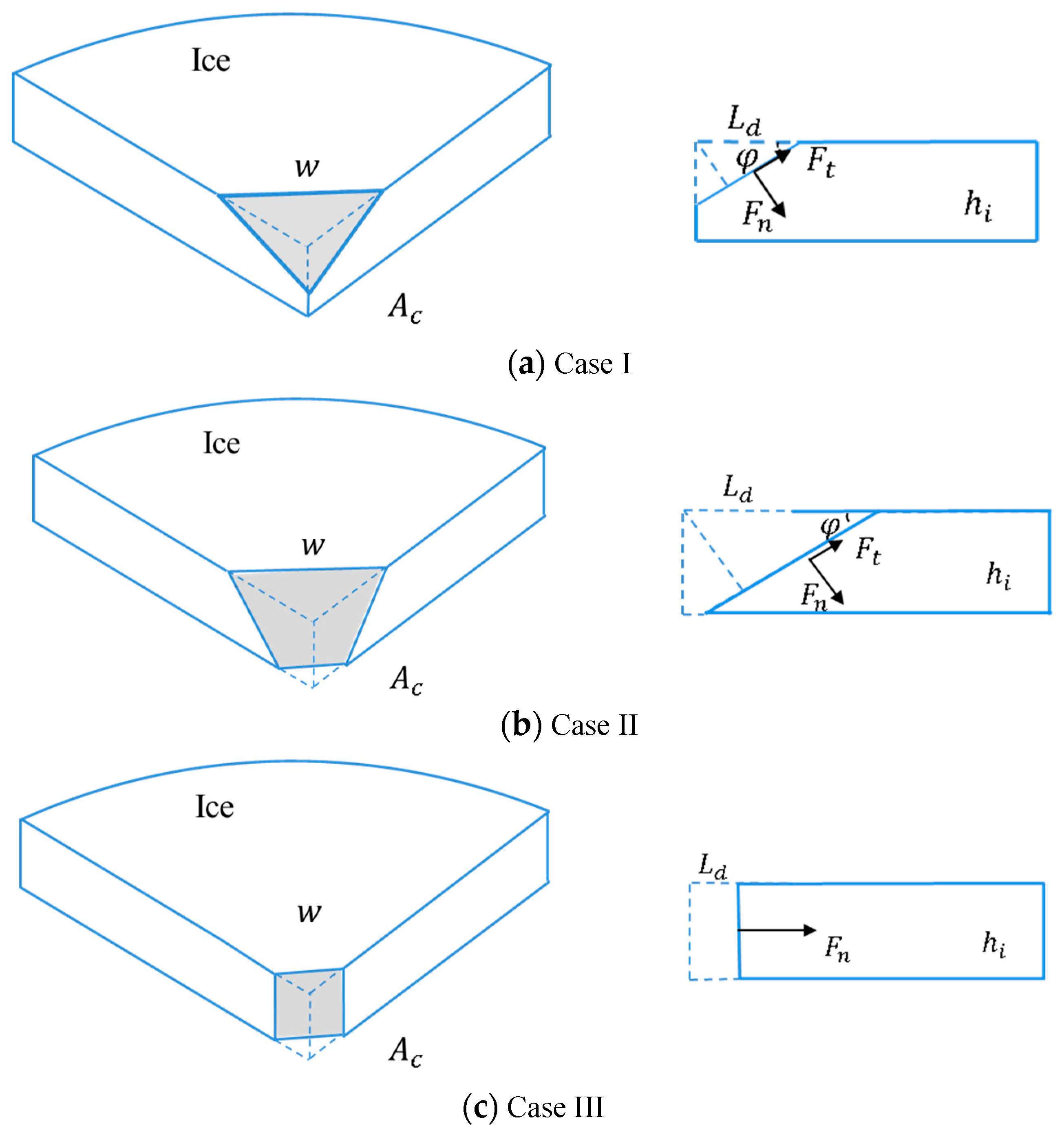
3.1. Validation with Model Test I
Barker et al. (2005) carried out a test campaign to measure the ice loads on offshore wind turbines in the Danish sea at the Canadian Hydraulics Centre of NRC (National Research Council) [
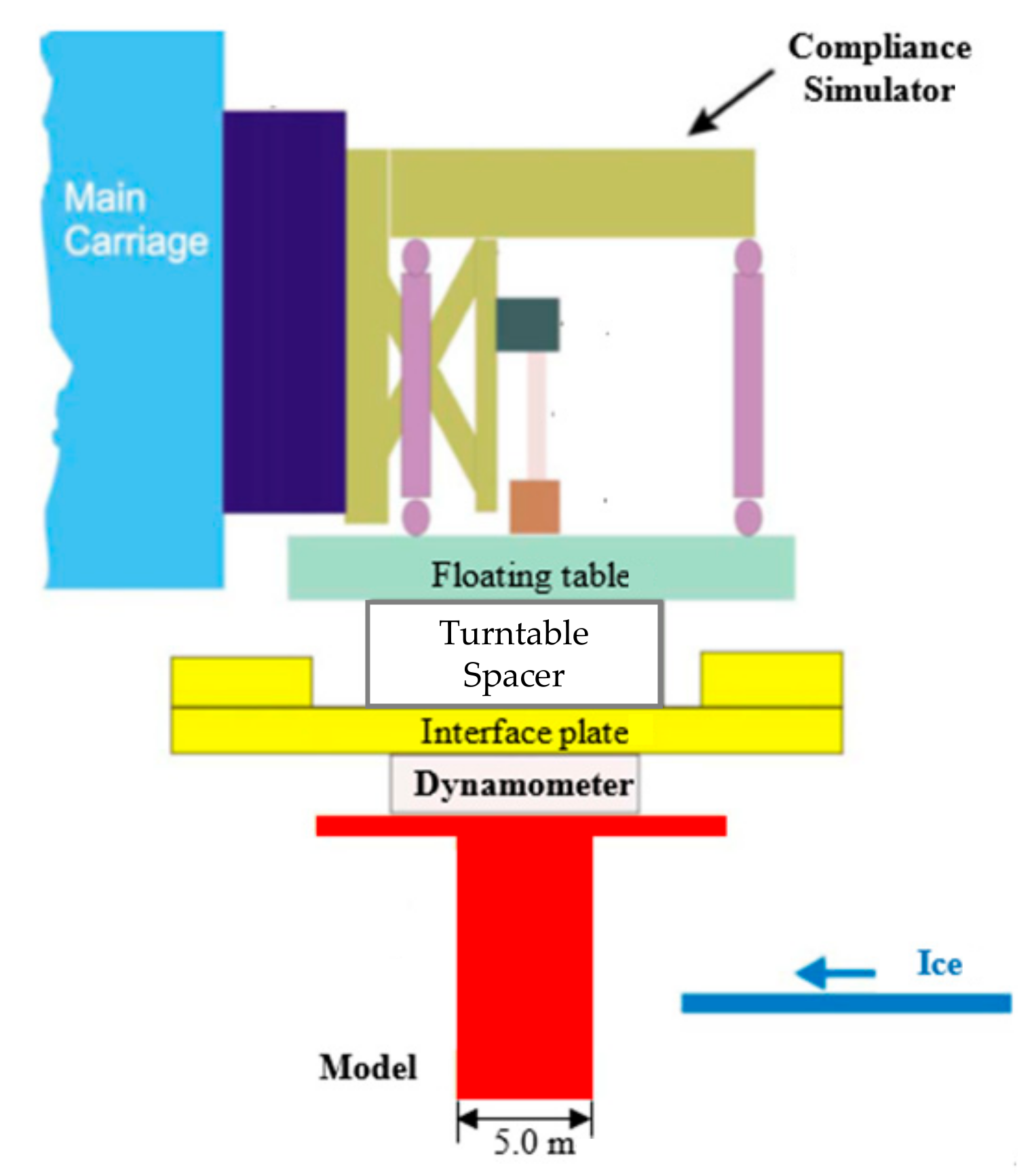
29]. The size of the tank is 21 m in length, 7 m in width, and 1.2 m in depth. Ice sheets are grown, tempered, or melted by adjusting the room’s air temperature. A main carriage could travel along the tank at a velocity of 3–650 mm/s. A small carriage pushes ice sheets towards the structures to be tested. A compliance simulator system was inflexibly fixed to a main carriage. A turntable spacer and interface plate were hung freely under a floating table. They were utilized to support the tested structure and also supply extra weight. All these components were applied to reproduce the main characteristics of wind turbine. The configuration setup is shown in
Figure 7. The sampling frequency is 100 Hz in the model tests.
Model tests with seven configurations were carried out. Only one configuration was selected for the present study. The cylinder model was rigidly fixed onto the main carriage. A geometric scale factor of 1:26 was set for model tests with the Froude and Cauchy scaling method. The diameter of the cylinder is 0.192 m in a model scale. One ice sheet was made for the tests.
Table 1 gives the ice properties and the test matrix. The dynamic friction coefficient between the ice and structure models was measured with a mean value of 0.07, which is used in the present simulation. The Poisson’s ratio in Equation (9) is taken as 0.3 [
35]. The elastic modulus is indirectly calculated from flexural strength in the simulation [
40].
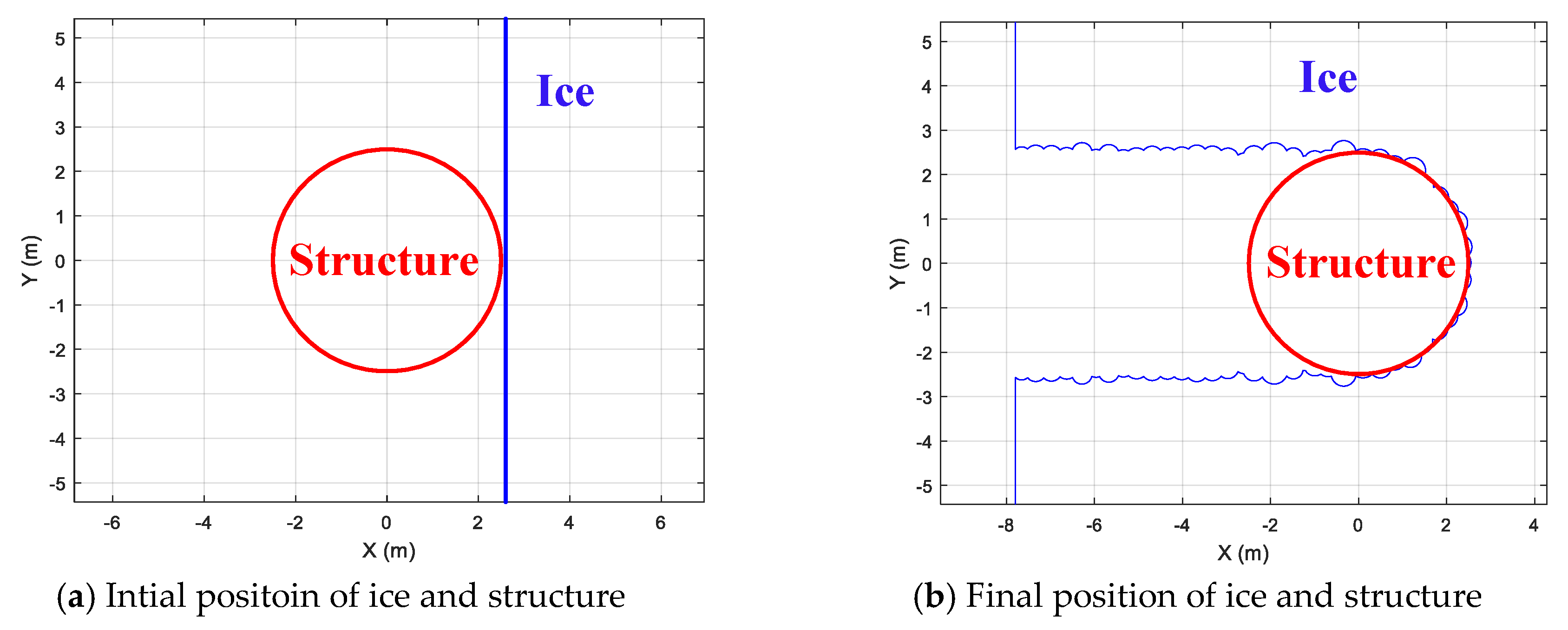
During the model tests, it was observed that continuous crushing with short durations occurred throughout the test series. The ice crushed against the cylinder at the contact surface and ice sheet was pulverized into very fine pieces. However, local flexural or buckling failures could be observed, and pure crushing events seldom occurred. Therefore, the ice-structure interaction process could be taken as non-simultaneous crushing. In the simulation, the structure is fixed and the level ice moves against the structure with a specific speed. The center of gravity for the structure is located at the origin, as shown in
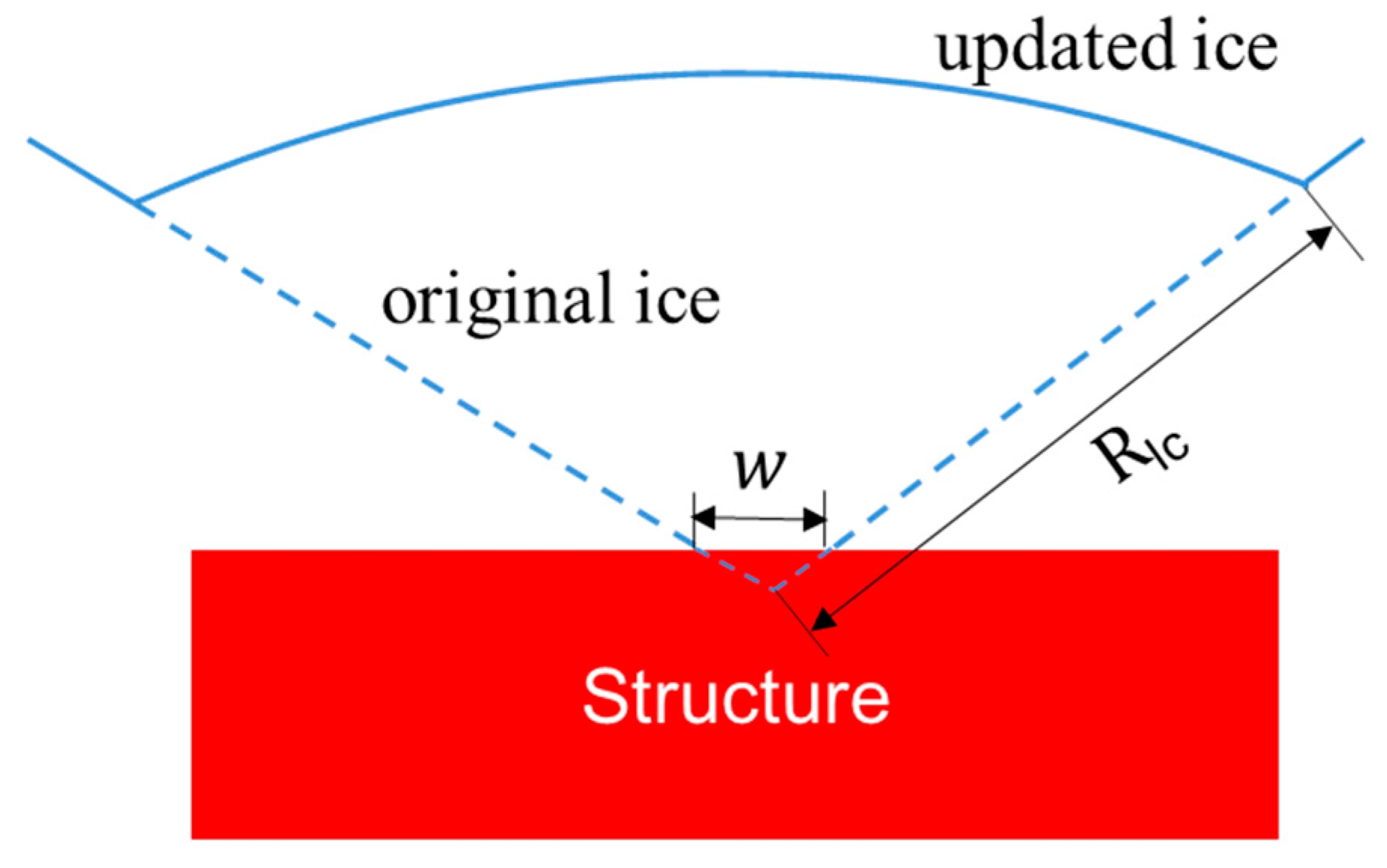
Figure 8. The initial ice boundary is a straight line that is very close to the structure. The right figure presents the ice boundary at the end of the simulation for test 105. It can be seen that the ice does not fail to crush perfectly.
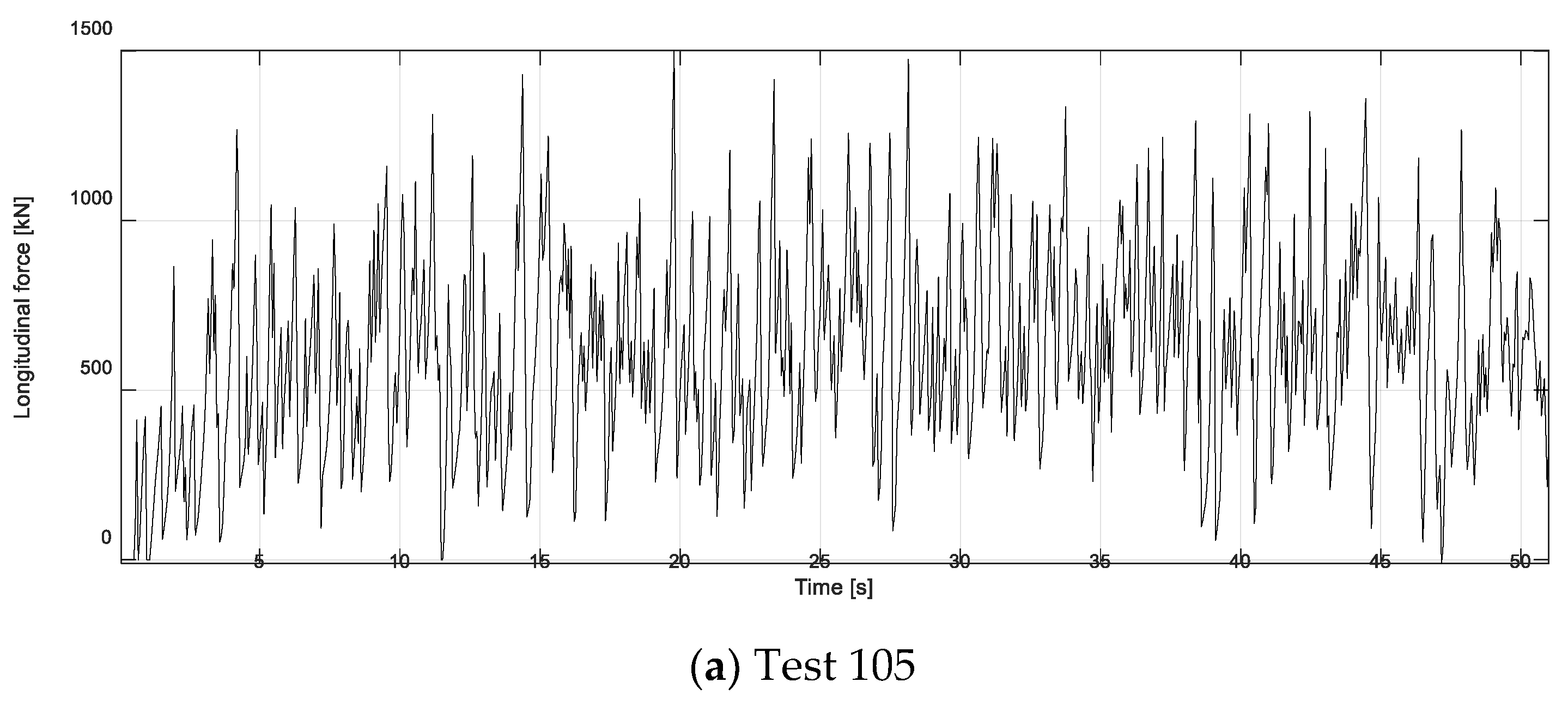
The ice force in a longitudinal direction is dominant to forces in other directions. Therefore, the longitudinal force is analyzed in this paper. The time series of the crushing force from the simulation of test 105 is given in
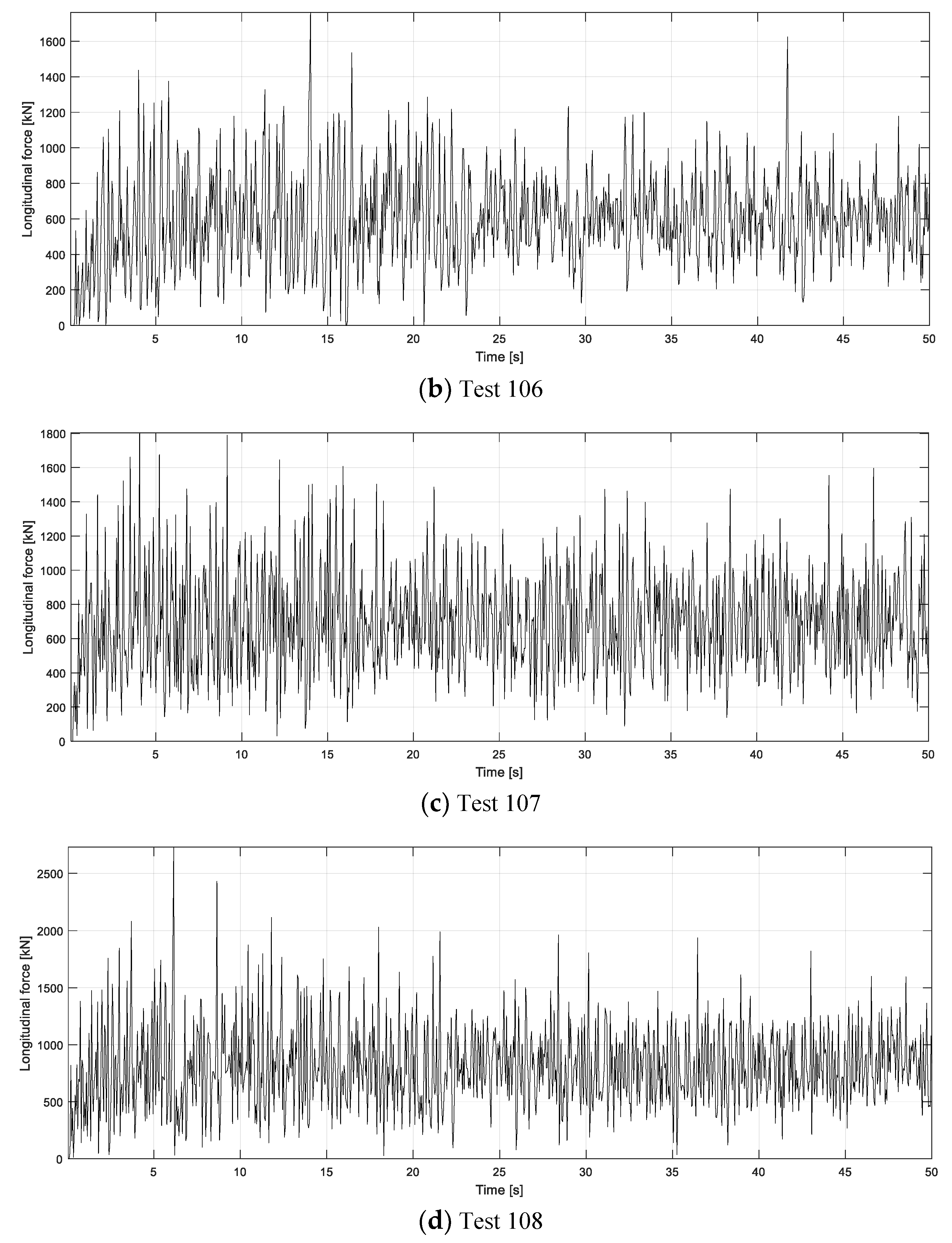
Figure 9a. It is found that ice force changes rapidly and fluctuates around the mean value. By setting up different ice drifting speeds, the other tests (106–108) are performed. The corresponding time series of the ice forces are presented in
Figure 9. The maximum ice forces derived from numerical simulation are tabulated in
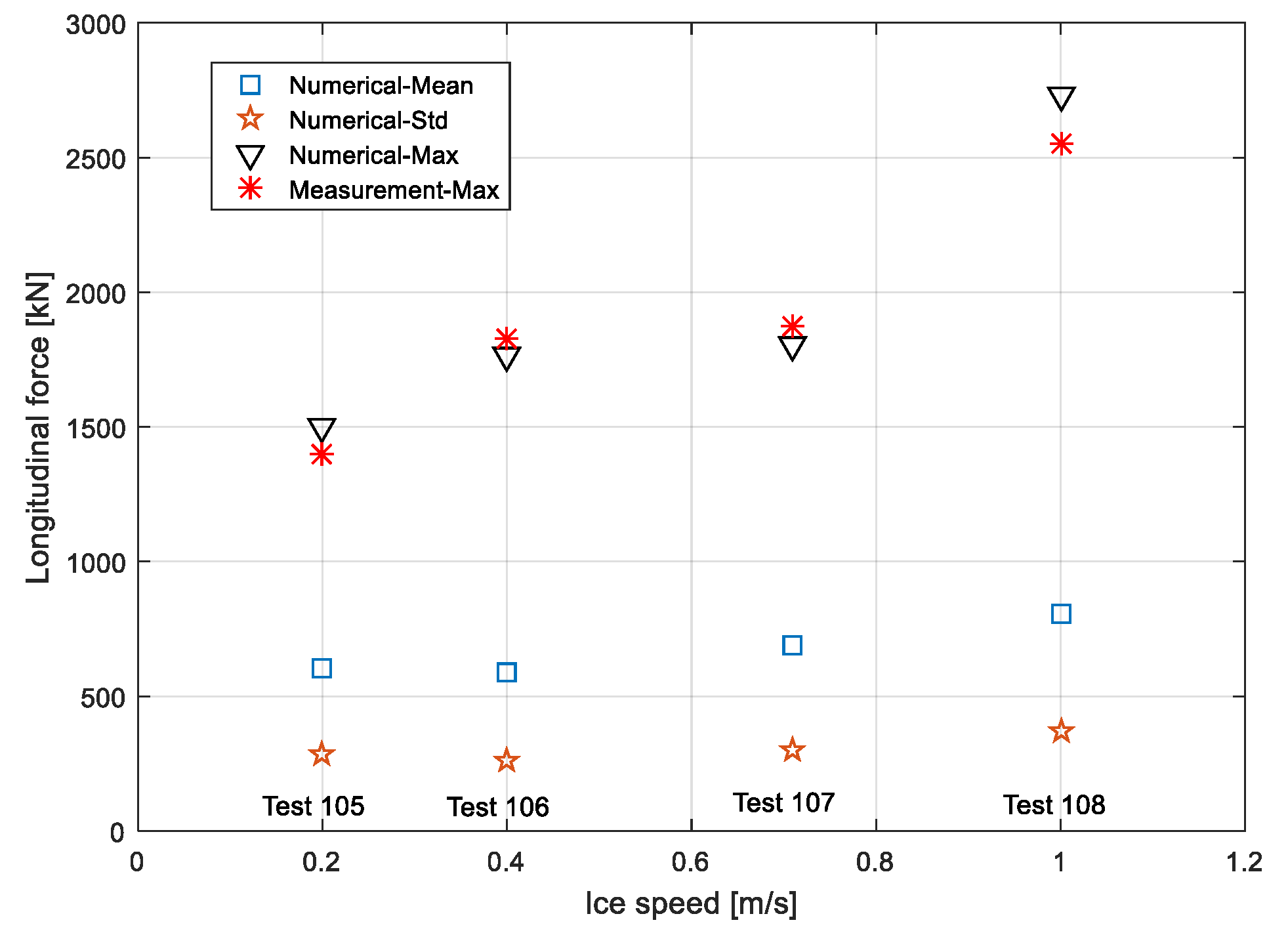
Table 2, where the measured data are also included as a comparison. The results show that the difference between the simulated and measured data ranges from 3.6% to 7.4%. The simulation results fit well with model’s test data. Both maximum data, average, and standard deviation of simulated force are also presented in
Figure 10 versus the ice drifting speed. The average and standard deviation of the force tend to increase when the ice drifting speed rises, but not linearly.
As presented in
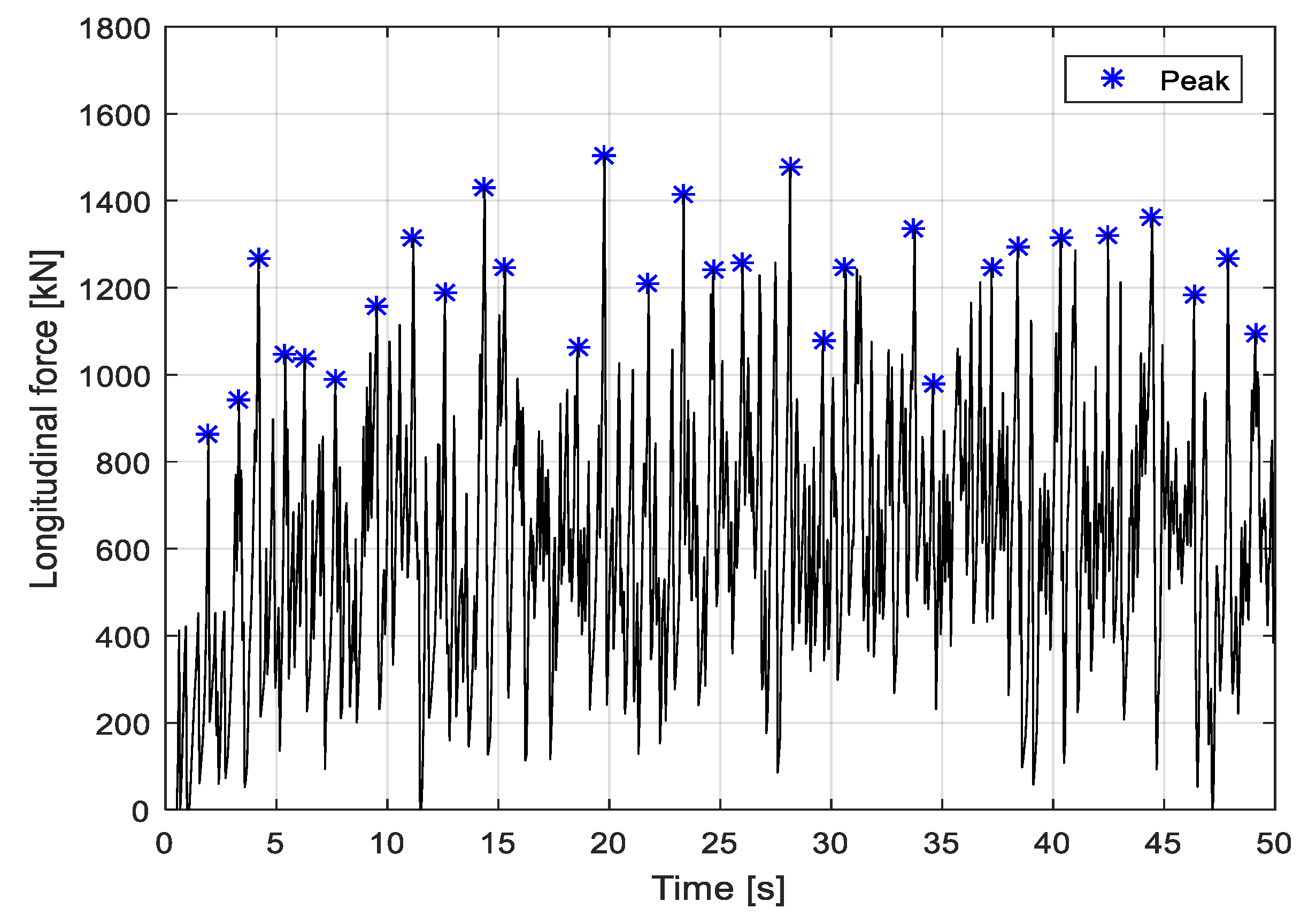
Figure 9, the time history of the simulated force for tests 105–108 show a strong non-linearity. This force is subjected to a rapid change and vibrates with many peaks corresponding to individual continuous icebreaking events as the ship advances. These peaks can be calculated and extracted from the time series of the ice force. The peaks for test 105 are presented in
Figure 11.
Then, the peaks derived in the time history of test 105 were collected. These peaks were then fitted based on the Weibull probabilistic model. The mathematical cumulative distribution function is shown as
where
k denotes the shape factor and λ denotes the scale factor.
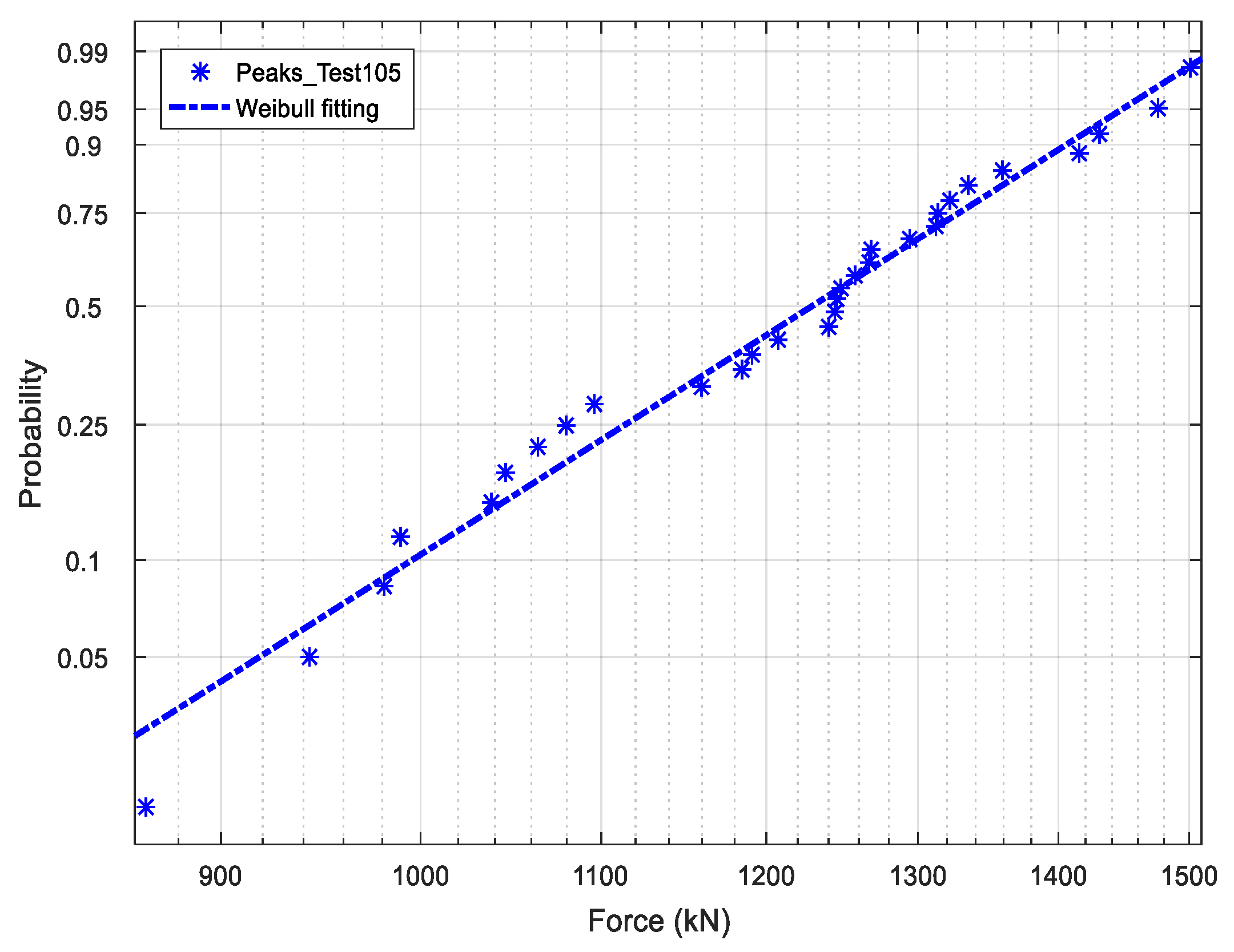
The fitting results for the simulated peaks are shown in
Figure 12. It is clear that the Weibull distribution is reasonable for both numerical simulation and model test data. Based on the simulation, the shape factor calculated is 6.97, and the scale factor is 1282 for test 105. The two factors for the other tests are also calculated. The results are shown in
Table 3.
3.2. Validation with Model Test II
Wu et al. (2018) carried out model tests for the foundations of 3 MW and 4 MW monopile wind turbines in the ice Basin of Tianjin University [
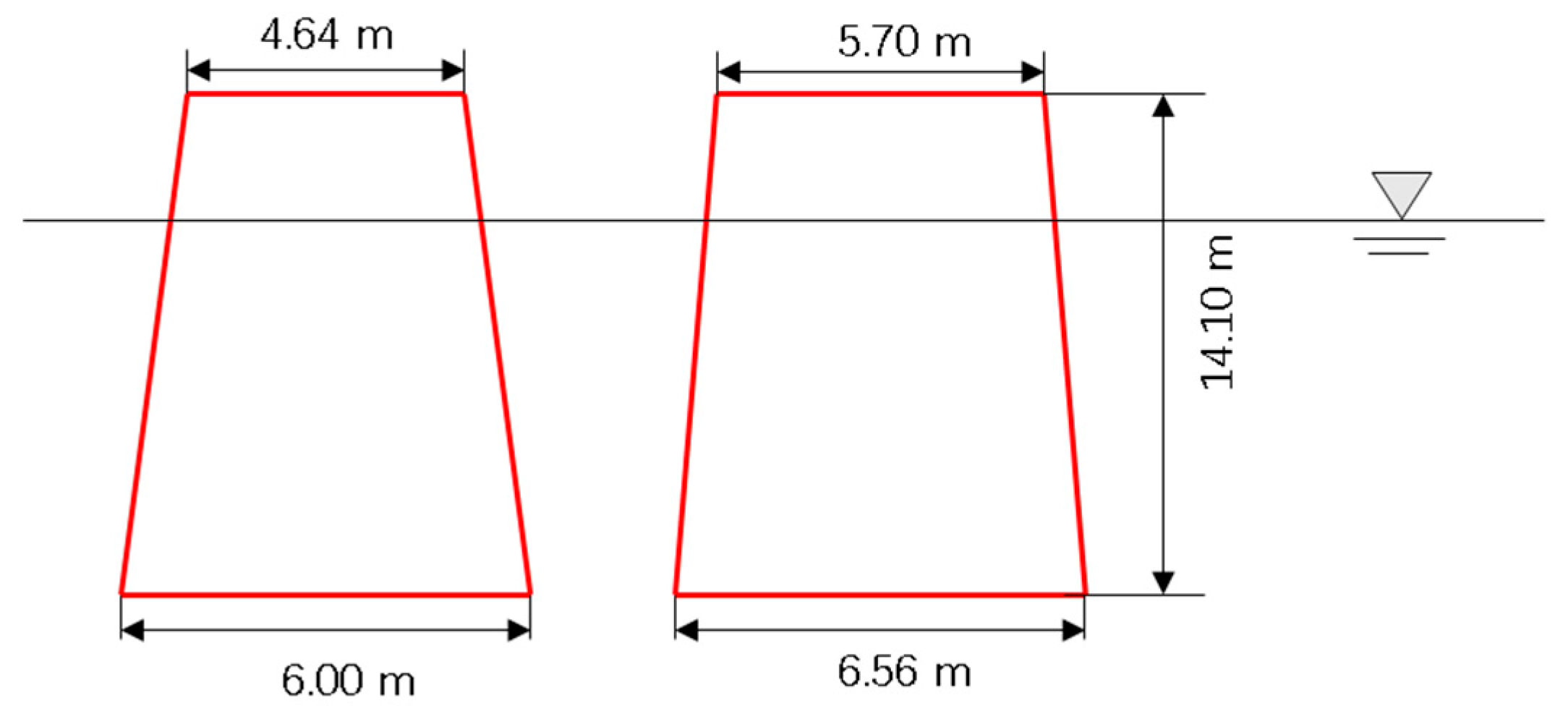
30]. The scale was set as 1:20. The ice tank was 40.0 m long, 6.0 m wide, and 1.8 m in depth. It was able to make an ice sheet with a thickness ranging from 1.0 to 30 cm. The foundations of the wind turbine towers were cone structures. The dimensions of the two icebreaking cones are shown in
Table 4. The sketch of two structure models is shown in
Figure 13. The model test to measure ice load on 3 MW structure is shown in
Figure 14. A force transducer was installed to measure ice force. The signals were recorded at a sampling frequency of 100 Hz in the model test.
The input of the numerical simulation is set as the same as that of the model tests. The target ice thickness is 0.4 m. The bending and crushing strength are expected to be 600 kPa and 2060 kPa, respectively. The ice drift velocity varies from 0.05 to 1.2 m/s in full scale. The specific test matrix with measured ice properties is presented in
Table 5. There is no information for the frictional coefficient of the ice-structure model [
30]. The friction is set as 0.1 in the following simulation.
Different failure modes were identified from the ice experiments. At a low speed, the level ice would crush against the cone and then fail in both the local and global buckling modes. The local buckling was more dominant than global bulking. An abnormally low ice load often occurred after the global buckling failure because large pieces of ice were fragmented from an intact ice sheet and there was almost no contact between the intact ice and the cone. This phenomenon is different for tests with a high speed. The global buckling event became less important as the speed increased. Ice would be pulverized into small rubble and fail in the buckling at some local zones.
Figure 15 gives a snapshot from the model test 306, which shows a non-simultaneous ice crushing scenario.
All tests shown in
Table 5 are simulated with ice speeds ranging from 0.05 to 1.2 m/s. Herein, the time evolution of the measured ice loads from four tests was selected and used for comparison due to non-simultaneous crushing failures at the contact area.
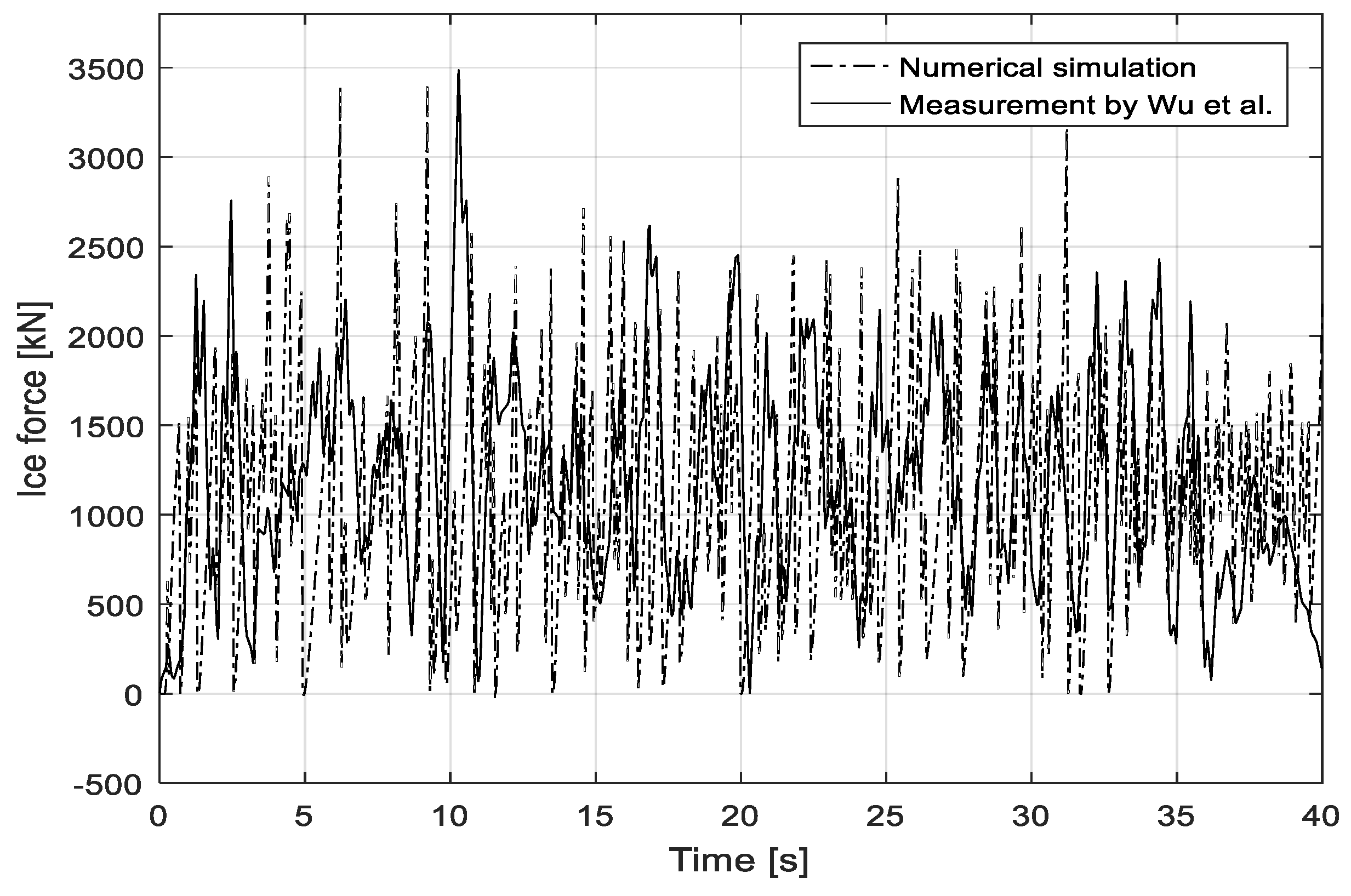
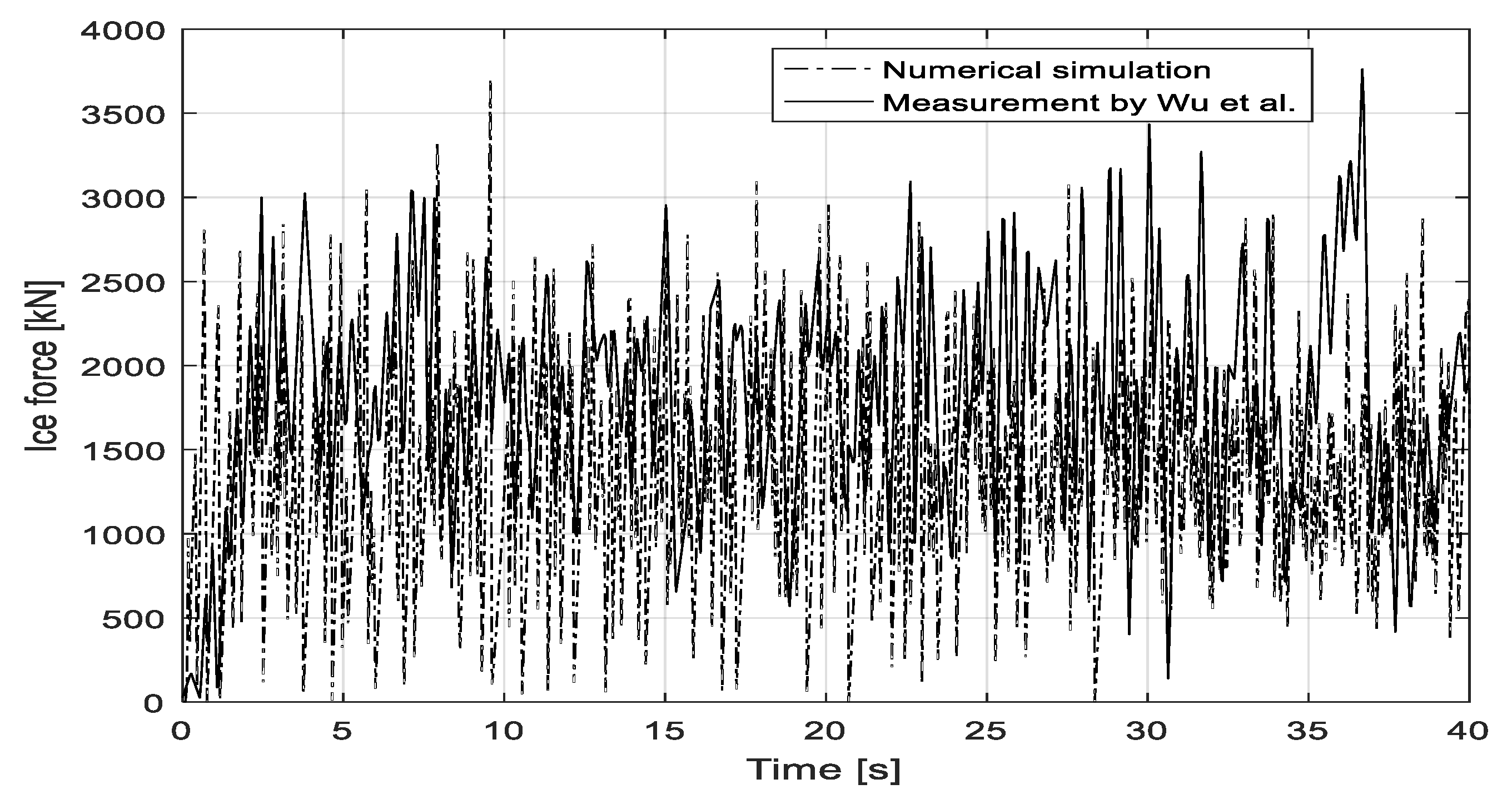
Figure 16 gives the simulated results of test 304 compared to those measured in the time domain where the drift speed is 0.6 m/s at full scale for the 3MW wind turbine’s tower. The simulation lasts 40 seconds, which is the same as the model test. The ice conditions are set as presented in
Table 5. In general, both the measured and simulated ice force show strong nonlinearity and vibration. Clearly, the two main phases, including loading and unloading, can be found from a time series of ice forces. The minimum ice force can drop to approximately zero, and the forces are cyclic with different peaks. By increasing the ice drift speed to 1.2 m/s, the time history of the simulated ice load from test 306 are shown compared to that measured in
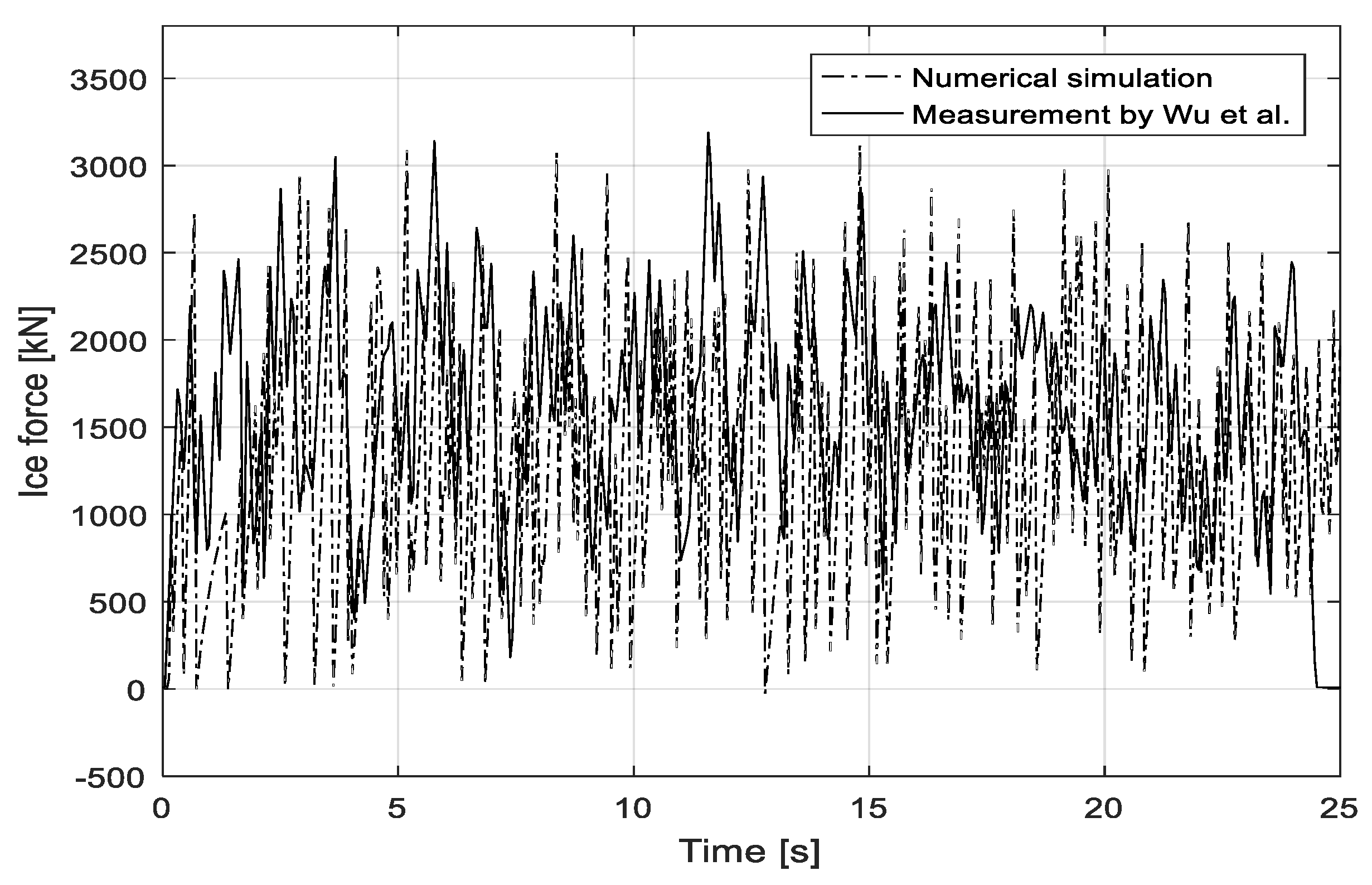
Figure 17. Similar ice force characteristics can be derived according to test 304.
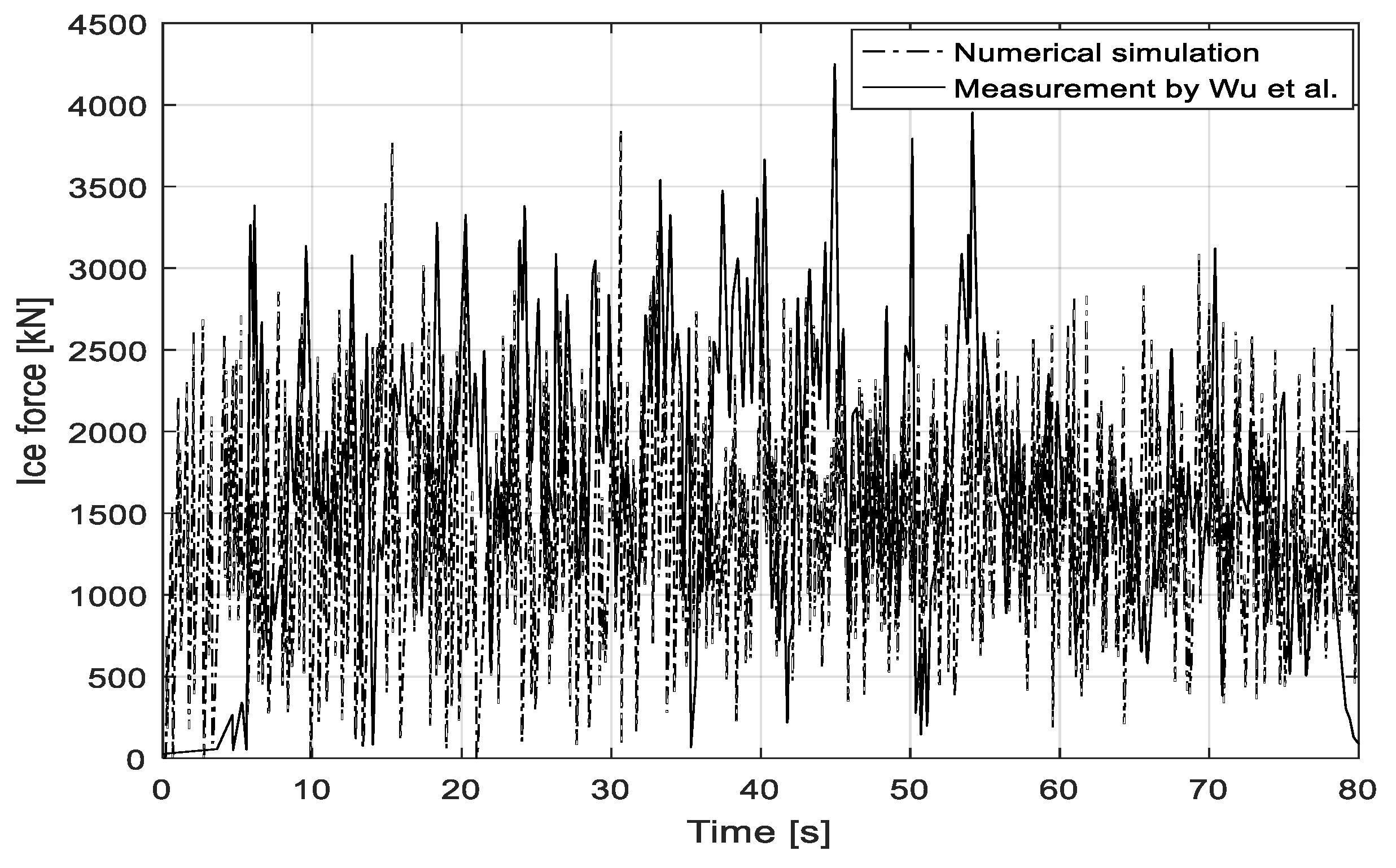
Using the structural model of a 4 MW wind turbine foundation, we continued to study ice forces for tests 404 and 406, where both the measured and simulated results are presented. The time history of ice loads for both tests are shown in
Figure 18 and
Figure 19, respectively. The difference between tests 304 and 404 or tests 306 and 406 lies in the structure. When comparing the maximum ice forces for test 304 and test 404 or test 306 and 406, the 4 MW wind turbine foundation is subjected to larger ice loads than the 3 MW wind turbine. This is because the diameter of the 4 MW wind turbine monopile at the mean waterline and slope is relatively large. The discrepancy between the measured and simulated ice forces for the four tests are tabulated in
Table 6. The statistics regarding the mean, standard deviation, and maximum values are presented for comparison. To sum up, the simulated mean force is underestimated, and the maximum difference is 20.5%. The standard deviation shows a difference of 1.7–28.2%. The error for the maximum value ranges from 1.6% to 9.4%.
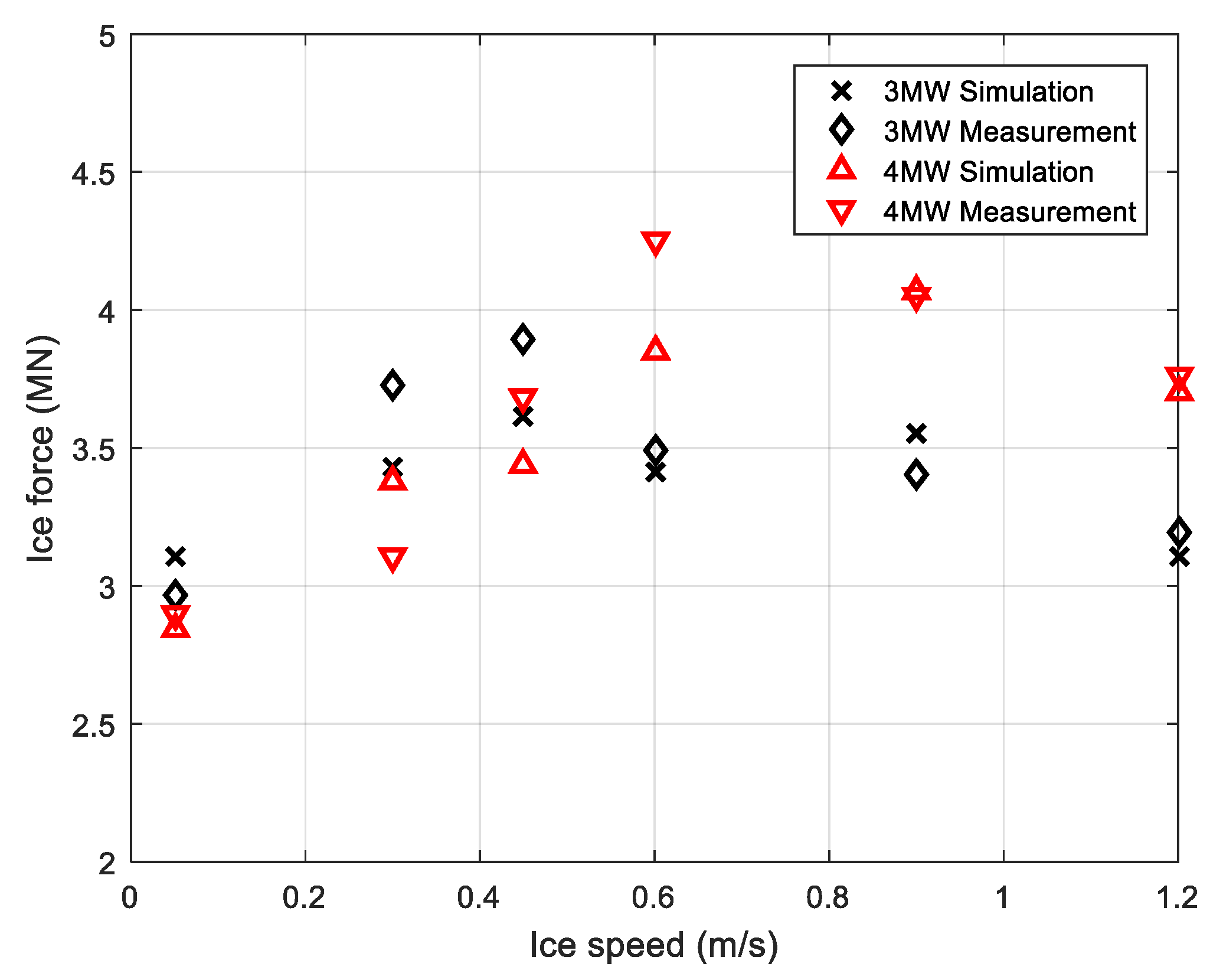
The other tests in
Table 5 are also simulated, and the corresponding maximum forces are presented in
Table 7. Due to the lack of a time series for the model test data, only the maximum ice forces from the model test data are given for comparison. These forces range from 2.97 to 3.89 MN for a 3 MW structure model and 2.90 to 4.05 MN for a 4 MW structure model. Generally speaking, the calculated results fit relatively well with the measured results. This result shows that errors are relatively small, and the maximum error is less than 9%. The largest difference is 8.68% and the smallest is 0.49%. The maximum ice force derived from both the numerical simulation and the model tests are compared in
Figure 20. The black solid line denotes the model test results while the dotted line denotes the numerical results. It is noted that the trends of the two lines agree well with each other. However, the peak of the maximum ice load from the simulation is smaller than that from the model test.
Moreover, the peaks of the time series of measured, and simulated ice forces are collected for tests 304, 306, 404, and 406. Weibull distributions are applied to fit these peaks approximately. The shape and scale factors for tests 304, 306, 404, and 406 are estimated from Weibull fitting. The standard error between the original peak values and the fitted data are also included in
Table 8. It can be seen that the errors for the shape factor are more than 10% and less than 15.7%. The scale factor error ranges from 1.8% to 4.4%.
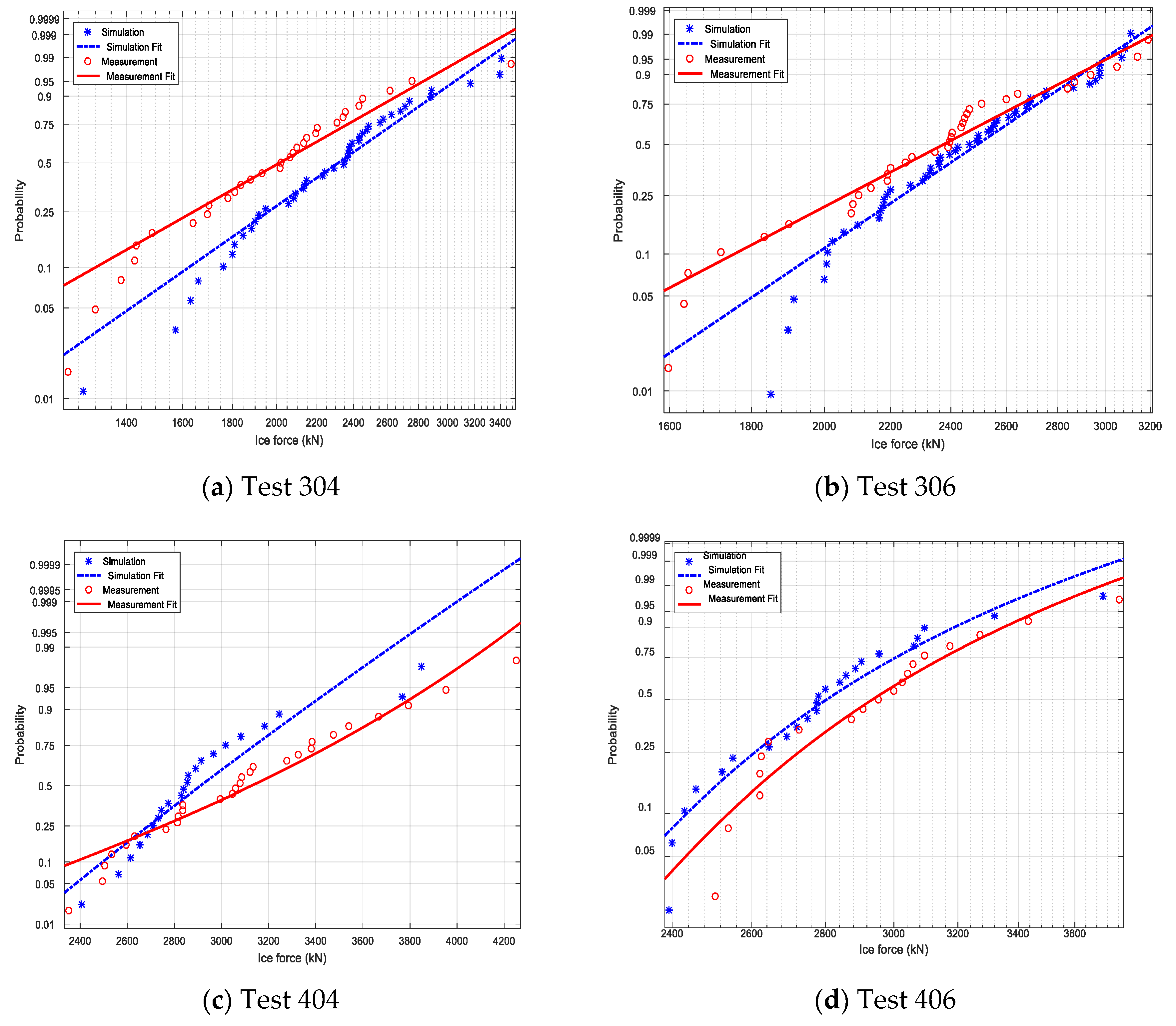
Both the measured and simulated results are plotted in
Figure 21. The red solid line denotes the measured results while the blue dotted line denotes the numerical results. For tests 304 and 306 (
Figure 21a,b), the simulation results are lower than the measurements, and the two lines tend to converge. For test 404 in
Figure 21c, the simulation results are larger than the measurement. They intersect at a relatively low force level and tend to deviate from each other. The scale factor is around 7% higher for the measured results than the simulated ones. For test 406 in
Figure 21d, the simulation data are slightly higher than the measured data. It should be noted that both the simulation and measured data fit well with the Weibull distribution for all four tests.
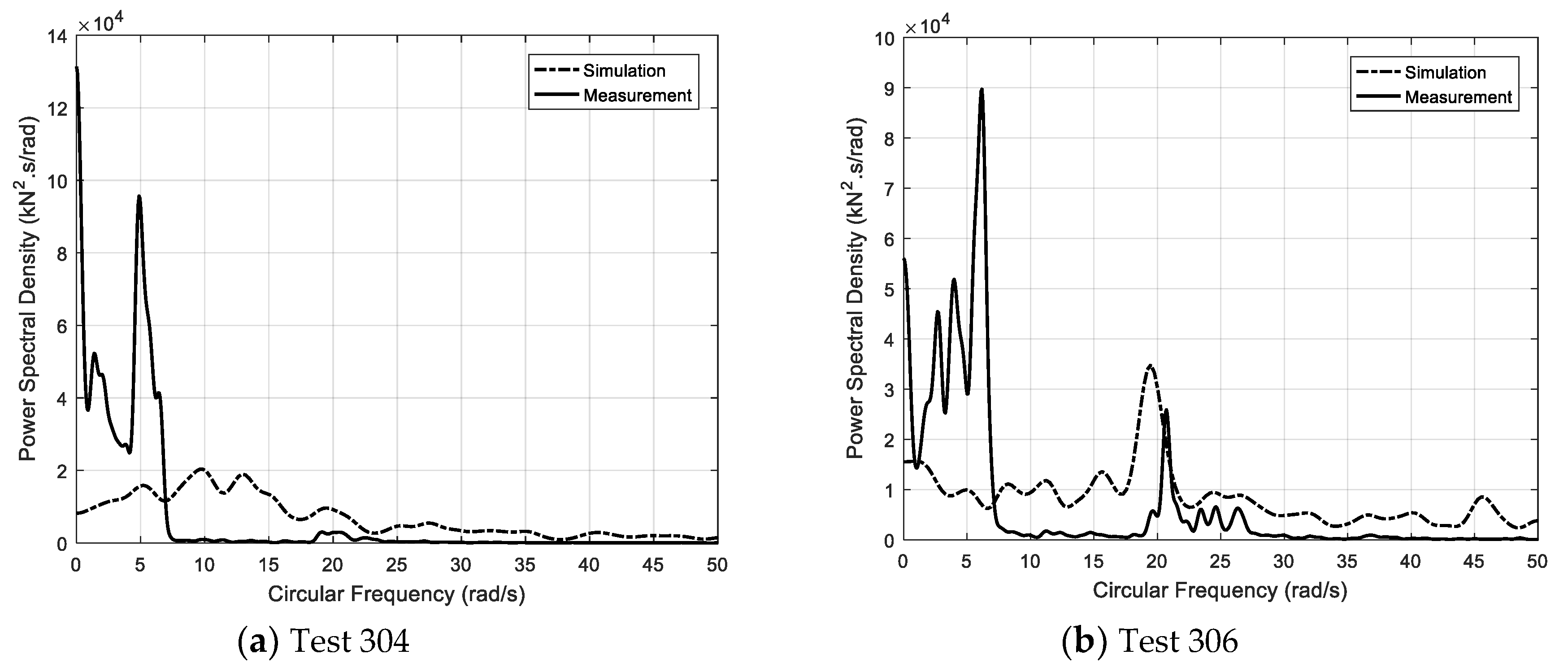
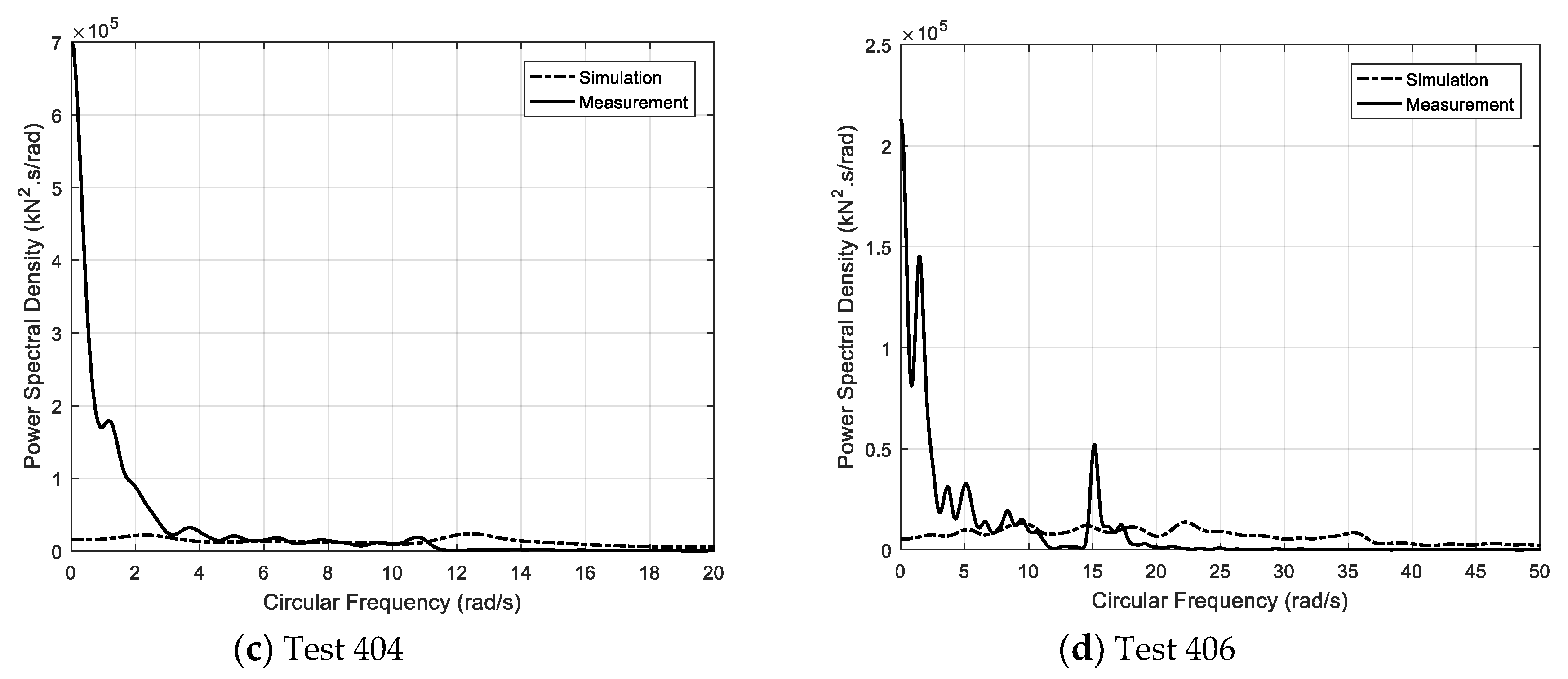
The power spectra of the simulated and measured ice loads (
Figure 14,
Figure 15,
Figure 16 and
Figure 17) are shown in
Figure 22. The simulated force spectrum is broad-banded comparison to the measured force spectrum. The power spectral density of the simulated force at a low frequency is much lower than that of the measured force. When looking at the spectrum for test 304 in
Figure 22a, it is clear that the energy is concentrated in a frequency range of less than 7 rad/s, and the dominant area is around 5.0 rad/s. Moreover, there exists a small amount of energy at around 20 rad/s. As the ice speed increases to 1.2 m/s, the main frequency increases slightly to 5.8 rad/s in
Figure 22b. In addition, the vibration is clearly triggered at a higher frequency of 21 rad/s. This phenomenon could be also found by studying the measured data for tests 404 and 406 in
Figure 22c,d. The main energy tends to shift from a low frequency range to a high range.