Power Beacon-Assisted Energy Harvesting in a Half-Duplex Communication Network under Co-Channel Interference over a Rayleigh Fading Environment: Energy Efficiency and Outage Probability Analysis
Abstract
1. Introduction
- The system model of a PB EH in an HD communication network under co-channel interference over a Rayleigh fading environment.
- The exact and asymptotic form expressions of the OP were derived.
- The EE of the model system and the influence of the primary system parameters on the performance of the proposed system were investigated.
- A Monte Carlo simulation was conducted to verify the analysis results using the primary system parameters.
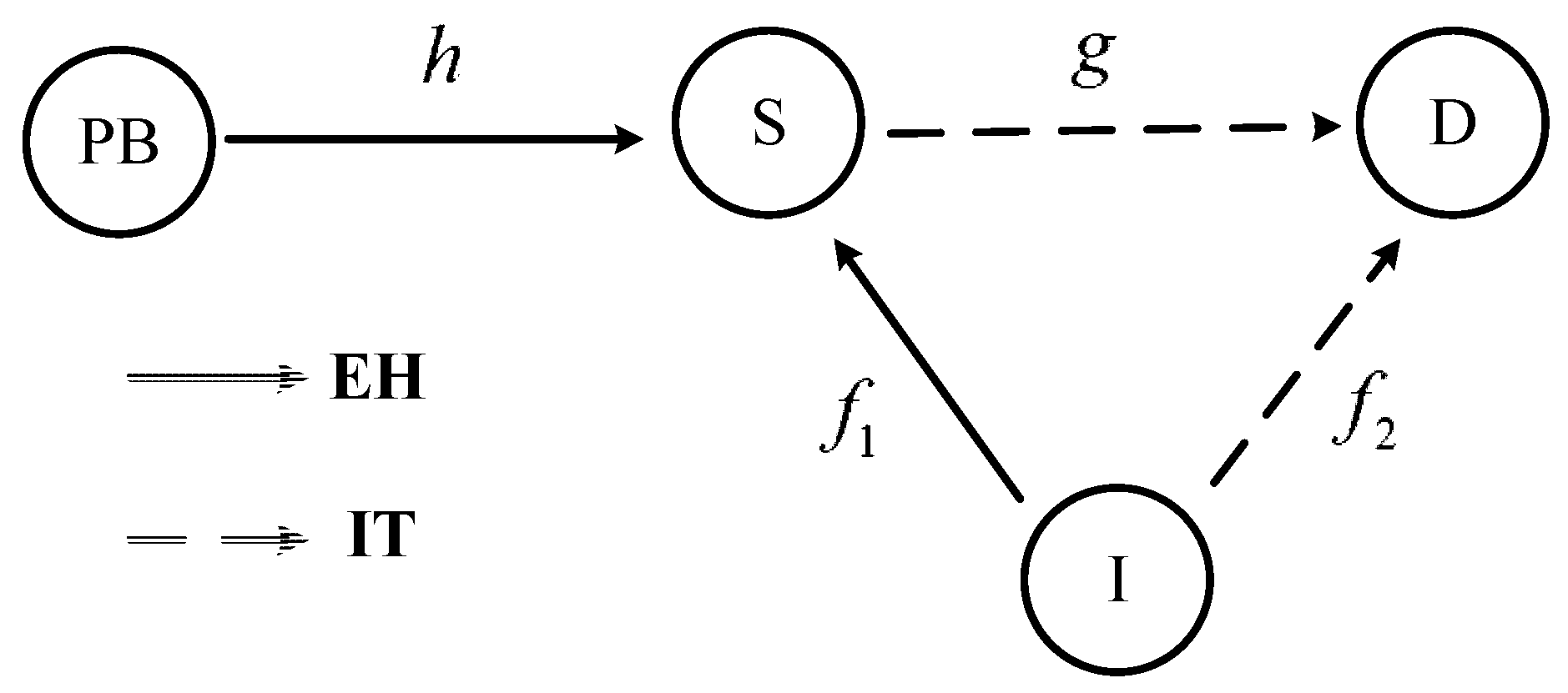
2. System Model
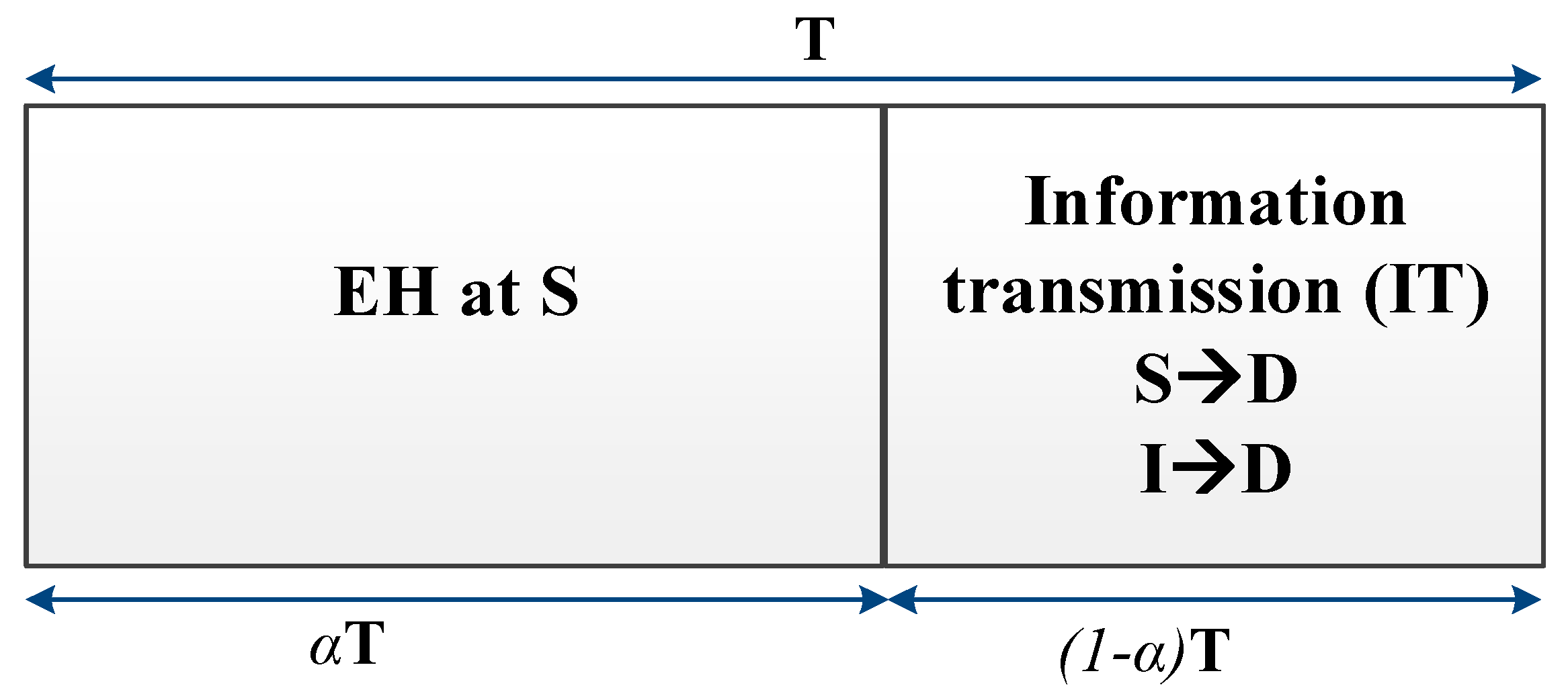
2.1. Energy Harvesting
2.2. Information Transmission
3. The System Performance
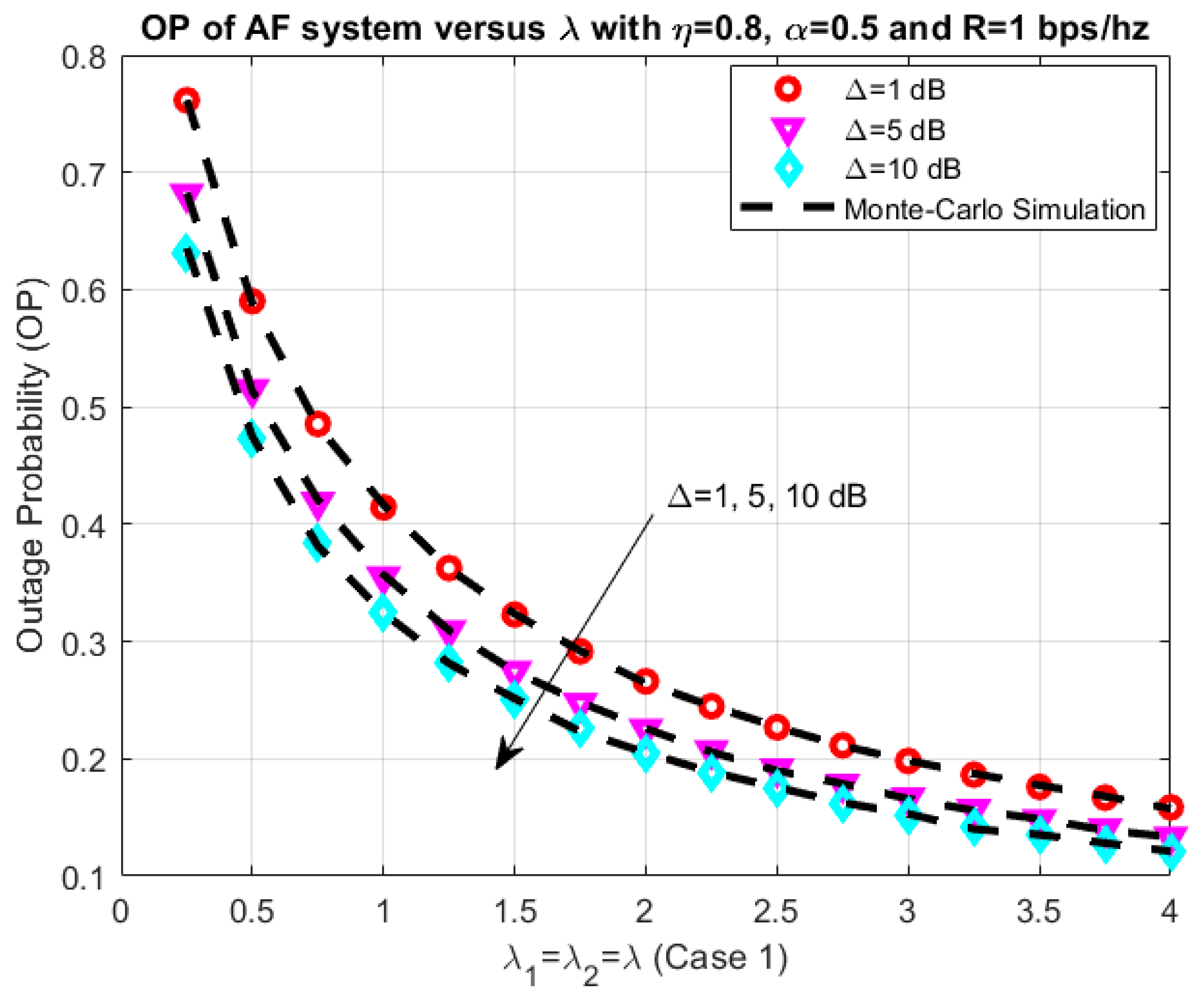
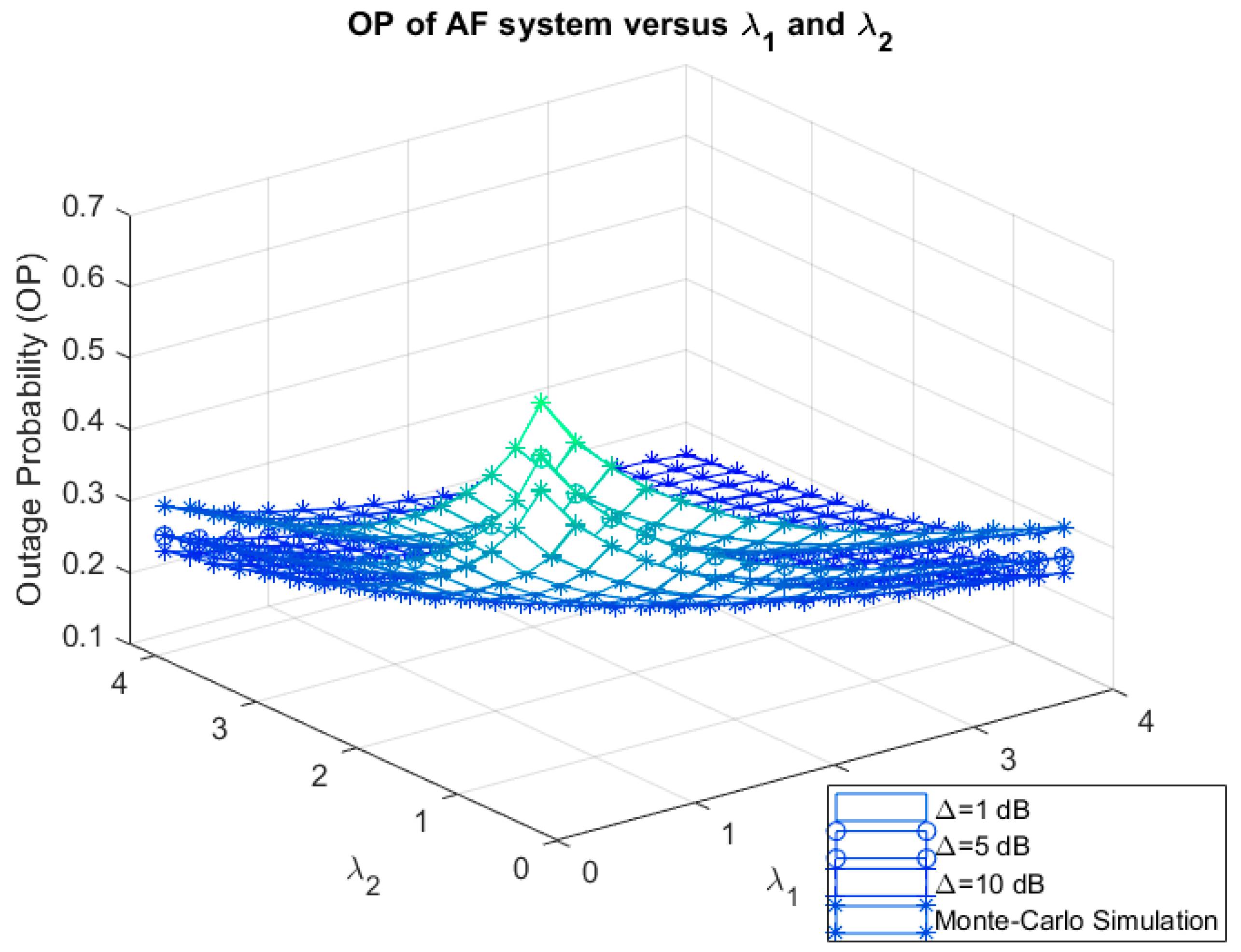
3.1. Outage Probability
3.1.1. Exact Analysis
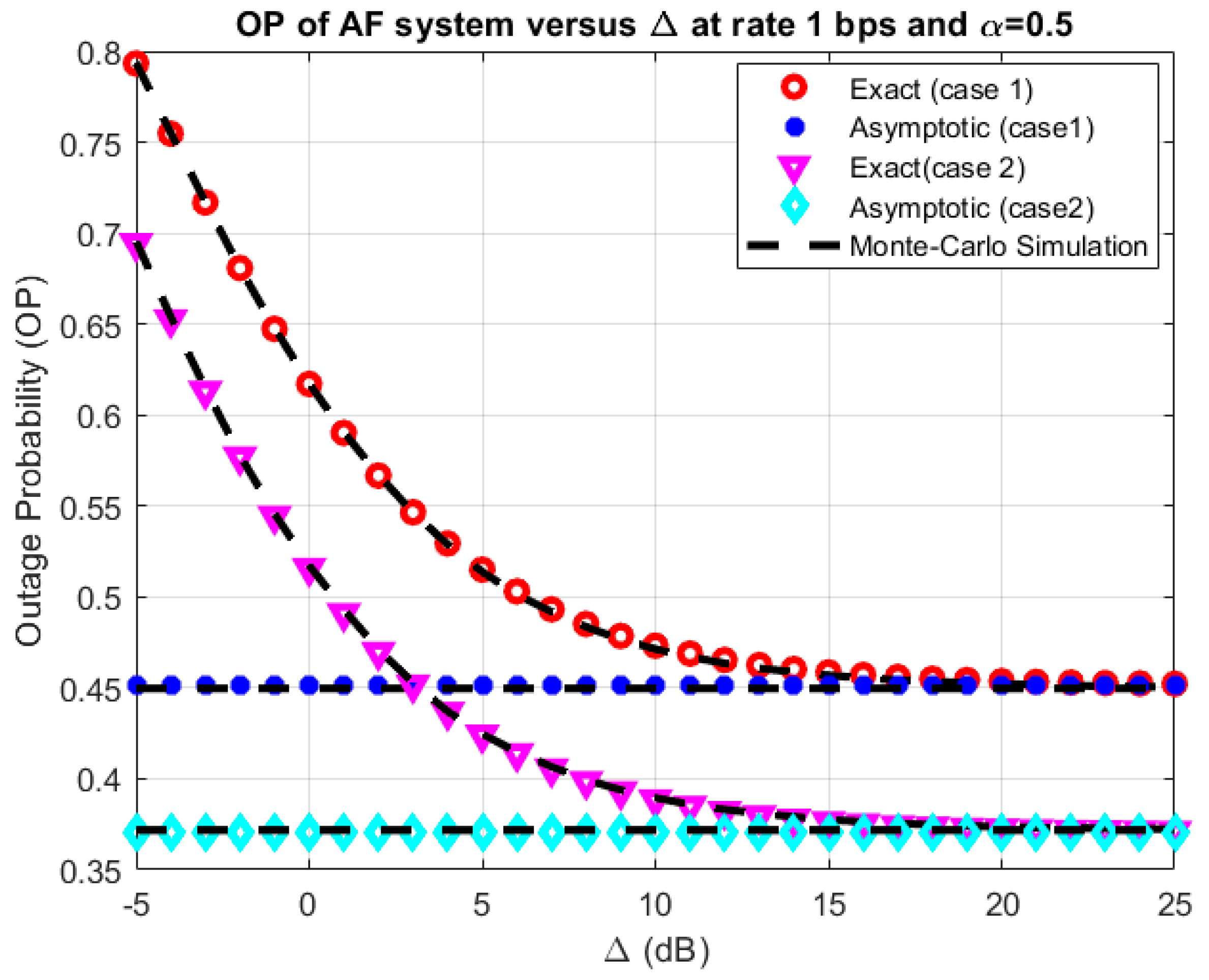
3.1.2. Asymptotic Analysis
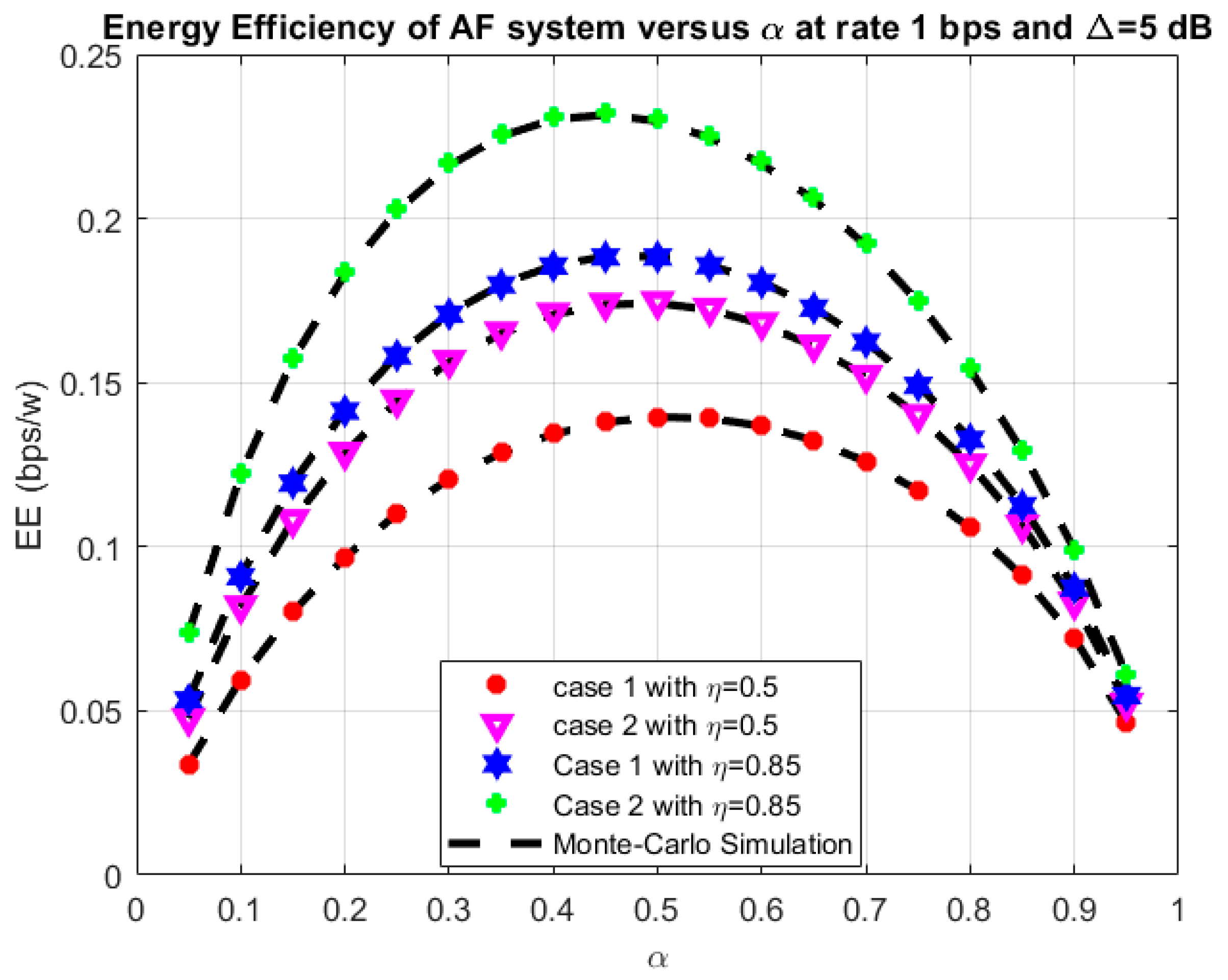
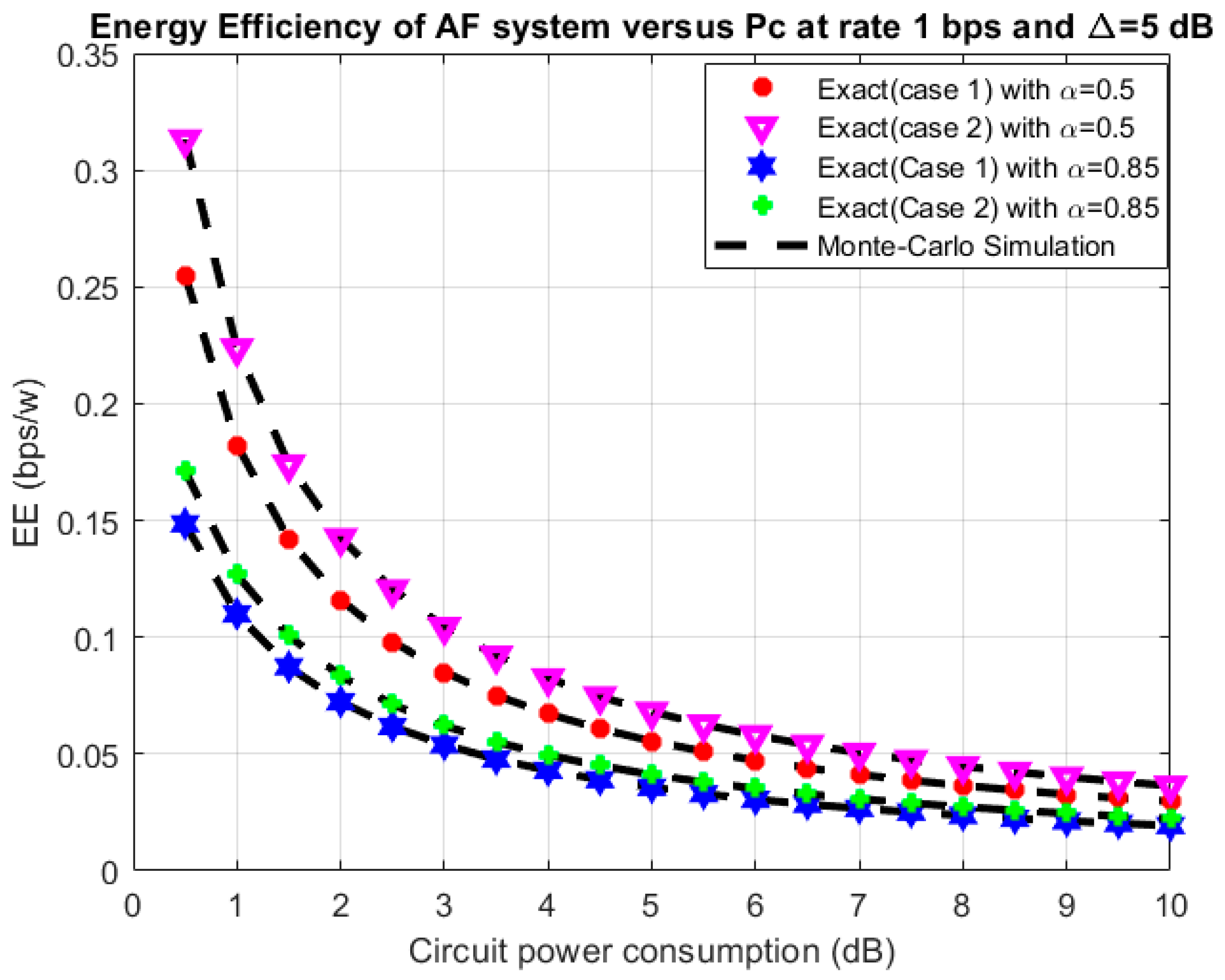
3.2. Energy Efficiency Analysis
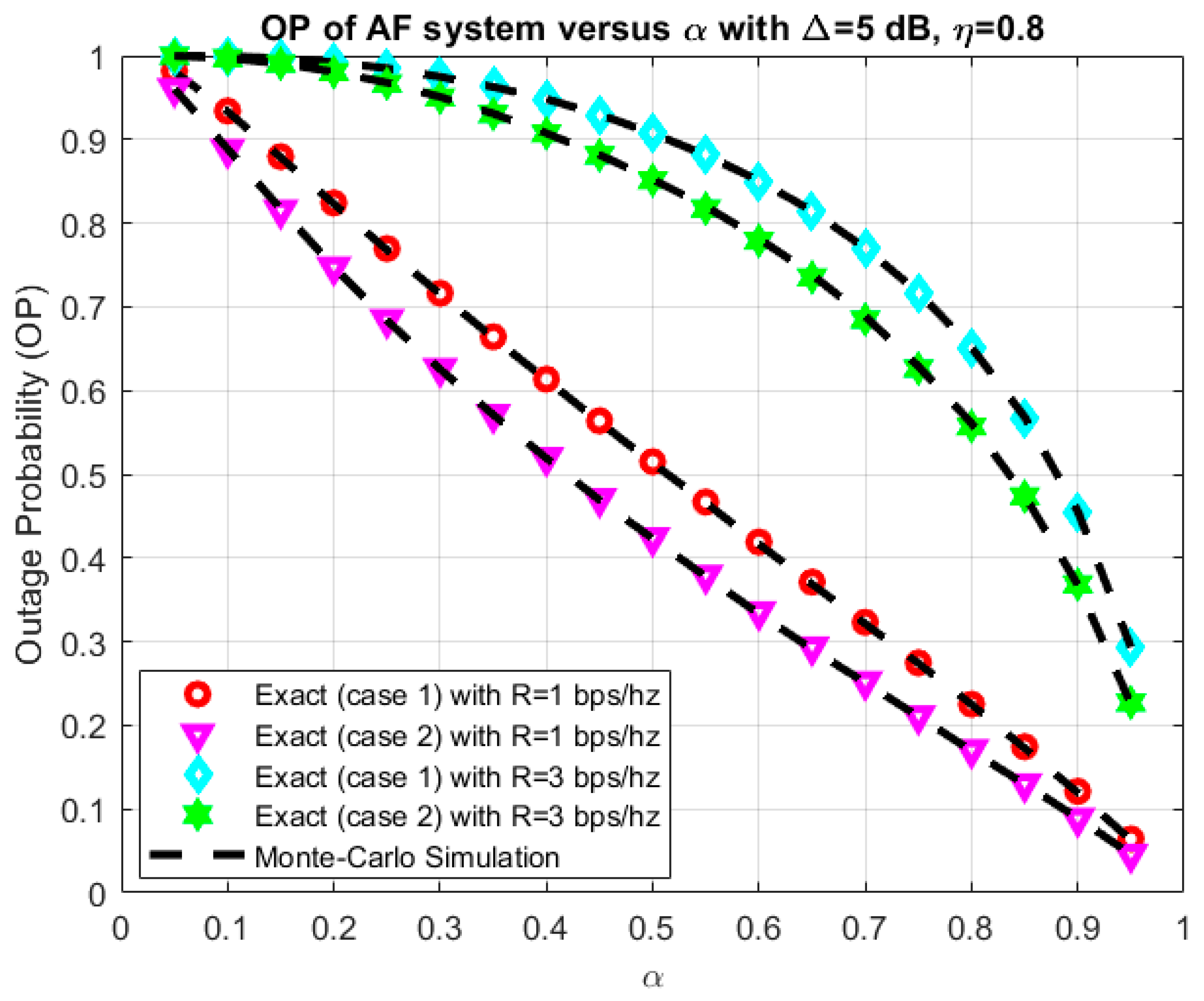
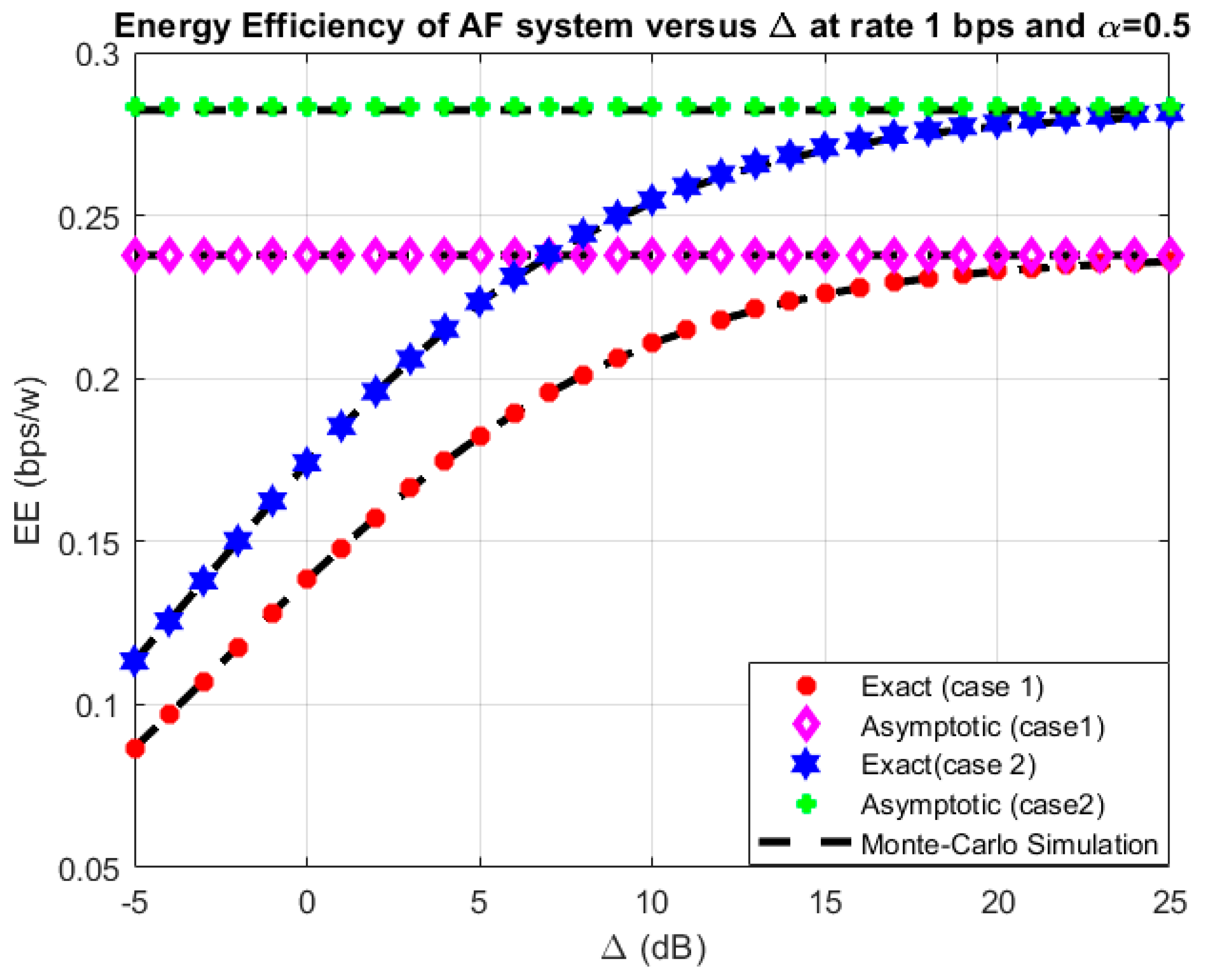
4. Results and Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wong, K.D. Fundamentals of Wireless Communication Engineering Technologies; John Wiley and Sons: Hoboken, NJ, USA, 2011. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Wireless powered communication: Opportunities and challenges. IEEE Commun. Mag. 2015, 53, 117–125. [Google Scholar] [CrossRef]
- Niyato, D.; Kim, D.I.; Maso, M.; Han, Z. Wireless Powered Communication Networks: Research Directions and Technological Approaches. IEEE Wirel. Commun 2017, 24, 2–11. [Google Scholar] [CrossRef]
- Yu, H.; Lee, H.; Jeon, H. What is 5G? Emerging 5G Mobile Services and Network Requirements. Sustainability 2017, 9, 1848. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Nguyen, T.-L.; Ha, D.-H.; Voznak, M. Performance Analysis of a User Selection Protocol in Cooperative Networks with Power Splitting Protocol-Based Energy Harvesting Over Nakagami-m/Rayleigh Channels. Electronics 2019, 8, 448. [Google Scholar] [CrossRef]
- Bi, S.; Ho, C.K.; Zhang, R. Recent Advances in Joint Wireless Energy and Information Transfer. In Proceedings of the 2014 IEEE Information Theory Workshop (ITW2014), Hobart, TAS, Australia, 2–5 November 2014. [Google Scholar] [CrossRef]
- Kawabata, H.; Ishibashi, K. RF Energy Powered Feedback-aided Cooperation. In Proceedings of the 2014 IEEE 25th Annual International Symposium on Personal, Indoor, and Mobile Radio Communication (PIMRC), Washington, DC, USA, 2–5 September 2014. [Google Scholar] [CrossRef]
- Huang, K.; Lau, V.K.N. Enabling Wireless Power Transfer in Cellular Networks: Architecture, Modeling and Deployment. IEEE Trans. Wirel. Commun. 2014, 13, 902–912. [Google Scholar] [CrossRef]
- Medepally, B.; Mehta, N.B. Voluntary Energy Harvesting Relays and Selection in Cooperative Wireless Networks. IEEE Trans. Wirel. Commun. 2010, 9, 3543–3553. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, R.; Ho, C.K. Wireless Information and Power Transfer: Architecture Design and Rate-energy. IEEE Trans. Commun. (GLOBECOM) 2013, 61, 4754–4761. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, R.; Chua, K.C. Wireless Information and Power Transfer: A Dynamic Power Splitting Approach. IEEE Trans. Commun. 2013, 61, 3990–4001. [Google Scholar] [CrossRef]
- Nasir, A.A.; Zhou, X.; Durrani, S.; Kennedy, R.A. Relaying Protocols for Wireless Energy Harvesting and Information Processing. IEEE Trans. Wirel. Commun. 2013, 12, 3622–3636. [Google Scholar] [CrossRef]
- Peng, C.L.; Li, F.W.; Liu, H. Optimal Power Splitting in Two-Way Decode-and-Forward Relay Networks. IEEE Commun. Lett. 2017, 21, 2009–2012. [Google Scholar] [CrossRef]
- Tan, N.; Nguyen, T.H.Q.; Minh, P.; Tran, T. Miroslav Voznak. Energy Harvesting over Rician Fading Channel: A Performance Analysis for Half-Duplex Bidirectional Sensor Networks under Hardware Impairments. Sensors 2018, 18, 1781. [Google Scholar]
- Do, D.T.; Van Nguyen, M.S.; Hoang, T.A.; Voznak, M. NOMA-Assisted Multiple Access Scheme for IoT Deployment: Relay Selection Model and Secrecy Performance Improvement. Sensors 2019, 19, 736. [Google Scholar] [CrossRef]
- Do, D.T.; Le, C.B. Application of NOMA in Wireless System with Wireless Power Transfer Scheme: Outage and Ergodic Capacity Performance Analysis. Sensors 2018, 18, 3501. [Google Scholar] [CrossRef]
- Zhou, X.; Li, Q. Energy Efficiency for SWIPT in MIMO Two-Way Amplify-and-Forward Relay Networks. IEEE Trans. Veh. Technol. 2018, 67, 4910–4924. [Google Scholar] [CrossRef]
- Lu, G.; Lei, C.; Ye, Y.; Shi, L.; Wang, T. Energy Efficiency Optimization for AF Relaying with TS-SWIPT. Energies 2019, 12, 993. [Google Scholar] [CrossRef]
- Nguyen, X.X.; Do, D. Optimal power allocation and throughput performance of full-duplex DF relaying networks with wireless power transfer-aware channel. EURASIP J. Wirel. Commun. Netw. 2017, 152. [Google Scholar] [CrossRef]
- Masood, Z.; Jung, S.P.; Choi, Y. Energy-Efficiency Performance Analysis and Maximization Using Wireless Energy Harvesting in Wireless Sensor Networks. Energies 2018, 10, 2917. [Google Scholar] [CrossRef]
- Ng, D.W.K.; Lo, E.S.; Schober, R. Wireless Information and Power Transfer: Energy Efficiency Optimization in OFDMA Systems. IEEE Trans. Wirel. Commun. 2013, 12, 6352–6370. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Nguyen, T.-L.; Ha, D.-H.; Voznak, M. Multisource Power Splitting Energy Harvesting Relaying Network in Half-Duplex System over Block Rayleigh Fading Channel: System Performance Analysis. Electronics 2019, 8, 67. [Google Scholar] [CrossRef]
- Zhang, J.; Haardt, M. Energy Efficient Two-Way Non-Regenerative Relaying for Relays with Multiple Antennas. IEEE Signal Process. Lett. 2015, 22, 1079–1083. [Google Scholar] [CrossRef]
- Zappone, A.; Bjornson, E.; Sanguinetti, L.; Jorswieck, E. Globally Optimal Energy-Efficient Power Control and Receiver Design in Wireless Networks. IEEE Trans. Signal Process. 2017, 65, 2844–2859. [Google Scholar] [CrossRef]
- Huang, Y.; Liu, M.; Liu, Y. Energy-Efficient SWIPT in IoT Distributed Antenna Systems. IEEE Internet Things J. 2018, 8, 2646–2656. [Google Scholar] [CrossRef]
- Chen, X.; Wang, X.; Chen, X. Energy-Efficient Optimization for Wireless Information and Power Transfer in Large-Scale MIMO Systems Employing Energy Beamforming. IEEE Wirel. Commun. Lett. 2013, 2, 667–670. [Google Scholar] [CrossRef]
- Guo, S.; Yang, Y.; Yu, H. Energy-Efficient Cooperative Transmission for SWIPT in Wireless Sensor Networks. In Wireless Power Transfer Algorithms, Technologies and Applications in Ad Hoc Communication Networks; Springer: Cham, Switzerland, 2016; pp. 253–281. [Google Scholar]
- Mao, S.; Leng, S.; Hu, J.; Yang, K. Energy-Efficient Resource Allocation for Cooperative Wireless Powered Cellular Networks. In Proceedings of the 2018IEEE International Conference on Communications (ICC), Kansas City, MO, USA, 20–24 May 2018. [Google Scholar]
- Zwillinger, D. Table of Integrals, Series, and Products; Elsevier Science: Amsterdam, The Netherlands, 2014. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh, T.H.Q.; Tran, P.T.; Voznak, M. Tran and Miroslav Voznak. Adaptive Energy Harvesting Relaying Protocol for Two-Way Half Duplex System Network over Rician Fading Channel. Wirel. Commun. Mob. Comput. 2018, 2018, 7693016. [Google Scholar] [CrossRef]
- Bhatnagar, M.R. On the Capacity of Decode-and-Forward Relaying over Rician Fading Channels. IEEE Commun. Lett. 2013, 17, 1100–1103. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Minh, T.H.Q.; Tran, P.T.; Voznak, M.; Duy, T.T.; Nguyen, T.-L.; Tin, P.T. Performance enhancement for energy harvesting based two-way relay protocols in wireless ad-hoc networks with partial and full relay selection methods. Ad Hoc Networks 2019, 84, 178–187. [Google Scholar] [CrossRef]
- Nguyen, T.N.; Tran, M.; Ha, D.-H.; Nguyen, T.-L.; Voznak, M. Energy harvesting based two-way full-duplex relaying network over a Rician fading environment: performance analysis. Proceedings of the Estonian Academy of Sciences 2019, 68, 111. [Google Scholar] [CrossRef]

© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Phan, V.-D.; Nguyen, T.N.; Tran, M.; Trang, T.T.; Voznak, M.; Ha, D.-H.; Nguyen, T.-L. Power Beacon-Assisted Energy Harvesting in a Half-Duplex Communication Network under Co-Channel Interference over a Rayleigh Fading Environment: Energy Efficiency and Outage Probability Analysis. Energies 2019, 12, 2579. https://doi.org/10.3390/en12132579
Phan V-D, Nguyen TN, Tran M, Trang TT, Voznak M, Ha D-H, Nguyen T-L. Power Beacon-Assisted Energy Harvesting in a Half-Duplex Communication Network under Co-Channel Interference over a Rayleigh Fading Environment: Energy Efficiency and Outage Probability Analysis. Energies. 2019; 12(13):2579. https://doi.org/10.3390/en12132579
Chicago/Turabian StylePhan, Van-Duc, Tan N. Nguyen, Minh Tran, Tran Thanh Trang, Miroslav Voznak, Duy-Hung Ha, and Thanh-Long Nguyen. 2019. "Power Beacon-Assisted Energy Harvesting in a Half-Duplex Communication Network under Co-Channel Interference over a Rayleigh Fading Environment: Energy Efficiency and Outage Probability Analysis" Energies 12, no. 13: 2579. https://doi.org/10.3390/en12132579
APA StylePhan, V.-D., Nguyen, T. N., Tran, M., Trang, T. T., Voznak, M., Ha, D.-H., & Nguyen, T.-L. (2019). Power Beacon-Assisted Energy Harvesting in a Half-Duplex Communication Network under Co-Channel Interference over a Rayleigh Fading Environment: Energy Efficiency and Outage Probability Analysis. Energies, 12(13), 2579. https://doi.org/10.3390/en12132579






