Evolutionary Multi-Objective Cost and Privacy Driven Load Morphing in Smart Electricity Grid Partition
Abstract
1. Introduction
2. Background
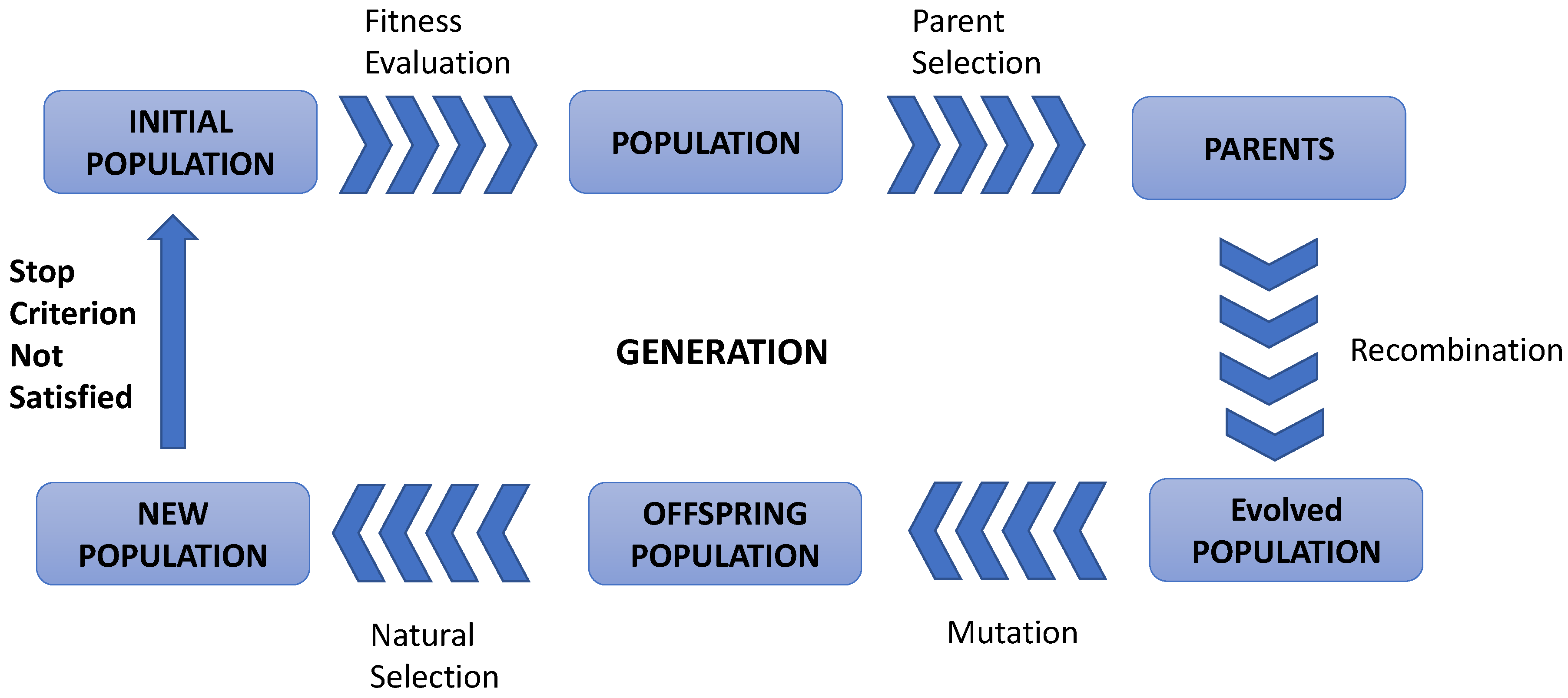
2.1. Introduction to Evolutionary Computing
- Maintenance of a set of candidate solutions (population);
- Fitness evaluation and sampling of the current population of solutions; and
- Recombination and mutation of solutions to generate new improved solutions.
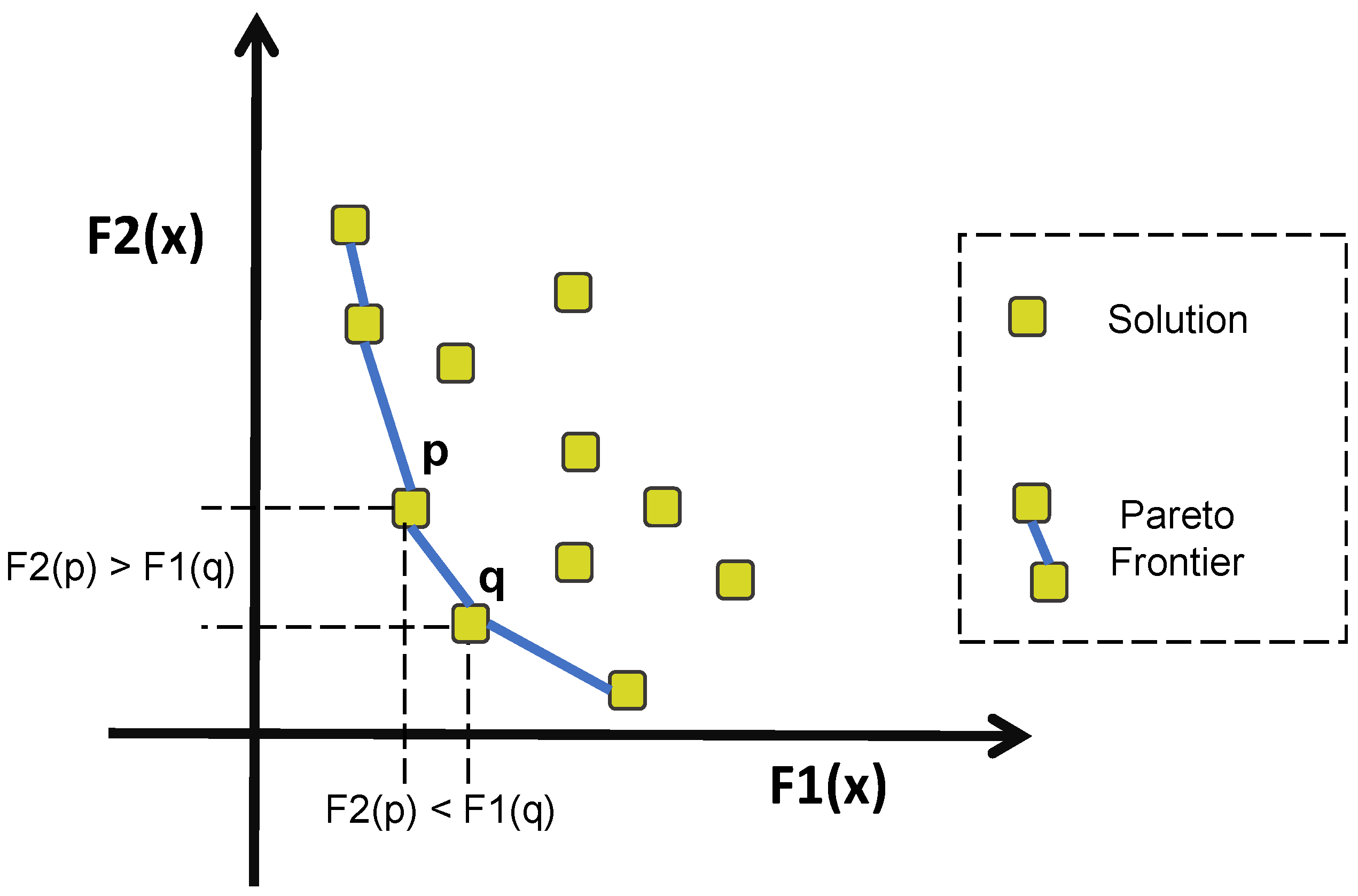
2.2. Pareto Optimality
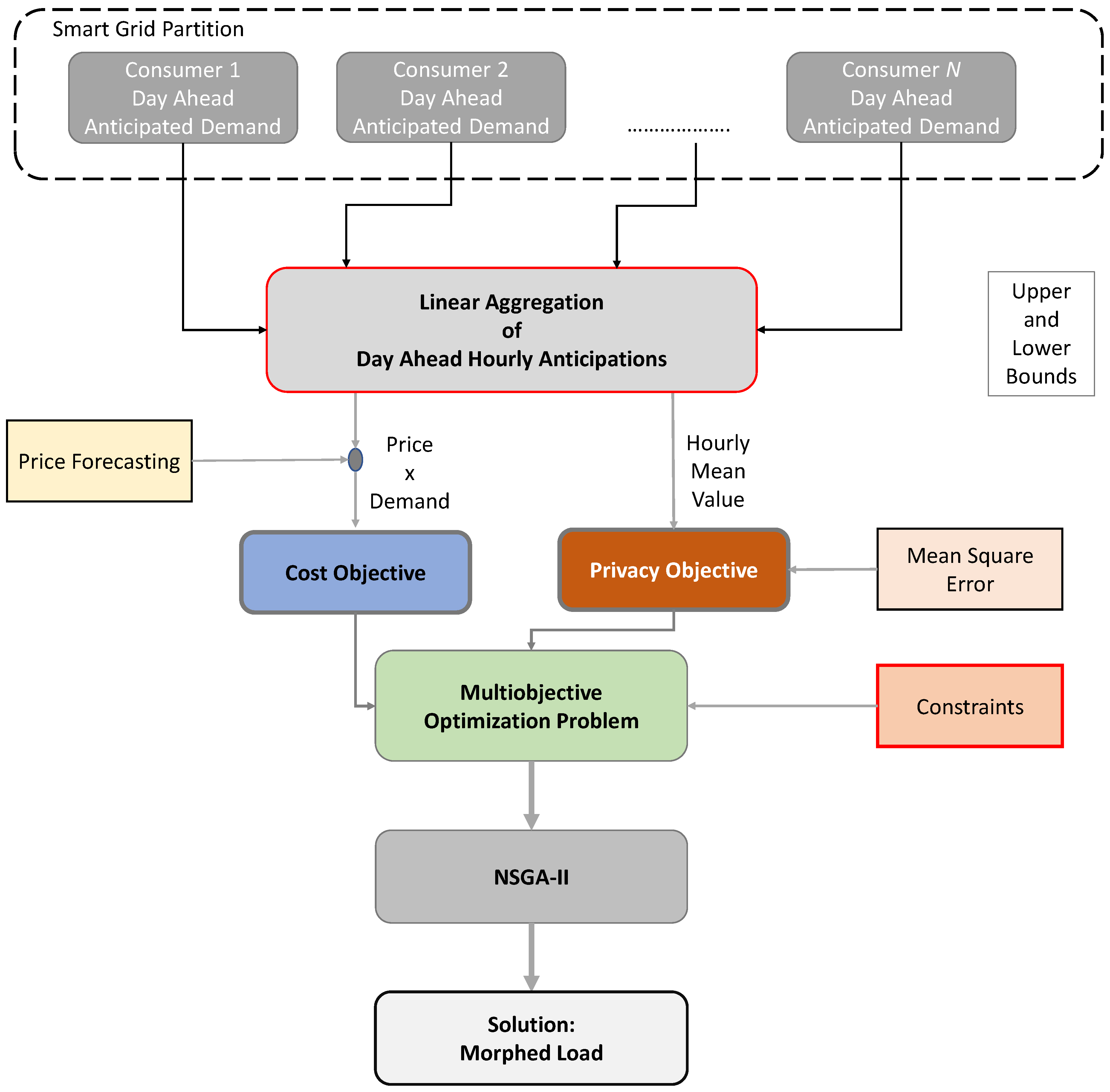
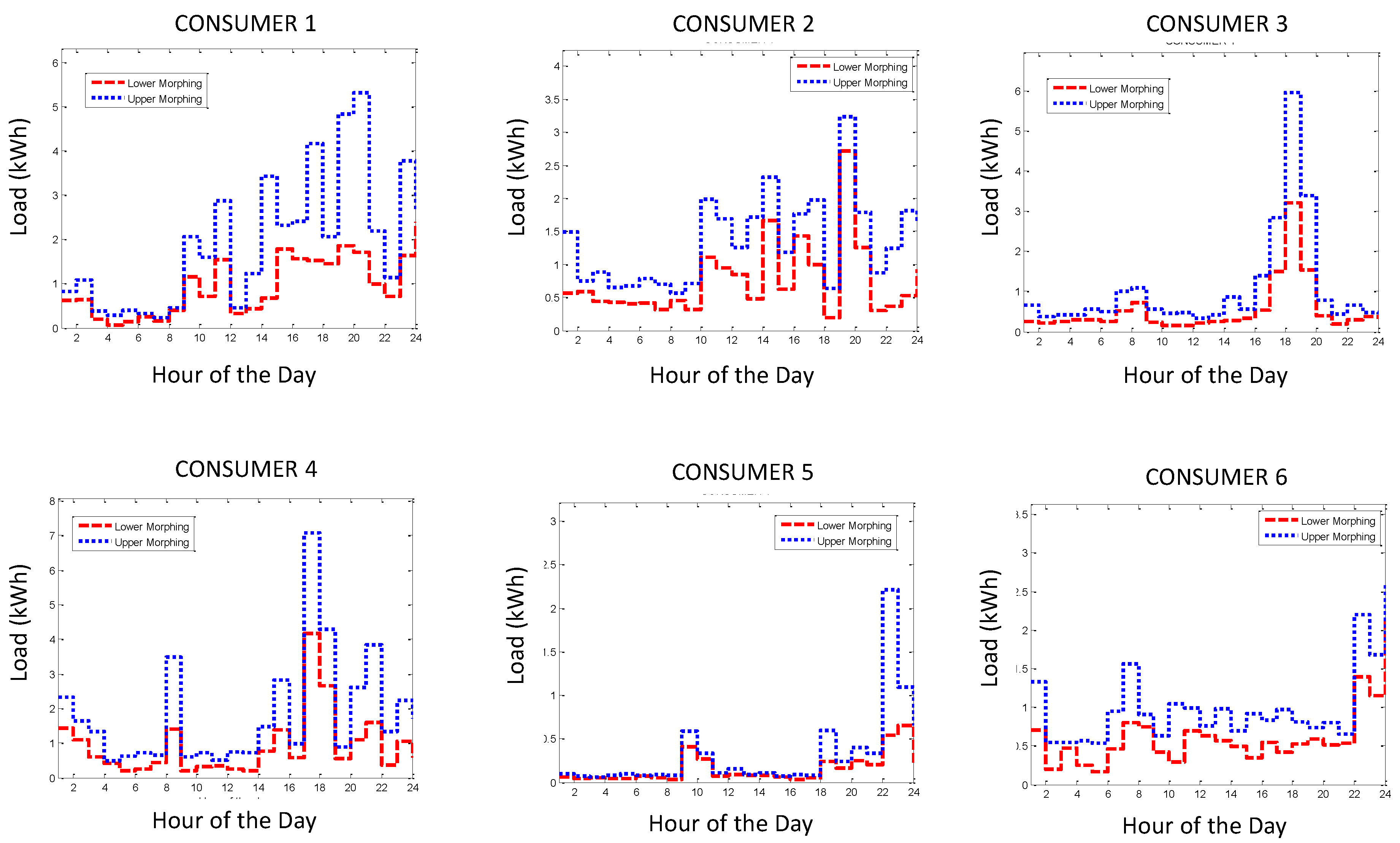
3. Grid Partition Load Morphing Methodology
4. Results
4.1. Problem Setup
- [0.7 × , ] for the lower bound;
- [, 1.3 × ] for the upper bound.
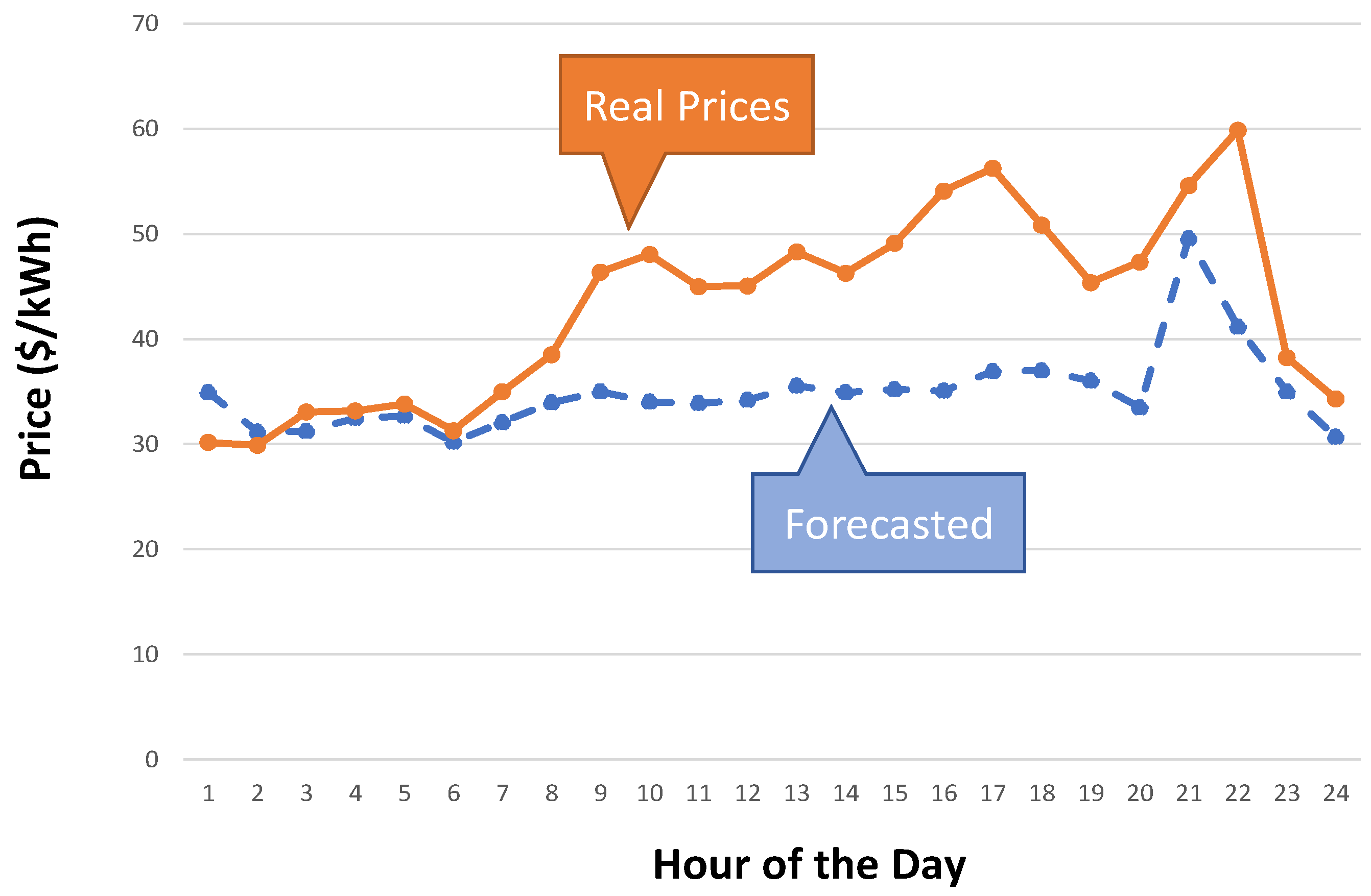
4.2. Tested Scenarios
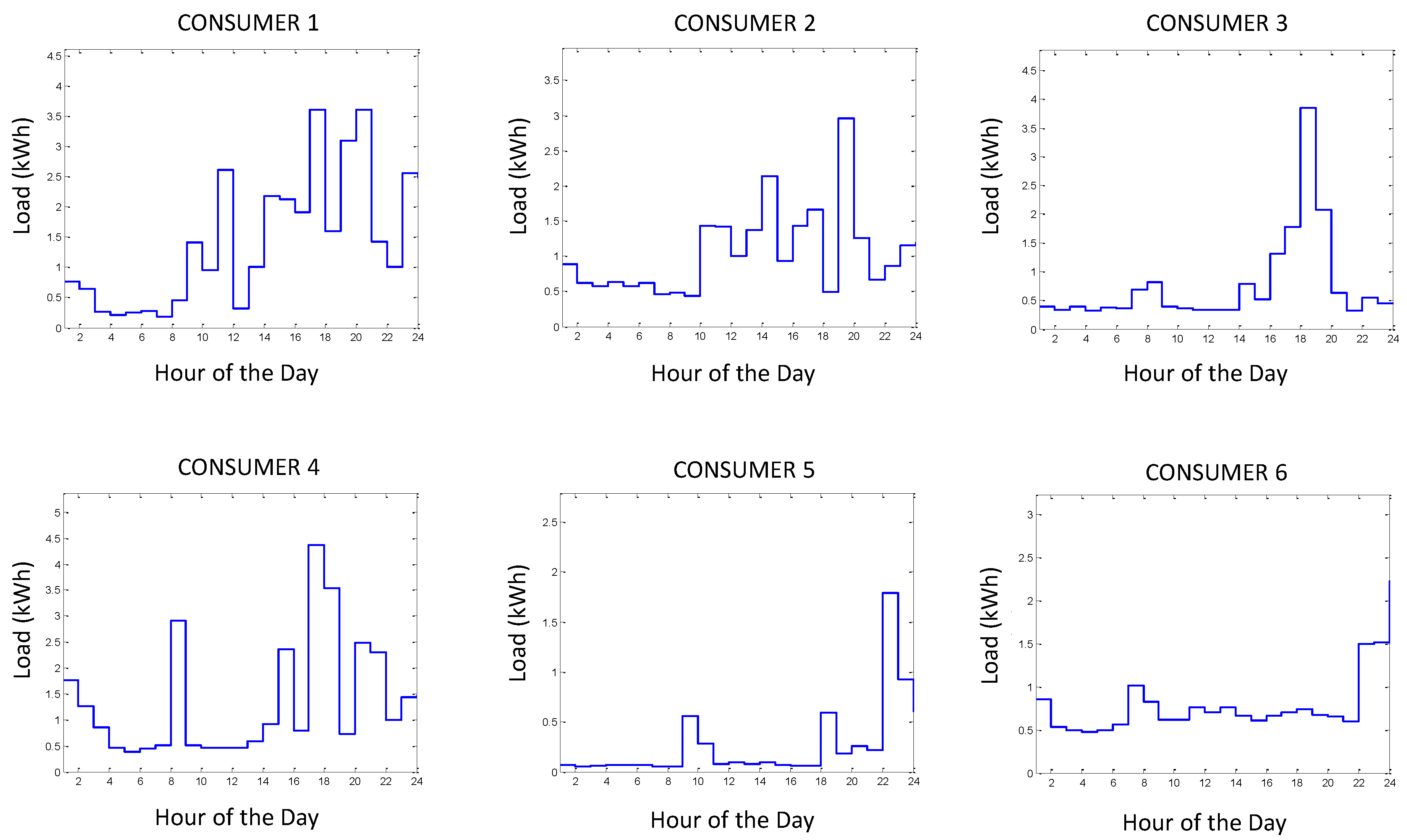
Scenario 1: Partition of Six Consumers
- Number of individuals: 30,
- Mutation probability: 0.01,
- Reproduction method: 15-point crossover,
- Max number of generations: 200,
- Selection of parents: Roulette method.
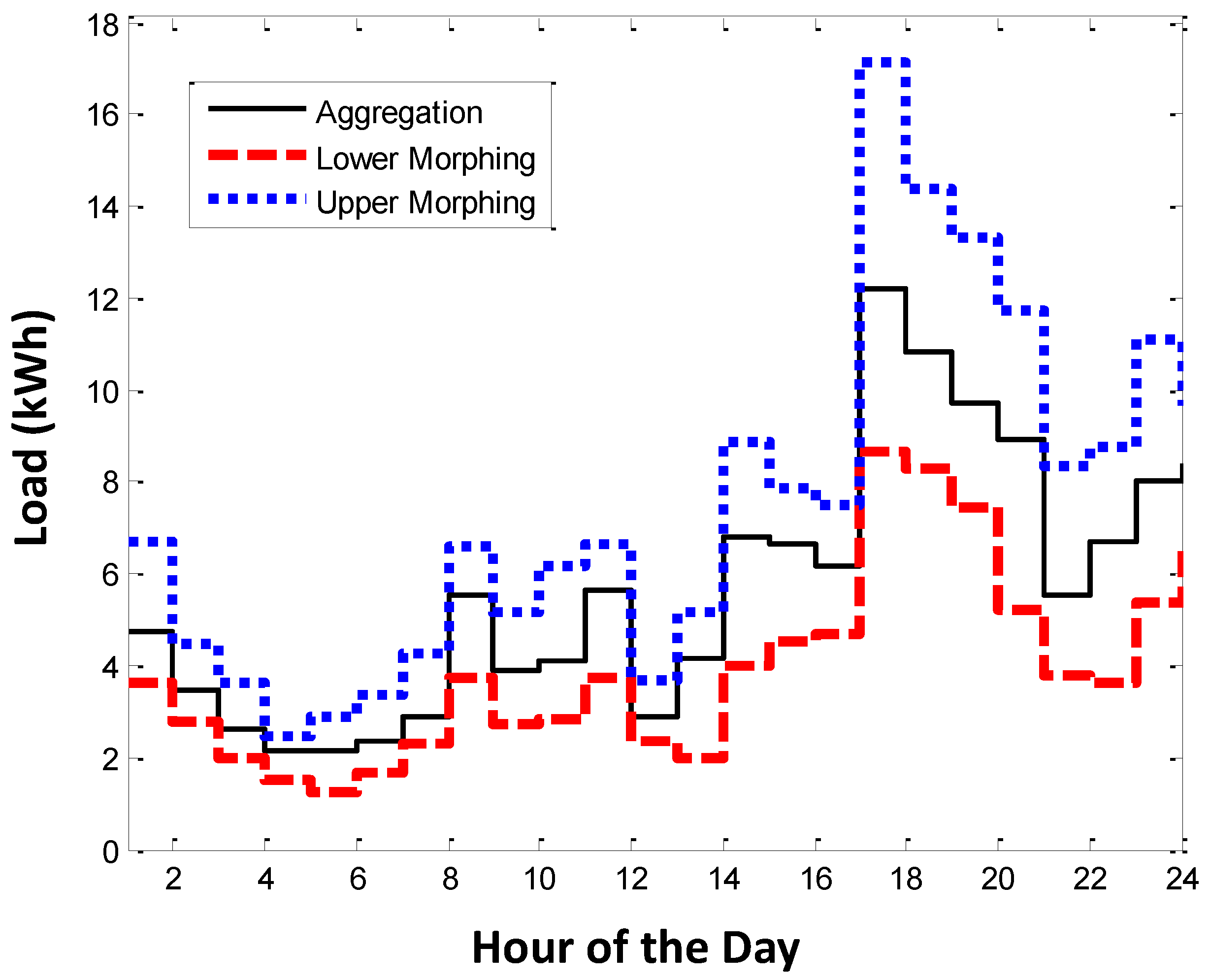
- The non-morphed forecasted cost (NMFC), taken as the forecasted price multiplied by the aggregated load.
- The non-morphed real cost (NMRC), taken as the real price multiplied by the aggregated load.
- The morphed forecasted cost (MFC), given by the forecasted price multiplied by the morphed aggregated load.
- The morphed real cost (MRC), given by the real price multiplied by the morphed aggregated load.
- The correlation coefficient (CC) between each individual consumer pattern and the final morphed pattern denoting the degree of privacy achieved.
4.3. Further Results
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Momoh, J. Smart Grid: Fundamentals of Design and Analysis; Wiley: New York, NY, USA, 2012; Chapter 1. [Google Scholar]
- Tsoukalas, L.H.; Gao, R. From Smart Grids to an Energy Internet: Assumptions, Architectures, and Requirements. In Proceedings of the 3rd IEEE International Conference on Electric Utility Deregulation and Restructuring and Power Technologies, Nanjing, China, 6–9 April 2008; p. 98. [Google Scholar]
- Alamaniotis, M.; Gatsis, N.; Tsoukalas, L.H. Virtual Budget: Integration of Load and Price Anticipation for Load Morphing in Price-Directed Energy Utilization. Electr. Power Syst. Res. 2018, 158, 284–296. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Tsoukalas, L.H.; Bourbakis, N. Virtual Cost Approach: Electricity Consumption Scheduling for Smart Grids/Cities in Price-Directed Electricity Markets. In Proceedings of the IISA 2014, Chania, Greece, 7–9 July 2014; pp. 38–43. [Google Scholar]
- Wang, W.; Xu, Y.; Khanna, M. A survey on the communication architectures in smart grid. Comput. Netw. 2011, 55, 3604–3629. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Tsoukalas, L.H.; Bourbakis, N. Anticipatory driven nodal electricity load morphing in smart cities enhancing consumption privacy. In Proceedings of the IEEE Manchester PowerTech, Manchester, UK, 18–22 June 2017; p. 6. [Google Scholar]
- Conejo, A.J.; Carrion, M.; Morales, L.M. Decision Making Under Uncertainty in Electricity Markets; Springer: London, UK, 2010. [Google Scholar]
- Frederiks, E.R.; Stenner, K.; Hobman, E.V. Household energy use: Applying Behavioural Economics to understand Consumer Decision-Making and Behaviour. Renew. Sustain. Energy Rev. 2015, 41, 1385–1394. [Google Scholar] [CrossRef]
- Anjos, M.F.; Gómez, J.A. Operations Research Approaches for Building Demand Response in a Smart Grid. In Leading Developments from INFORMS Communities; INFORMS: Catonsville, MD, USA, 2017; pp. 131–152. [Google Scholar]
- Setlhaolo, D.; Xia, X.; Zhang, J. Optimal scheduling of household appliances for demand response. Electr. Power Syst. Res. 2014, 116, 24–28. [Google Scholar] [CrossRef]
- Lujano-Rojas, J.M.; Monteiro, C.; Dufo-López, R.; Bernal-Agustín, J.L. Optimum residential load management strategy for real time pricing (RTP) demand response programs. Energy policy 2012, 45, 671–679. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Diaconita, V. Sliding Time Window Electricity Consumption Optimization Algorithm for Communities in the Context of Big Data Processing. IEEE Access 2019, 7, 13050–13067. [Google Scholar] [CrossRef]
- Oprea, S.V.; Bâra, A.; Ifrim, G. Flattening the electricity consumption peak and reducing the electricity payment for residential consumers in the context of smart grid by means of shifting optimization algorithm. Comput. Ind. Eng. 2018, 122, 125–139. [Google Scholar] [CrossRef]
- Gatsis, N.; Giannakis, G.B. Residential demand response with interruptible tasks: Duality and algorithms. In Proceedings of the 2011 50th IEEE Conference on Decision and Control and European Control Conference, Orlando, FL, USA, 12–15 December 2011; pp. 1–6. [Google Scholar]
- Oprea, S.V.; Bâra, A.; Reveiu, A. Informatics solution for energy efficiency improvement and consumption management of householders. Energies 2018, 11, 138. [Google Scholar] [CrossRef]
- Baharlouei, Z.; Hashemi, M.; Narimani, H.; Mohsenian-Rad, H. Achieving optimality and fairness in autonomous demand response: Benchmarks and billing mechanisms. IEEE Trans. Smart Grid 2013, 4, 968–975. [Google Scholar] [CrossRef]
- Safdarian, A.; Fotuhi-Firuzabad, M.; Lehtonen, M. A distributed algorithm for managing residential demand response in smart grids. IEEE Trans. Ind. Inform. 2014, 10, 2385–2393. [Google Scholar] [CrossRef]
- Khodaei, A.; Shahidehpour, M.; Choi, J. Optimal hourly scheduling of community-aggregated electricity consumption. J. Electr. Eng. Technol. 2013, 8, 1251–1260. [Google Scholar] [CrossRef]
- Verschae, R.; Kato, T.; Matsuyama, T. Energy management in prosumer communities: A coordinated approach. Energies 2016, 9, 562. [Google Scholar] [CrossRef]
- Verschae, R.; Kawashima, H.; Kato, T.; Matsuyama, T. Coordinated energy management for inter-community imbalance minimization. Renew. Energy 2016, 87, 922–935. [Google Scholar] [CrossRef]
- Shariatzadeh, F.; Mandal, P.; Srivastava, A.K. Demand response for sustainable energy systems: A review, application and implementation strategy. Renew. Sustain. Energy Rev. 2015, 45, 343–350. [Google Scholar] [CrossRef]
- Chrysikou, V.; Alamaniotis, M.; Tsoukalas, L.H. A Review of Incentive based Demand Response Methods in Smart Electricity Grids. Int. J. Monit. Surveill. Technol. Res. 2015, 3, 62–73. [Google Scholar] [CrossRef]
- Li, H.; Lin, X.; Yang, H.; Liang, X.; Lu, R.; Shen, X. EPPDR: An efficient privacy-preserving demand response scheme with adaptive key evolution in smart grid. IEEE Trans. Parallel Distrib. Syst. 2014, 25, 2053–2064. [Google Scholar] [CrossRef]
- Gong, Y.; Cai, Y.; Guo, Y.; Fang, Y. A privacy-preserving scheme for incentive-based demand response in the smart grid. IEEE Trans. Smart Grid 2016, 7, 1304–1313. [Google Scholar] [CrossRef]
- Wicker, S.; Thomas, R. A privacy-aware architecture for demand response systems. In Proceedings of the 44th Hawaii International Conference on System Sciences, Kauai, HI, USA, 4–7 January 2011; pp. 1–9. [Google Scholar]
- Beligianni, F.; Alamaniotis, M.; Fevgas, A.; Tsompanopoulou, P.; Bozanis, P.; Tsoukalas, L.H. An internet of things architecture for preserving privacy of energy consumption. In Proceedings of the 10th Mediterranean Conference on Power Generation, Transmission, Distribution and Energy Conversion (Med Power 2016), Belgrade, Serbia, 6–9 November 2016; pp. 1–8. [Google Scholar]
- Rahman, M.S.; Basu, A.; Kiyomoto, S.; Bhuiyan, M.A. Privacy-friendly secure bidding for smart grid demand-response. Inf. Sci. 2017, 379, 229–240. [Google Scholar] [CrossRef]
- Li, D.; Aung, Z.; Williams, J.R.; Sanchez, A. No peeking: privacy-preserving demand response system in smart grids. Int. J. Parallel Emerg. Distrib. Syst. 2014, 29, 290–315. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Bourbakis, N.; Tsoukalas, L.H. Enhancing privacy of electricity consumption in smart cities through morphing of anticipated demand pattern utilizing self-elasticity and genetic algorithms. Sustain. Cities Soc. 2019, 46, 101426. [Google Scholar] [CrossRef]
- Alamaniotis, M.; Tsoukalas, L.H.; Buckner, M. Privacy-driven electricity group demand response in smart cities using particle swarm optimization. In Proceedings of the 2016 IEEE 28th International Conference on Tools with Artificial Intelligence (ICTAI), San Jose, CA, USA, 6–8 November 2016; pp. 946–953. [Google Scholar]
- Alamaniotis, M. Morphing to the Mean Approach of Anticipated Electricity Demand in Smart City Partitions Using Citizen Elasticities. In Proceedings of the 2018 IEEE International Smart Cities Conference (ISC2), Kansas City, MO, USA, 16–19 September 2018; pp. 1–7. [Google Scholar]
- Alamaniotis, M.; Gatsis, N. Evolutionary Load Morphing in Smart Power System Partitions Ensuring Privacy and Minimizing Cost. In Proceedings of the 2018 Mediterranean Conference on Power Generation, Transmission, Distribution, and Energy Conversion (MEDPOWER 2018), Dubrovnik, Croatia, 12–15 November 2018; pp. 1–6. [Google Scholar]
- Commission for Energy Regulation (CER). (2012). CER Smart Metering Project—Electricity Customer Behaviour Trial, 2009–201 [dataset], 1st ed.; Irish Social Science Data Archive: Belfield, Irland, 2007; Available online: www.ucd.ie/issda/CER-electricity (accessed on 5 March 2019).
- Deb, K.; Pratap, A.; Agarwal, S.; Meyarivan, T.A.M.T. A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE Trans. Evol. Comput. 2002, 6, 182–197. [Google Scholar] [CrossRef]
- Ng, Y.K. The economic theory of clubs: Pareto optimality conditions. Economica 1973, 40, 291–298. [Google Scholar] [CrossRef]
- Eiben, A.E.; Smith, J.E. Introduction to Evolutionary Computing; Springer: Berlin/Heidelberg, Germany, 2003. [Google Scholar]
- Pareto, V. Manuale di Economica Politica; Societa Editrice Libraria: Milan, Italy, 1906; translated by Schwier, A.S., Manual of Political Economy; Schwier, A.S., Page, A.N., Eds.; Kelley: New York, NY, USA, 1971. [Google Scholar]
- Marler, R.; Arora, J. Survey of multi-objective optimization methods for engineering. Struct. Multidiscip. Optim. 2004, 26, 369–395. [Google Scholar] [CrossRef]
- Nasiakou, A.; Alamaniotis, M.; Tsoukalas, L.H.; Vavalis, M. Dynamic Data Driven Partitioning of Smart Grid Using Learning Methods. In Handbook of Dynamic Data Driven Applications Systems; Springer: Berlin/Heidelberg, Germany, 2018; pp. 505–526. [Google Scholar]
- Alamaniotis, M.; Tsoukalas, L.H. Utilization of virtual buffer in local area grids for electricity storage in smart power systems. In Proceedings of the 2017 IEEE North American Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar]
- Gao, R.; Tsoukalas, L.H. Implementing virtual buffer for electric power grids. In Proceedings of the International Conference on Computational Science, Beijing, China, 27–30 May 2007; Springer: Berlin/Heidelberg, Germany; pp. 1083–1089. [Google Scholar]
- Alamaniotis, M.; Bargiotas, D.; Bourbakis, N.G.; Tsoukalas, L.H. Genetic optimal regression of relevance vector machines for electricity pricing signal forecasting in smart grids. IEEE Trans. Smart Grid 2015, 6, 2997–3005. [Google Scholar] [CrossRef]
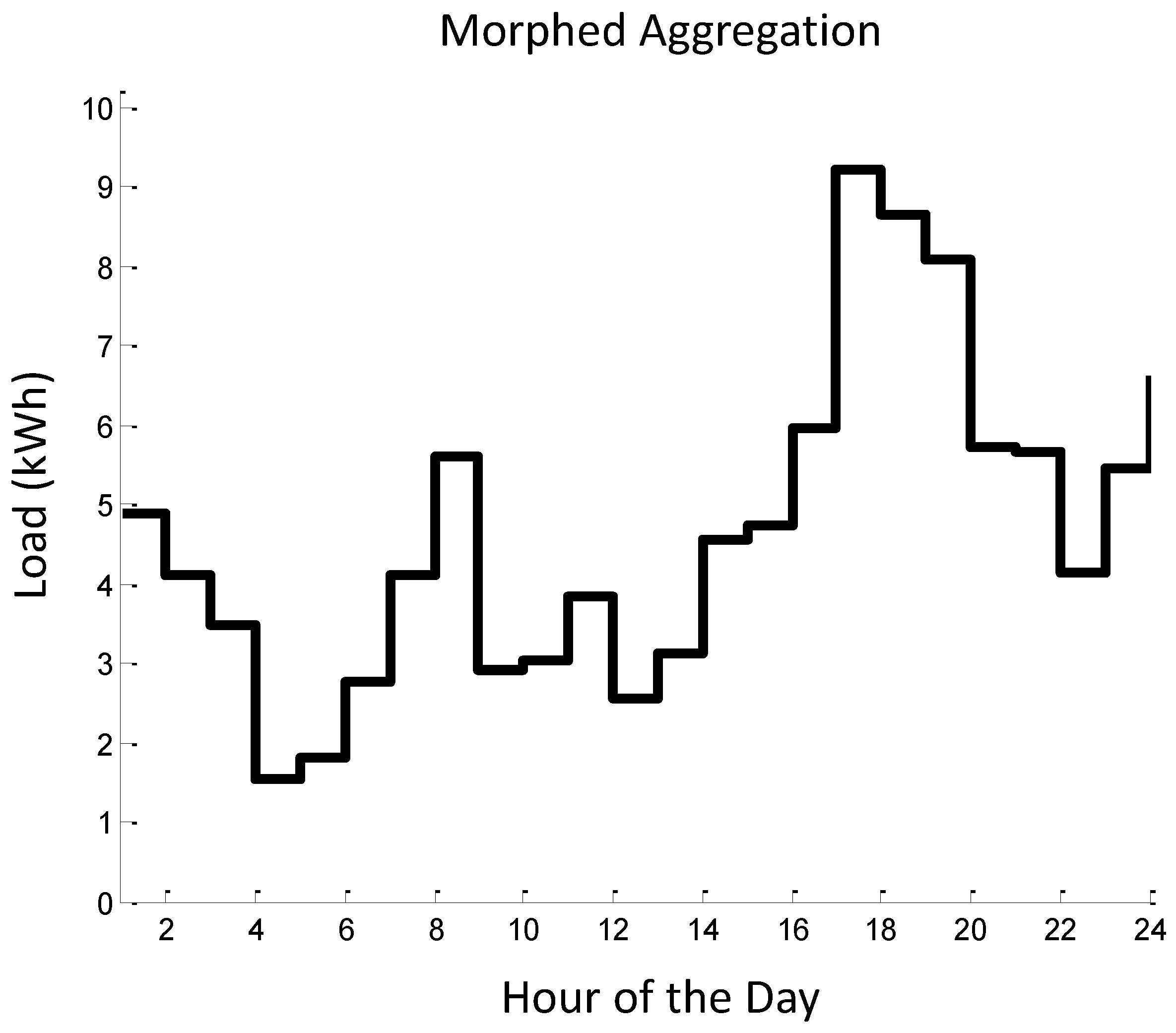
| Hour | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| Solution | 4.87 | 4.10 | 3.48 | 1.53 | 1.80 | 2.77 | 4.11 | 5.60 | 2.89 | 3.04 | 3.83 | 2.54 |
| Hour | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| Solution | 3.11 | 4.54 | 4.74 | 5.94 | 9.21 | 8.63 | 8.09 | 5.72 | 5.66 | 4.13 | 5.46 | 6.61 |
| Quantity | NMFC | MFC | NMRC | MRC | ||
| Value * | 4837 | 3978 | 6200 | 5016 | ||
| Consumer | #1 | #2 | #3 | #4 | #5 | #6 |
| CC value | 0.69 | 0.41 | 0.74 | 0.75 | 0.11 | 0.26 |
| NMFC ($) | MFC ($) | NMRC ($) | MRC ($) | Average Correlation (between Morphed and Consumers) | |
|---|---|---|---|---|---|
| Multi Objective (Our Method) | 6248 | 5077 | 8104 | 6577 | 0.427 |
| Single Objective: Consumer Cost | 6248 | 5556 | 8104 | 7185 | 0.449 |
| Single Objective: Consumer Privacy | 6248 | 5908 | 8104 | 7603 | 0.451 |
| NMFC ($) | MFC ($) | NMRC ($) | MRC ($) | Average Correlation (between Morphed and Consumers) | |
|---|---|---|---|---|---|
| Multi Objective (Our Method) | 6607 | 5635 | 8293 | 7039 | 0.269 |
| Single Objective: Consumer Privacy | 6607 | 6068 | 8293 | 7685 | 0.286 |
| Single Objective: Consumer Cost | 6607 | 6978 | 8293 | 8756 | 0.298 |
| NMFC ($) | MFC ($) | NMRC ($) | MRC ($) | Average Correlation (between Morphed and Consumers) | |
|---|---|---|---|---|---|
| Multi Objective (Our Method) | 30,421 | 25,792 | 39,385 | 33,073 | 0.327 |
| Single Objective: Consumer Cost | 30,421 | 27,230 | 39,380 | 35,100 | 0.320 |
| Single Objective: Consumer Privacy | 30,420 | 29,401 | 39,380 | 37,730 | 0.330 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alamaniotis, M.; Gatsis, N. Evolutionary Multi-Objective Cost and Privacy Driven Load Morphing in Smart Electricity Grid Partition. Energies 2019, 12, 2470. https://doi.org/10.3390/en12132470
Alamaniotis M, Gatsis N. Evolutionary Multi-Objective Cost and Privacy Driven Load Morphing in Smart Electricity Grid Partition. Energies. 2019; 12(13):2470. https://doi.org/10.3390/en12132470
Chicago/Turabian StyleAlamaniotis, Miltiadis, and Nikolaos Gatsis. 2019. "Evolutionary Multi-Objective Cost and Privacy Driven Load Morphing in Smart Electricity Grid Partition" Energies 12, no. 13: 2470. https://doi.org/10.3390/en12132470
APA StyleAlamaniotis, M., & Gatsis, N. (2019). Evolutionary Multi-Objective Cost and Privacy Driven Load Morphing in Smart Electricity Grid Partition. Energies, 12(13), 2470. https://doi.org/10.3390/en12132470






