Multivariable Regression Equivalent Model of Interconnected Active Distribution Networks Based on Boundary Measurement
Abstract
:1. Introduction
2. Multivariable Regression Equivalent Model
3. Algorithm for Regression Model
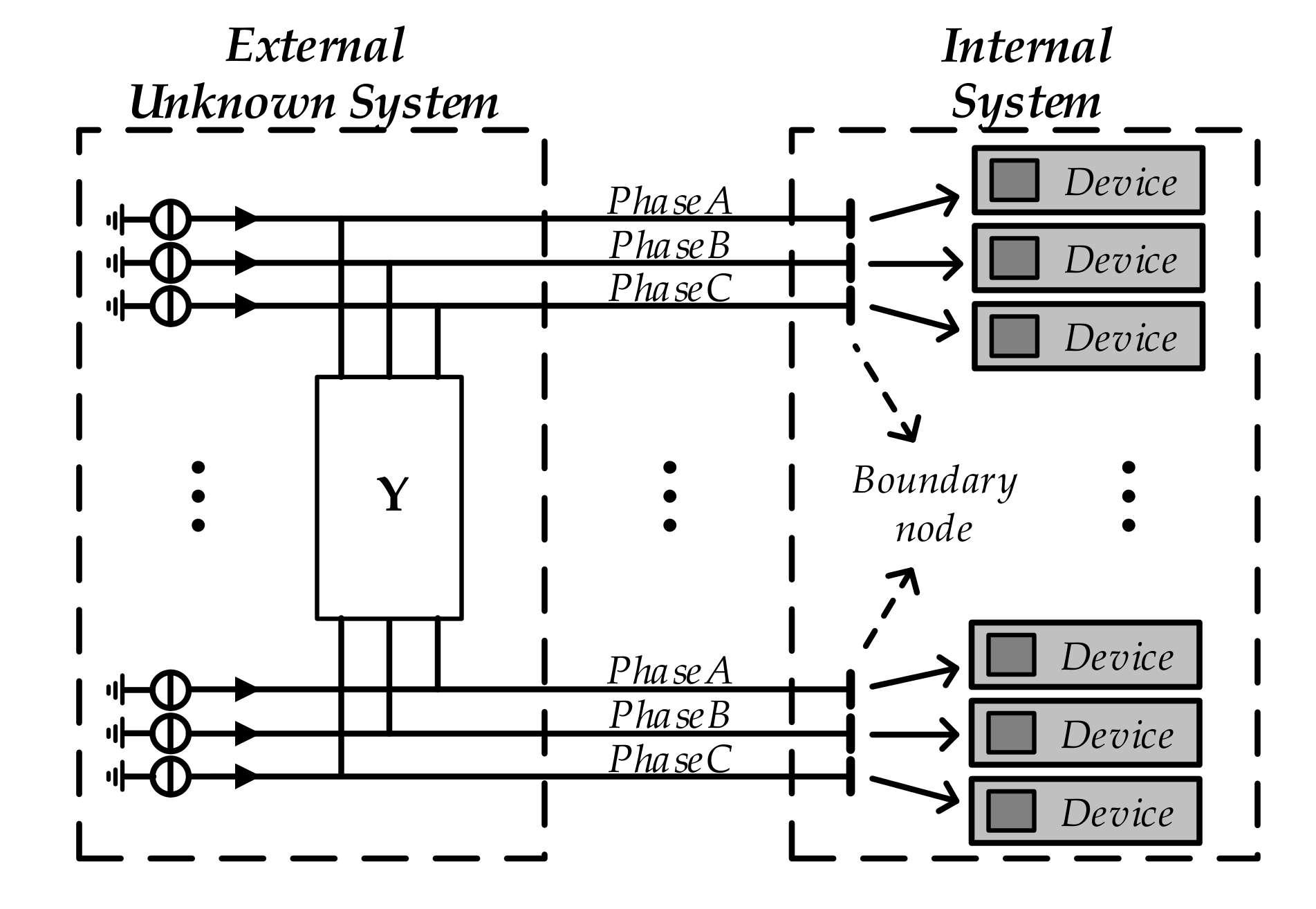
3.1. Collection Boundary Nodes Information
3.2. Maximum Likelihood Estimation of Equivalent Parameters
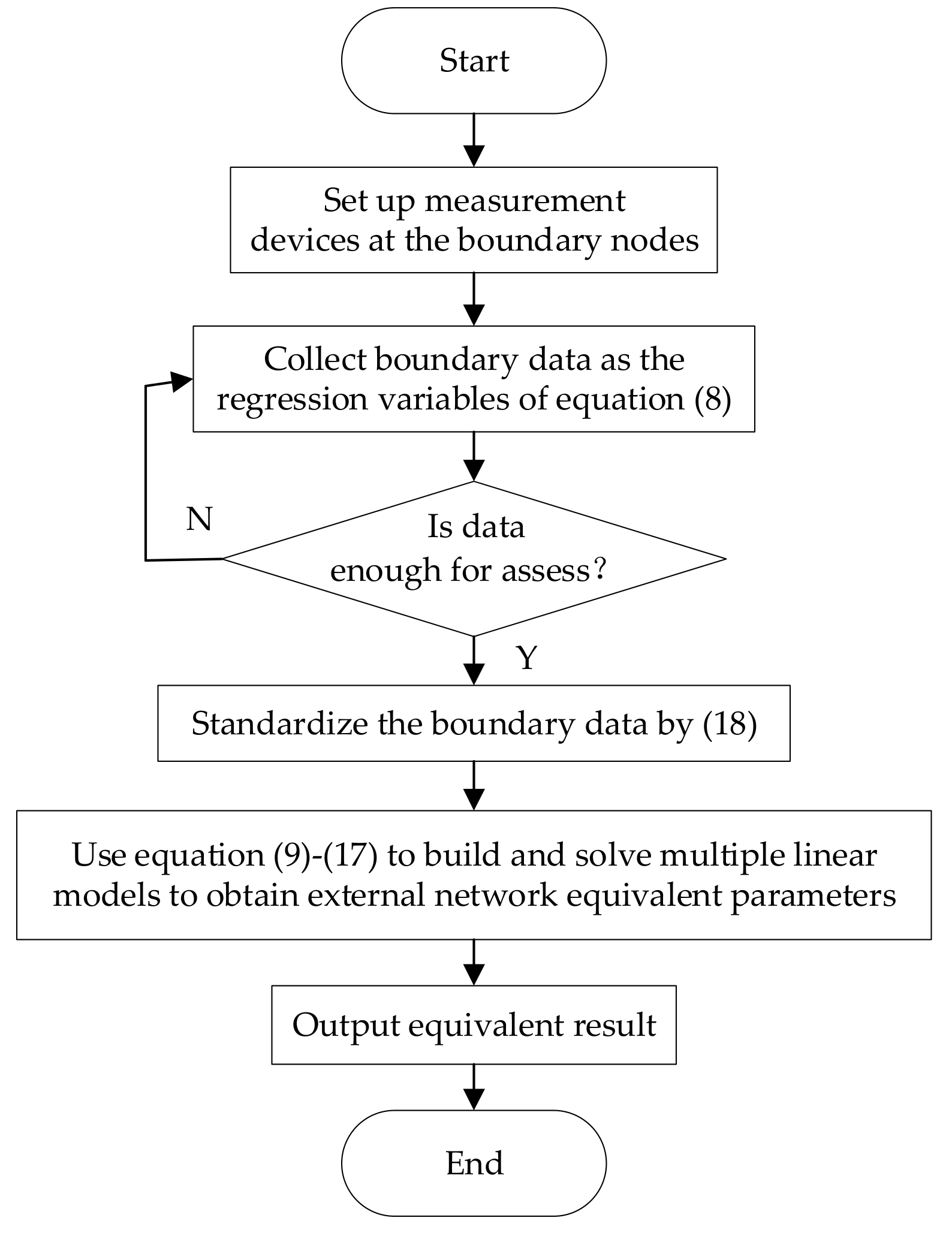
3.3. Equivalent Procedures
4. Simulation Verification
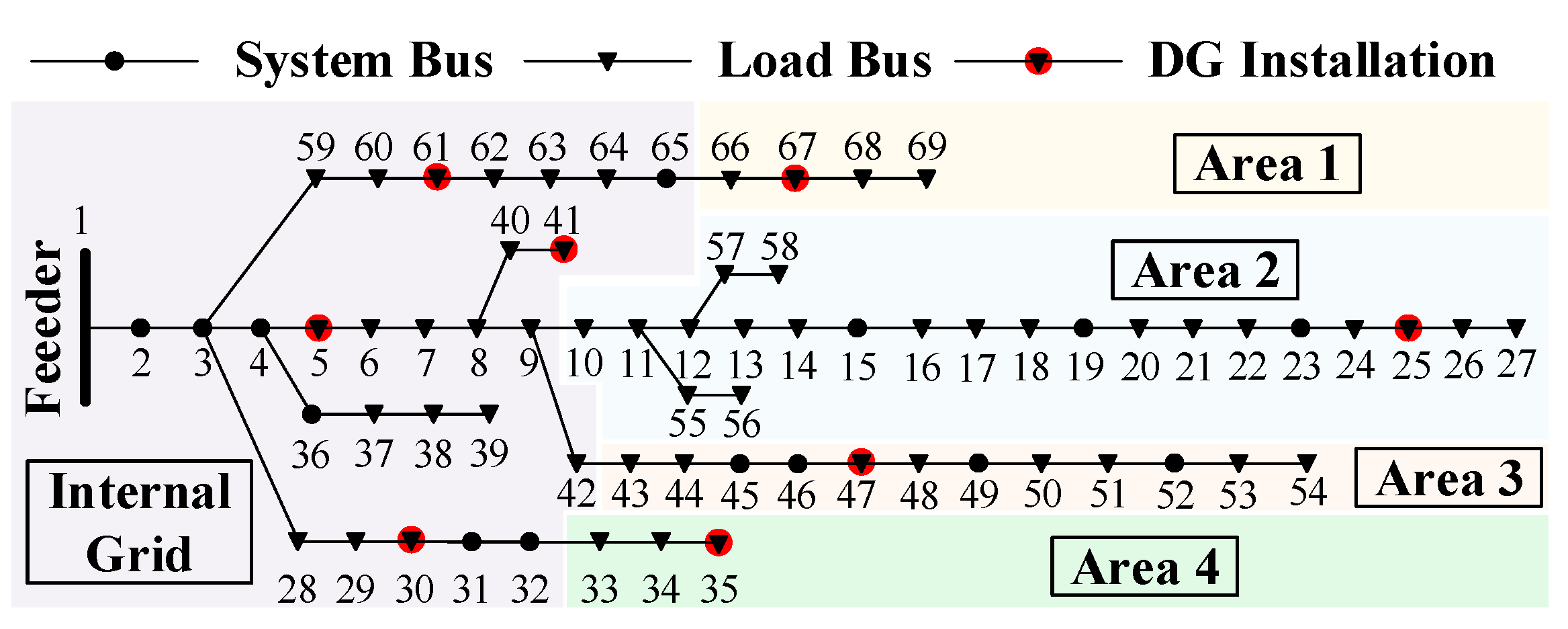
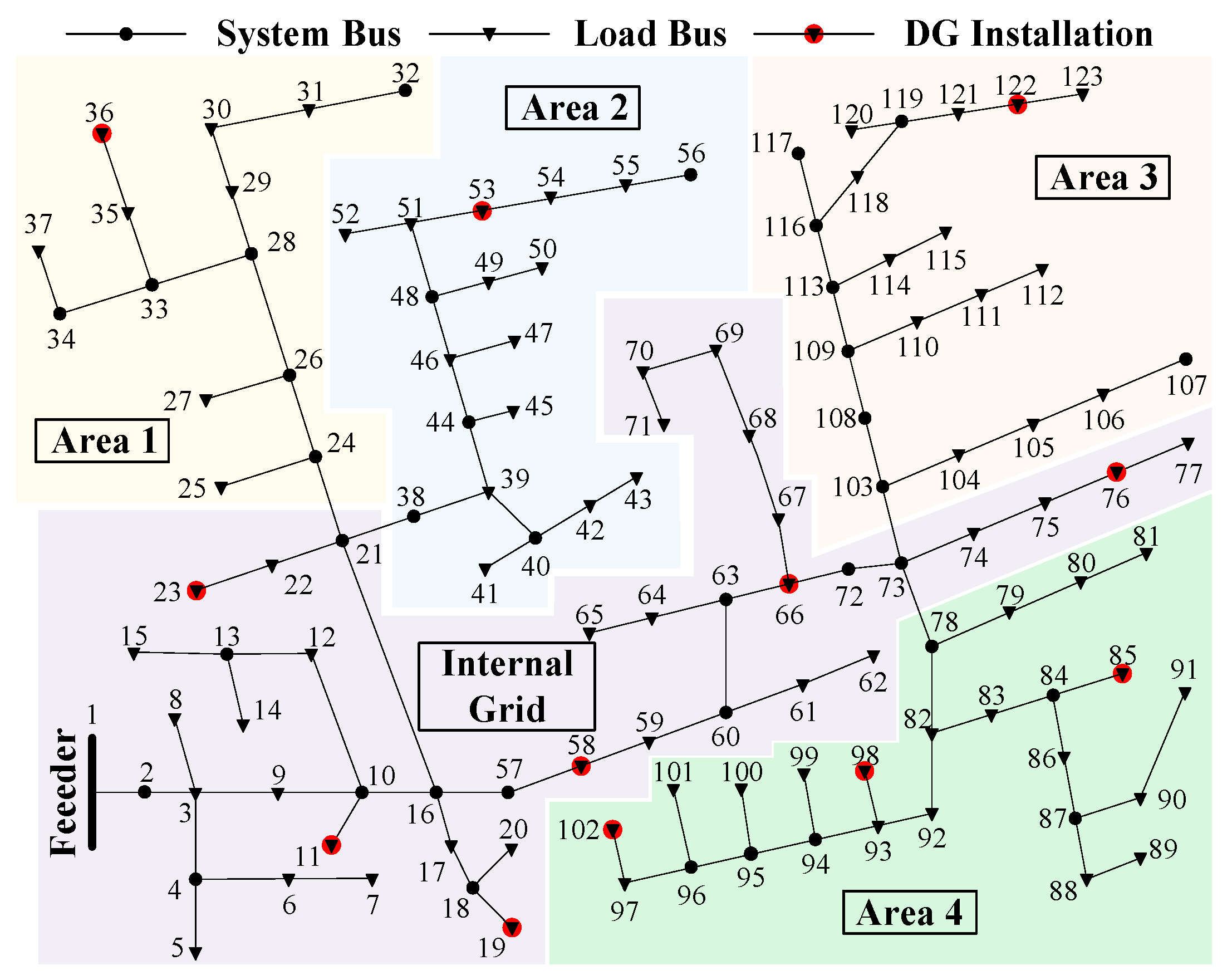
4.1. Test Systems
4.2. Scenarios Setting
4.2.1. Three Scenarios based on Case 1
4.2.2. Three Scenarios based on Case 2
4.3. Equivalent Error Indicators
4.4. Simulation Results of Case 1
4.4.1. Scenario 1
4.4.2. Scenario 2
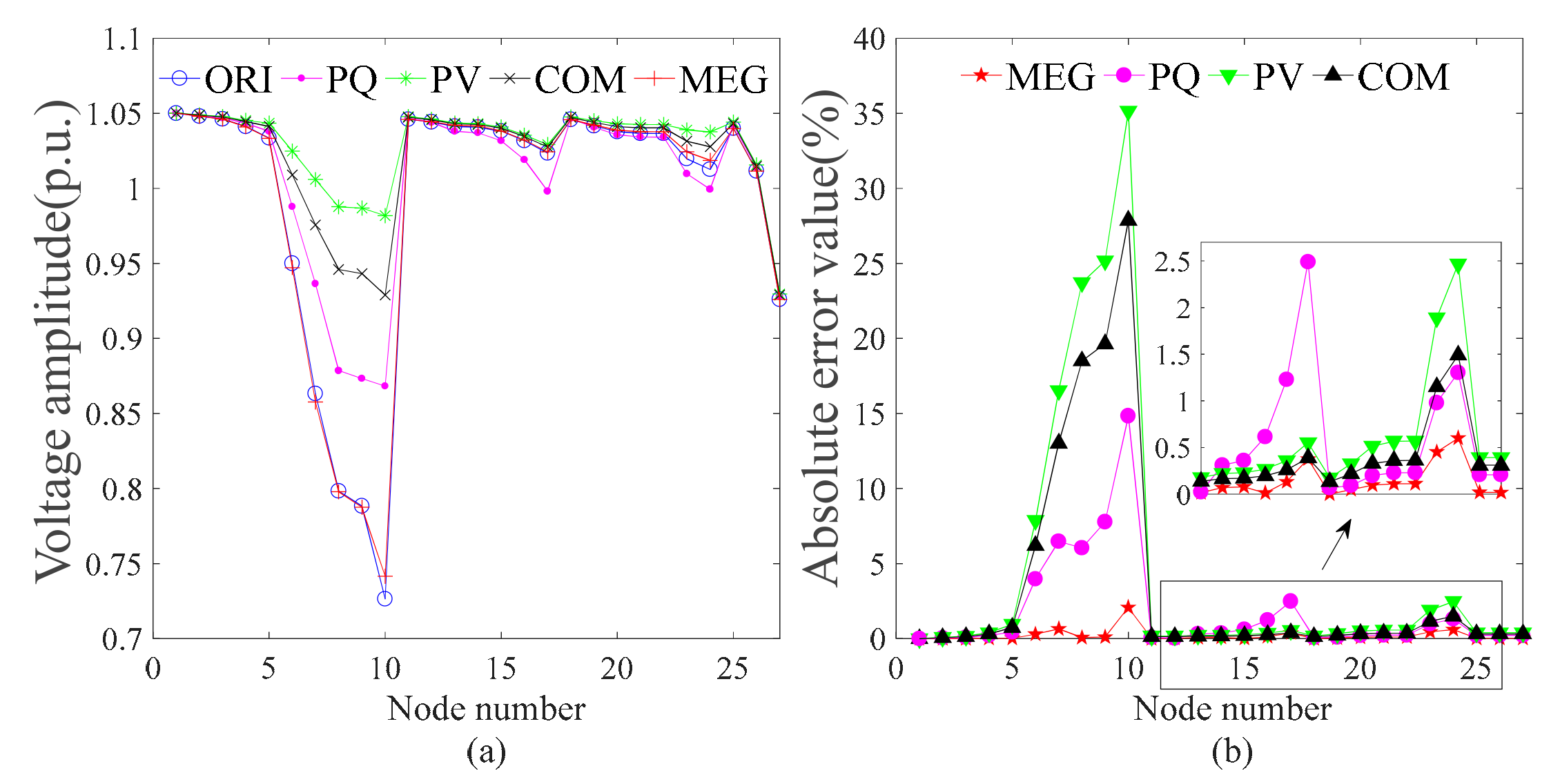
4.4.3. Scenario 3
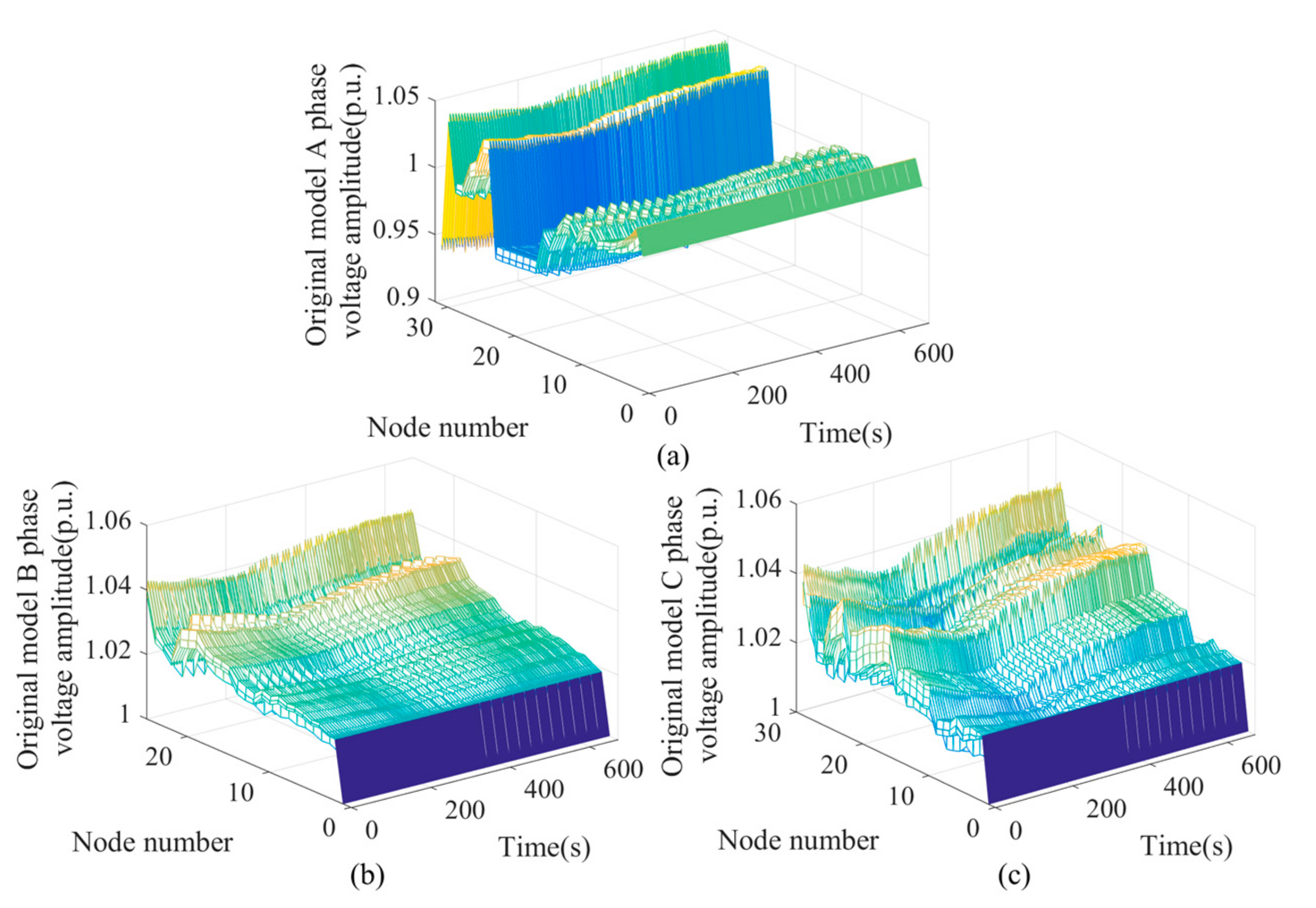
4.5. Simulation Results of Case 2
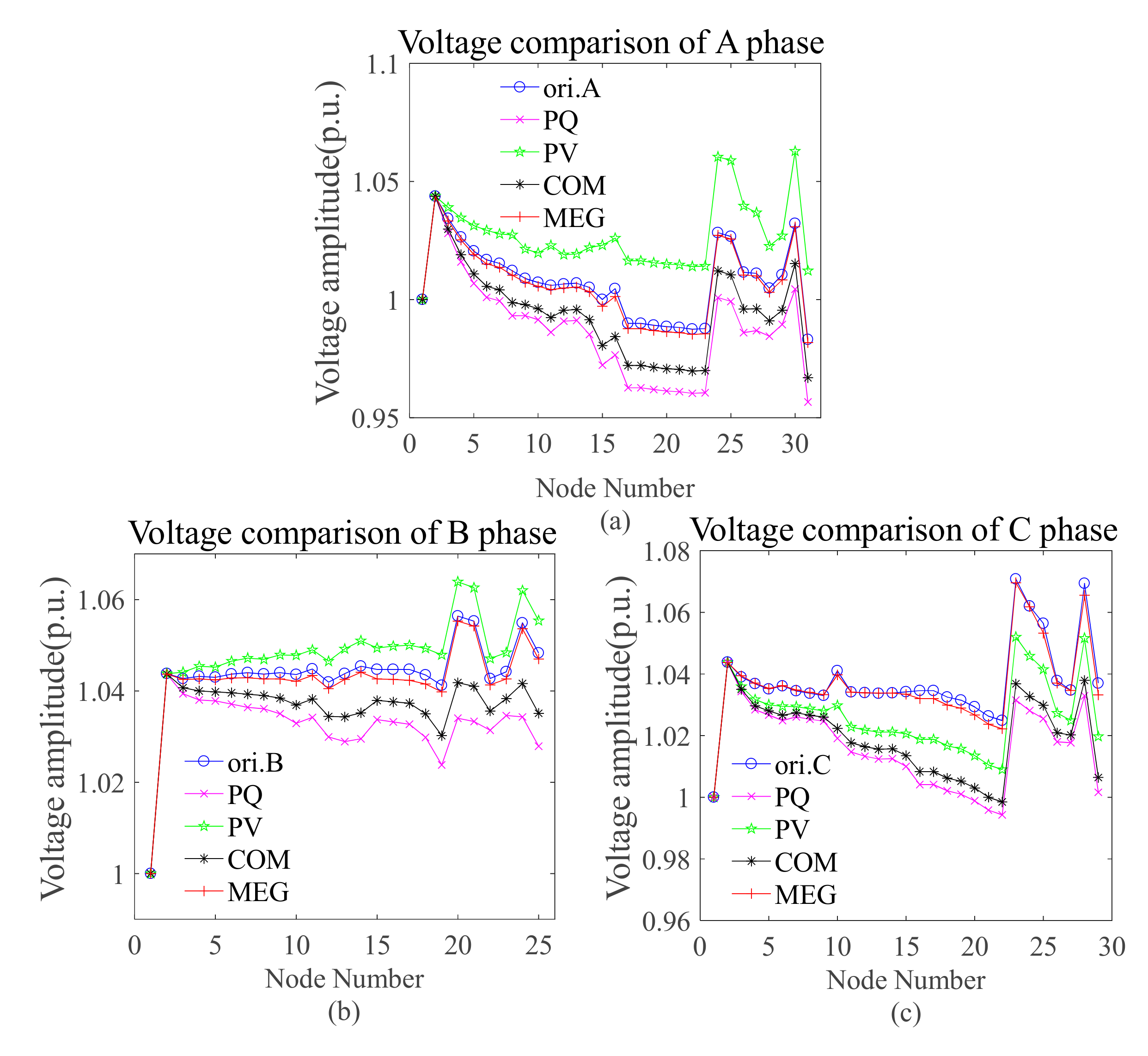
4.5.1. Scenario 1
4.5.2. Scenario 2
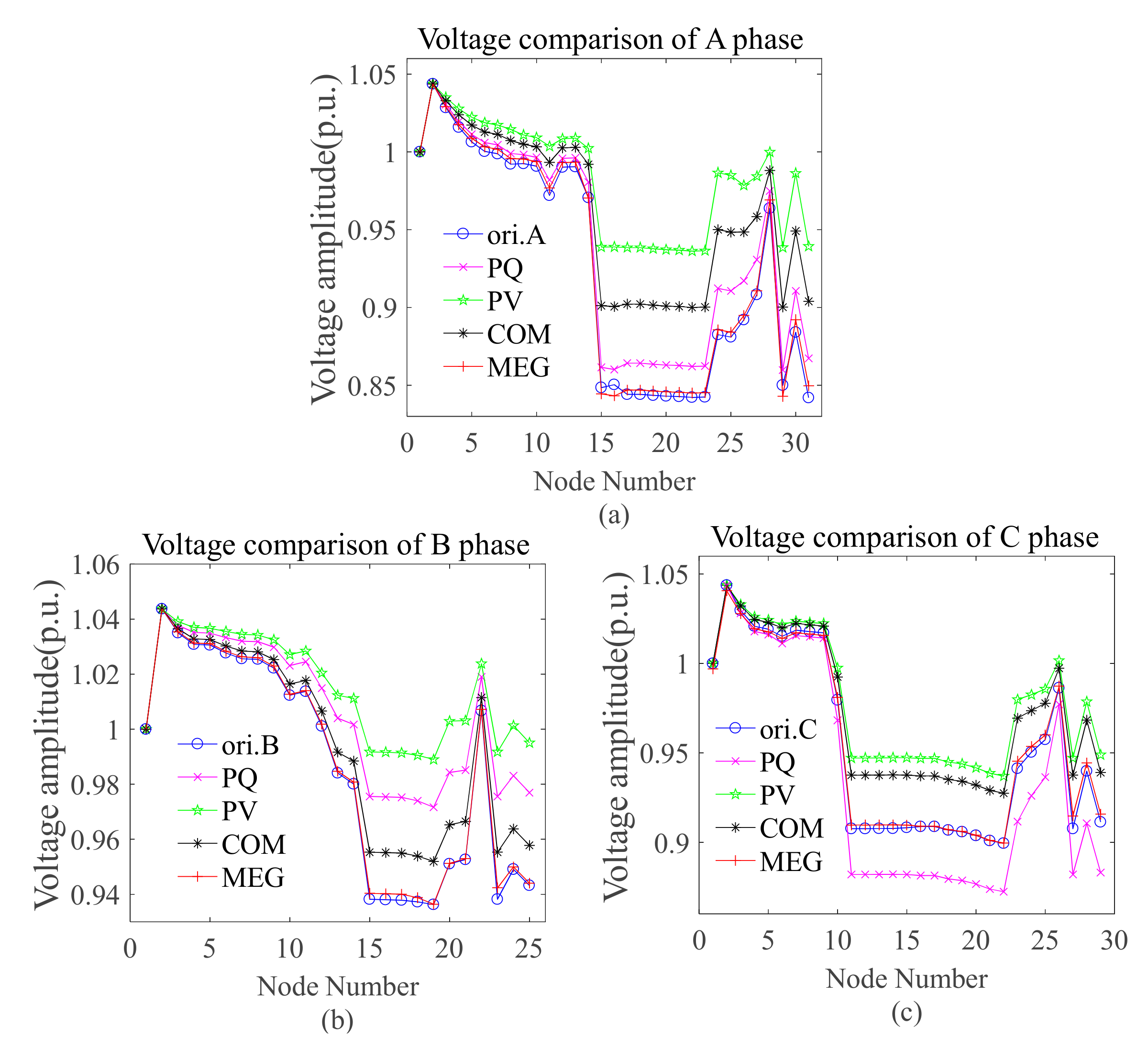
4.5.3. Scenario 3
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Luo, T.; Dolan, M.J.; Davidson, E.M.; Ault, G.W. Assessment of a new constraint satisfaction-based hybrid distributed control technique for power flow management in distribution networks with generation and demand response. IEEE Trans. Smart Grid 2015, 6, 271–278. [Google Scholar] [CrossRef]
- Zhang, C.; Wang, Q.; Wang, J.; Pinson, P.; Morales, J.M.; Ostergaard, J. Real-time procurement strategies of a proactive distribution company with aggregator-based demand response. IEEE Trans. Smart Grid 2018, 9, 766–776. [Google Scholar] [CrossRef]
- Haghighat, H.; Kennedy, S.W. A bilevel approach to operational decision making of a distribution company in competitive environments. IEEE Trans. Power Syst. 2012, 27, 1797–1807. [Google Scholar] [CrossRef]
- Millar, R.J.; Kazemi, S.; Lehtonen, M.; Saarijarvi, E. Impact of MV connected microgrids on MV distribution planning. IEEE Trans. Smart Grid 2012, 3, 2100–2108. [Google Scholar] [CrossRef]
- Vaccaro, A.; Popov, M.; Villacci, D.; Terzija, V. An integrated framework for smart microgrids modeling monitoring control communication and verification. Proc. IEEE 2011, 99, 119–132. [Google Scholar] [CrossRef]
- Aschmoneit, F.; Verstege, J. An external system equivalent for on-line steady-state generator outage simulation. IEEE Trans. Power Appar. Syst. 1979, 98, 770–779. [Google Scholar] [CrossRef]
- Milano, F.; Srivastava, K. Dynamic REI equivalents for short circuit and transient stability analyses. Electr. Power Syst. Res. 2009, 79, 878–887. [Google Scholar] [CrossRef]
- Deckmann, S.; Pizzolante, A.; Monticelli, A.; Stott, B.; Alsac, O. Studies on power system load flow equivalencing. IEEE Trans. Power Appar. Syst. 1980, 99, 2301–2310. [Google Scholar] [CrossRef]
- Angelos, E.W.S.; Asada, E.N. Improving state estimation with real-time external equivalents. IEEE Trans. Power Syst. 2016, 31, 1289–1296. [Google Scholar] [CrossRef]
- Liu, J.-H.; Chu, C.-C. Wide-area measurement-based voltage stability indicators by modified coupled single-port models. IEEE Trans. Power Syst. 2014, 29, 756–764. [Google Scholar] [CrossRef]
- Ju, P.; Handschin, E.; Wei, Z.; Schlucking, U. Sequential parameter estimation of a simplified induction motor load model. IEEE Trans. Power Syst. 1996, 11, 319–324. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, C.; Lin, F.; Li, W.; Wang, L.Y.; Zhao, J. Incorporating generator equivalent model into voltage stability analysis. IEEE Trans. Power Syst. 2013, 28, 4857–4866. [Google Scholar] [CrossRef]
- Shi, X.; Chen, G.; Ju, P.; Zhang, D. A new generalized load model of power systems and its applications. In Proceedings of the International Conference on Advanced Power System Automation and Protection, Beijing, China, 16–20 October 2011; pp. 2268–2271. [Google Scholar]
- Arefifar, S.A.; Xu, W. Online tracking of power system impedance parameters and field experiences. IEEE Trans. Power Deliv. 2009, 24, 1781–1788. [Google Scholar] [CrossRef]
- Milanovic, J.V.; Yamashita, K.; Villanueva, S.M.; Djokic, S.Z.; Korunovic, L.M. International industry practice on power system load modeling. IEEE Trans. Power Syst. 2013, 28, 3038–3046. [Google Scholar] [CrossRef]
- Rouhani, A.; Abur, A. Real-time dynamic parameter estimation for an exponential dynamic load model. IEEE Trans. Smart Grid. 2015, 7, 1530–1536. [Google Scholar] [CrossRef]
- Wang, Y.; Pordanjani, I.R.; Li, W.; Xu, W.; Chen, T.; Vaahedi, E.; Gurney, J. Voltage stability monitoring based on the concept of coupled single-port circuit. IEEE Trans. Power Syst. 2011, 26, 2154–2163. [Google Scholar] [CrossRef]
- Heydt, G.T. Thévenin’s theorem applied to the analysis of polyphase transmission circuits. IEEE Trans. Power Deliv. 2017, 32, 72–77. [Google Scholar] [CrossRef]
- Tomim, M.A.; Marti, J.R.; Filho, J.A.P.; Filho, J.A.P. Parallel transient stability simulation based on multi-area thévenin equivalents. IEEE Trans. Smart Grid 2017, 8, 1366–1377. [Google Scholar] [CrossRef]
- Sun, T.; Li, Z.; Rong, S.; Lu, J.; Li, W. Effect of load change on the Thevenin equivalent impedance of power system. Energies 2017, 10, 330. [Google Scholar] [CrossRef]
- An, T.; Zhou, S.; Yu, J.; Lu, W.; Zhang, Y. Research on illed-conditioned equations in tracking Thevenin equivalent parameters with local measurements. In Proceedings of the International Conference on Power System Technology, Chongqing, China, 22–26 October 2006; pp. 1–4. [Google Scholar]
- Abdelkader, S.M.; Morrow, D.J. Online thévenin equivalent determination considering system side changes and measurement errors. IEEE Trans. Power Syst. 2015, 30, 2716–2725. [Google Scholar] [CrossRef]
- Yu, J.; Dai, W.; Li, W.; Liu, X.; Liu, J. Optimal reactive power flow of interconnected power system based on static equivalent method using border PMU measurements. IEEE Trans. Power Syst. 2018, 33, 421–429. [Google Scholar] [CrossRef]
- Mousavi-Seyedi, S.S.; Aminifar, F.; Afsharnia, S. Parameter estimation of multiterminal transmission lines using joint PMU and SCADA data. IEEE Trans. Power Deliv. 2015, 30, 1077–1085. [Google Scholar] [CrossRef]
- Su, H.-Y.; Liu, T.-Y. A PMU-based method for smart transmission grid voltage security visualization and monitoring. Energies 2017, 10, 1103. [Google Scholar]
- Arava, V.S.N.; Vanfretti, L. A Method to estimate power system voltage stability margins using time-series from dynamic simulations with sequential load perturbations. IEEE Access 2018, 6, 43622–43632. [Google Scholar] [CrossRef]
- Abur, A.; Kim, H. Enhancement of external system modeling for state estimation [power systems]. IEEE Trans. Power Syst. 1996, 11, 1380–1386. [Google Scholar]
- Milanovic, J.V.; Zali, S.M. Validation of equivalent dynamic model of active distribution network cell. IEEE Trans. Power Syst. 2013, 28, 2101–2110. [Google Scholar] [CrossRef]
- Liu, J.-H.; Chu, C.-C. Long-term voltage instability detections of multiple fixed-speed induction generators in distribution networks using synchrophasors. IEEE Trans. Smart Grid 2015, 6, 2069–2079. [Google Scholar] [CrossRef]
- Shu, D.; Xie, X.; Dinavahi, V.; Zhang, C.; Ye, X.; Jiang, Q. Dynamic phasor based interface model for EMT and transient stability hybrid simulations. IEEE Trans. Power Syst. 2018, 33, 3930–3939. [Google Scholar] [CrossRef]
- Wang, C.; Qin, Z.; Hou, Y.; Yan, J. Multi-area dynamic state estimation with PMU measurements by an equality constrained extended kalman filter. IEEE Trans. Smart Grid 2018, 9, 900–910. [Google Scholar] [CrossRef]
- Von Meier, A.; Stewart, E.; McEachern, A.; Andersen, M.; Mehrmanesh, L. Precision micro-synchrophasors for distribution systems: a summary of applications. IEEE Trans. Smart Grid 2017, 8, 2926–2936. [Google Scholar] [CrossRef]
- Haase, R. Multivariate General Linear Models; SAGE Publications: Thousand Oaks, CA, USA, 2011; pp. 55–78. [Google Scholar]
- Knofczynski, G.T.; Mundfrom, D. Sample sizes when using multiple linear regression for prediction. Educ. Meas. 2008, 68, 431–442. [Google Scholar] [CrossRef]
- Baran, M.; Wu, F. Optimal capacitor placement on radial distribution systems. IEEE Trans. Power Deliv. 1989, 4, 725–734. [Google Scholar] [CrossRef]
- IEEE PES, Distribution Test Feeders. 2010. Available online: http://www.ewh.ieee.org/soc/pes/dsacom/testfeeders/index.html (accessed on 21 May 2018).
- Robbins, B.A.; Hadjicostis, C.N.; Dominguez-Garcia, A.D. A Two-stage distributed architecture for Voltage control in power distribution systems. IEEE Trans. Power Syst. 2013, 28, 1470–1482. [Google Scholar] [CrossRef]
- Lim, I.H.; Lee, S.J.; Choi, M.S.; Crossley, P. Multi-agent system-based protection coordination of distribution feeders. In Proceedings of the International Conference on Intelligent Systems Applications to Power Systems, Toki Messe, Niigata, Japan, 5–8 November 2007; pp. 1–6. [Google Scholar]






| Internal Grid | External Grid | ||||
|---|---|---|---|---|---|
| Name | Node | P(kW) | Name | Node | P(kW) |
| DG1 | 5 | 71.9 | DG5 | 25 | 44.3 |
| DG2 | 30 | 49.8 | DG6 | 35 | 66.7 |
| DG3 | 41 | 64.3 | DG7 | 47 | 132.9 |
| DG4 | 61 | 173.8 | DG8 | 67 | 113.8 |
| Internal Grid | External Grid | ||||||
|---|---|---|---|---|---|---|---|
| Name | Node | Phase | P(kW) | Name | Node | Phase | P(kW) |
| DG1 | 11 | B | 16.3 | DG7 | 36 | C | 82.6 |
| DG2 | 19 | C | 20.1 | DG8 | 53 | A | 184.9 |
| DG3 | 23 | A | 18.0 | B | 202.1 | ||
| DG4 | 58 | A | 12.3 | C | 303.3 | ||
| B | 32.9 | DG9 | 85 | A | 64.3 | ||
| C | 62.9 | B | 77.2 | ||||
| DG5 | 66 | A | 42.3 | C | 67.5 | ||
| B | 32.9 | DG10 | 98 | A | 92.9 | ||
| C | 62.9 | DG11 | 102 | B | 62.9 | ||
| DG6 | 76 | C | 67.3 | DG12 | 122 | A | 51.6 |
| Method | Without DG | With DG | ||
|---|---|---|---|---|
| emax (%) | eavg (%) | emax (%) | eavg (%) | |
| MEG | 0.48 | 0.21 | 1.823 | 0.03 |
| PV | 2.68 | 0.89 | 34.68 | 7.01 |
| PQ | 2.45 | 0.72 | 19.44 | 3.18 |
| COM | 1.78 | 0.63 | 27.34 | 5.23 |
| Error Indicator | MEG | PV | PQ | COM |
|---|---|---|---|---|
| emax (%) | 1.769 | 26.97 | 8.07 | 18.76 |
| eavg (%) | 0.17 | 5.64 | 1.80 | 4.68 |
| Method | emax (%) | eavg (%) | ||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| MEG | 0.33 | 0.23 | 0.44 | 0.16 | 0.13 | 0.16 |
| PV | 3.15 | 0.71 | 1.76 | 2.13 | 0.49 | 1.14 |
| PQ | 2.82 | 2.80 | 3.67 | 2.20 | 1.31 | 2.21 |
| COM | 2.02 | 1.38 | 3.18 | 1.43 | 0.83 | 1.89 |
| Method | emax(%) | eavg(%) | ||||
|---|---|---|---|---|---|---|
| A | B | C | A | B | C | |
| MEG | 1.27 | 0.44 | 1.11 | 0.16 | 0.13 | 0.16 |
| PV | 11.83 | 5.71 | 4.35 | 6.93 | 3.40 | 2.45 |
| PQ | 3.37 | 3.99 | 3.16 | 1.78 | 2.32 | 1.69 |
| COM | 4.82 | 11.4 | 7.14 | 2.76 | 6.84 | 4.01 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, A.; Huang, H.; Yang, W.; Li, H. Multivariable Regression Equivalent Model of Interconnected Active Distribution Networks Based on Boundary Measurement. Energies 2019, 12, 2339. https://doi.org/10.3390/en12122339
Zhang A, Huang H, Yang W, Li H. Multivariable Regression Equivalent Model of Interconnected Active Distribution Networks Based on Boundary Measurement. Energies. 2019; 12(12):2339. https://doi.org/10.3390/en12122339
Chicago/Turabian StyleZhang, Anan, Huang Huang, Wei Yang, and Hongwei Li. 2019. "Multivariable Regression Equivalent Model of Interconnected Active Distribution Networks Based on Boundary Measurement" Energies 12, no. 12: 2339. https://doi.org/10.3390/en12122339
APA StyleZhang, A., Huang, H., Yang, W., & Li, H. (2019). Multivariable Regression Equivalent Model of Interconnected Active Distribution Networks Based on Boundary Measurement. Energies, 12(12), 2339. https://doi.org/10.3390/en12122339





