A Generalized and Mode-Adaptive Approach to the Power Flow Analysis of the Isolated Hybrid AC/DC Microgrids
Abstract
1. Introduction
2. Primary Control in the Hierarchical Controlled AC/DC IHMG
2.1. Hierarchical Control Level
- Level 1 (primary control): The control object of this level achieves voltage/frequency control for interface devices of the distributed energy resources (DER). Moreover, the power sharing and optimal power management of resources can be obtained;
- Level 2 (secondary control): The control level utilizes the low speed communication network to compensate for the voltage and frequency deviations caused by the primary control level;
- Level 3 (tertiary control): There is a positive response in this control level for external dispatching instructions to maintain the effectiveness, economy, and reliability of the system.
2.2. The Primary Control of the DERs in the IHMG
2.3. The Primary Control of the IC in the IHMG
- IC can be a slack bus for the AC subgrid, compensating power mismatch in the AC subgrid in the weak systems, while the DC subgrid has a higher power surplus [34]. In this case, the IC can operate in grid-forming mode to perform frequency and voltage control of the AC subgrid;
- IC can be a slack bus for the DC subgrid with lower power surplus capacity than that of the AC subgrid. Moreover, IC can perform voltage control of the DC subgrid as a grid-forming unit in the DC subgrid;
- In order to achieve the equal loadings of subgrids, both subgrids of the IHMG should have similar power when the IC controls the transfer of the active power between the neighboring AC and DC subgrids. Moreover, in order to adapt the active power transfer between the two subgrids, IC measures the AC frequency and DC voltage and equalizes them by normalizing. The corresponding control strategies are as follows:where is the power transferred from the DC to the AC subgrids through the IC in the IHMG.
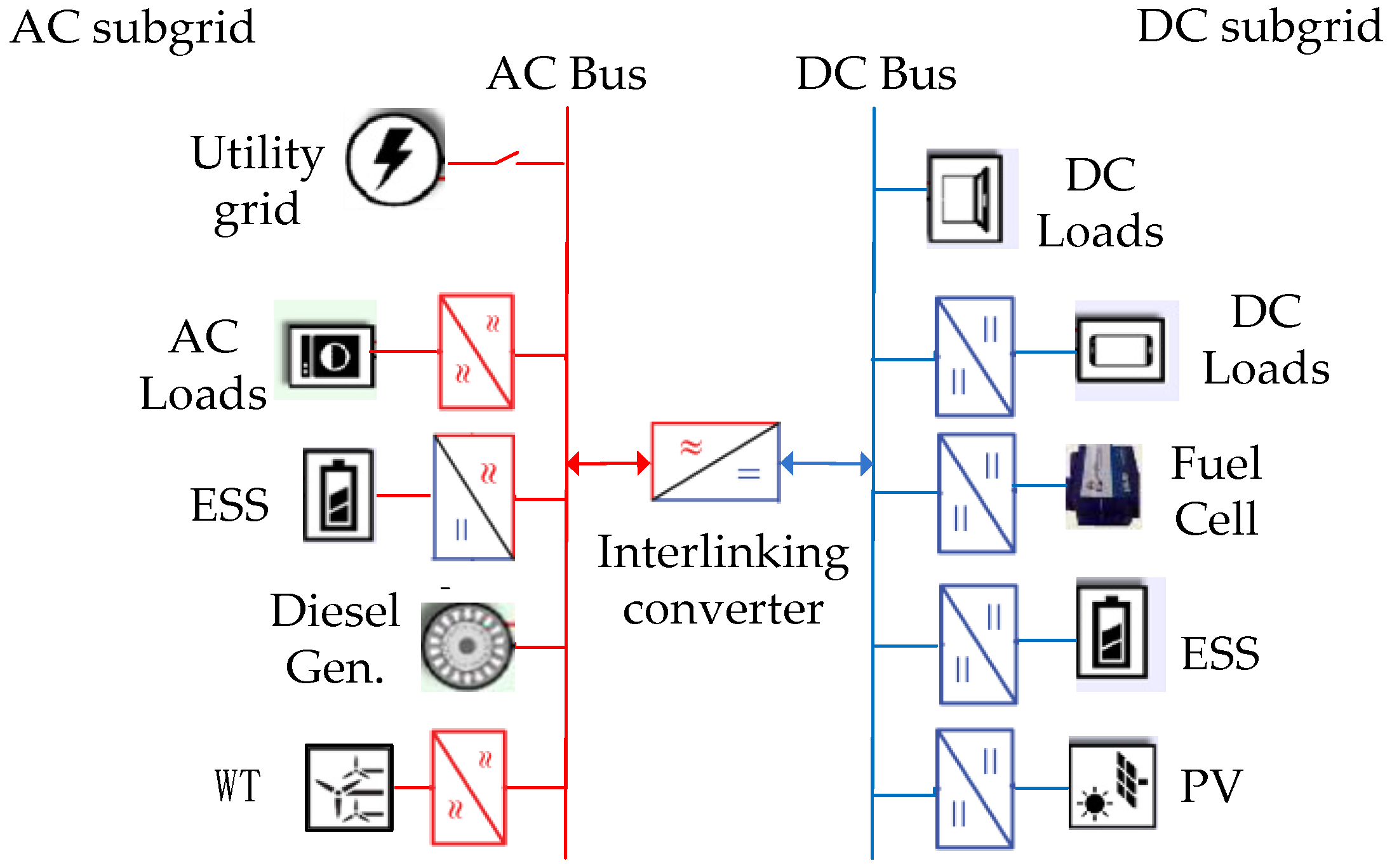
3. Definition of the Operating Modes in the AC/DC IHMG
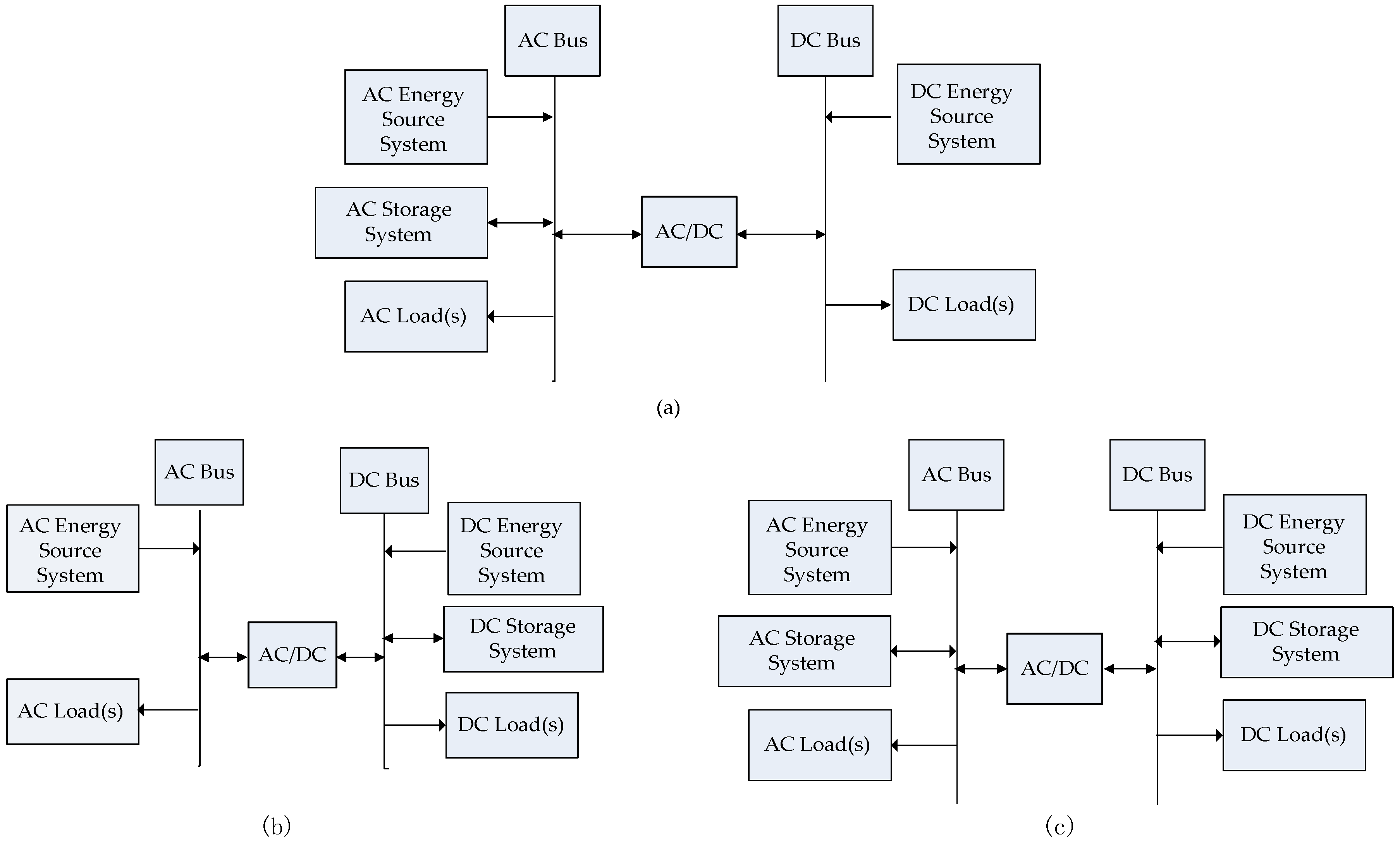
3.1. Classification of the AC/DC IHMG Configurations
- Disconnecting from the main network;
- Connecting the AC and DC subgrids through bidirectional AC/DC interfacing converters (ICs) to fulfill the bidirectional power flow between subgrids;
- Dividing the zones according to the DER type, such as RES, DG and ESS, and load type, such as AC or DC.
3.2. Primary Control Operating Modes
4. Formulation of the Unified PF Model
4.1. DER Model
4.2. Formulation of the Unified PF Model
- Unit-type vector W ((N + M) × 1): It describes the unit type (i.e., grid-following or grid forming) connected to the relevant bus in the AC/DC subgrid, as follows:
- (i)
- When = 1, the bus connects to the grid-forming unit;
- (ii)
- When = 0, the bus does not connect to the grid-following unit.
- Judgment vector D ((N + M) × 1): It checks for the coexistence of grid-forming units in both AC and DC subgrids:
- (i)
- When = 1, the grid-forming unit is available in both AC and DC subgrids;
- (ii)
- When = 0, the grid-forming unit is only installed separately in the AC or DC subgrids.
- Judgment vector U ((N + M) × 1): It checks for the existence of the grid-forming unit in each AC or DC subgrid:
- (i)
- When = 1, there are grid-forming units in the AC subgrid;
- (ii)
- When = 0, there is not grid-forming unit in the AC subgrid.
- The AC admittance matrix Y(N N):
- DC conductance matrix : The element in the matrix reflects the value of the conductance of the DC line that connects two buses.
4.3. Power Balance Equations
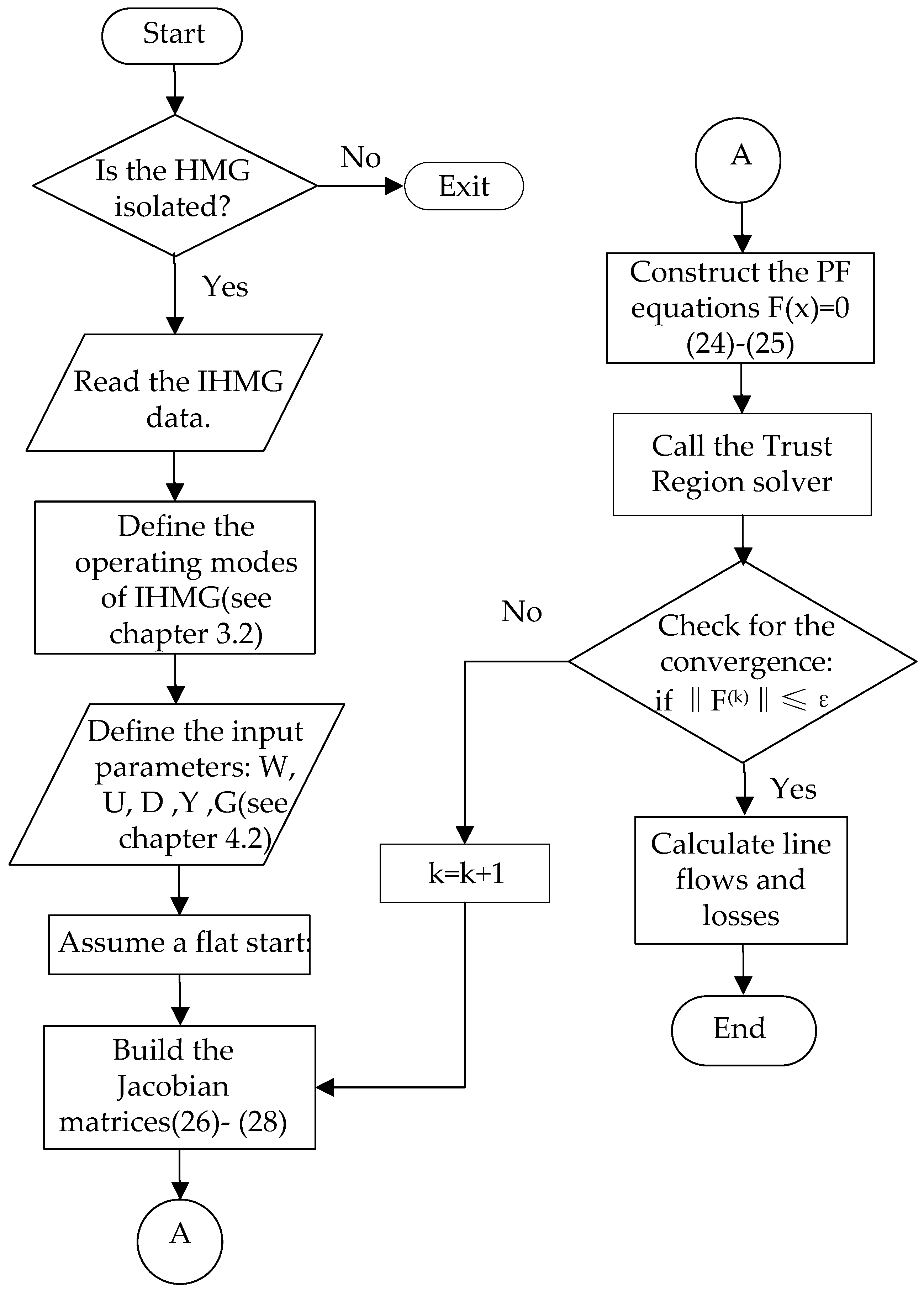
4.4. Solution Procedure
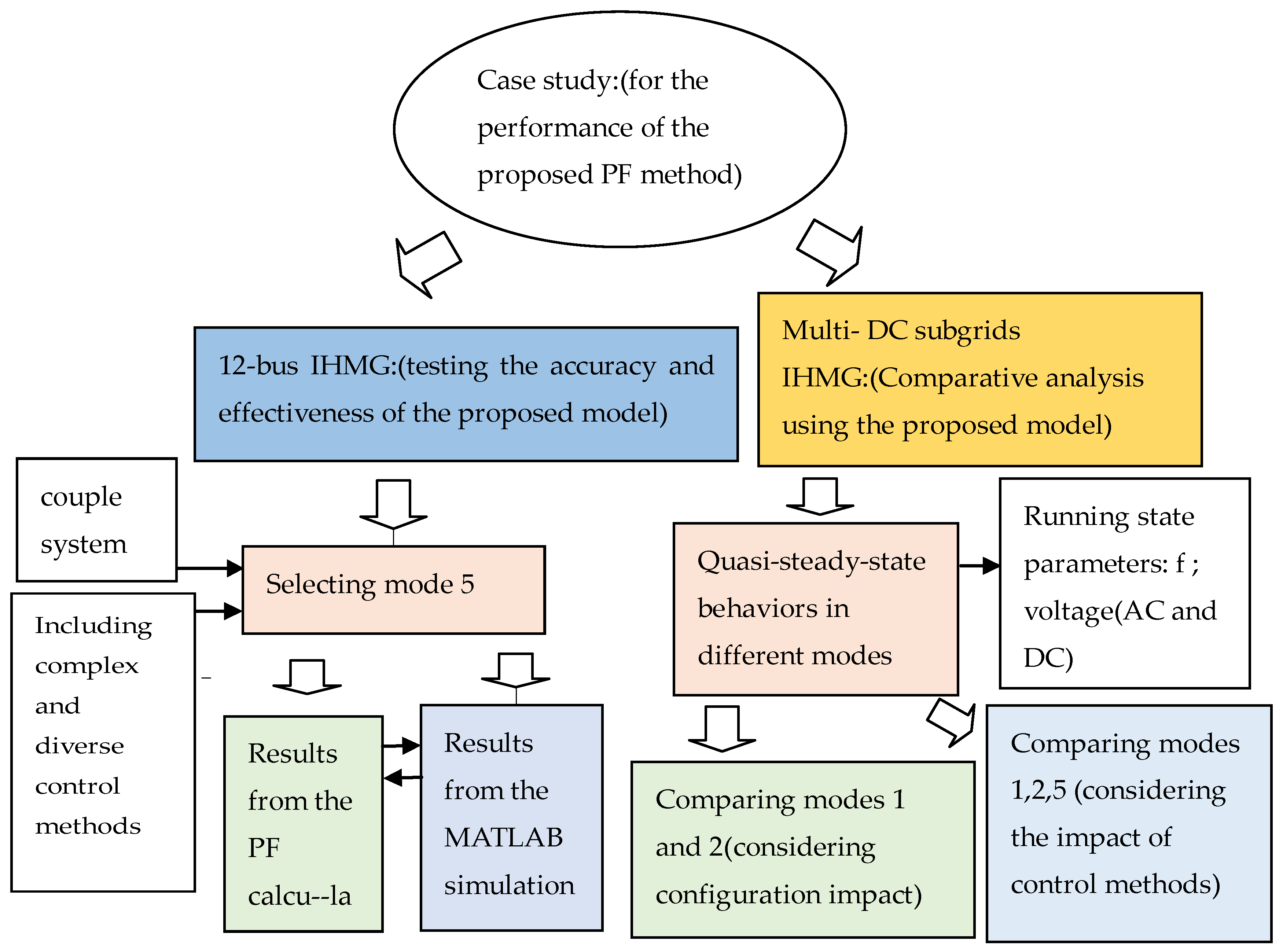
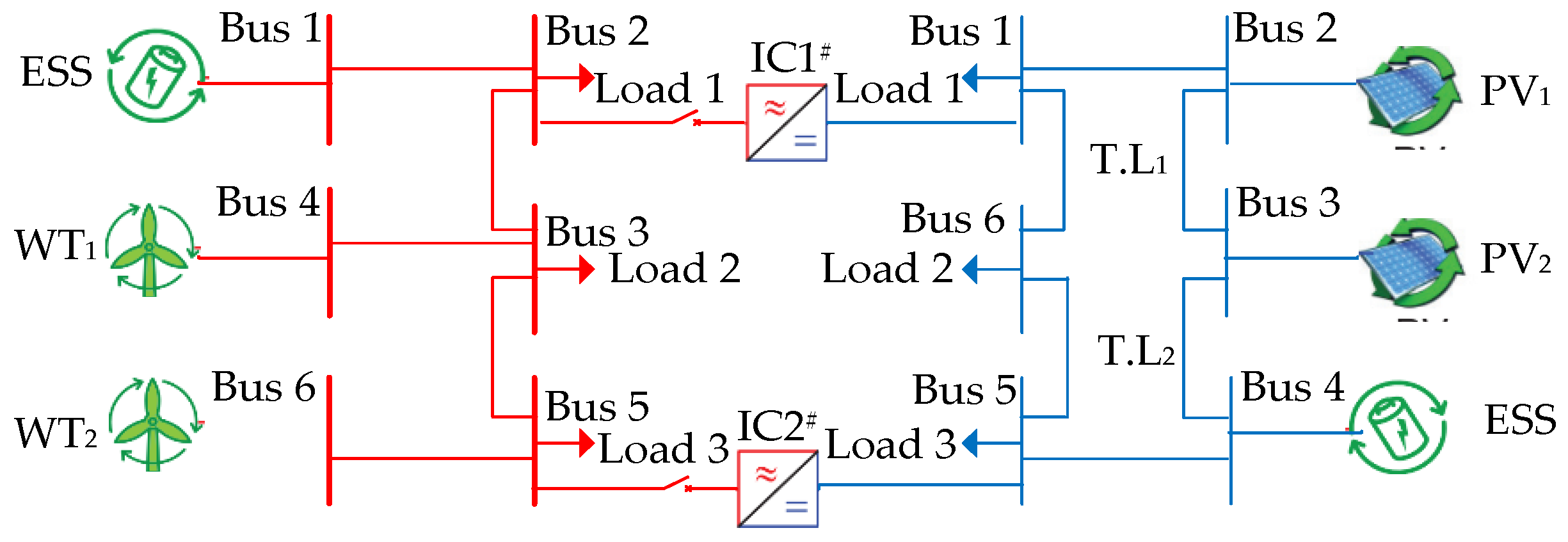
5. Cases Studies
5.1. Twelve-Bus Test System
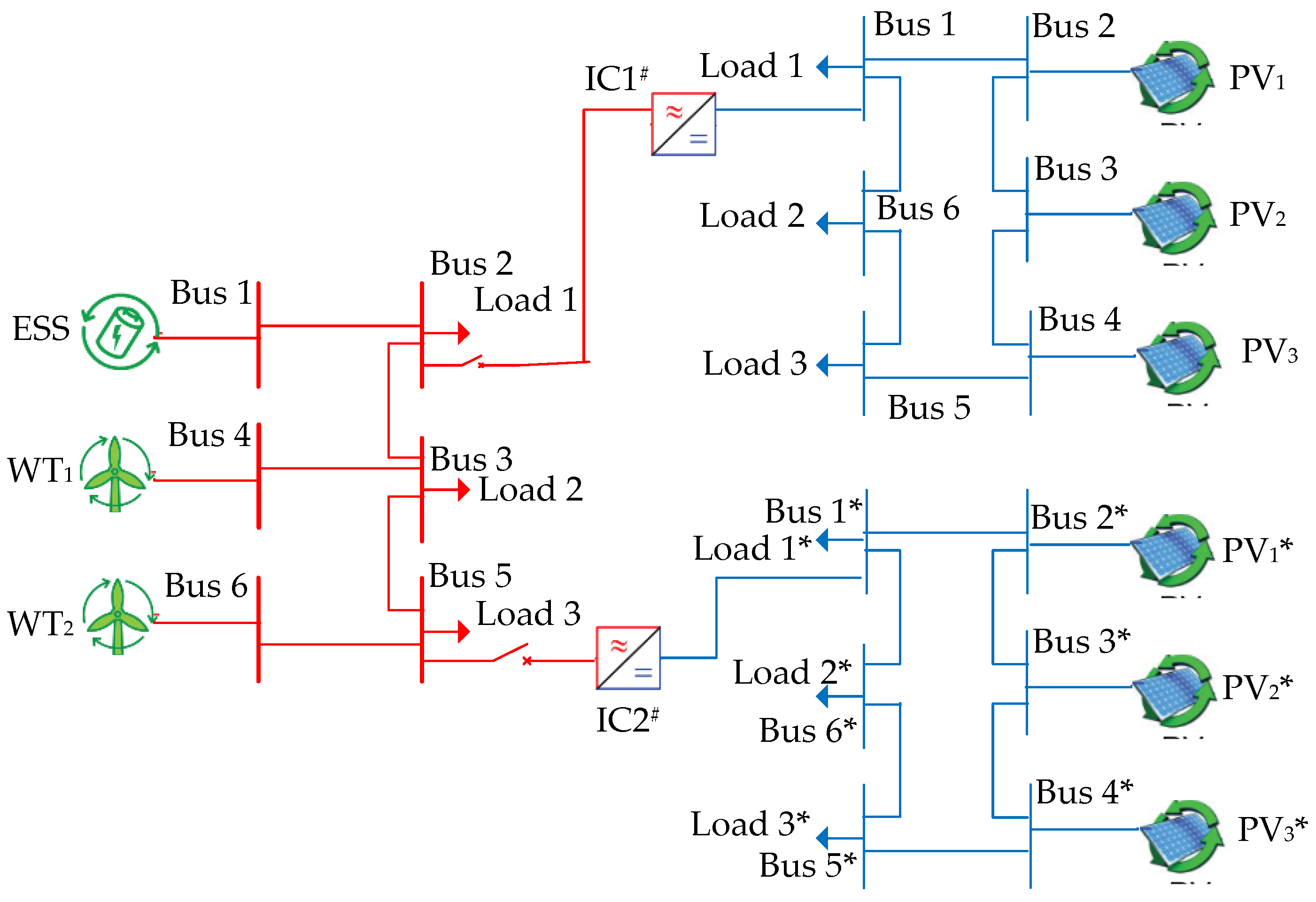
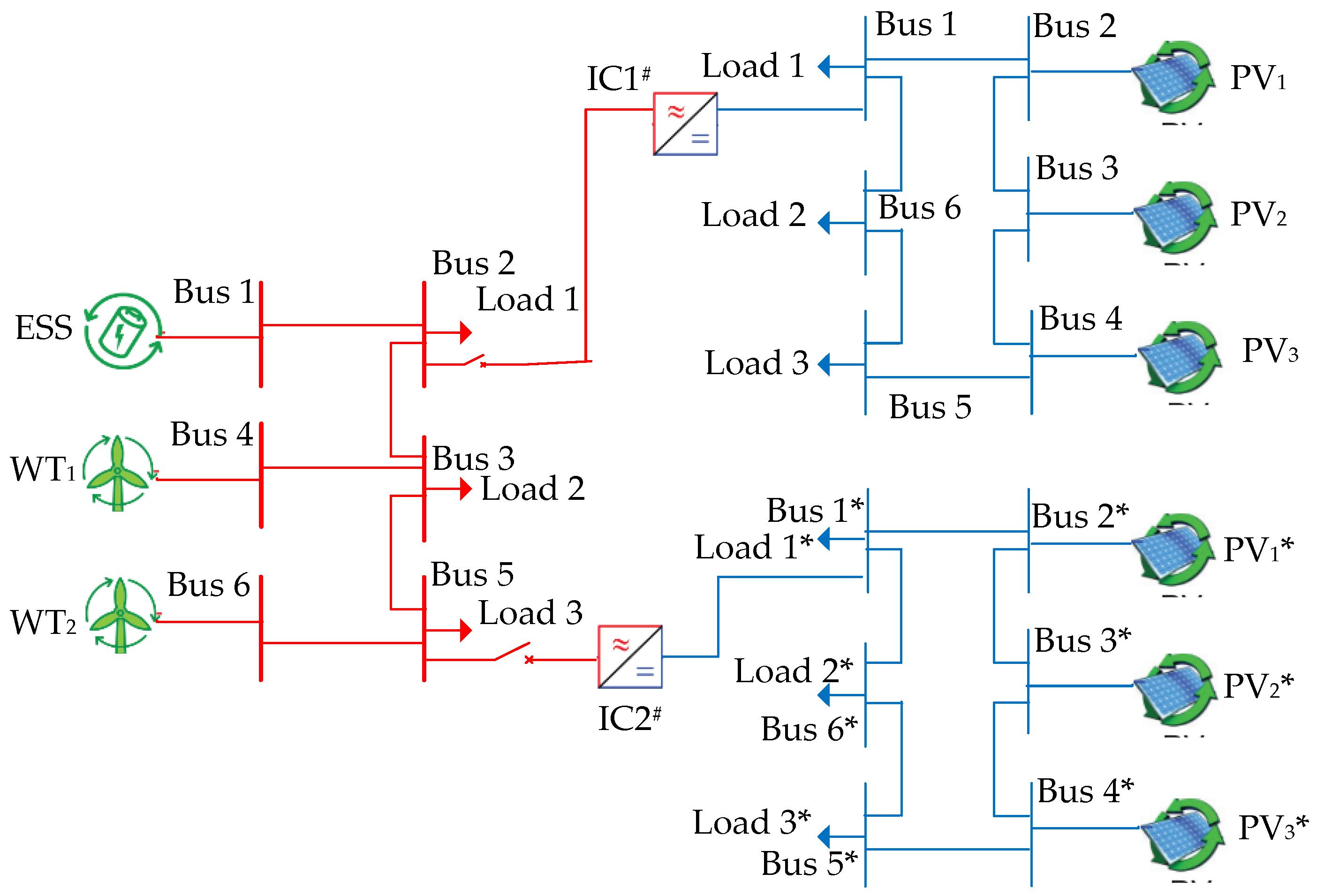
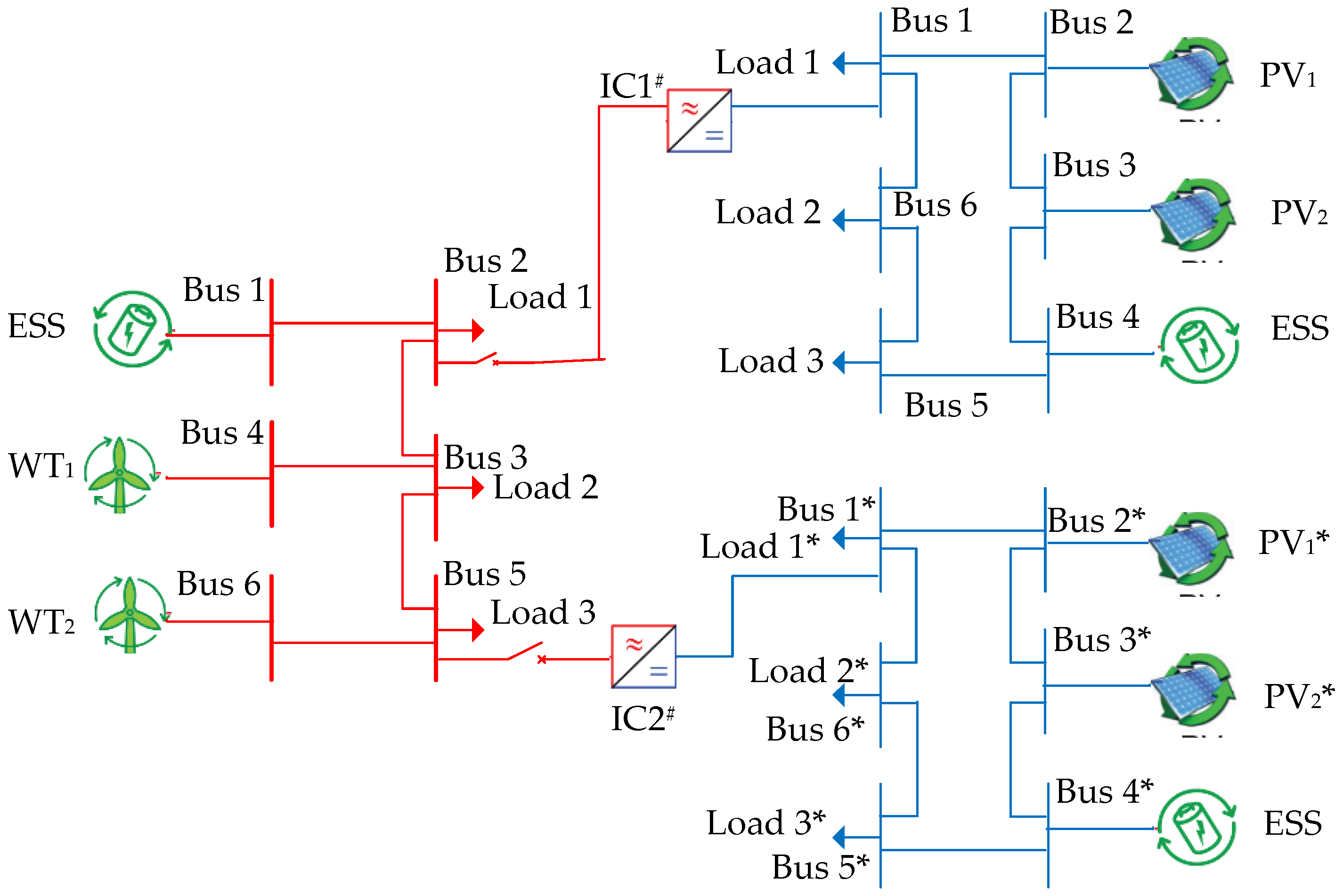
5.2. Multi-DC Subgrids IHMG Test System
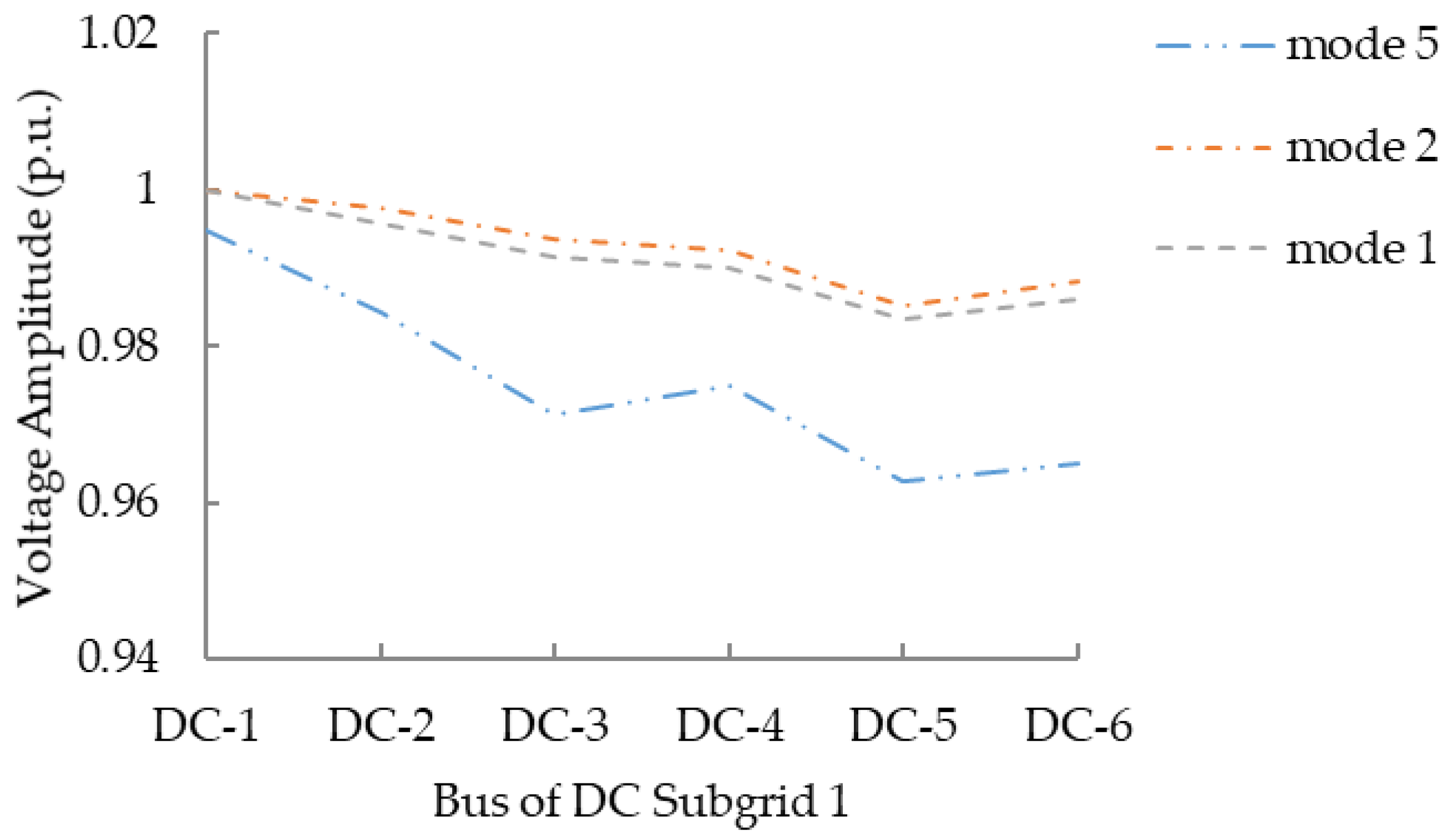
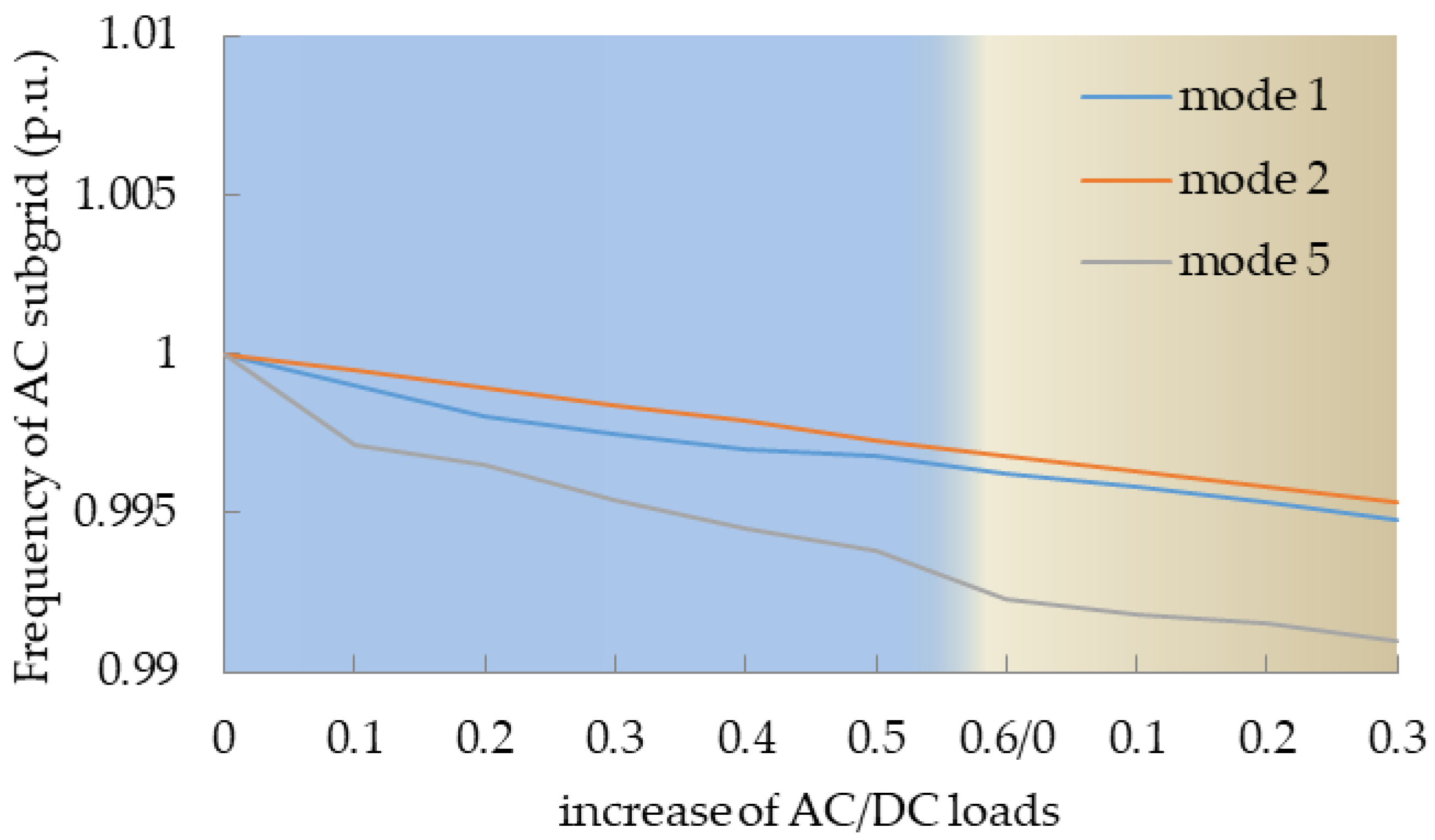
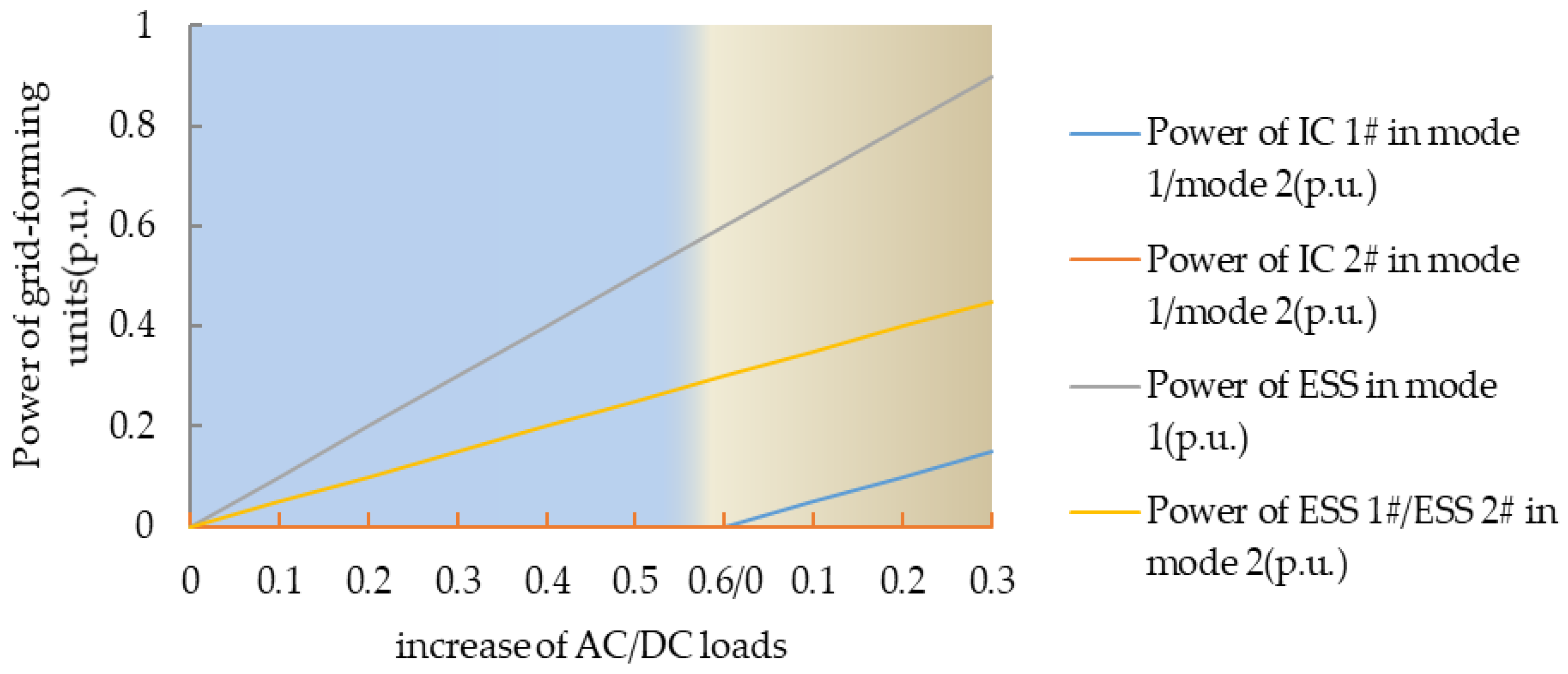
5.2.1. Algorithm Performance in the Normal Potation of the Multi-DC Subgrids System
5.2.2. Algorithm Performance in the Operation of the Multi-DC Subgrids IHMG System during Load Fluctuation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Wang, P.; Goel, L.; Liu, X.; Ghoo, F.H. Harmonizing AC and DC: A Hybrid AC/DC Future Grid Solution. IEEE Power Energy Mag. 2013, 11. [Google Scholar] [CrossRef]
- Han, Y.; Li, H.; Shen, P.; Coelho, E.A.A.; Guerrero, M. Review of Active and Reactive Power Sharing Strategies in Hierarchical Controlled Microgrids. IEEE Trans. Power Electron. 2017, 32, 2427–2451. [Google Scholar] [CrossRef]
- Guerrero, J.M.; Chandorkar, M.; Lee, T.L. Advanced Control Architectures for Intelligent Microgrids—Part I: Decentralized and Hierarchical Control. IEEE Trans. Ind. Electron. 2013, 60, 1254–1262. [Google Scholar] [CrossRef]
- Vandoorn, T.L.; Vasquez, J.C.; Kooning, J.D.; Guerrero, J.M.; Vandevelde, L. Microgrids: Hierarchical Control and an Overview of the Control and Reserve Management Strategies. IEEE Trans. Ind. Electron. 2013, 7, 42–55. [Google Scholar] [CrossRef]
- Palizban, O.; Kauhaniemi, K.; Guerrero, J.M. Microgrids in active network management—Part I: Hierarchical control, energy storage, virtual power plants, and market participation. Renew. Sustain. Energy Rev. 2014, 36, 428–439. [Google Scholar] [CrossRef]
- Palizban, O.; Kauhaniemi, K.; Guerrero, J.M. Microgrids in active network management—Part II: System operation, power quality and peotection. Renew. Sustain. Energy Rev. 2014, 36, 440–451. [Google Scholar] [CrossRef]
- Abdelaziz, M.M.A.; Ziz, M.M.F.; Farag, H.E.; El-Saadany, E.F. A multistage centralized control scheme for islanded microgrids with PEVs. IEEE Trans. Sustain. Energy 2014, 5, 927–937. [Google Scholar] [CrossRef]
- Nehrir, M.H.; Wang, C.; Strunz, K.; Aki, H.; Ramakumar, R.; Bing, J. A Review of Hybrid Renewable/Alternative Energy Systems for Electric Power Generation: Configurations, Control, and Applications. IEEE Trans. Sustain. Energy 2011, 2, 392–403. [Google Scholar] [CrossRef]
- Eghtedarpour, N.; Farjah, E. Power control and management in a hybrid AC/DC microgrid. IEEE Trans. Smart Grid 2014, 5, 1494–1505. [Google Scholar] [CrossRef]
- Unamunon, E.; Barrena, J.A. Hybrid ac/dc microgrids—Part II: Review and classification of control strategies. Renew. Sustain. Energy Rev. 2015, 52, 1123–1134. [Google Scholar] [CrossRef]
- Aneke, M.; Wang, M. Energy storage technologies and real life applications—A state of the art review. Appl. Energy 2016, 179, 350–377. [Google Scholar] [CrossRef]
- Ahn, S.J.; Park, J.W.; Chung, L.Y.; Moon, S.L.; Kang, S.H.; Nam, S.R. Power-Sharing Method of Multiple Distributed Generators Considering Control Modes and Configurations of a Microgrid. IEEE Trans. Power Deliv. 2010, 25, 2007–2016. [Google Scholar] [CrossRef]
- Bouzid, A.B.; Guerrero, J.M.; Cheriti, A.; Bouhamida, M.; Sicard, P.; Benghanem, M. A survey on control of electric power distributed generation systemsfor microgrid applications. Renew. Sustain. Energy Rev. 2015, 44, 751–766. [Google Scholar] [CrossRef]
- Hossain, M.A.; Pota, H.P.; Issa, W.; Hossain, M.J. Overview of AC Microgrid Controls withInverter-Interfaced Generations. Energies 2017, 10, 1300. [Google Scholar] [CrossRef]
- Nejabatkhah, F.; Li, Y.W. Overview of power management strategies of hybrid ac/dc microgrid. IEEE Trans. Power Electron. 2015, 30, 7072–7089. [Google Scholar] [CrossRef]
- Zhong, Q.C. Robust droop controller for accurate proportional load sharing among inverters operated in parallel. IEEE Trans. Ind. Electron. 2013, 60, 1281–1290. [Google Scholar] [CrossRef]
- Khorsandi, A.; Ashourloo, M.; Mokhtari, H. A decentralized control method for a low-voltage dc microgrid. IEEE Trans. Energy Convers. 2014, 29, 793–801. [Google Scholar] [CrossRef]
- Lu, X.; Guerrero, J.M.; Sun, K.; Vasquez, C. An improved droop control method for dc microgrids base on low bandwidth communication with dc bus voltage restoration and enhanced current sharing accuracy. IEEE Trans. Power Electron. 2014, 29, 1800–1812. [Google Scholar] [CrossRef]
- Piegari, L.; Tironi, E.; Musolino, V.; Grillo, S.; Tornelli, C. DC islands in ac smatrt grids. IEEE Trans. Power Electron. 2014, 29, 89–98. [Google Scholar]
- Dragičević, T.; Lu, X.; Vasquez, J.C.; Guerrero, J.M. DC Microgrids—Part I: A Review of Control Strategies and Stabilization Techniques. IEEE Trans. Power Electron. 2016, 31, 4876–4891. [Google Scholar]
- Unamuno, E.; Barrena, J.A. Primary control operation modes in islanded hybrid ac/dc microgrids. In Proceedings of the IEEE EUROCON 2015—International Conference on Computer as a Tool, Salamanca, Spain, 8–11 September 2015. [Google Scholar]
- Cimuca, G.O.; Saudemont, C.; Robyns, B.; Radulescu, M.M. Controland performance evaluation of a flywheel energy-storage system associated to a variable-speed wind generator. IEEE Trans. Power Electron. 2006, 53, 1074–1085. [Google Scholar]
- Loh, P.C.; Li, D.; Chai, Y.K.; Blaabjerg, F. Autonomous Operation of Hybrid MicrogridWith AC and DC Subgrids. IEEE Trans. Power Electron. 2012, 28, 2214–2223. [Google Scholar] [CrossRef]
- Loh, P.C.; Li, D.; Chai, Y.K.; Blaabjerg, F. Hybrid ac-dc microgrids with energy storages and progressive energy flow tuning. IEEE Trans. Power Electron. 2013, 28, 1533–1543. [Google Scholar] [CrossRef]
- Liu, X.; Wang, P.; Loh, P.C. A hybrid ac/dc microgid and its coordination control. IEEE Trans. Smart Grid 2011, 2, 278–286. [Google Scholar]
- Majumder, R. A hybrid microgrid with dc connection at back to back converters. IEEE Trans. Smart Grid 2014, 5, 251–259. [Google Scholar] [CrossRef]
- Xia, Y.; Peng, Y.G.; Yang, P.C.; Yu, M.; Wei, W. Distributed Coordination Control for Multiple Bidirectional Power Converters in a Hybrid AC/DC Microgrid. IEEE Trans. Power Electron. 2017, 32, 4949–4959. [Google Scholar] [CrossRef]
- Grainger, J.J.; Stevenson, W.D. Power System Analysis, 1st ed.; McGraw-Hill College: New York, NY, USA, 1994; pp. 1–361. [Google Scholar]
- Li, C.L.; Chaudhary, S.K.; Savaghebi, M.S.; Vasquez, J.C.; Guerrero, J.M. Power Flow Analysis for Low-Voltage AC and DC Microgrids Considering Droop Control and Virtual Impedance. IEEE Trans. Smart Grid 2017, 8, 2754–2764. [Google Scholar] [CrossRef]
- Wang, W.; Barnes, M. Power Flow Algorithms for Multi-Terminal VSC-HVDC With Droop Control. IEEE Trans. Power Syst. 2014, 29, 1721–1730. [Google Scholar] [CrossRef]
- Baradar, M.; Ghandhari, M. A Multi-Option Unified Power FlowApproach for Hybrid AC/DC Grids Incorporating Multi-TerminalVSC-HVDC. IEEE Trans. Power Syst. 2013, 28, 2376–2383. [Google Scholar] [CrossRef]
- Baradar, M.; Ghandhari, M.; Hertem, D.V. The modeling multi-terminal VSC-HVDC in power flow calculation using unified methodology. In Proceedings of the 2011 2nd IEEE PES International Conference and Exhibition on Innovative Smart Grid Technologies, Manchester, UK, 5–7 December 2011. [Google Scholar]
- Ahmed, H.M.A.; Eltantawy, A.B.; Salama, M.M.A. A Generalized Approach to the Load Flow Analysis of AC–DC Hybrid Distribution Systems. IEEE Trans. Power Syst. 2017, 33, 2117–2127. [Google Scholar] [CrossRef]
- Hamad, A.A.; Salama, M.M.; EL-Saadany, E.F. A Novel Load Flow Algorithm for Islanded AC/DC Hybrid Microgrids. IEEE Trans. Smart Grid 2019, 10, 1553–1566. [Google Scholar]
- Eajal, A.A.; Mohamed, A.A.; El-Saadany, E.F. A Unified Approach to the Power Flow Analysisof AC/DC Hybrid Microgrids. IEEE Trans. Sustain. Energy 2016, 7, 1145–1158. [Google Scholar] [CrossRef]
- Aprilia, E.; Meng, K.; Hosani, M.A.; Zeineldin, H.H. Unified Power Flow Algorithm for Standalone AC/DC Hybrid Microgrids. IEEE Trans. Smart Grid 2019, 10, 639–649. [Google Scholar] [CrossRef]
- Hamad, A.A.; Azzouz, M.A.; Saadany, E.F.E. A Sequential Power Flow Algorithm for Islanded Hybrid AC/DC Microgrids. IEEE Trans. Power Syst. 2016, 31, 3961–3970. [Google Scholar] [CrossRef]
- Aprilia, E.; Meng, K.; Dong, Z.Y.; Jia, Y.W.; Xu, Z. Hierarchical power flow algorithm for standalone hybrid AC/Multi-DC microgrids. In Proceedings of the 2017 IEEE Power & Energy Society General Meeting, Chicago, IL, USA, 16–20 July 2017. [Google Scholar]
- Golsorkhi, M.S.; Lu, D.D.C. A decentralized power flow control method for islanded microgrids using V-I droop. In Proceedings of the2014 22nd Iranian Conference on Electrical Engineering, Tehran, Iran, 20−22 May 2014. [Google Scholar]
- Beerten, J.; Cole, S.; Belmans, R. A sequential AC/DC power flow algorithm for networks containing Multi-terminal VSC HVDC systems. In Proceedings of the IEEE Power and Energy Society General Meeting, Providence, RI, USA, 25–29 July 2010. [Google Scholar]
- Narayanan, K.N.; Mitra, P. A comparative study of a sequential and simultaneous AC-DC power flow algorithms for a multi-terminal VSC-HVDC system. In Proceedings of the 2013 IEEE Innovative Smart Grid Technologies-Asia, Bangalore, India, 10–13 November 2013. [Google Scholar]
- Nocedal, J.; Wright, S.J. Numerical Optimization, 2nd ed.; Springer: New York, NY, USA, 2006; pp. 66–91. [Google Scholar]
- Chen, Y.C.; Dong, P.; Wu, Z.D. Analysis of power flow in wind farm with matpower. In Proceedings of the 2017 7th International Conference on Power Electronics Systems and Applications—Smart Mobility, Power Transfer & Security, Hong Kong, China, 12–14 December 2017. [Google Scholar]
- Zimmerman, R.D.; Daniel, R.; Murillo-Sanchez, C.E.; Thomas, R.J. MATPOWER: Steady-State Operations, Planning, and Analysis Tools for Power Systems Research and Education. IEEE Trans. Power Syst. 2011, 26, 12–19. [Google Scholar] [CrossRef]
- IEEE Guide for Design; Operationand Integration of Distributed Resource IslandSystems with Electric Power Systems; IEEE Std.: Piscataway, NJ, USA, 2011; pp. 1–54.
- Pogaku, N.; Prodanovic, M.; Green, T.C. Modeling, analysis and testing of autonomous operation of an inverter-based microgrid. IEEE Trans. Power Electron. 2007, 22, 623–625. [Google Scholar] [CrossRef]
- Hosseinzadeh, M.; Salmasi, F.R. Robust optimal power management system for a hybrid AC/DC micro-grid. IEEE Trans. Sustain. Energy 2015, 3, 675–687. [Google Scholar] [CrossRef]

| Unit Type in Mode 1 | Source Type | Control Type | Output Impedance | PF Model |
|---|---|---|---|---|
| AC ESS or DG | Non-Ideal Voltage source | Droop 1 | Finite, nonzero | Droop |
| RES | Ideal current source | MPPT | 0 | PQ |
| IC | DC Ideal Voltage source | Constant DC Voltage control | 0 | DC constant V |
| DC ESS or DG | - | - | - | - |
| Unit Type in Mode 3 | Source Type | Control Type | Output Impedance | PF Model |
|---|---|---|---|---|
| AC ESS or DG | - | - | - | - |
| RES | Ideal current source | MPPT | 0 | PQ |
| IC | AC Ideal Voltage source | Constant AC Voltage control | 0 | AC constant V |
| DC ESS or DG | Non-Ideal Voltage source | Droop 2 | Finite, nonzero | Droop |
| Unit Type in Mode 5 | Source Type | Control Type | Output Impedance | PF Model |
|---|---|---|---|---|
| AC ESS or DG | Non-Ideal Voltage source | Droop 1 | Finite, nonzero | Droop |
| RES | Ideal current source | MPPT | 0 | PQ |
| IC | Non-Ideal Voltage source | Droop 3 | Finite, nonzero | Droop |
| DC ESS or DG | Non-Ideal Voltage source | Droop 2 | Finite, nonzero | Droop |
| Subgrid | Bus Type | Number of Buses | Known Quantity | Unknown Quantity x = [xAC, xDC] | Number of Equations |
|---|---|---|---|---|---|
| AC | PQ | NR | Pn, Qn | Vn, | 2NR |
| Droop | ND | - | Pn, Qn, Vn, | 4ND | |
| Slack bus | 1 | Vn, | Pn, Qn | - | |
| DC | Const.P | MR | Pm | Vm | MR |
| Droop | MD | - | Pm, Vm | 2MD | |
| Const.V | M-MR-MD | Vm | Pm | M-MR-MD |
| Mode Type | Ui | Di | Wi |
|---|---|---|---|
| Mode 1 | 1 | 0 | 1 |
| Mode 3 | 0 | 0 | 0 |
| Mode 5 | 1 | 1 | 1 |
| Bus | Bus Type | Unified PF Results | MATLAB Results | ||
|---|---|---|---|---|---|
| Vn (p.u.) | θn (p.u.) | Vn (p.u.) | θn (p.u.) | ||
| 1(AC 1) | Droop | 0.9944 | 0.0337 | 0.9947 | 0.0330 |
| 2(AC 1) | Droop (IC AC) | 0.9928 | 0.0289 | 0.9932 | 0.0301 |
| 3(AC 1) | PQ | 0.9965 | 0.0234 | 0.9968 | 0.0256 |
| 4(AC 1) | PQ (MPPT) | 0.9957 | 0.0440 | 0.9960 | 0.0443 |
| 5(AC 1) | Droop (IC AC) | 0.9934 | 0.0956 | 0.9931 | 0.0900 |
| 6(AC 1) | PQ (MPPT) | 0.9994 | 0.0000 | 0.9997 | 0.0000 |
| (DC 2) | Droop (IC DC) | 1.0086 | - | 1.0082 | - |
| (DC 2) | P | 1.0012 | - | 1.0013 | - |
| (DC 2) | P | 0.9986 | - | 0.9981 | - |
| (DC 2) | Droop | 0.9979 | - | 0.9972 | - |
| (DC 2) | Droop (IC DC) | 1.0079 | - | 1.0076 | - |
| (DC 2) | R | 0.9970 | - | 0.9969 | - |
| Bus | Bus Type | Unified PF Results | MATLAB Results | ||
|---|---|---|---|---|---|
| PDR,n (p.u.) | QDR,n (p.u.) | PDR,n (p.u.) | QDR,n (p.u.) | ||
| 1(AC 1) | Droop | −0.1325 | — | −0.1361 | — |
| 4(AC 1) | PQ | 0.2668 | 0.2013 | 0.2698 | 0.2000 |
| 6(AC 1) | Droop | 0.5967 | 0.3034 | 0.5924 | 0.3001 |
| (DC 2) | P | 0.6098 | — | 0.6092 | — |
| (DC 2) | Droop | 0.0198 | — | 0.2001 | — |
| (DC 2) | Droop | 0.1998 | — | 0.1990 | — |
| IC | (p.u.) | (p.u.) | (p.u.) | (p.u.) | (p.u.) |
|---|---|---|---|---|---|
| 0.038 | 0.9928 | 1.0086 | −0.057 | - | |
| 0.052 | 0.9934 | 1.0079 | −0.077 | - |
| MG | Bus No. | Bus Type | (p.u.) | DR Type | MW | Mvar | (p.u.) | (p.u.) | (p.u.) |
|---|---|---|---|---|---|---|---|---|---|
| AC | 1 | Droop | 1.0 | DS | 0.8 | 0.6 | 1.0 | 0.0375 | 0.25 |
| 2 | Droop | 1.0 | - | - | - | 1.0 | 0.0625 | 0.4167 | |
| 3 | Z | 1.0 | - | - | - | 1.0 | - | - | |
| 4 | PQ | 1.0 | DG | 0.48 | 0.36 | 1.0 | - | - | |
| 5 | Droop | 1.0 | - | - | - | 1.0 | 0.0167 | - | |
| 6 | PQ | 1.0 | DG | 1.8 | 1.35 | 1.0 | - | - | |
| DC | 1 | Droop | 1.0 | - | - | - | - | 0.0781 | - |
| 2 | P | 1.0 | DG | 1.92 | - | - | - | - | |
| 3 | P | 1.0 | DG | 0.48 | - | - | - | - | |
| 4 | Droop | 1.0 | DS | 0.6 | - | - | 0.3125 | - | |
| 5 | R | 1.0 | - | - | - | - | - | - | |
| 6 | Droop | 1.0 | - | - | - | - | 0.25 | - |
| IC No. | AC Bus | DC Bus | (MW) | (Mvar) | (p.u.) | |||
|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 1 | 3.0 | 2.25 | 1.0 | 1.0 | 1.0 | 0.0667 |
| 2 | 5 | 5 | 3.0 | 2.25 | 1.0 | 1.0 | 1.0 | 0.0667 |
| MG | From | To | Load Connected to from Bus P(MW) Q(Mvar) | |||
|---|---|---|---|---|---|---|
| AC | 1 | 2 | 0.02646 | 0.01323 | - | |
| 2 | 3 | 0.04032 | 0.02016 | 0.4 | 0.3 | |
| 3 | 5 | 0.04032 | 0.02016 | 1.0 | 0.6 | |
| 5 | 6 | 0.02646 | 0.01323 | 0.8 | 0.6 | |
| 4 | 3 | 0.02646 | 0.01323 | - | ||
| DC | 1 | 2 | 0.4340 | - | 0.6 | |
| 2 | 3 | 0.2279 | - | - | ||
| 3 | 4 | 0.4100 | - | - | ||
| 4 | 5 | 0.4340 | - | - | ||
| 5 | 6 | 0.4100 | - | 1.4 | ||
| 6 | 1 | 0.2279 | - | 0.5 | ||
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xiao, Y.; Ren, C.; Han, X.; Wang, P. A Generalized and Mode-Adaptive Approach to the Power Flow Analysis of the Isolated Hybrid AC/DC Microgrids. Energies 2019, 12, 2253. https://doi.org/10.3390/en12122253
Xiao Y, Ren C, Han X, Wang P. A Generalized and Mode-Adaptive Approach to the Power Flow Analysis of the Isolated Hybrid AC/DC Microgrids. Energies. 2019; 12(12):2253. https://doi.org/10.3390/en12122253
Chicago/Turabian StyleXiao, Yu, Chunguang Ren, Xiaoqing Han, and Peng Wang. 2019. "A Generalized and Mode-Adaptive Approach to the Power Flow Analysis of the Isolated Hybrid AC/DC Microgrids" Energies 12, no. 12: 2253. https://doi.org/10.3390/en12122253
APA StyleXiao, Y., Ren, C., Han, X., & Wang, P. (2019). A Generalized and Mode-Adaptive Approach to the Power Flow Analysis of the Isolated Hybrid AC/DC Microgrids. Energies, 12(12), 2253. https://doi.org/10.3390/en12122253





