The Feasibility Appraisal for CO2 Enhanced Gas Recovery of Tight Gas Reservoir: Experimental Investigation and Numerical Model
Abstract
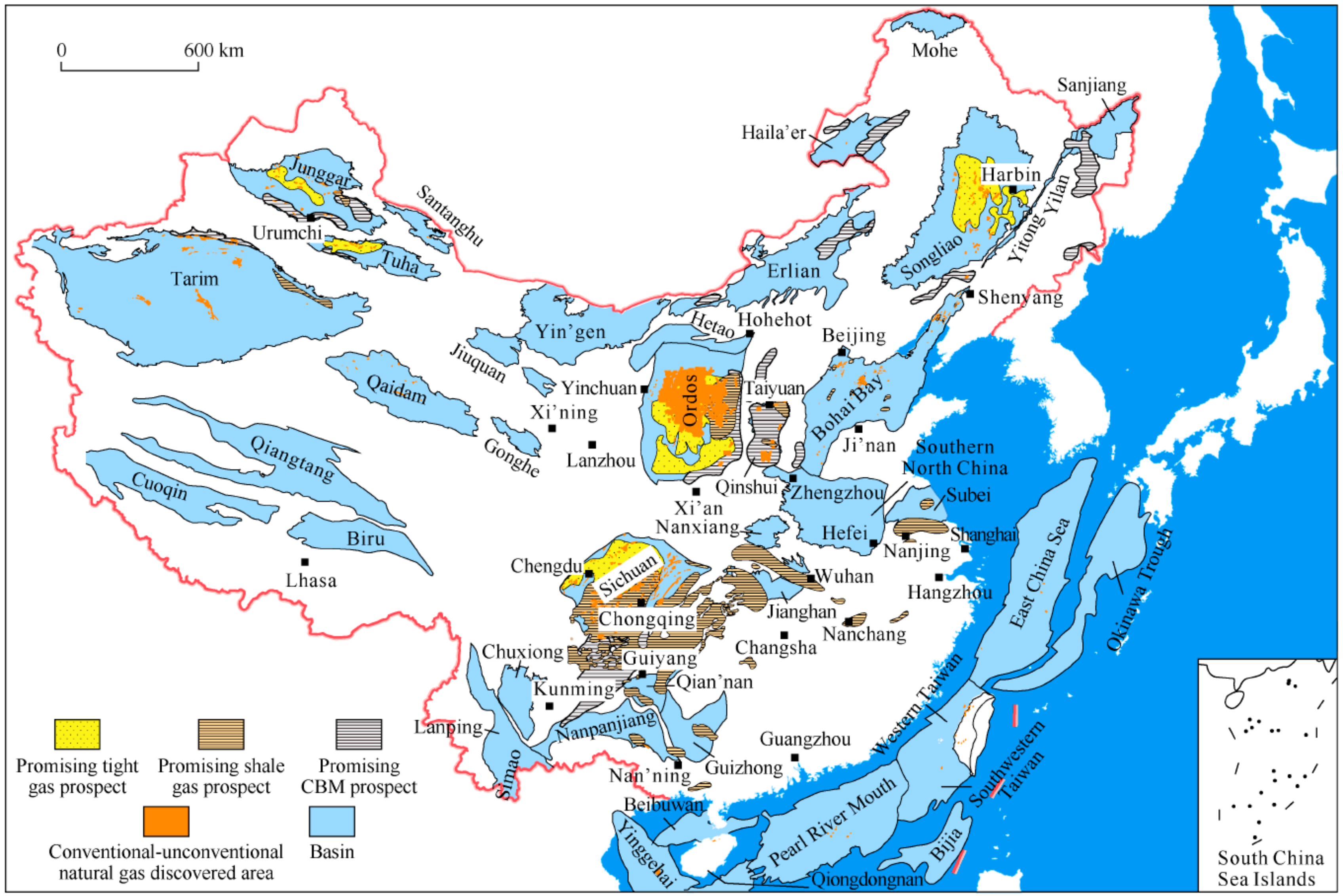
:1. Introduction
2. Material and Methods
2.1. Experiment
2.1.1. Material
2.1.2. Non-Equilibrium Phase Experiment
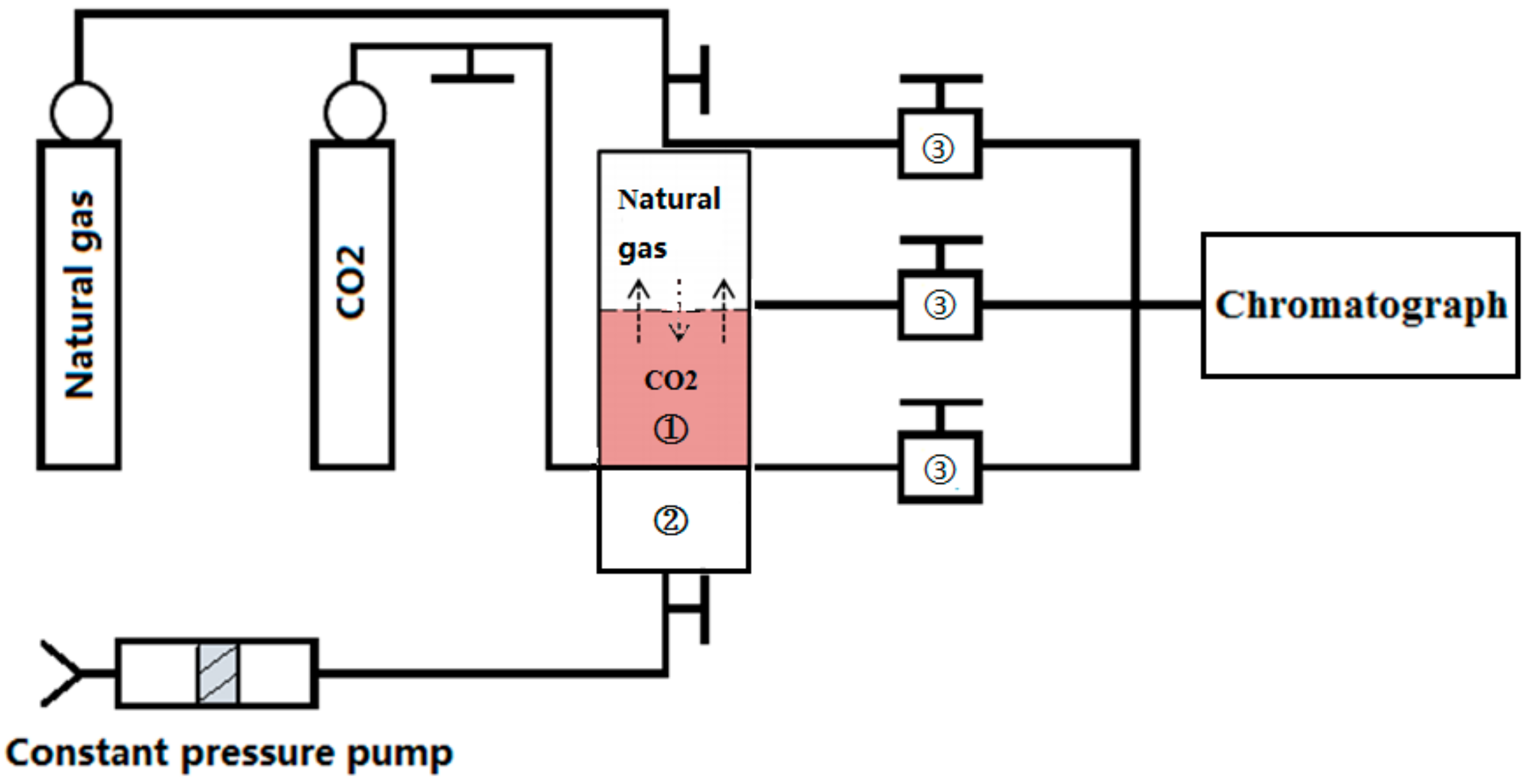
2.1.3. Supercritical CO2–Natural Gas Diffusion Experiment
2.1.4. Flooding Experiment
2.2. Numerical Model
2.2.1. Assumptions and Governing Model
2.2.2. Equilibrium Equation
Adjusted Peng–Robinson Equation of State
3. Results and Analysis
3.1. Experiment Results and Analysis
3.1.1. Non-Equilibrium Experiment
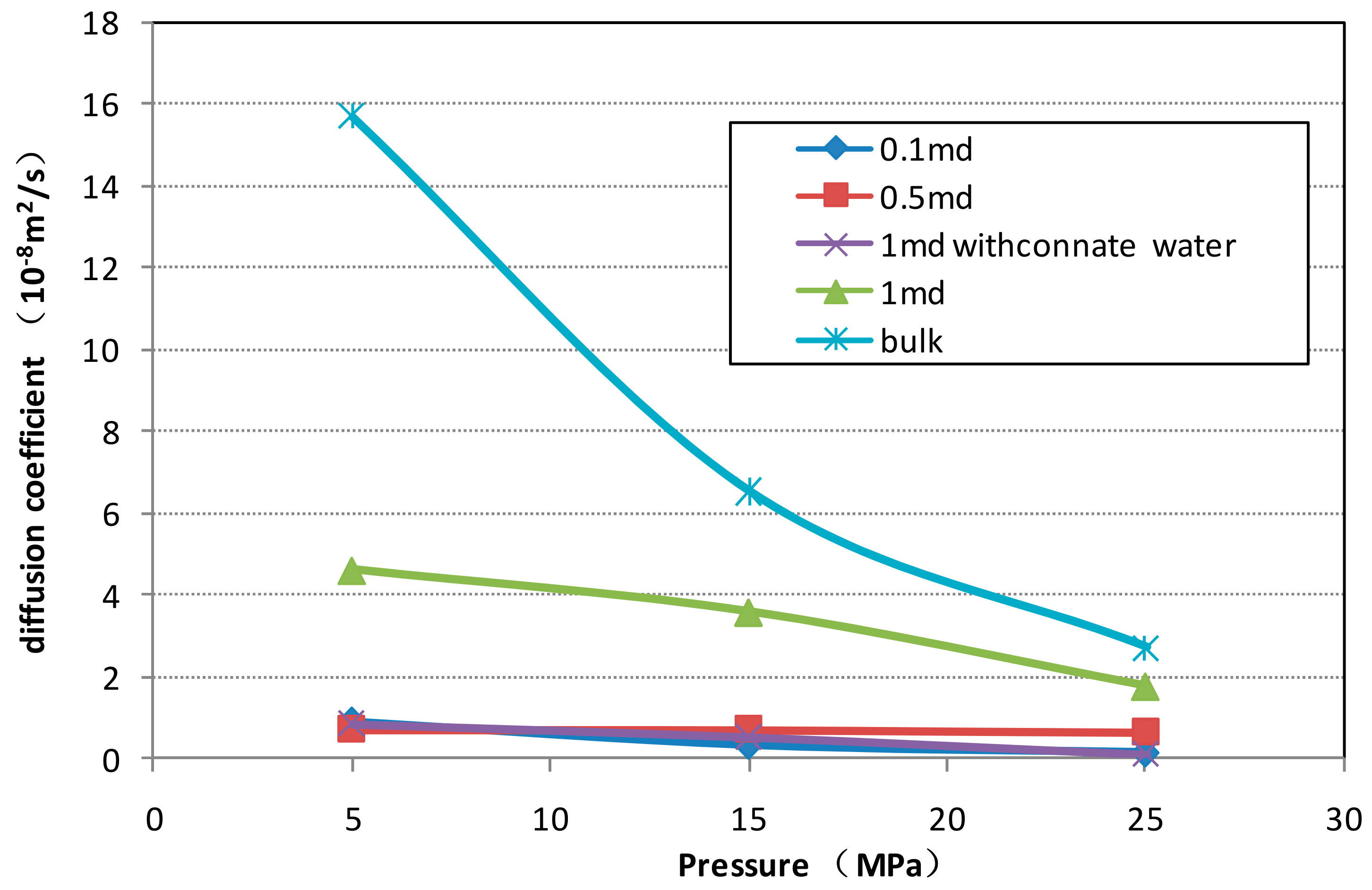
3.1.2. Diffusion Experiment
3.1.3. Long Core Model
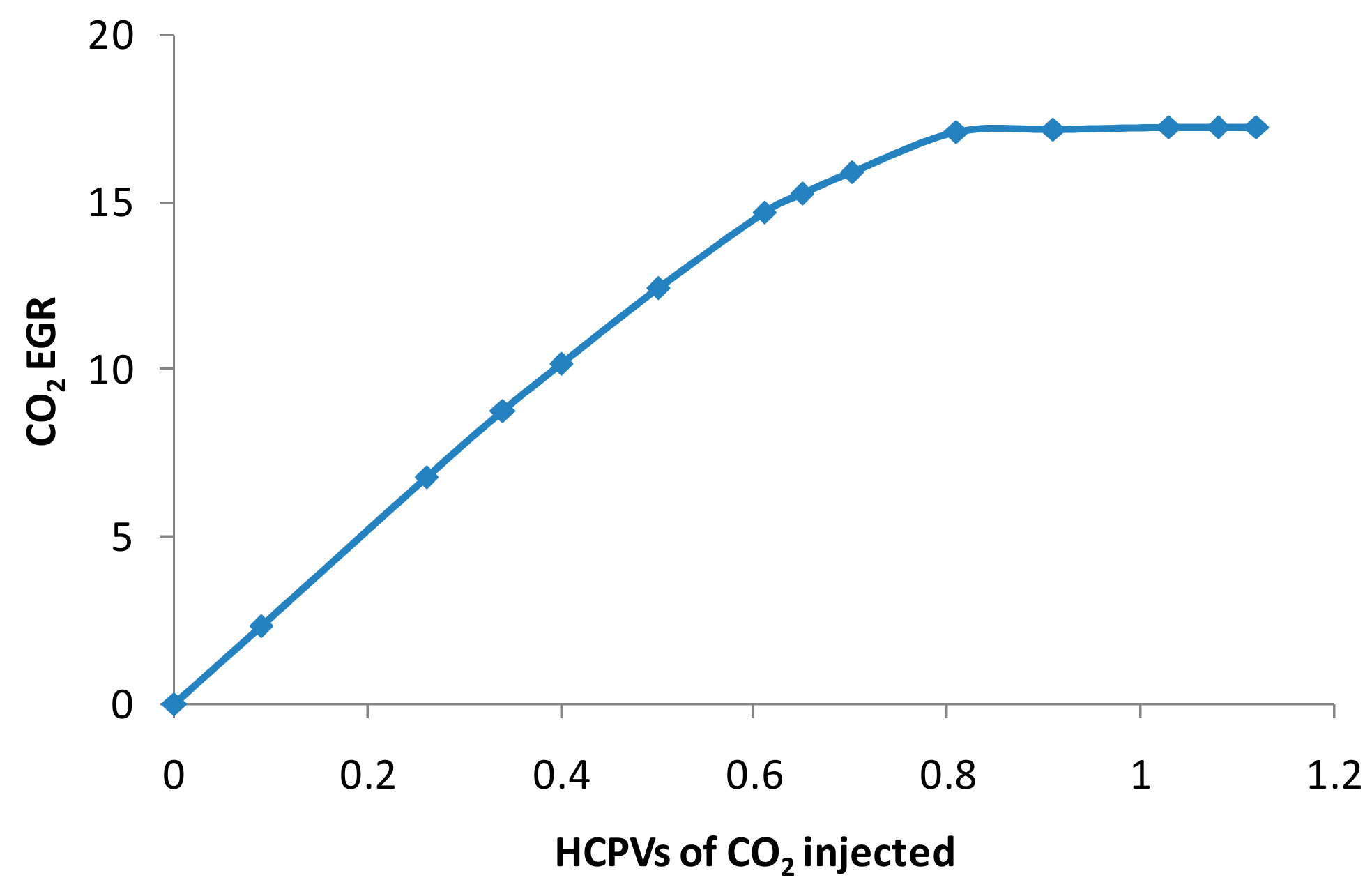
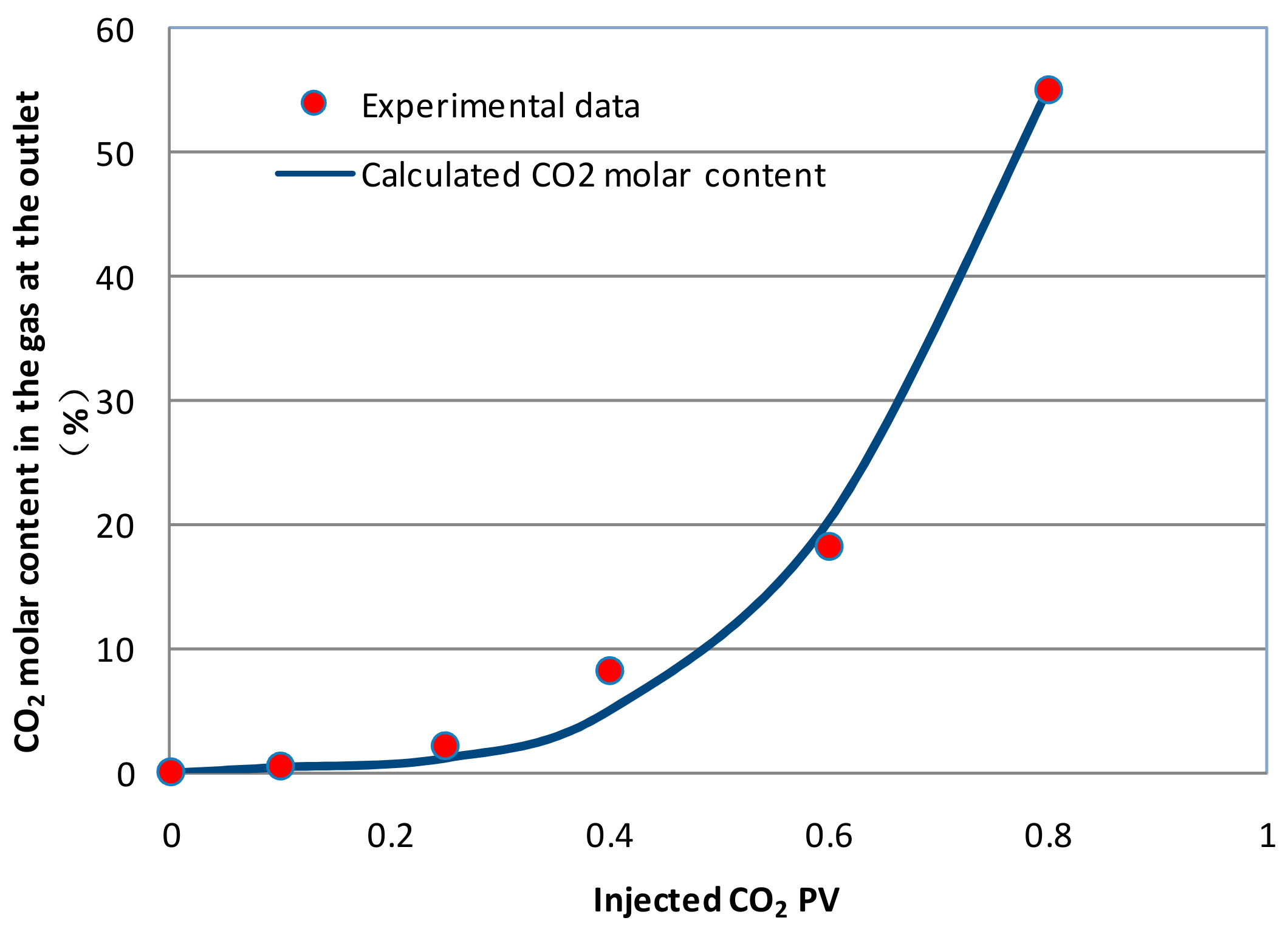
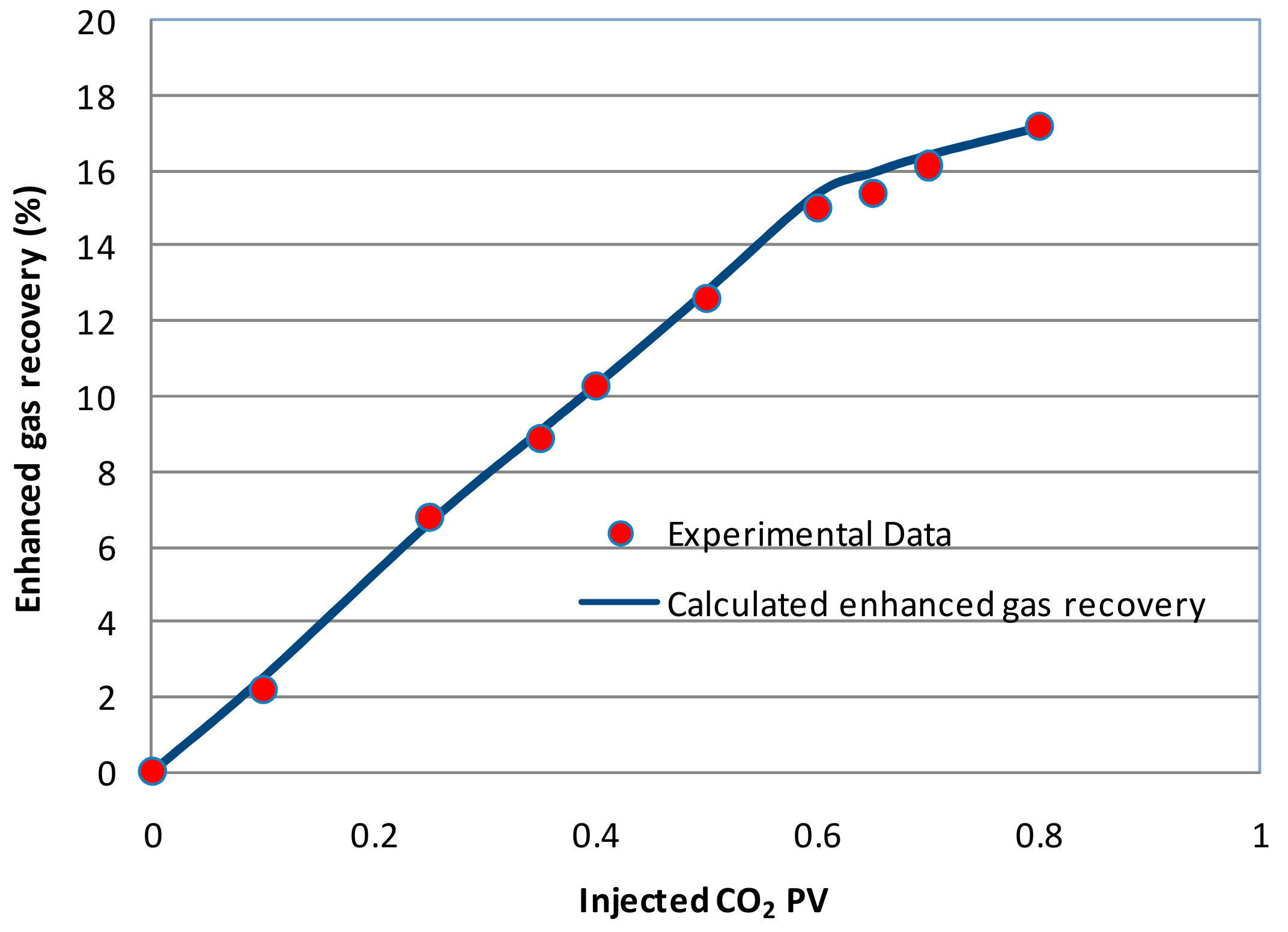
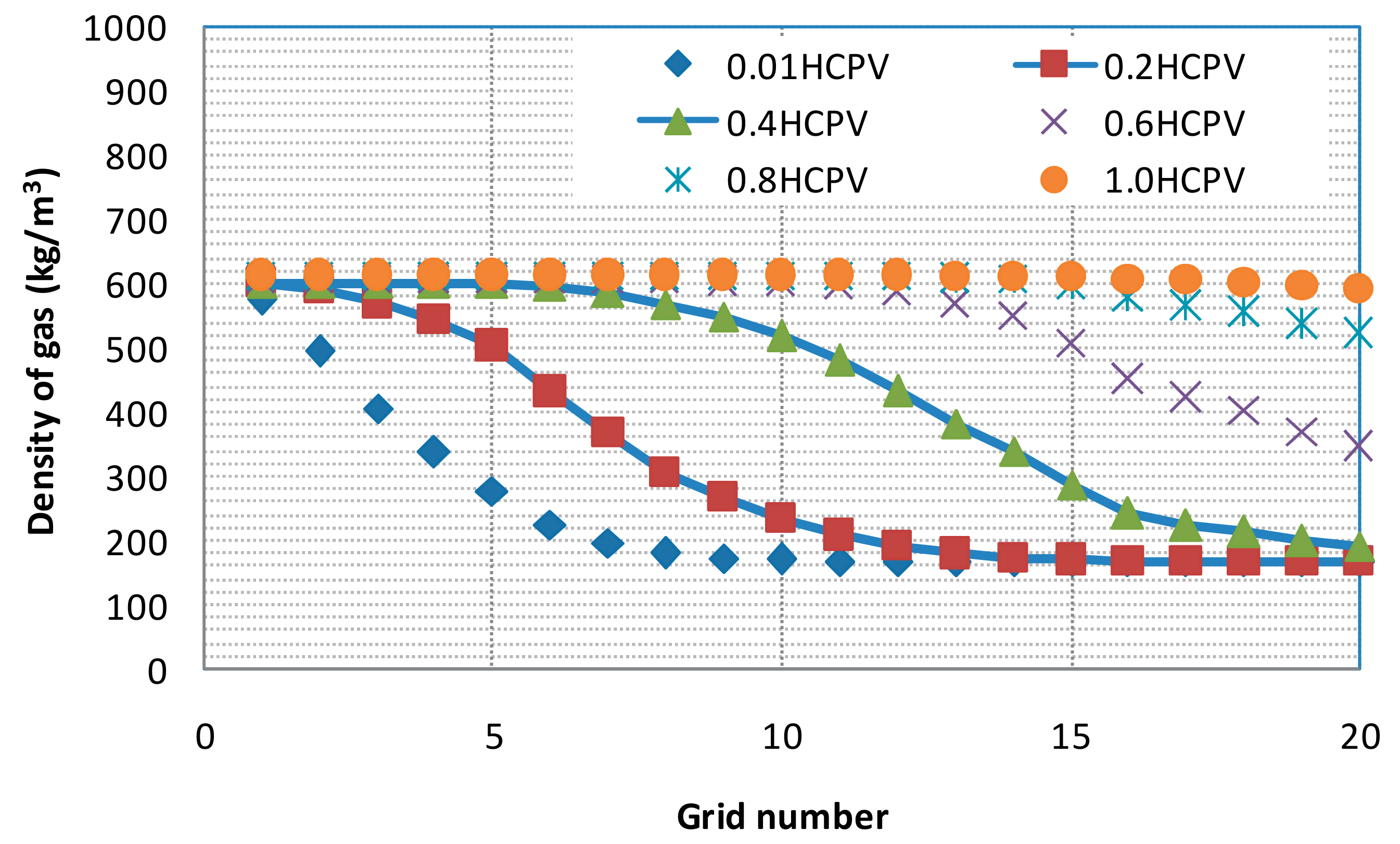
3.2. Numerical Model Verification
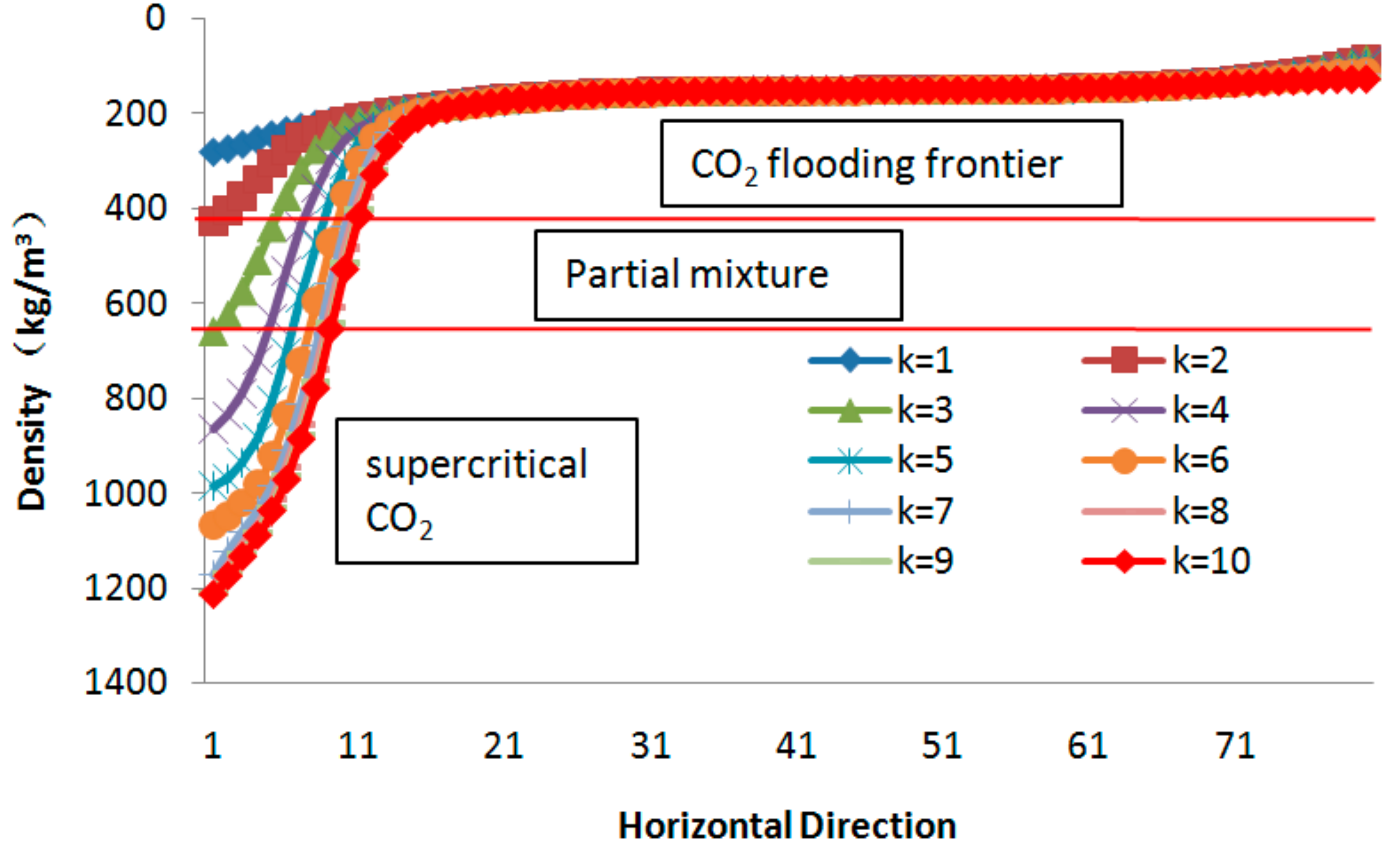
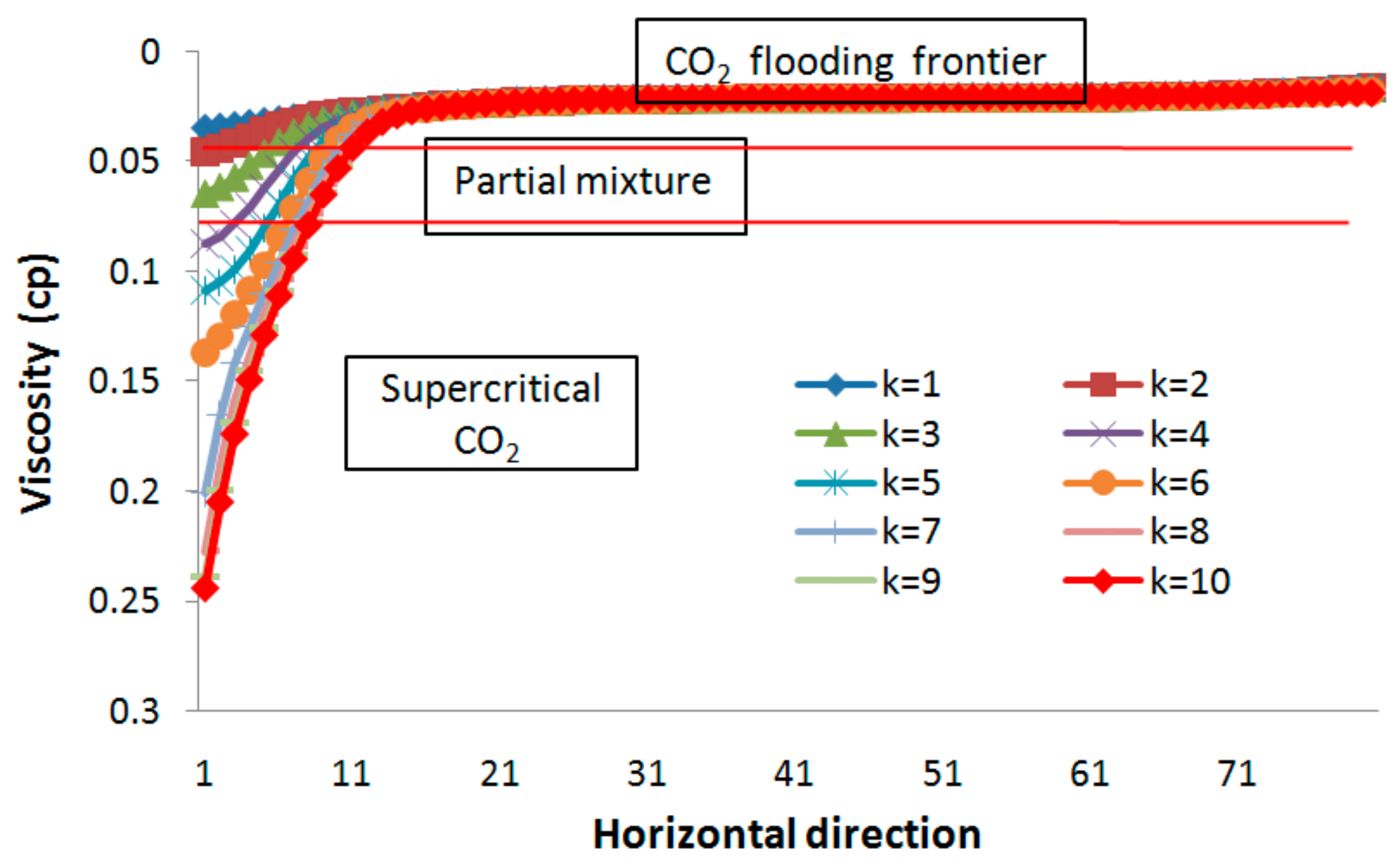
3.3. CO2 EGR Mechanism
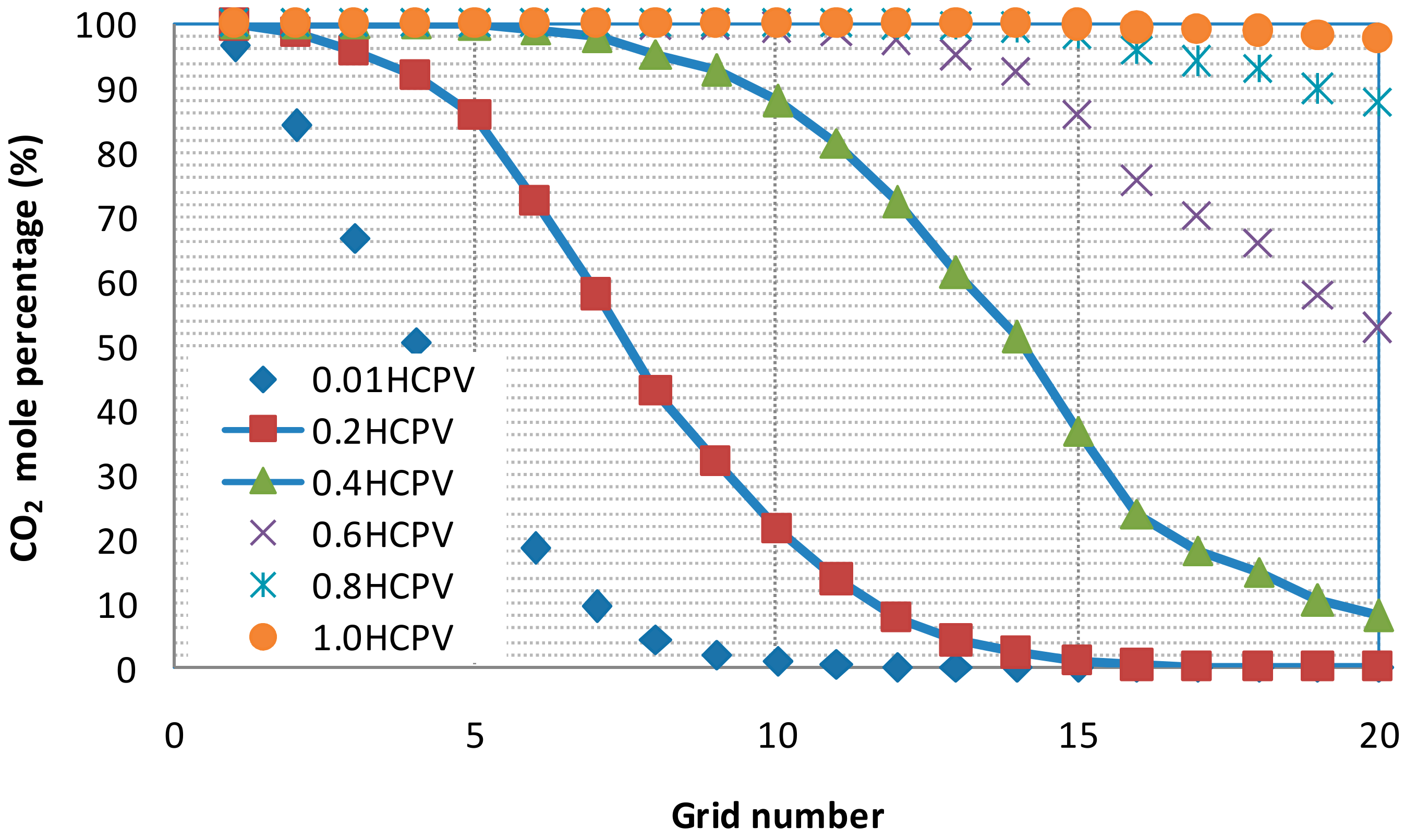
3.3.1. Partial Miscibility
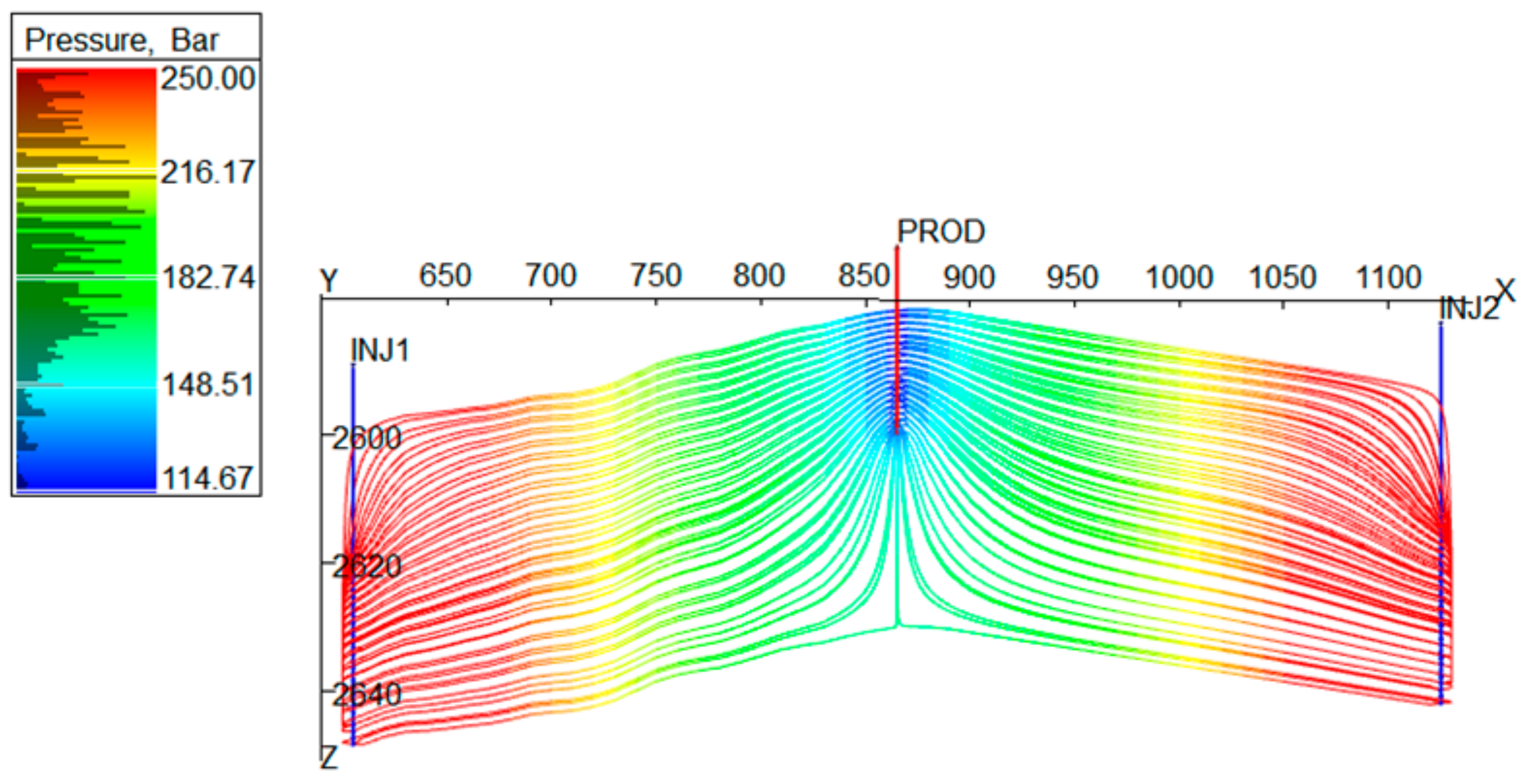
3.3.2. Pressure Maintenance
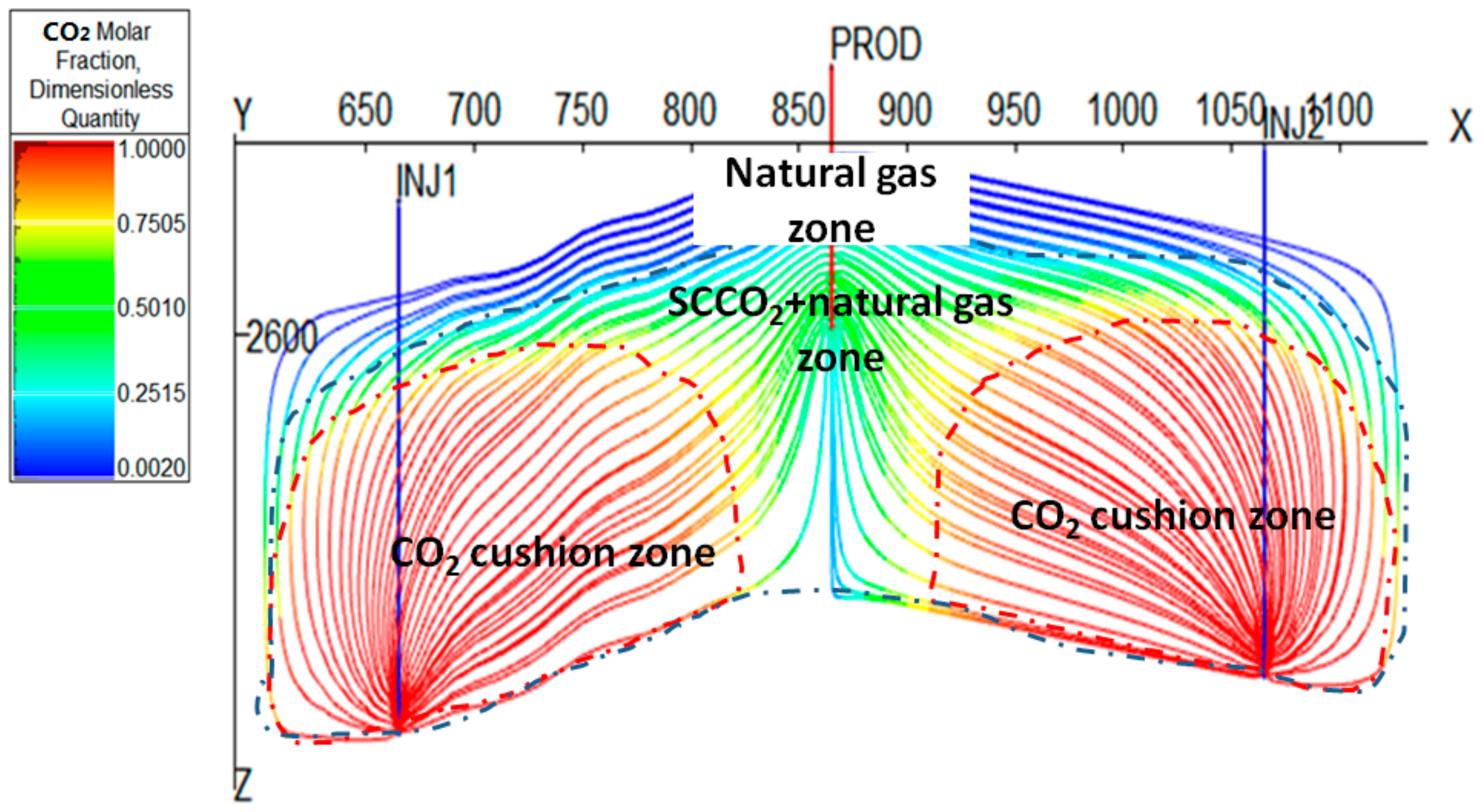
3.3.3. Cushion Gas Mechanism
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sheng, P.P.; Liao, X.W. The Technology of Carbon Dioxide Stored in Geological Media and Enhanced Oil Recovery, 1st ed.; Petroleum Industry Press: Beijing, China, 2009; pp. 1–4. [Google Scholar]
- IEA. Carbon Dioxide Utilization; Table 6; IEA Greenhouse Gas R&D Programme: Paris, France, 1997. [Google Scholar]
- Wang, H.; Ma, F.; Tong, X.; Liu, Z.; Zhang, X.; Wu, Z.; Li, D.; Wang, B.; Xie, Y.; Yang, L. Assessment of global unconventional oil and gas resources. Pet. Explor. Dev. 2016, 43, 850–862. [Google Scholar] [CrossRef]
- Jia, A.L. Progress and prospects of natural gas development technologies in China. Nat. Gas Ind. 2018, 38, 77–86. [Google Scholar] [CrossRef]
- Ma, X.H.; Jia, A.L.; Tan, J. Tight sand gas development technologies and practices in China. Pet. Explor. Dev. 2012, 39, 572–579. [Google Scholar] [CrossRef]
- Zou, C.N.; Yang, Z.; He, D.B. Theory, technology and prospects of conventional and unconventional natural gas. Pet. Explor. Dev. 2018, 45, 575–587. [Google Scholar] [CrossRef]
- Yuan, S.Y.; Wang, Q. New progress and prospect of oilfields development technologies in China. Pet. Explor. Dev. 2018, 45, 657–668. [Google Scholar] [CrossRef]
- Yuan, S.Y. Symposium of Gas Drive to Improve Oil Recovery, 1st ed.; Petroleum Industry Press: Beijing, China, 2016; pp. 1–15. [Google Scholar]
- Oldenberg, C.; Pruess, K.; Benson, S. Process modeling of CO2 injection into natural gas reservoirs for carbon sequestration and enhanced gas recovery. Energy Fuels 2001, 15, 293–298. [Google Scholar] [CrossRef]
- Oldenberg, C.; Benson, S. CO2 injection for Enhanced Gas Production and Carbon Sequestration. In Proceedings of the SPE International Petroleum Conference an Exhibition, Villahemosa, Mexico, 10–12 February 2002. SPE 74367. [Google Scholar]
- Sun, Y. Mechanism of Superciritical-CO2 Storage with Enhanced Gas Recovery in the Natural Gas Reservoirs. Ph.D. Thesis, Southwest Petroleum University, Chengdu, China, 2012. [Google Scholar]
- Dali, H.; Lihui, G.; Haocheng, L.; Meizhu, Z.; Feifei, C. Dynamic phase behavior of near-critical condensate gas reservoir fluids. Nat. Gas Ind. 2013, 33, 68–73. [Google Scholar]
- Mamora, D.D.; Seo, J.G. Enhanced gas recovery by carbon dioxide sequestration in depleted gas reservoir. In Proceedings of the SPE Annual International Petroleum Conference, San Antonio, TX, USA, 29 September–2 October 2002. [Google Scholar]
- Tang, Y.; Zhang, C.; Du, Z.M.; Cui, S.H.; Ma, Y.X.; Mi, H.G. Experiments on enhancing gas recovery and sequestration by CO2 displacement. Reserv. Eval. Dev. 2015, 5, 34–49. [Google Scholar]
- Nogueira, M.C.; Mamora, D.D. Effect of Flue Gas Impurities on the Process of Injection and Storage of CO2 in Depleted Gas Reservoirs. In Proceedings of the 2005 SPEBPA/DOE Exploration and Production Environmental Conference, Galveston, TX, USA, 7–9 March 2005. [Google Scholar]
- ATTurta, S.S.K.; Sim, A.K.; Singhal, B.F.; Hawkins, A. Basic investigation on enhanced gas recovery by gas-gas displacement. In Proceedings of the Petroleum Society’s 8th Canadian International Petroleum Conference, Calgary, AB, Canada, 12–14 June 2007. [Google Scholar]
- Shi, Y.; Jia, Y.; Pan, W.; Huang, L.; Yan, J.; Zheng, R. Potential Evaluation on CO2-EGR in tight and low permeability reservoirs. Nat. Gas Ind. 2017, 37, 62–69. [Google Scholar]
- Clemens, T.; Secklehner, S.; Mantatzis, K.; Jacobs, B. Enhanced Gas Recovery, Challenges shown at the Example of three Gas Fields. In Proceedings of the SPE EUROPEC/EAGE Annual Conference and Exhibition, Barcelona, Spain, 14–17 June 2010. [Google Scholar]
- Al-Hasami, A.; Ren, S.; Tohidi, B. CO2 Injection for enhanced gas recover and geo-storage: Reservoir simulation and economics. In Proceedings of the SPE EUROPEC/EAGE Annual Conference, Madrid, Spain, 13–16 June 2005. [Google Scholar]
- Rafiee, M.M.; Ramazanian, M. Simulation Study of Enhanced Gas Recovery Process Using a Compositional and a Black Oil Simulator. In Proceedings of the SPE Enhanced Oil Recovery Conference, Kuala Lumpur, Malaysia, 19–21 July 2011. [Google Scholar]
- Van der Meer, L.G.; Kreft, E.; Geel, C.R.; D’Hoore, D.; Hartman, J. CO2 storage and testing enhanced gas recovery in the K12-B reservoir. In Proceedings of the 23rd World Gas Conference, Amsterdam, The Netherlands, 5–9 June 2006. [Google Scholar]
- Kubus, P. CCS and CO2-Storage Possibilities in Hungary. In Proceedings of the SPE International Conference on CO2 Capture, Storage, and Utilization, New Orleans, LA, USA, 10–12 November 2010. [Google Scholar]
- Mathieson, A.; Midgley, J.; Dodds, K.; Wright, I.; Ringrose, P.; Saoul, N. CO2 Sequestration Monitoring and Verification Technologies Applied at Krechba, Algeria. Leading Edge 2010, 29, 216–222. [Google Scholar] [CrossRef]
- Mathieson, A.; Midgely, J.; Wright, I.; Saoula, N.; Ringrose, P. In Salah CO2 Storage JIP: CO2 sequestration monitoring and verification technologies applied at Krechba, Algeria. Energy Procedia 2010, 1063, 1–8. [Google Scholar] [CrossRef]
- Turgay, E.; Jamal, H.A.; Gregory, R.K. Basic Applied Reservoir Simulation—SPE Text Book Series Vol. 7, 1st ed.; Society of Petroleum Engineers Inc.: Houston, TX, USA, 2001; pp. 387–395. [Google Scholar]







© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jia, Y.; Shi, Y.; Pan, W.; Huang, L.; Yan, J.; Zhao, Q. The Feasibility Appraisal for CO2 Enhanced Gas Recovery of Tight Gas Reservoir: Experimental Investigation and Numerical Model. Energies 2019, 12, 2225. https://doi.org/10.3390/en12112225
Jia Y, Shi Y, Pan W, Huang L, Yan J, Zhao Q. The Feasibility Appraisal for CO2 Enhanced Gas Recovery of Tight Gas Reservoir: Experimental Investigation and Numerical Model. Energies. 2019; 12(11):2225. https://doi.org/10.3390/en12112225
Chicago/Turabian StyleJia, Ying, Yunqing Shi, Weiyi Pan, Lei Huang, Jin Yan, and Qingmin Zhao. 2019. "The Feasibility Appraisal for CO2 Enhanced Gas Recovery of Tight Gas Reservoir: Experimental Investigation and Numerical Model" Energies 12, no. 11: 2225. https://doi.org/10.3390/en12112225
APA StyleJia, Y., Shi, Y., Pan, W., Huang, L., Yan, J., & Zhao, Q. (2019). The Feasibility Appraisal for CO2 Enhanced Gas Recovery of Tight Gas Reservoir: Experimental Investigation and Numerical Model. Energies, 12(11), 2225. https://doi.org/10.3390/en12112225



