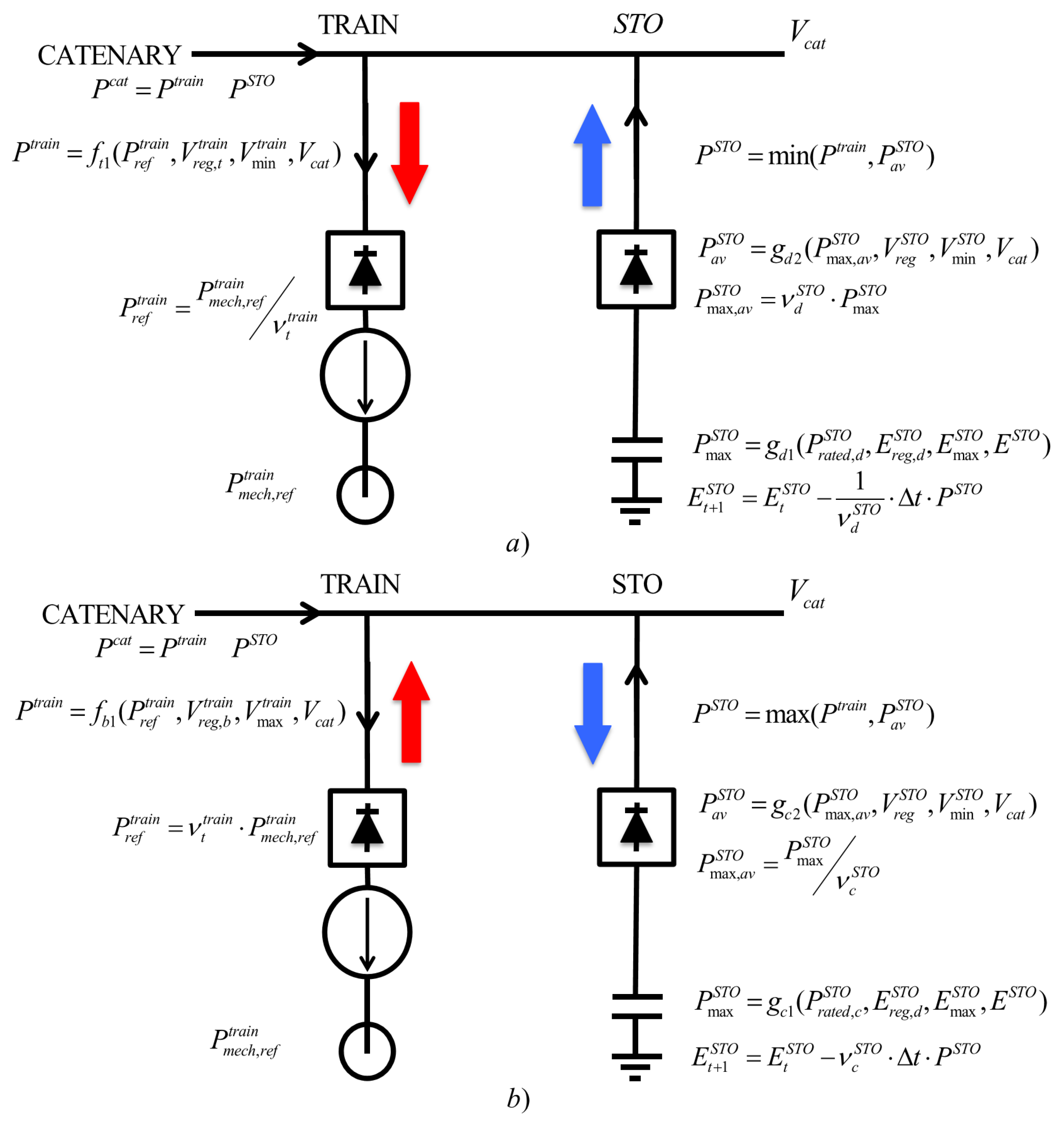
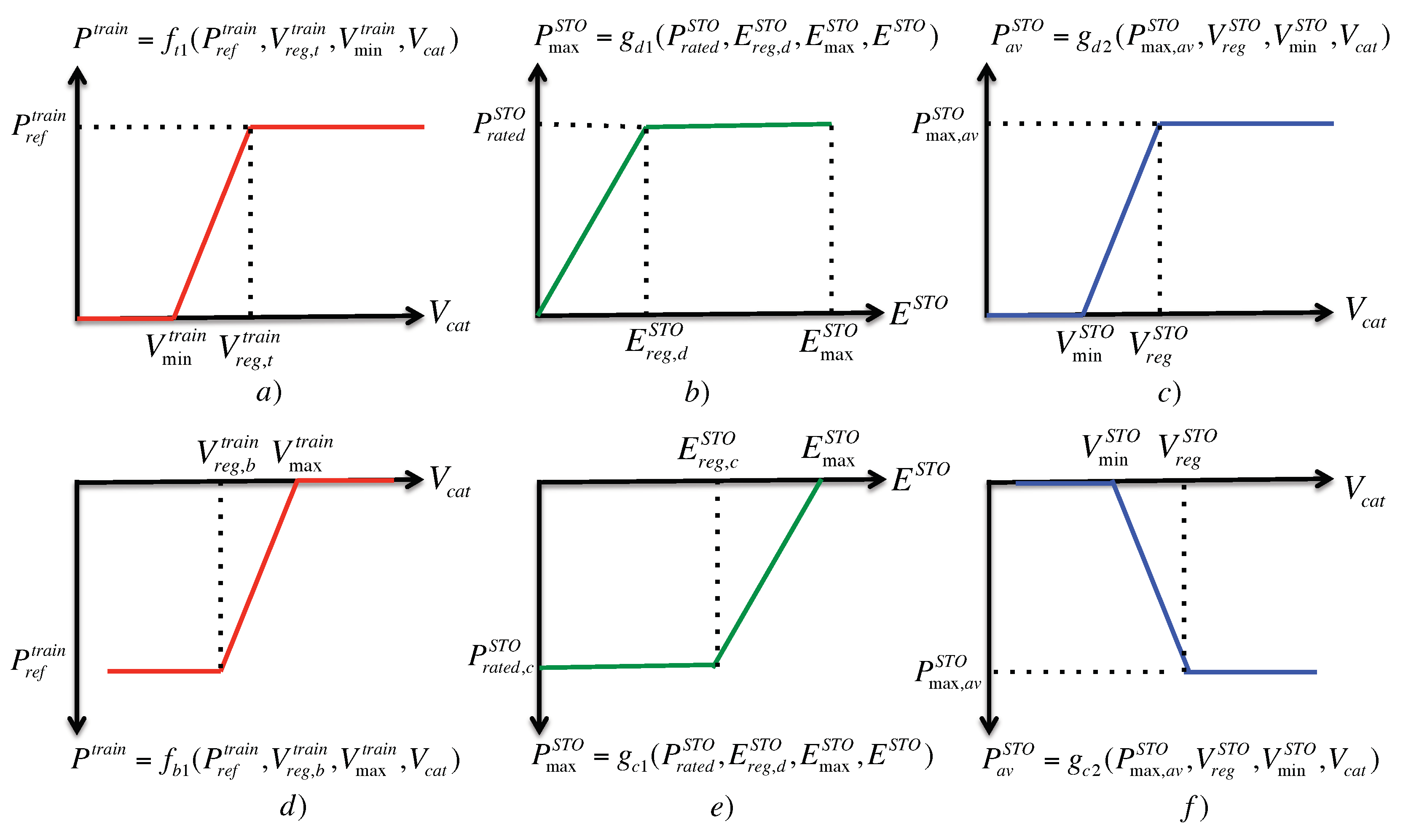
3.2. Rolling Stock
The train used in both lines was an electrical multiple unit (EMU). The whole unit was 2.940 m wide 4.265 m high and had a total length of 98.05 m, with an unladen weight of 157.3 t. The units were composed of five cars, the two ends having a driver’s cabin and a normal floor. The middle car had a normal floor, while the other two cars had a low floor. The five cars were supported on two types of bogies, the trailer bogie and the tractor. The tractor bogie was always shared between two cars. The train was designed to use a standard Iberian track gauge (1668 mm) at a maximum speed of 120 km/h with almost 1000 passengers, although it could reach 160 km/h with minor modifications. The maximum total power of the train was 2.2 MW, and it had regenerative braking. In the base case, the trains were not going to be equipped with on-board energy storage systems. However, we considered the possibility of adding an on-board accumulator system based on a hybrid battery/ultracapacitor technology. The power profiles obtained during the simulation in the accumulation system would help the manufacturer to determine the percentage of energy that must be stored in the battery or ultracap parts. The electromechanical efficiency of the trains in traction and braking modes (), as well as the electrochemical efficiency of the storage system in charging and discharging modes () were set to . The total accumulation system capacity () was 7 kWh, and the on-board energy storage device rated charging and discharging power () was 1 MW.
Regarding the protection curves of the trains and the storage elements, the minimum and the regulation voltage of the train in traction mode () were set to 1980 V and 2280 V. The same values have been selected for the minimum and regulation voltage of the energy storage system (). In braking mode, the regulation voltage and the maximum voltage of the squeeze control () were 3300 V and 3600 V, respectively. In the cases in which the on-board accumulation system was activated, the system would be initialized with no charge.
In
Table 2, the data summarizing the behavior of the trains in the different trips are collected. In the first column, we can observe the required mechanical power to complete the trip. It can be seen that the slope of the blue line was steeper because the difference between the power required for outward and return journeys was greater than on the red line. The average trip considering the two lines and both directions needed 229 kWh. The mechanical regeneration capacity in Column 2 is the available mechanical power that can be regenerated. Columns 3 and 4 contain the required electrical power and the electrical regeneration capacity considering already the efficiency of the electromechanical conversion. The electrical regeneration capacity was usually around 40% of the required electrical power, except in the S1 to S4 trip of the blue line. In this case, because the train ascended a steep slope, the regeneration capacity was much lower, around 22% of the required electrical power. In the fifth column, we can see the minimum electric consumption. This consumption was calculated as the required electrical power minus the electrical regeneration capacity. Off course, this is a theoretical consumption that considers that we took advantage of all electrical power available for regeneration. This is not true, mainly because of two reasons. First, part of the power that was available to be injected into the catenary was burned in the rheostatic braking system when the squeeze control was activated in order to maintain the catenary voltage below the maximum level. In addition, if the train was equipped with on-board accumulation, the efficiency of the electrochemical conversion during the charging and discharging process also reduced the percentage of available regenerated power that could be reused. For these reasons, we uses these minimum consumption figures as a theoretical ceiling to compare the different solutions, but we must be aware of the fact that we will not reach this theoretical ceiling.
3.4. Analysis of the Results
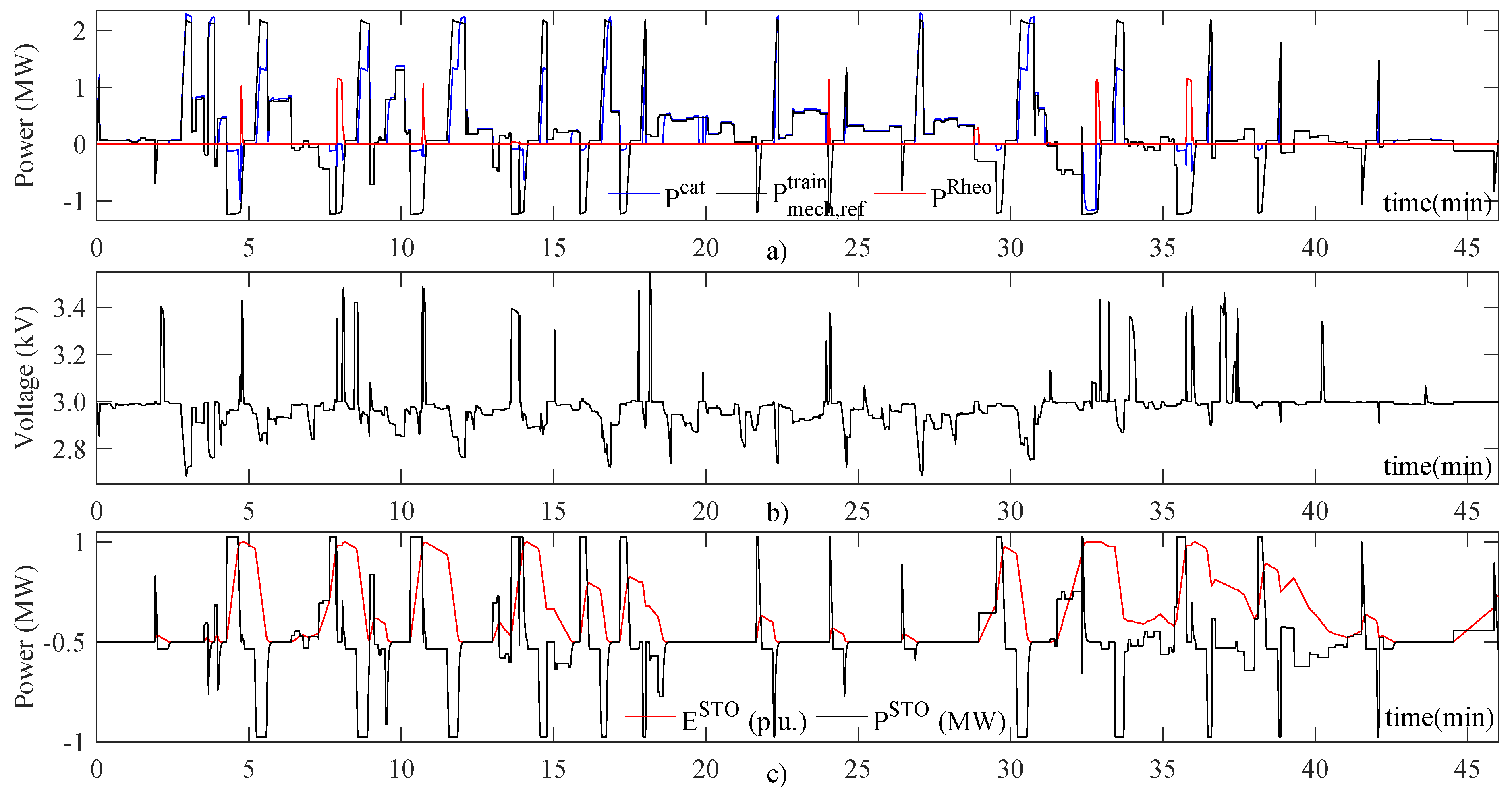
The above-described scenarios were simulated, and the obtained results are analyzed in this subsection. With the software used for simulation, we can obtain time-varying series of each electrical variable in the train or in the feeding network. An example of this detailed analysis can be observed in
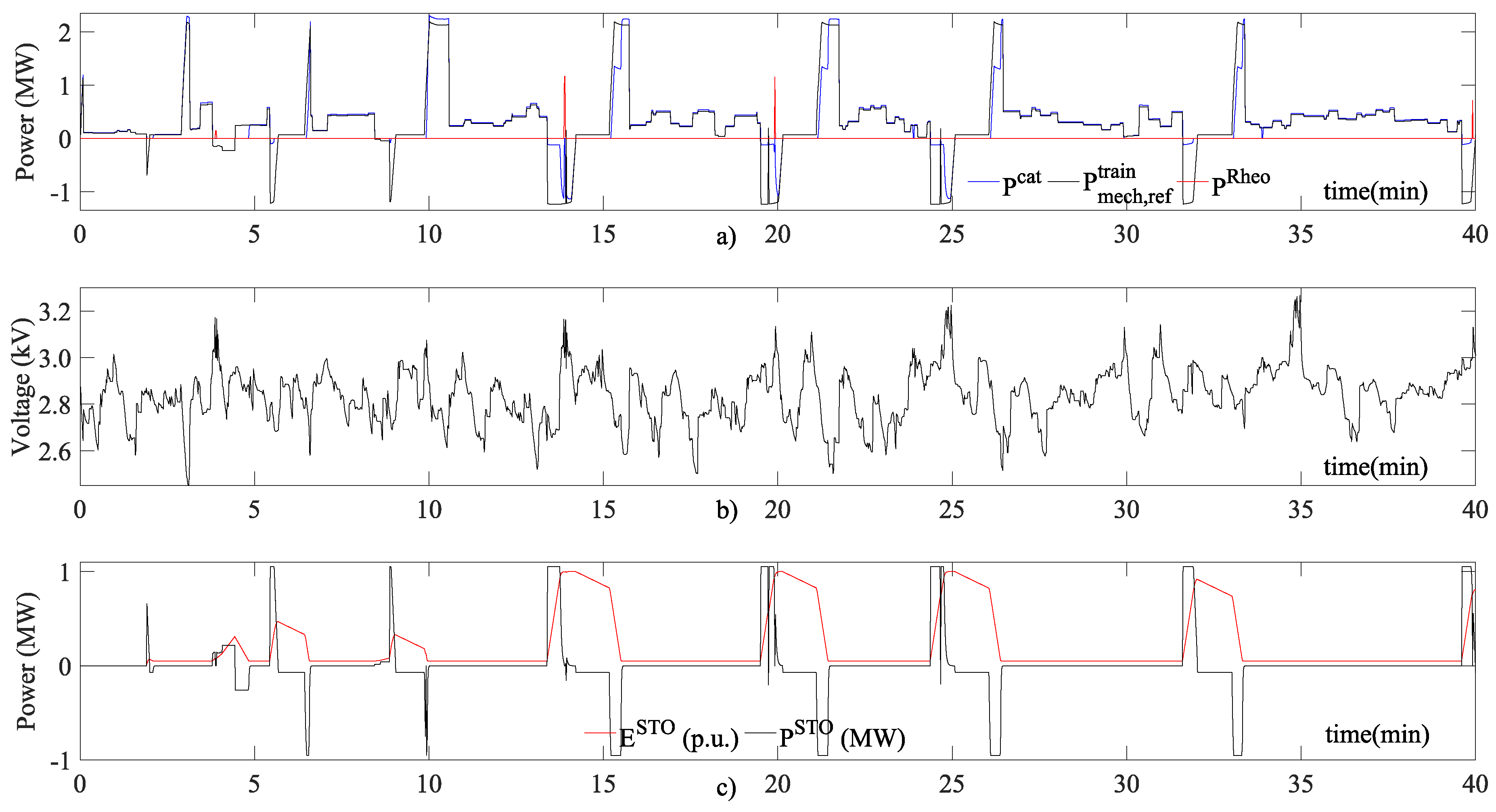
Figure 4, in which Train Number 4 on the red line route starting from S1 is represented in Scenario L1. It must be noticed how on seven occasions, the train burned part of the regenerated energy using the rheostatic system due to the high catenary voltage, even when the train was equipped with an energy storage system and the storage capacity was not full. It can be observed also how the power extracted/injected into the catenary differed from the train mechanical reference due to the efficiency of the electromechanical conversion process, but also because part of the power was provided by the energy storage system. In
Figure 5, the fourth train of the blue line starting from S1 is represented, in this case for the heavy traffic scenario (H1). It has to be remarked that the voltage level was much lower and the network receptivity higher. The burned power in this scenario was nearly zero since the overvoltage protection was only activated on four occasions with a very short duration.
The analysis of the time-varying curves was very interesting since it showed how electrical variables were correlated and it helped to understand the mathematical model proposed in the previous sections. However, in order to determine the effectiveness of the combination of the trains plus the infrastructure, another kind of analysis must be carried out. In
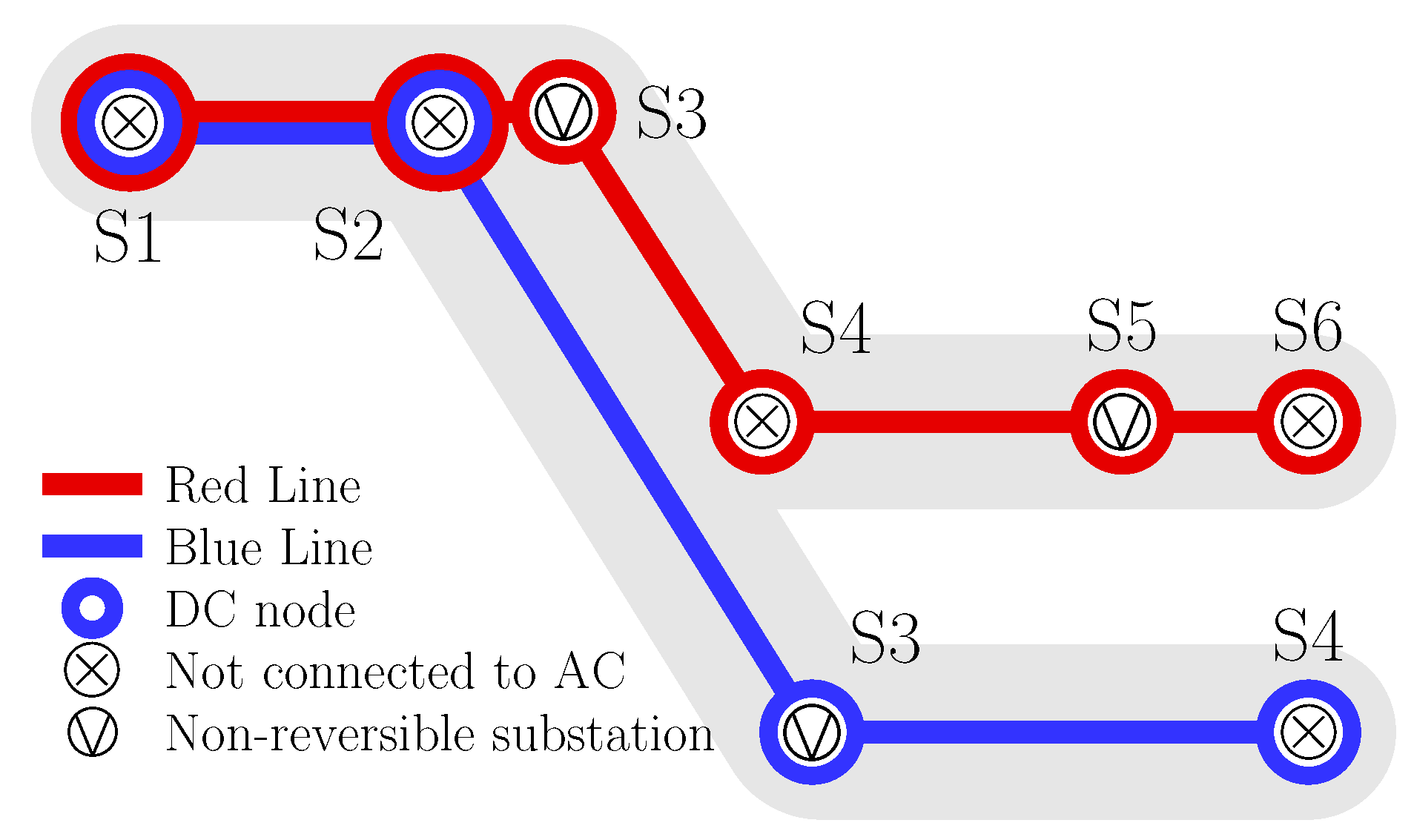
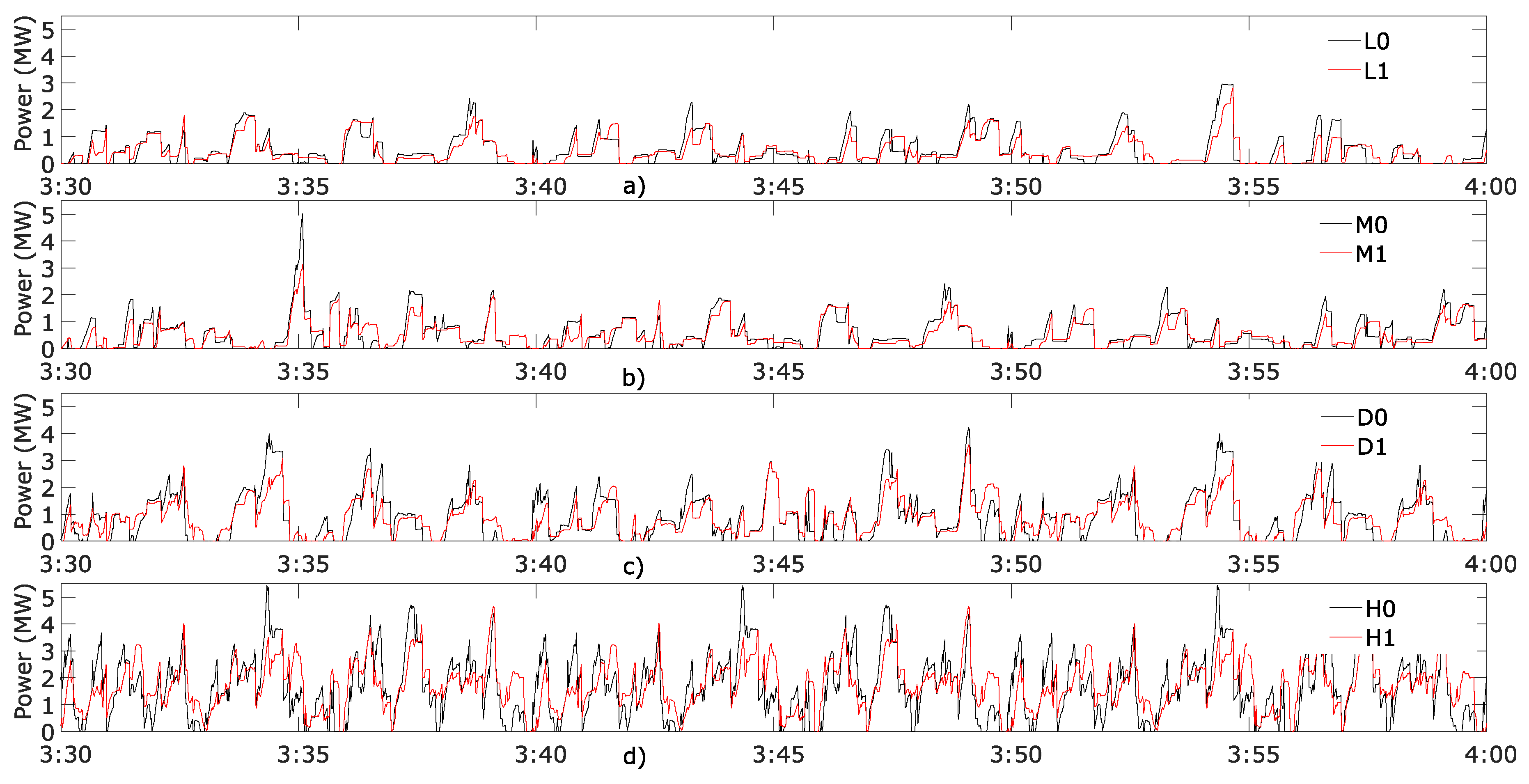
Figure 6 is represented the power extracted from the AC network at substation S5 of the red line during the first four hours of simulation for all scenarios. Each subfigure represents two scenarios with the same train headset, but with and without the accumulation system. The correlation between the power extracted from the AC network was higher in the low traffic scenarios.
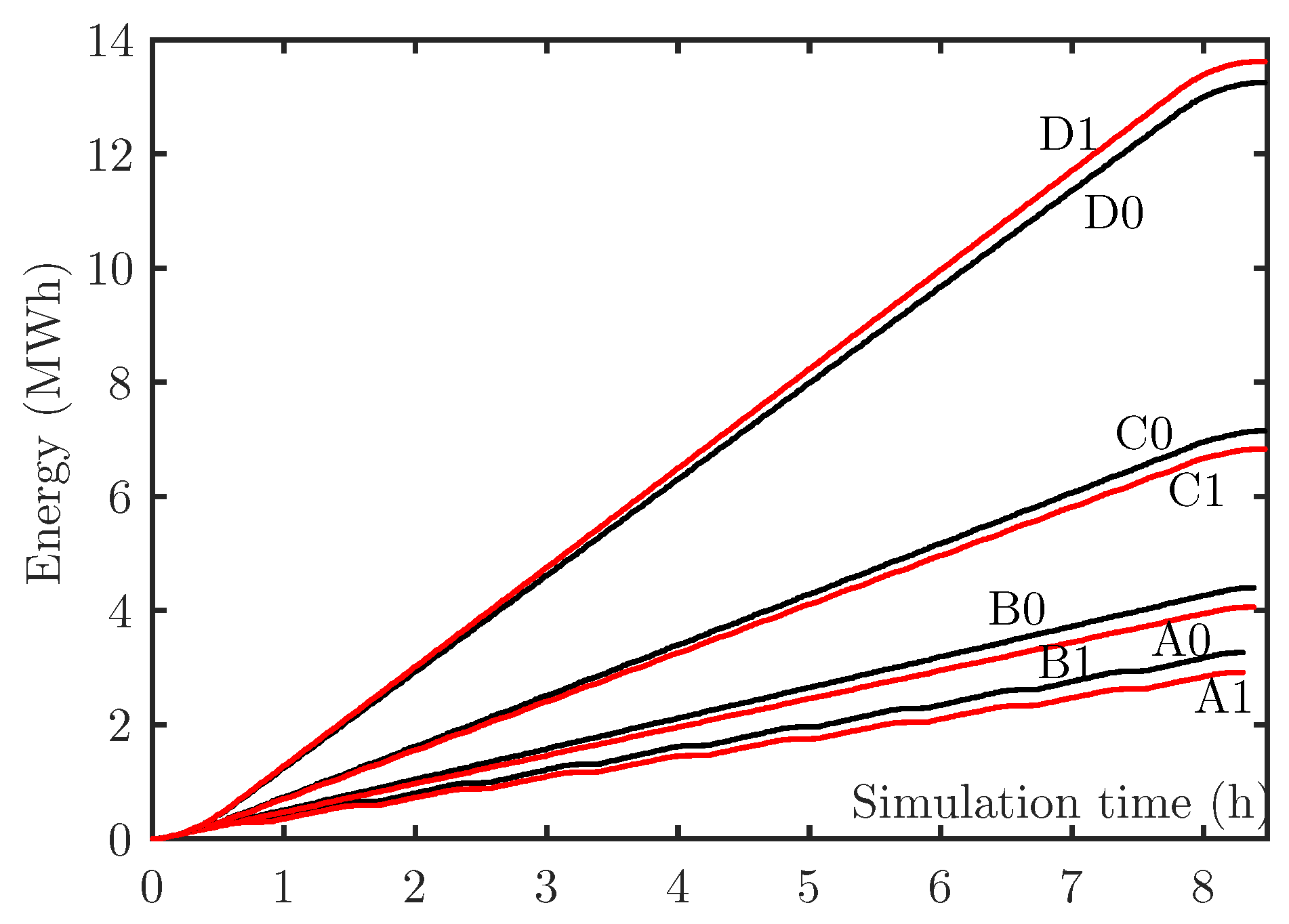
Figure 7 depicts the energy extracted from the AC network at substation S5 in the eight possible scenarios. It must be noticed that the red solid line represents always the scenarios with energy storage. Obviously, scenarios with the same traffic were quite correlated. It should be pointed out that in the light, medium, and dense traffic scenarios, the energy consumption from the AC network in the cases with energy storage systems was a little bit lower. Paradoxically, that is not the case for the heavy traffic scenario in which the energy consumed from the AC network was higher when the trains were equipped with energy storage systems. As will be observed, in heavy traffic scenarios, it was more efficient to share the energy surplus with other trains than storing it in the on-board accumulation system.
In
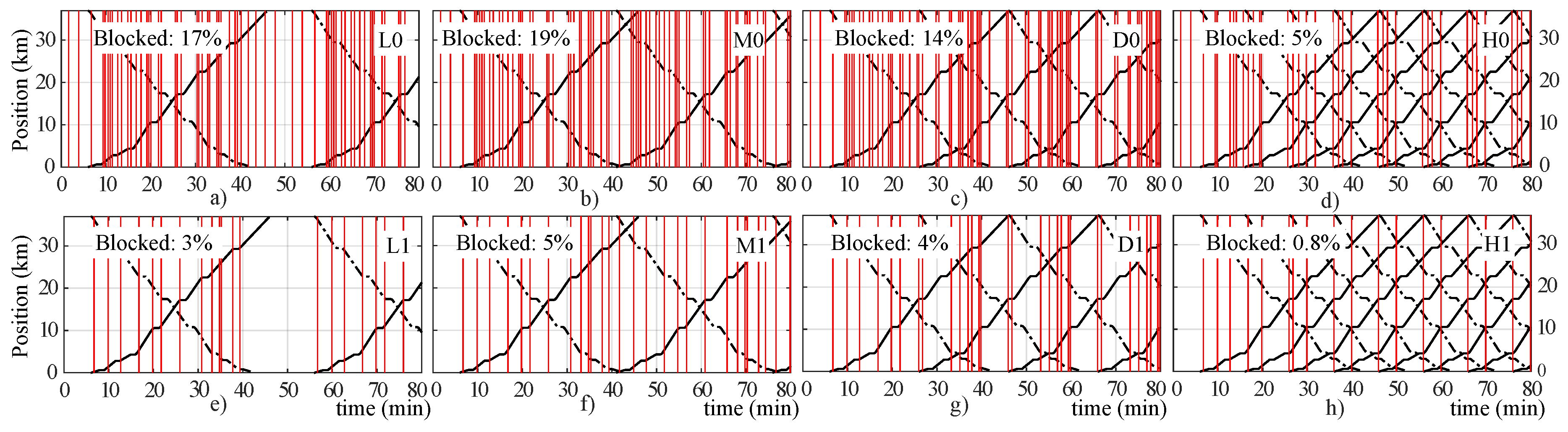
Figure 8, we represent the Marey diagrams of each scenario just for the red line. The horizontal axis represents time; in this case, we represented the first 80 min of simulation. In the vertical axis, we represent the position of the train. Solid black lines represent trains from S1 to S6, while dashed-dotted lines represent trains circulating from S6 to S1. Vertical red lines represent the instants at which all the substations were blocked at the same time. It must be noticed that in light, medium, and dense traffic scenarios, the percentage of instants in which all substations were blocked at the same time dropped drastically when we added on-board energy storage systems, improving this percentage by more than 10%. However, in the heavy traffic scenario, the percentage of blocking instants was already very low (5%) in the case without on-board accumulation. The installation of on-board accumulation in the heavy traffic scenario produced the blocking of all substations in only 0.8% of the cases.
In the next paragraphs, we will analyze the aggregated results obtained for the eight scenarios from three points of view. First, we will present a full summary of the system. Second, a summary from the point of view of the trains will be analyzed, and finally, we will show a summary from the point of view of the substations. The use of aggregated data help us to measure the impact of the on-board storage solution in different traffic scenarios for the same feeding infrastructure. In
Table 4, we summarize the most representative energies in the system; all the numbers are in MWh. In the first row, we have the electrical energy required by the trains. This energy is going to be the reference energy, since it only depends on the number of trains and does not depend on the equipment of the trains. This energy was the same with and without accumulation. For the light traffic scenario, the 40 trains required a total of 9.62 MWh. For the heavy scenario, the 188 trains required 45.2 MWh, the relation between the number of trains and the required electrical energy being linear. Something similar happened with the second and the third row, which represent the regeneration capacity and the minimum consumption, respectively. The regeneration capacity considers the electromechanical conversion efficiency, and the numbers obtained represent the electrical energy that could be used for injecting into the catenary or charging the storage system. The minimum consumption is a theoretical concept that cannot be reached since it is obtained by subtracting the regenerated capacity from the required electrical energy. Up to now, these numbers only depended on the traffic, and did not vary whether or not the trains had on-board energy storage equipment. The next row (fourth row) represents the energy demanded by the train at the catenary level. It differs from the electrical energy required by the trains for one reason in the case of trains without an accumulation system and two reasons in the case of trains with an on-board accumulation system. In the first case, the train demand was different from the electrical energy requirement because the over-current protection prevented the absorption of too much power in the case of low catenary voltage. In the second case, part of the electrical energy provided by the train can be provided by the on-board accumulation system.
As can be observed, for the light traffic scenario without accumulation, the trains absorbed 0.72 MWh less than the required energy, so we would have delays in the system. For the heavy traffic scenario, the difference was 1.3 MW. However, in order to compare the scenarios, it is better to compare percentages with respect to the required electrical energy. These percentages can be found in
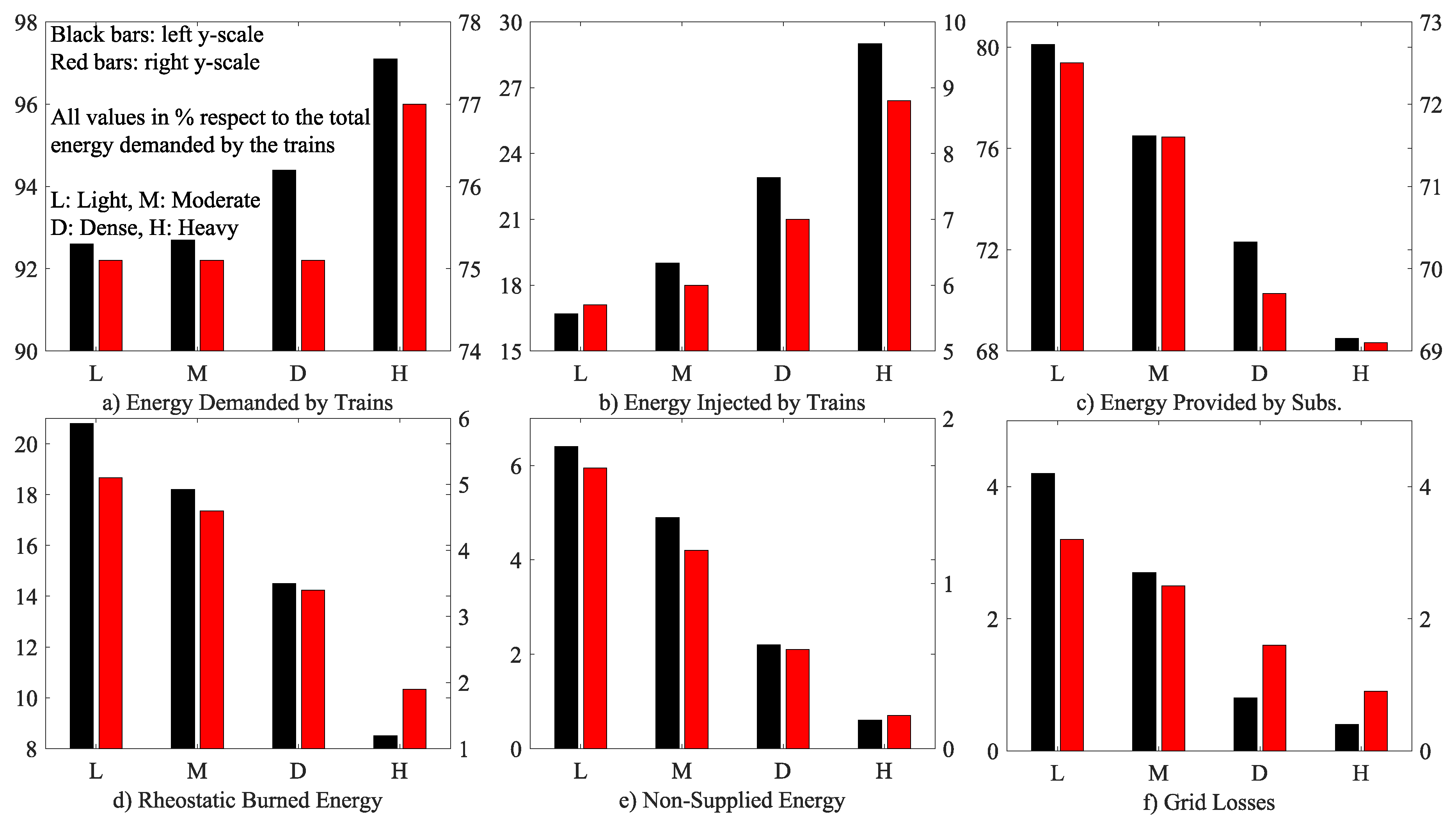
Table 5. The authors are fully aware that this second table is redundant, but we think that it is important to analyze at the same time the data in MWh and in percentage with respect to the required electrical energy. The train demand in the scenario L0 was 92.6% of the required electrical energy, which means that 6.4% of the required energy cannot be provided. In order to distinguish the correlations between the different variables with the different traffic scenarios with and without energy storage and extract conclusions about the trends of the energy savings and consumption, the energetic data in percentage with respect to the total energy demanded by the trains are also represented in
Figure 9. As can be observed, we had the same trends as the traffic increased for the cases with and without energy storage. However, even when the trend was the same, the values were very different, and it was necessary to add two different y-scales in order to compare the plots. The real energy demanded by the trains increased with the traffic, as well as the energy injected by the trains. That means that with denser traffic, the number of instants in which the overcurrent and overvoltage protections were activated was lower. We also reduced the energy provided by the substations and the grid losses when we increased the traffic.
The non-supplied energy in the case of the heavy traffic scenario without energy storage was only 0.6%. The non-supplied energy is represented in Row 9 of
Table 4 and
Table 5. This non-supplied energy in percentage is a good index of the network congestion, as it can be observed that the more trains in the system, the less the network congestion. In general, we can state that the installation of on-board energy storage always reduced the amount of non-supplied energy. In the worst scenario (light traffic), the non-supplied energy was reduced from 6.4–1.7% when we added storage to the trains. Row 5 represents the energy regenerated by the trains that was actually injected into the feeding system. Obviously, this energy increased with the traffic, but it was always reduced when we added energy storage to the trains. In Row 6, the trains’ net energy was obtained subtracting Row 5 (energy injected) from Row 4 (energy demanded). We can see that in the light, medium, and dense traffic scenario, the net energy was always lower when the trains were equipped with energy storage. However, the net energy was nearly the same in the scenarios H0 and H1. Row 7 represents the energy provided by the substations. It is very interesting to remark that even in the worst scenario (L0), the substations provided only 80% of the energy demanded by the trains, the rest being provided by other trains in braking mode. Again, for the light, medium, and dense traffic scenarios, the energy provided by the substations was reduced when we added the energy storage. In the heavy traffic scenario, this trend was inverted, and the energy provided by the substations was slightly higher when we added energy storage to the trains. This is because when we had many trains and they were very close to each other, it was more efficient to use the regenerated energy in other trains than the stored energy in the on-board accumulation system. This is coherent with the data obtained representing the losses in the feeding system (Row 10). In the heavy traffic scenario, the losses were higher when the trains were equipped with an energy storage system. Finally, Row 8 represents the energy burned in the rheostatic system of the train, in all cases, it suffered a significant reduction when we added the on-board accumulation system.
In
Table 6, we can observe the trains’ average behavior in the different trips and in all scenarios, as well as the average trip considering all possible routes in all scenarios. The table is split into four blocks. In the first one, we represent the total energy obtained from the catenary. It should be noticed that the slope of the blue line was steeper than the slope in the red line. That is the reason why the energy obtained from the catenary in the outward and return journeys was so different, as well as the energy injected into the catenary. It must be noted that for the average trip, the energy obtained from the catenary increased when we increased the traffic because the voltage was more stable (within the limits), and the non-supplied energy decreased. The minimum consumption (theoretical) for the average trip defined in
Table 2 was 151 kWh, and this number was obtained subtracting the electrical regeneration capacity from the required electrical energy. The best scenario in terms of average net consumption was H0 (heavy traffic without accumulation), with a net consumption of 164 kWh, only 5.8% above the theoretical consumption. Adding accumulation to the heavy traffic scenario increased the average trip net consumption by 1 kWh. In the rest of the scenarios, adding accumulation always improved the average trip net consumption. For instance, in the light traffic scenario, the net consumption for the average trip was 183 kWh without accumulation and 167 kWh with accumulation. It is very important to remark that when we considered the net consumption in the average trip for comparing with the theoretical limit, we were not considering the non-supplied energy that was quite high in the light, medium, and dense traffic scenarios without accumulation. When we added accumulation to the system, the non-supplied energy in the average trip was always lower than 2% with respect to the required electrical energy for the average trip; and in the case of heavy traffic, lower than 1%.
Table 7 contains the energy analysis of the substations for all scenarios; it is split into three blocks. The first block represents the energy injected into the DC traction system per each substation and the total. In the second block, we can observe the energy injected by each substation per train trip. Finally, this number is compared with the minimum theoretical consumption in Block 3. Again, we can observe that in the scenario H0, the total energy injected into all substations was only 9.3% above the minimum consumption.
Regarding the performance, both models (decoupled and integral) were equivalent from the point of view of the equations, and they provided the same result. However, the time savings on average when simulating the proposed decoupled model were around 20%. On average, the number of iterations of the decoupled model compared to the integral one was higher, from 6.5 iterations (average) to 7.9 iterations (average) per instant. The iterations using the decoupled model were faster. The average time to complete an iteration with the decoupled model was 0.39 ms, while the integral model spent 0.55 ms.