1. Introduction
Over the years several micro-ORC systems have been developed [
1] with the aim of understanding and improving the performance of different expander devices, pumping systems, and heat exchanger technology. Despite their effectiveness in energy recovery, micro-ORC systems are characterized by low-efficiency values, especially in cases where the net electric power is less than 10 kWe [
2]. In these applications, positive displacement machines are commonly used for expanding and pumping processes [
3]. Regarding the expander technology, the review by Bao and Zhao [
4] pointed out that, for micro energy systems, the volumetric expander technology is the most preferable in terms of efficiency and cost. In particular, scroll, screw, and rotary vane expanders are the most suitable for micro-ORC systems. When considering ORC systems of net electrical power output around 1 kWe, scroll and screw expanders are a well-known technology for energy conversion, but when the temperature of the hot source falls below 100 °C, other machines have to be used. For example, an innovative way to generate a small amount of electrical power (a few Watts) is to utilize free-piston expanders [
5,
6]. From the experimental side, the use of a positive displacement machine requires a specific test-rig to reproduce the actual operating conditions in terms of pressure, fluid characteristics and loads. Commonly, the presence of simplified prototypes and/or different working conditions could determine several differences between the actual machine performance and the measured ones. To help the experimental analysis, a lumped-parameter model is often used for extending the analysis to other operating conditions or other fluids [
7,
8], increasing the design capabilities and limiting the cost and time.
For the pump, no specific indication can be found in the literature, though a greater number of applications are equipped with a positive displacement machine, usually gear pumps. This widespread technology is common adopted for pressurizing the refrigerant (in most cases a certain percentage of oil mass fraction is added to the ORC systems to ensure the proper lubrication of the positive displacement machine) even if the gear pump operation is affected by two main issues, related to the (i) pressure pulsations and (ii) cavitation phenomenon.
Gear pumps are a class of robust positive displacement pumps that can work on a wide range of pressures and rotational speeds, but they are responsible for noise and vibration phenomena that could affect the circuit in which they operate. The damping effects provided by the pipeline are usually not able to eliminate the vibrations [
9,
10], which are also responsible for disturbances and, sometimes, the damage of measurement devices. Pulsations are due to the pressure ripples provided by the pump, which are driven by the engagement process and the position of the relief grooves [
11].
In several applications, micro-ORC systems are equipped with temperature probes, pressure transducers and flow meters. These devices are used to characterize the system and, in addition, for controlling its operating point when external conditions change, such as the electric load and the heat and sink temperature values. Noise and vibrations could, in turn, affect their operations and increase the uncertainty of the measuring process. In particular, the Coriolis flow meter (which is one of the most used technology in micro-ORC test benches) can be greatly affected due to its technology and measuring principle [
12]. Despite their accuracy and measuring performance, several analyses have been carried out over the year demonstrating how these devices could be affected by vibrations and pressure pulsations [
13,
14].
In addition, gear pumps are a class of positive displacement machine that shows high sensitivity to cavitation phenomena, in particular as a function of rotational speed. Higher rotational speed leads to higher volumetric efficiency but, at the same time, the pressure losses and the narrow gaps could cause local pressure drops that could lead to cavitation [
15,
16]. In ORC applications, this phenomenon is even more detrimental due to the thermodynamic state of the liquid pumped. In fact, the refrigerant in this section is very close to the saturated liquid curve and, so, even small pressure variations could originate phase change (from liquid to vapor) at the pump suction section. Cavitation produce erosion issues and is responsible for the reduction of the mass flow rate supplied by the pump. In this case, the control unit of the ORC system has to detect this discrepancy between the expected mass flow rate and the actual one and react by increasing the pump rotational speed.
Given this background, it is easy to understand how the use of a gear pump in a micro-ORC system needs to be analyzed and evaluated according to both the performance and reliability points of view. Pressure pulsations and cavitation affect the ORC system operation and the entire control system. Since these phenomena are mainly due to the pump operation, in this paper a time-dependent computational fluid dynamics (CFD) approach is proposed. The simulation strategy is based on a dynamic mesh approach, able to take into account the rotation and the engagement of the wheels, as well as the transient phenomena that affect the entire ORC. The dynamic mesh approach has been proven to be suitable for the analysis of such a machine, for discovering cavitation issues [
17,
18] and for calculating the performance [
19,
20].
The virtual model of the micro-ORC system is taken from an actual installation, described entirely by Bianchi et al. [
21]. The capabilities of CFD simulations for analyzing the ORC performance are proven [
22,
23]; however, in this work, a step forward on the simulation and explanations of such phenomena is performed. The criteria adopted in this paper are defined by the Whole ORC Model (WOM) [
22,
23], which is a new strategy for improving knowledge in micro-scale energy systems. The WOM strategy concept arises from evidence that the performance of every single device is affected by the operation of the other components/devices that operate in the same system. Including, in the same virtual CFD model, a higher number of components allows for an analysis of their interaction and adjusting the control logic, which can be an effective strategy for increasing system reliability.
Aim of the Paper and Novelty
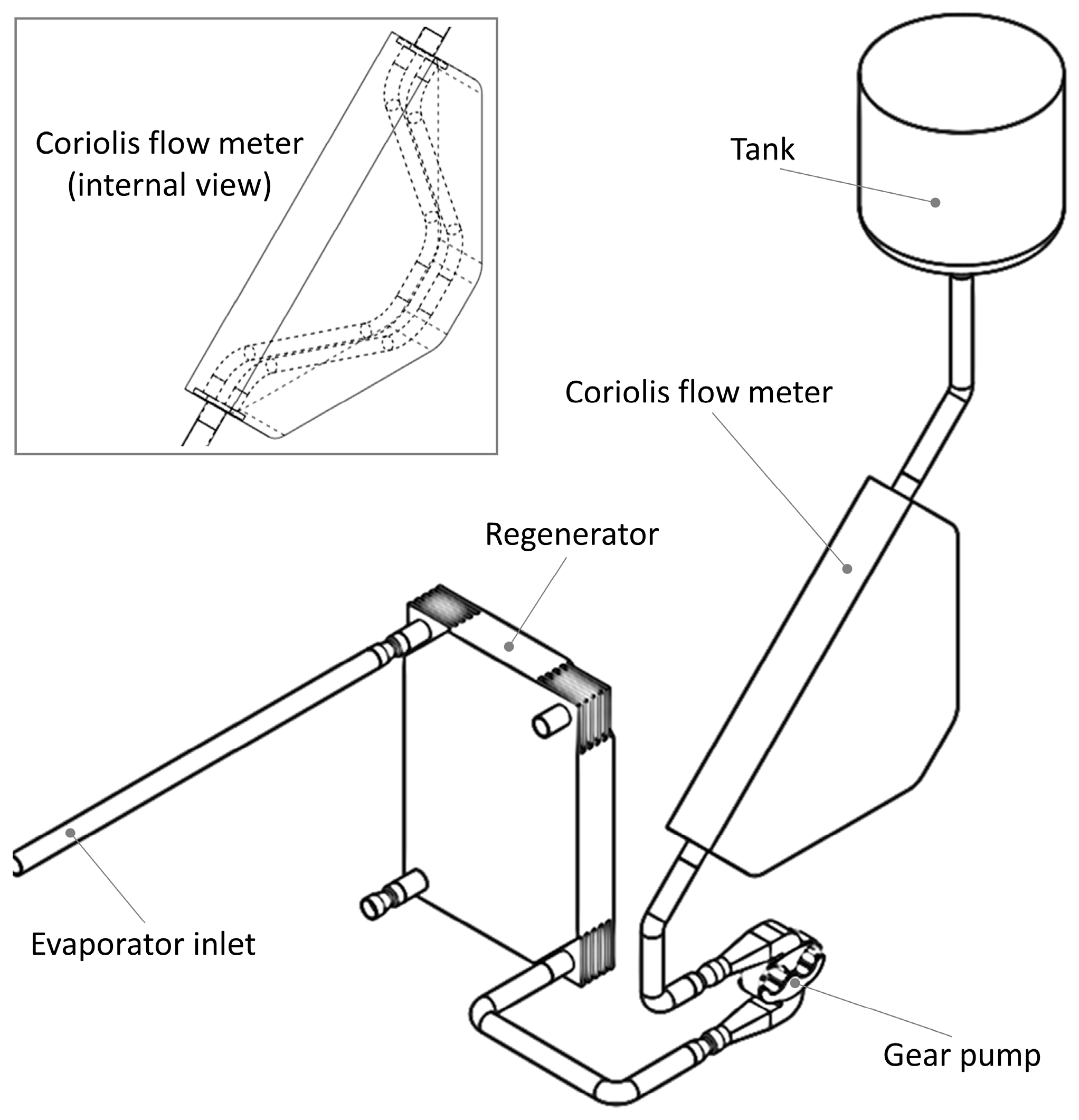
In this paper, a detailed analysis of pressure pulsation and cavitation phenomenon is carried out by means of transient CFD analysis. The numerical domain considered in the present analysis is depicted in
Figure 1 and corresponds to the virtual model of a portion of a real ORC system [
21]. As can be seen, starting from the liquid receiver (tank) (which collects the condensed liquid at the condenser outlet), the liquid passes through the Coriolis flow meter (CFM) (which is entirely modeled as reported in the internal view) and is processed by the pump. The pump is installed in the lower part of the circuit and is coupled with the system through an upstream and a downstream valve. The liquid refrigerant is then piped into the regenerator, which has the task of preheating it by removing heat from the refrigerant at the expander outlet. The virtual model depicts the actual installation in a very detailed form: bends, valves and tube-fittings are virtualized, generating a virtual test-bench. The innovative approach for studying the ORC operation reported in the present work is based on the application of a fully 3D transient numerical simulation of the entire system and allows us to analyze:
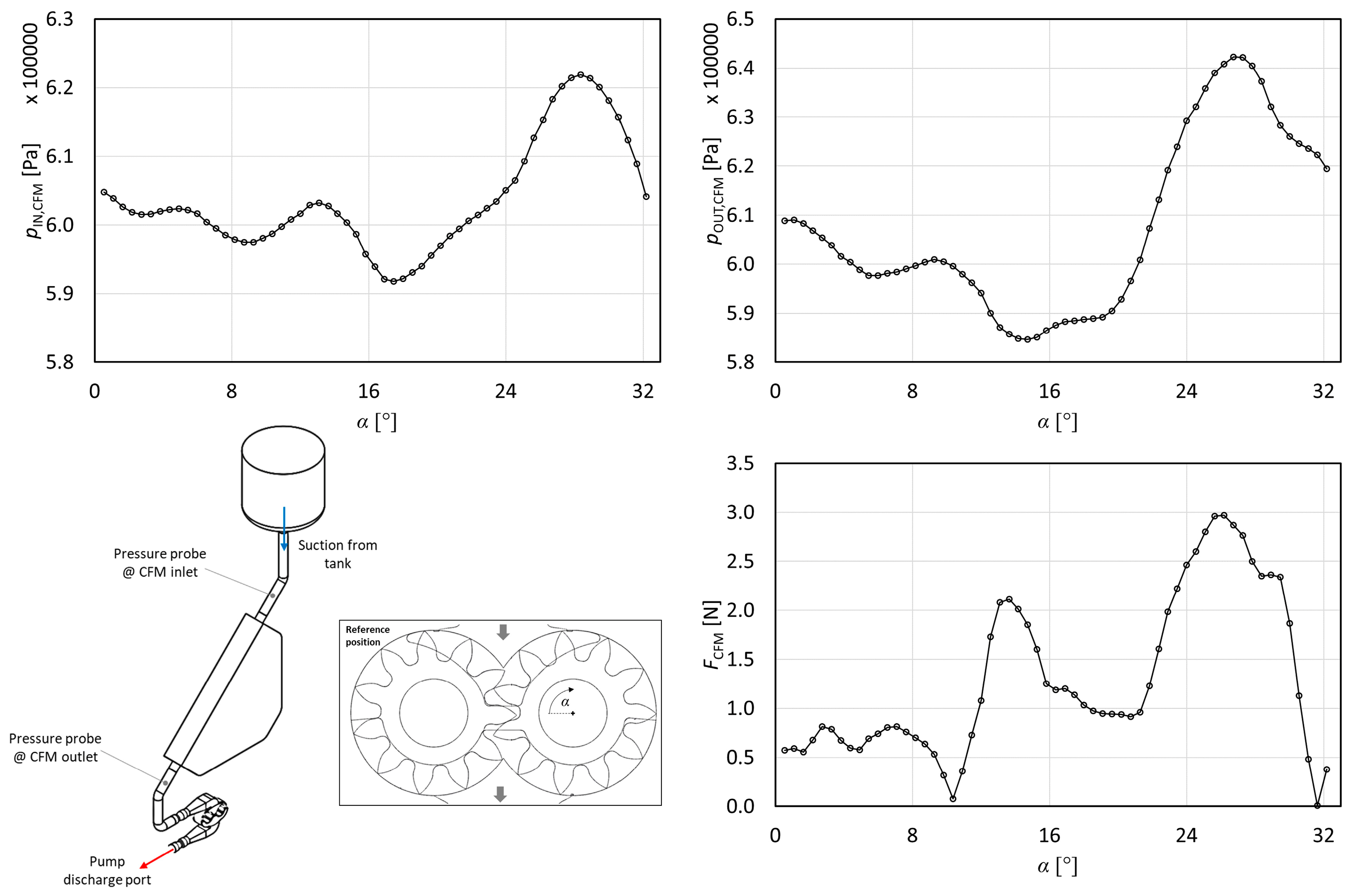
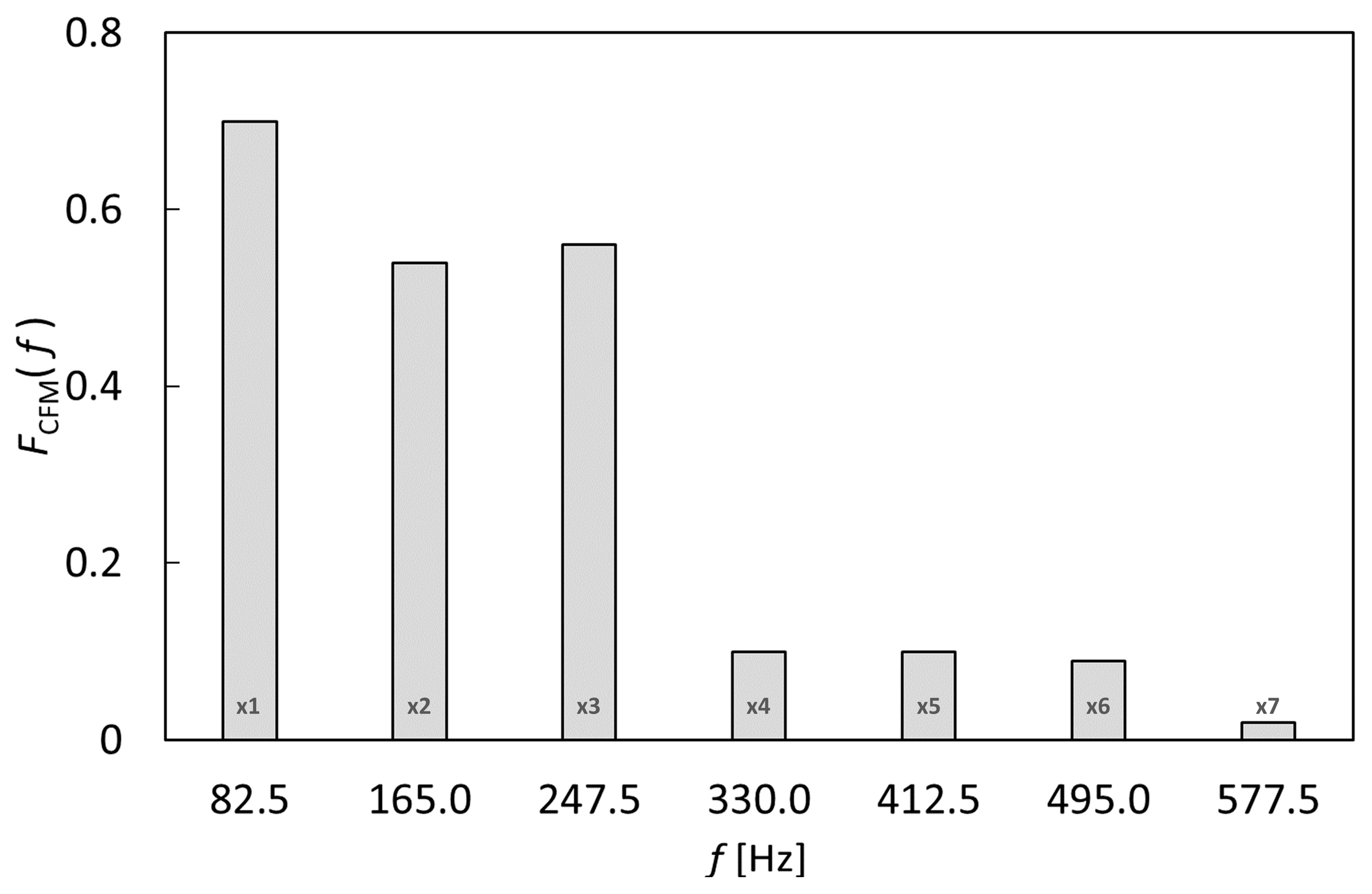
the effect of gear pump operation (in terms of pressure pulsation) on the CFM measurement performance. With the dynamic analysis it is possible to extract information about the frequency and magnitude of the vibrations, which can affect the CFM due to the gear pump operation;
the effect on the pump operation of the actual system layout and design. The virtualization of the ORC systems, which includes valves, bends, tank, regenerator, and measuring device (such as the CFM) allow for the determination of the actual flow conditions (in terms of velocity and pressure) at the inlet port of the gear pump;
the effect of cavitation on the pump operating points. By coupling the control system strategy and the CFD analysis, it is possible to detect how the cavitation phenomenon affects the ORC operation and which solution can be adopted for improving the control capability of the system, with the aim of preserving the performance and the reliability of each component.
2. Materials and Methods
As already pointed out, the virtual model of the ORC system is realized with reference to an actual installation. The operating conditions are taken directly from the experimental data described in [
21]. The experimental data are used for (i) validating the numerical results and (ii) feeding the numerical model with actual operating conditions, allowing the analysis of specific fluid dynamic effects (cavitation at the gear pump inlet and pressure pulsation on the CFM due to the gear pump operation), which can be difficult to detect by means of an experimental approach.
The prototypal micro-ORC energy system used as a reference was specifically designed for in-field operations but, at the same time, was equipped with several additional sensors/probes in order to detect its operating points and performance. The ORC system operates with R134a as a working fluid and its main components are as follows: (i) a brazed plate heat exchanger with 64 plates as evaporator, (ii) a brazed plate heat exchanger with 16 plates as a regenerator, (iii) a shell and tube heat exchanger as condenser, (iv) a volumetric three-piston radial engine used as expander, and finally, (v) a volumetric gear pump controlled by an inverter that supplies the organic fluid over the ORC system position under the liquid receiver (tank), realizing a column of water about 1 m high.
2.1. Computational Grid and Dynamic Mesh Approach
The numerical simulations and meshing phase are developed by means of the software Pumplinx 4.6.4 by Simerics Inc.
® (Bellevue, WA, USA). The virtual model depicted in
Figure 1 is discretized by means of a Cartesian grid (binary-tree mesh type) for the stationary domains (such as piping and gear pump body) and a body-fitted curvilinear mesh type for the rotary domains (such as the gear pump wheels).
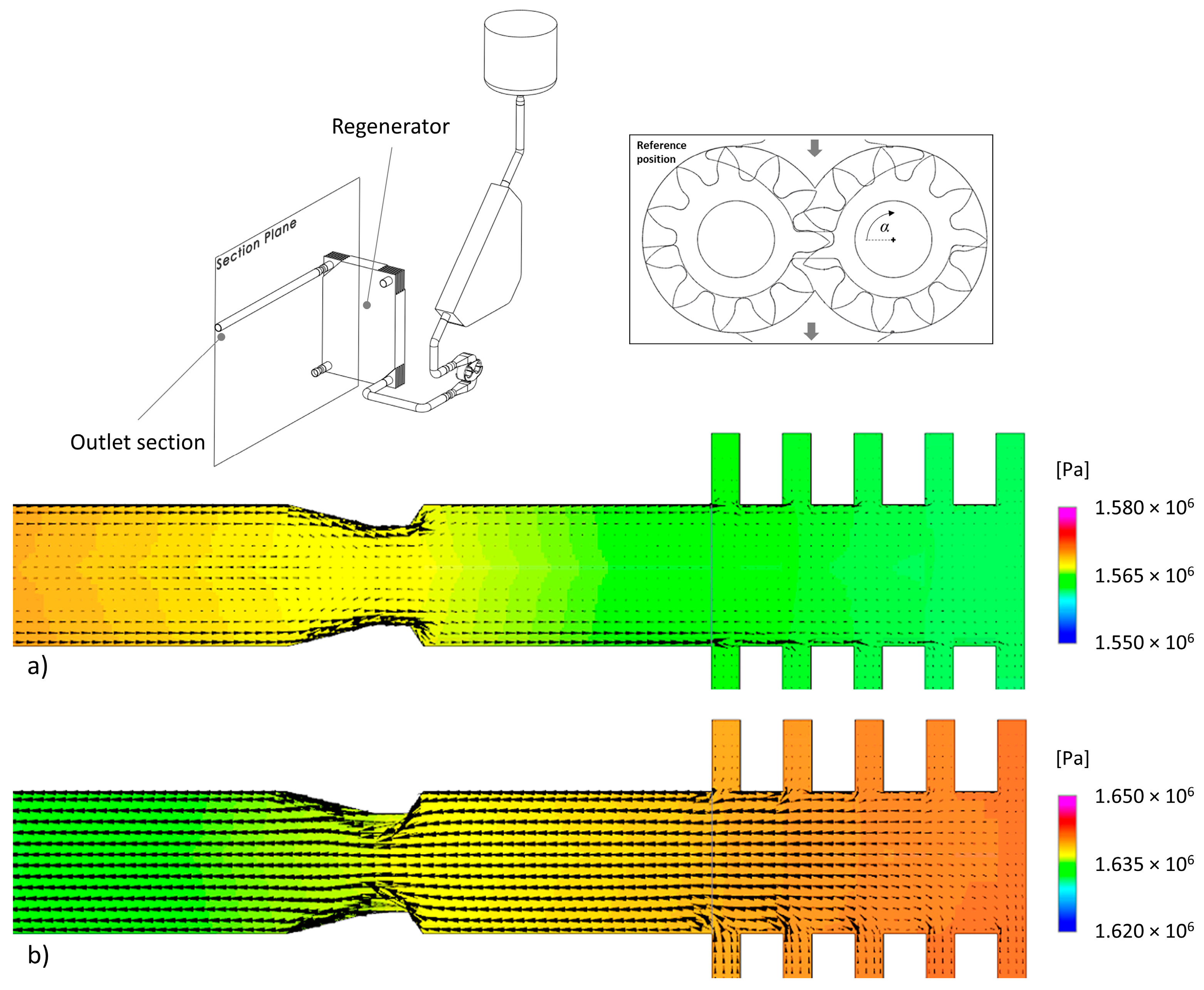
Figure 2 reports two mesh details of the stationary components: the outlet section of the regenerator and the inlet section of the CFM. The stationary mesh is composed of about 3 million elements. Finer grid elements are adopted at the variation of the passage area, especially in the proximity of the inlet and exit valves. Due to these geometric features, the element size of the mesh is adapted according to the passage area. In particular, in each section, an element number in the range of 20–30 was adopted along the pipe diameter. A detailed description of the element size adopted for the gap discretization is reported in the following section.
The dynamic mesh approach was adopted with the aim of analyzing the transient phenomenon generated by the gear pump operation. For this reason, particular attention was given to the mesh generation of this component. The internal volume of the gear pump has been discretized through a structured mesh able to account for the wheel rotation and engagement over the transient analysis. The rotation and engagement processes determine the modification of the internal shape of the computational domain at each time-step. The computational mesh of this section consists of about 300,000 hexahedral elements, which have been associated with a deformation algorithm able to simulate the rotation of the wheels and their engagement.
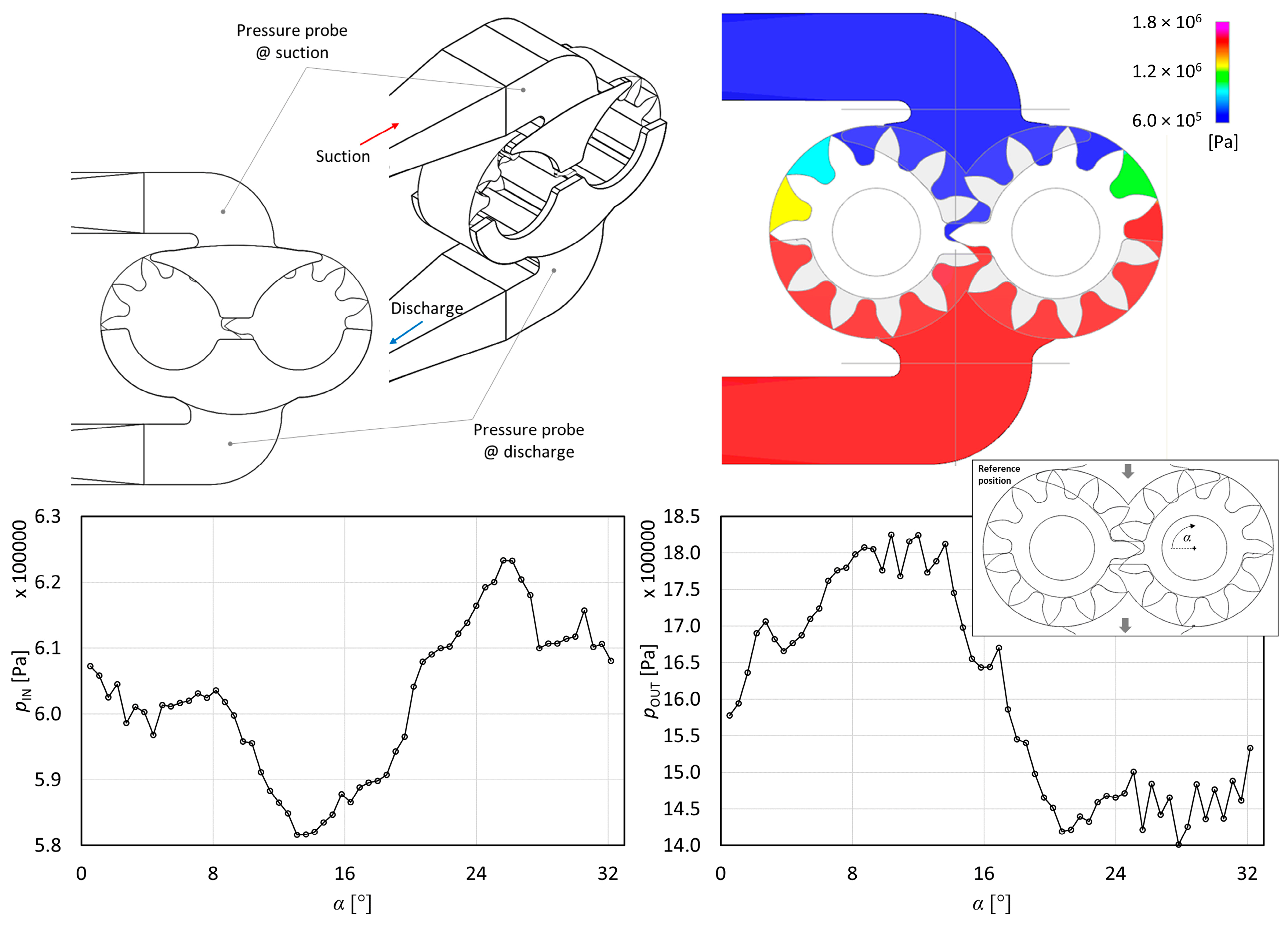
Figure 3 shows four successive instants related to the rotation and engaging of the gear pump wheels. It can be seen how the grid elements (in the vane) are able to adapt and change their shape, to accommodate the presence of the tooth of the opposite wheel. The rotating domain is connected to the suction and discharge ports through sliding interfaces able to couple the stationary and rotating domains. The subdivision between stationary and rotating domains inside the gear pump is depicted in
Figure 4. The suction and delivery ports of the gear pump are connected via sliding interfaces to the rotating domain.
The computational mesh, composed of about 3 million elements and depicted in
Figure 2,
Figure 3 and
Figure 4, is the result of a mesh sensitivity analysis (from 2 million to 4 million elements) that was carried out with the aim of validating the numerical results against the experimental data. A detailed comparison and quantification of the deviation between the numerical results and the actual ORC operation is reported in the following sections.
2.2. Gear Pump Virtual Model and Main Features
The pump displacement is equal to 7.5 × 10−6 m3. The volumetric flow rate provided by the gear pump can be adjusted according to the ORC requirements by varying the rotational velocity. This ideal displacement is affected by the unavoidable leakages that characterize these machines. By means of the present simulation strategy, it is possible to include in the fluid dynamic analysis all the leakages through the gaps: between the wheels and the pump casing (i.e., tooth flank—pump casing sides and tooth head—pump casing periphery) and the engagement region.
The liquid flows through these gaps according to the pressure gradient, from the discharge port to the suction port determining a volumetric efficiency lower than one. This phenomenon characterizes all rotating volumetric machines and is one of the main points of interest for the fluid dynamics simulation of this type of machine. In fact, an ideal positive displacement machine has to perfectly seal the suction port with respect to the discharge port, but the manufacturing processes and the necessity to reduce the friction between the moving and fixed parts determine the axial and radial gaps.
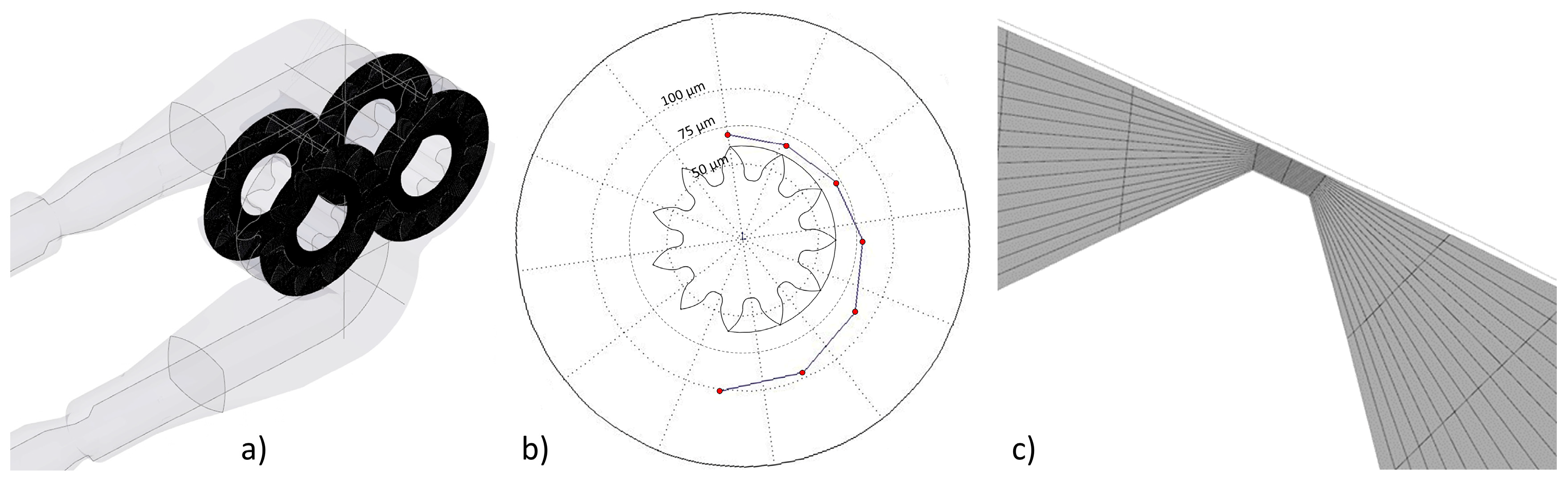
The axial gaps are due to the axial clearance that exists between the wheels and the pump case. In the present analysis, the axial gap is equal to 20 μm and contributes to a decrease in the volumetric efficiency of the gear pump. In
Figure 5a, the computational grid in the axial gaps is reported. It is realized by means of five layers of hexahedral elements and coupled with the rotating domain through a sling interface.
In a different way of the axial gaps, the clearance between the tooth head and the pump casing is a function of the angular position of the wheel and they vary in the range of 50–100 µm. Each angular position of the wheel is characterized by a different distance between the tooth head and the pump casing due to the eccentric position of the wheel. The eccentric position is related to the unbalanced pressure forces between the wheel region facing the delivery port (high pressure) and the wheel region facing the suction port (low pressure). The fluid pressure at the port acts on the overlocked wheel portion, generating a certain load. The fluid pressure at the delivery port is higher than the pressure value at the suction port; for this reason, the wheel is not concentric with respect to the pump casing but is located in an eccentric position responsible for the lower values for the tooth-head gap in the proximity of the suction port.
In
Figure 5b the magnitude of the gaps is reported by means of a polar diagram, in which the delivery section is in the lower part while the suction section is in the upper part. They vary (in particular, increase) starting from about 70 µm up to 100 µm.
In the tooth-head gap, thanks to the deformation strategy adopted for the computational mesh, the number of elements used to discretize that region is identical to the number of elements used to discretize the vane volume. In particular, 16 elements were adopted for the radial discretization of the gear pump vane, that allows a proper resolution of the flow field.
Figure 5c reports the computational mesh in correspondence of the gap between the tooth head and the pump case and shows the grid refinement in this particular region.
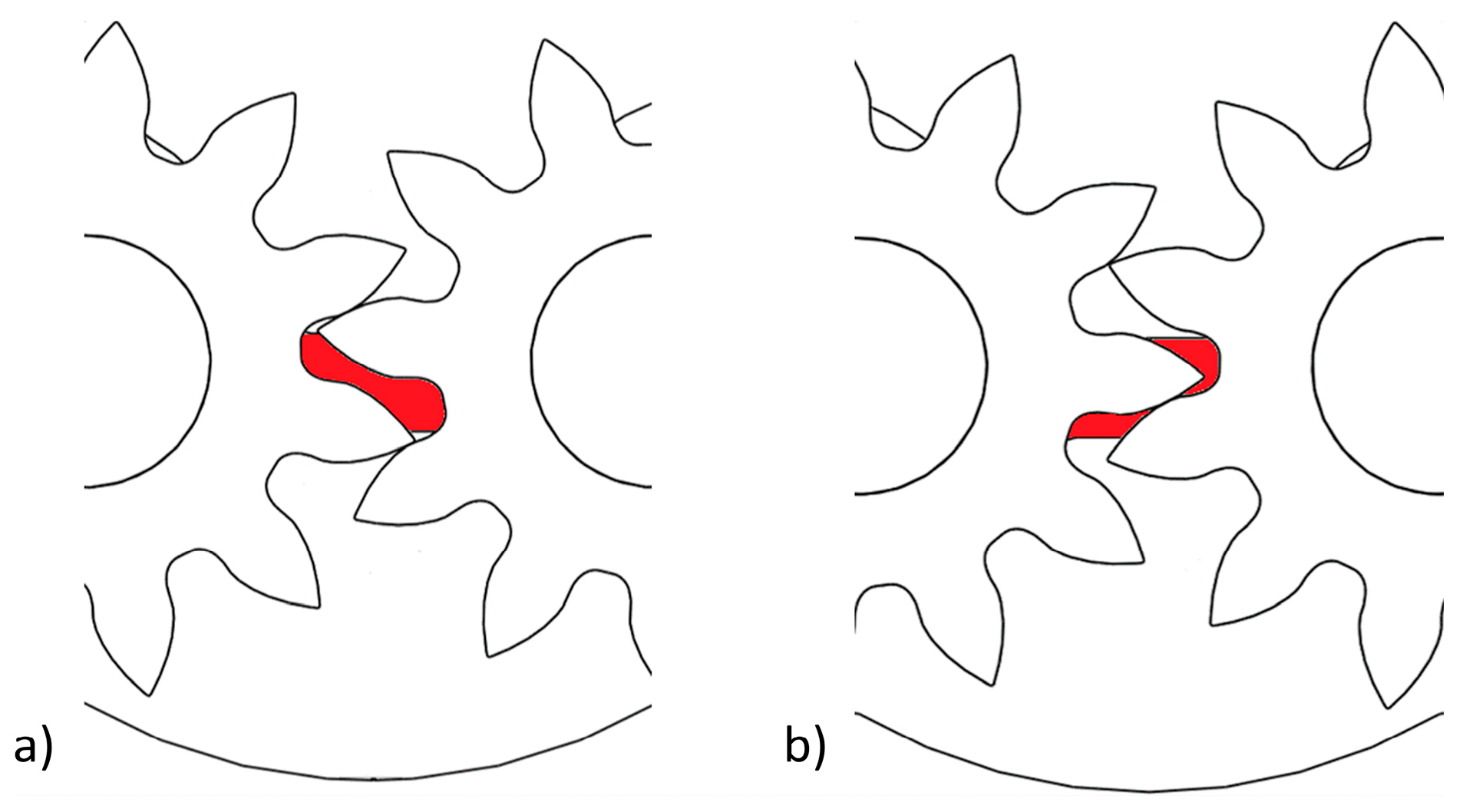
The last contribution to the reduction of volumetric efficiency is due to the engaging process. In the engaging region, when two teeth pairs come into contact, a trapped volume could arise and, in the case of the wrong design, it can experience a progressive volume reduction, leading to a sudden change in pressure [
11]. To avoid this, the trapped volume is always connected with the high- or low-pressure chamber. This role is performed by purpose-built pockets in the lateral side of the pump casing, named relief grooves, whose dimensions are very important to the resulting dynamic behavior. The shape and position of this relief groove are depicted in
Figure 6. The radial width of the relief groove must be balanced in order to (i) avoid the pressure rise caused by the trapped volume and (ii) limit the flow escaping from the delivery (high pressure) to the suction (low pressure) ports. As can be seen from the two successive instants shown in
Figure 6, the relief groove is firstly connected to the suction (upper) and discharge (lower) ports (see
Figure 6a) and then sealed by the contact between the two tooth pairs in contact (see
Figure 6b). In the latter position, the teeth in contact do not allow fluid flow from the delivery to the suction port.
In addition to the negative contribution to the volumetric efficiency, the backflow from the discharge to the suction port through the relief groove also determines pressure pulsations that could affect the flow field at the suction ports of the gear pump. In this region, a high-pressure jet of fluid coming from the groove experiences a sudden pressure drop increasing the pressure variation and the cavitation effects. This phenomenon, strongly related to the transient phenomena experienced by the gear pump, will be considered in the subsequent analysis of the results, with particular attention to the repercussions of this effect on cavitation and on the variation in pressure field induced by the CFM, which is installed upstream of (but close to) the gear pump.
2.3. Operating Conditions
The refrigerant (in the liquid phase) considered in the present analysis is the R134a (F3C-CH2-F). Over the modeled flow path, the liquid refrigerant experience the pressure rise provided by the gear pump. The aim of the present analysis is to show dynamic phenomena such as pressure pulsation and cavitation, and for this reason, the present analysis is carried out avoiding the thermal power exchanged at the regenerator and the heat dissipated with the environment.
Dealing with dynamic analysis, the boundary conditions of the present investigation are averaged values according to the gear pump rotation. The transient analysis is carried out adopting a time-step adequate to solve the 0.5° rotation of the gear wheels.
The liquid receiver (tank) is considered pressurized at a fixed pressure level of 601,325 Pa, while at the evaporator inlet, the imposed pressure is 1,601,325 Pa. These pressure boundary conditions are in line with the operating point reported in [
21], and are bounded by the heat source and sink constituted of water, having a temperature in the range 18–25 °C at the condenser and 60–90 °C at the evaporator.
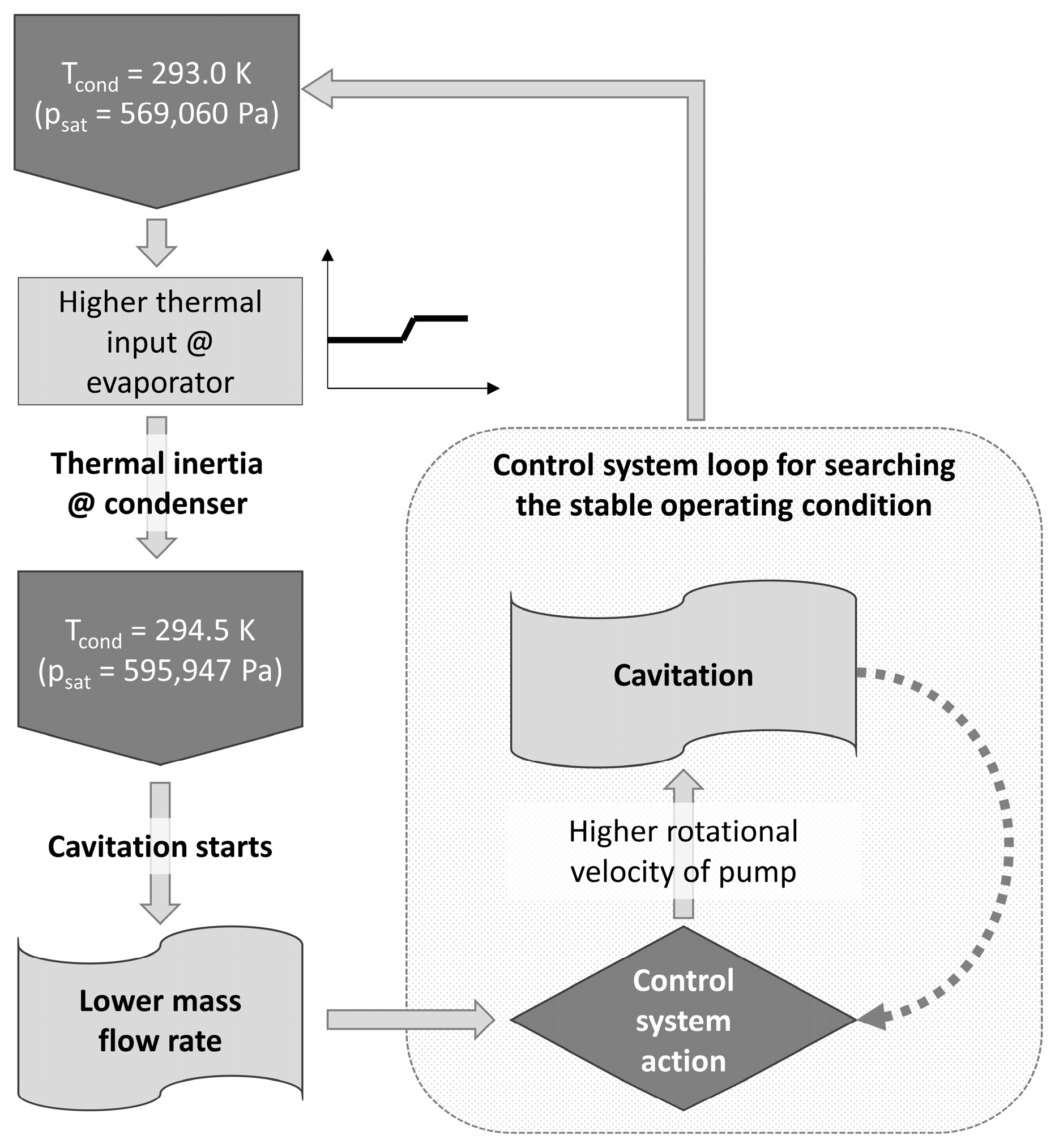
According to the pressure boundary condition, the gear pump rotational speed is adjusted (in the range from 450 rpm to 475 rpm) in order to guarantee a mass flow rate of about 0.1 kg/s, which is considered the target value for the present analysis. Since the pump operation is affected by the leakages and the cavitation phenomena, the target mass flow rate is guaranteed with different rotation speed related to the sub-cooling degree that occurs at the condenser. The sub-cooling degree determines the liquid saturation pressure, which represents the most important values for the cavitation phenomenon. Starting from a reference condition (which corresponds to 450 rpm, liquid temperature of 293 K and saturation pressure of 569,060 Pa), two additional operating points have been simulated according to the working parameter of the ORC control system (variation of the liquid temperature and pump rotational speed). Details about these two additional analyses will be reported later.
As described above, the suction section of the pump is affected by high-speed gradients of the fluid velocity due to the simultaneous presence of (i) wheel rotation and (i) backflow through the relief groove from the engaging region. These phenomena, associated with the thermodynamic condition of the liquid phase at the pump inlet (close to the saturated condition), and pressure losses introduced by the piping and fittings (pipes, valves, CFM, and bends) make the cavitation phenomenon one of the main issues of the present application (gear pump in a micro-ORC system).
2.4. Model Setup and Validation
With reference to the previous description, all the numerical simulations were carried out by imposing a constant static pressure at the inlet (601,325 Pa) and at the outlet (1,601,325 Pa) sections of the virtual model depicted in
Figure 1. For turbulence modeling, the
k–
ε turbulence model was adopted. A constant liquid density (1226 kg/m
3) and viscosity (2.02 × 10
−4 Pa s) values are also specified for each operating condition. The cavitation phenomenon is modeled by means of the equilibrium dissolve gas model implemented in Pumplinx 4.6.4 [
24].
As mentioned, the numerical model was validated against experimental data taken from [
21]. The sensitivity analysis of the computational mesh was carried out with the aim of reproducing the experimental results and, at the same time, limiting the computational effort.
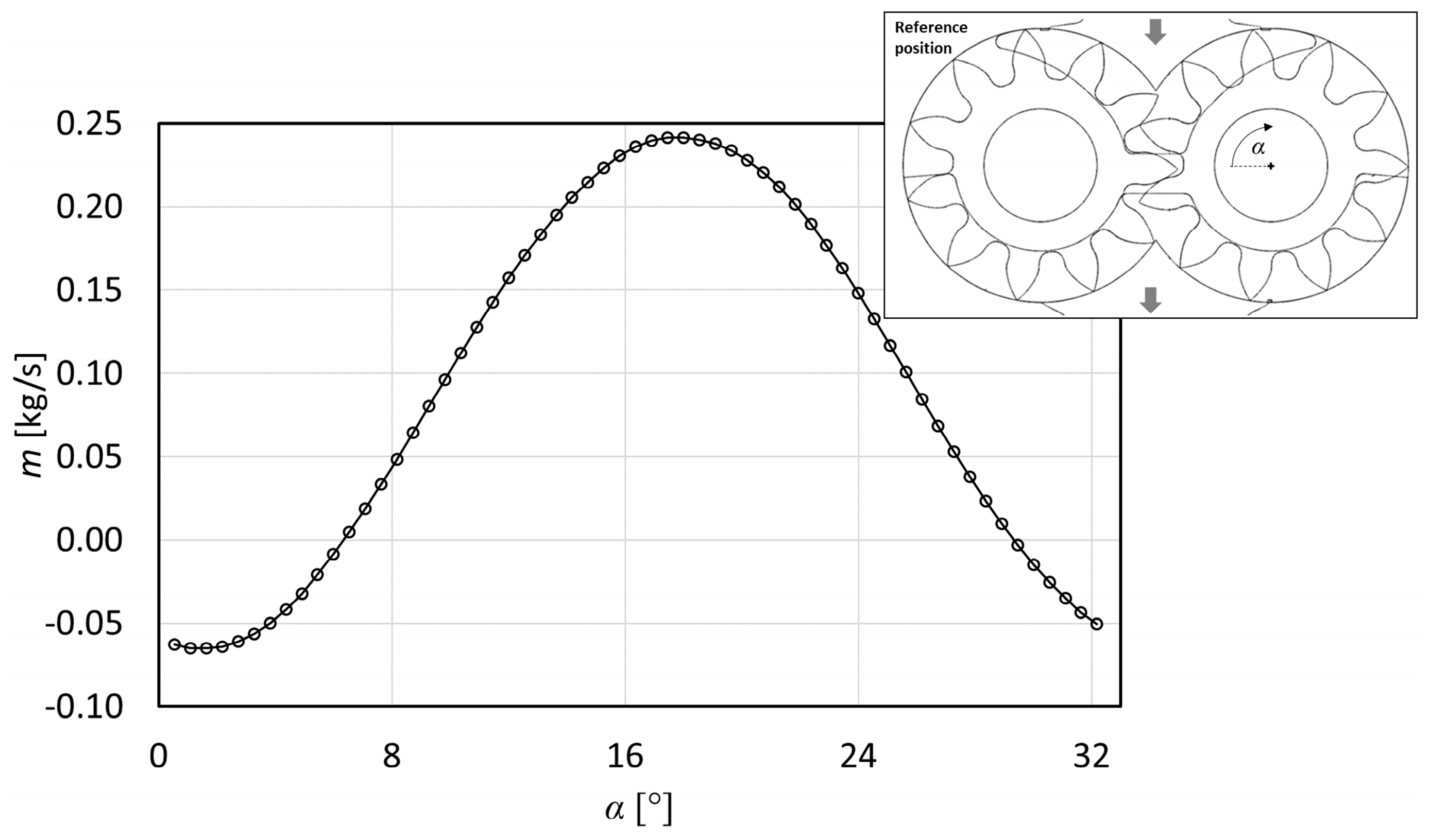
Figure 7 reports the comparison between the mass flow rate
m obtained from the experimental data and from the numerical solutions with respect to the gear pump rotational speed
ω. The mass flow rate values are taken as an averaged value of the instantaneous mass flow rate provided by the pump. The data are in reasonable agreement (error bars equal to 10%), especially in the range from 425 rpm to 525 rpm. For cases with lower values of rotational speed, the presence of a lubricant oil (in a fraction between 3% and 6%, see [
21]) allows the sealing process in the flank and radial gaps and, for this reason, the mass flow rate looks greater than the values obtained in numerical simulations.
5. Conclusions
In this paper, transient numerical simulations of a micro-ORC system branch have been carried out using a novel Whole Engine Model strategy. The aim of the present work was to analyze the fluid dynamic behavior of the gear pump operation on the system performance and control/measuring devices. The use of the dynamic model coupled with the dynamic mesh strategy allowed for the analysis of dynamic behavior such as pressure pulsation and cavitation phenomenon, related to the rotation and the engagement of gear pump wheels. With reference to the numerical results reported in this work, the main outcomes can be listed as follows:
the operation of the gear pump in a micro-ORC system determines pressure pulsations that could affect the measurement systems and system performance;
pressure pulsations affect the operation of the Coriolis flow meter installed downstream of the liquid receiver and upstream of the gear pump. The pressure pulsation results in an excitation force that is variable according to the gear pump wheel position;
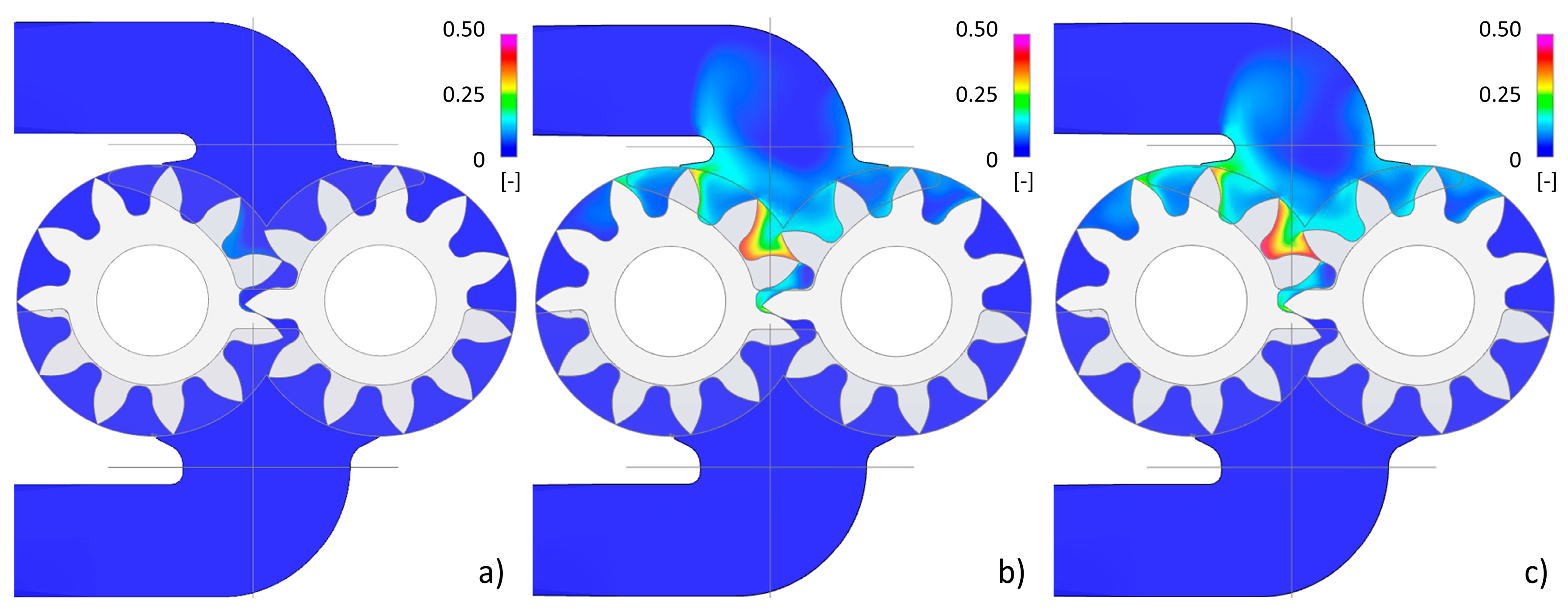
the sub-cooling degree affects the gear pump operation. The pressure losses generated by the piping, fittings and suction port geometry, together with the dynamic effects of wheel rotation, determine a pressure drop responsible for the cavitation phenomenon;
the cavitation phenomenon is promoted by the decreasing sub-cooling degree (which determines the saturation pressure of the liquid phase) and by the increasing pump rotational speed.
From the present analysis, it is clear that the actions of the control system affect the operation of every single component of an ORC system. The analyses have shown that certain transient conditions could determine several risks for the reliability and performance of components. Measuring performance can be preserved/improved by following specific guidelines, which involve both the design criteria of the devices and the control strategy of the ORC system. For example, the instantaneous variation of the evaporator thermal input could determine a cavitation phenomenon in the pump, which is subject to the action of the control system that requests more flow rate for increasing the energy exchanged at the evaporator. In this sense, numerical simulations of an actual installation may represent a valid support for better control and management of the systems, improving the performance, increasing the operating life, and reducing the risks of system damage.