Thermo-Hydro-Mechanical Coupled Modeling of Methane Hydrate-Bearing Sediments: Formulation and Application
Abstract
1. Introduction
2. Methodology
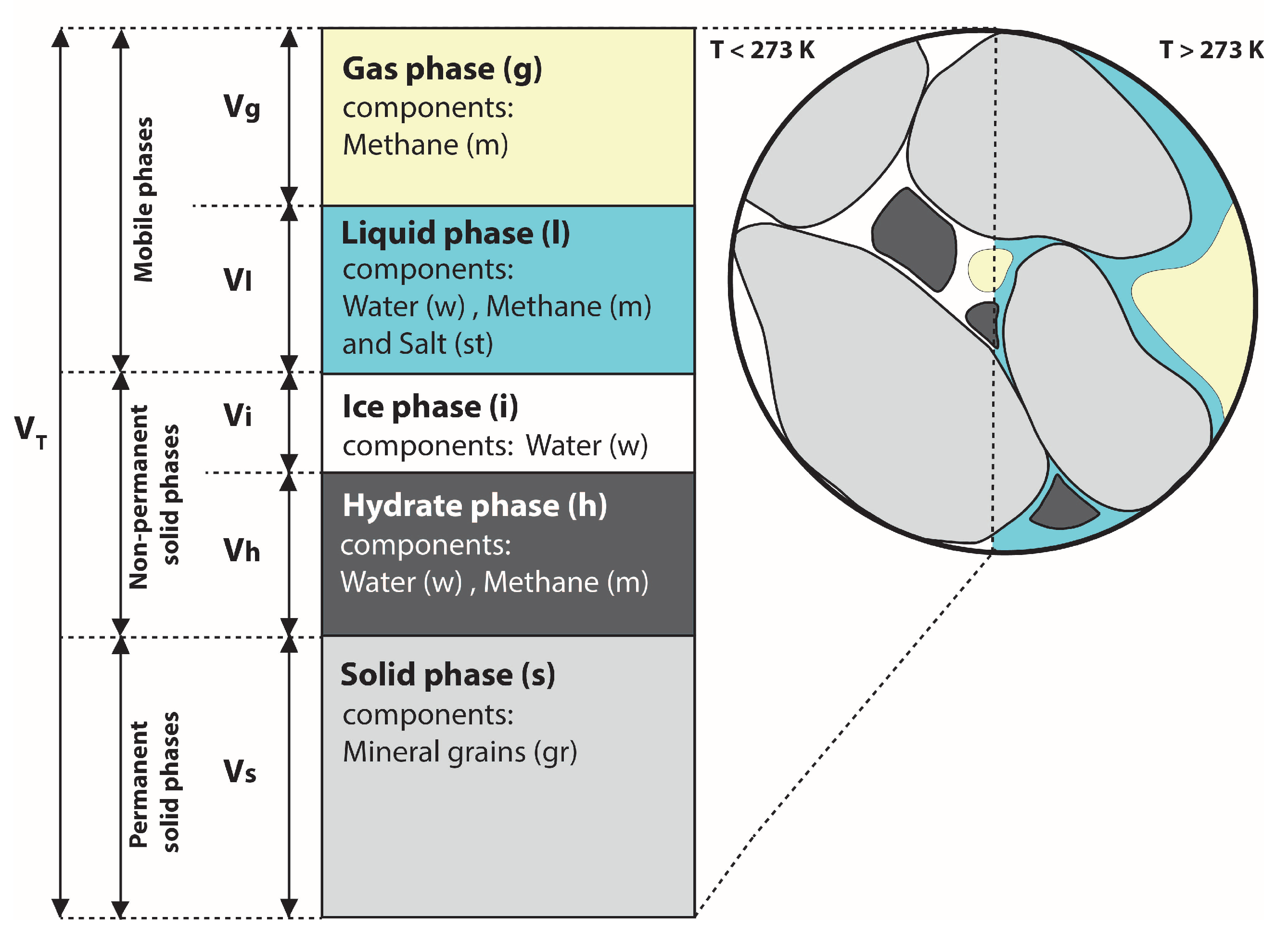
2.1. Components, Phases and Partial Saturations
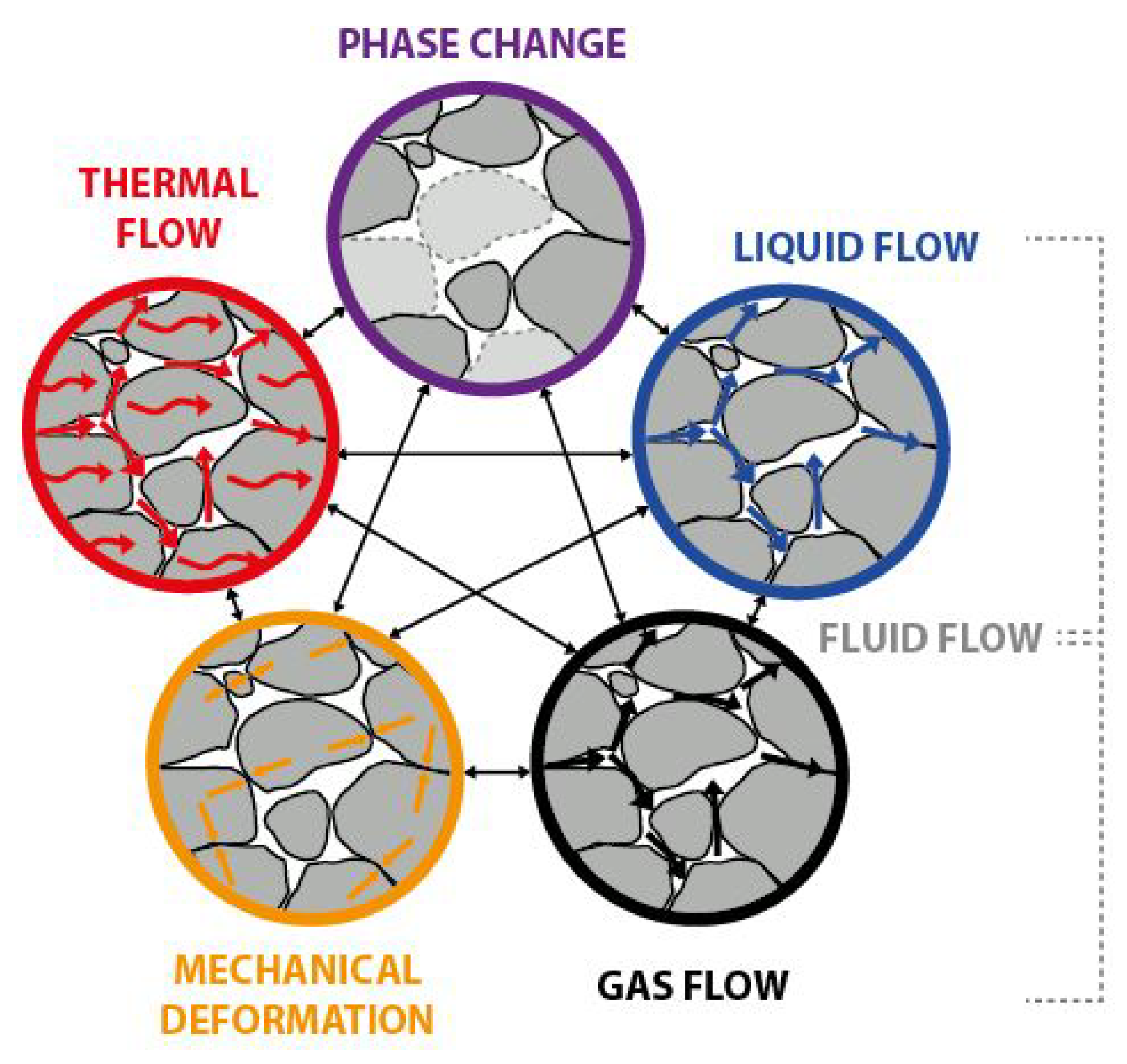
2.2. Multiphysical Coupled System
2.3. Governing Equations
- Mass balance of mineral grains:The mineral grains coincide with the permanent solid phase and define the skeletal structure of the porous medium. The mass conservation of this component can be written as:where is the flux of solid and can be expressed in terms of the solid velocity () as:Applying the chain rule for all the derivatives, Equation (3) can be rewritten as:Neglecting the gradients of density and porosity convected by the solid phase and under the assumption of small strain, Equation (5) can be rewritten as:where the term can be expressed in the form:and are Cartesian strains.
- Mass balance of methane:Methane component is present in liquid, gas and hydrate phases, and its total mass balance is expressed as:where , and are the volumetric mass of methane in the liquid, gas and hydrate phases, respectively. For a given temperature, pressure and salinity the term can be obtained according to [42,43], is equal to one as the gas phase is considered mono-component and assuming as 6.176.The mass flux terms and are the relative motion of methane in the liquid and gas phases, respectively, with respect to the solid phase. These terms are obtained as the sum of advective and diffusive flux terms as follows:The mass flux term denote the relative motion of methane in the hydrate phase with respect to the solid phase as a result of the medium deformation:The term is the external sink/source of methane per unit volume. Please note that because of the compositional approach adopted in the formulation, this term do not include methane mass changes from hydrate kinetics.
- Mass balance of water:Water is present in liquid, ice and hydrate phases but it is neglected as vapour in the gas phase. Thus, the water total mass balance of water is expressed as:where , and are the volumetric mass of water in the liquid, ice and hydrate phases, respectively. The term depends on the concentration of salt and methane dissolved in the liquid phase, is equal to one and .The mass flux term of water in liquid () is computed similarly as in Equation (9), while the flux terms in hydrate () and ice phases () are computed similarly as in Equation (11) for and , respectively.The is an external sink/source of water per unit volume and do not include water mass changes from hydrate kinetics.
- Mass balance of salt:Salt is present as a dissolved component in the liquid phase, and it is not allowed to precipitate as a solid phase. Its concentration modifies the liquid density, influences the solubility of methane and can inhibit hydrate stability conditions. The total mass balance of salt is expressed as:where is the volumetric mass of salt in the liquid phase. Changes in salt concentration due to “freshening” of the pore water can be used as a tracer of ongoing hydrate dissociation and/or ice melting.The flux term of salt in the liquid phase () is the relative motion of salt in the liquid phase with respect to the solid phase and is computed similarly as in Equation (9). Finally, the term is the external sink/source term of salt.
2.4. Numerical Solution Strategy
3. Results and Discussion
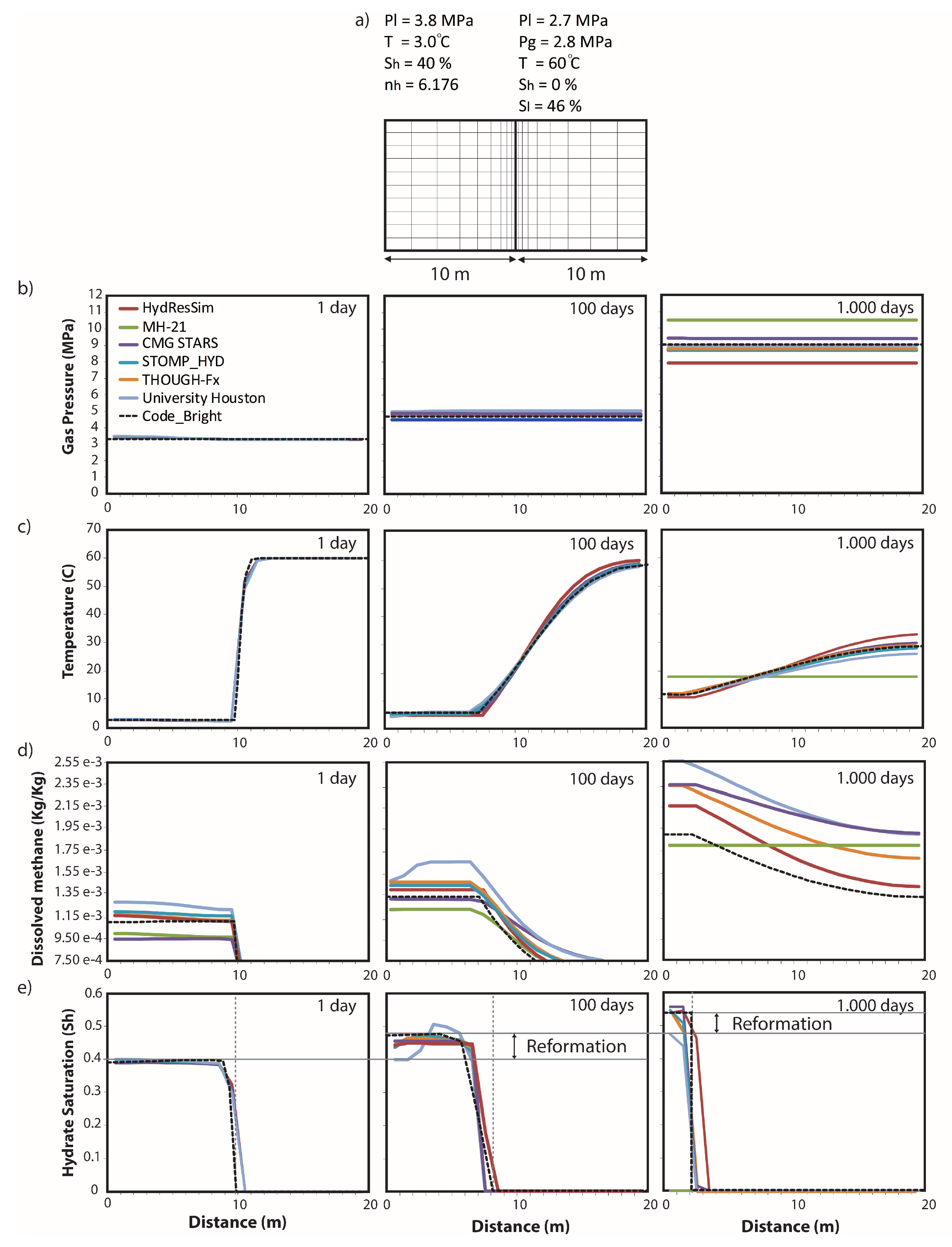
3.1. Thermo-Hydraulic Validation
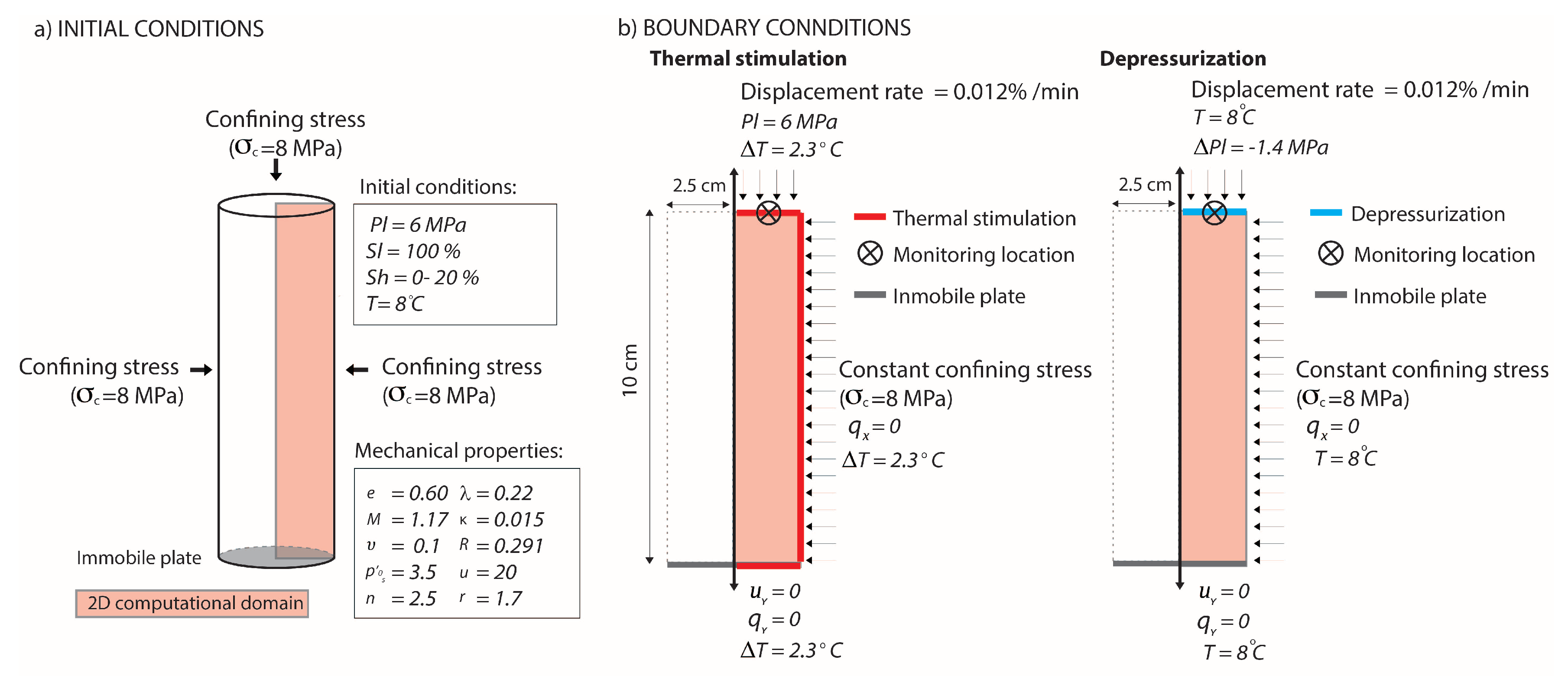
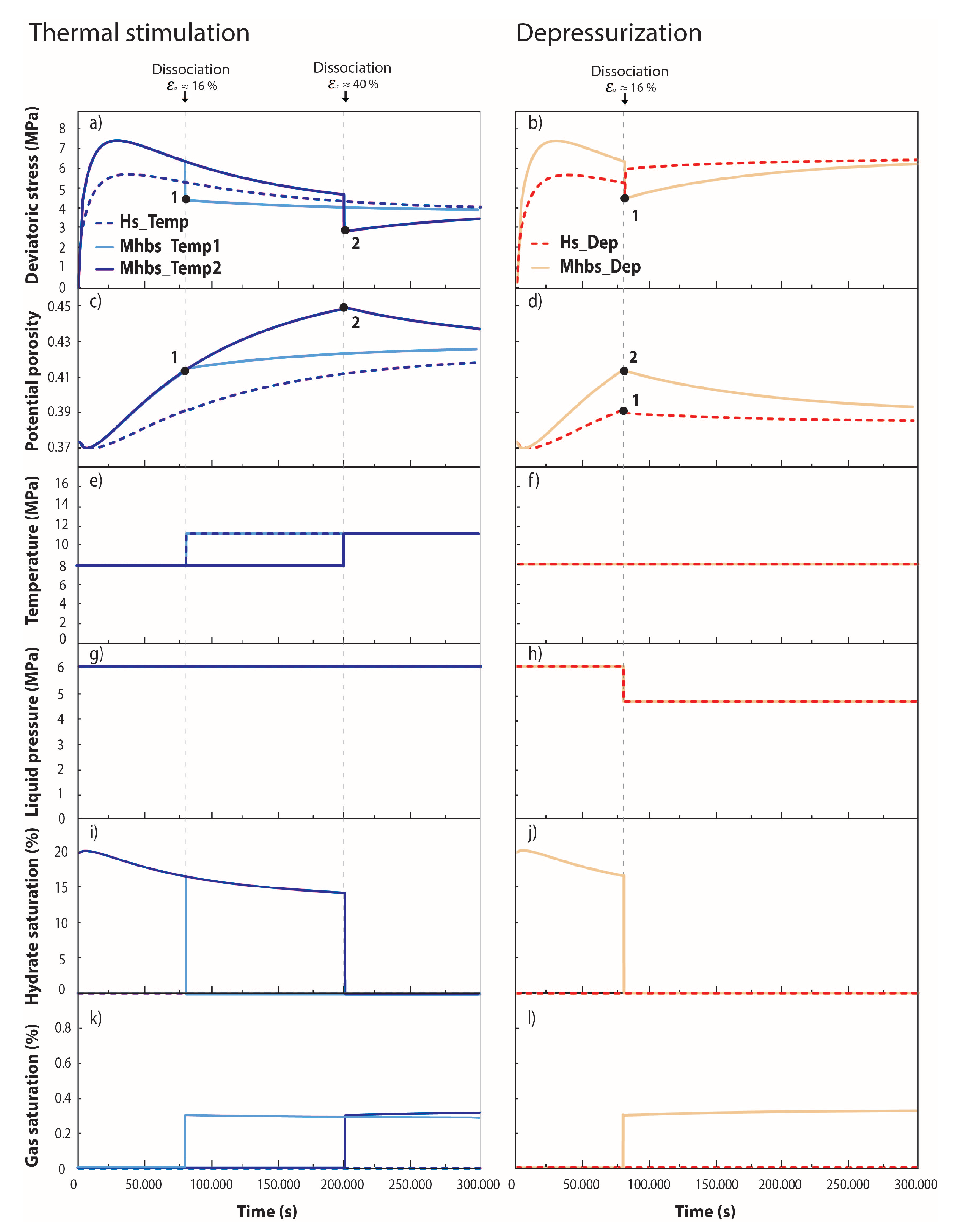
3.2. THM Modelling of Synthetic Experimental Tests
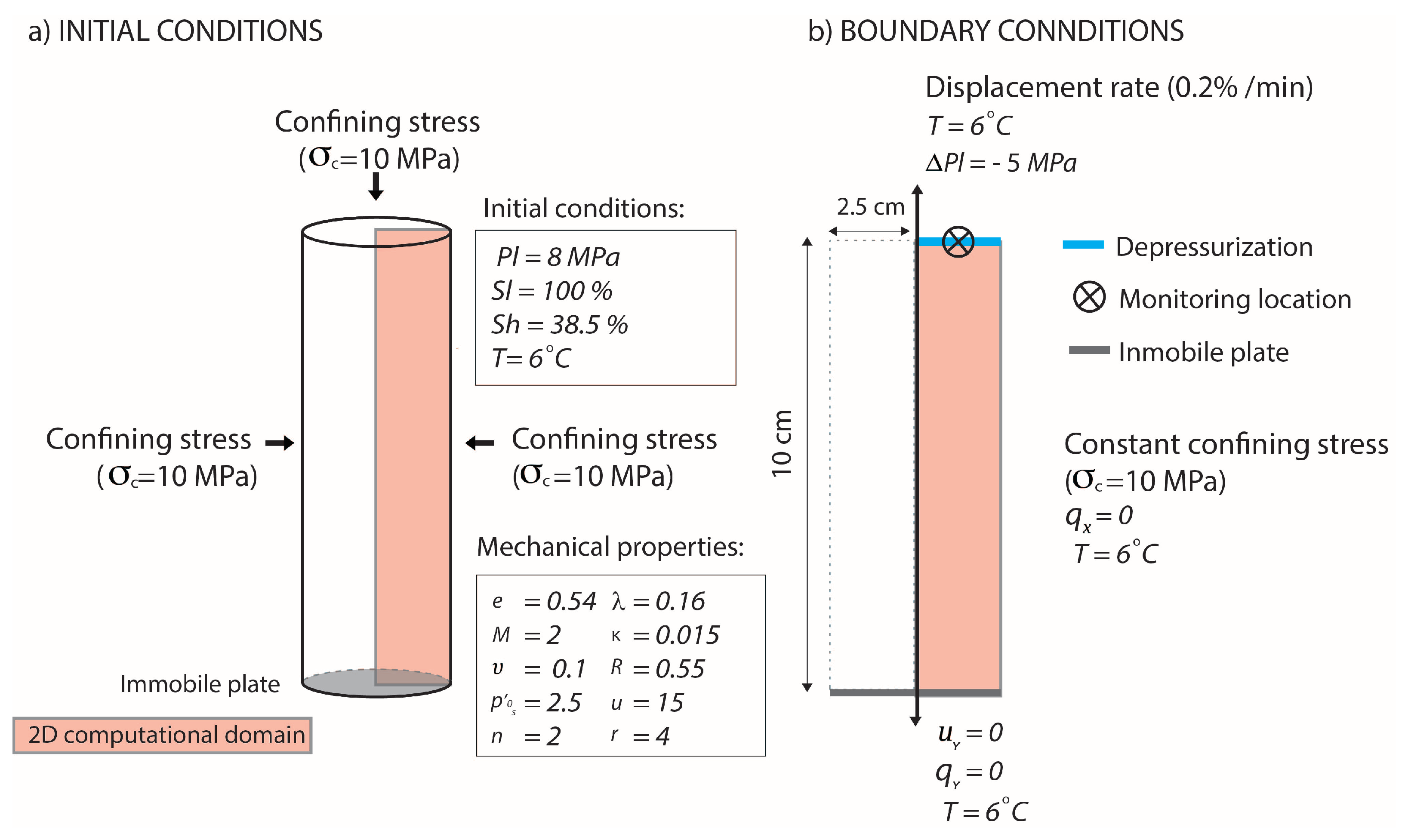
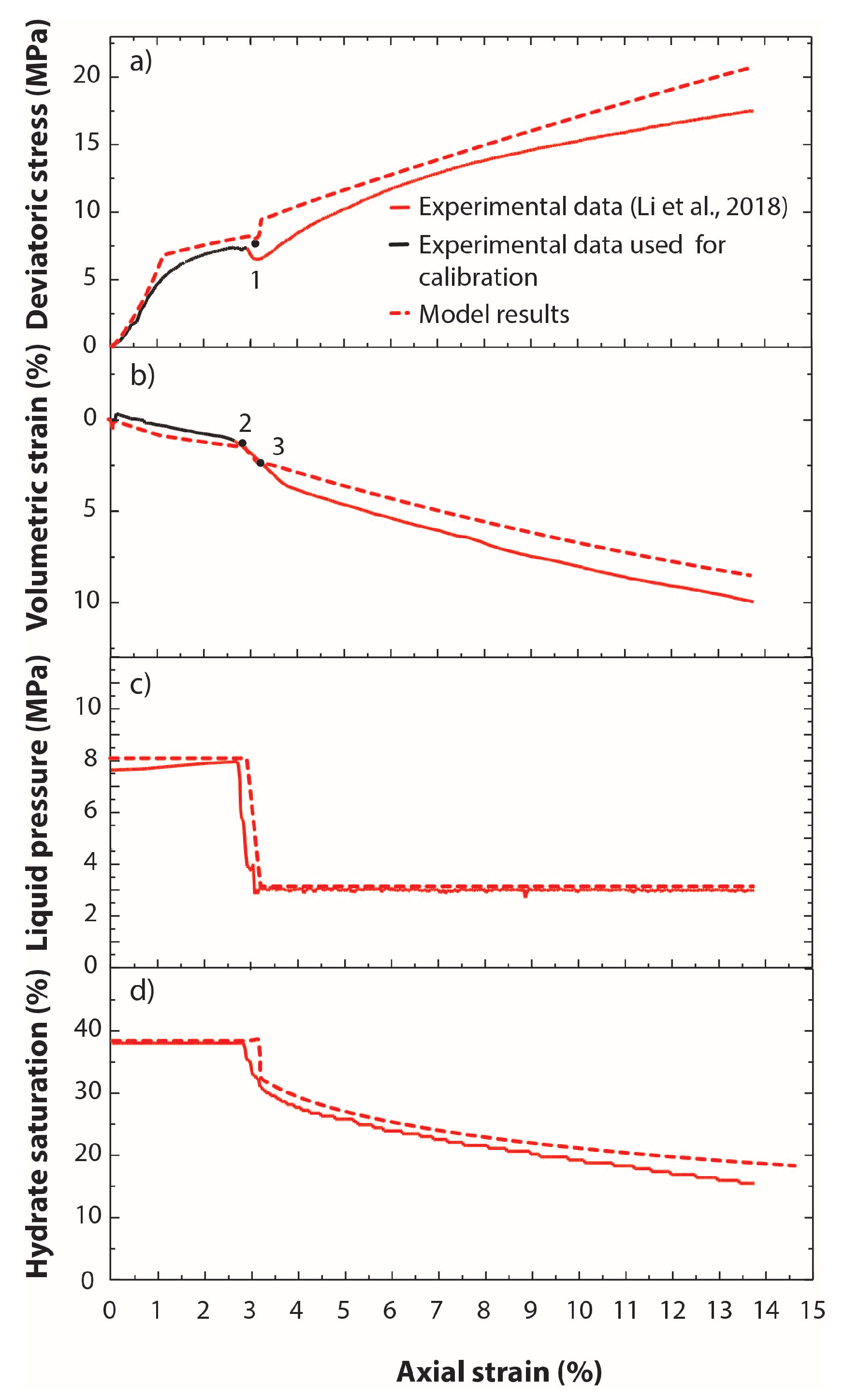
3.3. THM Modelling of the Experimental Tests of Li et al. (2018)
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| MHBS | Methane hydrate-bearing sediments |
| NETL | National Energy Technology Laboratory |
| P | Pressure |
| T | Temperature |
| TH | Thermo-hydraulic |
| THM | Thermo-hydro-mechanical |
| USGS | United States Geological Survey |
Appendix A. Development of Hydrate and Ice Mass Balance Equations
References
- Milkov, A.V. Global estimates of hydrate bound gas in marine sediments: How much is really out there? Earth Sci. Rev. 2004, 66, 183–197. [Google Scholar] [CrossRef]
- Krey, V.; Canadell, J.G.; Nakicenovic, N.; Abe, Y.; Andruleit, H.; Archer, D.; Grubler, A.; Hamilton, N.T.M.; Johnson, A.; Kostov, V.; et al. Gas hydrates: Entrance to a methane age or climate threat? Environ. Res. Lett. 2009, 4, 34007. [Google Scholar] [CrossRef]
- Muradov, N. Decarbonization at crossroads: The cessation of the positive historical trend or a temporary detour? Energy Environ. Sci. 2013, 6, 1060–1073. [Google Scholar] [CrossRef]
- Smith, C.A. Energy Resource Potential of Methane Hydrate: An Introduction to the Science and Energy Potential of a Unique Resource. 2011. Available online: www.netl.doe.gov (accessed on 23 May 2019).
- Birchwood, R.; Dai, J.; Shelander, D.; Boswell, R.; Collett, T.; Cook, A.; Dallimore, S.; Fujii, K.; Imasato, Y.; Fukuhara, M.; et al. Developments in gas hydrates. Oilfield Rev. 2010, 22, 18–33. [Google Scholar]
- Collett, T.S.; Johnson, A.H.; Knapp, C.C.; Boswell, R. Natural gas hydrates—Energy resource potential and associated geologic hazards. AAPG Mem. 2009, 89, 146–219. [Google Scholar]
- Ruppel, C.D. Gas hydrate in nature. U.S. Geol. Surv. Fact Sheet 2018, 2017–3080, 4. [Google Scholar]
- Hovland, M.; Gudmestad, O.T. Potential influence of gas hydrates on seabed installations. In Natural Gas Hydrates; Paull, C.K., Dillon, W.P., Eds.; Geophysical Monograph Series; American Geophysical Union: Washington, DC, USA, 2001; Volume 124, pp. 307–315. [Google Scholar]
- Nagel, N. Compaction and subsidence issues within the petroleum industry: From Wilmington to Ekofisk and beyond. Phys. Chem. Earth Part A Solid Earth Geod. 2001, 26, 3–14. [Google Scholar] [CrossRef]
- Ahmadi, G.; Ji, C.; Smith, D.H. Numerical solution for natural gas production from methane hydrate dissociation. J. Petroleum Sci. Eng. 2004, 41, 269–285. [Google Scholar] [CrossRef]
- Kurihara, M.; Ouchi, H.; Inoue, T.; Yonezawa, T.; Masuda, Y.; Dallimore, S.R.; Collett, T.S. Analysis of the JAPEX/JNOC/GSC et al. Mallik 5L-38 gas hydrate thermal-production test through numerical simulation. Bull. Geol. Surv. Can. 2005, 585, 111. [Google Scholar]
- Kwon, T.H.; Cho, G.C.; Santamarina, J.C. Gas hydrate dissociation in sediments: Pressure-temperature evolution. Geochem. Geophys. Geosyst. 2008, 9, Q03019. [Google Scholar] [CrossRef]
- Liu, Z.; Yu, X. Thermo-hydro-mechanical-chemical simulation of methane hydrate dissociation in porous media. Geotech. Geol. Eng. 2013, 13, 168–1691. [Google Scholar] [CrossRef]
- Moridis, G.J.; Kowalsky, M.; Pruess, K. TOUGH-Fx/HYDRATE v1.0 User’s Manual: A Code for the Simulation of System Behaviour in Hydrate-Bearing Geologic Media; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2008.
- Sultan, N.; Cochonat, P.; Foucher, J.P.; Mienert, J. Effect of gas hydrates melting on seafloor slope instability. Mar. Geol. 2004, 213, 379–401. [Google Scholar] [CrossRef]
- White, M.D.; Oostrom, M. STOMP Subsurface Transport Over Multiple Phase: User’s Guide; Pacific Northwest National Laboratory: Washington, DC, USA, 2006.
- Xu, W.; Ruppel, C. Predicting the occurrence, distribution, and evolution of methane gas hydrate in porous marine sediments. J. Geophys. Res. 1999, 104, 5081–5095. [Google Scholar] [CrossRef]
- Hyodo, M.; Yoneda, J.; Yoshimoto, N.; Nakata, Y. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed. Soils Found. 2013, 53, 299–314. [Google Scholar] [CrossRef]
- Masui, A.; Haneda, H.; Ogata, Y.; Aoki, K. Mechanical Properties of Sandy Sediment Containing Marine Gas Hydrates in Deep Sea Offshore Japan Survey Drilling in Nankai Trough. In Proceedings of the International Society of Offshore and Polar Engineers: Seventh ISOPE Ocean Mining Symposium, Lisbon, Portugal, 1–6 July 2007. [Google Scholar]
- Sultaniya, A.; Priest, J.; Clayton, C.R.I. Impact of formation and dissociation conditions on stiffness of a hydrate-bearing sand. Can. Geotech. J. 2018, 55, 988–998. [Google Scholar] [CrossRef]
- Li, D.; Wu, Q.; Wang, Z.; Lu, J.; Liang, D.; Li, X. Tri-axial shear tests on hydrate-bearing sediments during hydrate dissociation with depressurization. Energies 2018, 11, 1819. [Google Scholar] [CrossRef]
- Santamarina, J.C.; Dai, S.; Terzariol, M.; Jang, J.; Waite, W.F.; Winters, W.J.; Nagao, J.; Yoneda, J.; Konno, Y.; Fujii, T.; et al. Hydro-bio-geomechanical properties of hydrate-bearing sediments from Nankai Trough. Mar. Pet. Geol. 2015, 66, 434–450. [Google Scholar] [CrossRef]
- Yoneda, J.; Oshima, M.; Kida, M.; Kato, A.; Konno, Y.; Jin, Y.; Jang, J.; Waite, W.F.; Kumar, P.; Tenma, N. Permeability variation and anisotropy of gas hydrate-bearing pressure-core sediments recovered from the Krishna–Godavari Basin, offshore India. Mar. Pet. Geol. 2018. [Google Scholar] [CrossRef]
- Freij-Ayoub, R.; Tan, C.; Clennell, B.; Tohidi, B.; Yang, J. A wellbore stability model for hydrate bearing sediments. J. Pet. Sci. Eng. 2007, 57, 209–220. [Google Scholar] [CrossRef]
- Paull, C.K.; Ussler, W.; Dallimore, S.R.; Blasco, S.M.; Lorenson, T.D.; Melling, H.; Medioli, B.E.; Nixon, F.M.; McLaughlin, F.A. Origin of pingo-like features on the Beaufort Sea shelf and their possible relationship to decomposing methane gas hydrates. Geophys. Res. Lett. 2007, 34, L01603. [Google Scholar] [CrossRef]
- Pecher, I.; Henrys, S.; Ellis, S.; Chiswell, S.M.; Kukowski, N. Erosion of the seafloor at the top of the gas hydrate stability zone on the Hikurangi Margin, New Zealand. Geophys. Res. Lett. 2005, 32, L24603. [Google Scholar] [CrossRef]
- Schoderbek, D.; Farrell, H.; Hester, K.; Howard, J.; Raterman, K.; Silpngarmlert, S.; Martin, K.; Smith, B.; Klein, P. ConocoPhillips Gas Hydrate Production Test Final Technical Report, in United States Department of Energy; ConocoPhillips Company: Houston, TX, USA, 2013; p. 204. [Google Scholar]
- Booth, J.S.; Winters, W.J.; Dillon, W.P. Circumstantial evidence of gas hydrate and slope failure associations on the United States Atlantic continental margin. Ann. N. Y. Acad. Sci 1994, 715, 487–489. [Google Scholar] [CrossRef]
- Boswell, R.; Collett, T.S.; Myshakin, E.; Ajayi, T.; Seol, Y.; States, U. The Increasingly Complex Challenge of Gas Hydrate Reservoir Simulation. In Proceedings of the 9th International Conference on Gas Hydrates (IGCH9), Denver, CO, USA, 25–30 June 2017. [Google Scholar]
- Kimoto, S.; Oka, F.; Fushita, T. A chemo-thermo-mechanically coupled analysis of ground deformation induced by gas hydrate dissociation. Int. J. Mech. Sci. 2010, 52, 365–376. [Google Scholar] [CrossRef]
- Rutqvist, J. Status of the THOUGH-FLAC simulator and recent applications related to coupled fluid flow and crustal deformations. Comput. Geosci. 2011, 37, 739–750. [Google Scholar] [CrossRef]
- Kim, J.; Moridis, G.; Yang, D.; Rutqvist, J. Numerical studies on two way coupled fluid flow and geomechanics in hydrate deposits. SPE J. 2012, 17, 485–501. [Google Scholar] [CrossRef]
- Klar, A.; Uchida, S.; Soga, K.; Yamamoto, K. Explicitly coupled thermal flow mechanical formulation for gas hydrate sediments. SPE J. 2013, 18, 196–206. [Google Scholar] [CrossRef]
- Gupta, S.; Wohlmuth, B.; Helmig, R. Multi-rate time stepping schemes for hydro-geomechanical model for subsurface methane hydrate reservoirs. Adv. Water Resour. 2016, 91, 78–87. [Google Scholar] [CrossRef]
- Sun, X.; Luo, H.; Soga, K. A coupled thermal–hydraulic–mechanical–chemical (THMC) model for methane hydrate bearing sediments using COMSOL Multiphysics. J. Zhejiang Univ.-SCIENCE A 2018, 19, 600–623. [Google Scholar] [CrossRef]
- Sánchez, M.; Santamarina, C.; Teymouri, M.; Gai, X. Coupled numerical modeling of gas hydrate bearing sediments: From laboratory to field-scale analyses. J. Geophys. Res. Solid Earth 2018, 123, 10326–10348. [Google Scholar] [CrossRef]
- Olivella, S.; Gens, A.; Carrera, J.; Alonso, E.E. Numerical formulation for a simulator (CODE-BRIGHT) for the coupled analysis of saline media. Eng. Comput. 1996, 13, 87–112. [Google Scholar] [CrossRef]
- Alonso, E.; Pinyol, N.M. Numerical analysis of rapid drawdown: Applications in real cases. Water Sci. Eng. 2016, 9, 175–182. [Google Scholar] [CrossRef]
- Gens, A.; Sánchez, M.; Guimaräes, L.; Alonso, E.; Lloret, A.; Olivella, S.; Villar, M.V.; Huertas, F. A full scale in situ heating test for high level nuclear waste disposal: Observations, analysis and interpretation. Géotechnique 2009, 59, 377–399. [Google Scholar] [CrossRef]
- Vilarrasa, V.; Carrera, J.; Bolster, D.; Dentz, M. Semi analytical solution for CO2 plume shape and pressure evolution during CO2 injection in deep saline formations. Transp. Porous Media 2013, 97, 43–65. [Google Scholar] [CrossRef]
- De La Fuente, M.; Vaunat, J.; Marín-Moreno, H. A densification mechanism to model the mechanical effect of methane hydrates in sandy sediments. Numer. Anal. Methods Geomech. 2019. under review. [Google Scholar]
- Peng, D.Y.; Robinson, D.B. A new two-constant equation of state. Ind. Eng. Chem. Fundam. 1976, 15, 59–64. [Google Scholar] [CrossRef]
- Tishchenko, P.; Hensen, C.; Wallmann, K.; Wong, C.S. Calculation of the stability and solubility of methane hydrate in seawater. Chem. Geol. 2005, 219, 37–52. [Google Scholar] [CrossRef]
- Wilder, J.; Moridis, G.; Wilson, S.; Kurihara, M.; White, M.; Masuda, Y.; Anderson, B.J.; Collett, T.S.; Hunter, R.B.; Narita, H.; et al. An international effort to compare gas hydrate reservoir simulators. In Proceedings of the 6th International Conference on Gas Hydrates (ICGH), Vancouver, BC, Canada, 6–10 July 2008. [Google Scholar]
- Gupta, S.; Helmig, R.; Wohlmuth, B. Non-isothermal, multi-phase, multi-component flows through deformable methane hydrate reservoirs. Comput. Geosci. 2015, 19, 1063–1088. [Google Scholar] [CrossRef]
- Van Genuchten, M.T.T. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils. Soil Sci. Soc. Am. J. 1980, 44, 892–898. [Google Scholar] [CrossRef]
- Biot, M.A.; Willis, D.G. The Elastic Coefficients of the Theory of Consolidation. J. Appl. Mech. 1957, 24, 594–601. [Google Scholar]
- Waite, W.F. Thermal Properties of Methane Gas Hydrates. U.S. Geol. Surv. Fact Sheet 2007, 3041, 2. [Google Scholar]
- Gamwo, I.K.; Liu, Y. Mathematical modeling and numerical simulation of methane production in a hydrate reservoir. Ind. Eng. Chem. Res. 2010, 49, 5231–5245. [Google Scholar] [CrossRef]
- Mahabadi, N.; Zheng, X.; Jang, J. The effect of hydrate saturation on water retention curves in hydrate-bearing sediments. Geophys. Res. Lett. 2016, 43, 4279–4287. [Google Scholar] [CrossRef]
- IUPAC. Solubility Data Series; Methane, 27/28; Clever, H.L., Young, C.L., Eds.; Pergamon Press: Oxford, UK, 1987; pp. 50–55. [Google Scholar]
- Englezos, P.; Kalogerakis, N.; Dholabhai, P.D.; Bishnoi, P.R. Kinetics of Formation of Methane and Ethane Gas Hydrates. Chem. Eng. Sci. 1987, 42, 2647–2658. [Google Scholar] [CrossRef]
- Kim, H.C.; Bishnoi, P.R.; Heidemann, R.A.; Rizvi, S.S.H. Kinetics of methane hydrate decomposition. Chem. Eng. Sci. 1987, 42, 1645–1653. [Google Scholar] [CrossRef]
- Nishimura, S.; Gens, A.; Jardine, R.J.; Olivella, S. THM-coupled finite element analysis of frozen soil: Formulation and application. Géotechnique 2009, 59, 159–171. [Google Scholar] [CrossRef]
- Dai, S.; Lee, C.; Santamarina, J.C. Formation history and physical properties of sediments from the Mount Elbert gas hydrate stratigraphic test well, Alaska North Slope. Mar. Petroleum Geol. 2011, 28, 427–438. [Google Scholar] [CrossRef]
- Ghiassian, H.; Grozic, J.L.H. Strength behavior of methane hydrate bearing sand in undrained triaxial testing. Mar. Pet. Geol. 2013, 43, 310–319. [Google Scholar] [CrossRef]
- Hyodo, M.; Kajiyama, S.; Yoshimoto, N.; Nakata, Y. Triaxial behaviour of methane hydrate bearing sand. In Proceedings of the 10th International ISOPE Ocean Mining & Gas Hydrate Symposium OMS, Szczecin, Poland, 22–26 September 2013; pp. 126–134. [Google Scholar]
- Masui, A.; Haneda, H.; Ogata, Y.; Aoki, K. The effect of saturation degree of methane hydrate on the shear strength of synthetic methane hydrate sediments. In Proceedings of the 5th International Conference on Gas Hydrates, Trondheim, Norway, 12–16 June 2005; pp. 657–663. [Google Scholar]
- Miyazaki, K.; Masui, A.; Sakamoto, Y.; Aoki, K.; Tenma, N.; Yamaguchi, T. Triaxial compressive properties of artificial methane-hydrate-bearing sediment. J. Geophys. Res. Solid Earth 2011, 116, 1–11. [Google Scholar] [CrossRef]
- Soga, K.; Lee, L.S.; Ng, A.Y.M.; Klar, A. Characterisation and engineering properties of methane hydrate soils. Charact. Eng. Prop. Nat. Soils 2006, 4, 2591-1642. [Google Scholar]
- Waite, W.F.; Santamarina, J.C.; Cortes, D.D.; Dugan, B.; Espinoza, D.N.; Germaine, J.; Jang, J.; Jung, J.W.; Kneafsey, T.J.; Shin, H.; et al. Physical properties of hydrate-bearing sediments. Rev. Geophys. 2009, 47, 1–38. [Google Scholar] [CrossRef]
- Jung, J.W.; Santamarina, J.C.; Soga, K. Stress-strain response of hydrate-bearing sands: Numerical study using discrete element method simulations. J. Geophys. Res. Solid Earth 2012, 117, 1–12. [Google Scholar] [CrossRef]
- Pinkert, S.; Grozic, J.L.H.; Priest, J.A. Strain-Softening Model for Hydrate-Bearing Sands. Int. J. Geomech. 2015, 15, 04015007. [Google Scholar] [CrossRef]
- Pinkert, S.; Grozic, J.L.H. Prediction of the mechanical response of hydrate-bearing sands. J. Geophys. Res. Solid Earth 2014, 119, 4695–4707. [Google Scholar] [CrossRef]
- Sánchez, M.; Gai, X.; Santamarina, J.C. A constitutive mechanical model for gas hydrate bearing sediments incorporating inelastic mechanisms. Comput. Geotech. 2017, 84, 28–46. [Google Scholar] [CrossRef]
- Uchida, S. Numerical Investigation of Geomechanical Behaviour of Hydrate-Bearing Sediments. Ph.D. Thesis, University of Cambridge, Cambridge, UK, 2012. [Google Scholar]
- De La Fuente, M.; Vaunat, J.; Marín-Moreno, H. Composite model to reproduce the mechanical behaviour of Methane Hydrate Bearing Sediments. In Energy Geotechnics: Proceedings of the 1st International Conference on Energy Geotechnics, ICEGT; Wuttke, F., Bauer, S., Sanchez, M., Eds.; CRC Press: Boca Raton, FL, USA; Kiel, Germany, 2016; pp. 483–489. [Google Scholar]
- Jiang, M.; Zhu, F.; Liu, F.; Utili, S. A bond contact model for methane hydrate-bearing sediments with interparticle cementation. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1823–1854. [Google Scholar] [CrossRef]
- Lin, J.S.; Seol, Y.; Choi, J.H. An SMP critical state model for methane hydrate-bearing sands. Int. J. Numer. Anal. Methods Geomech. 2015, 32, 969–987. [Google Scholar] [CrossRef]
- Pinkert, S. Rowe’s stress-Dilatancy Theory for Hydrate-Bearing Sand. Int. J. Geomech. 2016, 17, 1–5. [Google Scholar] [CrossRef]
- Pinkert, S.; Grozic, J.L.H. Experimental verification of a prediction model for hydrate bearing sand. J. Geophys. Res. Solid Earth 2016, 121, 4147–4155. [Google Scholar] [CrossRef]
- Yu, H.S. CASM: A unified state parameter model for clay and sand. Int. J. Numer. Anal. Methods Geomech. 1998, 22, 621–653. [Google Scholar] [CrossRef]
- Hashiguchi, K. Subloading surface model in unconventional plasticity. Int. J. Solids Struct. 1989, 25, 917–945. [Google Scholar] [CrossRef]
- Yan, R.; Wei, C. Constitutive Model for Gas Hydrate-Bearing Soils Considering Hydrate Occurrence Habits. Int. J. Geomech. 2017, 17, 209–220. [Google Scholar] [CrossRef]
- Sloan, E.D.; Koh, C.A. Clathrate hydrates of natural gases. In Chemical Industries Series, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2007. [Google Scholar]
- Egeberg, P.K.; Dickens, G. Thermodynamic and pore water halogen constraints on gas hydrate distribution at ODP site 997 (Blake Ridge). Chem. Geol. 1999, 153, 53–79. [Google Scholar] [CrossRef]
- Hensen, C.; Zabel, M.; Pfeifer, K.; Schwenk, T.; Kasten, S.; Riedinger, N.; Schulz, H.D.; Boetius, A. Control of sulfate pore water profiles by sedimentary events and the significance of anaerobic oxidation of methane for the burial of sulfur in marine sediments. Geochim. Cosmochim. Acta 2003, 67, 2631–2647. [Google Scholar] [CrossRef]
- Davie, M.; Buffett, B. Sources of methane for marine gas hydrate: Inferences from a comparison of observations and numerical models. Earth Planet. Sci. Lett. 2003, 206, 51–63. [Google Scholar] [CrossRef]
- Sloan, S.W.; Abbo, A.J.; Sheng, D. Refined explicit integration of elasto-plastic models with automatic error control. Int. J. Num. Methods. Engrg. 2001, 18, 121–154. [Google Scholar]
- Allen, M.B.; Murphy, C.L. A Finite-Element Collocation Method for Variably Saturated Flow in Two Space Dimensions. Water Resour. Res. 1986, 22, 1537–1542. [Google Scholar] [CrossRef]
- Celia, M.A.; Boulotas, E.T.; Zarba, R. A General Mass Conservative Numerical Solution for the Unsaturated Flow Equation. Water Resour. Res. 1990, 26, 1483–1496. [Google Scholar] [CrossRef]
- Simo, J.; Taylor, R. Consistent tangent operators for rate-independent elastoplasticity. Comput. Methods Appl. Mech. Eng. 1985, 48, 101–118. [Google Scholar] [CrossRef]
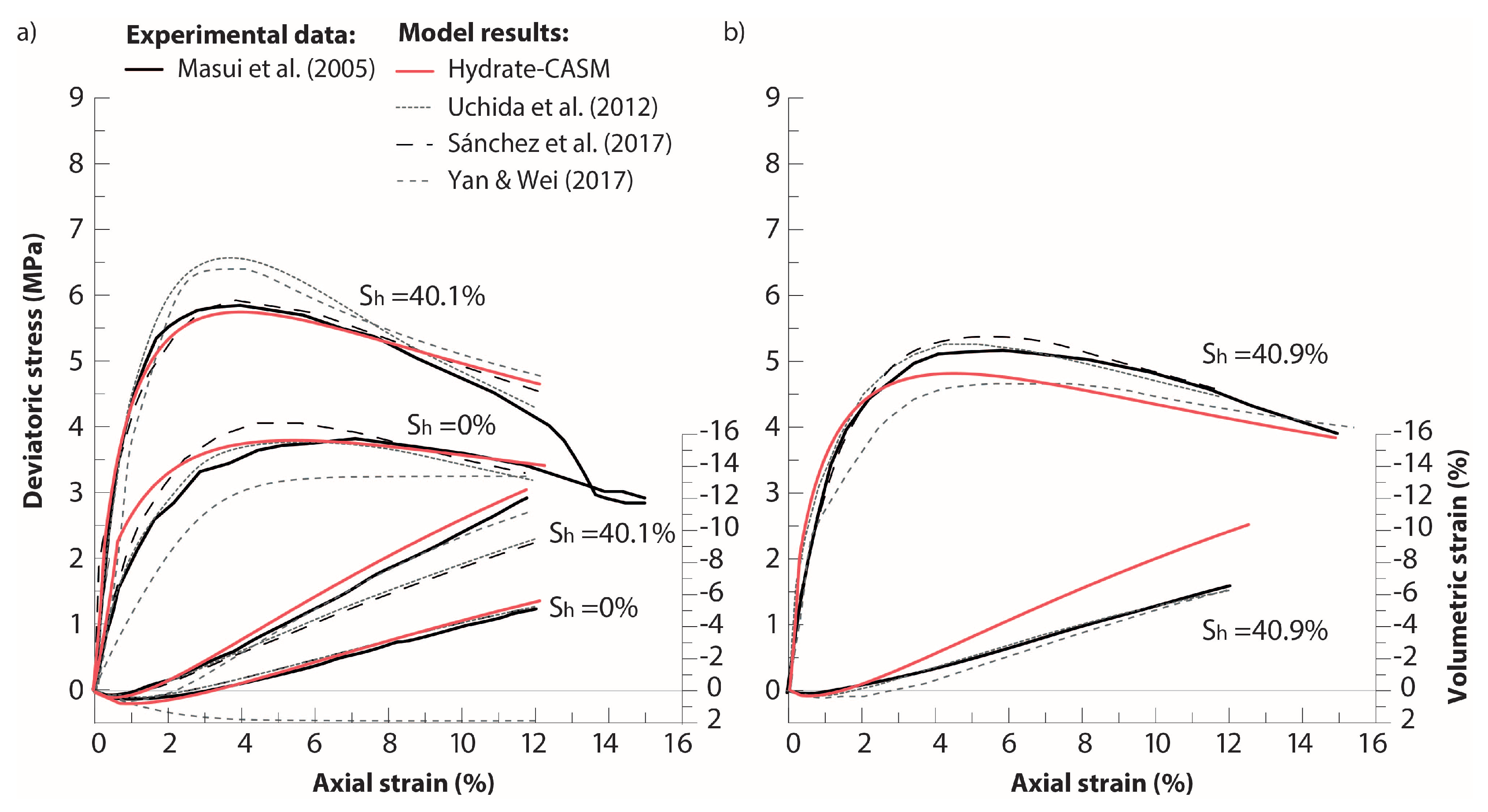
| Model Reference | Mechanical Approach |
|---|---|
| Kimoto et al. (2010) [30] | Viscoplasticity with dependency |
| Rutqvist (2011) [31] | Mohr-Coloumb elastoplasticity with dependency |
| Kim et al. (2012) [32] | Mohr-Coloumb elastoplasticity with dependency |
| Klar et al. (2013) [33] | Mohr-Coloumb elastoplasticity with dependency |
| Gupta et al. (2016) [34] | Poroelasticity with dependency |
| Sun et al. (2018) [35] | Thermodynamics-based elastoplastic model with dependency |
| Sánchez et al. (2018) [36] | Elastoplasticty with dependency + Damage model |
| Bulk volume | |
| Potential void space | |
| Potential porosity | |
| Available void space | |
| Available porosity | |
| Hydrate saturation | |
| Ice saturation | ) |
| Gas saturation | |
| Liquid saturation |
| Roman Symbols | |||
| Peng-Robinson EoS parameter | M | Slope of critical state line in p’-q space | |
| Viscosity parameter | Molecular mass of phase | ||
| Viscosity thermal function | n | Stress-state coefficient: yield surface shape parameter | |
| Hydrate surface area | Hydration number | ||
| Body forces | Mean effective stress | ||
| b | Peng-Robinson EoS constant | Van Genuchten parameter | |
| Viscosity parameter of phase | Isotropic yield stress of hydrate-free sediment | ||
| Specific heat of component in phase | Isotropic yield stress of MHBS | ||
| Mass change of phase | Hydrate phase equilibrium pressure | ||
| Diffusion coefficient of component in phase | Pressure of phase | ||
| e | Void ratio of hydrate-free sediment | Reference pressure for phase | |
| Available void ratio of the MHBS | Critical pressure | ||
| Hydrate void ratio | Pore pressure | ||
| Energy of phase | q | Deviatoric stress | |
| Energy of component in phase | Advective fuid flow | ||
| f | Hydrate-CASM yield function | r | Yield surface spacing ratio |
| External mass supply of component | R | Subloading ratio | |
| Internal/external energy supply | Regnault constant | ||
| Peng-Robinson EoS function | Rate of hydrate mass change | ||
| g | Gravity forces | S | Salinity |
| Diffusive flux of component in phase | Saturation of phase | ||
| Conductive heat flow | Effective liquid saturation | ||
| Energy dispersivity in phase | Maximum liquid saturation | ||
| Identity matrix | Residual liquid saturation | ||
| Mass flux of component in phase | t | Time | |
| Advective flux of energy of phase | Reference temperature | ||
| Intrinsic permeability of hydrate-free sediment | T | Temperature | |
| Intrinsic permeability of MHBS | Critical temperature | ||
| Relative permeability of phase | Hydrate phase equilibrium temperature | ||
| Solubility of methane in water | Reduced temperature | ||
| Hydrate dissociation constant | Displacement | ||
| Hydrate formation constant | u | Subloading parameter controlling the | |
| Latent heat of hydrate dissociation | plastic deformations before yielding | ||
| Latent heat of ice melting | v | Molar volume | |
| m | Van Genuchten parameter | V | Unitary volume |
| Greek Symbols | |||
| Biot’s coefficient | ∇ | Differential operator = () | |
| Thermal expansion coefficient of the liquid phase | Poisson’s ratio | ||
| ∂ | Partial derivative | Mass fraction of component in phase | |
| Norm of the incremental plastic strain | Viscosity of phase | ||
| Volumetric strain | Potential porosity | ||
| Cartesian strains | Available porosity | ||
| Solute variation | Density of phase | ||
| Slope of swelling line of hydrate-free sediment | Reference density of phase | ||
| Slope of swelling line of MHBS | Cauchy total stress (compression positive) | ||
| Swelling line slope reduction factor | Effective stress (compression positive) | ||
| Slope of normal compression line | Confining stress (compression positive) | ||
| Composite thermal conductivity | Volumetric mass of component in phase | ||
| Dry thermal conductivity | Tortuosity coefficient | ||
| Liquid saturated thermal conductivity | Peng-Robinson acentric factor | ||
| Phase | Specific Energy | Specific and Latent Heat |
|---|---|---|
| Gas (g) | = 2500 J (Kg K)−1 | |
| Hydrate (h) | = 2108 J (Kg K)−1; † = 3.39 e5 J Kg−1 | |
| Ice (i) | = 3144 J (Kg K)−1; † = 3.34 e5 J Kg−1 | |
| Liquid (l) | = 4184 J (Kg K)−1 | |
| + | = 2200 J (Kg K)−1 | |
| Solid (s) | = 874 J (Kg K)−1 |
| Constitutive Law | Equation | Dependent Variable |
|---|---|---|
| Advective fluid flow | ||
| Darcy’s law | Advective fluid flow, and | |
| Kozeny’s model | ||
| × m2 | ||
| exp | ||
| × MPa s; = 1808.5 K | ||
| × MPa s; = 119.4 K | ||
| Retention curve [46] | Saturation of mobile phases, and | |
| MPa | ||
| Liquid density [37] | Liquid density, | |
| = 1002.6 kg/m3 | ||
| MPa−1 | ||
| MPa | ||
| Gas density [42] | Gas density, | |
| J/mol K | ||
| MPa | ||
| K | ||
| Kg/mol | ||
| Non-advective fluid flow | ||
| Fick’s law | Diffusive flux, and | |
| exp | ||
| exp | ||
| Fourier’s law | Conductive heat flow, | |
| † | ||
| W/mK, W/mK | ||
| Stress-strain behavior | ||
| Effective stress [47] | Effective stress tensor, | |
| Hydrate-CASM [41] | Subloading yield function | Stress tensor, |
| Densification mechanism | ||
| = 0 if | ||
| if | ||
| Equilibrium Restriction | Equation | Dependent Variable |
|---|---|---|
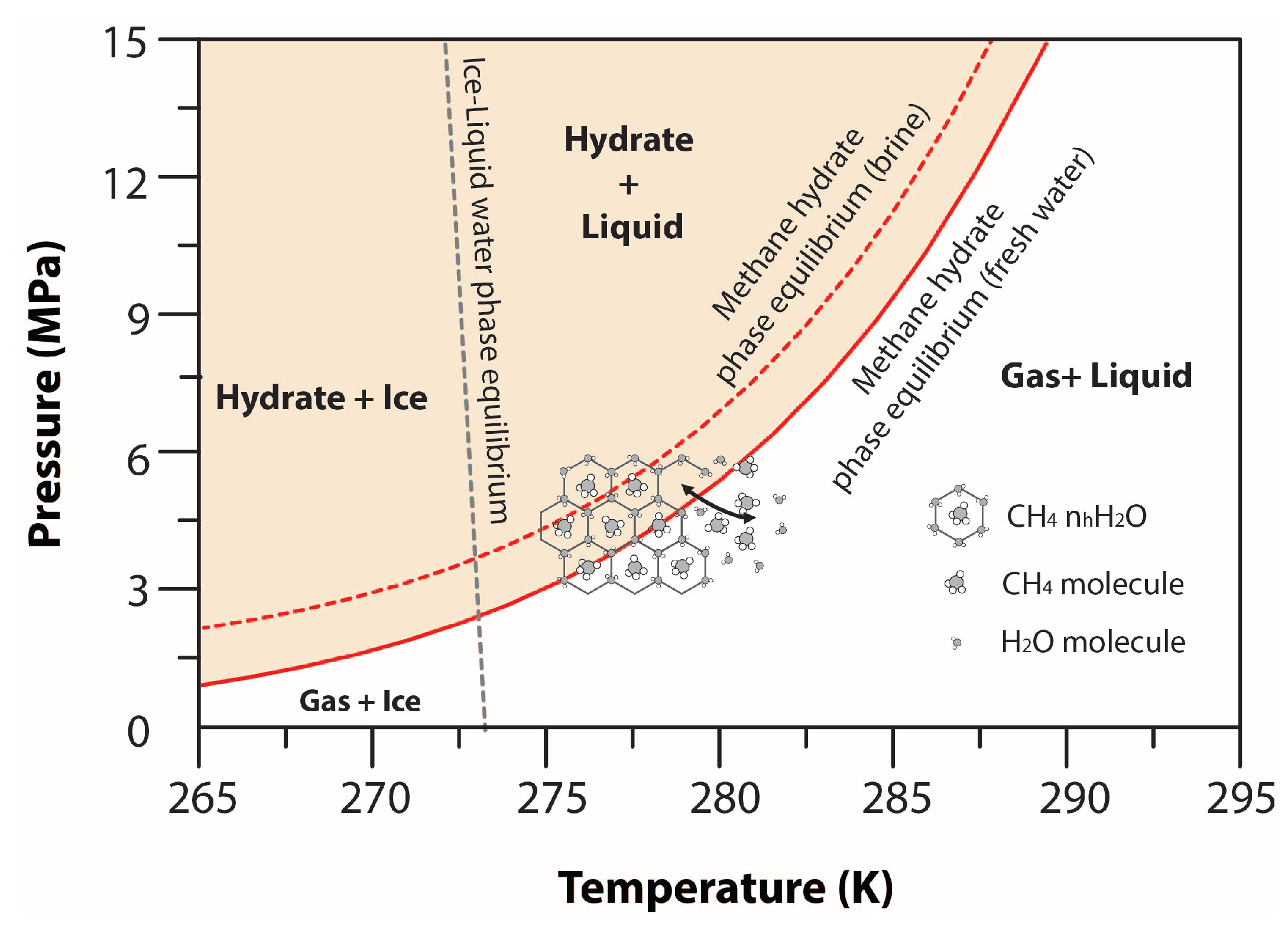
| Hydrate phase change | ||
| Hydrate phase boundary [43] | × × × × × × × × × × | Equilibrium pressure, |
| Methane solubility | Dissolved methane concentration, | |
| [43] | × × × × × × × × | |
| [51] | × | |
| × | ||
| × | ||
| Hydrate kinetic rate [52,53] | Hydrate mass change, | |
| exp | ||
| † | ||
| Ice phase change | ||
| Freezing characteristic function [54] | Ice saturation, | |
| Test Conditions | |||||
|---|---|---|---|---|---|
| Test Name | Temperature (°C) | Confining Pressure (MPa) | Liquid Pressure (MPa) | Hydrate Saturation (%) | Remarks |
| Hs_Temp | 8 → 11.3 | 8 | 6 | 0 | Thermal stimulation at |
| Mhbs_Temp1 | 8 → 11.3 | 8 | 6 | 20 | Thermal stimulation at |
| Mhbs_Temp2 | 8 → 11.3 | 8 | 6 | 20 | Thermal stimulation at |
| Hs_Dep | 8 | 8 | 6 → 4.6 | 0 | Depressurization at |
| Mhbs_Dep | 8 | 8 | 6 → 4.6 | 20 | Depressurization at |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
De La Fuente, M.; Vaunat, J.; Marín-Moreno, H. Thermo-Hydro-Mechanical Coupled Modeling of Methane Hydrate-Bearing Sediments: Formulation and Application. Energies 2019, 12, 2178. https://doi.org/10.3390/en12112178
De La Fuente M, Vaunat J, Marín-Moreno H. Thermo-Hydro-Mechanical Coupled Modeling of Methane Hydrate-Bearing Sediments: Formulation and Application. Energies. 2019; 12(11):2178. https://doi.org/10.3390/en12112178
Chicago/Turabian StyleDe La Fuente, Maria, Jean Vaunat, and Héctor Marín-Moreno. 2019. "Thermo-Hydro-Mechanical Coupled Modeling of Methane Hydrate-Bearing Sediments: Formulation and Application" Energies 12, no. 11: 2178. https://doi.org/10.3390/en12112178
APA StyleDe La Fuente, M., Vaunat, J., & Marín-Moreno, H. (2019). Thermo-Hydro-Mechanical Coupled Modeling of Methane Hydrate-Bearing Sediments: Formulation and Application. Energies, 12(11), 2178. https://doi.org/10.3390/en12112178





