1. Introduction
Demand response (DR) refers to ways of altering the power consumption of buildings, settlements, or other facilities, within a specific time frame, for economic return [
1]. It implies regulatory, technological, and market changes affecting the way energy is transacted and exploited. Demand response is strongly interlinked with the smart grid technological paradigm. By definition, consumers are able to adjust their power purchasing patterns according to dynamic exchange of information, incentives, and disincentives [
2]. Demand response is linked to sustainable development goal (SDG) 7 for ensuring access to affordable, reliable, sustainable, and modern energy for all [
3]. DR is directly linked to targets for increasing the share of renewables and improving energy efficiency in smart grids. Wide implementation of DR is expected to be complementary to SDG 13 as part of the efforts to keep global warming to well below 2 °C above pre-industrial levels.
Distributed energy resources (DER) and demand response (DR) are gradually gaining ground in this context with respect to (a) the reduction of peak loads, (b) maintaining grid balance, and (c) dealing with the volatility of renewable energy sources (RES). Maintaining grid balance is a prerequisite for the provision of high-quality power utility services affecting everyday life, as well as social and economic progress.
According to Reference [
4], demand-side management (DSM) measures can be categorized based on the timing and the impact of the measure into energy efficiency, time of use, demand response, and spinning reserve. Demand response is further classified into (i) incentive-based, including direct load control, interruptible/curtailable rates, emergency DR, capacity market programs, and demand bidding programs, and (ii) time-based, such as time of use (ToU) rates, critical peak pricing (CPP), and real-time pricing (RTP). In RTP, end customers are forwarded wholesale market prices a day or an hour before energy delivery. The main challenge in RTP is associated with the requirement for robust and continuous real-time communication between the energy provider and customers [
5]. Prices in RTP fluctuate as a consequence of wholesale market price variation and design aspects. Several RTP structures were assessed by utilities [
5].
In this framework, the idea of an open and transparent smart grid accommodating participants on a fair and inclusive basis is tied with (a) the allocation of actual costs for the generation, transmission, and distribution to the various stakeholders, and (b) the transition to a very high share of clean energy resources in the electricity generation mix. Undoubtedly, the smart grid of the next decade needs to ensure very high penetration of RES, as well as gradual replacement of fossil fuels and other power sources associated with high environmental risks. Grid energy efficiency is currently related, among others, to requirements for significant levels of spinning reserves and low-efficiency generators compromising environmental sustainability. In DR, consumers are incentivized to control their consumption in time to follow high RES production, contribute to the decrease of demand peaks, and lead to an improved overall energy efficiency at grid level.
The potential benefits of DR for customers, system operation, market efficiency, and reliability of the power system were critically evaluated based on different innovative technologies, real case studies, and research projects [
2,
6,
7].
On the contrary, there are several factors slowing down the widespread implementation of DR as reported by various authors reflecting various human intrinsic, economic, social, technological, and regulatory aspects, as discussed in References [
8,
9,
10]. In terms of the infrastructure modernization necessary for DR to take place, smart meters and advanced metering infrastructure (AMI) have a fundamental role to play. Advanced metering infrastructure, such as smart meters, is an essential part of the smart grid for utilities to be able to monitor and control any point of energy consumption/production or distribution in the grid. AMI and smart meters are also essential for consumers to be able to monitor their consumption and react to information about prices or DR events in real time. Various forms of possible DR program types and interactions between stakeholders involved such as utilities, aggregators, and resources are defined in the Open ADR standard [
11].
Adding flexibility in power consumption provides a sound basis for improving the grid’s environmental performance. Reduction of peak loads at grid level could lead to a lower level of operation for generation plants of high running cost, low efficiency, and low environmental performance. DR potential in the United States (US) alone could lead to peak load reductions of 150 GW, an equivalent of approximately 2000 peaking plants [
12].
A thorough review of existing DR programs available to US commercial and residential customers by numerous independent system operators (ISOs) and regional transmission organizations (RTOs) was provided in Reference [
13]. Such programs include real-time demand, real-time price (RT-Price), day-ahead load response (DALRP), day-ahead demand response program (DADRP), and more. In RT-Price, consumers can choose to reduce their load in real time as a response to prices exceeding a certain value. A detailed classification and survey of DR programs in smart grids with respect to pricing and optimization algorithms is available in Reference [
14]. In day-ahead real-time pricing (DARTP) programs, the predicted next day’s real-time prices are announced to customers and used for billing their consumption. DARTP is reported as one of the solutions which was tested and found effective in achieving flatter demand, reduction of losses, shorter peak-to-peak distance, and a higher load factor.
In DR, the consumer becomes a prosumer with an important active role in the transaction of energy on a day-to-day basis. This calls for new tools and services to allow for interoperable bidirectional flow of dynamic information along with increased environmental and social awareness. Hence, DR is identified as an important field for technological and market innovations aligned with climate change mitigation policies and the transition to sustainable smart grids in the near future.
In this direction, a wide range of demand response techniques were applied and documented according to the type of the loads and the installed facility equipment [
15,
16]. Customers can change their electricity pattern and participate in DR by reducing their use of electricity, by shifting consumption to another time period, and by self-generating electricity [
17]. In this context, the adjustment of the heating, ventilation, and air conditioning (HVAC) temperature set points is reported as an effective way to exploit the thermal mass of the building to reduce peaks or shift loads. Changing thermostat settings or reducing the operational time of HVAC systems, and decreasing artificial lighting levels are some of the main load curtailment techniques [
15,
17].
HVAC is among the major energy loads of the building sector [
18]. The operation of the HVAC system is of great significance with respect to the energy efficiency of a building overall. It is linked to the technical attributes of the technology employed and to the way systems are controlled, i.e., settings and embedded intelligence, which in turn define the actual operational performance and indoor comfort conditions. Many researchers investigated the potential of applying advanced controls and optimization techniques to evaluate the potential for energy efficiency improvements with respect to the operation of HVAC systems [
19,
20,
21,
22,
23,
24,
25,
26].
A mixed-integer linear problem (MILP) for real-time cost optimization of building HVAC was proposed by Risbeck et al. [
27]. This study focuses on the optimization of equipment usage in HVAC commercial systems. In their study, building temperature dynamics were either considered linear and used to estimate cooling or heating loads, or assumed to be available as a forecast of hot and cold water demand. Pompeiro et al. applied dynamic programming and genetic algorithm (GA) optimization to maximize thermal comfort and minimize the HVAC cost with photovoltaic (PV) production and storage in an experimental facility [
28]. Their approach concentrated mainly on the exploitation of energy from the PV and storage. The operation of the HVAC was controlled based on indoor temperature measurements and restricted in low, medium, and high HVAC operating modes. A time of use pricing scheme of three tariffs was used in the optimization of a small experimental room. An experimental evaluation of an HVAC system under variable pricing was conducted in Reference [
29]. A linear model of temperature evolution was developed by correlating past values of temperature with HVAC modules turned on/off at any instance in time. The approach was validated in an experimental facility, demonstrating reduced cost with respect to a normal thermostat in two different ToU pricing schemes. In Reference [
30], a MIP configuration was proposed to optimize HVAC operation based on a comfort/cost trade-off. The approach determined when each one out of a set of many HVAC units was turned on and off based on common goals. Cost reductions of 4.73%, 4.5%, 11.2%, and 8.5% in two different scenarios were achieved. In Reference [
31], direct load control and set point regulation of aggregated HVAC systems for frequency regulation in smart grids were investigated. A simplified HVAC model was used to evaluate temperature evolution and power consumption. Results demonstrated acceptable variations of temperature and on/off operations associated with smaller tracking errors compared to direct load controls and sliding-mode control strategies. In Reference [
32], a model predictive control framework to determine optimal control profiles of HVAC systems in demand response was proposed. This approach used a non-linear autoregressive neural network configuration to model the thermal behavior of the building zone and to simulate HVAC control strategies as a response to a demand response signal. The optimal control problem was formed as a mixed-integer non-linear problem (MINLP), taking into account on-site energy storage and energy generation systems with night set-up, demand-limiting and pre-cooling HVAC control strategies. Results for a day in August indicated reliable prediction levels for zone temperature and power. Cost savings, in the case of a varying pricing signal, of 14.25% to 15.26% for demand-limiting and optimal control without energy generation and storage were achieved. In the case of optimal control combined with energy generation and storage, cost savings of 30.95% were obtained. Particle swarm optimization was used in Reference [
33] to optimize the operation of residential HVAC systems based on a multi-objective scheduling problem taking into account day-ahead (DA) electricity price, outdoor temperature forecast, and user preferences. A cooling scenario with DA pricing was demonstrated where a decrease of HVAC energy consumption of 6.54% and a reduction of 18.71% in electricity cost were achieved.
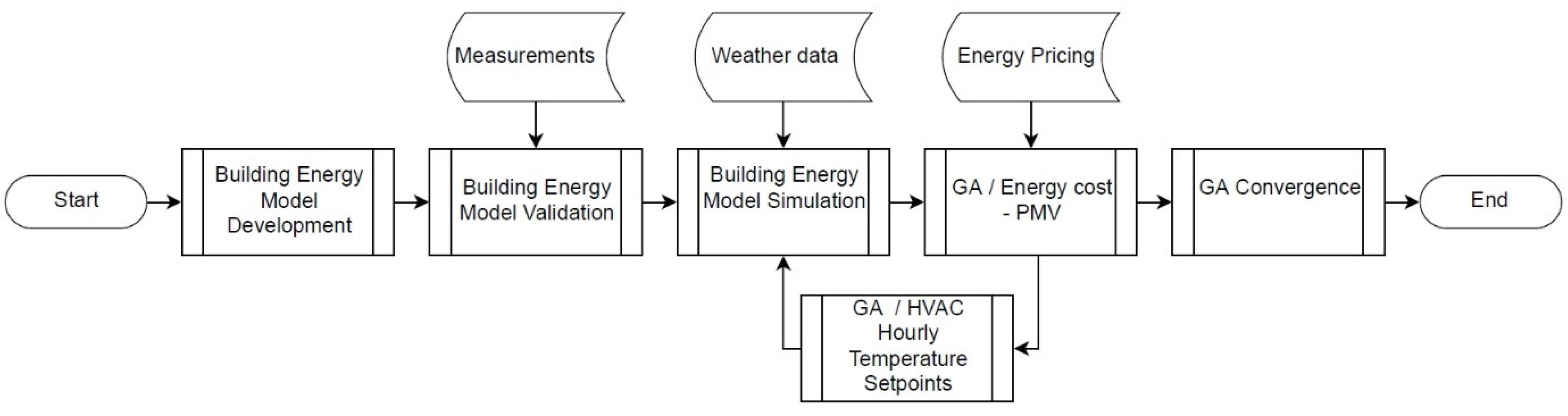
The purpose of this paper is to investigate GA optimisation in HVAC temperature set point control, based on day-ahead pricing information, for realizing profits as a reward for exploiting flexibility in consumption. Cost of energy is used as the first optimization criterion which encapsulates energy consumption. Using energy consumption as the optimization criterion instead would lead to suboptimum performance with respect to cost, which is the main incentive behind changes in power consumption. Most importantly, minimizing on-site energy consumption does not guarantee optimum environmental performance, since it does not take into account where, when, and how energy is generated. On the other hand, having cost of energy as one criterion in the objective function provides an indirect way to account for operational aspects of the power grid and induce change. Reduction of energy on-site consumption is, in any case, considered and evaluated, since it is a well-established measure of the energy efficiency of buildings.
The contribution of this work resides on the combination of the following aspects:
An original demand response optimization scheme is developed to include cost of energy and predicted mean vote (PMV) as the two criteria merged into one objective function. Along with HVAC hourly set points used as the variables of GA optimization, the developed approach constitutes a powerful assessment and decision tool which can be used to identify and ultimately apply dominant HVAC set point patterns based on actual weather conditions and preferences with regard to indoor conditions.
The optimization algorithm coupled with the validated dynamic thermal model of the building enables the assessment of energy cost, energy savings, and thermal comfort for a wide range of temperature set point patterns and RTP schemes.
The developed approach is designed to assess RTP schemes based on real DA market information to take advantage of price fluctuations which reflect current market operations in the optimization process.
In
Section 2, the methodology and infrastructure of the case study building are presented. Results obtained during the optimization process are analyzed in
Section 3. Finally,
Section 4 highlights the main conclusions and recommendations for future work.
3. Results and Discussion
The generic GA optimization scheme analyzed in the previous section was applied to include working hours (9:00 a.m. to 6:00 p.m.) plus two hours before (7:00–9:00 a.m.) and two hours after (6:00–8:00 p.m.). This was considered essential to study the effects of preheating or precooling of the building and maintaining internal conditions at sensible temperature values for some time after working hours to account for the fact that some people may still occupy the building. Optimization was conducted for the main industrial thermal zone of the building, which occupies a total area of 1327 m2 and a height of 8 m, surrounded by various other spaces including offices, meeting rooms, and other facilities on two floors. Following a number of trials, the population size of the GA was set to 50, the crossover fraction was set to 0.8, and the maximum number of iterations was set to 4,600 in order to examine a wide range of different solutions. Based on the set of the results, solutions were obtained to identify the set point patterns associated with optimum levels of energy and cost savings, as well as compliance with well-established standards of thermal comfort and temperature set point drift. The approach was designed to evaluate energy cost on a 24-h time frame. Representative results for four winter days, two days for autumn, one for summer, and one for spring are presented to account for different seasonal climatic conditions, heating and cooling modes, and DA pricing profiles.
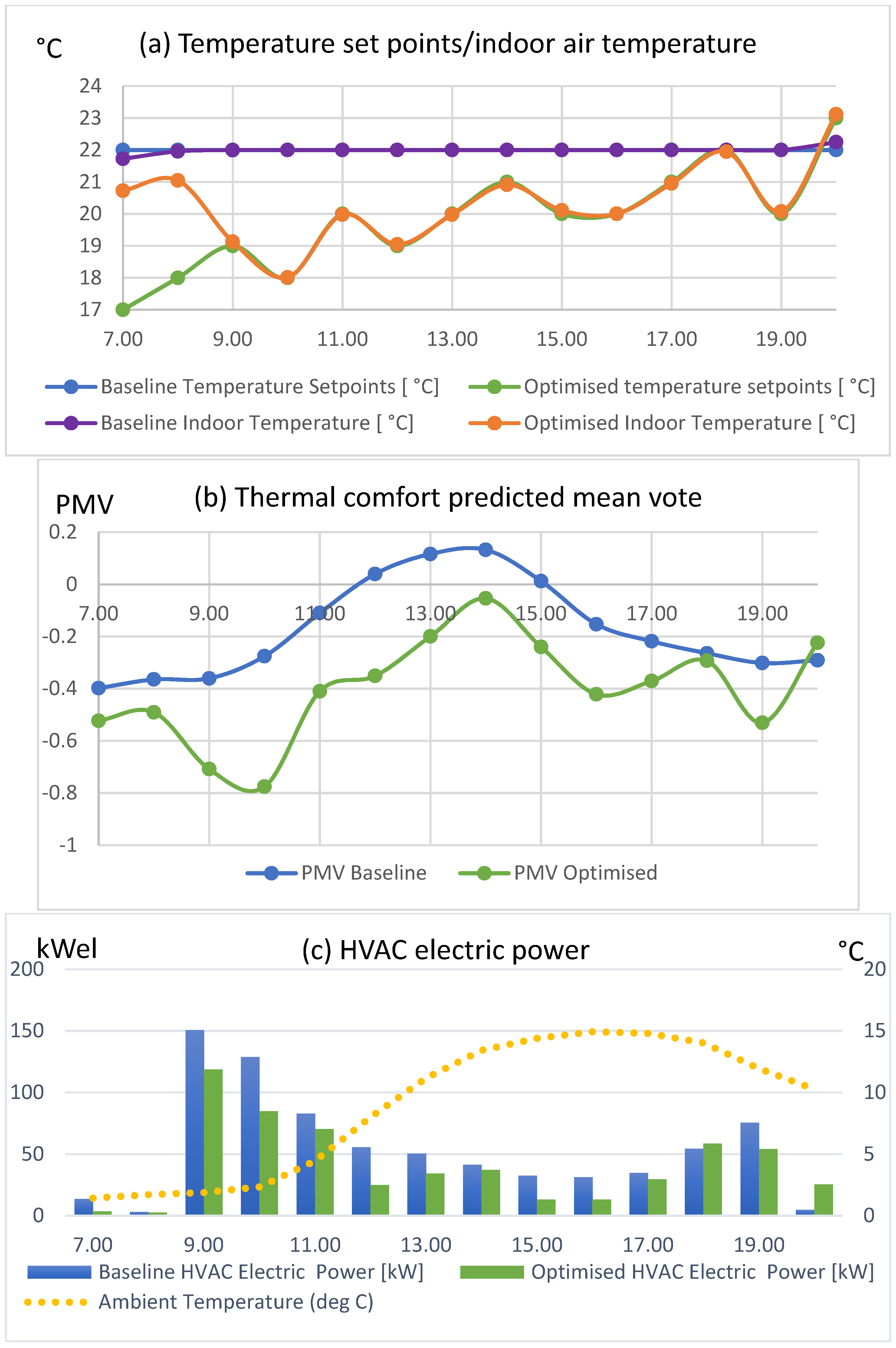
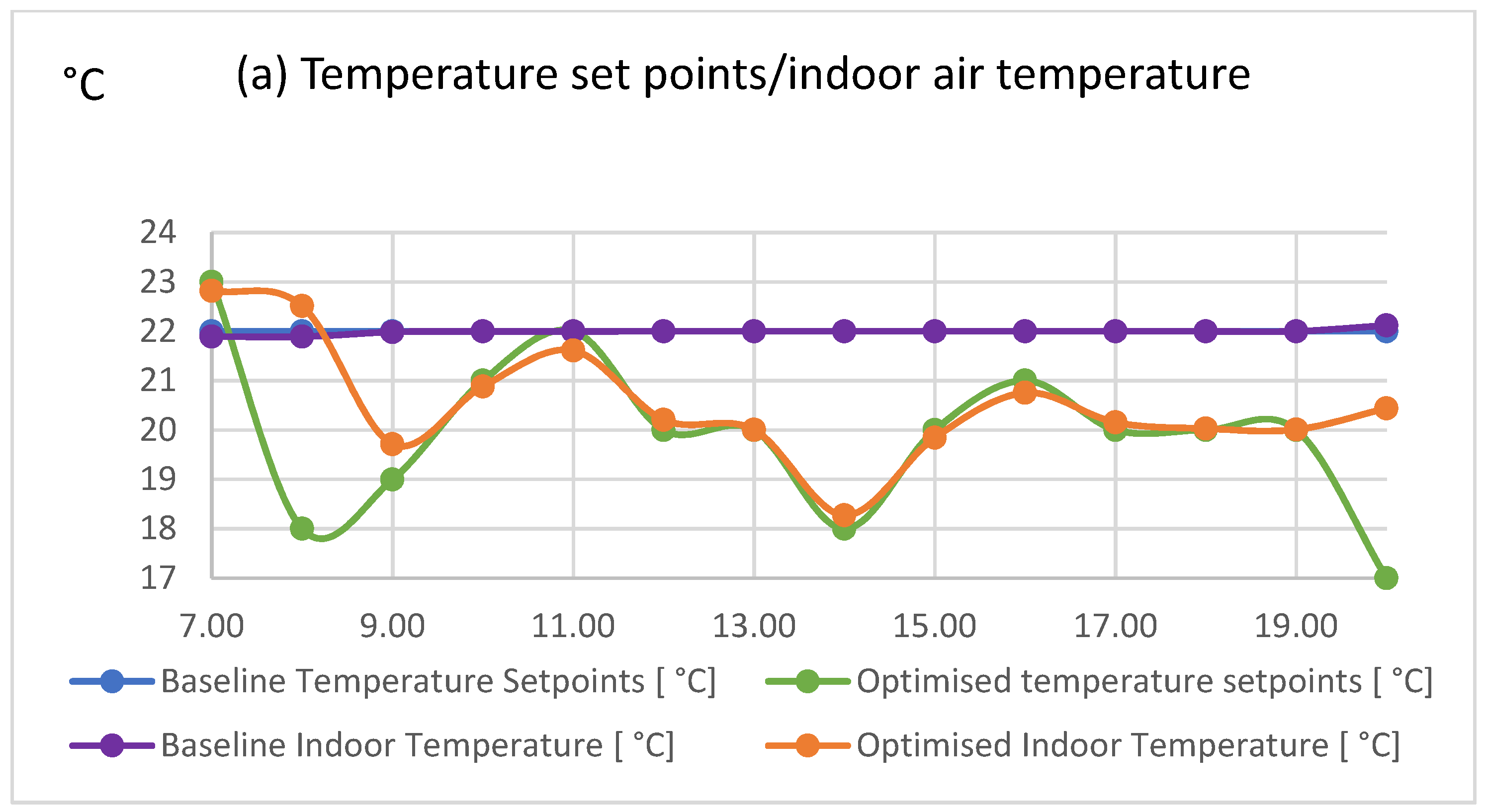
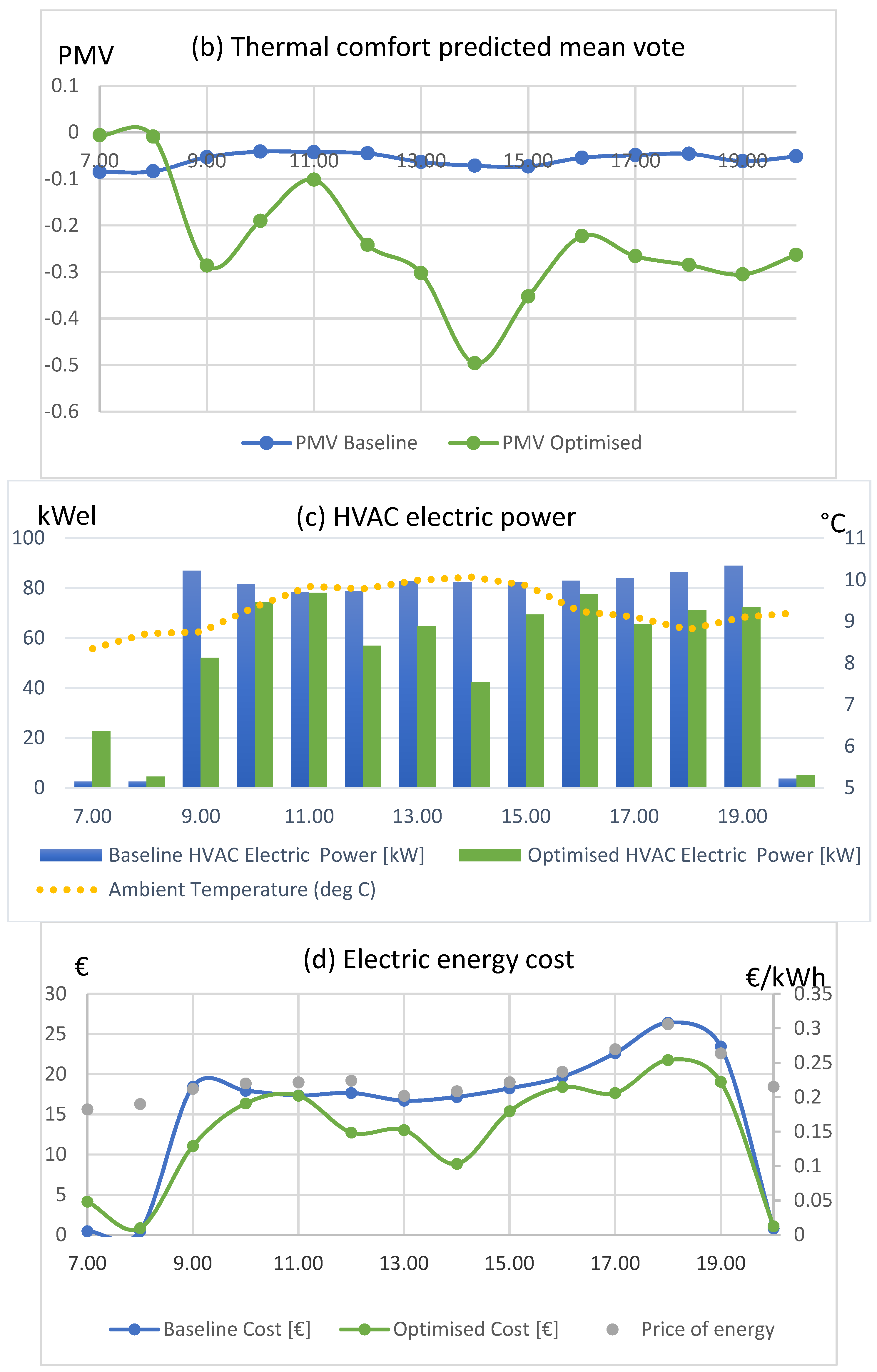
Scenario 1: 25 January 2018 (Winter)
Results from the GA HVAC optimization on 25 January 2018 are presented in
Figure 3 below. In the optimized scenario of this case, set points during working hours were selected, on an hourly basis, to be between 18 °C and 22 °C, as shown in
Figure 3a, and the energy of the HVAC was reduced from 759.88 kWh to 570.13 kWh, a reduction of 25% (
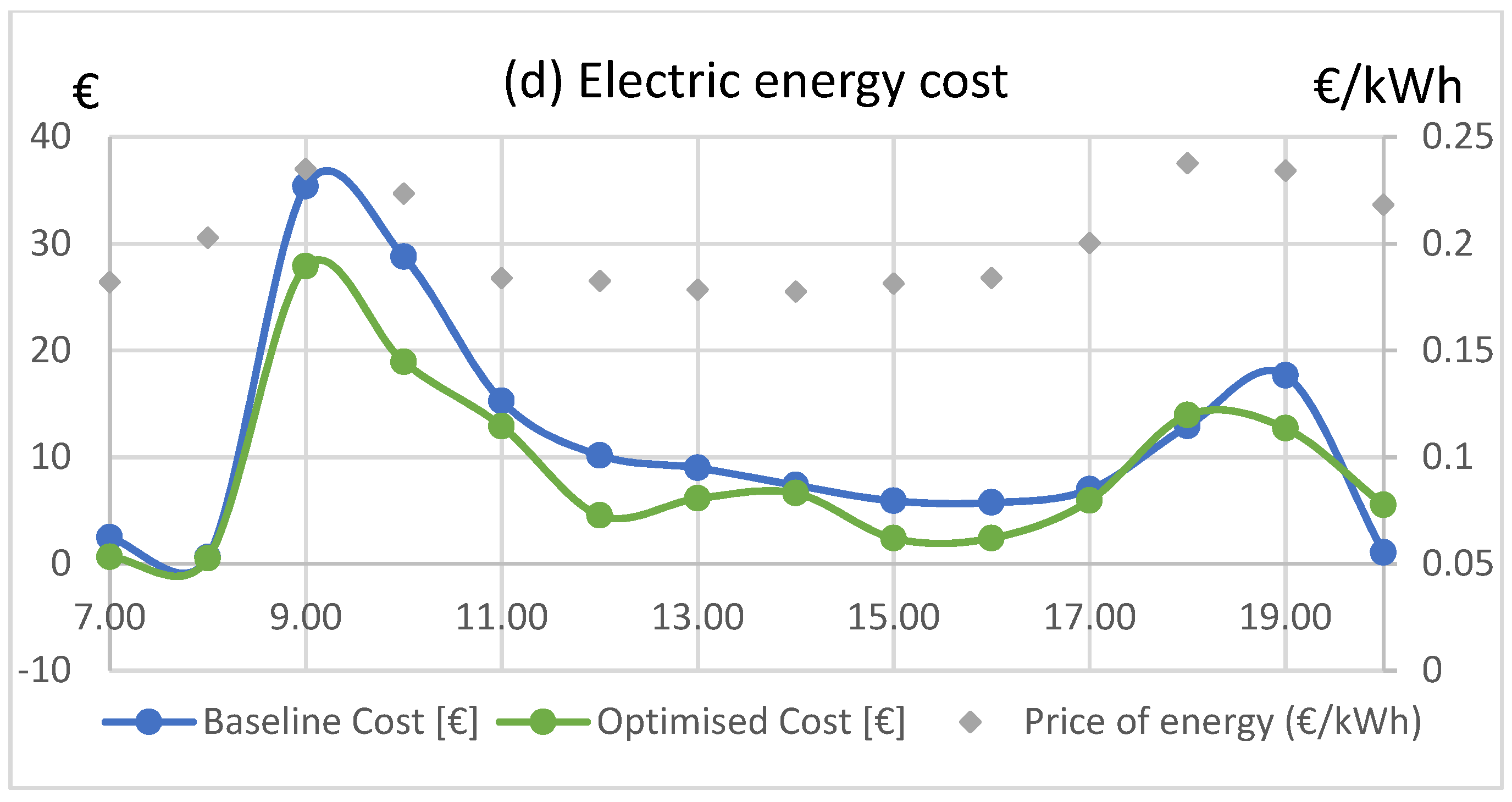
Figure 3c). Energy cost (
Figure 3d) was decreased from €159.3 to €121.03, which is equal to 25.0% savings. The HVAC power was kept lower in the optimized scenario, except during hours 6:00 and 8:00 p.m. At the baseline scenario, the PMV varied from −0.36 to 0.13, while, at the optimized scenario, from −0.78 to −0.05 (
Figure 3b). The average PMV varied from −0.14 to −0.38, which corresponds to a PPD increase from 6.28% to 9.13% between the baseline and optimized scenario. In this case, a trade-off between thermal comfort and energy consumption was found to be associated with significant cost savings at times of high pricing rates but also during low pricing zones.
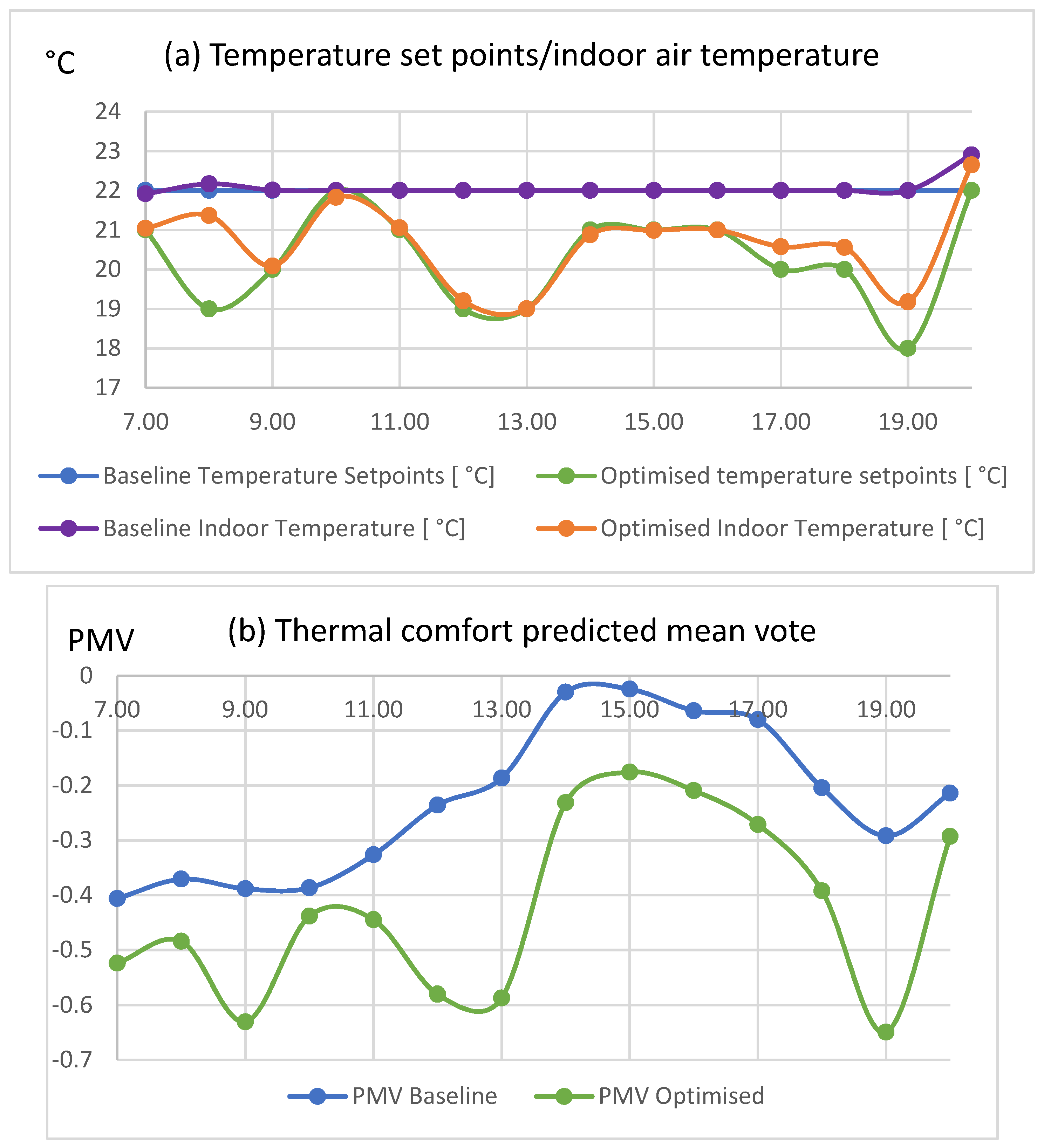
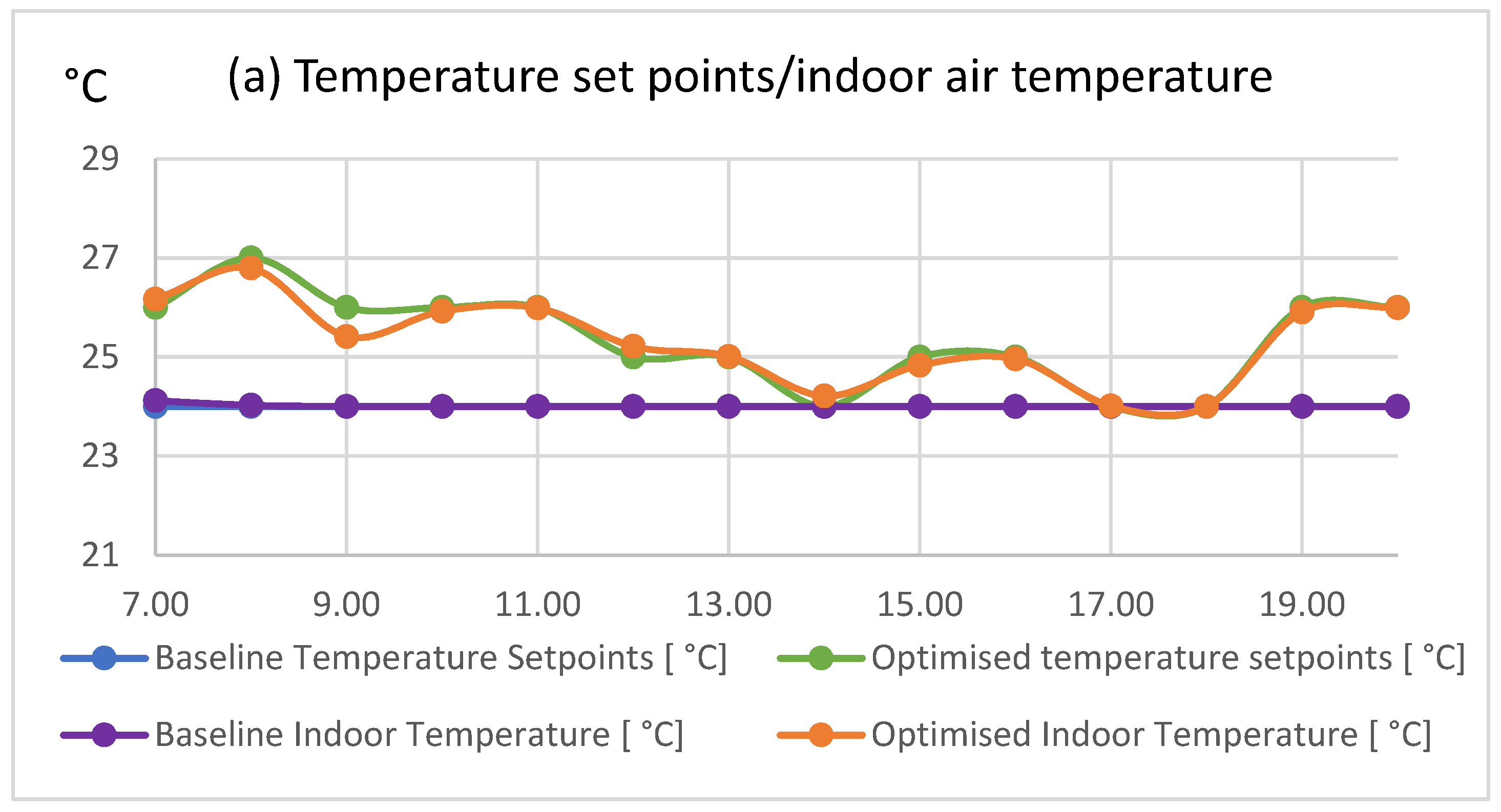
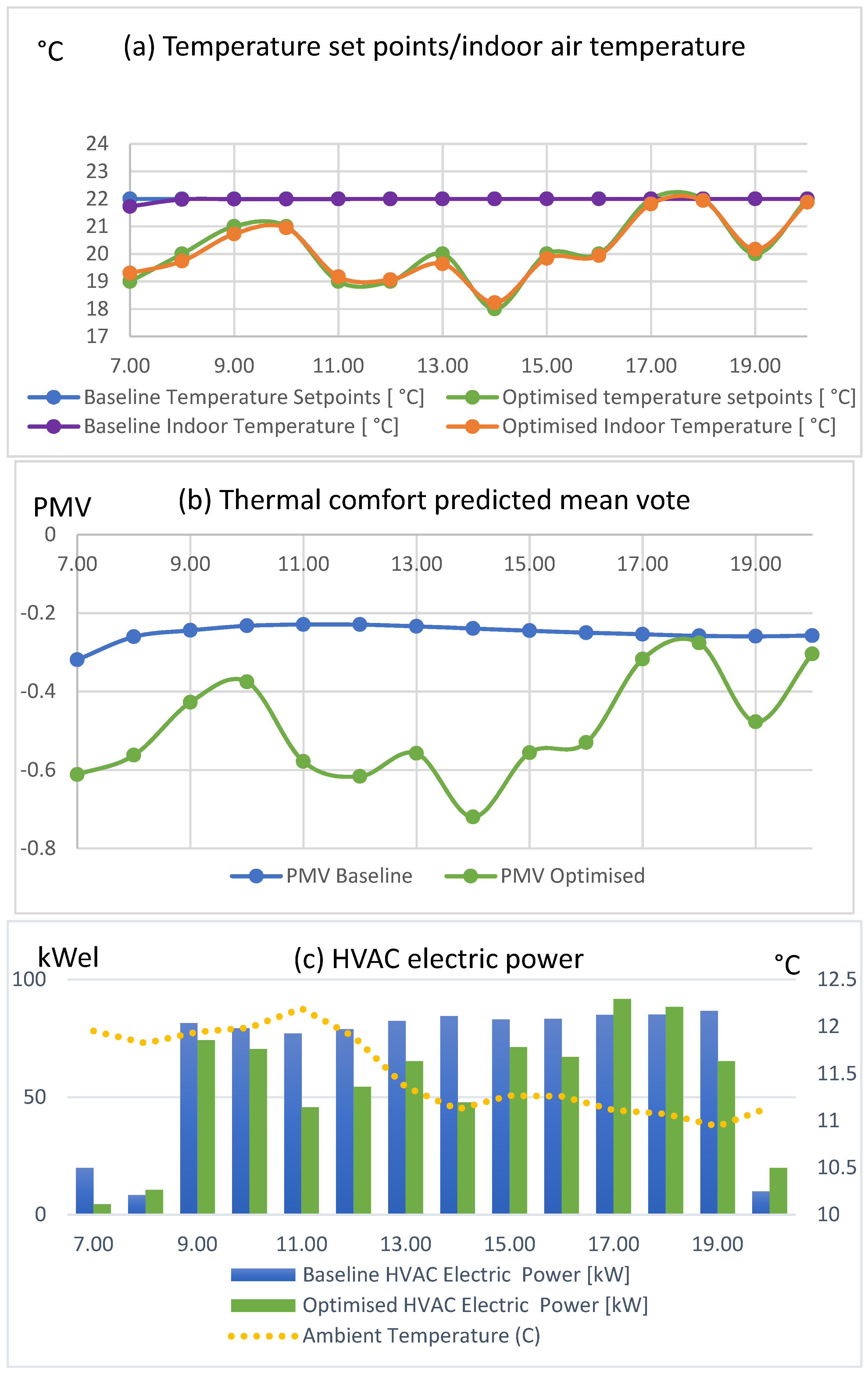
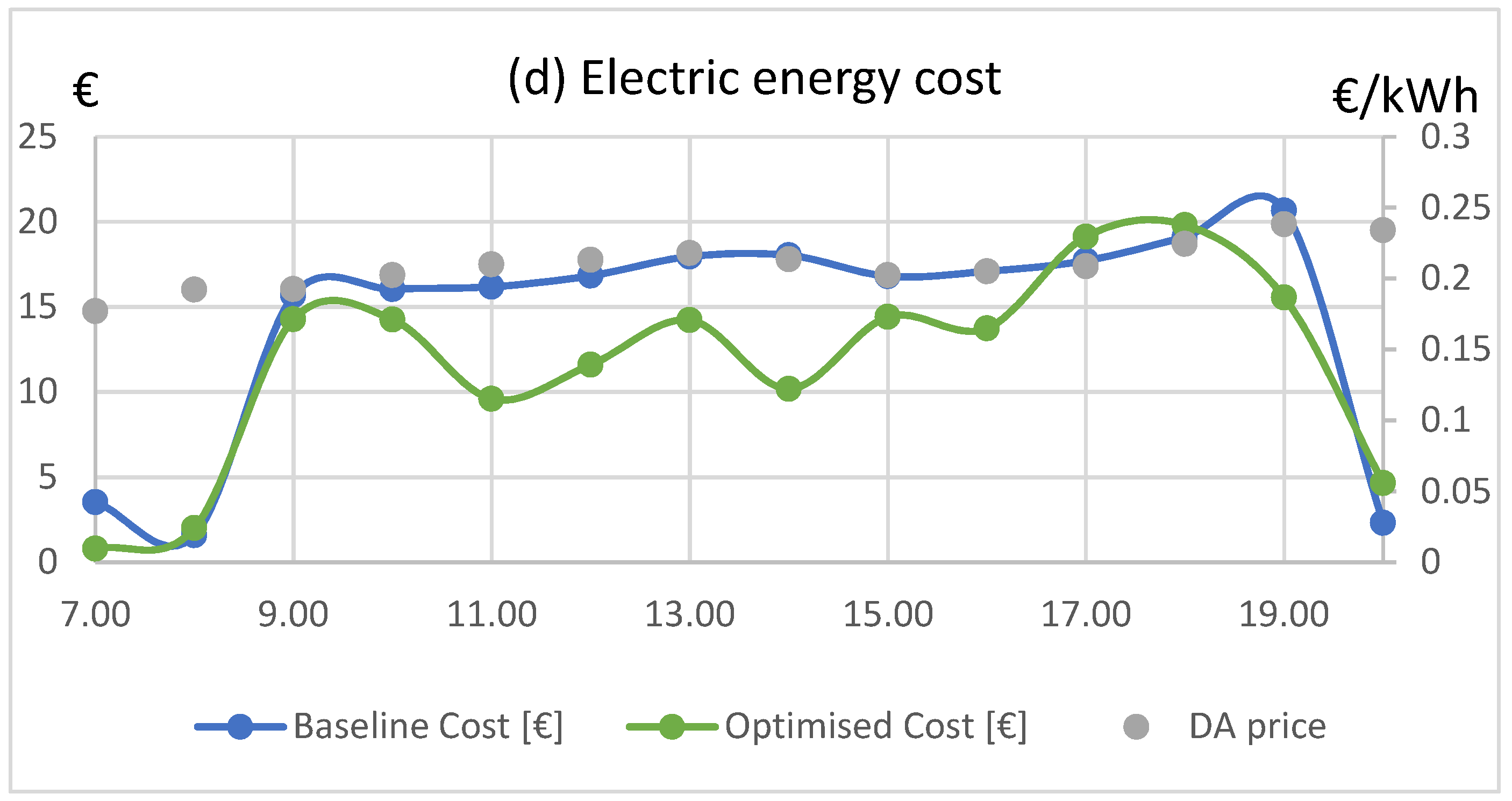
Scenario 2: 27 March 2018 (Spring)
Results from the GA HVAC optimization on 27 March 2018 are presented in
Figure 4 below. In the optimized scenario of this case, set points were dynamically altered between 19 °C and 22 °C within working hours (
Figure 4a), and the energy of the HVAC was reduced from 610.91 kWh to 463.43 kWh (
Figure 4c), a reduction of 24.1%. Energy cost (
Figure 4d) was decreased from €121.02 to €94.05, which is equal to 22.3% savings. The HVAC power was lower in the optimized scenario, except during hours 10:00 a.m. and 8:00 p.m. (outside working hours). At the baseline scenario, the PMV varied from −0.39 to −0.02, while, at the optimized scenario, PMV varied from −0.65 to −0.18 (
Figure 4b). The average PMV varied from −0.2 to −0.41, which corresponds to a PPD increase from 6.47% to 9.28% between the baseline and optimized scenario. Similarly, in this case, cost savings occurred mostly early in the morning and late in the evening when prices were relatively high. Some savings were also observed around 12:00–1:00 p.m. just before prices got to the lowest level of that particular day.
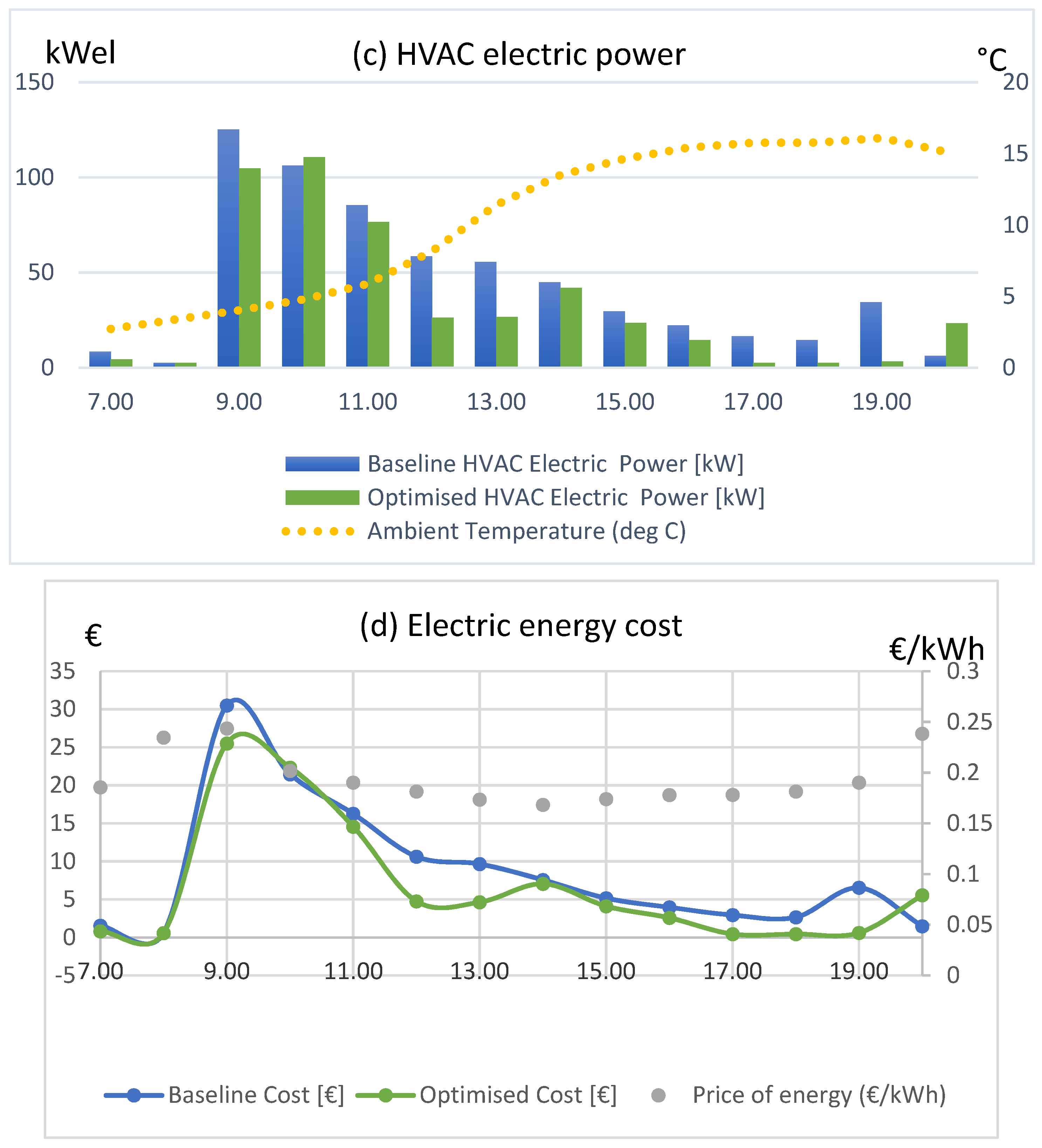
Scenario 3: 15 August 2018 (Summer)
Results from the GA HVAC optimization on 15 August 2018 are presented in
Figure 5 below. In the optimized scenario, temperature set points varied, on an hourly basis, from 26 °C to 24 °C, within working hours (
Figure 5a), whereas the energy of the HVAC (
Figure 5c) was reduced from 1447.83 kWh to 1175.93 kWh, a reduction of 18.8%. Energy cost (
Figure 5d) was decreased from €295.26 to €238.57, which is equal to 19.2% savings. The mean PMV for working hours was improved from −0.2 to −0.007, and the PPD was decreased from 6.42% to 5.03%. In the optimized solution, HVAC power was lower during all hours except 2:00, 5:00, and 6:00 p.m. following the set points changing from higher to lower values down to 24 °C. In this scenario, cost savings occurred throughout the day, while they were more evident during hours of high prices compared to neighbor regions. The PMV was improved as the fixed cooling set point caused thermal discomfort and unnecessary high energy consumption levels for most hours during the day.
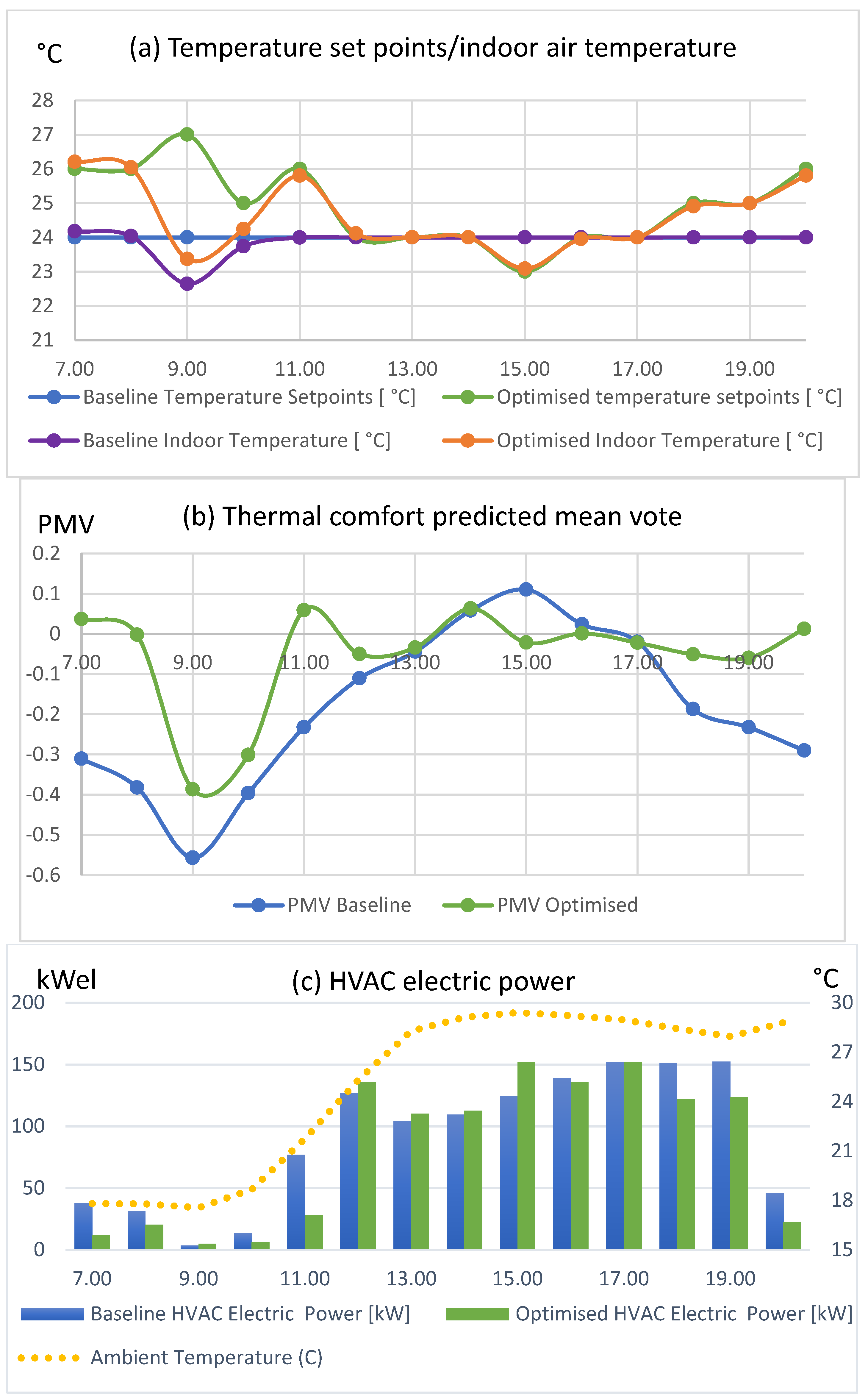
Scenario 4: 10 September 2018 (Autumn)
Scenario 4 results from the GA HVAC optimization on 10 September 2018 are presented in
Figure 6 below. In this case, the energy of the HVAC (
Figure 6c) was reduced from 1268.47 kWh to 1136.29 kWh, a reduction of 10.4%, while energy cost (
Figure 6d) was decreased from €311.59 to €280.68, a reduction of 9.9%. The slight difference in the mean PMV for working hours from −0.144 to −0.073 corresponds to a PPD decrease by 1.1%. The PMV at the baseline scenario varied from −0.56 up to 0.11, while, in the optimized scenario, PMV varied from −0.39 to 0.06 (
Figure 6b). HVAC power values (
Figure 6c) in the optimized scenario exceeded their respective values in the baseline scenario at times of low prices with respect to the neighboring regions and specifically from 12:00–3:00 p.m. Baseline energy consumption was unnecessarily high during morning hours as it coincided with significant negative PMV levels, while efficient performance was observed in the optimized scenario where the set point was kept at the highest allowed level. Indoor temperature (
Figure 6a) deviated from the set point temperature for both the baseline and the optimized scenario between 9:00 and 10:00 a.m. In the optimized scenario, the HVAC energy consumption remained at low levels due to the negative PMV levels during the same time period. Another interesting observation was that the PMV in the baseline scenario significantly increased over time during the day, despite the fact that the indoor temperature was kept constant, which was mainly due to the effect of radiative temperature on thermal comfort.
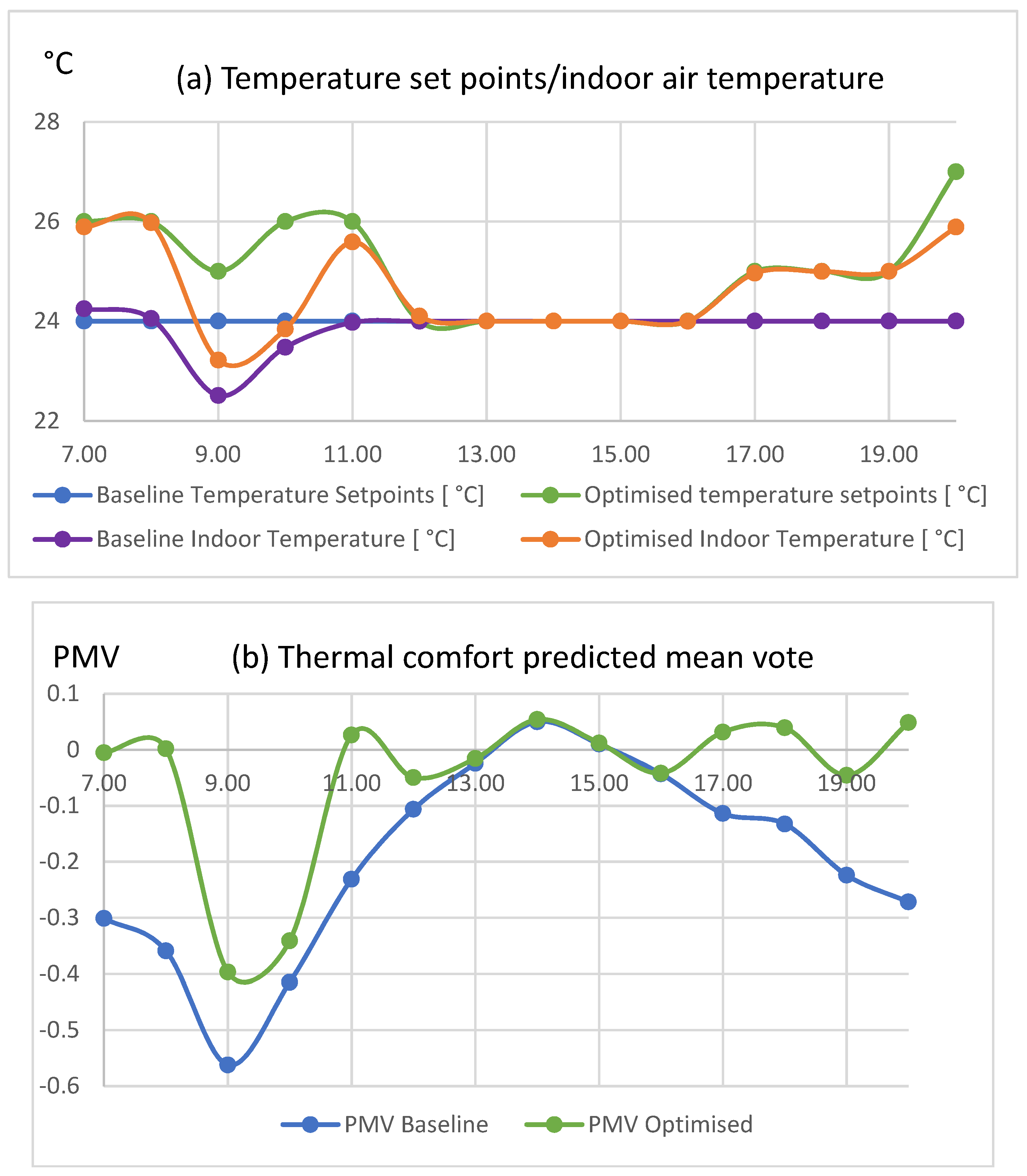
Scenario 5: 21 September 2018 (Autumn)
Results from the GA HVAC optimization on 21 September 2018 are presented in
Figure 7 below. In the optimized scenario, set points within working hours fluctuated between 26 °C and 24 °C (
Figure 7a), while the energy of the HVAC was reduced from 1248.69 kWh to 1078.16 kWh (
Figure 7c), a reduction of 13.7%. Energy cost (
Figure 7d) was decreased from €298.07 to €253.79, which is equal to savings of 14.9%. The mean PMV for working hours was improved from −0.172 to −0.056, and the respective PPD was decreased from 6.4% to 5.4%. In this case, the optimized PMV (
Figure 7b) reflected improved thermal conditions, since it oscillated in the region −0.40 to 0.05 in the optimized scenario, while, in the baseline scenario, it varied between −0.56 and 0.05. Energy savings were achieved by keeping the temperature set points at higher levels, while the PMV was at negative levels during early morning and late afternoon working hours. Slightly higher HVAC power levels (
Figure 7c) were observed during hours 12:00–3:00 p.m., coinciding with the lowest energy prices during the day.
Scenario 6: 20 November 2018 (Winter)
Results from the GA HVAC optimization on 20 November 2018 are presented in
Figure 8 below. Temperature set points in the optimized scenario were dynamically controlled from 17 °C to 23 °C (18 °C to 22 °C within working hours;
Figure 8a). In the optimized scenario, the energy of the HVAC was reduced from 923.75 kWh to 756.67 kWh, a reduction of 18.1% (
Figure 8c). Energy cost, shown in
Figure 8d, was decreased from €217.33 to €177.66, which is equal to savings of 17.4%. PMV in the optimized scenario varied from −0.50 to −0.10, whereas, in the baseline scenario, it varied between −0.07 and −0.05 (
Figure 8b). The mean PMV for working hours was increased from −0.055 to −0.276, and the respective PPD was increased by 1.4%. PMV was kept at small negative values and above −0.3 for most hours, except for 2:00 and 3:00 p.m., where PMV was −0.49 and −0.35, respectively. HVAC power in the optimized scenario was kept at lower levels compared to the baseline for all working hours (except early morning hours).
Scenario 7: 22 November 2018 (Winter)
Results from the GA HVAC optimization on 22 November 2018 are presented in
Figure 9 below. Optimized temperature set points, as presented in
Figure 9a, varied from 19 °C to 22 °C. In the optimized scenario, the energy of the HVAC was reduced from 717.77 kWh to 631.61 kWh, a reduction of 12.0% (
Figure 9c). Energy cost (
Figure 9d) was decreased from €179.59 to €159.01, which is equal to savings of 11.5%. PMV in the optimized scenario (
Figure 9b) varied between −0.25 and −0.01 and, in the baseline scenario, PMV varied between −0.03 and −0.01. The mean PMV for working hours was increased from −0.016 to −0.110, and the respective PPD was increased by 0.4%. Significant energy savings occurred during hours of high prices, corresponding to hours 9:00 a.m., 1:00 p.m., and 3:00–6:00 p.m., while the PMV was kept at small negative levels down to −0.25.
Scenario 8: 25 November 2018 (Winter)
Optimization results for HVAC optimization on 25 November 2018 are available in
Figure 10. Temperature set points varied from 18 °C to 22 °C in the optimized solution (
Figure 10a). In this scenario, HVAC energy consumption (
Figure 10c) was reduced from 944.85 kWh to 776.17 kWh, a decrease of 17.9% compared to the baseline. Daily cost (
Figure 10d) was reduced from €199.52 to €164.26, a reduction of 17.7%. The mean PMV was decreased from −0.244 in the baseline scenario to −0.478, which is equivalent to a PPD increase of 4.2% (
Figure 10b). HVAC consumption in the optimized scenario exceeded the baseline levels slightly during hours 8:00 a.m., and 5:00 and 6:00 p.m. A compromise between maintaining comfort within tolerable levels while maximizing cost savings was reached.