A Hierarchical Optimisation of a Compressed Natural Gas Station for Energy and Fuelling Efficiency under a Demand Response Program
Abstract
1. Introduction
1.1. Background
1.2. Improving the CNG Station Operation Efficiency
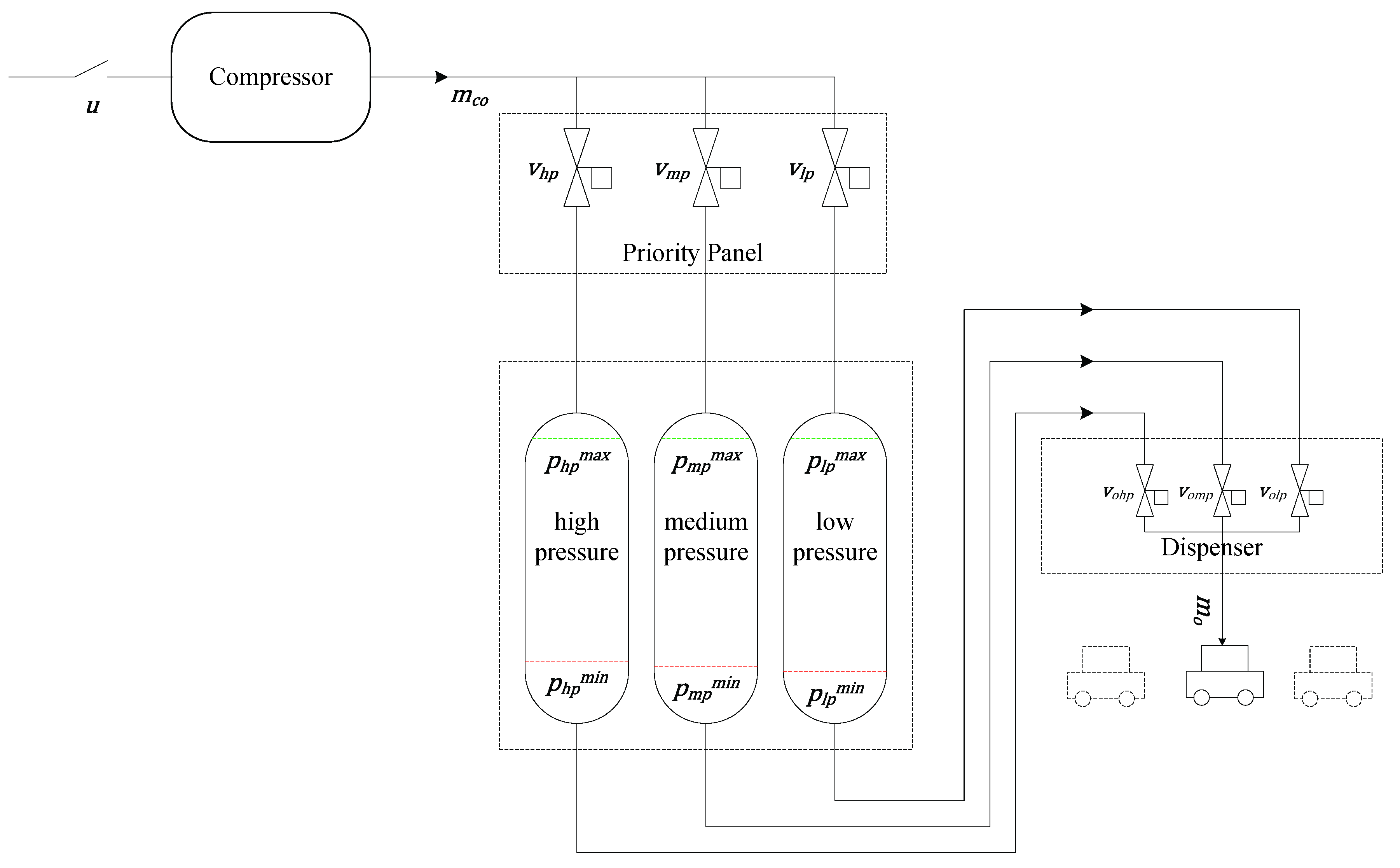
2. System Modelling and Formulation
2.1. The Energy Cost Minimisation Layer
2.1.1. Objective Function
2.1.2. Constraints
2.1.3. Algorithm
2.2. Gas Flow Optimisation Layer
2.2.1. Objective Function
2.2.2. Constraints
2.2.3. Algorithm
- For the current sampling instant k, the controller minimises the objective function in Equation (26) and finds an optimum solution for the control variables , , , , and , subject to the constraints set out in Section 2.2.2.
- From the solution, only the first elements of the solution , , , , and are implemented.
- The states , , and are measured to be fed back.
- The value of k is set to and system states, inputs and outputs are updated.
- Steps 1–4 are repeated until k reaches a value predetermined to mark the end of the control period.
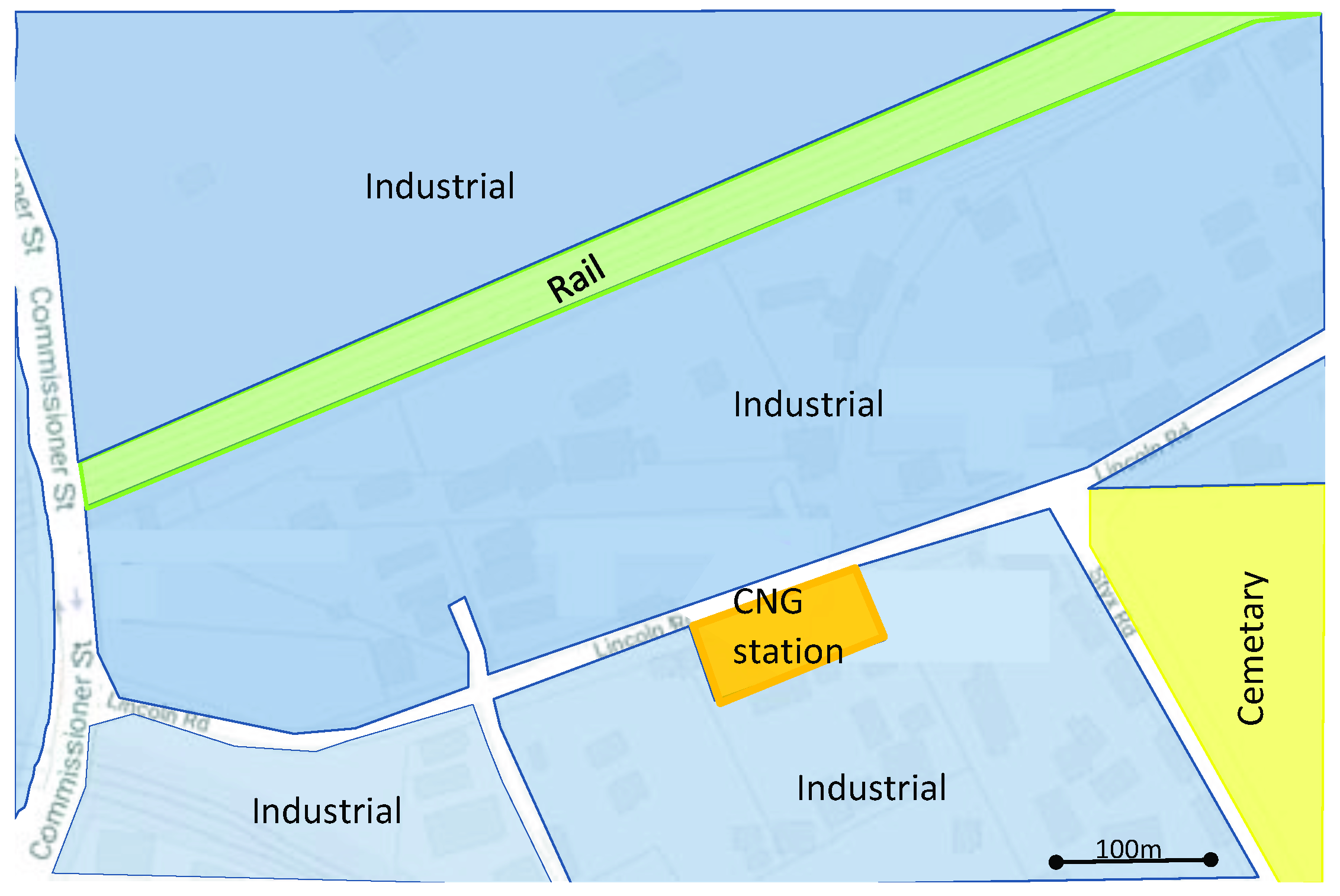
3. Case Study
4. Results
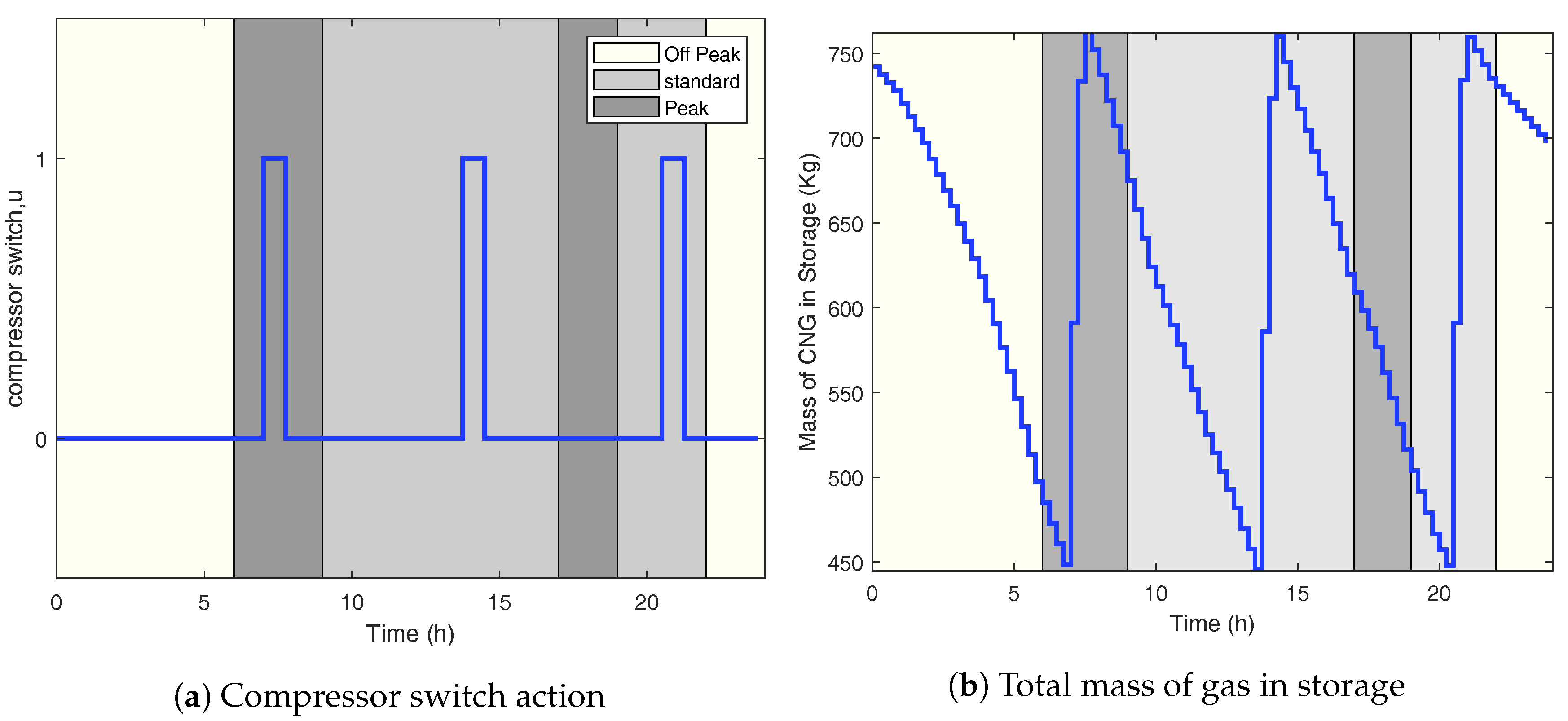
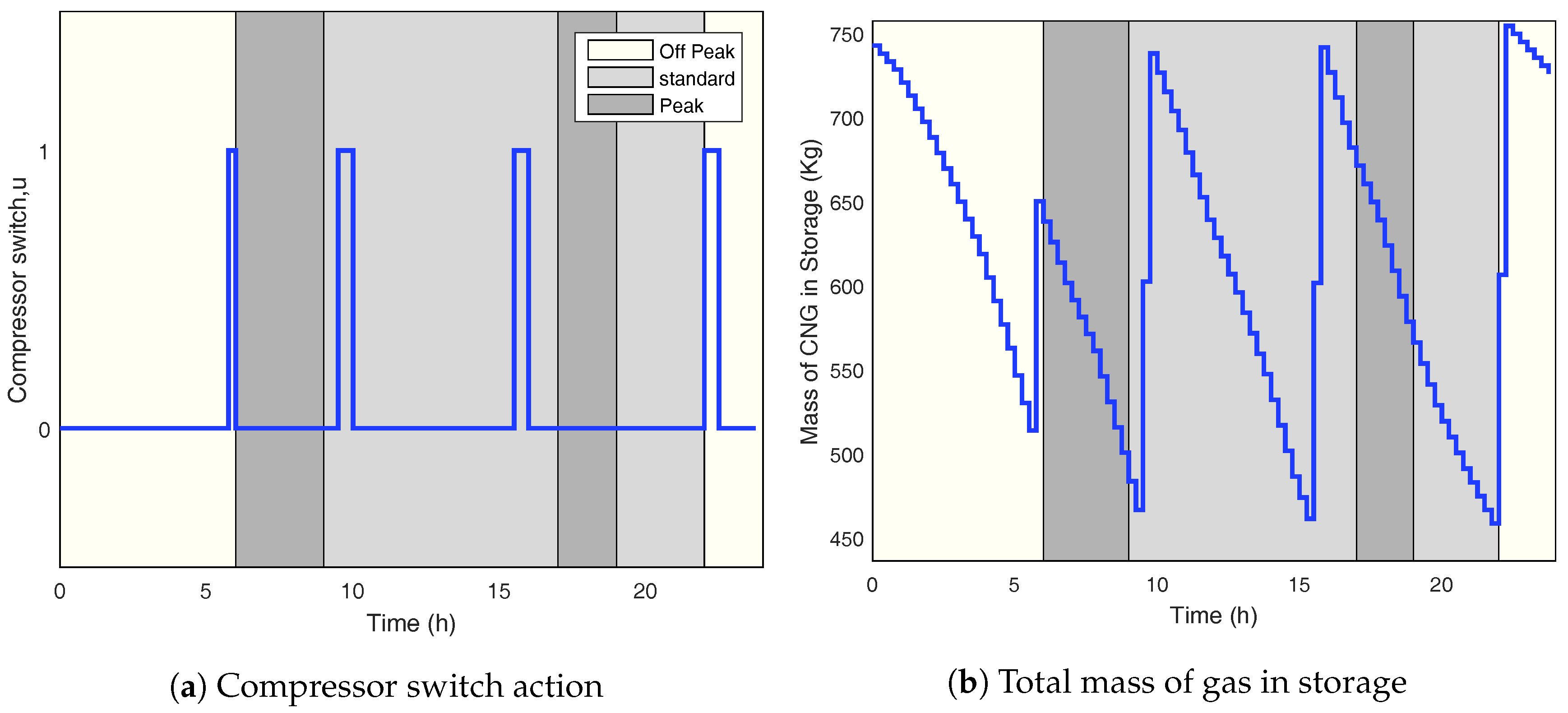
4.1. Energy Cost Minimisation Layer Results
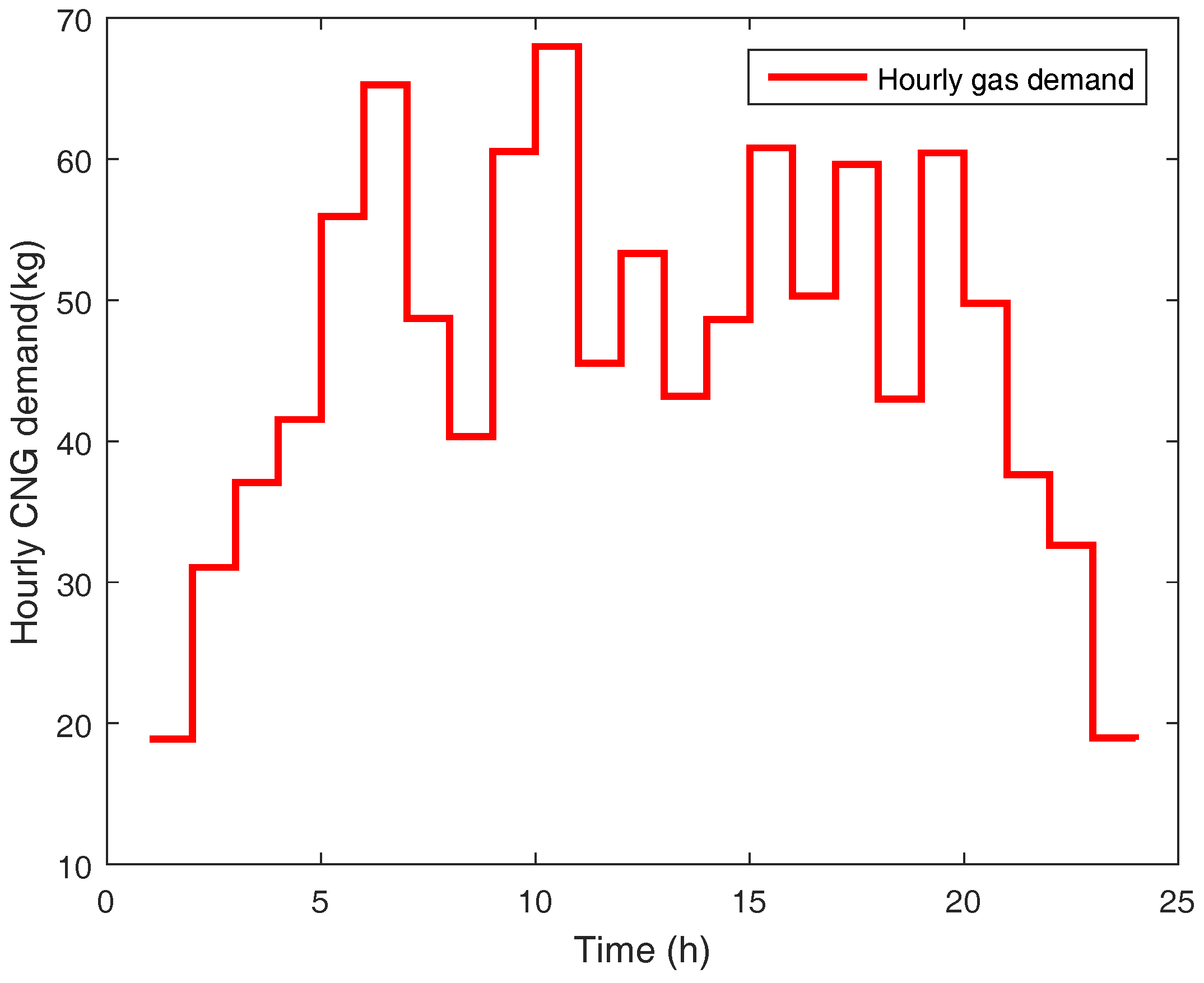
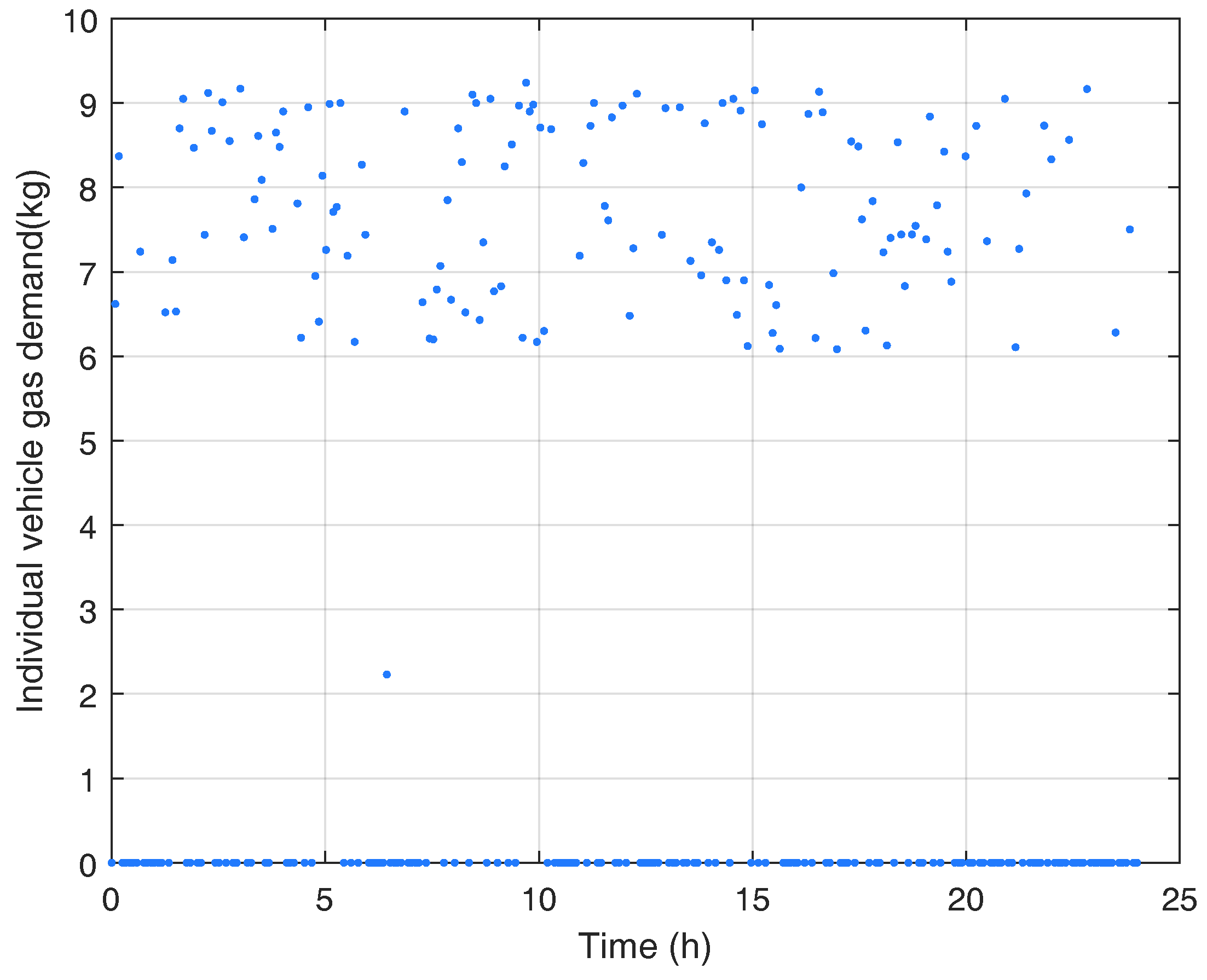
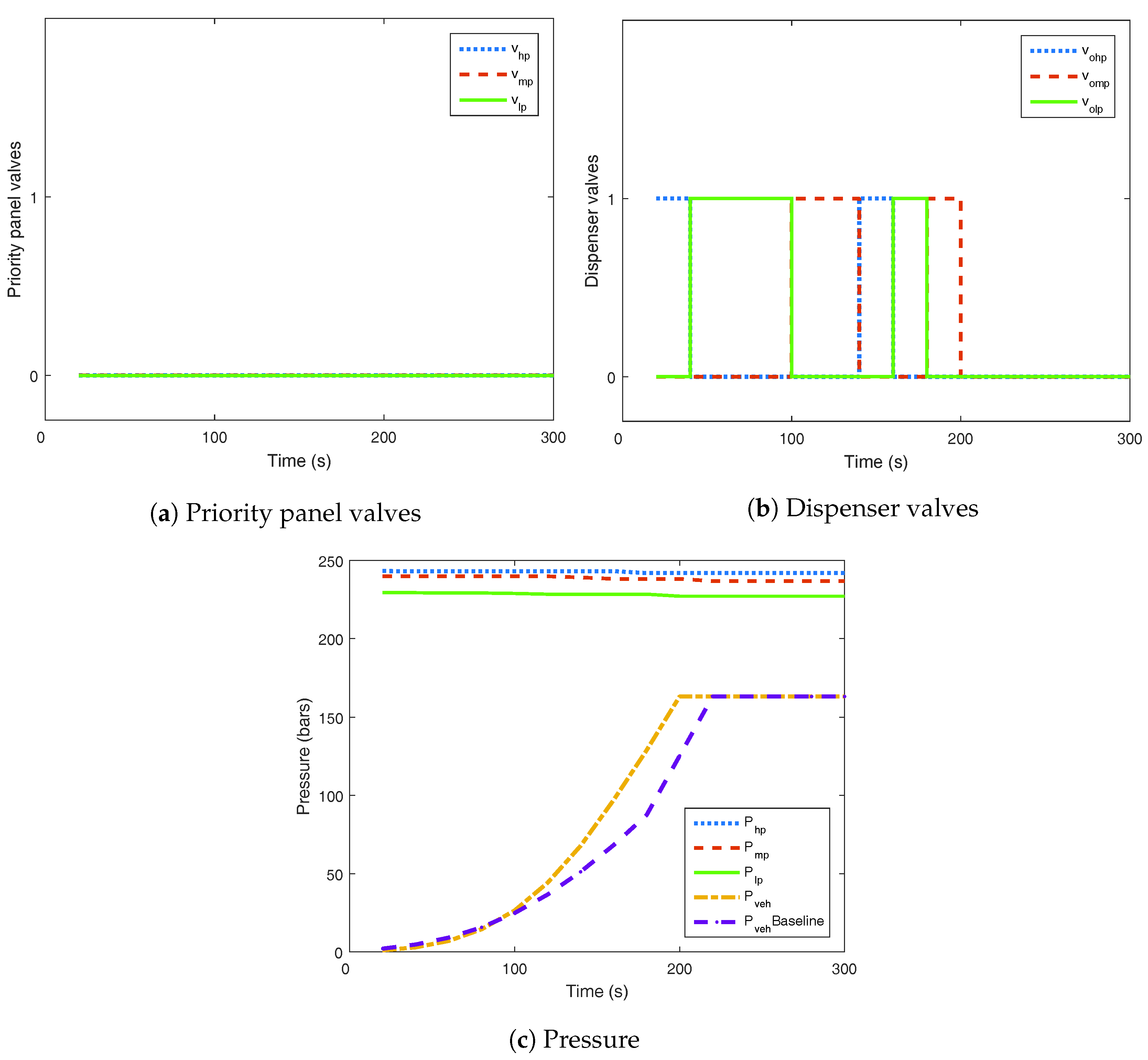
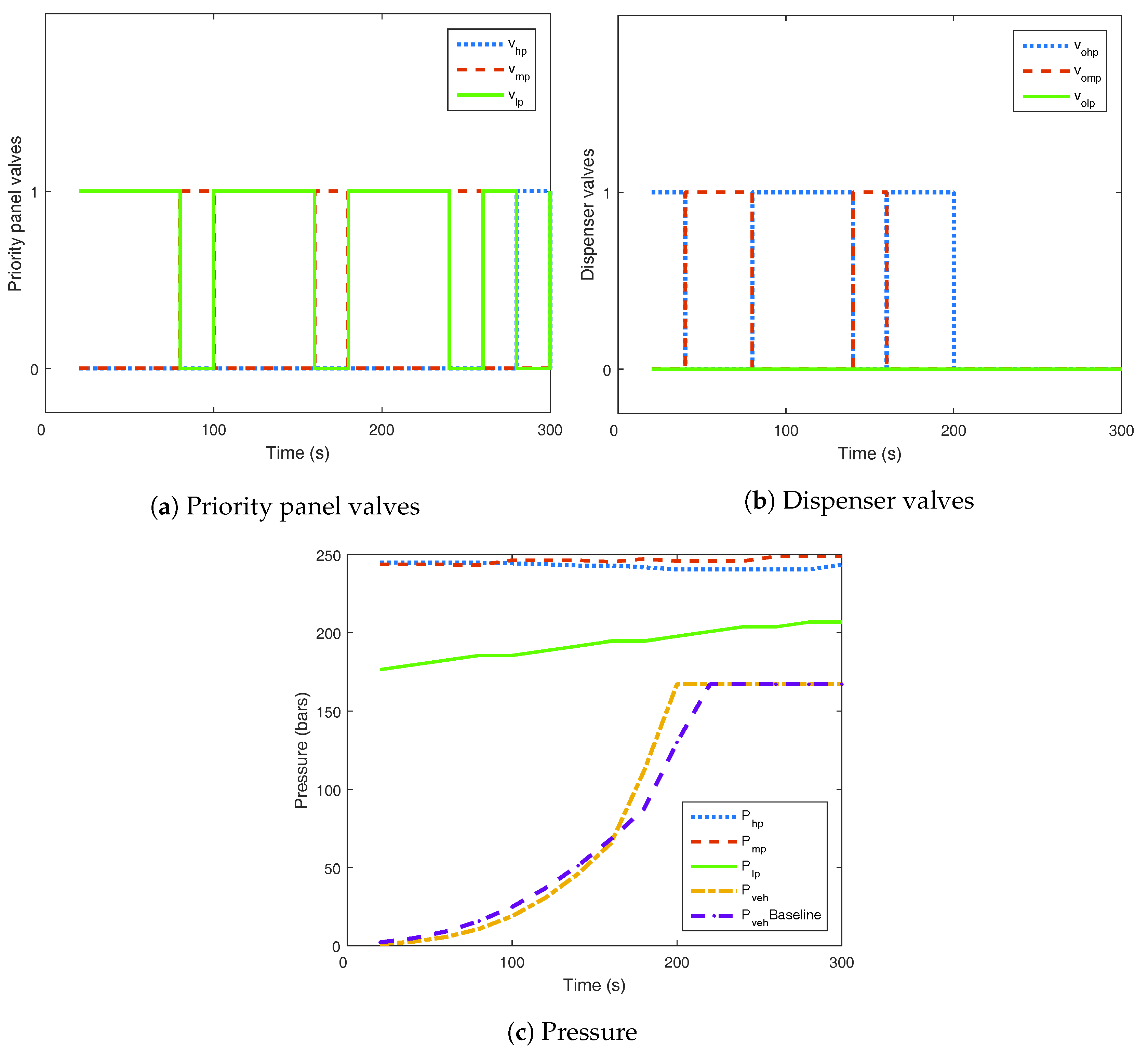
4.2. Gas Flow Optimisation Layer Results
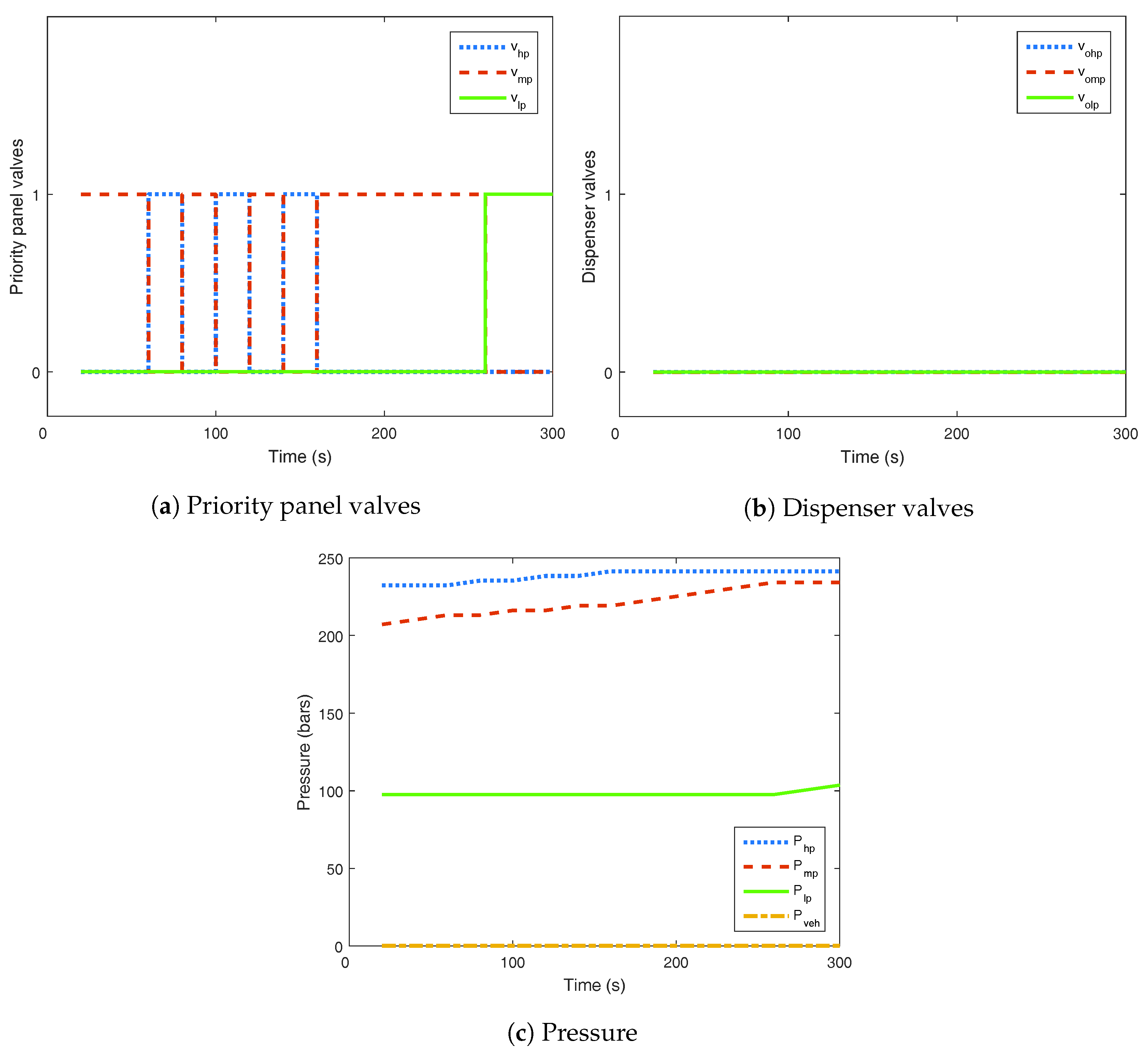
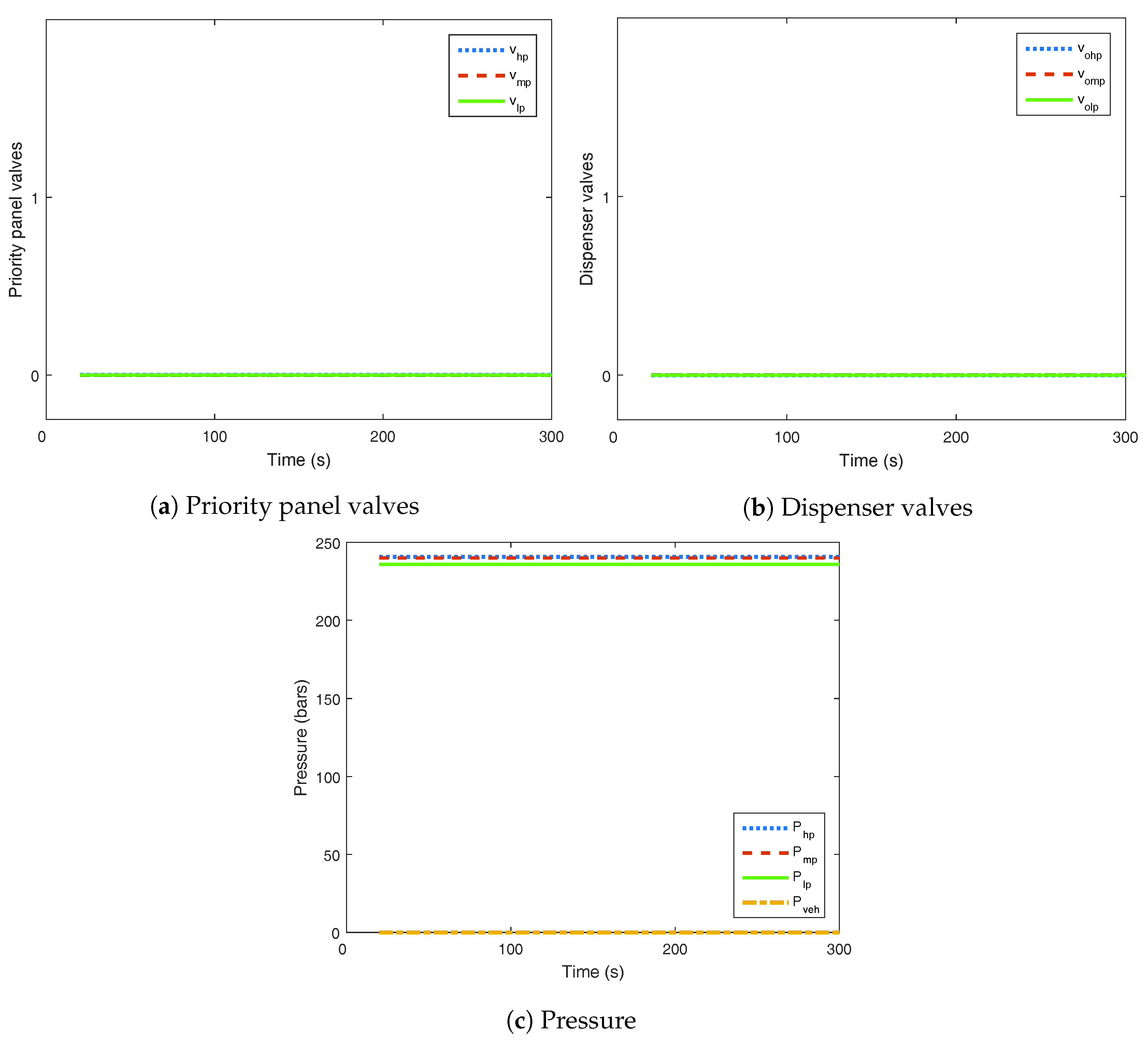
4.2.1. Vehicle Filling with the Compressor Off
4.2.2. Vehicle Filling with the Compressor On
4.2.3. Cascade Reservoir Filling without Vehicle Fuelling
4.2.4. Control Action during Idle Time
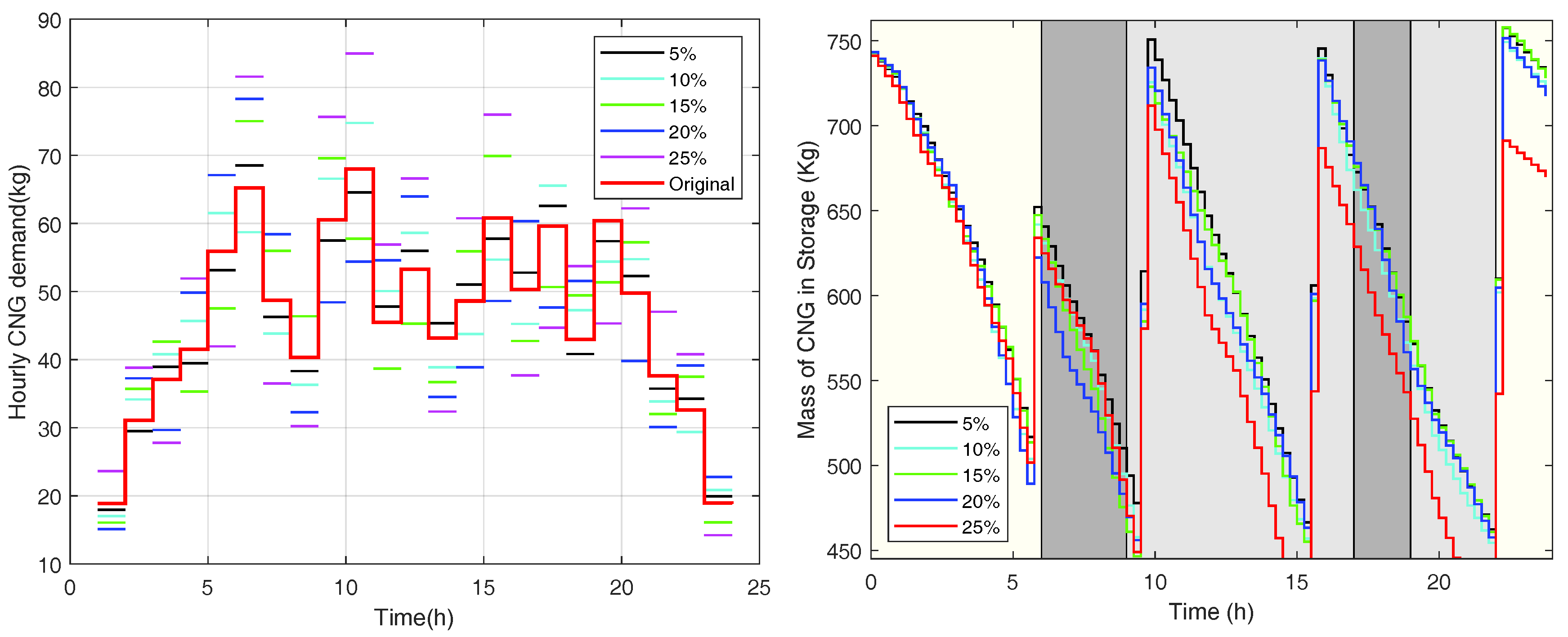
4.3. Sensitivity Analysis
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| Area of dispenser valve orifice (m2) | |
| Co-efficient of discharge of dispenser valve orifice | |
| Specific heat capacity of CNG at constant pressure (J/KgK) | |
| Specific heat capacity of CNG at constant volume (J/KgK) | |
| Objective function of the upper layer | |
| Objective function of the lower layer | |
| m | Mass of gas (kg) |
| Maximum mass of gas for the cascade storage (kg) | |
| Minimum mass of gas for the cascade storage (kg) | |
| Gas demand (kg) | |
| Instantaneous mass flow rate from high pressure, medium pressure and low | |
| pressure reservoirs to vehicle tank (kg/h) | |
| Instantaneous total mass flow rate from cascade storage to vehicle tank (kg/h) | |
| Compressor outlet mass flow rate (kg/h) | |
| M | Molar mass (kg) |
| Molecular weight of the air (g) | |
| Molecular weight of the gas (g) | |
| N | Upper layer control horizon |
| Lower layer model predictive control prediction horizon | |
| n | Gas quantity (moles) |
| P | Pressure (bars) |
| Compressor motor power rating (kW) | |
| Price of electricity under TOU tariff (currency/kW h) | |
| Pressure in high, medium and low pressure reservoirs (bars) | |
| Maximum pressure for high pressure, medium pressure and low pressure reservoirs (bars) | |
| Minimum pressure for high pressure, medium pressure and low pressure reservoirs (bars) | |
| Target vehicle pressure (bars) | |
| Vehicle pressure (bars) | |
| Capacity of the compressor under standard conditions (Nm3/h) | |
| R | Universal gas constant (L bar/K mol) |
| Sampling period (s) | |
| T | Absolute temperature (K) |
| u | State of compressor switch |
| State of priority panel valves for high pressure, medium pressure and low pressure reservoirs | |
| State of dispenser valves for high pressure, medium pressure and low pressure reservoirs | |
| V | Volume of cascade reservoir tanks (L) |
| Volume of high, medium and low pressure reservoirs (L) | |
| z | Compressibility factor of CNG |
| ϱ | Weighting factor for the upper layer |
| ς | Weighting factor for the lower layer |
| γ | ratio of specific heats |
| Density of air under standard conditions (kg/m3) | |
| Density of gas in high pressure, medium pressure and low pressure reservoirs (kg/m3) |
References
- Davies, J.; Grant, M.; Venezia, J.; Aamidor, J. US Transportation Sector Greenhouse Gas Emissions: Trends, Uncertainties and Methodological Improvements. In TRB 2007 Annual Meeting; Transport Research Board: Washington, DC, USA, 2007. [Google Scholar]
- Yeh, S. An empirical analysis on the adoption of alternative fuel vehicles: The case of natural gas vehicles. Energy Policy 2007, 35, 5865–5875. [Google Scholar] [CrossRef]
- Ou, X.; Zhang, X.; Zhang, X.; Zhang, Q. Life cycle GHG of NG-based fuel and electric vehicle in China. Energies 2013, 6, 2644–2662. [Google Scholar] [CrossRef]
- Mikolajková-Alifov, M.; Pettersson, F.; Björklund-Sänkiaho, M.; Saxén, H. A Model of Optimal Gas Supply to a Set of Distributed Consumers. Energies 2019, 12, 351. [Google Scholar] [CrossRef]
- Kuby, M. The opposite of ubiquitous: How early adopters of fast-filling alt-fuel vehicles adapt to the sparsity of stations. J. Transp. Geogr. 2019, 75, 46–57. [Google Scholar] [CrossRef]
- Chala, G.; Abd Aziz, A.; Hagos, F. Natural Gas Engine Technologies: Challenges and Energy Sustainability Issue. Energies 2018, 11, 2934. [Google Scholar] [CrossRef]
- Greene, D.L. Survey evidence on the importance of fuel availability to the choice of alternative fuels and vehicles. Energy Stud. Rev. 1998, 8, 215–231. [Google Scholar] [CrossRef][Green Version]
- Newhouse, N.L.; Liss, W.E. Fast Silling of NGV Fuel Containers; Technical Report; SAE Technical Paper; SAE: Warrendale, PA, USA, 1999. [Google Scholar]
- Chen, S.; Xie, G.; LI, Q.; Chang, K. Comparison among LNG, CNG and L-CNG Filling Stations. Gas Heat 2007, 7, 006. [Google Scholar]
- Khadem, J.; Saadat-Targhi, M.; Farzaneh-Gord, M. Mathematical modeling of fast filling process at CNG refueling stations considering connecting pipes. J. Nat. Gas Sci. Eng. 2015, 26, 176–184. [Google Scholar] [CrossRef]
- Albadi, M.H.; El-Saadany, E. A summary of demand response in electricity markets. Electr. Power Syst. Res. 2008, 78, 1989–1996. [Google Scholar] [CrossRef]
- Kagiri, C.; Zhang, L.; Xia, X. Optimal energy cost management of a CNG fuelling station. In Proceedings of the Control Conference Africa, Johannesburg, South Africa, 7–8 December 2017; Volume 50, pp. 94–97. [Google Scholar]
- Khamforoush, M.; Moosavi, R.; Hatami, T. Compressed natural gas behavior in a natural gas vehicle fuel tank during fast filling process: Mathematical modeling, thermodynamic analysis, and optimization. J. Nat. Gas Sci. Eng. 2014, 20, 121–131. [Google Scholar] [CrossRef]
- Kountz, K.; Blazek, C.; Liss, W. A new natural gas dispenser control system. In International Gas Research Conference; Government Institutes Inc.: Rockville, MD, USA, 1998; Volume 4, pp. 135–145. [Google Scholar]
- Kountz, K.J.; Blazek, C.F.; Christopher, F. NGV Fuelling Station and Dispenser Control Systems; Technical Report; Gas Research Institute: Chicago, IL, USA, 1997. [Google Scholar]
- Kountz, K. Modeling the fast fill process in natural gas vehicle storage cylinders. In 207th ACS National Meeting-Division of Fuel Chemistry; American Chemical Society: San Diego, CA, USA, 1994. [Google Scholar]
- Farzaneh-Gord, M. Compressed natural gas-Single reservoir filling process. Int. Gas Eng. Manag. 2008, 48, 16–18. [Google Scholar]
- Thomas, G.; Goulding, J.; Munteam, C. Measurement, Approval and Verification of CNG Dispensers; Technical Report; National Weights and Measures Laboratory: London, UK, 1999.
- Farzaneh-gord, M.; Hashemi, S.; Farzaneh-kord, A. Thermodynamics Analysis of Cascade Reserviors Filling Process of Natural Gas Vehicle Cylinders. World Appl. Sci. 2008, 5, 143–149. [Google Scholar]
- Deymi-Dashtebayaz, M.; Gord, M.F.; Rahbari, H.R. Studying transmission of fuel storage bank to NGV cylinder in CNG fast filling station. J. Braz. Soc. Mech. Sci. Eng. 2012, 34, 429–435. [Google Scholar] [CrossRef]
- Frick, M.; Axhausen, K.W.; Carle, G.; Wokaun, A. Optimization of the distribution of compressed natural gas (CNG) refueling stations: Swiss case studies. Transp. Res. Part D Transp. Environ. 2007, 12, 10–22. [Google Scholar] [CrossRef]
- Bang, H.J.; Stockar, S.; Muratori, M.; Rizzoni, G. Modeling and analysis of a CNG residential refueling system. In ASME 2014 Dynamic Systems and Control Conference; American Society of Mechanical Engineers: New York, NY, USA, 2014. [Google Scholar]
- Smith, M.; Gonzales, J. Costs Associated with Compressed Natural Gas Vehicle Fueling Infrastructure; Technical Report; National Renewable Energy Laboratory (NREL): Golden, CO, USA, 2014.
- Kagiri, C.; Zhang, L.; Xia, X. Compressor and priority panel optimization for an energy efficient CNG fuelling station. In Proceedings of the IEEE 11th Asian Control Conference (ASCC), Gold Coast, QLD, Australia, 17–20 December 2017; pp. 2200–2203. [Google Scholar]
- Xia, X.; Zhang, J.; Cass, W. Energy management of commercial buildings—A case study from a POET perspective of energy efficiency. J. Energy S. Afr. 2012, 23, 23–31. [Google Scholar]
- Spees, K.; Lave, L.B. Demand response and electricity market efficiency. Electr. J. 2007, 20, 69–85. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, L. Industrial energy systems in view of energy efficiency and operation control. Annu. Rev. Control 2016, 42, 299–308. [Google Scholar] [CrossRef]
- Kagiri, C.; Zhang, L.; Xia, X. Optimization of a compressed natural gas station operation to minimize energy cost. In Proceedings of the 9th International Conference on Applied Energy, Cardiff, UK, 21–24 August 2017; pp. 2003–2008. [Google Scholar]
- Kagiri, C.; Wanjiru, E.M.; Zhang, L.; Xia, X. Optimized response to electricity time-of-use tariff of a compressed natural gas fuelling station. Appl. Energy 2018, 222, 244–256. [Google Scholar] [CrossRef]
- Allgöwer, F.; Zheng, A. Nonlinear Model Predictive Control; Birkhäuser: Basel, Switzerland, 2012; Volume 26. [Google Scholar]
- Qin, S.J.; Badgwell, T.A. A survey of industrial model predictive control technology. Control Eng. Pract. 2003, 11, 733–764. [Google Scholar] [CrossRef]
- Xia, X.; Zhang, J. Operation efficiency optimisation modelling and application of model predictive control. IEEE/CAA J. Autom. Sin. 2015, 2, 166–172. [Google Scholar]
- Kountz, K.J.; Liss, W.E.; Blazek, C.F. Automated Process and System for Dispensing Compressed Natural Gas. U.S. Patent 5,810,058, 22 September 1998. [Google Scholar]
- Shipley, E. Study of Natural Gas Vehicles (NGV) during the Fast Fill Process. Master’s Thesis, West Virginia University, Morgantown, WV, USA, 2002. [Google Scholar]
- Nguyen, H.H.; Uraikul, V.; Chan, C.W.; Tontiwachwuthikul, P. A comparison of automation techniques for optimization of compressor scheduling. Adv. Eng. Softw. 2008, 39, 178–188. [Google Scholar] [CrossRef]
- Nguyen, H.H.; Chan, C.W. Applications of artificial intelligence for optimization of compressor scheduling. Eng. Appl. Artif. Intell. 2006, 19, 113–126. [Google Scholar] [CrossRef]
- Mathaba, T.; Xia, X.; Zhang, J. Analysing the economic benefit of electricity price forecast in industrial load scheduling. Electr. Power Syst. Res. 2014, 116, 158–165. [Google Scholar] [CrossRef]
- Wanjiru, E.M.; Xia, X. Energy-water optimization model incorporating rooftop water harvesting for lawn irrigation. Appl. Energy 2015, 160, 521–531. [Google Scholar] [CrossRef][Green Version]
- Saadat-Targhi, M.; Khadem, J.; Farzaneh-Gord, M. Thermodynamic analysis of a CNG refueling station considering the reciprocating compressor. J. Nat. Gas Sci. Eng. 2016, 29, 453–461. [Google Scholar] [CrossRef]
- Calvert, J.G. Glossary of atmospheric chemistry terms (Recommendations 1990). Pure Appl. Chem. 1990, 62, 2167–2219. [Google Scholar] [CrossRef]
- Farzaneh-Gord, M.; Deymi-Dashtebayaz, M. Optimizing natural gas fueling station reservoirs pressure based on ideal gas model. Pol. J. Chem. Technol. 2013, 15, 88–96. [Google Scholar] [CrossRef]
- Cilliers, C.; van der Zee, L.; Kleingeld, M. Cost savings on mine dewatering pumps by reducing preparation-and comeback loads. In Proceedings of the IEEE International Conference on the Industrial and Commercial Use of Energy (ICUE), Cape Town, South Africa, 19–20 August 2014; pp. 1–8. [Google Scholar]
- Cilliers, C. Cost Savings on Mine Dewatering Pumps by Reducing Preparation- and Comeback Loads. Master’s Thesis, North West University, Potchefstroom, South Africa, 2014. [Google Scholar]
- van Tonder, A.; Kleingeld, M.; Marais, J. Investigating demand response potential in a mining group. In Proceedings of the IEEE Industrial and Commercial Use of Energy Conference (ICUE), Cape Town, South Africa, 20–21 August 2013; pp. 1–5. [Google Scholar]
| Parameter | Value |
|---|---|
| 1.225 kg/m3 | |
| 0.61 | |
| 1.304 | |
| 0.028966 g | |
| 0.0164 g | |
| R | 0.083145 LbarK−1mol−1 |
| T | 294.15 K |
| Gas Level Disturbance | 4th Vehicle(s) | 38th Vehicle(s) |
|---|---|---|
| 5% | 200 | 200 |
| 10% | 200 | 200 |
| 15% | 200 | 200 |
| 20% | 200 | 200 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kagiri, C.; Zhang, L.; Xia, X. A Hierarchical Optimisation of a Compressed Natural Gas Station for Energy and Fuelling Efficiency under a Demand Response Program. Energies 2019, 12, 2165. https://doi.org/10.3390/en12112165
Kagiri C, Zhang L, Xia X. A Hierarchical Optimisation of a Compressed Natural Gas Station for Energy and Fuelling Efficiency under a Demand Response Program. Energies. 2019; 12(11):2165. https://doi.org/10.3390/en12112165
Chicago/Turabian StyleKagiri, Charles, Lijun Zhang, and Xiaohua Xia. 2019. "A Hierarchical Optimisation of a Compressed Natural Gas Station for Energy and Fuelling Efficiency under a Demand Response Program" Energies 12, no. 11: 2165. https://doi.org/10.3390/en12112165
APA StyleKagiri, C., Zhang, L., & Xia, X. (2019). A Hierarchical Optimisation of a Compressed Natural Gas Station for Energy and Fuelling Efficiency under a Demand Response Program. Energies, 12(11), 2165. https://doi.org/10.3390/en12112165





