Micromechanical Investigation of Stress Relaxation in Gas Hydrate-Bearing Sediments Due to Sand Production
Abstract
:1. Introduction
2. Sand Migration Effect on Stresses
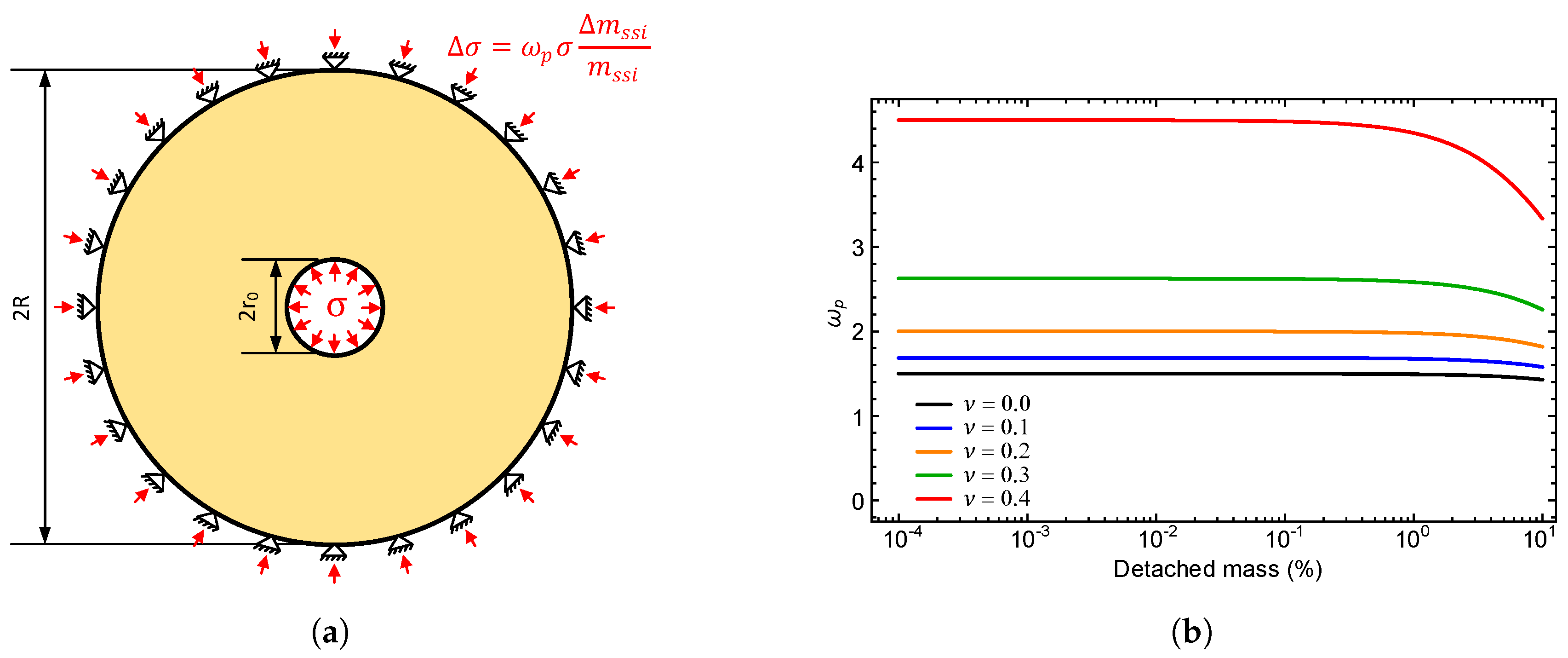
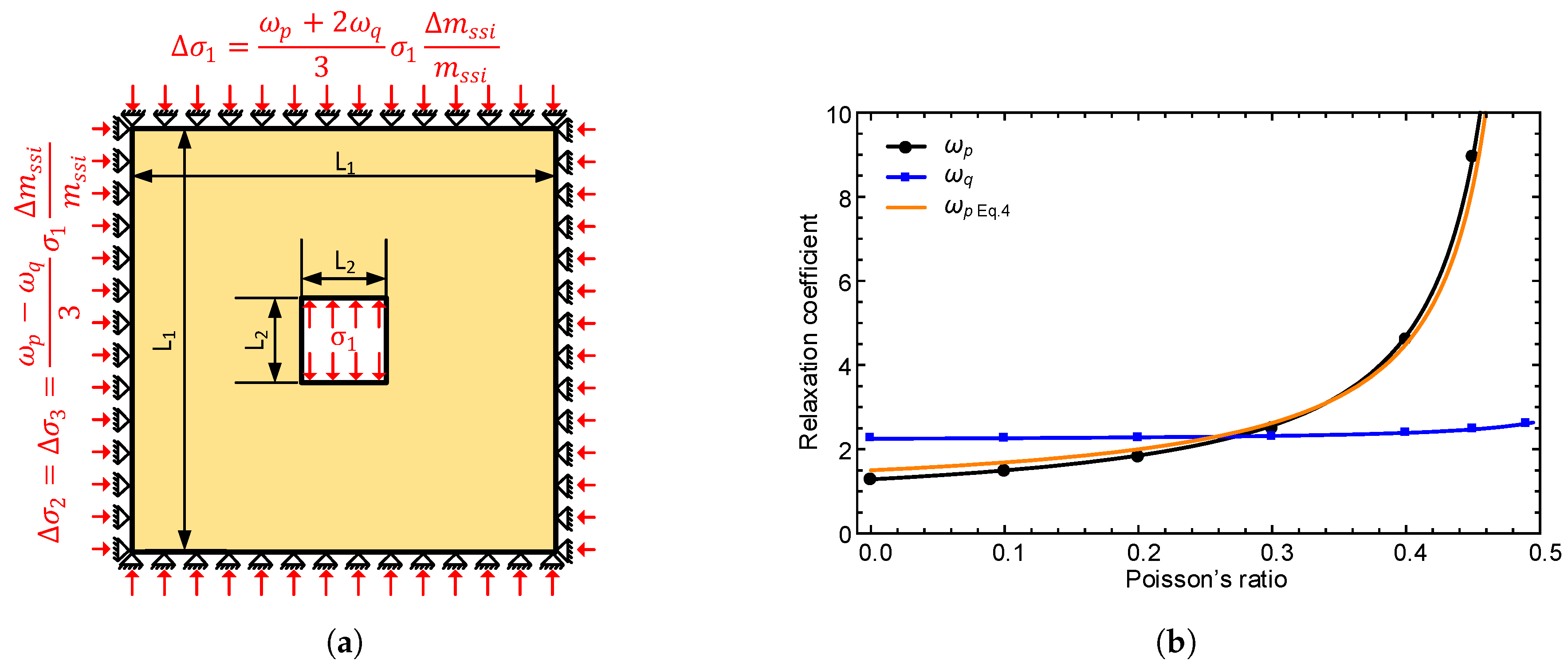
3. Elasticity-Based Stress Relaxation
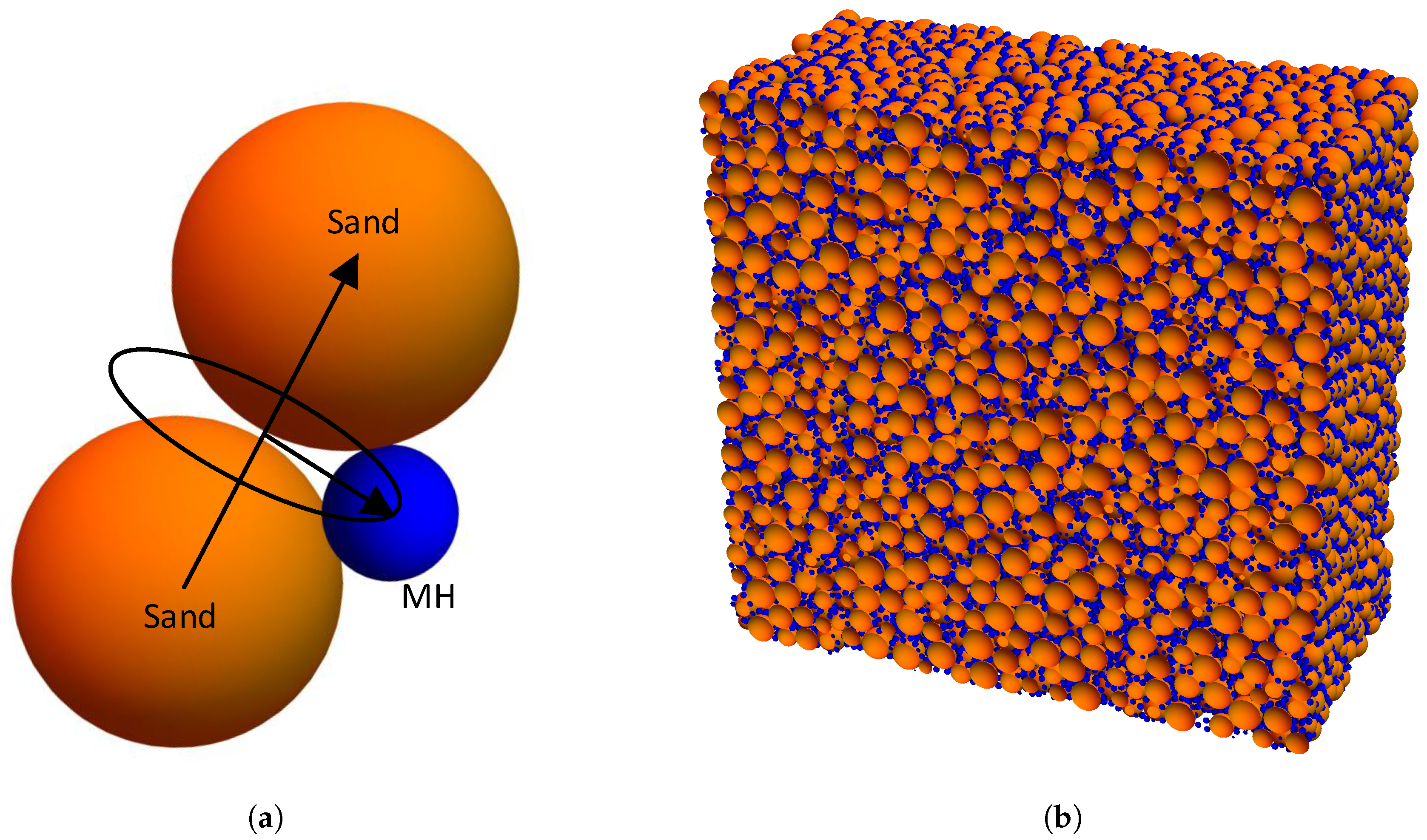
4. Random DEM Model
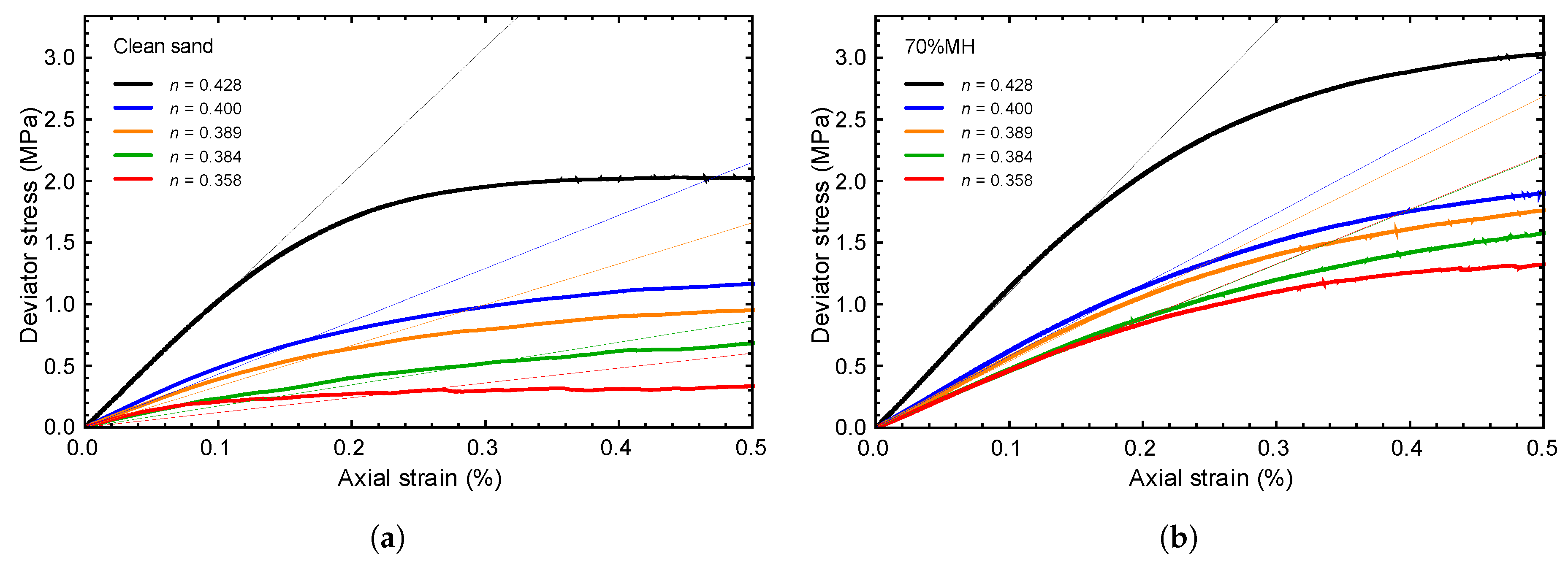
4.1. Clean Sand Skeleton
4.1.1. Analysis and Results
4.1.2. Discussion
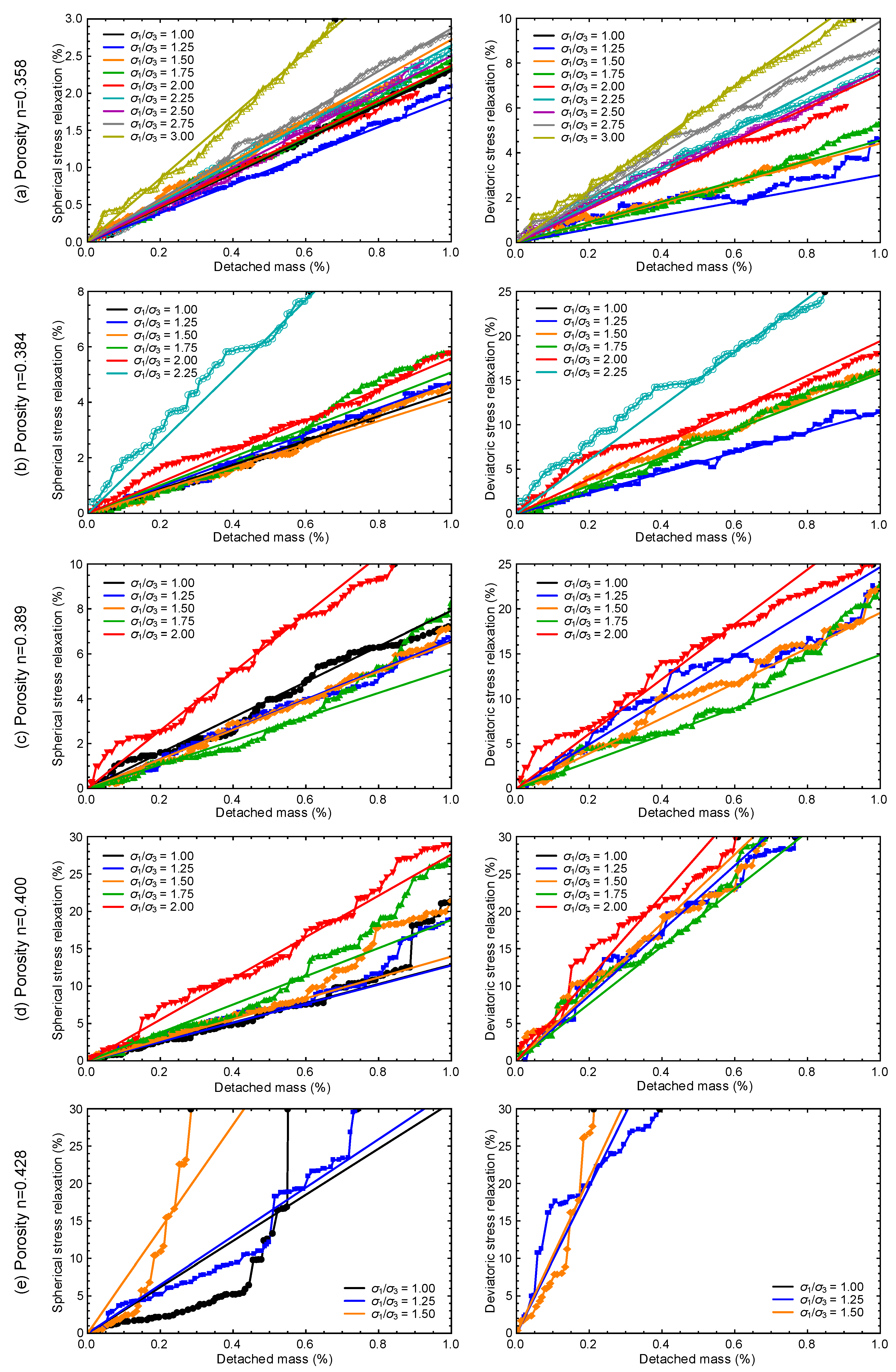
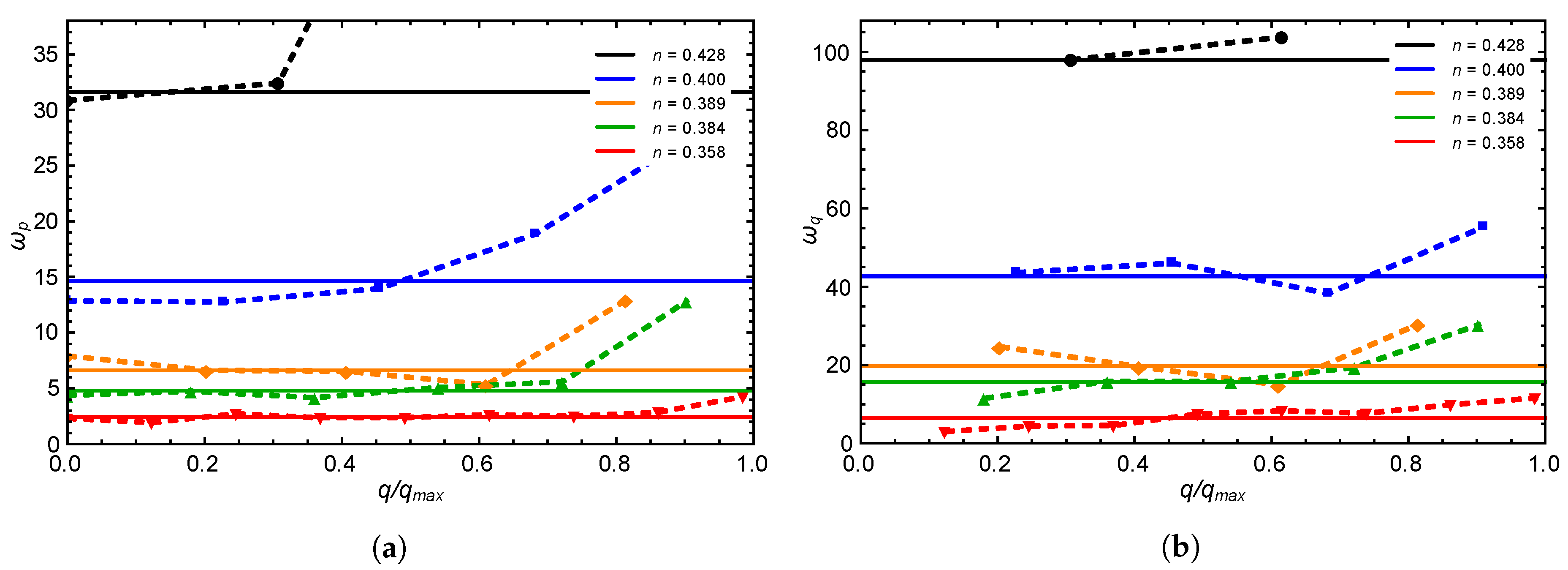
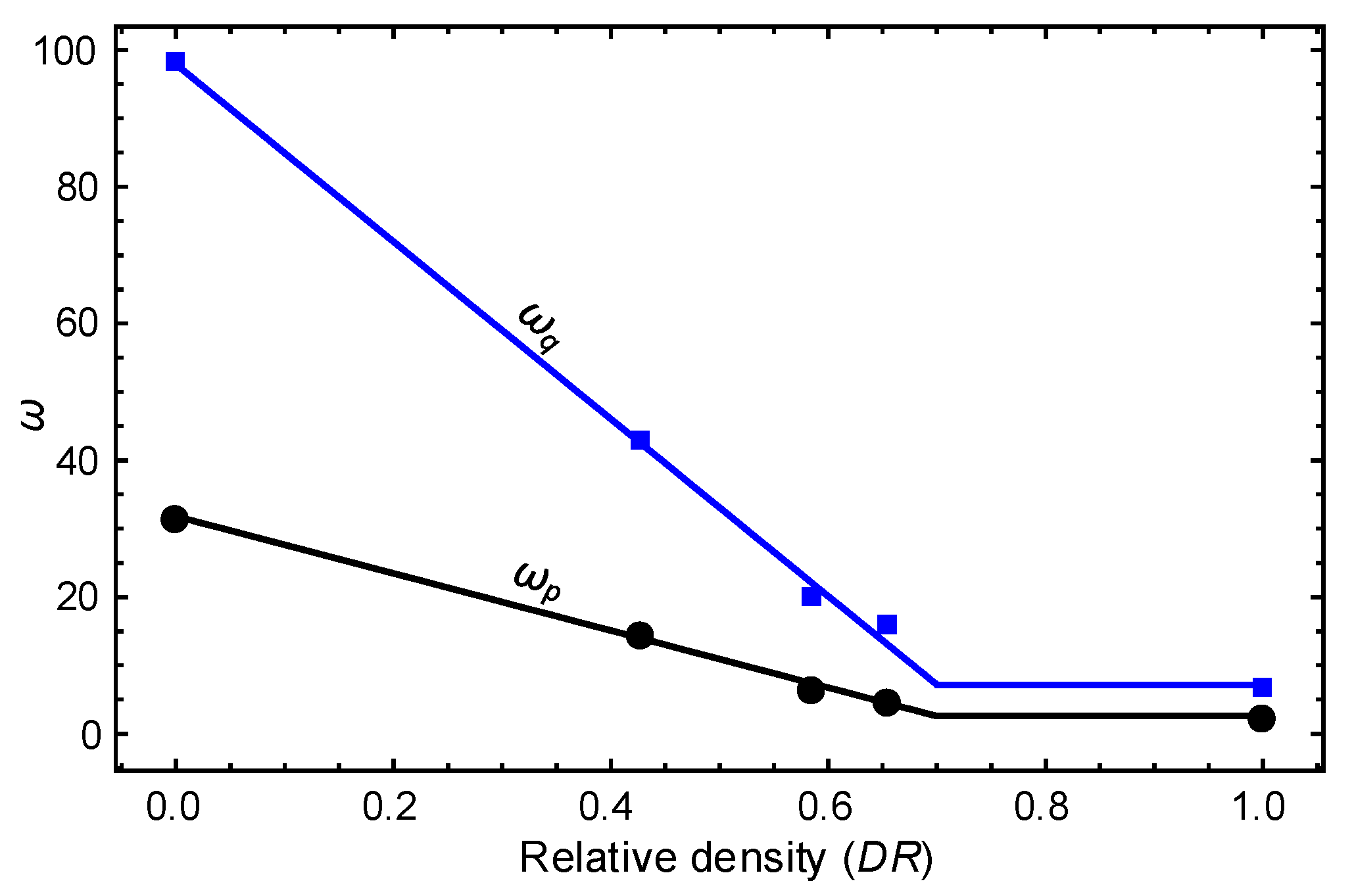
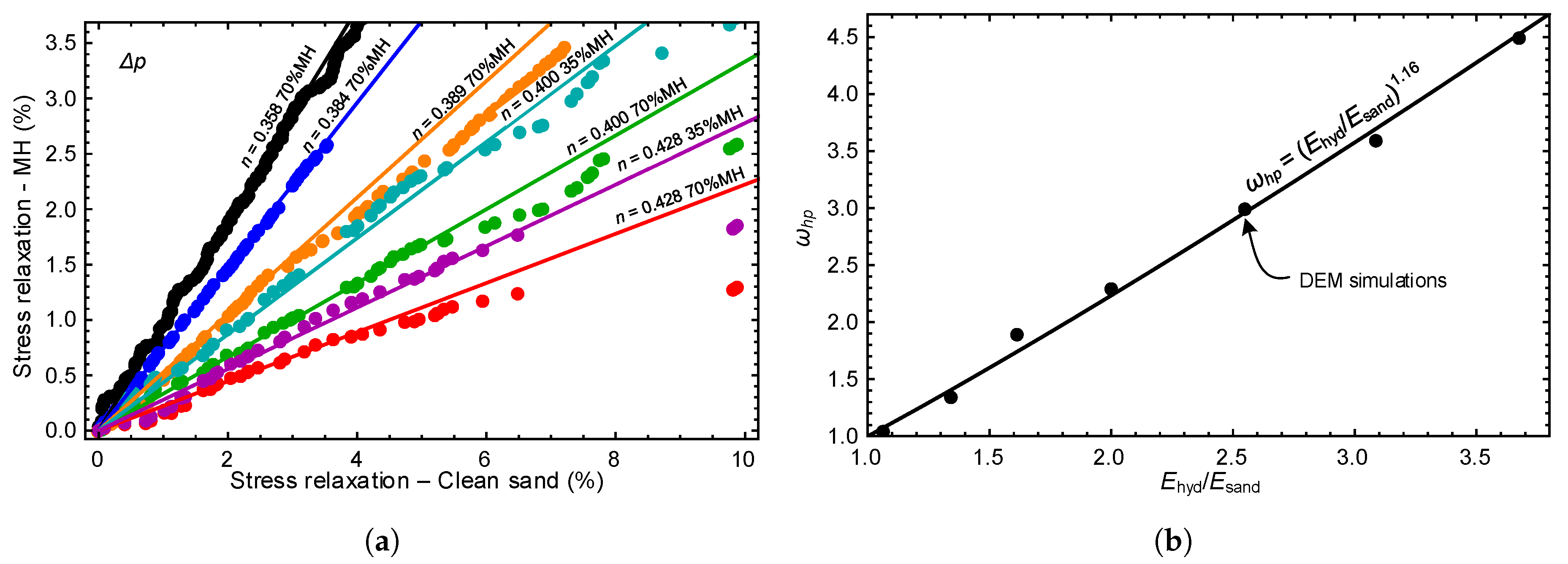
4.2. Hydrate-Bearing Sediments
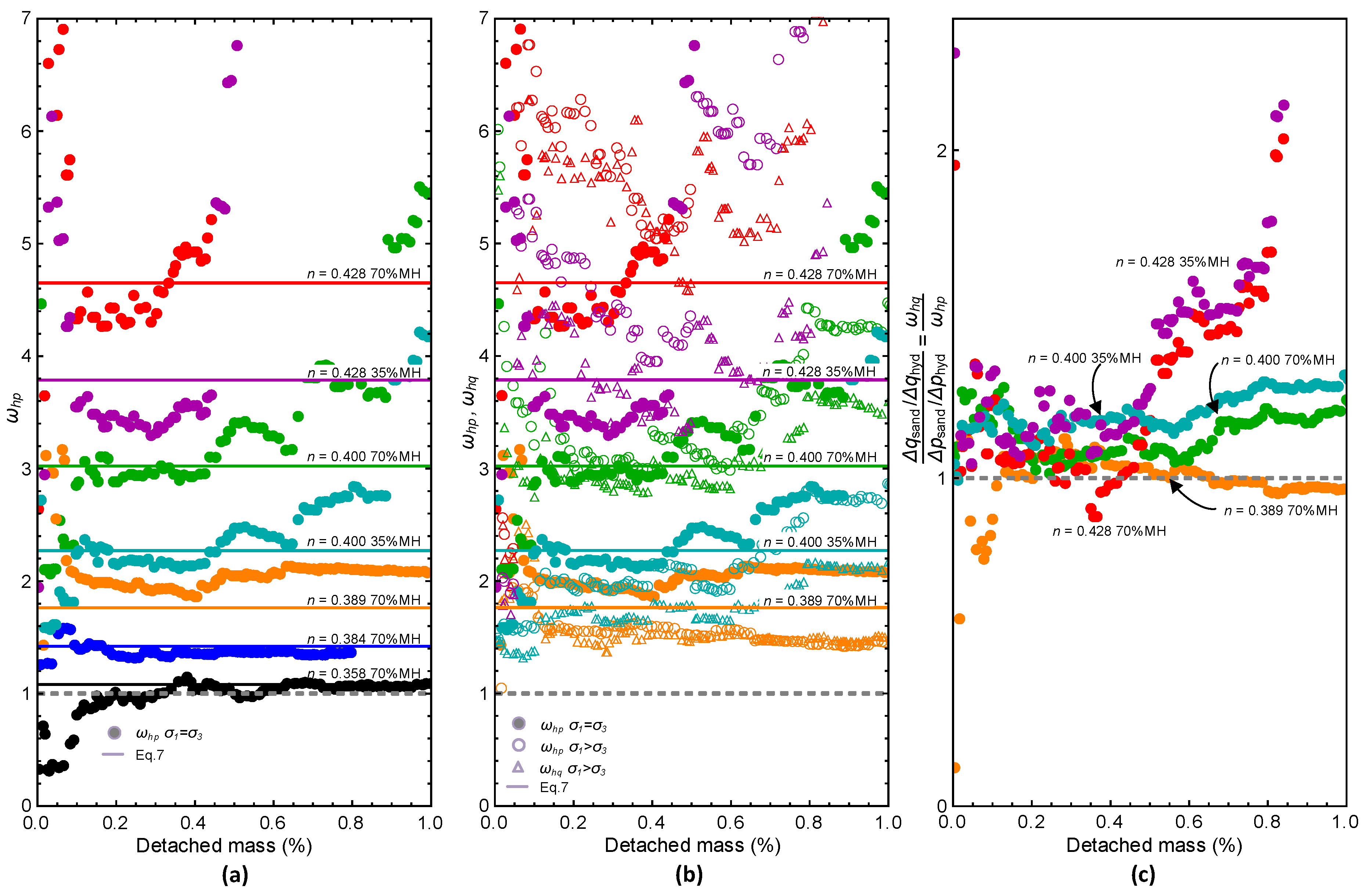
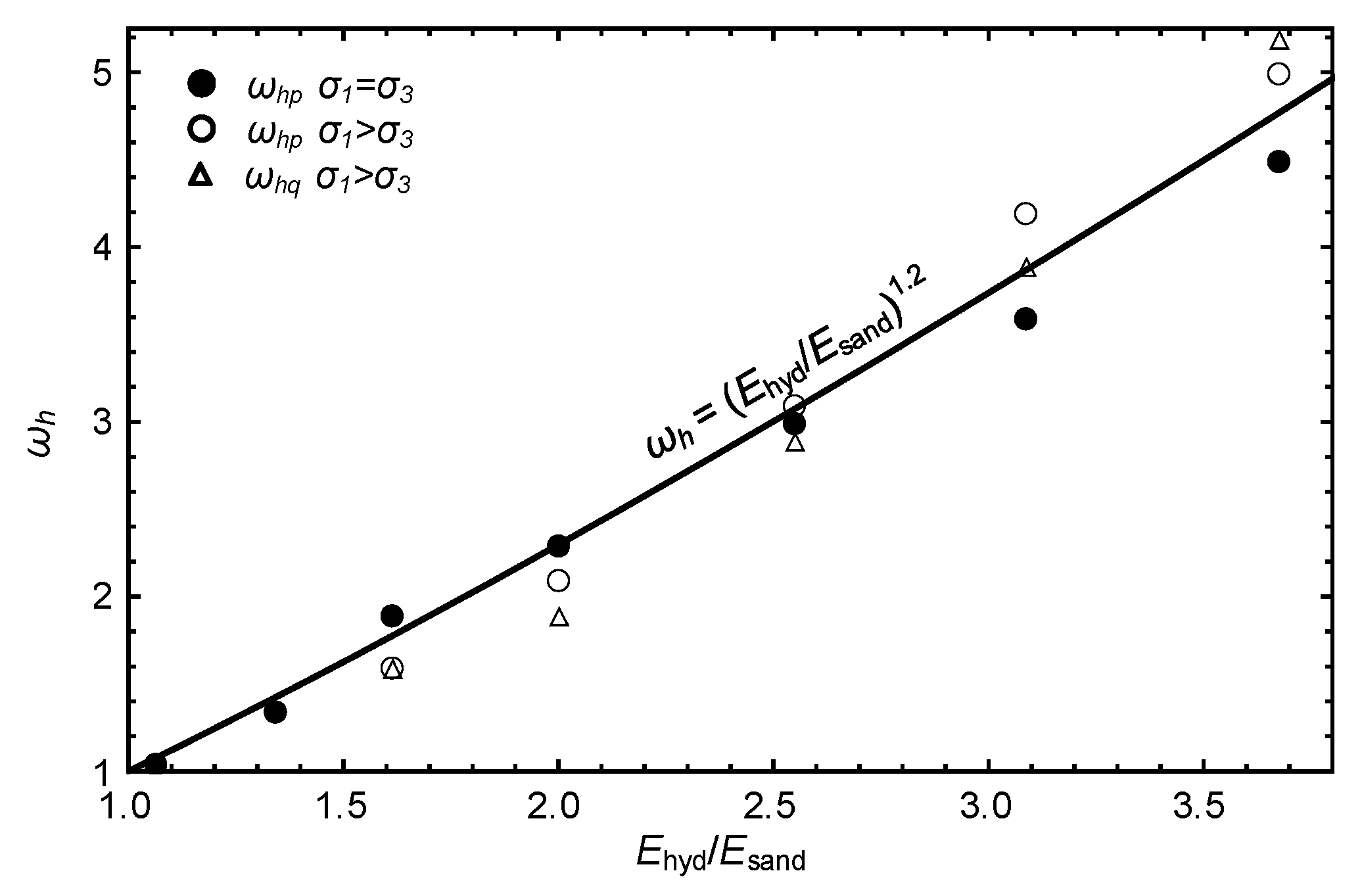
4.2.1. Analysis and Results
4.2.2. Discussion
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Milkov, A.V. Global estimates of hydrate-bound gas in marine sediments: How much is really out there? Earth-Sci. Rev. 2004, 66, 183–197. [Google Scholar] [CrossRef]
- Klauda, J.B.; Sandler, S.I. Global Distribution of Methane Hydrate in Ocean Sediment. Energy Fuels 2005, 19, 459–470. [Google Scholar] [CrossRef]
- Archer, D.; Buffett, B.; Brovkin, V. Ocean methane hydrates as a slow tipping point in the global carbon cycle. Proc. Natl. Acad. Sci. USA 2009, 106, 20596–20601. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Boswell, R.; Collett, T.S. Current perspectives on gas hydrate resources. Energy Environ. Sci. 2011, 4, 1206–1215. [Google Scholar] [CrossRef]
- Johnson, A.H. Global resource potential of gas hydrate–a new calculation. Nat. Gas Oil 2011, 304, 285–4541. [Google Scholar]
- Englezos, P.; Kalogerakis, N.; Dholabhai, P.; Bishnoi, P. Kinetics of formation of methane and ethane gas hydrates. Chem. Eng. Sci. 1987, 42, 2647–2658. [Google Scholar] [CrossRef]
- Kvenvolden, K.A.; Rogers, B.W. Gaia’s breath—Global methane exhalations. Mar. Pet. Geol. 2005, 22, 579–590. [Google Scholar] [CrossRef]
- Waite, W.F.; Stern, L.A.; Kirby, S.H.; Winters, W.J.; Mason, D.H. Simultaneous determination of thermal conductivity, thermal diffusivity and specific heat in sI methane hydrate. Geophys. J. Int. 2007, 169, 767–774. [Google Scholar] [CrossRef] [Green Version]
- Sung, W.M.; Huh, D.G.; Ryu, B.J.; Lee, H.S. Development and application of gas hydrate reservoir simulator based on depressurizing mechanism. Korean J. Chem. Eng. 2000, 17, 344–350. [Google Scholar] [CrossRef]
- Dallimore, S. Overview of science program, JAPEX/JNOC/GSC Mallik 2L-38 gas hydrate research well. In Scientific Results from Japex/JNOC/GSC Mallik 2L-38 Gas Hydrate Research Well; Geological Survey of Canada: Ottawa, ON, Canada, 1999. [Google Scholar]
- Collett, T. Growing interest in gas hydrates. Oilfield Rev. 2000, 12, 43–57. [Google Scholar]
- Uchida, T.; Tsuji, T. Petrophysical Properties of Natural Gas Hydrates-Bearing Sands and Their Sedimentology in the Nankai Trough. Resour. Geol. 2004, 54, 79–87. [Google Scholar] [CrossRef]
- Dallimore, S.R.; Collett, T.S. Scientific Results from the Mallik 2002 Gas Hydrate Production Research Well Program, Mackenzie Delta, Northwest Territories, Canada; Geological Survey of Canada: Ottawa, ON, Canada, 2005. [Google Scholar]
- Hyndman, R.; Spence, G. A seismic study of methane hydrate marine bottom simulating reflectors. J. Geophys. Res. Solid Earth 1992, 97, 6683–6698. [Google Scholar] [CrossRef]
- Nur, A. BSR and methane hydrates: New challenges for geophysics and rock physics. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 6–9 May 1996. [Google Scholar]
- Andreassen, K.; Mienert, J.; Bryn, P.; Singh, S.C. A double gas-hydrate related bottom simulating reflector at the Norwegian continental margin. Ann. N. Y. Acad. Sci. 2000, 912, 126–135. [Google Scholar] [CrossRef]
- Yuan, J.; Edwards, R. The assessment of marine gas hydrates through electrical remote sounding: Hydrate without a BSR? Geophys. Res. Lett. 2000, 27, 2397–2400. [Google Scholar] [CrossRef]
- Archer, D. Methane hydrate stability and anthropogenic climate change. Biogeosciences 2007, 4, 521–544. [Google Scholar] [CrossRef] [Green Version]
- Koh, C.A.; Sloan, E.D. Natural gas hydrates: Recent advances and challenges in energy and environmental applications. AIChE J. 2007, 53, 1636–1643. [Google Scholar] [CrossRef]
- Milkov, A. Worldwide distribution of submarine mud volcanoes and associated gas hydrates. Mar. Geol. 2000, 167, 29–42. [Google Scholar] [CrossRef]
- Grozic, J. Interplay between gas hydrates and submarine slope failure. In Submarine Mass Movements and Their Consequences; Springer: Dordrecht, The Netherlands, 2010; pp. 11–30. [Google Scholar]
- Mascle, J.; Mary, F.; Praeg, D.; Brosolo, L.; Camera, L.; Ceramicola, S.; Dupre, S. Distribution and geological control of mud volcanoes and other fluid/free gas seepage features in the Mediterranean Sea and nearby Gulf of Cadiz. Geo-Mar. Lett. 2014, 34, 89–110. [Google Scholar] [CrossRef]
- Yelisetti, S.; Spence, G.D.; Riedel, M. Role of gas hydrates in slope failure on frontal ridge of northern Cascadia margin. Geophys. J. Int. 2014, 199, 441–458. [Google Scholar] [CrossRef] [Green Version]
- Shimizu, H.; Kumazaki, T.; Kume, T.; Sasaki, S. Elasticity of single-crystal methane hydrate at high pressure. Phys. Rev. B 2002, 65, 212102. [Google Scholar] [CrossRef]
- Masui, A.; Haneda, H.; Ogata, Y.; Aoki, K. Effects of Methane Hydrate Formation On Shear Strength of Synthetic Methane Hydrate Sediments. In International Society of Offshore and Polar Engineers; International Society of Offshore and Polar Engineers: Seoul, Korea, 2005. [Google Scholar]
- Pinkert, S. Rowe’s Stress-Dilatancy Theory for Hydrate-Bearing Sand. Int. J. Geomech. 2016, 17, 06016008. [Google Scholar] [CrossRef]
- Yoneda, J.; Masui, A.; Konno, Y.; Jin, Y.; Kida, M.; Katagiri, J.; Nagao, J.; Tenma, N. Pressure-core-based reservoir characterization for geomechanics: Insights from gas hydrate drilling during 2012–2013 at the eastern Nankai Trough. Mar. Pet. Geol. 2017, 86, 1–16. [Google Scholar] [CrossRef]
- Choi, J.H.; Dai, S.; Lin, J.S.; Seol, Y. Multi-Stage Triaxial Tests on Laboratory-Formed Methane Hydrate-Bearing Sediments. J. Geophys. Res. Solid Earth 2018. [Google Scholar] [CrossRef]
- Soga, K.; Lee, S.; Ng, M.; Klar, A. Characterisation and engineering properties of methane hydrate soils. Charact. Eng. Prop. Nat. Soils 2006, 4, 2591–2642. [Google Scholar]
- Jung, J.W.; Santamarina, J.C.; Soga, K. Stress-strain response of hydrate-bearing sands: Numerical study using discrete element method simulations. J. Geophys. Res. (Solid Earth) 2012, 117, B04202. [Google Scholar] [CrossRef]
- Uchida, S.; Soga, K.; Yamamoto, K. Critical state soil constitutive model for methane hydrate soil. J. Geophys. Res. Solid Earth 2012, 117. [Google Scholar] [CrossRef]
- Jiang, M.; Zhu, F.; Liu, F.; Utili, S. A bond contact model for methane hydrate-bearing sediments with interparticle cementation. Int. J. Numer. Anal. Methods Geomech. 2014, 38, 1823–1854. [Google Scholar] [CrossRef]
- Lin, J.S.; Seol, Y.; Choi, J.H. An SMP critical state model for methane hydrate-bearing sands. Int. J. Numer. Anal. Methods Geomech. 2015, 39, 969–987. [Google Scholar] [CrossRef]
- Sánchez, M.; Gai, X.; Santamarina, J.C. A constitutive mechanical model for gas hydrate bearing sediments incorporating inelastic mechanisms. Comput. Geotech. 2017, 84, 28–46. [Google Scholar] [CrossRef] [Green Version]
- Cohen, E.; Klar, A. A cohesionless micromechanical model for gas hydrate-bearing sediments. Granul. Matter 2019, 21, 36. [Google Scholar] [CrossRef] [Green Version]
- Moridis, G.J. Numerical studies of gas production from methane hydrates. In Proceedings of the SPE Gas Technology Symposium, Society of Petroleum Engineers, Calgary, AL, USA, 30 April–2 May 2002. [Google Scholar]
- Klar, A.; Soga, K. Coupled deformation-flow analysis for methane hydrate production by depressurized wells. In Proceedings of the 3rd Biot Conference on Poromechanics, Oklahoma City, OK, USA, 25–27 May 2005. [Google Scholar]
- Rutqvist, J.; Moridis, G.J. Coupled hydrologic, thermal and geomechanical analysis of well bore stability in hydrate-bearing sediments. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2008. [Google Scholar]
- Kurihara, M.; Sato, A.; Funatsu, K.; Ouchi, H.; Yamamoto, K.; Numasawa, M.; Ebinuma, T.; Narita, H.; Masuda, Y.; Dallimore, S.R.; et al. Analysis of production data for 2007/2008 Mallik gas hydrate production tests in Canada. In Proceedings of the International Oil and Gas Conference and Exhibition in China, Society of Petroleum Engineers, Beijing, China, 8–10 June 2010. [Google Scholar]
- Klar, A.; Soga, K.; Ng, M. Coupled deformation–flow analysis for methane hydrate extraction. Geotechnique 2010, 60, 765–776. [Google Scholar] [CrossRef]
- Janicki, G.; Schlüter, S.; Hennig, T.; Lyko, H.; Deerberg, G. Simulation of methane recovery from gas hydrates combined with storing carbon dioxide as hydrates. J. Geol. Res. 2011, 2011, 462156. [Google Scholar] [CrossRef]
- Klar, A.; Uchida, S.; Soga, K.; Yamamoto, K. Explicitly Coupled Thermal Flow Mechanical Formulation for Gas-Hydrate Sediments. SPE J. 2013, 18, 196–206. [Google Scholar] [CrossRef]
- Gupta, S.; Helmig, R.; Wohlmuth, B. Non-isothermal, multi-phase, multi-component flows through deformable methane hydrate reservoirs. Comput. Geosci. 2015, 19, 1063–1088. [Google Scholar] [CrossRef] [Green Version]
- Uchida, S.; Klar, A.; Yamamoto, K. Sand production model in gas hydrate-bearing sediments. Int. J. Rock Mech. Min. Sci. 2016, 86, 303–316. [Google Scholar] [CrossRef]
- Qorbani, K.; Kvamme, B.; Kuznetsova, T. Using a reactive transport simulator to simulate CH4 production from bear island basin in the Barents Sea utilizing the depressurization method. Energies 2017, 10, 187. [Google Scholar] [CrossRef]
- Sánchez, M.; Santamarina, C.; Teymouri, M.; Gai, X. Coupled Numerical Modeling of Gas Hydrate-Bearing Sediments: From Laboratory to Field-Scale Analyses. J. Geophys. Res. Solid Earth 2018, 123, 10–326. [Google Scholar] [CrossRef]
- Yan, C.; Li, Y.; Cheng, Y.; Wang, W.; Song, B.; Deng, F.; Feng, Y. Sand production evaluation during gas production from natural gas hydrates. J. Nat. Gas Sci. Eng. 2018, 57, 77–88. [Google Scholar] [CrossRef]
- Hunter, R.B.; Collett, T.S.; Boswell, R.; Anderson, B.J.; Digert, S.A.; Pospisil, G.; Baker, R.; Weeks, M. Mount Elbert Gas Hydrate Stratigraphic Test Well, Alaska North Slope: Overview of scientific and technical program. Mar. Pet. Geol. 2011, 28, 295–310. [Google Scholar] [CrossRef]
- Dallimore, S.R.; Wright, J.F.; Nixon, F.M.; Kurihara, M.; Yamamoto, K.; Fujii, T.; Fujii, K.; Numasawa, M.; Yasuda, M.; Imasato, Y.; et al. Geologic and Porous Media Factors Affecting the 2007 Production Response Characteristics of the Jogmec/Nrcan/Aurora Mallik Gas Hydrate Production Research Well. In Proceedings of the 6th International Conference on Gas Hydrates, Vancouver, BC, Canada, 6–10 July 2008. [Google Scholar]
- Yamamoto, K.; Terao, Y.; Fujii, T.; Ikawa, T.; Seki, M.; Matsuzawa, M.; Kanno, T. Operational overview of the first offshore production test of methane hydrates in the Eastern Nankai Trough. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 5–8 May 2014. [Google Scholar]
- Hancock, S.; Collett, T.; Dallimore, S.; Satoh, T.; Inoue, T.; Huenges, E.; Henninges, J.; Weatherill, B. Overview of thermal-stimulation production-test results for the JAPEX/JNOC/GSC et al. Mallik 5L-38 gas hydrate production research well. Bull.-Geol. Surv. Can. 2005, 585, 135. [Google Scholar]
- Schoderbek, D.; Farrell, H.; Howard, J.; Raterman, K.; Silpngarmlert, S.; Martin, K.; Smith, B.; Klein, P. ConocoPhillips Gas Hydrate Production Test; Technical Report; National Energy Technology Laboratory: Pittsburgh, PA, USA; Morgantown, WV, USA, 2013. [Google Scholar]
- Moridis, G.J.; Reagan, M.T. Strategies for Gas Production from Oceanic Class 3 Hydrate Accumulations; Technical Report; Ernest Orlando Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2007. [Google Scholar]
- Klar, A.; Deerberg, G.; Janicki, G.; Schicks, J.; Riedel, M.; Fietzek, P.; Mosch, T.; Tinivella, U.; De La Fuente Ruiz, M.; Gatt, P.; et al. Marine Gas Hydrate Technology: State of the Art and Future Possibilities for Europe. Final Report of WG2 of COST Action ES 1405. 2019. Available online: http://oceanrep.geomar.de/46367/ (accessed on 28 May 2019).
- Uchida, S.; Klar, A.; Charas, Z.; Yamamoto, K. Thermo-Hydro-Mechanical Sand Production Model in Hydrate-Bearing Sediments. In Proceedings of the EAGE International Workshop on Geomechanics and Energy—The Ground as Energy Source and Storage, Lausanne, Switzerland, 26–28 November 2013; pp. 1–11. [Google Scholar]
- Lee, J.; Ahn, T.; Lee, J.; Kim, S. Laboratory test to evaluate the performance of sand control screens during hydrate dissociation process by depressurization. In Proceedings of the ISOPE Ocean Mining Symposium, Szczecin, Poland, 22–26 September 2013; pp. 150–153. [Google Scholar]
- Cohen, E.; Klar, A.; Uchida, S.; Yamamoto, K. Micromechanical investigation of sand production in gas hydrate-bearing sediments. In Proceedings of the 9th International Conference on Gas Hydrates, Denver, CO, USA, 25–30 June 2017; p. 1652. [Google Scholar]
- Uchida, S.; Lin, J.S.; Myshakin, E.M.; Seol, Y.; Boswell, R. Numerical simulations of sand migration during gas production in hydrate-bearing sands interbedded with thin mud layers at site NGHP-02-16. Mar. Pet. Geol. 2018. [Google Scholar] [CrossRef]
- Itasca. PFC3D Ver. 4.0- User Manual; Itasca: Minneapolis, MN, USA, 2008. [Google Scholar]
- Hyodo, M.; Yoneda, J.; Yoshimoto, N.; Nakata, Y. Mechanical and dissociation properties of methane hydrate-bearing sand in deep seabed. Soils Found. 2013, 53, 299–314. [Google Scholar] [CrossRef] [Green Version]
- Brugada, J.; Cheng, Y.P.; Soga, K.; Santamarina, J.C. Discrete element modelling of geomechanical behaviour of methane hydrate soils with pore-filling hydrate distribution. Granul. Matter 2010, 12, 517–525. [Google Scholar] [CrossRef]
- Shen, Z.; Jiang, M. DEM simulation of bonded granular material. Part II: Extension to grain-coating type methane hydrate bearing sand. Comput. Geotech. 2016, 75, 225–243. [Google Scholar] [CrossRef]
- Yu, Y.; Cheng, Y.P.; Xu, X.; Soga, K. Discrete element modelling of methane hydrate soil sediments using elongated soil particles. Comput. Geotech. 2016. [Google Scholar] [CrossRef]
- Chaouachi, M.; Falenty, A.; Sell, K.; Enzmann, F.; Kersten, M.; Haberthür, D.; Kuhs, W.F. Microstructural evolution of gas hydrates in sedimentary matrices observed with synchrotron X-ray computed tomographic microscopy. Geochem. Geophys. Geosyst. 2015, 16, 1711–1722. [Google Scholar] [CrossRef] [Green Version]
- Cundall, P.A. Computer Simulations of Dense Sphere Assemblies. Stud. Appl. Mech. 1988, 20, 113–123. [Google Scholar] [CrossRef]
- Ergun, S. Fluid flow through packed columns. Chem. Eng. Prog. 1952, 48, 89–94. [Google Scholar]
| Property | Sand | Methane-Hydrate |
|---|---|---|
| Particle diameter (mm) | 0.25–0.15 | |
| Inter-particle friction (-) | ||
| Density (kg/m) | 2600 | 900 |
| Shear modulus (Pa) | ||
| Poisson’s ratio (-) |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cohen, E.; Klar, A.; Yamamoto, K. Micromechanical Investigation of Stress Relaxation in Gas Hydrate-Bearing Sediments Due to Sand Production. Energies 2019, 12, 2131. https://doi.org/10.3390/en12112131
Cohen E, Klar A, Yamamoto K. Micromechanical Investigation of Stress Relaxation in Gas Hydrate-Bearing Sediments Due to Sand Production. Energies. 2019; 12(11):2131. https://doi.org/10.3390/en12112131
Chicago/Turabian StyleCohen, Eitan, Assaf Klar, and Koji Yamamoto. 2019. "Micromechanical Investigation of Stress Relaxation in Gas Hydrate-Bearing Sediments Due to Sand Production" Energies 12, no. 11: 2131. https://doi.org/10.3390/en12112131
APA StyleCohen, E., Klar, A., & Yamamoto, K. (2019). Micromechanical Investigation of Stress Relaxation in Gas Hydrate-Bearing Sediments Due to Sand Production. Energies, 12(11), 2131. https://doi.org/10.3390/en12112131





