3D Evolutionary Reconstruction of Scalar Fields in the Gas-Phase
Abstract
1. Introduction
2. The Evolutionary Reconstruction Scheme
| Algorithm 1 Evolutionary reconstruction technique. | |
| 1: Start | |
| 2: | ▹ Read GA and image settings |
| 3: | ▹ Read reference images |
| 4: | ▹ Create stochastic mask |
| 5: | ▹ Initialize population |
| 6: | ▹ Evaluate Fitness |
| 7: | ▹ Calculate ranks |
| 8: | ▹ Get best chromosome |
| 9: while and do | |
| 10: | ▹ Perform evolution step |
| 11: | ▹ Evaluate fitness |
| 12: | ▹ Calculate ranks |
| 13: | ▹ Get best chromosome |
| 14: if and then | |
| 15: | ▹ Re-create stochastic mask |
| 16: end if | |
| 17: | |
| 18: end while | |
| 19: End | |
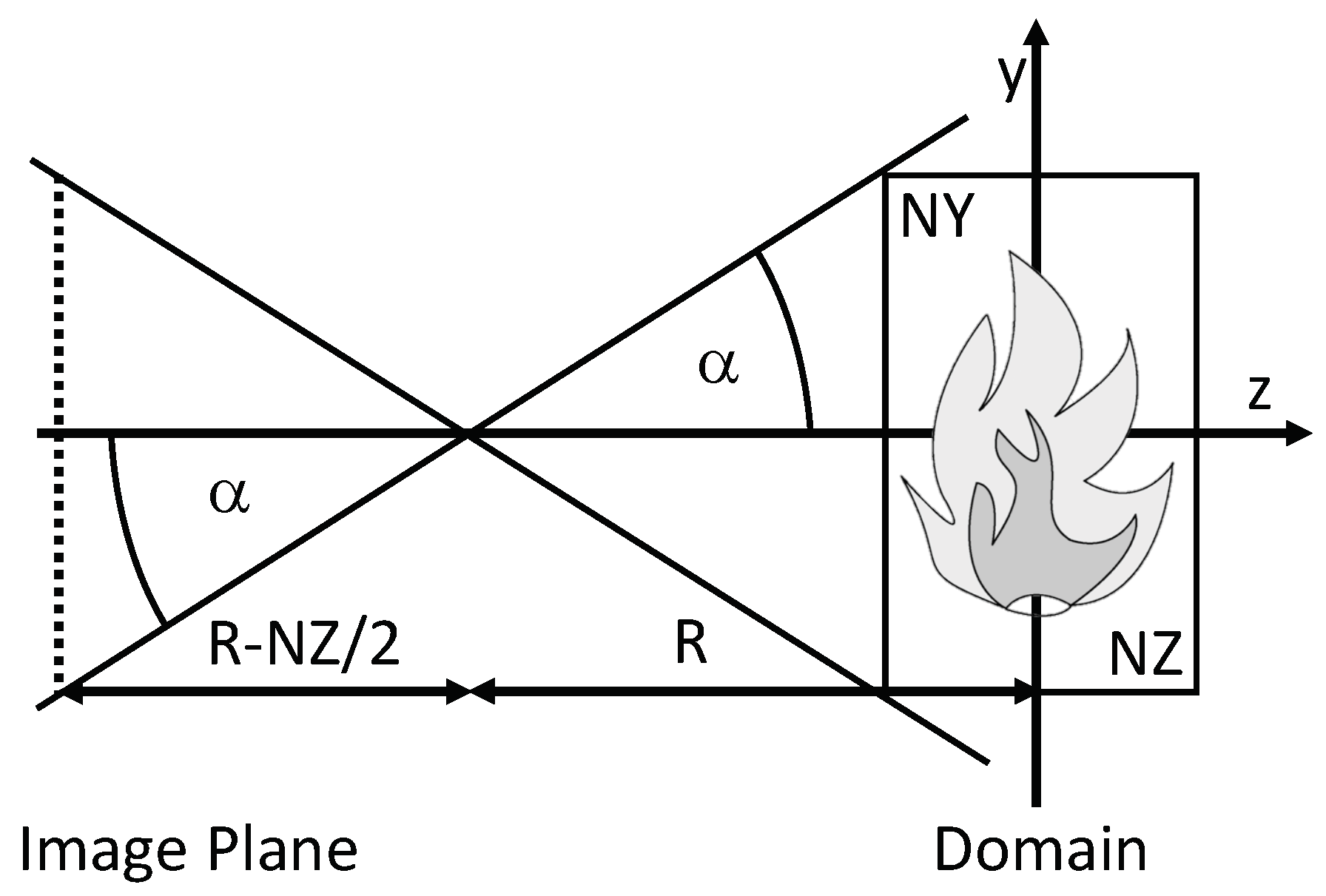
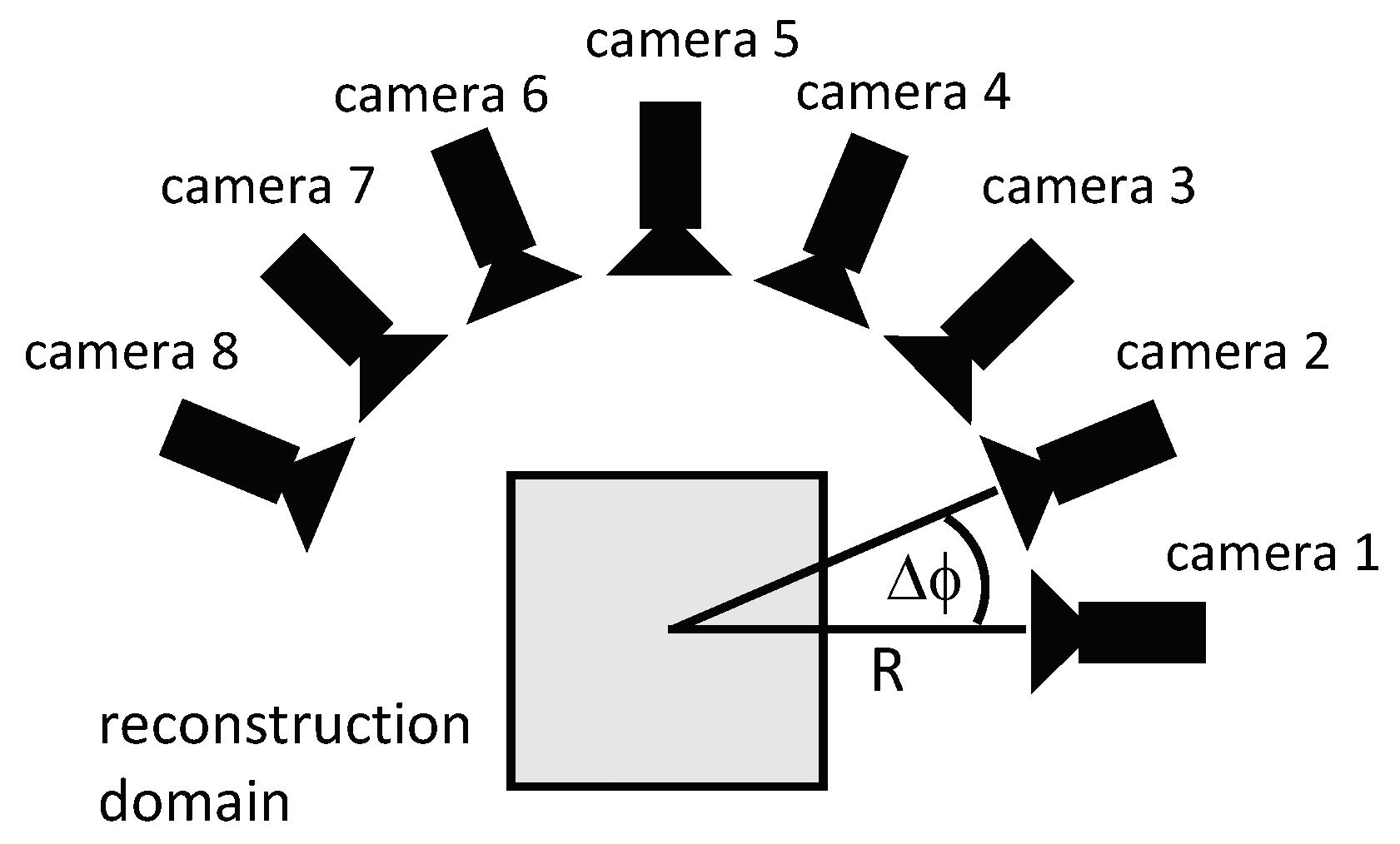
2.1. Ray-Tracing
2.2. The Genetic Algorithm
| Algorithm 2 Evolution Step | |
| 1: function Evolution_Step(POP, MSK) | ▹ Input is the population and mask |
| 2: for do | |
| 3: | ▹ Select two chromosomes |
| 4: | ▹ Merge to offspring |
| 5: | |
| 6: if then | |
| 7: | ▹ Apply mutation operator |
| 8: end if | |
| 9: if then | |
| 10: | ▹ Apply annihilation operator |
| 11: end if | |
| 12: if then | |
| 13: | ▹ Apply filter operator |
| 14: end if | |
| 15: end for | |
| 16: | ▹ Copy to new population |
| 17: return POP | |
| 18: end function | |
2.3. The Stochastic Mask
| Algorithm 3 First stage Metropolis sampling step. | |
| 1: function MetropolisStep1() | ▹ input is a start location |
| 2: | ▹ |
| 3: | ▹ |
| 4: for do | |
| 5: | |
| 6: | |
| 7: if then | |
| 8: if then | |
| 9: return | |
| 10: end if | |
| 11: else | |
| 12: return | |
| 13: end if | |
| 14: end for | |
| 15: end function | |
| Algorithm 4 Second stage Metropolis sampling step. | |
| 1: function MetropolisStep2() | ▹ input is a start location |
| 2: | ▹ |
| 3: | ▹ |
| 4: if then | |
| 5: return | |
| 6: else | |
| 7: return | |
| 8: end if | |
| 9: end function | |
3. Phantom Study on Numerical Data
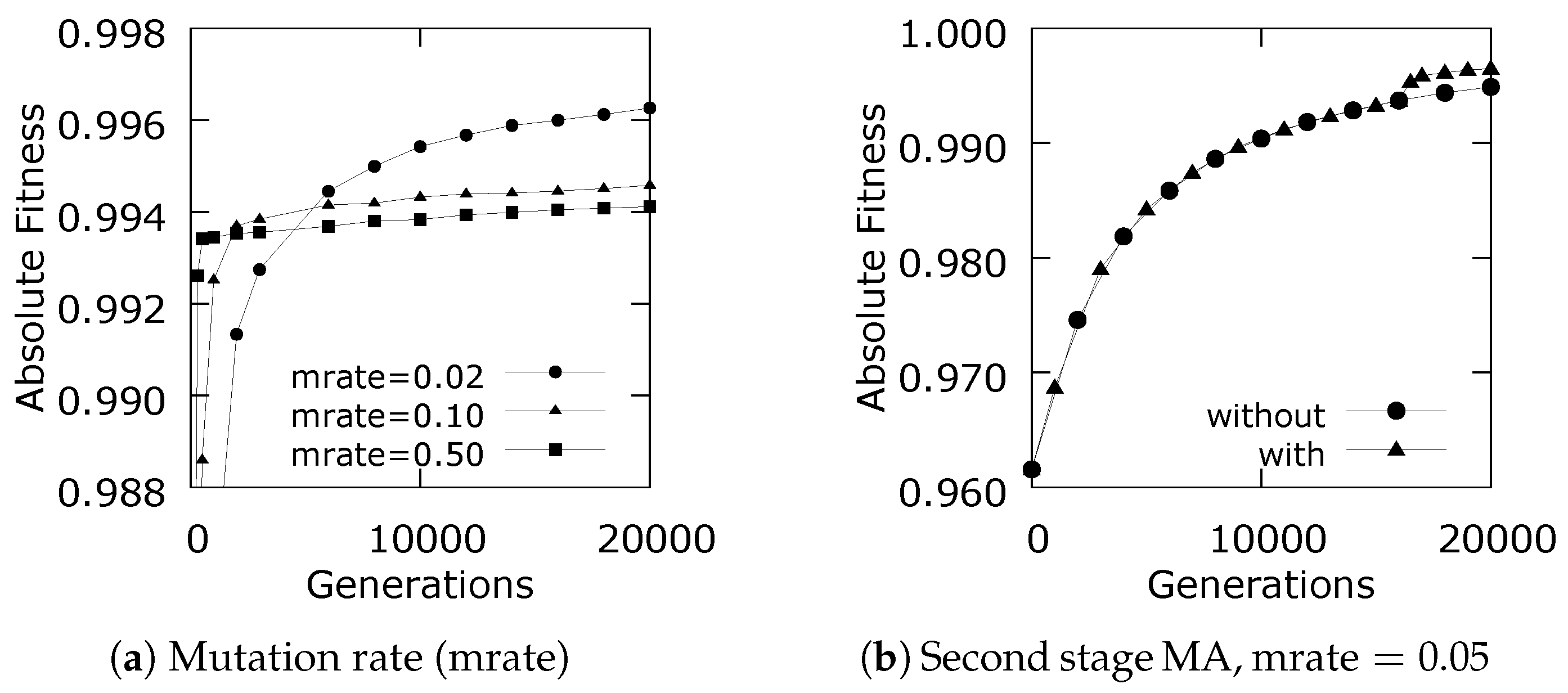
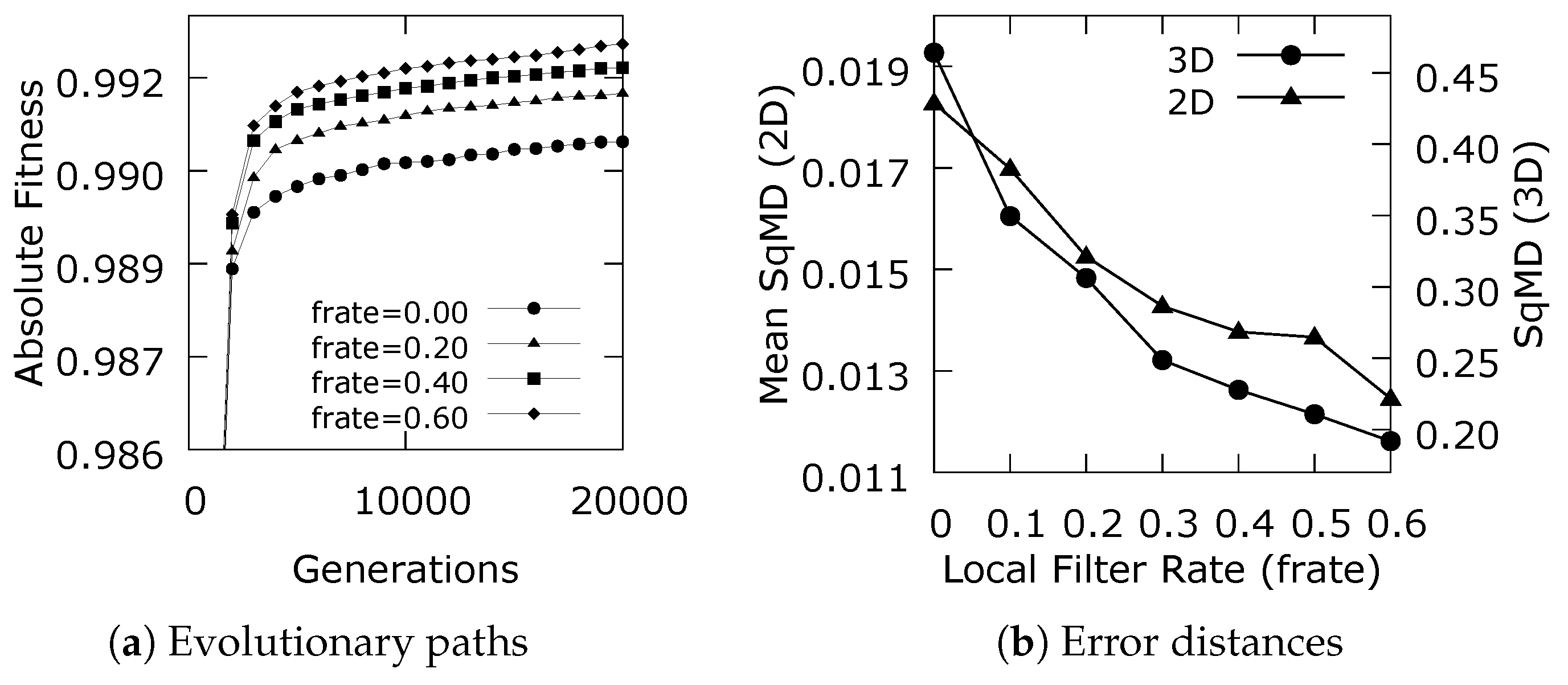
3.1. Parameter Study on Canonical Phantom Data
3.2. Phantom Study on Three Generic Flame Types
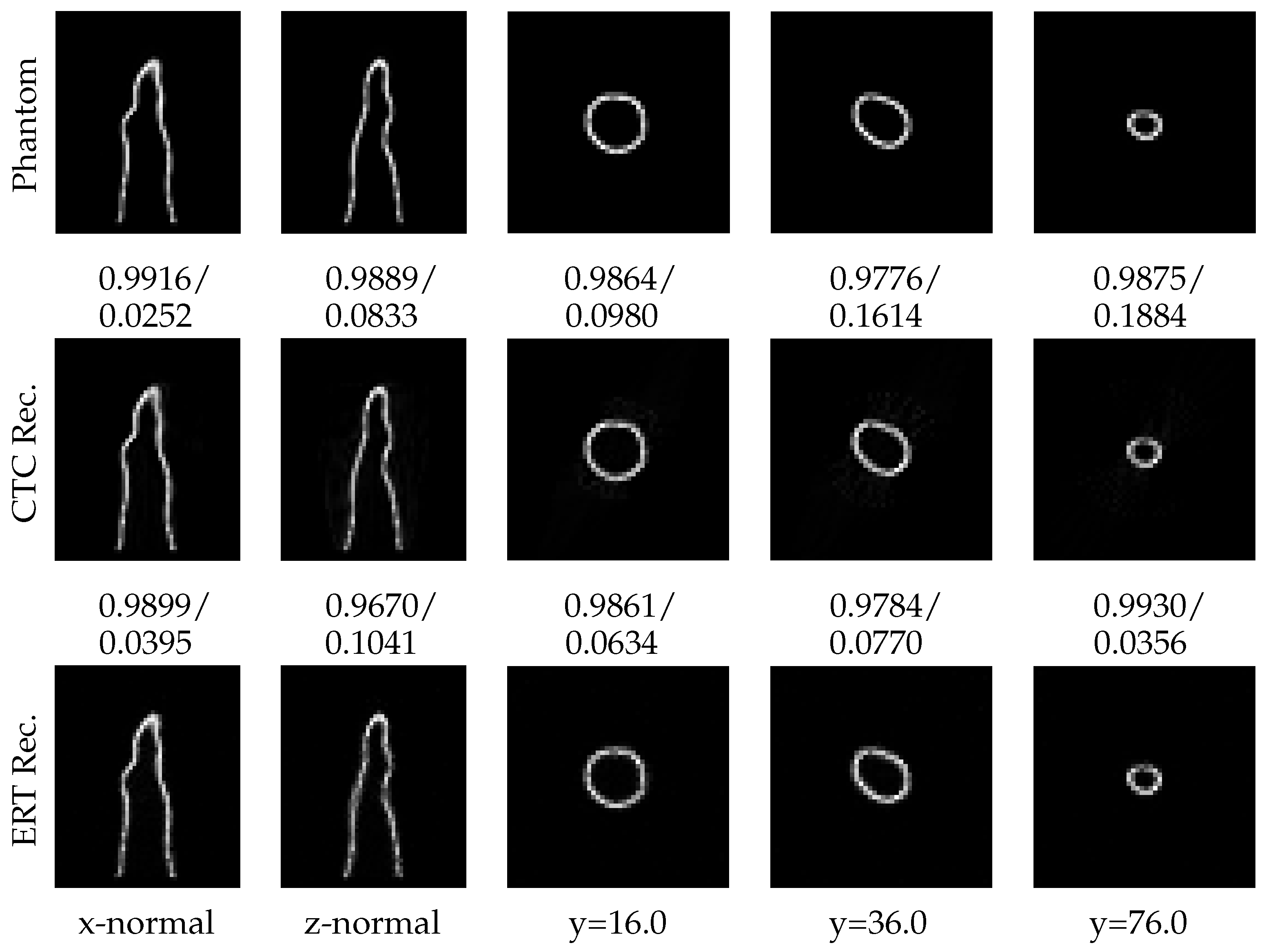
3.3. The Bunsen Flame Phantom
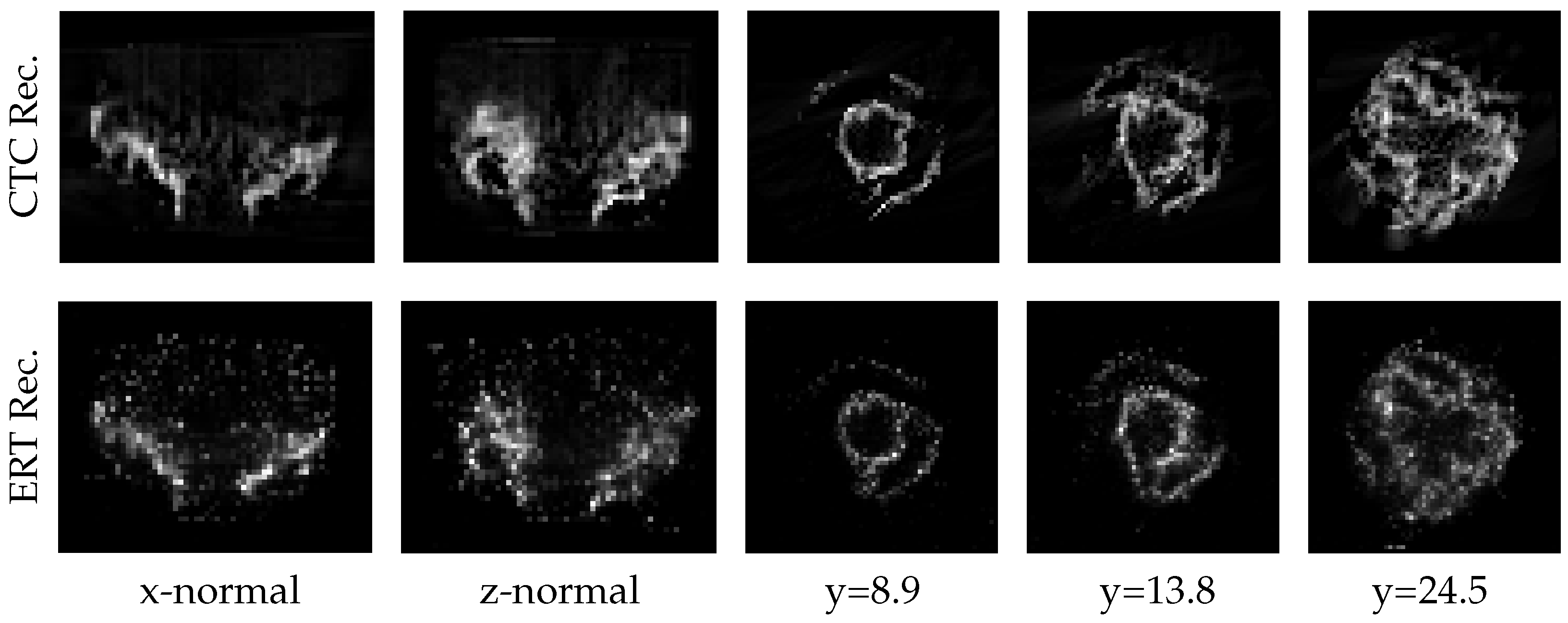
3.4. The Swirl Flame Phantom
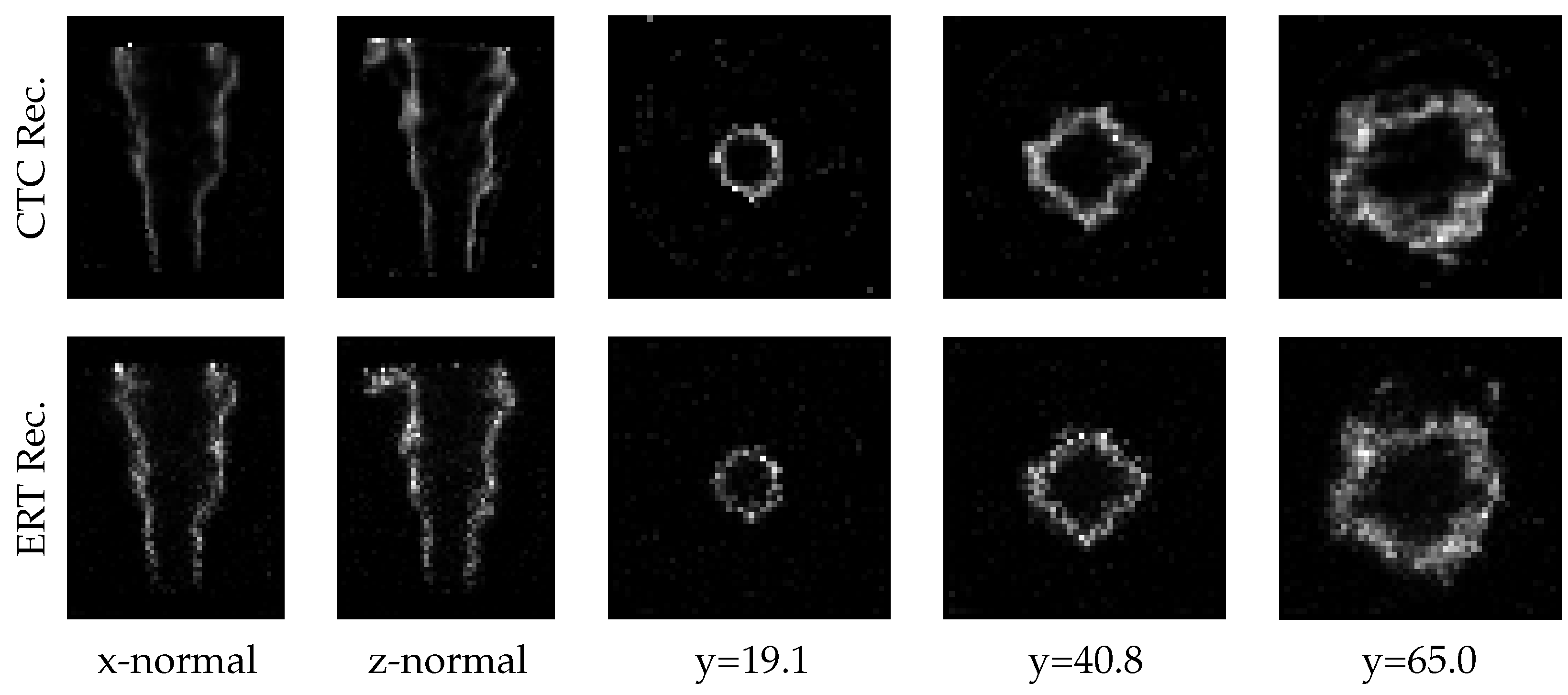
3.5. The Cambridge–Sandia Stratified Flame Phantom
4. Applications to Experimental Data
4.1. The Bunsen Flame
4.2. The Swirl Flame
4.3. The Cambridge-Sandia Stratified Flame
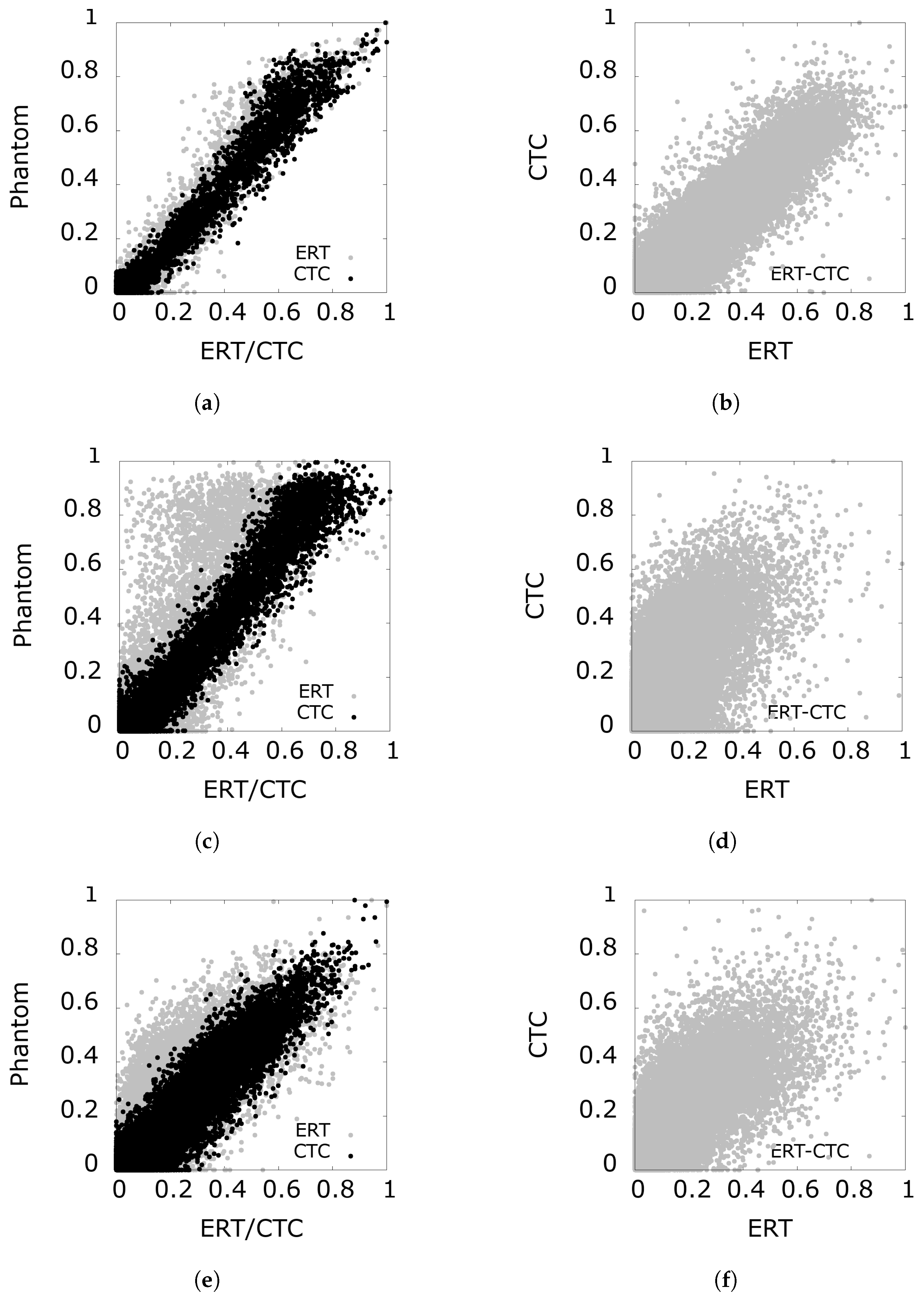
5. Quantitative Comparisons—Phantoms and Experiments
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Sivathanu, Y.; Lim, J.; Joseph, R. Statistical absorption tomography for turbulent flows. J. Quant. Spectrosc. Radiat. Transf. 2001, 68, 611–623. [Google Scholar] [CrossRef]
- Liu, C.; Cao, Z.; Lin, Y.; Xu, L.; McCann, H. Online cross-sectional monitoring of a swirling flame using TDLAS tomography. IEEE Trans. Instrum. Meas. 2018, 67, 1338–1348. [Google Scholar] [CrossRef]
- Liu, C.; Xu, L. Laser absorption spectroscopy for combustion diagnosis in reactive flows: A review. Appl. Spectrosc. Rev. 2019, 54, 1–44. [Google Scholar] [CrossRef]
- Agrawal, A.K.; Butuk, N.K.; Gollahalli, S.R.; Griffin, D. Three-dimensional rainbow schlieren tomography of a temperature field in gas flows. Appl. Opt. 1998, 37, 479–485. [Google Scholar] [CrossRef]
- Grauer, S.; Unterberger, A.; Rittler, A.; Daun, K.J.; Kempf, A.; Mohri, K. Instantaneous 3D flame imaging by background-oriented schlieren tomography. Combust. Flame 2018, 196, 284–299. [Google Scholar] [CrossRef]
- Hertz, H.M.; Faris, G.W. Emission tomography of flame radicals. Opt. Lett. 1988, 13, 351–353. [Google Scholar] [CrossRef] [PubMed]
- Ishino, Y.; Ohiwa, N. Three-Dimensional Computerized Tomographic reconstruction of instantaneous distribution of chemiluminescence of a turbulent premixed flame. JSME Int. J. Ser. Fluids Therm. Eng. 2005, 48, 34–40. [Google Scholar] [CrossRef][Green Version]
- Floyd, J.; Kempf, A.M. Computed Tomography of Chemiluminescence (CTC): High resolution and instantaneous 3D measurements of a matrix burner. Proc. Combust. Inst. 2011, 33, 751–758. [Google Scholar] [CrossRef]
- Floyd, J.; Geipel, P.; Kempf, A.M. Computed Tomography of Chemiluminescence (CTC): 3D time resolved measurements of a turbulent opposed jet flame. Combust. Flame 2011, 158, 376–391. [Google Scholar] [CrossRef]
- Anikin, N.B.; Suntz, R.; Bockhorn, H. Tomographic reconstruction of 2D-OH*-chemiluminescence distributions in turbulent diffusion flames. Appl. Phys. B 2012, 107, 591–602. [Google Scholar] [CrossRef]
- Hossain, M.; Lu, G.; Yan, Y. Optical fiber imaging based tomographic reconstruction of burner flames. IEEE Trans. Instrum. Meas. 2012, 61, 1417–1425. [Google Scholar] [CrossRef]
- Worth, N.A.; Dawson, J.R. Tomographic reconstruction of OH* chemiluminescence in two interacting turbulent flames. Meas. Sci. Technol. 2012, 24, 024013. [Google Scholar] [CrossRef]
- Hossain, M.M.; Lu, G.; Sun, D.; Yan, Y. Three-dimensional reconstruction of flame temperature and emissivity distribution using optical tomographic and two-colour pyrometric techniques. Meas. Sci. Technol. 2013, 24, 074010. [Google Scholar] [CrossRef]
- Li, X.; Ma, L. Capabilities and limitations of 3D flame measurements based on computed tomography of chemiluminescence. Combust. Flame 2015, 162, 642–651. [Google Scholar] [CrossRef]
- Wang, J.; Song, Y.; Li, Z.H.; Kempf, A.; He, A.Z. Multi-directional 3D flame chemiluminescence tomography based on lens imaging. Opt. Lett. 2015, 40, 1231–1234. [Google Scholar] [CrossRef] [PubMed]
- Mohri, K.; Görs, S.; Schöler, J.; Rittler, A.; Dreier, T.; Schulz, C.; Kempf, A. Instantaneous 3D imaging of highly turbulent flames using computed tomography of chemiluminescence. Appl. Opt. 2017, 56, 7385–7395. [Google Scholar] [CrossRef]
- Unterberger, A.; Röder, M.; Giese, A.; Al-Halbouni, A.; Kempf, A.; Mohri, K. 3D instantaneous reconstruction of turbulent industrial flames using Computed Tomography of Chemiluminescence (CTC). J. Combust. 2018, 2018, 5373829. [Google Scholar] [CrossRef]
- Schröder, A.; Geisler, R.; Elsinga, G.E.; Scarano, F.; Dierksheide, U. Investigation of a turbulent spot and a tripped turbulent boundary layer flow using time-resolved tomographic PIV. Exp. Fluids 2008, 44, 305–316. [Google Scholar] [CrossRef]
- Weinkauff, J.; Michaelis, D.; Dreizler, A.; Böhm, B. Tomographic PIV measurements in a turbulent lifted jet flame. Exp. Fluids 2013, 54, 1624. [Google Scholar] [CrossRef]
- Herman, G.T. Fundamentals of Computerized Tomography: Image Reconstruction from Projections, 2nd ed.; Springer: New York, NY, USA, 2009. [Google Scholar]
- Gordon, R. A tutorial on art (algebraic reconstruction techniques). IEEE Trans. Nucl. Sci. 1974, 21, 78–93. [Google Scholar] [CrossRef]
- Hansen, P.C. Rank-Deficient and Discrete Ill-Posed Problems: Numerical Aspects of Linear Inversion; SIAM: Philadelphia, PA, USA, 1998. [Google Scholar]
- Cai, W.; Kaminski, C.F. Tomographic absorption spectroscopy for the study of gas dynamics and reactive flows. Prog. Energy Combust. Sci. 2017, 59, 1–31. [Google Scholar] [CrossRef]
- Daun, K.J.; Grauer, S.J.; Hadwin, P.J. Chemical species tomography of turbulent flows: Discrete ill-posed and rank deficient problems and the use of prior information. J. Quant. Spectrosc. Radiat. Transf. 2016, 172, 58–74. [Google Scholar] [CrossRef]
- Grauer, S.J.; Hadwin, P.J.; Daun, K.J. Bayesian approach to the design of chemical species tomography experiments. Appl. Opt. 2016, 55, 5772–5782. [Google Scholar] [CrossRef]
- Kihm, K.D.; Okamoto, K.; Tsuru, D.; Ko, H.S. Adoption of a genetic algorithm (GA) for tomographic reconstruction of line-of-sight optical images. Exp. Fluids 1996, 22, 137–143. [Google Scholar] [CrossRef]
- Kihm, K.D.; Lyons, D.P. Optical tomography using a genetic algorithm. Opt. Lett. 1996, 21, 1327–1329. [Google Scholar] [CrossRef] [PubMed]
- Wu, C.; Cheng, Y.; Ding, Y.; Wei, F.; Jin, Y. A novel X-ray computed tomography method for fast measurement of multiphase flow. Chem. Eng. Sci. 2007, 62, 4325–4335. [Google Scholar] [CrossRef]
- Yang, X.; van Ommen, J.R.; Mudde, R.F. Comparison of genetic algorithm and algebraic reconstruction for X-ray tomography in bubbling fluidized beds. Powder Technol. 2014, 253, 626–637. [Google Scholar] [CrossRef]
- Yang, X.; Van Ommen, J.R.; Schoormans, J.; Mudde, R.F. A hybrid tomographic reconstruction algorithm for high speed X-ray tomography. Comput. Phys. Commun. 2015, 196, 27–35. [Google Scholar] [CrossRef]
- Batenburg, K.J. An evolutionary algorithm for discrete tomography. Discret. Appl. Math. 2005, 151, 36–54. [Google Scholar] [CrossRef][Green Version]
- Valenti, C. A genetic algorithm for discrete tomography reconstruction. Genet. Prog. Evol. Mach. 2008, 9, 85–96. [Google Scholar] [CrossRef]
- Di Gesù, V.; Lo Bosco, G.; Millonzi, F.; Valenti, C. A memetic approach to discrete tomography from noisy projections. Pattern Recogn. 2010, 43, 3073–3082. [Google Scholar] [CrossRef]
- Olmi, R.; Bini, M.; Priori, S. A genetic algorithm approach to image reconstruction in electrical impedance tomography. IEEE Trans. Evol. Comput. 2000, 4, 83–88. [Google Scholar] [CrossRef]
- Proch, F.; Domingo, P.; Vervisch, L.; Kempf, A.M. Flame resolved simulation of a turbulent premixed bluff-body burner experiment. Part I: Analysis of the reaction zone dynamics with tabulated chemistry. Combust. Flame 2017, 180, 321–339. [Google Scholar] [CrossRef]
- Proch, F.; Domingo, P.; Vervisch, L.; Kempf, A.M. Flame resolved simulation of a turbulent premixed bluff-body burner experiment. Part II: A-priori and a-posteriori investigation of sub-grid scale wrinkling closures in the context of artificially thickened flame modeling. Combust. Flame 2017, 180, 340–350. [Google Scholar] [CrossRef]
- Holland, J.H. Adaptation in Natural and Artificial Systems, 2nd ed.; University of Michigan Press: Ann Arbor, MI, USA, 1992. [Google Scholar]
- Michalewicz, Z. Genetic Alogrithms + Data Structures = Evolution Programs, 3rd ed.; Springer: New York, NY, USA, 1996. [Google Scholar]
- Winter, A. vlib API (Version1.2) [Computer Software]. 2001. Available online: http://vg.swan.ac.uk/vlib/ (accessed on 24 December 2017).
- Chen, M.; Winter, A.; Rodgman, D.; Treavett, S. Enriching volume modelling with scalar fields. In Data Visualization: The State of The Art; Post, F., Bonneau, G.P., Nielson, G., Eds.; Kluwer Academic Publishers: Boston, MA, USA, 2003. [Google Scholar]
- Winter, A.; Chen, M. vlib: A Volume Graphics API. In Volume Graphics 2001; Springer: New York, NY, USA, 2001. [Google Scholar]
- Winter, A.; Chen, M. Image-Swept Volumes. Comput. Graph. Forum 2002, 21, 441–450. [Google Scholar] [CrossRef]
- Aggarwal, C.C.; Hinneburg, A.; Keim, D.A. On the surprising behavior of distance metrics in high dimensional space. In Database Theory—ICDT 2001; Van den Bussche, J., Vianu, V., Eds.; Springer: Berlin/Heidelberg, Germany, 2001; pp. 420–434. [Google Scholar]
- Burkhardt, J. TRUNCATED_NORMAL The Truncated Normal Distribution (Version 03.04.2015) [Computer Software]. 2015. Available online: https://people.sc.fsu.edu/~jburkardt/f_src/truncated_normal/truncated_normal.html (accessed on 20 December 2017).
- Metropolis, N.; Rosenbluth, A.; Rosenbluth, M.; Teller, A.; Teller, E. Equations of State Calculations by Fast Computing Machines. J. Chem. Phys. 1953, 21, 1087–1092. [Google Scholar] [CrossRef]
- Hastings, W. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 1970, 57, 97–109. [Google Scholar] [CrossRef]
- Chib, S.; Greenberg, E. Understanding the Metropolis-Hastings algorithm. Am. Stat. 1995, 49, 327–335. [Google Scholar]
- Michel, M. Irreversible Markov Chains by the Factorized Metropolis Filter: Algorithms and Applications in Particle Systems and Spin Models. Ph.D. Thesis, PSL Research University, Paris, France, 2016. [Google Scholar]
- Pettit, M.; Coriton, B.; Gomez, A.; Kempf, A. Large-Eddy Simulation and experiments on non-premixed highly turbulent opposed jet flows. Proc. Combust. Inst. 2011, 33, 1391–1399. [Google Scholar] [CrossRef]
- Proch, F.; Kempf, A.M. Numerical analysis of the Cambridge stratified flame series using artificial thickened flame LES with tabulated premixed flame chemistry. Combust. Flame 2014, 161, 2627–2646. [Google Scholar] [CrossRef]
- Meier, W.; Keck, O.; Noll, B.; Kunz, O.; Stricker, W. Investigations in the TECFLAM swirling diffusion flame: Laser Raman measurements and CFD calculations. Appl. Phys. B 2000, 71, 725–731. [Google Scholar] [CrossRef]
- Schneider, C.; Dreizler, A.; Janicka, J. Fluid dynamical analysis of atmospheric reacting and isothermal swirling flows. Flow Turbul. Combust. 2005, 74, 103–127. [Google Scholar] [CrossRef]
- Sweeney, M.S.; Hochgreb, S.; Dunn, M.J.; Barlow, R.S. The structure of turbulent stratified and premixed methane/air flames I: Non-swirling flows. Combust. Flame 2012, 159, 2896–2911. [Google Scholar] [CrossRef]
- Sweeney, M.S.; Hochgreb, S.; Dunn, M.J.; Barlow, R.S. The structure of turbulent stratified and premixed methane/air flames II: Swirling flows. Combust. Flame 2012, 159, 2912–2929. [Google Scholar] [CrossRef]
- Nambully, S.; Domingo, P.; Moureau, V.; Vervisch, L. A filtered-laminar-flame PDF sub-grid-scale closure for LES of premixed turbulent flames: II. Application to a stratified bluff-body burner. Combust. Flame 2014, 161, 1775–1791. [Google Scholar] [CrossRef]
- Nambully, S.; Domingo, P.; Moureau, V.; Vervisch, L. A filtered-laminar-flame PDF sub-grid scale closure for LES of premixed turbulent flames. Part I: Formalism and application to a bluff-body burner with differential diffusion. Combust. Flame 2014, 161, 1756–1774. [Google Scholar] [CrossRef]








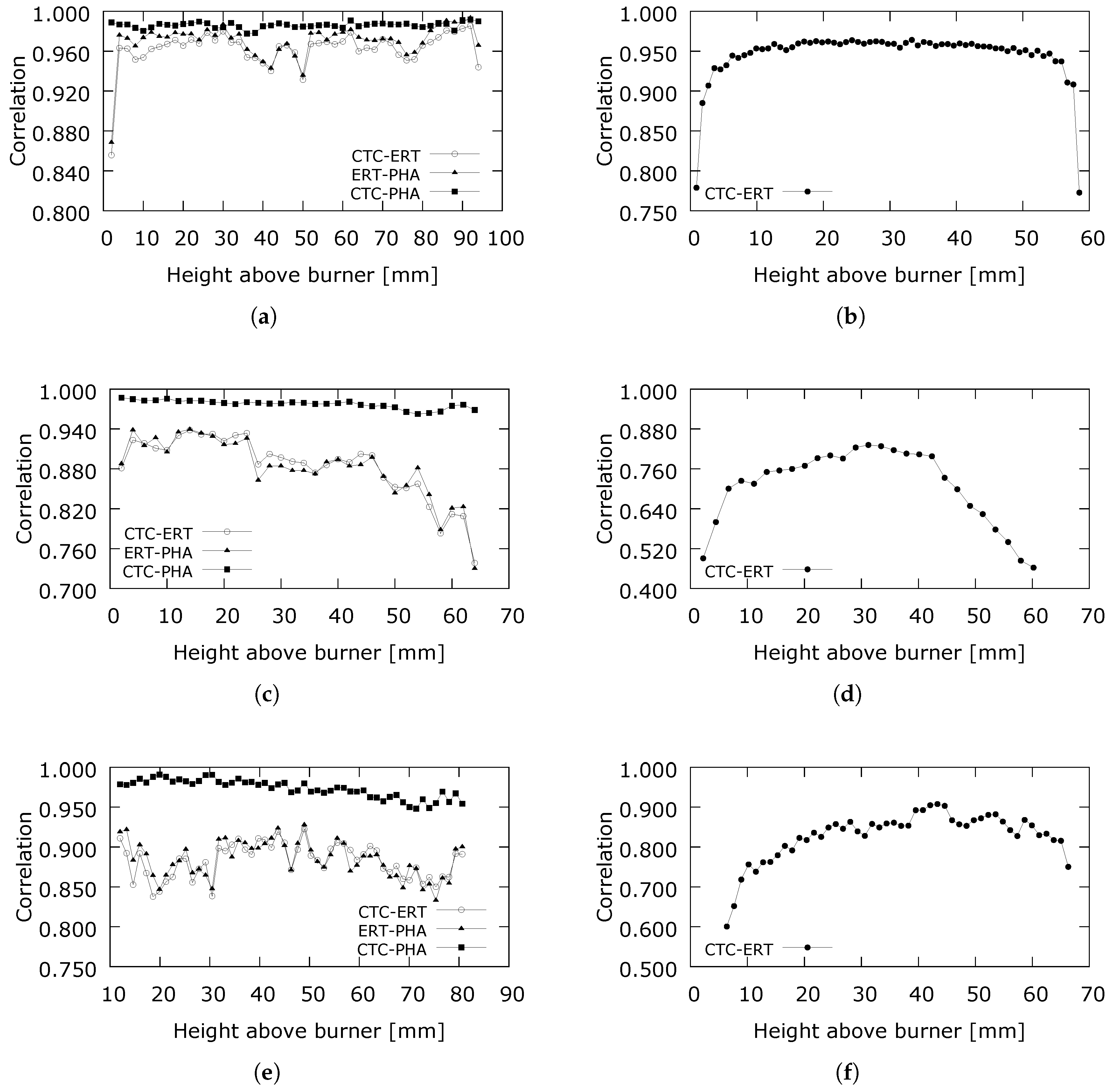
| Parameter | Air | / | |
|---|---|---|---|
| outer-flow | 441.7 | 34.8 | 0.75 |
| inner-flow | 144.0 | 11.4 | 0.75 |
| co-flow | 765.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Unterberger, A.; Kempf, A.; Mohri, K. 3D Evolutionary Reconstruction of Scalar Fields in the Gas-Phase. Energies 2019, 12, 2075. https://doi.org/10.3390/en12112075
Unterberger A, Kempf A, Mohri K. 3D Evolutionary Reconstruction of Scalar Fields in the Gas-Phase. Energies. 2019; 12(11):2075. https://doi.org/10.3390/en12112075
Chicago/Turabian StyleUnterberger, Andreas, Andreas Kempf, and Khadijeh Mohri. 2019. "3D Evolutionary Reconstruction of Scalar Fields in the Gas-Phase" Energies 12, no. 11: 2075. https://doi.org/10.3390/en12112075
APA StyleUnterberger, A., Kempf, A., & Mohri, K. (2019). 3D Evolutionary Reconstruction of Scalar Fields in the Gas-Phase. Energies, 12(11), 2075. https://doi.org/10.3390/en12112075





