Interval Energy Flow Analysis in Integrated Electrical and Natural-Gas Systems Considering Uncertainties
Abstract
:1. Introduction
- Interval energy flow model of IENGS is built to reflect the various uncertainties brought by electrical load, power generation, and gas load, and the Krawczyk–Moore interval iterative method is used to solve interval energy flow equations and verify its correctness with the comparison to Monte Carlo simulation.
- The influence of each kind of uncertainty brought by electrical load, power generation, and gas load has been investigated, and especially the impact of uncertainty in power system on gas system and the impact of uncertainty in gas system on power system are analyzed.
- The convergence of energy flow is analyzed when the uncertainty level of electrical load is increased to verify the approach’s effectiveness.
2. Energy Flow Model in IENGS Considering Uncertainties
2.1. Steady-State Energy Flow Model without Consideration of Uncertainty
2.1.1. Power Flow Model
2.1.2. Gas Flow Model
- (1)
- known-pressure node. Gas supply of this node is sufficient and the pressure is a given reference value to compute all other unknown nodal pressures, which is similar to slack buses in power systems.
- (2)
- known-injection node. Gas consumption and injection are known while pressure is unknown for the node, which is analogous to the PQ buses in power systems.
2.1.3. Coupling Model
2.1.4. Steady-State Energy Flow Balance Equation
2.2. Interval Energy Flow Modeling Considering Uncertainty
2.2.1. Uncertainties in Interval Forms
2.2.2. Energy Flow Model Using Interval Mathematics
3. Interval Energy Flow Analysis based on Krawczyk–Moore Iterative Method
3.1. Krawczyk–Moore Iterative Method in Energy Flow Analysis
3.2. Improvement of the Krawczyk–Moore Iterative Process with Affine Arithmetic
3.2.1. Affine Arithmetic
3.2.2. Improvement in Iterative Process with Affine Arithmetic
3.3. Interval Energy Flow Analysis Process
4. Case Study
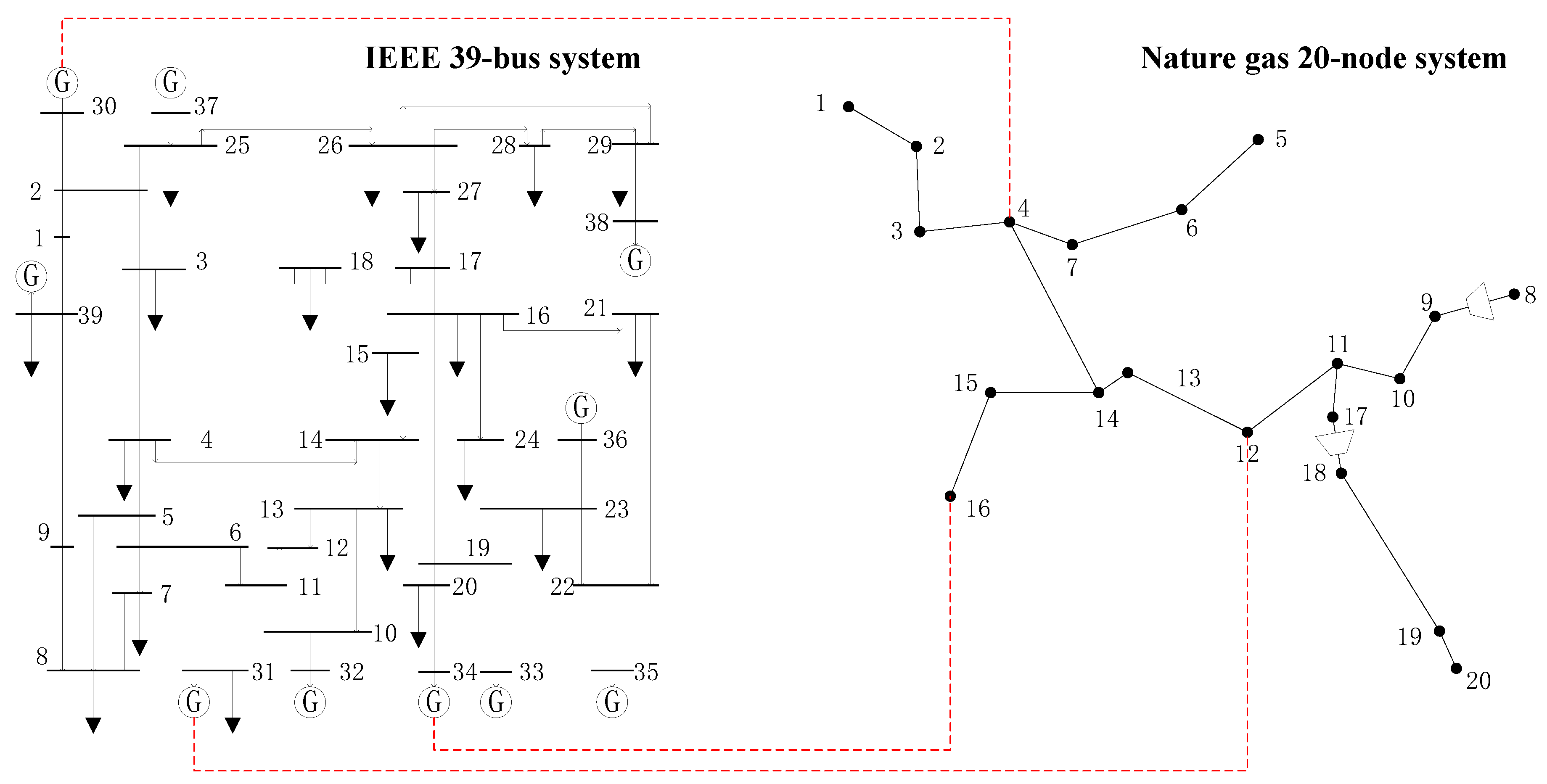
4.1. Thirty-Nine-Bus Electrical System Coupled with 20-Node Gas System
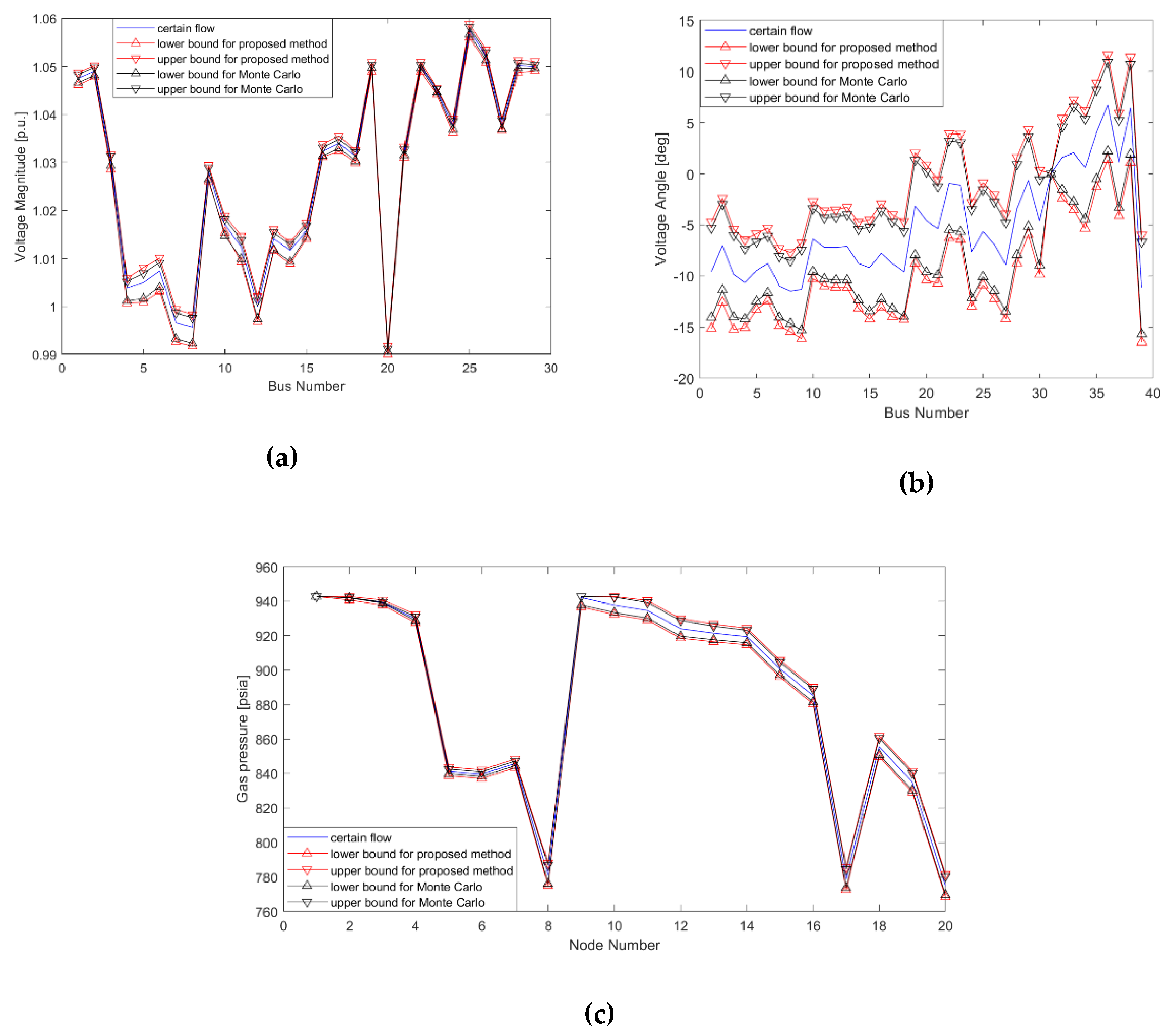
4.2. Comparison with Monte Carlo Simulation
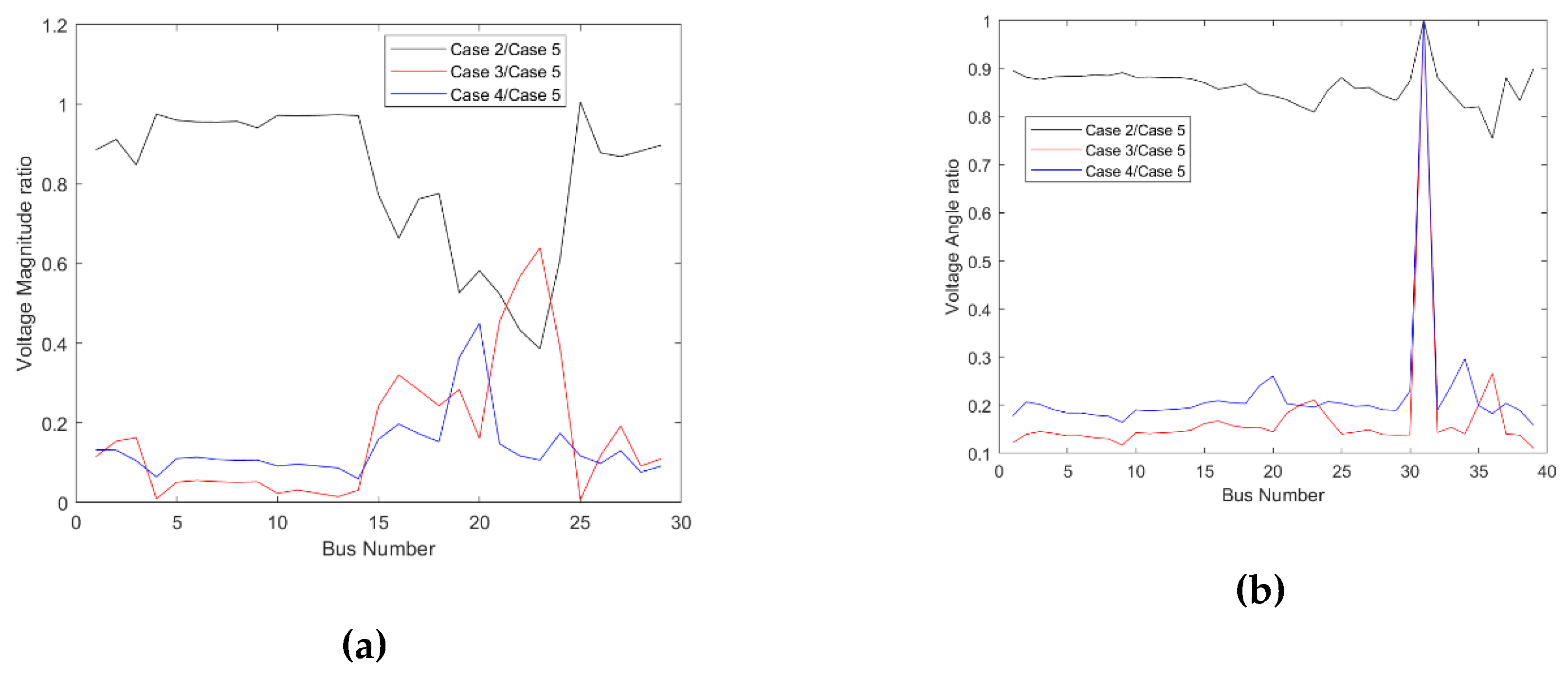
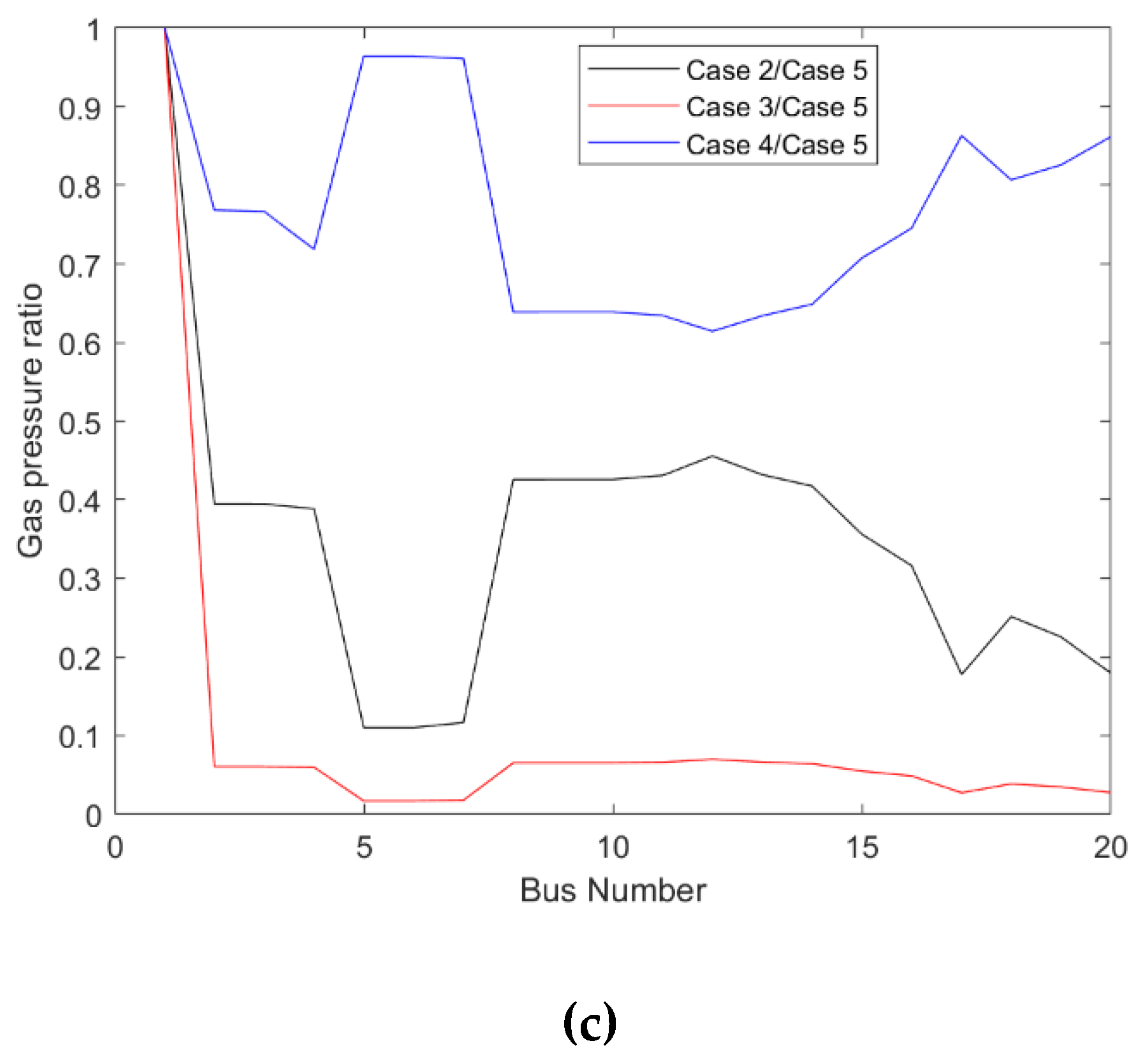
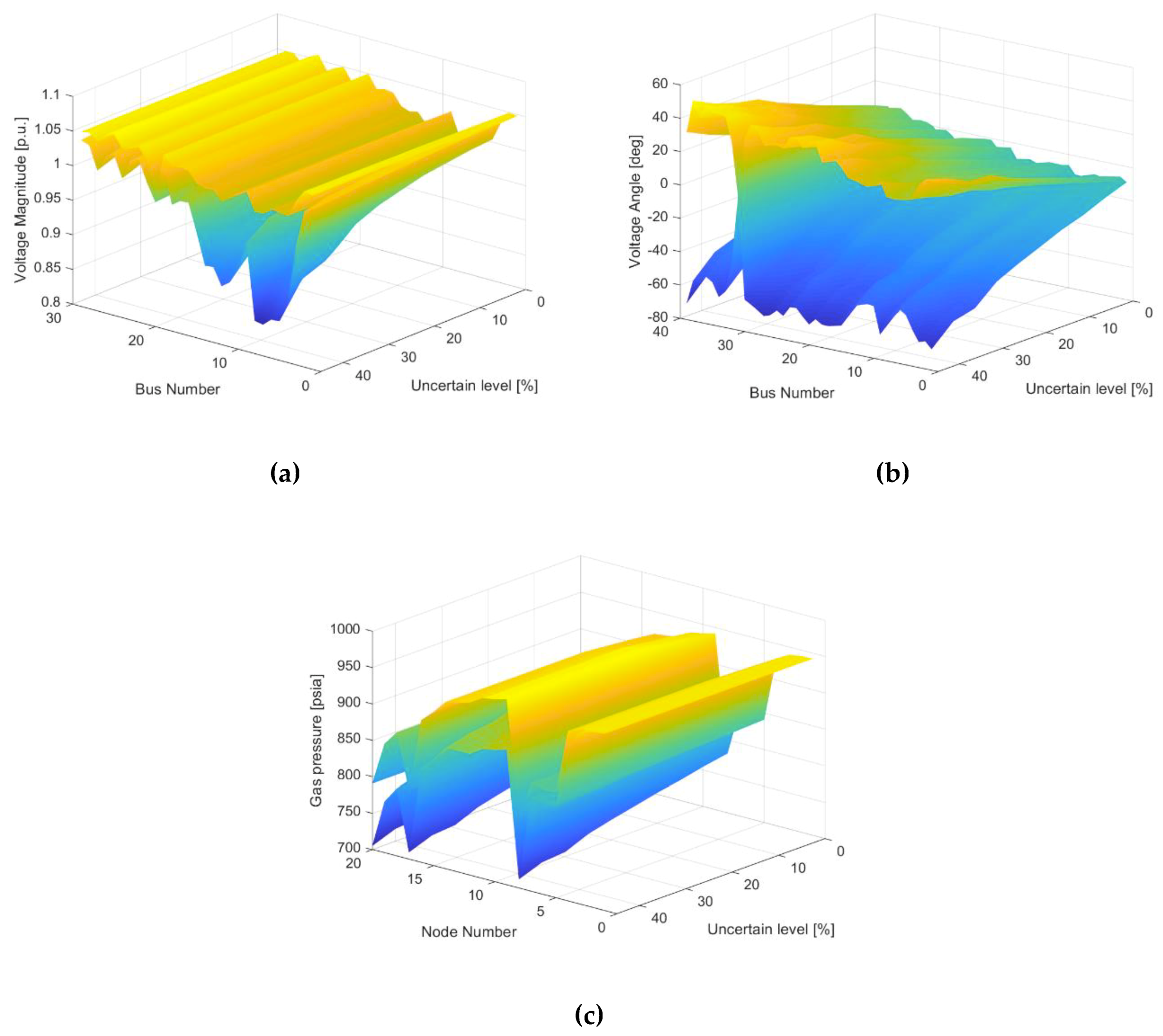
4.3. Uncertain Energy Flow Analysis
4.4. Convergence Analysis of Uncertain Energy Flow
5. Conclusions
- Uncertainty caused by the power system (variation of electrical load or power generation) will be delivered to the gas system by coupling nodes. Similarly, uncertainty caused by the gas system (variation of gas load) will be delivered to the power system by coupling nodes.
- Accumulation of uncertainties brought by multiple sources will also will expand the variation of the whole system.
- Uncertainty on the increase brought by a single source (variation of electrical load, power generation, or gas load) will expand the variation of the whole system.
Author Contributions
Funding
Conflicts of Interest
References
- Henderson, M.; Shahidehpour, M. Continuing to grow: natural gas usage rising in electricity generation. IEEE Power Energy Mag. 2014, 12, 12–19. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Sun, Y.; Zang, H.; Zhu, Y. Optimal power and gas flow with a limited number of control actions. IEEE Trans. Smart Grid 2018, 9, 5371–5380. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. An integrated steady-state operation assessment of electrical, natural gas, and district heating networks. IEEE Trans. Power Syst. 2016, 31, 3636–3647. [Google Scholar] [CrossRef]
- Li, Y.; Zou, Y.; Cao, Y.; Tan, Y.; Cao, Y.; Liu, X.; Shahidehpour, M.; Tian, S.; Bu, F. Optimal stochastic operation of integrated low-carbon electric power, natural gas, and heat delivery system. IEEE Trans. Sustain. Energy 2018, 9, 273–283. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Cheung, K.W.; Wang, D. Identifying optimal energy flow solvability in electricity-gas integrated energy systems. IEEE Trans. Sustain. Energy 2017, 8, 846–854. [Google Scholar] [CrossRef]
- Wang, C.; Wei, W.; Wang, J.; Bai, L.; Liang, Y.; Bi, T. Convex optimization based distributed optimal gas-power flow calculation. IEEE Trans. Sustain. Energy 2018, 9, 1145–1156. [Google Scholar] [CrossRef]
- Ding, T.; Hu, Y.; Bie, Z. Multi-Stage stochastic programming with nonanticipativity constraints for expansion of combined power and natural gas systems. IEEE Trans. Power Syst. 2018, 33, 317–328. [Google Scholar] [CrossRef]
- Shao, C.; Shahidehpour, M.; Wang, X.; Wang, B. Integrated planning of electricity and natural gas transportation systems for enhancing the power grid resilience. IEEE Trans. Power Syst. 2017, 32, 4418–4429. [Google Scholar] [CrossRef]
- Qiu, J.; Dong, Z.Y.; Zhao, J.H.; Meng, K.; Zheng, Y.; Hill, D.J. Low carbon oriented expansion planning of integrated gas and power systems. IEEE Trans. Power Syst. 2015, 30, 1035–1046. [Google Scholar] [CrossRef]
- Zhao, B.; Conejo, A.J.; Sioshansi, R. Coordinated expansion planning of natural gas and electric power systems. IEEE Trans. Power Syst. 2018, 33, 3064–3075. [Google Scholar] [CrossRef]
- Gil, M.; Dueñas, P.; Reneses, J. Electricity and natural gas interdependency: comparison of two methodologies for coupling large market models within the European regulatory framework. IEEE Trans. Power Syst. 2016, 31, 361–369. [Google Scholar] [CrossRef]
- Qiu, J.; Zhao, J.; Yang, H.; Dong, Z.Y. Optimal Scheduling for prosumers in coupled transactive power and gas systems. IEEE Trans. Power Syst. 2018, 33, 1970–1980. [Google Scholar] [CrossRef]
- Massrur, H.R.; Niknam, T.; Aghaei, J.; Shafie-khah, M.; Catalão, J.P.S. Fast decomposed energy flow in large-scale integrated electricity–gas–heat energy systems. IEEE Trans. Sustain. Energy 2018, 9, 1565–1577. [Google Scholar] [CrossRef]
- Martinez-Mares, A.; Fuerte-Esquivel, C.R. A unified gas and power flow analysis in natural gas and electricity coupled networks. IEEE Trans. Power Syst. 2012, 27, 2156–2166. [Google Scholar] [CrossRef]
- Xu, X.; Jia, H.; Chiang, H.D.; Yu, D.C.; Wang, D. Dynamic modeling and interaction of hybrid natural gas and electricity supply system in microgrid. IEEE Trans. Power Syst. 2015, 30, 1212–1221. [Google Scholar] [CrossRef]
- Zeng, Q.; Fang, J.; Li, J.; Chen, Z. Steady-state analysis of the integrated natural gas and electric power system with bi-directional energy conversion. Appl. Energy 2016, 184, 1483–1492. [Google Scholar] [CrossRef]
- Kuczyński, S.; Łaciak, M.; Olijnyk, A.; Szurlej, A.; Wlodek, T. Techno-economic assessment of turboexpander application at natural gas regulation stations. Energies 2019, 12, 755. [Google Scholar] [CrossRef]
- Borelli, D.; Devia, F.; Brunenghi, M.M.; Schenone, M.; Spoladore, A. Waste energy recovery from natural gas distribution Network: CELSIUS Project Demonstrator in Genoa. Sustainability 2015, 7, 16703–16719. [Google Scholar] [CrossRef]
- Liu, X.; Mancarella, P. Modelling, assessment and Sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems. Appl. Energy 2016, 167, 336–352. [Google Scholar] [CrossRef]
- Shabanpour-Haghighi, A.; Seifi, A.R. Simultaneous integrated optimal energy flow of electricity, gas, and heat. Energy Conver. Manag. 2015, 101, 579–591. [Google Scholar] [CrossRef]
- Pan, Z.; Guo, Q.; Sun, H. Interactions of district electricity and heating systems considering time-scale characteristics based on quasi-steady multi-energy flow. Appl. Energy 2016, 167, 230–243. [Google Scholar] [CrossRef]
- Erdener, B.C.; Pambour, K.A.; Lavin, R.B.; Dengiz, B. An integrated simulation model for analysing electricity and gas systems. Int. J. Electr. Power Energy Syst. 2014, 61, 410–420. [Google Scholar] [CrossRef]
- Ghanaatian, M.; Lotfifard, S. Control of flywheel energy storage systems in the presence of uncertainties. IEEE Trans. Sustain. Energy 2019, 10, 36–45. [Google Scholar] [CrossRef]
- Niloofar, G.; Shabestari, M.; Parisa, M.; Ali, M.; Subhashish, B. State-space modeling and reachability analysis for a dc microgrid. In Proceedings of the Applied Power Electronics Conference and Exposition (APEC) 2019, Anaheim, CA, USA, 7–8 February 2019. [Google Scholar]
- Gharibpour, H.; Monsef, H.; Ghanaatian, M. The comparison of two control methods of power swing reduction in power system with UPFC compensator. In Proceedings of the 20th Iranian Conference on Electrical Engineering (ICEE2012), Tehran, Iran, 15–17 May 2012. [Google Scholar] [CrossRef]
- Luo, J.; Shi, L.; Ni, Y. A solution of optimal power flow incorporating wind generation and power grid uncertainties. IEEE Access 2018, 6, 1. [Google Scholar] [CrossRef]
- Chen, S.; Wei, Z.; Sun, G.; Cheung, K.W.; Sun, Y. Multi-linear probabilistic energy flow analysis of integrated electrical and natural-gas systems. IEEE Trans. Power Syst. 2017, 32, 1970–1979. [Google Scholar] [CrossRef]
- Ding, T.; Bo, R.; Li, F.; Guo, Q.; Sun, H.; Gu, W.; Zhou, G. Interval power flow analysis using linear relaxation and optimality-based bounds tightening (OBBT) methods. IEEE Trans. Power Syst. 2015, 30, 177–188. [Google Scholar] [CrossRef]
- Wang, Z.; Alvarado, F.L. Interval arithmetic in power flow analysis. IEEE Trans. Power Syst. 1992, 7, 1341–1349. [Google Scholar] [CrossRef]
- Qiao, Z.; Guo, Q.; Sun, H.; Pan, Z.; Liu, Y.; Xiong, W. An interval gas flow analysis in natural gas and electricity coupled networks considering the uncertainty of wind power. Appl. Energy 2017, 201, 343–353. [Google Scholar] [CrossRef]
- Li, Q.; An, S.; Gedra, T.W. Solving natural gas load flow problems using electric load flow techniques. In Proceedings of the North American Power Symposium, Rolla, MO, USA, 14–16 September 2003. [Google Scholar]
- Moore, R.E. Methods and Applications of Interval Analysis; Society for Industrial and Applied Mathematics: Philadelphia, PA, USA, 1979; ISBN 0-89871-161-4. [Google Scholar]
- Mori, H.; Yuihara, A. Calculation of multiple power flow solutions with the Krawczyk method. In Proceedings of the 1999 IEEE International Symposium on Circuits and Systems VLSI, Orlando, FL, USA, 30 May–2 June 1999. [Google Scholar] [CrossRef]
- Ding, T.; Cui, H.; Gu, W.; Wan, Q. An uncertainty power flow algorithm based on interval and affine arithmetic. Autom. Electr. Power Syst. 2012, 36, 51–55. [Google Scholar] [CrossRef]
- Ding, T.; Li, F.; Li, X.; Sun, H.; Bo, R. Interval radial power flow using extended DistFlow formulation and Krawczyk iteration method with sparse approximate inverse preconditioner. IET Gener. Transm. Distrib. 2015, 9, 1998–2006. [Google Scholar] [CrossRef]
- Figueiredo, D.; Henrique, L.; Jorge, S. Affine arithmetic: concepts and applications. Numer. Algorithms 2004, 37, 147–158. [Google Scholar] [CrossRef]
- Wang, S.; Han, L.; Wu, L. Uncertainty tracing of distributed generations via complex affine arithmetic based unbalanced three-phase power flow. IEEE Trans. Power Syst. 2015, 30, 3053–3062. [Google Scholar] [CrossRef]
- Wolf, D.; Smeers, Y. The gas transmission problem solved by an extension of the simplex algorithm. Manag. Sci. 2000, 46, 1454–1465. [Google Scholar] [CrossRef]
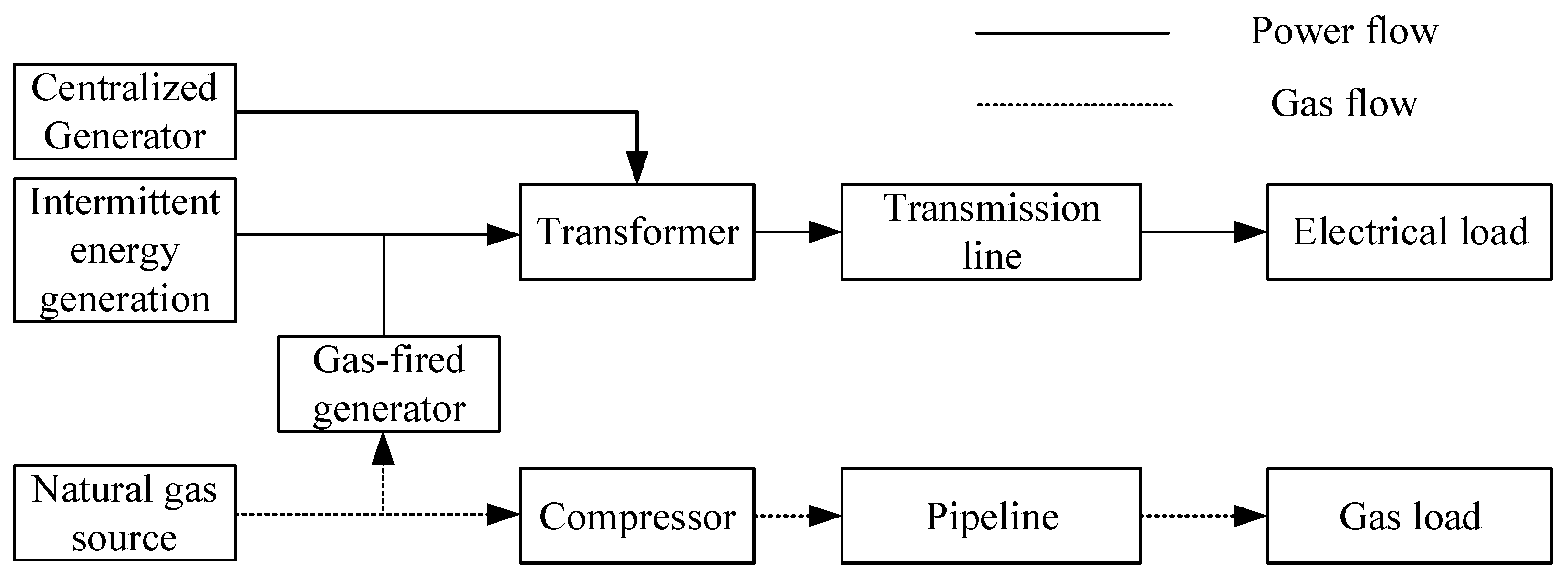


| Terms | Power System | Natural-Gas System |
|---|---|---|
| Element | Line Transformer | Pipeline Compressor |
| Variable | Amplitude, Phase angle Active power, Reactive power | Pressure Injection |
| Node type | PQ bus, PV bus Slack bus | Known injection node Known pressure node |
| Node | Source (MSCF3/Hour) | Load (MSCF3/Hour) |
|---|---|---|
| 1 | 21.613 | 0 |
| 2 | 9.632 | 0 |
| 3 | 0 | 5.7666 |
| 4 | 0 | 0 |
| 5 | 0.562 | 0 |
| 6 | 0 | 5.9358 |
| 7 | 0 | 7.7339 |
| 8 | 29.6466 | 0 |
| 9 | 0 | 0 |
| 10 | 0 | 9.3672 |
| 11 | 0 | 0 |
| 12 | 0 | 3.1194 |
| 13 | 5.2824 | 0 |
| 14 | 2.0703 | 0 |
| 15 | 0 | 10.1764 |
| 16 | 0 | 14.978 |
| 17 | 0 | 0 |
| 18 | 0 | 0 |
| 19 | 0.3016 | 0 |
| 20 | 0 | 2.8237 |
| Number | Power Bus | Gas Node | α | β | γ |
|---|---|---|---|---|---|
| 1 | 30 | 4 | 0 | 7 | 0 |
| 2 | 31 | 12 | 0 | 7 | 0 |
| 3 | 34 | 16 | 0 | 7 | 0 |
| Bus | Certain Power Flow Results of Scenario 1 | Interval Power Flow Results by Proposed Approach of Scenario 2 | Interval Power Flow Results by MC Simulation of Scenario 2 | |||
|---|---|---|---|---|---|---|
| U | δ | [U] | [δ] | [U] | [δ] | |
| 4 | 1.0038 | −10.6546 | [1.0007, 1.0059] | [−15.0646, −6.4446] | [1.0012, 1.0052] | [−14.2234, −7.3382] |
| 9 | 1.0281 | −11.2997 | [1.0261, 1.0294] | [−16.1506, −6.7488] | [1.0265, 1.0289] | [−15.2939, −7.4510] |
| 13 | 1.0142 | −7.0959 | [1.0116, 1.0161] | [−11.1179, −3.2738] | [1.0119, 1.0154] | [−10.3979, −4.0105] |
| 18 | 1.0313 | −9.6156 | [1.0299, 1.0326] | [−14.7713, −4.6599] | [1.0303, 1.0322] | [−13.9605, −5.6291] |
| 23 | 1.0450 | −1.1221 | [1.0441, 1.0455] | [−6.4243, 3.8801] | [1.0446, 1.0453] | [−5.6517, 3.0626] |
| 27 | 1.0379 | −8.9173 | [1.0367, 1.0392] | [−14.2173, −3.9173] | [1.0370, 1.0388] | [−13.4650, −4.7830] |
| 30 | 1.0475 | −4.5918 | [1.0475, 1.0475] | [−9.8479, 0.3643] | [1.0475, 1.0475] | [−8.9419, −0.5602] |
| 32 | 0.9831 | 1.6155 | [0.9831, 0.9831] | [−2.4121, 5.4430] | [0.9831, 0.9831] | [−1.5599, 4.5918] |
| 34 | 1.0123 | 0.6263 | [1.0123, 1.0123] | [−5.3464, 6.1989] | [1.0123, 1.0123] | [−4.4250, 5.3869] |
| Node | Certain Gas Flow Results of Scenario 1 | Interval Gas Flow Results by Proposed Approach of Scenario 2 | Interval Gas Flow Results by MC Simulation of Scenario 2 |
|---|---|---|---|
| v | [v] | [v] | |
| 1 | 942.70 | [942.70, 942.70] | [942.70, 942.70] |
| 2 | 942.00 | [940.72,942.70] | [941.92,942.08] |
| 4 | 929.82 | [927.46,932.29] | [928.66,931.09] |
| 6 | 839.52 | [837.03,842.12] | [838.23,840.92] |
| 10 | 937.71 | [932.22,942.70] | [933.42,942.32] |
| 12 | 924.09 | [918.54,929.97] | [919.74,928.77] |
| 14 | 919.49 | [914.73,924.37] | [915.93,923.17] |
| 16 | 885.24 | [880.34,890.27] | [881.54,889.07] |
| 18 | 855.54 | [849.64,861.79] | [850.84,860.59] |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, S.; Yuan, S. Interval Energy Flow Analysis in Integrated Electrical and Natural-Gas Systems Considering Uncertainties. Energies 2019, 12, 2043. https://doi.org/10.3390/en12112043
Wang S, Yuan S. Interval Energy Flow Analysis in Integrated Electrical and Natural-Gas Systems Considering Uncertainties. Energies. 2019; 12(11):2043. https://doi.org/10.3390/en12112043
Chicago/Turabian StyleWang, Shouxiang, and Shuangchen Yuan. 2019. "Interval Energy Flow Analysis in Integrated Electrical and Natural-Gas Systems Considering Uncertainties" Energies 12, no. 11: 2043. https://doi.org/10.3390/en12112043
APA StyleWang, S., & Yuan, S. (2019). Interval Energy Flow Analysis in Integrated Electrical and Natural-Gas Systems Considering Uncertainties. Energies, 12(11), 2043. https://doi.org/10.3390/en12112043





