Transient Temperature Calculation and Multi-Parameter Thermal Protection of Overhead Transmission Lines Based on an Equivalent Thermal Network
Abstract
1. Introduction
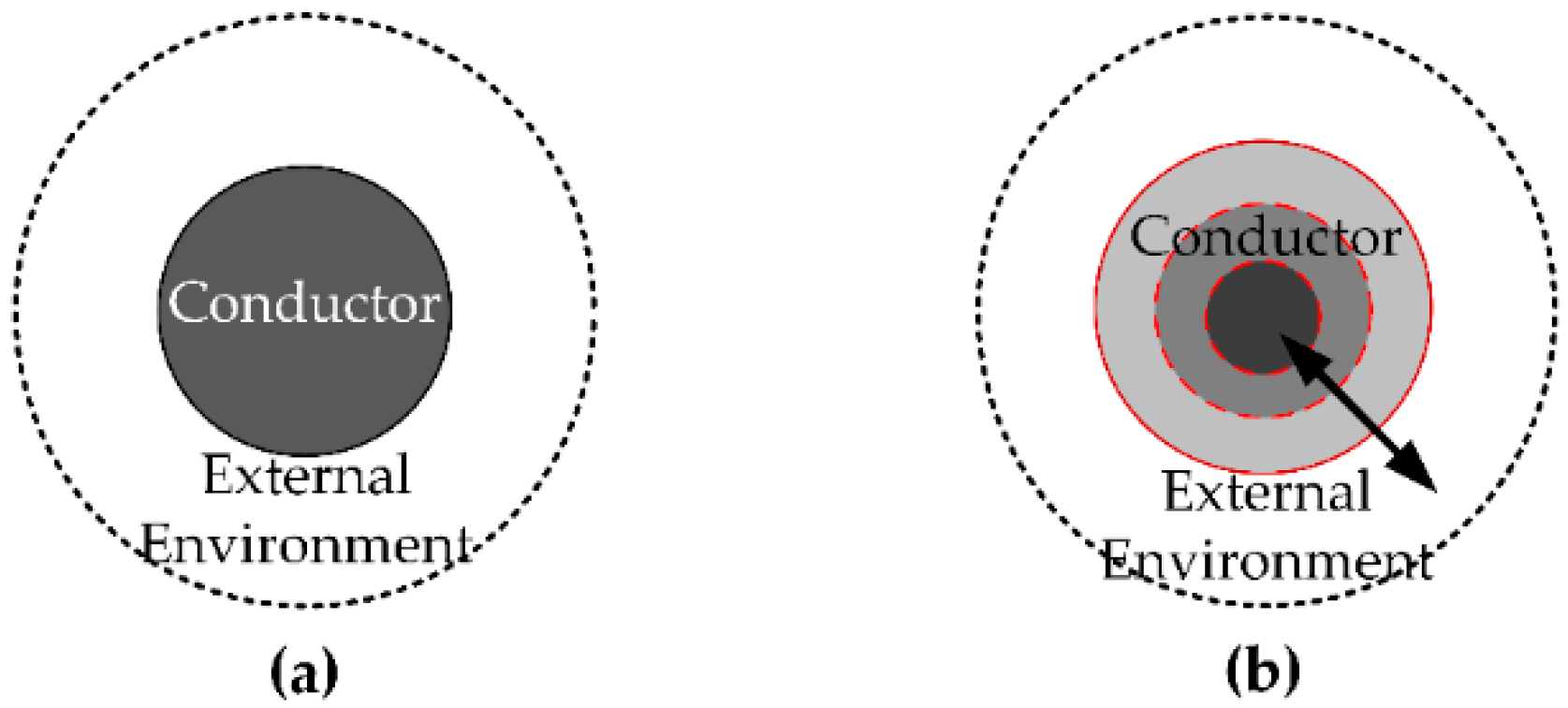
2. ETN Modeling of Overhead Transmission Lines
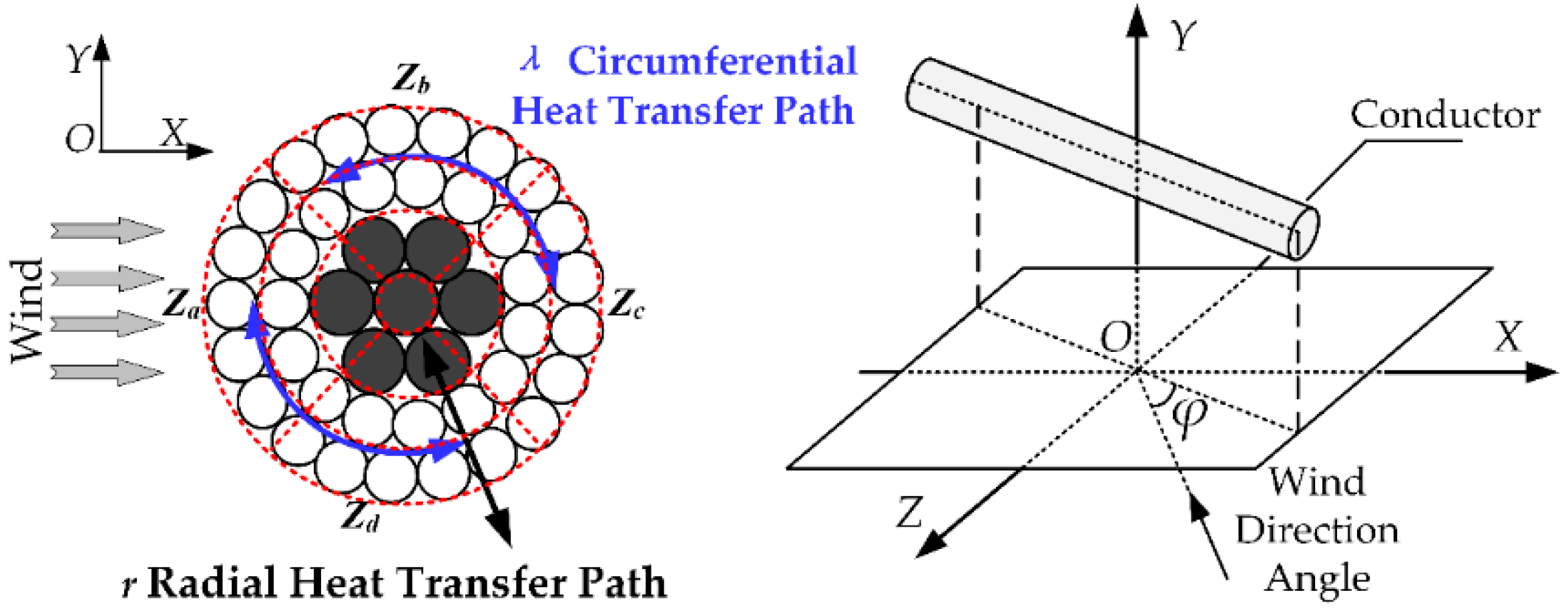
2.1. Heat Transfer Analysis of Overhead Transmission Line Cross-Section
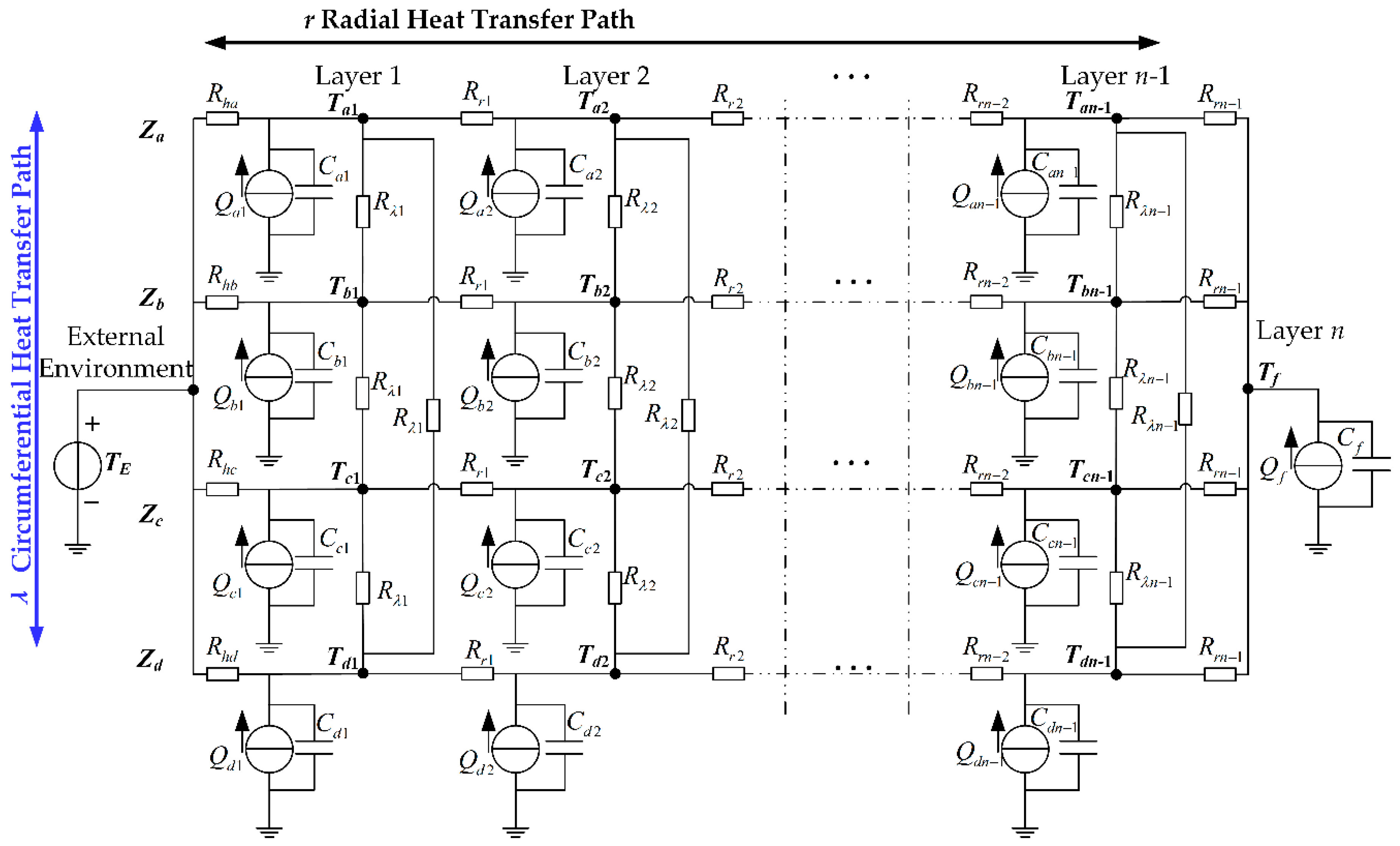
2.2. ETN of Overhead Transmission Lines
3. Transient Temperature Calculation Method for Overhead Transmission Line Based on the ETN
3.1. Determination of ETN Parameters
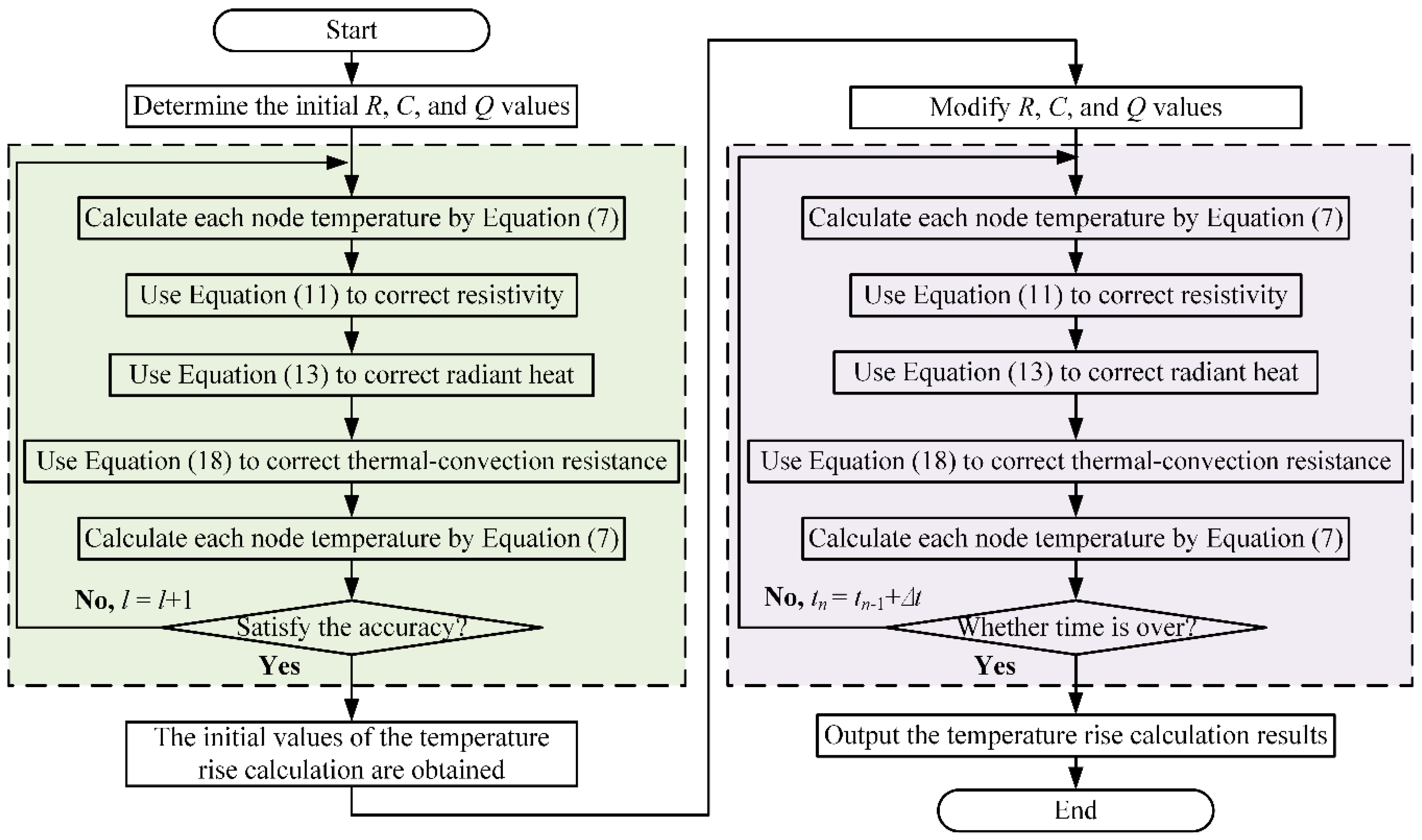
3.2. Transient Temperature Calculation Method with Nonlinear Iteration
- Step 1:
- Acquire conductor parameters, meteorological parameters, and current, and determine the initial values of Q, C, and R of the ETN by Equations (8)–(18). The initial temperature of each node is ambient temperature TE.
- Step 2:
- Calculate temperature of each node by Equation (7), and modify resistivity, radiant heat of nodes, and thermal convection resistance by Equations (11), (13) and (18), correspondingly. Thus, the temperature values of each node of the ETN can be solved.
- Step 3:
- Assess whether the temperature difference between two adjacent iterations satisfies the control precision (considered 0.01 °C in this paper). Otherwise, set the number of iterations l to l + 1, and continue the calculation until the temperature difference is less than that of the given precision.
- Step 4:
- Adjust the Joule heat of nodes of the ETN by current. Use the temperature value outputted in Step 3 as the initial value of the transient temperature rise response calculation for subsequent iterations.
- Step 5:
- Determine whether the calculation is completed. Otherwise, set time tn = tn−1 + ∆t for the calculation until the calculation time is equal to the prescribed time.
- Step 6:
- Obtain the calculation results of the transient temperature rise response, and the calculation is completed.
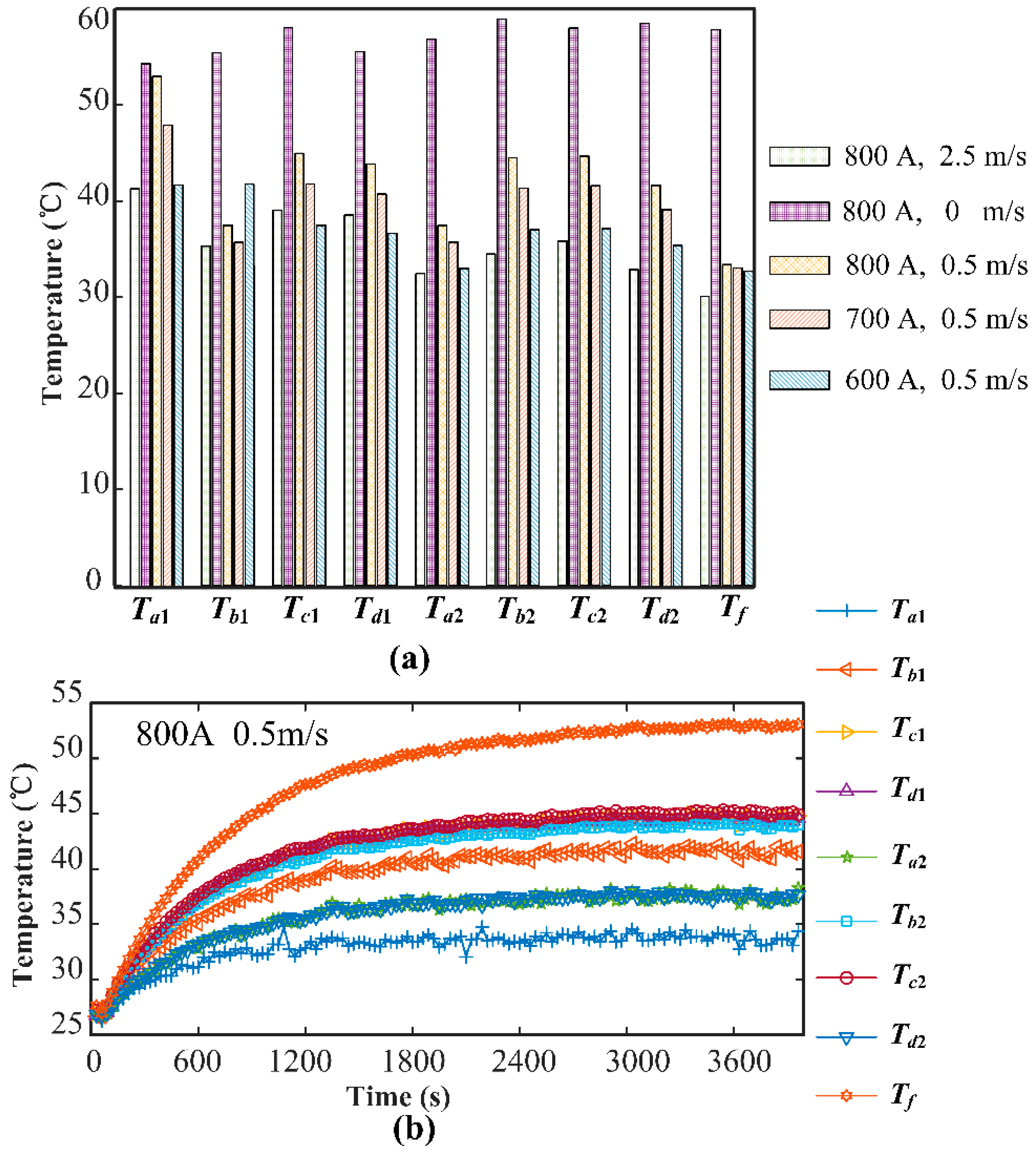
4. Experimental Verification of the Model and Calculation Method
4.1. Temperature Rise Test Platform of Overhead Transmission Lines
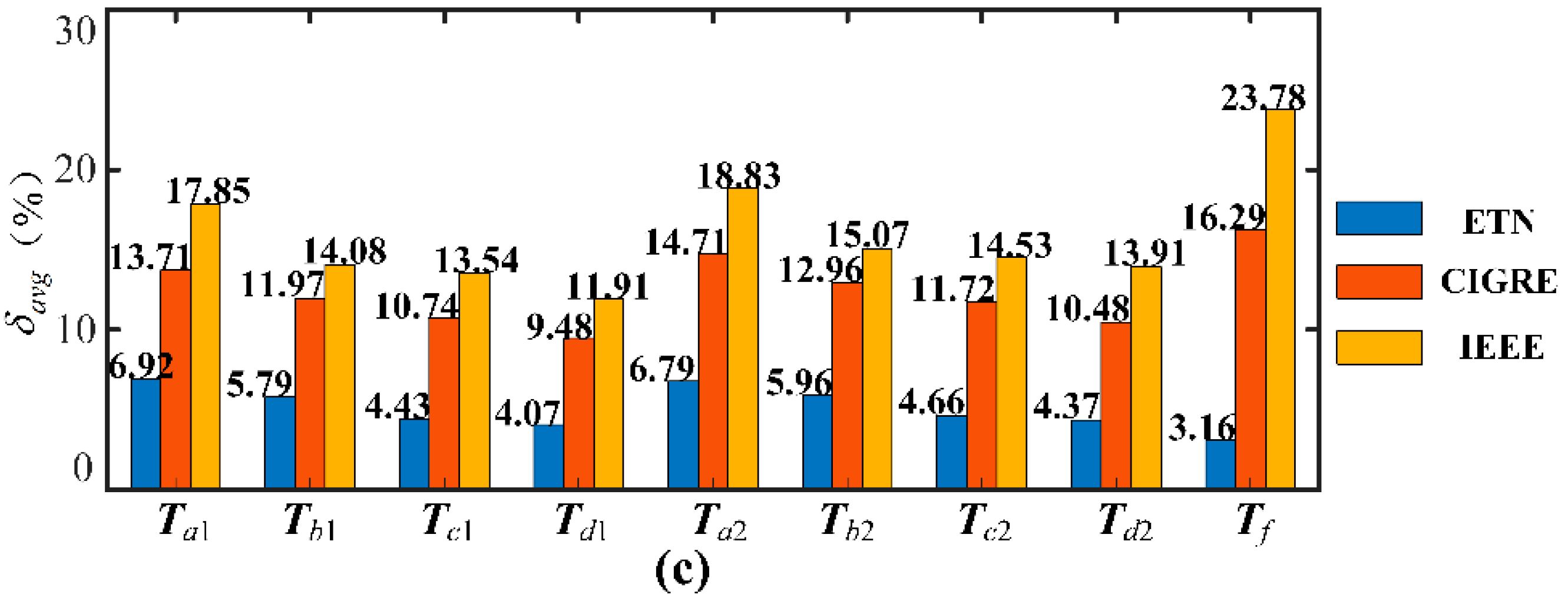
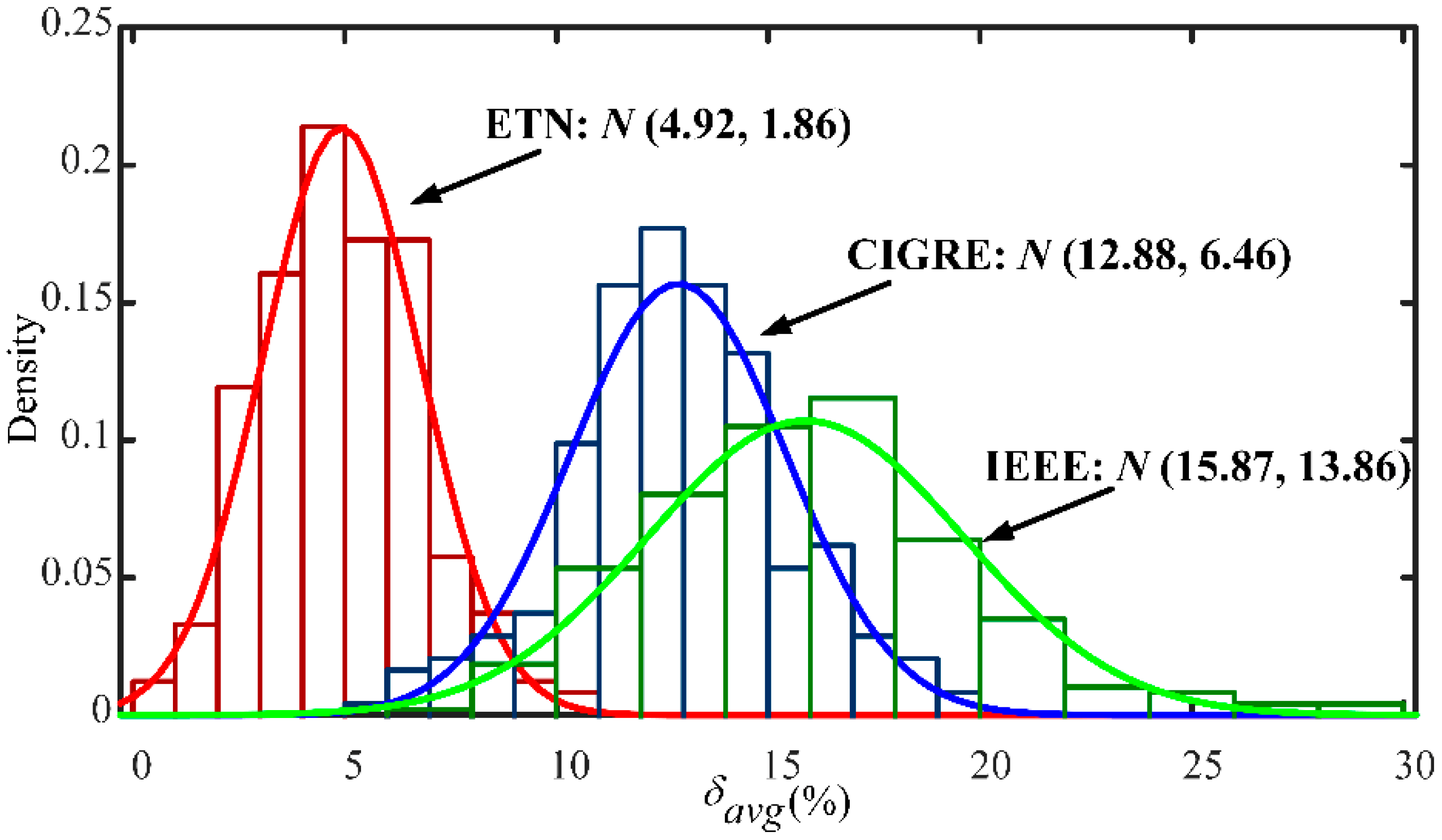
4.2. Verification of the Model and Calculation Method
4.3. Extrapolation and Validation
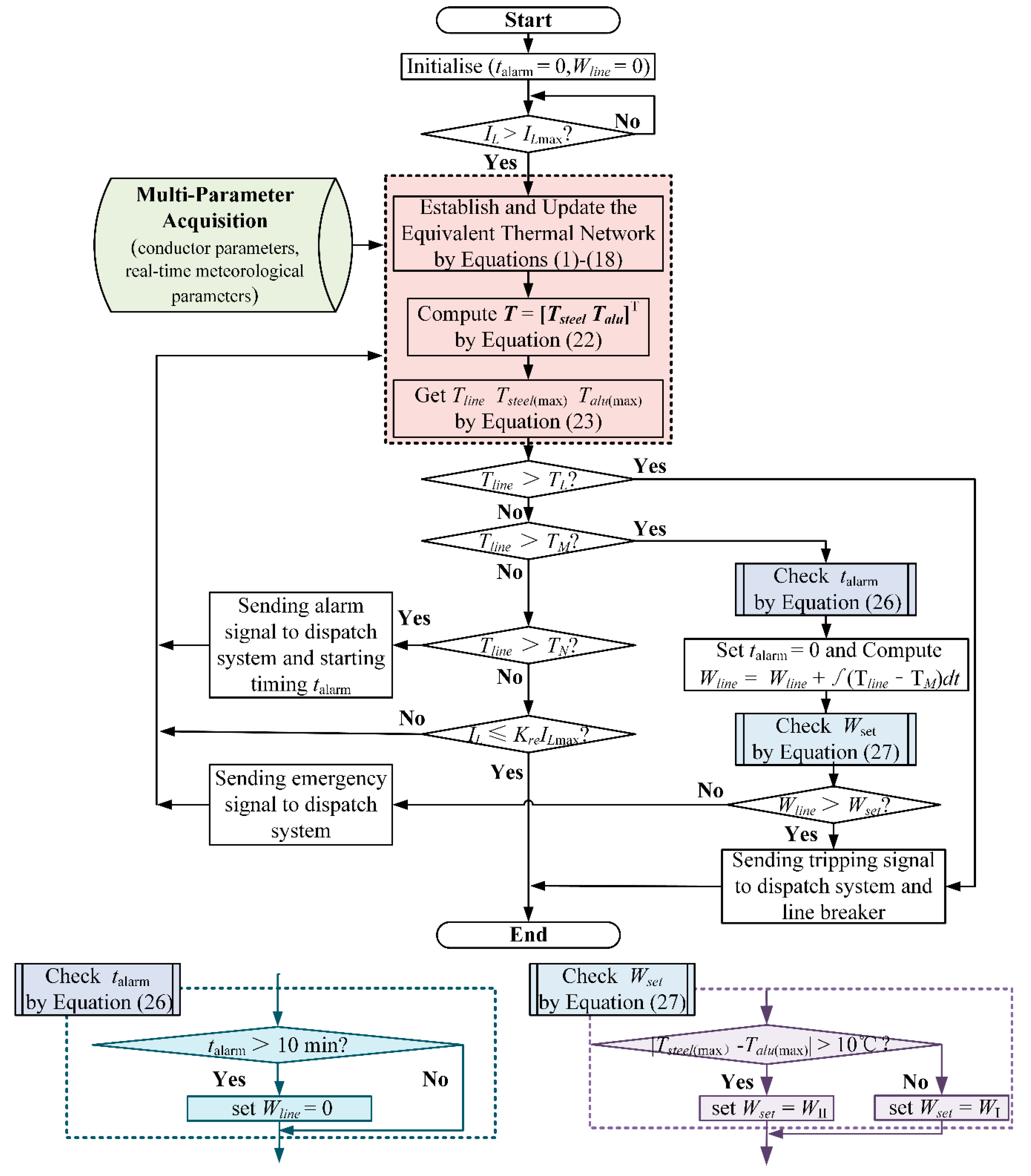
5. MPTP Based on the Transient Temperature of Overhead Transmission Lines
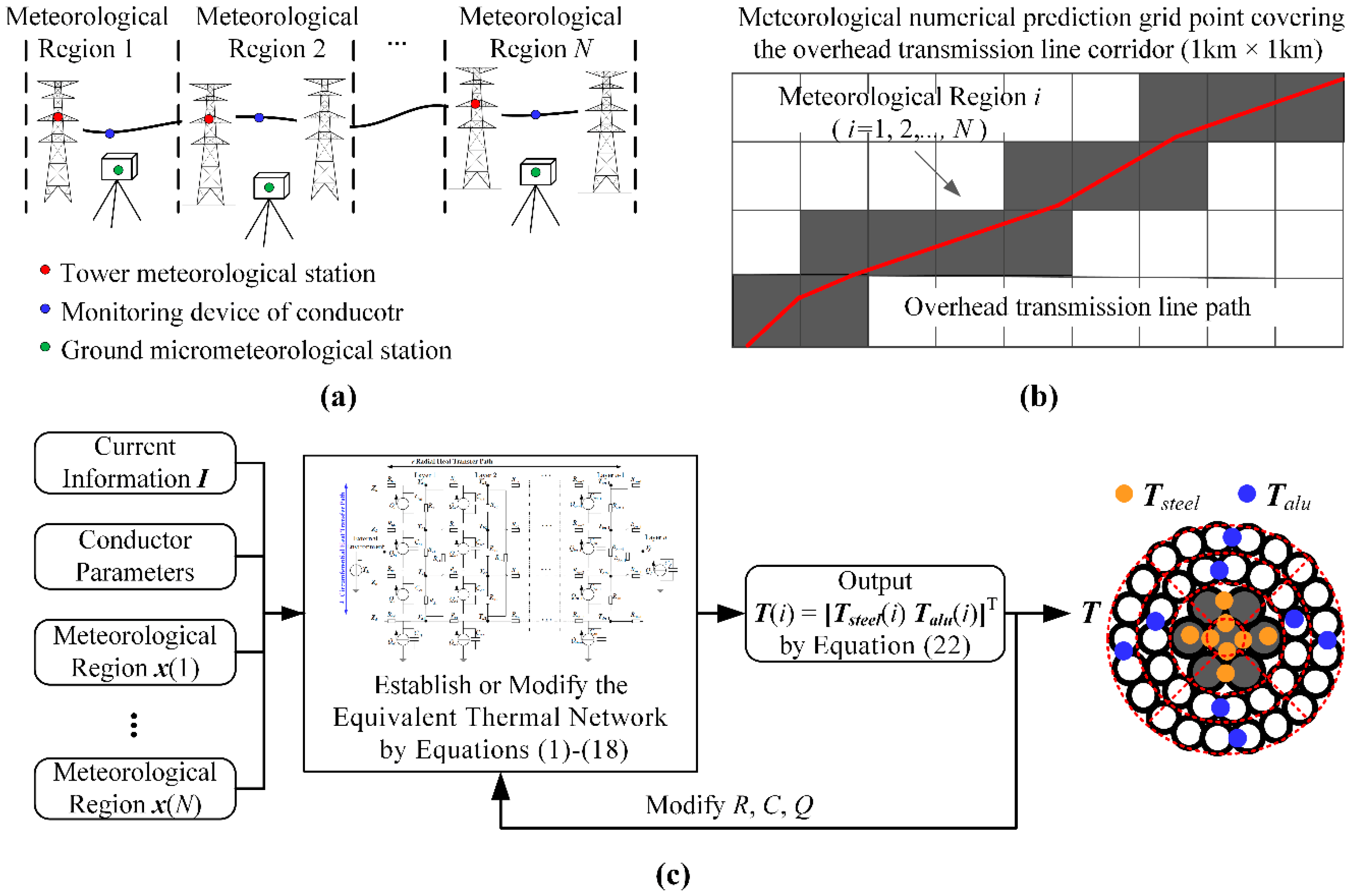
5.1. Transient Temperature Estimation of the Entire Overhead Transmission Lines
5.2. MPTP Strategy of Overhead Transmission Lines
- Step 1:
- Initialize talarm and Wline to 0. Determine whether the operating current IL is greater than the maximum load current ILmax. Proceed to Step 2 when the start-up criterion of protection IL > ILmax is satisfied.
- Step 2:
- Obtain the meteorological parameters around the transmission line and conductor parameters. Then, modify the ETN in real-time by Equations (22) and (23), and calculate the transient temperature rise response. Proceed to Step 3.
- Step 3:
- Assess whether the calculated Tline is greater than the limit temperature TL. Send a trip signal to the dispatching system and the breaker of the transmission line to remove the line when criterion Tline > TL is satisfied. End the MPTP algorithm. Proceed to Step 4 when the Tline does not exceed TL.
- Step 4:
- Determine whether the calculated Tline is greater than the emergency temperature TM. Otherwise, proceed to Step 5. Evaluate the talarm using Equation (26) when criterion Tline > TM is satisfied, and calculate the temperature–time integral Wline. Then, verify the emergency thermal setting value Wset using Equation (27), and compare the values of Wline and Wset. If the criterion Wline > Wset is satisfied, a trip signal to the dispatching system and the breaker cuts off the line, and the algorithm ends. If the criterion Wline > Wset is not satisfied, an emergency warning signal is sent to the dispatching system, and the algorithm returns to Step 2 to continue the calculation of transient temperature rise and thermal safety assessment for transmission line.
- Step 5:
- Assess whether the calculated Tline is greater than the alarm temperature TN. Send an alarm signal to the dispatching system and start the talarm when criterion Tline > TL is satisfied. Furthermore, return to Step 2. Proceed to Step 6 when criterion Tline > TN is unsatisfied.
- Step 6:
- Determine whether operating current IL is lower than return current KreILmax (Kre is the return coefficient, generally set to 0.9). End the protection algorithm when criterion IL ≤ KreILmax is satisfied. Otherwise, return to Step 2, and continue the calculation of the transient temperature rise response and thermal safety assessment of the transmission line.
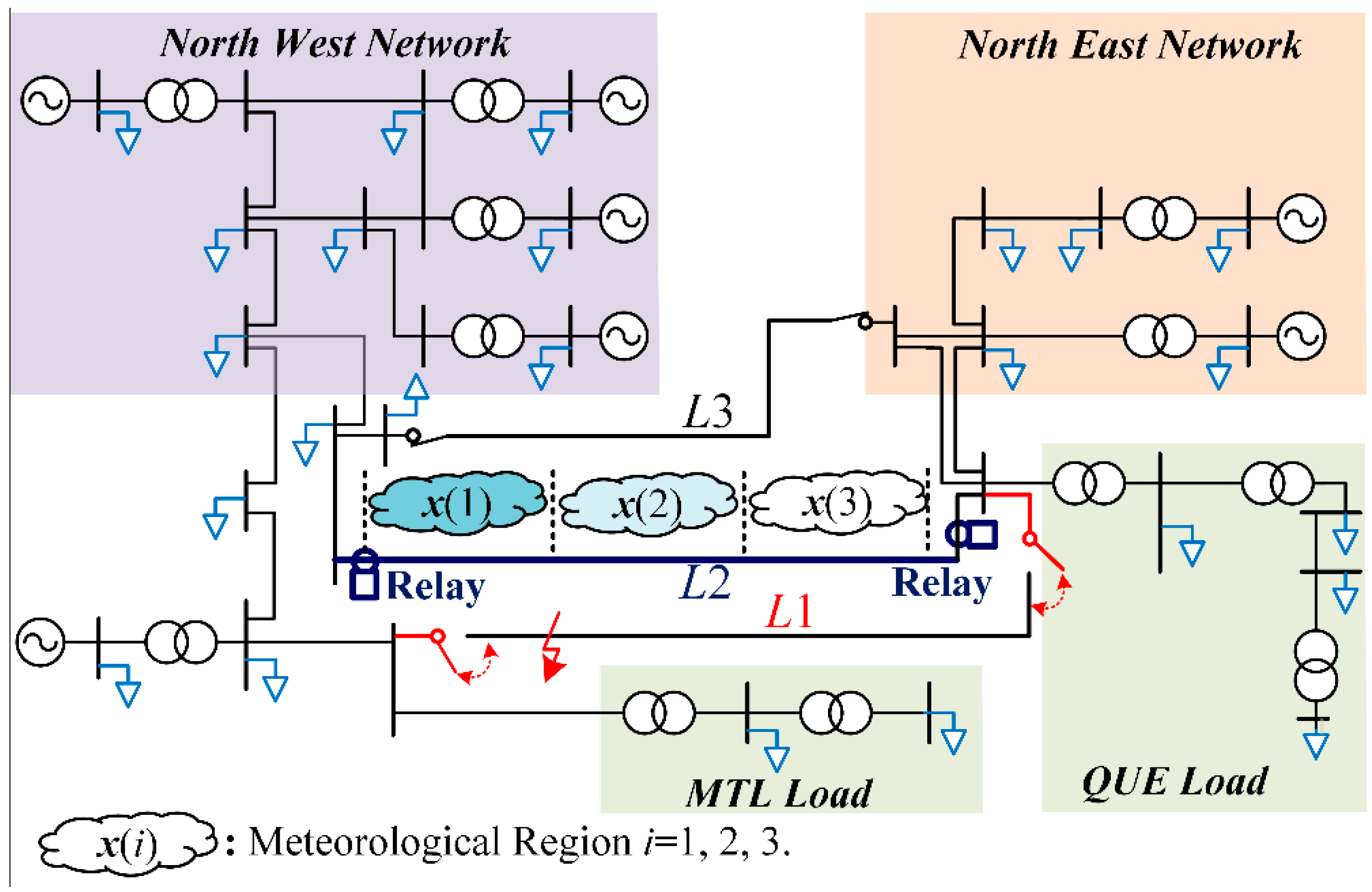
6. Case Study for Protection of Overhead Transmission Lines
6.1. Test System
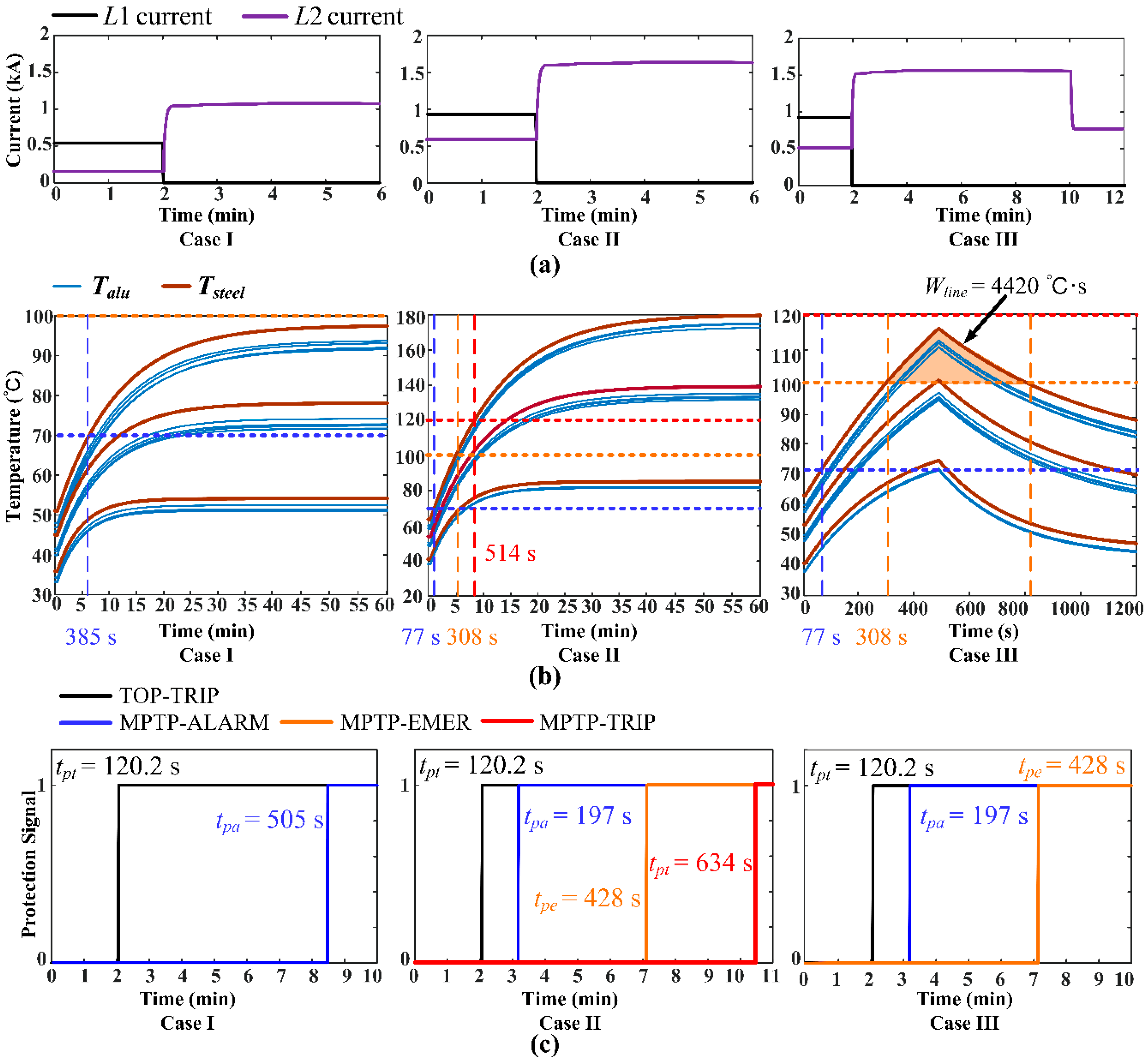
6.2. Results and Discussion
- Case I:
- Line L3 is in a normal operation, Line L1 trips at t = 120 s due to a fault, and Line L2 is overloaded.
- Case II:
- Line L3 is disconnected due to maintenance, Line L1 trips at t = 120 s due to a fault, and Line L2 is overloaded.
- Case III:
- Line L3 is disconnected due to maintenance, Line L1 trips at t = 120 s due to a fault, and Line L2 is overloaded, which is in accordance with Case II. However, the power flow is adjusted by power system security and stability controls. Thus, the current of Line L2 is reduced at t = 600 s.
7. Conclusions
- Conductor cross-section heat transfers under overloading conditions can be characterized in three types, namely, radial and circumferential heat conduction, convection, and radiation. The ETN can integrate the above-mentioned types and simultaneously reflect the temperature-dependent characteristics of resistivity, thermal convection resistance, and radiant heat flux. The comparison of the calculated results with the experimental results shows that the calculation precision of the ETN is better than the IEEE and CIGRE standard models. The calculated relative error does not exceed 7.59% under 95% confidence interval.
- The transient temperature estimation of transmission lines based on ETN can objectively characterize the dynamic safety state of the entire line. In comparison with the DTLR, the proposed method can better reflect the effects of non-uniform meteorological distribution along the line and the different temperature rise responses in different parts of the transmission line.
- The MPTP of the transmission line can provide more time than the TOP when eliminating overloads. The delay time of the MPTP does not reduce transmission line security, which is derived from the electro-thermal coupling analysis of the line. The MPTP calculation time can satisfy the engineering requirements, as confirmed by the case study.
Author Contributions
Funding
Conflicts of Interest
Appendix A
Appendix B
| Name | Model Number | Main Specification |
|---|---|---|
| Steel frame | Self-made | 0.8 × 0.8 × 2.0 m |
| Large current generator | SDDL-5000Q | Rated capacity: 30 kVA Output current: 0–5000 A Accuracy: 0.1 % |
| Controllable blower | HB-429 | Wind speed: 0–10 m/s |
| Current transformer | LXZK-0.66 | Ratio: 3200/5 A Rated Burden: 15 VA Accuracy: 0.2 % |
| Temperature sensor | PT1000 | Range: −70 °C–+500 °C Accuracy: ±0.03 °C (class 1/10B) |
| Ultrasonic anemometer | HY-WDS3 | Range: 0–60 m/s, 0–359° Resolution: 0.01 m/s, 0.1° |
| Radiation intensity measuring instrument | SPN1 | Range: 0–2000 W/m2 Resolution: 0.6 W/m2 |
| Multi-channel data acquisition device | Agilent 34970A & 34901A | Scan rate:250 Channels/s Resolution: 22 bits |
| Parameter | Value |
|---|---|
| Conductor outside diameter D0 (mm) | 26.82 |
| Steel core diameter (mm) | 7.5 |
| Aluminum outer strand diameter (mm) | 3.22 |
| Sectional area (mm2) | 425.24 |
| Emissivity ε 1 | 0.9 |
| Solar absorptivity δ 2 | 0.9 |
| Steel specific heat capacity at 20 °C, cs (J/kg· °C) | 481 |
| Aluminum specific heat capacity at 20 °C, ca (J/kg· °C) | 897 |
| Steel mass per unit length, ms (kg/m) | 0.267 |
| Aluminum mass per unit length, ma (kg/m) | 1.079 |
| Mass per unit length of steel (kg/m) | 1.349 |
References
- Abdullah, A.M.; Butler, K. Distance protection zone 3 misoperation during system wide cascading events: The problem and a survey of solutions. Electr. Power Syst. Res. 2018, 154, 151–159. [Google Scholar] [CrossRef]
- Ebrahim, V. Practical Power System Operation; Wiley-IEEE: Upper Saddle River, NJ, USA, 2014; ISBN 9781118394021. [Google Scholar]
- Bakar, A.A.; Yatim, F.M.; Yusof, S.; Othman, M.R. Analysis of overload conditions in distance relay under severe system contingencies. Int. J. Electr. Power Energy Syst. 2010, 32, 345–350. [Google Scholar] [CrossRef]
- Pavlatos, C.; Vita, V. Linguistic representation of power system signals. In Electricity Distribution; Energy Systems Series; Springer: Berlin/Heidelberg, Germany, 2016; pp. 285–295. [Google Scholar] [CrossRef]
- Andersson, G.; Donalek, P.; Farmer, R. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 2005, 20, 1922–1928. [Google Scholar] [CrossRef]
- Dong, X.; Cao, R.; Wang, B.; Shi, S.; Bak, D. India blackout and three functions of protective relay. Power Syst. Prot. Control 2013, 41, 19–25. [Google Scholar] [CrossRef]
- Rosas, C.M.; Sole, R. Analysis of major failures in Europe’s power grid. Int. J. Electr. Power Energy Syst. 2011, 33, 805–808. [Google Scholar] [CrossRef]
- Dong, X. Analytic method to calculate and characterize the sag and tension of overhead lines. IEEE Trans. Power Del. 2016, 31, 2064–2071. [Google Scholar] [CrossRef]
- Cooper, I.P.; Kopsidas, K.; Boumecid, B. Overhead line design considerations for conductor creep mitigation. IET Gener. Transm. Distrib. 2016, 10, 2424–2432. [Google Scholar] [CrossRef]
- IEEE. IEEE Std 1283-2013: IEEE Guide for Determining the Effects of High-Temperature Operation on Conductors, Connectors, and Accessories; IEEE Standard Association: Washington, DC, USA, 2013. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, W.; Shen, J. Online tracking of transmission-line parameters using SCADA data. IEEE Trans. Power Del. 2016, 31, 674–682. [Google Scholar] [CrossRef]
- Douglass, D.; Chisholm, W.; Davidson, G.; Grant, I.; Lindsey, K.; Lancaster, M.; Lawry, D.; McCarthy, T.; Nascimento, C.; Pasha, M.; et al. Real-time overhead transmission-line monitoring for dynamic rating. IEEE Trans. Power Deliv. 2016, 31, 921–927. [Google Scholar] [CrossRef]
- Zhou, Z.; Wang, X.; Du, D.; Li, Y.; Li, M. A coordination strategy between relay protection and stability control under overload conditions. Proc. CSEE 2013, 33, 146–155. [Google Scholar]
- Cong, Y.; Regulski, P.; Wall, P.; Osborne, M.; Terzija, V. On the use of dynamic thermal-line ratings for improving operational tripping schemes. IEEE Trans. Power Del. 2016, 31, 1891–1990. [Google Scholar] [CrossRef]
- Staszewski, Ł.; Rebizant, W. DLR-supported overcurrent line protection for blackout prevention. Elect. Power Syst. Res. 2018, 155, 104–110. [Google Scholar] [CrossRef]
- Carneiro, J.; Ferrarini, L. A probabilistic protection against thermal overloads of transmission lines. Electr. Power Syst. Res. 2011, 81, 1874–1880. [Google Scholar] [CrossRef]
- IEEE. IEEE Std 738-2012: IEEE Standard for Calculating the Current-Temperature Relationship of Bare Overhead Conductors; IEEE Standard Association: Washington, DC, USA, 2013. [Google Scholar]
- CIGRE Working Group B2. 42. Guide for Thermal Rating Calculations of Overhead Lines; Technical Brochure 601; CIGRE: Paris, France, 2014; Available online: https://e-cigre.org/publication/601-guide-for-thermal-ratingcalculations-of-overhead-lines (accessed on 15 August 2018).
- Arroyo, A.; Castro, P.; Martinez, R.; Manana, M.; Madrazo, A.; Lecuna, R.; Gonzalez, A. Comparison between IEEE and CIGRE thermal behavior standards and measured temperature on a 132-kV overhead power line. Energies 2015, 8, 13660–13671. [Google Scholar] [CrossRef]
- Sugihara, H.; Funaki, T.; Yamaguchi, N. Evaluation method for real-time dynamic line ratings based on line current variation model for representing forecast error of intermittent renewable generation. Energies 2017, 10, 503. [Google Scholar] [CrossRef]
- Alvarez, D.L.; Silva, F.M.F.D.; Mombello, E.E.; Bak, C.L.; Rosero, J.A. Conductor temperature estimation and prediction at thermal transient state in dynamic line rating application. IEEE Trans. Power Deliv. 2018, 33, 2236–2245. [Google Scholar] [CrossRef]
- Sarajlić, M.; Pihler, J.; Sarajlić, N.; Štumberger, G. Identification of the heat equation parameters for estimation of a bare overhead conductor’s temperature by the differential evolution algorithm. Energies 2018, 11, 2061. [Google Scholar] [CrossRef]
- Chatzipanagiotou, P.; Chatziathanasiou, V. Dynamic thermal analysis of a power line by simplified RC model networks: Theoretical and experimental analysis. Int. J. Electr. Power Energy Syst. 2019, 106, 288–293. [Google Scholar] [CrossRef]
- Liu, G.; Rung, B.; Zhnag, M. A transient model for overhead transmission line dynamic rating based on thermal circuit method. Autom. Electr. Power Syst. 2012, 16, 58–62. [Google Scholar] [CrossRef]
- Liu, G.; Ruan, B.; Lin, J.; Yang, M.; Zhang, M.; Xu, Z. Steady-state model of thermal circuit method for dynamic overhead lines rating. High Voltage Eng. 2013, 39, 1107–1113. [Google Scholar] [CrossRef]
- Zhang, X.; Ying, Z.; Chen, Y.; Chen, X. A thermal model for calculating axial temperature distribution of overhead conductor under laboratory conditions. Elect. Power Syst. Res. 2019, 166, 223–231. [Google Scholar] [CrossRef]
- Ying, Z.; Du, Z.; Feng, K.; Liu, Y.; Wu, J. Radial thermal circuit model and parameter calculation method for high voltage overhead transmission line. Trans. Chin. Electrotech. Soc. 2016, 31, 13–21. [Google Scholar]
- Ying, Z.; Kai, F.; Du, Z.; Liu, Y.; Wu, J. Thermal circuit modeling of the relationship between current and axial temperature for high voltage overhead conductor. Proc. CSEE 2015, 35, 2887–2895. [Google Scholar] [CrossRef]
- Makhkamova, I.; Mahkamov, K.; Taylor, P. CFD thermal modelling of Lynx overhead conductors in distribution networks with integrated renewable energy driven generators. Appl. Thermal Eng. 2013, 58, 522–535. [Google Scholar] [CrossRef]
- Farzaneh, M.; Farokhi, S.; Chisholm, W. Electrical Design of Overhead Power Transmission Lines; McGraw-Hill: New York, NY, USA, 2012; ISBN 9780071771917. [Google Scholar]
- Stephan, K. Heat and Mass Transfer; Springer: Singapore, 2017; ISBN 9783540295266. [Google Scholar]
- Cotton, I.; The, J. Critical span identification model for dynamic thermal rating system placement. IET Gener. Transm. Distrib. 2015, 16, 2644–2652. [Google Scholar] [CrossRef]
- Greenwood, D.M.; Gentle, J.P.; Myers, K.S.; Davison, P.J.; West, I.J.; Bush, J.W.; Ingram, G.L.; Troffaes, M.C. A comparison of real time thermal rating systems in the U.S. and the UK. IEEE Trans. Power Deliv. 2014, 29, 1849–1858. [Google Scholar] [CrossRef]
- Lo, C.F.; Yang, Z.L.; Pielke, R.A. Assessment of three dynamical climate downscaling methods using the Weather Research and Forecasting (WRF) model. J. Geophys. Res. 2008, 13, 91–112. [Google Scholar] [CrossRef]
- Verbois, H.; Huva, R.; Rusydi, A.; Walsh, W. Solar irradiance forecasting in the tropics using numerical weather prediction and statistical learning. Solar Energy 2018, 162, 265–277. [Google Scholar] [CrossRef]
- China Association for Engineering Construction Standardization, CECS. Load Code for the Design of Building Structure; China Architecture Building Press: Beijing, China, 2012; ISBN 9787112071050. [Google Scholar]
- Yi, D.; Yangchun, C.; Wanli, Z.; Jiedong, L. Dynamic Capacity Increasing Technology of High Voltage Overhead Transmission Line; China Electric Power Press: Beijing, China, 2013; ISBN 9787512341951. [Google Scholar]
- CIGRE Working Group B2. 42. Guide to the Operation of Conventional Conductor Systems above 100 °C; Technical Brochure 643; CIGRE: Paris, France, 2015; Available online: https://e-cigre.org/publication/643-guide-to-the-operation-of-conventional-conductor-systems-above-100c (accessed on 15 August 2018).
- The Mathworks. Initializing a 29-Bus 7-Power Plant Network with the Load FlowTool of Powergui. 2018. Available online: https://ww2.mathworks.cn/help/physmod/sps/examples/initializing-a-29-bus-7-power-plant-network-with-the-load-flow-tool-of-powergui.html (accessed on 15 August 2018).



| Current (A) | Wind Speed (m/s) |
|---|---|
| 300 | 0 |
| 400 | 0.5 |
| 500 | 1.0 |
| 600 | 1.5 |
| 700 | 2.0 |
| 800 | 2.5 |
| 900 | 3.0 |
| Current (A) | Air Temperature ( °C) | Wind Speed (m/s) |
|---|---|---|
| 1000 | 15 | 0.5 |
| 1100 | 20 | 2.0 |
| 1200 | 35 | 3.0 |
| Regions | Air Temperature ( °C) | Wind Speed 1 (m/s) | Radiation Intensity (W/m2) |
|---|---|---|---|
| x(1) | 30 | 4.0 | 800 |
| x(2) | 35 | 2.0 | 1200 |
| x(3) | 40 | 1.0 | 1000 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, J.; Xiong, X.; Chen, J.; Wang, W.; Wang, J. Transient Temperature Calculation and Multi-Parameter Thermal Protection of Overhead Transmission Lines Based on an Equivalent Thermal Network. Energies 2019, 12, 67. https://doi.org/10.3390/en12010067
Hu J, Xiong X, Chen J, Wang W, Wang J. Transient Temperature Calculation and Multi-Parameter Thermal Protection of Overhead Transmission Lines Based on an Equivalent Thermal Network. Energies. 2019; 12(1):67. https://doi.org/10.3390/en12010067
Chicago/Turabian StyleHu, Jian, Xiaofu Xiong, Jing Chen, Wei Wang, and Jian Wang. 2019. "Transient Temperature Calculation and Multi-Parameter Thermal Protection of Overhead Transmission Lines Based on an Equivalent Thermal Network" Energies 12, no. 1: 67. https://doi.org/10.3390/en12010067
APA StyleHu, J., Xiong, X., Chen, J., Wang, W., & Wang, J. (2019). Transient Temperature Calculation and Multi-Parameter Thermal Protection of Overhead Transmission Lines Based on an Equivalent Thermal Network. Energies, 12(1), 67. https://doi.org/10.3390/en12010067




