Closed-Form Solution of Radial Transport of Tracers in Porous Media Influenced by Linear Drift
Abstract
1. Introduction
2. Radial Diffusion Models with Drift
3. Mathematical Formulation of the Radial Transport Equation with Linear Drift
3.1. Introducing the Linear Drift
3.2. Analytical Solution
3.3. Weak-Form Numerical Solution of the Tracer Transport Equation
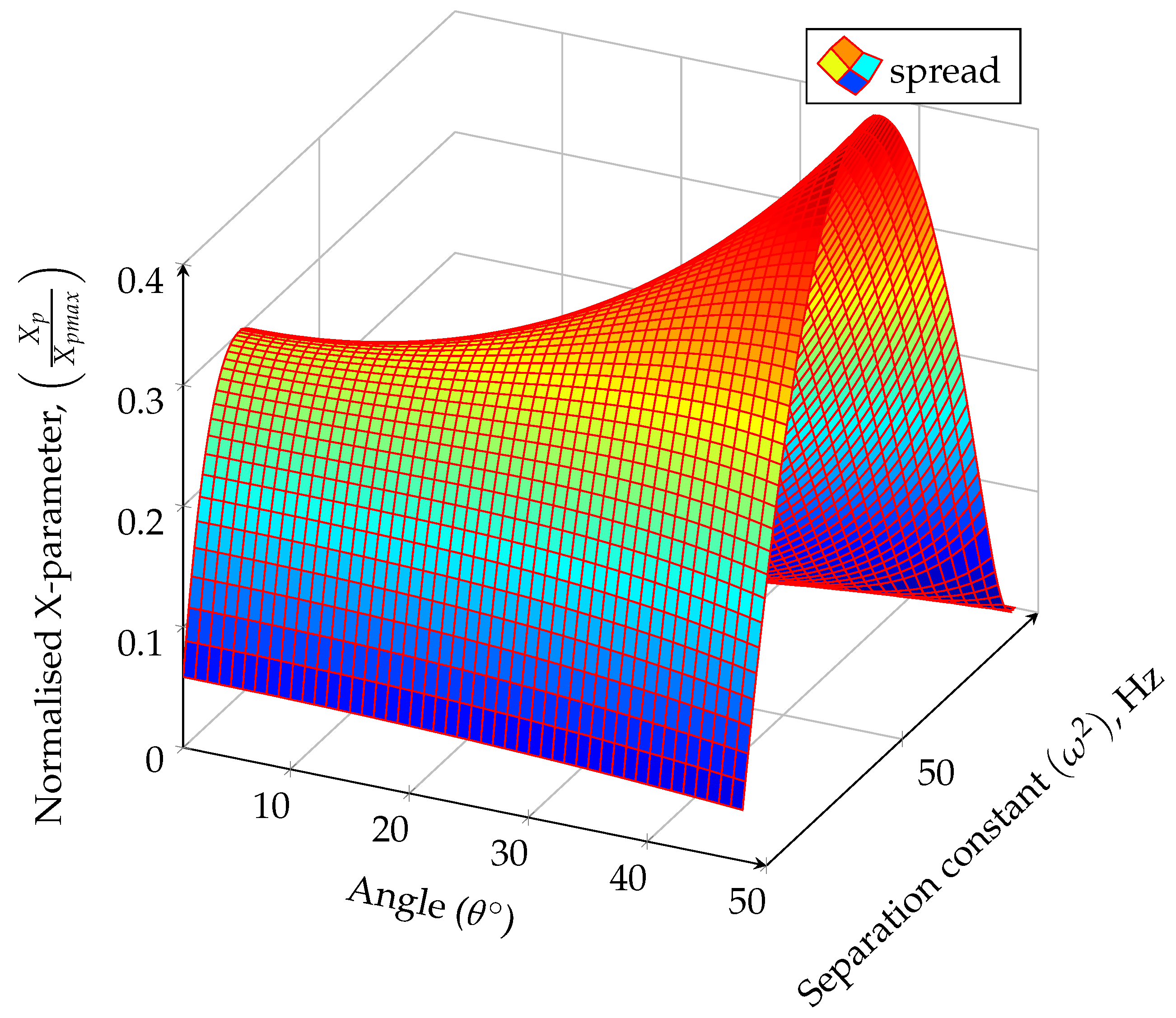
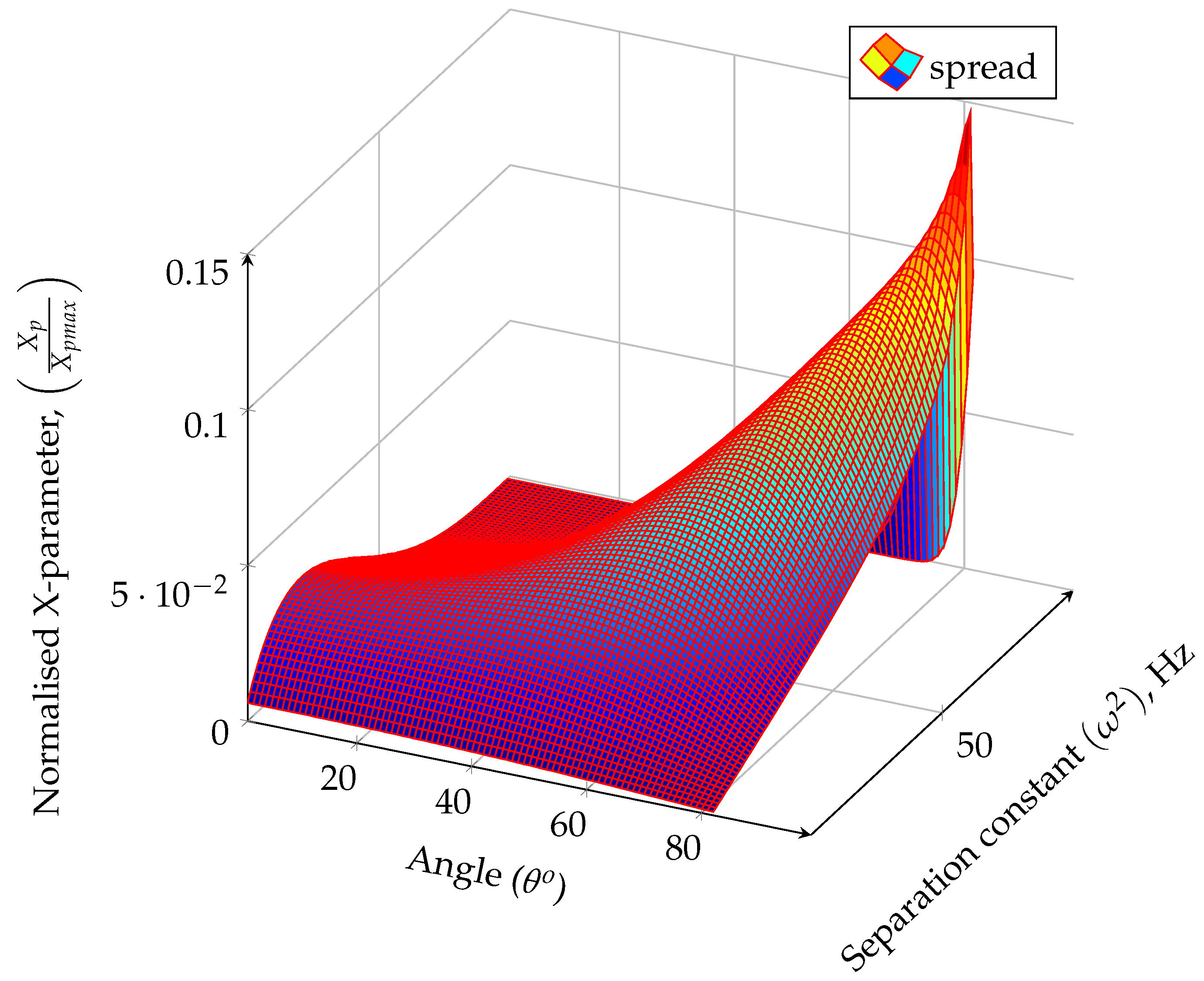
3.3.1. Separation Constant
3.3.2. Boundary and Initial Conditions
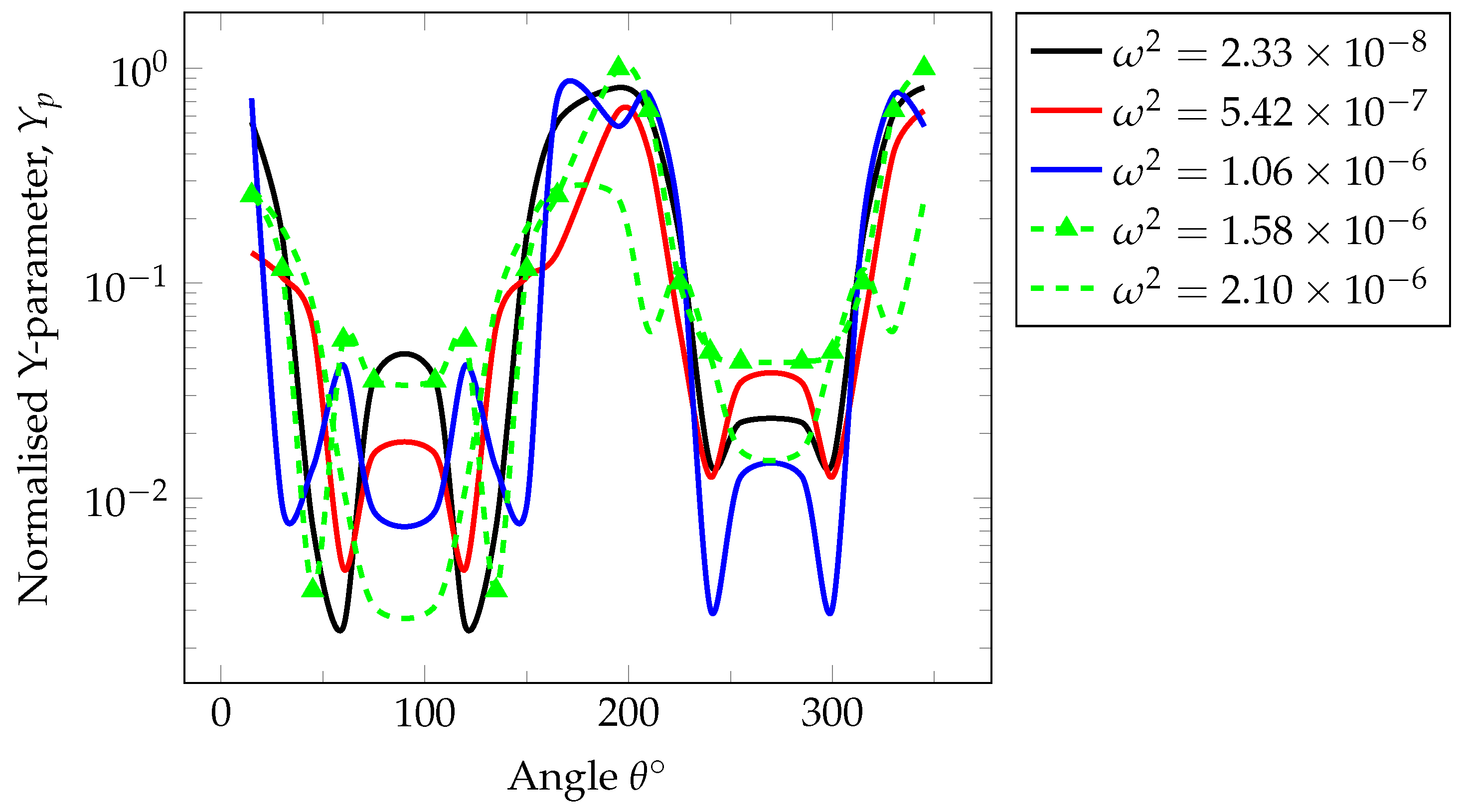
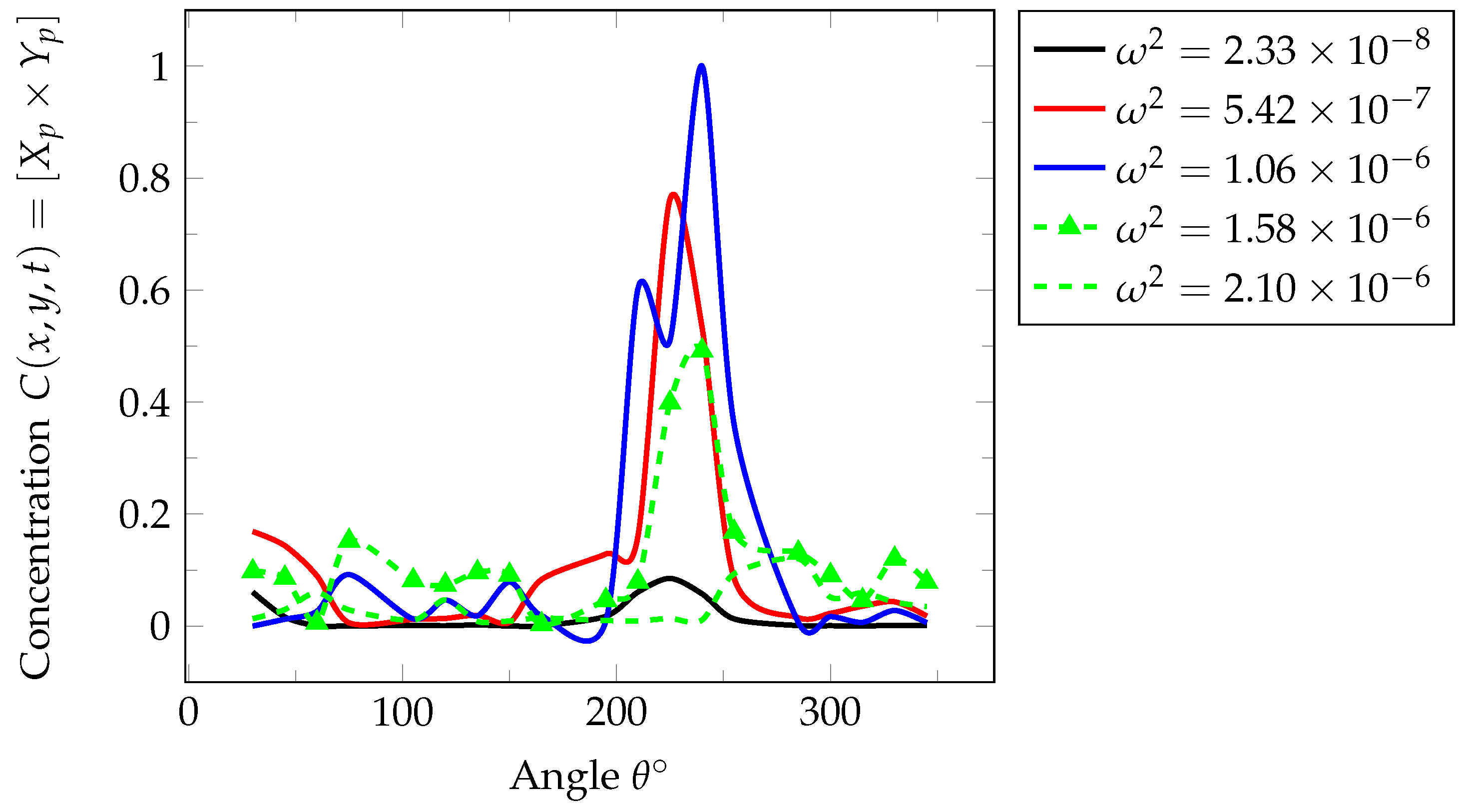
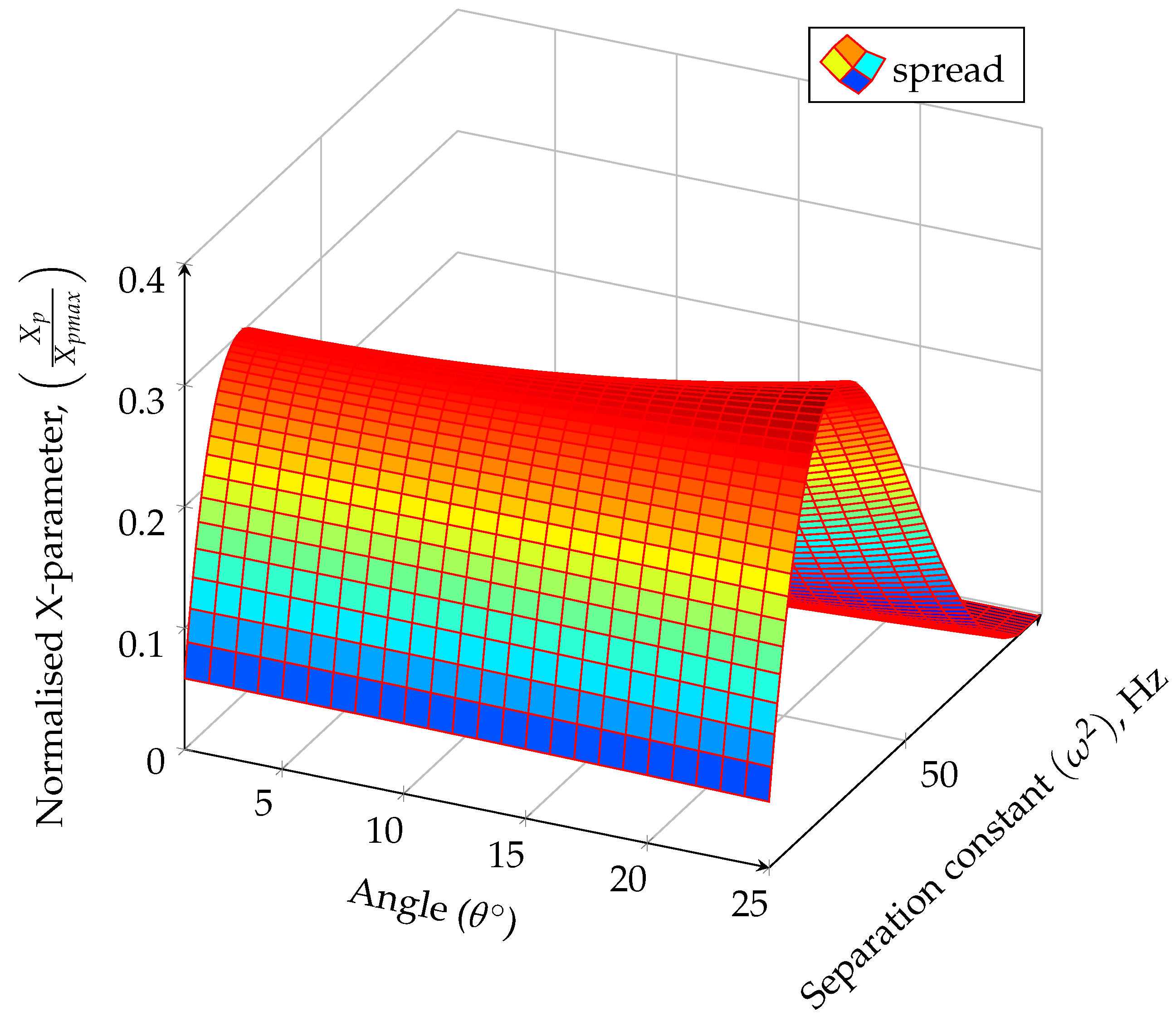
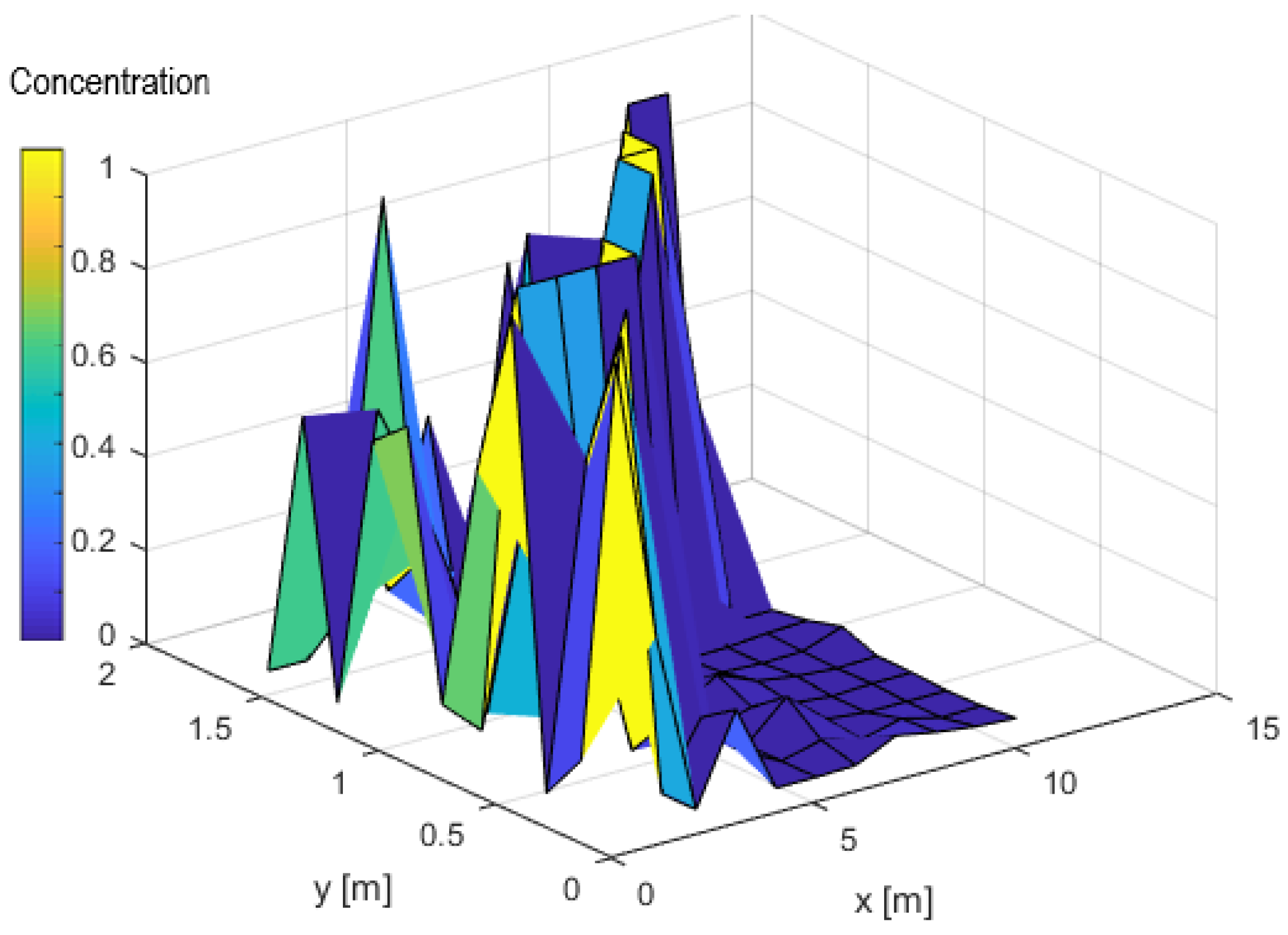
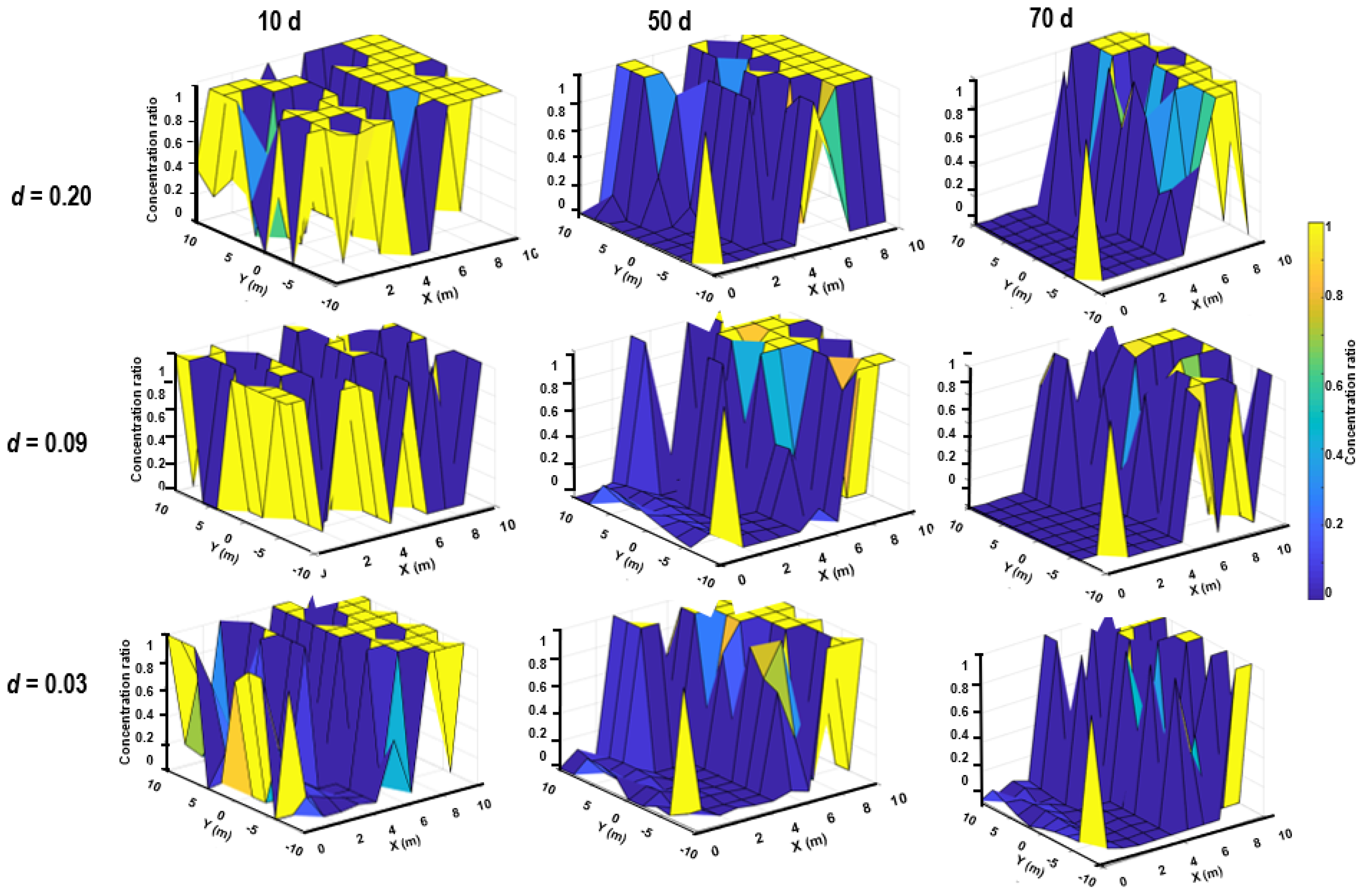
4. Analysis of Results
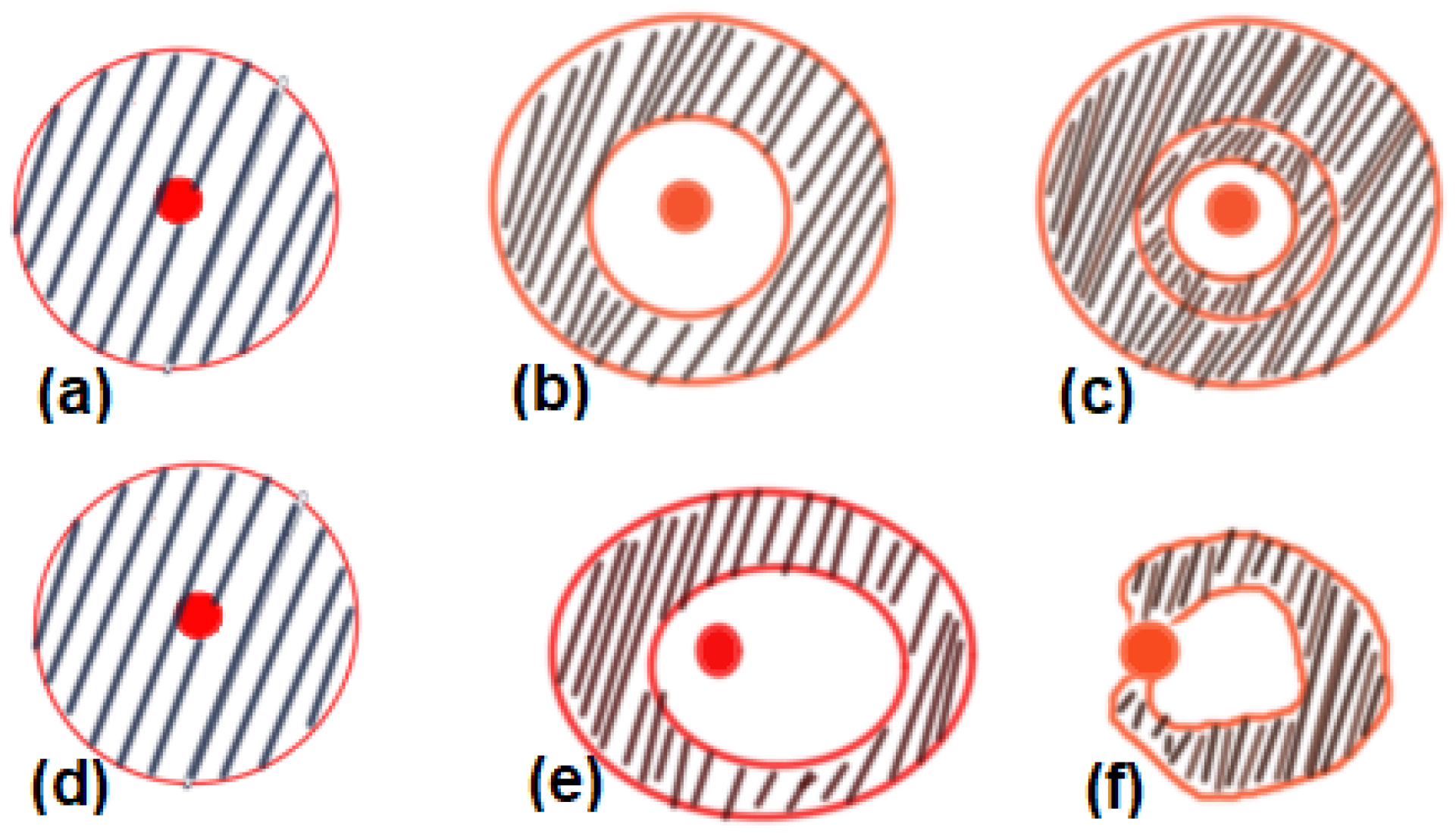
Linear Drift Effect and Concentration Distribution Profile
5. Conclusions
- A new closed-form analytical solution to the radial transport of tracers in porous media under the influence of linear drift and radial convection was developed. The radial transport equation was cast in the form of the Whittaker equation after adopting variable transformation and an exact solution for the tracer concentration derived therefrom.
- The weak-form solution was developed by splitting the transformed equation, adopting a common separation constant and invoking inverse Laplace transformation using the Euler inversion algorithm.
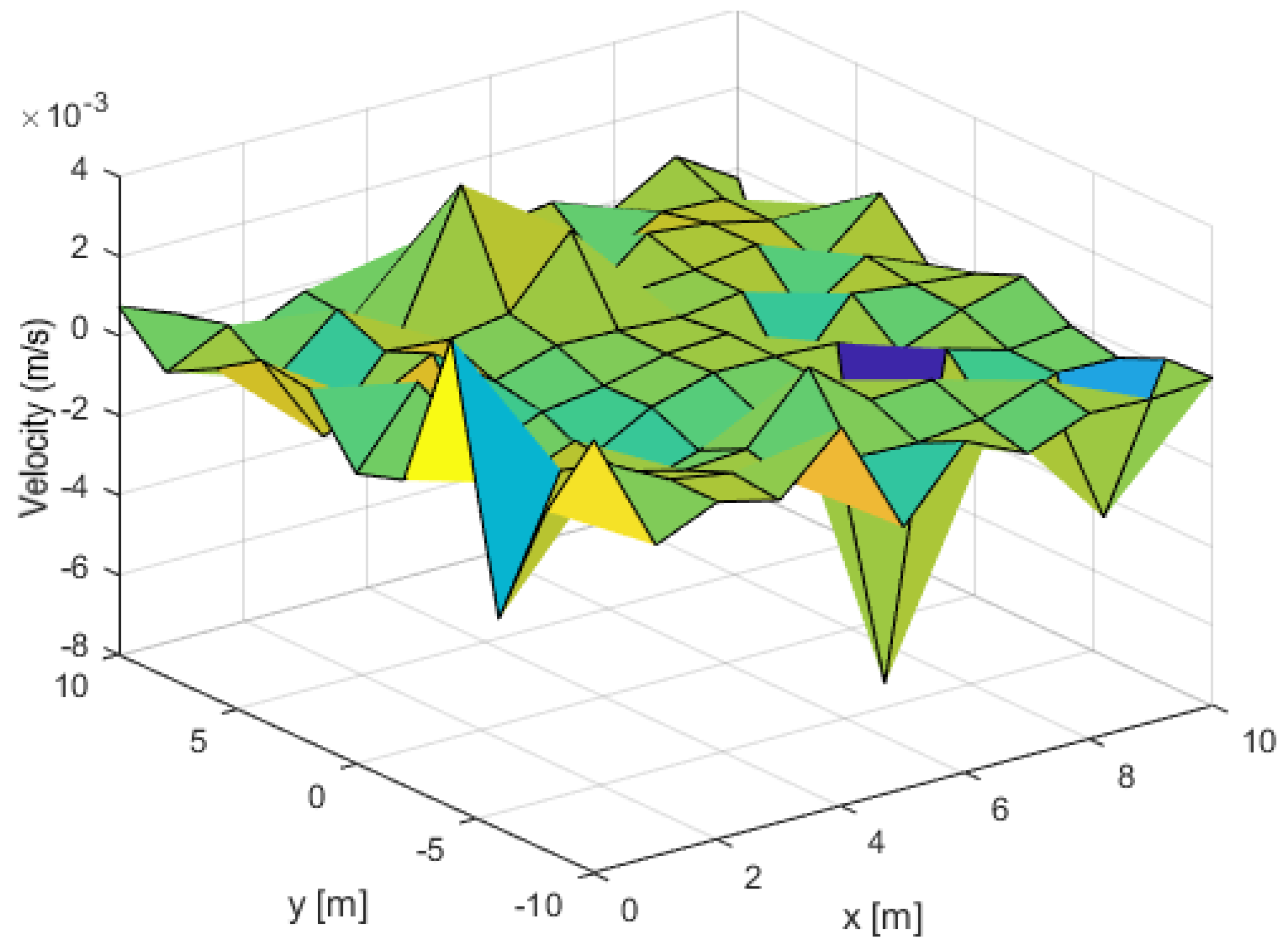
- Variable transformation from a radial to a Cartesian coordinate system was used to analyse the concentration distribution profiles in three-dimensional graphical plots.
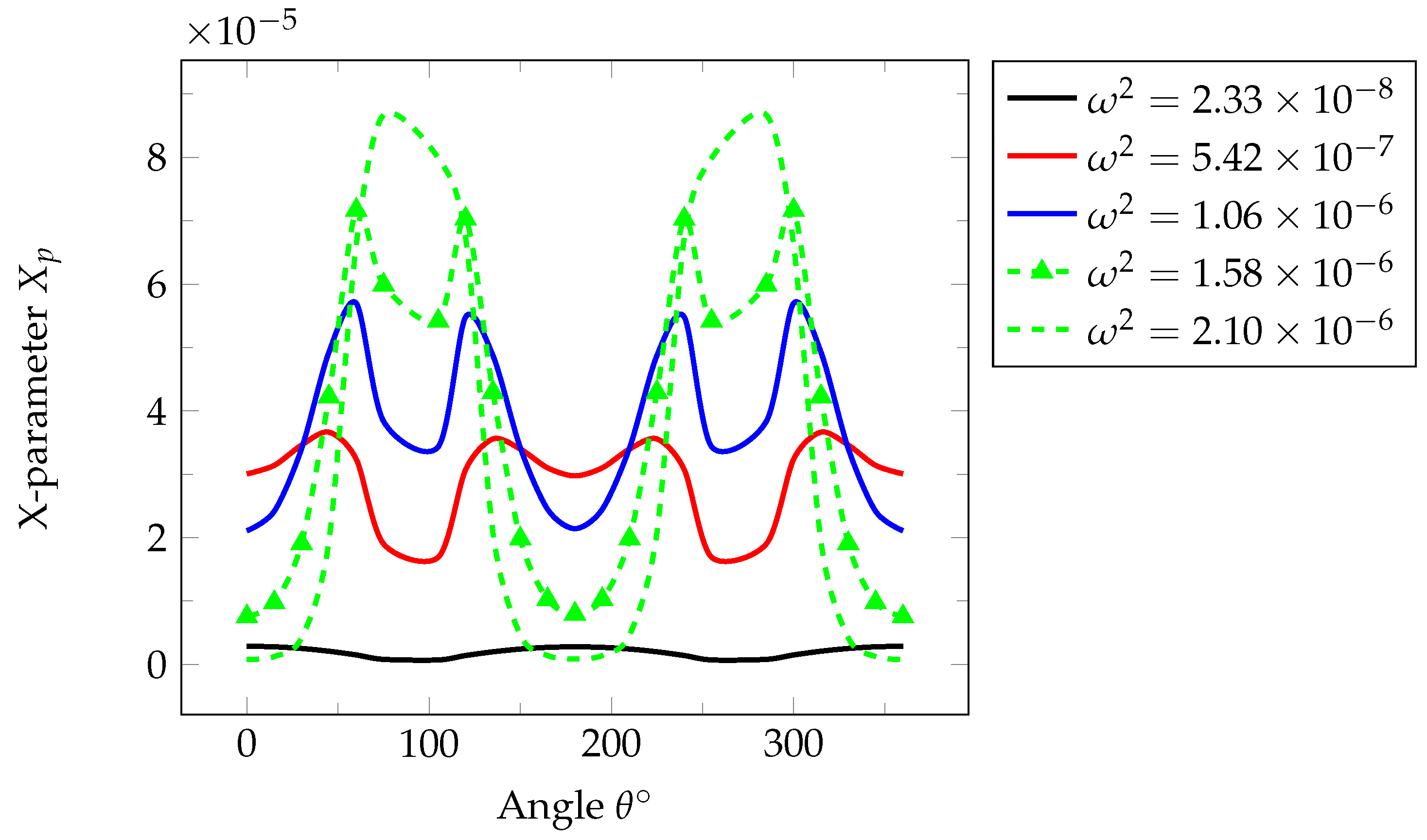
- The obtained solutions are generally stable and dependent on the precision with which the separation constant can be determined. This is important because the exponential term in the inversion formula may amplify the numerical error. The maximum error quantified by the separation constant is .
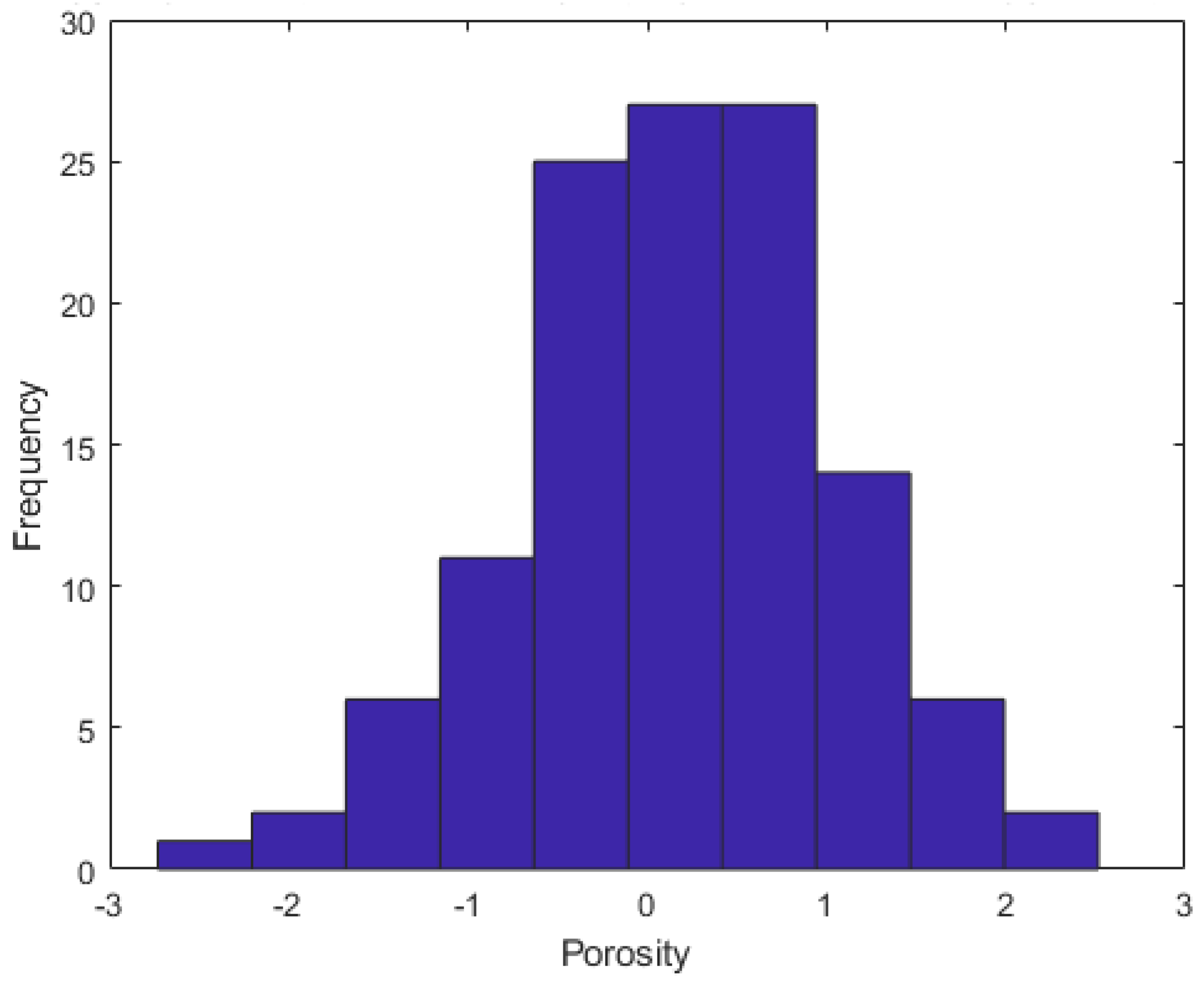
- The influence of linear drift on the concentration profiles was evaluated in the x-direction for a system with nonhomogeneous porosity distribution and variable velocity profiles.
- The results of the analyses indicated that the effect of linear drift on the tracer concentration profile is dependent on system heterogeneity and progressively becomes more pronounced at later times.
- Practical application was demonstrated in a typical EOR process involving the injection of chemicals (e.g., surfactants or polymers), but without a chemical reaction. Another possible application is a single-well chemical tracer injection method for measuring residual oil saturation and fluid flow behaviour and characterisation in porous media.
- This work can be extended to the analysis of systems involving variation of tracer injection intensity, where spreading may occur in the r- or x-y plane. The developed solution can also be extended to systems where moderate-to-high intensity tracer flow with linear drift manifests. In this case, the tangential velocity component of the drift velocity becomes significant and will have to be included in the solution approach.
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| Gamma function | |
| Whittaker and Kummer function parameters defined in the text | |
| Chemical reaction constant, (d) | |
| Laplace operator | |
| Absolute value of the separation constant | |
| Porosity, dimensionless | |
| Angle, () | |
| A | Constant of integration |
| Airy function of the 1st kind | |
| Airy function of the 2nd kind | |
| C | Tracer concentration |
| D | Flow hydrodynamic dispersion (m/s) |
| d | Drift ratio |
| Molecular diffusion constant | |
| Shear mixing constant | |
| h | Formation thickness, (m) |
| i | Unit vector along the x-axis |
| j | Unit vector along the y-axis |
| k | Unit vector along the z-axis |
| L | Length of dispersion, (m) |
| Q | Injection rate, (m/s) |
| r | Radial distance from the well, (m) |
| Dimensionless well-bore radius | |
| Well-bore radius, (m) | |
| s | Laplace parameter |
| Saturation of the mobile fluid phase | |
| Mobile fluid phase saturation, dimensionless | |
| t | Time, (s or d) |
| u | Velocity along the x-axis without linear drift, (m/s) |
| Tricomi Kummer U-function with parameters (a,b,z) | |
| Linear drift velocity, (m/s) | |
| Velocity at the well-bore (m/s) | |
| Velocity along the y-axis, (m/s) | |
| Whittaker function with parameters () | |
| x | x-coordinate variable |
| y | y-coordinate variable |
| D | dimensionless |
| d | drift |
| m | molecular |
| p | phase |
| r | reaction |
| w | well-bore |
Appendix A. Derivation of the Transport Flow Equation with Linear Drift
Appendix B. Analytical Solution—Dimensionless Representation and Inverse Laplace Transform
Appendix C. Weak-Form Solution—Separation Constant and Extended Confluent Hypergeometric Functions
References
- Baldwin, D.E. Prediction of Tracer Performance in a Five-Spot Pattern. J. Pet. Technol. 1966, 18, 513–517. [Google Scholar] [CrossRef]
- Rubin, J.; James, R.V. Dispersion affected transport of reacting solutes in saturated porous media: Galerkin Method applied to equilibrium-controlled exchange in unidirectional steady water flow. Water Resour. Res. 1973, 9, 1332–1356. [Google Scholar] [CrossRef]
- Moreno, L.; Neretnieks, I.; Klockars, C.E. Evaluation of Some Tracer Test in the Granitic Rock at FinnsjöRn; SKBF/KBS Tech; Technical Report 83-38; Nuclear Fuel Safety Project; SKB: Stockholm, Sweden, 1983. [Google Scholar]
- Herbert, A.W.; Hodgkinson, D.P.; Lever, D.A.; Rae, J.; Robinson, P.C. Mathematical modelling of radionuclide migration in groundwater. Q. J. Eng. Geol. 1986, 19, 109–120. [Google Scholar] [CrossRef]
- Mabuza, S.; Čanić, S.; Muha, B. Modeling and analysis of reactive solute transport in deformable channels with wall adsorption-desorption. Math. Methods Appl. Sci. 2016, 39, 1780–1802. [Google Scholar] [CrossRef]
- Vetter, O.J.; Zinnow, K.P. Evaluation of Well-to-Well Tracers for Geothermal Reservoirs; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 1981; Volume 14.
- Tomich, J.F.; Dalton, R.L.J.; Deans, H.A.; Shallenberger, L.K. Single-Well Tracer Method To Measure Residual Oil Saturation. J. Pet. Technol. 1973, 25, 211–218. [Google Scholar] [CrossRef]
- Bear, J. Dynamics of Fluids in Porous Media; Dover Civil and Mechanical Engineering; Dover Publications: Mineola, NY, USA, 2013. [Google Scholar]
- Zhou, R.; Zhan, H. Reactive solute transport in an asymmetrical fracture-rock matrix system. Adv. Water Resour. 2018, 112, 224–234. [Google Scholar] [CrossRef]
- Landa-Marbán, D.; Radu, F.A.; Nordbotten, J.M. Modeling and Simulation of Microbial Enhanced Oil Recovery Including Interfacial Area. Transp. Porous Media 2017, 120, 395–413. [Google Scholar] [CrossRef]
- Noetinger, B.; Roubinet, D.; Russian, A.; Borgne, T.L.; Delay, F.; Dentz, M.; de Dreuzy, J.; Gouze, P. Random Walk Methods for Modeling Hydrodynamic Transport in Porous and Fractured Media from Pore to Reservoir Scale. Transp. Porous Media 2016, 115, 345–385. [Google Scholar] [CrossRef]
- Zlotnik, V.A.; Logan, J.D. Boundary conditions for convergent radial tracer tests and effect of well bore mixing volume. Water Resour. Res. 1996, 32, 2323–2328. [Google Scholar] [CrossRef]
- Carslaw, H.S.; Jaeger, J.C. Conduction of Heat in Solids; Clarendon Press: Oxford, UK, 1959. [Google Scholar]
- Falade, G.K.; Brigham, W.E. Analysis of Radial Transport of Reactive Tracer in Porous Media. SPE Reserv. Eng. 1989, 4, 85–90. [Google Scholar] [CrossRef]
- Attinger, S.; Abdulle, A. Effective velocity for transport in heterogeneous compressible flows with mean drift. Phys. Fluids 2008, 20, 016102. [Google Scholar] [CrossRef]
- Vergassola, M.; Avellaneda, M. Scalar transport in compressible flow. Phys. D Nonlinear Phenom. 1997, 106, 148–166. [Google Scholar] [CrossRef]
- Moench, A.F.; Ogata, A. A numerical inversion of the Laplace transform solution to radial dispersion in a porous medium. Water Resour. Res. 1981, 17, 250–252. [Google Scholar] [CrossRef]
- Stehfest, H. Algorithm 368: Numerical inversion of Laplace transforms. Assoc. Comput. Mach. J. 1970, 13, 47–49. [Google Scholar]
- Abramowitz, M.; Stegun, I.A. Handbook of Mathematical Functions, Appl. Math. Ser. 55; National Bureau of Standards: Gaithersburg, MD, USA, 1964; p. 1046.
- Mashayekhizadeh, V.; Dejam, M.; Ghazanfari, M.H. The Application of Numerical Laplace Inversion Methods for Type Curve Development in Well Testing: A Comparative Study. Pet. Sci. Technol. 2011, 29, 695–707. [Google Scholar] [CrossRef]
- De-Hoog, F.R.; Knight, D.H.; Stokes, A.N. An Improved Method for Numerical Inversion of Laplace Transforms. SIAM J. Sci. Stat. Comput. 1982, 3, 357–366. [Google Scholar] [CrossRef]
- Dubner, H.; Abate, J. Numerical Inversion of Laplace Transforms by Relating Them to the Finite Fourier Cosine Transform. Assoc. Comput. Mach. J. 1968, 15, 115–123. [Google Scholar] [CrossRef]
- Zakian, V. Numerical inversion of Laplace transform. Electron. Lett. 1969, 5, 120–121. [Google Scholar] [CrossRef]
- Schapery, R.A. Approximate methods of transform inversion for viscoelastic stress analysis. In Proceedings of the 4th U.S. National Congress on Applied Mechanics, Berkeley, CA, USA, 18–21 June 1962; pp. 1075–1085. [Google Scholar]
- Brzeziński, D.W.; Ostalczyk, P. Numerical calculations accuracy comparison of the Inverse Laplace Transform algorithms for solutions of fractional order differential equations. Nonlinear Dyn. 2016, 84, 65–77. [Google Scholar] [CrossRef]
- Fick, A. Ueber Diffusion. Ann. Phys. 1855, 94, 59–86. (In German) [Google Scholar] [CrossRef]
- Skellam, J. Random Dispersal in Theoretical Populations. Biometrika 1951, 38, 196–218. [Google Scholar] [CrossRef] [PubMed]
- Whittaker, E.T. An expression of certain known functions as generalized hypergeometric functions. Bull. Am. Math. Soc. 1903, 10, 125–134. [Google Scholar] [CrossRef]
- Gaver, D.P. Observing stochastic processes and approximate transform inversion. Oper. Res. 1966, 14, 444–459. [Google Scholar] [CrossRef]
- Talbot, A. The accurate numerical inversion of Laplace transforms. IMA J. Appl. Math. 1979, 23, 97–120. [Google Scholar] [CrossRef]
- Abate, J.; Whitt., W. The Fourier-series method for inverting transforms of probability distributions. Queueing Syst. 1992, 10, 5–88. [Google Scholar] [CrossRef]
- Abate, J.; Whitt., W. Numerical inversion of Laplace transforms of probability distributions. Oper. Res. Soc. Am. J. Comput. 1995, 7, 36–43. [Google Scholar] [CrossRef]
- McClure, T. Numerical Inverse Laplace Transform. 2018. Available online: https://uk.mathworks.com/matlabcentral/fileexchange/39035-numerical-inverse-laplace-transform (accessed on 16 August 2017).
- Avdis, E.; Whitt, W. Power Algorithms for Inverting Laplace Transforms. INFORMS J. Comput. 2007, 19, 341–355. [Google Scholar] [CrossRef]
- Campos, L. On some solutions of the extended confluent hypergeometric differential equation. J. Comput. Appl. Math. 2001, 137, 177–200. [Google Scholar] [CrossRef]
- Spanier, J.; Oldham, K.B. An Atlas of Functions; Taylor & Francis/Hemisphere: Bristol, PA, USA, 1987. [Google Scholar]
- Slater, L.J. The Second Form of Solutions of Kummer’s Equations; Confluent Hypergeometric Functions; Cambridge University Press: Cambridge, UK, 1960. [Google Scholar]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Akanji, L.T.; Falade, G.K. Closed-Form Solution of Radial Transport of Tracers in Porous Media Influenced by Linear Drift. Energies 2019, 12, 29. https://doi.org/10.3390/en12010029
Akanji LT, Falade GK. Closed-Form Solution of Radial Transport of Tracers in Porous Media Influenced by Linear Drift. Energies. 2019; 12(1):29. https://doi.org/10.3390/en12010029
Chicago/Turabian StyleAkanji, Lateef T., and Gabriel K. Falade. 2019. "Closed-Form Solution of Radial Transport of Tracers in Porous Media Influenced by Linear Drift" Energies 12, no. 1: 29. https://doi.org/10.3390/en12010029
APA StyleAkanji, L. T., & Falade, G. K. (2019). Closed-Form Solution of Radial Transport of Tracers in Porous Media Influenced by Linear Drift. Energies, 12(1), 29. https://doi.org/10.3390/en12010029




