Sample Entropy Based Net Load Tracing Dispatch of New Energy Power System
Abstract
:1. Introduction
2. Characteristics of Net Loads and SampEn Calculation
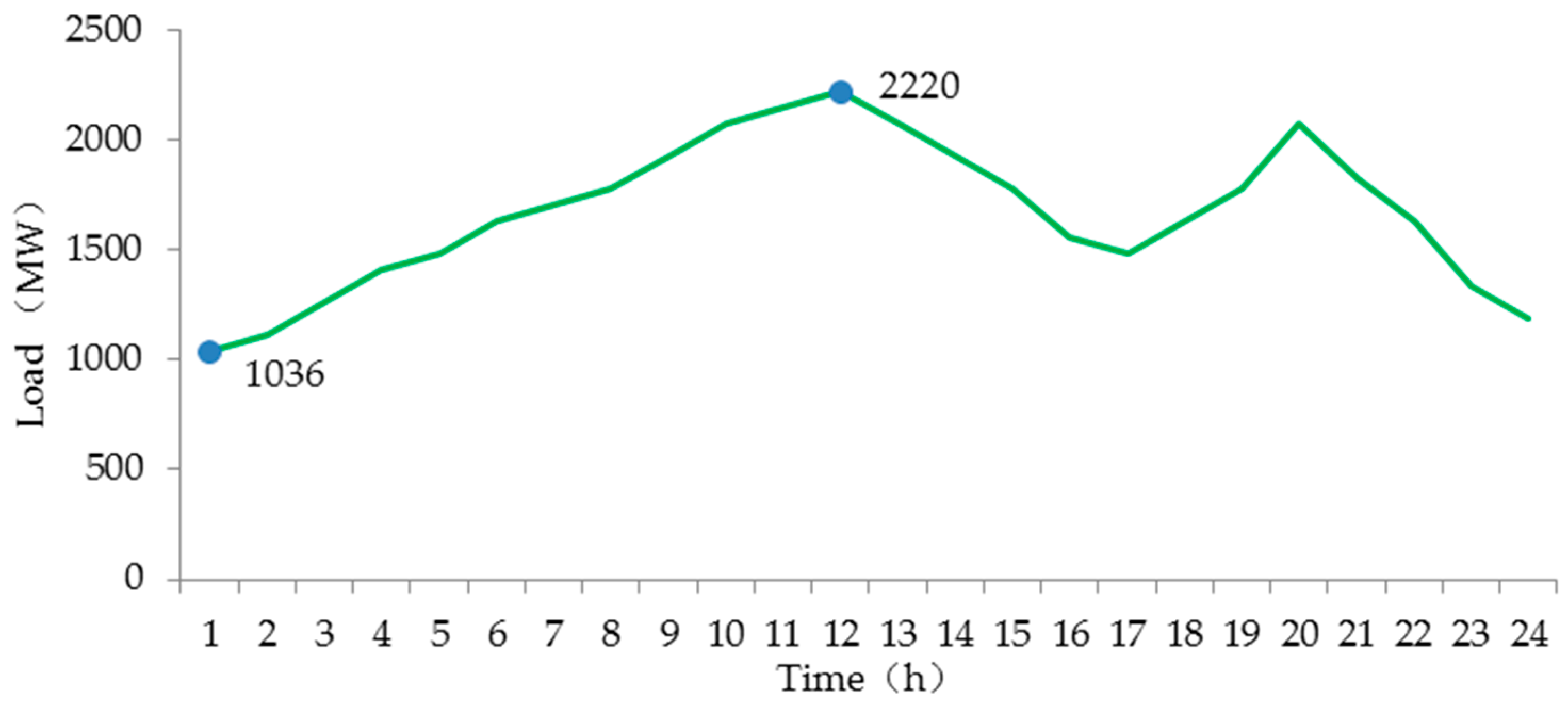
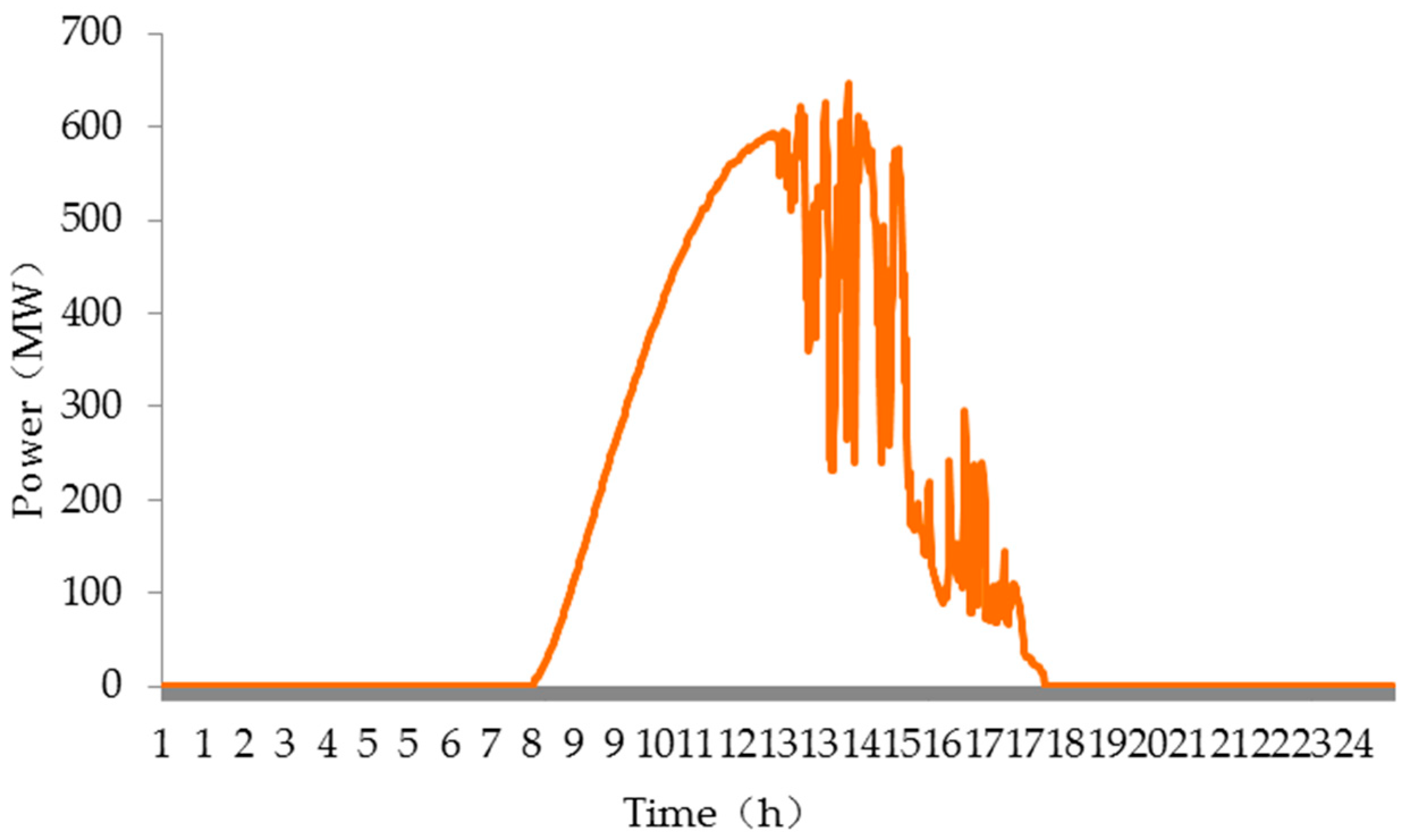
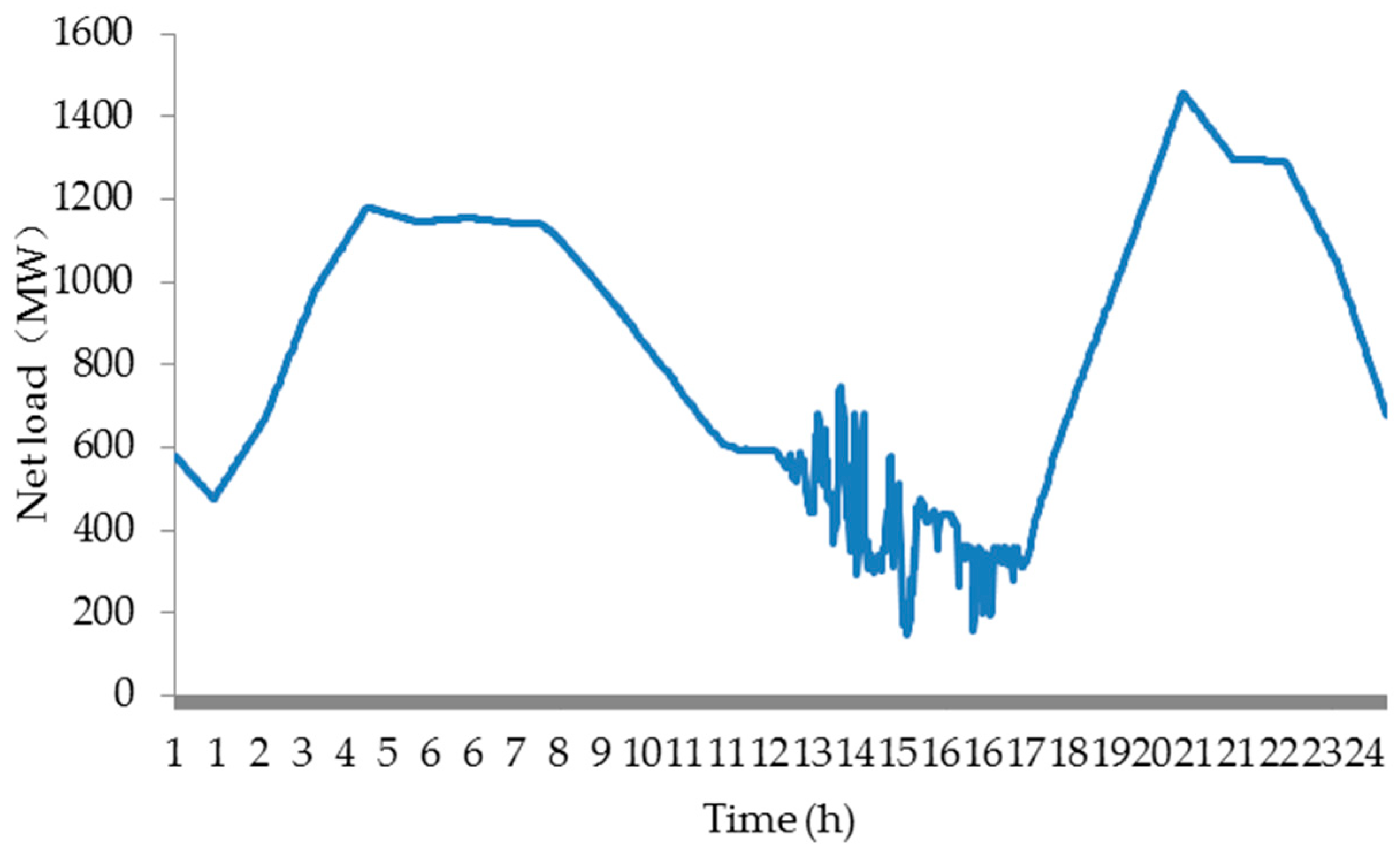
2.1. Net Loads Description
2.2. SampEn of Net Loads in New Energy Power System
2.3. SampEn Application of Net Loads
3. New Energy Net Load Tracing Dispatch Strategy Based on SampEn
3.1. Generating Mode of Thermal Generators
3.2. Power Dispatch Model Based on SampEn
3.2.1. Objective Functions
3.2.2. Power Balance Equations and Constraint Functions
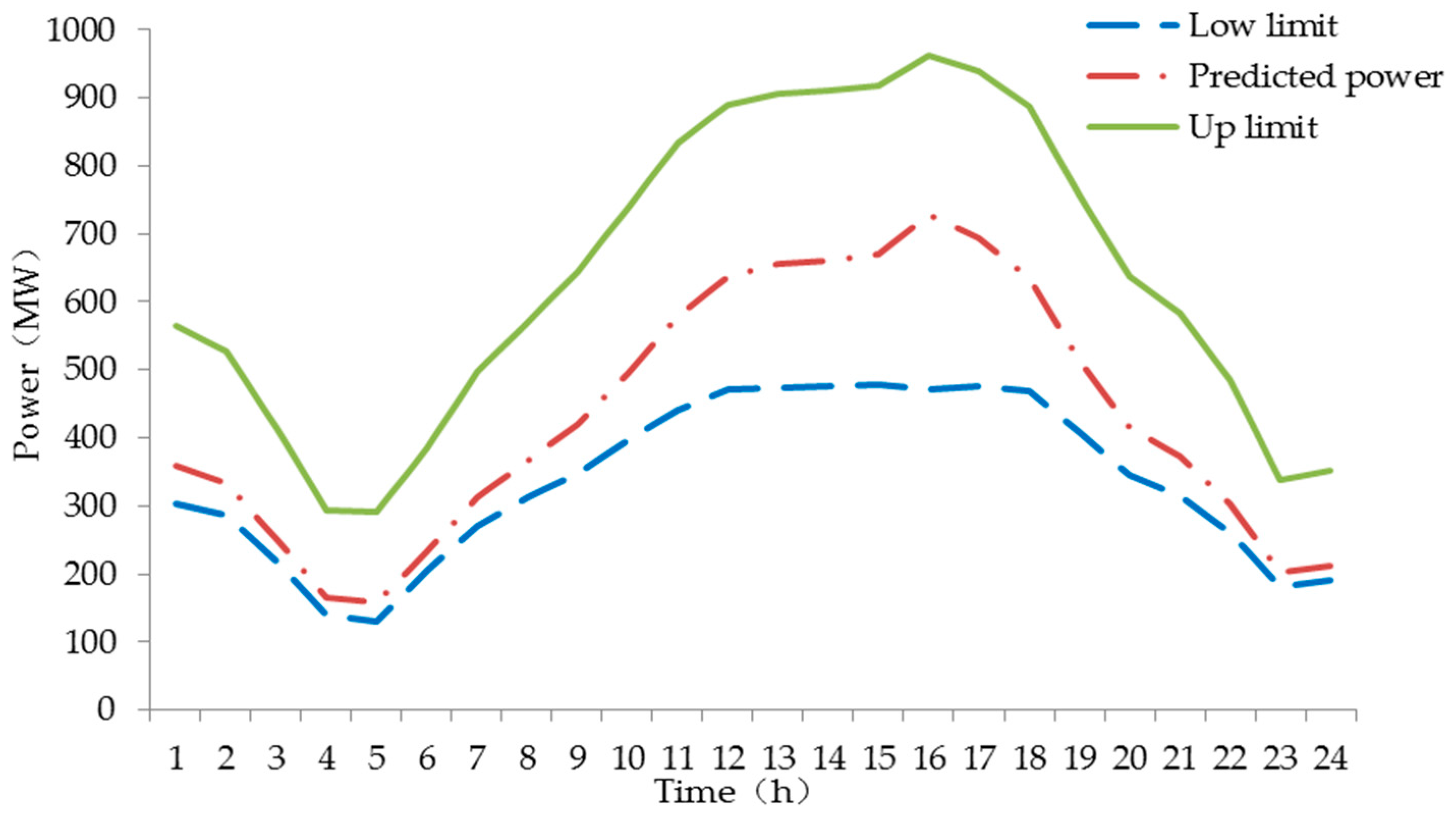
3.2.3. Stochastic Variables
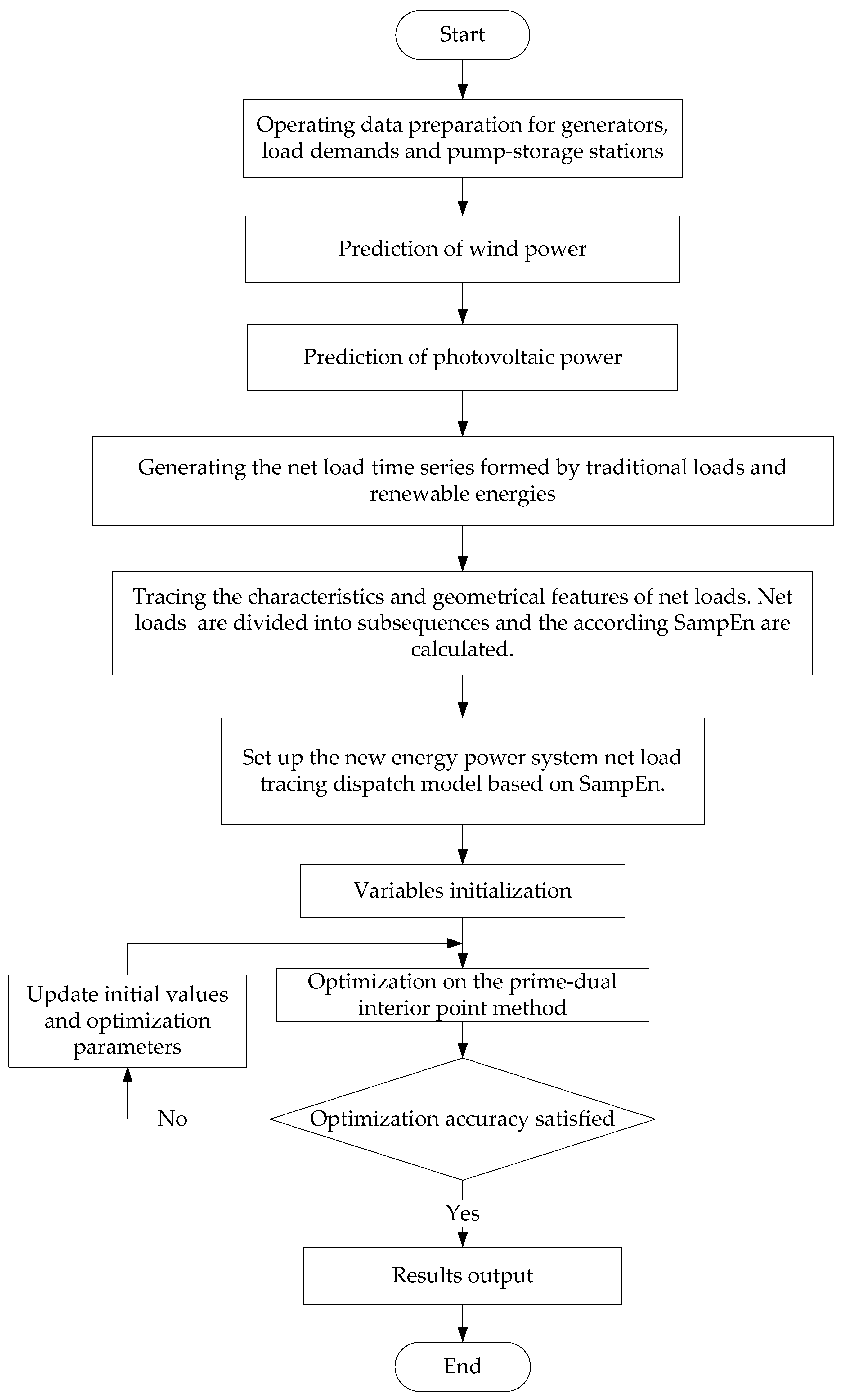
3.3. Power Dispatch Strategy Process Based On SampEn
4. Case Study
4.1. SampEn Calculation
4.2. Result Comparison and Analysis of Cases
- Case 1: power dispatch without SampEn and the wind power reserve confidence degree is 0.9.
- Case 2: power dispatch based on SampEn at wind power reserve confidence degree of 0.9.
- Case 3: power dispatch without SampEn and the wind power reserve confidence degree is 0.95.
- Case 4: power dispatch based on SampEn at wind power reserve confidence degree of 0.95.
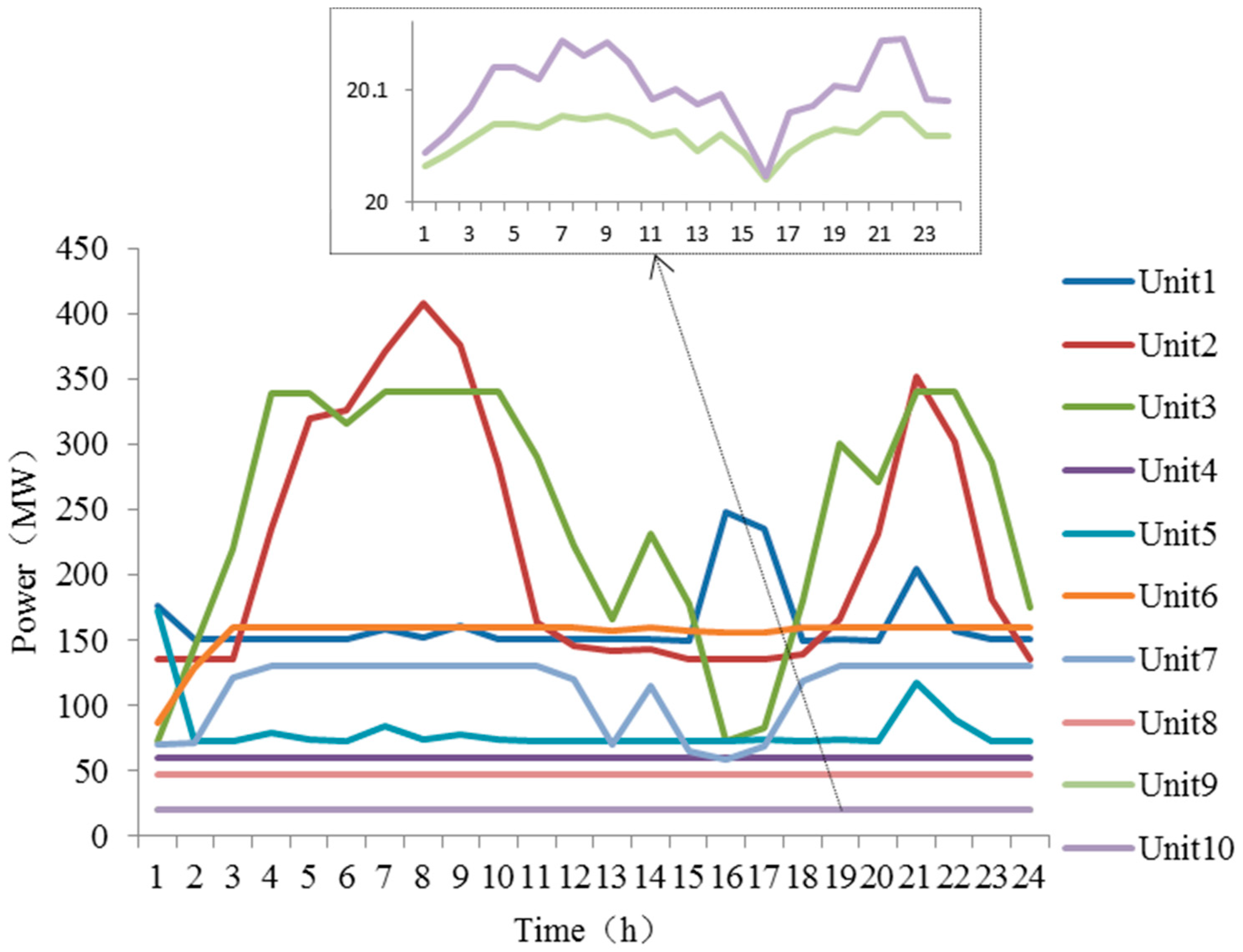
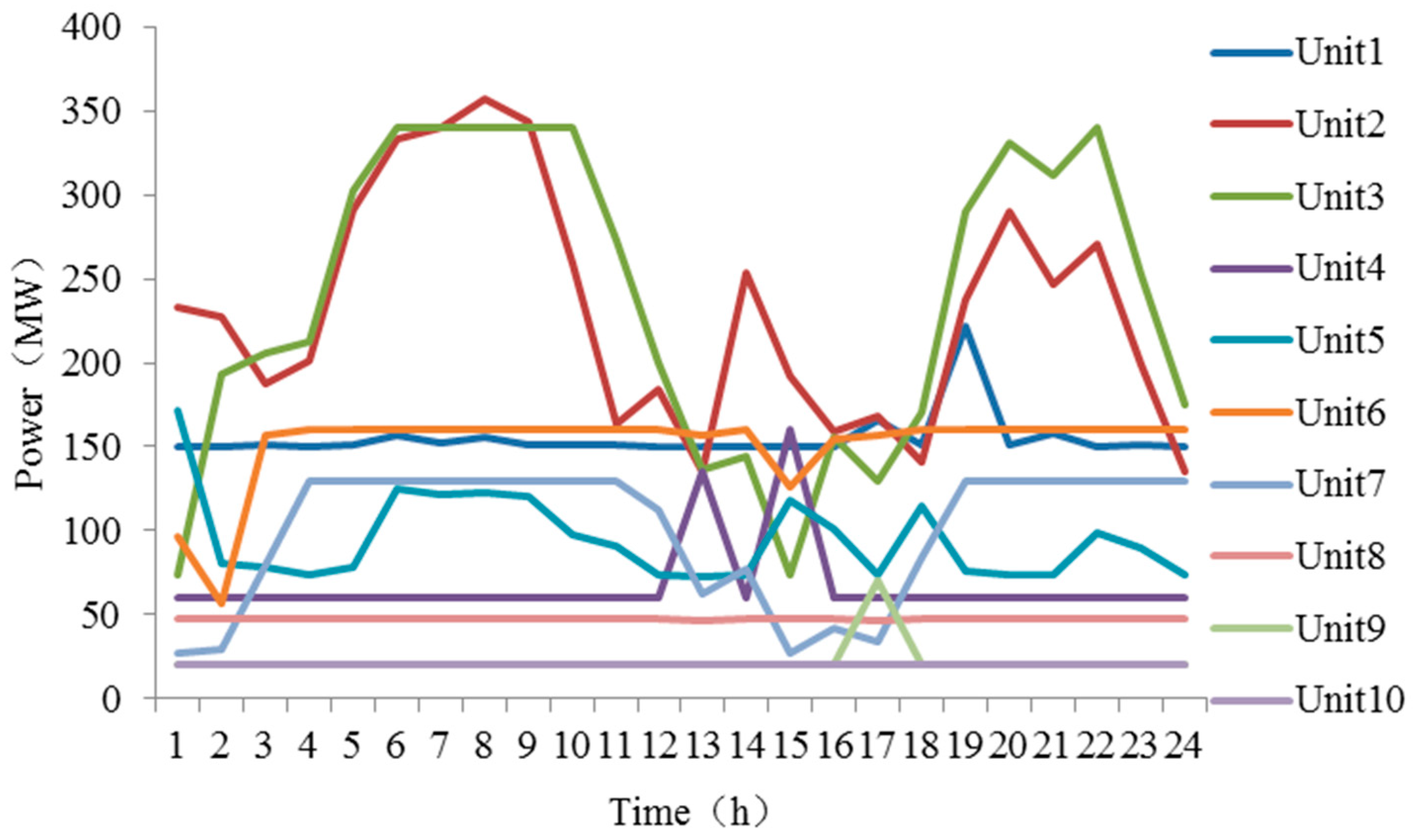
4.2.1. Results in Case 1
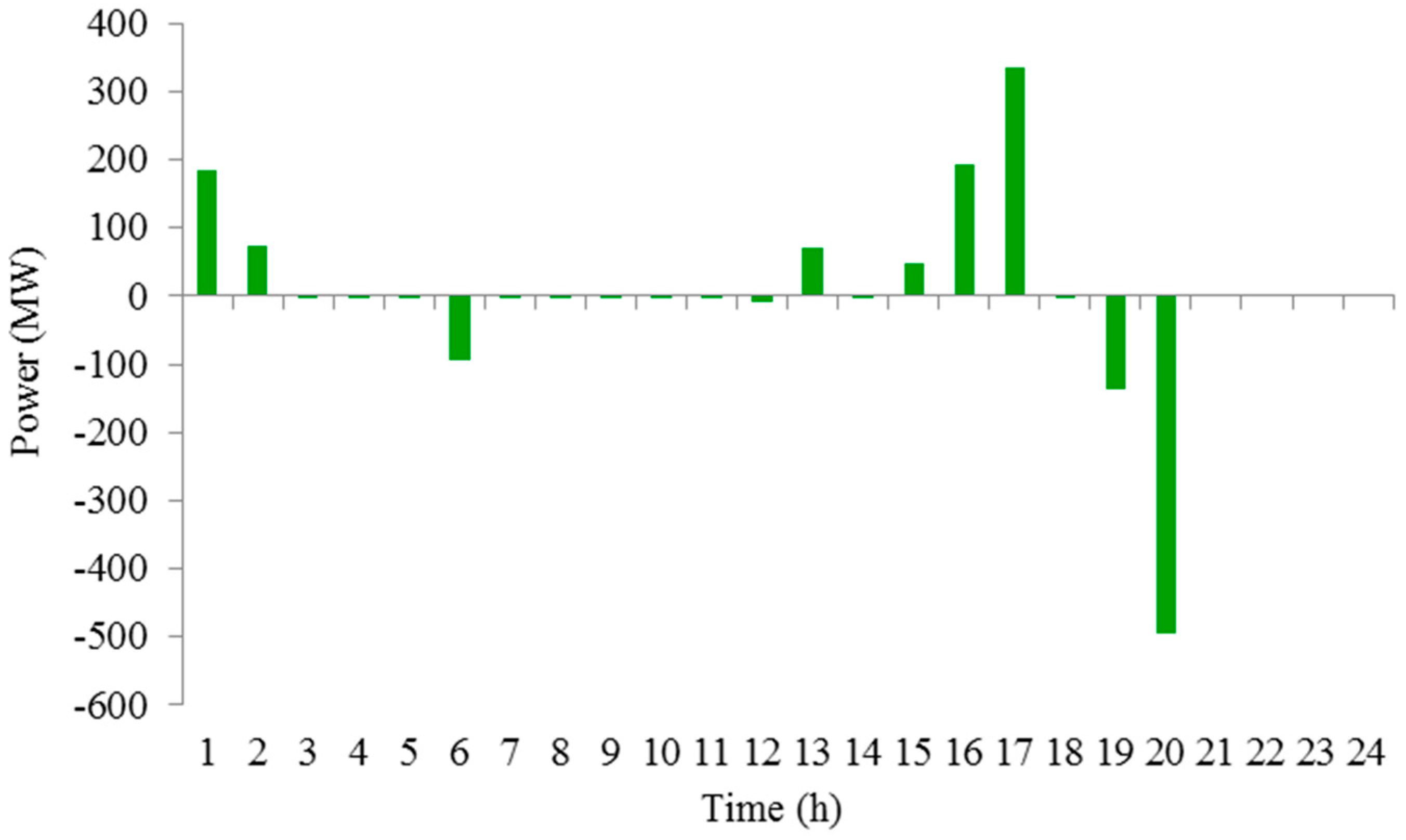
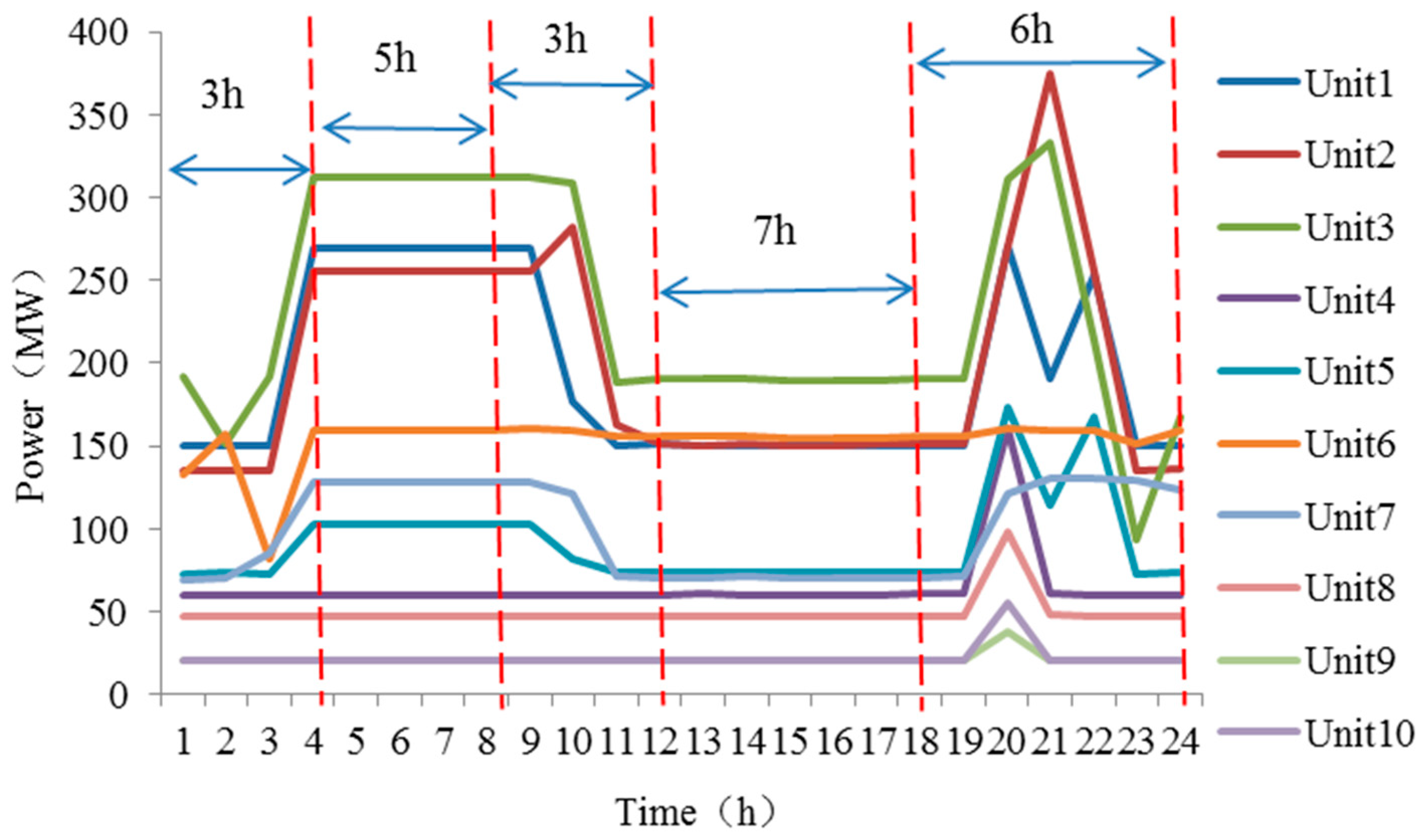
4.2.2. Results in Case 2
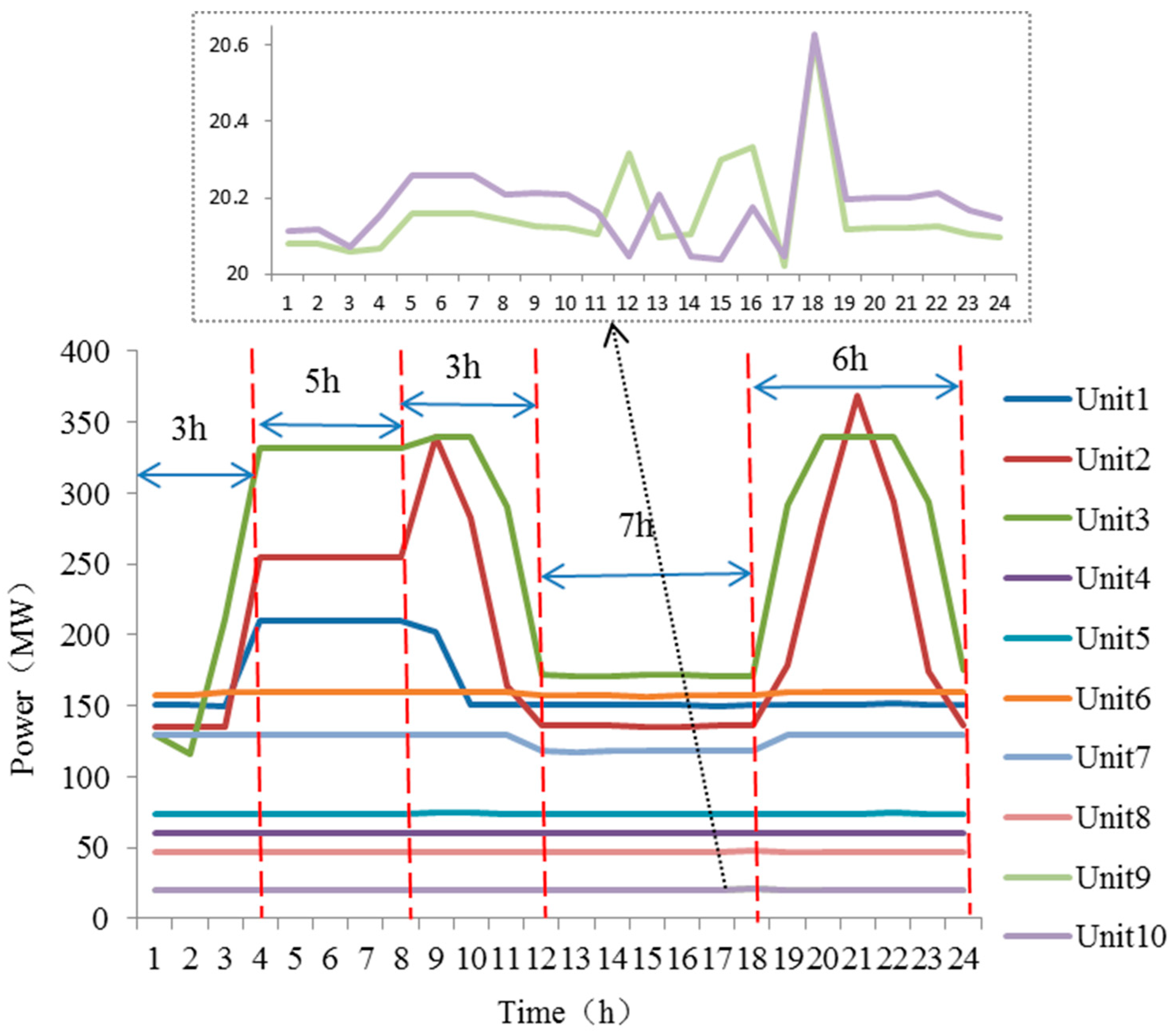
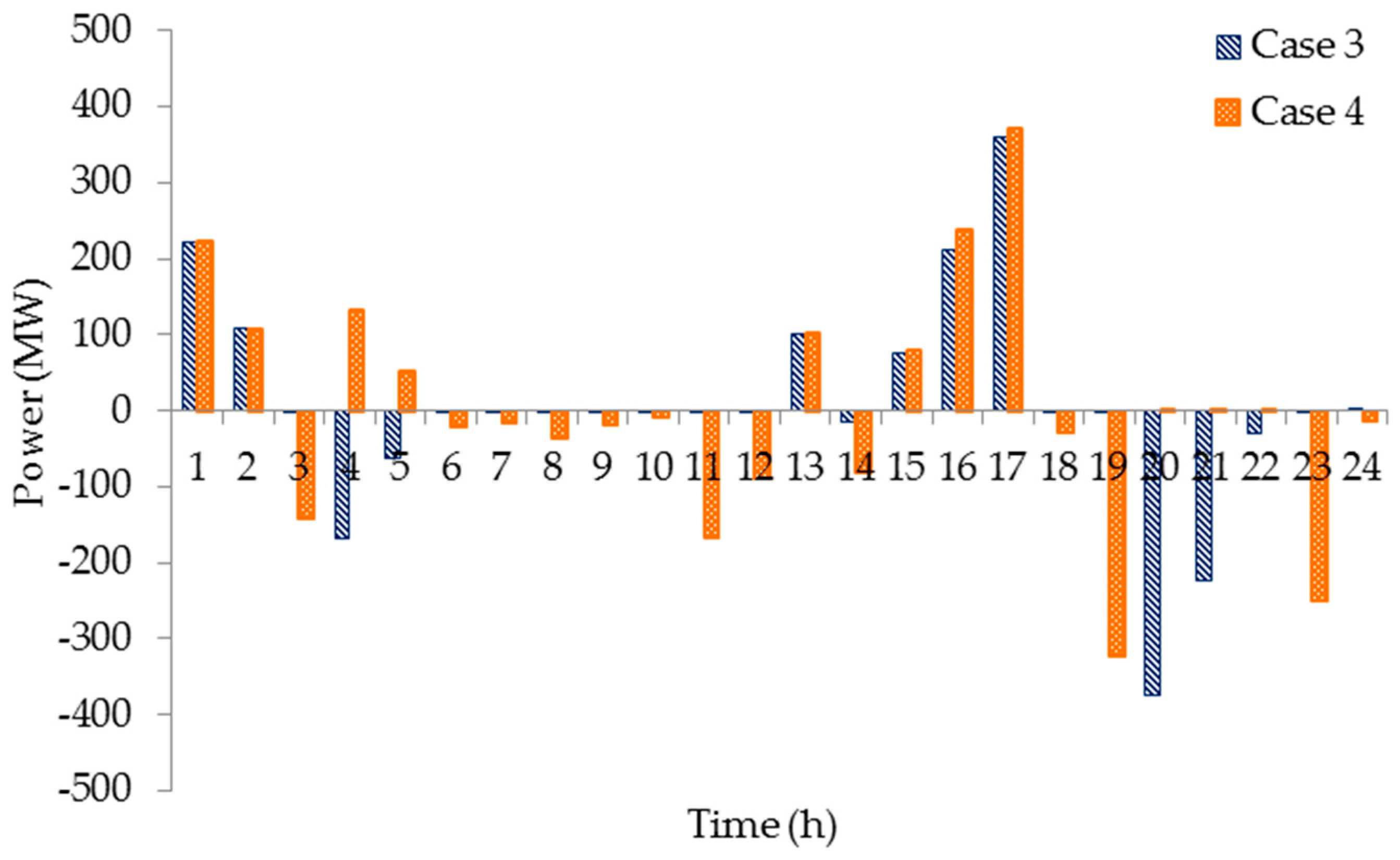
4.2.3. Results in Case 3
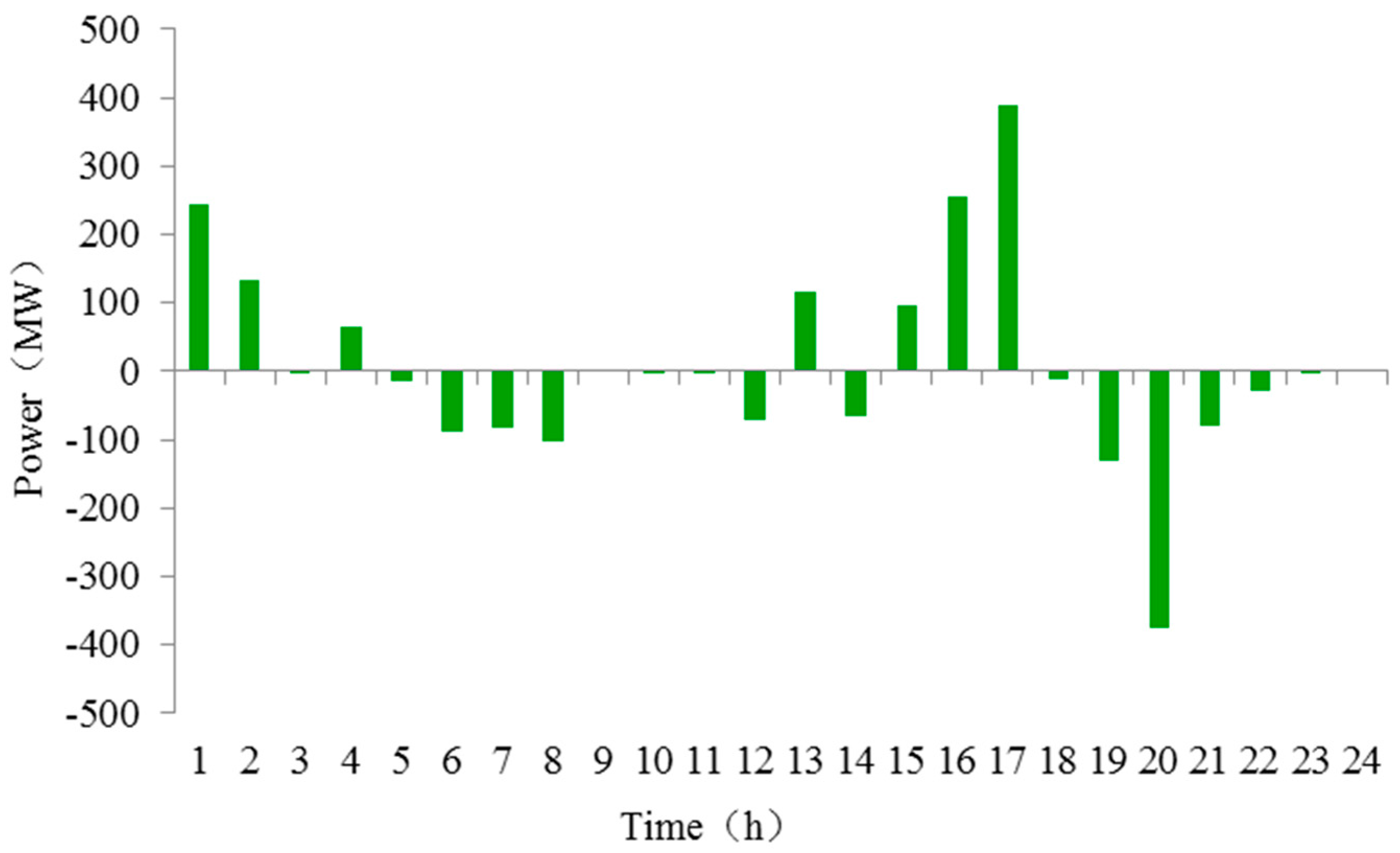
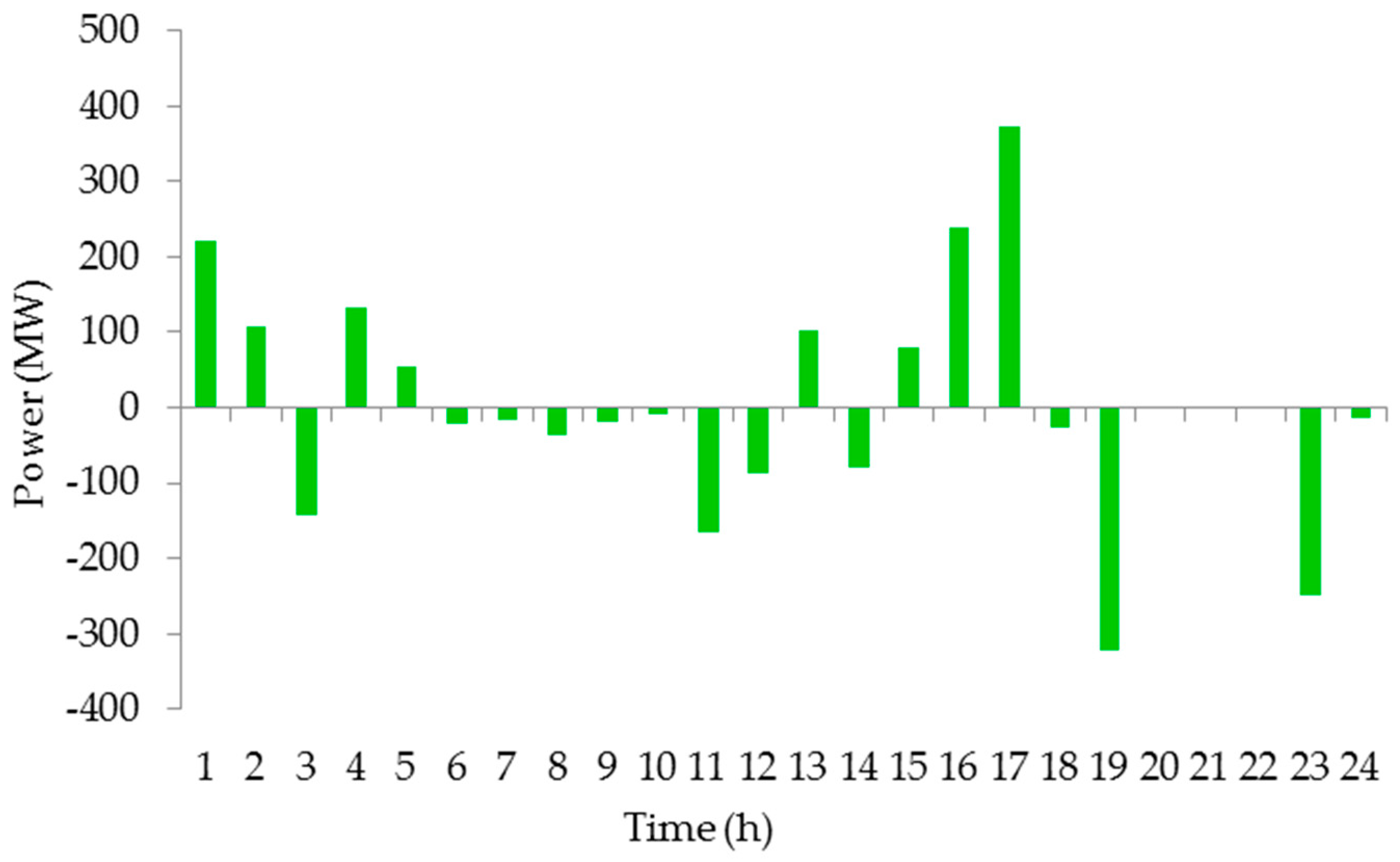
4.2.4. Results in Case 4
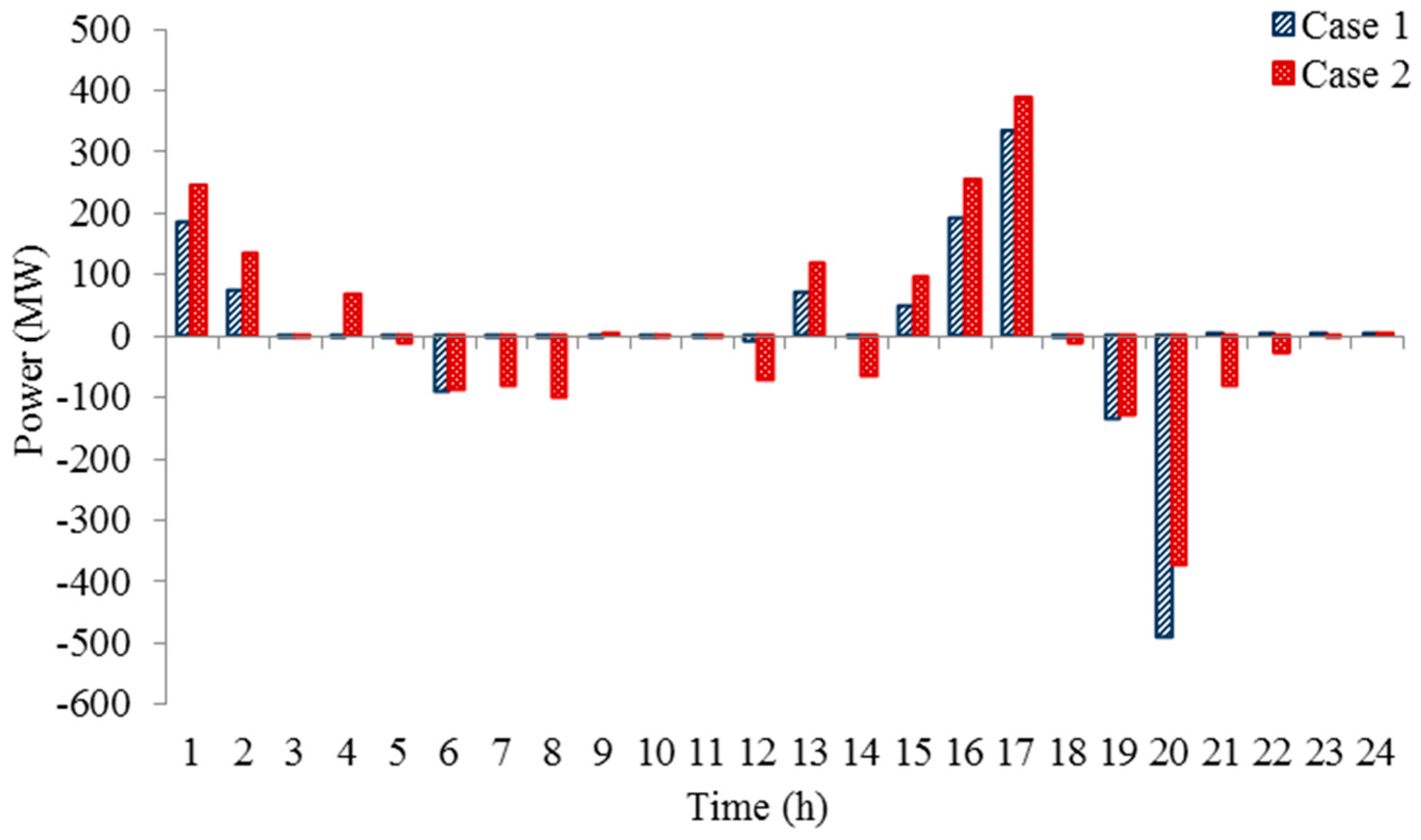
4.2.5. Result Comparison of Case 1 and Case 2
4.2.6. Result Comparison of Case 3 and Case 4
4.3. Discussion
4.3.1. Power Outputs Analysis of Thermal Generators
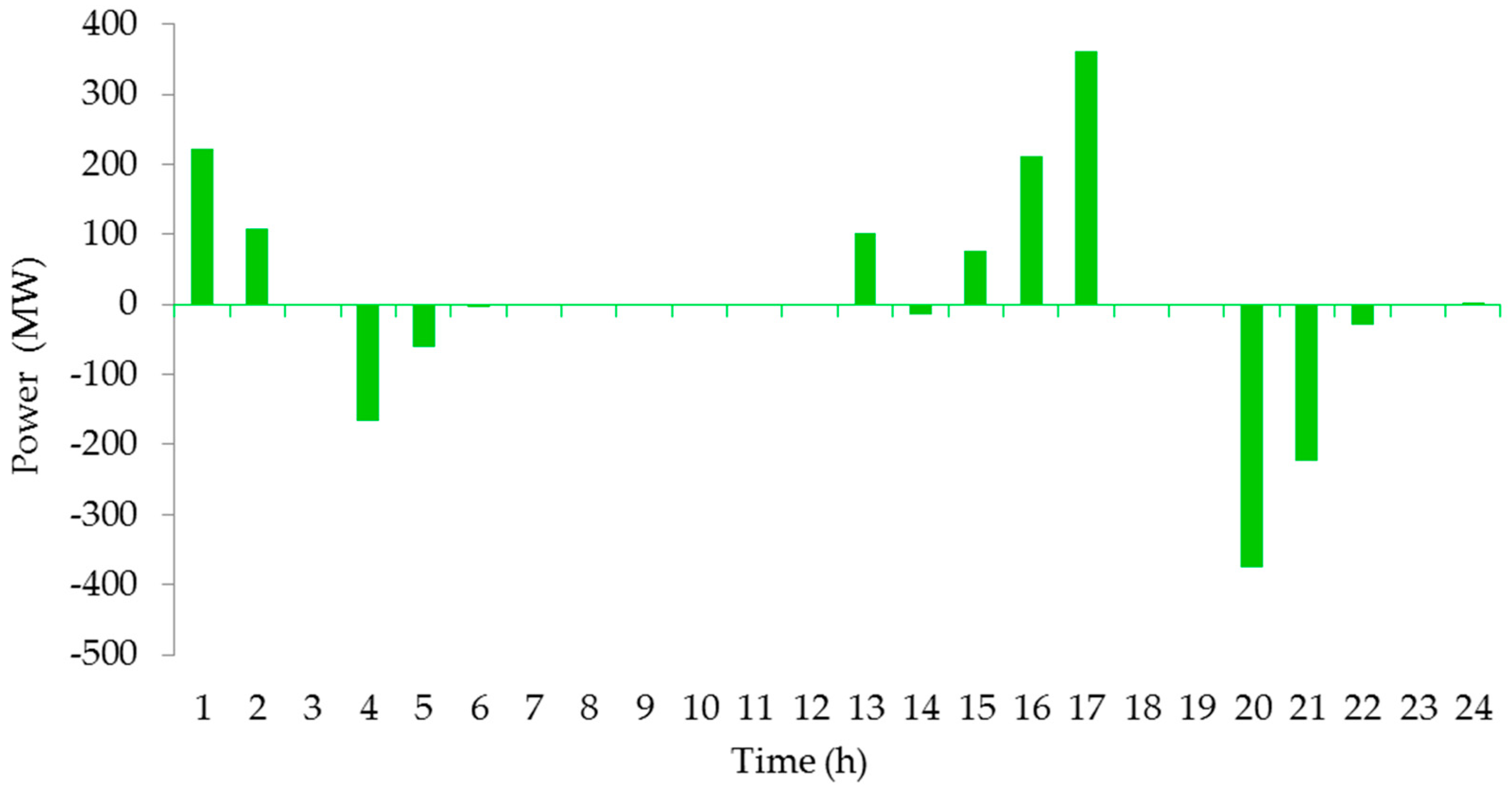
4.3.2. Power Output Analysis of Pumped Storage
4.3.3. Power Output Analysis of the Cases with and Without SampEn
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Zhou, X.X.; Chen, S.Y.; Lu, Z.X.; Huang, Y.H.; Ma, S.C.; Zhao, Q. Technology features of the new generation power system in China. Proc. CSEE 2018, 38, 1893–1904. [Google Scholar]
- Krishnan, S.H.; Ezhilarasi, D.; Uma, G.; Umapathy, M. Pyroelectric-based solar and wind energy harvesting system. IEEE Trans. Sustain. Energy 2014, 5, 73–81. [Google Scholar] [CrossRef]
- Hsiao, C.C.; Jhang, J.W.; Siao, A.S. Study on pyroelectric harvesters integrating solar radiation with wind power. Energies 2015, 8, 7465–7477. [Google Scholar] [CrossRef]
- Xu, F.; Li, L.L.; Chen, Z.X.; Tu, M.F.; Ding, Q. Generation scheduling model and application with fluctuation reduction of unit output. Autom. Electr. Power Syst. 2012, 36, 45–50+102. [Google Scholar]
- Wood, A.J.; Wollenberag, B.F. Power Generation Operation and Control; Wiley: New York, NY, USA, 1996. [Google Scholar]
- Bai, J.H.; Xin, S.X.; Liu, J.; Zheng, K. Roadmap of realizing the high penetration renewable energy in China. Proc. CSEE 2015, 35, 3699–3705. [Google Scholar]
- Huber, M.; Dimkova, D.; Hamacher, T. Integration of wind and solar power in Europe: Assessment of flexibility requirements. Energy 2014, 69, 236–246. [Google Scholar] [CrossRef] [Green Version]
- Min, C.G.; Kim, M.K. Net load carrying capability of generating units in power systems. Energies 2017, 10, 1221. [Google Scholar] [CrossRef]
- Zhou, B.R.; Geng, G.C.; Jiang, Q.Y. Hydro-thermal-wind coordination in day-ahead unit commitment. IEEE Trans. Power Syst. 2016, 31, 4626–4637. [Google Scholar] [CrossRef]
- Jiang, R.; Wang, J.; Guan, Y. Robust unit commitment with wind power and pumped storage hydro. IEEE Trans. Power Syst. 2012, 27, 800–810. [Google Scholar] [CrossRef]
- Hu, S.B.; Sun, H.; Peng, F.X.; Zhou, W.; Cao, W.P.; Su, A.L.; Chen, X.D.; Sun, M.Z. Optimization strategy for economic power dispatch utilizing retired EV batteries as flexible loads. Energies 2018, 11, 1657. [Google Scholar] [CrossRef]
- Ortega-Vazquez, M.A.; Kirschen, D.S. Estimating the spinning reserve requirements in systems with significant wind power generation penetration. IEEE Trans. Power Syst. 2009, 24, 114–124. [Google Scholar] [CrossRef]
- Papavasiliou, A.; Oren, S.S.; O’Neill, R.P. Reserve requirements for wind power integration: A scenario-based stochastic programming framework. IEEE Trans. Power Syst. 2011, 26, 2197–2206. [Google Scholar] [CrossRef]
- Matos, M.A.; Bessa, R.J. Setting the operating reserve using probabilistic wind power forecasts. IEEE Trans. Power Syst. 2011, 26, 594–603. [Google Scholar] [CrossRef]
- Lannoye, E.; Flynn, D.; O’Malley, M. Assessment of power system flexibility: A high-level approach. In Proceedings of the IEEE Power & Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–8. [Google Scholar]
- Wu, Y.K.; Chang, L.T.; Su, P.E.; Hsieh, T.Y.; Jan, B.S. Assessment of potential variability of net load following the integration of 3 GW wind power in Taiwan. Energy Procedia 2016, 100, 117–121. [Google Scholar] [CrossRef]
- Marannino, P.; Granelli, G.P.; Montagna, M.; Silvestri, A. Different time-scale approaches to the real power dispatch of thermal units. IEEE Trans. Power Syst. 1990, 5, 169–176. [Google Scholar] [CrossRef]
- Generation Dispatching Plan of Electricity Market on Generation Side. Available online: http://tech.bjx.com.cn/html/20071227/59347.shtml (accessed on 25 December 2018).
- Cataliotti, A.; Cervellera, C.; Cosentino, V.; Di Cara, D.; Gaggero, M.; Maccio, D.; Marsala, G.; Ragusa, A.; Tine, G. An Improved Load Flow Method for MV Networks Based on LV Load Measurements and Estimations. IEEE Trans. Instrum. Meas. 2018, 68, 430–438. [Google Scholar] [CrossRef]
- Cataliotti, A.; Cosentino, V.; Di Cara, D.; Tinè, G. LV Measurement Device Placement for Load Flow Analysis in MV Smart Grids. IEEE Trans. Instrum. Meas. 2016, 65, 999–1006. [Google Scholar] [CrossRef]
- Xygkis, T.C.; Korres, G.N. Optimized measurement allocation for power distribution systems using mixed integer sdp. IEEE Trans. Instrum. Meas. 2017, 66, 2967–2976. [Google Scholar] [CrossRef]
- Xygkis, T.C.; Korres, G.N.; Manousakis, N.M. Fisher information based meter placement in distribution grids via the d-optimal experimental design. IEEE Trans. Smart Grid 2018, 9, 1452–1461. [Google Scholar] [CrossRef]
- Pegoraro, P.A.; Angioni, A.; Pau, M.; Monti, A.; Muscas, C.; Ponci, F.; Sulis, S. Bayesian approach for distribution system state estimation with non-gaussian uncertainty models. IEEE Trans. Instrum. Meas. 2017, 66, 2957–2966. [Google Scholar] [CrossRef]
- Zhang, L.; Yang, J.; Jian, X.H.; Zhang, F.; Han, X.S. Unit Commitment with Energy Storage Considering Operation Flexibility at Sub-hourly Time-scales. Autom. Electr. Power Syst. 2018, 42, 48–56. [Google Scholar]
- Zhai, J.Y.; Ren, J.W.; Zhou, M.; Li, Z. Multi-Time Scale Fuzzy Chance Constrained Dynamic Economic Dispatch Model for Power System with Wind Power. Power Syst. Technol. 2016, 40, 1094–1099. [Google Scholar]
- Yong, T.; Yao, J.; Yang, S.; Yang, Z. Ramp enhanced unit commitment for energy scheduling with high penetration of renewable generation. In Proceedings of the 2015 IEEE Power & Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015. [Google Scholar]
- Zhao, D.M.; Yin, J.F. Fuzzy random chance constrained preemptive goal programming scheduling model considering source-side and load-side uncertainty. Trans. China Electrotech. Soc. 2018, 33, 1076–1085. [Google Scholar]
- Li, P.; Wand, X.Y.; Han, P.F. Risk Analysis of Microgrid Optimal Operation Scheduling under Double Uncertainty Environment. Proc. CSEE 2017, 37, 4296–4303. [Google Scholar]
- Guo, P.; Wen, J.; Zhu, D.D.; Wang, W.Z.; Liu, W.Y. The Coordination Control Strategy for Large-Scale Wind Power Consumption Based on Source-Load Interactive. Trans. China Electrotech. Soci. 2017, 32, 1–9. [Google Scholar]
- Zhang, X.H.; Zhao, C.M.; Liang, J.X.; Li, K.; Zhong, J.Q. Robust Fuzzy Scheduling of Power Systems Considering Bilateral Uncertainties of Generation and Demand Side. Autom. Electr. Power Syst. 2018, 42, 67–75. [Google Scholar]
- Gangammanavar, H.; Sen, S.; Zavala, V.M. Stochastic optimization of sub-hourly economic dispatch with wind energy. IEEE Trans. Power Syst. 2016, 31, 949–959. [Google Scholar] [CrossRef]
- Wang, J.D.; Wang, J.H.; Liu, C.; Ruiz, J.P. Stochastic unit commitment with sub-hourly dispatch constraints. Appl. Energy 2013, 105, 418–422. [Google Scholar] [CrossRef]
- Zhang, X.Y.; Yang, J.Q.; Zhang, X.J. Dynamic economic dispatch incorporating multiple wind farms based on FFT simplified chance constrained programming. J. Zhengjiang Univ. (Eng. Sci.) 2017, 51, 976–983. [Google Scholar]
- Shaker, H.; Zareipour, H.; Wood, D. Impacts of large-scale wind and solar power integration on California’s net electrical load. Renew. Sustain. Energy Rev. 2016, 58, 761–774. [Google Scholar] [CrossRef]
- Yin, Y.; Shang, P.J.; Andrew, C.A.; Peng, C.K. Multiscale joint permutation entropy for complex time series. Physica A 2019, 515, 388–402. [Google Scholar] [CrossRef]
- Cuadras, A.; Romero, R.; Ovejas, V.J. Entropy characterisation of overstressed capacitors for lifetime prediction. J. Power Sources 2016, 336, 272–278. [Google Scholar] [CrossRef]
- Hsiao, C.C.; Liang, B.H. The generated entropy monitored by pyroelectric sensors. Sensors 2018, 18, 3320. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.Y. The Theory of Approximate Entropy and its Application. Chin. J. Med. Phys. 2009, 26, 1543–1546. [Google Scholar]
- Chou, C.M. Complexity analysis of rainfall and runoff time series based on sample entropy in different temporal scales. Stoch. Environ. Res. Risk Assess. 2014, 28, 1401–1408. [Google Scholar] [CrossRef]
- Richman, J.S.; Moorman, J.R. Physiological time-series analysis using approximate entropy and sample entropy. Am. J. Physiol. Heart Circ. Physiol. 2000, 278, 2039–2049. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.C.; Liu, K.P.; Qin, L.; Fang, N.C. Wind Power Multi-Step Interval Prediction Based on Ensemble Empirical Mode Decomposition-Sample Entropy and Optimized Extreme Learning Machine. Power Syst. Technol. 2016, 40, 2045–2051. [Google Scholar]
- Al-Angari, H.M.; Sahakian, A.V. Use of sample entropy approach to study heart rate variability in obstructive sleep apnea syndrome. IEEE Trans. Bio-Med. Eng. 2007, 54, 1900–1904. [Google Scholar] [CrossRef]
- Xu, W. The Complexity Algorithms Research of Chaotic Sequences Based on Entropy Theory. Ph.D. Thesis, Heilongjiang University, Harbin, China, 2017. [Google Scholar]
- Zhang, X.Q.; Liang, J.; Zhang, X.; Zhang, F.; Zhang, L.; Xu, B. Combined Model for Ultra Short-term Wind Power Prediction Based on Sample Entropy and Extreme Learning Machine. Proc. CSEE 2013, 33, 33–40. [Google Scholar]
- Cheng, W.S.; Zhang, H.F. A dynamic economic dispatch model incorporating wind power based on chance constrained programming. Energies 2015, 8, 233–256. [Google Scholar] [CrossRef]
- Shen, Z.; Xie, S.Q.; Pan, C.Y. Probability and Statistics; High Education Press: Beijing, China, June 2008; pp. 139–143, 161–163. [Google Scholar]
- Attaviriyanupap, P.; Kita, H.; Tanaka, E.; Hasegawa, J. A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function. IEEE Trans. Power Syst. 2002, 17, 411–416. [Google Scholar] [CrossRef]
- Zhang, X.H.; Zhao, J.Q.; Chen, X.Y. Multi-objective Unit Commitment Fuzzy Modeling and Optimization for Energy-saving and Emission Reduction. Proc. CSEE 2010, 30, 71–76. [Google Scholar]
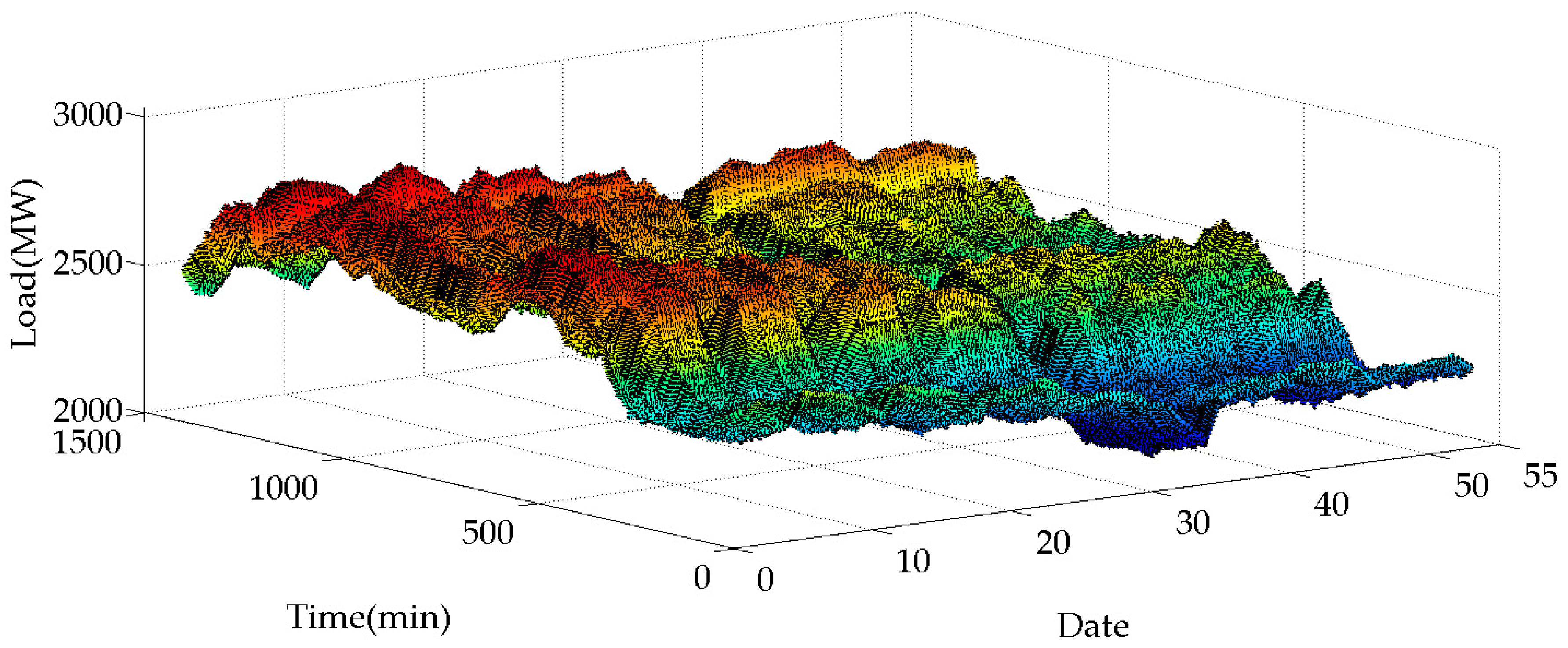
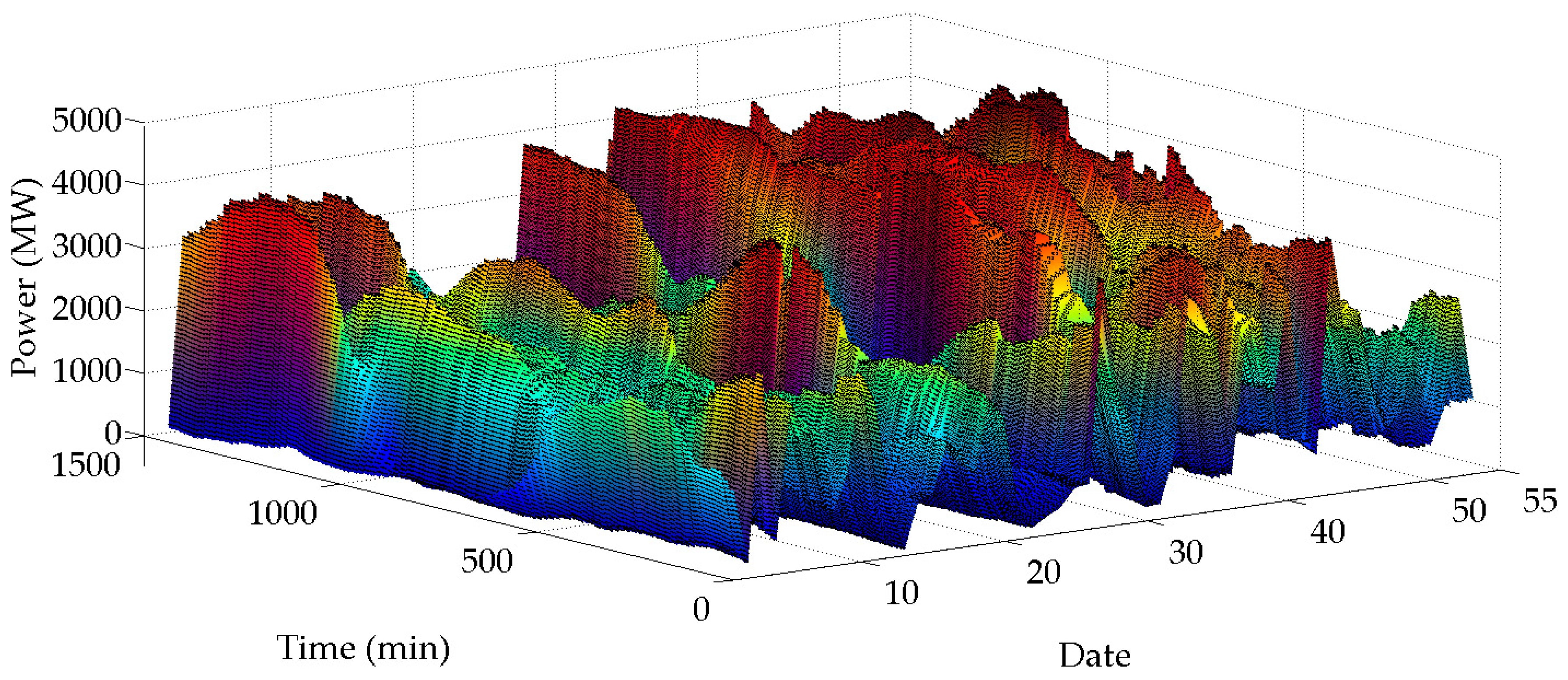
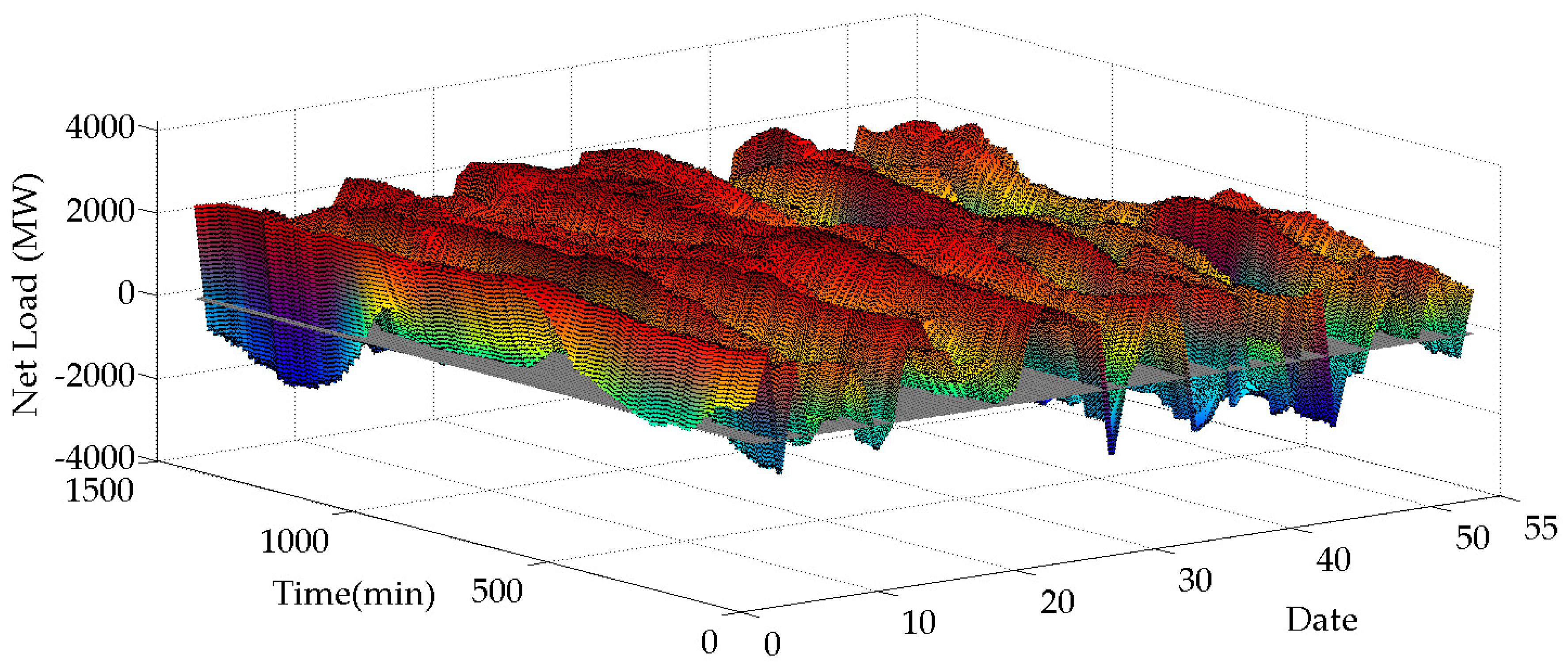
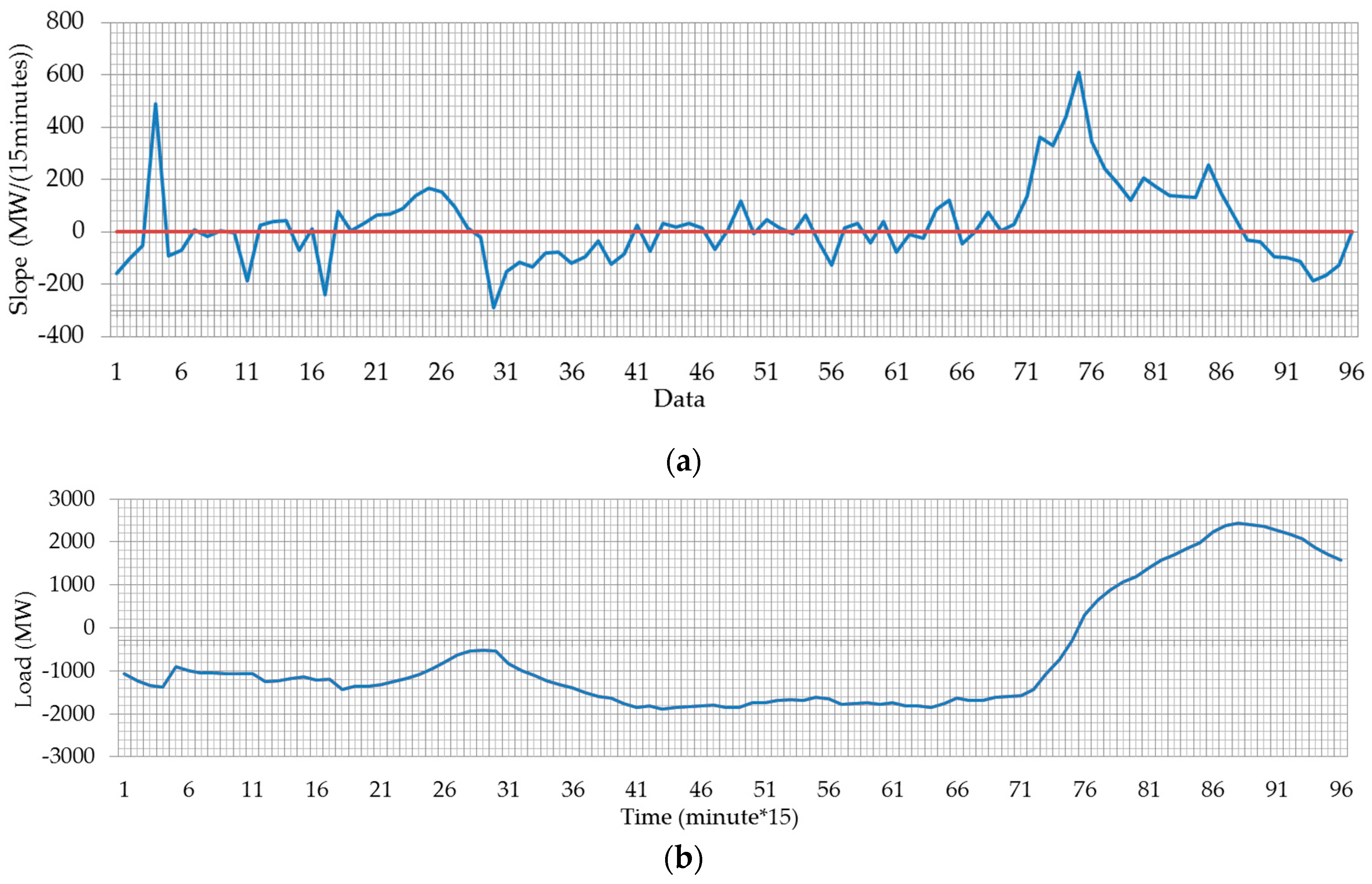
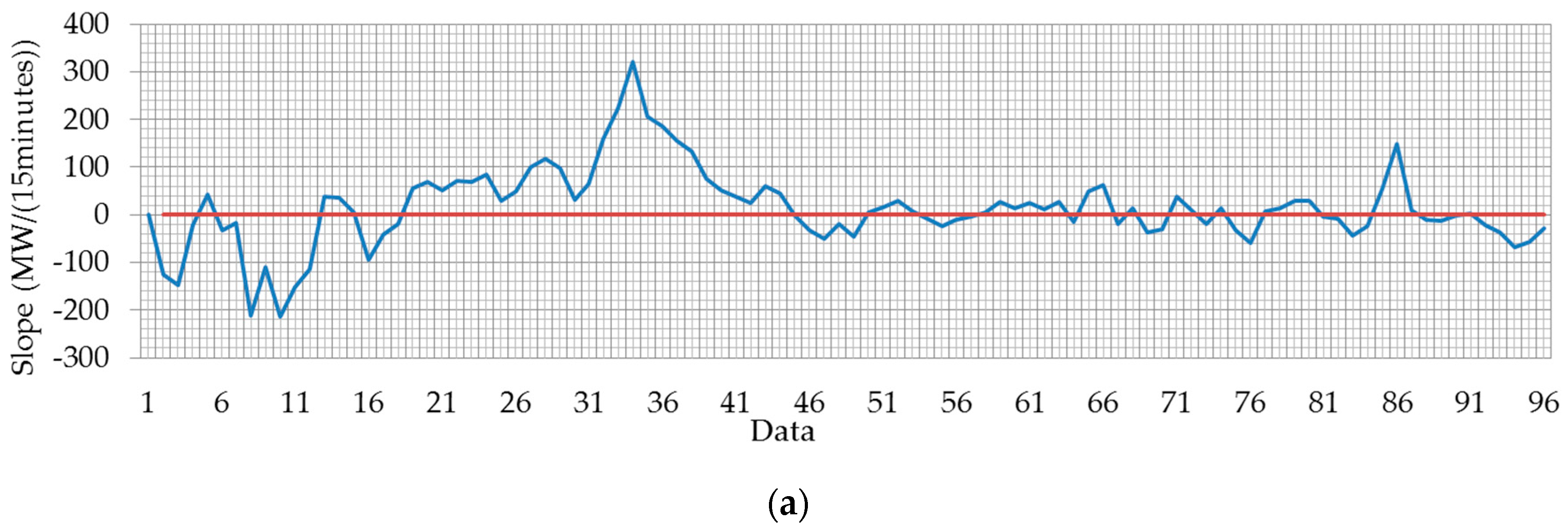
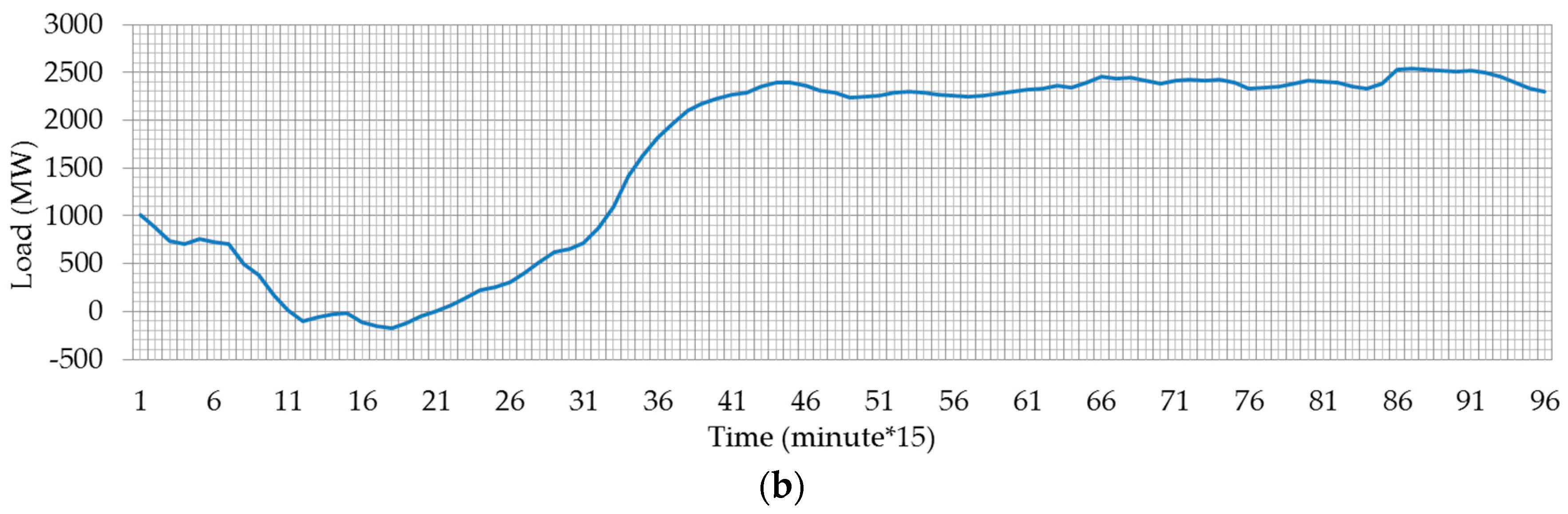
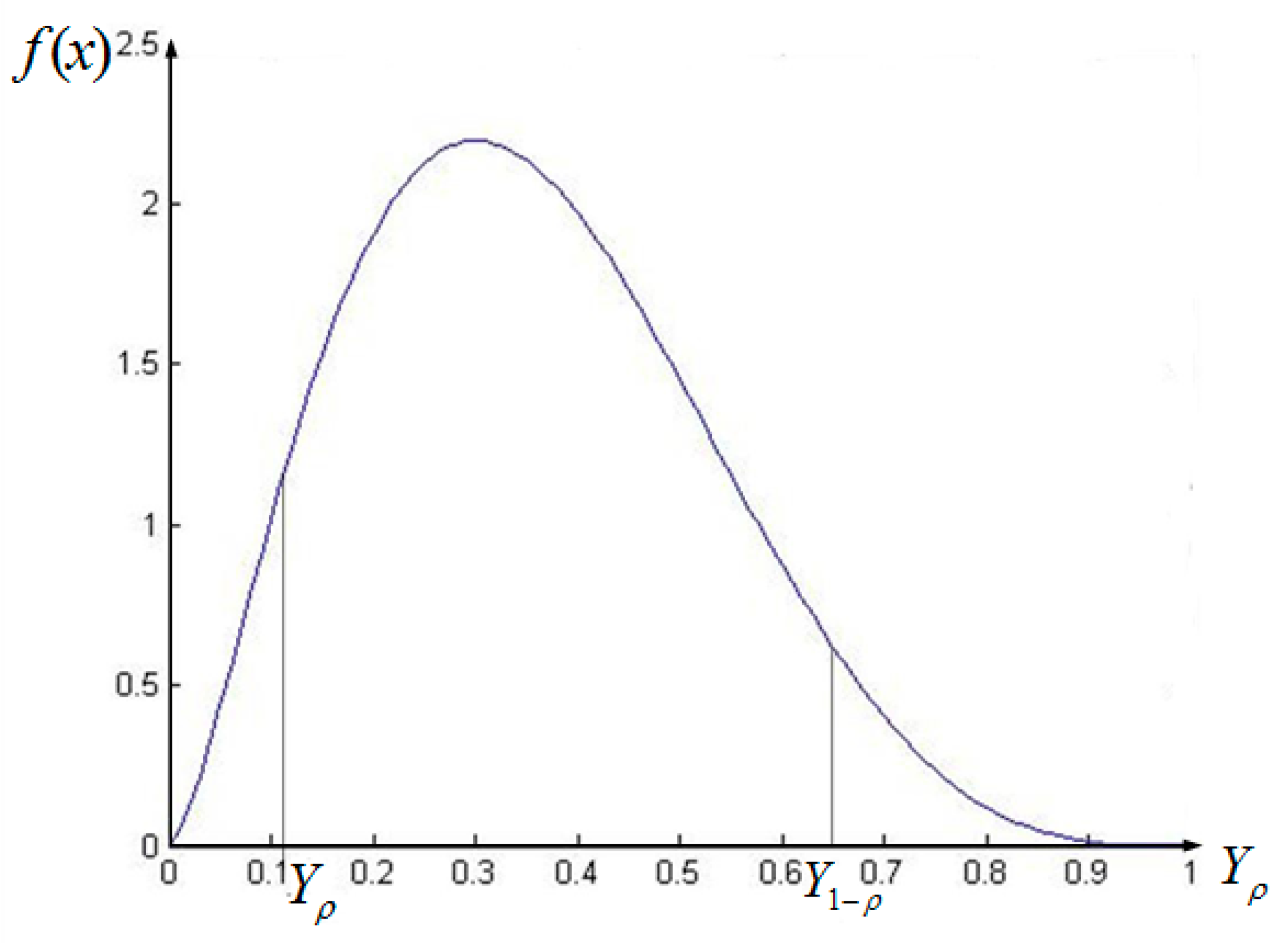
| Date | Time | Slope Sign Changing Amount | Percentage of Slope Sign Changing | Valley-to-Peak | Slope Sign Changing Amount/Valley-to-Peak | SampEn |
|---|---|---|---|---|---|---|
| 0411 | 1–18 | 11 | 0.61 | 731.61 | 0.0150 | 0.42 |
| 19–41 | 3 | 0.13 | 457.95 | 0.0066 | 0.18 | |
| 42–69 | 15 | 0.54 | 247.65 | 0.0606 | 0.74 | |
| 70–96 | 1 | 0.04 | 795.91 | 0.0013 | 0.08 | |
| 0303 | 1–45 | 6 | 0.13 | 2582.03 | 0.0023 | 0.04 |
| 46–96 | 18 | 0.35 | 340.37 | 0.0529 | 0.72 |
| Parameters | Unit1 | Unit2 | Unit3 | Unit4 | Unit5 | Unit6 | Unit7 | Unit8 | Unit9 | Unit10 |
|---|---|---|---|---|---|---|---|---|---|---|
| (MW) | 470 | 460 | 340 | 300 | 243 | 160 | 130 | 120 | 80 | 55 |
| (MW) | 150 | 135 | 73 | 60 | 73 | 57 | 20 | 47 | 20 | 20 |
| a (10−3 $/MW2h) | 0.43 | 0.63 | 0.39 | 0.70 | 0.79 | 0.56 | 2.11 | 4.80 | 109.08 | 9.51 |
| B ($/MWh) | 21.60 | 21.05 | 20.81 | 23.90 | 21.62 | 17.87 | 16.51 | 23.23 | 19.58 | 22.54 |
| C ($/h) | 958.20 | 1313.6 | 604.97 | 471.60 | 480.29 | 601.75 | 502.70 | 639.40 | 455.60 | 692.40 |
| UR | 120 | 120 | 120 | 100 | 100 | 100 | 50 | 50 | 50 | 50 |
| DR | 120 | 120 | 120 | 100 | 100 | 100 | 50 | 50 | 50 | 50 |
| ($/MWh) | 14.7 | 15.5 | 15.2 | 17.8 | 19.3 | 19.8 | 18.7 | 21.7 | 23.4 | 25.2 |
| ($/MWh) | 15.2 | 14.8 | 15.1 | 18.6 | 21.2 | 19.5 | 19 | 22 | 23.1 | 25.6 |
| ($/MWh) | 3.13 | 3.08 | 3.75 | 4.17 | 5.88 | 9.71 | 9.09 | 13.7 | 16.67 | 28.57 |
| ($/MWh) | 3.13 | 3.08 | 3.75 | 4.17 | 5.88 | 9.71 | 9.09 | 13.7 | 16.67 | 28.57 |
| Time Periods (h) | SampEn | SampEn Proportion |
|---|---|---|
| 1–4 | 0.04 | 5% |
| 4–8 | 0.14 | 16% |
| 8–12 | 0.08 | 2% |
| 12–18 | 0.61 | 71% |
| 18–24 | 0.06 | 6% |
| Parameters | Case 1 | Case 2 | Percentage Optimization of Case 2 Compared to Case 1 |
|---|---|---|---|
| Operation cost (105 $) | 7.1744 | 7.1712 | 0.04% |
| Up ramping power (MW) | 1636.27 | 918.59 | 43.86% |
| Down ramping power (MW) | 1526.61 | 869.37 | 43.05% |
| Throughput of pumped storage (MW) | 1636.03 | 2358.29 | 44.15% |
| Parameters | Case 3 | Case 4 | Percentage Optimization of Case 4 Compared to Case 3 |
|---|---|---|---|
| Operation cost (105 $) | 7.2082 | 7.1903 | 0.25% |
| Up ramping power (MW) | 1932.88 | 1681.89 | 12.99% |
| Down ramping power (MW) | 1860.82 | 1623.47 | 12.76% |
| Throughput of pumped storage (MW) | 1955.61 | 2497.82 | 27.73% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, S.; Peng, F.; Gao, Z.; Ding, C.; Sun, H.; Zhou, W. Sample Entropy Based Net Load Tracing Dispatch of New Energy Power System. Energies 2019, 12, 193. https://doi.org/10.3390/en12010193
Hu S, Peng F, Gao Z, Ding C, Sun H, Zhou W. Sample Entropy Based Net Load Tracing Dispatch of New Energy Power System. Energies. 2019; 12(1):193. https://doi.org/10.3390/en12010193
Chicago/Turabian StyleHu, Shubo, Feixiang Peng, Zhengnan Gao, Changqiang Ding, Hui Sun, and Wei Zhou. 2019. "Sample Entropy Based Net Load Tracing Dispatch of New Energy Power System" Energies 12, no. 1: 193. https://doi.org/10.3390/en12010193
APA StyleHu, S., Peng, F., Gao, Z., Ding, C., Sun, H., & Zhou, W. (2019). Sample Entropy Based Net Load Tracing Dispatch of New Energy Power System. Energies, 12(1), 193. https://doi.org/10.3390/en12010193





