Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation
Abstract
1. Introduction
- The substitution of the discontinuous signum function by linear ones [27]. This method is the well-known SMC based on a boundary layer. This proposition allows the reduction of the chattering phenomenon. However, the finite-time convergence feature is no longer guaranteed. The latter is very desirable when critical convergence time is required.
- Higher Order Sliding Mode (HOSM) [30,31,32]. The idea consists of making the switching control term act on the control input derivative, which makes the control input fed into the system continuous. This method gives better performances since it allows higher precision and reduces the chattering phenomenon. However, this approach requires some information, as the first time derivative of the selected sliding surface is not always available for measurements, making the implementation difficult.
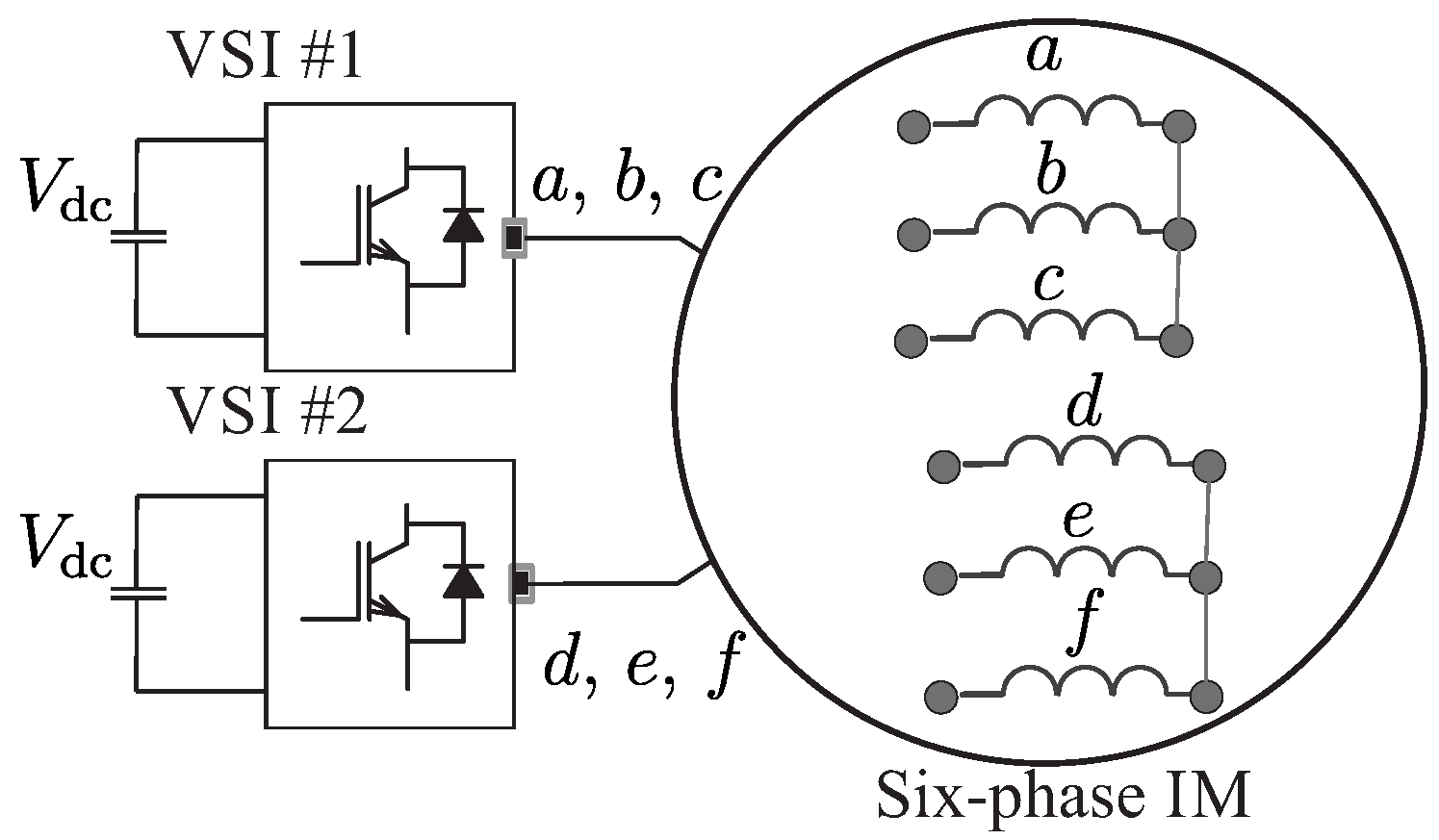
2. Six-Phase IM and VSI Model
3. Controller Design and Stability Analysis
3.1. Outer Speed Control Loop
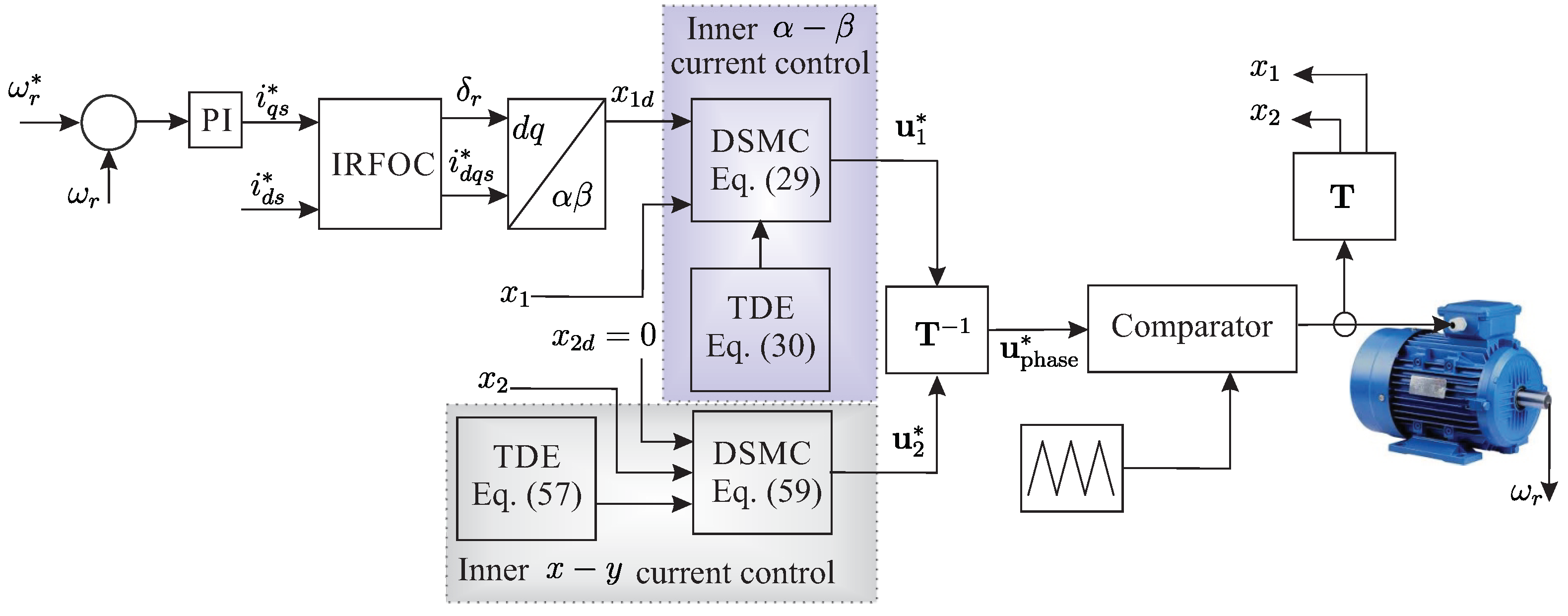
3.2. Inner Current Control Loop
3.2.1. Control of Stator Current in the Sub-Space
- Consider the first case where , then , and:If the condition in (31) is satisfied, then .Moreover, can be written as:Hence:since and , then the above inequality is always true.
- Consider the second case where . This implies and . Then, let us rewrite as follows:which is always true since .Moreover, can be rewritten as:Since and , then, it is obvious that the inequality in (15) is always true.
- Consider the third case where , then:Hence:
- Consider the first case where and for all . Then:Hence, it is obvious that ensures that:It follows that:which is contradictory to the fact that .
- Consider the second case where and for all . Then:Once again, it is obvious that verifies:It follows that:which is contradictory to the fact that .
3.2.2. Control of Stator Current in the Sub-Space
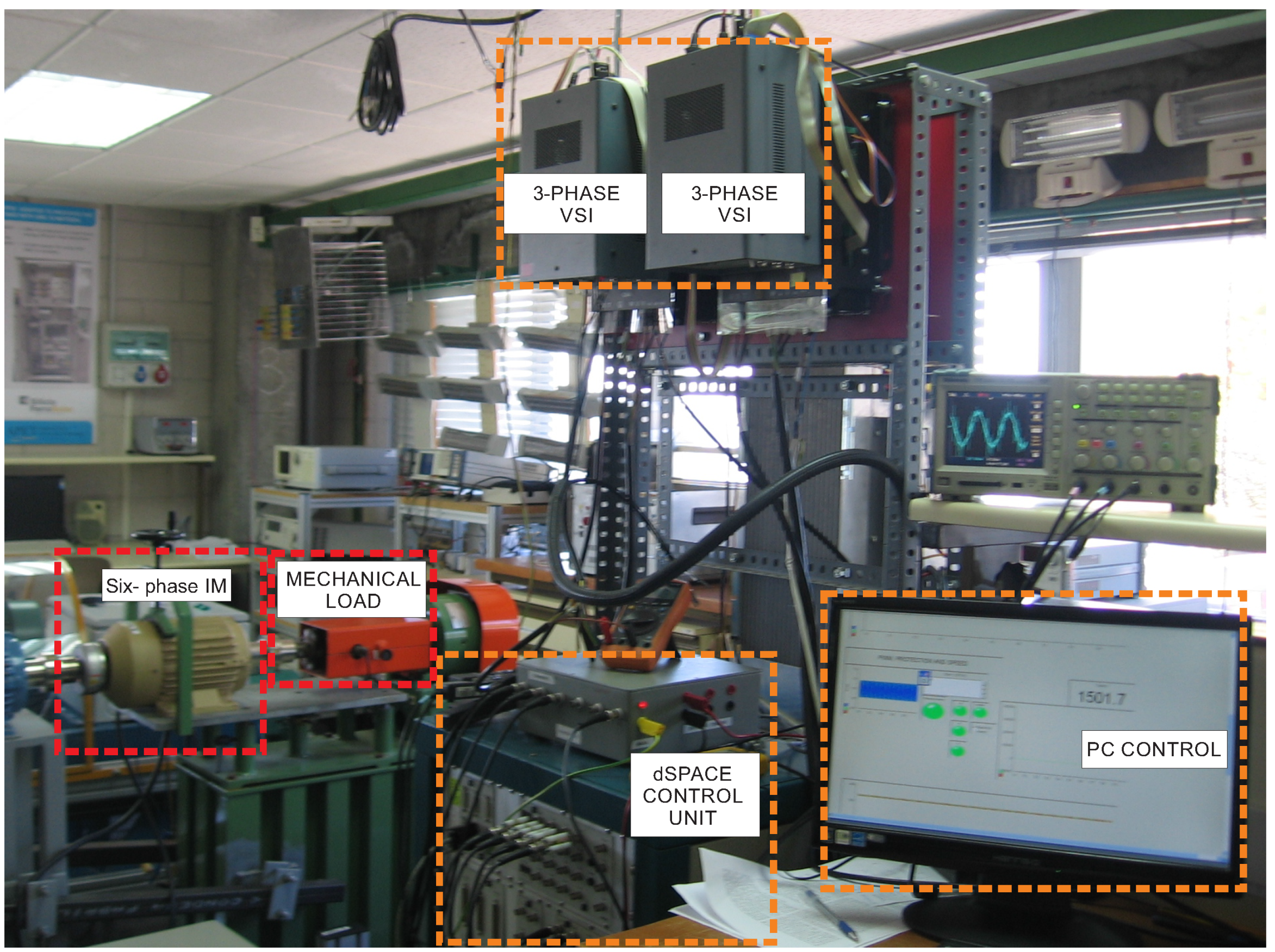
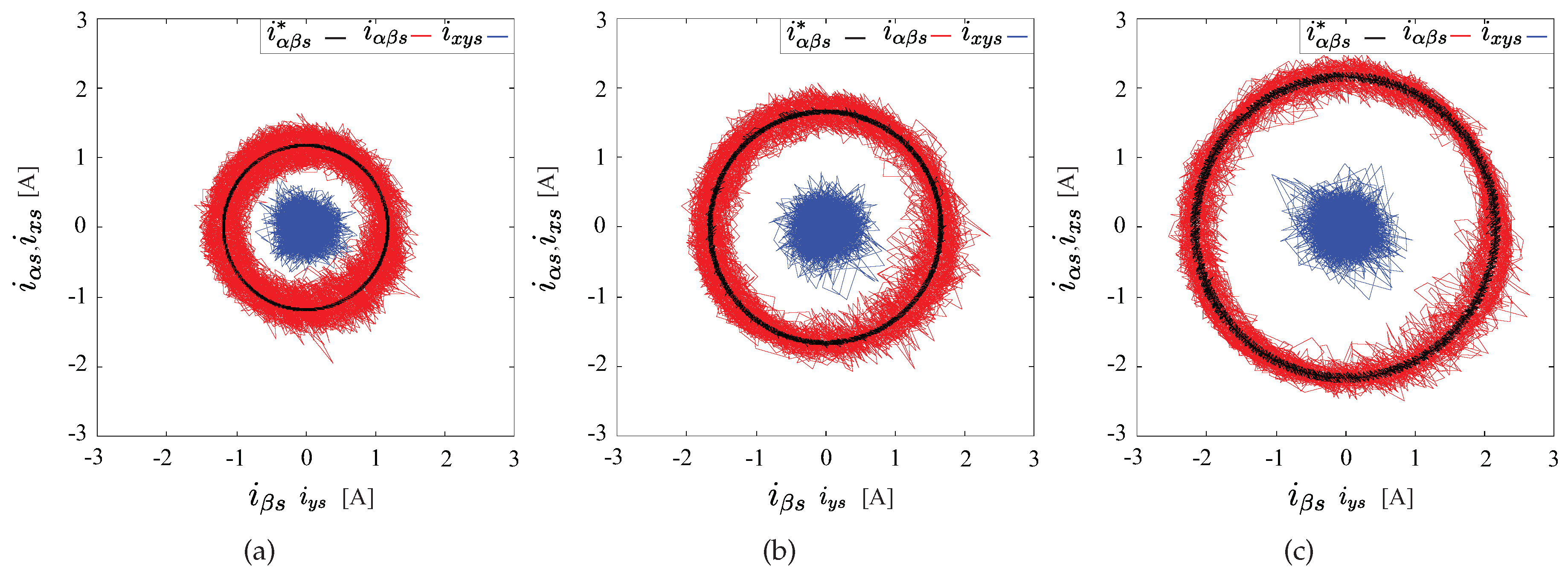
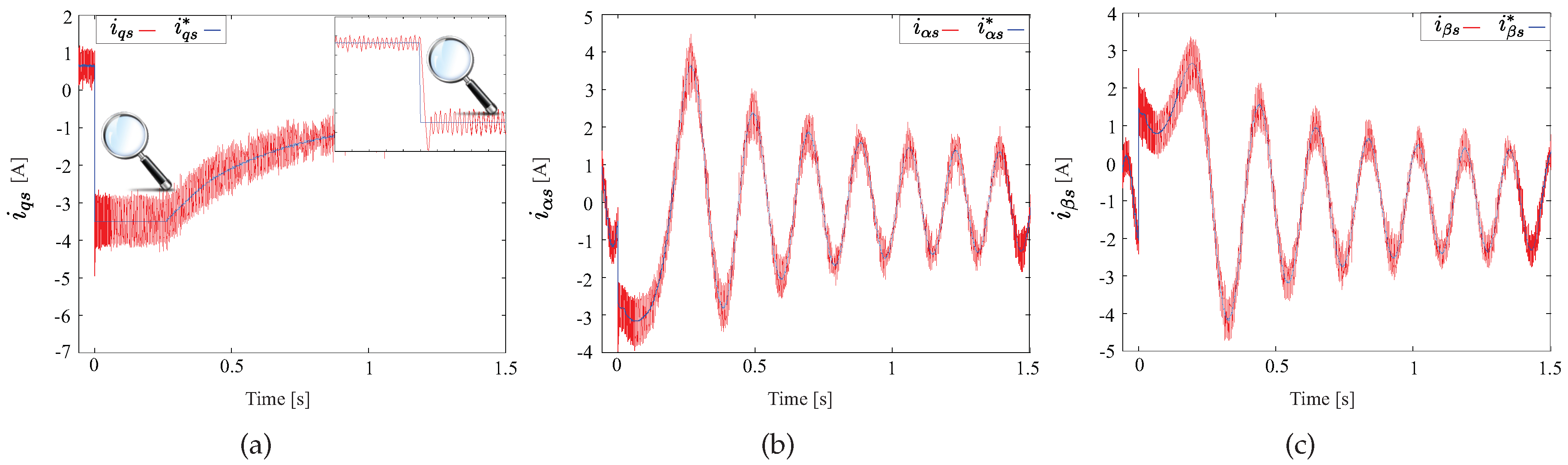
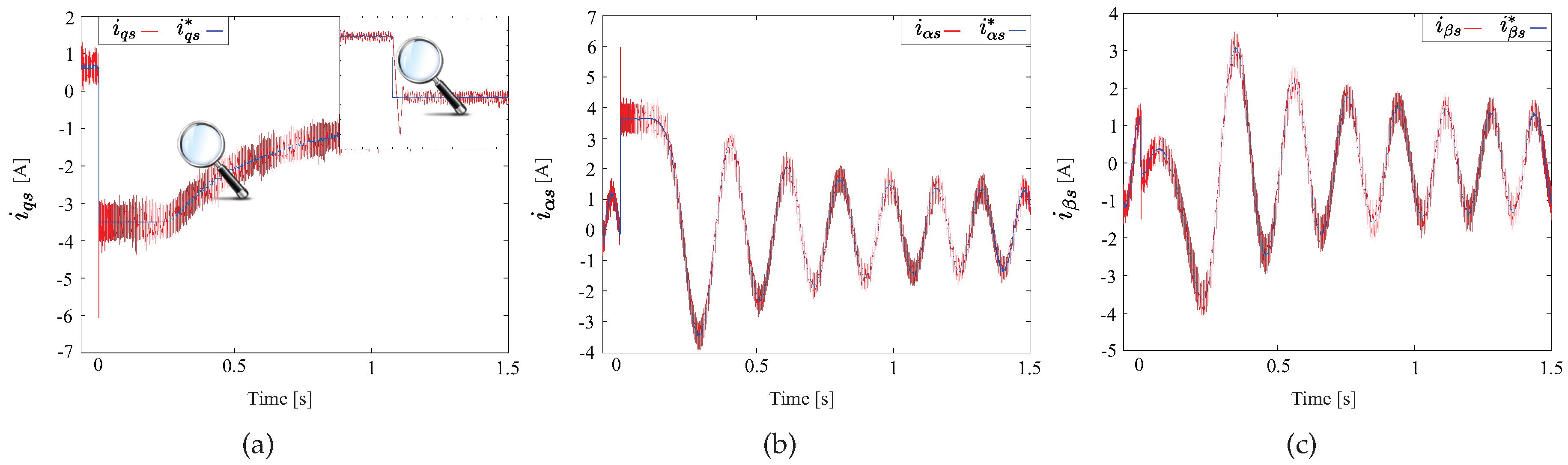
4. Experimental Results
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DSMC | Discrete-Time Siding Mode Control |
| FF | Form Factor |
| IM | Induction Machine |
| IRFOC | Indirect Rotor Field-Oriented Control |
| MSE | Mean Squared Error |
| RMS | Root Mean Square |
| PI | Proportional-Integral |
| SMC | Sliding Mode Control |
| TDE | Time Delay Estimation |
| THD | Total Harmonic Distortion |
| VSD | Vector Space Decomposition |
| VSI | Voltage Source Inverter |
References
- Barrero, F.; Duran, M.J. Recent Advances in the Design, Modeling, and Control of Multiphase Machines: Part I. IEEE Trans. Ind. Electron. 2016, 63, 449–458. [Google Scholar] [CrossRef]
- Duran, M.J.; Barrero, F. Recent Advances in the Design, Modeling, and Control of Multiphase Machines: Part II. IEEE Trans. Ind. Electron. 2016, 63, 459–468. [Google Scholar] [CrossRef]
- Levi, E. Advances in Converter Control and Innovative Exploitation of Additional Degrees of Freedom for Multiphase Machines. IEEE Trans. Ind. Electron. 2016, 63, 433–448. [Google Scholar] [CrossRef]
- Zoric, I.; Jones, M.; Levi, E. Arbitrary Power Sharing Among Three-Phase Winding Sets of Multiphase Machines. IEEE Trans. Ind. Electron. 2018, 65, 1128–1139. [Google Scholar] [CrossRef]
- Yepes, A.G.; Malvar, J.; Vidal, A.; López, O.; Doval-Gandoy, J. Current harmonics compensation based on multiresonant control in synchronous frames for symmetrical n-phase machines. IEEE Trans. Ind. Electron. 2015, 62, 2708–2720. [Google Scholar] [CrossRef]
- Lim, C.; Levi, E.; Jones, M.; Rahim, N.; Hew, W.P. FCS-MPC based current control of a five-phase induction motor and its comparison with PI-PWM control. IEEE Trans. Ind. Electron. 2014, 61, 149–163. [Google Scholar] [CrossRef]
- Taheri, A.; Rahmati, A.; Kaboli, S. Efficiency improvement in DTC of six-phase induction machine by adaptive gradient descent of flux. IEEE Trans. Power Electron. 2012, 27, 1552–1562. [Google Scholar] [CrossRef]
- Riveros, J.A.; Barrero, F.; Levi, E.; Duran, M.J.; Toral, S.; Jones, M. Variable-speed five-phase induction motor drive based on predictive torque control. IEEE Trans. Ind. Electron. 2013, 60, 2957–2968. [Google Scholar] [CrossRef]
- Gregor, R.; Rodas, J. Speed sensorless control of dual three-phase induction machine based on a Luenberger observer for rotor current estimation. In Proceedings of the 38th Annual Conference on IEEE Industrial Electronics Society (IECON), Montreal, QC, Canada, 25–28 Octorber 2012; pp. 3653–3658. [Google Scholar] [CrossRef]
- Ayala, M.; Gonzalez, O.; Rodas, J.; Gregor, R.; Doval-Gandoy, J. A speed-sensorless predictive current control of multiphase induction machines using a Kalman filter for rotor current estimator. In Proceedings of the 2016 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Toulouse, France, 2–4 November 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Rodas, J.; Barrero, F.; Arahal, M.R.; Martín, C.; Gregor, R. Online estimation of rotor variables in predictive current controllers: a case study using five-phase induction machines. IEEE Trans. Ind. Electron. 2016, 63, 5348–5356. [Google Scholar] [CrossRef]
- Rodas, J.; Martín, C.; Arahal, M.R.; Barrero, F.; Gregor, R. Influence of Covariance-Based ALS Methods in the Performance of Predictive Controllers with Rotor Current Estimation. IEEE Trans. Ind. Electron. 2017, 64, 2602–2607. [Google Scholar] [CrossRef]
- Guzman, H.; Duran, M.J.; Barrero, F.; Zarri, L.; Bogado, B.; Prieto, I.G.; Arahal, M.R. Comparative study of predictive and resonant controllers in fault-tolerant five-phase induction motor drives. IEEE Trans. Ind. Electron. 2016, 63, 606–617. [Google Scholar] [CrossRef]
- Bermudez, M.; Gonzalez-Prieto, I.; Barrero, F.; Guzman, H.; Duran, M.J.; Kestelyn, X. Open-Phase Fault-Tolerant Direct Torque Control Technique for Five-Phase Induction Motor Drives. IEEE Trans. Ind. Electron. 2017, 64, 902–911. [Google Scholar] [CrossRef]
- Baneira, F.; Doval-Gandoy, J.; Yepes, A.G.; López, O.; Pérez-Estévez, D. Control Strategy for Multiphase Drives With Minimum Losses in the Full Torque Operation Range Under Single Open-Phase Fault. IEEE Trans. Power Electron. 2017, 32, 6275–6285. [Google Scholar] [CrossRef]
- Rodas, J.; Guzman, H.; Gregor, R.; Barrero, B. Model predictive current controller using Kalman filter for fault-tolerant five-phase wind energy conversion systems. In Proceedings of the 7th International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Vancouver, BC, Canada, 27–30 June 2016; pp. 1–6. [Google Scholar] [CrossRef]
- Echeikh, H.; Trabelsi, R.; Mimouni, M.F.; Iqbal, A.; Alammari, R. High performance backstepping control of a fivephase induction motor drive. In Proceedings of the 2014 IEEE 23rd International Symposium on Industrial Electronics (ISIE), Istanbul, Turkey, 1–4 June 2014; pp. 812–817. [Google Scholar] [CrossRef]
- Echeikh, H.; Trabelsi, R.; Iqbal, A.; Bianchi, N.; Mimouni, M.F. Comparative study between the rotor flux oriented control and non-linear backstepping control of a five-phase induction motor drive—An experimental validation. IET Power Electron. 2016, 9, 2510–2521. [Google Scholar] [CrossRef]
- Kali, Y.; Rodas, J.; Saad, M.; Gregor, R.; Bejelloun, K.; Doval-Gandoy, J. Current Control based on Super-Twisting Algorithm with Time Delay Estimation for a Five-Phase Induction Motor Drive. In Proceedings of the 2017 International Electric Machines and Drives Conference (IEMDC), Miami, FL, USA, 21–24 May 2017; pp. 1–8. [Google Scholar] [CrossRef]
- Kali, Y.; Rodas, J.; Saad, M.; Gregor, R.; Bejelloun, K.; Doval-Gandoy, J.; Goodwin, G. Speed Control of a Five-Phase Induction Motor Drive using Modified Super-Twisting Algorithm. In Proceedings of the 2018 International Symposium on Power Electronics, Electrical Drives, Automation and Motion (SPEEDAM), Amalfi, Italy, 20–22 June 2018; pp. 938–943. [Google Scholar] [CrossRef]
- Ayala, M.; Gonzalez, O.; Rodas, J.; Gregor, R.; Kali, Y.; Wheeler, P. Comparative Study of Non-linear Controllers Applied to a Six-Phase Induction Machine. In Proceedings of the 2018 International Conference on Electrical Systems for Aircraft, Railway, Ship Propulsion and Road Vehicles & International Transportation Electrification Conference (ESARS-ITEC), Nottingham, UK, 7–9 November 2018; pp. 1–6. [Google Scholar]
- Fnaiech, M.A.; Betin, F.; Capolino, G.A.; Fnaiech, F. Fuzzy logic and sliding-mode controls applied to six-phase induction machine with open phases. IEEE Trans. Ind. Electron. 2010, 57, 354–364. [Google Scholar] [CrossRef]
- Utkin, V. Sliding Mode in Control and Optimization; Springer: Berlin, Germany, 1992. [Google Scholar]
- Utkin, V.; Guldner, J.; Shi, J. Sliding Mode Control in Electromechanical Systems; Taylor-Francis: Abingdon, UK, 1999. [Google Scholar]
- Fridman, L. An averaging approach to chattering. IEEE Trans. Autom. Control 2001, 46, 1260–1265. [Google Scholar] [CrossRef]
- Boiko, I.; Fridman, L. Analysis of Chattering in Continuous Sliding-mode Controllers. IEEE Trans. Autom. Control 2005, 50, 1442–1446. [Google Scholar] [CrossRef]
- Young, K.D.; Utkin, V.I.; Ozguner, U. A control engineer’s guide to sliding mode control. IEEE Trans. Control Syst. Technol. 1999, 7, 328–342. [Google Scholar] [CrossRef]
- Drakunov, S.; Utkin, V. Sliding mode observers. Tutorial. In Proceedings of the 34th IEEE Conference on Decision and Control, New Orleans, LA, USA, 13–15 December 1995; pp. 3376–3378. [Google Scholar] [CrossRef]
- Yan, X.G.; Edwards, C. Nonlinear robust fault reconstruction and estimation using a sliding mode observer. Automatica 2007, 43, 1605–1614. [Google Scholar] [CrossRef]
- Levant, A. Higher-order sliding modes, differentiation and output-feedback control. Int. J. Control 2003, 76, 924–941. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Benjelloun, K.; Fatemi, A. Discrete-time second order sliding mode with time delay control for uncertain robot manipulators. Robot. Auton. Syst. 2017, 94, 53–60. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Benjelloun, K.; Khairallah, C. Super-twisting algorithm with time delay estimation for uncertain robot manipulators. Nonlinear Dyn. 2018, 93, 557–569. [Google Scholar] [CrossRef]
- Kali, Y.; Saad, M.; Benjelloun, K.; Benbrahim, M. Sliding Mode with Time Delay Control for MIMO Nonlinear Systems with Unknown Dynamics. In Proceedings of the 2015 International Workshop on Recent Advances in Sliding Modes (RASM), Istanbul, Turkey, 9–11 April 2015; pp. 1–6. [Google Scholar] [CrossRef]
- Kali, Y.; Rodas, J.; Gregor, R.; Saad, M.; Benjelloun, K. Attitude Tracking of a Tri-Rotor UAV based on Robust Sliding Mode with Time Delay Estimation. In Proceedings of the 2018 International Conference on Unmanned Aircraft Systems (ICUAS), Dallas, TX, USA, 12–15 June 2018; pp. 346–351. [Google Scholar] [CrossRef]
- Bandal, V.; Bandyopadhyay, B.; Kulkarni, A.M. Design of power system stabilizer using power rate reaching law based sliding mode control technique. In Proceedings of the 2005 International Power Engineering Conference, Singapore, 29 November–2 December 2005; pp. 923–928. [Google Scholar] [CrossRef]
- Gonzalez, O.; Ayala, M.; Rodas, J.; Gregor, R.; Rivas, G.; Doval-Gandoy, J. Variable-Speed Control of a Six-Phase Induction Machine using Predictive-Fixed Switching Frequency Current Control Techniques. In Proceedings of the 9th IEEE International Symposium on Power Electronics for Distributed Generation Systems (PEDG), Charlotte, NC, USA, 25–28 June 2018; pp. 1–6. [Google Scholar] [CrossRef]
- Harnefors, L.; Saarakkala, S.E.; Hinkkanen, M. Speed Control of Electrical Drives Using Classical Control Methods. IEEE Trans. Ind. Appl. 2013, 49, 889–898. [Google Scholar] [CrossRef]
- Jung, J.H.; Chang, P.; Kang, S.H. Stability Analysis of Discrete Time Delay Control for Nonlinear Systems. In Proceedings of the 2007 American Control Conference, New York City, NY, USA, July 11–13 2007; pp. 5995–6002. [Google Scholar] [CrossRef]
- Qu, S.; Xia, X.; Zhang, J. Dynamics of Discrete-Time Sliding-Mode-Control Uncertain Systems With a Disturbance Compensator. IEEE Trans. Ind. Electron. 2014, 61, 3502–3510. [Google Scholar] [CrossRef]
- Yepes, A.G.; Riveros, J.A.; Doval-Gandoy, J.; Barrero, F.; López, O.; Bogado, B.; Jones, M.; Levi, E. Parameter identification of multiphase induction machines with distributed windings Part 1: Sinusoidal excitation methods. IEEE Trans. Energy Convers. 2012, 27, 1056–1066. [Google Scholar] [CrossRef]
- Riveros, J.A.; Yepes, A.G.; Barrero, F.; Doval-Gandoy, J.; Bogado, B.; Lopez, O.; Jones, M.; Levi, E. Parameter identification of multiphase induction machines with distributed windings Part 2: Time-domain techniques. IEEE Trans. Energy Convers. 2012, 27, 1067–1077. [Google Scholar] [CrossRef]
| Parameter | Value | Parameter | Value | Parameter | Value |
|---|---|---|---|---|---|
| () | 6.9 | (mH) | 626.8 | (kW) | 2 |
| () | 6.7 | (rpm) | 3000 | (kg·m) | 0.07 |
| (mH) | 5.3 | (mH) | 654.4 | (kg·m/s) | 0.0004 |
| (mH) | 614 | P | 1 | (V) | 400 |
| Sampling | Frequency | 8 kHz | ||||
| MSE | MSE | MSE | MSE | MSE | MSE | |
| 500 | 0.2502 | 0.2602 | 0.1875 | 0.1729 | 0.2494 | 0.2609 |
| 1000 | 0.2937 | 0.3021 | 0.2326 | 0.2280 | 0.3039 | 0.2919 |
| 1500 | 0.3000 | 0.3050 | 0.2491 | 0.2456 | 0.3327 | 0.2689 |
| Sampling | Frequency | 16 kHz | ||||
| MSE | MSE | MSE | MSE | MSE | MSE | |
| 500 | 0.1867 | 0.1883 | 0.1931 | 0.1851 | 0.1830 | 0.1919 |
| 1000 | 0.1797 | 0.1779 | 0.2078 | 0.1975 | 0.1795 | 0.1780 |
| 1500 | 0.1731 | 0.1786 | 0.2342 | 0.2291 | 0.1767 | 0.1750 |
| Sampling | Frequency | 8 kHz | |||||
| THD | THD | RMS ripple | RMS ripple | FF | FF | MSE | |
| 500 | 29.6198 | 30.7074 | 0.2598 | 0.2492 | 1.0811 | 1.0300 | 1.3432 |
| 1000 | 17.8543 | 18.0026 | 0.2890 | 0.3005 | 1.0203 | 1.0405 | 2.2250 |
| 1500 | 17.8761 | 18.0059 | 0.2593 | 0.3194 | 1.0084 | 1.1389 | 2.4146 |
| Sampling | Frequency | 16 kHz | |||||
| THD | THD | RMS ripple | RMS ripple | FF | FF | MSE | |
| 500 | 21.6914 | 22.6592 | 0.1895 | 0.1829 | 1.0466 | 1.0164 | 1.6508 |
| 1000 | 15.3291 | 14.8507 | 0.1751 | 0.1783 | 1.0087 | 1.0151 | 2.8814 |
| 1500 | 11.1020 | 11.2140 | 0.1707 | 0.1712 | 1.0040 | 1.0134 | 3.1855 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kali, Y.; Ayala, M.; Rodas, J.; Saad, M.; Doval-Gandoy, J.; Gregor, R.; Benjelloun, K. Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation. Energies 2019, 12, 170. https://doi.org/10.3390/en12010170
Kali Y, Ayala M, Rodas J, Saad M, Doval-Gandoy J, Gregor R, Benjelloun K. Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation. Energies. 2019; 12(1):170. https://doi.org/10.3390/en12010170
Chicago/Turabian StyleKali, Yassine, Magno Ayala, Jorge Rodas, Maarouf Saad, Jesus Doval-Gandoy, Raul Gregor, and Khalid Benjelloun. 2019. "Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation" Energies 12, no. 1: 170. https://doi.org/10.3390/en12010170
APA StyleKali, Y., Ayala, M., Rodas, J., Saad, M., Doval-Gandoy, J., Gregor, R., & Benjelloun, K. (2019). Current Control of a Six-Phase Induction Machine Drive Based on Discrete-Time Sliding Mode with Time Delay Estimation. Energies, 12(1), 170. https://doi.org/10.3390/en12010170









