Abstract
Decentralized energy production offers an increased share of renewable energy and autonomy compared to the conventional, grid-only solution. However, under the net-metering scheme, the energy losses in batteries translate into financial losses to an investor seeking to move away from grid-only electricity and set up a residential PV+Battery microgrid. Our paper examines a hypothetical support scheme for such a project, designed to balance the economic disadvantage through partially supporting the acquisition of batteries, and thus ensure that the microgrid solution is more attractive than no investment. For this we develop four case studies based on experiments carried out in Greece, Italy, Denmark and Finland. Using the minimization of the Net Present Cost for each project, we compare the PV+Battery solution to the grid-only scenario over 25 years, for a range of electricity prices. The results illustrate first how the success of this project depends on the price of electricity. Second, we find that under current conditions in the respective countries the need for battery support varies between zero in Denmark and 86% in Italy, which reflects how the disadvantages of net metering can only be counterbalanced by either very high electricity price or very high solar resource. Our paper contributes thus to the discussion about the favourable environment for batteries in residential microgrids.
1. Introduction
Reports forecasting the development of electricity networks by 2050 point out that there will be increased decentralized energy generation in cities to help meeting climate change mitigation and decarbonization goals [1] and the growing demand for smart solutions and energy flexibility [2,3]. In the EU, Microgrids (MGs) exploit the full advantage of distributed energy resources [4], and at the same time their cost ranges are projected to further drop by 50–75% over the next 15 years [5]. In the anticipation of these developments the study of microgrids investment draws special attention.
Microgrids are understood to be small-scale grids that serve their load with a mix of resources and can be connected or not to the main grid. They are regarded as building blocks of smart grids, with control capabilities that allow distribution networks to also operate when isolated from the main grid, in case of faults or other external disturbances or disasters [6]. It is worth noting that in current perception MGs operate largely at low voltage (LV) and include, unless specified otherwise, one or more renewable energy sources (RES), thus promoting decentralization and helping the transition away from fossil fuels and nuclear power.
Densely populated urban environments do not provide the necessary space for hydro or biomass plants, nor the quality of the wind resource necessary for large wind turbines—therefore solar energy remains the single renewable resource that can be harvested efficiently within urban residential areas. However, the fraction of renewable energy used from residential PV units can be further increased through the inclusion of storage systems—e.g., batteries, flywheels, capacitors, etc. In fact, including storage provides a series of advantages: increased autonomy for the end user, decongestion of the main grid, grid stabilization, power quality management, reliability supervision, loads shifting and grid operational support [7], and the option found to be most suitable for short-term storage are regarded to be batteries [8]. This is why the European Energy Union has deemed that “energy storage should participate in the system and be rewarded” [9].
In addition to the favourable economic perspectives and to the political encouragement, the take-up of MGs that include storage can be further facilitated by the District Network Operator (DNO). The bidirectional power flow and the intermittency of RES cause congestion on LV networks, as well as under/over voltages, overloads and line losses [10]. By facilitating the development of Decentralized Energy Resources (DER) solutions and encouraging energy storage, DNOs can avoid these problems for themselves.
However from the point of view of energy balance and economic rationale, under the net-metering scheme, using storage alongside PV units proves sub-optimal. The problem comes from the battery losses: with each charge-discharge cycle an amount of energy, instead of being injected into and then retrieved from the main grid, is in fact lost.
This paper examines the situation in which a greenfield investment is considered for a grid-connected residential microgrid consisting of a PV unit and a storage unit (batteries). The research focuses on four case studies based on real-life experiments, adapted to cover the same load (8 households) and similar proportions between PV production, self-consumption, and storage. We compare the Net Present Cost (NPC) of these investments for the next 25 years with the cost of using only electricity from the main grid (no investment, baseline scenario). Due to the losses in the battery, the PV+Battery solution prevents the investor to reach maximum profitability with the MG system, and for this reason we propose a support scheme in which the acquisition of the battery is partly covered by a third party (e.g., local government, other stakeholders). The objective of the investigation is to set a benchmark for the battery support that is required in order to keep the NPC of the PV+Battery system lower than the one from the baseline scenario. Our paper calculates the benchmark 50 values in the countries of the respective case studies and draws conclusions from the difference in results.
The benefits for society and the environment outlined earlier are up until now not reflected in the costs and benefits borne by the private actor investing in a microgrid. As such, the contribution of this paper is that it delivers the first investigation, to the best of the authors’ knowledge, into both a possible support scheme specifically targeting the inclusion of batteries in microgrids, as well as a comprehensive analysis of the drivers dictating the cost of such a scheme, providing valuable insights for policymakers.
1.1. Literature Review
Economic investigation of MGs is on the one hand strongly connected to the technological specifications of the MGs considered: e.g., equipment, components, size. On the other hand, the economic insights are also strongly influenced by policy in form of incentives, subsidies, tax deductions or reductions, etc. Therefore the economic research of MGs tends to be case-specific, and a majority of academic papers on this topic either are driven by case studies, or focus on a country-specific policy or technological scope (components used in a MG).
In our paper we have limited the scope in type and size (residential, case studies, 8 households) and policy (net metering, EU). We understand a microgrid to be a community renewable energy project (as in [11,12]) and the operationalization is aligned with the concepts of community renewable energy projects, including the spectrums proposed for range of actors and distribution of financial benefit [13]. Our literature review is therefore targeted on residential microgrids, their relationship with DNOs, studies of experimental set-ups similar to our scope, and specifically residential MGs consisdting in PV+Battery, specifically the Li-Ion batteries which are consodered to be today’s state-of-art [14]. The conclusions of the literature review, detailed in the subsections below, are the following:
- Research agrees that batteries in PV-powered grid-connected residential MGs have many advantages but under the net-metering scheme they can only be made profitable through support; however no investigation or simulation of a specific support measure could be found.
- Academic literature confirms that, from a technological point of view, DNOs can be potentially interested in an uptake of residential MGs;
- As a method of evaluation, the techno-economic assessment (TEA) with tools such as the HOMER software is commonly used for studies similar to ours.
1.2. Residential, PV+Battery MGs
A review of 45 existing, simulated and experimental MGs, of which five were comparable to our study, concludes that a combination of different RES together with storage has a significant economic potential, especially for storage systems sized to cover lower ratios of Stored energy/PV Output [15]. A similar study, examining 13 MGs against academic literature, found that including storage is an essential success factor for decentralized generation [16]. However a review of 17 studies, of which 6 in the EU, found that the costs exceeded the benefits under current conditions in the smart grid systems that were analyzed [17]. Overall, literature research finds several types of incentives that can encourage the implementation of storage systems: availability of third-party financing, high demand charges, technology cost reductions, and market developments [18]. Net metering, on the other hand, is found to be less conducive to battery profitability [19].
Regarding individual case studies, a particularly comprehensive insight can be drawn from Italy, where several pilot projects of medium and LV MGs have been studied. In those cases, storage systems are necessary if the presence of RES is to expand [20], and two case studies confirm that using storage systems improved power quality [21]. A study in the Milan urban area supports the case for energy storage by calculating savings from unnecessary grid expansions based on distributed generation (DG) energy including storage [22]. The same pilot project in the Milan area reported that the local Internet infrastructure was able to provide the intra-MG communication [23]. In Helsinki it was possible to demonstrate how MGs with storage can improve the urban network [24]. In the UK, a solution for the promotion of DG has been found to be via incentives for lowering carbon emissions through storage [22], whereas in Portugal the inclusion of storage has been the key to identifying the economic boundaries in the relationship with the DNO (Idem).
The recent paper of Li et al. [25] carries out an analysis similar to ours on residential MGs in Japan under a feed-in tariff (FiT), and concludes that the inclusion of batteries depends on support schemes and that, among others, increased electricity pricing can improve the attractiveness of a PV+Battery system. In Switzerland, on the other hand, the storage system would only become attractive in a residential MG (also under FiT) once the cost of batteries is halved [26]. In the case of Germany, also using FiT, the current conditions are favourable for standalone PV units, and in the absence of other incentives the uptake in battery adoption will synchronize with the decrease of battery prices [27]. In fact, a study of both countries reveals that higher electricity prices contribute to the profitability of PV+Battery systems [28], as confirmed by the comparative study of Germany, Spain, France and Italy [29]. For a MG in Italy, under the net-metering scheme, similar conclusions have been reached; however in an analysis for 10 years project lifetime and with storage costs higher than the ones regarded in this paper [30]. A study of several sizing and subsidy combinations, also in Italy, confirms that PV+Battery systems can reach profitability through either subsidies or high self-consumption rates [31].
Other than with direct support, incentives such as real time energy pricing combined with capacity block pricing could contribute to a wider adoption of batteries in residential MGs [32]. Alternatively, economic valuation can be changed in favour of batteries if energy storage is regarded as a distinct asset class within the electric value chain [33], or if resilience and power quality also get included in the calculations [34]. Resilience, in this case, is the capability of energy systems to withstand macro-grid outages by islanding and meeting critical loads. An Australian case study also finds that the benefits which the network derives from from battery contributions such as reducing residential evening peaks, if monetized by the investor, can compensate the econmic losses of the PV+Battery system [35]. Under these circumstances, combining renewables and storage into Virtual Power Plants promises financial benefit [36].
1.3. Residential Microgrids versus DNOs
Dealing with individual prosumers causes an increased bidirectional power flow, which has an impact on the bus voltages and on the power losses, all the more severe in LV networks due to high ratio of active/reactive power of the lines [37]. In fact, the bidirectional traffic on the lines is a problem for DNOs “particularly in radial LV networks, where renewable intermittency and bidirectional power flow may cause critical problems such as under/over voltages, line overloads and high energy losses. System operators consider the worst-case scenarios for the assessment of the impacts of new integrations and usually they prefer passive methods to mitigate the negative effects” [10]. Traditional distribution network practice is often described as ‘fit and forget’ [38], but as the volume of connected DG increases, the amount of available network capacity becomes exhausted and, if more DG is to be accommodated, some improvements become necessary [39].
From the point of view of the residential consumers, increasing self-sufficiency is more attractive for higher-demand consumers (as opposed to single-household consumers) due to the scale effect of pooling the storage capabilities [40]; that means that a number of residential consumers bundled in a MG can profit more from the pooled benefit than from an individual relationship with the DNO.
Cooperation between utilities and customers has the potential for cost and energy savings while balancing the benefits between the participants (provided that the mutual dependence of energy consumption cost among consumers is fairly addressed) [41]. The DNOs, today’s de facto electricity providers to the end consumer, are thus required to adjust to new business models that are not necessarily based on volume sales (kWh), but still are expected to remain important players if they consider selling other services such as balancing and security [42].
1.4. Economic Assessment of Microgrids
Incipient economic studies of MGs have focused on minimizing either the capital investments or the operational costs of a MG (see [43]). However, with the improvement of computational capabilities, it is now state-of-the art to carry out a full TEA that takes into account all the variables and constraints. The TEA is part of the business case of MGs, which is key to argumentation in their favour [44]. Currently there is an array of pieces of software available for TEA of microgrids [45,46]. Out of these solutions, we found that HOMER was the software used most widely in case studies researching microgrid optimization, sizing and economic evaluation.
HOMER is driven by the minimization of NPC [47], which is an indicator further explained in Section 2.1. The NPC includes the acquisition, installation and replacement cost (CapEx), as well as the O&M and fuel cost (OpEx) during the system lifetime. All the cash flows are measured from the moment of the system operation and take into account such country-specific indicators like inflation, discount and interest rate [48].
2. Method
For our study we analyze a MG system consisting of the following:
- A residential load sized to 8 households
- A PV unit sized to cover ca. 70% of the yearly consumption
- A connection to the main grid under the net-metering scheme
- A storage unit sized to cover ca. 19% of the yearly consumption
The exact specifications of each system can be found in Appendix A. Each system is duplicated for each country of the case studies (Greece, Italy, Denmark and Finland) with minimum adjustments. The detailed description of the analyzed systems is presented in Section 2.2; the design of the case studies based on the real-life experiments carried out in each location is further detailed in Appendix A. The indicators, parameters and methods used for the software analysis are detailed in Section 2.1.
2.1. TEA of the System
For the TEA we used the HOMER software to calculate and minimize the NPC of the MG project, while at the same time checking for renewable fraction. It is worth pointing out that in the evaluation of investment projects, the indicators NPV and NPC can be used for the same output: NPV is a function to maximize, whereas its opposite, the NPC, is to be minimized.
The following cost components are considered: capital, replacement, O&M, fuel, emissions penalties, and buying power from the grid. Residual value of equipment at the end of the project lifetime, as well as the earnings from selling electricity to the grid give the revenue. “HOMER calculates the total NPC by summing up the total discounted cash flows in each year of the project lifetime” [49].
Based on the MG components—PV unit, battery and grid connection—the NPC is calculated for each feasible combination of the three under the given parameters (incl. the price of electricity and load):
- Grid-only, which corresponds to our baseline scenario ()
- Grid+PV, which means covering the load with a PV unit backed by the main grid under the net-metering scheme ()
- Grid +Battery+PV, in which the load is served by a PV unit backed primarily by storage and secondarily by the main grid under the net-metering scheme ()
- Grid+Battery, which is regarded as an impractical solution and therefore discarded.
Given the three values calculated at (1), (2) and (3), the goal of the rational investor is to select the configuration which yields the lowest NPC. As outlined in the introduction, the system including a battery is inferior to a PV-only system under net metering due to the energy losses in the battery. Having a PV+Battery system can lead to one of the two situations which we illustrate with the following intervals:
and
The focus of this research are systems which do include a battery and are still an attractive investment compared to the grid-only scenario, as formulated in interval (1). As explained in Section 3.1, having a MG investment project in interval (1) or (2) depends, by way of design, on the price of electricity from the main grid and on the capital cost of the storage system.
In order to ensure a “jump” from interval (2) to interval (1), two parameter sweeps were carried out for 2 scenarios, as detailed in Section 2.3.
It is however important to acknowledge that the use of the NPV indicator is disputed as a driver for investment decision for investments with characteristics such as irreversibility, uncertainty, flexible timing, and lumpiness [50]. In our study we use the NPC indicator (the opposite of NPV) not for real-life investment decisions, but for the purpose of comparison.
2.2. Case Studies
Original data for the case studies has been collected during four research visits within the Transnational Access program of ERIGrid under H2020, to research facilities in Greece, Italy, Denmark and Finland. The host facilities have each provided various MG components as detailed in Table A3 in Appendix A, with which a number of different operation scenarios in grid-connected and islanded mode were carried out. In parallel with the technical experiments, economic data has been collected, so as to enable a TEA using the HOMER software.
The data collection was driven by the input requirements of the software, and included three types of parameters:
- Geographically determined economic and environmental parameters, which depend on each country and are assumed to be fixed (sun radiation intensity, inflation rate, electricity price);
- Technical parameters of the examined systems, referring to technical capacity and performance levels of equipment pieces, as well as the relationships and proportions between them. These have been provided by the host facilities (if necessary an equivalent has been recalculated to match equipment pieces provided by the software database) and further resized to fit the 8-household objective;
- Economic parameters including equipment prices and O&M costs. Acquisition prices have been partly collected from online retail sources, partly provided by the host facilities.
A full summary of the input parameters can be found in Appendix B.
2.2.1. Geographically Determined Economic and Environmental Parameters
Having each system located in a different country we have taken into account the local environmental and environmentally impacted parameters for each setting:
- latitude and longitude (software database)
- GHI radiation (software database)
- temperature resource (software database)
- load profiles (software database combined with experimental data)
- PV generation profiles (software database combined with experimental data, for details see Appendix A)
The country-specific economic indicators that contribute to the calculation of of each system are outlined in Table 1.

Table 1.
Overview of economic indicators for the case studies.
2.2.2. Technical Parameters
The case studies investigated in this paper are based on four sets of experiments, each carried out at a different research facility. In addition to the geographically dependent economic and environmental variables, each facility was equipped with system components of different sizes, capacities, performance levels, ages, etc. Therefore, in order to enable comparisons between systems, it was necessary to develop new systems by resizing, adjusting and adapting the examined configurations (Appendix A provides an overview of the original set-ups on which the MGs studied in this paper are based).
First, the systems have been aligned with the research scope and reduced to include only a PV unit, storage and the respective load. Then, all systems have been resized so as to reach one fixed size: households, which is a mean of the system sizes regarded in the experiments, and we consider to be a reasonable size for an urban residential microgrid, comparable with other case studies (e.g., [54]). The differences between the systems are driven by the load size and environmental conditions: based on them, the PV units were sized to cover similar proportions of the consumption, as were the battery capacity values. The calculations are presented step by step in Appendix A.
At this point it is worth detailing the adjustments requested by the constraints of the HOMER software.
HOMER is a TEA tool to estimate the main indicators of a MG project and carry out sensitivity analyses [49]. The way it is designed it assumes a greenfield investment: the project starts from scratch, with all components installed at the same time. Real-life investments are not always as straightforward; in fact, the systems on which the aforementioned experiments have been carried out, had been extended and improved over several years, ending up with PV panels and batteries of various sizes, ages and efficiency levels.
In order to solve this problem we retained the capacity levels of the equipment, but for the HOMER simulations we substituted them with new equipment pieces selected from the software database. The resulting simulations were carried out on MG systems set to start their lifetime in 2018, with equipment prices at the level of 2018, for a project lifetime of 25 years—but emulating the performance of the real-life systems used in the experiments (i.e., substituting PV panels older than 10 years with newer ones but at 80% of the original performance level, following the technology depreciation curve [55]). The two major changes were the use of Li-Ion batteries as a standard for the storage system, and the use of generic polycrystalline PV units.
Table 2 provides a summary of the technical indicators of the system, as they result from the calculations detailed in Appendix A.

Table 2.
Technical data of the 8-households case study systems with battery.
In Table 2 the first two horizontal sections (5 lines) describe a MG system without a battery (PV+G). In this scenario, in the example of Greece (column 1), the ratio between the yearly PV production and the yearly consumption of the households is 77.65%, given by the sizing of components based on the real-life experiment carried out at the Greek research facility CRES. This system, designed to operate load-first (PV output destined primarily for consumption, only excess electricity sold), achieves a level of renewable penetration of 60.10% of the total consumption. This value is lower than the 77.65%: the difference reflects the fact that not all of the energy produced by the PV unit is being used, but whenever the production exceeds the demand the surplus energy is being fed into the main grid, which is consistent with the project design.
In the lower part of the table we regard the same MG, to which we add a storage system sized to cover ca. 19% of the yearly energy consumption. In the same Greek scenario from column 1, the Battery is charged on account of 29% of the total PV production. The value of 29% is calculated at the end of each year by regarding the hour-by-hour operation of the system and distinguishing from the PV production the amount directly used by the consumer, the amount stored in the batteries, and finally the amount left to sell to the grid.
On line 8, the ratio Battery Output/Consumption provides the verification of the initial constraint of 19% autonomy, now calculated via software with the selected equipment pieces and results in values between 18.9% and 20.15%, which comply with the initial constraint. The battery output (minus battery losses), once fed back into the MG, counts towards the fraction of renewable energy use, hence the increase in renewable fraction from 60.10% before battery to 68.70% with battery in the Greek set-up. In fact, on each column we can identify significant increases of renewable fraction due to the inclusion of a battery in the system.
Figure 1 exemplifies the behaviour of the system during 2 randomly selected days over the year.
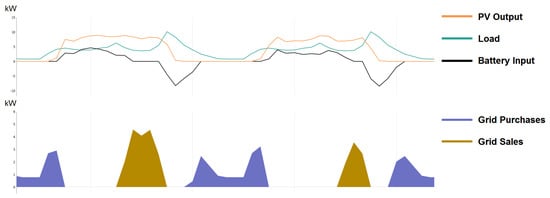
Figure 1.
Example of the functioning of the components of a system from Table 2 (upper graph) and the parallel exchange with the grid (lower graph)—graphical adaptation from author’s experiments. Load convention presupposes that negative battery input (in black) stands for discharge.
The battery dispatch strategy is oriented towards maximizing the renewable fraction, therefore the control parameters include “prohibit grid from charging battery” and “prohibit sales from battery”. In fact, maximization of the renewable fraction implies a minimization of the exchange with the main grid, as follows: load is primarily served by PV output, secondarily by battery, and only if none of them can provide electricity draw from the main grid; for PV output, first serve load, secondarily charge battery, and if there is surplus, feed it into the main grid; finally, the battery can only be charged from the PV output, and can only discharge to meet load.
2.2.3. Economic Parameters
For our research we have decided to distribute the capital expenditures on the main hardware items. In other words, we regard the PV unit as a whole, but translating this perspective into HOMER means that the only cost carrier are the PV panels; all the other components of the PV unit (wires, controllers, converters, installation costs) are artificially set to zero. The same applies to the storage system. In this context, Table 3 provides an overview of the purchase prices of the MG components as found at various online retailers and/or provided by the host facilities. The prices do not include VAT.

Table 3.
Overview of PV unit prices.
The PV unit prices have been calculated based on retail prices featured on online resellers, excluding VAT. As mentioned above, the equipment pieces used in the real-life experiments were of different ages and performance levels, whereas the software input requirements suppose all capital expenditures on the same level, set to today’s values, therefore all prices considered for the analysis are on the level of 2018.
2.3. Scenario Analyses
For our research we carry out two scenario analyses: one by varying the price of electricity from the main grid () and keeping the price of battery constant at zero, and one by varying the acquisition price of the storage system until for the fixed electricity price. For both scenarios we define the following roles for the participants:
- Investor: can be the consumer (i.e., the households, in which case it is the “prosumer”) or another private investor willing to set up a grid-connected MG (PV+Battery) for the 8 households. The decision of the investor is 0 or 1, whether to invest or not, and it is based on whether the investment brings savings compared to the baseline scenario ().
- Supporter: can be the policy maker and/or the DNO or any other stakeholder interested in the advantages of decentralizing the electricity production (see the introduction). The Supporter is willing to cover partly or fully the cost of including a storage system over the 25 years of project lifetime, but not willing to facilitate savings (profit) for the Investor ().
The interest of the Investor is to receive as much contribution from the Supporter as possible. This however goes against the interest of the Supporter, as from their point of view the Investor is already being helped with battery acquisition (fully or partially), it would not be rational to support them in making further profits.
We are interested in the relationship between and and compare them by means of a ratio. We denote the savings in NPC that the investor achieves by including a battery with an indicator which we express in percentage.
For example a value of means that and the project cost of the MG is lower than the cost in the baseline scenario, thus achieving savings for the investor in the MG project. The level of savings is 10% of .
The confronting interests of the Investor and the Supporter are reconciled when , which is when . From Equation (3) it follows that this can be achieved by either maximizing by increasing , or by minimizing by supporting the acquisition of the battery—depending on whether Equation (1) or (2) applies to the specific case.
Our paper investigates the two possibilities through two policy scenarios:
Scenario 1: Having a load of households served by a PV unit primarily and connected to the main grid secondarily, under the net-metering scheme, the Supporter can decide to provide storage system for free (due to software requirements, the calculations were carried out considering the capital cost of the battery = 1 € + cost of the converter = 1 €; all other costs related to the storage system (capital, installation, maintenance, replacement, etc) were set to zero) for 25 years. In this scenario the Investor is required to provide only the PV unit. Our parameter sweep in Scenario 1 determines for which .
Scenario 2: Having learned from Scenario 1 that the current electricity prices incur significant savings in NPC for the Investor, it is reasonable for the Supporter to contribute with less than the full price of the battery. Under this scenario we calculate the contribution that the Supporter would have to make to support the inclusion of storage systems in order to make the MG project more attractive than the baseline (minimize until it equals given ).
The baseline scenario (grid-only) is calculated to serve as reference for both Scenario 1 and 2, and represents the cost of using electricity from the main grid only over the next 25 years (no investment). The price of electricity is regarded as unchanged for the 25-year projection, as are the inflation and discount rate, and the average household consumption and profile. However, the estimates calculated under this strong assumption serve as a benchmark, and are to be further compared to other estimates made under the same assumption. For this reason we have calculated the benchmark values for different prices of electricity (15 values in Table 4 and Table 5, 59 values in Figure 2 and Figure 4, and in the extended versions, Appendix C).

Table 4.
Values of in €, for different values of . Observed data in bold.

Table 5.
Variation of for a PV+Battery system, storage system provided for free.
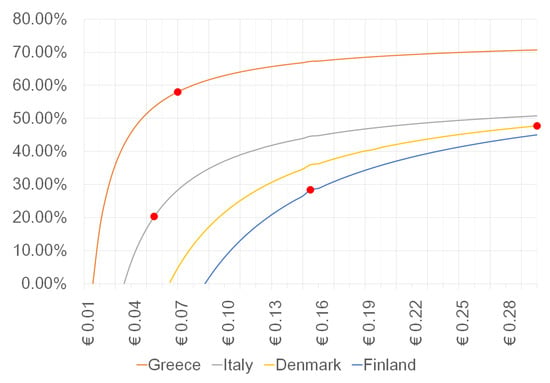
Figure 2.
increasing with the increase of in each country. Highlighted in red are the points corresponding to the level of savings provided at the current in the respective countries.
In Scenario 2 we set to achieve by minimizing until it reaches its minimum, that matches the value of for the fixed, given :
But the actual is related to the market price of the battery, which we set to 200 €/kWh [5]. In this scenario we obtain the minimized value of through the contribution of the Supporter, which is subtracted from the cost of the project. We denote the share of battery price which is contributed by the Supporter with :
The investigation of Scenario 2 determines how the market price of the battery is shared between the Supporter and the Investor in order to reconcile the interests of the two, at . We express the breakdown of the battery price with the following equation:
3. Results
The focus of this investigation is grid-connected residential MGs, each consisting of households, a PV unit and a storage system, with case studies located in Greece, Italy, Denmark and Finland. We investigate the inclusion of a battery under the net-metering scheme, and confront the problem that microgrids with battery are economically inferior to the grid-only scenario. As a solution, we examine the possibility that the acquisition of batteries is supported, and determine the amount and cost sharing between a Supporter and the Investor for which the microgrid project is economically attractive. Our paper further investigates the factors that drive these outcomes.
In the following subsections, the results of the TEA under the two scenarios are presented. The definition of scenarios and of the participants (Investor and Supporter) are detailed in the Method Section 2.
3.1. Results from Case Studies
Table 4 provides an overview of the baseline scenario (grid-only) with a sensitivity analysis on the electricity price () in each country (the values for observed data are highlighted in bold). The values of the for each represent, in fact, the total price of using only electricity from the main grid over the next 25 years: × annual consumption × 25 years. We consider the prices of electricity at the level from the time of the experiments (Table 1), and influenced only by inflation rate for the 25 years of project lifetime. We argue that the estimates obtained in this way serve as a conservative benchmark due to the fact that we also leave unchanged all other parameters (inflation rate, consumption per household).
The values of current electricity prices are highlighted in bold in Table 4, along with the corresponding values. In Denmark, for example, using the main grid for the next 25 years would cost 116,884 €; however if electricity would cost 0.20 €/kWh, the same Danish system would pay 77,922 € for the 25 years of use.
3.1.1. Scenario 1: Battery and Replacements for Free
As detailed in the Method Section 2.3 we first considered Scenario 1, a hypothetical public policy in which batteries are given out for free to prosumers (and replaced twice for free) over 25 years.
Table 5 summarizes the values of with a sensitivity analysis on , and reveals the following. For example in Finland, if = 0.01 €/kWh, installing a MG system with a battery for free yields an NPC of the project 492% greater than the baseline scenario from Table 4. In other words, if electricity is as cheap as 0.01 €/kWh, then setting up a microgrid, even with a battery for free, is still an unwise investment due to the installation costs of the PV unit. However if is gradually increased, the investment in a MG gradually becomes more attractive until, in the Finnish case, around the value of = 0.09 €/kWh when it breaks even with the baseline scenario and the disadvantage of the MG are at 0% compared to the grid-only scenario. In fact, for the current price of electricity in Finland at 0.158 €/kWh, setting up a microgrid saves 28% in NPC over 25 years (assuming that the battery and replacements are for free).
The graphic representation of Table 5 in Figure 2 offers additional insights. Based on the premises of Scenario 1 (see Section 2.3), one way of achieving is by increasing , which can happen if the price of electricity on the main grid increases. From Figure 2 we learn that the curves become “flatter” with the increase of , but have different slopes on the left side of the figure, for lower prices of electricity. For example in the Greek case, where we set €/kWh, an increase of to a €/kWh yields (in spite of the more expensive electricity!) an increase of savings from 17,153 € at to an amount of 18,728 € at a . The curve of for Greece is steeper than the others for low prices of electricity, which suggests that even small increases in the price of electricity can yield significant increases in savings for the investor. This option is of course less effective for “flatter” curves such as the evolution of savings for Italy for high electricity prices. Also, Figure 2 illustrates the significantly higher potential for savings in the Greek environment. The complete data source for Figure 2 can be found in Appendix D.
The simulation of Scenario 1 anchors the premises for Scenario 2: it visualizes to what extent are the savings to the prosumer dependent on and sensitive to the price of electricity (Figure 2), and it confirms that, for the current prices of electricity, a PV+Battery system brings significant savings to the Investor, if the battery is provided for free (Table 5).
3.1.2. Scenario 2: Storage Costs Shared
From Scenario 1 we learned that in Italy, for example, if the battery is provided for free, the Investor will achieve savings of 20% with the PV+Battery system, compared to the grid-only scenario. Since the Supporter is already providing a battery for free and not interested in facilitating further profits to the Investor, in Scenario 2 we consider the point where to be the break-even point where the interest of both participants are reconciled.
In Scenario 2 the electricity price for each case was held unchanged at the value of the observed during the time of the experiment. For these values is known (Table 4), the was calculated with the market price of the battery of 200 €/kWh [5], and finally and are based on Equations (5)–(7) (see Section 2).
Table 6 includes for reference the necessary storage capacity in each case. Additionally, represents the total price of a battery + two further replacements thereof during 25 years at today’s market price. Since the storage systems need different capacities across the four case studies in order to maintain each the 19% Storage/Consumption ratio, the absolute values of and are supported by including in Table 6 the investment per kWh nominal capacity installed. This indicator provides a clearer overview of how much the Investor and the Supporter contribute to each kWh storage. We find that between Greece and Finland, even though the storage requirements are significantly different (30 vs. 91.2 kWh), the Investors in both countries will be willing to pay comparable amounts of money for each kWh of storage capacity (567 vs. 395 €).

Table 6.
Sharing of battery purchase at market price between Investor and Supporter—in absolute values, in percentage, and per kWh capacity.
Figure 3 visualizes the share in battery investment required for between Supporter (orange) and Investor (grey), and shows that in Greece the Investor is capable of financing up to 94.4% of the total price of the storage system while keeping the PV+Battery system more attractive than the grid-only scenario. At the same time, the Supporter is required to contribute with at least 5.6% to the battery, in order to make sure that the PV+Battery system is attractive to the Investor. The high level of autonomy is correlated with the good GHI index of the location and with the comparatively lower price of the PV unit (the scaled annual average of the GHI resource used for the calculations is 4.94 kWh/m/day in Greece, compared to 3.68 in Italy, 2.90 in Denmark and 2.49 in Finland; for battery prices see Table 3). Solutions towards the full autonomy of the Investor include increases of (as per Scenario 1), batteries with the same price but higher roundtrip efficiency (in our simulation: ≥86%), or lower price of the existing batteries.
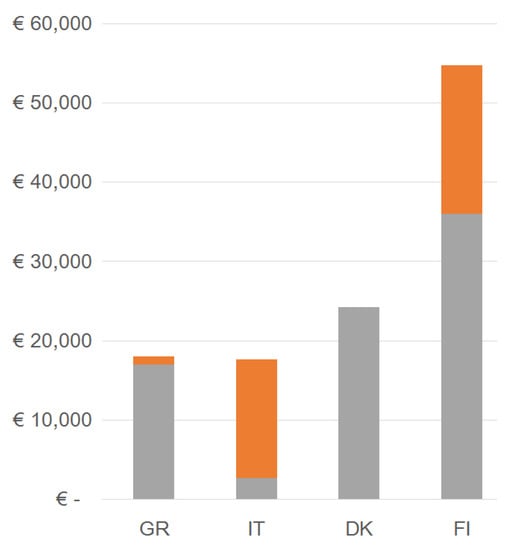
Figure 3.
(grey) and (orange).
In Italy on the other hand, in order for a similar system to succeed, the Supporter is required to contribute with at least 84.7% of the battery price, as the Investor is willing to pay only up to 2700 € (with a ) for the required storage system. Explanations for the low level of autonomy for the Investor could include the differences in PV output between summer and winter, as the location in Milan is often covered in fog during winter; a different location would arguably deliver improved results. Solutions towards better profitability of the PV+Battery system (and, hence, an increased autonomy of the Investor) can include a variation of storage capacity as suggested in the literature research section.
Scenario 2 reveals that in Denmark the solution for is that the Investor can afford to contribute a maximum of € for the battery, but in reality the price of the battery would not exceed 26,264 €. This implies that in Denmark the required contribution from the Supporter is €, and already as is, without additional support. By setting up a PV+Battery microgrid, a Danish investor saves ca. 31,500 € compared to the grid-only scenario, which is mostly due to the high price of grid electricity.
Finally in the Finnish case the Investor is willing to pay up to 65.79% of the necessary 54,720 € for a battery, which requires the Supporter to contribute with the remaining 34.21% in order for the project to succeed. Given the necessary size of the battery, the level of autonomy of the Investor can be regarded as encouraging. Also, Figure 2 suggests that at a higher electricity price the savings would be greater still, thus making the battery more attractive. Alternatively, tying the size of the storage system to the median PV output instead of the consumption could also provide more economic efficiency—or, indeed, identifying a new energy mix altogether. Results from Scenario 1 and 2 are summarized in Table 7.

Table 7.
Summary of findings for observed grid electricity prices.
Table 7 follows the narrative which includes Scenario 1 and 2. For example under the current conditions in Greece, an Investor set to build a MG with PV and a battery received free of charge will be saving 17,153 € compared to the no-investment option. These potential savings translate into a willingness to pay up to 17,153 € for a storage system, and should this sum not cover the whole market price of the storage system, a third party would be called for support. We find that the 17,153 € represent 94.4% of the battery investment cost.
Both Scenario 1 and Scenario 2 are focused on the solution PV+Battery, and are oriented and optimized towards maximizing the share of renewables. Our paper examines the performance of PV+Battery compared to the grid-only scenario under net metering, and investigates a hypothetical support scheme that would make the PV+Battery solution competitive. However, as indicated in the Method Section 2.1, Equations (1) and (2), from the economic point of view the PV-alone solution is always superior under the net-metering scheme. In this case the greenfield Investor is confronted with the choice: setting up a PV unit alone, with no support, or setting up a PV+Battery system, with the battery supported. In both cases the Investor yields significant savings compared to no investment—but in the case of PV alone the savings are greater still than in the case of PV+Battery. The argumentation in favour of the lower savings can rely on increasing the renewable share, but there is room for research whether the unrealized savings can be compensated by the advantages of the battery and the network-savings advantages of the DNO.
Figure 4 refers to Scenario 1 applied in Greece: the higher the price of electricity, the higher are the realized savings of PV+Battery system (orange). The total potential savings of a PV-only system are the sum of the orange and blue segments. In other words, the blue segments indicate how far are the realized savings from the highest possible savings (in €). For Investors who already have a PV unit in place but not battery, the net-metering scheme is offering what is effectively an ideal (zero-losses) battery for free, which is difficult to replace with a real-life battery that has a purchase price and energy losses. Further research is required to determine whether a similar support scheme is feasible for an addition of battery to a PV unit already in use, under net metering, knowing that even for optimal sizing and high-efficiency Li-Ion batteries, such systems are not profitable [57].
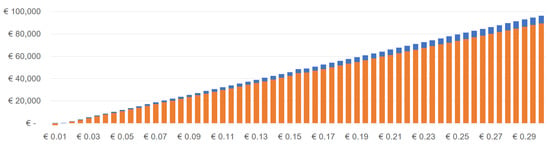
Figure 4.
Realized savings due to PV+Battery (orange) and potential additional savings from PV alone (blue)—in Greece, battery for free.
Figure A1, Figure A2, Figure A3, Figure A4, Figure A5, Figure A6, Figure A7 and Figure A8 in Appendix C detail the proportions for each case study, in absolute values (€) and in percentage. These figures reveal the fact that, again, a higher price of electricity is less unfavourable for the PV+Battery solution, because for higher the realized savings are closer to the potential savings. However, under the net-metering scheme, the PV+Battery solution is always inferior to the PV-alone solution, which illustrates to what extent the goal of maximizing the share of renewable energy goes against economic efficiency for the rational Investor.
The analysis in Scenarios 1 and 2 reveals that the electricity price is the main driver for the profitability of PV+Battery systems, and the storage size is secondary. The largest required capacity is at the northernmost latitude in Finland, yet here the Supporter is required to contribute only with 34.21% (18,720 €) to the total investment—compared with 84.7% (14,940 €) in Italy. In these two cases, comparable sums of money support vastly different storage capacities.
As outlined in the introduction and supported by the findings, the drivers behind the effort to support PV+Battery MG systems not rely on economic advantages, since for the greenfield Investor the PV-alone system is the most efficient one under the net-metering scheme. The remaining arguments in favour of batteries include autonomy, decongestion of main grid, and an increase of renewable fraction in the residential electricity sector.
From Table 8 we learn that PV+Battery MG systems provide a stronger environmental advantage than similar PV-only systems. In the case with the lowest national renewable fraction (Greece), the potential for improvement is also the highest, so the argument in favour of including a battery in order to increase the renewable fraction is also the strongest. It is also encouraging that the Danish case, where the renewable share argument is the weakest (3.29% true increase), is also where the argument is not needed, since the Investor is compelled to cover the full cost of the battery for economic reasons. However for the Italian and the Finnish case there is room for further investigation, whether an increase of 4–5% in true renewable share is strong enough an argument for the required support.

Table 8.
True share of renewable energy in the electricity mix.
4. Conclusions
Under the net-metering scheme PV+Battery microgrid systems prove economically inefficient: instead of retrieving from the main grid the same amount of energy as the one that has been injected during excess PV production, the consumer is bound to retrieve from the battery less energy than the amount saved, due to the losses of the storage technology. This paper investigated a support scheme with which the investment in a microgrid with PV+Battery is made to be more attractive than purchasing the electricity from the main grid alone, by having the cost of batteries partly supported by a third party. The rationale for this type of support was that both the policy makers and the DNOs would have an interest in supporting microgrids with PV and batteries: arguments on the part of the policy makers included the increase in renewable energy share, while the interest of DNOs include the avoidance of extra costs brought by the bidirectional power flow on the LV lines.
To this end we have developed four case studies based on real-life experiments carried out in Greece, Italy, Denmark and Finland, and regarded a standardized MG project consisting of 8 households, a PV unit to cover ca 70% of the consumption and a storage unit to cover ca 19% of the consumption over 25 years. All four MGs were connected to the main grid under the net-metering scheme, and subject to all the country-specific conditions including electricity price and weather. For each of the four MG projects we have calculated two values of the NPC: , the benchmark cost of supplying the consumers with electricity from the main grid over the 25 years, and , the indicator for a grid-connected PV+Battery project. The focus of the study was to determine when (which makes the PV+Battery project more attractive than the grid-only scenario). The investigation of the case studies was carried out under two scenarios: (1) batteries provided for free, and (2) the acquisition of the storage system were supported in part (e.g., by subsidies).
Under Scenario 1 we confirmed that the inclusion of batteries, even for free, is not an attractive investment when the price of electricity on the main grid is very low. However by varying the price of electricity we found that at the observed levels of electricity prices in the respective countries, all MG investments with a battery for free will make significant savings compared to being supplied by the main grid only. In Scenario 2 we took the perspective of the party providing the support for batteries (e.g., the government) and calculated the benchmark contribution that would support the purchase of a battery to a level that would keep the MG project an attractive investment (). We found that the sharing of storage costs differs significantly between the case studies, and we found that under the net-metering scheme the PV+Battery systems are sustainable either for very high prices of electricity (Denmark), or for very high PV potential (Greece).
This investigation has a twofold contribution. First, it quantifies the relationship between the price of electricity on the main grid and the profitability of the battery. This relationship, illustrated as a curve, helps understand how the inclusion of batteries can be supported not by increasing the contribution to the acquisition, but for varying prices of electricity provided to the MG. Second, by evaluating the value with which the Supporter can contribute to sharing the battery price with the Investor, as well as by pointing out the level of unrealized savings, we provide a benchmark for further investigations.
Our study demonstrates the limits of the net-metering scheme: while the use of batteries always comes with economic disadvantages under net metering, the attractiveness of a PV+Battery system depends strictly on whether they are outweighed by the advantages provided by exceptional circumstances (such as very high solar resource or very high electricity price). In other words, for MG projects that do not benefit from such advantages, the net-metering scheme discourages the adoption of batteries. On the level of the single project, improvements to the profitability can be made by resizing the components, considering capacity tariffs, or simply waiting for the battery prices to decrease. On a regional or country level, an agreement with the DNOs would be helpful, in which value could be assigned to the services provided by MGs (such as line decongestion, flexibility and resilience) as suggested by academic research and outlined in the introduction. Furthermore, regarding the results from the perspective of the EU policy, it becomes apparent that, all else equal, the substantial difference in electricity prices is what leads identical projects to be successful in one country and less successful in the next.
Overall, our work provides useful orientation for stakeholders who, encouraged by the favourable policy landscape and by the equally encouraging perspectives in storage technology improvements, are considering setting up PV+Battery residential microgrids.
Author Contributions
Conceptualization by I.S., H.P. and S.V.P.; methodology, I.S., H.P., S.V.P.; software, I.S.; formal analysis, I.S. and K.M.; data curation, I.S.; writing—original draft preparation, I.S.; writing—review and editing, H.P., S.V.P. and K.M.; visualization, I.S.; supervision, H.P. and S.V.P.; funding acquisition, I.S., H.P., S.V.P.
Funding
The access to research facilities and experiments was funded through the Transnational Access Programme of ERIGrid Research Infrastructure.
Acknowledgments
This research has been performed using the ERIGrid Research Infrastructure and is part of a project that has received funding from the European Union’s Horizon 2020 Research and Innovation Programme under the Grant Agreement No. 654113. The support of the European Research Infrastructure ERIGrid and its partners CRES, RSE, DTU and VTT is very much appreciated. This document does not represent an official position of the European Commission.
Conflicts of Interest
The authors declare no conflict of interest. The funders had no role in the design of the study; in the collection, analyses, or interpretation of data; in the writing of the manuscript, or in the decision to publish the results.
Abbreviations
The following abbreviations are used in this manuscript:
| CRES | Centre for Renewable Energy and Saving |
| DER | Decentralized Energy Resources |
| DG | Distributed Generation |
| DNO | District Network Operator |
| DTU | Danish Technical University |
| FiT | Feed-in Tariff |
| H2020 | EU Horizon 2020 Programme |
| IRR | Internal Rate of Return |
| LV | Low Voltage |
| MG | Microgrid |
| MV | Medium Voltage |
| NPC | Net Present Cost |
| NPV | Net Present Value |
| PV | Photovoltaic |
| RES | Renewable Energy Sources |
| RSE | Ricerca sul Sistema Energetico |
| TEA | Techno-economic assessment |
| VTT | Finnish Technical Research Centre |
Appendix A. System Description
The systems analyzed in the paper are based on four real-life experimental set-ups summarized below in Table A1.

Table A1.
Sizing of PV units and load in the real-life experiments.
Table A1.
Sizing of PV units and load in the real-life experiments.
| GR | IT | DK | FI | |
|---|---|---|---|---|
| System Consumption (kWh/year) | 10,715 | 96,678 | 16,060 | 4105 |
| PV Production (kWh/year) | 8320 | 58,187 | 10,306 | 2764 |
| PV Capacity (kWp) | 3.36 | 30.34 | 10 | 3.03 |
| Fraction Production:Consumption | 77.65% | 60.19% | 64.17% | 67.34% |
In the set-up of the experiment in Finland the components had been oversized intentionally so as to compensate the age and losses of the battery and diminish the risk of a black-out. Additionally, the household served by the microgrid worked as a smart home, thus having a different load profile and consumption than conventional homes. In order to bring the Finnish system on a level comparable with the other systems, we set the fraction PV Production:Household Consumption (P:C) to 67.34% which is the arithmetic mean of the other three systems. The load considered for our simulation is switched to a conventional residential load with the average household consumption in Finland [56]. Based on these new parameters and on the capacity factor of the PV unit (provided by the catalogue in the database of HOMER), we calculated the system listed here and used further in our simulations.
In the next step all systems were brought on the same size and we decided to consider the system size to be 8 households. The resizing has been calculated so as to maintain the P:C ratio from the original set-up, as outlined in Table A2.

Table A2.
Adaptation of the experimental set-ups, without storage.
Table A2.
Adaptation of the experimental set-ups, without storage.
| GR | IT | DK | FI | |
|---|---|---|---|---|
| Avg Household cons [56] (kWh/year) | 3758 | 2432 | 3878 | 8041 |
| Resized to 8 households (kWh/year) | 30,064 | 19,456 | 31,024 | 64,328 |
| Production resized (kWh/year) | 23,344.14 | 11,709.86 | 19,908.68 | 43,315.56 |
| Capacity factor | 28.27% | 21.90% | 11.80% | 10.40% |
| Rated capacity for new PV (kW) | 9.43 | 6.10 | 9.26 | 47.55 |
| Renewable fraction without battery | 60.10% | 49.50% | 48.80% | 49.20% |
Since the resizing has to be completed with equipment available in real-life, we acknowledge the possibility that the minor changes in equipment can ultimately influence the economic indicators. In our case, we are looking at the difference in NPC between the microgrid system and the baseline scenario (grid-only); we found that this difference was affected by the resizing by a magnitude of −2.02% … +0.62%, which we find to be a reasonable error term for our purposes.
To these systems we add a Li-Ion battery sized to provide ca. 19% of the total annual consumption, based on the lowest value found in the experiments. The technical specifications are based on the catalogue equipment pieces provided by HOMER, selected so as to match the peak load under the constraint of 19%:

Table A3.
Adaptation of the experimental set-ups.
Table A3.
Adaptation of the experimental set-ups.
| GR | IT | DK | FI | |
|---|---|---|---|---|
| Total load with 8 HHs (kWh/year) | 30,064 | 19,456 | 31,024 | 64,328 |
| PV Production (kWh/year) | 23,344 | 11,710 | 19,909 | 43,316 |
| Battery type | sonnenbatterie 4–6 kWh eco | LGchemRESU10 [9.8 kWh] | CAT TimeShift 6.74 | Samsung M8194 M2 [7.6 kWh] |
| Battery Discharge power (kW) | 4.00 | 5.00 | 6.52 | 7.60 |
| Battery nominal capacity (kWh/cell) | 6.00 | 9.80 | 6.74 | 7.60 |
| Nr of cells/strings | 5 | 3 | 6 | 12 |
| Usable nominal storage capacity per charge at given SoC (kWh) | 24 | 24.4 | 32.4 | 73 |
| Roundtrip efficiency | 86% | 95% | 95% | 90% |
| Energy In (kWh/year) | 6761 | 3850 | 6576 | 13,567 |
| Energy Out (kWh/year) | 5837 | 3678 | 6251 | 12,279 |
| Nr of cycles/year | 282 | 158 | 203 | 186 |
| Converter to match peak load (kW) | 10 | 11 | 17 | 36 |
| Fraction Battery intake: PV production | 29% | 33% | 33% | 31% |
| Fraction Battery Output: Consumption | 19.42% | 18.90% | 20.15% | 19.09% |
| Renewable fraction with battery | 68.70% | 56.90% | 55.90% | 55.10% |
| Increase in renewable fraction compared to Table A2 | 14.31% | 14.95% | 14.55% | 11.99% |
Appendix B. Overview of System Input Indicators
Full List of indicators taken into account by the HOMER software for the techno-economic assessment and the calculation of NPC and renewable fraction. Second column of Table A4 features the source for the value of each indicator: HB (HOMER database, or automatic calculations based on previous input values), EX (Experiment), 3P (third-party source) or AS (Assumption). The 3rd column provides observations, adjustments, sources, etc.

Table A4.
Full list of indicators taken into account for the TEA.
Table A4.
Full list of indicators taken into account for the TEA.
| Indicator | Source | Notes |
|---|---|---|
| Discount rate | 3P | [53] |
| Inflation Rate | 3P | www.tradingeconomics.com |
| Annual capacity shortage | 0 (zero) | No shortage acceptable |
| Project lifetime | 25 years | standard |
| PV capacity | EX | ---- |
| PV capital cost | EX | adjusted with online retail resources, excl. VAT |
| PV Replacement cost | AS | Assume zero residual value after the lifetime of a PV unit |
| PV O&M cost per kW capacity | EX | As provided by experts at the host facilities |
| PV derating factor | HB | ---- |
| PV electrical bus (AC/DC) | AS | Assumed AC in all systems, converter included with the PV unit |
| PV Capacity optimization | AS | none |
| Consider temperature effects? | AS | Yes, in order to caption major geographical differences |
| Temperature effect on power | HB | ---- |
| Ground reflectance | HB | ---- |
| Tracking system | EX | No |
| Nominal operating cell temp | HB | ---- |
| Efficiency at standard testing conditions | HB | ---- |
| GHI Input | HB, EX | database standard solar resource scaled to match experimental data |
| GHI Scaled annual average | HB, EX | As calculated |
| Load Peak Month | AS | January or August, depending on geography |
| Load Profile | HB, EX | database standard load resource scaled to match experimental data |
| Load Random Variability | HB | statstical variance |
| Load Day-to-day | HB | ----- |
| Load timestep | EX | 1 h |
| Load type | AS | residential, as per research scope |
| Load peak month profile | HB, EX | database standard load resource scaled to match experimental data |
| Load Average energy baseline | EX | ---- |
| Load Average energy scaled | EX | ---- |
| Load Average power baseline | EX | ---- |
| Load Average power scaled | EX | ---- |
| Load Peak baseline | EX | ---- |
| Load Peak scaled | HB, EX | ---- |
| Load factor baseline | HB, EX | ---- |
| Load factor scaled | HB, EX | as calculated |
| Load Scaled annual average | HB, EX | as calculated |
| Load Efficiency advanced | AS | not regarded |
| Storage type | AS | Li-Ion, state of the art technology on level 2018 |
| Storage Nominal Voltage | HB, EX | As follows from the equipment type selected |
| Storage Nominal Capacity | HB, EX | As follows from the equipment type selected |
| Storage Quantity (nr of cells) | HB, AS | As calculated in order to cover power and energy demand |
| Storage roundtrip efficiency | HB | corresponds to the specs of the equipment selected |
| Storage Capital cost | 3P | Based on the equipment type selected |
| Storage Replacement | AS | Assumed zero residual value after the lifetime of a battery |
| Storage O&M | AS | assumed zero, in order to leave only one cost driver for the total investment cost of the storage system |
| Storage Throughput | EX | automatically calculated |
| Storage String size Storage Quantity (nr of cells) | HB, EX | As calculated in order to obtain power and energy demand |
| Storage Initial state of charge | AS | zero %, otherwise more energy in the system than produced or purchased |
| Storage Minimum state of charge | AS | 20%, a real-life reasonable average for the lifetime of the battery |
| Storage Minimum storage life | AS | 8 years for batteries used very intensively, that should be replaced twice over the 25 years |
| Converter Type | HB, EX | Calculated as necessary |
| Converter Capacity | HB, EX | As calculated to cover the demand |
| Converter Capital | AS | 1 € assumed, in order to leave only one cost driver for the total investment cost of the storage system |
| Converter Replacement cost | AS | Zero assumed, in order to leave only one cost driver for the total investment cost of the storage system |
| Converter O&M | AS | Zero assumed, in order to leave only one cost driver for the total investment cost of the storage system |
| Converter Capacity optimization | AS | None |
| Converter Lifetime | AS | 25 years assumed |
| Converter Efficiency | HB | 95% |
| Converter Parallel with AC generator? | HB | yes, required |
| Converter Rectifier Input | HB | ----- |
| Converter Relative capacity | HB | ----- |
| Converter Efficiency | HB | ----- |
| Grid electricity price | EX | ---- |
| Grid pricing sysyem | AS | Net Metering, as per research scope |
| Grid Controller | HB | ---- |
| Grid Emissions | HB | ---- |
| CO2 | HB | ---- |
| CO | HB | ---- |
| Unburned Hydrocarbons | HB | ---- |
| Particulate Matter | HB | ---- |
| SO2 | HB | ---- |
| NOx | HB | ---- |
| Controller Homer Cycle Charge | HB | ---- |
| Controller Capital | AS | Assumed zero, to leave just the battery to be the cost carrier |
| Controller Replacement | AS | zero |
| Controller O&M | AS | zero |
| Controller Lifetime | AS | 25 years |
| Apply Setpoint state of charge | HB | ---- |
| Allow diesel-off generation | ----- | not the case |
| Allow generators to operate simultaneously | ----- | not the case |
| Allow systems with generator capacity less than peak load | ----- | not the case |
Appendix C. Evolution of Savings for the Investor, in €, Compared to the Baseline Scenario and to the Best-Case Scenario, Varying with the Price of Electricity
For the Greek case, if the battery is provided for free to the PV+Battery MG system, the value of (orange) increases with , as do the unrealized potential savings (blue) if the system were supplied by PV alone (Figure A1). However, in proportional terms, i.e., if the segments in Figure A1 are normalized to 100% each, we note that the proportion of unrealized savings (blue) decreases with the increase of —Figure A2.
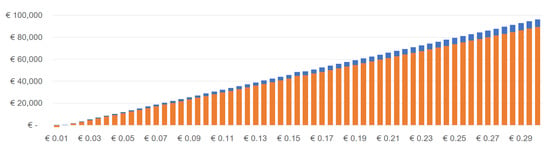
Figure A1.
Savings in € compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Greece, battery for free.
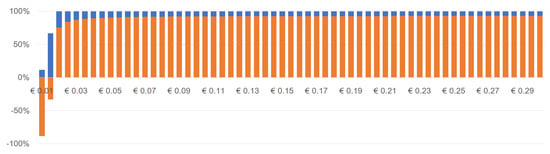
Figure A2.
Savings in Percentage compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Greece, battery for free.
Similarly, the same trend is confirmed for Italy in Figure A3 and Figure A4, with the observation that the proportional increase of (orange) reaches a ”stable” level sooner, for lower .
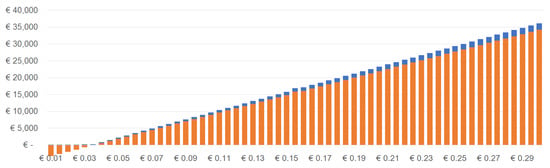
Figure A3.
Savings in € compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Italy, battery for free.
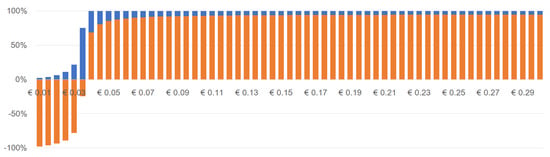
Figure A4.
Savings in Percentage compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Italy, battery for free.
The Danish and the Finnish case are presented in Figure A5–Figure A6, and Figure A7–Figure A8, respectively.
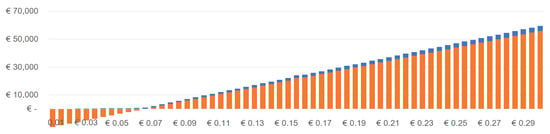
Figure A5.
Savings in € compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Denmark, battery for free.
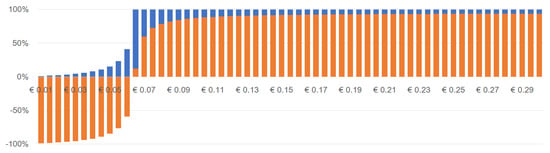
Figure A6.
Savings in Percentage compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Denmark, battery for free.
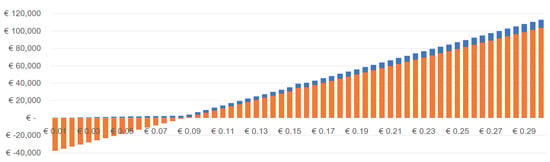
Figure A7.
Savings in € compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Finland, battery for free.
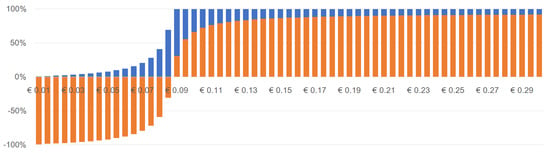
Figure A8.
Savings in Percentage compared to the baseline scenario (Grid-only) and to the best-case scenario (PV+G)—In Finland, battery for free.
Appendix D. Source Data for Tables and Figures

Table A5.
Values of and generated by HOMER and visualized in Figure 2.
Table A5.
Values of and generated by HOMER and visualized in Figure 2.
| €/kWh | GREECE | ITALY | DENMARK | FINLAND | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| (€) | (€) | (€) | (€) | (€) | (€) | (€) | (€) | (€) | (€) | (€) | (€) | |
| 0.01 | 4224 | 5970 | −1746 | 2247 | 5558 | −3311 | 3896 | 16,815 | −12,919 | 7681 | 45,472 | −37,791 |
| 0.015 | 6335 | 6507 | −172 | 3370 | 6034 | −2664 | 5844 | 17,579 | −11,735 | 11,522 | 46,872 | −35,350 |
| 0.02 | 8447 | 7043 | 1404 | 4494 | 6511 | −2017 | 7792 | 18,342 | −10,550 | 15,363 | 48,273 | −32,910 |
| 0.025 | 10,553 | 7580 | 2973 | 5617 | 6987 | −1370 | 9740 | 19,106 | −9366 | 19,204 | 49,673 | −30,469 |
| 0.03 | 12,671 | 8117 | 4554 | 6741 | 7464 | −723 | 11,688 | 19,869 | −8181 | 23,044 | 51,073 | −28,029 |
| 0.035 | 14,782 | 8654 | 6128 | 7864 | 7940 | −76 | 13,636 | 20,633 | −6997 | 26,885 | 52,474 | −25,589 |
| 0.04 | 16,894 | 9191 | 7703 | 8988 | 8417 | 571 | 15,584 | 21,396 | −5812 | 30,726 | 53,874 | −23,148 |
| 0.045 | 19,006 | 9728 | 9278 | 10,111 | 8893 | 1218 | 17,532 | 22,160 | −4628 | 34,567 | 55,274 | −20,707 |
| 0.05 | 21,118 | 10,264 | 10,854 | 11,235 | 9369 | 1866 | 19,481 | 22,923 | −3442 | 38,407 | 56,675 | −18,268 |
| 0.055 | 23,229 | 10,801 | 12,428 | 12,358 | 9846 | 2512 | 21,429 | 23,687 | −2258 | 42,248 | 58,075 | −15,827 |
| 0.06 | 25,341 | 11,338 | 14,003 | 13,482 | 10,322 | 3160 | 23,377 | 24,450 | −1073 | 46,089 | 59,475 | −13,386 |
| 0.065 | 27,453 | 11,875 | 15,578 | 14,605 | 10,799 | 3806 | 25,325 | 25,214 | 111 | 49,930 | 60,876 | −10,946 |
| 0.07 | 29,565 | 12,412 | 17,153 | 15,729 | 11,275 | 4454 | 27,273 | 25,982 | 1291 | 53,770 | 62,276 | −8506 |
| 0.075 | 31,676 | 12,948 | 18,728 | 16,852 | 11,752 | 5100 | 29,221 | 26,741 | 2480 | 57,611 | 63,676 | −6065 |
| 0.08 | 33,788 | 13,485 | 20,303 | 17,976 | 12,228 | 5748 | 31,169 | 27,509 | 3660 | 61,452 | 65,077 | −3625 |
| 0.085 | 35,900 | 14,022 | 21,878 | 19,099 | 12,705 | 6394 | 33,117 | 28,268 | 4849 | 65,292 | 66,477 | −1185 |
| 0.09 | 38,012 | 14,559 | 23,453 | 20,223 | 13,180 | 7043 | 35,065 | 29,036 | 6029 | 69,133 | 67,878 | 1255 |
| 0.095 | 40,124 | 15,096 | 25,028 | 21,346 | 13,658 | 7688 | 37,013 | 29,795 | 7218 | 72,974 | 69,278 | 3696 |
| 0.10 | 42,235 | 15,633 | 26,602 | 22,470 | 14,133 | 8337 | 38,961 | 30,563 | 8398 | 76,815 | 70,678 | 6137 |
| 0.105 | 44,347 | 16,169 | 28,178 | 23,593 | 14,610 | 8983 | 40,909 | 31,322 | 9587 | 80,655 | 72,079 | 8576 |
| 0.11 | 46,459 | 16,706 | 29,753 | 24,717 | 15,087 | 9630 | 42,857 | 32,085 | 10,772 | 84,496 | 73,479 | 11,017 |
| 0.115 | 48,571 | 17,243 | 31,328 | 25,840 | 15,563 | 10,277 | 44,805 | 32,849 | 11,956 | 88,337 | 74,879 | 13,458 |
| 0.12 | 50,682 | 17,780 | 32,902 | 26,936 | 16,040 | 10,896 | 46,753 | 33,612 | 13,141 | 92,178 | 76,280 | 15,898 |
| 0.125 | 52,794 | 18,317 | 34,477 | 28,087 | 16,516 | 11,571 | 48,702 | 34,376 | 14,326 | 96,018 | 77,680 | 18,338 |
| 0.13 | 54,906 | 18,853 | 36,053 | 29,210 | 16,993 | 12,217 | 50,650 | 35,139 | 15,511 | 99,859 | 79,080 | 20,779 |
| 0.135 | 57,018 | 19,390 | 37,628 | 30,334 | 17,469 | 12,865 | 52,598 | 35,903 | 16,695 | 103,700 | 80,481 | 23,219 |
| 0.14 | 59,129 | 19,927 | 39,202 | 31,457 | 17,946 | 13,511 | 54,546 | 36,666 | 17,880 | 107,540 | 81,881 | 25,659 |
| 0.145 | 61,241 | 20,464 | 40,777 | 32,581 | 18,422 | 14,159 | 56,494 | 37,430 | 19,064 | 111,381 | 83,281 | 28,100 |
| 0.15 | 63,353 | 21,001 | 42,352 | 33,704 | 18,899 | 14,805 | 58,442 | 38,193 | 20,249 | 115,222 | 84,682 | 30,540 |
| 0.158 | 66,732 | 21,860 | 44,872 | 35,502 | 19,661 | 15,841 | 61,559 | 39,415 | 22,144 | 121,367 | 86,922 | 34,445 |
| 0.16 | 67,576 | 22,074 | 45,502 | 35,951 | 19,851 | 16,100 | 62,338 | 39,720 | 22,618 | 122,903 | 87,483 | 35,420 |
| 0.165 | 69,688 | 22,611 | 47,077 | 37,075 | 20,328 | 16,747 | 64,286 | 40,484 | 23,802 | 126,744 | 88,883 | 37,861 |
| 0.17 | 71,800 | 23,148 | 48,652 | 38,198 | 20,804 | 17,394 | 66,234 | 41,247 | 24,987 | 130,585 | 90,283 | 40,302 |
| 0.175 | 73,912 | 23,685 | 50,227 | 39,322 | 21,281 | 18,041 | 68,182 | 42,011 | 26,171 | 134,426 | 91,684 | 42,742 |
| 0.18 | 76,023 | 24,222 | 51,801 | 40,445 | 21,757 | 18,688 | 70,130 | 42,774 | 27,356 | 138,266 | 93,084 | 45,182 |
| 0.185 | 78,135 | 24,758 | 53,377 | 41,569 | 22,234 | 19,335 | 72,078 | 43,538 | 28,540 | 142,107 | 94,484 | 47,623 |
| 0.19 | 80,247 | 25,295 | 54,952 | 42,692 | 22,710 | 19,982 | 74,026 | 44,301 | 29,725 | 145,948 | 95,885 | 50,063 |
| 0.195 | 82,359 | 25,832 | 56,527 | 43,816 | 23,187 | 20,629 | 75,794 | 45,065 | 30,729 | 149,789 | 97,285 | 52,504 |
| 0.20 | 84,471 | 26,369 | 58,102 | 44,939 | 23,662 | 21,277 | 77,922 | 45,828 | 32,094 | 153,629 | 98,685 | 54,944 |
| 0.205 | 86,582 | 26,906 | 59,676 | 46,063 | 24,140 | 21,923 | 79,870 | 46,592 | 33,278 | 157,470 | 100,086 | 57,384 |
| 0.21 | 88,694 | 27,443 | 61,251 | 47,186 | 24,616 | 22,570 | 81,819 | 47,355 | 34,464 | 161,311 | 101,486 | 59,825 |
| 0.215 | 90,806 | 27,979 | 62,827 | 48,310 | 25,092 | 23,218 | 83,767 | 48,119 | 35,648 | 165,151 | 102,886 | 62,265 |
| 0.22 | 92,918 | 28,516 | 64,402 | 49,433 | 25,569 | 23,864 | 85,715 | 48,882 | 36,833 | 168,992 | 104,287 | 64,705 |
| 0.225 | 95,029 | 29,053 | 65,976 | 50,557 | 26,045 | 24,512 | 87,663 | 49,646 | 38,017 | 172,833 | 105,687 | 67,146 |
| 0.23 | 97,141 | 29,590 | 67,551 | 51,680 | 26,522 | 25,158 | 89,611 | 50,409 | 39,202 | 176,674 | 107,088 | 69,586 |
| 0.235 | 99,253 | 30,127 | 69,126 | 52,804 | 26,998 | 25,806 | 91,559 | 51,173 | 40,386 | 180,514 | 108,488 | 72,026 |
| 0.24 | 101,365 | 30,663 | 70,702 | 53,927 | 27,475 | 26,452 | 93,507 | 51,936 | 41,571 | 184,355 | 109,888 | 74,467 |
| 0.245 | 103,476 | 31,200 | 72,276 | 55,050 | 27,951 | 27,099 | 95,455 | 52,700 | 42,755 | 188,196 | 111,289 | 76,907 |
| 0.25 | 105,588 | 31,737 | 73,851 | 56,174 | 28,428 | 27,746 | 97,403 | 53,463 | 43,940 | 192,037 | 112,689 | 79,348 |
| 0.255 | 107,700 | 32,274 | 75,426 | 57,297 | 28,904 | 28,393 | 99,351 | 54,227 | 45,124 | 195,877 | 114,089 | 81,788 |
| 0.26 | 109,812 | 32,811 | 77,001 | 58,421 | 29,380 | 29,041 | 101,299 | 54,990 | 46,309 | 199,718 | 115,490 | 84,228 |
| 0.265 | 111,923 | 33,348 | 78,575 | 59,544 | 29,857 | 29,687 | 103,247 | 55,754 | 47,493 | 203,559 | 116,890 | 86,669 |
| 0.27 | 114,035 | 33,884 | 80,151 | 60,668 | 30,333 | 30,335 | 105,195 | 56,517 | 48,678 | 207,400 | 118,290 | 89,110 |
| 0.275 | 116,147 | 34,421 | 81,726 | 61,791 | 30,810 | 30,981 | 107,143 | 57,281 | 49,862 | 211,240 | 119,691 | 91,549 |
| 0.28 | 118,259 | 34,958 | 83,301 | 62,915 | 31,286 | 31,629 | 109,091 | 58,044 | 51,047 | 215,081 | 121,091 | 93,990 |
| 0.285 | 120,371 | 35,495 | 84,876 | 64,038 | 31,763 | 32,275 | 111,039 | 58,808 | 52,231 | 218,922 | 122,491 | 96,431 |
| 0.29 | 122,482 | 36,032 | 86,450 | 65,162 | 32,239 | 32,923 | 112,988 | 59,571 | 53,417 | 222,762 | 123,892 | 98,870 |
| 0.295 | 124,594 | 36,568 | 88,026 | 66,285 | 32,716 | 33,569 | 114,936 | 60,335 | 54,601 | 226,603 | 125,292 | 101,311 |
| 0.30 | 126,706 | 37,105 | 89,601 | 67,409 | 33,191 | 34,218 | 116,884 | 61,103 | 55,781 | 230,444 | 126,692 | 103,752 |
References
- European Commission. Energy Roadmap 2050. Technical Report. 2012. Available online: https://ec.europa.eu/energy/sites/ener/files/documents/ (accessed on 10 December 2018).
- Clarke, T.; Lambert, E.; Deavis-Marks, M.; Ceccarelli, A.; Zoppi, T.; Jung, O.; Chai, M.; Chen, Y.; Vasenev, A.; Montoya, L. Improving the Robustness of Urban Electricity Networks. Technical report, Ethos Energy, University of Florence, FTW, Queen Mary University of London, University of Twente. 2015. Available online: http://ireneproject.eu/wp-content/uploads (accessed on 10 December 2018).
- IEA. Smart Grids in Distribution Networks: Roadmap Development and Implementation. Technical Report. IEA, 2015. Available online: www.iea.org/publications (accessed on 10 December 2018).
- Yan, J.; Zhai, Y.; Wijayatunga, P.; Mohamed, A.M.; Campana, P.E. Renewable energy integration with mini/micro-grids (editorial). Appl. Energy 2017, 201, 241–244. [Google Scholar] [CrossRef]
- IRENA. Innovation Outlook: Renewable Mini-Grids. Technical report. IRENA, Abu Dhabi, 2016. Available online: www.irena.org/publications (accessed on 10 December 2018).
- Schwaegerl, C.; Tao, L. Quantification of Technical, Economic, Environmental and Social Benefits of Microgrid Operation. In Microgrids: Architectures and Control; Hatziargyriou, N., Ed.; Wiley IEEE Press: Chichester, UK, 2014; Chapter 7; pp. 275–313. [Google Scholar]
- Mohammed, Y.S.; Mustafa, M.W.; Bashir, N. Hybrid renewable energy systems for off-grid electric power: Review of substantial issues. Renew. Sustain. Energy Rev. 2014, 35, 527–539. [Google Scholar] [CrossRef]
- Blanco, H.; Faaij, A. A review at the role of storage in energy systems with a focus on Power to Gas and long-term storage. Renew. Sustain. Energy Rev. 2018, 81, 1049–1086. [Google Scholar] [CrossRef]
- European Commission. Energy Storage—The Role of Electricity. Technical Report. European Commission, Brussels, 2017. Available online: https://ec.europa.eu/energy/en/topics/technology-and-innovation/energy-storage (accessed on 10 December 2018).
- Zehir, M.A.; Batman, A.; Sonmez, M.A.; Font, A.; Tsiamitros, D.; Stimoniaris, D.; Kollatou, T.; Bagriyanik, M.; Ozdemir, A.; Dialynas, E. Impacts of microgrids with renewables on secondary distribution networks. Appl. Energy 2017, 201, 308–319. [Google Scholar] [CrossRef]
- Van Der Schoor, T.; Scholtens, B. Power to the people: Local community initiatives and the transition to sustainable energy. Renew. Sustain. Energy Rev. 2015, 43, 666–675. [Google Scholar] [CrossRef]
- Becker, S.; Kunze, C.; Vancea, M. Community energy and social entrepreneurship: Addressing purpose, organisation and embeddedness of renewable energy projects. J. Clean. Prod. 2017, 147, 25–36. [Google Scholar] [CrossRef]
- Hicks, J.; Ison, N. An exploration of the boundaries of ‘community’ in community renewable energy projects: Navigating between motivations and context. Energy Policy 2018, 113, 523–534. [Google Scholar] [CrossRef]
- Yu, H.J.J. A prospective economic assessment of residential PV self-consumption with batteries and its systemic effects: The French case in 2030. Energy Policy 2018, 113, 673–687. [Google Scholar] [CrossRef]
- Mariam, L.; Basu, M.; Conlon, M.F. Microgrid: Architecture, policy and future trends. Renew. Sustain. Energy Rev. 2016, 64, 477–489. [Google Scholar] [CrossRef]
- Soshinskaya, M.; Crijns-Graus, W.H.; Guerrero, J.M.; Vasquez, J.C. Microgrids: Experiences, barriers and success factors. Renew. Sustain. Energy Rev. 2014, 40, 659–672. [Google Scholar] [CrossRef]
- Moretti, M.; Djomo, S.N.; Azadi, H.; May, K.; De Vos, K.; Van Passel, S.; Witters, N. A systematic review of environmental and economic impacts of smart grids. Renew. Sustain. Energy Rev. 2017, 68, 888–898. [Google Scholar] [CrossRef]
- Miller, L.; Carriveau, R. A review of energy storage financing—Learning from and partnering with the renewable energy industry. J. Energy Storage 2018, 19, 311–319. [Google Scholar] [CrossRef]
- Sauhats, A.; Zemite, L.; Petrichenko, L.; Moshkin, I.; Jasevics, A. Estimating the Economic Impacts of Net Metering Schemes for Residential PV Systems with Profiling of Power Demand, Generation, and Market Prices. Energies 2018, 11, 3222. [Google Scholar] [CrossRef]
- Coppo, M.; Pelacchi, P.; Pilo, F.; Pisano, G.; Soma, G.G.; Turri, R. The Italian smart grid pilot projects: Selection and assessment of the test beds for the regulation of smart electricity distribution. Electr. Power Syst. Res. 2015, 120, 136–149. [Google Scholar] [CrossRef]
- Bianco, G.; Noce, C.; Sapienza, G. Enel Distribuzione projects for renewable energy sources integration in distribution grid. Electr. Power Syst. Res. 2015, 120, 118–127. [Google Scholar] [CrossRef]
- Crispim, J.; Braz, J.; Castro, R.; Esteves, J. Smart Grids in the EU with smart regulation: Experiences from the UK, Italy and Portugal. Util. Policy 2014, 31, 85–93. [Google Scholar] [CrossRef]
- Delfanti, M.; Fasciolo, E.; Olivieri, V.; Pozzi, M. A2A project: A practical implementation of smart grids in the urban area of Milan. Electr. Power Syst. Res. 2015, 120, 2–19. [Google Scholar] [CrossRef]
- Siirto, O.; Hyvärinen, M.; Loukkalahti, M.; Hämäläinen, A.; Lehtonen, M. Improving reliability in an urban network. Electr. Power Syst. Res. 2015, 120, 47–55. [Google Scholar] [CrossRef]
- Li, Y.; Gao, W.; Ruan, Y. Performance investigation of grid-connected residential PV-battery system focusing on enhancing self-consumption and peak shaving in Kyushu, Japan. Renew. Energy 2018, 127, 514–523. [Google Scholar] [CrossRef]
- Pena-Bello, A.; Burer, M.; Patel, M.K.; Parra, D. Optimizing PV and grid charging in combined applications to improve the profitability of residential batteries. J. Energy Storage 2017, 13, 58–72. [Google Scholar] [CrossRef]
- Dietrich, A.; Weber, C. What drives profitability of grid-connected residential PV storage systems? A closer look with focus on Germany. Energy Econ. 2018, 74, 399–416. [Google Scholar] [CrossRef]
- Parra, D.; Patel, M.K. Effect of tariffs on the performance and economic benefits of PV-coupled battery systems. Appl. Energy 2016, 164, 175–187. [Google Scholar] [CrossRef]
- Zsiborács, H.; Baranyai, N.H.; Vincze, A.; Háber, I.; Pintér, G. Economic and Technical Aspects of Flexible Storage Photovoltaic Systems in Europe. Energies 2018, 11, 1445. [Google Scholar] [CrossRef]
- Cerino Abdin, G.; Noussan, M. Electricity storage compared to net metering in residential PV applications. J. Clean. Prod. 2018, 176, 175–186. [Google Scholar] [CrossRef]
- Cucchiella, F.; D’Adamo, I.; Gastaldi, M. The economic feasibility of residential energy storage combined with PV panels: The role of subsidies in Italy. Energies 2017, 10, 1434. [Google Scholar] [CrossRef]
- Milis, K.; Peremans, H.; Van Passel, S. Steering the adoption of battery storage through electricity tariff design. Renew. Sustain. Energy Rev. 2018, 98, 125–139. [Google Scholar] [CrossRef]
- Zame, K.K.; Brehm, C.A.; Nitica, A.T.; Richard, C.L.; Schweitzer, G.D. Smart grid and energy storage: Policy recommendations. Renew. Sustain. Energy Rev. 2018, 82, 1646–1654. [Google Scholar] [CrossRef]
- Laws, N.D.; Anderson, K.; DiOrio, N.A.; Li, X.; McLaren, J. Impacts of valuing resilience on cost-optimal PV and storage systems for commercial buildings. Renew. Energy 2018, 127, 896–909. [Google Scholar] [CrossRef]
- Shaw-Williams, D.; Susilawati, C.; Walker, G. Value of residential investment in photovoltaics and batteries in networks: A techno-economic analysis. Energies 2018, 11, 1022. [Google Scholar] [CrossRef]
- Robert, F.C.; Sisodia, G.S.; Gopalan, S. A critical review on the utilization of storage and demand response for the implementation of renewable energy microgrids. Sustain. Cities Soc. 2018, 40, 735–745. [Google Scholar] [CrossRef]
- Zehir, M.A.; Batman, A.; Sonmez, M.A.; Font, A.; Tsiamitros, D.; Stimoniaris, D.; Kollatou, T.; Bagriyanik, M.; Ozdemir, A.; Dialynas, E. Impact of Renewable Based Microgrid Supply/Demand Profiles on Low Voltage Distribution Networks. Energy Procedia 2016, 103, 231–236. [Google Scholar] [CrossRef]
- CIGRE. Planning and Optimization Methods for Active Distribution Systems. Technical Report. August 2014. Available online: https://www.researchgate.net/publication/283569552_Planning_and_optimization_methods_for_active_distribution_systems (accessed on 10 December 2018).
- Bell, K.; Gill, S. Delivering a highly distributed electricity system: Technical, regulatory and policy challenges. Energy Policy 2018, 113, 765–777. [Google Scholar] [CrossRef]
- McKenna, R. The double-edged sword of decentralized energy autonomy. Energy Policy 2018, 113, 747–750. [Google Scholar] [CrossRef]
- Haider, H.T.; See, O.H.; Elmenreich, W. A review of residential demand response of smart grid. Renew. Sustain. Energy Rev. 2016, 59, 166–178. [Google Scholar] [CrossRef]
- Carvalho, P.; Marques, R.C. Computing economies of scope using robust partial frontier nonparametric methods. Water 2016, 8, 82. [Google Scholar] [CrossRef]
- Asano, H.; Bando, S. Economic Analysis of Microgrids. In Proceedings of the Power Conversion Conference, Nagoya, Japan, 2–5 April 2007; pp. 654–658. [Google Scholar]
- Quashie, M.; Bouffard, F.; Joós, G. Business cases for isolated and grid connected microgrids: Methodology and applications. Appl. Energy 2017, 205, 105–115. [Google Scholar] [CrossRef]
- Allegrini, J.; Orehounig, K.; Mavromatidis, G.; Ruesch, F.; Dorer, V.; Evins, R. A review of modelling approaches and tools for the simulation of district-scale energy systems. Renew. Sustain. Energy Rev. 2015, 52, 1391–1404. [Google Scholar] [CrossRef]
- Connolly, D.; Lund, H.; Mathiesen, B.V.; Leahy, M. A review of computer tools for analysing the integration of renewable energy into various energy systems. Appl. Energy 2010, 87, 1059–1082. [Google Scholar] [CrossRef]
- Al-falahi, M.D.; Jayasinghe, S.D.; Enshaei, H. A review on recent size optimization methodologies for standalone solar and wind hybrid renewable energy system. Energy Convers. Manag. 2017, 143, 252–274. [Google Scholar] [CrossRef]
- Tezer, T.; Yaman, R.; Yaman, G. Evaluation of approaches used for optimization of stand-alone hybrid renewable energy systems. Renew. Sustain. Energy Rev. 2017, 73, 840–853. [Google Scholar] [CrossRef]
- HOMER. HOMER Pro Version 3.12 online User Manual. HOMER Energy, 2016. Available online: https://www.homerenergy.com/products/pro/docs/3.12/index.html (accessed on 3 January 2019).
- Basher, S.A.; Raboy, D.G. The misuse of net present value in energy efficiency standards. Renew. Sustain. Energy Rev. 2018, 96, 218–225. [Google Scholar] [CrossRef]
- TradingEconomics. Country Indicators. Available online: https://tradingeconomics.com/countries (accessed on 10 December 2018).
- Papadopoulos, M.; Karteris, M.M. An assessment of the Greek incentives scheme for photovoltaics. Energy Policy 2009, 37, 1945–1952. [Google Scholar] [CrossRef]
- Grant Thornton and Clean Energy Pipeline. Renewable Energy Discount Rate Survey Results—2017. Available online: https://www.grantthornton.co.uk/globalassets/1.-member-firms/united-kingdom/pdf/documents/renewable-energy-discount-rate-survey-2017.pdf (accessed on 10 December 2018).
- Comodi, G.; Giantomassi, A.; Severini, M.; Squartini, S.; Ferracuti, F.; Fonti, A.; Nardi Cesarini, D.; Morodo, M.; Polonara, F. Multi-apartment residential microgrid with electrical and thermal storage devices: Experimental analysis and simulation of energy management strategies. Appl. Energy 2015, 137, 854–866. [Google Scholar] [CrossRef]
- Hesse, H.C.; Schimpe, M.; Kucevic, D.; Jossen, A. Lithium-ion battery storage for the grid—A review of stationary battery storage system design tailored for applications in modern power grids. Energies 2017, 10, 2107. [Google Scholar] [CrossRef]
- World Energy Council. Average Electricity Consumption Per Electrified Household. 2016. Available online: https://wec-indicators.enerdata.net/household-electricity-use.html (accessed on 10 December 2018).
- Goebel, C.; Cheng, V.; Jacobsen, H.A. Profitability of residential battery energy storage combined with solar photovoltaics. Energies 2017, 10, 976. [Google Scholar] [CrossRef]
- Eurostat. Share of Energy from Renewable Sources, Energy Indicator: Share of Renewable Energy in Electricity. Available online: http://appsso.eurostat.ec.europa.eu/nui/submitViewTableAction.do (accessed on 10 December 2018).
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).