Modelling Hourly Global Horizontal Irradiance from Satellite-Derived Datasets and Climate Variables as New Inputs with Artificial Neural Networks

Abstract

More accurate data of hourly Global Horizontal Irradiance (GHI) are required in the field of solar energy in areas with limited ground measurements. The aim of the research was to obtain more precise and accurate hourly GHI by using new input from Satellite-Derived Datasets (SDDs) with new input combinations of clear sky (Cs) and top-of-atmosphere (TOA) irradiance on the horizontal surface and with observed climate variables, namely Sunshine Duration (SD), Air Temperature (AT), Relative Humidity (RH) and Wind Speed (WS). The variables were placed in ten different sets as models in an artificial neural network with the Levenberg–Marquardt training algorithm to obtain results from training, validation and test data. It was applied at two station types in northeast Iraq. The test data results with observed input variables (correlation coefficient (r) = 0.755, Root Mean Square Error (RMSE) = 33.7% and bias = 0.3%) are improved with new input combinations for all variables (r = 0.983, RMSE = 9.5% and bias = 0.0%) at four automatic stations. Similarly, they improved at five tower stations with no recorded SD (from: r = 0.601, RMSE = 41% and bias = 0.7% to: r = 0.976, RMSE = 11.2% and bias = 0.0%). The estimation of hourly GHI is slightly enhanced by using the new inputs.

1. Introduction

Several studies have estimated Global Horizontal Irradiance (GHI) from various methods, but a higher temporal resolution of GHI is likely necessary for several applications such as photovoltaic panel and concentrated solar power projects. Recently, the demand for GHI has increased for solar energy projects. This is owing to problems related to non-renewable energies, a lack of other energy sources, increasing the use of energy and potential availability of solar energy [1,2,3,4]. Stations with long historical measurements of GHI are limited because of the cost of installation and maintenance, and issues related to the pyranometers [5]. Therefore, several studies have tried to estimate GHI empirically from the early 20th century until now from other climate variables, namely, Sunshine Duration (SD), Air Temperature (AT), cloud cover, and other variables, using the top-of-atmosphere irradiance on the horizontal surface (TOA) [6,7,8,9,10,11] and with linear regression models [12,13,14]. Recently, machine learning approaches have also been broadly used [15,16], which mostly include Artificial Neural Networks (ANNs), which will be discussed in a later section, Support Vector Machines, Random Forest [5,17,18] and some other machine learning models [19,20]. Some of these and other approaches have used satellite image data and interpolation techniques to cover the limitation of spatial resolution [3,21,22,23].

Geostationary satellites such as Meteosat First Generation (MFG), Meteosat Second Generation (MSG)/Spinning Enhanced Visible, Infrared Imager (SEVIRI), the Japanese Geostationary Meteorological Satellite (GMS), and the Geostationary Operational Environmental Satellite system (GOES) are considered to be more acceptable for obtaining high temporal resolution of GHI data than other satellites. Heliosat-2 is a method that has been widely used for converting satellite images to GHI. The reader is referred to Refs [24,25] for further information about Heliosat-2. Some other approaches can also be found in the literature with the same aim [26,27]. Consequently, several datasets and services are providing GHI data with various spatial and temporal resolutions globally. More detailed information about them can be found in [28]. The HelioClim-3 (HC3) and Copernicus Atmosphere Monitoring Service (CAMS) Radiation Service (CRS) are the most widely used Satellite-Derived Datasets (SDDs) which cover Europe, Africa and Asia [29]. They provide GHI data at the sub-hourly scale and have been built using the Heliosat-2 and Heliosat-4 algorithms, respectively. Their data have been validated in several climate regions, with overall results that show good agreements with quality-controlled ground data [30,31,32,33]. Full information and its availability can be found in [29]. Therefore, this study will use hourly GHI data from HC3 version-5 (HC3v5) and CRS version-3 (CRSv3) and combine them with climate variable ground data in an ANN algorithm for modelling GHI in areas where recorded GHI ground data are scarce.

SDDs have also been utilised with ground data to improve GHI datasets. For instance, Journee et al. in two different studies have merged SDD from MFG and MSG with GHI ground data to make a solar map over Belgium using kriging interpolation [34,35]. A map of GHI has been created by the combination of those datasets. SDDs are also important for other uses, such as for showing long-term trends of GHI over Europe and updating existing records [36]. It has also been used for a crop estimation model [37] and to obtain a coefficient of regression for calibrating a model for the same purpose [38]. Those studies revealed that SDDs are affordable for improving the results of GHI estimation.

Other research has used ANN models to analyse satellite images for estimating GHI and other components of solar radiation. For example, Meteosat-6 images have been analysed to estimate monthly GHI over Turkey [39]. Similarly, Meteosat-9 images have also been used with extra data in a model in Andalusia, Spain [40]. ANNs have also been used with Heliosat-2 for converting multi-spectral MSG images to estimate hourly GHI [41]. In addition, images from the Japanese Multifunctional Transport Satellites (MTSAT) have been analysed and combined with other data in an ANN for predicting GHI [42]. Other studies have analysed satellite images for obtaining climate variable data (such as land surface temperature) which were then paired with ground measurements in a model to estimate GHI [43,44]. Another case is Qin et al. [45], who input monthly precipitation calculated from TRMM satellite data with surface temperature from the Moderate Resolution Imaging Spectroradiometer (MODIS) to a model with GHI as an output. These papers have examined the use of ANNs with some climate parameters from satellite images to estimate GHI, but the high temporal availability of those parameters is limited.

ANNs have also been used to forecast GHI with various data and over various time intervals. For example, HC3, climate variables and other inputs have been analysed in ANN models to forecast GHI in intra-day and 1–6 h ahead in Gran Canary, Spain in two different studies [46,47]. They demonstrated that the SDD improved the forecasting results. Cloud properties and metric velocity data from satellite images with ground data have been used in an ANN model to forecast GHI at 30, 60, 90 and 120 min time scales [48]. Clear sky irradiance on a horizontal surface (Cs) and weather research data have been used to forecast 24 h ahead with an ANN model [49]. Hybrid ANN models have also been used to forecast one hour ahead [2,50]. Those papers demonstrated the role of ANNs in forecasting GHI at various time scales, and the role of SDDs and Cs as inputs to improve the model results. Another study has utilised machine learning algorisms to forecast GHI on a tilted panel based on several inputs namely climate variables, satellite data and solar position [19].

ANNs are considered one of the most powerful algorithms to find relationships between dependent and independent variables. They have been used broadly in literature to estimate GHI and other solar components with different types of data. For instance, geographical and meteorological parameters at different time scales as various inputs have been used with ANN models for a variety of climate regions and countries. For example, two cities in Oman [51]; eight cities [52] and nine cities [53] in China; 195 cities in Nigeria [54]; 27 stations [55], seven cities [56] and 30 cities [57] in Turkey; five stations in Argentina [12]; six cities in the Yucatan peninsula, Mexico [18]; five cities in Italy [58]; four cities in the USA; and two cities [59], 10 cities [60] and 12 cities in Iran [61]; and Cairo city in Egypt [17]. Generally, the results of those models in the literature show good agreement with ground data. This indicates the importance of various types of ANN models and algorithms for estimating GHI. However, those studies mainly focused on daily timescales and in a few cases on monthly scales, not at an hourly time scale, which is the focus of this study.

After an extensive review of recent literature, only four studies have been found that have used ANNs to estimate GHI on the hourly timescale. The studies focused on one city each in Algeria [62], Malaysia [63] and Morocco [64], and on five cities in North Africa and Jordan [5]. They are fully described and compared to this study in

Table 1. The literature for estimating Global Horizontal Irradiance (GHI) with Artificial Neural Networks (ANN) models on hourly time scales.

Reference	Inputs	Neurons in the Hidden Layer	Training Algorithm	Best RMSE
[62]	SD, AT, RH, WS, TOA, precipitation, Pressure, Declination, Zenith angle and Wind direction	1–8 By 1 or 2	feed-forward backpropagation Levenberg–Marquardt	13.3%
[63]	AT, RH, sunshine ratio, Day number, Month number, Number of an hour per day	3 and 6	Firefly algorithm	18.9%
[64]	SD, AT, RH, WS, Declination angle, GHI daily, daylight hours, TOA, a sunshine fraction	10, 15 and 20	feed-forward Levenberg–Marquardt	13.1%
[5]	TOA, Solar time and Day number	100, 180, 210 and 300	-	17%
This study	SD, At, RH, WS, Cs, TOA, HC3v5 and CRSv3	20–140 by 10	feed-forward backpropagation Levenberg–Marquardt	?

. On the other hand, other studies have estimated Direct Normal Irradiance (DNI) [58,65], Diffuse Horizontal Irradiance (DHI) [66,67] and have forecasted GHI, as mentioned in the previous paragraphs using ANN models on hourly time scales.

The studies (Table 1) also used other machine learning approaches with ANNs, estimated other solar components and estimated timescales, whereas the descriptions in the table are focused on the ANNs for estimating hourly GHI.

It seems clear from the literature that studies using SDDs and combining them with observed climate variables (SD, AT, Relative Humidity (RH) and Wind Speed (WS)) and with TOA and Cs as several new input combinations in an ANN model to estimate hourly GHI are limited. The aim of this study was to model hourly GHI in areas with few ground measurements by using new input variable combinations, which have not been seen in the previously mentioned studies on hourly scales or even on daily scales.

2. Materials and Methods

2.1. Study Site, Ground Data and Satellite-Derived Datasets

The case study is located between latitudes [34°08′20″–37°22′36″], and longitudes [42°32′00″–46°14′29″] in northeast Iraq. The Mediterranean Sea and semi-arid climate regions are seen in the area according to the Koppen classification [68] (Figure 1).

The hourly ground data of SD AT, RH and WS and GHI, were collected from two station types. First, the data from tower stations are all the above variables except SD. The pyranometer used for recording GHI in these stations is the Kipp and Zonen CMP6 Pyranometer. The data were collected for the period 2011–2014 from five stations, some of which lacked data from some years, from the Ministry of Electricity, Kurdistan Regional Government (KRG) (

Table 2. Tower stations with hourly data of Air Temperature (AT), Relative Humidity (RH) and Wind Speed (WS) and GHI at ground measurements with GHI of two Satellite-Derived Datasets (SDDs) and with calculated clear sky (Cs) and top-of-atmosphere (TOA) irradiance.

Station	Coordinates (Degrees)		Elevation a.s.l (m)	Period (dd/mm/yy)
Batufa	37.1764 N	43.0236 E	947	01/01/2011–31/12/2013
Enjaksor	37.0603 N	42.4353 E	509	01/01/2011–31/12/2014
Hojava	37.0075 N	43.0369 E	933	01/01/2011–31/12/2013
Jazhnikan	36.3564 N	43.9556 E	430	01/01/2011–31/10/2013
Tarjan	36.1258 N	43.7353 E	276	01/01/2011–31/12/2013

). Others are automatic stations at which SD is also recorded as well as the above variables. The GHI equipped in these stations is the Vaisala QMS101 Pyranometer. The data were collected from 2013–2016 by the General Directorate of Meteorology and Seismology, KRG, for four stations (

Table 3. Automatic stations as data in Table 2, plus SD.

Station	Coordinates (Degrees)		Elevation a.s.l (m)	Period (dd/mm/yy)
Halsho	36.2097 N	45.2598 E	1105	01/01/2013–31/12/2016
Bazian	35.6021 N	45.1376 E	892	01/04/2014–30/12/2016
Maydan	34.9194 N	45.6224 E	330	01/01/2014–31/12/2016
Kalar	34.6244 N	45.3049 E	218	01/01/2014–31/12/2016

). Both datasets are missing date from some months or years.

The SDDs, which are HC3v5 and CRSv3 with Cs and TOA, are collected from the Solar Radiation Data (SoDa) portal [29]. The SDDs are calculated with the Heliosat-2 and Heliosat-4 algorithms, utilising cloud properties from MSG images; full details can be found at [29,32,69,70]. The temporal resolution of MSG image is 15 min, and its spatial resolution is 5 km in the case study. The data were provided by SoDa based on those resolutions from 15 min, sub-hourly, hourly and monthly data with aggregation. Cs uses the McClear sky model data; full details about this can be found at [71]. The McClear sky is a model for providing hourly GHI under clear-sky conditions which are based on several inputs (solar zenith angle, ground albedo, ozone and water vapour column, aerosol, gases, time interval, location and its elevation) some of the inputs are measured with physical low, and some others came from satellite products [71]. The TOA is irradiance of the sun at the top of the atmosphere, which is calculated, based on blackbody radiation with Stefan–Boltzmann law, and it is adjusted with the sun-earth distance. Then it is multiplied by the cosine of the solar zenith angle of an area to calculate it on a horizontal plane of that area [72]. TOA and Cs are available at SoDa.

2.2. Quality Control of GHI Measurements and Evolution of SDDs

A full quality control procedure was applied to all nine stations of ground measurements to detect systematic errors, to select questionable data and to find gaps and not applicable (NA) values. The quality control procedure is published in a study with full details [73].

The station data were harmonised with SDDs (HC3v5 and CRSv3) and with TOA and Cs. All data were merged into one dataset. The dataset was configured based on true solar time when the solar elevation angle was above 15°. Systematic errors, NA values and a few questionable data points were then removed. In this way, the SDDs are evaluated against quality-controlled ground data. The validation is published in full detail in another study [30].

The output data from the nine stations in the study area in the two mentioned studies from which ground measurements were tested [73] and SDDs were evaluated [30], were used in this study.

2.3. Data Pre-Processing

The data were normalised to 0–1, as is recommended for the ANNs. The input normalised data of SD, AT, RH, WS, Cs, TOA, HC3v5 and CRSv3 were set as ten different inputs. Each input contained some of the above variables in both tower and automatic stations (

Table 4. Inputs and output to the ANN models.

Models	Inputs (Automatic Stations)	Inputs (Tower Stations)	Output
M1	SD, AT, RH, WS	AT, RH, WS	GHI
M2	SD, AT, RH, WS, Cs	AT, RH, WS, Cs	GHI
M3	SD, AT, RH, WS, TOA	AT, RH, WS, TOA	GHI
M4	SD, AT, RH, WS, HC3v5	AT, RH, WS, HC3v5	GHI
M5	SD, AT, RH, WS, CRSv3	AT, RH, WS CRSv3	GHI
M6	SD, AT, RH, WS, Cs, TOA	AT, RH, WS, Cs, TOA	GHI
M7	SD, AT, RH, WS, Cs, HC3v5	AT, RH, WS, Cs, HC3v5	GHI
M8	SD, AT, RH, WS, Cs, CRSv3	AT, RH, WS, Cs CRSv3	GHI
M9	SD, AT, RH, WS, Cs, TOA, HC3v5	AT, RH, WS, Cs, TOA, HC3v5	GHI
M10	SD, AT, RH, WS, Cs, TOA, CRSv3	SD, AT, RH, WS, Cs, TOA, CRSv3	GHI

). Each set of input combinations were named model-1 (M1) to model-10 (M10). Hereafter, each combination of inputs in each station M1–M10 was trained, and the results were presented using those names, as demonstrated in Table 4. The data in each station were randomly distributed for each model from M1–M10 as training (70%), validation (15%) and test (15%) data.

2.4. Artificial Neural Networks

ANNs are soft computing techniques which are based on how the human brain works. ANNs are considered one of the most powerful algorithms for finding a relationship between inputs and outputs. They have been used broadly in the literature for modelling GHI and have been described in detail (Section 1). ANNs contain three primary layers, which are the input layer, hidden layer and output layer (Figure 2). The weight and bias in each layer’s neurons are adjusted based on the activation function and algorithms for training the model, which depend on error minimising between the desired output and the target.

The neural network fitting toolbox (nftool) of MATLAB R2016a academic use [74] was used in this study. After the data were normalised to 0–1 and inputs and outputs were designated as M1–M10 for each station, the data were divided into training, validation and test sets. The Levenberg–Marquardt backpropagation algorithm was used to train each model with activation functions, sigmoid in the hidden layer and linear in the output layer (Figure 2). The number of neurons in the hidden layer for each model was selected after several tests based on the performance and balance of under or overfitting among the training, validation and test datasets. All other processes such as initial weight and bias and connections between layers were automatically completed.

The Levenberg–Marquardt algorithm was used due to its reduced time required for convergence, and its results are better than others such as the Bayesian Regularization and Scaled Conjugate Gradient in the case of modelling GHI [54,75,76,77]. However, another reason is that we compared the initial results of Levenberg–Marquardt to the other two training algorithms and its results were better than they were. Therefore, it was the only method utilised in this study.

The methodology steps are illustrated in Figure 3.

2.5. Evaluation Criteria

The performance and reliability of the results for models M1–M10 for training, validation and test data against ground measurements were evaluated by statistical indicators such as correlation coefficient (r) in Equation (1), the bias in Equation (2), and the relative bias in Equation (3), the root mean square error (RMSE) in Equation (4), and the relative RMSE (rRMSE) in Equation (5).

$$r=\frac{{{\displaystyle \sum }}_{i=1}^n\left(Xi-\overline{X}\right)\left(Yi-\overline{Y}\right)}{\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Xi-\overline{X}\right)}^2}\sqrt{{{\displaystyle \sum }}_{i=1}^n{\left(Yi-\overline{Y}\right)}^2}}$$

(1)

$$Bias=\frac{{{\displaystyle \sum }}_{i=1}^n\left(Yi-Xi\right)}{n}$$

(2)

$$rBias=\frac{Bias}{MeanXi}\ast 100$$

(3)

$$RMSE=\sqrt{\frac{{{\displaystyle \sum }}_{i=1}^n{\left(Yi-Xi\right)}^2}{n}}$$

(4)

$$rRMSE=\frac{RMSE}{MeanXi}\ast 100$$

(5)

where n = the number of observations, Xi = the GHI of ground data and Yi = the estimated GHI.

3. Results

The results of hourly GHI with ANN models from M1–M10 based on variable inputs for training, validation and test data were averaged for four automatic stations and five tower stations and are presented in

Table 5. Statistical results of hourly GHI models averaged for each model M1–M10 for tower stations. Mean, bias and RMSE units are W/m².

Models	Train						Validation						Test
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	517.2	−0.4	−0.1	206.6	40	0.617	516.2	0.2	0.0	208.4	40.2	0.600	511	3.4	0.7	209.5	41	0.601
M2	516.2	3.7	0.7	103.4	20	0.919	513.6	4.0	0.8	105.4	20.4	0.916	516.7	2.3	0.4	104.4	20.2	0.917
M3	514.8	1.7	0.3	111.6	21.6	0.905	518.8	−0.4	−0.1	112.8	21.6	0.903	519.7	−1.7	−0.3	111.8	21.5	0.903
M4	515.8	1.8	0.3	62	12.2	0.971	518.4	1.0	0.2	62.6	12	0.971	516.7	1.5	0.3	62.9	12.2	0.971
M5	515.6	0.2	0.0	76	15	0.957	516.4	1.0	0.2	76.6	14.8	0.956	517.2	1.7	0.3	75.6	14.6	0.958
M6	516	−0.6	−0.1	95	18.4	0.932	514	−0.8	−0.2	98.4	19.4	0.927	518.7	0.9	0.2	98.1	18.9	0.929
M7	515.6	−1.5	−0.3	59.8	11.4	0.974	513	−1.1	−0.2	60.4	11.6	0.973	521.1	−2.0	−0.4	60.4	11.6	0.973
M8	515.8	−0.7	−0.1	73	14.2	0.961	519.2	−1.4	−0.3	74.2	14.2	0.960	514	−0.1	0.0	75.3	14.6	0.958
M9	515.6	0.4	0.1	59.2	11.4	0.974	518.6	0.4	0.1	59.6	11.4	0.974	516.3	0.3	0.1	60	11.6	0.974
M10	517.2	1.3	0.2	55.8	10.8	0.977	512.6	1.8	0.4	58.2	11.4	0.975	513.8	−0.2	0.0	57.8	11.2	0.976

and

Table 6. As in Table 5, but for automatic stations.

Models	Train						Validation						Test
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	485	−0.2	−0.1	160.5	33.0	0.743	481.2	1.2	0.2	162.0	33.8	0.736	482.2	1.4	0.3	163.6	33.7	0.755
M2	484.2	0.4	0.1	54.3	11.5	0.974	486.5	−0.2	0.0	55.8	11.5	0.973	479.9	0.7	0.1	56.8	11.8	0.974
M3	484.5	−0.6	−0.1	55.5	11.8	0.973	479.2	−1.2	−0.3	59.0	12.3	0.970	485.4	−2.0	−0.4	58.8	12.1	0.971
M4	484	0.0	0.0	53.8	11.3	0.975	488	0.8	0.2	54.5	11.3	0.974	480.4	−0.5	−0.1	54.6	11.4	0.976
M5	484.7	1.5	0.3	58.8	12.5	0.970	480.5	2.0	0.4	61.8	13.0	0.967	484.4	1.6	0.3	60.0	12.4	0.970
M6	482.5	−0.7	−0.1	52.8	10.8	0.976	491.2	−1.3	−0.3	54.0	11.0	0.974	482.6	−0.5	−0.1	54.1	11.2	0.976
M7	483.5	1.2	0.3	46.0	9.3	0.982	486.5	0.4	0.1	47.3	9.5	0.981	483.3	1.1	0.2	47.6	9.8	0.981
M8	484	0.1	0.0	48.5	10.3	0.979	481.7	−0.1	0.0	50.0	10.3	0.978	486	0.3	0.1	49.5	10.2	0.980
M9	484	0.7	0.1	43.5	9.0	0.984	480	0.0	0.0	44.3	9.3	0.983	487.9	−0.2	0.0	46.3	9.5	0.983
M10	484.5	0.3	0.1	44.5	9.5	0.983	483.2	0.6	0.1	45.3	9.3	0.982	482.1	0.3	0.1	47.2	9.8	0.982

respectively. However, the same results with the number of neurons in the hidden layer, number of datasets used and mean of GHI ground data for every individual station types are presented in

Table A1. Statistical results of hourly GHI models and neuron numbers in the hidden layer for Batufa tower station. Mean, bias and RMSE units are W/m².

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	523	0.03	0.01	211	40	0.654	514	7.11	1.38	212	41	0.639	512	9.87	1.93	215	42	0.639	70
M2	523	3.34	0.64	110	21	0.919	511	7.61	1.49	112	22	0.914	517	4.54	0.88	110	21	0.92	80
M3	519	2.68	0.52	115	22	0.912	528	−0.42	−0.08	117	22	0.906	518	−0.18	−0.03	120	23	0.904	140
M4	517	0.93	0.18	66	13	0.971	534	0.86	0.16	65	12	0.973	522	0.3	0.06	66	13	0.972	70
M5	518	−0.6	−0.12	83	16	0.955	523	1.11	0.21	79	15	0.959	528	0.18	0.03	82	16	0.956	70
M6	521	1.32	0.25	100	19	0.932	506	1.41	0.28	108	21	0.923	533	0.83	0.16	101	19	0.935	90
M7	522	−5.23	−1	64	12	0.974	514	−2.29	−0.45	66	13	0.971	519	−4.86	−0.94	64	12	0.973	70
M8	521	0.53	0.1	79	15	0.959	525	−1.32	−0.25	80	15	0.957	513	0.63	0.12	81	16	0.957	70
M9	519	2.51	0.48	64	12	0.974	526	1.79	0.34	64	12	0.974	522	1.5	0.29	65	12	0.973	50
M10	522	−0.55	−0.11	61	12	0.976	513	0.98	0.19	63	12	0.975	521	0.07	0.01	61	12	0.976	90

,

Table A2. As in Table A1, but for Enjaksor tower station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	BIAS	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	518	−1.36	−0.26	207	40	0.608	521	−3.85	−0.74	208	40	0.6	515	−2.67	−0.52	209	41	0.596	90
M2	518	−2.02	−0.39	103	20	0.919	520	−2.97	−0.57	105	20	0.916	512	−0.57	−0.11	104	20	0.917	120
M3	514	2.27	0.44	112	22	0.903	530	0.42	0.08	113	21	0.901	524	−1.84	−0.35	113	22	0.898	100
M4	514	0.21	0.04	57	11	0.976	529	−2.32	−0.44	57	11	0.975	524	0.04	0.01	57	11	0.976	60
M5	517	3.93	0.76	75	15	0.958	521	2.45	0.47	75	14	0.958	517	4.09	0.79	75	15	0.959	90
M6	518	−0.83	−0.16	98	19	0.926	519	−2.64	−0.51	102	20	0.92	517	4.12	0.8	100	19	0.925	70
M7	519	0.24	0.05	54	10	0.979	512	−1.03	−0.2	56	11	0.977	519	−2.45	−0.47	56	11	0.977	60
M8	517	5.47	1.06	73	14	0.96	521	4.34	0.83	73	14	0.961	519	4.49	0.87	72	14	0.961	50
M9	516	−0.45	−0.09	54	10	0.978	525	0.56	0.11	55	10	0.977	520	0.49	0.09	54	10	0.979	60
M10	520	0.73	0.14	52	10	0.98	513	0.63	0.12	51	10	0.98	511	−0.14	−0.03	52	10	0.98	100

,

Table A3. As in Table A1, but for Hojava tower station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	504	−1.63	−0.32	205	41	0.634	514	−6.44	−1.25	207	40	0.618	491	6.66	1.36	208	42	0.621	90
M2	504	5.03	1	106	21	0.918	495	0.47	0.09	106	21	0.916	509	−0.44	−0.09	103	20	0.92	90
M3	504	1.82	0.36	112	22	0.908	503	−0.78	−0.16	111	22	0.906	501	1.25	0.25	110	22	0.908	90
M4	503	0.45	0.09	64	13	0.97	501	0.11	0.02	64	13	0.97	509	0.3	0.06	65	13	0.969	80
M5	504	−2	−0.4	79	16	0.955	498	2.35	0.47	83	17	0.947	504	−1.46	−0.29	79	16	0.955	80
M6	501	−4.56	−0.91	98	20	0.93	512	−0.81	−0.16	100	20	0.925	504	−3.23	−0.64	99	20	0.927	100
M7	501	−3.24	−0.65	64	13	0.97	507	−2.2	−0.43	62	12	0.972	511	−2.67	−0.52	64	13	0.97	80
M8	504	−4.46	−0.88	75	15	0.959	504	−3.53	−0.7	78	15	0.957	500	−6.12	−1.22	78	16	0.957	80
M9	504	0.32	0.06	64	13	0.971	503	−0.83	−0.17	64	13	0.97	499	2.7	0.54	63	13	0.971	80
M10	502	4.01	0.8	57	11	0.976	514	4.16	0.81	63	12	0.972	499	2.56	0.51	61	12	0.974	80

,

Table A4. As in Table A1, but for Jazhnikan tower station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	518	−1.85	−0.36	208	40	0.59	518	−0.13	−0.03	208	40	0.584	519	−6.91	−1.33	209	40	0.586	100
M2	516	8.12	1.57	99	19	0.924	516	10.19	1.97	102	20	0.918	530	3.36	0.63	102	19	0.917	110
M3	518	0.99	0.19	108	21	0.907	512	0.03	0.01	111	22	0.906	526	−1.78	−0.34	109	21	0.903	110
M4	521	3.41	0.65	62	12	0.97	509	3.59	0.71	63	12	0.97	516	3.67	0.71	66	13	0.968	120
M5	518	−1.5	−0.29	72	14	0.96	521	−3.16	−0.61	75	14	0.958	514	2.21	0.43	71	14	0.96	100
M6	518	0.63	0.12	89	17	0.938	514	−1.4	−0.27	91	18	0.934	522	0.39	0.07	96	18	0.927	130
M7	514	−0.4	−0.08	58	11	0.974	524	−1.07	−0.2	60	11	0.973	530	0.01	0	60	11	0.972	120
M8	517	−2.8	−0.54	70	14	0.963	524	−3.44	−0.66	69	13	0.964	516	−0.39	−0.08	75	15	0.955	140
M9	516	−0.58	−0.11	56	11	0.976	525	−1.27	−0.24	57	11	0.976	523	−3.2	−0.61	59	11	0.974	140
M10	520	3.27	0.63	53	10	0.979	503	3.45	0.69	59	12	0.972	523	0.65	0.12	59	11	0.973	130

,

Table A5. As in Table A1, but for Tarjan tower station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	523	3.01	0.58	202	39	0.598	514	4.39	0.85	207	40	0.557	517	11.55	2.23	207	40	0.552	100
M2	520	3.83	0.74	99	19	0.917	526	4.76	0.9	102	19	0.917	518	5.33	1.03	102	20	0.912	80
M3	519	0.89	0.17	111	21	0.895	521	−1.26	−0.24	112	21	0.894	528	−6.07	−1.15	106	20	0.907	70
M4	524	4.08	0.78	61	12	0.97	519	2.51	0.48	64	12	0.969	510	3.79	0.74	62	12	0.967	100
M5	521	1.2	0.23	71	14	0.959	519	2.33	0.45	71	14	0.959	523	2.82	0.54	71	14	0.959	20
M6	522	0.49	0.09	90	17	0.932	519	−0.66	−0.13	91	18	0.935	518	1.22	0.24	93	18	0.929	80
M7	522	1.01	0.19	59	11	0.972	508	0.95	0.19	58	11	0.972	527	0.18	0.03	59	11	0.972	60
M8	520	−2.17	−0.42	68	13	0.962	522	−2.81	−0.54	71	14	0.96	521	0.41	0.08	71	14	0.96	60
M9	523	0.1	0.02	58	11	0.973	514	1.69	0.33	58	11	0.974	517	−0.04	−0.01	60	12	0.971	40
M10	522	−1.16	−0.22	56	11	0.975	520	−0.32	−0.06	55	11	0.975	516	−4.35	−0.84	57	11	0.973	60

,

Table A6. As in Table A1, but for Halsho automatic station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	482	1.13	0.23	153	32	0.835	468	2.39	0.51	153	33	0.834	474	8.11	1.71	155	33	0.827	80
M2	479	−0.76	−0.16	57	12	0.979	487	−1.08	−0.22	59	12	0.977	472	1.11	0.24	61	13	0.976	120
M3	478	−2.87	−0.6	62	13	0.974	475	0.32	0.07	67	14	0.97	485	−3.28	−0.68	66	14	0.972	120
M4	481	−0.11	−0.02	55	11	0.98	476	2.36	0.5	55	12	0.98	474	−0.49	−0.1	56	12	0.98	60
M5	477	0.64	0.13	60	13	0.976	481	1.44	0.3	62	13	0.974	484	0.31	0.06	62	13	0.975	100
M6	479	−0.52	−0.11	58	12	0.978	482	−0.14	−0.03	57	12	0.978	477	1.6	0.34	60	13	0.976	40
M7	478	1.45	0.3	49	10	0.984	479	1.37	0.29	50	10	0.984	481	1.81	0.38	49	10	0.984	20
M8	478	−0.37	−0.08	51	11	0.983	481	0.95	0.2	54	11	0.981	482	0.65	0.13	51	11	0.983	30
M9	477	−0.14	−0.03	48	10	0.985	483	1.54	0.32	48	10	0.985	484	−0.1	−0.02	49	10	0.984	50
M10	476	0.4	0.08	47	10	0.985	489	0	0	46	9	0.986	481	0.73	0.15	49	10	0.985	40

,

Table A7. As in Table A1, but for Bazian automatic station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	482	−0.46	−0.1	166	34	0.724	477	−3.28	−0.69	168	35	0.712	468	5.49	1.17	168	36	0.716	70
M2	480	3.41	0.71	62	13	0.966	482	0.25	0.05	63	13	0.965	473	0.78	0.16	62	13	0.967	60
M3	479	−0.11	−0.02	60	13	0.968	475	−0.63	−0.13	63	13	0.965	484	−1.32	−0.27	61	13	0.967	70
M4	477	0.94	0.2	55	12	0.973	490	4.31	0.88	55	11	0.973	477	1.11	0.23	56	12	0.973	50
M5	480	2.78	0.58	61	13	0.967	471	4.94	1.05	64	14	0.963	483	2.97	0.61	61	13	0.969	60
M6	478	−0.31	−0.06	57	12	0.971	484	−0.26	−0.05	61	13	0.967	476	0.88	0.18	58	12	0.971	70
M7	478	2.47	0.52	50	10	0.979	486	−0.62	−0.13	50	10	0.978	476	−2.14	−0.45	50	11	0.978	20
M8	480	−0.04	−0.01	52	11	0.976	476	2.2	0.46	53	11	0.976	476	1.18	0.25	53	11	0.975	20
M9	478	2.6	0.54	46	10	0.982	484	0.74	0.15	46	10	0.982	477	2.93	0.61	48	10	0.979	40
M10	480	0.37	0.08	46	10	0.981	480	1.82	0.38	47	10	0.98	472	−0.31	−0.07	49	10	0.978	50

,

Table A8. As in Table A1, but for Maydan automatic station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	503	0.06	0.01	165	33	0.723	501	13.04	2.6	170	34	0.701	507	−0.72	−0.14	169	33	0.7	60
M2	503	−0.1	−0.02	43	9	0.983	506	−1.09	−0.22	45	9	0.982	499	−0.16	−0.03	46	9	0.982	60
M3	506	0.42	0.08	45	9	0.982	494	1.64	0.33	48	10	0.98	498	0.02	0	47	9	0.981	50
M4	503	0.17	0.03	48	10	0.98	509	−1.94	−0.38	50	10	0.978	499	0.19	0.04	49	10	0.978	60
M5	504	−2.29	−0.45	54	11	0.974	499	−2.64	−0.53	59	12	0.969	505	−2.93	−0.58	57	11	0.971	70
M6	500	−1.41	−0.28	42	8	0.984	514	−1.11	−0.22	43	8	0.983	506	−3.86	−0.76	44	9	0.982	80
M7	504	0.96	0.19	37	7	0.988	499	1.26	0.25	39	8	0.986	503	2.02	0.4	40	8	0.986	60
M8	503	0.16	0.03	40	8	0.986	503	−0.32	−0.06	42	8	0.984	505	0.28	0.06	43	9	0.983	60
M9	505	0.6	0.12	35	7	0.989	488	−1.37	−0.28	35	7	0.989	511	−2.43	−0.48	39	8	0.987	50
M10	504	0.33	0.07	38	8	0.987	502	0.18	0.04	40	8	0.986	500	−0.46	−0.09	41	8	0.985	70

and

Table A9. As in Table A1, but for Kalar automatic station.

Models	Train						Validation						Test						Neurons
	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r	Mean	Bias	%	RMSE	%	r
M1	473	−1.63	−0.34	158	33	0.689	479	−7.26	−1.52	157	33	0.695	479	−9.24	−1.93	161	34	0.705	70
M2	475	−0.91	−0.19	55	12	0.968	471	1.17	0.25	56	12	0.966	475	0.84	0.18	56	12	0.966	60
M3	475	0.03	0.01	55	12	0.968	473	−6.31	−1.33	58	12	0.965	474	−3.22	−0.68	58	12	0.962	50
M4	475	−1.14	−0.24	57	12	0.966	477	−1.44	−0.3	58	12	0.964	473	−2.85	−0.6	57	12	0.964	60
M5	478	4.84	1.01	60	13	0.962	471	4.31	0.92	62	13	0.96	464	6.89	1.48	60	13	0.961	90
M6	473	−0.48	−0.1	54	11	0.97	485	−3.77	−0.78	55	11	0.969	471	−0.73	−0.15	52	11	0.971	80
M7	474	−0.02	0	48	10	0.976	482	−0.47	−0.1	50	10	0.975	472	2.12	0.45	51	11	0.972	60
M8	475	0.77	0.16	51	11	0.972	467	−3.03	−0.65	51	11	0.972	479	−1.02	−0.21	51	11	0.972	40
M9	476	−0.21	−0.04	45	9	0.979	465	−0.77	−0.17	48	10	0.975	477	−0.66	−0.14	48	10	0.977	40
M10	478	0.03	0.01	47	10	0.977	462	0.34	0.07	48	10	0.976	474	1.05	0.22	49	10	0.973	60

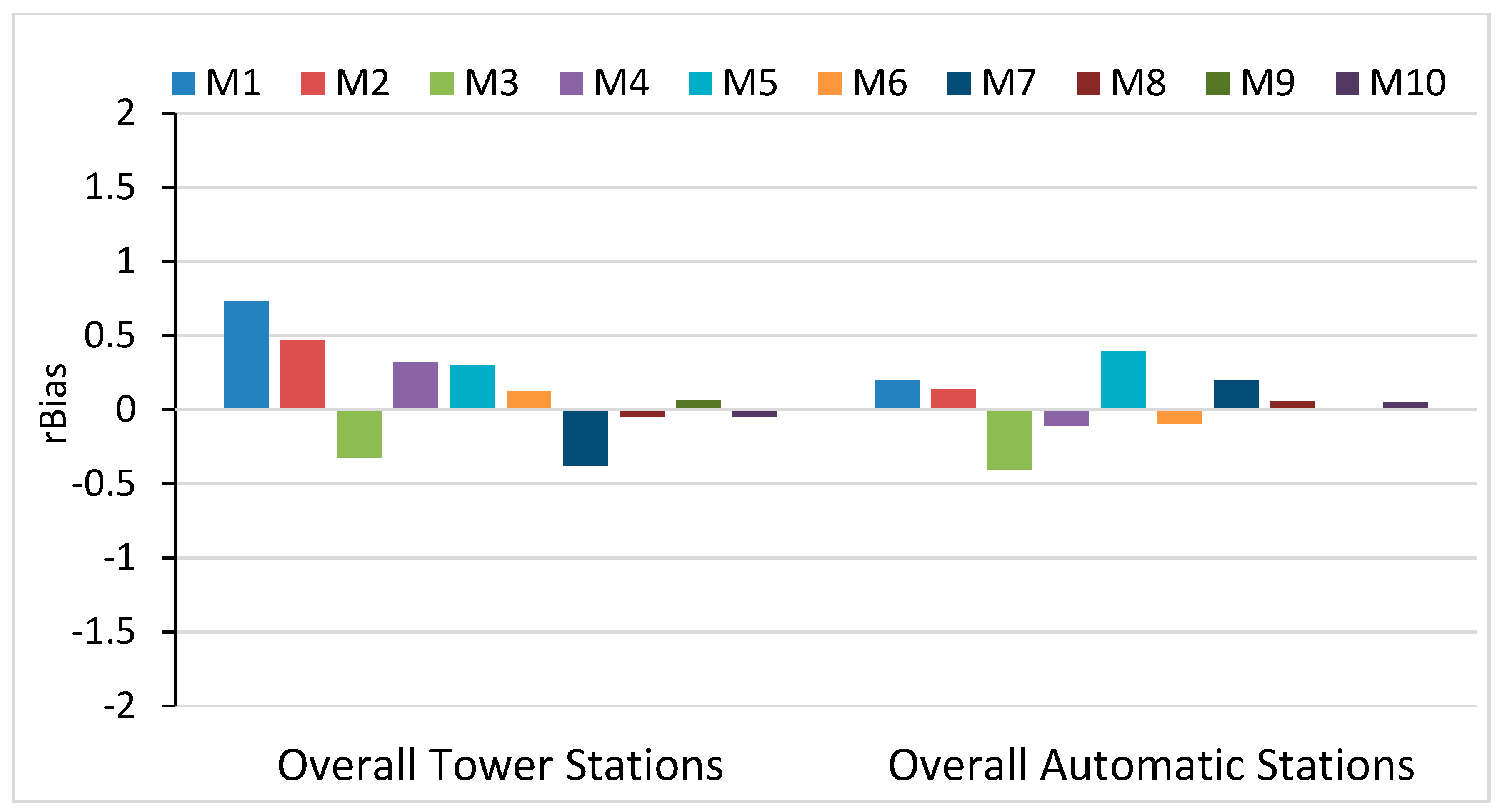
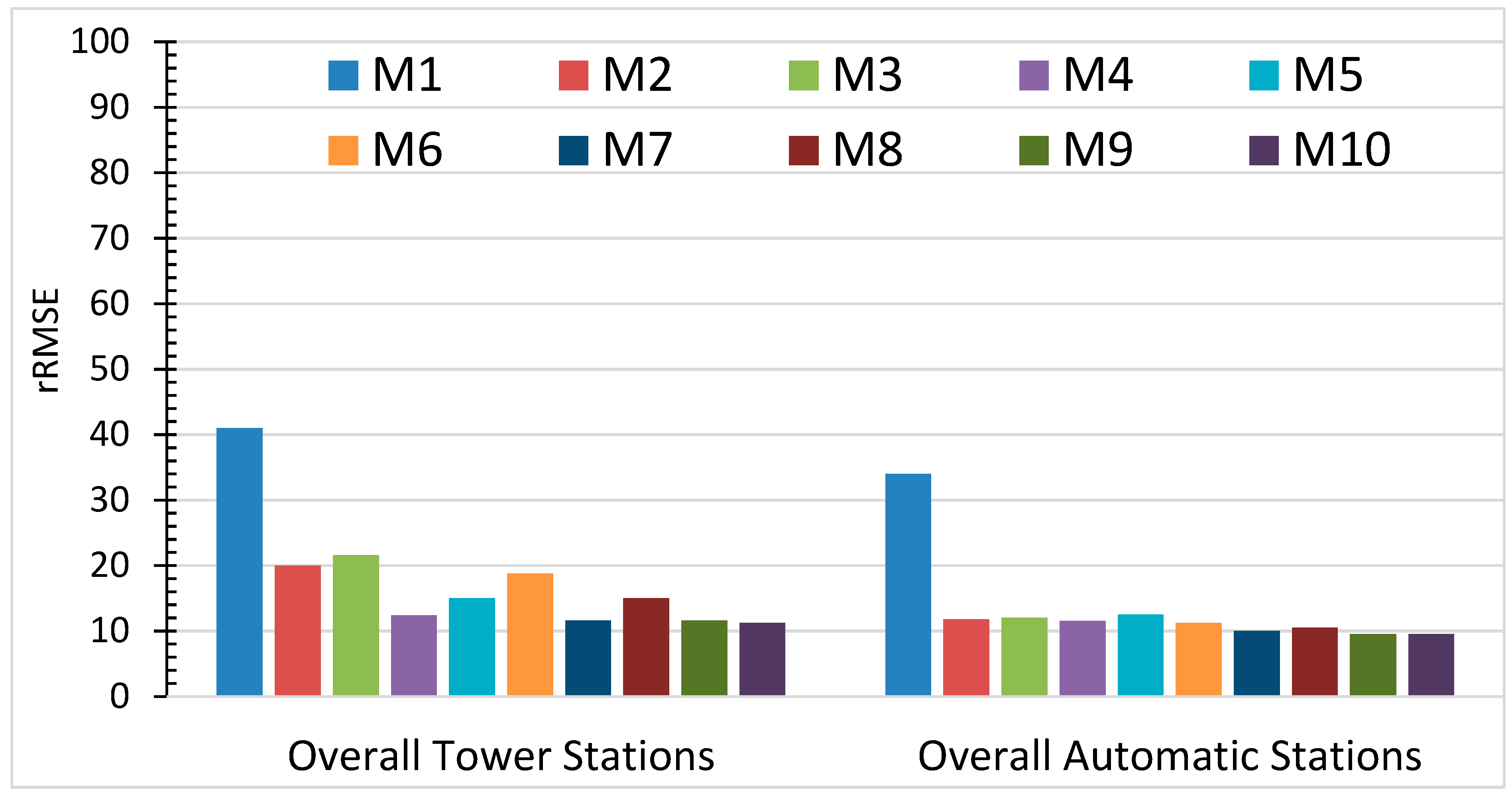
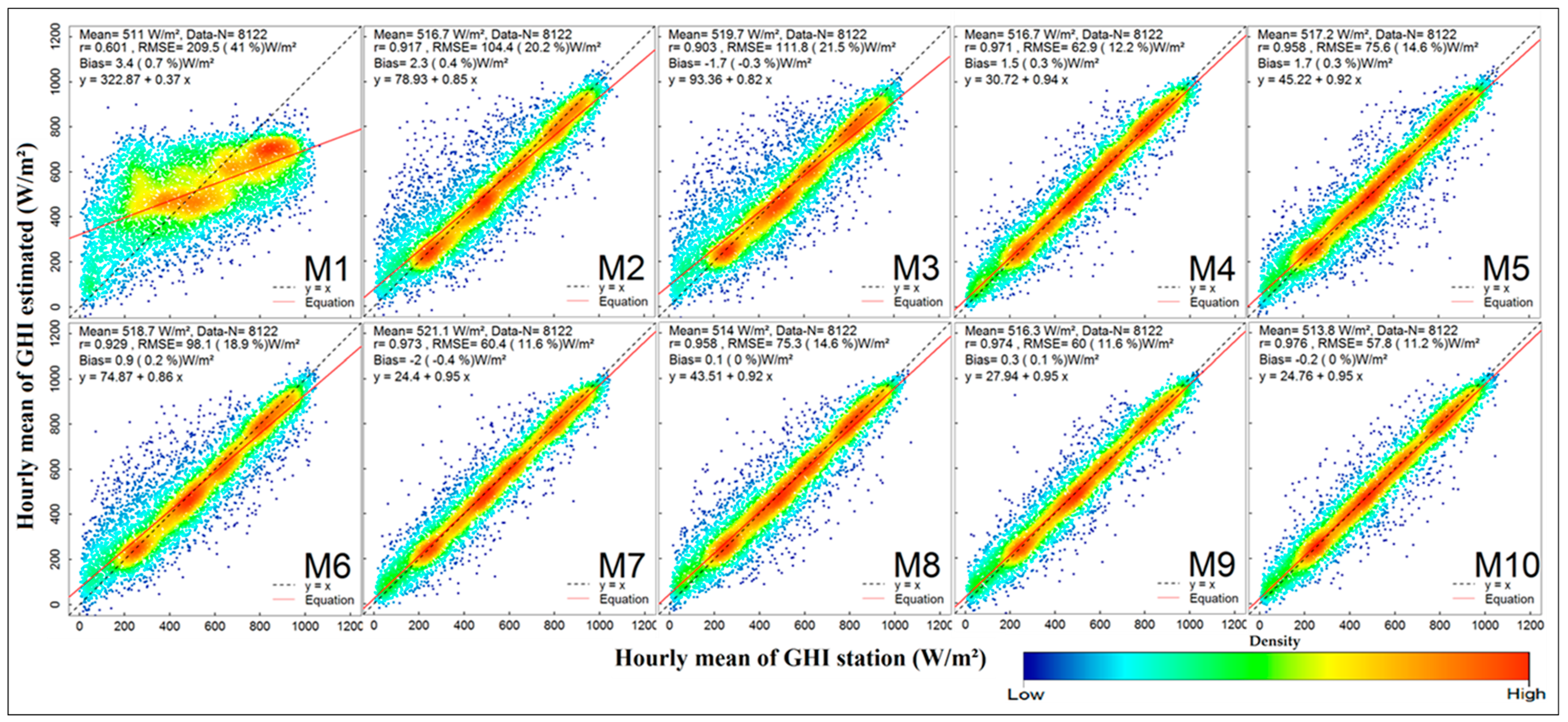
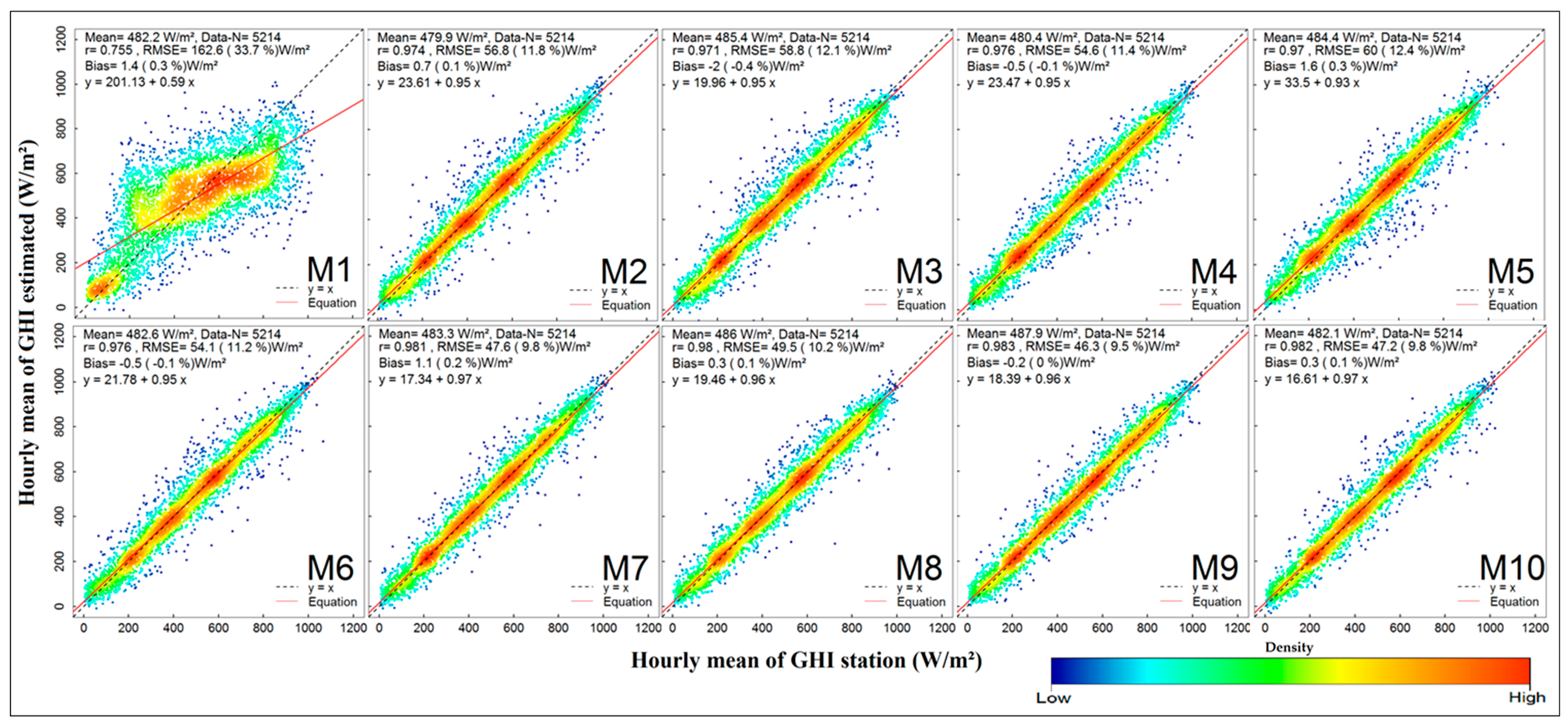
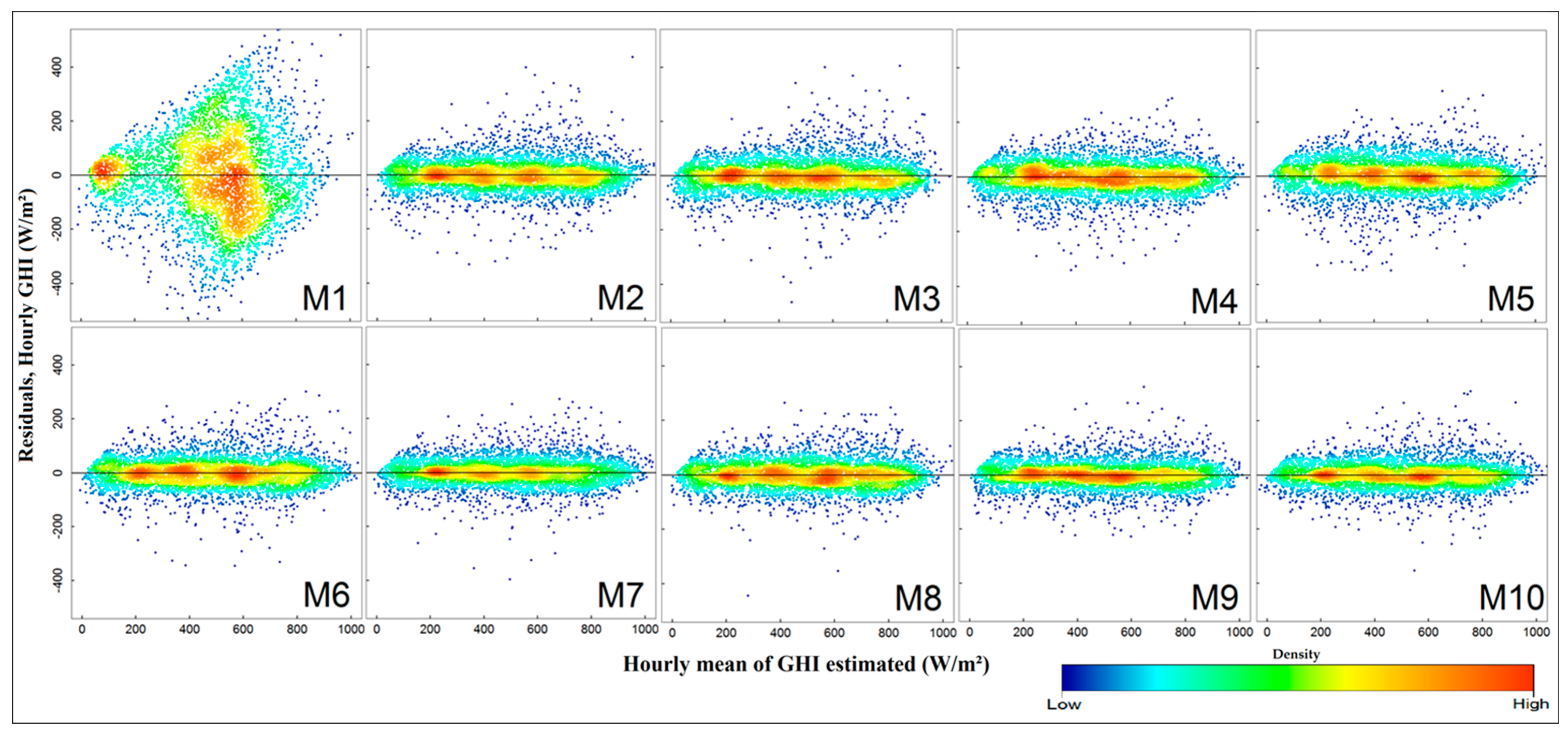
with two Figure A1 and Figure A2 of relative bias and RMSE of test data for further demonstration. Figure 4 and Figure 5 show a further comparison of the relative bias and RMSE between the models and the station types in the test data. In addition, the results of M1–M10 in the test data are shown with scatterplots of ground vs models and estimated vs residuals in Figure 6, Figure 7, Figure 8 and Figure 9 for both station types respectively.

As can be seen in Table 5 (tower stations) and Table 6 (automatic stations), there is no significant difference (the differences are lower than 3% in all individual cases) when comparing training and validation data with test data, which is in line with the stated methodology. Therefore, the results will be presented and discussed according to the models’ independent test data, which is more important to demonstrate the reliability of each model.

The overall results of GHI estimation by ANN models compared to ground data show the better performance of automatic stations than tower stations in all models based on r values, bias and RMSE (Table 5 and Table 6, Figure 4, Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9).

The lowest r value range among the models are 0.601 and 0.755 in M1 for both station types, respectively. The highest r value is 0.983 in M9 automatic stations and 0.976 in M10 tower stations. Other r values range from 0.903–0.982 in both station types (Table 5 and Table 6). Despite both high and low r values, the values of M3 and M5 compared to other remaining values are low in automatic stations. This is also true for M2, M3 and M6 to others at tower stations.

The values of bias were significantly low in all cases in the study area, which is under 1% of mean ground data for M1–M10. In the tower stations, the highest bias was recorded in M1 (3.4 W/m²) 0.7%. It was 0.4% (2.3 W/m²) in M2, a negative bias of −0.4% (−2 W/m²) in M7 and the others’ rates were below 0.3%. However, in the automatic stations, the highest bias was recorded in M3 (−2 W/m²) −0.4%. It was 0.3% in M1 and M5, and the others were below that value. The lowest bias was recorded at M8, M9 and M10, which were close to zero in both station types (Table 5 and Table 6, Figure 4). Figure 4 demonstrates the low rates of relative bias among M1-M10 for both station types.

The RMSE results showed similarity with bias. The highest RMSE in tower stations was recorded in M1 (209.5 W/m² 41%). It decreased to 111.8 W/m² (21.5%) and to 104.4 W/m² (20.2%) in M3 and M2 respectively. The lowest recorded RMSE values were 57.8 W/m² (11.2%), 60 W/m² (11.6%) and 60.4 W/m² (11.6%) in M10, M9 and M7 respectively. Other rates are between 12–19%.

On the other hand, the RMSE at automatic stations are low compared to tower stations for each model. However, the highest one was recorded in M1 (163.6 W/m² 33.7%). It decreased to 60 W/m² (12.4%) in M3. The lowest RMSE was recorded in M9 (46.3 W/m² 9.5%) and there were slightly higher values in M7 (47.6 W/m² 9.8%) and M10 (47.2 W/m² 9.8%). The other remaining values were between 10–12% (Table 5 and Table 6, Figure 5). Figure 5 shows the stability of relative RMSE in automatic stations after M1 among the other models whereas it shows fluctuations for tower stations for the same situation.

Those rates of RMSE can be noted clearly by a close look at the scatterplots of each model in Figure 6 (tower stations) and Figure 8 (automatic stations), which are demonstrating the results of hourly GHI models in test data against ground measurements. The observations are concentrated around the 1:1 line in better performance models (M8, M9 and M10), where the regression lines are correspondingly close to the 1:1 line. The opposite is seen in M1 for both station types. However, in models M2, M3 and M6 (tower stations) the observations are far from the 1:1 line and the regression line in red is not close to the 1:1 line, corresponding to high recorded RMSE compared to other models (Figure 6).

Figure 7 (for tower stations) and Figure 9 (for automatic stations) show the scatterplots of residuals against estimated hourly GHI of test data in each model. The clustered patterns of residuals are seen only in M1 in both station types whereas all other residuals are randomly distributed and the densities of observation are around zero. However, low performance can be noted at M2, M3 and M6 (Figure 7).

4. Discussion

The hourly GHI was estimated over nine stations in Iraq by using observed inputs (SD, AT, RH and WS), calculated inputs (TOA and Cs) and new input from SDDs (HC3v5 or CRSv3) to the ten M1-M10 ANN models based on the number and combination of inputs. The results of the overall performance are r values from 0.601–0.976, bias from −0.4–0.0–0.7% and RMSE from 11.2–41% at tower stations and r values from 0.755–0.983, bias from −0.4–0.0–0.3% and RMSE from 9.5–33.7% at automatic stations. Excellent performance was recorded in M9 (9.5%), and M10 (11.2%) and low performance was recorded in M1 at automatic and tower stations respectively. The better results of those models at hourly time scales compared to the previous studies for similar estimation (Table 1) are related to the new inputs such as Cs, TOA and SDDs together in this study.

The overall better performance, with a lower percent of automatic stations than tower stations in all models, is obtained by the use of SD as inputs in automatic stations—SD is unrecorded in tower stations. It is also reported [6,62,64,77] that the role of SD increases the performance of models.

The low performance of M1 in both station types is related to the small number of inputs, which do not include any of the calculated inputs. The calculated inputs such as Cs have a unique role to increase the model performance as seen in M2 compared to M1 in both stations. This is in agreement to improved results in some limited studies which used Cs as inputs either for modelling or forecasting GHI [47,49,78,79].

The low recorded bias in most of the models is related to the good estimation of GHI by ANN models as mentioned in several studies [12,17,62,64]. We presented the overall bias among stations, which led to a decrease in the bias because of positive bias in some stations and negative bias in others in the same model, whereas the bias in all individual stations was lower than 2% except one case of 2.2% (Table A1, Table A2, Table A3, Table A4, Table A5, Table A6, Table A7, Table A8 and Table A9, Figure A1).

The fluctuation of RMSE among models at tower stations and its stability among models at automatic stations (Figure 5 and Figure A2, Table 5 and Table 6) are mainly related to the role of SD, which was used as input in the later ones. The highest record of RMSE in M1 in both station types is related to inputs which contain only four climate variables. This is reported by literature where GHI was estimated at a daily time scale [55,77]. The improved performance in M2 and M3 compared to M1 is related to the use of additional variables of Cs and TOA in those models respectively (Table 4). Hence, the low performance of M2, M3 and M6 compared to better performance in M4 and M5 are related to the use of SDDs as new inputs with climate variables. This has been reported by studies which have used SDDs in foresting GHI [46,47]. The better performance of M7 and M8 compared to the previous M1–M6 is related to the use of Cs with SDDs in those models. The role of Cs is mentioned in literature [49,79], but in those cases, it was not combined with SDDs. The overall better performances of M9 and M10 from the other models (M1–M8) are related to the combination of all variables in those models. These demonstrate the better performance of this study compared to similar studies [5,62,63,64].

The performance of HC3v5 as input with only four climate variables is better than CRSv3 as demonstrated in the comparison between M4 and M5 in both station types, whereas in other models (M7–M10) the difference between them are minimal. The former result (M4–M5) is related to the accurate reproduction of the GHI ground data by HC3v5 as described in the literature [30,32,33]. The latter (M7–M10) is related to the use of Cs and TOA as separate inputs.

This study revealed that using SDDs, Cs, and TOA with climate variables in ANN models has improved the results of estimation for hourly GHI with an overall r value of 0.980, bias lower than 2% and RMSE lower than 10% compared to similar studies with no combination of those inputs [5,62,63,64].

The results of this study demonstrate that this way of modelling allows the retrieval or management of a dataset of GHI for decades where the inputs are available, but where GHI is not recorded as in most areas in the case study and similar regions with a scarcity of ground data, it can be achieved by using the trained models.

The new inputs of SDDs and Cs which improved the results are easily and openly available for most regions [29] unlike other variables such as cloud cover and SD [21,73,80]. Therefore, the mentioned new variables can be used for modelling and forecasting the solar components for better results.

The limitations are principally as follows: This study estimated GHI but no other solar components, which are required directly in fields such as DNI in concentrated solar power. Hence, some studies have estimated DNI and DHI from GHI [64,81,82]. However, further research is required for that in this type of area with a scarcity of ground data. Another limitation is the scarcity of long-term GHI ground data at timescales beyond five years or more, which are better for training this kind of model.

5. Conclusions

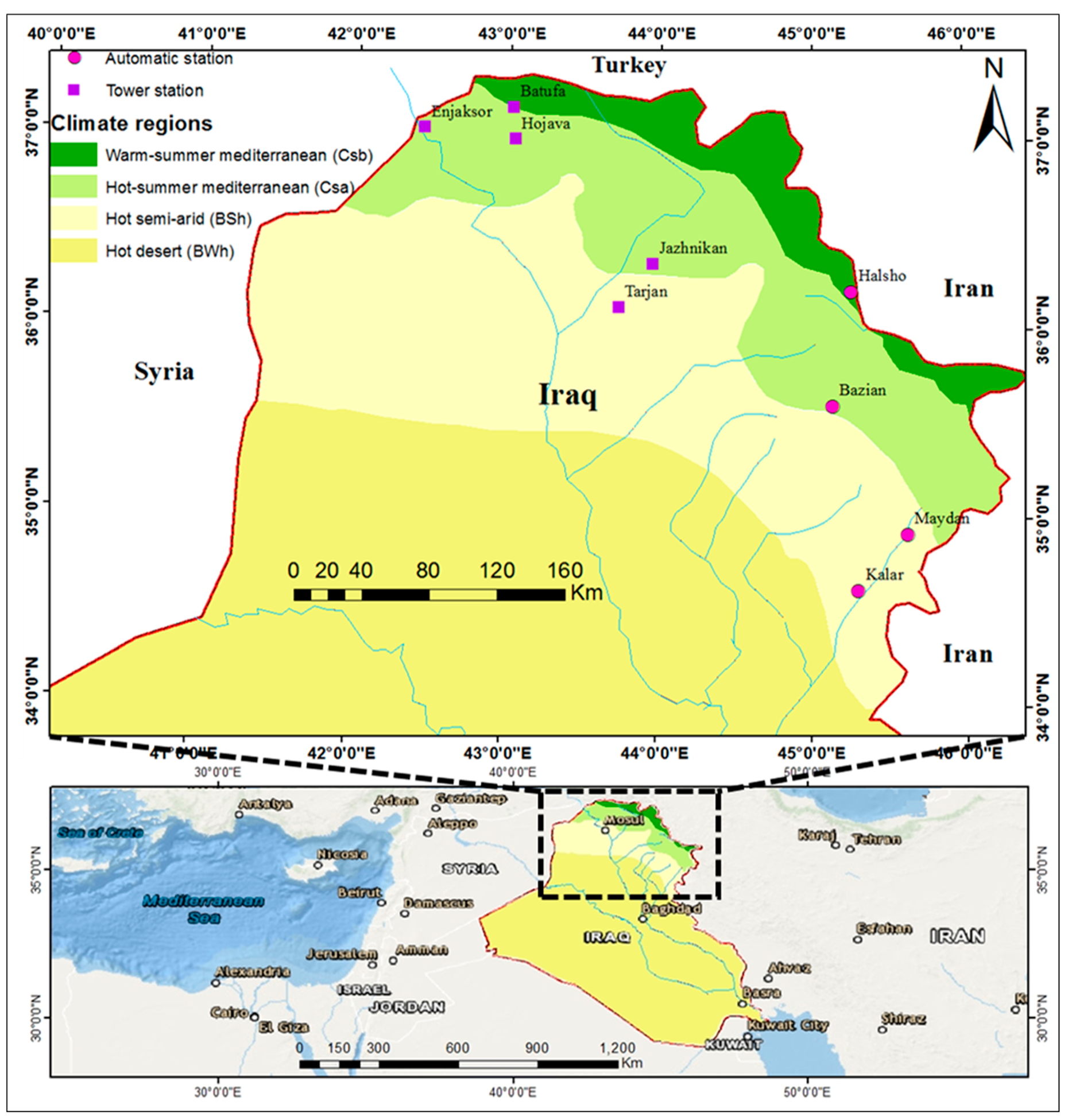
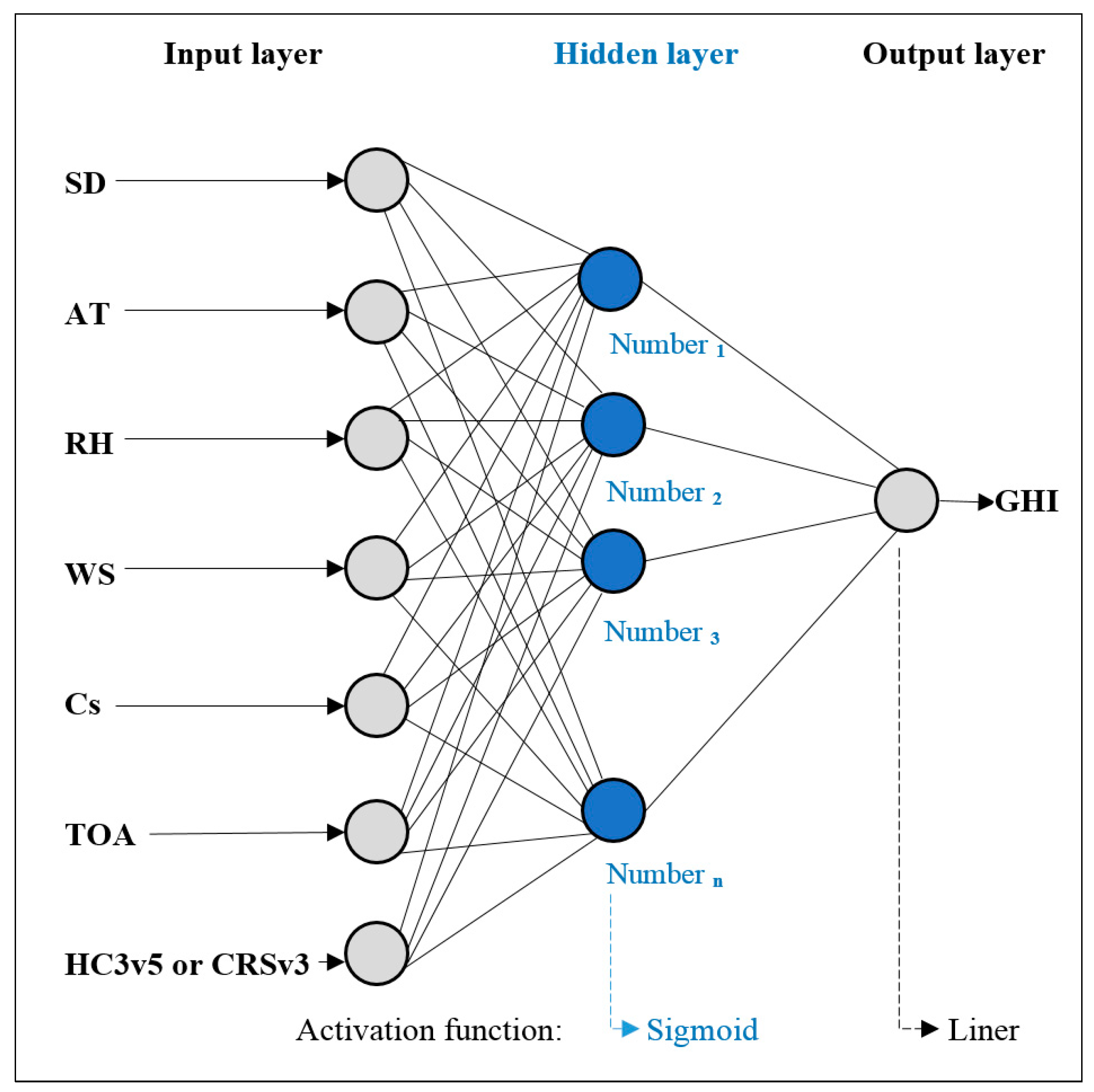
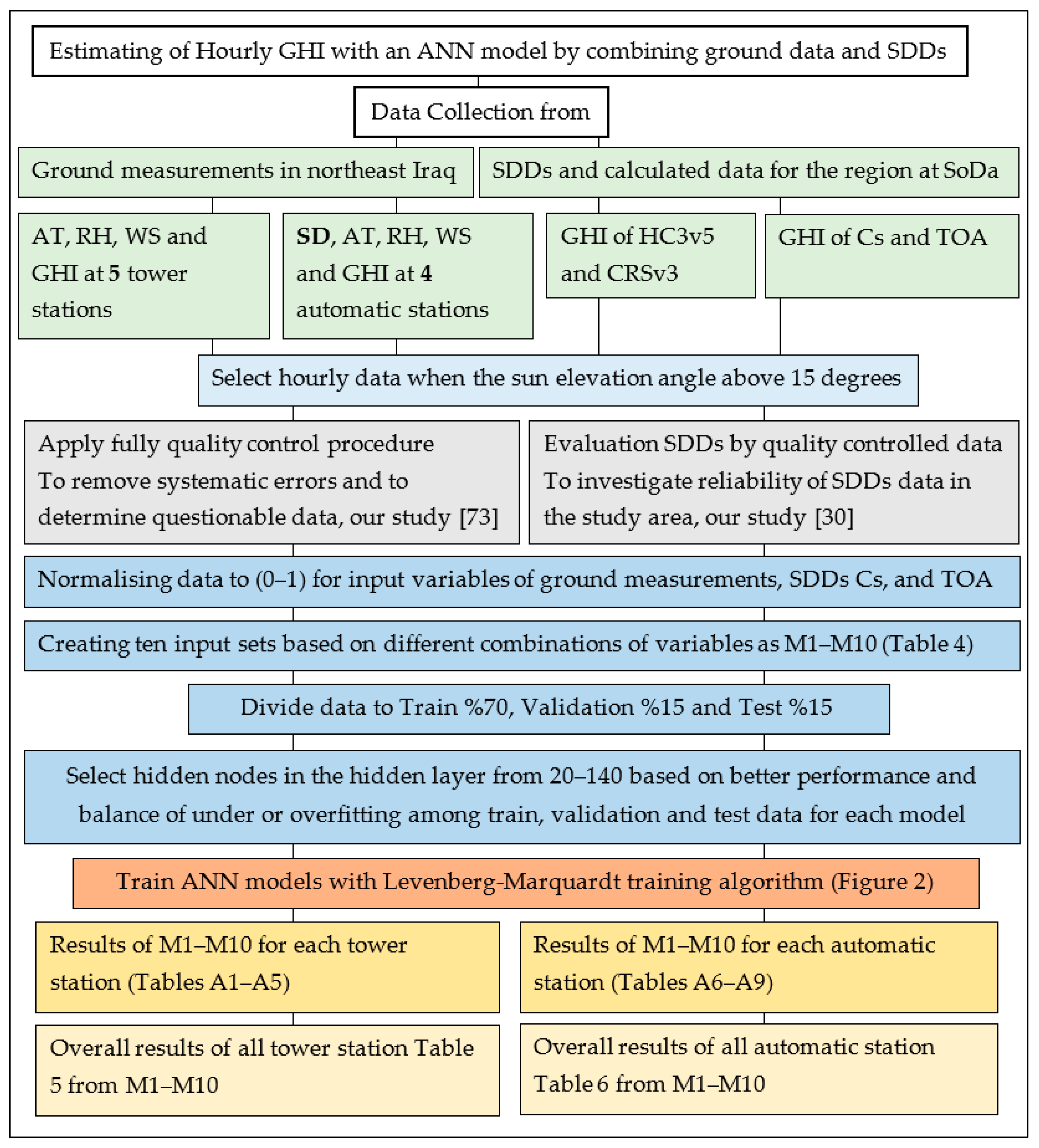
This paper aimed to use a new input of SDDs together with Cs, TOA and observed climate variables SD, AT, RH and WS as new input combinations in ten ANN models to estimate GHI at the hourly time scale with a Levenberg–Marquardt training algorithm. The inputs were arranged into ten different sets, as models M1–M10, to demonstrate the role of new inputs. The data at four automatic stations of all the above variables and five tower stations without SD in northeast Iraq were used.

The test results demonstrated a good improvement from M1 to M10 based on adding the new inputs such as TOA with observed variables (M3), Cs with observed variables (M2), SDDs with all observed climate variables (M4–M5), other combinations (M6–M8) and all together (M9–M10) with low percent fluctuation between both station types. The best results are r = 0.983, RMSE = 9.5% and bias = 0.0% in M9 and r = 0.976, RMSE = 11.2% and bias = 0.0% in M10 and the worst results are r = 0.755, RMSE = 33.7% and bias = 0.3% in M1 and r = 0.601, RMSE = 41% and bias = 0.7% in M1 at automatic and tower stations, respectively.

This study demonstrated the role of new input combinations for estimating hourly GHI with high accuracy. While the models have been trained with a few years of data, it would be better to train them with more years of data with such algorithms.

Further research is required for using new inputs with other machine learning approaches and empirical models.