Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting
Abstract
1. Introduction
2. Literature Review
- (i)
- We train LSTM and GRU deep learning models with single and multiple time scale sequences. This will allow capturing the dynamic features in longer sequences to accurately forecast aggregate electric load while targeting predictions that are robust against time variations.
- (ii)
- We compare the LSTM and GRU models with ANN, boosting and bagging decision trees ensemble models in both single and multiple time scale sequences. The best performing model is selected for our benchmark.
3. Background
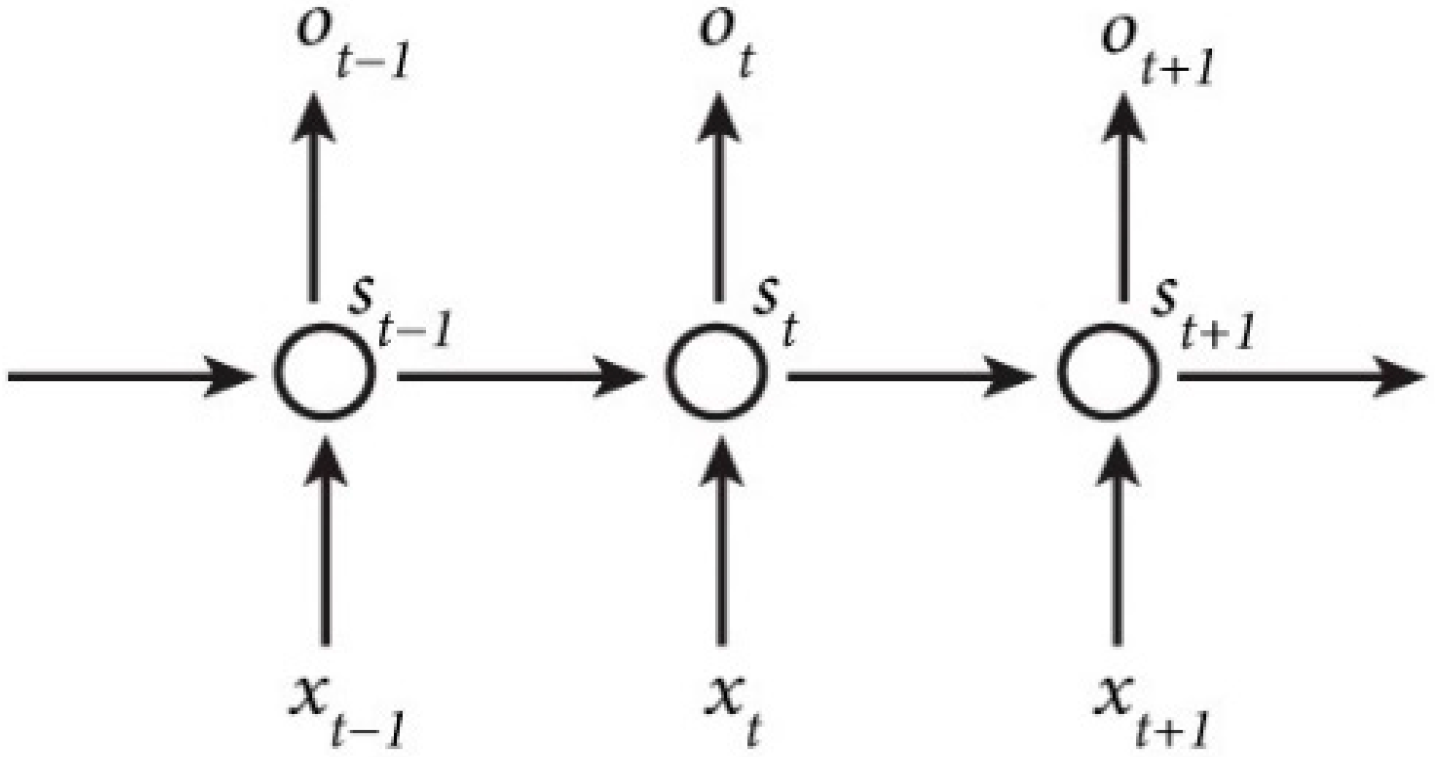
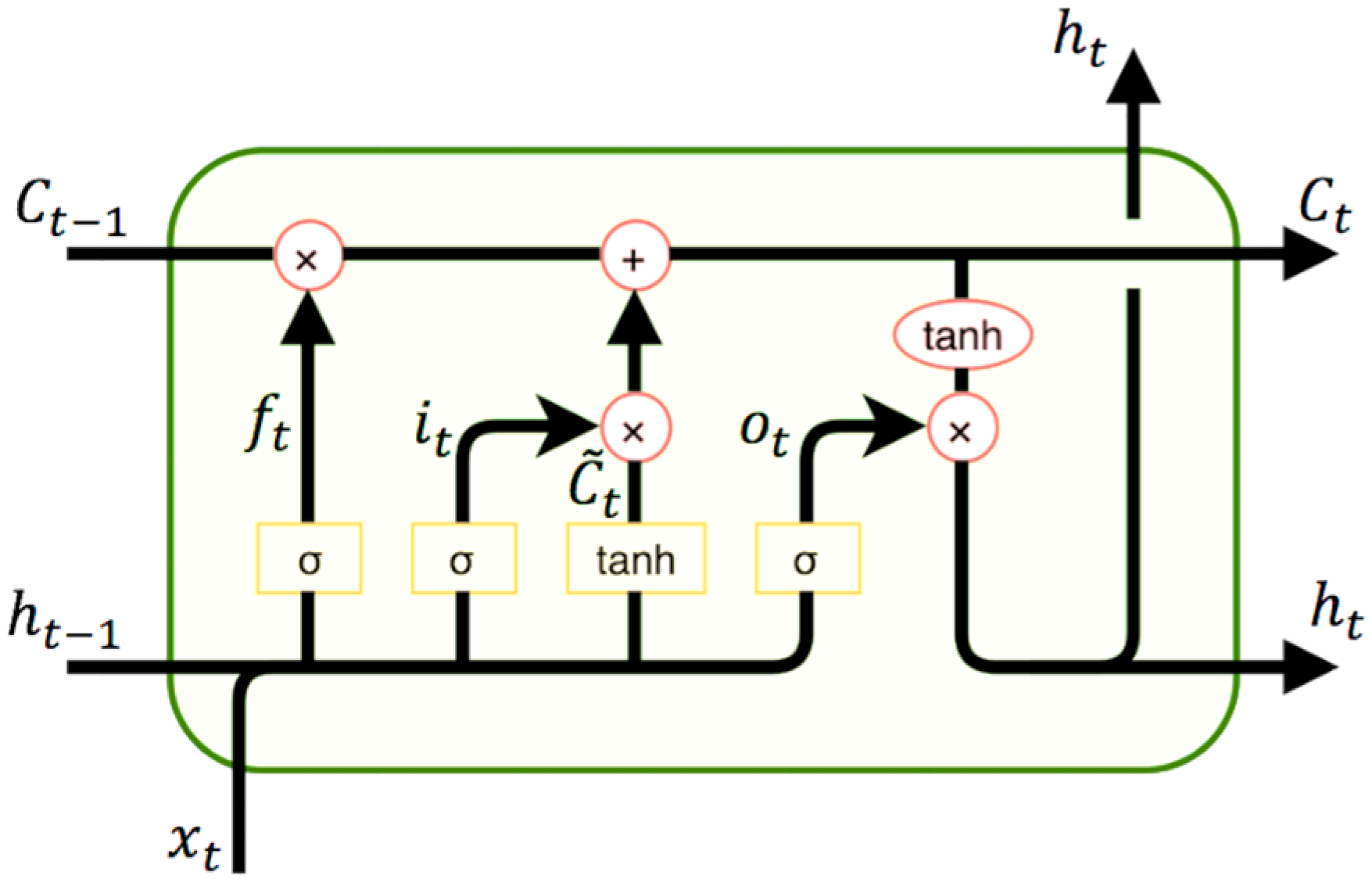
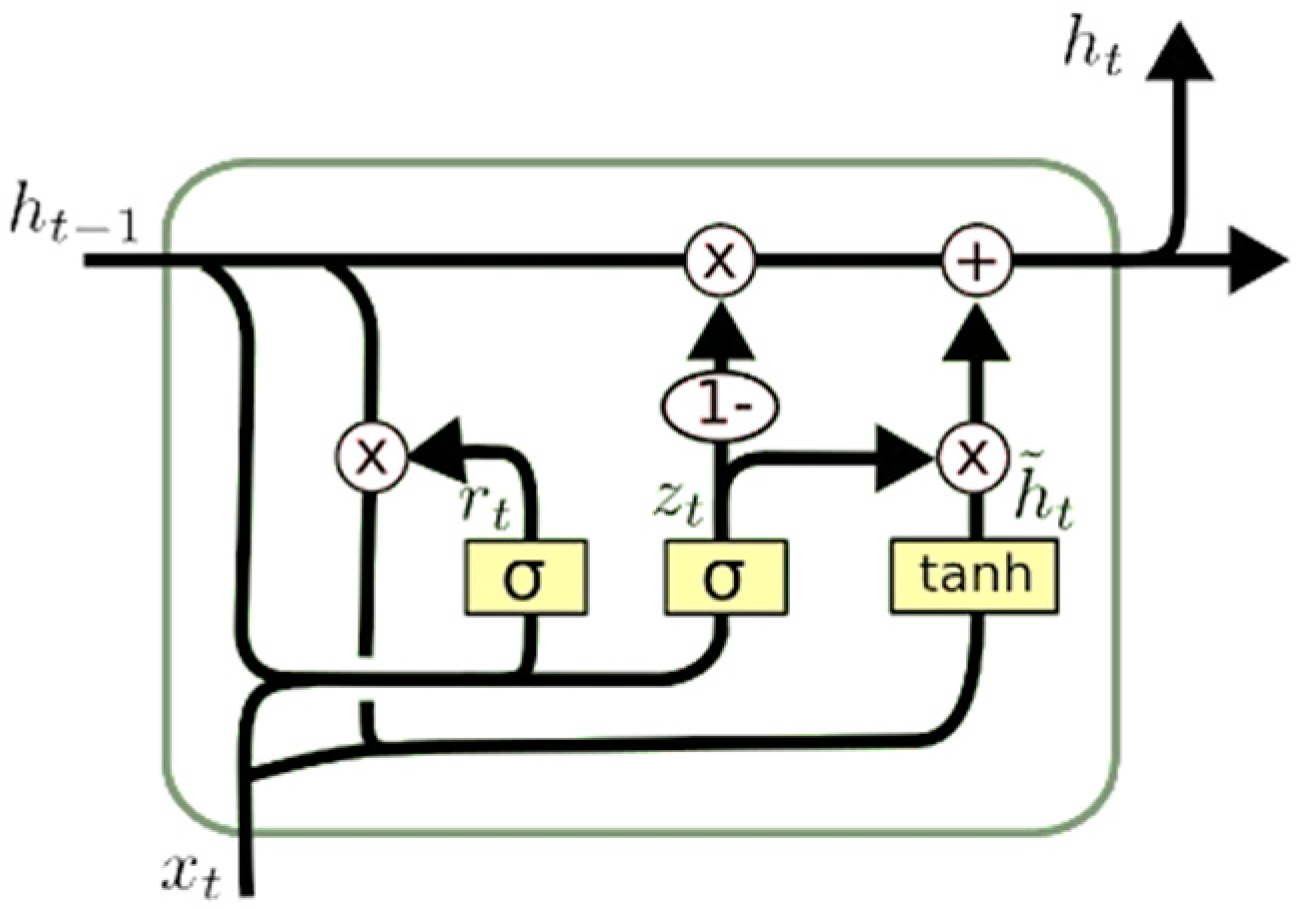
3.1. From RNN to LSTMs and GRUs
3.2. Ensemble Approaches
3.3. Performance Metrics for Evaluation
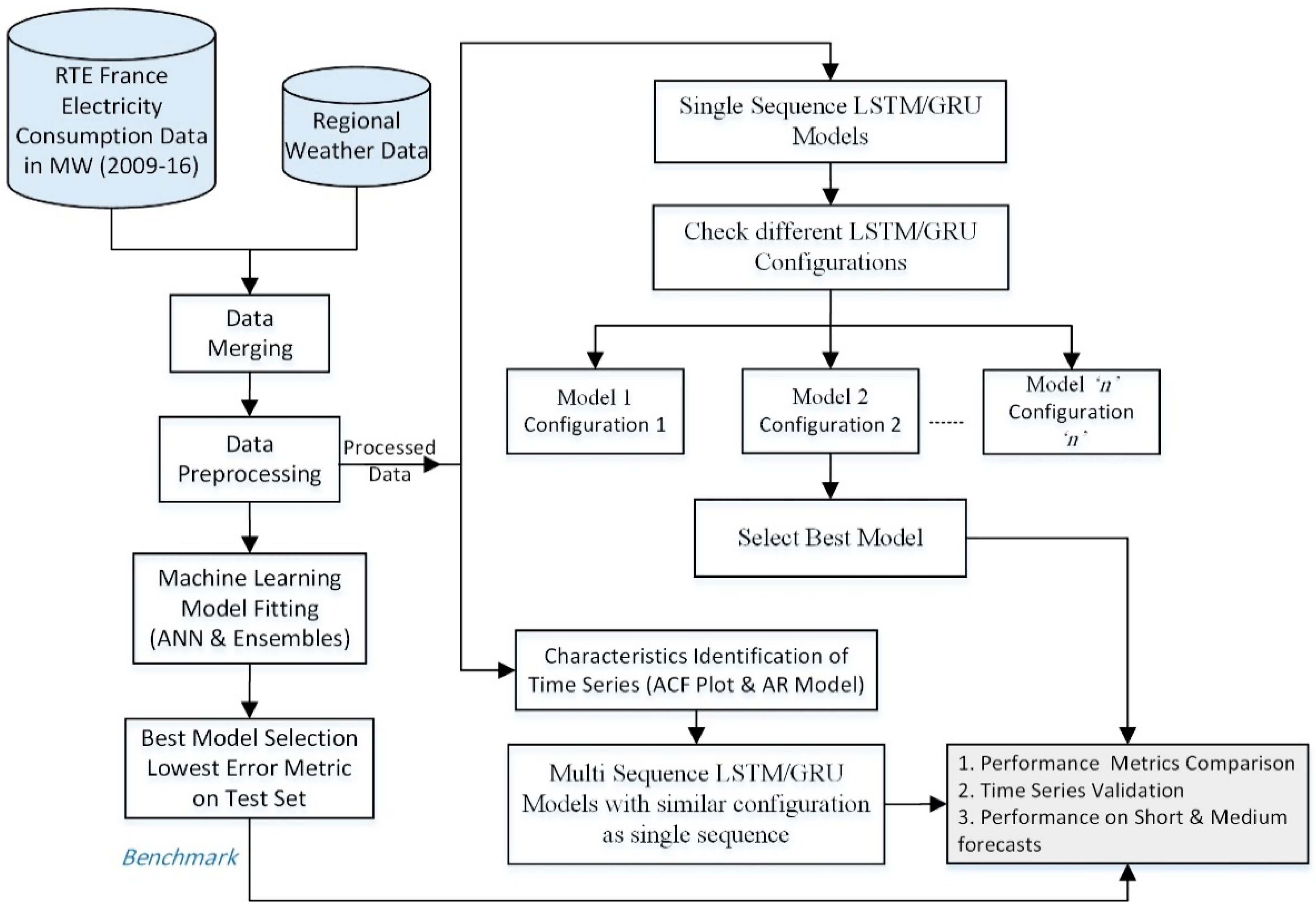
4. Forecasting Methodology
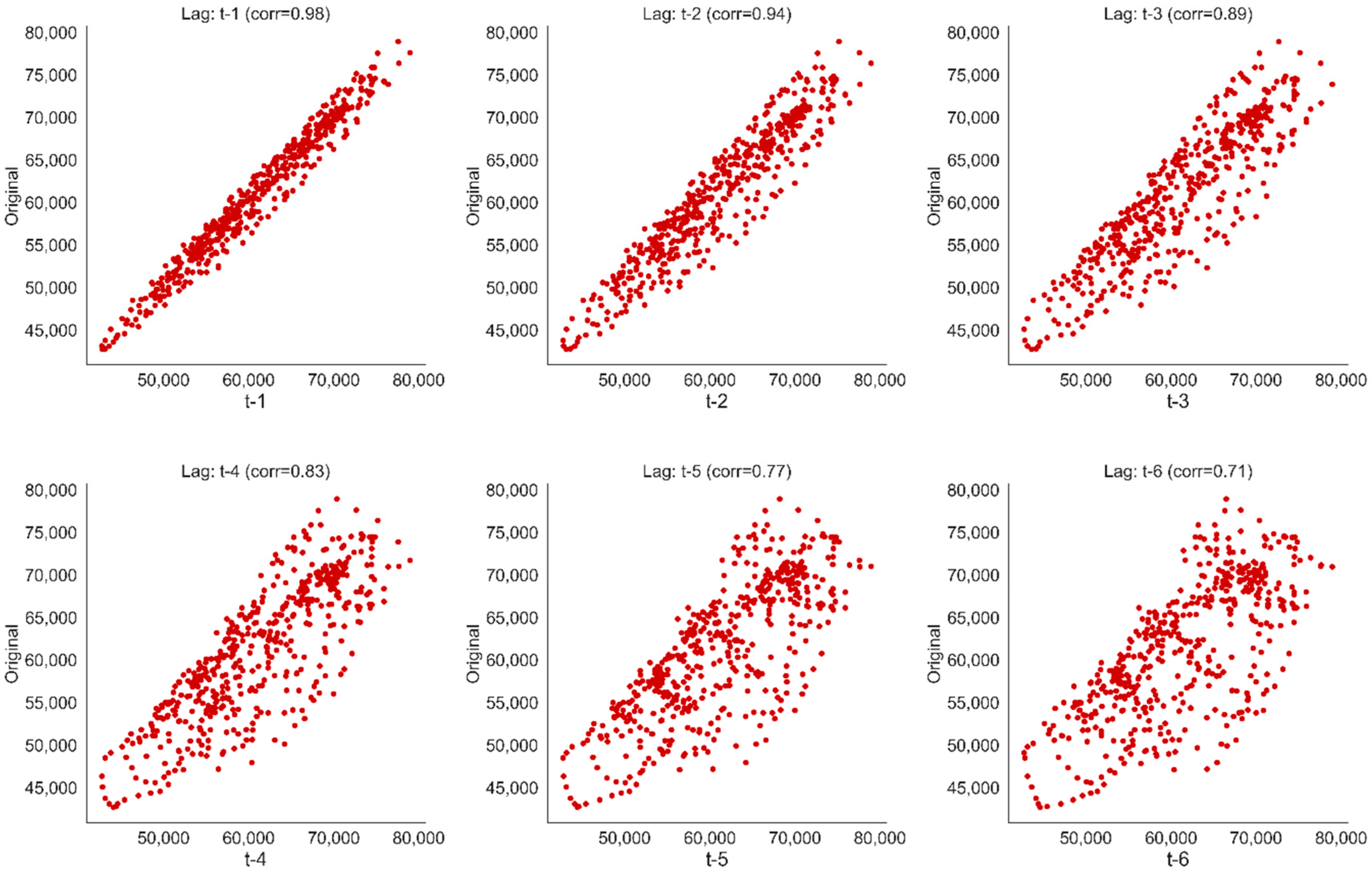
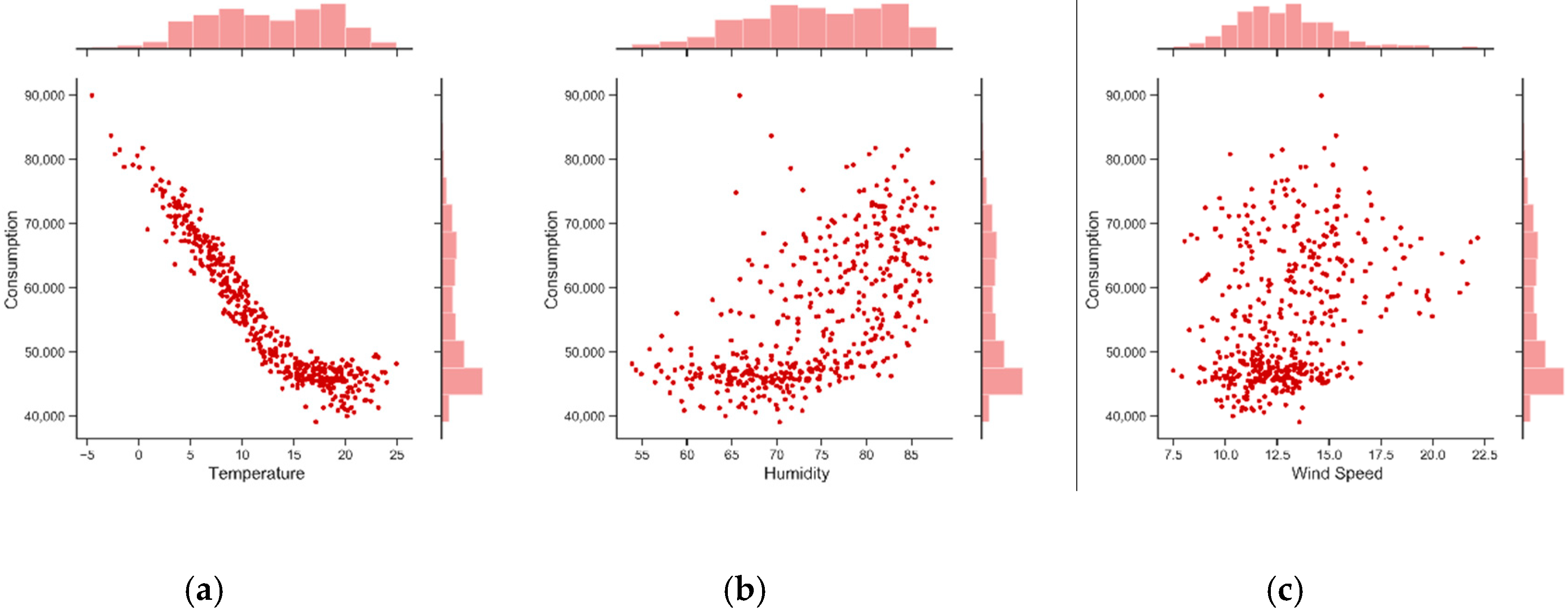
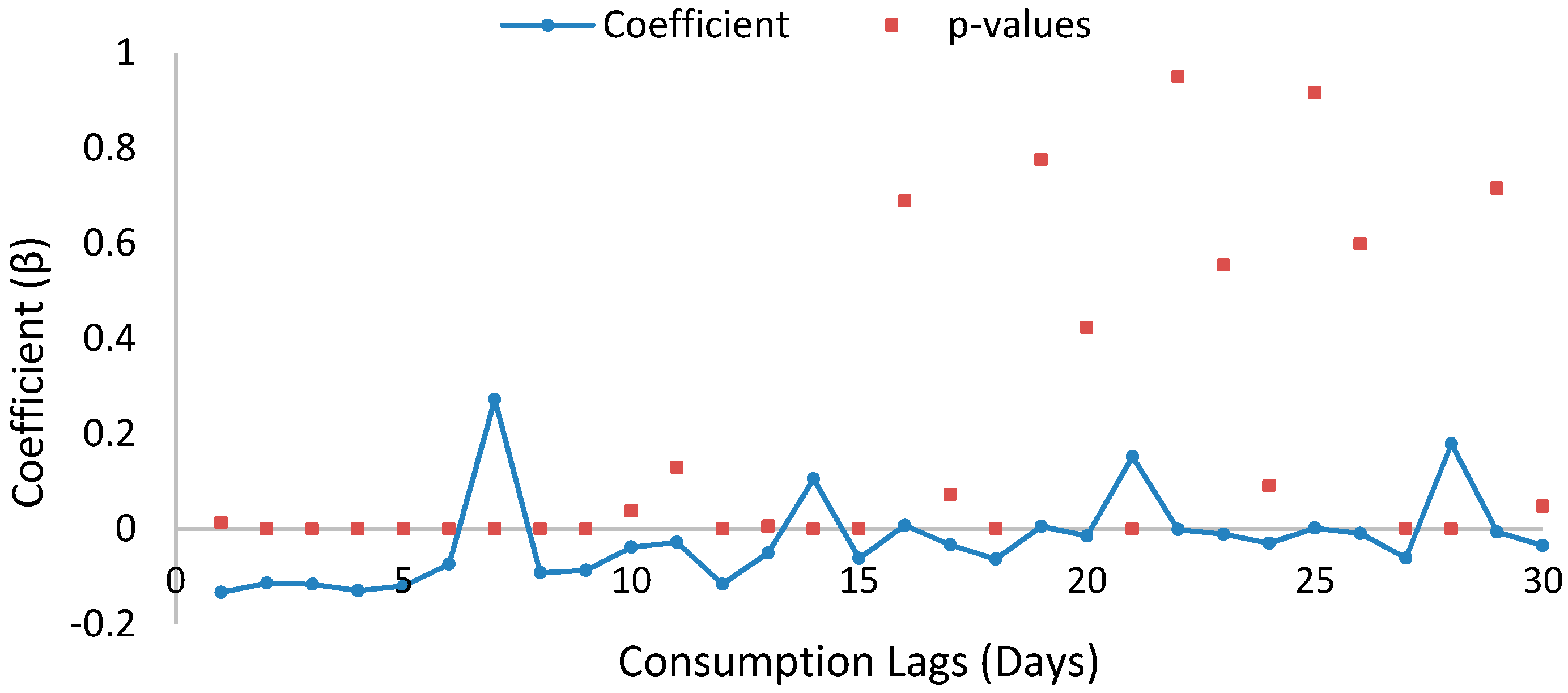
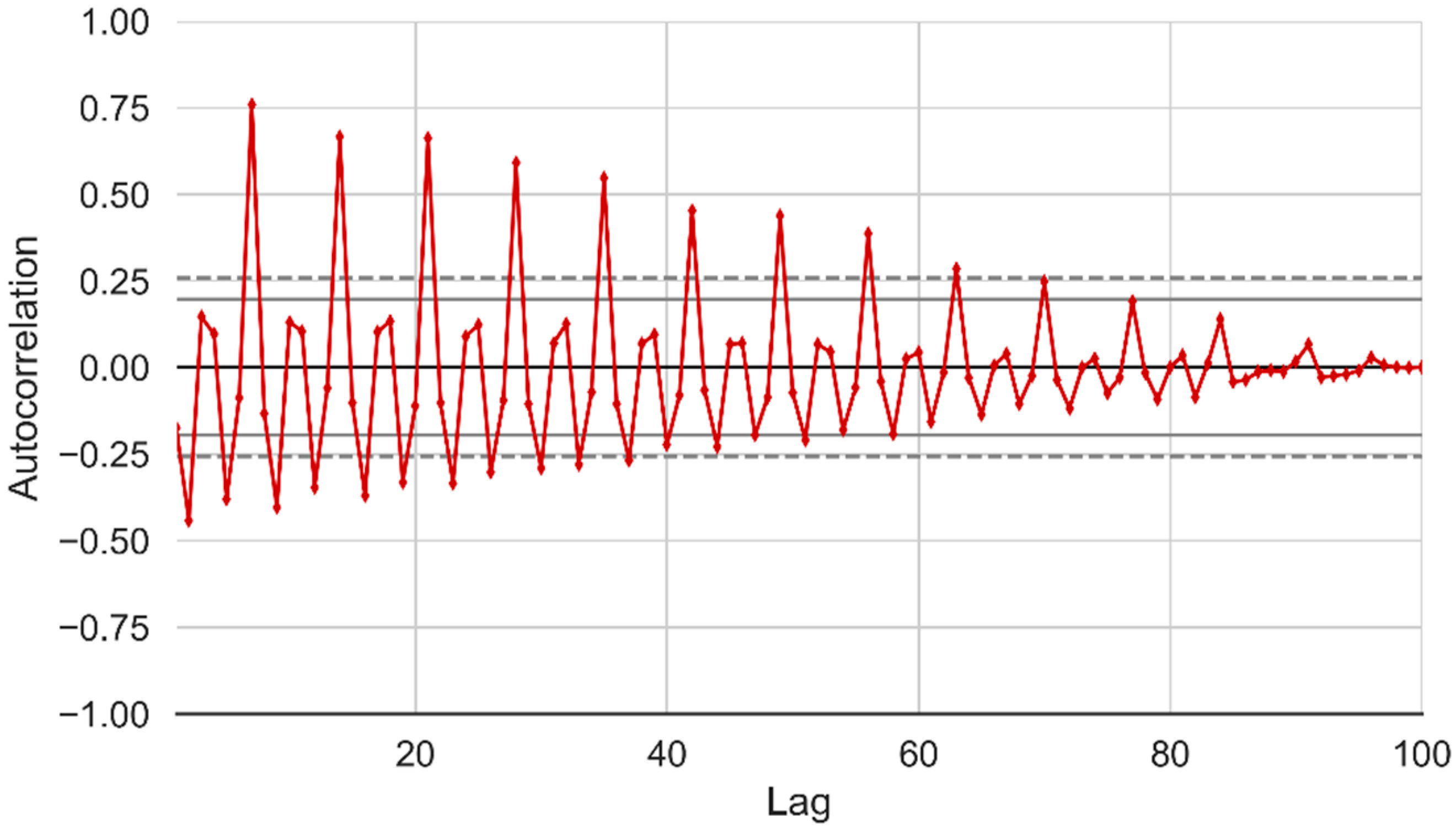
4.1. Exploratory Data Analysis
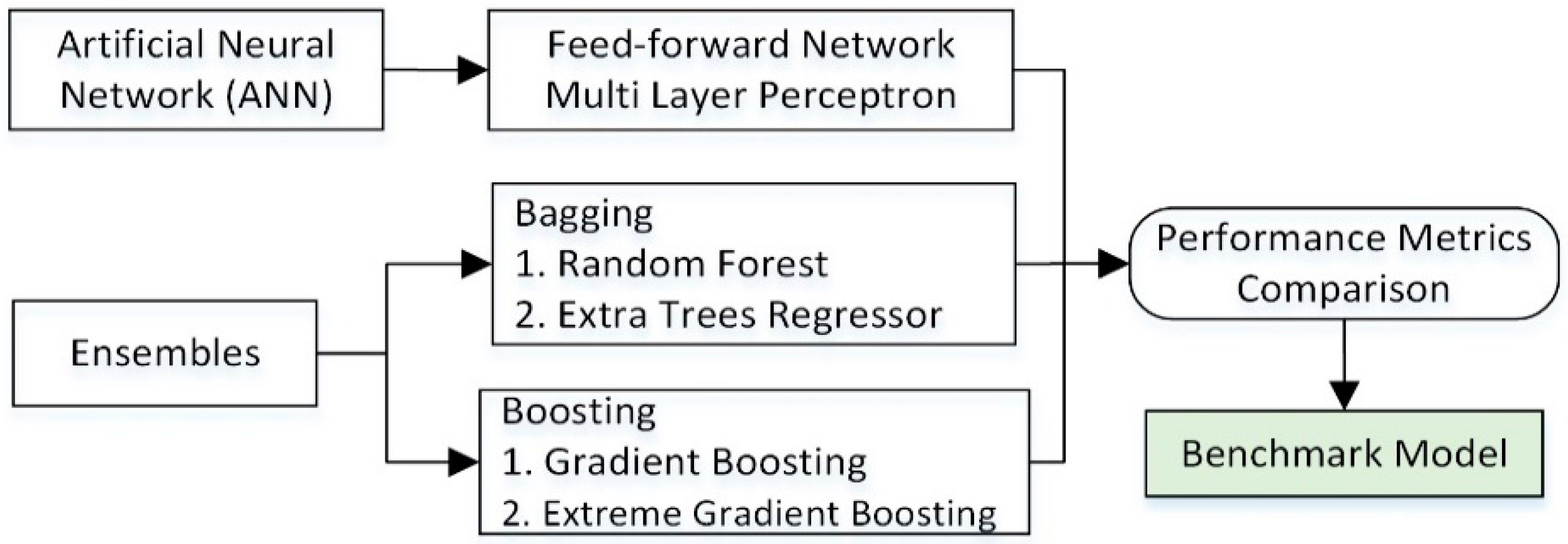
4.2. Selecting Machine Learning Benchmark Model
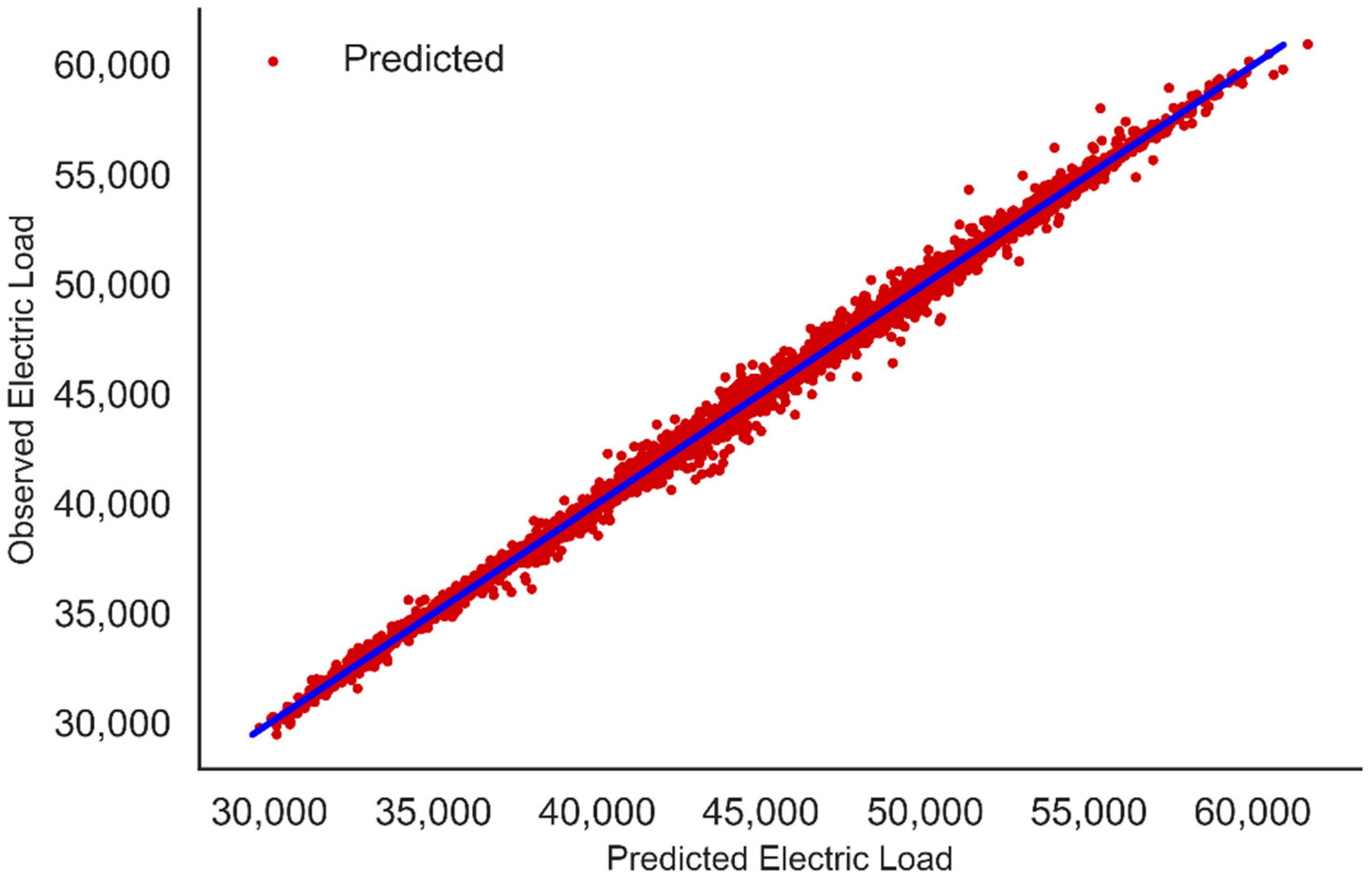
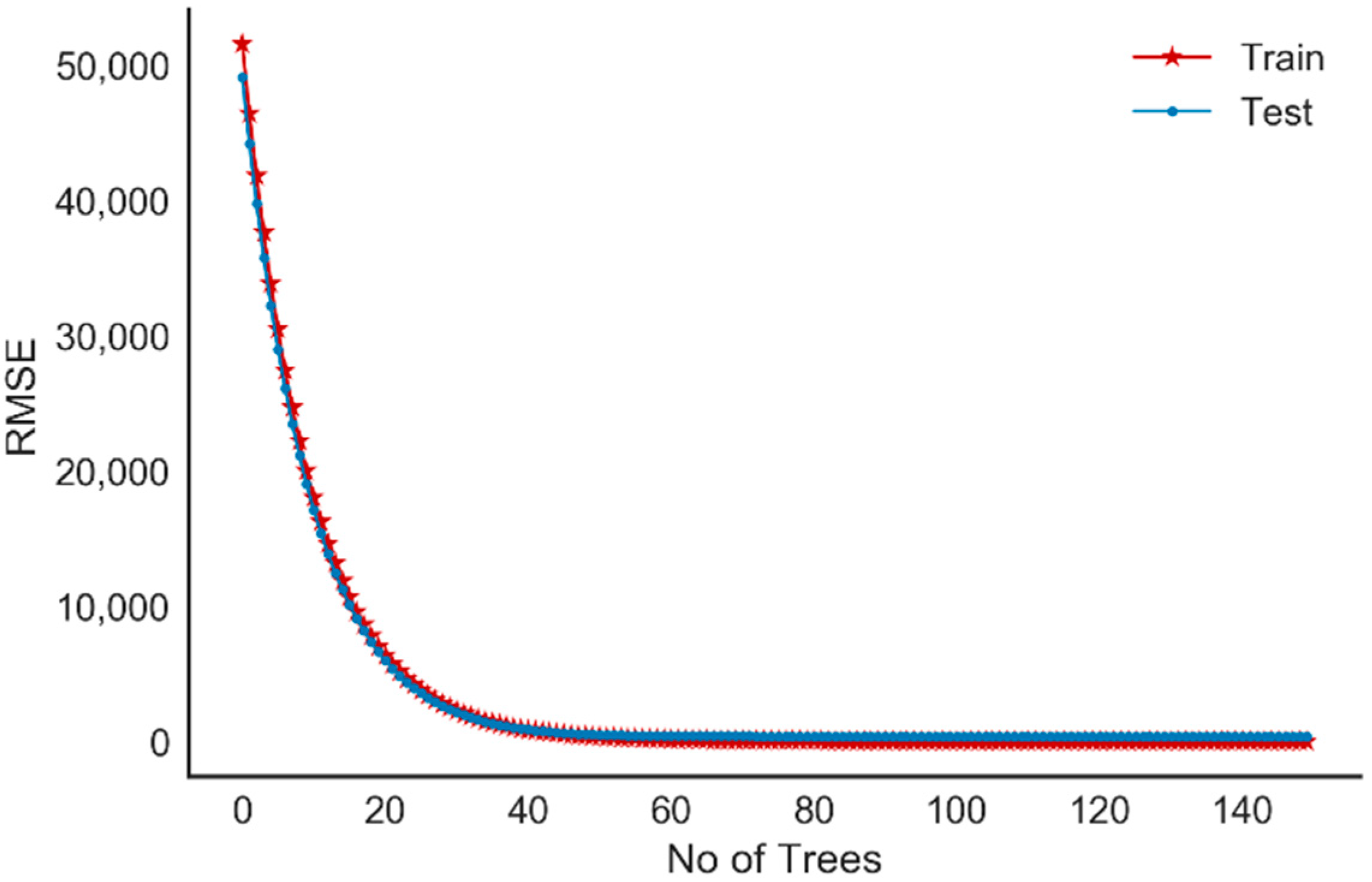
Checking Overfitting for XGBoost Model
4.3. LSTM-RNN Model Training
5. Experimental Results
5.1. Models with Single-Sequence Input
5.2. Models with Multi-Sequence Input
6. Models Validation
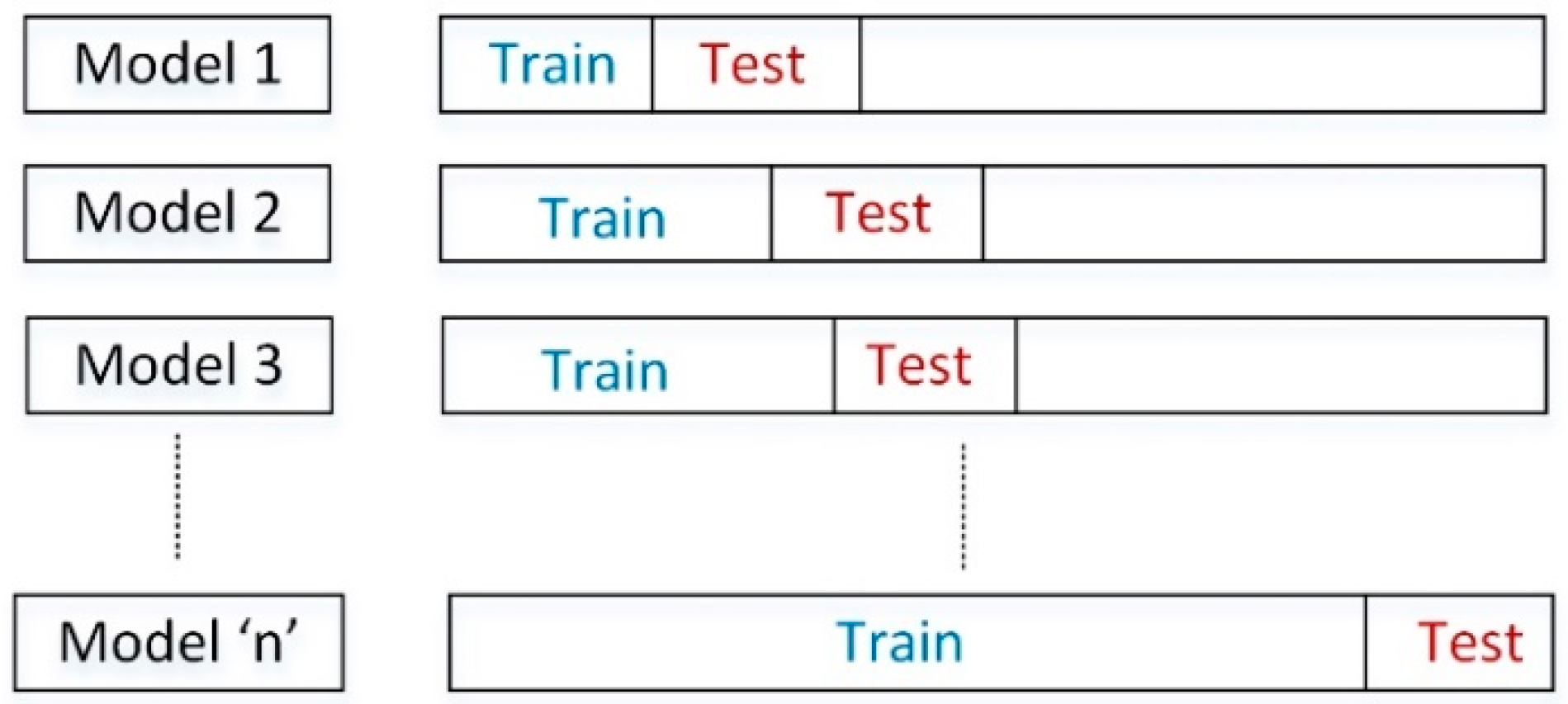
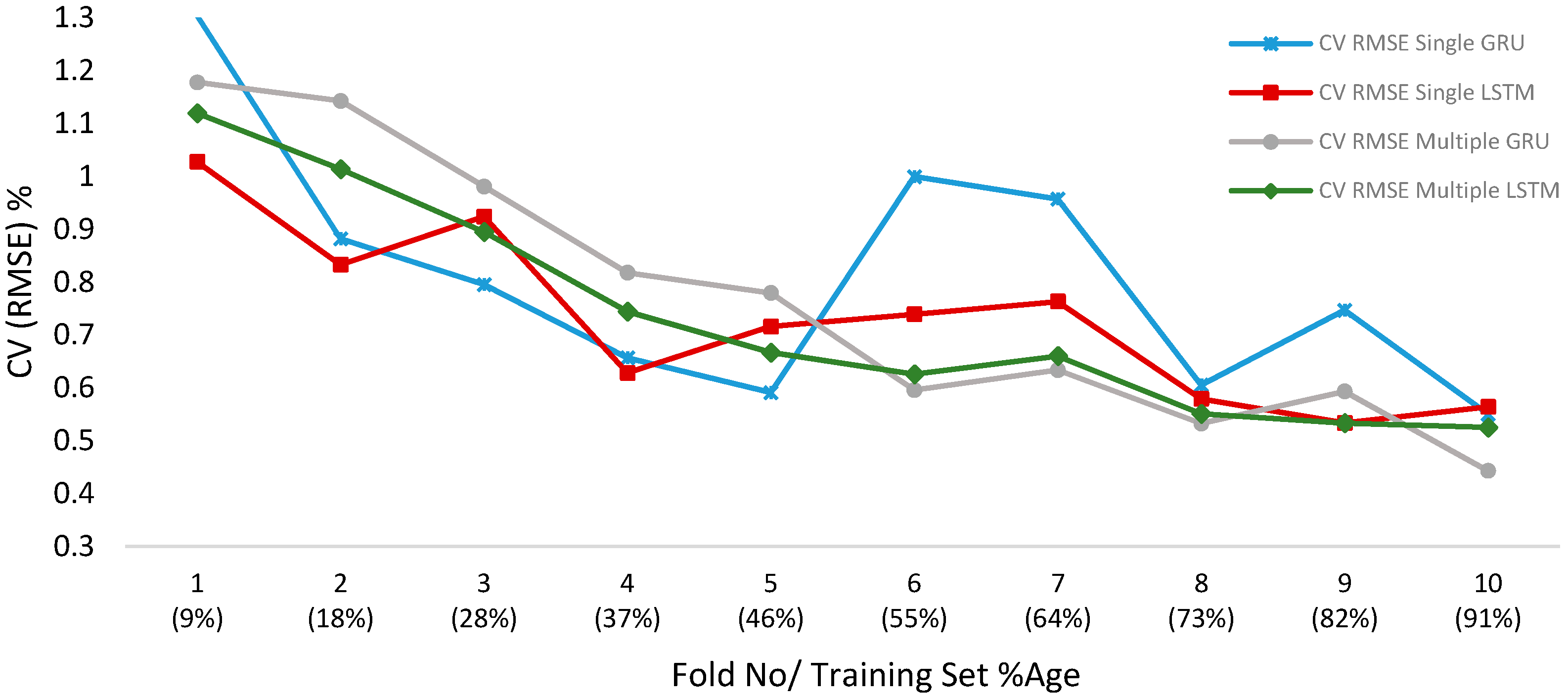
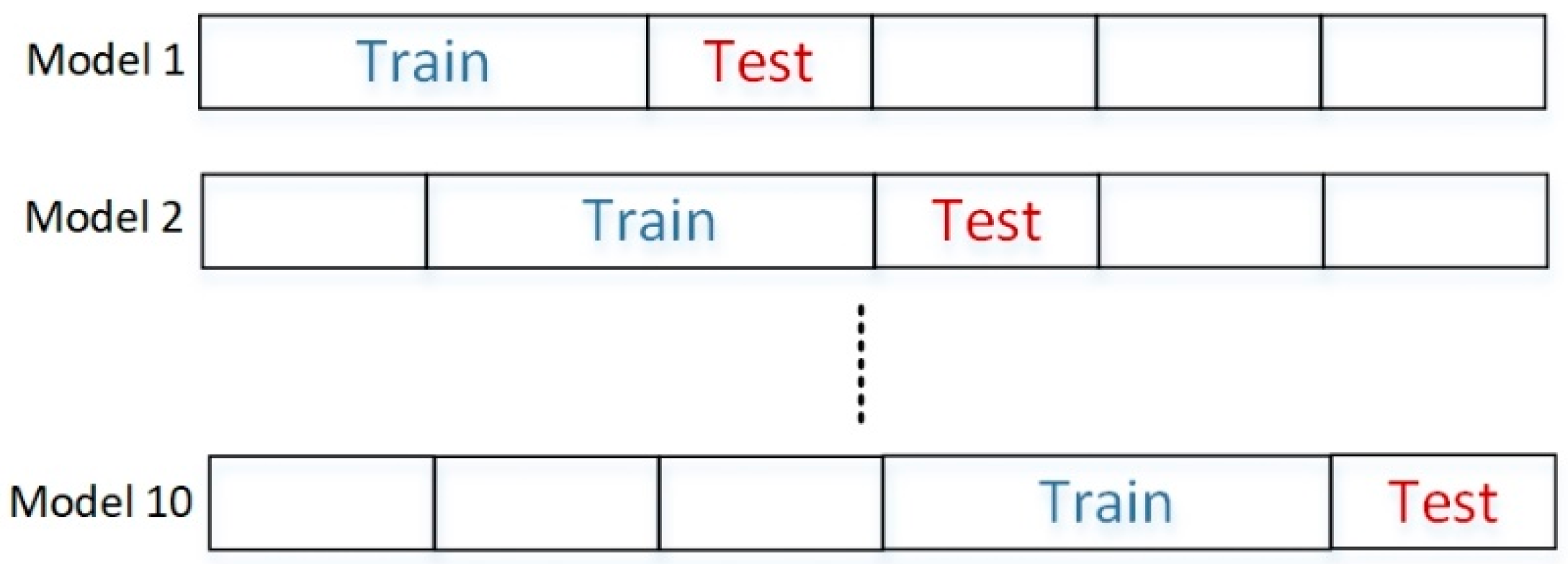
6.1. Models Validation Using Time Series Split
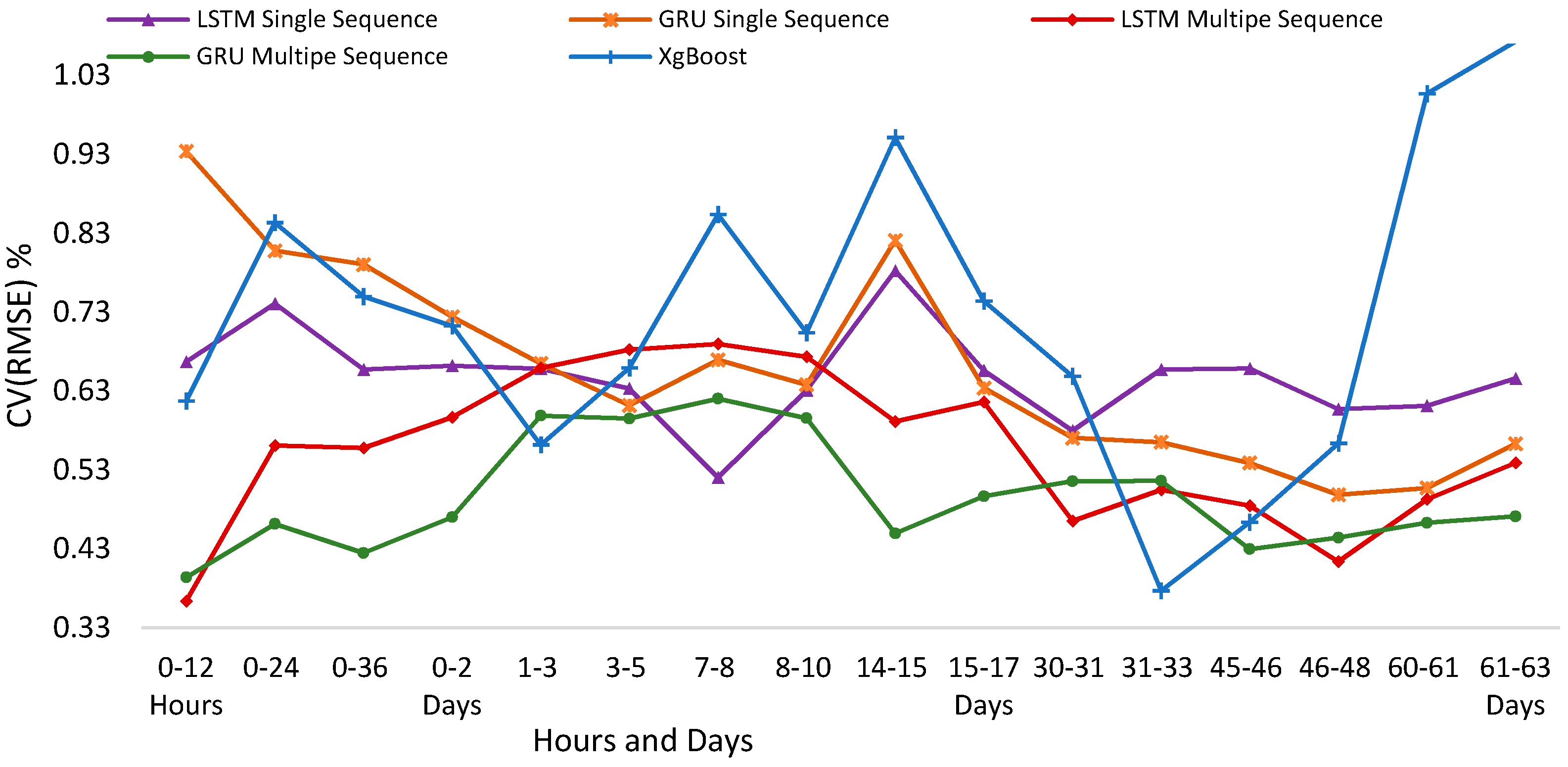
6.2. Validation on Short and Medium Term Forecasting Horizons
6.3. Validation Using Sliding Window Approach: t-Test for the Difference in Means
6.4. Comparison with other Studies
6.5. Threat to Validity
7. Conclusions
Author Contributions
Funding
Conflicts of Interest
Nomenclature
| ACF | autocorrelation function |
| ANN | artificial neural network |
| AR | Autoregressive |
| ARIMA | autoregressive integrated moving average |
| CV | coefficient of variation |
| DNN | deep neural networks |
| GRU | gated recurrent unit |
| LSTM | Long short term memory |
| MAE | mean absolute error |
| MAPE | Mean absolute percentage error |
| MLP | multi-layer perceptron |
| RNN | Recurrent neural networks |
| RMSE | root mean squared error |
| STLF | short-term load forecasting |
| SVM | support vector machines |
References
- Stoft, S. Power system economics. J. Energy Lit. 2002, 8, 94–99. [Google Scholar]
- Zhang, G.P. Time series forecasting using a hybrid ARIMA and neural network model. Neurocomputing 2003, 50, 159–175. [Google Scholar] [CrossRef]
- Box, G.E.; Jenkins, G.M.; Reinsel, G.C. Time Series Analysis: Forecasting and Control; John Wiley & Sons: Hoboken, NJ, USA, 2011; Volume 734. [Google Scholar]
- Hernandez, L.; Baladron, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J.; Massana, J. A survey on electric power demand forecasting: Future trends in smart grids, microgrids and smart buildings. IEEE Commun. Surv. Tutor. 2014, 16, 1460–1495. [Google Scholar] [CrossRef]
- Graves, A.; Jaitly, N. Towards end-to-end speech recognition with recurrent neural networks. In Proceedings of the International Conference on Machine Learning, Beijing, China, 21–26 June 2014; pp. 1764–1772. [Google Scholar]
- Mao, J.; Xu, W.; Yang, Y.; Wang, J.; Huang, Z.; Yuille, A. Deep captioning with multimodal recurrent neural networks (m-rnn). arXiv, 2014; arXiv:1412.6632. [Google Scholar]
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the Neural Information Processing Systems 2014, Montréal, QC, Canada, 8–13 December 2014; pp. 3104–3112. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. LSTM can solve hard long time lag problems. In Proceedings of the Neural Information Processing Systems 1997, Denver, CO, USA, 5 May 1997; pp. 473–479. [Google Scholar]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv, 2014; arXiv:1406.1078. [Google Scholar]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M. Optimal deep learning LSTM model for electric load forecasting using feature selection and genetic algorithm: Comparison with machine learning approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Wang, Z.; Srinivasan, R.S. A review of artificial intelligence based building energy use prediction: Contrasting the capabilities of single and ensemble prediction models. Renew. Sustain. Energy Rev. 2017, 75, 796–808. [Google Scholar] [CrossRef]
- Liu, N.; Tang, Q.; Zhang, J.; Fan, W.; Liu, J. A hybrid forecasting model with parameter optimization for short-term load forecasting of micro-grids. Appl. Energy 2014, 129, 336–345. [Google Scholar] [CrossRef]
- Ryu, S.; Noh, J.; Kim, H. Deep neural network based demand side short term load forecasting. Energies 2016, 10, 3. [Google Scholar] [CrossRef]
- Hagan, M.T.; Behr, S.M. The time series approach to short term load forecasting. IEEE Trans. Power Syst. 1987, 2, 785–791. [Google Scholar] [CrossRef]
- Taylor, J.W. Short-term electricity demand forecasting using double seasonal exponential smoothing. J. Oper. Res. Soc. 2003, 54, 799–805. [Google Scholar] [CrossRef]
- Taylor, J.W.; De Menezes, L.M.; McSharry, P.E. A comparison of univariate methods for forecasting electricity demand up to a day ahead. Int. J. Forecast. 2006, 22, 1–16. [Google Scholar] [CrossRef]
- Park, D.C.; El-Sharkawi, M.A.; Marks, R.J.; Atlas, L.E.; Damborg, M.J. Electric load forecasting using an artificial neural network. IEEE Trans. Power Syst. 1991, 6, 442–449. [Google Scholar] [CrossRef]
- Hernandez, L.; Baladrón, C.; Aguiar, J.M.; Carro, B.; Sanchez-Esguevillas, A.J.; Lloret, J. Short-term load forecasting for microgrids based on artificial neural networks. Energies 2013, 6, 1385–1408. [Google Scholar] [CrossRef]
- Hippert, H.S.; Pedreira, C.E.; Souza, R.C. Neural networks for short-term load forecasting: A review and evaluation. IEEE Trans. Power Syst. 2001, 16, 44–55. [Google Scholar] [CrossRef]
- Yukseltan, E.; Yucekaya, A.; Bilge, A.H. Forecasting electricity demand for Turkey: Modeling periodic variations and demand segregation. Appl. Energy 2017, 193, 287–296. [Google Scholar] [CrossRef]
- Zhang, F.; Deb, C.; Lee, S.E.; Yang, J.; Shah, K.W. Time series forecasting for building energy consumption using weighted Support Vector Regression with differential evolution optimization technique. Energy Build. 2016, 126, 94–103. [Google Scholar] [CrossRef]
- Papadopoulos, S.; Karakatsanis, I. Short-term electricity load forecasting using time series and ensemble learning methods. In Proceedings of the IEEE Power and Energy Conference at Illinois (PECI), Champaign, IL, USA, 20–21 February 2015; pp. 1–6. [Google Scholar]
- Dudek, G. Short-term load forecasting using random forests. In Intelligent Systems’ 2014; Springer: Cham, Switzerland, 2015; pp. 821–828. [Google Scholar]
- Wang, W.; Shi, Y.; Lyu, G.; Deng, W. Electricity Consumption Prediction Using XGBoost Based on Discrete Wavelet Transform. DEStech Trans. Comput. Sci. Eng. 2017. [Google Scholar] [CrossRef]
- Hossen, T.; Plathottam, S.J.; Angamuthu, R.K.; Ranganathan, P.; Salehfar, H. Short-term load forecasting using deep neural networks (DNN). In Proceedings of the 2017 North American IEEE Power Symposium (NAPS), Morgantown, WV, USA, 17–19 September 2017; pp. 1–6. [Google Scholar]
- He, W. Load forecasting via deep neural networks. Procedia Comput. Sci. 2017, 122, 308–314. [Google Scholar] [CrossRef]
- Zheng, H.; Yuan, J.; Chen, L. Short-Term Load Forecasting Using EMD-LSTM Neural Networks with a Xgboost Algorithm for Feature Importance Evaluation. Energies 2017, 10, 1168. [Google Scholar] [CrossRef]
- Colah.github.io. Understanding LSTM Networks—Colah’s Blog. Available online: http://colah.github.io/posts/2015-08-Understanding-LSTMs (accessed on 24 August 2018).
- Patterson, J.; Gibson, A. Deep Learning: A Practitioner’s Approach; O’Reilly Media, Inc.: Sevvan, CA, USA, 2017. [Google Scholar]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. arXiv, 2014; arXiv:1412.3555. [Google Scholar]
- Wei, Y.; Zhang, X.; Shi, Y.; Xia, L.; Pan, S.; Wu, J.; Zhao, X. A review of data-driven approaches for prediction and classification of building energy consumption. Renew. Sustain. Energy Rev. 2018, 82, 1027–1047. [Google Scholar] [CrossRef]
- Yildiz, B.; Bilbao, J.I.; Sproul, A.B. A review and analysis of regression and machine learning models on commercial building electricity load forecasting. Renew. Sustain. Energy Rev. 2017, 73, 1104–1122. [Google Scholar] [CrossRef]
- RTE France. Bilans Électriques Nationaux. Available online: http://www.rte-france.com/fr/article/bilans-electriques-nationaux (accessed on 7 February 2018).
- sklearn.model_selection.TimeSeriesSplit—scikit-learn 0.20.1 Documentation. 2018. Available online: https://scikit-learn.org/stable/modules/generated/sklearn.model_selection.TimeSeriesSplit.html (accessed on 20 March 2018).
- Massana, J.; Pous, C.; Burgas, L.; Melendez, J.; Colomer, J. Short-term load forecasting in a non-residential building contrasting models and attributes. Energy Build. 2015, 92, 322–330. [Google Scholar] [CrossRef]
- Wang, Z.; Wang, Y.; Srinivasan, R.S. A novel ensemble learning approach to support building energy use prediction. Energy Build. 2018, 159, 109–122. [Google Scholar] [CrossRef]




| Model | RMSE | CV (RMSE) | MAE |
|---|---|---|---|
| ANN | 725.89 | 1.311 | 559.63 |
| Random Forest | 527.25 | 0.952 | 368.91 |
| Extra Trees Regressor | 492.13 | 0.889 | 346.44 |
| Gradient Boosting | 455.84 | 0.823 | 320.72 |
| Extreme Gradient Boosting | 440.16 | 0.795 | 311.43 |
| No | Hyperparameter | Option |
|---|---|---|
| 1 | Time Lags | 10, 20, 30, 40 |
| 2 | No of Hidden Layers | 1, 2, 3, 4 |
| 3 | No of Neurons in Hidden layer | 30, 40, 50, 60 |
| 4 | Batch Size | 50 to 200 |
| 5 | Epochs | 50 to 150 |
| 6 | Activation Function | Sigmoid, hyperbolic tangent (tanh) and rectified linear unit (ReLU) |
| 7 | Optimizers. | ADAM (adaptive moment estimation), SGD (Stochastic gradient descent), RMSProp (Root Mean Square Propagation) |
| Metrics | LSTM Model 30 Lags | GRU Model 30 Lags | XGBoost Model Metrics |
|---|---|---|---|
| RMSE | 346.34 | 339.22 | 440.16 |
| CV(RMSE) | 0.622 | 0.611 | 0.795 |
| MAE | 257.05 | 251.66 | 311.43 |
| No | Model Inputs | Errors LSTM | Errors GRU | ||||
|---|---|---|---|---|---|---|---|
| Input 1 | Input 2 | Input 3 | MAE | RMSE | MAE | RMSE | |
| 1 | Immediate 10 | 2 days, 10 lags | 3 days, 10 lags | 315.41 | 394.70 | 352.34 | 270.56 |
| 2 | Immediate 10 | 1 day, 10 lags | 1 week, 10 lags | 220.79 | 293.74 | 233.18 | 312.64 |
| 3 | Immediate 10 | 1 week, 10 lags | 2 week 10 lags | 293.02 | 388.35 | 234.62 | 326.48 |
| 4 | Immediate 10 | 1 week, 10 lags | 1 Month, 10 lags | 252.05 | 351.15 | 324.67 | 434.19 |
| 5 | Immediate 10 | 1 month,10 lags | 2 Month, 10 lags | 389.45 | 512.40 | 380.26 | 490.10 |
| 6 | Immediate 20 | 1 day, 20 lags | 1 week, 20 Lags | 251.16 | 327.48 | 202.15 | 266.57 |
| 7 | Immediate 20 | 1 day, 20 lags | 2 week, 20 Lags | 239.58 | 314.53 | 242.14 | 317.08 |
| 8 | Immediate 20 | 1 week, 20 lags | 2 week, 20 Lags | 291.51 | 386.30 | 251.84 | 353.36 |
| 9 | Immediate 20 | 1 week, 20 lags | 1 month,20 Lags | 332.86 | 417.32 | 234.87 | 334.80 |
| 10 | Immediate 20 | 1 month 20 lags | 2 Month, 20 lags | 323.88 | 428.79 | 473.01 | 585.77 |
| Metric/Model | Single Sequence | Multiple Sequence | |||
|---|---|---|---|---|---|
| LSTM | GRU | LSTM | GRU | ||
| MAE | Mean | 294.81 | 342.28 | 307.12 | 329.27 |
| Std. Deviation | 66.84 | 103.96 | 87.61 | 110.61 | |
| RMSE | Mean | 403.47 | 446.62 | 404.94 | 425 |
| Std. Deviation | 89.65 | 129.03 | 115.18 | 142.02 | |
| Model | Standard Deviation CV(RMSE) % | Variance | 95% Upper Bound for σ |
|---|---|---|---|
| Single-sequence LSTM | 0.126 | 0.016 | 0.186 |
| Multiple-sequence LSTM | 0.071 | 0.005 | 0.099 |
| Model | Mean CV (RMSE) (%) | Variance |
|---|---|---|
| Single Sequence LSTM | 0.64231 | 0.004023 |
| Multiple Sequence LSTM | 0.58994 | 0.001603 |
| Ref. | MAPE (%) | Horizon | Features | Approach |
|---|---|---|---|---|
| [20] | 1.34–3.59 | Annual Predictions | Harmonics of sinusoidal variations | Linear regression |
| [22] | 1.32–2.62 | Day ahead | Past loads, Std dev, calendar features (month, day, hour) | SARIMA, SARIMAX, random forests gradient boosting regression trees |
| [23] | 0.92–2.64 | Day ahead | Past loads | Random forest |
| [25] | 1.19–3.29 | 90 days | Weather and load data | Deep neural network |
| [35] | 0.06–4.68 | 90 days | Electrical load, weather, indoor and calendar data. | MLR, MLP, SVR |
| [36] | 2.97–4.62 | 2 weeks ahead | Meteorological, occupancy, calendar | Ensemble bagging trees |
| [Present work] | 0.48–0.55 | Day, weak, month, year | Multi-sequence past loads | LSTM |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting. Energies 2019, 12, 149. https://doi.org/10.3390/en12010149
Bouktif S, Fiaz A, Ouni A, Serhani MA. Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting. Energies. 2019; 12(1):149. https://doi.org/10.3390/en12010149
Chicago/Turabian StyleBouktif, Salah, Ali Fiaz, Ali Ouni, and Mohamed Adel Serhani. 2019. "Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting" Energies 12, no. 1: 149. https://doi.org/10.3390/en12010149
APA StyleBouktif, S., Fiaz, A., Ouni, A., & Serhani, M. A. (2019). Single and Multi-Sequence Deep Learning Models for Short and Medium Term Electric Load Forecasting. Energies, 12(1), 149. https://doi.org/10.3390/en12010149





