Implementation Strategy of Convolution Neural Networks on Field Programmable Gate Arrays for Appliance Classification Using the Voltage and Current (V-I) Trajectory
Abstract
1. Introduction
2. Background and Related Work
2.1. V-I Shapes and NILM
2.2. Convolution Neural Network Backgroud
2.3. FPGA Implementations of NILM and CNNs
3. Materials and Methods
3.1. Dataset
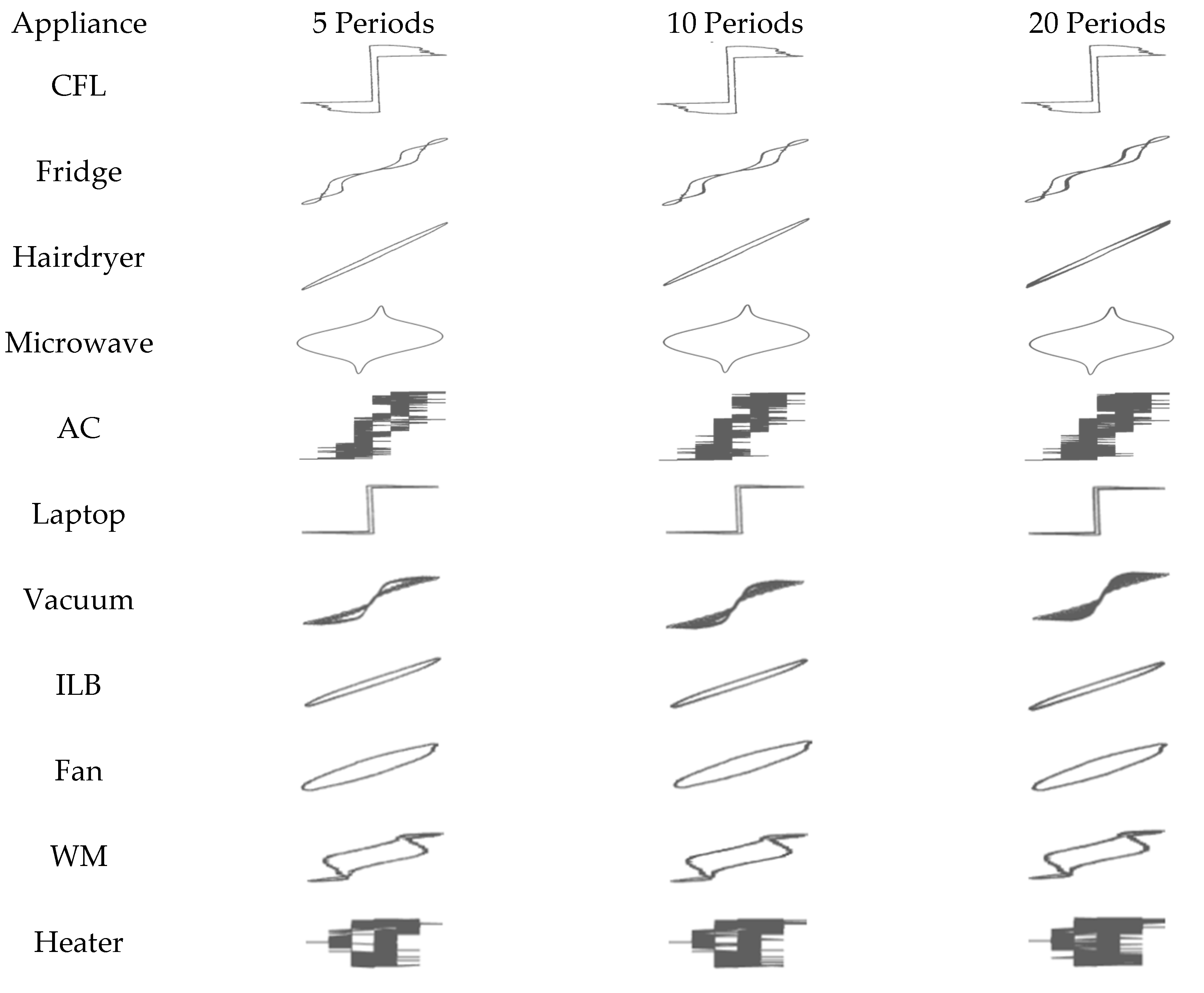
3.2. Data Pre-Processing
3.3. CNN for Appliance Classification
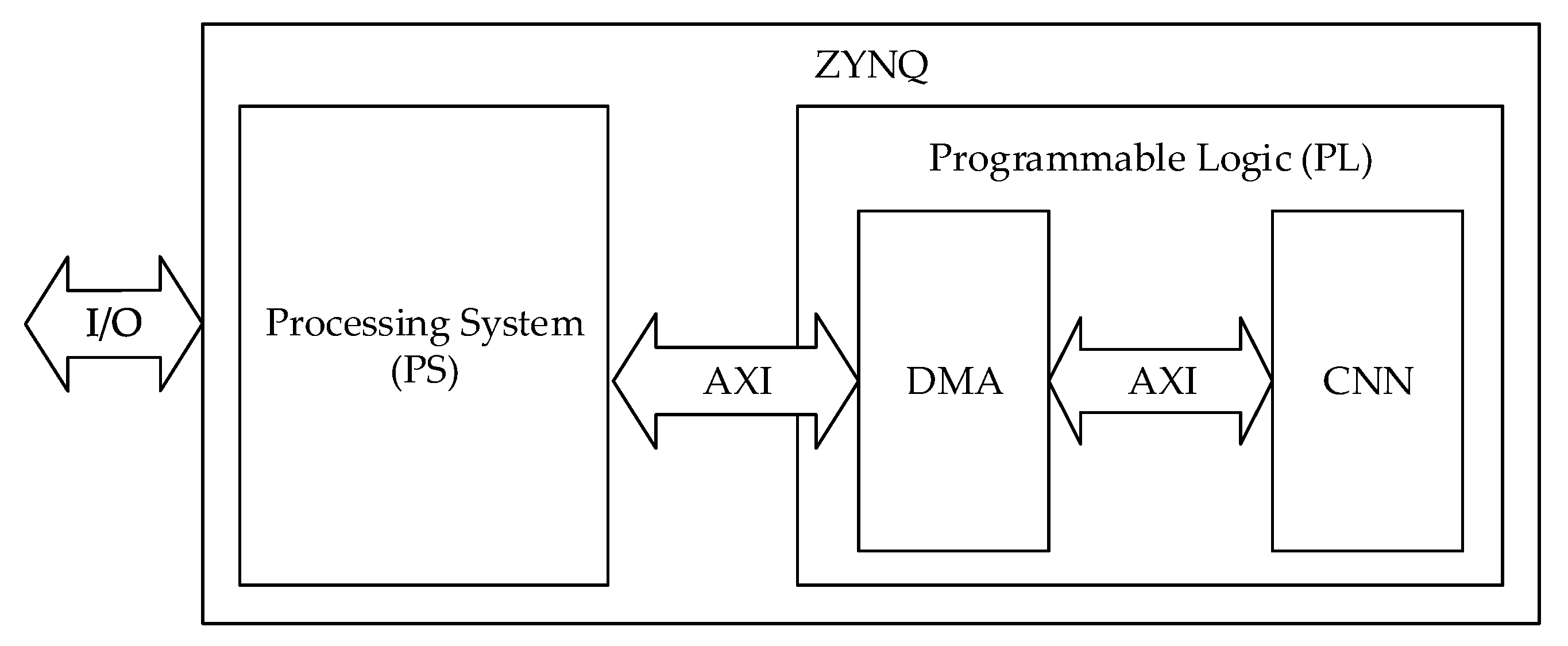
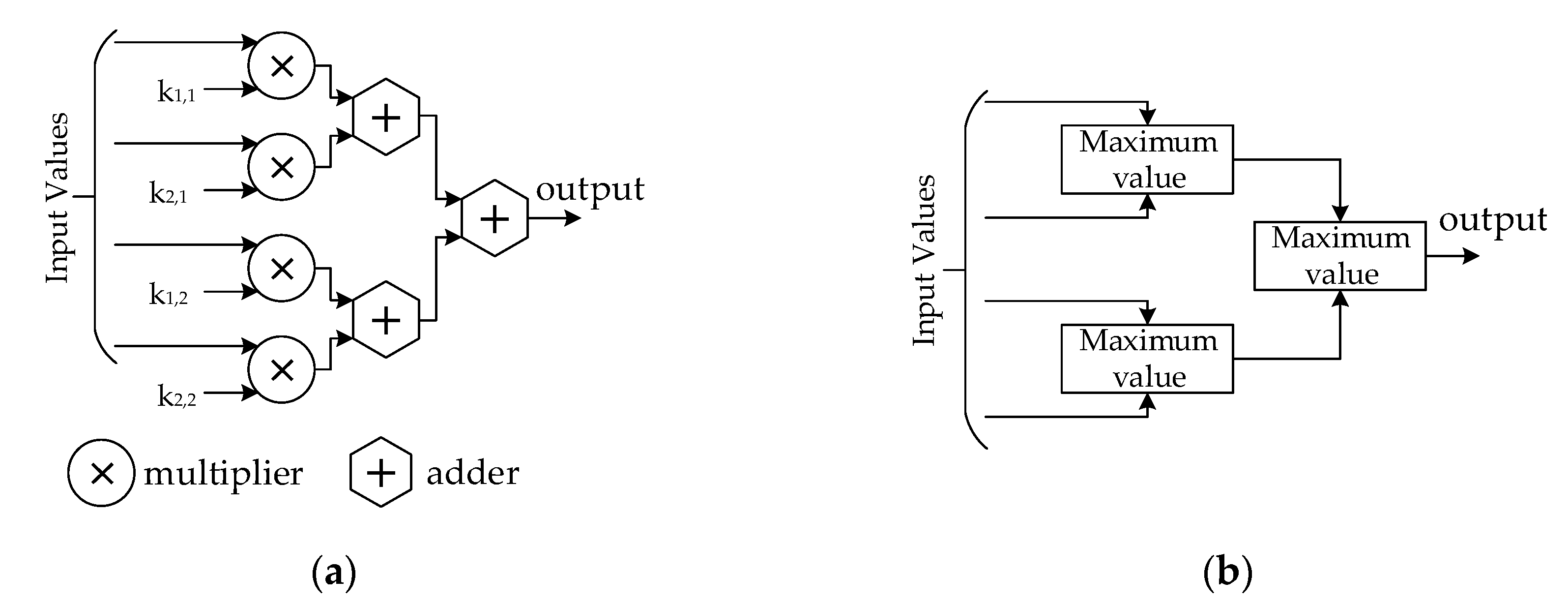
3.4. CNN Implementation on FPGA
3.5. Evaluation Metrics
3.6. Power and Temperature Effects on the FPGA
4. Results and Discussion
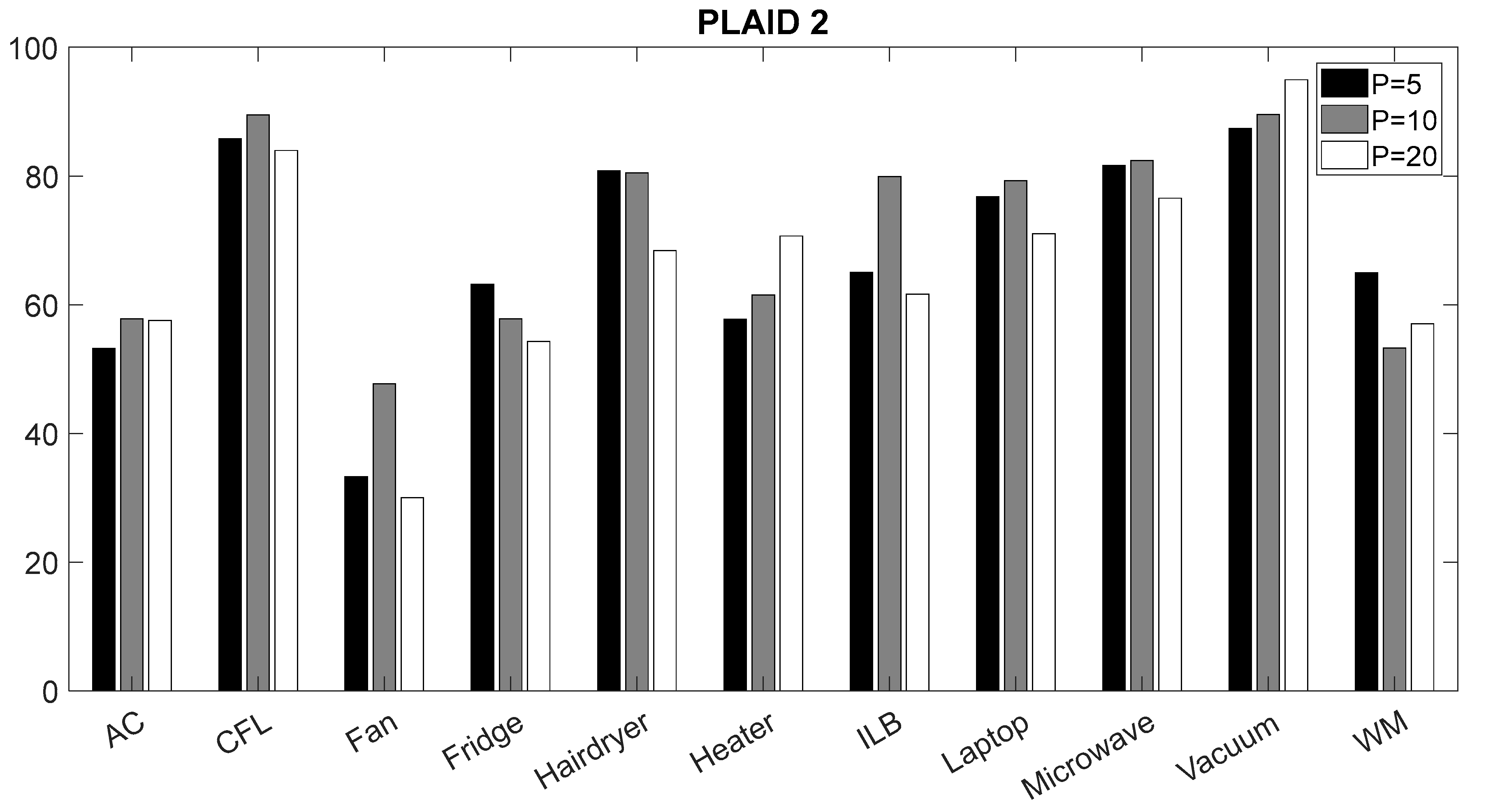
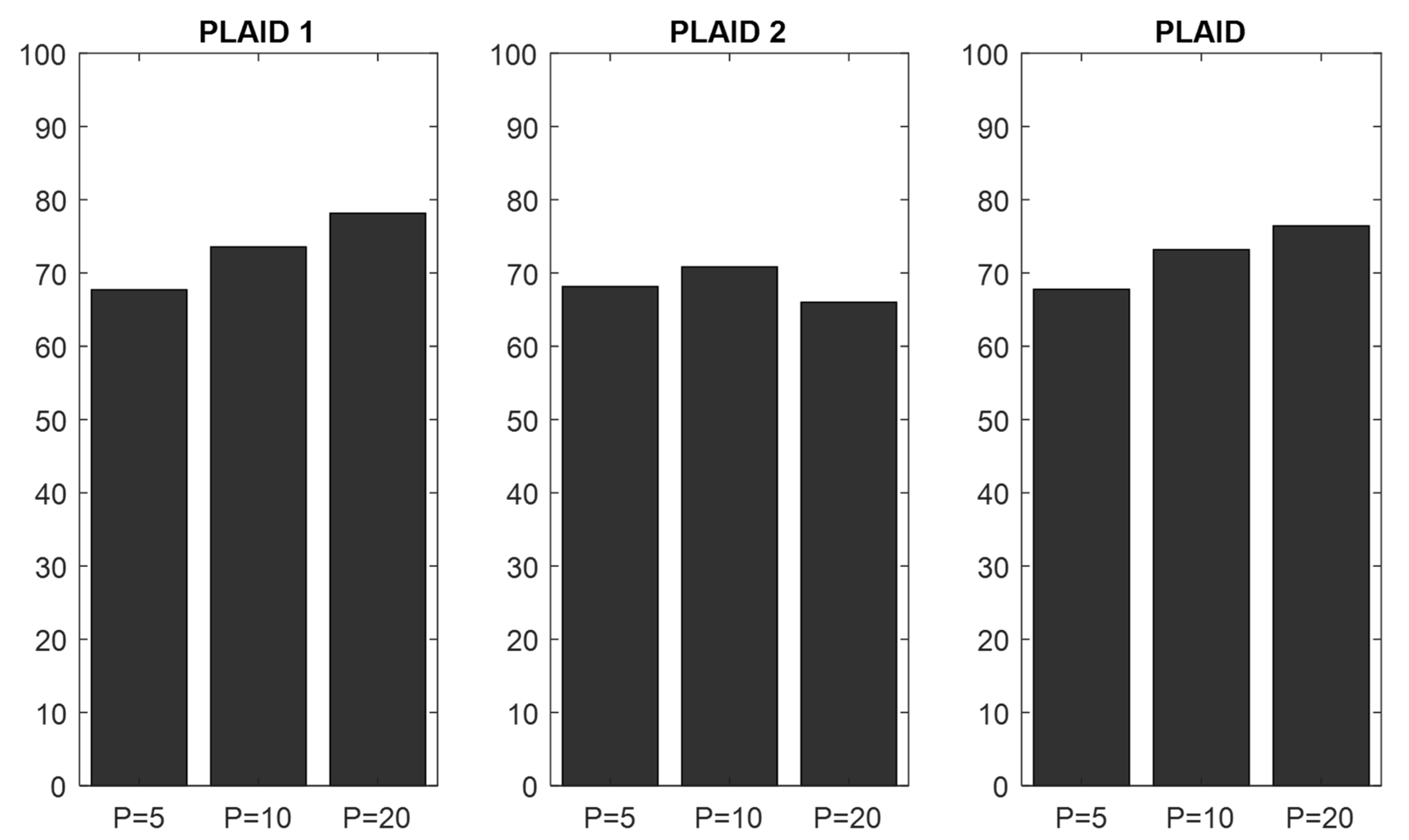
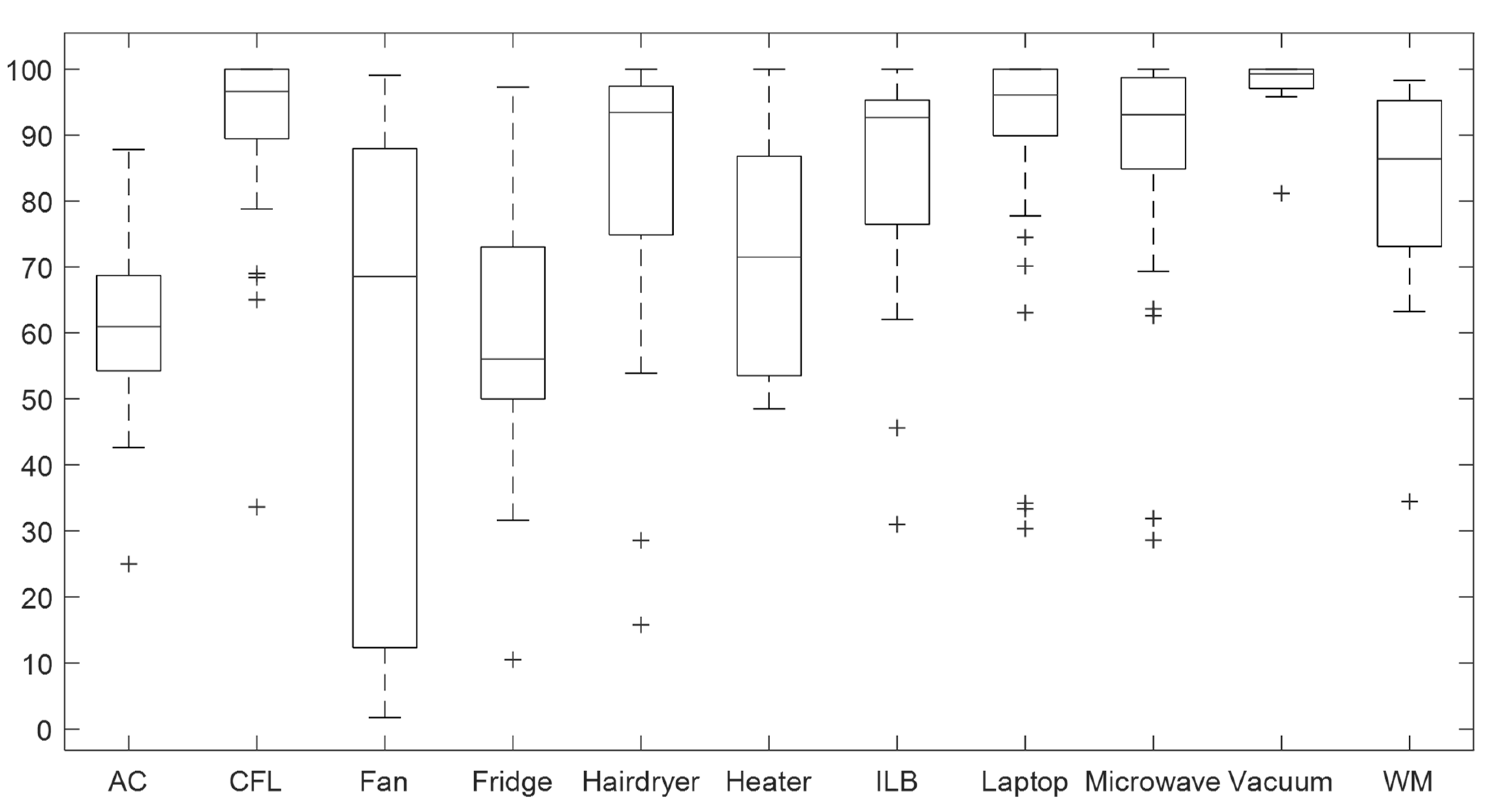
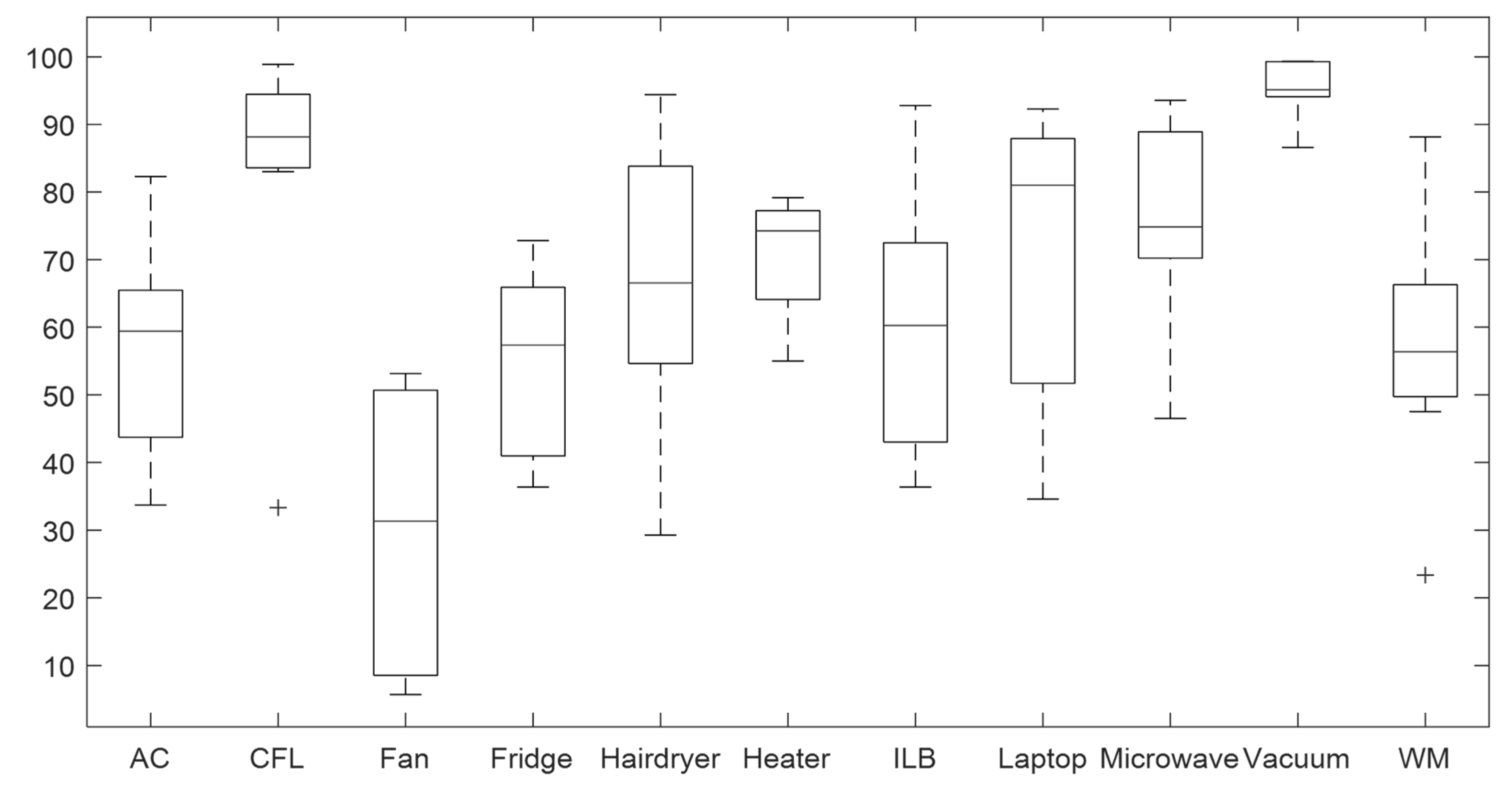
4.1. Validation of the CNN Classifier According to Window Sizes
4.2. Performance and Cost
4.3. Comparison Results
5. Conclusion and Future Work Directions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hart, G.W. Nonintrusive appliance load monitoring. Proc. IEEE 1992, 80, 1870–1891. [Google Scholar] [CrossRef]
- Armel, K.C.; Gupta, A.; Shrimali, G.; Albert, A. Is disaggregation the holy grail of energy efficiency? The case of electricity. Energy Policy 2013, 52, 213–234. [Google Scholar] [CrossRef]
- Esa, N.F.; Abdullah, M.P.; Hassan, M.Y. A review disaggregation method in Non-intrusive Appliance Load Monitoring. Renew. Sustain. Energy Rev. 2016, 66, 163–173. [Google Scholar] [CrossRef]
- Nalmpantis, C.; Vrakas, D. Machine learning approaches for non-intrusive load monitoring: from qualitative to quantitative comparation. Artif. Intell. Rev. 2018, 1–27. [Google Scholar] [CrossRef]
- Pereira, L.; Nunes, N. Performance evaluation in non-intrusive load monitoring: Datasets, metrics, and tools—A review. Wiley Interdiscip. Rev. Data Min. Knowl. Discov. 2018. [Google Scholar] [CrossRef]
- Gao, J.; Kara, E.C.; Giri, S.; Bergés, M. A feasibility study of automated plug-load identification from high-frequency measurements. In Proceedings of the 2015 IEEE Global Conference on Signal and Information Processing (GlobalSIP), Orlando, FL, USA, 14–16 December 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 220–224. [Google Scholar]
- Lam, H.Y.; Fung, G.S.K.; Lee, W.K. A novel method to construct taxonomy electrical appliances based on load signatures. IEEE Trans. Consum. Electron. 2007, 53, 653–660. [Google Scholar] [CrossRef]
- Hassan, T.; Javed, F.; Arshad, N. An Empirical Investigation of V-I Trajectory Based Load Signatures for Non-Intrusive Load Monitoring. IEEE Trans. Smart Grid 2014, 5, 870–878. [Google Scholar] [CrossRef]
- De Baets, L.; Ruyssinck, J.; Develder, C.; Dhaene, T.; Deschrijver, D. Appliance classification using VI trajectories and convolutional neural networks. Energy Build. 2018, 158, 32–36. [Google Scholar] [CrossRef]
- Kostyk, T.; Herkert, J. Societal Implications of the Emerging Smart Grid. Commun. ACM 2012, 55, 34–36. [Google Scholar] [CrossRef]
- McLaughlin, S.; McDaniel, P.; Aiello, W. Protecting Consumer Privacy from Electric Load Monitoring. In Proceedings of the 18th ACM Conference on Computer and Communications Security; CCS ’11, Chicago, IL, USA, 17–21 October 2011; pp. 87–98. [Google Scholar]
- Barbosa, P.; Brito, A.; Almeida, H. A Technique to provide differential privacy for appliance usage in smart metering. Inf. Sci. 2016, 370–371, 355–367. [Google Scholar] [CrossRef]
- Cao, H.; Liu, S.; Wu, L.; Guan, Z.; Du, X. Achieving differential privacy against non-intrusive load monitoring in smart grid: A fog computing approach. Concurr. Comput. Pract. Exp. 2018. [Google Scholar] [CrossRef]
- Kolter, Z.; Matthew, J. REDD: A public data set for energy disaggregation research. In Proceedings of the Data Mining Applications in Sustainability (SustKDD), San Diego, CA, USA, 21 August 2011. [Google Scholar]
- Iksan, N.; Sembiring, J.; Haryanto, N.; Supangkat, S.H. Appliances identification method of non-intrusive load monitoring based on load signature of V-I trajectory. In Proceedings of the International Conference on Information Technology Systems and Innovation (ICITSI), Bandung, Indonesia, 16–19 November 2015; IEEE: Piscataway, NJ, USA, 2015; pp. 1–6. [Google Scholar]
- Gao, J.; Giri, S.; Kara, E.C.; Bergés, M. PLAID: A public dataset of high-resoultion electrical appliance measurements for load identification research. In Proceedings of the 1st ACM Conference on Embedded Systems for Energy-Efficient Buildings—BuildSys, Memphis, TN, USA, 3–6 November 2014; Volume 14, pp. 198–199. [Google Scholar]
- Barsim, K.S.; Mauch, L. Bin Neural Network Ensembles to Real-time Identification of Plug-level Appliance Measurements. In Proceedings of the 3rd International Workshop on Non-Intrusive Load Monitoring, Vancouver, BC, Canada, 14–15 May 2016. [Google Scholar]
- Du, L.; He, D.; Harley, R.G.; Habetler, T.G. Electric Load Classification by Binary Voltage-Current Trajectory Mapping. IEEE Trans. Smart Grid 2016, 7, 358–365. [Google Scholar] [CrossRef]
- De Baets, L.; Develder, C.; Dhaene, T.; Deschrijver, D. Automated classification of appliances using elliptical fourier descriptors. In Proceedings of the 2017 IEEE International Conference on Smart Grid Communications (SmartGridComm), Dresden, Germany, 23–27 October 2017; IEEE: Piscataway, NJ, USA, 2017; pp. 153–158. [Google Scholar]
- Kahl, M.; UI Haq, A.; Kriechbaumer, T.; Hans-Arno, J. WHITED—A Worldwide Household and Industry Transient Energy Data Set. In Proceedings of the 3rd International NILM Workshop, Vancouver, BC, Canada, 14–15 May 2016. [Google Scholar]
- Fukushima, K.; Miyake, S. Neocognitron: A new algorithm for pattern recognition tolerant of deformations and shifts in position. Pattern Recognit. 1982, 15, 455–469. [Google Scholar] [CrossRef]
- Mamalet, F.; Garcia, C. Simplifying ConvNets for fast learning. In Proceedings of the Lecture Notes in Computer Science (Including Subseries Lecture Notes in Artificial Intelligence and Lecture Notes in Bioinformatics), Rome, Italy, 10–14 September 2012; Volume 7553, LNCS. pp. 58–65. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Ren, J.S.J.; Xu, L. On Vectorization of Deep Convolutional Neural Networks for Vision Tasks. In Proceedings of the AAAI'15 Twenty-Ninth AAAI Conference on Artificial Intelligence, Austin, TX, USA, 25–30 January 2015; pp. 1840–1846. [Google Scholar]
- Stutz, D. Understanding Convolutional Neural Networks. Nips 2016 2014, 1–23. [Google Scholar] [CrossRef]
- Nagi, J.; Ducatelle, F. Max-pooling convolutional neural networks for vision-based hand gesture recognition. In Proceedings of the 2011 IEEE International Conference on Signal and Image Processing Applications (ICSIPA), Kuala Lumpur, Malaysia, 16–18 November 2011; IEEE: Piscataway, NJ, USA, 2011; pp. 342–347. [Google Scholar] [CrossRef]
- Haykin, S. Neural Networks: A Comprehensive Foundation; Macmillan: New York, NY, USA, 1994; pp. 107–116. [Google Scholar]
- Memisevic, R.; Zach, C. Gated softmax classification. In Proceedings of the Advances in Neural Information Processing Systems 23 (NIPS 2010), Vancouver, BC, USA, 6–9 December 2010. [Google Scholar]
- Pereira, L.; Ribeiro, M.; Jardim, N. Engineering and deploying a hardware and software platform to collect and label non-intrusive load monitoring datasets. In Proceedings of the Sustainable Internet and ICT for Sustainability (SustainIT), Funchal, Portugal, 6–7 December 2017; pp. 1–9. [Google Scholar]
- Remscrim, Z.; Paris, J.; Leeb, S.B.; Shaw, S.R.; Neuman, S.; Schantz, C.; Muller, S.; Page, S. FPGA-based spectral envelope preprocessor for power monitoring and control. In Proceedings of the Twenty-Fifth Annual IEEE Applied Power Electronics Conference and Exposition (APEC), Palm Springs, CA, USA, 21–25 February 2010; IEEE: Piscataway, NJ, USA, 2010; pp. 2194–2201. [Google Scholar]
- Trung, K.N.; Zammit, O.; Dekneuvel, E.; Nicolle, B.; Van, C.N.; Jacquemod, G. An innovative non-intrusive load monitoring system for commercial and industrial application. In Proceedings of the 2012 International Conference on Advanced Technologies for Communications, Hanoi, Vietnam, 10–12 October 2012; IEEE: Piscataway, NJ, USA, 2012; pp. 23–27. [Google Scholar]
- LogiCORE IP Block Memory Generator v6.2; DS512; Xilinx: San Jose, CA, USA, 1 March 2011; Available online: https://www.xilinx.com/support/documentation/ip_documentation/blk_mem_gen/v6_2/blk_mem_gen_ds512.pdf (accessed on 12 September 2018).
- Säckinger, E.; Boser, B.E.; Jackel, L.D. A neurocomputer board based on the ANNA neural network chip. In Proceedins of the NIPS’91 4th International Conference on Neural Information Processing Systems, Denver, CO, USA, 2–5 December 1991; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1991; pp. 773–780. [Google Scholar]
- Sackinger, E.; Boser, B.E.; Bromley, J.; LeCun, Y.; Jackel, L.D. Application of the ANNA Neural Network Chip to High-Speed Character Recognition. IEEE Trans. Neural Netw. 1992, 3, 498–505. [Google Scholar] [CrossRef] [PubMed]
- Säckinger, E.; Graf, H.P. A system for high-speed pattern recognition and image analysis. In Proceedings of the Fourth International Conference on Microelectronics for Neural Networks and Fuzzy Systems, Turin, Italy, 26–28 September 1994; IEEE: Piscataway, NJ, USA, 1994. [Google Scholar] [CrossRef]
- Korekado, K.; Morie, T.; Nomura, O.; Ando, H.; Nakano, T.; Matsugu, M.; Atsushi, I. A convolutional Neural Network VLSI for image Recognition Using Merged/Mixed Analoge-Digital Architecture. In Proceedings of the KES: Knowledge-Based Intelligent Information and Engineering, Oxford, UK, 3–5 September 2003; pp. 169–176. [Google Scholar]
- Fieres, B.; Grubl, A.; Philipp, S.; Meier, K.; Schemmel, J.; Schurmann, F. A Platform for Parallel Operation of VLSI Neural Networks. In Proceedings of the BICS, Scotland, UK, 29 August–1 September 2004. [Google Scholar]
- Farabet, C.; Poulet, C.; Han, J.Y.; LeCun, Y. CNP: An FPGA-based processor for Convolutional Networks. In Proceedings of the FPL 09: 19th International Conference on Field Programmable Logic and Applications, Prague, Czech Republic, 31 August–2 September 2009; IEEE: Piscataway, NJ, USA, 2009; pp. 32–37. [Google Scholar]
- Zhang, C.; Li, P.; Sun, G.; Guan, Y.; Xiao, B.; Cong, J. Optimizing FPGA-based Accelerator Design for Deep Convolutional Neural Networks. In Proceedings of the 2015 ACM/SIGDA International Symposium on Field-Programmable Gate Arrays—FPGA, Monterey, CA, USA, 22–24 February 2015; pp. 161–170. [Google Scholar]
- Baptista, D.; Sousa, L.; Morgado-Dias, F. Configurable N-fold Hardware Architecture for Convolutional Neural Networks. In Proceedings of the International Conference on Biomedical Engineering and Applications—ICBEA18, Funchal, Portugal, 9–12 July 2018. [Google Scholar]
- Ovtcharov, K.; Ruwase, O.; Kim, J.; Fowers, J.; Strauss, K.; Chung, E.S. Accelerating Deep Convolutional Neural Networks Using Specialized Hardware; Microsoft Research: Cambridge, UK, 2015. [Google Scholar]
- Cloutier, J.; Cosatto, E.; Pigeon, S.; Boyer, F.R.; Simard, P.Y. VIP: An FPGA-based processor for image processing and neural/nnetworks. Proceedings of Fifth International Conference on Microelectronics for Neural Networks, Lausanne, Switzerland, 12–14 February 1996; IEEE: Piscataway, NJ, USA, 1996; pp. 330–336. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. Adam: A Method for Stochastic Optimization. In Proceedings of the 3rd International Conference for Learning Representations, San Diego, CA, USA, 7–9 May 2015. [Google Scholar]
- Zynq-7000 All Programmable SoC Data Sheet: Overview; DS190; Xilinx: San Jose, CA, USA, 2017; Volume 190.
- Mason, J.C.; Handscomb, D.C. Chebyshev Polynomials; Chapman & Hall/CRC Press LLC: Boca Raton, Florida, USA, 2003; ISBN 0849303559. [Google Scholar]
- Baptista, D.; Morgado-Dias, F. Low-resource hardware implementation of the hyperbolic tangent for artificial neural networks. Neural Comput. Appl. 2013, 23, 601–607. [Google Scholar] [CrossRef]
- Nascimento, I.; Jardim, R.; Morgado-Dias, F. Hyperbolic tangent implementation in hardware: A new solution using polynomial modeling of the fractional exponential part. Neural Comput. Appl. 2013, 23, 363–369. [Google Scholar] [CrossRef]
- Power Methodology Guide; UG786; Xilinx: San Jose, CA, USA, 2011; Volume 786, p. 54. Available online: https://www.xilinx.com/support/documentation/sw_manuals/xilinx13_1/ug786_PowerMethodology.pdf (accessed on 12 September 2018).
- Vivado Design Suite User Guide Design Analysis and Closure Techniques; UG906; Xilinx: San Jose, CA, USA, 2012; Volume 906, Available online: https://www.xilinx.com/support/documentation/sw_manuals/xilinx2017_3/ug906-vivado-design-analysis.pdf (accessed on 12 September 2018).
- Zynq-7000 All Programmable SoC DC and AC Switching Characteristics; DS191; Xilinx: San Jose, CA, USA, 2014; Volume 187, Available online: https://www.xilinx.com/support/documentation/data_sheets/ds187-XC7Z010-XC7Z020-Data-Sheet.pdf (accessed on 12 September 2018).
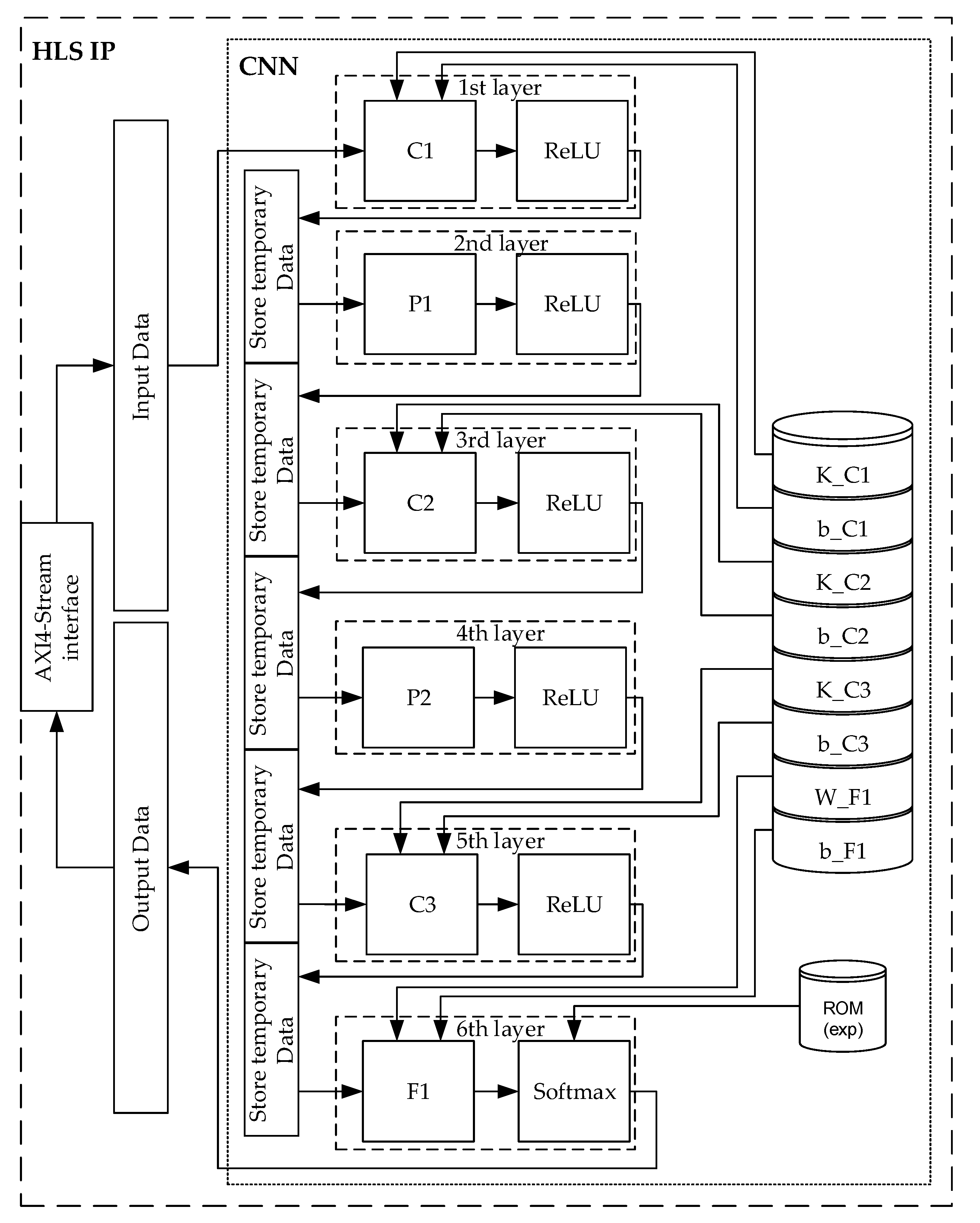
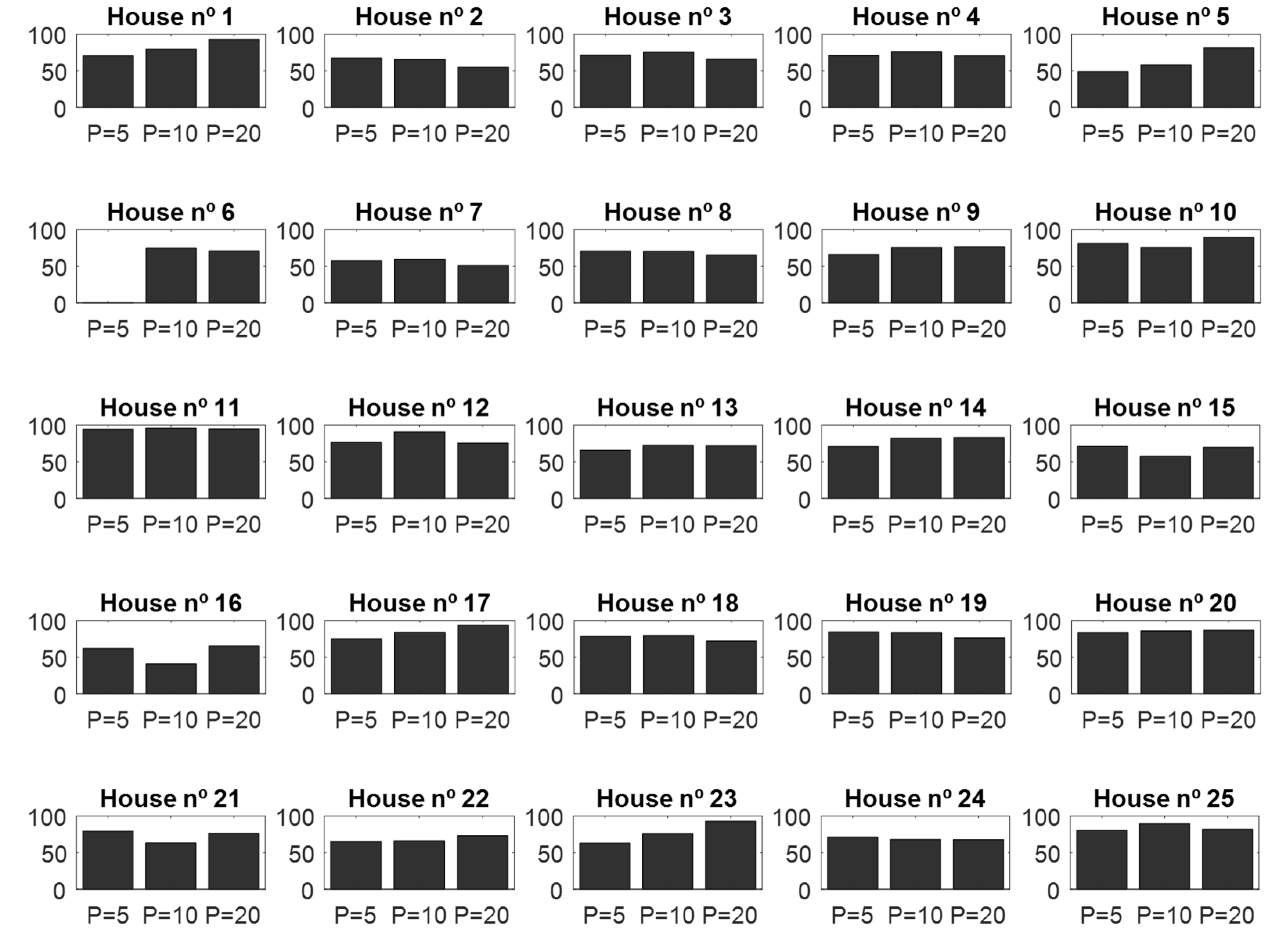
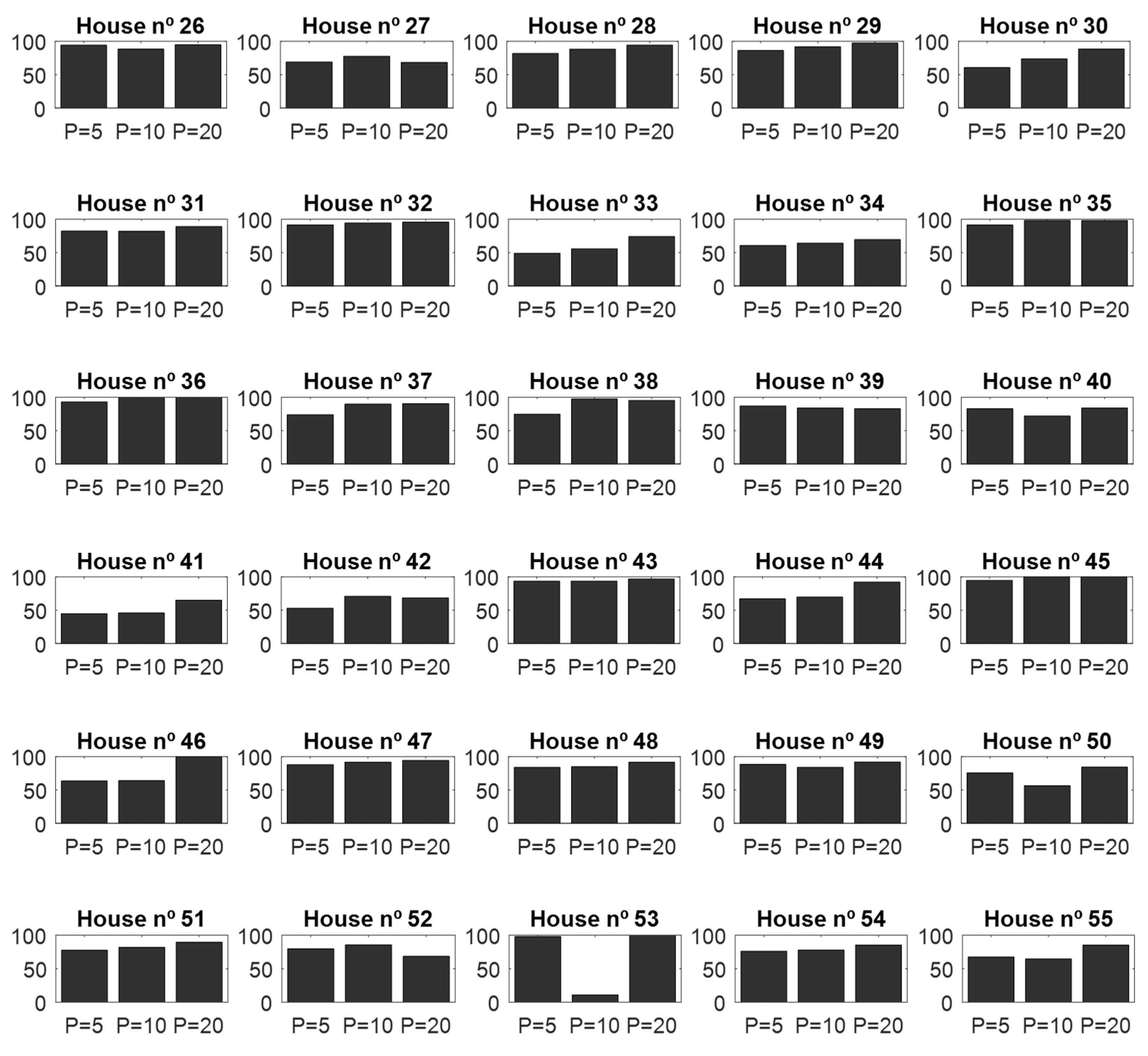
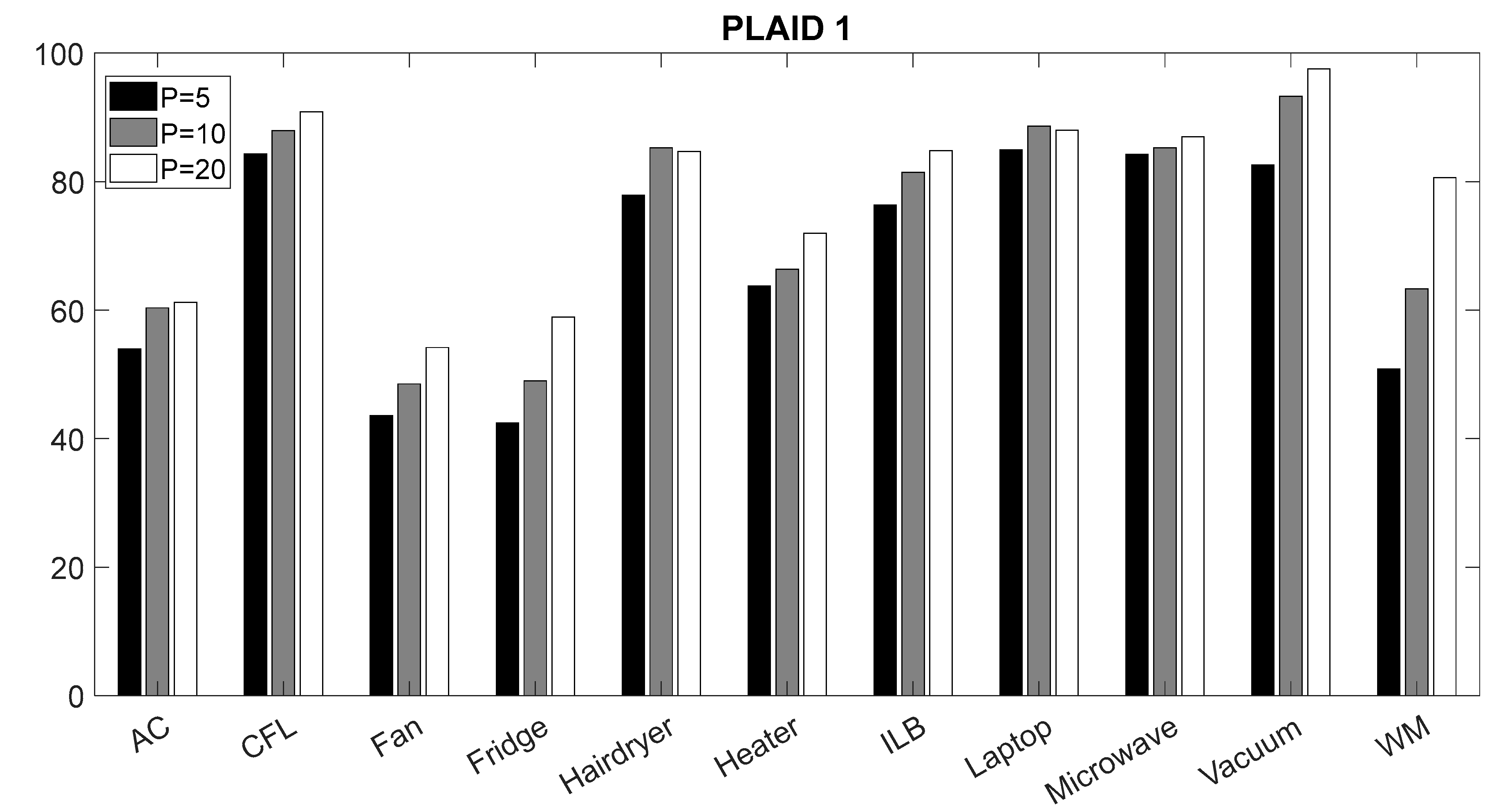
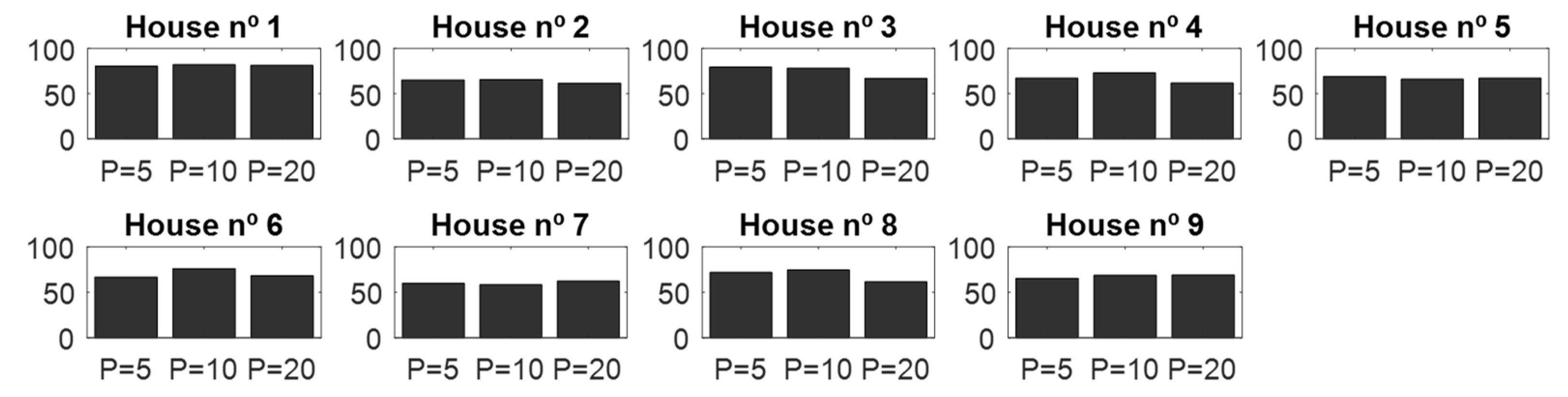
| Layer | Kernel/Pooling Window | Layer Size |
|---|---|---|
| Input | - | 1@50X50 |
| Convolution—stride 1 (C1) | [4@3X3] | 4@48X48 |
| Pooling—stride 2 (P1) | [4@2X2] | 4@24X24 |
| Convolution—stride 1 (C2) | [6@3X3] | 6@22X22 |
| Pooling—stride 2 (P2) | [6@2X2] | 6@11X11 |
| Convolution—stride 1 (C3) | [18@3X3] | 18@9X9 |
| Full out (F1) | - | 11 |
| Resources | LUT | 47.25% (25,138 of 53,200) |
| LUTRAM | 1.41% (246 of 17400) | |
| FF | 13.05% (13,884 of 10,6400) | |
| BRAM | 36.43% (51 of 140) | |
| DSP | 71.82% (158 of 220) | |
| BUFG | 3.13% (1 of 32) | |
| Latency (ms) | ≅ 5.7 | |
| Power | Dynamic (W) | 1.701 |
| Device Static (W) | 0.167 | |
| Total On-Chip Power (W) | 1.868 | |
| Junction Temperature (°C) | 46.5 | |
| Thermal Margin (°C) | 38.5 | |
| Effective thermal resistance to air (°C/W) | 11.5 | |
| Appliance | Convolutional Neural Networks [9] | Neural Network Ensembles [17] | Our Classifier | |
|---|---|---|---|---|
| PLAID 1 | PLAID 1 | PLAID 1 | PLAID 2 | |
| CFL | 95.60% | 69.8% | 90.86% | 83.96% |
| Fridge | 50.93% | 96.9% | 58.91% | 54.32% |
| Hairdryer | 79.76% | 74.1% | 84.70% | 68.40% |
| Microwave | 93.14% | 74.0% | 86.98% | 76.54% |
| AC | 46.65% | 92.6% | 61.20% | 57.55% |
| Laptop | 97.94% | 77.4% | 88.01% | 71.01% |
| Vacuum | 97.91% | 88.2% | 97.55% | 94.94% |
| ILB | 80.58% | 95.6% | 84.83% | 61.63% |
| Fan | 60.12% | 98.6% | 54.18% | 30.04% |
| WM | 68.82% | 96.1% | 80.62% | 57.02% |
| Heater | 82.23% | 89.4% | 71.92% | 70.67% |
| Total | 77.61% | 86.61% | 78.16% | 66.01% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Baptista, D.; Mostafa, S.S.; Pereira, L.; Sousa, L.; Morgado-Dias, F. Implementation Strategy of Convolution Neural Networks on Field Programmable Gate Arrays for Appliance Classification Using the Voltage and Current (V-I) Trajectory. Energies 2018, 11, 2460. https://doi.org/10.3390/en11092460
Baptista D, Mostafa SS, Pereira L, Sousa L, Morgado-Dias F. Implementation Strategy of Convolution Neural Networks on Field Programmable Gate Arrays for Appliance Classification Using the Voltage and Current (V-I) Trajectory. Energies. 2018; 11(9):2460. https://doi.org/10.3390/en11092460
Chicago/Turabian StyleBaptista, Darío, Sheikh Shanawaz Mostafa, Lucas Pereira, Leonel Sousa, and Fernando Morgado-Dias. 2018. "Implementation Strategy of Convolution Neural Networks on Field Programmable Gate Arrays for Appliance Classification Using the Voltage and Current (V-I) Trajectory" Energies 11, no. 9: 2460. https://doi.org/10.3390/en11092460
APA StyleBaptista, D., Mostafa, S. S., Pereira, L., Sousa, L., & Morgado-Dias, F. (2018). Implementation Strategy of Convolution Neural Networks on Field Programmable Gate Arrays for Appliance Classification Using the Voltage and Current (V-I) Trajectory. Energies, 11(9), 2460. https://doi.org/10.3390/en11092460








