THD Reduction in Wind Energy System Using Type-4 Wind Turbine/PMSG Applying the Active Front-End Converter Parallel Operation

Abstract

In this paper, the active front-end (AFE) converter topology for the total harmonic distortion (THD) reduction in a wind energy system (WES) is used. A higher THD results in serious pulsations in the wind turbine (WT) output power and several power losses at the WES. The AFE converter topology improves the capability, efficiency, and reliability in the energy conversion devices; by modifying a conventional back-to-back converter, from using a single voltage source converter (VSC) to use pVSC connected in parallel, the AFE converter is generated. The THD reduction is achieved by applying a different phase shift angle at the carrier of digital sinusoidal pulse width modulation (DSPWM) switching signals of each VSC. To verify the functionality of the proposed methodology, the WES simulation in Matlab-Simulink^® (Matlab r2015b, Mathworks, Natick, MA, USA) is analyzed, and the experimental laboratory tests using the concept of rapid control prototyping (RCP) and the real-time simulator Opal-RT Technologies^® (Montreal, QC, Canada) is achieved. The obtained results show a type-4 WT with a total output power of 6 MVA, generating a THD reduction up to 5.5 times of the total WES current output by Fourier series expansion.

1. Introduction

Nowadays, the number of wind energy systems (WES) has increased dramatically, as evidence of this; in 2013, WES were installed in more than 80 countries, generating a power of 240 GW [1], in 2014, the generation reached a capacity of 369.9 GW [2], in 2015, a production of 432.883 GW was generated [3]. By the end of 2016 a global generation of 487 GW was installed [4], and in 2021 the installed capacity is expected to exceed 800 GW [5]. Within the types of variable speed wind turbines (WT) there are three types: Type-2 (squirrel-cage induction generator (SCIG)), type-3 (double-fed induction generator (DFIG)) and type-4 (squirrel-cage induction generator (SCIG)/permanent magnet synchronous generator (PMSG) with full-scale back-to-back converter); in which, type-2 has a 10% variability in the rotor, type-3 has a 30% variability, and type-4 has 60% in the variability of the rotor speed [6]. The type-3 (DFIG) wind turbine schemes constitute the majority of variable speed commerce applications; however, the type-4 WT with a PMSG (WT-PMSG) is an attractive and the best option since this is not directly connected to the grid, presenting advantages such as: High efficiency, increased reliability, major variable speed operation, and low cost in maintenance and installation, due the absence of gearboxes [7]. In the type-4 WT-PMSG installation the important aspects to prevent are associated problems with the wind-nature fluctuations. For example: The flicker generation is mainly caused by load flow changes, due to its continuous operation [8]; a power factor not unity, this characteristic happens as the modulation index of the back-to-back converter is not high [9]. Voltage sags occur by the sudden changes in the rotor speed of the type-4 WT-PMSG and cause a decrement in the transferred power from the dc-link to the grid [10]. A higher total harmonic distortion (THD) is mainly produced by the power converters switching, this results in serious pulsations in the type-4 WT-PMSG output power and in several power losses at the WES [11,12]. All these problems can be mitigated through the full-scale back-to-back converter in the type-4 WT-PMSG scheme, and this generates the following advantages [13,14,15,16]: (i) Bidirectional power flow; (ii) adjustable dc-link voltage; (iii) a sinusoidal grid-side current with an exchange of active and reactive power. These advantages are possible because the generated whole power by the type-4 WT-PMSG on the AC grid is supplied through the back-to-back converter.

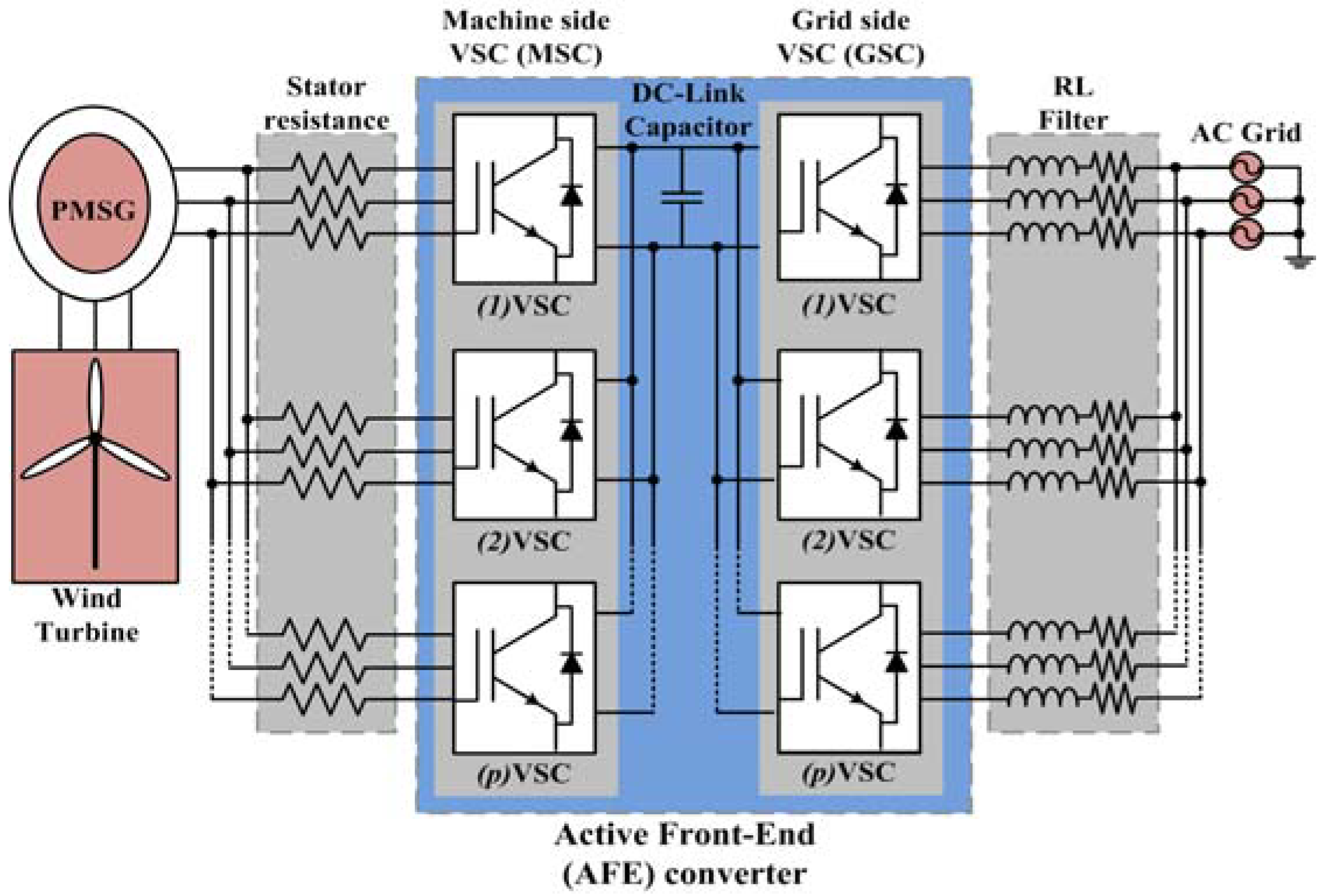
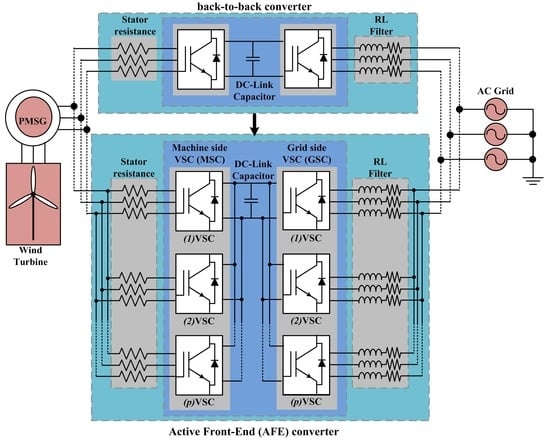
However, its implementation is very difficult, since this must handle very high powers of up to 6 MVA. Notwithstanding, the Active Front-End (AFE) converter topology provides a viable and efficient solution to improve the power transfer capacity and reliability of the WES quality; the AFE converter is generated by modifying a conventional back-to-back converter, from using a single voltage source converter (VSC) to use pVCS connected in parallel, as shown in Figure 1. As evidence, in [3] the authors describe the principal WT manufacturers, those in low voltage and medium voltage technologies are classified, generating power ratings of >3 MVA and <3 MVA, respectively. In the open literature there exists some research works that address the AFE converter topology applied to WES; for example, in [17] the authors analytically and experimentally present the control method for the current balance in an AFE power converter of 600 kVA, this is a very important topic in the parallel connection of power converters, however, the authors make the AFE converter analysis connecting only two VSCs in parallel, generating: A THD of 4.32% (three times higher than in our research work with THD of 1.23%); in addition, they use the space vector modulation for the switching of VSCs, which generates a more complex control if pVSC in parallel are connected.

The main goal of this work is the AFE converter topology application for the THD reduction in a WES and the increase of power transfer between the WT and the AC grid; generating greater capability, efficiency, and reliability in the energy conversion at the WES.

Contributions from this Work

In this paper, the AFE converter topology applied in the THD reduction at WES is made. Through the AFE converter parallel topology the following advantages were possible:

(i)

Increased the converter power capacity.

(ii)

Minimized size of each VSC unit, which manages a portion of the total nominal power.

(iii)

A reduced ripple on the injected current, which improves the voltage quality at the Point of Common Coupling (PCC).

(iv)

An increased equivalent switching frequency, generating a smaller passive filter on the AC-side.

(v)

The possibility of THD Reduction at the WES, modifying the Digital sinusoidal pulse width modulation (DSPWM) switching signals in each VSC.

To verify the functionality and robustness of the proposed methodology, an AFE converter formed with three VSCs connected in parallel is incorporated, as shown in Figure 1. The WES simulation in Matlab-Simulink^® is analyzed, and the experimental laboratory tests using the concept of rapid control prototyping (RCP) and the real-time simulator Opal-RT^® is achieved. The obtained results show a WES prototyping that incorporates a type-4 wind turbine with a total output power of 6 MVA and a THD reduction of up to 5.5 times.

This paper is organized as follows: Section 2 details the modeling of the Type-4 WT-PMSG; first, the modeling power transfer control between the WT-PMSG and AFE converter is generated; subsequently, the modeling of the machine-side VSC control, DC-link control and the grid-side VSC control of the AFE converter is analyzed, and finally, the design of the AFE converter system parameters is presented. Section 3 presents the modeling of the DSPWM Technique Applied in the THD Reduction. Section 4 shows the simulated results of a study case for WES. Section 5 presents the real-time simulation results of a study case for WES using Opal-RT Technologies^®. Finally, in Section 6, the conclusions are presented.

2. Modeling of the Type-4 WT-PMSG

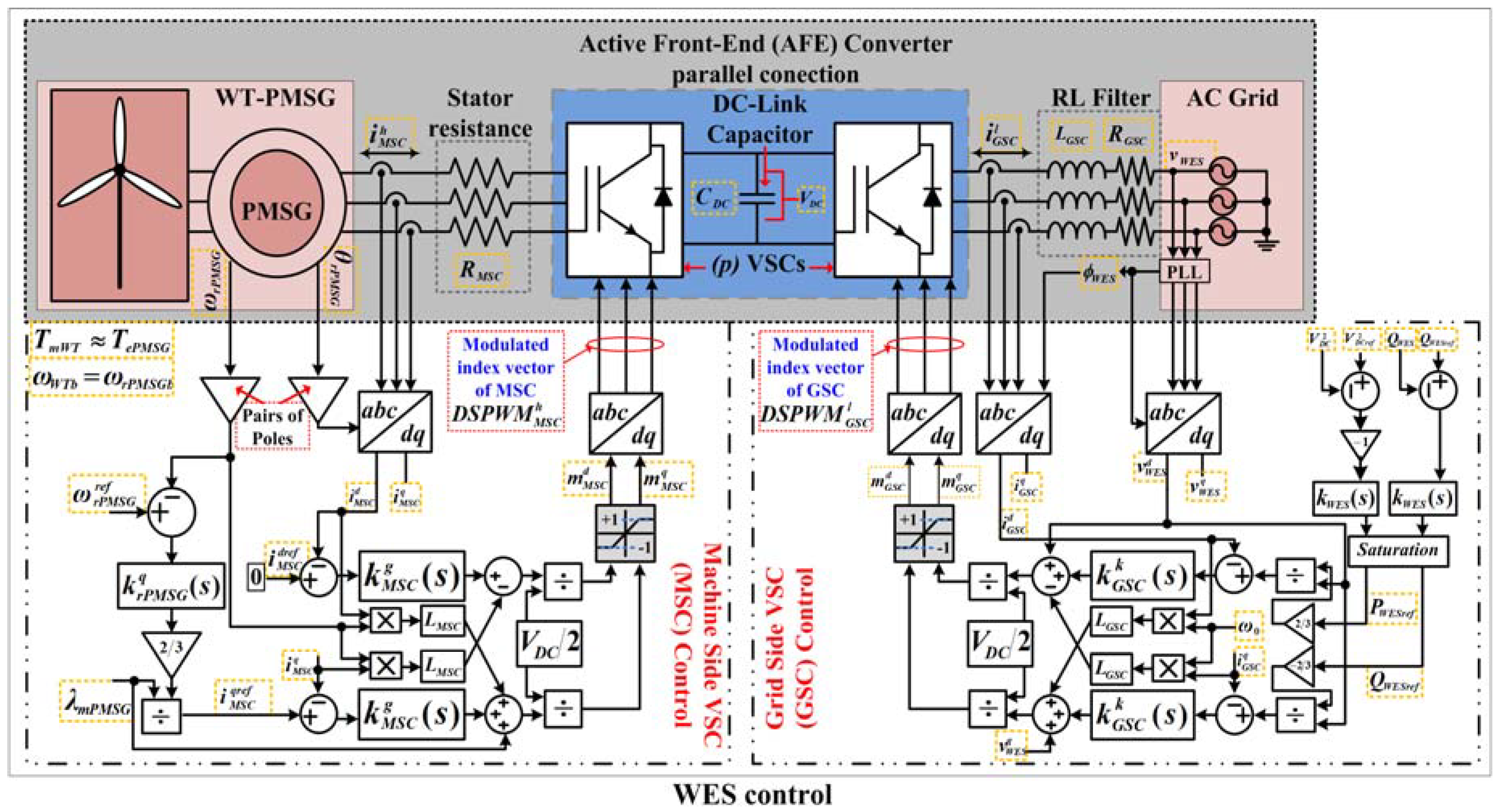
The AFE converter structure consists in two power electronics converters: A machine-side VSC (MSC) to provide power conversion between medium AC voltage and low DC voltage levels, and a grid-side VSC (GSC) to generate the voltages required by the consumers [18], for which, the next sections describe the control modeling of MSC and GSC and these are shown in Figure 2.

2.1. Modeling of the Machine-Side VSC Control at AFE Converter

The MSC provides the rotor flux frequency control, thus enabling the rotor shaft frequency to optimally track wind speed [19]. The time-domain relationship of the VSC AC-side is given by:

$$\left[d\left(i_{MSC}^h\left(t\right)\right)/dt\right]=-\left(R_{MSC}^h/L_{MSC}^h\right)\left[i_{MSC}^h(t)\right]+\left(1/L_{MSC}^h\right)\left[v_{MSC}^h\left(t\right)\right]-\left(1/L_{MSC}^h\right)\left[v_{WT-PMSG}^h\left(t\right)\right]$$

(1)

where h is the MSC three-phase vector (a,b,c), L_MSC is the PMSG armature inductance, R_MSC is the PMSG stator phase resistance, v_MSC and i_MSC are the MSC voltage and current, respectively, v_WT-PMSG is the generated WT-PMSG voltage.

Then, the dq reference frame model derived from the AC-side of the MSC, including the inductances cross-coupling, is described as:

$$\left[\frac{d(i_{MSC}^d(t))}{dt}\right]=-\left(\frac{R_{MSC}^d}{L_{MSC}^d}\right)\left[i_{MSC}^d\left(t\right)\right]+\left(\frac{{\omega }_{rPMSG}{L}_{MSC}^q}{L_{MSC}^d}\right)\left[i_{MSC}^q\left(t\right)\right]+\left[\frac{v_{MSC}^d(t)}{L_{MSC}^d}\right]-\left[\frac{v_{WT-PMSG}^d(t)}{L_{MSC}^d}\right]$$

(2a)

$$\left[\frac{d(i_{MSC}^q(t))}{dt}\right]=-\left(\frac{R_{MSC}^q}{L_{MSC}^q}\right)\left[i_{MSC}^q(t)\right]-\left(\frac{{\omega }_{rPMSG}{L}_{MSC}^d}{L_{MSC}^q}\right)\left[i_{MSC}^d(t)\right]-\left[\frac{({\lambda }_{mPMSG})({\omega }_{rPMSG})}{L_{MSC}^q}\right]+\left[\frac{v_{MSC}^q(t)}{L_{MSC}^q}\right]-\left[\frac{v_{WT-PMSG}^q(t)}{L_{MSC}^q}\right]$$

(2b)

where ω_rPMSG is the PMSG rotor angular velocity; λ_mPMSG is the maximum flux linkage generated by the PMSG rotor magnets and transferred to the stator windings.

The generated MSC voltage is given by:

$$\left[v_{MSC}^g(t)\right]=\left(1/2\right)\left[m_{MSC}^g(t)*V_{DC}(t)\right]$$

(3)

where g is the dq components reference frame vector of the MSC, VDC is the DC-link voltage, $m_{MSC}^g$ is the modulated index vector.

Making $L_{MSC}=L_{MSC}^d=L_{MSC}^q$, the presence of ω_rPMSGL_MSC in (2) indicates the coupled dynamics between $i_{MSC}^d$ and $i_{MSC}^q$. To decouple these dynamics, the $i_{MSC}^q$ vector signals are changed, based in the dq reference frame, i.e.,

$$\left[m_{MSC}^d(t)\right]=\left(2/V_{DC}(t)\right)\left[{{\rm E}}_{MSC}^d(t)-\left(\left({\omega }_{rPMSG}·L_{MSC}\right)i_{MSC}^q(t)\right)+v_{WT-PMSG}^d(t)\right]$$

(4a)

$$\left[m_{MSC}^q(t)\right]=\left(2/V_{DC}(t)\right)\left[{{\rm E}}_{MSC}^q(t)+\left(\left({\omega }_{rPMSG}·L_{MSC}\right)i_{MSC}^d(t)\right)+{\lambda }_{mPMSG}{\omega }_{rPMSG}+v_{WT-PMSG}^q(t)\right]$$

(4b)

where $E_{MSC}^d(t)$ and $E_{MSC}^q(t)$ are two additional control inputs.

The MSC plant is obtained by substituting (4) into (3), subsequently, (3) is substituting into (2) generating a first order lineal system that, in Equation (5) is described.

$$\left[{{\rm E}}_{MSC}^g(t)\right]=L_{MSC}\left[d{i}_{MSC}^g(t)/dt\right]+R_{MSC}\left[i_{MSC}^g(t)\right]$$

(5)

Equation (5) in the time domain is represented; its representation in the frequency domain is shown in (6); which describes a decoupled and first-order linear system, controlled through $E_{MSC}^g(s)$.

$$\left[{{\rm E}}_{MSC}^g(s)\right]=\left(s{L}_{MSC}+R_{MSC}\right)\left[i_{MSC}^g(s)\right]$$

(6)

Rewriting equation (6), the transfer function representing the MSC plant is given, i.e.,

$$\left[i_{MSC}^g(s)\right]=\left[{{\rm E}}_{MSC}^g(s)\right]{\left(s{L}_{MSC}+R_{MSC}\right)}^{-1}$$

(7)

With the purpose of tracking the $i_{MSC}^g(s)$ reference commands in the loop, the proportional-integral (PI) compensators are used, obtaining:

$$\left[{{\rm E}}_{MSC}^g(s)\right]\approx \left[k_{MSC}^g(s)\right]=\left[\frac{({\alpha }_{MSC}sk{p}_{MSC}^g+{\alpha }_{MSC}k{i}_{MSC}^g)}{{\alpha }_{MSC}s}\right]=\left[\left(\frac{{\alpha }_{MSC}}{s}\right)\left(\frac{(sk{p}_{MSC}^g+k{i}_{MSC}^g)}{{\alpha }_{MSC}}\right)\right]$$

(8)

where $k{p}_{MSC}^g$ and $k{i}_{MSC}^g$ are the proportional and integral gains, respectively, α_MSC=2.2/τ_MSC is the MSC bandwidth of the closed loop control and τ_MSC is compensator response time.

Substituting Equation (8) into (7), the closed-loop transfer function $\left[{\iota }_{MSC}^g(s)\right]$ is formed:

$$\left[{\iota }_{MSC}^g(s)\right]\approx \left[i_{MSC}^{gref}(s)-i_{MSC}^g(s)\right]=\left[\left(\frac{{\alpha }_{MSC}}{s}\right)\left(\frac{sk{p}_{MSC}^g(s)+k{i}_{MSC}^g(s)}{{\alpha }_{MSC}}\right)\left(\frac{1}{s{L}_{MSC}(s)+R_{MSC}(s)}\right)\right]$$

(9)

If in open loop the expression (9) tends to be ∞ when $s=j\omega \to 0$, this guarantees that, in closed loop the system will not have a phase shift delay.

Based on (9), the relation between the plant pole and the PI compensator zero is obtained through (10), generating the $k{p}_{MSC}^g$ and $k{i}_{MSC}^g$ control gains.

$$\left[k{p}_{MSC}^g\right]=\left[{\alpha }_{MSC}{L}_{MSC}\right]=\left[\left(2.2/{\tau }_{MSC}\right)L_{MSC}\right]$$

(10a)

$$\left[k{i}_{MSC}^g\right]=\left[{\alpha }_{MSC}{R}_{MSC}\right]=\left[\left(2.2/{\tau }_{MSC}\right)R_{MSC}\right]$$

(10b)

Compensator response time, τ_MSC, in the range from 5 to 0.5 ms is selected, in this case a τ_MSC = 2.2 ms is designated.

2.2. Modeling Power Transfer Control between the WT-PMSG and AFE Converter

In the WT-PMSG power transfer modeling the following power-speed characteristics are considered [20]: (i) The base angular velocity of the WT is determined by the base rotor angular velocity of the PMSG, ω_WTb = ω_rPMSGb; (ii) the WES base power is determined by the WT-PMSG nominal power, P_WESb = P_WT-PMSGb; iii) the output base power of the AFE converter is determined by the base WES power, P_AFEb = P_WESb; this power is transferred from WT to PMSG through the electric torque, this is represented by:

$$\left[T_{ePMSG}\right]=\left(3/2\right)\left[\left((L_{MSC}^d-L_{MSC}^q)i_{MSC}^d{i}_{MSC}^q\right)+({\lambda }_{mPMSG}{i}_{MSC}^q)\right]$$

(11)

where T_ePMSG is the PMSG electrical torque, $L_{MSC}^d$ and $L_{MSC}^q$ are the dq reference frame components of the PMSG armature inductance.

However, considering that the rotor has a cylindrical geometry, then it is established that, $L_{MSC}^d=L_{MSC}^q$ [21], generating (12):

$$\left[T_{ePMSG}\right]=\left((3/2){\lambda }_{mPMSG}\right)\left[i_{MSC}^q\right]$$

(12)

Then, to realize the WT-PMSG variable speed control, it is necessary to generate the plant model that represents it. Therefore, in (13) the dynamic characteristics are shown as a time function so that it represents:

$$\left[\frac{d({\omega }_{rPMSG})}{dt}\right]=\frac{1}{2H}\left[T_{mWT}-T_{ePMSG}-D{\omega }_{rPMSG}(t)\right]$$

(13)

where D is the PMSG viscous damping, H is the inertia constant (s), T_mWT is the WT mechanical torque.

Equation (13) analyzes the WT-PMSG in the time domain; however, the WT-PMSG plant representation requires a transfer function to design the ω_rPMSG control. By using Laplace transformation, the WT-PMSG plant in the frequency domain is represented, i.e.,

$$\left[{\omega }_{rPMSG}(s)\right]=\left[\left(T_{mWT}-T_{ePMSG}\right){\left(2Hs+D\right)}^{-1}\right]$$

(14)

Equation (14) shows a multiple inputs single output system (MISO); however, because in steady state it is valid that T_mWT ≈ T_ePMSG, then, in the control design it is considered that T_mWT = 0; generating a single input single output system (SISO), as shown in (15).

$$\left[\frac{{\omega }_{rPMSG}(s)}{-T_{ePMSG}}\right]=\left[\frac{1}{2Hs+D}\right]$$

(15)

With the purpose of tracking the ω_rPMSG reference commands in the closed-loop transfer function, the proportional-integral (PI) compensators are used. The feedback loop $\left[{\iota }_{rPMSG}^q(s)\right]$ is:

$$\left[{\iota }_{rPMSG}^q(s)\right]=\left[{\omega }_{rPMSG}^{ref}(s)-{\omega }_{rPMSG}(s)\right]=\left[\left(\frac{{\alpha }_{PMSG}}{s}\right)\left(\frac{(sk{p}_{rPMSG}^q+k{i}_{rPMSG}^q)}{{\alpha }_{PMSG}}\right)\left(\frac{1}{(2Hs+D)}\right)\right]$$

(16)

where $k{p}_{rPMSG}^q$ and $k{i}_{rPMSG}^q$ are the proportional and integral gains, respectively.

From (16), the relation between the plant pole and PI compensator zero is obtained and the control gains using the next expression are generated:

$$\left[k{p}_{rPMSG}^q\right]=\left[2H{\alpha }_{PMSG}\right]=\left[\left(2.2/{\tau }_{PMSG}\right)2H\right]$$

(17a)

$$\left[k{i}_{rPMSG}^q\right]=\left[{\alpha }_{PMSG}D\right]=\left[\left(2.2/{\tau }_{PMSG}\right)D\right]$$

(17b)

where the subscript τ_PMSG is the response time by the closed loop of the WT-PMSG first-order transfer function. This is selected according to the WT-PMSG transferred power and this must be at least ten times higher than τ_MSC.

2.3. Modeling of the Grid-Side VSC Control of the AFE Converter

The GSC is used to keep the DC-link constant, transferring the generated power between the WT-PMSG and AC grid. The time-domain relationship of the VSC AC-side is given by:

$$\left[d\left(i_{GSC}^l(t)\right)/dt\right]=-\left(R_{GSC}^l/L_{GSC}^l\right)\left[i_{GSC}^l(t)\right]+\left(1/L_{GSC}^l\right)\left[v_{GSC}^l(t)\right]-\left(1/L_{GSC}^l\right)\left[v_{WES}^l(t)\right]$$

(18)

where l is the VSC three-phase vector (a,b,c ), L_GSC and R_GSC are the RL filter parameters through which the AFE converter is connected to the grid, v_GSC and i_GSC are the GSC voltage and current, respectively; v_WES is the generated WES voltage.

Then, from (18) the derived dq model is described as:

$$L_{GSC}\left(d{i}_{GSC}^d(t)/dt\right)=\left({\omega }_0·L_{GSC}\right)\left[i_{GSC}^q(t)\right]-\left(R_{GSC}\right)\left[i_{GSC}^d(t)\right]+\left[v_{GSC}^d(t)\right]-\left[v_{WES}^d(t)\right]$$

(19a)

$$L_{GSC}\left(d{i}_{GSC}^q/dt\right)=-\left({\omega }_0·L_{GSC}\right)\left[i_{GSC}^d(t)\right]-\left(R_{GSC}\right)\left[i_{GSC}^q(t)\right]+\left[v_{GSC}^q(t)\right]-\left[v_{WES}^q(t)\right]$$

(19b)

where ω₀ is the WES angular frequency; the generated GSC voltages are given by:

$$v_{GSC}^k(t)=\left(V_{DC}/2\right)\left[m_{GSC}^k(t)\right]$$

(20)

where k is the dq components reference frame vector of the grid-side VSC, $m_{GSC}^k$ is the modulated index vector.

Making $L_{GSC}=L_{GSC}^d=L_{GSC}^q$, the presence of ω₀L_GSC in (19) indicates the coupled dynamics between $i_{GSC}^d$ and $i_{GSC}^q$. Decoupling these dynamics changes $m_{GSC}^d$ and $m_{GSC}^q$, based in the dq reference frame, i.e.,

$$\left[m_{GSC}^d(t)\right]=\left(2/V_{DC}(t)\right)\left[{{\rm E}}_{GSC}^d(t)-\left(\left({\omega }_0\cdot L_{GSC}\right)i_{GSC}^q(t)\right)+v_{WES}^d(t)\right]$$

(21a)

$$\left[m_{GSC}^q(t)\right]=\left(2/V_{DC}(t)\right)\left[{{\rm E}}_{GSC}^q(t)+\left(\left({\omega }_0\cdot L_{GSC}\right)i_{GSC}^d\left(t\right)\right)+v_{WES}^q(t)\right]$$

(21b)

where $E_{GSC}^d(t)$ and $E_{GSC}^q(t)$ are two additional control inputs.

The GSC plant is obtained by substituting (21) into (20), subsequently, (20) is substituting into (19) generating a first order lineal system, this in Equation (22) is described as:

$$L_{GSC}\left[d{i}_{GSC}^k(t)/dt\right]=\left[{{\rm E}}_{GSC}^k(t)\right]-R_{GSC}\left[i_{GSC}^k(t)\right]$$

(22)

The frequency domain of the Equation (22) is shown in (23); which describes a decoupled, first-order, linear system, controlled through $E_{GSC}^k(s)$. Also, Equation (23) represents the grid-side VSC plant.

$$\left[i_{GSC}^k(s)\right]=\left[{{\rm E}}_{GSC}^k(s)\right]{\left(s{L}_{GSC}+R_{GSC}\right)}^{-1}$$

(23)

With the purpose of tracking the $i_{GSC}^k(s)$ reference commands in the closed loop, the proportional-integral (PI) compensators are used, obtaining:

$$\left[{{\rm E}}_{GSC}^k(s)\right]\approx \left[k_{GSC}^k(s)\right]=\left[\frac{({\alpha }_{GSC}sk{p}_{GSC}^k+{\alpha }_{GSC}k{i}_{GSC}^k)}{{\alpha }_{GSC}s}\right]=\left[\left(\frac{{\alpha }_{GSC}}{s}\right)\left(\frac{(sk{p}_{GSC}^k+k{i}_{GSC}^k)}{{\alpha }_{GSC}}\right)\right]$$

(24)

where $k{p}_{GSC}^k$ and $k{i}_{GSC}^k$ are the proportional and integral gains, respectively.

The feedback loop ${\iota }_{GSC}^k(s)$ is:

$$\left[{\iota }_{GSC}^k(s)\right]=\left[i_{GSC}^{kref}(s)-i_{GSC}^k(s)\right]=\left[\left(\frac{{\alpha }_{GSC}}{s}\right)\left(\frac{(sk{p}_{GSC}^k+k{i}_{GSC}^k)}{{\alpha }_{GSC}}\right)\left(\frac{1}{s{L}_{GSC}+R_{GSC}}\right)\right]$$

(25)

The relation between the plant pole and the PI compensator zero is obtained in (26), generating the $k{p}_{GSC}^k$ and $k{i}_{GSC}^k$ control gains and α_GSC=2.2/τ_GSC is the GSC bandwidth of the closed-loop control.

$$\left[k{p}_{GSC}^k\right]=\left[{\alpha }_{GSC}{L}_{GSC}\right]=\left[\left(2.2/{\tau }_{GSC}\right)L_{GSC}\right]$$

(26a)

$$\left[k{i}_{GSC}^k\right]=\left[{\alpha }_{GSC}{R}_{GSC}\right]=\left[\left(2.2/{\tau }_{GSC}\right)R_{GSC}\right]$$

(26b)

where τ_GSC is selected from 5 to 0.5 ms based on the transferred power.

2.4. The DC-Side Control of the AFE Converter

GSC improves the DC-link control. The time-domain relationship of the DC-link of the AFE converter is given by:

$$\left[d{V}_{DC}(t)/dt\right]=\left[I_{DC}(t)/C_{DC}\right]-\left[V_{DC}(t)/\left(C_{DC}·R_{DC}\right)\right]$$

(27)

The sum of currents entering the capacitor is:

$$\left[I_{DC}(t)\right]=\frac{1}{2}{\displaystyle \sum _{l=a}^c{m}_{GSC}^l(t)\left[i_{GSC}^l(t)\right]}$$

(28)

The functionality of the AFE converter requires that:

$$V_{DC}\ge \left|2\left(v_{WESL-L}\right)\right|$$

(29)

The DC-link control is calculated through the stored energy in the capacitor, that is,

$$\left[U_{DC}(s)\right]=\left(C_{DC}/2\right)\left[V_{DC}^2(s)\right]$$

(30)

where U_DC is the stored energy in the capacitor and C_DC is the DC-link capacitance.

Considering that U_DC(s) ≈ P_GSCref(s), and using the d reference frame component of grid-side VSC plant described in (22) the DC-link control is made, generating the active power control, that is:

$$\left[P_{GSCref}(s)\right]=\left(C_{DC}/2\right)\left[V_{DCref}^2(s)-V_{DC}^2(s)\right]\left[E_{GSC}^d(s)\right]$$

(31)

The reactive power control is made with the q reference frame component of the GSC plant described in (22), that is,

$$\left[Q_{GSCref}(s)\right]=\left[Q_{WESref}(s)-Q_{WES}(s)\right]\left[{{\rm E}}_{GSC}^d(s)\right]$$

(32)

where Q_WES is the presented reactive power at the WES.

It is important to consider that, the subscript τ_WES presented in (32) must be at least ten times higher than τ_GSC.

2.5. System Parameters Design of the AFE Converter

The correct operation of the type-4 WT control depends on the precise design of the AFE converter parameters; thus, the element’s values of the MSC are obtained from the WT-PMSG nominal power, P_WT-PMSG, that is: the current is i_MSC = (2/3)(P_WT-PMSG/v_MSC); the machine-side impedance is Z_MSCt = v_MSC/i_MSC, thus, the MSC works with 15% of the total WT-PMSG impedance, i.e., Z_MSC = (0.15)Z_MSCt; from the WT-PMSG characteristics the following parameters are taken: L_MSC, R_MSG, D, H. The element’s values of the GSC are obtained from the WES nominal power, but to achieve P_WES = P_WT-PMSG i_GSC is generated using i_MSC = (2/3)(P_WES/v_GSC); the grid-side impedance is Z_GSCt=v_GSC/i_GSC the GSC works with 15% of the total WES impedance, i.e.,: Z_GSC = (0.15)Z_GSCt; therefore, L_GSC is calculated with L_GSC = Z_GSC/ω₀, the R_GSC value varies according to the transferred power, in a range from 0.1 Ω to 0.5 Ω; the base WES capacitance C_WES is calculated with C_WES = 1/(Z_GSCω₀). Then, a better time response in the WES feedback is achieved, since the L_MSC and R_MSC values are used in (10), H and D values are used in (17), L_GSC and R_GSC values are used in (26), to obtain the system feedback gains. It is important to establish that from the generated active power by the GSC, v_WES is kept constant in the presence of any perturbation; for which, it is essential to calculate the correct capacitance value that maintains the DC-link compensation. This is determined from the base DC-link capacitance, i.e., C_DC = (3/8)C_WES, determining the store energy in Equation (30).

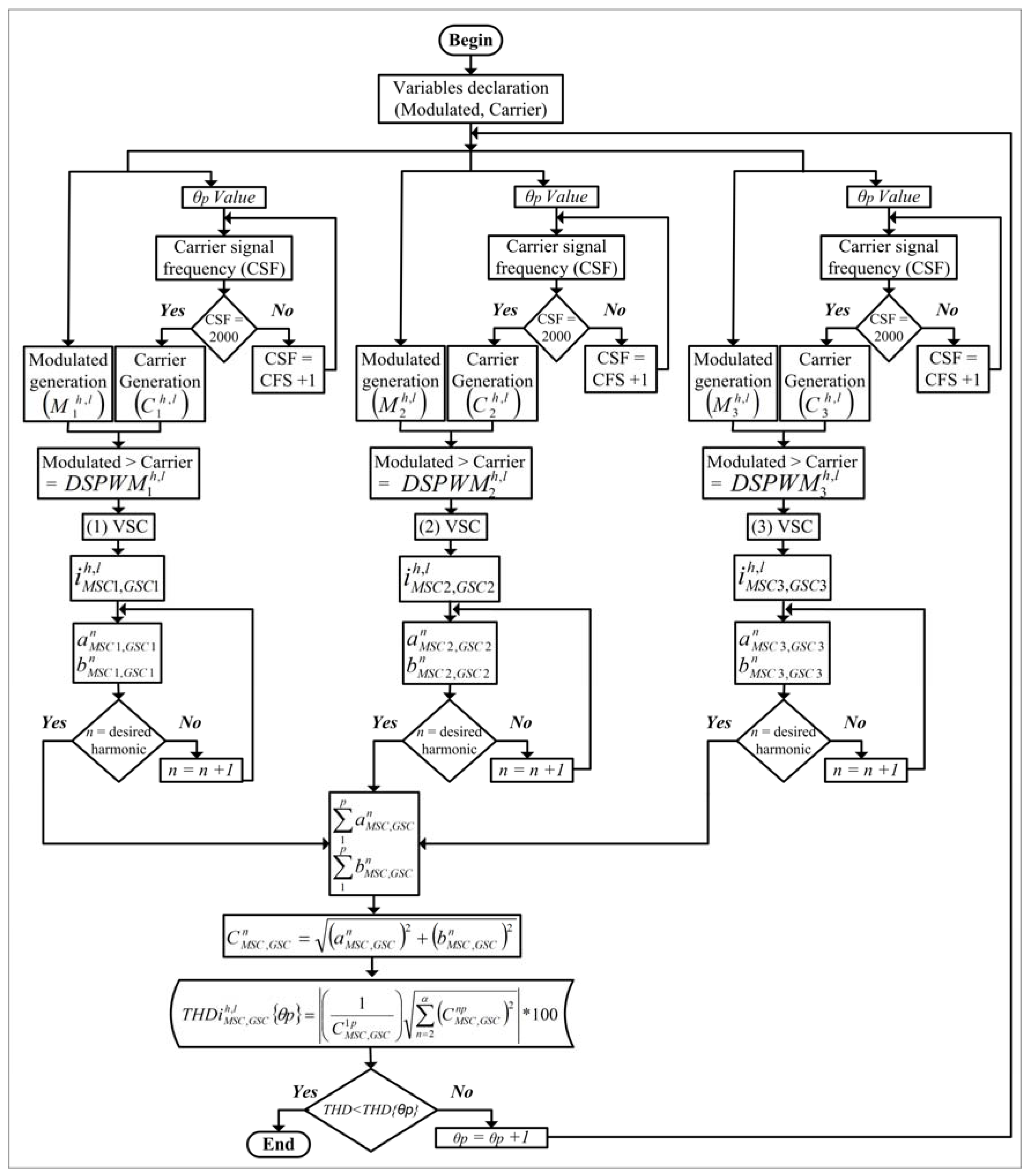
3. Modeling of the DSPWM Technique Applied in the THD Reduction

Digital modulation techniques are the most generalized framework in the control of modern power electronics converters applications. Digital sinusoidal pulse width modulation (DSPWM) is a modulation technique created by the internal generation of the modulated and carrier signals using a digital controller [22].

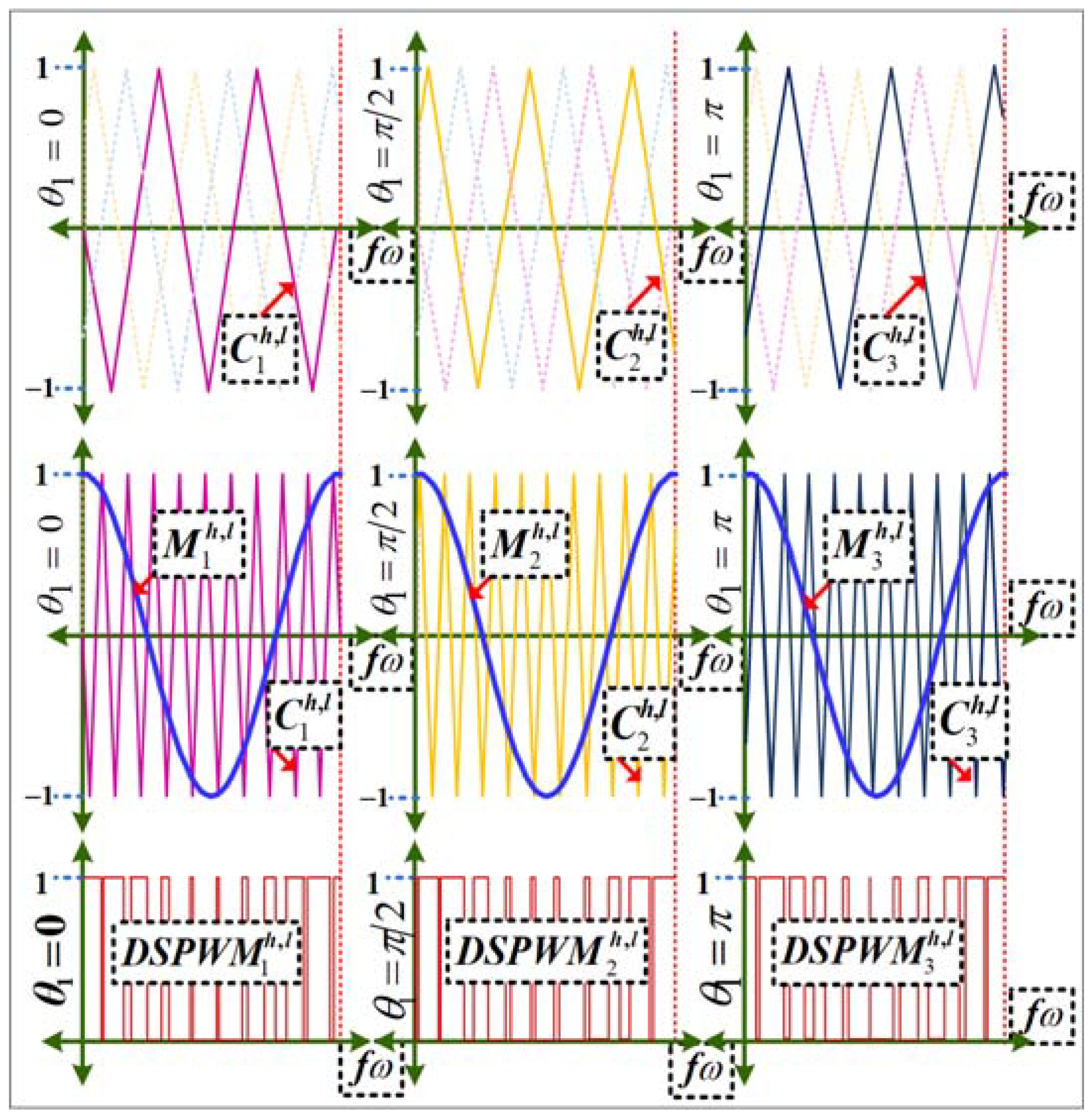
THD reduction is achieved by modifying the DSPWM switching signals in each VSC. This is carried out by applying a different phase shift angle in each carrier signal of each VSC; the modulated signal angle is not changed. Then, the output signals (voltage or current) of each VSC are added. In this paper, the AFE converter is built with three VSC connected in parallel. Figure 3 shows the comparison between the modulated (without phase shift angle) and carrier (with phase shift angle) signals, generating the DSPWM signal (phase a) corresponding to each VSC connected in parallel. The correct phase shift angle between each carrier signal is established putting up different values of total phase shift angle at the WES, see Figure 2. The analysis is shown in

Table 1. Analysis of different phase shift at the carrier signal.

Total Phase Shift (θp)	Carrier Phase Shift in Each VSC			% Total Harmonic Distortion (THD)
	θ1	θ2	θ3
0	0	0	0	6.8%
π/6	0	π/18	π/9	4.33%
π/3	0	π/9	2π/9	1.99%
π/2	0	π/6	π/3	2.054%
2π/3	0	2π/9	4π/9	1.271%
5π/6	0	5π/18	5π/9	1.608%
π	0	π/3	2π/3	4.616%
7π/6	0	7π/18	7π/9	5.635%
4π/3	0	4π/9	8π/9	2.864%
3π/2	0	π/2	π	1.239%
5π/3	0	5π/9	10π/9	1.36%
11π/6	0	11π/18	11π/9	1.867%
2π	0	2π/3	4π/3	2.756%

.

In Table 1 it is observed that the angle that generates a lower THD is 3π/2; hence, this angle divides the number of VSCs placed in parallel, i.e.,

$${\theta }_p=(3\pi /2)/p$$

(33)

where p is the number of VSC connected in parallel and θ_p is the carrier signal phase shift angle of each VSC.

The n-harmonics content is calculated through the Fourier series expansion, i.e.,

$$F(t)=C_0+{\displaystyle \sum _{n=1}^{\infty }\left(C_{MSC,GSC}^n\cos \left(n{\omega }_{0}t+\sigma \right)\right)}$$

(34)

where n is the harmonic number, $C_{MSC,GSC}^n=\sqrt{{(a_{MSC,GSC}^n)}^2+{(b_{MSC,GSC}^n)}^2}$, $\sigma ={\tan }^{-1}(b_{MSC,GSC}^n/a_{MSC,GSC}^n)$ and $C_0=a_0/2$.

The magnitude of each harmonic is calculated by,

$$a_{MSC,GSC}^n=\frac{2}{T}\left({\displaystyle {\int }_{-T/2}^{T/2}F(t)\cos (n{\omega }_{0}t)d{\omega }_{0}t}\right)$$

(35)

$$b_{MSC,GSC}^n=\frac{2}{T}\left({\displaystyle {\int }_{-T/2}^{T/2}F(t)\sin (n{\omega }_{0}t)d{\omega }_{0}t}\right)$$

(36)

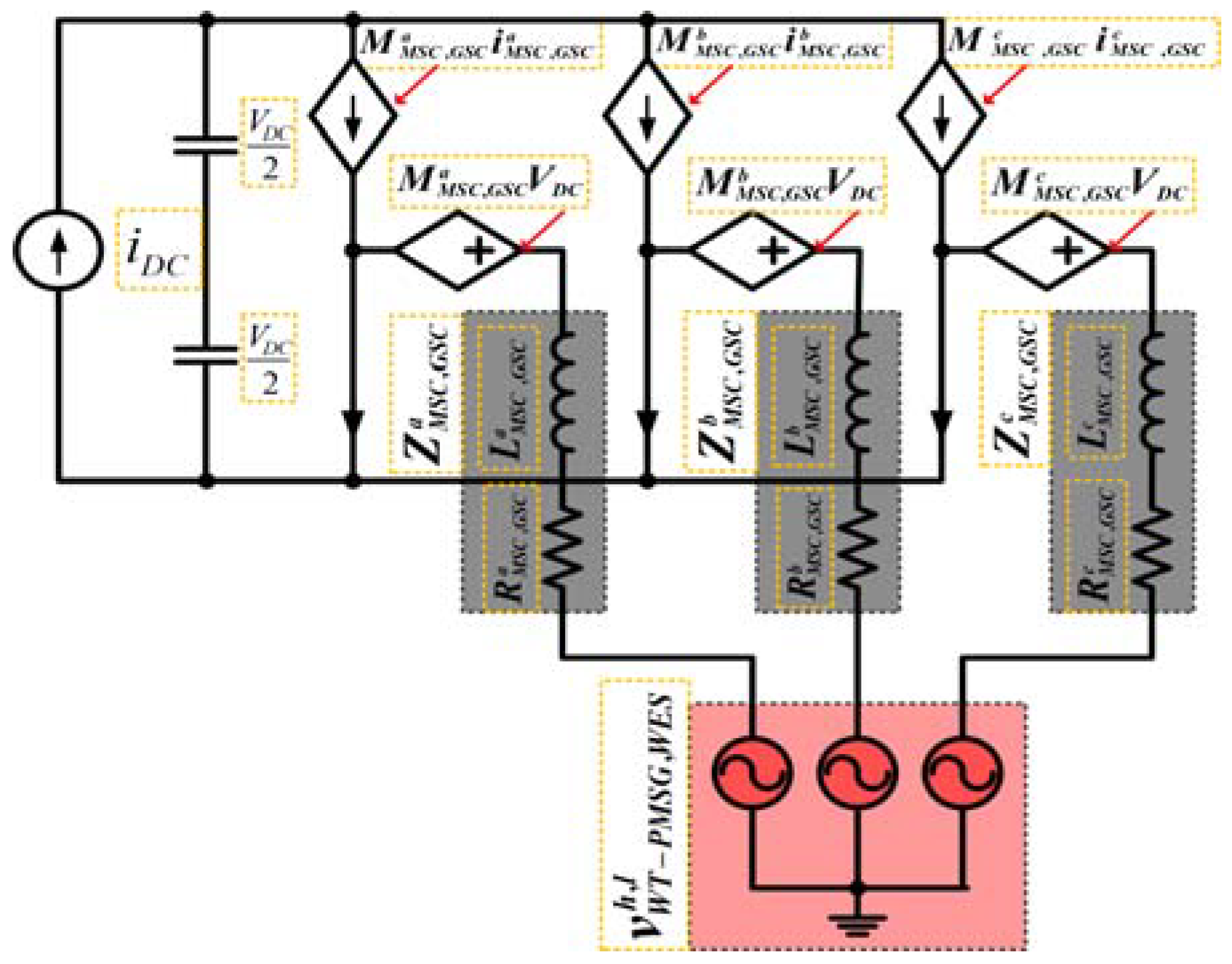
To calculate the THD in the AFE converter, the individually equivalent circuit of each three-phase VSC is analyzed.

A three-phase VSC equivalent circuit is shown in Figure 4.

The three-phase VSC is represented by the next equation,

$${\left[\begin{array}{ccc}2(Z\ast i^a)& -(Z\ast i^b)& -(Z\ast i^c)\\ -(Z\ast i^a)& 2(Z\ast i^b)& -(Z\ast i^c)\\ -(Z\ast i^a)& -(Z\ast i^b)& 2(Z\ast i^c)\end{array}\right]}_{MSC,GSC}=\left[{\left(\begin{array}{c}{v}^a-v^b\\ v^b-v^c\\ v^c-v^a\end{array}\right)}_{MSC,GSC}-{\left(\begin{array}{c}{v}^a-v^b\\ v^b-v^c\\ v^c-v^a\end{array}\right)}_{WT-PMSG,WES}\right]$$

(37)

Using Kirchhoff’s current law (KCL), the currents flowing towards the MSC or/and GSC node must be equal to the currents leaving the MSC or/and GSC node, i.e.,

$$i_{MSC,GSC}^c=-\left(i_{MSC,GSC}^a+i_{MSC,GSC}^b\right)$$

(38)

Replacing equation (38) in (37) gives line-to-line current of the MSC or/and GSC, i.e.,

$$\left[\begin{array}{c}{i}_{MSC,GSC}^{ab}\\ i_{MSC,GSC}^{bc}\\ i_{MSC,GSC}^{ca}\end{array}\right]=\left(\frac{1}{3Z_{MSC,GSC}^{h,l}}\right)\left({\left[\begin{array}{c}{v}^a-v^b\\ v^b-v^c\\ v^c-v^a\end{array}\right]}_{WT-PMSG,WES}-{\left[\begin{array}{c}{v}^a-v^b\\ v^b-v^c\\ v^c-v^a\end{array}\right]}_{MSC,GSC}\right)$$

(39)

where v_WT-PMSG represents the WT-PMSG voltage, v_WES exemplifies the WES voltage, v_MSC,GSC is the VSC AC-side output voltage of MSC or/and GSC, and $Z_{MSC,GSC}^{h,l}$ is the AC-side filter of MSC or/and GSC.

The v_MSC,GSC value depends on $M_{MSC,GSC}^{h,l}$ signal modulation. The modulated and carrier signals implement the DSPWM technique of Figure 3; these have modulation frequencies of 60Hz (ω₀) and 7kHz (fω), respectively.

The carrier signal is composed by an up-slope and a down-slope, calculated as,

$$C_{t_{1}p}=1-\left(\left(4/f\omega \right)\left({\omega }_0{t}_1-{\theta }_p\right)\right)$$

(40)

$$C_{t_{2}p}=\left(\left(4/f\omega \right)\left({\omega }_0{t}_2-\left(f\omega /2\right)-{\theta }_p\right)\right)-1$$

(41)

where C_t1,t2p is the composed carrier signal, θ_p is phase shift angle of each VSC, fω is switching frequency of the carrier signal, t₁ is the time for the up-slope, t₂ is the time for the down-slope.

Time t₁ for up-slope is:

$${\theta }_p\le t_1\le \left(\left(f\omega /2\right)+{\theta }_p\right)$$

(42)

Time t₂ for down-slope is:

$$\left(\left(f\omega /2\right)+{\theta }_p\right)\le t_2\le \left(f\omega +{\theta }_p\right)$$

(43)

Modulated signals in each VSC are described by the carrier signal time, that is:

$$\begin{array}{l}{M}_{t_{1}p}^{h,l}=\cos (t_1+\phi )\\ M_{t_{2}p}^{h,l}=\cos (t_2+\phi )\end{array}$$

(44)

where h,l = a,b,c the VSC phases in MSC and GSC, respectively, and φ is the corresponding angle of each phase in the modulated signal.

The comparison between modulated and carrier signals defines the DSPWM signal, its representation is:

$$\begin{array}{l}DSPW{M}_{t_{1}p}^{h,l}=\left|M_{t_{1}p}^{h,l}\le C_{t_{1}p}\right|\\ DSPW{M}_{t_{2}p}^{h,l}=\left|M_{t_{2}p}^{h,l}\le C_{t_{2}p}\right|\end{array}$$

(45)

Multiplying the DSPWM signal and DC voltage amplitude generates the VSCs output voltage for each phase value in MSC and GSC, i.e.,

$$v_{MSC,GSC}^{h,l}=V_{DC}*DSPW{M}_{MSC,GSC}^{h,l}$$

(46)

The WT-PMSG voltage $v_{WT-PMSG}^h$ is generated by,

$$\begin{array}{l}{v}_{t_{1}WT-PMSG}^h=PMSG\left(\cos \left({\omega }_{rPMSG}{t}_1+{\theta }_{rPMSG}\right)\right)\\ v_{t_{2}WT-PMSG}^h=PMSG\left(\cos \left({\omega }_{rPMSG}{t}_2+{\theta }_{rPMSG}\right)\right)\end{array}$$

(47)

where PMSG is the WT-PMSG amplitude voltage and ϕ is the corresponding angle of each phase in the three-phase WT-PMSG.

And the WES voltage $v_{WES}^l$ is produced by,

$$\begin{array}{l}{v}_{t_{1}WES}^l=WES\left(\cos \left({\omega }_0{t}_1+{\varphi }_{WES}\right)\right)\\ v_{t_{2}WES}^l=WES\left(\cos \left({\omega }_0{t}_2+{\varphi }_{WES}\right)\right)\end{array}$$

(48)

where WES is the AC grid amplitude voltage and ϕ_WES is the corresponding angle of each phase in the three-phase WES grid.

The output current in each VSC is calculated as,

$$\begin{array}{l}\left[i_{t_{1}MSC,GSC}^{h,l}\right]=(1/(3Z_{MSC,GSC}))\left(\left[v_{t_{1}WT-PMSG,WES}^{h,l}\right]-\left[v_{t_{1}MSC,GSC}^{h,l}\right]\right)\\ \left[i_{t_{2}MSC,GSC}^{h,l}\right]=(1/(3Z_{MSC,GSC}))\left(\left[v_{t_{2}WT-PMSG,WES}^{h,l}\right]-\left[v_{t_{2}MSC,GSC}^{h,l}\right]\right)\end{array}$$

(49)

The harmonic content spectrum to obtain the THD is required. By using (35), (36), and (49) the spectrum is calculated as,

$$a_{MSC,GSC}^n=\left(\frac{2}{T}\right)\left[\left({\displaystyle {\int }_{{\theta }_p}^{\left(f\omega /2\right)+{\theta }_p}\left(i_{t_{1}MSC,GSC}^{h,l}\cos \left(n{\omega }_0{t}_1\right)\right)d{\omega }_0{t}_1}\right)+\left({\displaystyle {\int }_{\left(f\omega /2\right)+{\theta }_p}^{f\omega +{\theta }_p}\left(i_{t_{1}MSC,GSC}^{h,l}\cos \left(n{\omega }_0{t}_2\right)\right)d{\omega }_0{t}_2}\right)\right]$$

(50)

$$b_{MSC,GSC}^n=\left(\frac{2}{T}\right)\left[\left({\displaystyle {\int }_{{\theta }_p}^{\left(f\omega /2\right)+{\theta }_p}\left(i_{t_{1}MSC,GSC}^{h,l}sin\left(n{\omega }_0{t}_1\right)\right)d{\omega }_0{t}_1}\right)+\left({\displaystyle {\int }_{\left(f\omega /2\right)+{\theta }_p}^{f\omega +{\theta }_p}\left(i_{t_{2}MSC,GSC}^{h,l}sin\left(n{\omega }_0{t}_2\right)\right)d{\omega }_0{t}_2}\right)\right]$$

(51)

For the harmonic content of the output current signal, the magnitude of the individual harmonics is calculated for each VSC connected in parallel to the MSC and GSC and these are added, i.e.,

$$a_{MSC,GSC}^{n1}+a_{MSC,GSC}^{n2}+\dots +a_{MSC,GSC}^{np}$$

(52)

$$b_{MSC,GSC}^{n1}+b_{MSC,GSC}^{n2}+\dots +b_{MSC,GSC}^{np}$$

(53)

where p is the number of VSCs placed in parallel and n is the number of harmonics.

The THD in the AFE converter output current is,

$$THD{i}_{MSC,GSC}^{h,l}=\left|\left(\frac{1}{C_{MSC,GSC}^{1p}}\right)\sqrt{{\displaystyle \sum _{n=2}^{\infty }{\left(C_{MSC,GSC}^{np}\right)}^2}}\right|\ast 100$$

(54)

where $C_{MSC,GSC}^{1p}$ is the fundamental harmonic magnitude and $C_{MSC,GSC}^{np}$ is the n^tth harmonic magnitude.

Finally, the lower THD content in the output current of the AFE converter is generated when the output current signals of each VSC are added, i.e.,

$$i_{MSC,GSC}^{h,l}=i_{MSC1,GSC1}^{h,l}+i_{MSC2,GSC2}^{h,l}+\dots +i_{MSCp,GSCp}^{h,l}$$

(55)

Figure 5 shows the flow diagram that describes the generated method for a lower harmonic content, represented from Equations (33) to (55).

4. Simulation Results: Study Case for WES

In this paper, Matlab-Simulink^® (Matlab r2015b, Mathworks, Natick, MA, USA) and Opal-RT Technologies^® module (OP-5600) (Montreal, QC, Canada) are the main elements in the WES real-time simulation, since the OP-5600 module uses the rapid control prototyping (RCP) concept, which allows testing of the control law without the need for any programming code.

In Figure 2, the simulated WES is shown. It contains a WT-PMSG to supply the MSC, the AFE parallel converter and the infinite bus (considered as an ideal voltage source) to supply the GSC. The MSC and GSC are connected to WT-PMSG and the AC grid through RL filters, both converters are formed by three VSCs connected in parallel and each one is designed to possess a power and voltage of 2 MVA and 2.5 kV, respectively. The characteristics of the WT-PMSG are described in

Table 2. Wind turbine-permanent magnet synchronous generator (WT-PMSG) characteristics.

Wind Turbine (WT)
Nominal output power	2 MW	Base wind speed	12 m/s
Pitch angle	45 deg	base generator speed	1.2 pu
Permanent Magnet Synchronous Generator (PMSG)
Mechanical input	−8.49 × 105 N.m.	Stator resistance	8.2 × 10−4 Ω
Armature inductance	1.6 × 10−3 H	Flux linkage	5.82
Viscous damping	4.04 × 103 N.m.s	Inertia	2.7 × 106 kg.m2
Pole pairs	4	Rotor type	Round

.

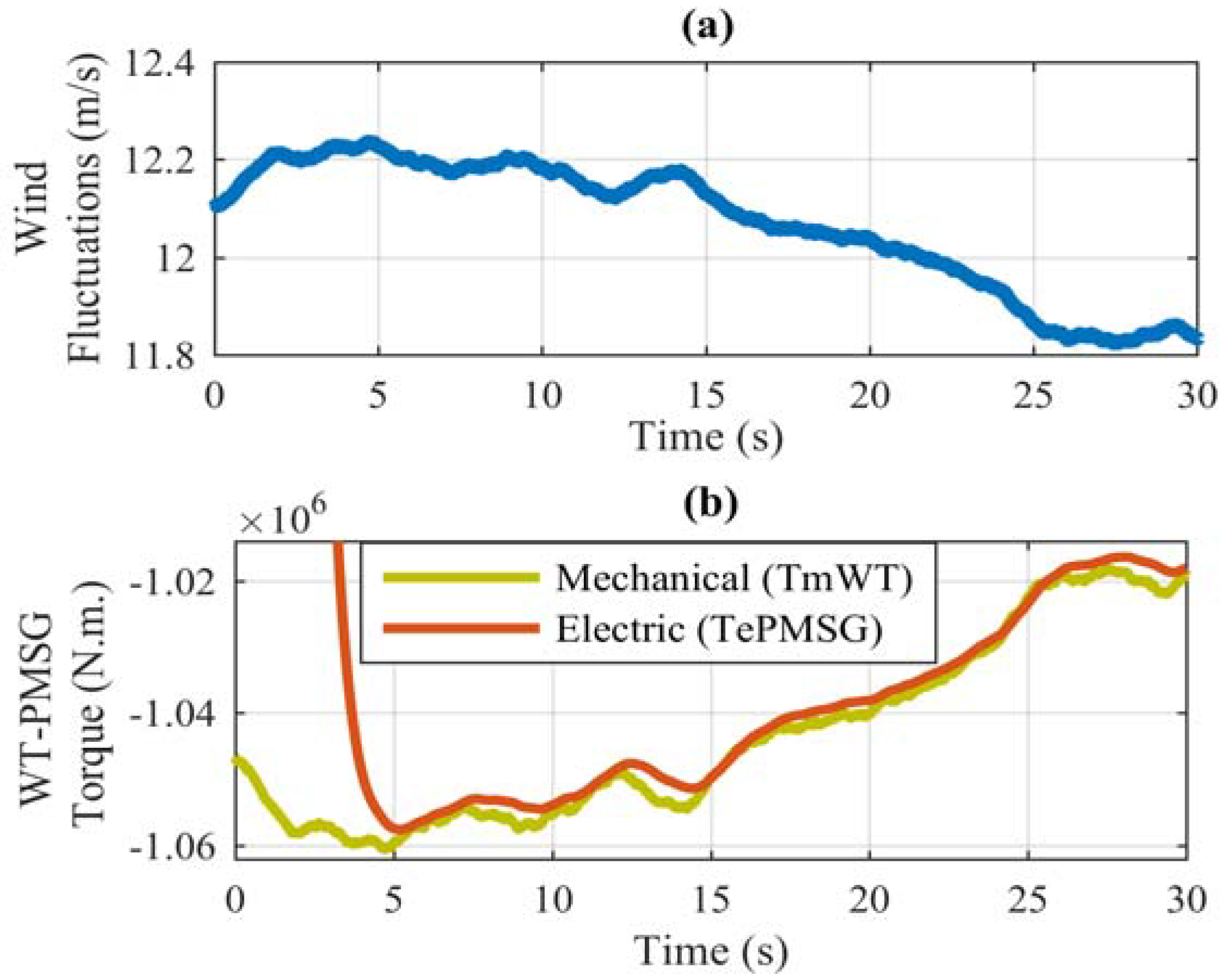
To verify the correct WES operation in Figure 2, in Figure 6 the behavior of the WT mechanical torque and the PMSG electric torque are analyzed.

Figure 6a details the wind fluctuations applied to the WT, which are generated in Matlab-Simulink^® by a rotor wind model developed by RISOE National Laboratory based on Kaimal spectra. Figure 6b shows the behavior of the WT mechanical torque and the PMSG electric torque in the presence of wind fluctuations. It is possible to observe that the electric torque follows the mechanical torque behavior, due to the effective structure of the MSC closed-loop control.

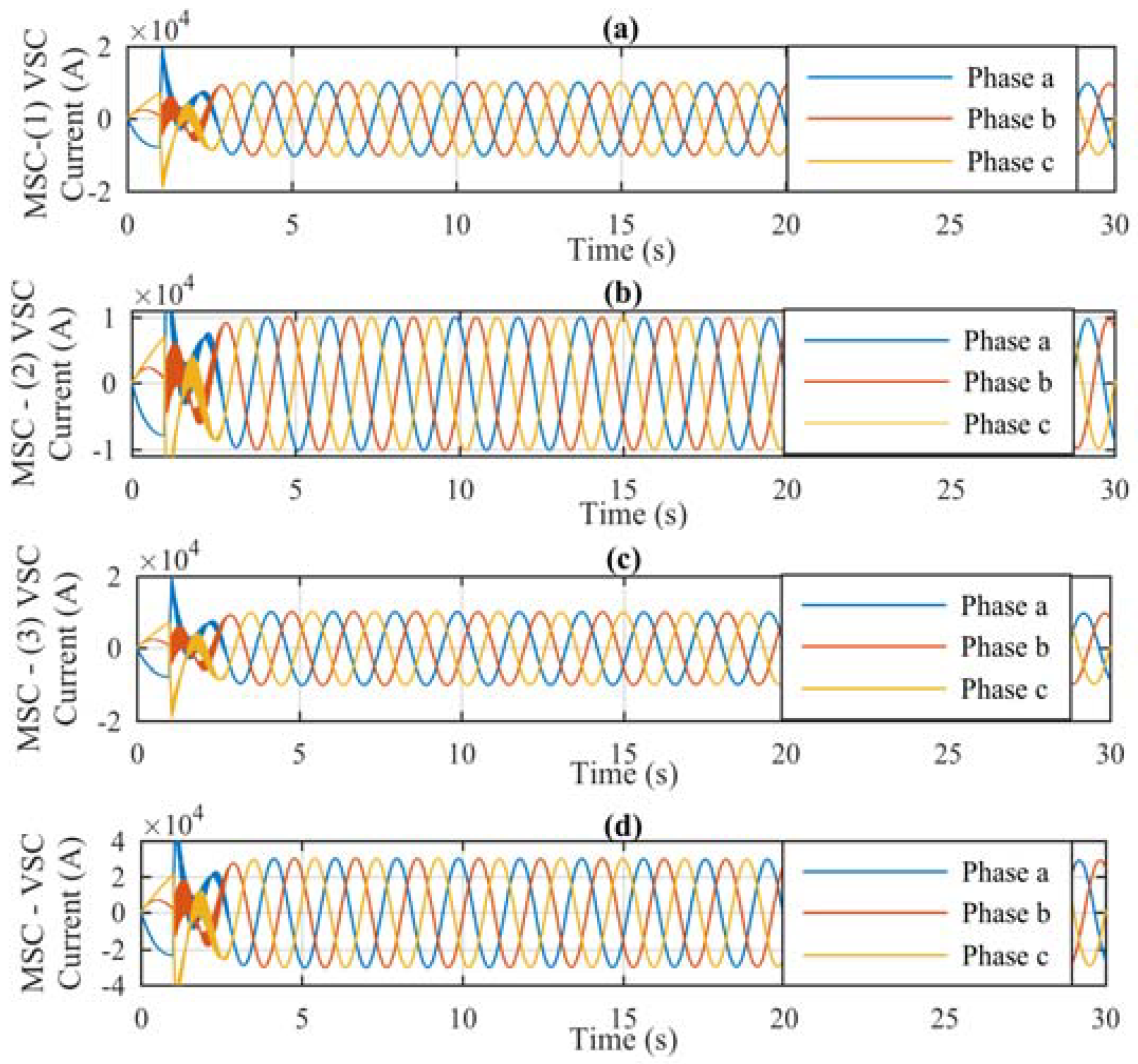
Figure 7 shows the generated current by the WT-PMSG, which is controlled through the MSC of the AFE parallel converter. Because the MSC is formed using the parallel connection of three VSCs, each VSC can handle one third of the total current generated by the WT; Figure 7a–c illustrates the current in the (1), (2), and (3) VSCs, respectively, and in Figure 7d the MSC total current is shown.

While, the main MSC function is the rotor flux frequency control, generating the power conversion between medium AC voltage and low DC voltage levels, the most important GSC function is to keep the DC-link constant, transferring the generated power between the WT-PMSG and AC grid in the voltages required by the consumers.

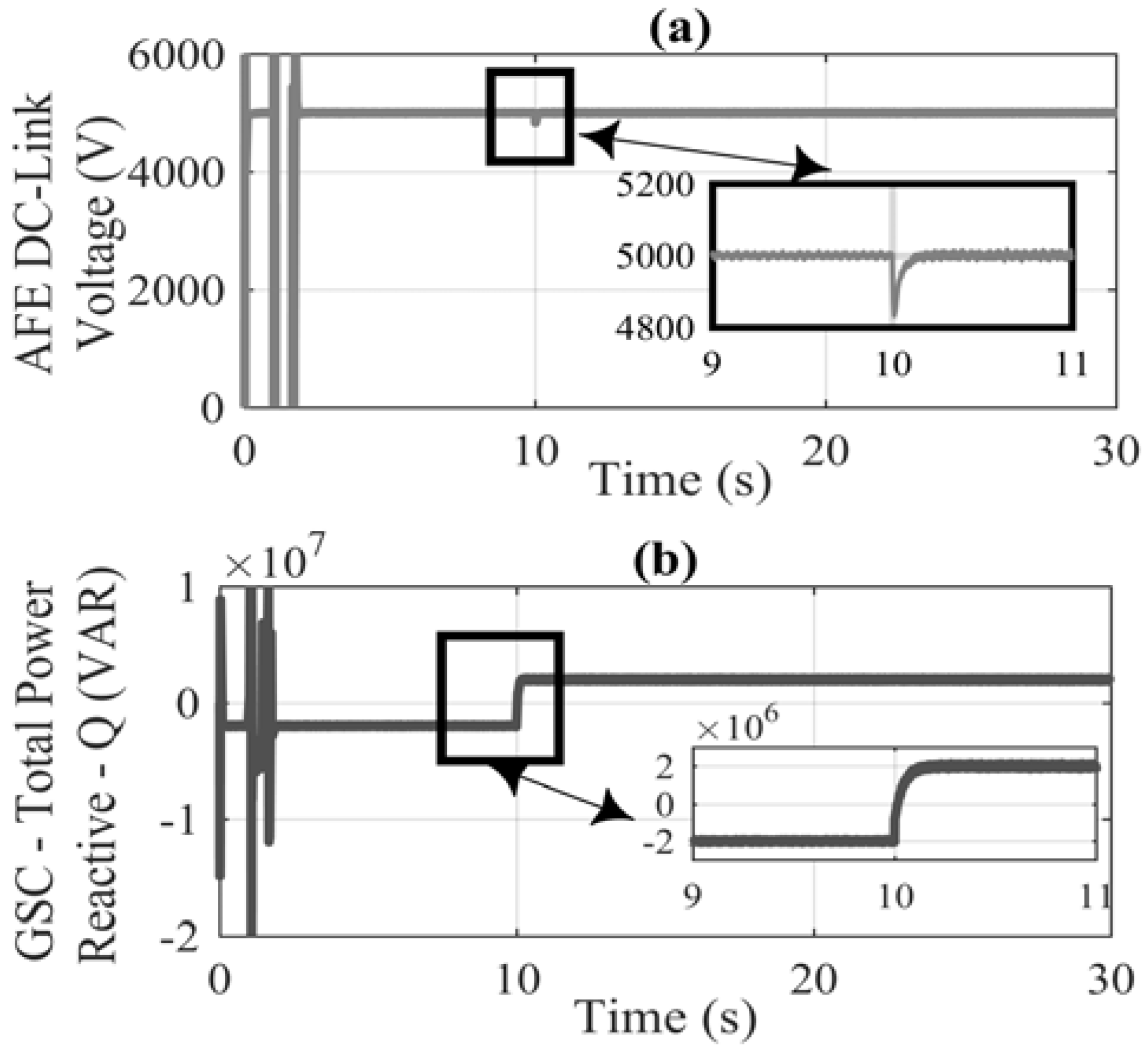
Figure 8a shows that the DC-link remains constant at 5kV, because, when the MSC requires a reactive power exchange, due to the wind fluctuations of Figure 6a, the GSC restores the DC-Link, and at the same time injects the needed reactive power, as shown in Figure 8b.

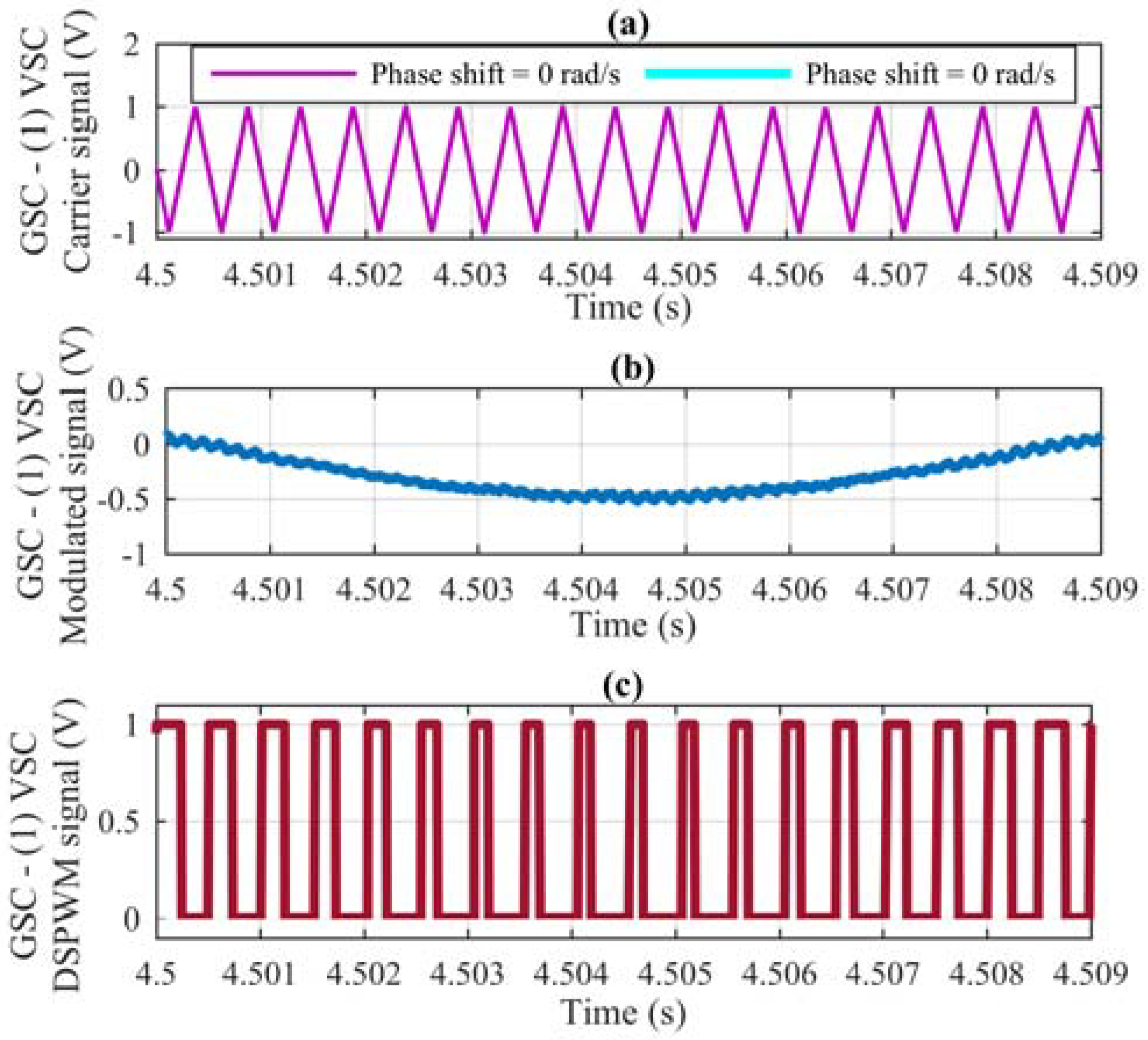
Figure 9, Figure 10 and Figure 11 detail the applied DSPWM to each of the VSCs connected in parallel for the correct operation of the GSC, at the stability time from 4.5 to 4.509 ms. In Figure 9, it can be seen that both the carrier signal of Figure 9a and the modulated signal of Figure 9b start at the same time, i.e., the carrier signal does not present any phase shift, generating the DSPWM signal in Figure 9c, this is applied to the first VSC connected in parallel in the GSC. 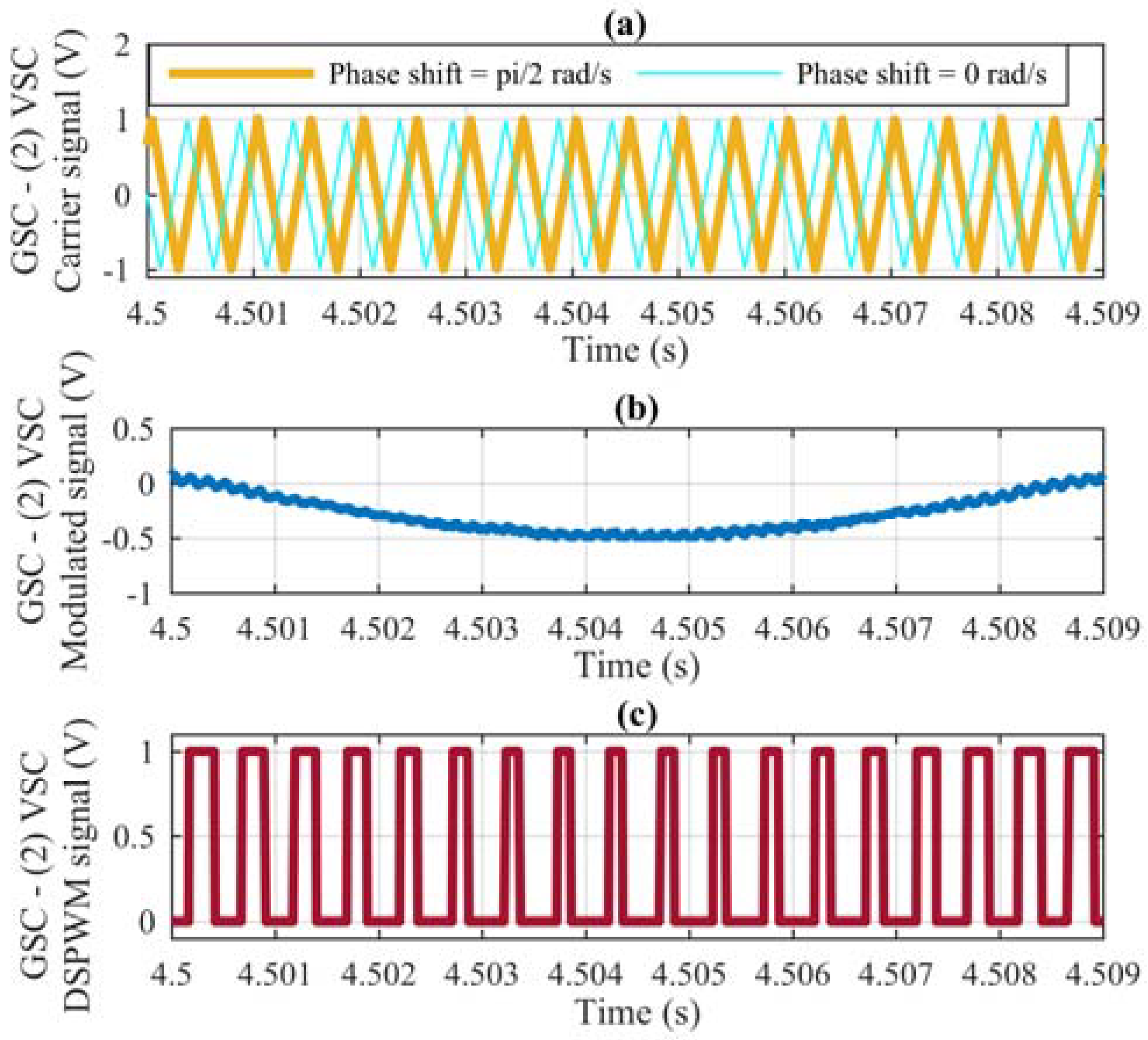In Figure 10, the DSPWM generation applied to the second VSC connected in parallel to the GSC is shown; in Figure 10a, a phase shift of π/2 (rad/s) in the carrier signal is observed. This is compared with the modulated signal of Figure 10b, originating the DSPWM with the phase shift of Figure 10c. 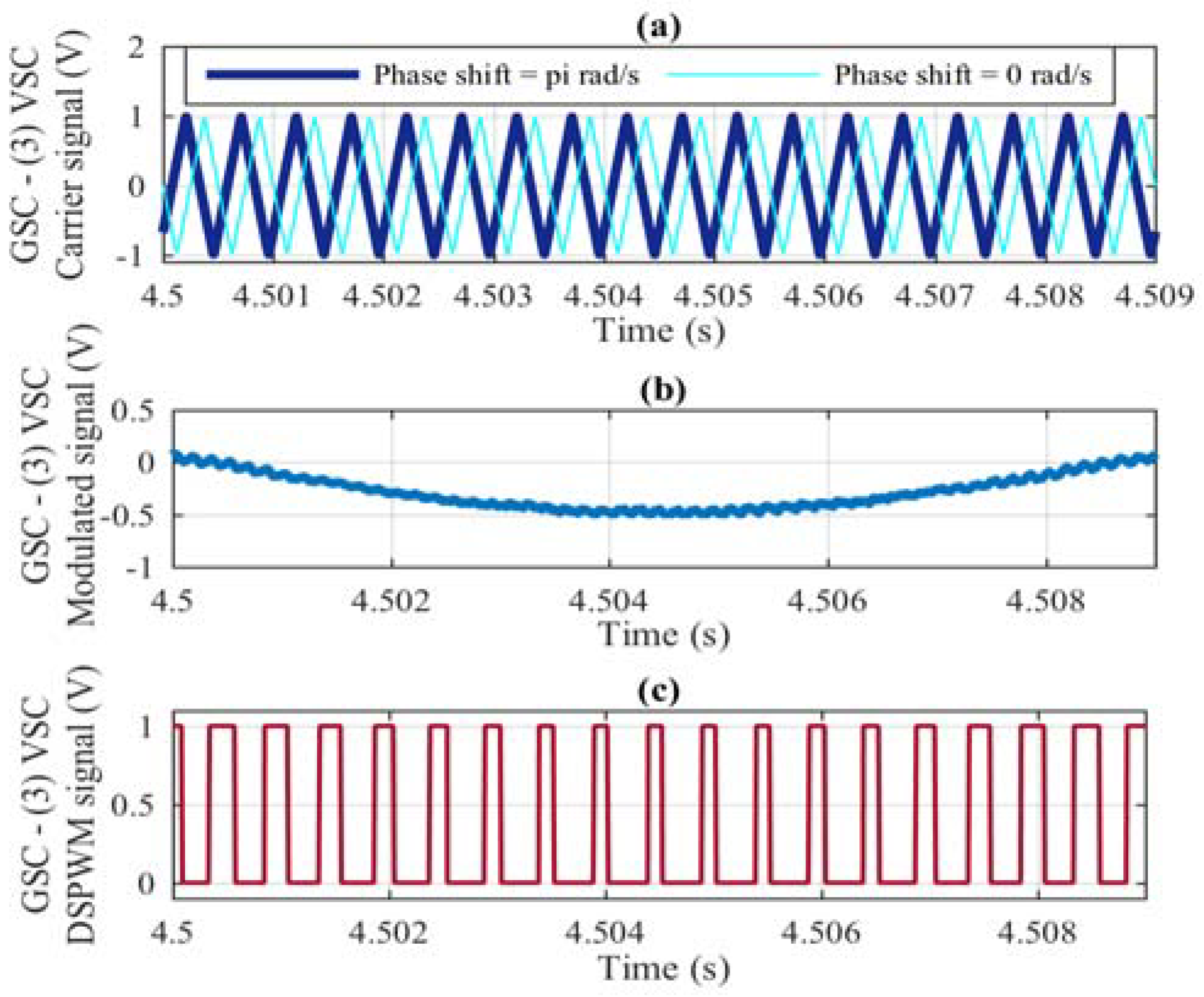Finally, in Figure 11, the DSPWM signal applied to the third VSC connected in parallel of the GSC is presented; in Figure 11a the carrier is observed with a phase shift of π (rad/s) with respect to the modulated signal of Figure 11b, generating the DSPWM of Figure 11c.

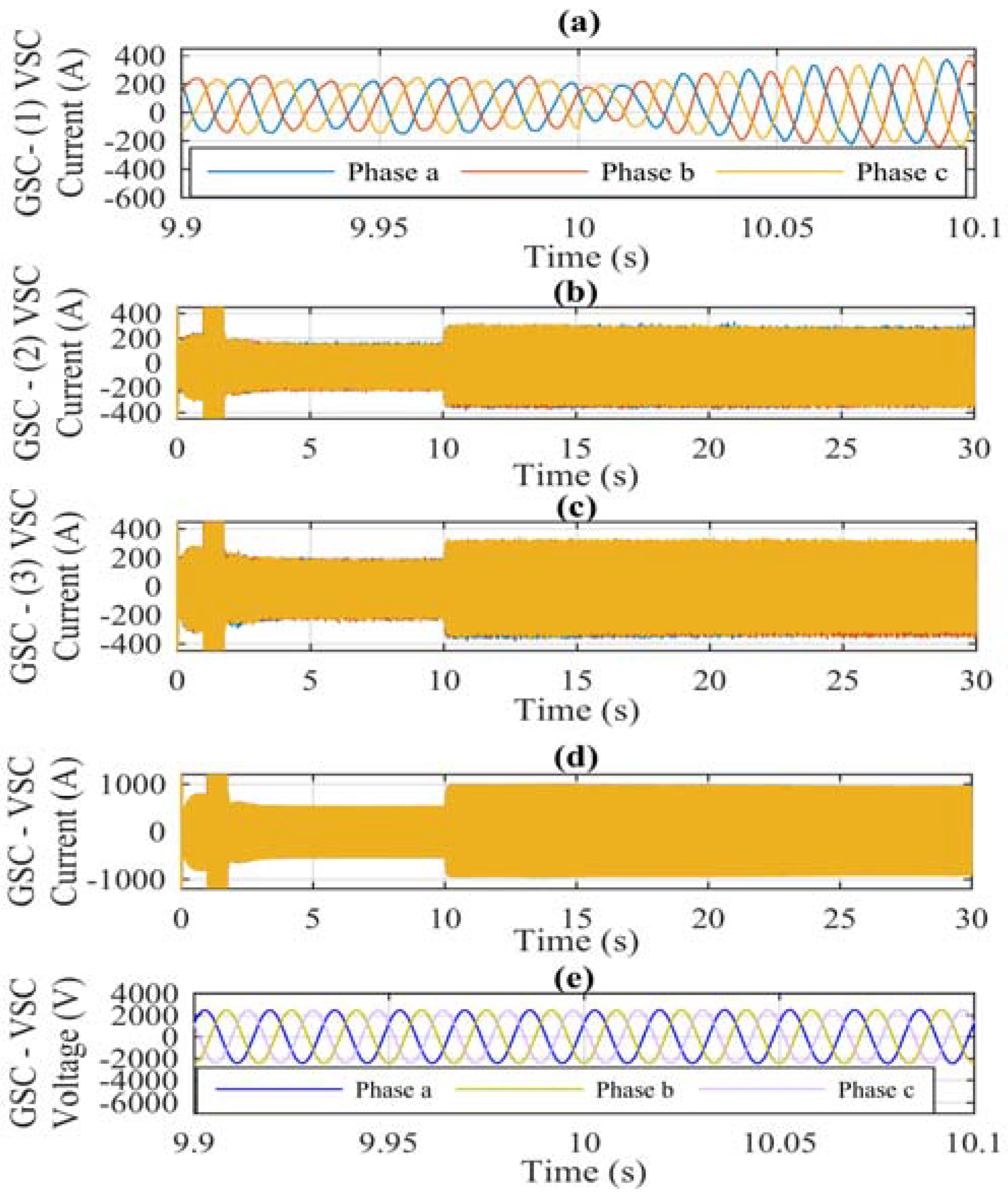
Figure 12 shows the electrical variables present at the GSC when the corresponding phase shift in the carriers of each VSC connected in parallel is performed, according to Equation (33). Figure 12a shows the (1) VSC current generated due to the phase shift at the carrier of Figure 9a; in which, a zoom in time is made from 9.9 to 10.1 s, observing the current magnitude and behavior in the presence of the reactive power exchange at Figure 8b. Figure 12b shows the (2) VSC current generated due the phase shift at the carrier of Figure 10a; Figure 12c shows the (3) VSC current generated due the phase shift at the carrier of Figure 11a; in Figure 12a–c, each current magnitude is 330 A, generating a total GSC current of 990 A, as seen in Figure 12d; Figure 12e details a zoom in time from 9.9 to 10.1 s, observing the generated voltage at the GSC, the magnitude of which corresponds to 2500 V.

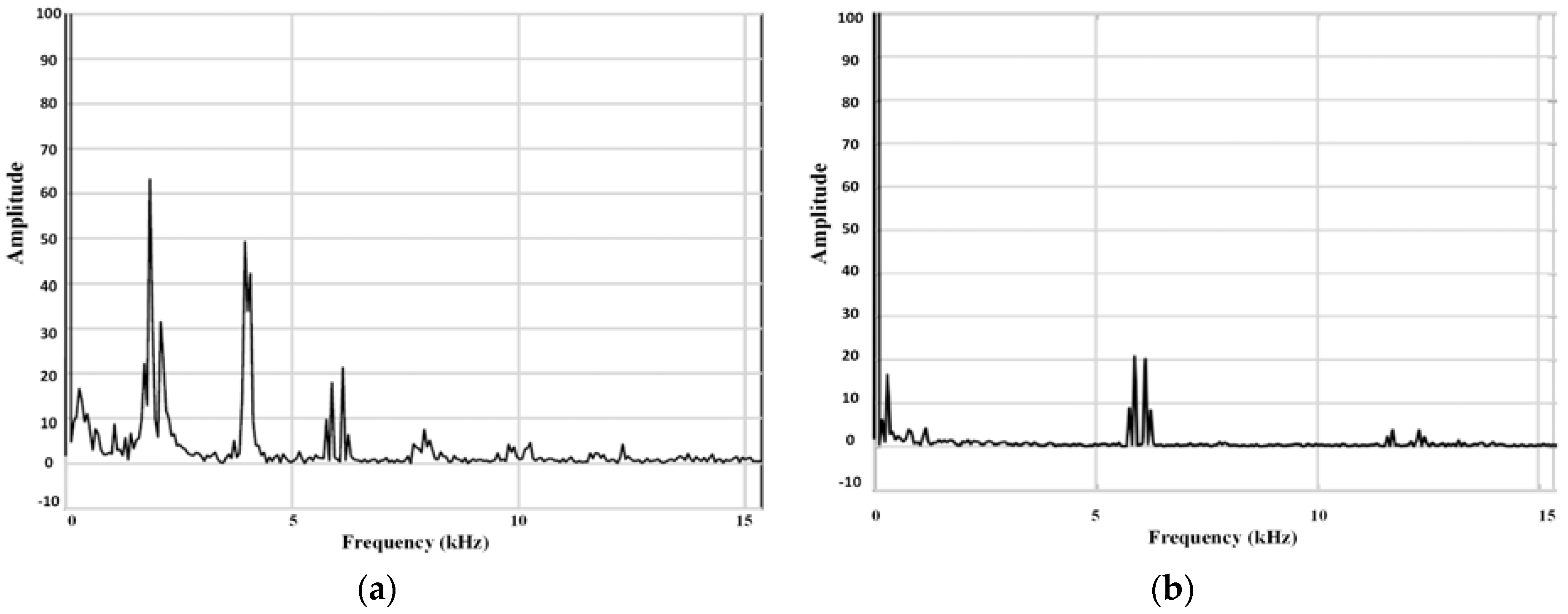
Finally, the current THD is shown in Figure 13; Figure 13a contents the THD without any phase shift between carriers of each VSC of the AFE converter, which corresponds to 6.8%. Please observe that, in Figure 13b, when the corresponding phase shift is performed in the carriers, the current THD is reduced to 1.239%, as specified in Table 1. The Figure 13 shows the harmonics magnitude reduction or even their elimination, once the phase shift between carriers has been made. The THD was reduced by approximately 5.5 times.

5. Real Time Simulation Results: Study Case for WES using Opal-RT Technologies^®

To verify the robustness of the applied control in the AFE converter and the THD reduction at the WES, the grid of Figure 2 in real time using the Opal-RT Technologies^® is simulated; generating an RCP concept that tests the WES dynamics without the need for any programming code. Specifically, the VSC of the AFE converter is composed by the insulated gate bipolar transistor (IGBTs), these use a switching frequency of 7 kHz. Figure 14a shows the wind fluctuations generated by a rotor wind model developed by RISOE National Laboratory based on Kaimal spectra. Figure 14b contains the mechanical torque behavior generated by the wind turbine, and in response to the applied control at the MSC, the PMSG electric torque is able to follow the same behavior.

Figure 15 presents the main electrical variables of the WES simulated in real time by OPAL-RT^®. Figure 15a contains the current portion that handles the first VSC connected in parallel; as can be seen, as only three VSCs are connected in parallel, each one handles only a third of the total current generated by the MSC. The total current is presented in Figure 15b, and this is transferred by the WT-PMSG to the AC grid through the AFE converter. In Figure 15c, the generated voltage by the MSC is observed. It is important to mention that the main objective of the GSC is to support the constant DC-link in the presence of any disturbance (such as voltage/current variations due to wind fluctuations or reactive power exchanges by the behavior of the WT). This is evidenced in Figure 15d and is possible due to the applied control robustness. Figure 15e shows the GSC ability to exchange reactive power, that is, the ability of the injection/absorption of 6 MVA into the AC grid. Figure 15f contains the handled current portion by the first VSC connected in parallel at the GSC; similarly, as only three VSCs are connected in parallel, each one handles only a third of the total current generated by the GSC; the total current is presented in Figure 15g. Finally, in Figure 15h, the handled voltage by the GSC is observed, this is taken from the PCC attached to the AC grid. The THD of the handled total current by the GSC is generated through the OPAL-RT^®. The generated THD without phase shift between the carriers of each VSC connected in parallel corresponds to 8.85%. The produced THD once the phase shift between the carriers of each VSC is made corresponds to 2.18%, and the phase shift from equation (33) is calculated; therefore, it is demonstrated that making the WES real-time simulation and applying the phase shift between the carriers of each VSC, the THD can be reduced up to four times.

Finally, it is important to mention that, the block –written to file– produces the results of Figure 14 and Figure 15 in the MATLAB–Simulink^® interface; this allows plotting the variables in MATLAB windows in order to have a better presentation.

6. Conclusions

In this paper, the AFE converter topology has been analyzed for the THD reduction in a WES. The WES has been formed by a WT-PMSG connected to the AC grid through an AFE converter. The AFE converter topology has been made from the use of a single VSC to use pVCS connected in parallel.

The effective THD reduction has been made through the variation in the DSPWM technique applied to each VSC, that is, applying a different phase shift angle at the carrier signals of each VSC connected in parallel, while the modulated signal angle has been kept constant.

To verify the robustness to the applied control, the WES control law has been simulated in real time using the Opal-RT Technologies^®, generating an RCP concept, which tests the WES dynamics without the need for any programming code.

The obtained results have shown a type-4 WT with total output power of 6MVA generates a THD reduction up to 5.5 times of the total WES current output by Fourier series expansion.