Full-Speed Range Encoderless Control for Salient-Pole PMSM with a Novel Full-Order SMO

Abstract

For salient-pole permanent magnet synchronous motor (PMSM), the amplitude of extended back electromotive force (EEMF) is determined by rotor speed, stator current and its derivative value. Theoretically, even at extremely low speed, the back EEMF can be detected if the current in q-axis is changing. However, it is difficult to detect the EEMF precisely due to the current at low speed. In this paper, novel full-order multi-input and multi-output discrete-time sliding mode observer (SMO) is built to detect the rotor position. With the proposed rotor position estimation technique, the motor can start up from standstill and reverse between positive and negative directions without a position sensor. The proposed method was evaluated by experiment.

1. Introduction

Permanent magnet synchronous motor (PMSM) has many benefits, such as high efficiency, high power density, and good dynamic performance, which has been widely used in various kinds of industrial and domestic applications [1,2].

As is well known, rotor position is required in high-performance control of PMSM, which is usually obtained by using an external dedicated sensor. However, the position sensor may increase cost, weight, volume, and complexity; reduce reliability; and restrict the application area [3,4].

To detect the rotor position information directly from the model of PMSM, various kinds of strategies have been proposed up to date, such as voltage model based methods [5,6], Kalman filter based methods [7,8], and state observers based methods [9,10]. Among them, sliding mode observer (SMO) is a very promising option [11,12,13].

The SMO-based rotor position estimation algorithm of salient-pole PMSM is more complicated than that of non-salient pole PMSM [14]. In $\alpha \beta$ coordinate system, the state equations of salient-pole PMSM are coupled with each other. The amplitude of the extended back electromotive force (EEMF) is determined by rotor speed, stator current and its derivative value. It is a challenge to estimate the EEMF accurately [12,13].

To obtain the rotor position of salient-pole PMSM, some SMO-based methods have been proposed. To facilitate digital control applications, a discrete-time SMO is constructed in [11], and a kind of position extraction algorithm is proposed to mitigate the oscillations. In [14], a rotor position estimation method based on extended flux model is proposed, while a discrete-time SMO and a position compensator are designed. A full-order discrete-time SMO-based position sensorless control method is introduced in [15], where the modeling uncertainties and external disturbances are considered.

However, in these studies, two single input and single output (SISO) SMO are built in $\alpha$-axis and $\beta$-axis, respectively, while the effect of coupling is neglected. A signum function or a sigmoid function is used as switching function, which cannot guarantee the convergence in the boundary layer [16]. During load (torque and/or speed) variations, it is a challenge to estimate the EEMF accurately [13]. Due to unwanted chattering, a filter is required to achieve desired back EEMF signal, which may cause phase shift and estimation error in the rotor position.

In this paper, an alternative rotor position estimation strategy for salient-pole PMSM is proposed. To improve the estimation results, the transient state of back EEMF is considered [17]. A fourth-order state equation of salient-pole PMSM in $\alpha \beta$ coordinate system is established; the state vector consists of currents and back EEMF. As the state vector is four-dimensional and input vector is two-dimensional, a novel multiple input and multiple output (MIMO) sliding mode observer is built for the system. To facilitate digital control applications, the sliding mode observer is studied in the discrete-time field. Pole placement technique [18,19] is used to design the switching surface; desired dynamic characteristics can be achieved through eigenvalue placement. To force the state trajectories reach and subsequently remain on the eventual sliding surface with a good movement quality, free hierarchical law is adopted as switching scheme, and discretized reaching law [20] is used to design the quasi-sliding mode and reaching process. Reaching law approach has many merits, such as guaranteeing robustness, reducing chattering, and revealing the motion mechanism of the system [21].

This paper is organized as follows: the SMO-based position sensorless control strategies for salient-pole PMSM are introduced in Section 1. In Section 2, a full-order state equation of salient-pole PMSM is built. In Section 3, a full-order SMO is proposed to detect the back EEMF and rotor position. In Section 4, the experimental results of the proposed position sensorless control are given. The paper is concluded in Section 5.

2. Full-Order State Equation of Salient-Pole PMSM

The model of salient-pole PMSM is shown in Figure 1. A, B and C are the three phase windings, $\alpha \beta$ represents the stationary reference frame, and $dq$ means the rotating reference frame.

Figure 1. Illustration of the salient-pole permanent magnet synchronous motor (PMSM) model.

The motor equation in $dq$ coordinate frame is expressed as Equation (1) [11].

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{u}_d\hfill \\ u_q\hfill \end{array}\right]& =\left[\begin{array}{cc}R+P{L}_d,& -\omega L_q\\ \omega L_q,& R+P{L}_d\end{array}\right]\left[\begin{array}{c}{i}_d\hfill \\ i_q\hfill \end{array}\right]\hfill \\ & +\left[\begin{array}{cc}0,& 0\\ \omega (L_d-L_q),& -P(L_d-L_q)\end{array}\right]\left[\begin{array}{c}{i}_d\hfill \\ i_q\hfill \end{array}\right]\hfill \\ & +\left[\begin{array}{c}0\\ \omega {\psi }_{PM}\end{array}\right]\hfill \end{array}$$

(1)

where P is a derivative operator; $R_s$ is stator resistance; $\omega$ is electrical rotor speed; $\theta$ is electrical rotor angle; ${\psi }_{PM}$ is PM flux linkage; $L_d,L_q$ are stator inductances; $u_d,u_q$ are stator voltages; and $i_d,i_q$ are stator currents.

To facilitate the rotor position estimation, inverse Park transformation is used to transform Equation (1) into $\alpha \beta$ coordinate frame, as shown in Equation (2).

$$\begin{array}{cc}\hfill \left[\begin{array}{c}{u}_{\alpha }\hfill \\ u_{\beta }\hfill \end{array}\right]& =\left[\begin{array}{cc}R+P{L}_d,& \omega (L_d-L_q)\\ -\omega (L_d-L_q),\hfill & R+P{L}_d\end{array}\right]\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]\hfill \\ & +\{(L_d-L_q)(\omega i_d-P{i}_q)+\omega {\psi }_{PM}\}\left[\begin{array}{c}-\sin \theta \hfill \\ \cos \theta \end{array}\right]\hfill \end{array}$$

(2)

As is shown in Equation (2), the state equations in $\alpha$-axis and $\beta$-axis couples with each other. The second term in the right side of Equation (2) is the EEMF; the amplitude of the EEMF is determined by rotor speed, stator current and its derivative value.

The differential of $i_q$ exists in the EEMF. Even the motor is standstill, only if the current $i_q$ changes, the EEMF is not zero. This property is useful for the motor to start up from zero speed and reverse from one direction to the other.

Let $\eta$ denotes the term $(L_d-L_q)(\omega i_d-P{i}_q)+\omega {\psi }_{PM}$, then the current model of PMSM is shown as Equation (3).

$$\begin{array}{cc}\hfill \left[\begin{array}{c}P{i}_{\alpha }\hfill \\ P{i}_{\beta }\hfill \end{array}\right]& =\frac{1}{L_d}\left[\begin{array}{cc}-R,& -\omega (L_d-L_q)\\ \omega (L_d-L_q),& -R\end{array}\right]\left[\begin{array}{c}{i}_{\alpha }\\ i_{\beta }\end{array}\right]\hfill \\ & +\frac{1}{L_d}\left[\begin{array}{c}{u}_{\alpha }\\ u_{\beta }\end{array}\right]-\frac{1}{L_d}\left[\begin{array}{c}{e}_{\alpha }\\ e_{\beta }\end{array}\right]\hfill \end{array}$$

(3)

$e_{\alpha }$ and $e_{\beta }$ in Equation (3) are EEMF, which can be expressed as Equation (4). In conventional second-order SMO-based encoderless control methods, the derivatives of the EMF terms are assumed to be zero ($de/dt=0$), so the dynamic performance is limited [17,22].

$$\left[\begin{array}{c}{e}_{\alpha }\\ e_{\beta }\end{array}\right]=\eta \left[\begin{array}{c}-\sin \theta \\ \cos \theta \end{array}\right]$$

(4)

The differential equation of EEMF is shown as Equation (5) [23].

$$\left[\begin{array}{c}P{e}_{\alpha }\\ P{e}_{\beta }\end{array}\right]=\omega \left[\begin{array}{c}-e_{\beta }\\ e_{\alpha }\end{array}\right]$$

(5)

Combining Equations (3) and (5), a full-order state equation of PMSM is shown in Equation (6).

$$\left[\begin{array}{c}P{e}_{\alpha \beta }\\ P{i}_{\alpha \beta }\end{array}\right]=\left[\begin{array}{cc}{A}_{11}\hfill & O\hfill \\ A_{21}\hfill & A_{22}\hfill \end{array}\right]\left[\begin{array}{c}{e}_{\alpha \beta }\\ i_{\alpha \beta }\end{array}\right]+\left[\begin{array}{c}O\\ B_1\end{array}\right]u_{\alpha \beta }$$

(6)

where,

$$\begin{array}{c}{i}_{\alpha \beta }={[i_{\alpha },i_{\beta }]}^T,e_{\alpha \beta }={[e_{\alpha },e_{\beta }]}^T,u_{\alpha \beta }={[u_{\alpha },u_{\beta }]}^T\hfill \\ A_{11}=\omega J_2,A_{21}=-B_1=-\frac{1}{L_d}{I}_2,\hfill \\ A_{22}=-\frac{R}{L_d}{I}_2+\omega \frac{L_d-L_q}{L_d}{J}_2,\hfill \\ I_2=\left[\begin{array}{cc}1\hfill & 0\hfill \\ 0\hfill & 1\hfill \end{array}\right],J_2=\left[\begin{array}{cc}0\hfill & -1\hfill \\ 1\hfill & 0\hfill \end{array}\right],O=\left[\begin{array}{cc}0\hfill & 0\hfill \\ 0\hfill & 0\hfill \end{array}\right]\hfill \end{array}$$

3. Full-Order Sliding Mode Observer Design

Based on motor state Equation (6), estimated state equation is shown in Equation (7).

$$\begin{array}{cc}\hfill \left[\begin{array}{c}P{\widehat{e}}_{\alpha \beta }\\ P{\widehat{i}}_{\alpha \beta }\end{array}\right]& =\left[\begin{array}{cc}{A}_{11}\hfill & O\hfill \\ A_{21}\hfill & A_{22}\hfill \end{array}\right]\left[\begin{array}{c}{\widehat{e}}_{\alpha \beta }\\ {\widehat{i}}_{\alpha \beta }\end{array}\right]\hfill \\ & +\left[\begin{array}{c}O\hfill \\ B_1\hfill \end{array}\right]u_{\alpha \beta }+\left[\begin{array}{c}M\\ N\end{array}\right]z_{\alpha \beta }\hfill \end{array}$$

(7)

where ${\widehat{i}}_{\alpha \beta }$ are estimated currents; ${\widehat{e}}_{\alpha \beta }$ are estimated EEMF; $z_{\alpha }$ and $z_{\beta }$ are inputs of the estimator, $z_{\alpha }=f({\widehat{i}}_{\alpha }-i_{\alpha })$; $z_{\beta }=f({\widehat{i}}_{\beta }-i_{\beta })$; $M=m{I}_2$; and $N=n{I}_2$.

Subtracting Equation (6) from Equation (7), estimation errors are shown in Equation (8).

$$\left[\begin{array}{c}P{\overline{e}}_{\alpha \beta }\\ P{\overline{i}}_{\alpha \beta }\end{array}\right]=\left[\begin{array}{cc}{A}_{11}\hfill & O\hfill \\ A_{21}\hfill & A_{22}\hfill \end{array}\right]\left[\begin{array}{c}{\overline{e}}_{\alpha \beta }\\ {\overline{i}}_{\alpha \beta }\end{array}\right]+\left[\begin{array}{c}M\\ N\end{array}\right]z_{\alpha \beta }$$

(8)

where ${\overline{e}}_{\alpha \beta }={\widehat{e}}_{\alpha \beta }-e_{\alpha \beta }$ and ${\overline{i}}_{\alpha \beta }={\widehat{i}}_{\alpha \beta }-i_{\alpha \beta }$.

Equation (8) is a Multi-Input and Multi-Output (MIMO) system, which can be expressed as Equation (9).

$${\dot{x}}_0=A{x}_0+Bz$$

(9)

where $x_0\in R^4$ is a state vector, and $z\in R^2$ is a input vector.

A linear transformation shown as Equation (10) is used to transform Equation (9) into a regular form that has reduced-order, simpler computation, and equivalent dynamics [24].

$$\begin{array}{c}x=T{x}_0\\ T=\left[\begin{array}{cc}{I}_2\hfill & -M{N}^{-1}\hfill \\ 0\hfill & I_2\hfill \end{array}\right]\end{array}$$

(10)

After transformation, the regular form of the sliding mode observer is shown as Equation (11).

$$\begin{array}{c}\dot{x}=\tilde{A}x+\tilde{B}z\hfill \end{array}$$

(11)

where,

$$\begin{array}{c}\tilde{A}=TA{T}^{-1}=\left[\begin{array}{cc}{\tilde{A}}_{11}& {\tilde{A}}_{12}\\ {\tilde{A}}_{21}& {\tilde{A}}_{22}\end{array}\right],\tilde{B}=TB=\left[\begin{array}{c}0\\ M\end{array}\right],\hfill \\ {\tilde{A}}_{11}=A_{11}-\frac{m}{n}{A}_{21},{\tilde{A}}_{21}=A_{21},{\tilde{A}}_{22}=\frac{m}{n}{A}_{21}+A_{22}\hfill \\ {\tilde{A}}_{12}=(A_{11}-\frac{m}{n}{A}_{21})\frac{m}{n}{I}_2-\frac{m}{n}{A}_{22}\hfill \end{array}$$

To facilitate digital processor applications, the SMO is studied in discrete-time field. The discrete-time form of the SMO in Equation (11) is expressed as Equation (12).

$$\begin{array}{c}x(k+1)=Dx(k)+Ez(k)\hfill \end{array}$$

(12)

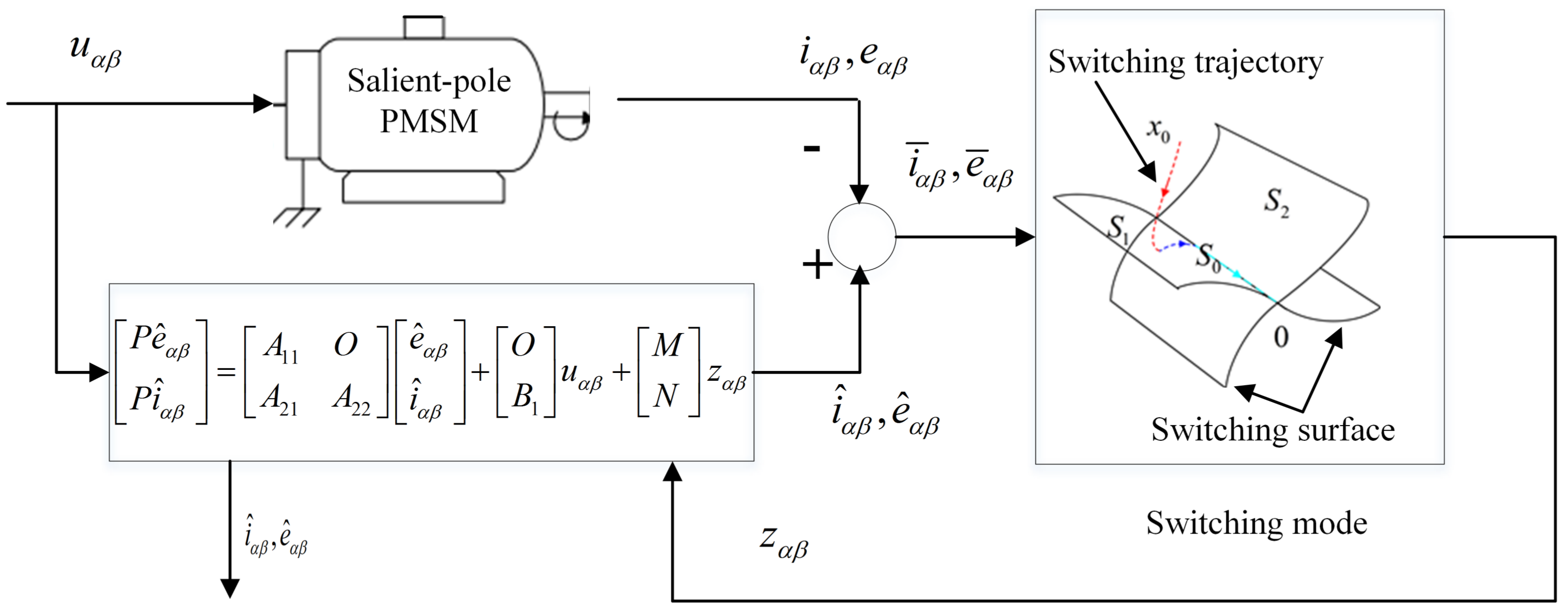
For the Multiple Input and Multiple Output (MIMO) system, a SMO is designed to estimate the currents and back EEMF in $\alpha$-axis and $\beta$-axis. The scheme is shown as Figure 2.

Figure 2. Sliding mode observer diagram.

The design of the sliding mode control involves two parts: switching surfaces and switching trajectory, as shown in Figure 2. The switching surfaces are designed to ensure the system has desired dynamic characteristics. System state trajectories should reach and remain on the eventual switching surface [19,21].

The dynamics of the system only depends on switching surfaces and is not influenced by system structure and parameter uncertainties [13].

Linear switching surfaces are used in the variable structure control. There are two inputs, so two switching surfaces are designed, which are shown as $S_1$ and $S_2$ in Figure 2.

$$S_i(k)=\tilde{C}x(k)$$

(13)

where $i=1,2$, $\tilde{C}\in R^{2\times 4}$

The eventual switching surface is $S_0$, which is shown as Equation (14).

$$S_0=S_1\cap S_2$$

(14)

When the sliding mode is enforced in the switching surface, the system’s dynamic characteristics are determined by sliding eigenvalues [19].

In the following, the matrix $\tilde{C}$ is expressed as $\tilde{C}=[{\tilde{C}}_1,{\tilde{C}}_2]$, ${\tilde{C}}_1\in R^{2\times 2}$ and ${\tilde{C}}_2\in R^{2\times 2}$ are unknown.

As the design of switching surface is not affected by ${\tilde{C}}_2$, it can take any arbitrary value [18,19]. To simplify the switching function, ${\tilde{C}}_2$ is set as a unit matrix $I_2$.

Equation (12) can be expressed as Equation (15), and the switching function Equation (13) can be expressed as Equation (16).

$$\begin{array}{c}{x}_1(k+1)=D_{11}{x}_1(k)+D_{12}{x}_2(k)\hfill \\ x_2(k+1)=D_{21}{x}_1(k)+D_{22}{x}_1(k)+Ez(k)\hfill \end{array}$$

(15)

$$S(k)=\tilde{C}x(k)={\tilde{C}}_1{x}_1(k)+{\tilde{C}}_2{x}_2(k)$$

(16)

Equation (16) can be transformed to Equation (17).

$$\begin{array}{c}{x}_1(k)=x_1(k)\hfill \\ x_2(k)={\tilde{C}}_2^{-1}S(k)-{\tilde{C}}_2^{-1}{C}_1{x}_1(k)\hfill \end{array}$$

(17)

Substituting Equation (17) into Equation (15):

$$\begin{array}{c}{x}_1(k+1)=(D_{11}-D_{12}{\tilde{C}}_2^{-1}{\tilde{C}}_1)x_1(k)+D_{12}{\tilde{C}}_2^{-1}S(k)\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill S(k+1)=& [{\tilde{C}}_1{D}_{11}+{\tilde{C}}_2{D}_{21}]x_1(k)\hfill \\ & -[({\tilde{C}}_1{D}_{12}+{\tilde{C}}_2{D}_{22}){\tilde{C}}_2^{-1}{\tilde{C}}_1]x_1(k)\hfill \\ & +({\tilde{C}}_1{D}_{12}+{\tilde{C}}_2{D}_{22}){\tilde{C}}_2^{-1}S(k)+{\tilde{C}}_{2}Ez(k)\hfill \end{array}$$

(19)

When the switching trajectory arrives at the switching surface, $S(k)\approx 0$. Substituting $S(k)=0$ into Equation (18):

$$\begin{array}{c}{x}_1(k+1)=(D_{11}-D_{12}F)x_1(k)\hfill \\ F={\tilde{C}}_2^{-1}{\tilde{C}}_1,F\in R^{2\times 2}\hfill \end{array}$$

(20)

Assume the desired poles of the system are ${\lambda }_1$ and ${\lambda }_2$.

$$\det (\lambda I_2-(D_{11}-D_{12}F))=(\lambda -{\lambda }_1)(\lambda -{\lambda }_2)$$

(21)

Matrix F can be calculated based on Equation (21), and ${\tilde{C}}_1$ can be obtained according to F and Equation (20). The switching functions are achieved by substituting ${\tilde{C}}_1$ and ${\tilde{C}}_2$ into Equation (13).

In this control system, there are three switching surfaces $(S_0,S_1,S_2)$. Free-order switching scheme is adopted, as shown in Figure 2.

Discrete-time reaching law is used to design the sliding mode trajectory, which is shown as Equation (22).

$$\begin{array}{c}S(k+1)-S(k)=-q{T}_{s}S(k)-\epsilon T_s\mathrm{sgn}(S(k))\\ \epsilon >0,q>0,1-q{T}_s>0\end{array}$$

(22)

where $\epsilon \in R^{2\times 2}$ and $q\in R^{2\times 2}$ are diagonal matrices.

According to Equations (12) and (13), $S(k+1)$ can be expressed as Equation (23).

$$S(k+1)=\tilde{C}x(k+1)=\tilde{C}Dx(k)+\tilde{C}Ez(k)$$

(23)

Combining Equations (22) and (23), inputs of the system $z(k)$ are shown as Equation (24).

$$z(k)={(\tilde{C}E)}^{-1}[\tilde{C}(I_4-D)x(k)-\epsilon T_s\mathrm{sgn}(S(k))-q{T}_s\tilde{C}x(k)]$$

(24)

Substituting Equation (24) into Equation (12), the sliding mode trajectory is shown as Equation (25).

$$\begin{array}{cc}\hfill x(k+1)=& (D+E{(\tilde{C}E)}^{-1}\tilde{C}(I_2-D))x(k)\hfill \\ & -(E{(\tilde{C}E)}^{-1}q{T}_s\tilde{C})x(k)\hfill \\ & -E{(\tilde{C}E)}^{-1}\epsilon T_s\mathrm{sgn}(S(k))\hfill \end{array}$$

(25)

Substituting Equation (24) into the discrete-time form of Equation (7), state variables of the system, including currents $(i_{\alpha },i_{\beta })$ and EEMF signals $(e_{\alpha },e_{\beta })$, can be achieved.

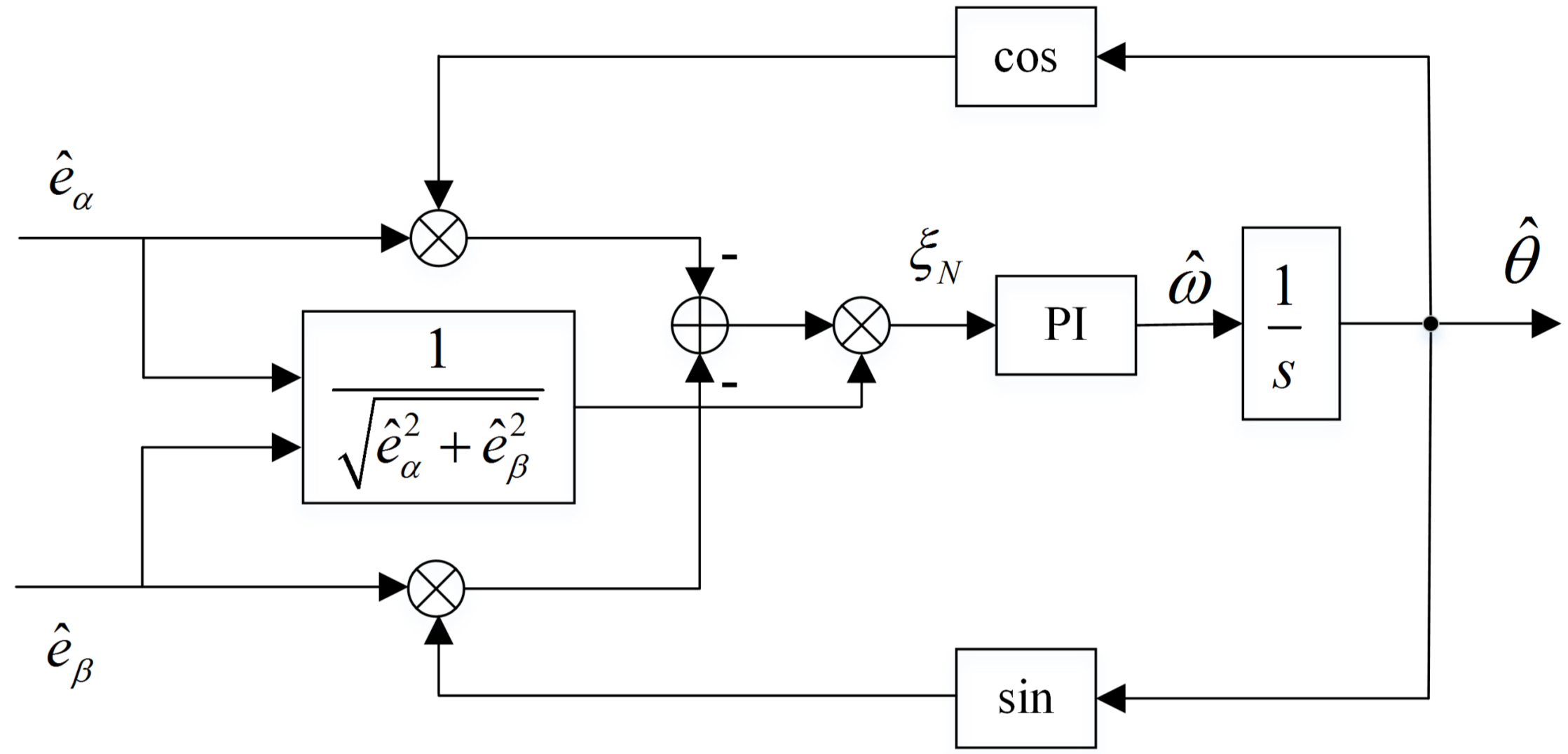
An angle-tracking observer (ATO) is used to estimate rotor angle and speed from estimated EEMF signals [22,25]. Because the amplitude of EEMF changes with speed, normalization is adopted in the observer. The position error is shown as Equation (26).

$${\xi }_N=-\frac{1}{\sqrt{{\widehat{e}}_{\alpha }^2+{\widehat{e}}_{\beta }^2}}({\widehat{e}}_{\alpha }\cos {\widehat{\theta }}_e+{\widehat{e}}_{\beta }\sin {\widehat{\theta }}_e)$$

(26)

The scheme of the ATO is shown as Figure 3, and rotor position is achieved by Equation (27).

$${\widehat{\theta }}_e=\frac{1}{s}(K_p+\frac{K_i}{s}){\xi }_N$$

(27)

where $K_p$ and $K_i$ are parameters of the PI regulator in Figure 3.

Figure 3. Angle-tracking observer.

4. Experimental Results

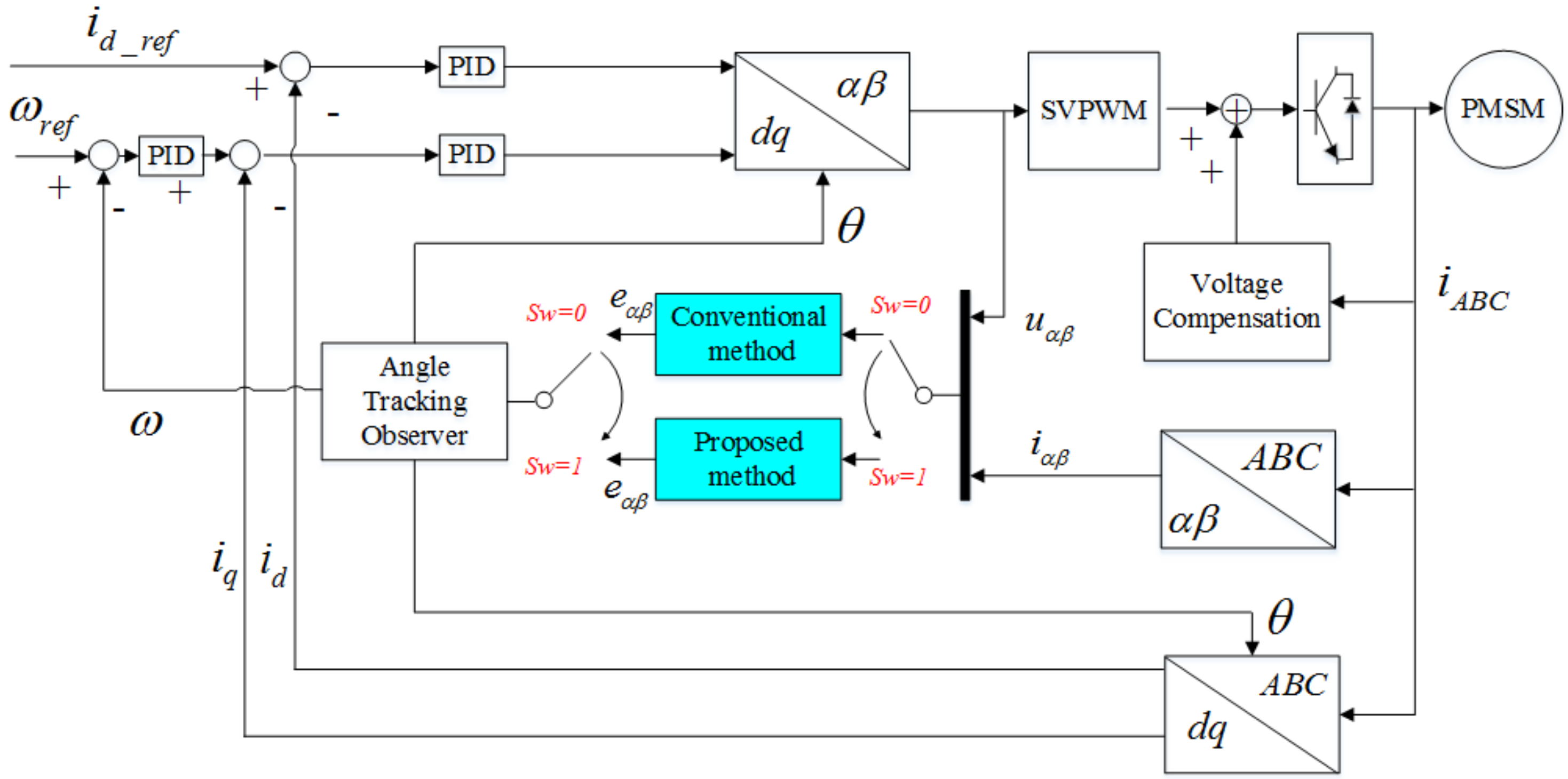
The proposed encoderless method is shown as Figure 4. A conventional full-order discrete-time SMO-based position sensorless control method [15] and the proposed method are compared under the same condition. When $Sw=1$, the proposed method is used, otherwise the conventional method is used. The comparison includes computation time, speed variation and torque variation. To show the effectiveness of the proposed method in low speed range, speed reversal experiment and startup experiment are implemented.

Figure 4. Rotor position and speed estimation diagram.

The test bench is shown as Figure 5. The inverter is a specially designed two-level three phase voltage source inverter, the type of the MOSFETS (IXFR180N10, IXYS corporation, Leiden, Netherlands) is IXFR180N10, and the current sensor is T60404-N4646-X100. The parameters of the salient-pole PMSM are shown in Table 1. The ratio between amplitude of back EEMF and speed is very low, which is a severe condition for back EEMF based position sensorless control methods when working in low speed range.

Figure 5. The test bench.

Table 1. Parameters of the tested IPMSM.

Parameter	Value
Rated torque	2 Nm
Rated current/voltage (rms)	50 A/13 V
Number of pole pairs	5
$d/q$-axis inductance	0.05/0.095 mH
Resistance	18 mΩ
Rated speed	2000 rpm
The moment of inertia	0.00187 kg·m2
PM flux linkage	0.00707 Vs

A DC motor is mechanically coupled with the salient-pole PMSM to produce the load torque, an adjustable resistor that connected to the terminal of the DC motor is used to change the load torque. An absolute encoder is used to measure the actual position used for comparison. Both the switching frequency and sampling frequency are 10 kHz.

In the figures shown in the Experimental Results, “Red” represents the reference signals, “Black” means measured signals, “Green” represents the signals that are achieved by using convention method and “Blue” denotes the signals that are obtained by using the proposed method.

4.1. Computation Load Comparison

To evaluate the computational load of the two methods, computation time are compared. In this experiment, the turnaround time is used as a criterion, which can be read directly from the control desk of dSAPCE. The turnaround time includes the communication time, data conversion time, code implementation time and data saving time. Except for code implementation time, the other times of the two methods are the same.

The turnaround time of the two strategies is shown in Table 2. Compared with the conventional method, the time increase of the proposed method is 3.4% of the sampling period.

Table 2. Turnaround time comparison of the conventional method and the proposed method.

Time	Value
Conventional method $t_1$ (μs)	8.9
Proposed method $t_2$ (μs)	12.3
Increased time $t_2-t_1$ (μs)	3.4
Sampling period $Ts$ (μs)	100
Increased time percentage $(t_2-t_1)/T_s$	3.4%

4.2. Speed Variation Comparison

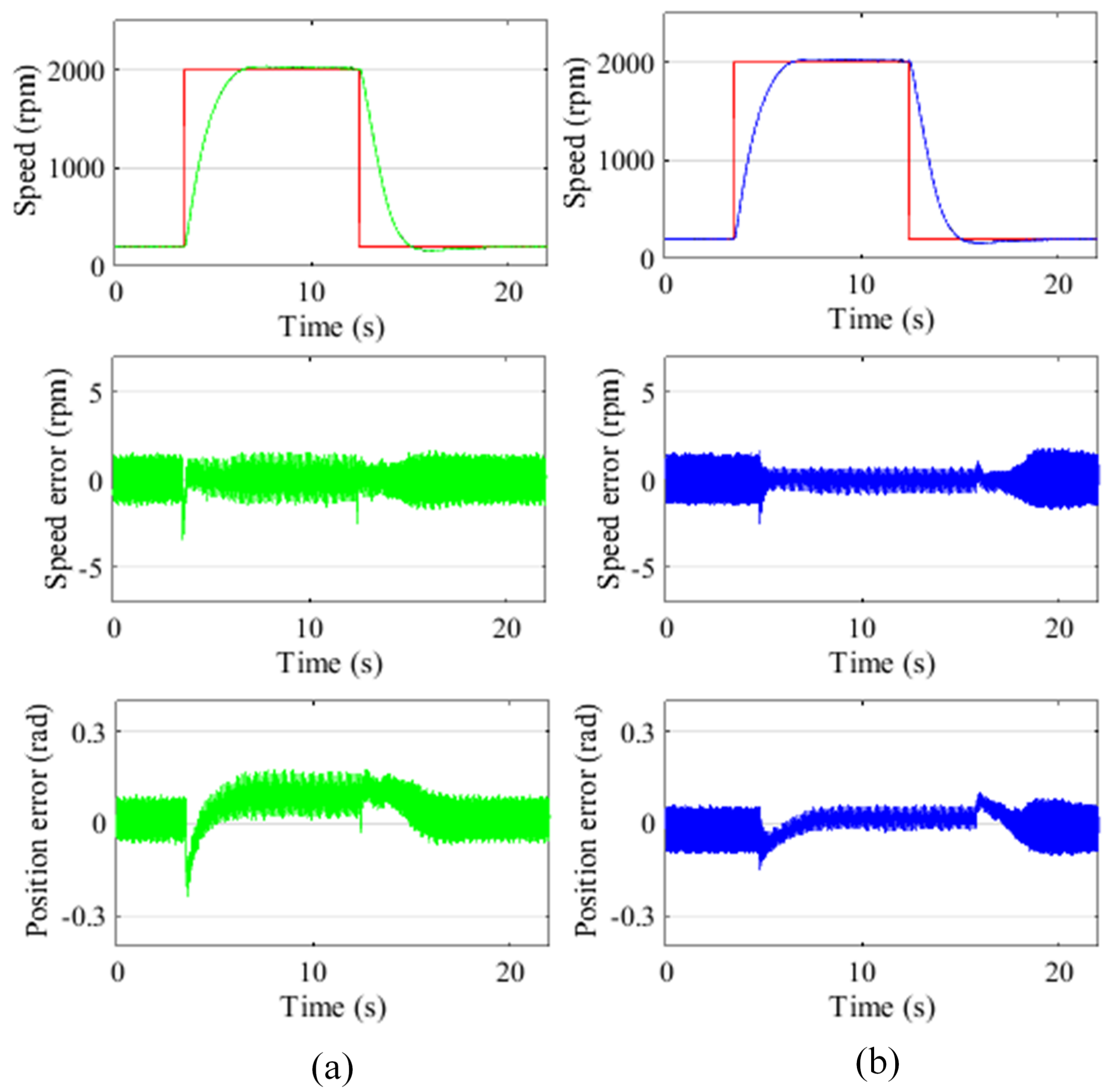
In this experiment, the motor accelerates from 100 rpm to 2000 rpm and then decelerates to 100 rpm without load torque. To make a fair comparison, the switching surface of the proposed method is adjusted to make the estimation error between the proposed method and conventional method is approximately equal at 100 rpm.

During this process, the reference speed, measured speed, estimated speed, speed estimation error and electrical position estimation error are given in Figure 6. The experimental results of the conventional method are shown in Figure 6a, while the experimental results of the proposed method are shown in Figure 6b.

Figure 6. The speed changes from 100 rpm (0.05 p.u.) to 2000 rpm (1 p.u.): (a) conventional method; and (b) proposed method. “Red Line” represents the reference signals, “Green Line” represents the signals that are achieved by using convention method and “Blue Line” denotes the signals that are obtained by using the proposed method.

The experimental results show that, at 100 rpm, the speed estimation errors of the two methods are almost the same. With the increase of speed, the speed estimation error of the proposed method is smaller than that of the conventional method. At 2000 rpm, the speed estimation error of the proposed method is about 50% of the conventional method.

At 100 rpm, the electrical rotor position estimation errors of the two methods are similar. During the speed variation process, the maximum electrical rotor position estimation error of the conventional method is −0.2 rad, and the maximum electrical rotor position estimation error of the proposed method is −0.1 rad. At 2000 rpm, the phase lag of the conventional method is 0.1 rad, and the phase lag of the proposed method is zero.

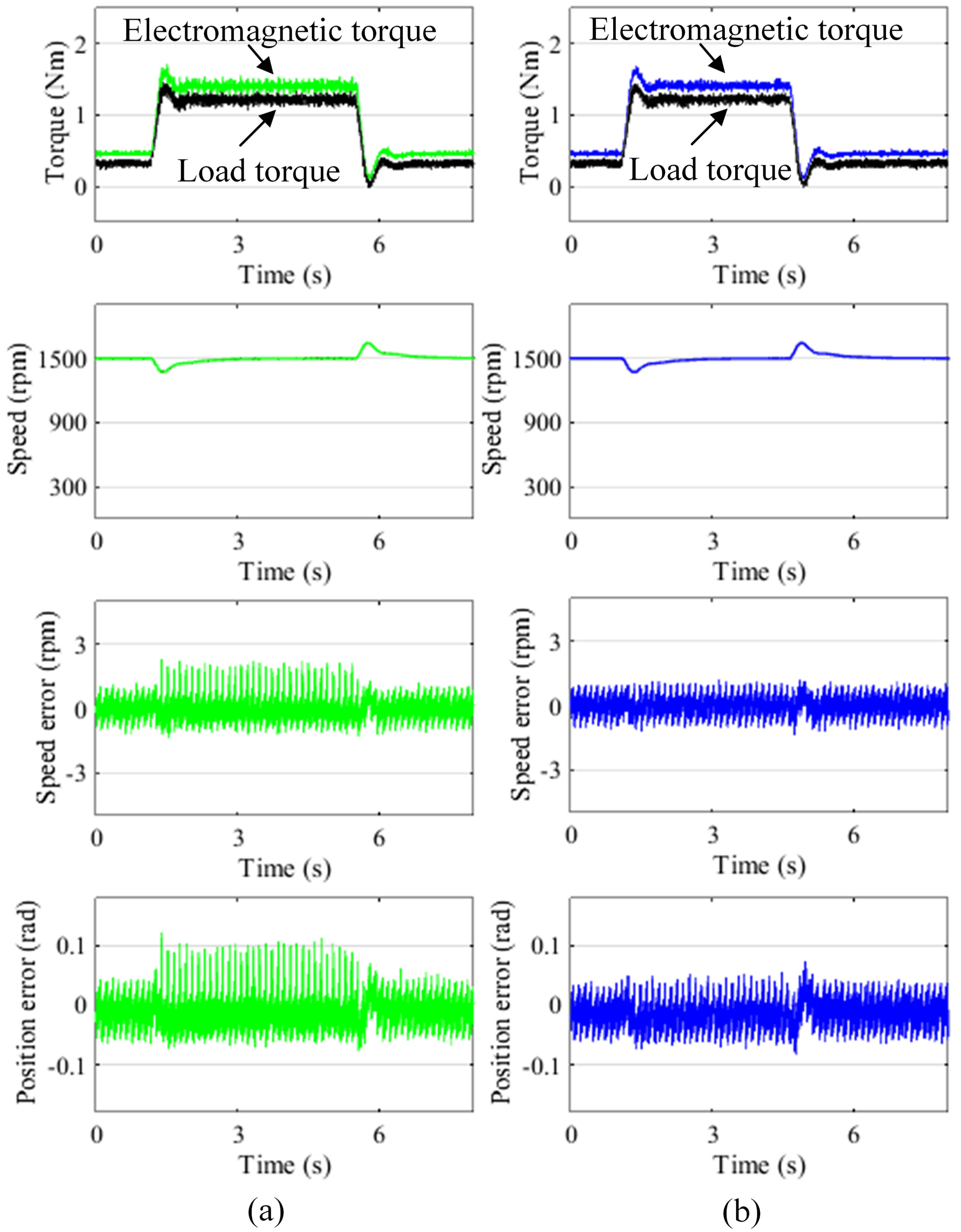
4.3. Torque Variation Comparison

In this experiment, the motor operates under speed control; the speed is 1500 rpm (0.75 p.u.). In the beginning, the load torque is 0.2 Nm (0.1 p.u.), a load torque 1.2 Nm (0.6 p.u.) is provided to the motor as a disturbance, and then the load torque is reduced to 0.2 Nm (0.1 p.u.). During the torque variation process, the electromagnetic torque, load torque, measured speed, estimated speed, electrical position estimation error and speed estimation error are shown as Figure 7.

Figure 7. The load torque changes from 0.2 Nm (0.1 p.u.) to 1.2 Nm (0.6 p.u.): (a) conventional method; and (b) proposed method. “Black Line” means measured signals, “Green Line” represents the signals that are achieved by using convention method and “Blue Line” denotes the signals that are obtained by using the proposed method.

The experimental results show that, during the torque disturbance process, both the electrical rotor position and speed estimation errors of the proposed method are significantly lower than those of the conventional method.

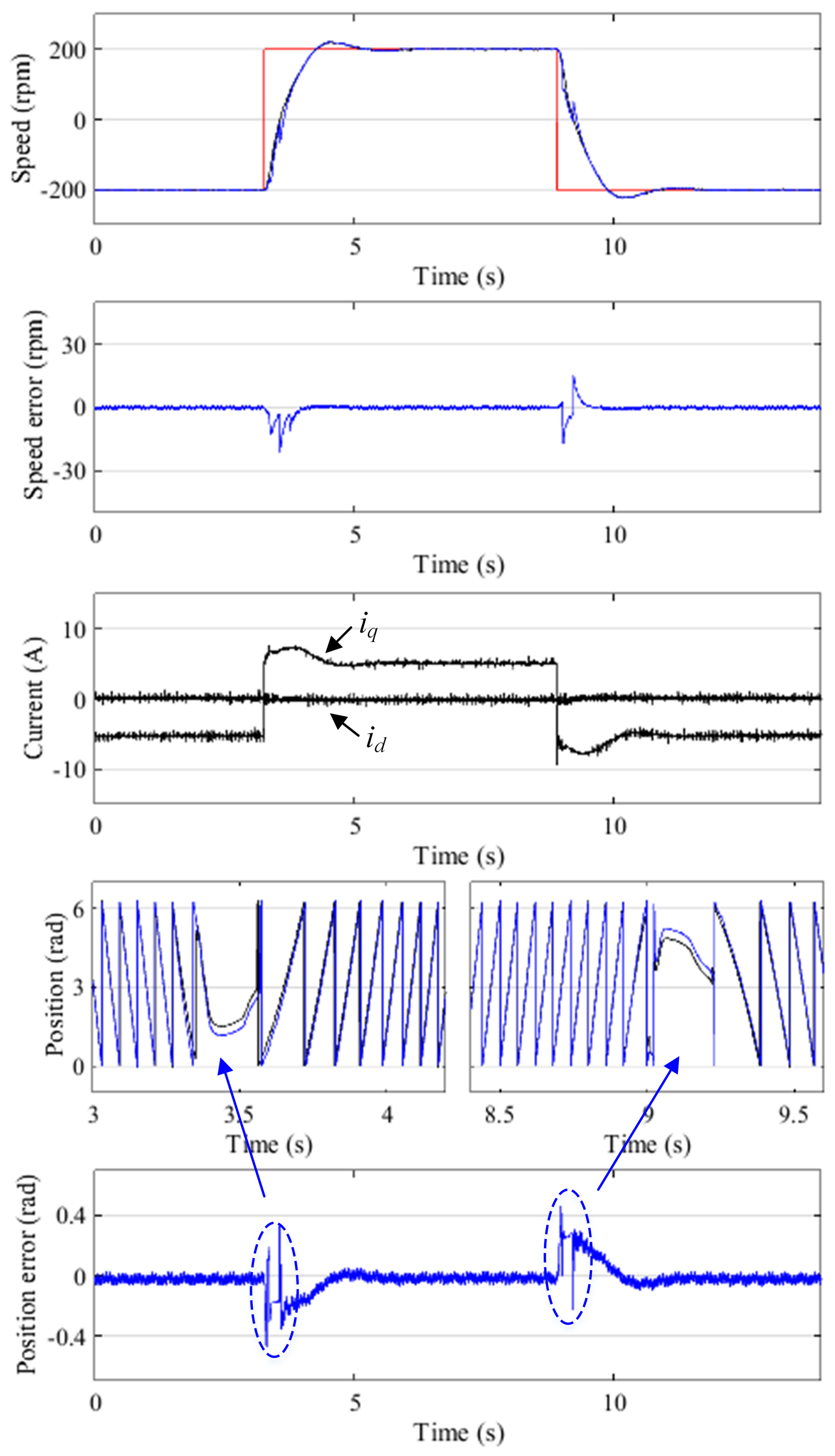
4.4. Speed Reversal

With the conventional full-order discrete-time SMO, the motor can not reverse from one direction to the other without position sensor in this experiment. Therefore, in this section, only the experimental results of the proposed method are shown.

The motor reverses between 200 rpm (0.1 p.u.) and −200 rpm (−0.1 p.u.). The reference speed, measured speed, estimated speed, measured rotor position, estimated rotor position, currents in d-axis and q-axis, speed estimation error and electrical position estimation error are shown in Figure 8.

Figure 8. The speed changes between 200 rpm (0.1 p.u.) and −200 rpm (−0.1 p.u.). “Red Line” represents the reference signals, “Black” means measured signals and “Blue Line” denotes the signals that are obtained by using the proposed method.

The experimental results show that the motor can reverse successfully from one direction to the other. During the reversal process, the maximum electrical rotor position and speed estimation errors occur around zero speed. The maximum electrical rotor position estimation error is 0.4 rad, and the maximum rotor speed estimation error is 15 rpm.

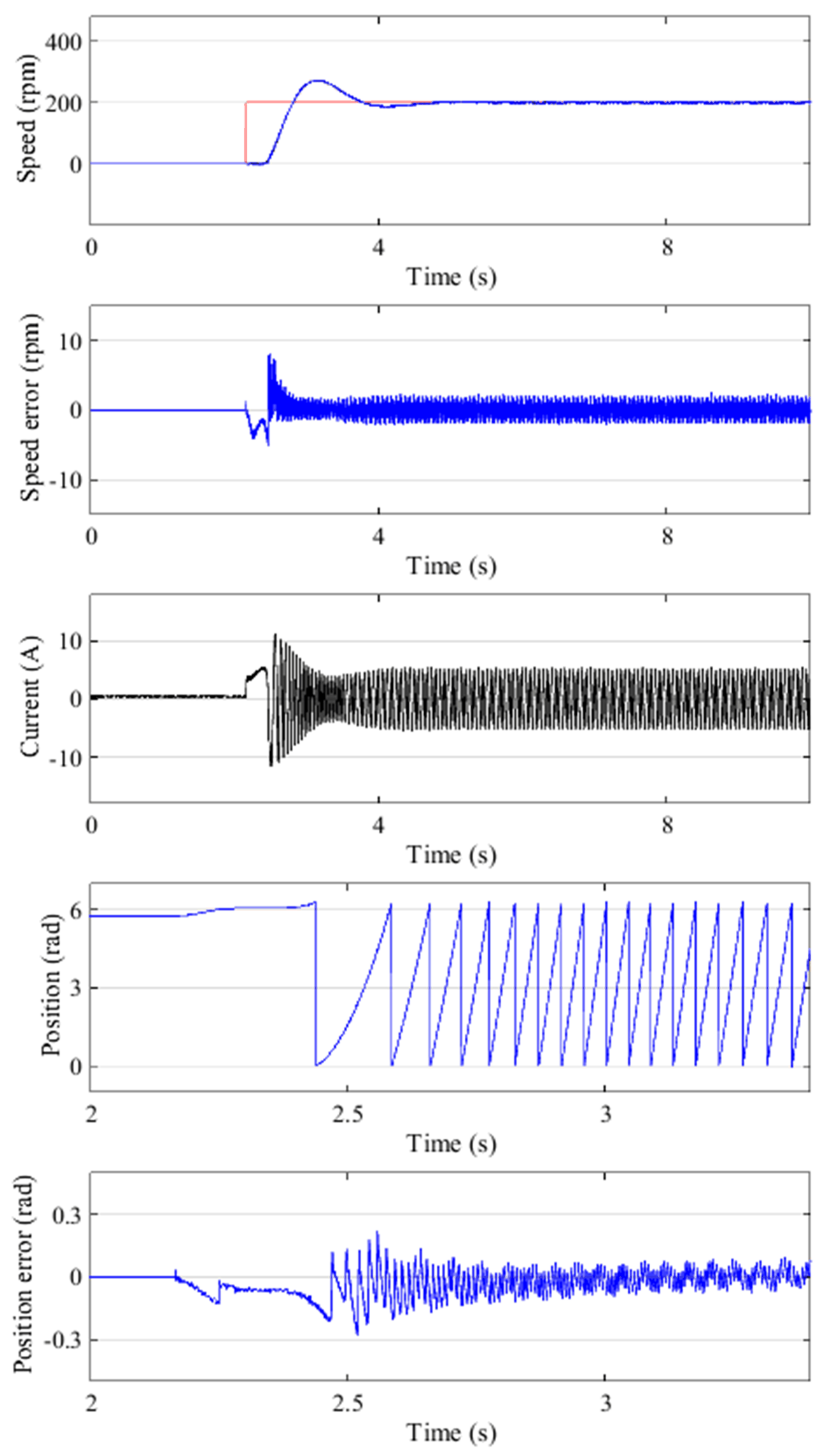
4.5. Start up from Standstill

With the conventional full-order discrete-time SMO, the motor cannot start up from standstill in this experiment. Therefore, in this section, only the experimental results of the proposed method are shown.

The initial rotor position is achieved by initial rotor position Estimation [26]. During the startup process, the reference speed, measured speed, estimated speed, measured rotor position, estimated rotor position, phase current, electrical position estimation error and speed estimation error are shown in Figure 9.

Figure 9. The motor starts up from zero speed to 200 rpm (0.1 p.u.).

The experimental results show that the motor can start up successfully from standstill. During the startup process, the maximum speed estimation error is 8 rpm and the maximum electrical rotor position estimation error is −0.27 rad.

5. Conclusions

This paper proposes a novel position sensorless control strategy for PMSM considering saliency. A novel full-order SMO is built to estimate the rotor position. The effectiveness of the proposed method is validated on a low voltage salient-pole PMSM.

The performance of a conventional full-order SMO-based position sensorless control method and the proposed method are compared under the same condition. The computational burden of the proposed method is higher than that of the conventional method. In the test bench, the computation time increase is 3.4% of the sampling period. With the rapid development of fast microprocessors, the computational time increase can be ignored.

During speed variation and torque variation process, the performance of the proposed method is obviously better than that of the conventional method. The rotor speed estimation error and position estimation error of the proposed method are about 50% of the conventional method. During speed variations, there is no phase lag in the proposed method. Based on the proposed method, the motor can reverse between positive and negative directions and start up from standstill without a position sensor.

The rotor position is estimated based on the the differential of $i_q$, so the proposed method can be used for salient-pole PMSM with different load at stand still and low speed. However, due to the restriction of the test bench, it is incapable of producing satisfied load torque at low speed. In the next step, a new test bench will be built to repeat the experiments under heavy mechanical load at zero speed and low speed.

The proposed position sensorless control method can be used for salient-pole PMSMs in electrical car, robot joints, etc., where startup and low speed operation of PMSM are required.