Distributed Adaptive Primal Algorithm for P2P-ETS over Unreliable Communication Links
Abstract
1. Introduction
- We propose a DAP routing algorithm to efficiently route energy request information in a network of proactive prosumers until a consensus is reached. The robustness of the proposed DAP routing algorithm is tested against unreliability and other link constraints that have impacts on the optimal communication amongst the trading prosumers, compared to the existing literature that assumes perfect communication links exists among the energy trading entities [12,17,18,19];
- The algorithm tends to reduce communication delay resulting from long queuing of messages. This is achieved by setting a limiting indicator on the communication link using the gradient update of the link states to adaptively route the messages via less congested paths, compared to [25] that calculate the shortest path based on link state marginal cost. With the limiting indicator and gradient update, the delay cost function associated with maximum capacity utilization is maximally reduced;
- As a result of the adaptive nature of the proposed routing algorithm, future grids will benefit through reduced delay and lower bandwidth requirement. This can be observed from the result which shows a 20% reduction in delay compared to hop-by-hop adaptive link state routing algorithm [25]. Further, in contrast to [8,15] that examined delay and packet loss, we tested the robustness of the proposed DAP routing algorithm to more stringent communication network constraints including delay, packet loss, congestion and different network topologies. The result shows that these constraints if not checked, would impact negatively the communication and transactions of the energy trading entities.
2. Literature Review
3. Problem Formulation
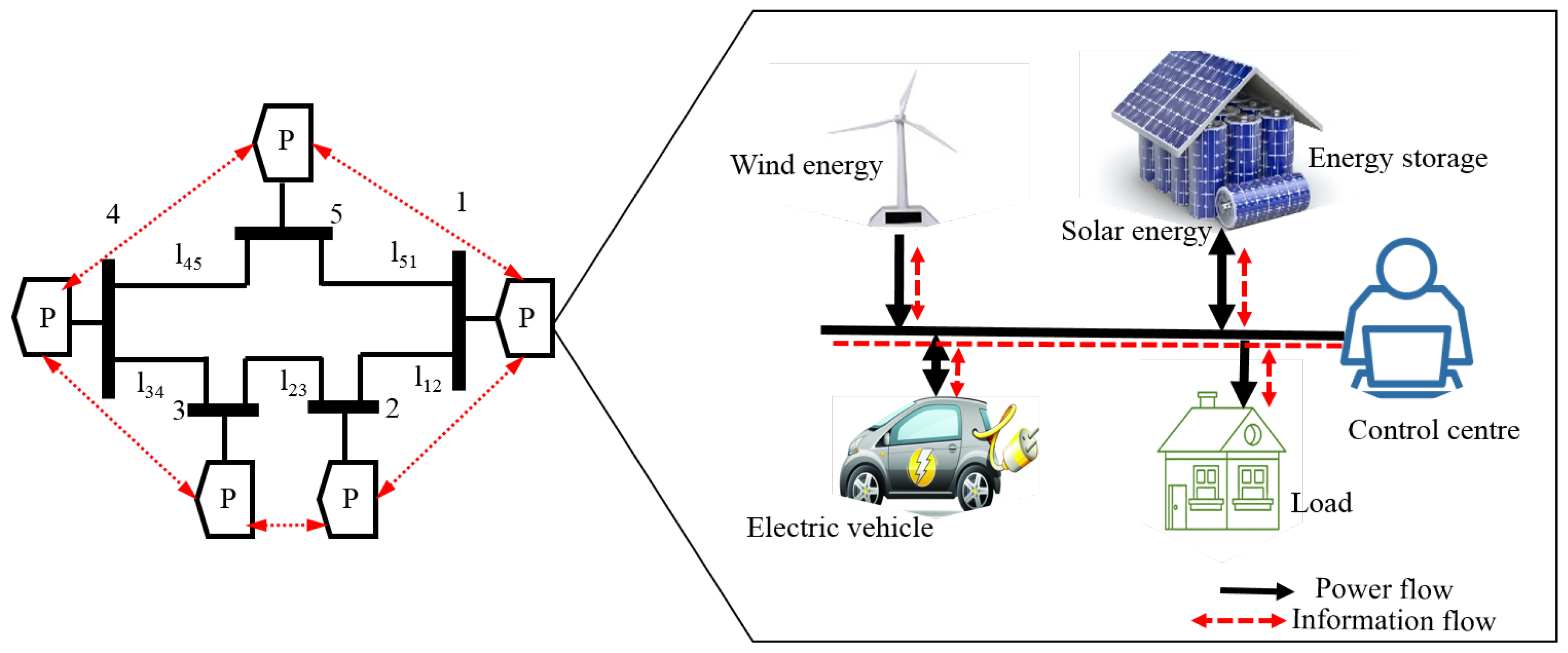
3.1. Communication Network
3.2. Multi-Commodity Network Flow Model
4. DAP-Adaptive Routing Algorithm
4.1. The Proposed DAP Iterative Algorithm
4.2. Implication of Model Solution to P2P-ETS
| Algorithm 1 Proposed DAP Routing Algorithm. |
|
5. Simulation and Result Analysis
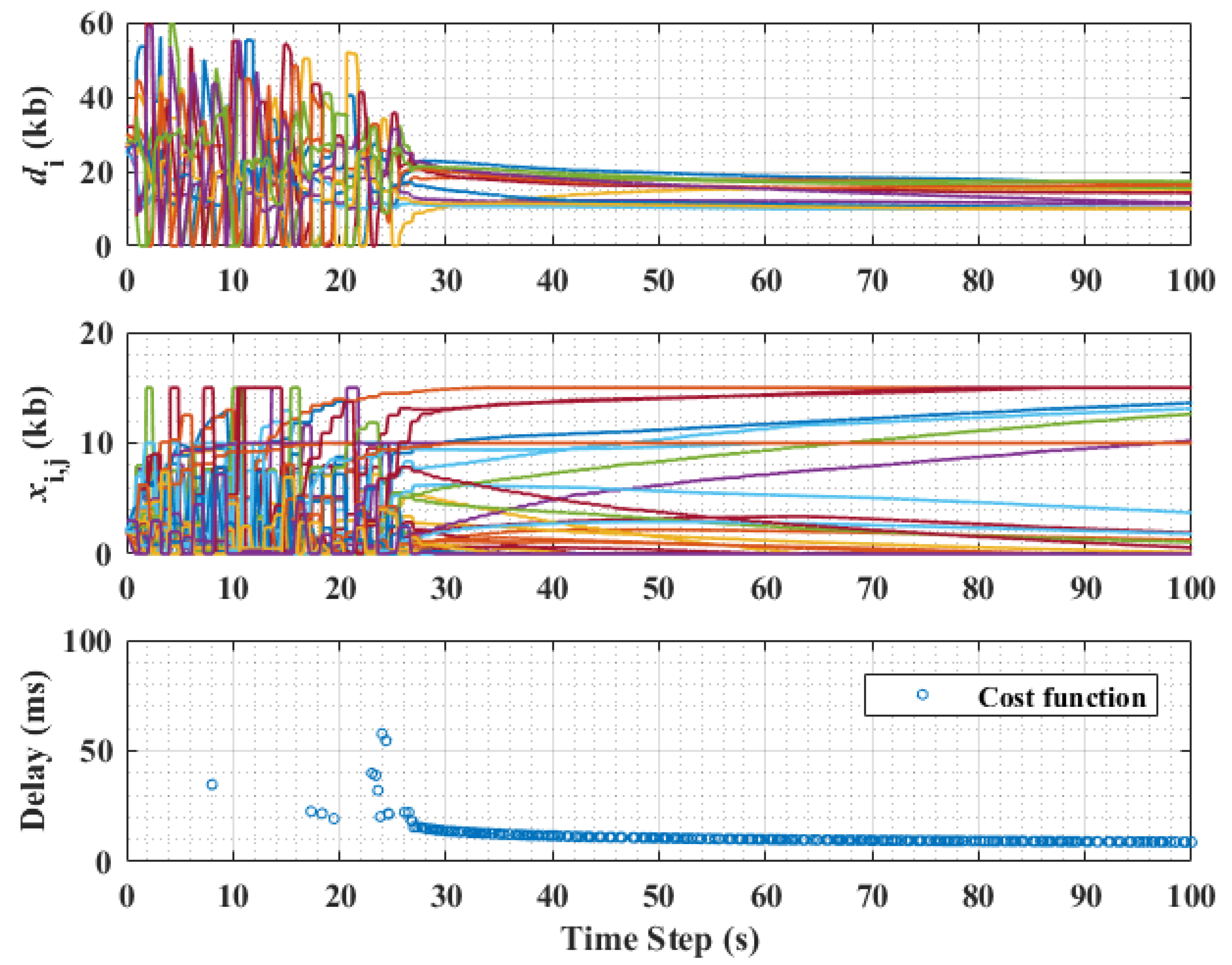
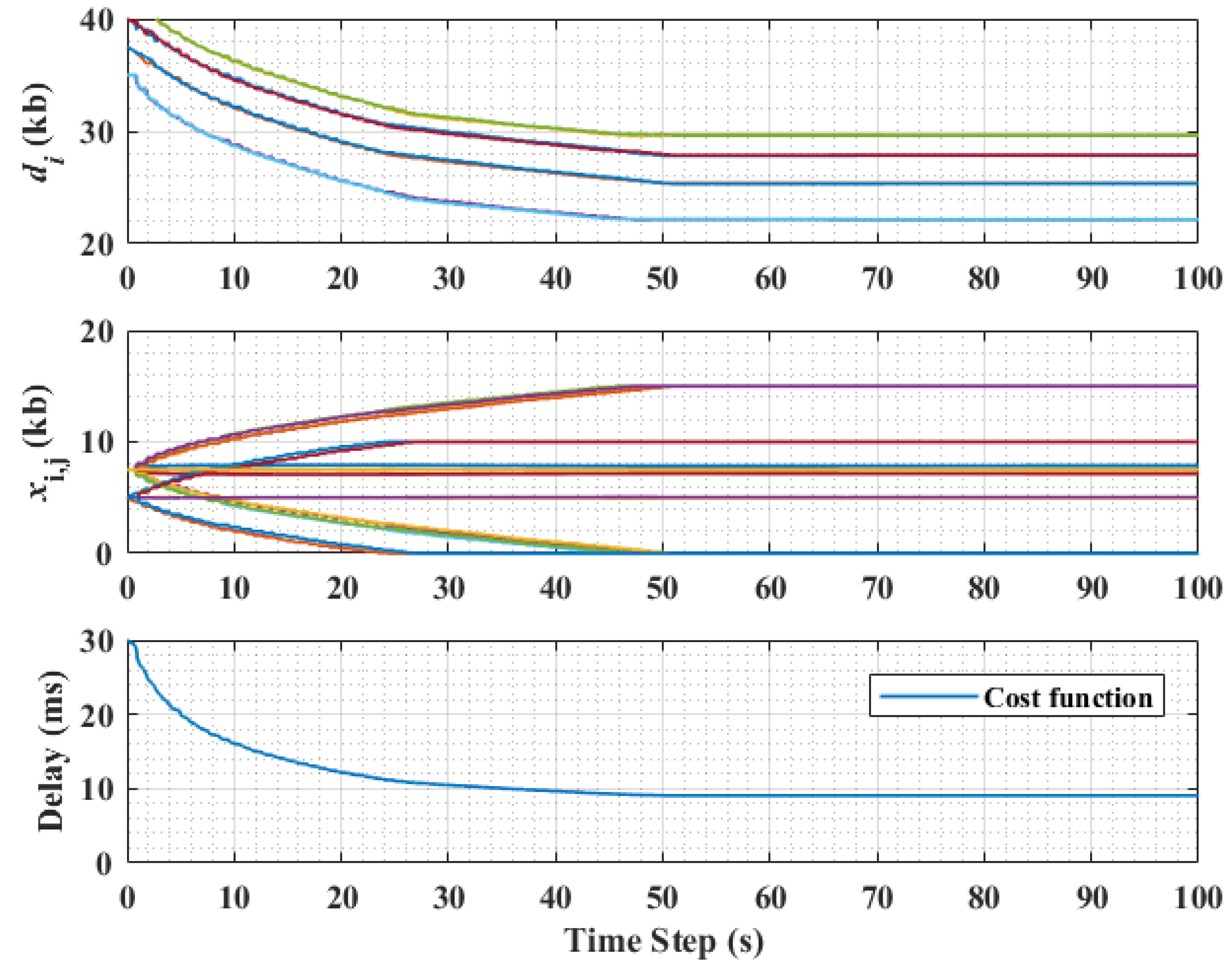
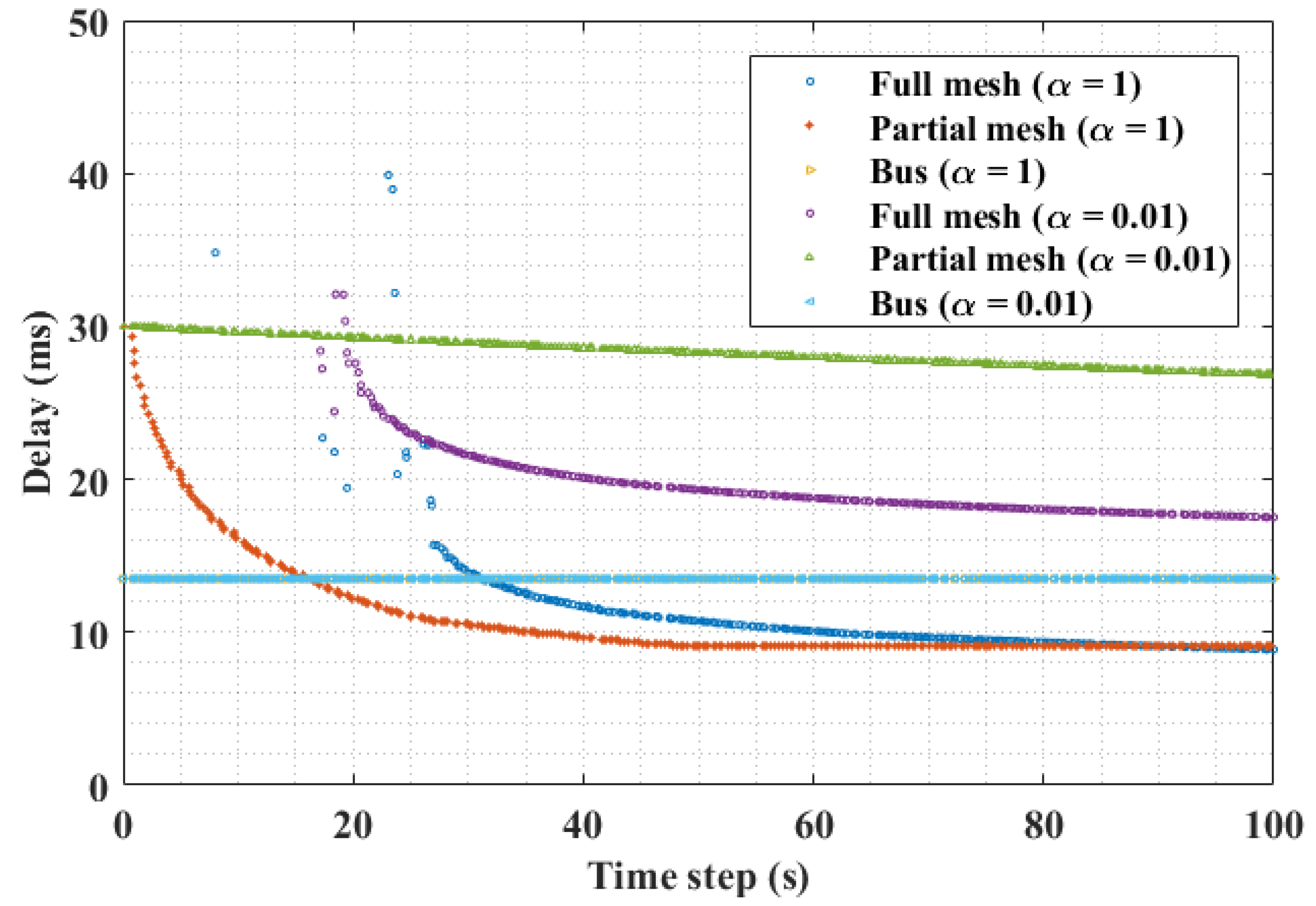
5.1. Performance Analysis of the DAP Routing Algorithm
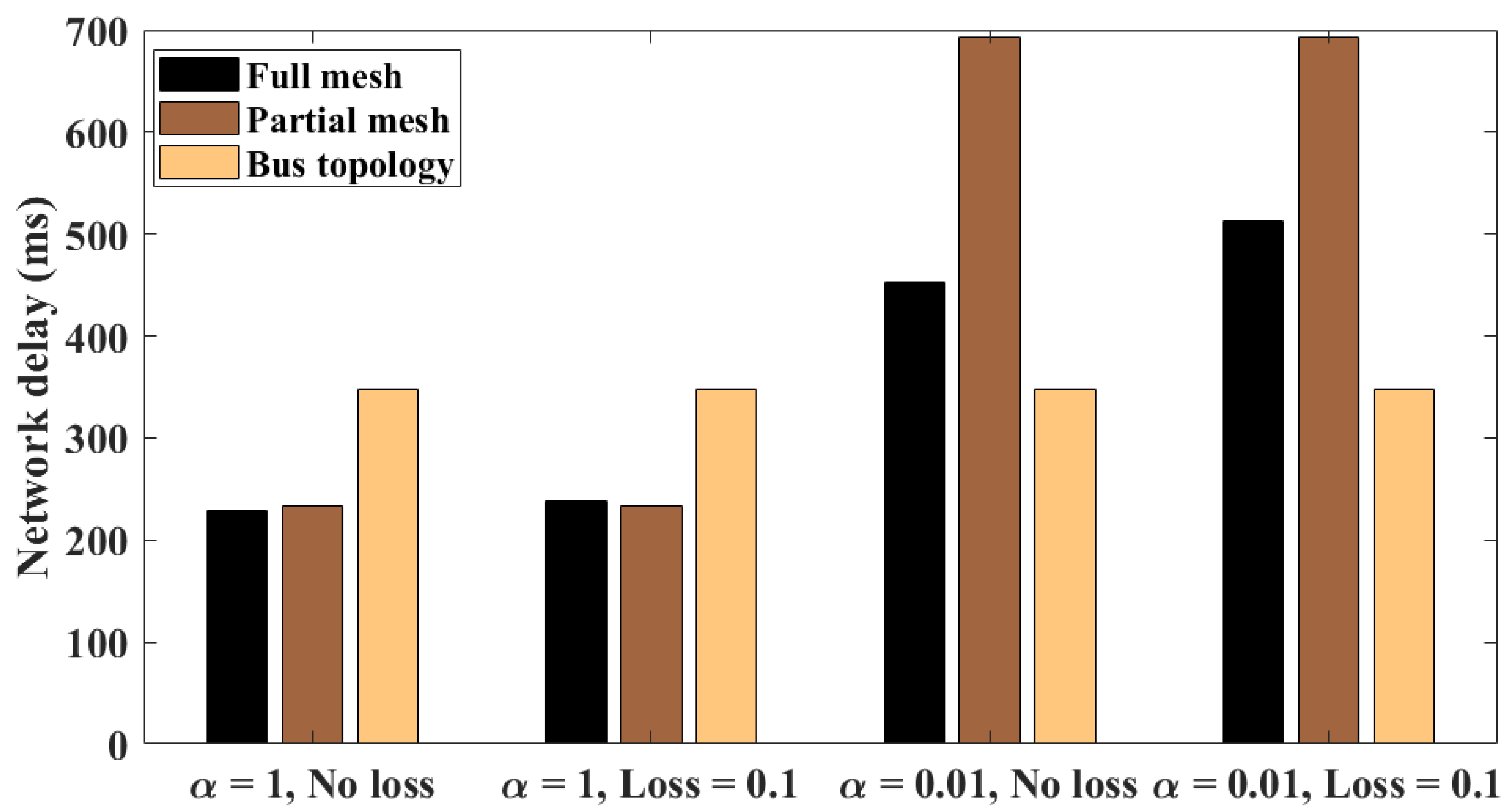
5.2. Cases of Unreliable Communication Link and Varying Step Sizes
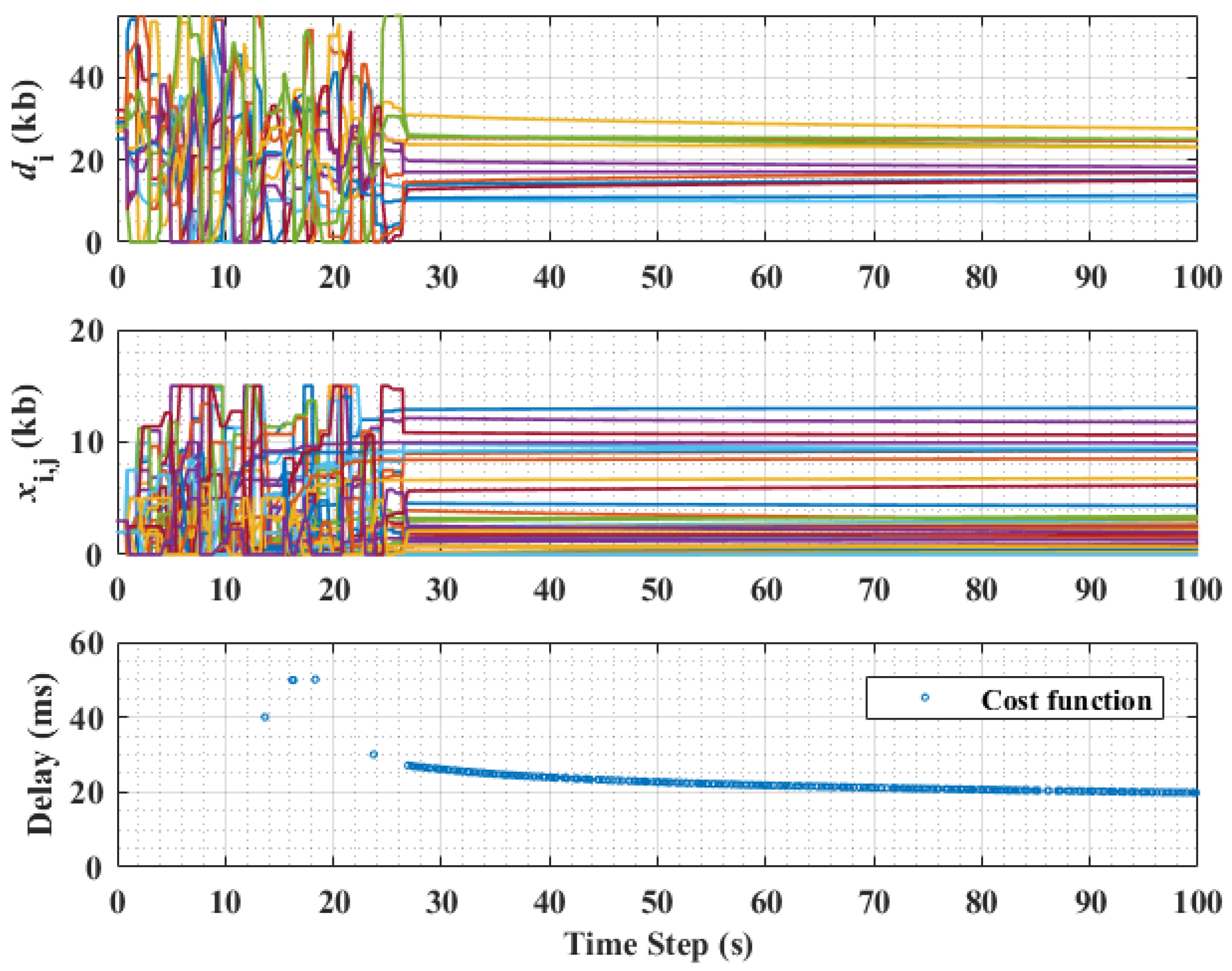
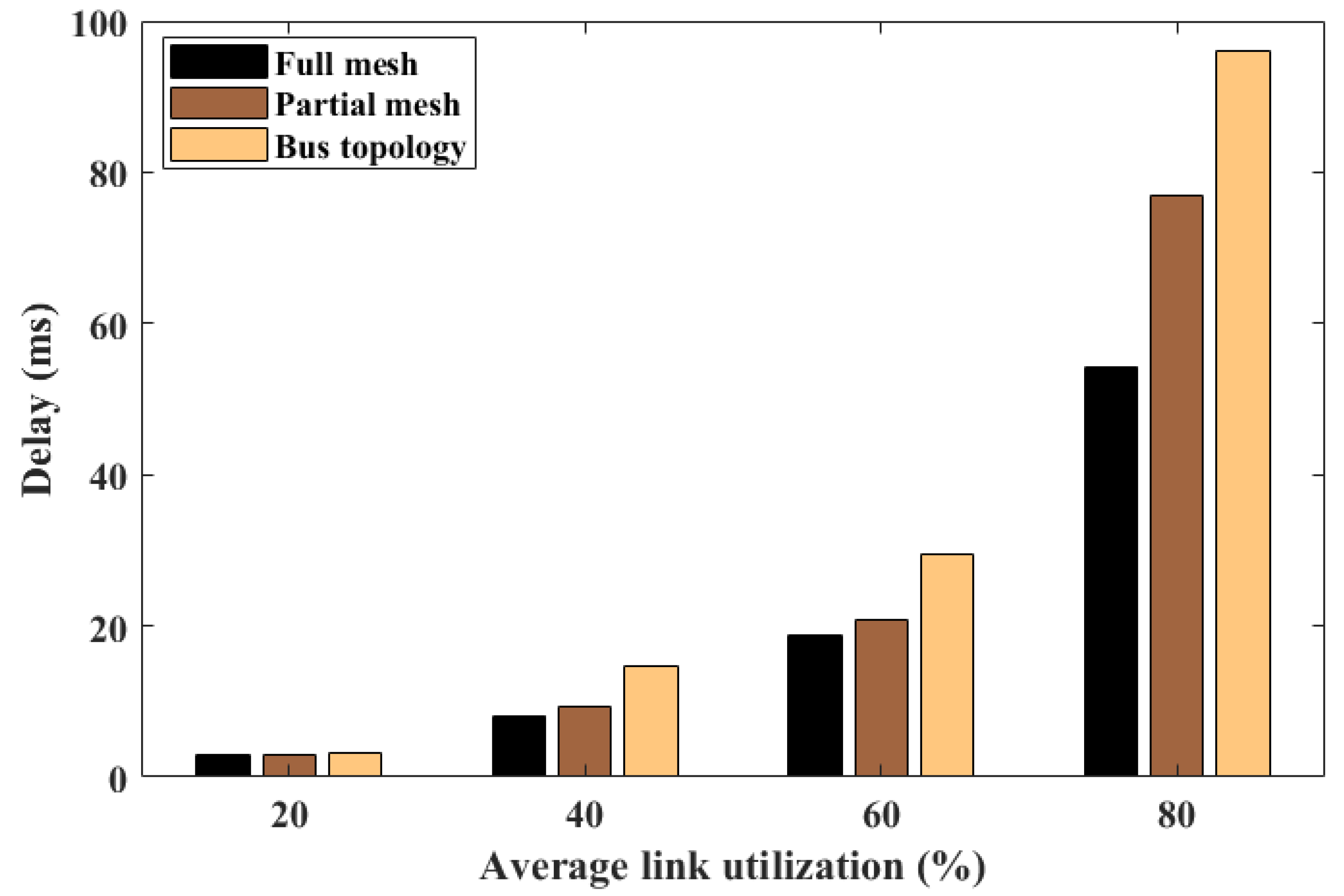
5.3. Evaluating Congestion on the Communication Link
5.4. Scalability Check to Increasing Number of Prosumers
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Abbreviations
| DAP | Distributed Adaptive Primal algorithm |
| MCF | Multicommodity flow network |
| ETS | Energy trading and sharing |
| The time-varying network graph | |
| Interconnected nodes representing the prosumers | |
| Set of network links connecting the prosumers | |
| Energy demand messages transmitted by each prosumer in the network | |
| Total energy demand messages in the network | |
| The flow on link corresponding to commodity d | |
| Total traffic flow on link | |
| Signal loss probability on link | |
| Source prosumer transmitting | |
| Destination prosumer receiving | |
| Bandwidth capacity on link | |
| Network delay function of link | |
| Link utilization indicator for each link in the network | |
| Peer capacity utilization indicator | |
| Egress link from a source or intermediary peer | |
| Ingress link to an intermediary or destination peer | |
| Order of n |
References
- Jogunola, O.; Ikpehai, A.; Anoh, K.; Adebisi, B.; Hammoudeh, M.; Son, S.Y.; Harris, G. State-of-the-art and prospects for peer-to-peer transaction-based energy system. Energies 2017, 10, 2016. [Google Scholar] [CrossRef]
- Anoh, K.; Adebisi, B.; Jogunola, O.; Hammoudeh, M. Cooperative Hybrid Wireless-Powerline Channel Transmission for Peer-To-Peer Energy Trading and Sharing System. In Proceedings of the International Conference on Future Networks and Distributed Systems, Cambridge, UK, 19–20 July 2017; p. 7. [Google Scholar]
- Jogunola, O.; Ikpehai, A.; Anoh, K.; Adebisi, B.; Hammoudeh, M.; Gacanin, H.; Harris, G. Comparative Analysis of P2P Architectures for Energy Trading and Sharing. Energies 2017, 11, 62. [Google Scholar] [CrossRef]
- Liu, N.; Yu, X.; Wang, C.; Li, C.; Ma, L.; Lei, J. Energy sharing model with price-based demand response for microgrids of peer-to-peer prosumers. IEEE Trans. Power Syst. 2017, 32, 3569–3583. [Google Scholar] [CrossRef]
- Sha’aban, Y.; Ikpehai, A.; Adebisi, B.; Rabie, K. Bi-Directional Coordination of Plug-In Electric Vehicles with Economic Model Predictive Control. Energies 2017, 10, 1507. [Google Scholar] [CrossRef]
- Magnússon, S.; Weeraddana, P.C.; Fischione, C.A. Distributed approach for the optimal power-flow problem based on ADMM and sequential convex approximations. IEEE Trans. Control Netw. Syst. 2015, 2, 238–253. [Google Scholar] [CrossRef]
- Zhang, Z.; Chow, M.Y. Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid. IEEE Trans. Power Syst. 2012, 27, 1761–1768. [Google Scholar] [CrossRef]
- Wu, J.; Yang, T.; Wu, D.; Kalsi, K.; Johansson, K.H. Distributed optimal dispatch of distributed energy resources over lossy communication networks. IEEE Trans. Smart Grid 2017, 8, 3125–3137. [Google Scholar] [CrossRef]
- Anoh, K.; Ikpehai, A.; Bajovic, D.; Jogunola, O.; Adebisi, B.; Vukobratovic, D.; Hammoudeh, M. Virtual Microgrids: A Management Concept for Peer-to-Peer Energy Trading. In Proceedings of the the 2nd International Conference on Future Networks & Distributed Systems, Amman, Jordan, 26–27 June 2018. [Google Scholar]
- Anoh, K.; Bajovic, D.; Adebisi, B.; Vukobratovic, D.; Jakoveticx, D.; Cosovic, M. Distributed Energy Trading with Communication Constraints. In Proceedings of the 2018 IEEE PES Innovative Smart Grid Technologies Europe (ISGT Europe 2018), Sarajevo, Bosnia and Herzeqovina, 21–25 October 2018. [Google Scholar]
- Liu, N.; Wang, J.; Wang, L. Distributed energy management for interconnected operation of combined heat and power-based microgrids with demand response. J. Modern Power Syst. Clean Energy 2017, 5, 478–488. [Google Scholar] [CrossRef]
- Zhou, Y.; Ci, S.; Li, H.; Yang, Y.A. New framework for peer-to-peer energy sharing and coordination in the energy internet. In Proceedings of the 2017 IEEE International Conference on Communications (ICC), Paris, France, 21–25 May 2017; pp. 1–6. [Google Scholar]
- Gregoratti, D.; Matamoros, J. Distributed energy trading: The multiple-microgrid case. IEEE Trans. Ind. Electron. 2015, 62, 2551–2559. [Google Scholar] [CrossRef]
- Liu, M.; Shi, Y.; Liu, X. Distributed MPC of aggregated heterogeneous thermostatically controlled loads in smart grid. IEEE Trans. Ind. Electron. 2016, 63, 1120–1129. [Google Scholar] [CrossRef]
- Yang, T.; Lu, J.; Wu, D.; Wu, J.; Shi, G.; Meng, Z.; Johansson, K.H. A distributed algorithm for economic dispatch over time-varying directed networks with delays. IEEE Trans. Ind. Electron. 2017, 64, 5095–5106. [Google Scholar] [CrossRef]
- Bahrami, S.; Amini, M.H.; Shafie-khah, M.; Catalao, J.P. A Decentralized Renewable Generation Management and Demand Response in Power Distribution Networks. IEEE Trans. Sustain. Energy 2018. [Google Scholar] [CrossRef]
- Yang, T.; Wu, D.; Sun, Y.; Lian, J. Minimum-time consensus-based approach for power system applications. IEEE Trans. Ind. Electron. 2016, 63, 1318–1328. [Google Scholar] [CrossRef]
- Xing, H.; Mou, Y.; Fu, M.; Lin, Z. Distributed bisection method for economic power dispatch in smart grid. IEEE Trans. Power Syst. 2015, 30, 3024–3035. [Google Scholar] [CrossRef]
- Dominguez-Garcia, A.D.; Cady, S.T.; Hadjicostis, C.N. Decentralized optimal dispatch of distributed energy resources. In Proceedings of the 2012 IEEE 51st IEEE Conference on Decision and Control (CDC), Maui, HI, USA, 10–13 December 2012; pp. 3688–3693. [Google Scholar]
- Zhang, Z.; Chow, M.Y. The influence of time delays on decentralized economic dispatch by using incremental cost consensus algorithm. In Control and Optimization Methods for Electric Smart Grids; Springer: Berlin, Germany, 2012; Volume 371, pp. 313–326. [Google Scholar]
- Yang, S.; Tan, S.; Xu, J.X. Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- Yang, T.; Wu, D.; Sun, Y.; Lian, J. Impacts of time delays on distributed algorithms for economic dispatch. In Proceedings of the IEEE Power Energy Society General Meeting, Denver, CO, USA, 26–30 July 2015; pp. 1–5. [Google Scholar]
- Marino, P.P. Optimization of Computer Networks: Modeling and Algorithms: A Hands-on Approach; John Wiley & Sons: Hoboken, NJ, USA, 2016. [Google Scholar]
- Bertsekas, D.P. Convex Optimization Algorithms; Athena Scientific Belmont: Belmont, MA, USA, 2015. [Google Scholar]
- Michael, N.; Tang, A. Halo: Hop-by-hop adaptive link-state optimal routing. IEEE/ACM Trans. Netw. 2015, 23, 1862–1875. [Google Scholar] [CrossRef]
- Safdarian, A.; Fotuhi-Firuzabad, M.; Lehtonen, M. A distributed algorithm for managing residential demand response in smart grids. IEEE Trans. Ind. Inform. 2014, 10, 2385–2393. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Incentivizing energy trading for interconnected microgrids. IEEE Trans. Smart Grid 2018, 9, 2647–2657. [Google Scholar] [CrossRef]
- Amini, M.H.; Bahrami, S.; Kamyab, F.; Mishra, S.; Jaddivada, R.; Boroojeni, K.; Weng, P.; Xu, Y. Decomposition Methods for Distributed Optimal Power Flow: Panorama and Case Studies of the DC Model. In Classical and Recent Aspects of Power System Optimization; Elsevier: New York, NY, USA, 2018; pp. 137–155. [Google Scholar]
- Almasalma, H.; Claeys, S.; Mikhaylov, K.; Haapola, J.; Pouttu, A.; Deconinck, G. Experimental Validation of Peer-to-Peer Distributed Voltage Control System. Energies 2018, 11, 1304. [Google Scholar] [CrossRef]
- Nedic, A.; Ozdaglar, A. Distributed subgradient methods for multi-agent optimization. IEEE Trans. Autom. Control 2009, 54, 48–61. [Google Scholar] [CrossRef]
- Su, L.; Vaidya, N.H. Robust multi-agent optimization: Coping with packet-dropping link failures. arXiv, 2016; arXiv:1606.08904. [Google Scholar]
- Dominguez-Garcia, A.D.; Hadjicostis, C.N.; Vaidya, N.H. Resilient networked control of distributed energy resources. IEEE J. Sel. Areas Commun. 2012, 30, 1137–1148. [Google Scholar] [CrossRef]
- Hadjicostis, C.N.; Vaidya, N.H.; Domínguez-García, A.D. Robust distributed average consensus via exchange of running sums. IEEE Trans. Autom. Control 2016, 61, 1492–1507. [Google Scholar] [CrossRef]
- Carli, R.; Notarstefano, G.; Schenato, L.; Varagnolo, D. Analysis of Newton-Raphson Consensus for multi-agent convex optimization under asynchronous and lossy communications. arXiv, 2017; arXiv:1704.06147. [Google Scholar]
- Varagnolo, D.; Zanella, F.; Cenedese, A.; Pillonetto, G.; Schenato, L. Newton-Raphson consensus for distributed convex optimization. IEEE Trans. Autom. Control 2016, 61, 994–1009. [Google Scholar] [CrossRef]
- Rehmani, M.H.; Reisslein, M.; Rachedi, A.; Erol-Kantarci, M.; Radenkovic, M. Integrating Renewable Energy Resources Into the Smart Grid: Recent Developments in Information and Communication Technologies. IEEE Trans. Ind. Inform. 2018, 14, 2814–2825. [Google Scholar] [CrossRef]
- Manfren, M. Multi-commodity network flow models for dynamic energy management–Mathematical formulation. Energy Procedia 2012, 14, 1380–1385. [Google Scholar] [CrossRef]
- Pióro, M.; Medhi, D. Routing, Flow, and Capacity Design in Communication and Computer Networks; Elsevier: New York, NY, USA, 2004. [Google Scholar]
- Trdlicka, J.; Hanzálek, Z. Distributed algorithm for energy optimal multi-commodity network flow routing in sensor networks. In Proceedings of the International Conference on Wireless Communications & Signal Processing (WCSP), Suzhou, China, 21–23 October 2010; pp. 1–6. [Google Scholar]
- Lisser, A.; Mahey, P. Multicommodity Flow Problems and Decomposition in Telecommunications Networks. In Handbook of Optimization in Telecommunications; Springer: Berlin, Germany, 2006; pp. 241–267. [Google Scholar]
- Adhikari, R.; Aste, N.; Manfren, M. Multi-commodity network flow models for dynamic energy management–Smart Grid applications. Energy Procedia 2012, 14, 1374–1379. [Google Scholar] [CrossRef]
- Koushik, K.; Saswati, S.; Leandros, T. Optimization based rate control for multipath sessions. In Teletraffic Science and Engineering; Elsevier: New York, NY, USA, 2001; Volume 4, pp. 805–816. [Google Scholar]
- Net2Plan. Net2Plan: The Open-Source Network Planner. Available online: http://net2plan.com/index.php (accessed on 8 July 2018).



| Ref. | Energy Netw. | No of Peers | Method | Network Constraints | |||
|---|---|---|---|---|---|---|---|
| Delay | Loss | Netw. Util. | Conges. | ||||
| [8] | Yes | 5 | Gradient Push-sum | No | Yes | No | No |
| [15] | Yes | Up to 14 | Gradient Push-sum | Yes | No | No | No |
| [13] | Yes | 4 | Subgradient | No | No | No | No |
| [14] | Yes | 3 | Subgradient | No | No | No | No |
| [12] | Yes | Up to 64 | ADMM | No | No | No | No |
| [25] | No | Up to 50 | MC | Yes | No | Yes | Yes |
| DAP | Yes | Up to 30 | MC Subgradient | Yes | Yes | Yes | Yes |
| Simulation Parameter | Value |
|---|---|
| Demand/message request | 45, 35, 35, 40 (kb) |
| 0.01, 1 | |
| Signal loss probability | 0.1 |
| Total link capacity | = 400 kb |
| Asynchronous message update | 0–5 time steps |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jogunola, O.; Adebisi, B.; Anoh, K.; Ikpehai, A.; Hammoudeh, M.; Harris, G.; Gacanin, H. Distributed Adaptive Primal Algorithm for P2P-ETS over Unreliable Communication Links. Energies 2018, 11, 2331. https://doi.org/10.3390/en11092331
Jogunola O, Adebisi B, Anoh K, Ikpehai A, Hammoudeh M, Harris G, Gacanin H. Distributed Adaptive Primal Algorithm for P2P-ETS over Unreliable Communication Links. Energies. 2018; 11(9):2331. https://doi.org/10.3390/en11092331
Chicago/Turabian StyleJogunola, Olamide, Bamidele Adebisi, Kelvin Anoh, Augustine Ikpehai, Mohammad Hammoudeh, Georgina Harris, and Haris Gacanin. 2018. "Distributed Adaptive Primal Algorithm for P2P-ETS over Unreliable Communication Links" Energies 11, no. 9: 2331. https://doi.org/10.3390/en11092331
APA StyleJogunola, O., Adebisi, B., Anoh, K., Ikpehai, A., Hammoudeh, M., Harris, G., & Gacanin, H. (2018). Distributed Adaptive Primal Algorithm for P2P-ETS over Unreliable Communication Links. Energies, 11(9), 2331. https://doi.org/10.3390/en11092331








