Game-Theory Modeling for Social Welfare Maximization in Smart Grids
Abstract
:1. Introduction
- As an revolutionary game based on the Stackelberg game structure, it is necessary to study that the players (demands and generators) obtain the each other’s energy parameters, such as the time-varying electricity price and an amount of electricity consumption with spying on each other’s energy strategy to effectively and adaptively maximize their profit.
- We propose two energy strategies for profit maximization for both the generators and EUs (Generator’s Best-Pricing and Power-Generation Strategy in Section 3.1, Demand’s Best Electricity-Usage Strategy in Section 3.2) based on the Stackelberg game as an evolutionary game where the players (demands and generators) alternately perform their energy strategy with spying on each other’s energy strategy to update their own energy parameters to achieve profit maximization over time in smart grid demand response. Whenever the generators and the EUs execute their energy strategy in the proposed Stackelberg game structure, the generators acquire the optimal power consumption calculated by the EU, and the EUs obtain the optimal electricity price calculated by the generator. To the best knowledge of the authors, this game structure based on the aforementioned parameter exchange (optimal power consumption and optimal electricity price) for profit maximization in the smart grid demand response is first studied.
- We newly formulate a generator profit function including the additional parameter, the electricity-consumption of EUs, compared with that of the conventional profit function [26] since the profit of generators can be influenced by the electricity-consumption of EUs.
- We greatly improve the monetary profit of the generators and EUs using the proposed two energy strategies by optimizing the amount of the power generation and the electricity price in the generator side, and electricity consumption in the EU side.
- As one of the simple and powerful electricity-usage control strategy of the demand that is applicable to the time-varying electricity market, we newly propose a market-adaptive electricity-usage scheduling algorithm which maximizes the demand’s profit by calculating the amount of power that should be consumed according to the time-varying electricity price.
- The proposed profit maximization algorithm can solve the existing PAR reduction problem because the energy usage immediately increases as the electricity price goes down, and the energy usage goes down as the price goes up according to the proposed game structure. It is also possible to alleviate the problem that the price greatly fluctuates because if the price changes greatly, the power plant will lose its benefits and will not be able to withstand it. The problem of making power generation stable is consistent with reducing PAR, which is one of DR’s ultimate goals. Stable power generation can reduce useless power generation, which makes our energy resources the most efficient to use, and can contribute to addressing issues such as global warming in the energy industry.
2. System Model and Problem Formulation
2.1. Generator Profit
2.2. EU Profit
2.3. Optimization of the Problem Formulation Based on the Stackelberg Game Model
3. Profit Maximization
3.1. Generator’s Best-Pricing and Power-Generation Strategy
| Algorithm 1. Generator’s Profit Maximization (lines 3–8, performed by the generator, master-loop algorithm). |
| 1: Input: time set . 2: While , do 3: Input: active generator set (positive zero), . 4: Initialize . 5: Update and from Slave-loop algorithm (“Algorithm 3”). 6: If 7: Return optimal parameters and optimal profit of generators, . 8: else Update and , then Go to line 5. |
| Algorithm 2. Energy-User’s Profit Maximization (Market-adaptive Electricity-Usage Scheduling Algorithm, lines 9–17, performed by the EU). |
| 9: Input: , active EU set 10: For do 11: Calculate with according to (26). 12: Calculate with according to (25). 13: Calculate with according to (27). 14: Update with and according to (28). 15: end for 16: Calculate with (7). 17: Let . 18: end while |
| Algorithm 3. Slave-loop Algorithm of the Generator’s Profit Maximization. |
| 1: Input: active generator set . . . 2: While and are not converged do 3: for do 4: Update with (18), with (19), with (20), with (21), with (22), with (23), and with (24). 5: end for 6: Let . 7: end while |
3.2. Demand’s Best Electricity-Usage Strategy
3.3. Complexity Analysis
3.4. Schematic Overview and Application of Proposed Algorithms
- The game players, generators and EUs, interact with observing the each other’s energy strategy for profit maximization. The generators observe the electricity consumption of the EUs, and the EUs observe the electricity price of the generators in the proposed game operation.
- The proposed profit maximization game was constructed as an iterative algorithm where the energy strategies (Algorithms 1 and 2) are repeatedly performed up to the specified number of times, for example 24 times as 24 h a day.
- In the EU side, the implementation method of the proposed profit maximization algorithm is as follows: The proposed profit maximization algorithm and formulas is applicable to general demand response applications between generators and EUs such as, residential households, electrical appliances, new smart appliances and internet of things (IoT) devices as a real-world scenario. In the EU side which can be used at high priced hours, we can effectively reduce electricity charges by adjusting the energy usage according to the electricity price with the proposed Market-Adaptive Electricity-Usage Scheduling Algorithm (Algorithm 2 in the manuscript). To implement the Market-Adaptive Electricity-Usage Scheduling Algorithm, automatic electricity usage controller can be needed to be implemented and connected to EU applications (the residential households, IoT devices and etc.). The automatic electricity usage controller can be developed by porting a functional software which quickly and dynamically performs the automatic electricity usage control to an AMI or an EMC. In the case of AMI and EMC, it is possible to transmit and receive electricity price information in real time through power line communications in smart grid. Based on this, the proposed algorithm can be fully implemented and operate to achieve energy usage optimization and electricity charge savings. To summarize, EUs should choose their appliances or facilities to automatically control their energy usage to maximize monetary profit, and if they are connected to a smart meter or EMC equipped with our proposed algorithms, the proposed profit maximization system will simply be able to operate. We think that the proposed system can be implemented in the direction of utilizing existing infrastructure such as the smart meter and EMC.
- On the generator side, the implementation method of the proposed profit maximization algorithm is as follows: In order to realize the optimal power generation and optimal pricing based on the proposed algorithm in the generators side, the generators should be able to integrate and manage the total power generation and the electricity price by forming a coalitional for profit maximization themselves. Or as a top authority for power generators that are already integrated and managed by the government can implement the proposed coalitional game theory methods. Or a third party such as a power retailer that runs various demand response programs can implement the proposed game theory. If the proposed algorithm is implemented and operated, it should be able to interact with another game player, energy user, with through power line communication or wireless local area network (WLAN) on the smart grid for information communication, such as real-time electricity price and electricity consumption exchange required by this algorithm.
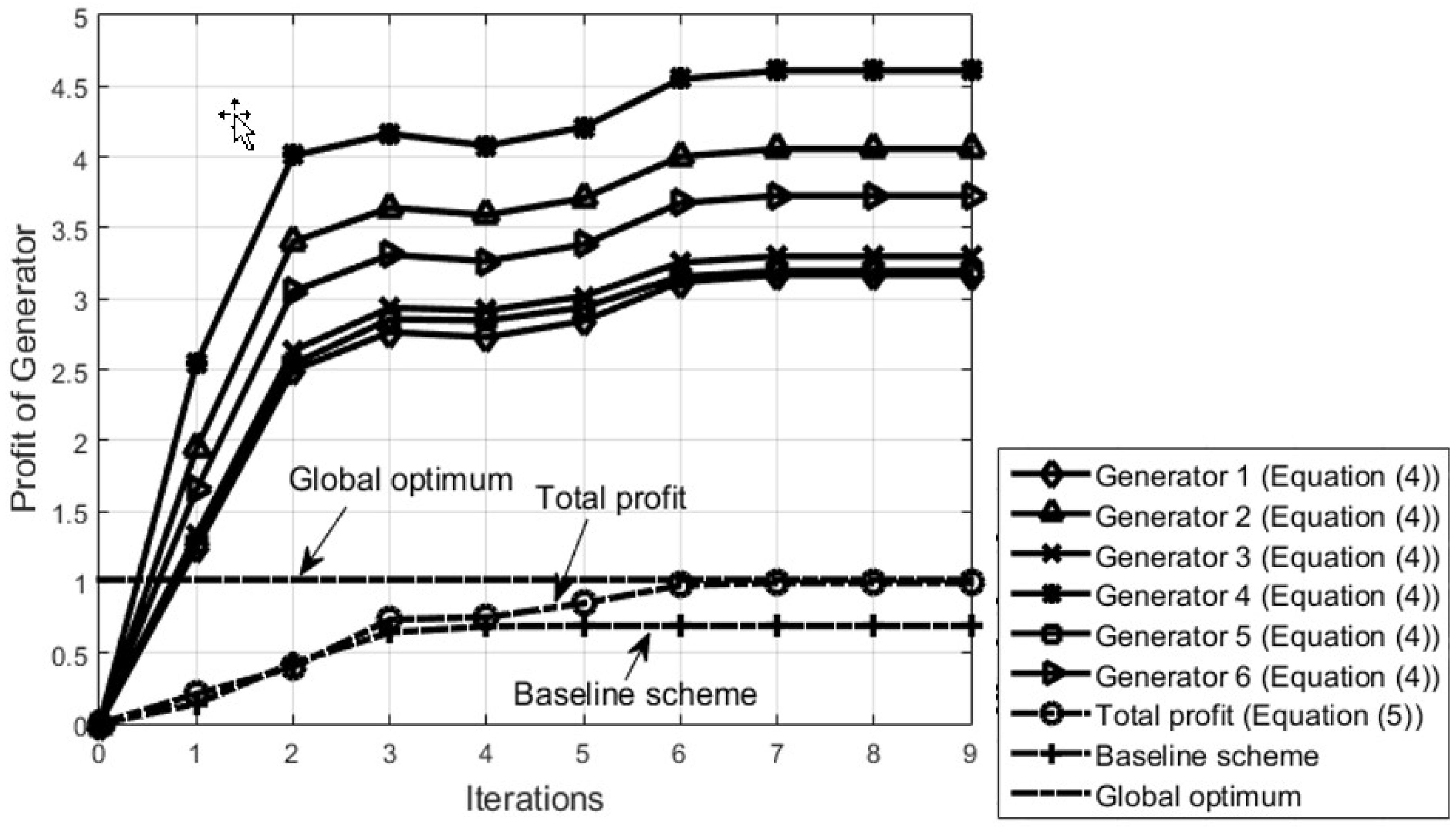
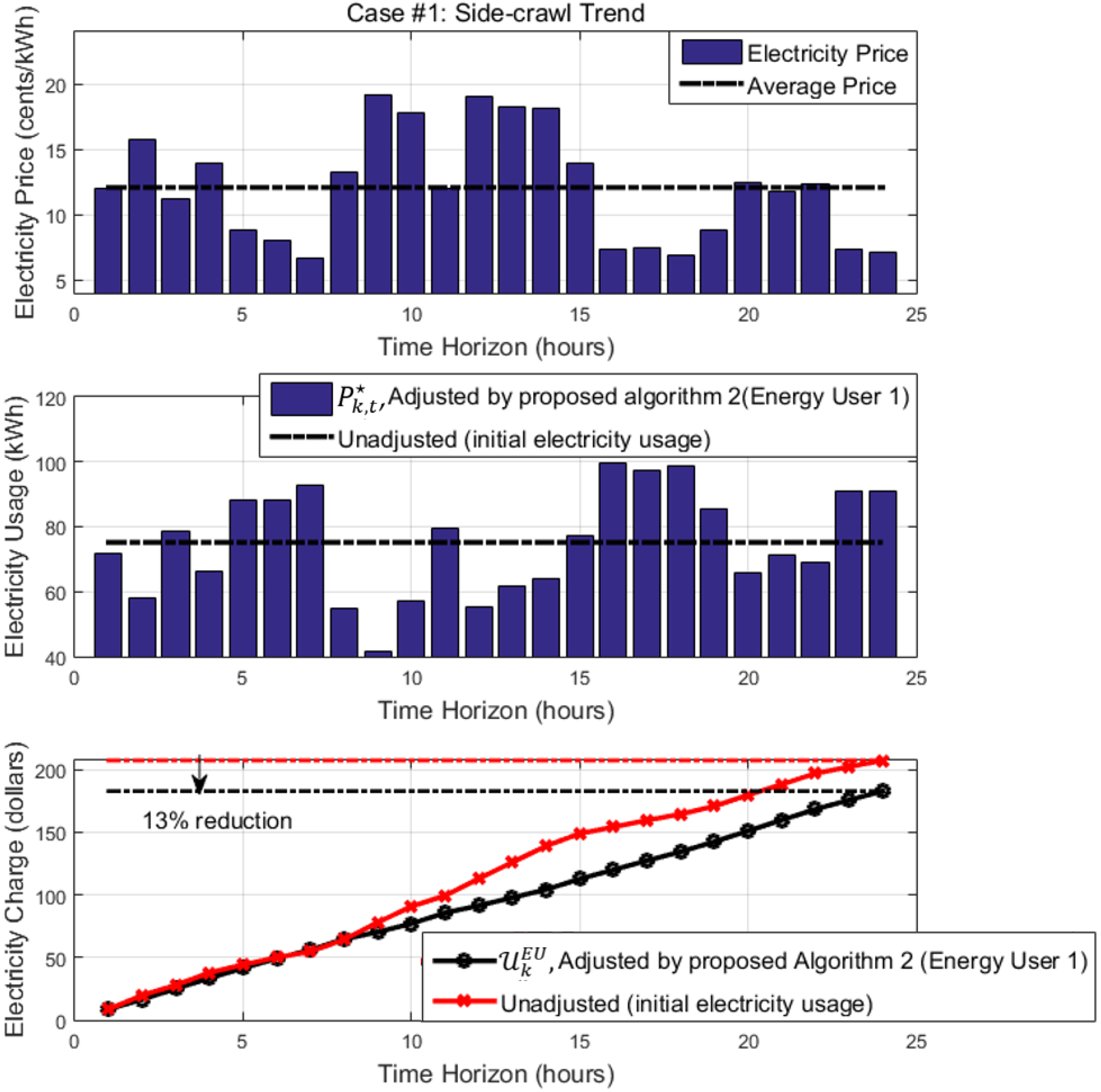
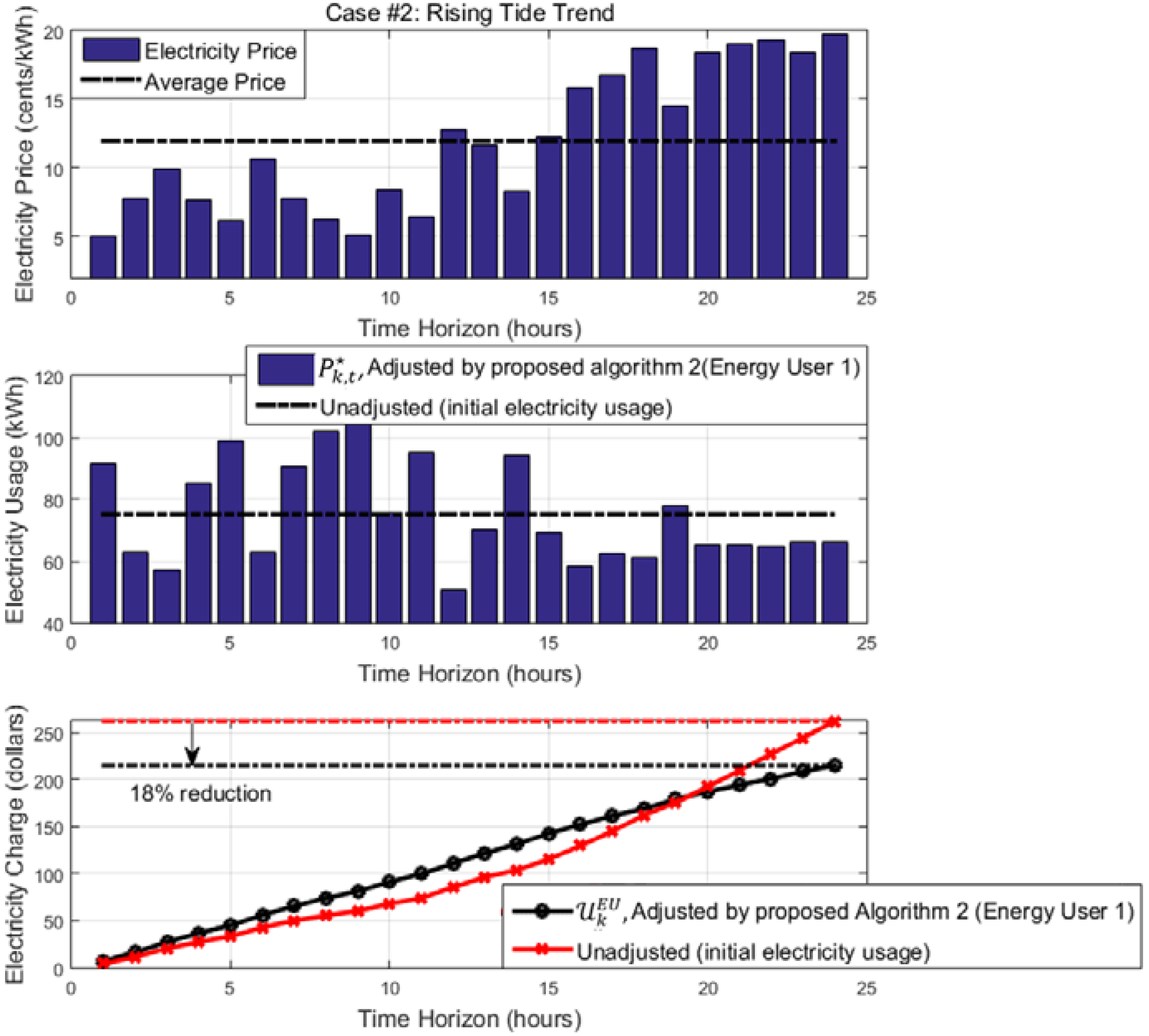
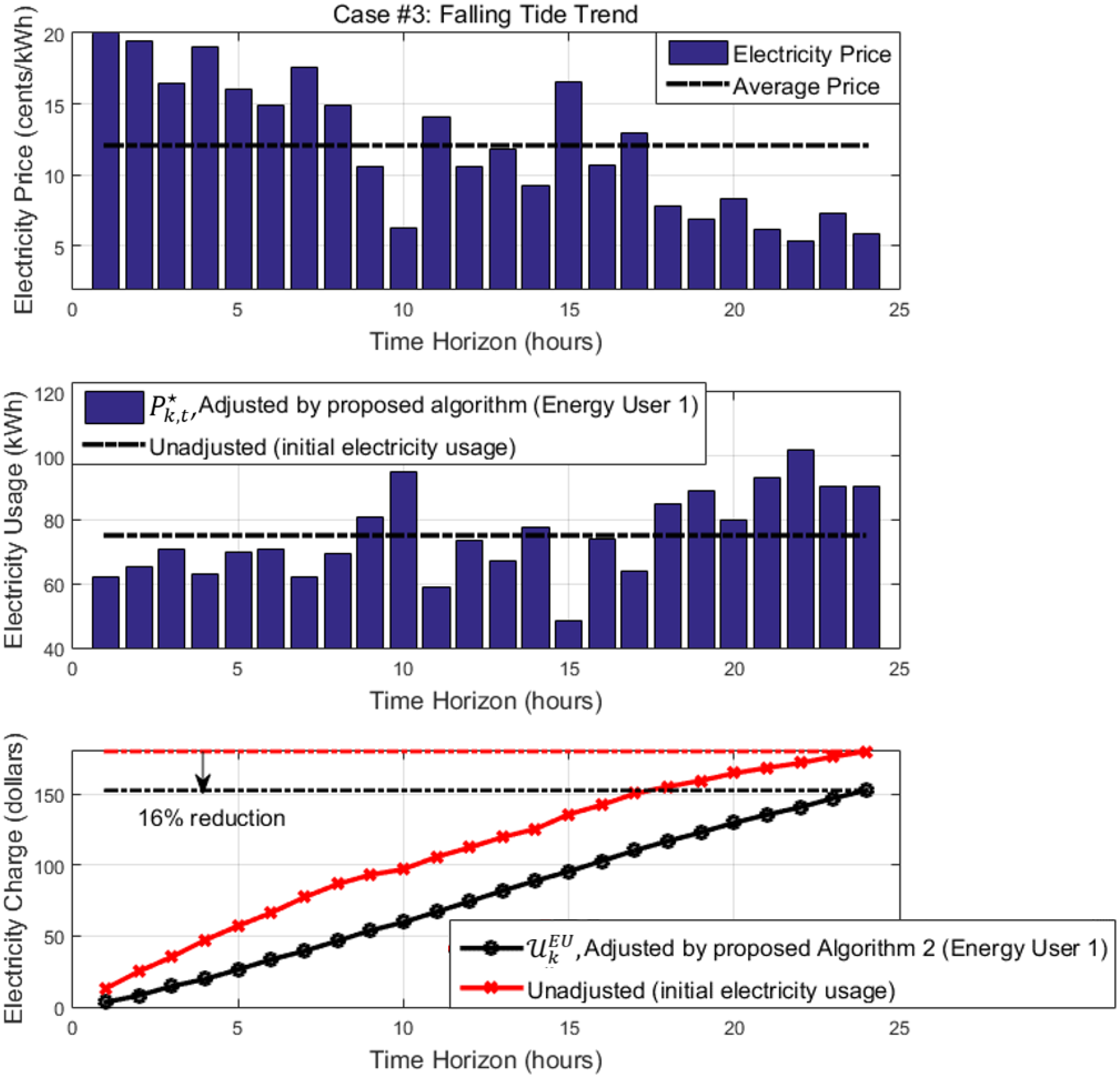
4. Simulation Results
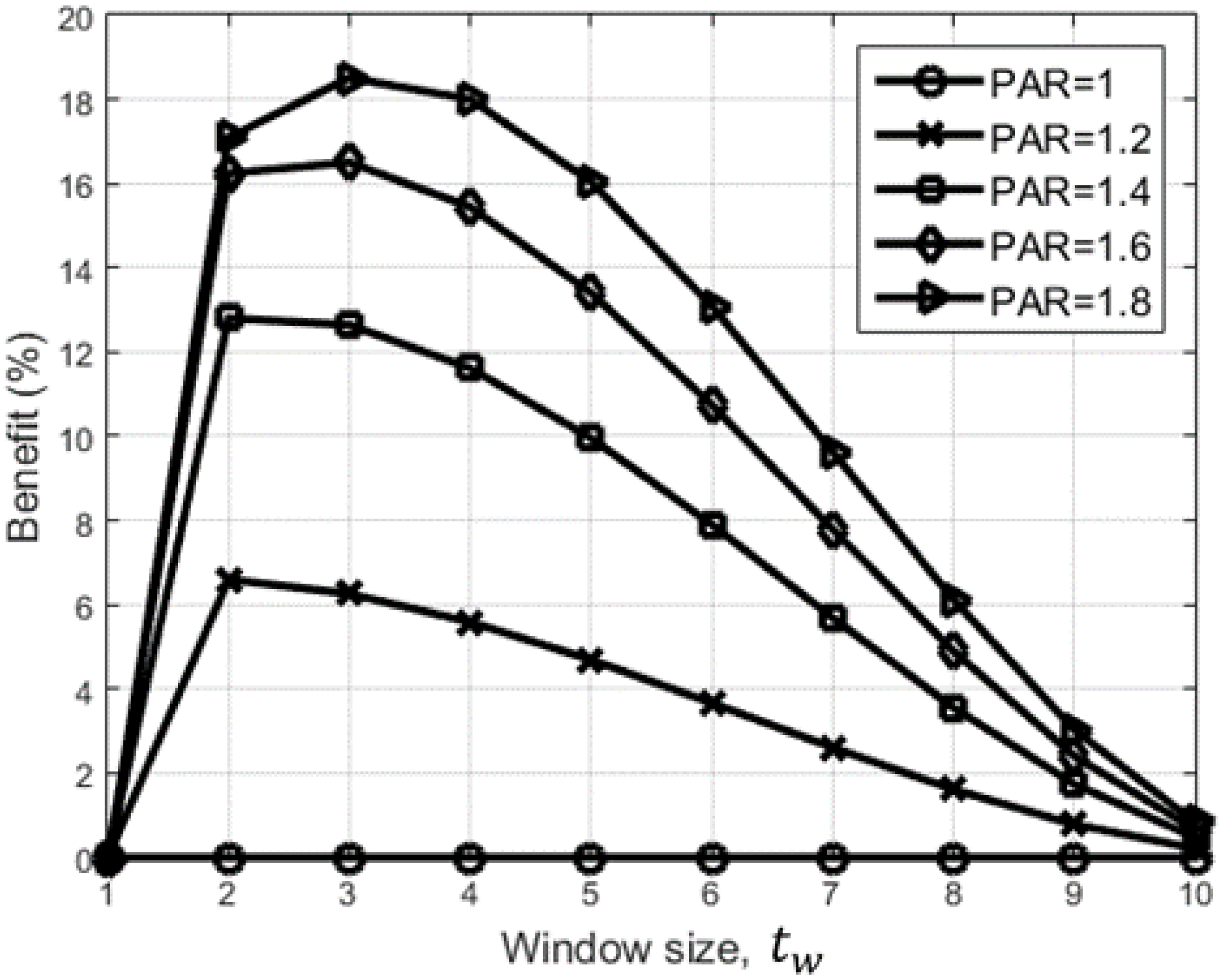
Summary of Simulation Results and Insights
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Siano, P. Demand response and smart grids-A survey. Renew. Sustain. Energy Rev. 2014, 30, 461–478. [Google Scholar] [CrossRef]
- Wood, A.J.; Wollenberg, B.F. Power Generation, Operation, and Control; John Wiley & Sons: Hoboken, NJ, USA, 2012. [Google Scholar]
- Zakariazadeh, A.; Jadid, S.; Siano, P. Smart microgrid energy and reserve scheduling with demand response using stochastic optimization. Int. J. Elect. Power Energy Syst. 2014, 63, 523–533. [Google Scholar] [CrossRef]
- Deng, R.; Yang, Z.; Chow, M.-Y.; Chen, J. A survey on demand response in smart grids: Mathematical models and approaches. IEEE Access 2017, 11, 570–582. [Google Scholar] [CrossRef]
- Chen, X.; Wei, T.; Hu, S. Uncertainty-aware household appliance scheduling considering dynamic electricity pricing in smart home. IEEE Trans. Smart Grid 2013, 4, 932–941. [Google Scholar] [CrossRef]
- Power Smart Pricing. Available online: http://www.powersmartpricing.org/ (accessed on 12 May 2018).
- Kim, T.; Poor, H. Scheduling power consumption with price uncertainty. IEEE Trans. Smart Grid 2011, 2, 519–527. [Google Scholar] [CrossRef]
- Ibars, C.; Navarro, M.; Giupponi, L. Distributed Demand Management in Smart Grid with a Congestion Game. In Proceedings of the First IEEE International Conference on Smart Grid Communications, Gaithersburg, MD, USA, 4–6 October 2010; pp. 495–500. [Google Scholar] [CrossRef]
- Kishore, S.; Snyder, L. An Innovative RTP-based Residential Power Scheduling Scheme for Smart Grids. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Prague, Czech Republic, 22–27 May 2011; pp. 5956–5959. [Google Scholar] [CrossRef]
- Bu, S.; Yu, F.R.; Liu, P.X. Dynamic pricing for demand-side management in the smart grid. In Proceedings of the IEEE Online Conference on Green Communications, New York, NY, USA, 26–29 September 2011; pp. 47–51. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Akorede, M.F.; Marzband, M.; Vechiu, L.; Pouresmaeil, E. CVaR-based energy management scheme for optimal resilience and operational cost in commercial building microgrids. Int. J. Elec. Power Energy Syst. 2018, 100, 1–9. [Google Scholar] [CrossRef]
- Tavakoli, M.; Shokridehaki, F.; Marzband, M.; Godina, R.; Pouresmaeil, E. A two stage hierarchical control approach for the optimal energy management in commercial building microgrids based on local wind power and PEVs. Sustain. Cities Soc. 2018, 41, 332–340. [Google Scholar] [CrossRef]
- Marzband, M.; Azarinejadian, F.; Savaghebi, M.; Pouresmaeil, E.; Guerrero, J.M.; Lightbody, G. Smart transactive energy framework in grid-connected multiple home microgrids under independent and coalition operations. Renew. Energy 2018, 126, 95–106. [Google Scholar] [CrossRef]
- Marzband, M.; Fouladfar, M.H.; Akorede, M.F.; Lightbody, G.; Pouresmaeil, E. Framework for smart transactive energy in home-microgrids considering coalition formation and demand side management. Sustain. Cities Soc. 2018, 40, 136–154. [Google Scholar] [CrossRef]
- Tushar, W.; Yuen, C.; Smith, D.B.; Poor, H.V. Price discrimination for energy trading in smart grid: A game theoretic approach. IEEE Trans. Smart Grid 2017, 8, 1790–1801. [Google Scholar] [CrossRef]
- Yu, M.; Hong, S.H. A real-time demand-response algorithm for smart grids: A Stackelberg game approach. IEEE Trans. Smart Grid 2016, 7, 879–888. [Google Scholar] [CrossRef]
- Ye, M.; Hu, G. Game design and analysis for price-based demand response: An aggregate game approach. IEEE Trans. Cybern. 2017, 47, 720–730. [Google Scholar] [CrossRef] [PubMed]
- Hong, S.G.; Hwang, Y.M.; Lee, S.Y.; Shin, Y.; Kim, D.I.; Kim, J.Y. Game-theoretic modeling of backscatter wireless sensor networks under smart interference. IEEE Commun. Lett. 2018, 22, 804–807. [Google Scholar] [CrossRef]
- Lee, C.; Park, L.; Cho, S. Light-weight Stackelberg game theoretic demand response scheme for massive smart manufacturing systems. IEEE Access 2018, 6, 23316–23324. [Google Scholar] [CrossRef]
- Esfahani, M.M.; Hariri, A.; Mohammed, O.A. A multiagent-based game-theoretic and optimization approach for market operation of multi-microgrid systems. IEEE Trans. Ind. Informat. 2018, 1, 1–12. [Google Scholar] [CrossRef]
- Marzband, M.; Javadi, M.; Pourmousavi, S.A.; Lightbody, G. An advance retail electricity market for active distribution systems and home microgrid interoperability based on game theory. Electr. Power Syst. Res. 2018, 157, 187–199. [Google Scholar] [CrossRef]
- Nekouei, E.; Alpcan, T.; Chattopadhyay, D. Game-theoretic frameworks for demand response in electricity markets. IEEE Trans. Smart Grid 2015, 6, 748–758. [Google Scholar] [CrossRef]
- Asr, N.R.; Ojha, U.; Zhang, Z.; Chow, M.Y. Incremental welfare consensus algorithm for cooperative distributed generation/demand response in smart grid. IEEE Trans. Smart Grid 2014, 5, 2836–2845. [Google Scholar]
- Soliman, S.A.-H.; Mantawy, A.-A.H. Modern Optimization Techniques with Applications in Electric Power Systems; Springer: Berlin, Germany, 2011. [Google Scholar]
- Zhang, Z.; Chow, M.-Y. Convergence analysis of the incremental cost consensus algorithm under different communication network topologies in a smart grid. IEEE Trans. Power Syst. 2012, 27, 1761–1768. [Google Scholar] [CrossRef]
- Yang, S.; Tan, S.; Xu, J.-X. Consensus based approach for economic dispatch problem in a smart grid. IEEE Trans. Power Syst. 2013, 28, 4416–4426. [Google Scholar] [CrossRef]
- Kar, S.; Hug, G.; Mohammadi, J.; Moura, J.M.F. Distributed state estimation and energy management in smart grids: A consensus innovations approach. IEEE J. Sel. Top. Signal Process. 2014, 8, 1022–1038. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, S.; Huang, H.; Ranjan, R.; Zomaya, A.Y.; Wang, L. Game theoretic market driven smart home scheduling considering energy balancing. IEEE Syst. J. 2017, 11, 910–921. [Google Scholar] [CrossRef]
- Dinkelbach, W. On nonlinear fractional programming. Manag. Sci. 1967, 13, 492–498. [Google Scholar] [CrossRef]
- Boyed, S.P.; Vandenberghe, L. Convex Optimization; Cambridge University Press: Cambridge, UK, 2004. [Google Scholar]
- Azizi, S.; Dobakhshari, A.S.; Sarmadi, S.A.N.; Ranjbar, A.M. Optimal PMU placement by an equivalent linear Formulation for exhaustive search. IEEE Trans. Smart Grid 2012, 3, 174–182. [Google Scholar] [CrossRef]
- Ma, K.; Hu, G.; Spanos, C.G. Distributed energy consumption control via real-time pricing feedback in smart grid. IEEE Trans. Control Syst. Technol. 2014, 22, 1907–1914. [Google Scholar] [CrossRef]



| Notations | Meanings of Notations |
|---|---|
| , | The set of energy users (EUs) |
| , | The set of generators |
| , | Total scheduling time set |
| The constant time length | |
| (cents/kWh) | The electricity price per unit energy |
| (kWh) | The amount of the actual providable power |
| (kWh) | The transmission losses |
| (kWh) | The total amount of generated power |
| (cents) | The cost to generate power for generator i |
| , , and | The fitting parameters of the cost function |
| The coefficient for power loss | |
| and | The minimum and maximum bound of |
| The profit function for generator i | |
| The total profit for all generators | |
| Real profit of generators | |
| Maximum achievable profit of the generator i | |
| The amount of the electricity usage of UE k | |
| The amount of electricity to be used in the future divided by the remaining time | |
| The additional or abandoned electricity usage | |
| The electricity charge for UE k | |
| The total electricity charge for all UEs | |
| The Stackelberg game where is a player set that is composed of generators and EUs, is the constraint set, and is the profit set | |
| and | The minimum and maximum prices of the electricity |
| and | The minimum and maximum electricity-usage |
| The minimum required electricity consumption | |
| The optimum solution of P1 | |
| and | The optimized value of , and |
| A set of feasible solutions | |
| The Lagrange dual function of P3 | |
| , and | The Lagrange multipliers |
| and | The number of iterations for the master-loop and slave-loop in Algorithm 1 |
| , and | The iteration steps for optimization |
| The base price as the historical average of | |
| The window size of the time slots | |
| The total electricity charge accumulated for |
| Generator Parameters | ||||||
|---|---|---|---|---|---|---|
| Node | ||||||
| 1 | 0.0024 | 5.56 | 30 | 0.00021 | 60 | 339.69 |
| 2 | 0.0056 | 4.32 | 25 | 0.00031 | 25 | 479.10 |
| 3 | 0.0072 | 6.60 | 25 | 0.00011 | 28 | 290.4 |
| 4 | 0.0047 | 3.14 | 16 | 0.00022 | 40 | 306.34 |
| 5 | 0.0091 | 7.54 | 6 | 0.00041 | 35 | 593.80 |
| 6 | 0.0046 | 4.76 | 12 | 0.000121 | 30 | 443.41 |
| Demand Parameters | |||||
|---|---|---|---|---|---|
| Node | Node | ||||
| 1 | 50 | 100.34 | 7 | 80 | 137.93 |
| 2 | 100 | 159.13 | 8 | 50 | 84.19 |
| 3 | 40 | 80.56 | 9 | 50 | 104.06 |
| 4 | 30 | 123.98 | 10 | 78 | 119.36 |
| 5 | 80 | 109.55 | 11 | 103 | 176.19 |
| 6 | 40 | 76.34 | 12 | 67 | 147.26 |
| Energy Strategy | Gain of Profit |
|---|---|
| Algorithm 1: Generator Profit Maximization | About 45% (compared to existing (beseline scheme) scheme) |
| Algorithm 2: Energy User Profit Maximization | 15.6% on average (compared to that of when algorithm was not applied) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hwang, Y.M.; Sim, I.; Sun, Y.G.; Lee, H.-J.; Kim, J.Y. Game-Theory Modeling for Social Welfare Maximization in Smart Grids. Energies 2018, 11, 2315. https://doi.org/10.3390/en11092315
Hwang YM, Sim I, Sun YG, Lee H-J, Kim JY. Game-Theory Modeling for Social Welfare Maximization in Smart Grids. Energies. 2018; 11(9):2315. https://doi.org/10.3390/en11092315
Chicago/Turabian StyleHwang, Yu Min, Issac Sim, Young Ghyu Sun, Heung-Jae Lee, and Jin Young Kim. 2018. "Game-Theory Modeling for Social Welfare Maximization in Smart Grids" Energies 11, no. 9: 2315. https://doi.org/10.3390/en11092315
APA StyleHwang, Y. M., Sim, I., Sun, Y. G., Lee, H.-J., & Kim, J. Y. (2018). Game-Theory Modeling for Social Welfare Maximization in Smart Grids. Energies, 11(9), 2315. https://doi.org/10.3390/en11092315






