On Energy Management Control of a PV-Diesel-ESS Based Microgrid in a Stand-Alone Context
Abstract
:1. Introduction
- In terms of control, an IMC strategy based on resonant regulator is proposed.
- In terms of energy management, the EMC is tested first using a standard SOC profile emulating the microgrid different states. Then real data are used to simulate the load and solar radiations. Furthermore, the second case SOC profile is estimated using the system parameters and the extracted data.
- The proposed ESS control strategy, IMC operating mode, and PMC one are experimentally validated.
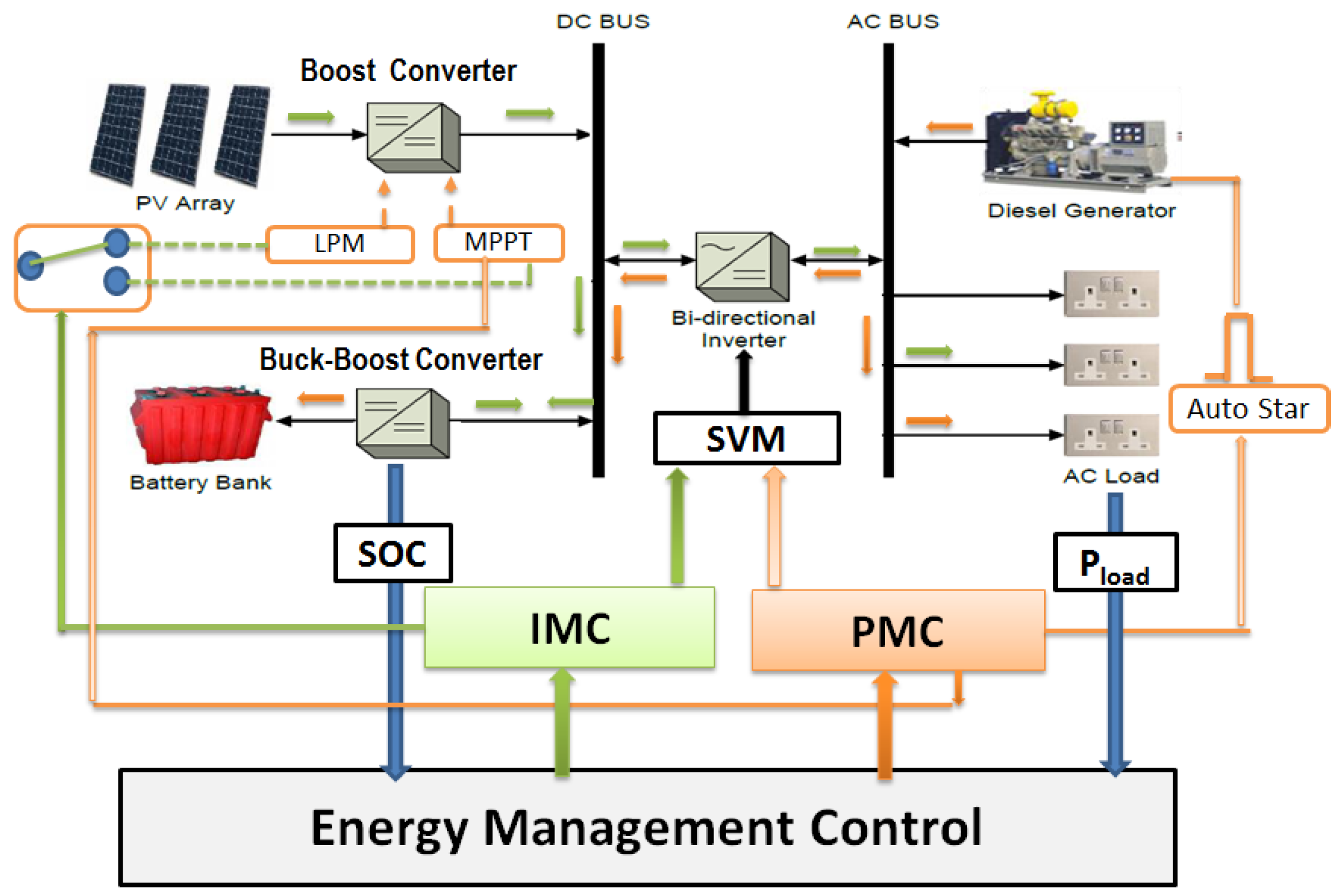
2. System Structure and Modeling
2.1. PVG Model
2.2. DG Model
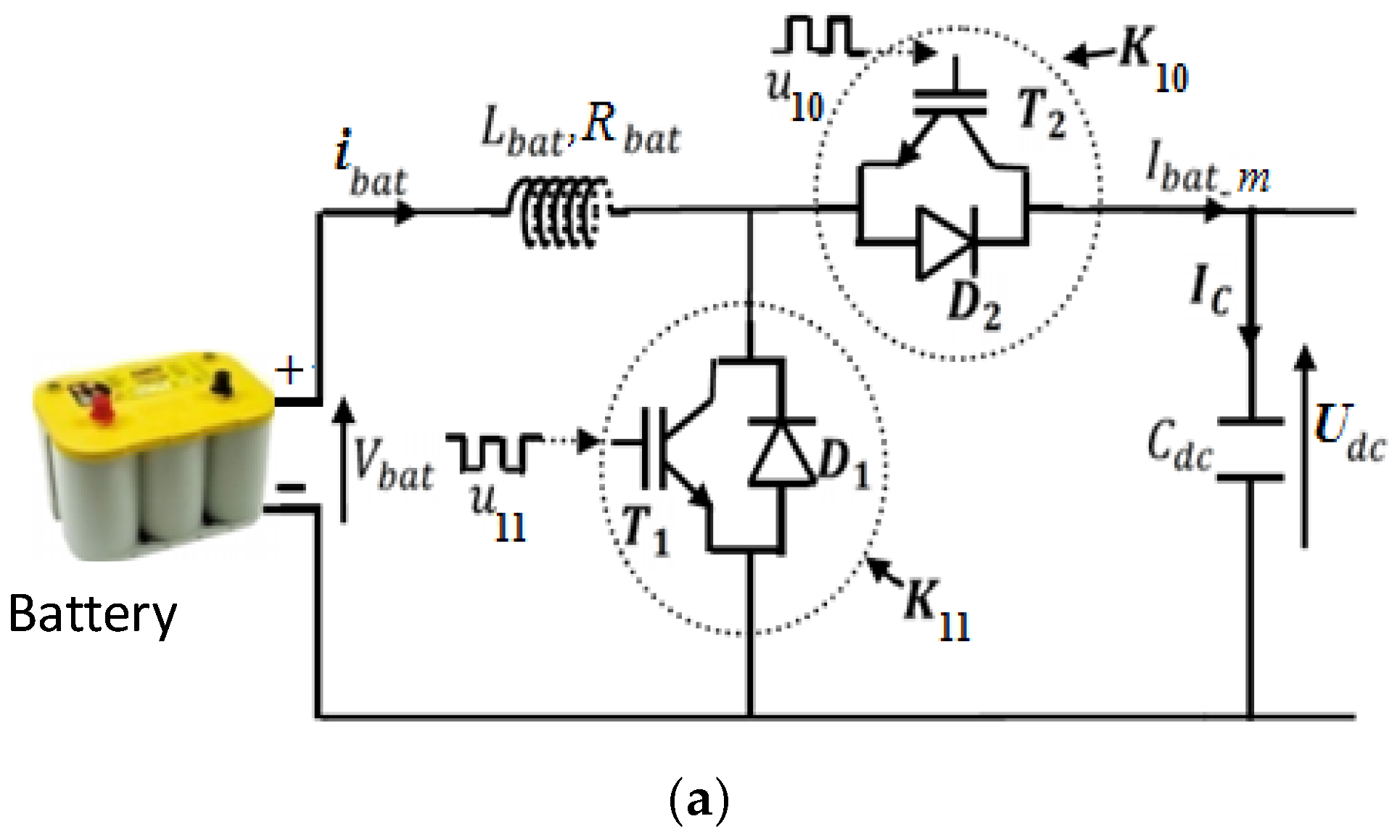
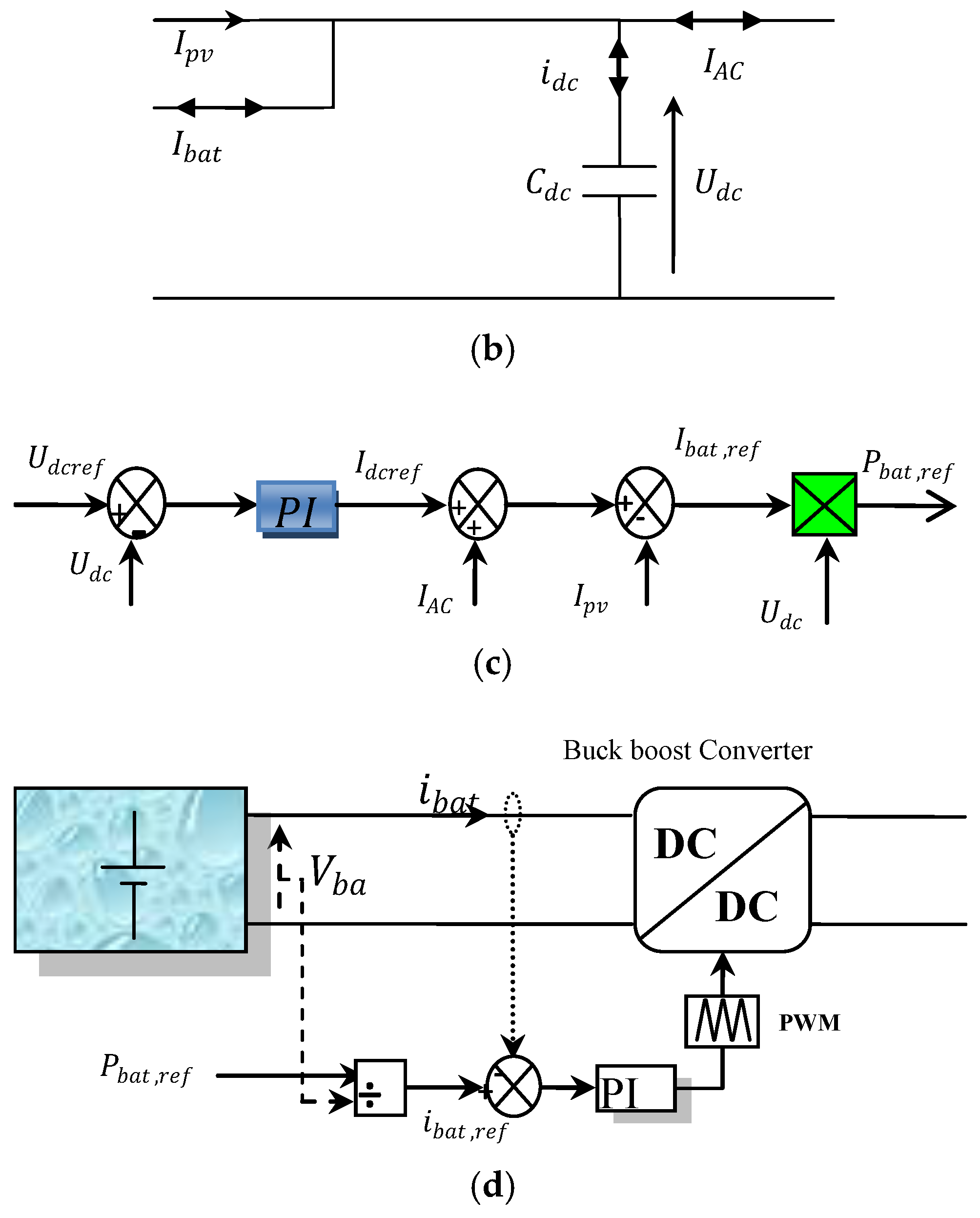
2.3. Battery Model
3. Energy Management Control and Supervisory Algorithm
3.1. ESS Control Strategy
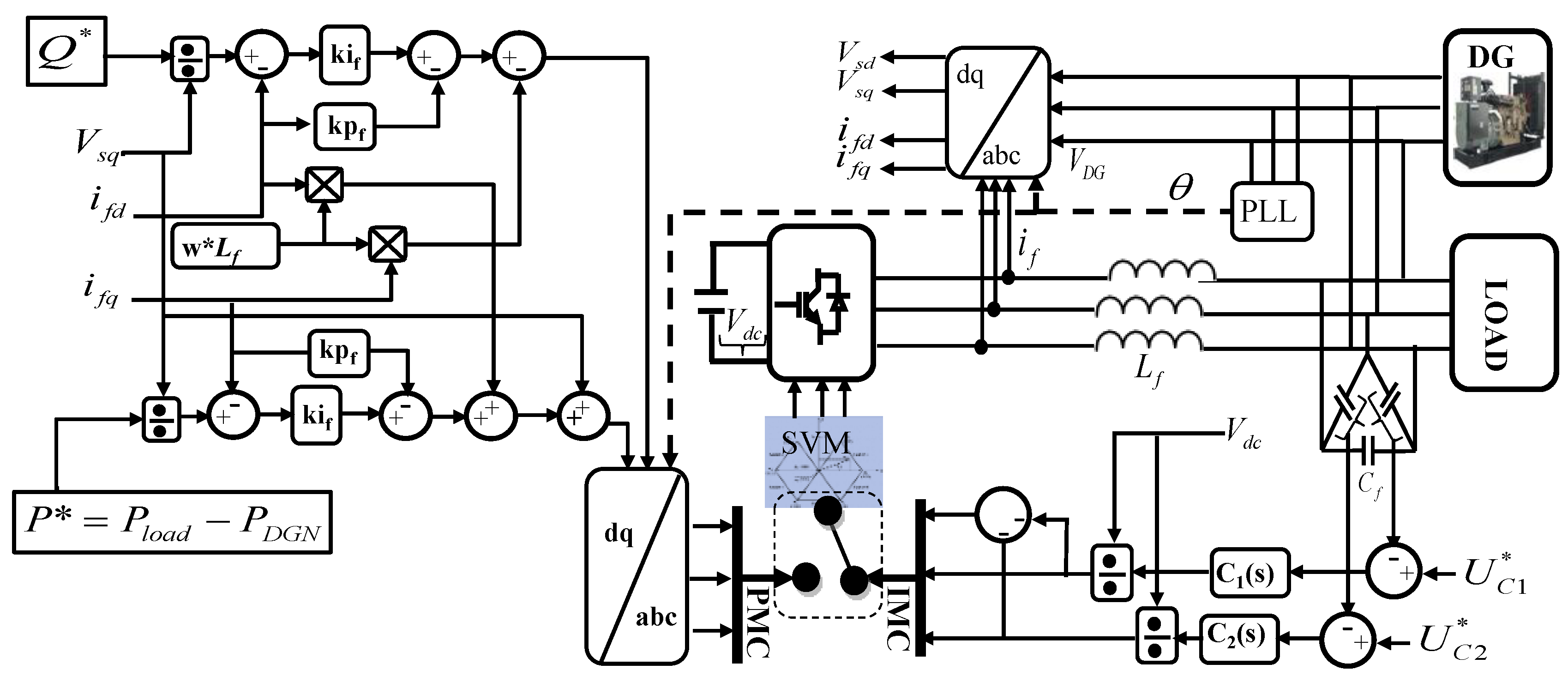
3.2. Isolated Mode Control (IMC)
3.3. Parallel Mode Control (PMC)
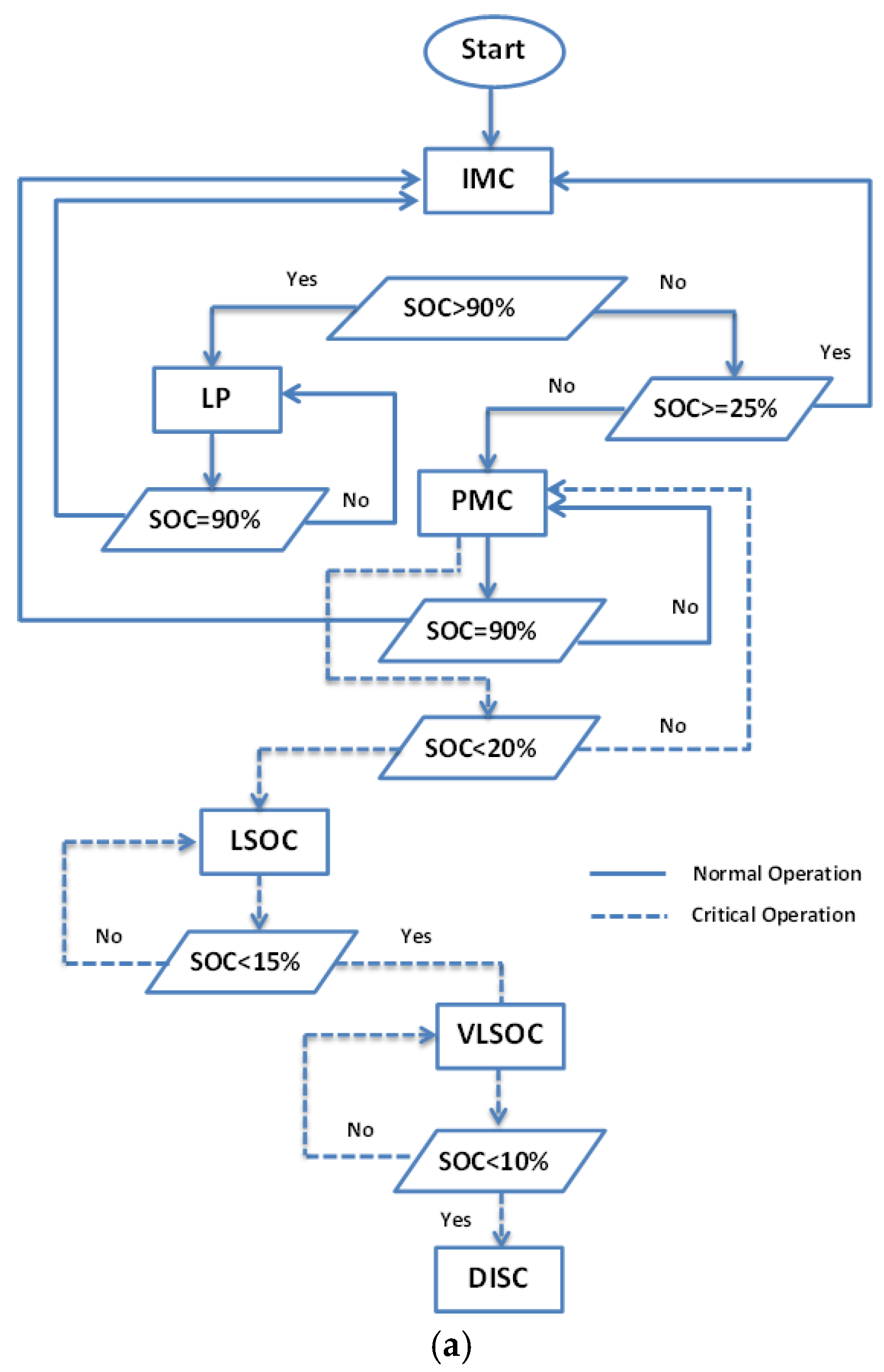
3.4. Supervisory Algorithm
3.4.1. ESS Supervision
3.4.2. DG Supervision
- The DG start-up must be load-out and delayed with about 3 to 5 seconds after it starts to avoid operation during its transient.
- When solicited, the DG runs at its nominal point in all possible operating scenarios regardless load changes.
- The DG will stop only if the SOC reaches its maximum.
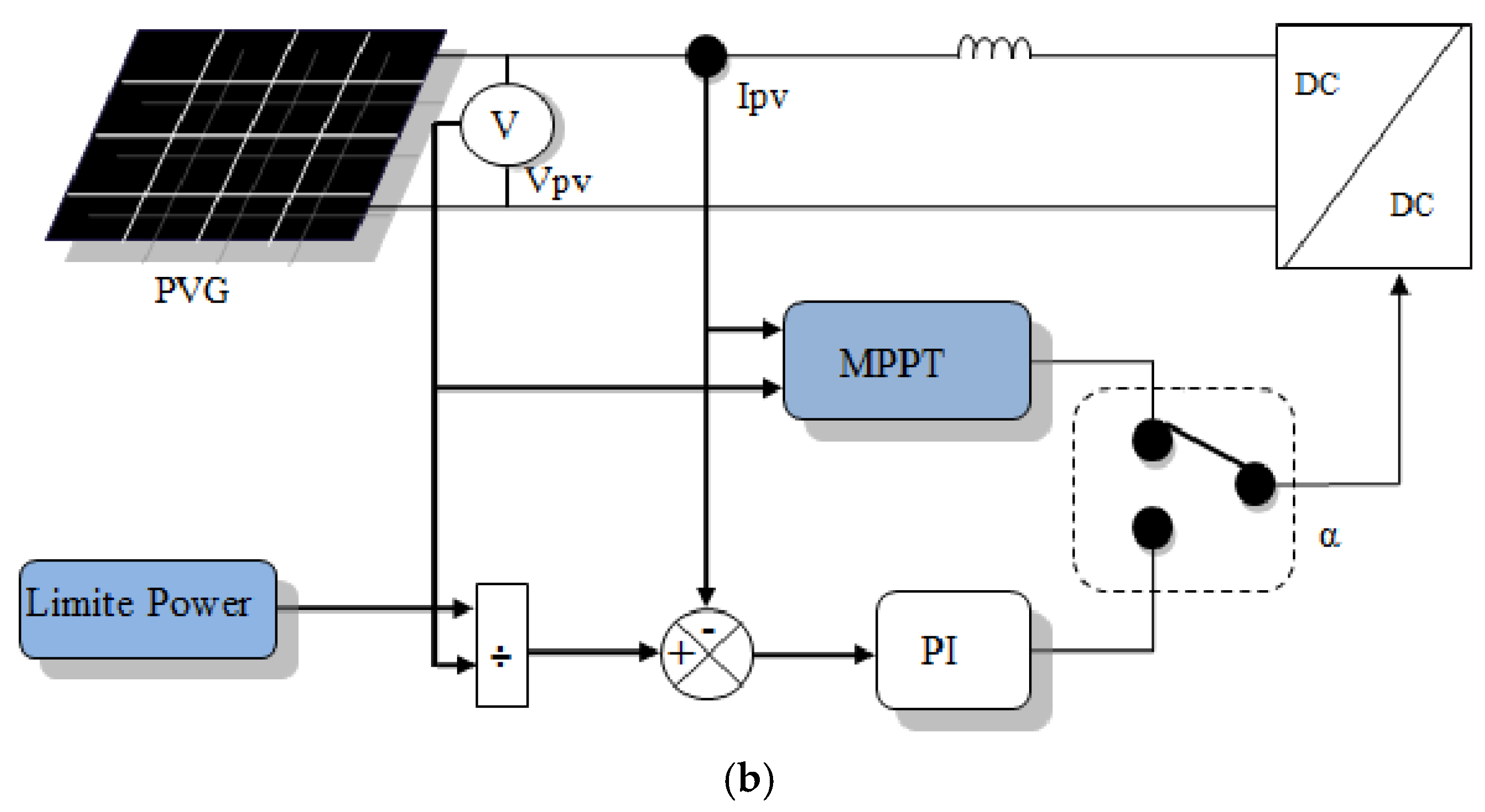
3.4.3. PVG Supervision
3.4.4. Load Supervision
- When the DG does not start.
- When there is a malfunction in the DC/AC converter. Therefore, the energy surplus produced by the DG is not transferred to the ESS and the SOC continues to decrease.
- When there is a malfunction in the DC/DC buck/boost converter related to the ESS.
4. Simulation Results
4.1. Discussion
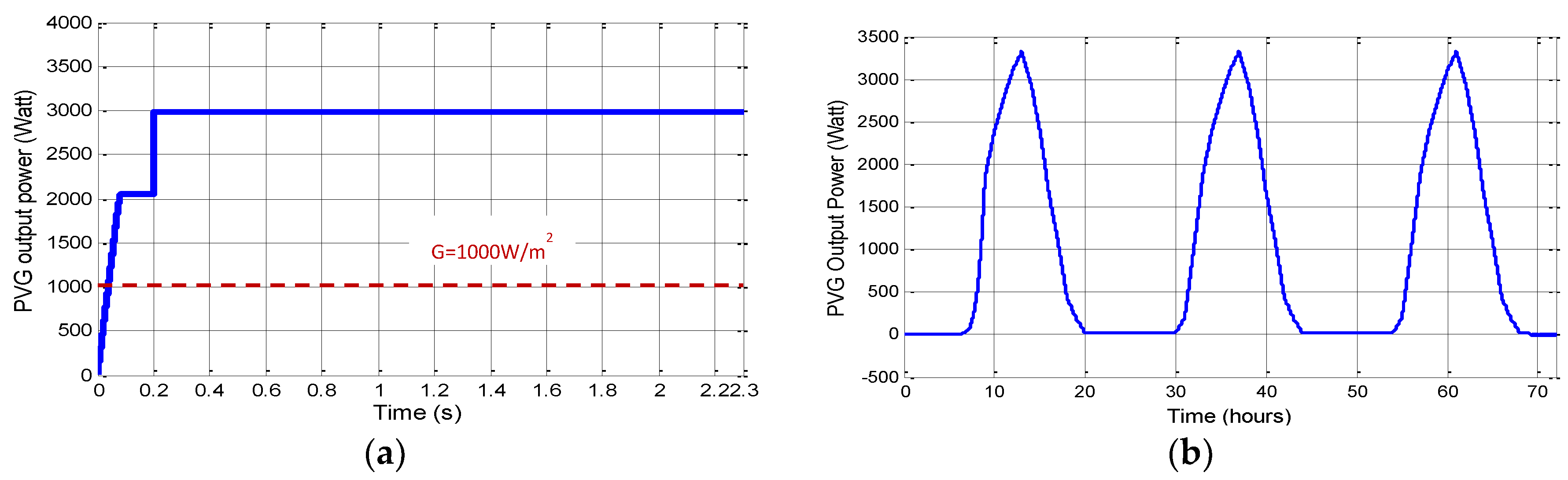
4.1.1. Emulated SOC
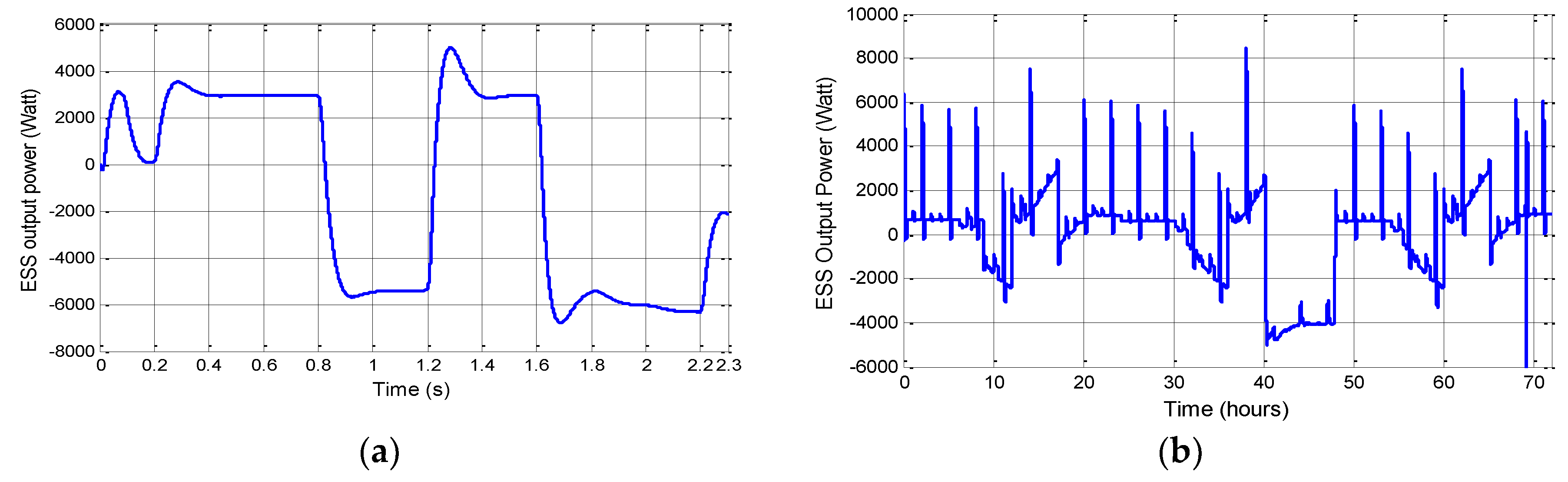
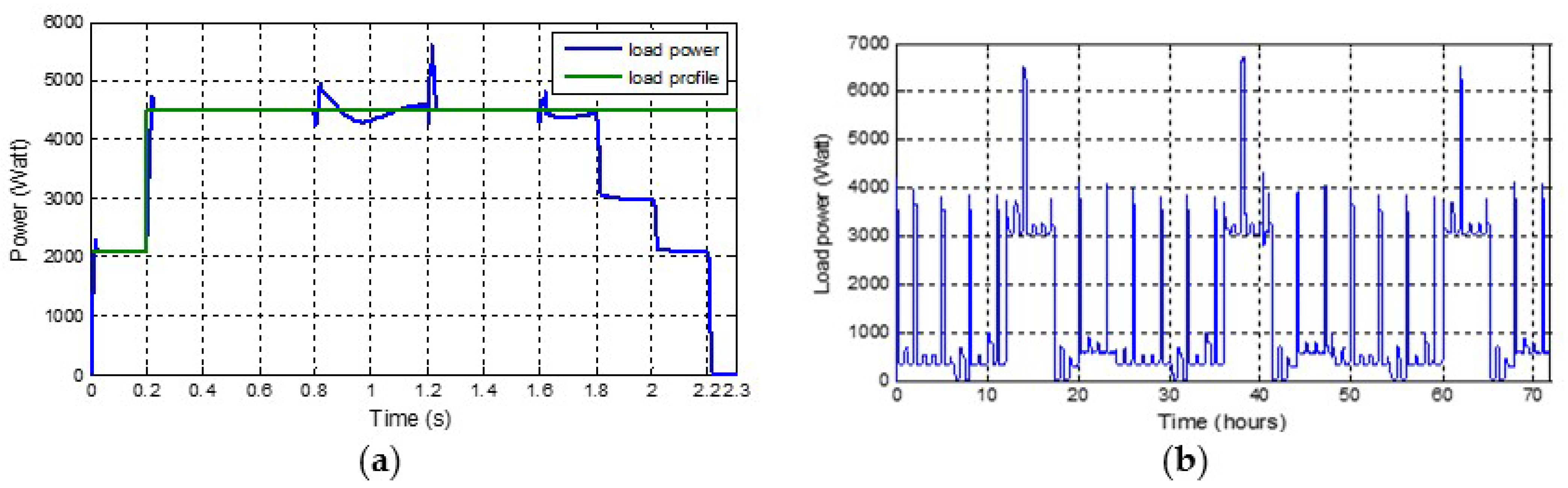
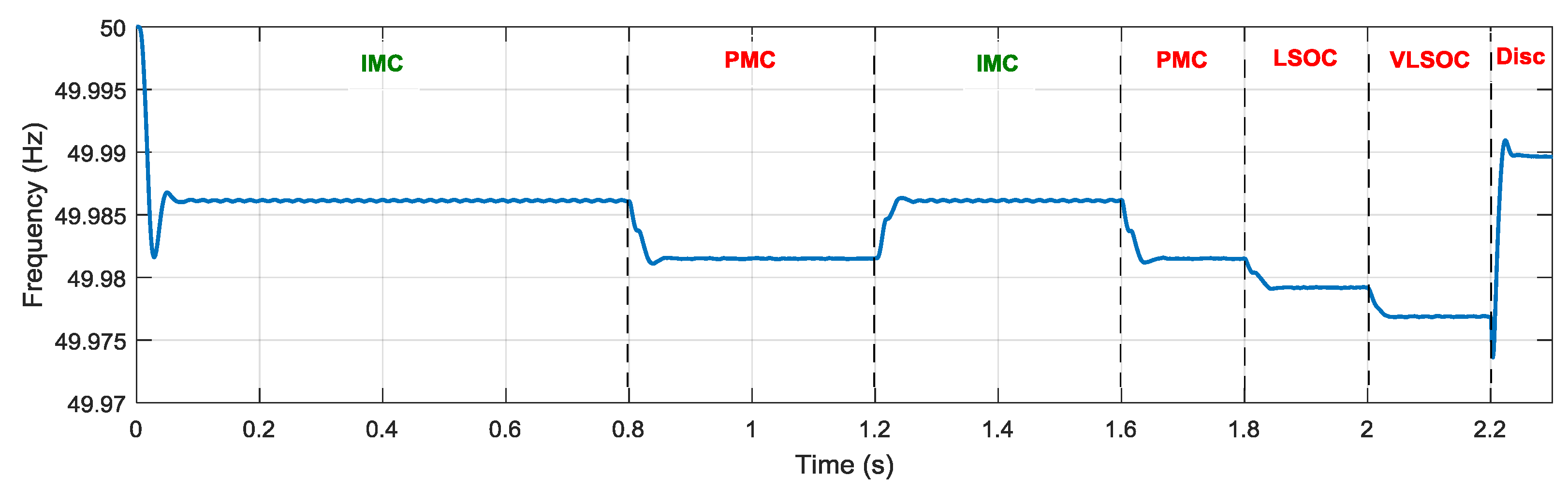
- From 0 to 0.2 s, the batteries are charged (SOC > SOCmax) and the PVG power produced exceeds the load requirement. The LP mode is then activated.
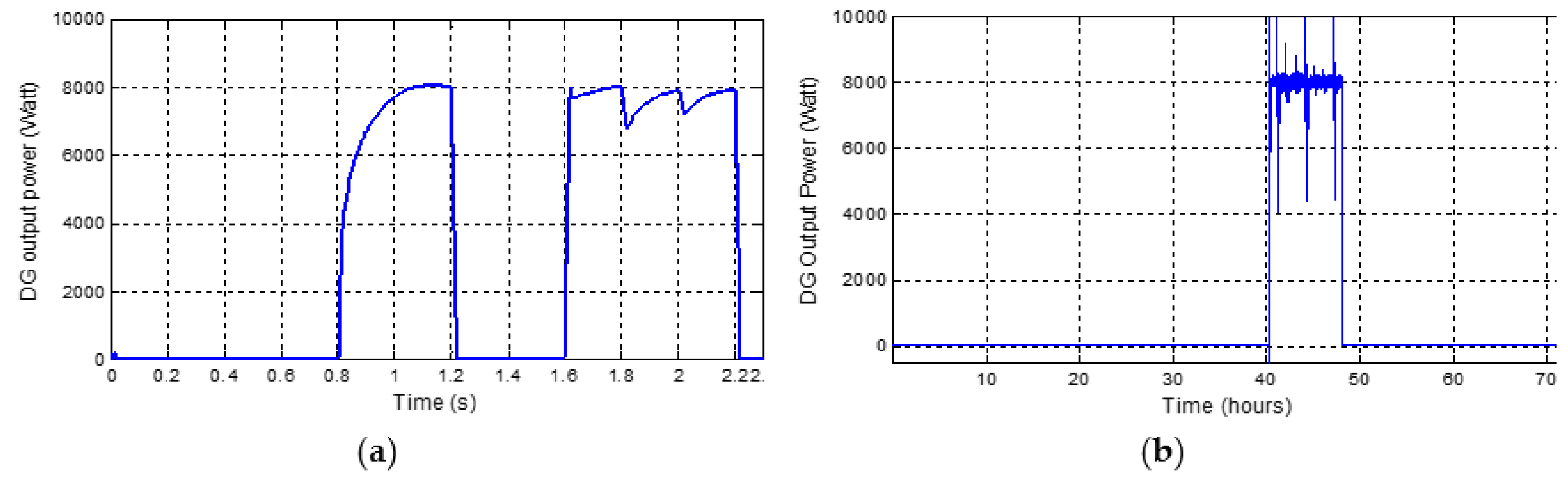
- From 0.8 to 1.2 s, the SOC riches its lower limit value SOCmin. The DG is solicited with a nominal operating regime, assumed equal to 8kW (Figure 10a), to supply the load power and charge the ESS. The system is then in the PMC operating mode until the SOC riches the limit value SOCmax.
- From 1.2 to 1.6 s, the SOC riches its upper limit value SOCmax. The IMC operating mode is then reactivated.
- From 1.6 to 1.8 s the SOC riches its lower limit value SOCmin. The PMC operating mode is then reactivated.
- From 1.8 to 2 s, the SOC is less than 20%. The supervisory algorithm disconnects then the load with the lowest priority (P3) and the system is in a low state of charge (LSOC) operating mode.
- From 2 to 2.2 s, the ESS continues its discharging (10% < SOC < 15%) and the P2 load is then disconnected. P1 is the load that is still connected to the system that is in a very low state of charge (VLSOC) operating mode.
- At 2.2 s, the SOC drops below 10%. All the loads are disconnected and the system is in the disconnection (DISC) mode.
4.1.2. Estimated SOC
- One second of simulation corresponds to one hour of operation. For a simulation step of 5 µs, this allows assuming a constant ESS current during 0.018 s.
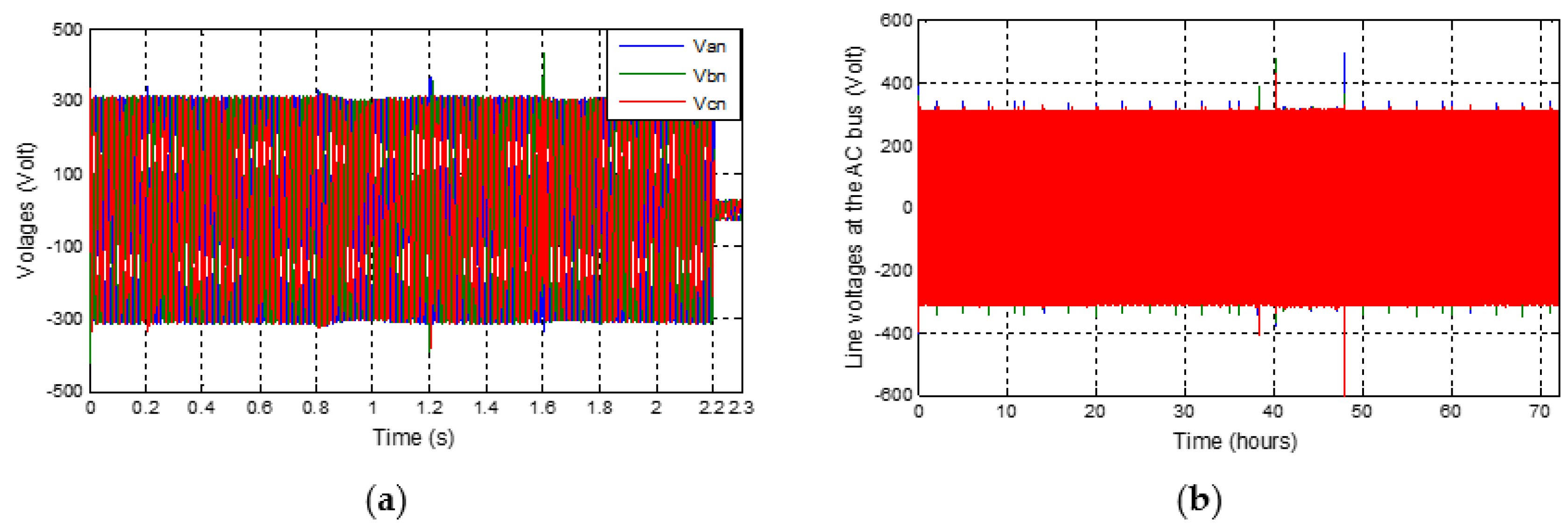
- The SOC is now estimated (Figure 6b) and the microgrid is simulated for 3 days (72 s of simulation).
- The system has been simulated using the MATLAB-Simulink environment for a daily radiation profile of the Adrar region and the load profile of three Saharan cabins, as previously mentioned. The achieved simulation results are given by Figure 7b, Figure 8b, Figure 9b, Figure 10b and Figure 11b. Here, it can be noticed that:
- From 0 to 40 h, 25% < SOC < 90%. Both PVG and ESS provide the load required power. The system is then in the IMC operating mode with 40 hours of autonomy.
- From 40 to 48 h, the SOC riches its lower limit value SOCmin. The DG is solicited with a nominal operating regime to supply the load power and charge the ESS. The system is then in the PMC operating mode until the SOC riches the limit value SOCmax.
- From 48 to 72 h, the ESS is charged (SOC = 90%). The DG is disconnected, the IMC operating mode is reactivated and the system operating cycle is therefore 2 days.
4.1.3. Stability Analysis
5. Experimental Validations
5.1. Discussion
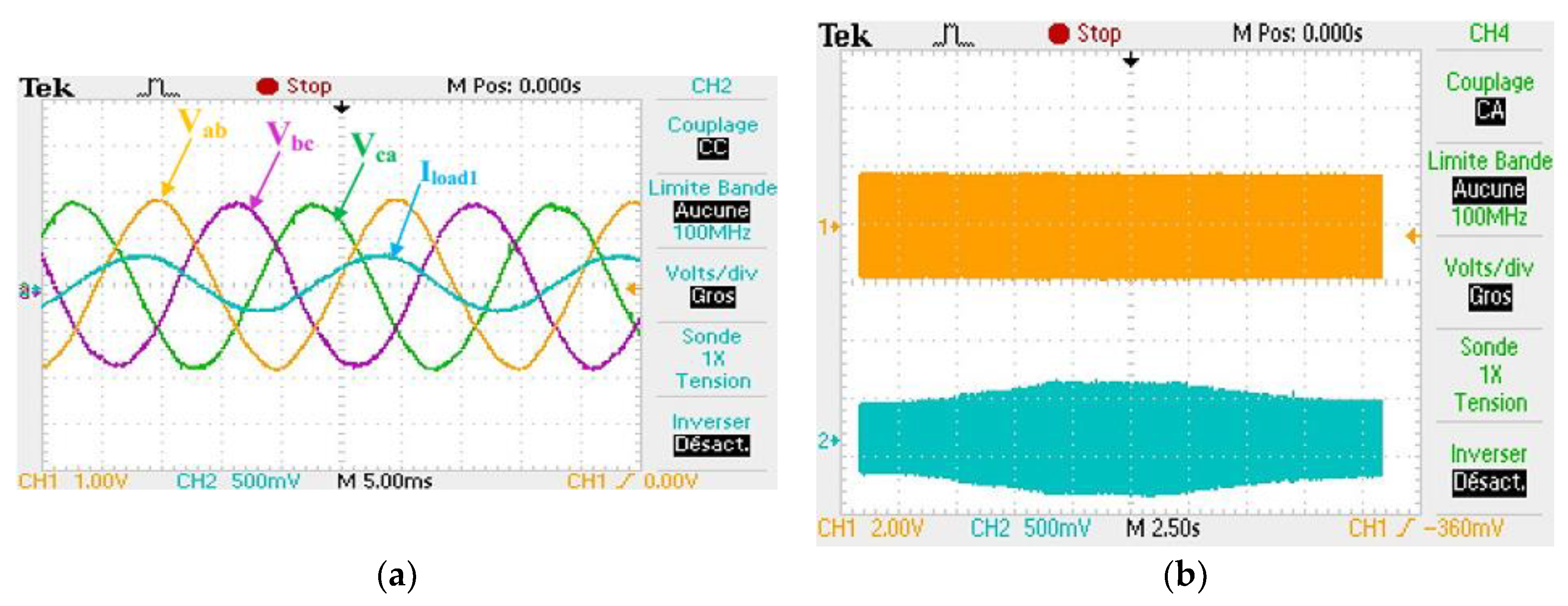
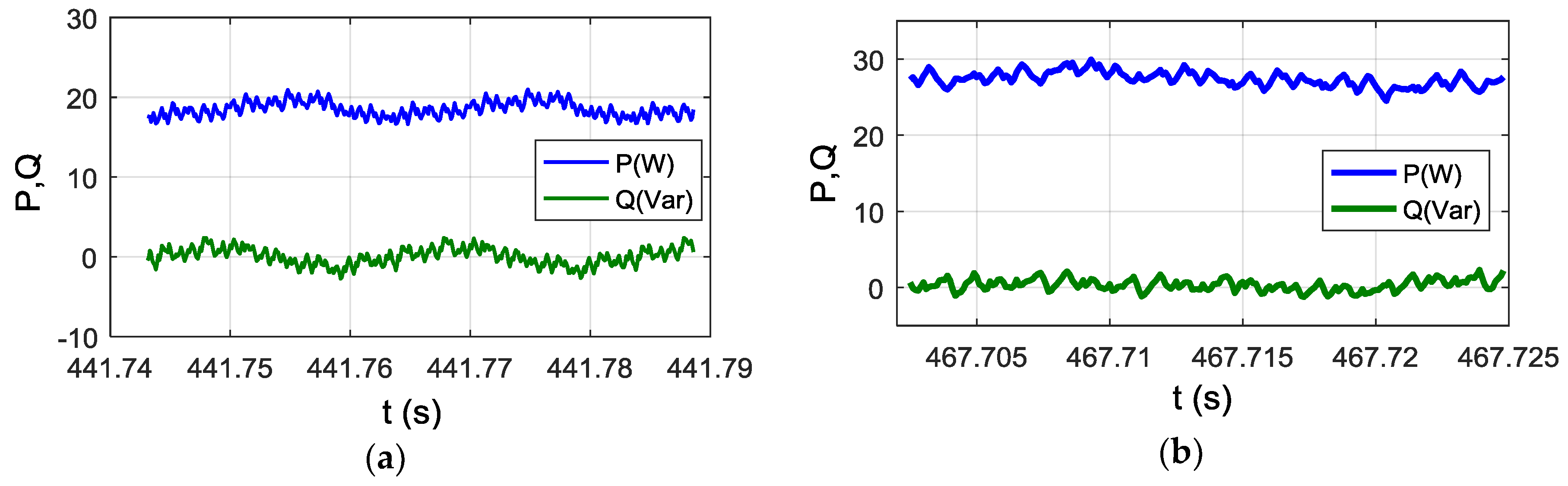
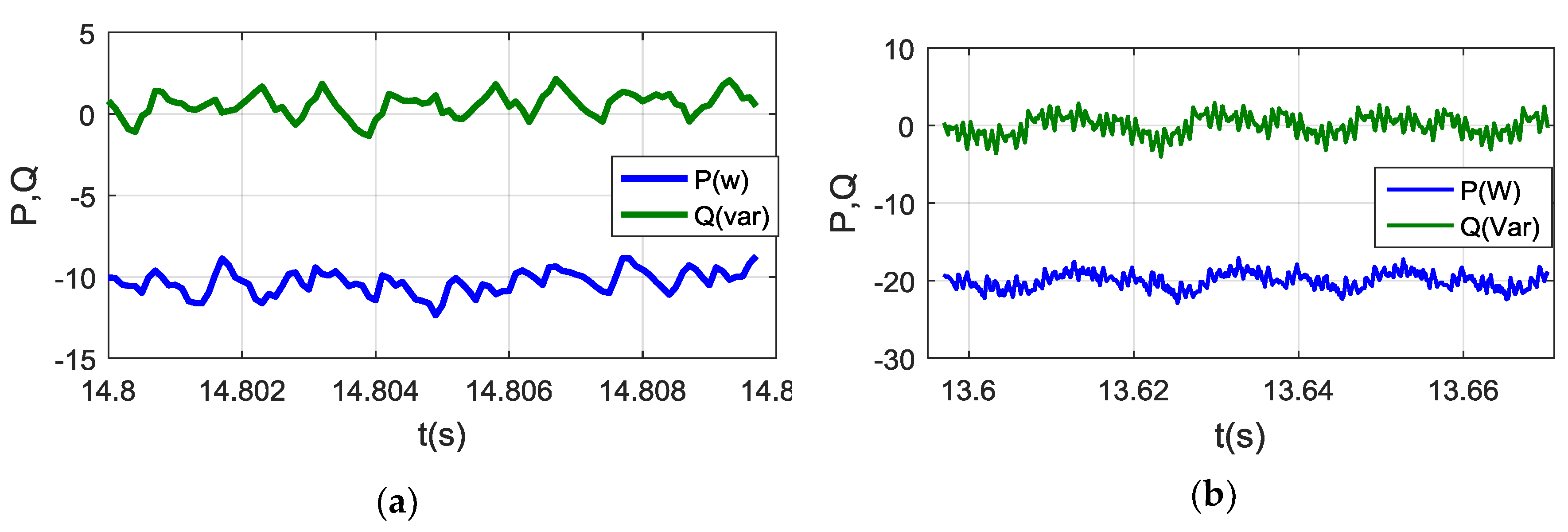
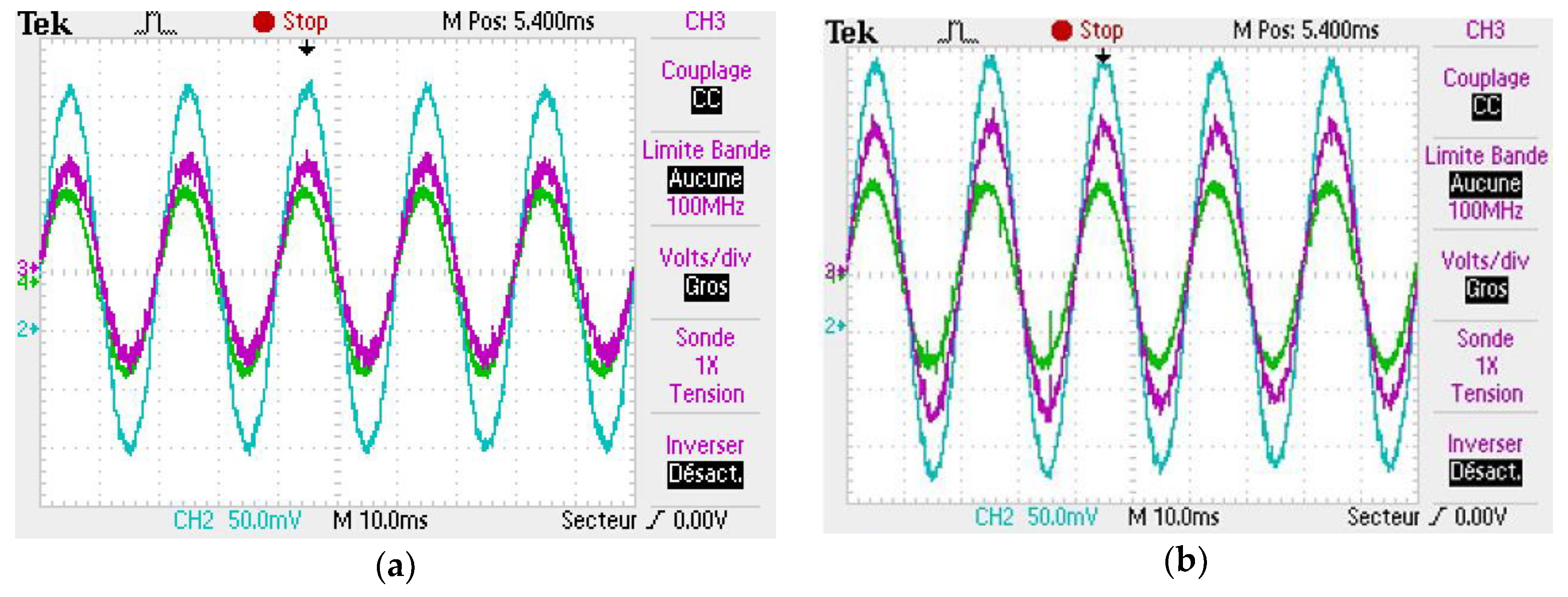
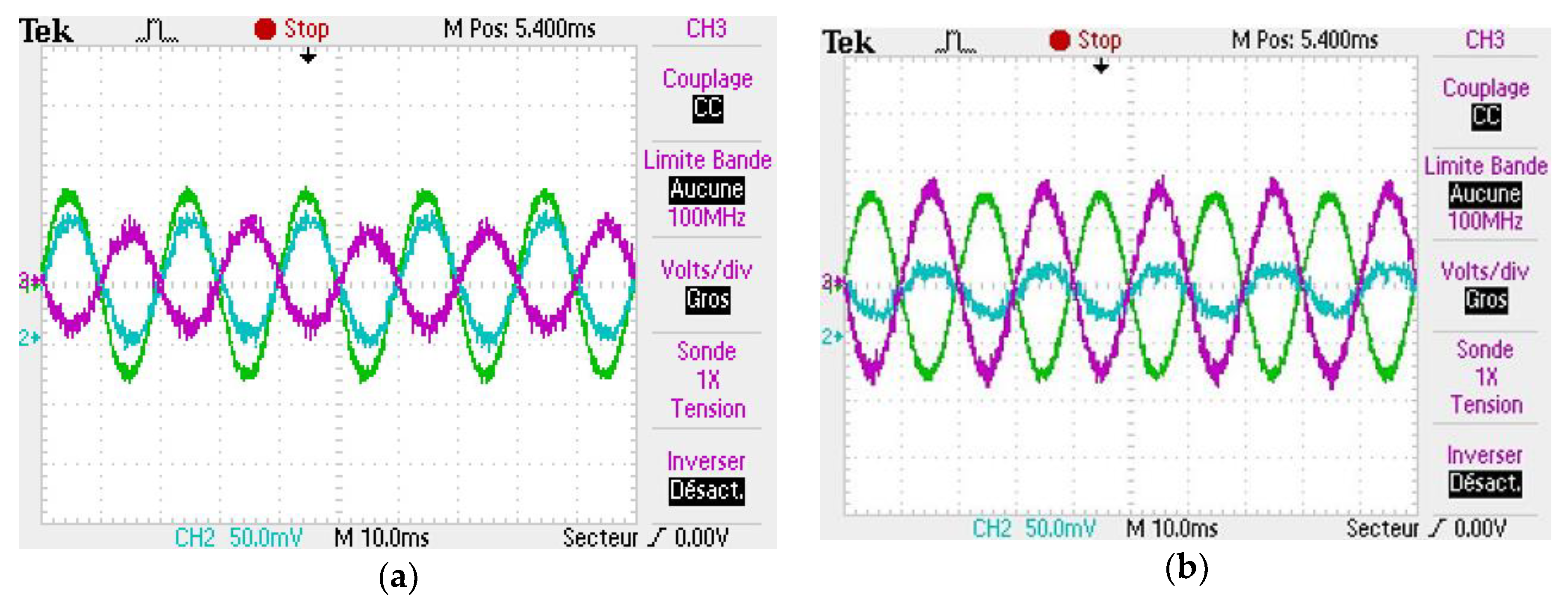
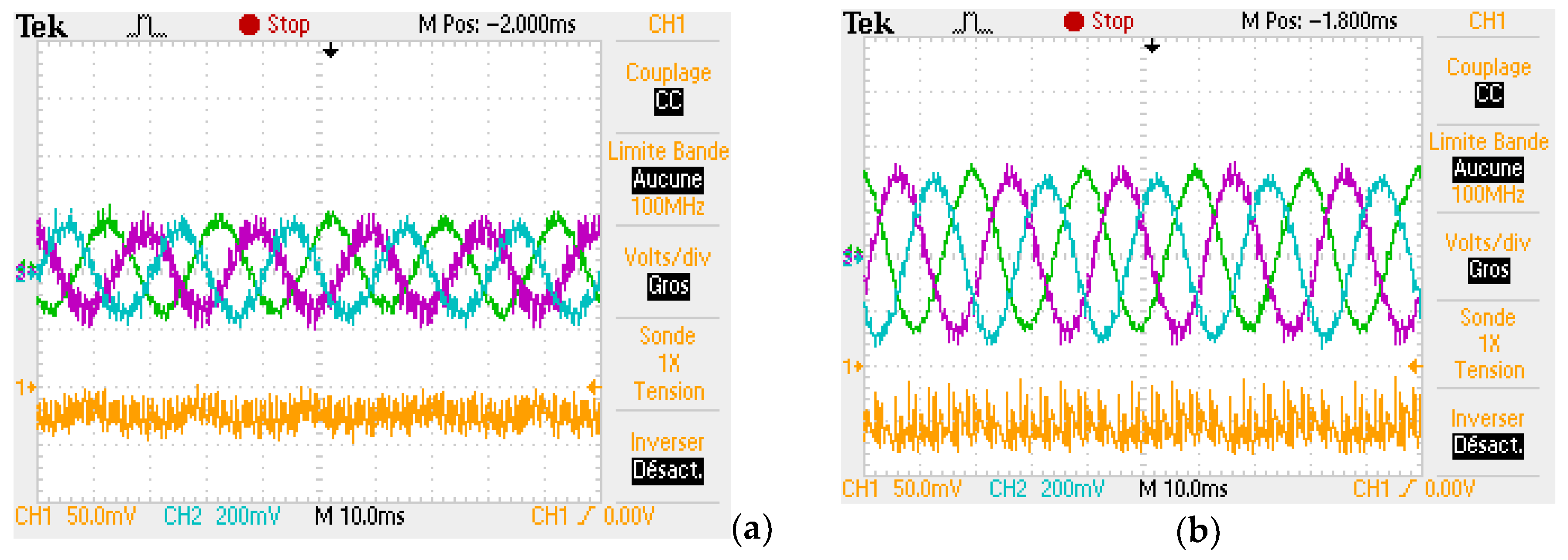
5.1.1. ESS Control Validation
5.1.2. IMC Validation
5.1.3. PMC Validation
6. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Appliances | Nbr | Power | DUD | TP | DEC |
|---|---|---|---|---|---|
| TV | 1 | 80 W | 5 h | 80 W | 400 Wh |
| Fridge | 1 | 800 W | 4 h | 800 W | 3200 Wh |
| Lights | 1 | 40 W | 1 h | 40 W | 40 Wh |
| Neon light | 2 | 40 W | 8 h | 80 W | 640 Wh |
| Bathroom lamp | 1 | 40 W | 2 h | 40 W | 80 Wh |
| Water heater | 1 | 800 W | 2 h | 800 W | 1600 Wh |
| Computer | 1 | 100 W | 4 h | 100 W | 400 Wh |
| Air conditioner | 1 | 1000 W | 3 h | 1000 W | 3000 Wh |
| Coffee maker | 1 | 150 W | 1 h | 150 W | 150 Wh |
| Total | 3090 W | 9510 Wh | |||
Symbols and Abbreviations
| Iph | Photocurrent; |
| I0 | Diode saturation current; |
| q | Coulomb constant (1.602 × 10−19 C) |
| k | Boltzmann’s constant (1.38 × 10−23 J/K) |
| T | Cell temperature (K); |
| Rs | Series cell resistance (Ω); |
| Rp | Parallel cell resistance (Ω); |
| Ns | Number of series panel; |
| Np | Number of parallel panel; |
| Ipv, Vpv | PV array output current and voltage (V); |
| G | Solar radiation (W/m2); |
| SOC | State of Charge; |
| h | Number of engine cycles; |
| MPPT | Maximum Power Point Tracking; |
| ESS | Energy Storage System; |
| dq | Direct- and Quadrature axes; |
| We | System angular frequency; |
| JT | Total inertia; |
| DT | Total friction coefficient; |
| PLL | Phase-locked loop; |
| P, Q | Active power and reactive power; |
| Tmec | Diesel engine torque; |
| Φ | Fuel flow; |
| C | Fuel flow control signal; |
| Te | Electromagnetic torque; |
| τ1 | Diesel engine delay time; |
| τ2 | Actuator time constant; |
| Ka | Actuator gain; |
| P&O | Perturb & Observ; |
| SVM | Space Vector Modulation; |
| THD | Total Harmonic Distortion. |
References
- Stambouli, A.B.; Khiat, Z.; Flazi, S.; Kitamura, Y. A review on the renewable energy development in Algeria: Current perspective, energy scenario and sustainability issues. Renew. Sustain. Energy Rev. 2012, 16, 4445–4460. [Google Scholar] [CrossRef]
- Himri, Y.; Malik, A.S.; Stambouli, A.B.; Himri, S.; Draoui, B. Review and use of the Algerian renewable energy for sustainable development. Renew. Sustain. Energy Rev. 2009, 13, 1584–1591. [Google Scholar] [CrossRef]
- Bajpai, P.; Dash, V. Hybrid renewable energy systems for power generation in stand-alone applications: A review. Renew. Sustain. Energy Rev. 2012, 16, 2926–2939. [Google Scholar] [CrossRef]
- Khelif, A.; Talha, A.; Belhamel, M.; Arab, A.H. Feasibility study of hybrid Diesel-PV power plants in the southern of Algeria: Case study on AFRA power plant. Int. J. Electr. Power Energy Syst. 2012, 43, 546–553. [Google Scholar] [CrossRef]
- Sekhar, P.C.; Mishra, S. Storage free smart energy management for frequency control in a Diesel-PV-fuel cell-based hybrid AC microgrid. IEEE Trans. Neural Networks Learn. Syst. 2016, 27, 1657–1671. [Google Scholar] [CrossRef] [PubMed]
- Wen, S.; Lan, H.; Hong, Y.; Yu, D.C.; Zhang, L.; Cheng, P. Allocation of ESS by interval optimization method considering impact of ship swinging on hybrid PV/Diesel ship power system. Appl. Energy 2016, 175, 158–167. [Google Scholar] [CrossRef]
- Ahadi, A.; Kang, S.; Lee, J. A novel approach for optimal combinations of wind, PV, and energy storage system in Diesel-free isolated communities. Appl. Energy 2016, 170, 101–115. [Google Scholar] [CrossRef]
- Bui, V.; Hussain, A.; Kim, H. Optimal operation of microgrids considering auto-configuration function using multiagent system. Energies 2017, 10, 1484. [Google Scholar] [CrossRef]
- Ou, T.; Hong, C. Dynamic operation and control of microgrid hybrid power systems. Energy 2014, 66, 314–323. [Google Scholar] [CrossRef]
- Zhu, B.; Tazvinga, H.; Xia, X. Switched model predictive control for energy dispatching of a photovoltaic-Diesel-battery hybrid power system. IEEE Trans. Control. Syst. Technol 2015, 23, 1229–1236. [Google Scholar]
- Philip, J.; Jain, C.; Kant, K.; Singh, B.; Mishra, S.; Chandra, A.; Al-Haddad, K. Control and implementation of a standalone solar photovoltaic hybrid system. IEEE Trans. Ind. Appl. 2016, 52, 3472–3479. [Google Scholar] [CrossRef]
- Rashed, M.; Elmitwally, A.; Kaddah, S. New control approach for a PV-Diesel autonomous power system. Electr. Power Syst. Res. 2008, 78, 949–956. [Google Scholar] [CrossRef]
- Elmitwally, A.; Rashed, M. Flexible operation strategy for an isolated PV-Diesel microgrid without energy storage. IEEE Trans. Energy Convers. 2011, 26, 235–244. [Google Scholar] [CrossRef]
- Lan, H.; Bai, Y.; Wen, S.; Yu, D.C.; Hong, Y.; Dai, J.; Cheng, P. Modeling and stability analysis of hybrid PV/Diesel/ESS in ship power system. Inventions 2016, 1, 5. [Google Scholar] [CrossRef]
- Datta, M.; Senjyu, T.; Yona, A.; Funabashi, T.; Kim, C.H. A frequency-control approach by photovoltaic generator in a PV-Diesel hybrid power system. IEEE Trans. Energy Convers. 2011, 26, 559–571. [Google Scholar] [CrossRef]
- Kim, Y.S.; Kim, E.S.; Moon, S.I. Frequency and voltage control strategy of standalone microgrids with high penetration of intermittent renewable generation systems. IEEE Trans. Power Syst. January 2016, 31, 718–728. [Google Scholar] [CrossRef]
- Wang, H.; Huang, J. Joint investment and operation of microgrid. IEEE Trans. Smart Grid 2017, 8, 833–845. [Google Scholar] [CrossRef]
- Urtasun, A.; Sanchis, P.; Barricarte, D.; Marroyo, L. Energy management strategy for a battery-Diesel stand-alone system with distributed PV generation based on grid frequency modulation. Renew. Energy 2014, 66, 325–336. [Google Scholar] [CrossRef]
- Long, B.; Jeong, T.W.; Lee, J.D.; Jung, Y.C.; Chong, K.T. Energy management of a hybrid AC-DC micro-grid based on a battery testing system. Energies 2015, 8, 1181–1194. [Google Scholar] [CrossRef]
- Ashari, M.; Nayar, C.V. An optimum dispatch strategy using set points for a photovoltaic (PV)–Diesel–battery hybrid power system. Sol. Energy 1999, 66, 1–9. [Google Scholar] [CrossRef]
- Arafat, M.N.; Palle, S.; Sozer, Y.; Husain, I. Transition control strategy between standalone and grid-connected operations of voltage-source inverters. IEEE Trans. Ind. Appl. 2012, 48, 1516–1525. [Google Scholar] [CrossRef]
- Arafat, M.N.; Elrayyah, A.; Sozer, Y. An effective smooth transition control strategy using droop based synchronization for parallel inverters. IEEE Trans. Ind. Appl. 2015, 51, 2443–2454. [Google Scholar] [CrossRef]
- Sekhar, P.C.; Mishra, S.; Sharma, R. Data analytics based neuro-fuzzy controller for Diesel-photovoltaic hybrid AC microgrid. IET Gener. Transm. Distrib. 2015, 9, 193–207. [Google Scholar] [CrossRef]
- Mishra, S.; Ramasubramanian, D.; Sekhar, P.C. A seamless control methodology for a grid connected and isolated PV-Diesel microgrid. IEEE Trans. Power Syst. 2013, 28, 4393–4404. [Google Scholar] [CrossRef]
- Belila, A.; Tabbache, B. A control strategy of hybrid system Diesel-photovoltaic-battery for stand-alone applications. In Proceedings of the 2015 IEEE EEEIC, Rome, Italy, 10–13 June 2015; pp. 860–865. [Google Scholar]
- Belila, A.; Tabbache, B.; Berkouk, E.M.; Benbouzid, M.E.H. Integration of a storage system in a hybrid system ‘Diesel-Photovoltaic’ for stand-alone applications. In Proceedings of the 2017 IEEE EEEIC, Milan, Italy, 6–9 June 2017; pp. 1–6. [Google Scholar]
- Yazdani, A.; Di Fazio, A.R.; Ghoddami, H.; Russo, M.; Kazerani, M.; Jatskevich, J.; Strunz, K.; Leva, S.; Martinez, J.A. Modeling guidelines and a benchmark for power system simulation studies of three-phase single-stage photovoltaic systems. IEEE Trans. Power Deliv. 2011, 26, 1247–1264. [Google Scholar] [CrossRef]
- Mishra, S.; Ramasubramanian, D. Improving the small signal stability of a PV-DE-dynamic load-based microgrid using an auxiliary signal in the PV control loop. IEEE Trans. Power Syst. 2016, 30, 166–176. [Google Scholar] [CrossRef]
- Ou, T.; Lu, K.; Huang, C. Improvement of transient stability in a hybrid power multi-system using a designed NIDC (Novel Intelligent Damping Controller). Energies 2017, 10, 488. [Google Scholar] [CrossRef]
- Merabet, A.; Ahmed, K.T.; Ibrahim, H.; Beguenane, R.; Ghias, A.M.Y.M. Energy management and control system for laboratory scale microgrid based wind-PV-battery. IEEE Trans. Sustain. Energy 2017, 8, 145–154. [Google Scholar] [CrossRef]
- Fakham, H.; Lu, D.; Francois, B. Power control design of a battery charger in a hybrid active PV generator for load-following applications. IEEE Trans. Industrial Electron. 2011, 58, 85–94. [Google Scholar] [CrossRef]
- Shen, J.; Khaligh, A. A supervisory energy management control strategy in a battery ultracapacitor hybrid energy storage system. IEEE Trans. Transp. Electrif. 2015, 1, 223–231. [Google Scholar] [CrossRef]
- Bacha, S.; Munteanu, I.; Bratcu, A.I. Power Electronic Converters Modeling and Control with Case Studies; Springer: London, UK, 2014. [Google Scholar]
- Rocabert, J.; Luna, A.; Blaabjerg, F.; Rodríguez, P. Control of power converters in AC microgrids. IEEE Trans. Power Electron. 2012, 27, 4734–4749. [Google Scholar] [CrossRef]
- Degobert, P.; Remy, G.; Zeng, J.; Barre, P.J.; Hautier, J.P. High-performance control of the permanent magnet synchronous motor using self-tuning multiple-frequency resonant controllers. In Proceedings of the 2006 IEEE SSST, Cookeville, TN, USA, 5–7 March 2006; pp. 382–386. [Google Scholar]
- Tuyen, N.D.; Dzung, P.Q. Space vector modulation for an indirect matrix converter with improved input power factor. Energies 2017, 10, 588. [Google Scholar] [CrossRef]
- El Tawil, T.; Charpentier, J.F.; Benbouzid, M.E.H. Sizing and rough optimization of a hybrid renewable-based farm in a stand-alone marine context. Renew. Energy 2018, 115, 1134–1143. [Google Scholar] [CrossRef]
- Ramli, M.A.M.; Hiendro, A.; Twaha, S. Economic analysis of PV/Diesel hybrid system with flywheel energy storage. Renew. Energy 2015, 78, 398–405. [Google Scholar] [CrossRef]
- Choi, Y.; Kim, H. Optimal scheduling of energy storage system for self-sustainable base station operation considering battery wear-out cost. Energies 2016, 9, 462. [Google Scholar] [CrossRef]





| ESS Parameters | PVG Parameters | ||
| Battery capacity | 12 V, 150 Ah | PVG Rated power | 3.2 kW |
| Number of batteries | 12 in serial | Panel rated power | 135 W |
| CDC | 0.047 F | ns | 8 |
| r | 1 Ω | np | 3 |
| l | 0.05 H | DG Parameters | |
| ksi | 1/sqrt(2) | DG Rated power | 10 kVA (8 kW) |
| tr | 0.01 s | τ1 | 0. 3 s |
| ω1 | 4/(trksi), | τ2 | 0.05 s |
| UDC | 650 V | ka | 2.7 |
| DT | 0.1 pu | ||
| JT | 0.005 pu | ||
| IMC Parameters | PMC Parameters | ||
| ωn | 1/sqrt(LfCf) | KiPLL | −295.17 |
| P | 1000 | KpPLL | −1.37 |
| c0 | 1.38 × 1014 | Kif | −522.23 |
| c1 | 6.58 × 1011 | Kpf | −28.34 |
| c2 | 8.96 × 108 | Filter Parameters | |
| c3 | 9.09 × 105 | Rf | 8.66 Ω, |
| d0 | 2.21 × 108 | Lf | 46 mH |
| d1 | 4.60 × 104 | Cf | 30 μF |
| PVG-DG-ESS (Proposed EMC) | DG only | |
|---|---|---|
| DG Operation (%) | 16.66 | 10 |
| Consumed fuel (Lbs) | 36 | 216 |
| Fuel total cost (US$) | 12.52 | 75.13 |
| PVG-DG-ESS (Proposed EMC) | PVG-ESS Microgrid (IMC) | |
|---|---|---|
| Number of cycle | Operation time: 8 hours = 16.66% | |
| 8.4 | 3 | |
| Number of cycles/OC | Operation time: OC = 48 hours | |
| 8.4 × 6 = 50.4 | 8.4 × 5 + 3 = 45 | |
| Wear cost gain (%/OC) | 10.71 | |
| Wear cost gain (%/h) | 0.223 | |
| 1 | PC computer | 5 | Scope | 10 | Three-phase inverter |
| 2 | PCI6052E; | 6 | voltages and currents measurement | 11 | DC/DC converter’s |
| 3 | PV panels | 7 | Resistive load; | 12 | ESS (battery). |
| 4 | Currents measurement | 8, 9 | LC filters; |
| IMC | PMC | LC Filter | ESS | ||||
|---|---|---|---|---|---|---|---|
| c0 | 1.38×1014 | KiPLL | −295.17 | Rf | 8.66 Ω, | Cbat | 12 V, 100 Ah |
| c1 | 6.58 × 1011 | KpPLL | −1.37 | Lf | 46 mH | CDC | 0.047 F |
| c2 | 8.96 × 108 | Kif | −522.23 | Cf | 30 μF | UDC | 48 V |
| c3 | 9.09 × 105 | Kpf | −28.34 | ||||
| d0 | 2.21 × 108 | ||||||
| d1 | 4.60 × 104 | ||||||
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Belila, A.; Benbouzid, M.; Berkouk, E.-M.; Amirat, Y. On Energy Management Control of a PV-Diesel-ESS Based Microgrid in a Stand-Alone Context. Energies 2018, 11, 2164. https://doi.org/10.3390/en11082164
Belila A, Benbouzid M, Berkouk E-M, Amirat Y. On Energy Management Control of a PV-Diesel-ESS Based Microgrid in a Stand-Alone Context. Energies. 2018; 11(8):2164. https://doi.org/10.3390/en11082164
Chicago/Turabian StyleBelila, Ahmed, Mohamed Benbouzid, El-Madjid Berkouk, and Yassine Amirat. 2018. "On Energy Management Control of a PV-Diesel-ESS Based Microgrid in a Stand-Alone Context" Energies 11, no. 8: 2164. https://doi.org/10.3390/en11082164
APA StyleBelila, A., Benbouzid, M., Berkouk, E.-M., & Amirat, Y. (2018). On Energy Management Control of a PV-Diesel-ESS Based Microgrid in a Stand-Alone Context. Energies, 11(8), 2164. https://doi.org/10.3390/en11082164







