On the Accuracy of Three-Dimensional Actuator Disc Approach in Modelling a Large-Scale Tidal Turbine in a Simple Channel
Abstract
1. Introduction
2. Background
2.1. Description of Telemac3D
2.2. Theory of the RANS Actuator Disc
2.3. Limitation of the Actuator Disc Approach
- The overall turbine structure is not being represented and thus affecting the turbulence in the near wake region, known to be 2–5 rotor diameters downstream of the turbines.
- Kinematics of turbulence, such as vortices trailing from the edges of a blade cannot be replicated, and thus, they must be properly parameterized.
- Energy extraction due to mechanical motion of the turbine rotor cannot be reproduced, instead the energy removed from the disc will be converted into small scale turbulence eddies behind the disc. However, the influence of swirl on the far region is assumed to be minimal.
- This concept cannot be used to investigate the performance of a turbine (e.g., maximum power produced) since it does not include the blades.
2.4. Benchmarking and Data Validation
- Flume dimensions are: 21 m long, 1.35 m wide, and tank depth of 0.3 m.
- Perforated disc with diameter of 0.1 m was used, where the porosity ranged from 0.48 m to 0.35 m (corresponding to coefficient of thrust, .
- The flow speed was approximately set to 0.3 m/s, with mean U velocity component of 0.25 m/s.
- The vertical velocity profile was developed to closely match the 1/7th power law, with uniform velocity near the open surface.
- An acoustic Doppler velocimeter was employed to measure downstream fluid velocities, starting from 3 to 20-disc diameters in a longitudinal direction, as well as up to a 4-disc diameter in the lateral axis.
3. Methodology
3.1. Actuator Disc Representation in Telemac3D
- (a)
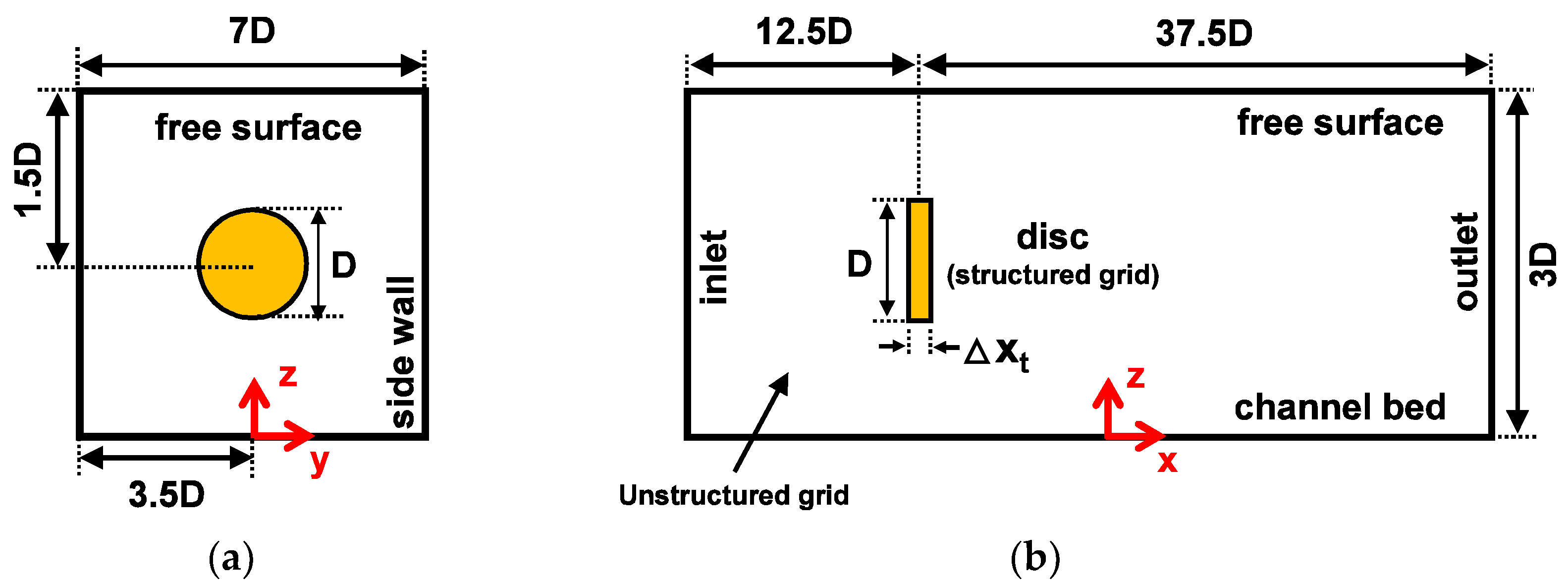
- The turbine arrangement and the overall dimensions of the domain used in this study is presented in Figure 1, where the disc was located 250 m from the channel inlet. Additionally, its z and y axis centreline were fixed at a 30-m mid-depth and 70-m from the side wall.
- (b)
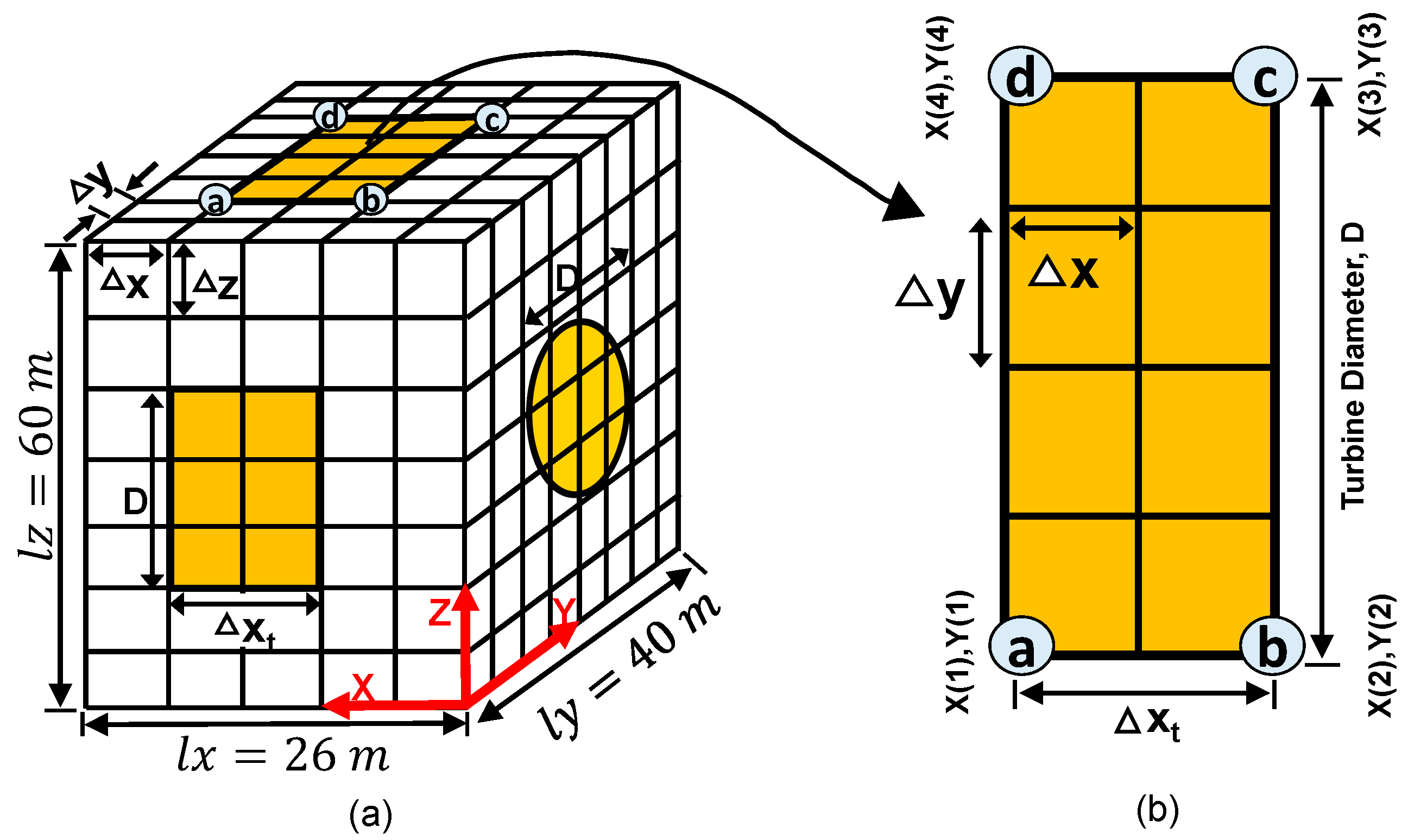
- The use of a structured grid at the turbine position was chosen as it would allow for a better representation of the turbine shape, as well as maintaining the distance between nodes for refinement purposes. Figure 2 provides the graphical information on the dimensions and pertinent parameters concerning the implementation of the structured grid in the domain. The size of the structured grid (i.e., lx = 26 m, ly = 40 m and lz = 60 m) were deliberately set to be larger than the turbine diameter (D = 20 m) and its width ( 2 m) to allow for numerical tolerance upon the execution of the momentum sink in the TRISOU subroutine. The grid element spacing within this structured grid are denoted by , and Δz in the x, y, and z directions, respectively. For the simulations, lx, ly, and lz were kept constant, but the dimensions of , , and were varied and their impact on the wake characteristics was investigated and the results are presented in Section 4.
- (c)
- The location of the disc (i.e., the turbine) in the domain was specified by four nodes in the horizontal plane (see Figure 2a), denoted as a, b, c, and d, which will act as the enclosure for the turbine. The coordinate of each node was represented by a pair of x and y. The distance between and refers to the turbine diameter, D, while the distance between and corresponds to the disc thickness, .
- (d)
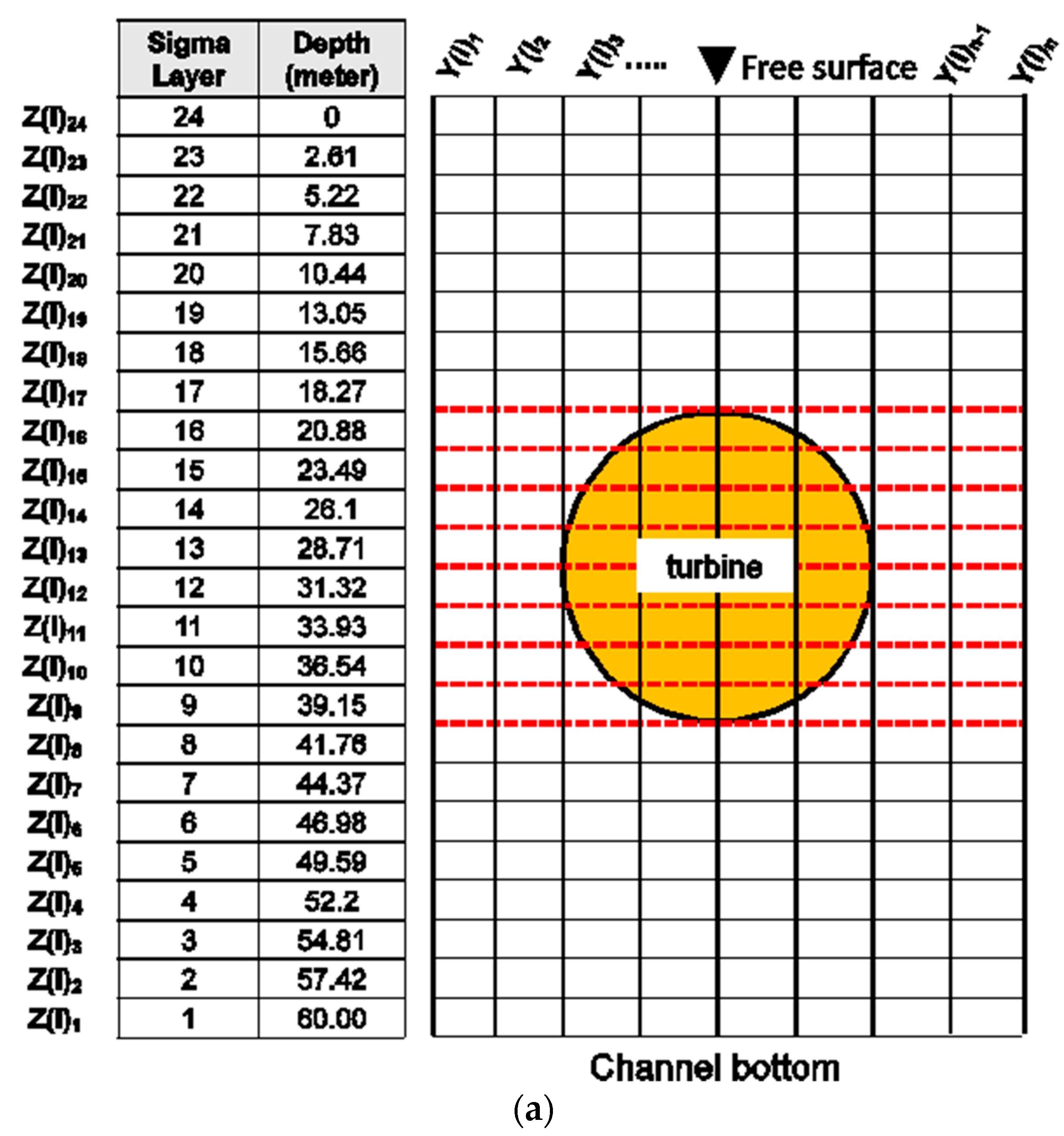
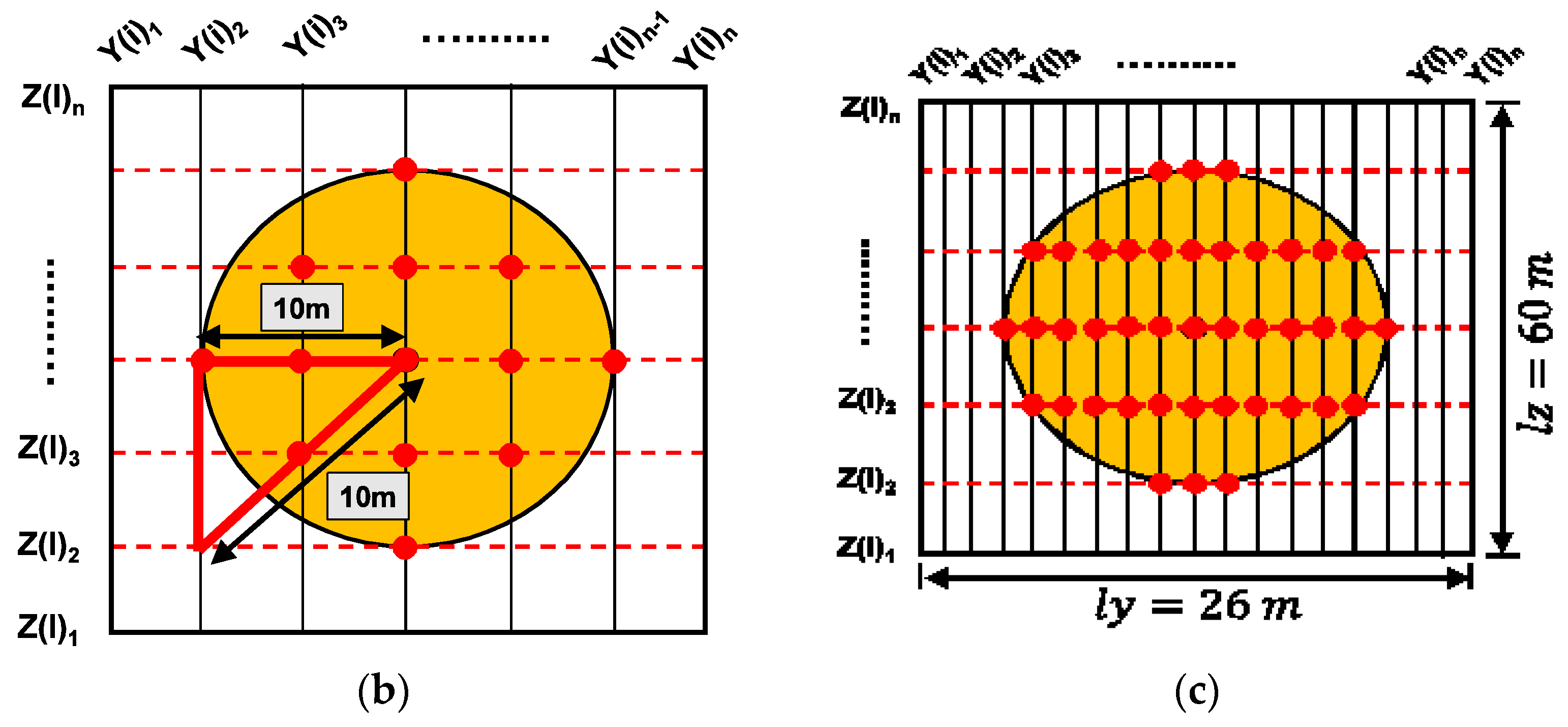
- Although several mesh transformation options are available in the Telemac3D module, the sigma coordinate system was chosen to represent the depth due to its simplicity, as shown in Figure 3a. In fact, the interval between the vertical planes, as well as the mesh density in the y direction, must be carefully selected since the intersections between the z and y axis nodes will determine the accuracy of disc frame. Coarser mesh density in both the y and z axis will result in a limited number of nodes available within the disc surface area, as shown in Figure 3b. Whereas, Figure 3c portrays unbalanced concentration of the nodes when one of the axis uses a very fine grid resolution compare to the other. Section 4.3.2 will elaborate further on this subject matter.
- (e)
- Once the optimal resolution for both and was established, the momentum source term (see Equation (6)) was applied into the model through the existing nodes within the 10-m radius from the disc centre, Figure 3b. For this purpose, Equation (9) was employed to locate all the relevant nodes that formulate the disc’s 20-m frame.
3.2. Model Set-Up
3.3. Boundary Condition
3.4. Turbulence Input
4. Models’ Sensitivity and Validation
4.1. Validation Metric
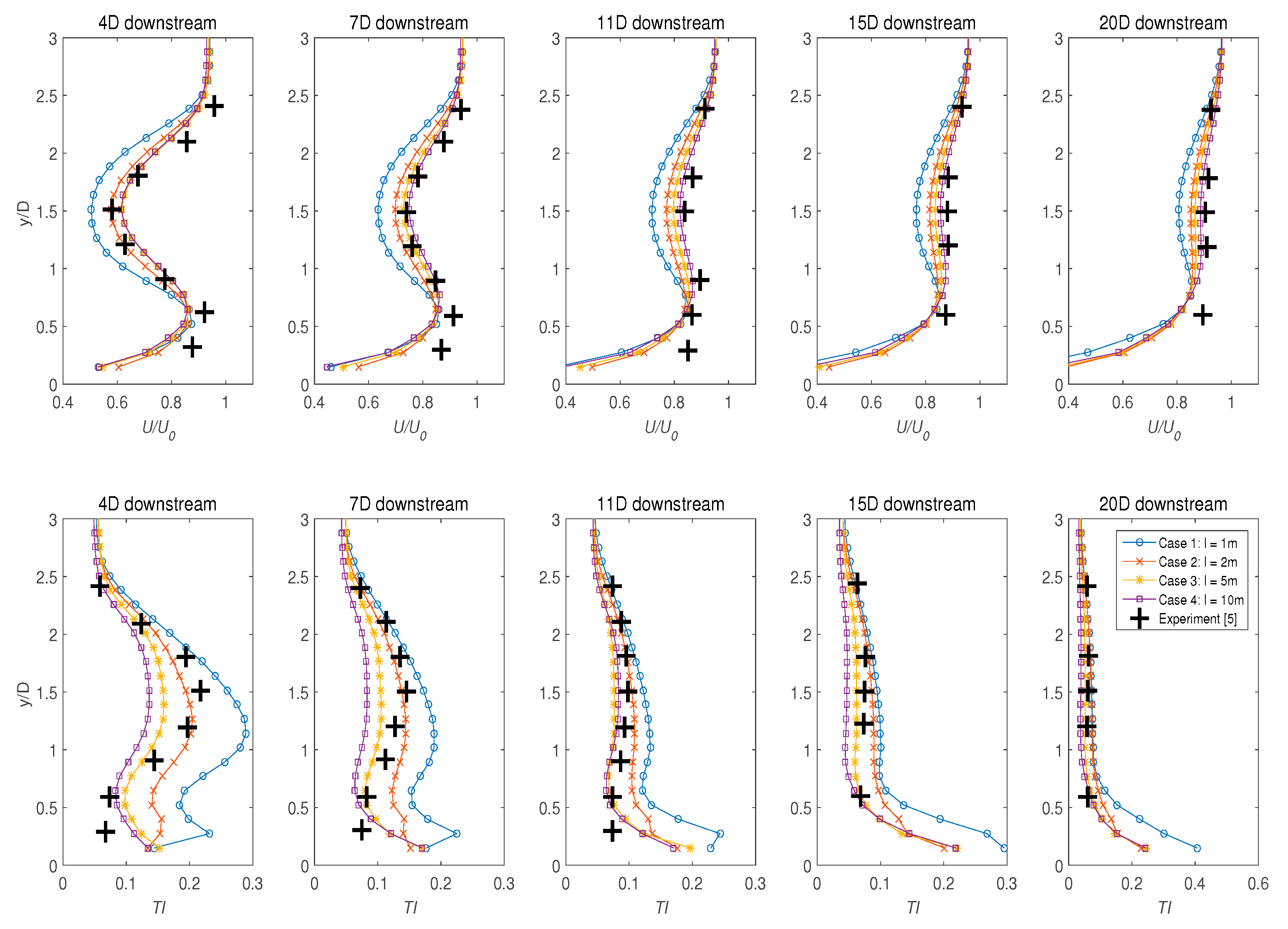
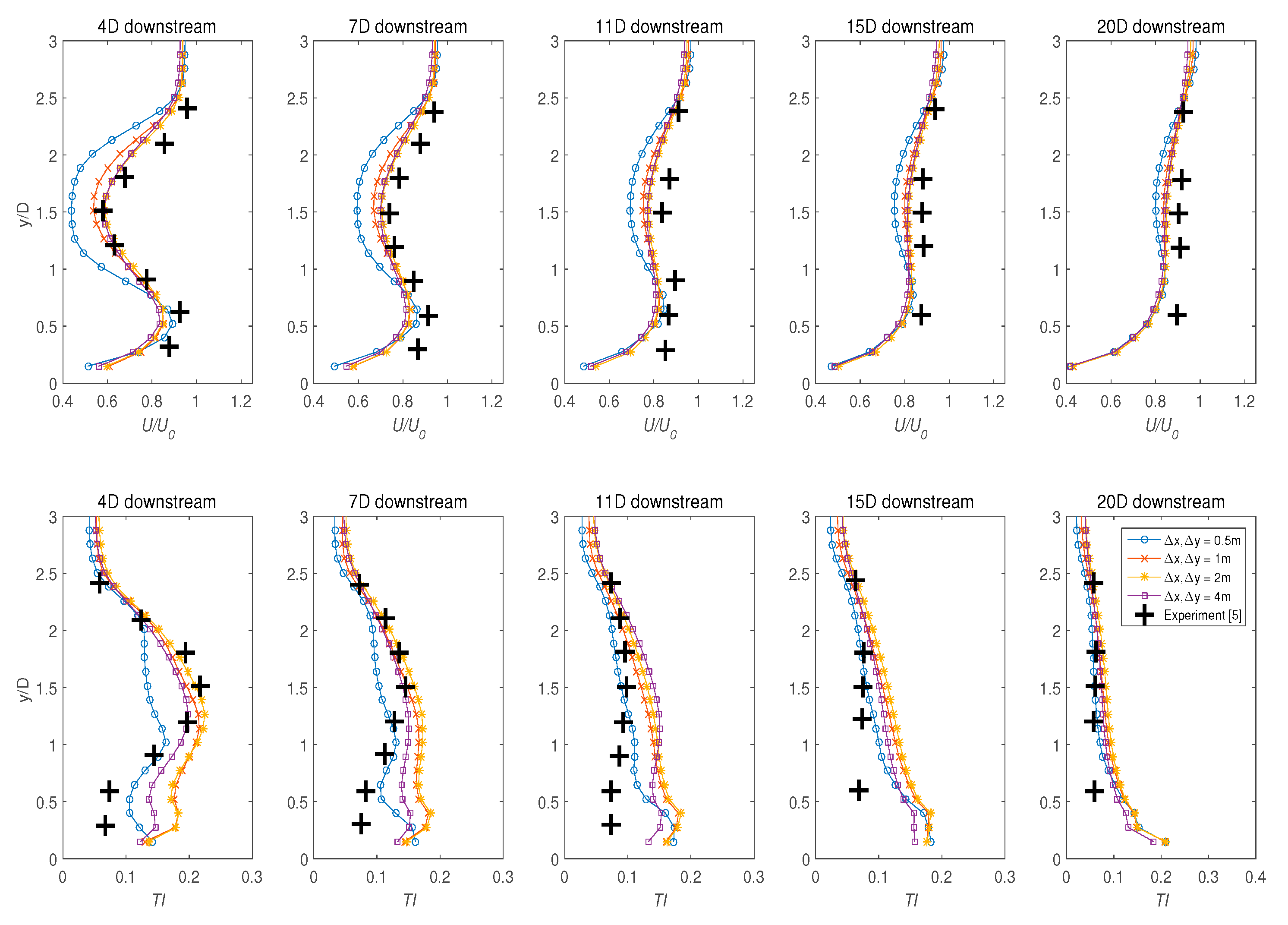
4.2. Mesh Dependence Test
4.3. Sensitivity of the Structured Grid at Turbine Location
4.3.1. Influence of the Disc Thickness,
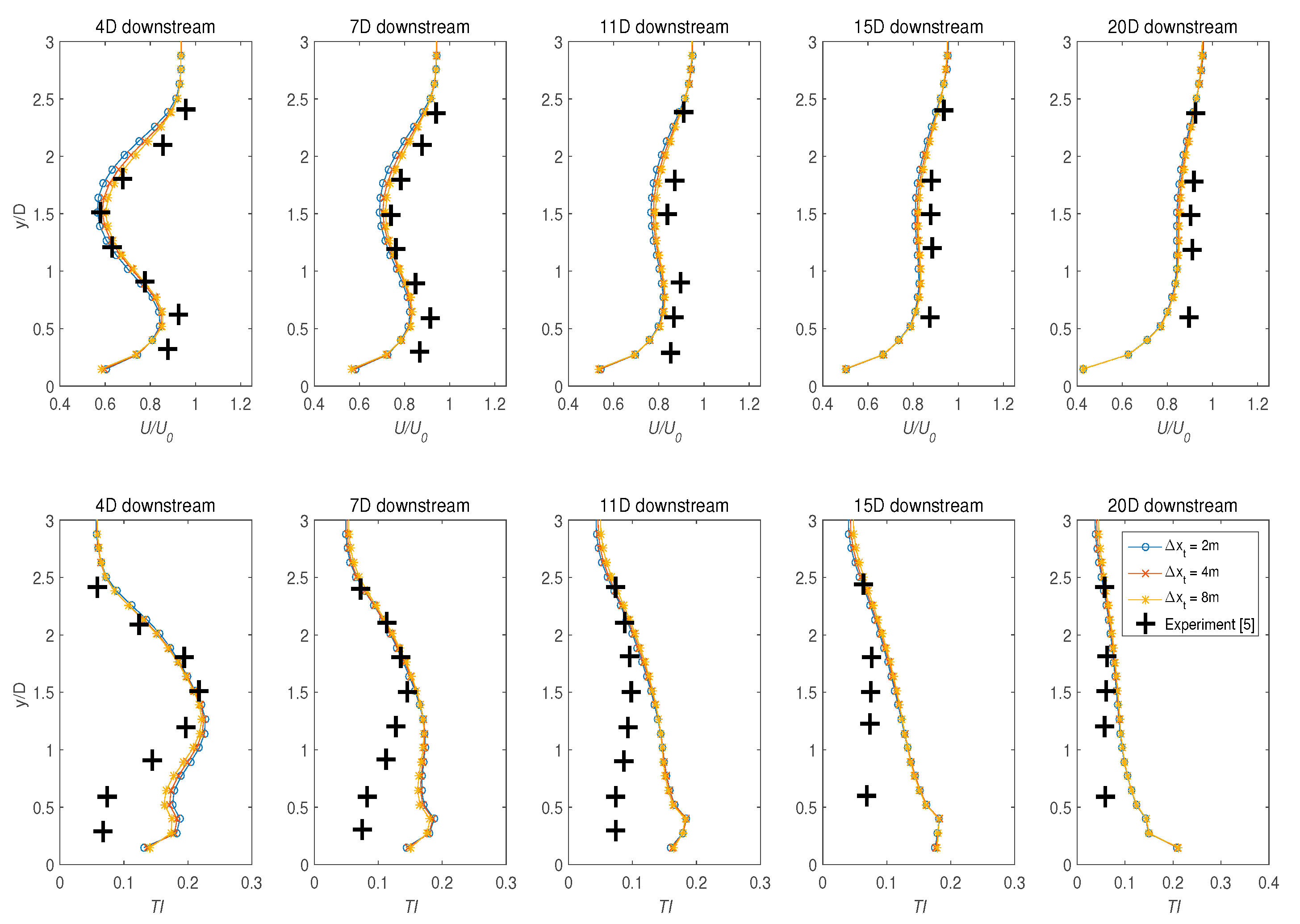
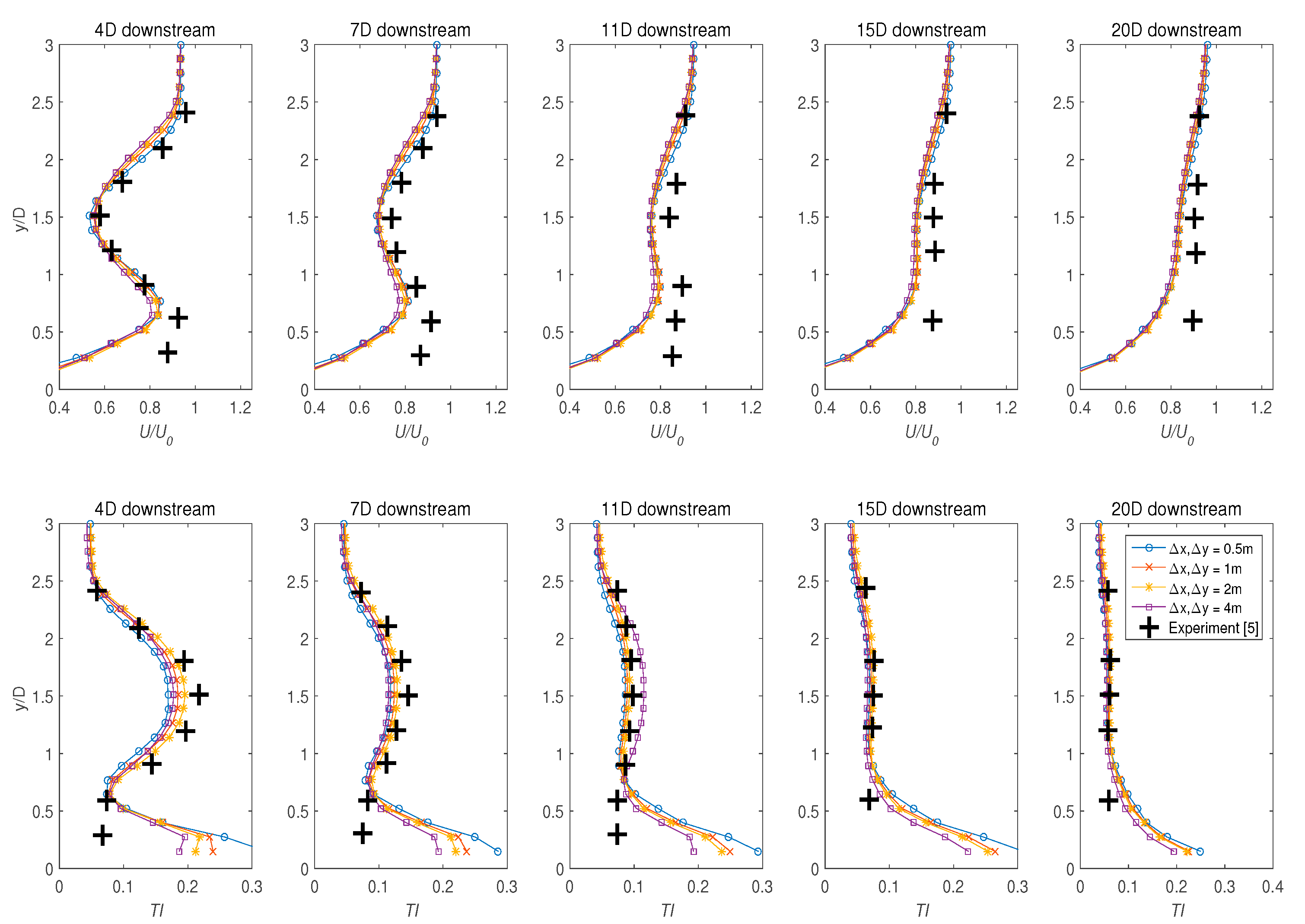
4.3.2. Resolution of the Structured Grid ()
4.3.3. Grid Resolution for
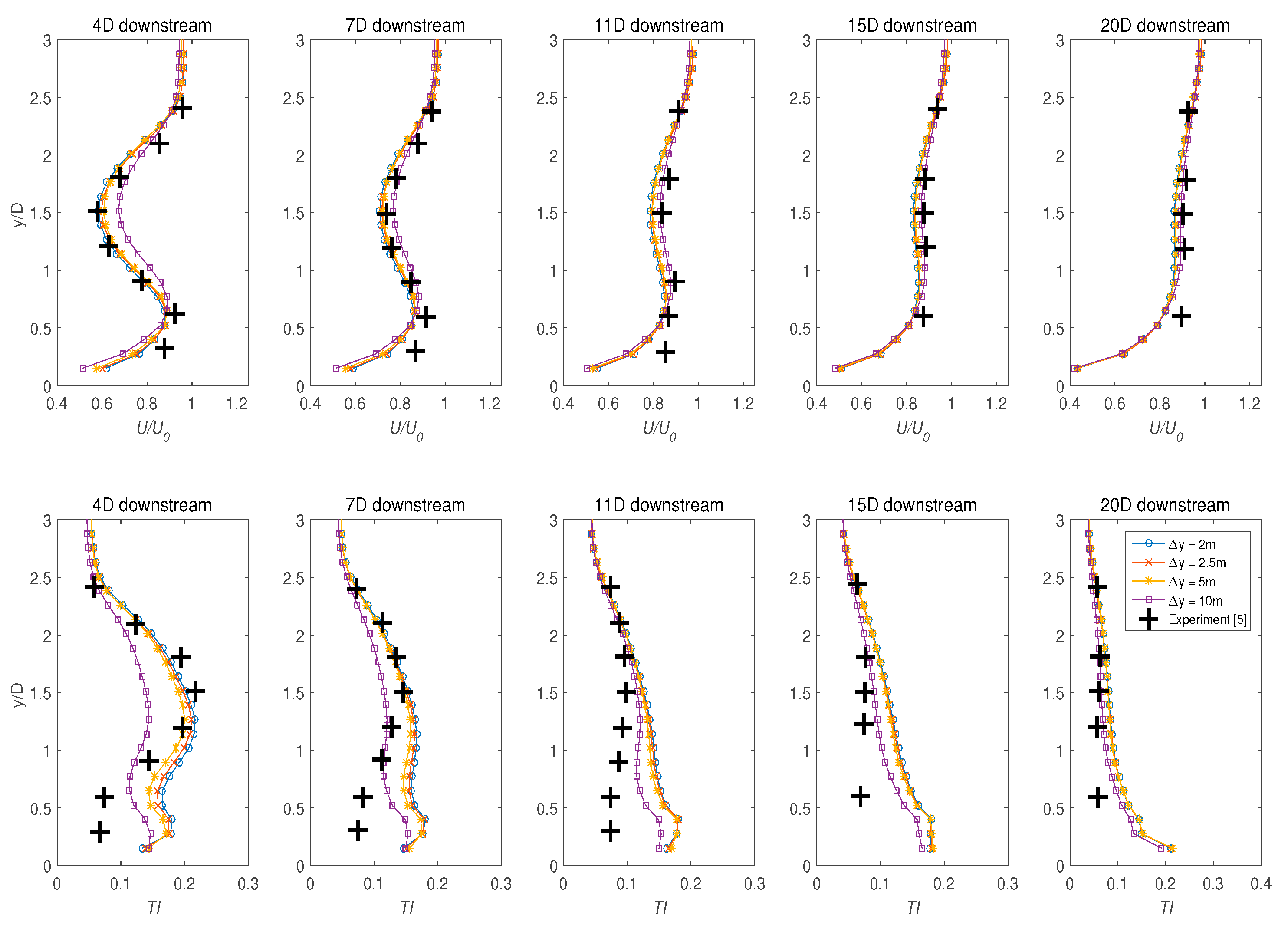
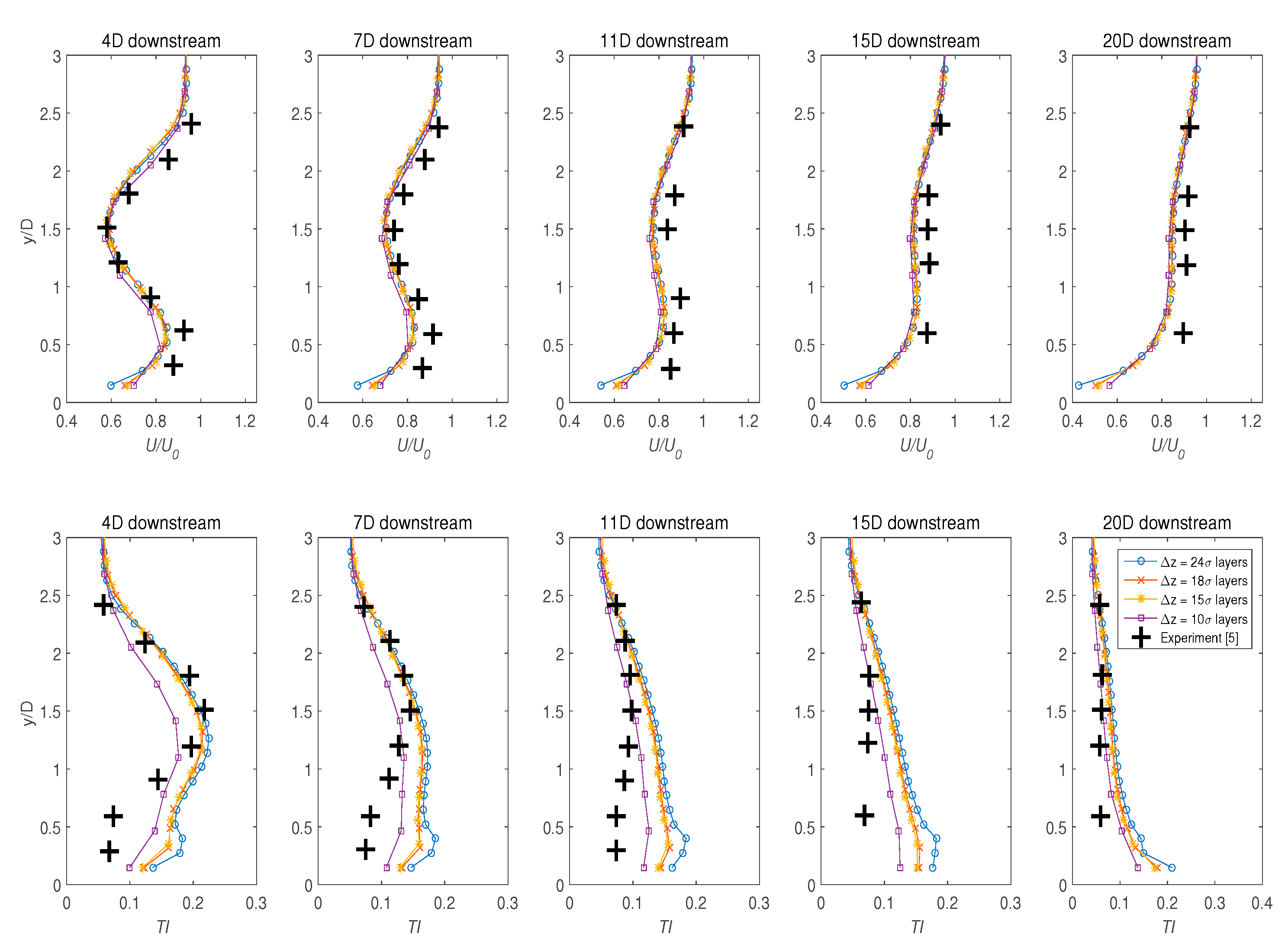
4.4. Sensitivity of the Vertical Resolutions,
4.5. Hydrostatic vs. Non-Hydrostatic Pressure Models
5. Conclusions
- The results demonstrated that the numerical model was highly sensitive to the mesh refinement upstream and downstream of the turbine, where coarser models tended to underestimate both the velocity retardation and TI.
- Altering the thickness of the turbine () had negligible impact on the downstream wakes and turbulence mixings.
- Numerical accuracy of the model was found to be highly susceptible to changes in the grid density of the turbine enclosure. The optimal structured grid density of Δx = 2 m, and Δy = 2 m satisfactorily modelled both the velocity deficit and the TI.
- The importance of the grid spacing in y direction () in characterising the thrust and also the shape of the disc was also highlighted.
- The influence of vertical resolutions (Δz) in representing the depth of the channel on the model was investigated to find a balance between computational efficiency and numerical accuracy. The findings indicated that appropriate adjustment on both the horizontal and vertical planes must be attained to accomplish the optimal ratio between the nodes resolution in both z and y orientation. Note that the optimal structured grid density found in this study was limited to the computational resources available to the authors. The methodology presented in this article, however, are still valid for a more refined grid implementation.
- The impact of the hydrostatic and non-hydrostatic pressure assumptions on the predicted output were examined, where both models exhibit nearly indistinguishable flow retardation characteristics behind the simulated disc. However, for the TI, only the non-hydrostatic model was able to match the experimental result, while the hydrostatic solver failed to properly resolve the turbulence mixing in the wake regions between 4D and 15D.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Neill, S.P.; Litt, E.J.; Couch, S.J.; Davies, A.G. The impact of tidal stream turbines on large-scale sediment dynamics. Renew. Energy 2009, 34, 2803–2812. [Google Scholar] [CrossRef]
- Robins, P.E.; Neill, S.P.; Lewis, M.J. Impact of tidal-stream arrays in relation to the natural variability of sedimentary processes. Renew. Energy 2014, 72, 311–321. [Google Scholar] [CrossRef]
- Chatzirodou, A.; Karunarathna, H.; Mainland, S.; Firth, P.; Park, S. Impacts of tidal energy extraction on sea bed morphology. Coast. Eng. 2014, 1, 33. [Google Scholar] [CrossRef]
- Sun, X.; Chick, J.P.; Bryden, I.G. Laboratory-scale simulation of energy extraction from tidal currents. Renew. Energy 2008, 33, 1267–1274. [Google Scholar] [CrossRef]
- Harrison, M.E.; Batten, W.M.J.; Myers, L.E.; Bahaj, A.S. Comparison between CFD simulations and experiments for predicting the far wake of horizontal axis tidal turbines. IET Renew. Power Gener. 2010, 4, 613–627. [Google Scholar] [CrossRef]
- Adcock, T.A.; Draper, S.; Nishino, T. Tidal power generation–A review of hydrodynamic modelling. Proc. Inst. Mech. Eng. Part A J. Power Energy 2015, 299, 755–771. [Google Scholar] [CrossRef]
- Daly, T.; Myers, L.E.; Bahaj, A.S. Modelling of the flow field surrounding tidal turbine arrays for varying positions in a channel. Philosophical Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2018, 371, 20120246. [Google Scholar] [CrossRef] [PubMed]
- Lartiga, C.; Crawford, C. Actuator Disk Modeling in Support of Tidal Turbine Rotor Testing. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010; pp. 1–6. [Google Scholar]
- Roc, T.; Conley, D.C.; Greaves, D. Methodology for tidal turbine representation in ocean circulation model. Renew. Energy 2013, 51, 448–464. [Google Scholar] [CrossRef]
- Nguyen, V.T.; Guillou, S.S.; Thiebot, J.; Cruz, A.S. Modelling turbulence with an Actuator Disk representing a tidal turbine. Renew. Energy 2016, 97, 625–635. [Google Scholar] [CrossRef]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows: Modelling with the Finite Element Method; John Wiley & Sons: West Sussex, UK, 2007. [Google Scholar]
- Desombre, J. TELEMAC-3D OPERATING MANUAL (Release 6.2); EDF R&D: Paris, France, 2013. [Google Scholar]
- Hervouet, J.M.; Jankowski, J. Comparing numerical simulations of free surface flows using non-hydrostatic Navier-Stokes and Boussinesq equations. Electricité de France; Bauwesen der Universität Hannover; Unpublished work. 2000. [Google Scholar]
- Burton, T.; Jenkins, N.; Sharpe, D.; Bossanyi, E. Wind Energy Handbook; John Wiley & Sons: Weat Sussex, UK, 2011. [Google Scholar]
- Batten, W.M.J.; Harrison, M.E.; Bahaj, A.S. The accuracy of the actuator disc-RANS approach for predicting the performance and far wake of a horizontal axis tidal stream turbine. Philos. Trans. R. Soc. Lond. A Math. Phys. Eng. Sci. 2013, 371, 20120293. [Google Scholar] [CrossRef] [PubMed]
- Taylor, G. The Scientific Papers of Sir Geoffrey Ingram Taylor; Cambridge University Press: Cambridge, UK, 1963. [Google Scholar]
- Whelan, J.; Thomson, M.; Graham, J.M.R.; Peiro, J. Modelling of free surface proximity and wave induced velocities around a horizontal axis tidal stream turbine. In Proceedings of the 7th European Wave and Tidal Energy Conference, Porto, Portugal, 11–13 September 2007. [Google Scholar]
- Belloni, C.; Willden, R.H.J. A computational study of a bi-directional ducted tidal turbine. In Proceedings of the 3rd International Conference on Ocean Energy, Bilbao, Spain, 6–8 October 2010. [Google Scholar]
- Myers, L.E.; Bahaj, A.S. Experimental analysis of the flow field around horizontal axis tidal turbines by use of scale mesh disk rotor simulators. Ocean Eng. 2010, 37, 218–227. [Google Scholar] [CrossRef]
- Troldborg, N.; Sørensen, J.N.; Mikkelsen, R.F. Actuator Line Simulation of Wake of Wind Turbine Operating in Turbulent Inflow. J. Phys. Conf. Ser. 2007, 75, 012063. [Google Scholar] [CrossRef]
- Sforza, S.P.M.; Smorto, M. Three-dimensional wakes of simulated wind turbines. AIAA J. 1981, 19, 1101–1107. [Google Scholar] [CrossRef]
- Legrand, C. Assessment of Tidal Energy Resource: Marine Renewable Energy Guides; European Marine Energy Centre: London, UK, 2009. [Google Scholar]
- Scott, N.C.; Smeed, M.R.; McLaren, A.C. Pentland Firth Tidal Energy Project Grid Options Study Prepared for: Highlands and Islands Enterprise; Xero Energy: Glasgow, UK, 2009. [Google Scholar]
- Carbon Trust. PhaseII: UK Tidal Stream Energy Resource Assessment; Black & Veatch Ltd.: London, UK, 2005. [Google Scholar]
- Rahman, A.; Venugopal, V. Inter-Comparison of 3D Tidal Flow Models Applied To Orkney Islands and Pentland Firth. In Proceedings of the 11th European Wave and Tidal Energy Conference (EWTEC 2015), Nantes, France, 6–11 September 2015. [Google Scholar]
- Salim, S.M.; Cheah, S.C. Wall y+ Strategy for Dealing with Wall-bounded Turbulent Flows. In Proceedings of the International MultiConference of Engineers and Computer Scientists (IMECS), Hong Kong, China, 18–20 March 2009. [Google Scholar]
- Kalitzin, G.; Medic, G.; Iaccarino, G.; Durbin, P. Near-wall behavior of RANS turbulence models and implications for wall functions. J. Comput. Phys. 2005, 204, 265–291. [Google Scholar] [CrossRef]
- Osalusi, E.; Side, J.; Harris, R. Reynolds stress and turbulence estimates in bottom boundary layer of fall of warness. Int. Commun. Heat Mass Transf. 2009, 36, 412–421. [Google Scholar] [CrossRef]
- Osalusi, E.; Side, J.; Harris, R. Structure of turbulent flow in emec’s tidal energy test site. Int. Commun. Heat Mass Transf. 2009, 36, 422–431. [Google Scholar] [CrossRef]
- Macenri, J.; Reed, M.; Thiringer, T. Influence of tidal parameters on SeaGen flicker performance. Philos. Trans. A Math. Phys. Eng. Sci. 2013, 371, 20120247. [Google Scholar] [CrossRef] [PubMed]
- Myers, L.E.; Bahaj, A.S. An experimental investigation simulating flow effects in first generation marine current energy converter arrays. Renew. Energy 2012, 37, 28–36. [Google Scholar] [CrossRef]
- Giles, J.; Myers, L.; Bahaj, A.; Shelmerdine, B. The downstream wake response of marine current energy converters operating in shallow tidal flows. In Proceedings of the World Renewable Energy Congress, Linkoping, Sweden, 8–13 May 2011. [Google Scholar]
- Milne, I.A.; Sharma, R.N.; Flay, R.G.J.; Bickerton, S. Characteristics of the onset flow turbulence at a tidal-stream power site. Philos. Trans. R. Soc. A 2013, 371, 20120196. [Google Scholar] [CrossRef] [PubMed]
- Thomson, J.; Polagye, B.; Durgesh, V.; Richmond, M.C. Measurements of turbulence at two tidal energy sites in puget sound, WA. IEEE J. Ocean. Eng. 2012, 37, 363–374. [Google Scholar] [CrossRef]
- Mycek, P.; Gaurier, B.; Germain, G.; Pinon, G.; Rivoalen, E. Experimental study of the turbulence intensity effects on marine current turbines behaviour. Part I: One single turbine. Renew. Energy 2014, 66, 729–746. [Google Scholar] [CrossRef]
- Barthelmie, R.J.J.; Folkerts, L.; Larsen, G.C.C.; Rados, K.; Pryor, S.C.C.; Frandsen, S.T.T.; Lange, B.; Schepers, G. Comparison of wake model simulations with offshore wind turbine wake profiles measured by sodar. J. Atmos. Ocean. Technol. 2006, 23, 888–901. [Google Scholar] [CrossRef]
- IEC. Wind Turbines–Part 21: Measurement and Assessment of Power Quality Characteristics of Grid Connected Wind Turbines IEC 61400-21; IEC: Geneva, Switzerland, 2008. [Google Scholar]
- Milne, I.A.; Sharma, R.N.; Flay, R.G.J.; Bickerton, S. The Role of Onset Turbulence on Tidal Turbine Blade Loads. In Proceedings of the 17th Australasian Fluid Mechanics Conference 2010, Auckland, New Zealand, 5–9 December 2010; pp. 1–8. [Google Scholar]
- Rohatgi, A. WebPlotDigitizer. 2013. Available online: http://arohatgi.info/WebPlotDigitizer/ (accessed on 20 April 2016).


| Telemac3D Subroutines | Function |
|---|---|
| CONDIM | To set the initial condition for the model’s depth and velocity profile |
| VEL_PROF_Z | To specify the vertical velocity profile at the channel inlet |
| KEPCL3 and KEPINI | To be used with k-epsilon turbulence model |
| TRISOU | To implement the source terms for the momentum equations |
| Numerical Parameters | Input/Values |
|---|---|
| Law of the bottom friction and the corresponding friction coefficient | Chezy (44) |
| Turbulence model | k- turbulence models |
| Hydrostatic assumption | True |
| Initial condition | “PARTICULAR” where the initial elevation is set to 60 m |
| Vertical resolutions | 24 sigma layers |
| Boundary condition on the bottom | Slip condition |
| Boundary forcing | Inlet: prescribed flowrate, Q = 21,840 m3/s Outlet: prescribed elevation, H = 60 m |
| Resistance coefficient, K | 2 (corresponding to CT = 0.89) |
| Refinement Details | Centreline Velocity at Various Longitudinal Positions from Actuator Disc (m/s) | |||||
|---|---|---|---|---|---|---|
| Mesh Size | Number of Elements | 5D Upstream | 4D Downstream | 7D Downstream | 11D Downstream | 20D Downstream |
| Case 1 (1 m) | 925,536 | 2.683 | 1.515 | 1.903 | 2.153 | 2.418 |
| Case 2 (2 m) | 316,584 | 2.680 | 1.735 | 2.092 | 2.315 | 2.554 |
| Case 3 (5 m) | 101,496 | 2.690 | 1.853 | 2.186 | 2.391 | 2.600 |
| Case 4 (10 m) | 72,936 | 2.694 | 1.846 | 2.247 | 2.464 | 2.659 |
| Sigma Layers | Distance between Planes (in Meter) | Number of Mesh Elements |
|---|---|---|
| 24 | 2.61 | 317,928 |
| 18 | 3.53 | 238,446 |
| 15 | 4.29 | 198,705 |
| 10 | 6.66 | 132,470 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rahman, A.; Venugopal, V.; Thiebot, J. On the Accuracy of Three-Dimensional Actuator Disc Approach in Modelling a Large-Scale Tidal Turbine in a Simple Channel. Energies 2018, 11, 2151. https://doi.org/10.3390/en11082151
Rahman A, Venugopal V, Thiebot J. On the Accuracy of Three-Dimensional Actuator Disc Approach in Modelling a Large-Scale Tidal Turbine in a Simple Channel. Energies. 2018; 11(8):2151. https://doi.org/10.3390/en11082151
Chicago/Turabian StyleRahman, Anas, Vengatesan Venugopal, and Jerome Thiebot. 2018. "On the Accuracy of Three-Dimensional Actuator Disc Approach in Modelling a Large-Scale Tidal Turbine in a Simple Channel" Energies 11, no. 8: 2151. https://doi.org/10.3390/en11082151
APA StyleRahman, A., Venugopal, V., & Thiebot, J. (2018). On the Accuracy of Three-Dimensional Actuator Disc Approach in Modelling a Large-Scale Tidal Turbine in a Simple Channel. Energies, 11(8), 2151. https://doi.org/10.3390/en11082151







