Flow Simulation of Artificially Induced Microfractures Using Digital Rock and Lattice Boltzmann Methods
Abstract
1. Introduction
2. Methodology
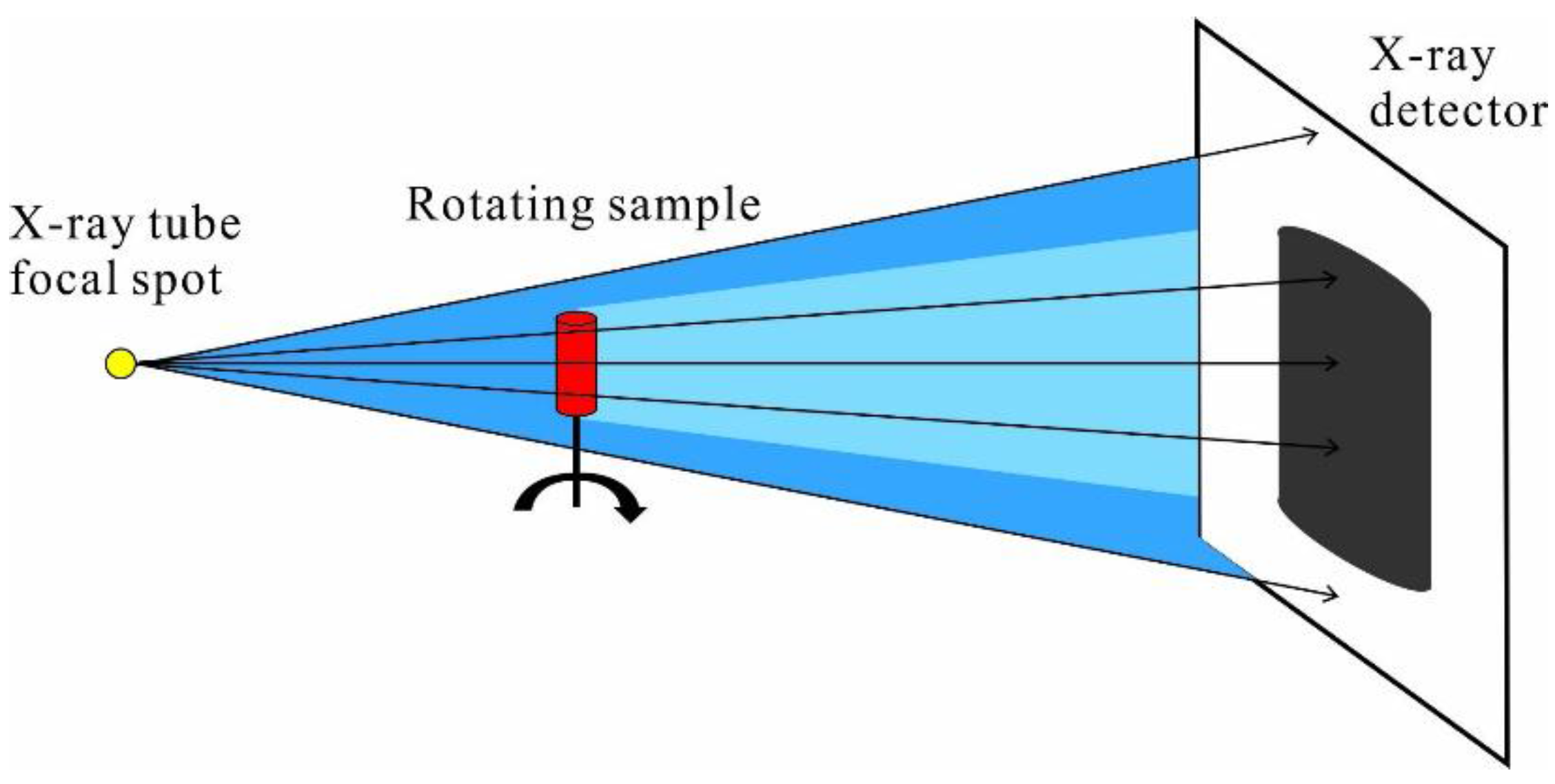
2.1. The 3D Digital Core
2.2. Fractal Theory and Fractal Dimension
2.2.1. The Concept of “Fractals”
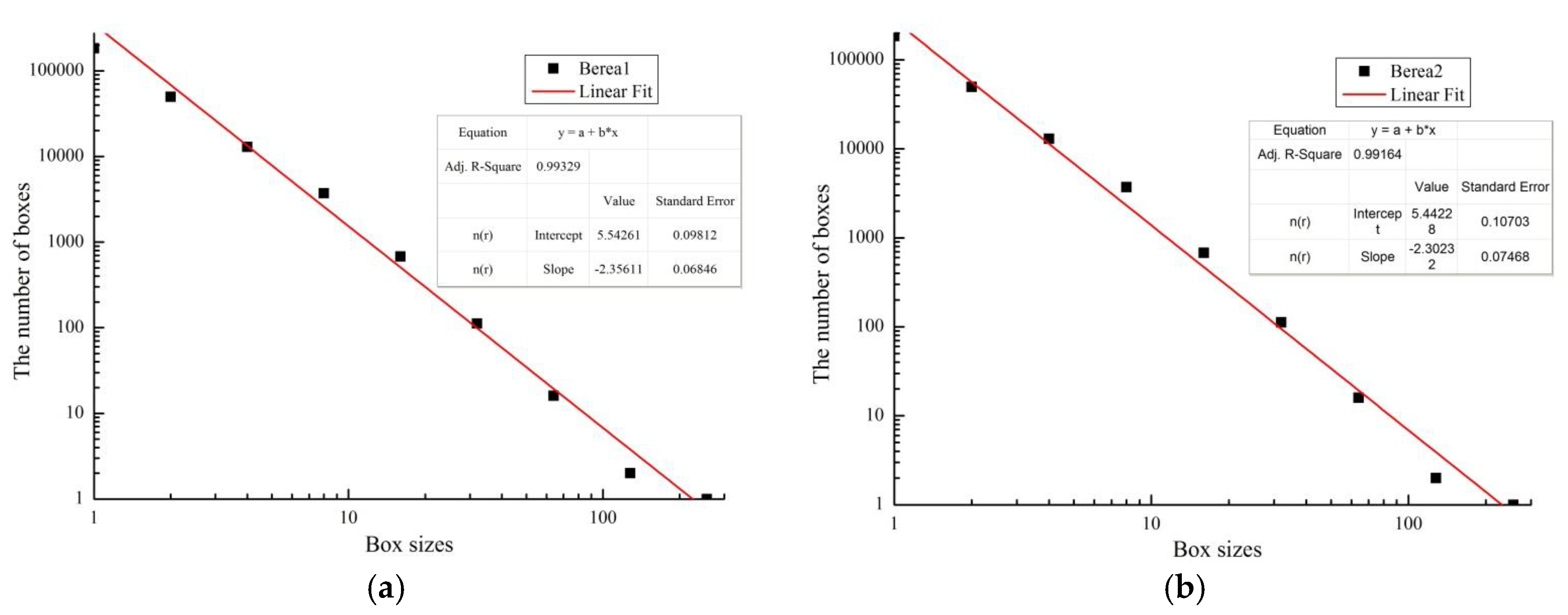
2.2.2. The Box-Counting Method and Fractal Dimension
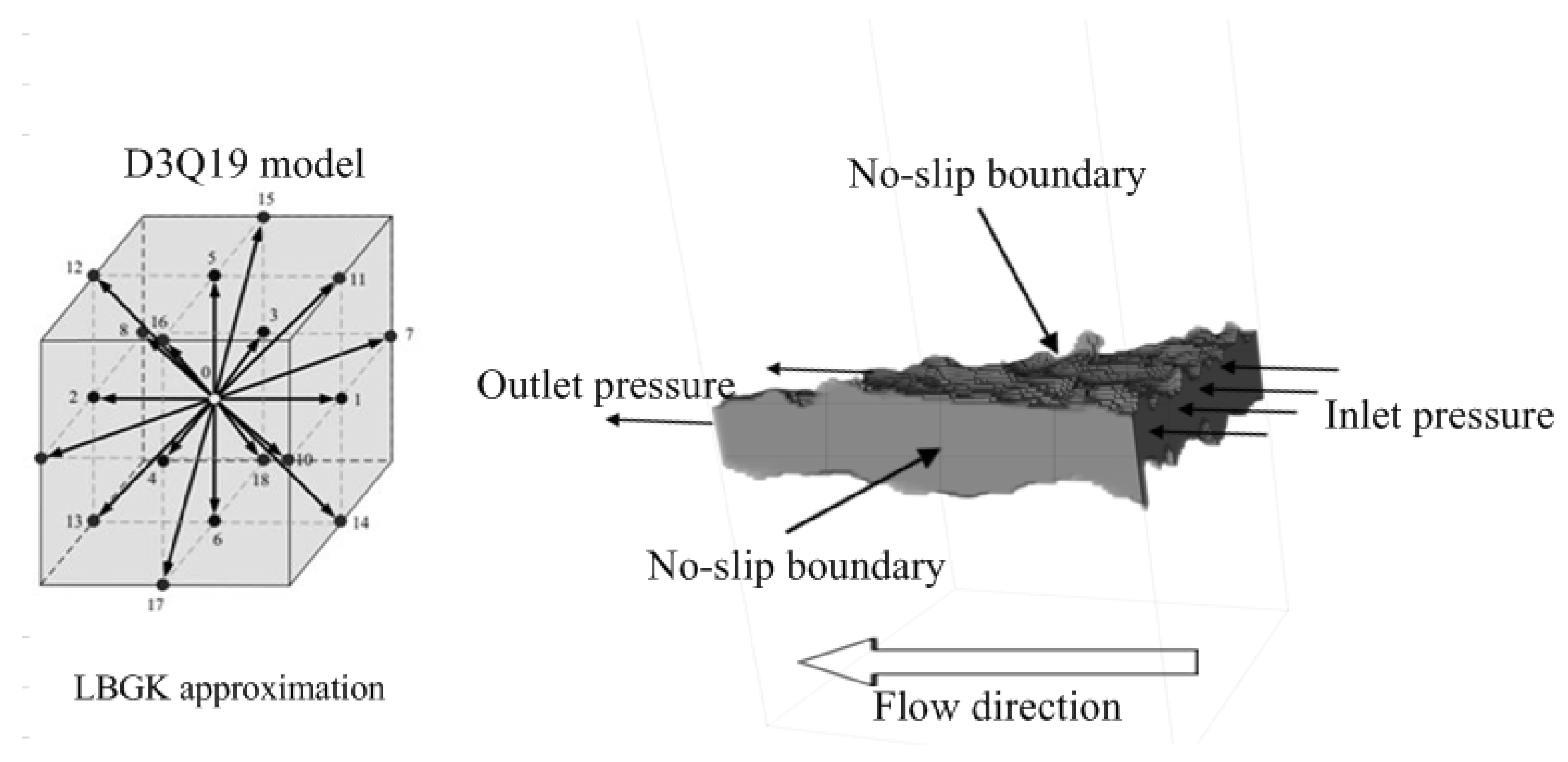
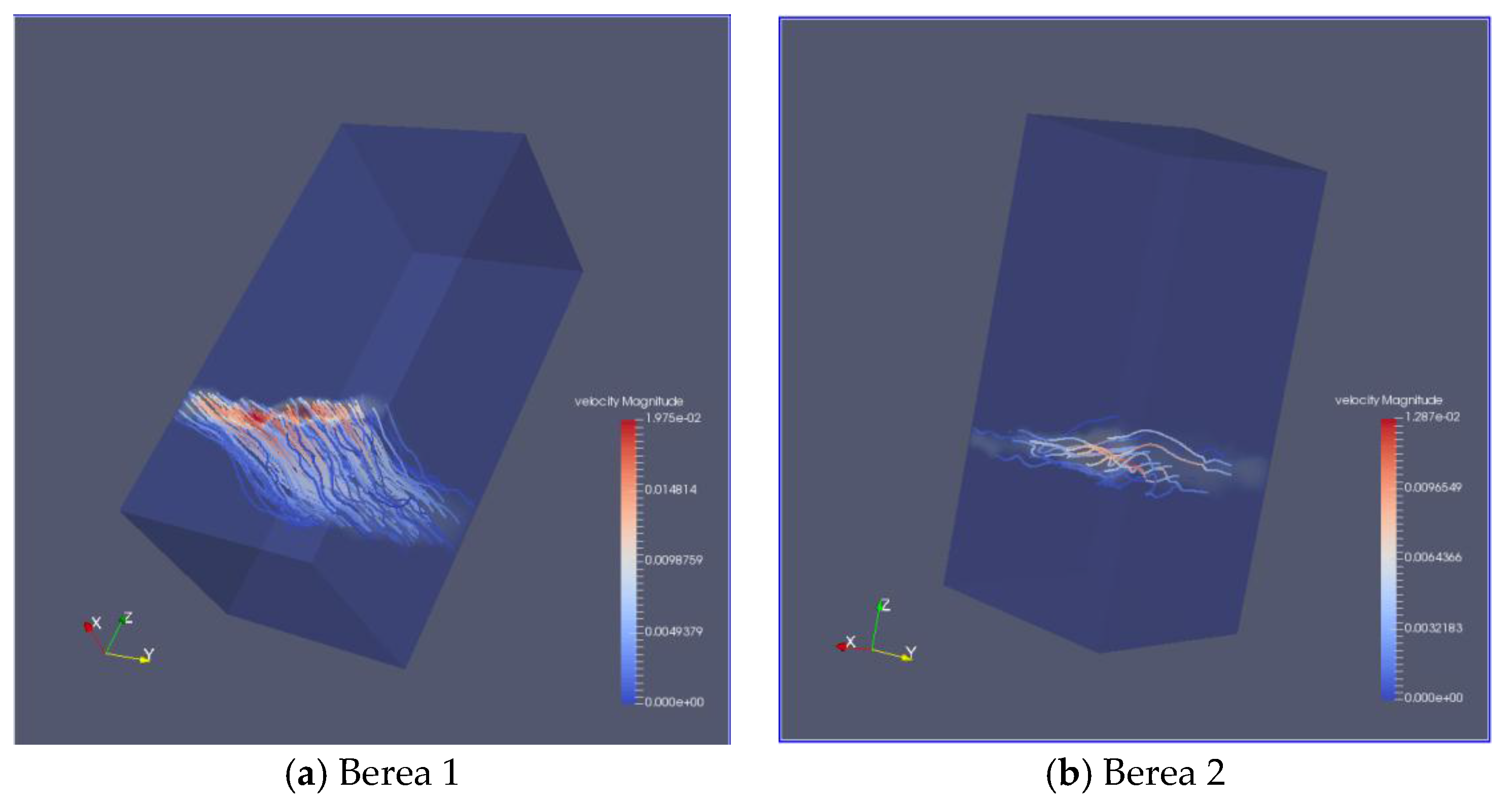
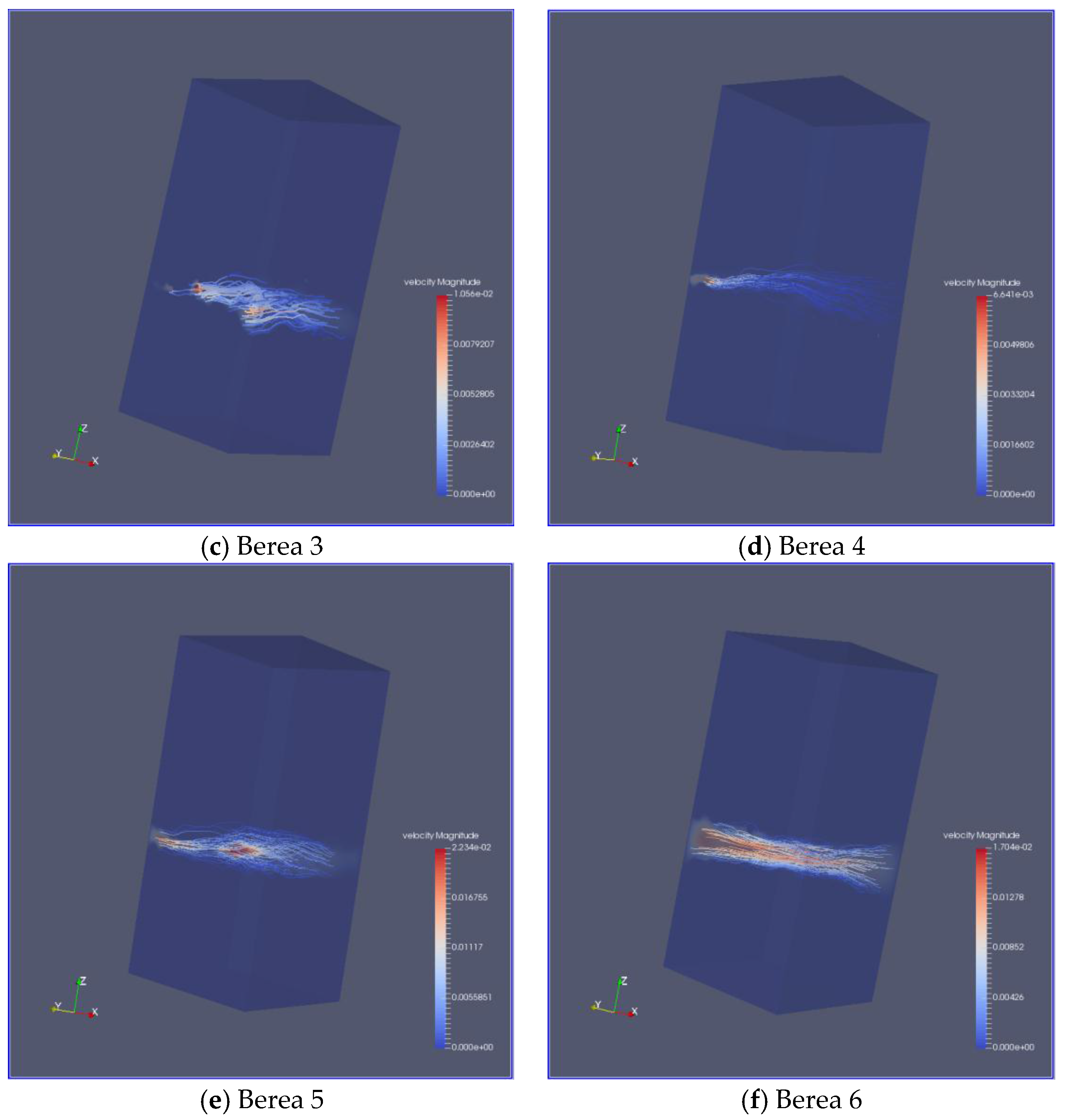
2.3. The Calculating of Permeability by LBM
3. Results and Discussion
3.1. The Digital Rocks of Fractures
3.2. Fractal Dimension Calculating of Fractures
3.3. The Permeability of Fractures
3.4. The Relations of Permeability and Other Parameters
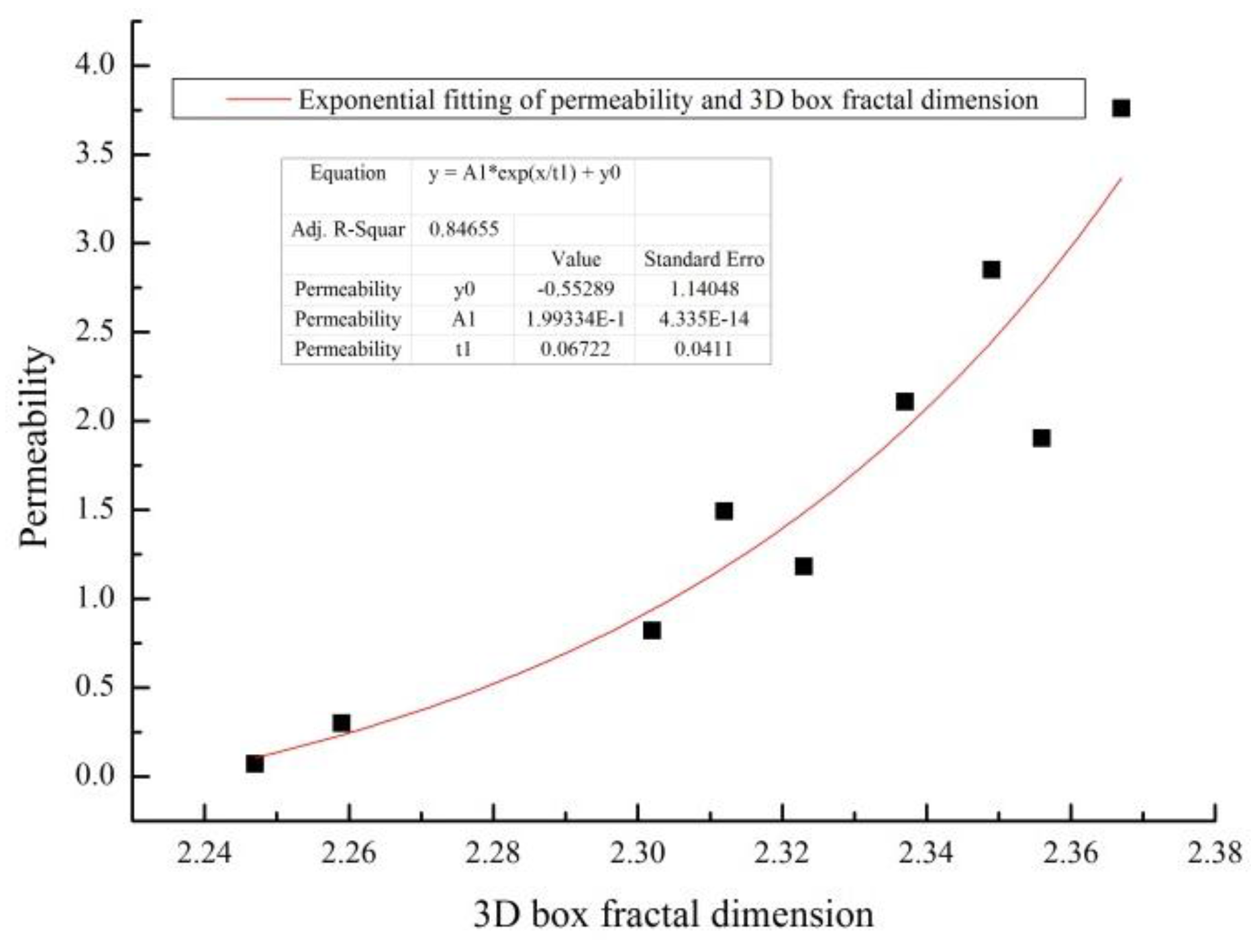
3.4.1. Permeability versus 3D Box Fractal Dimension
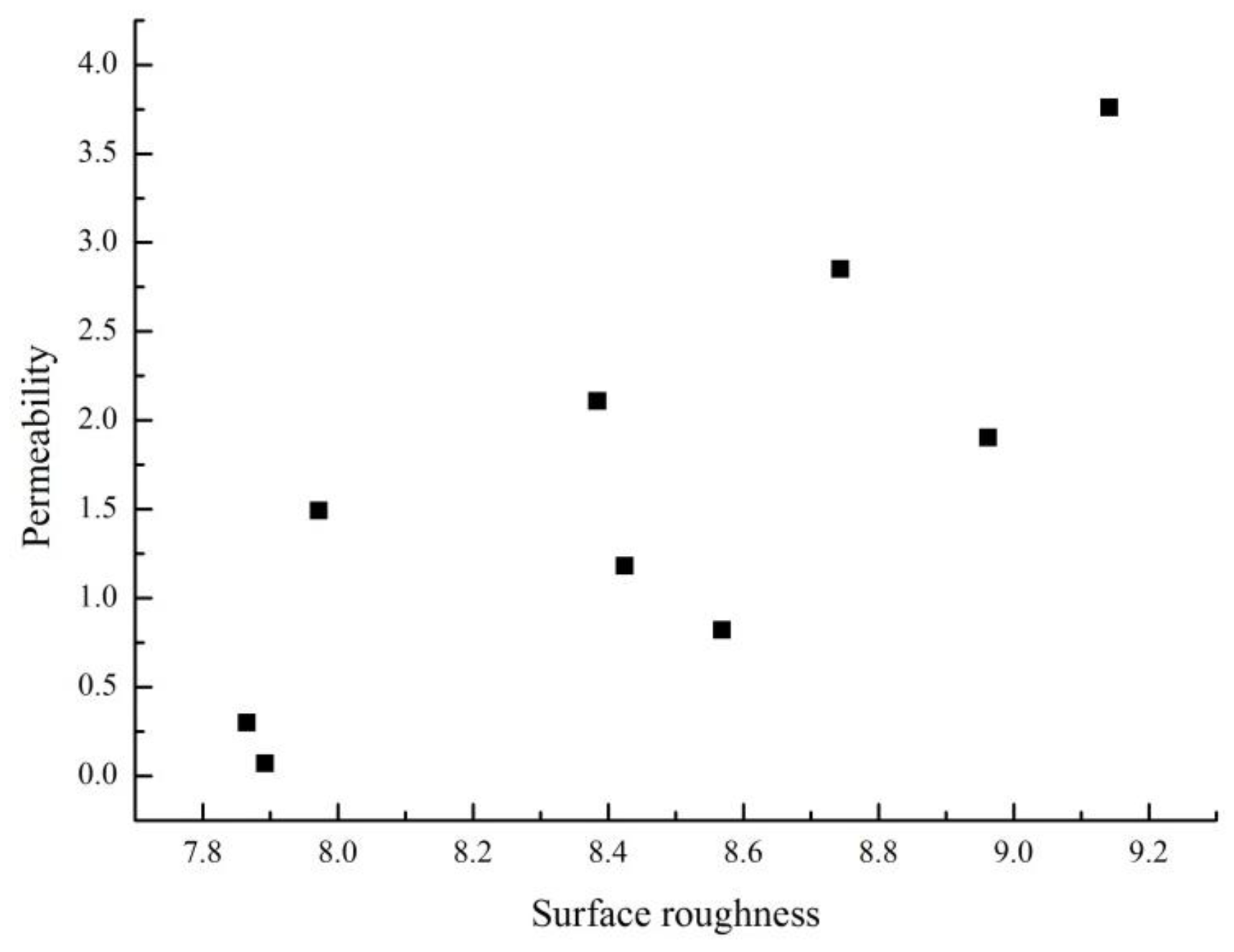
3.4.2. Permeability versus Surface Roughness
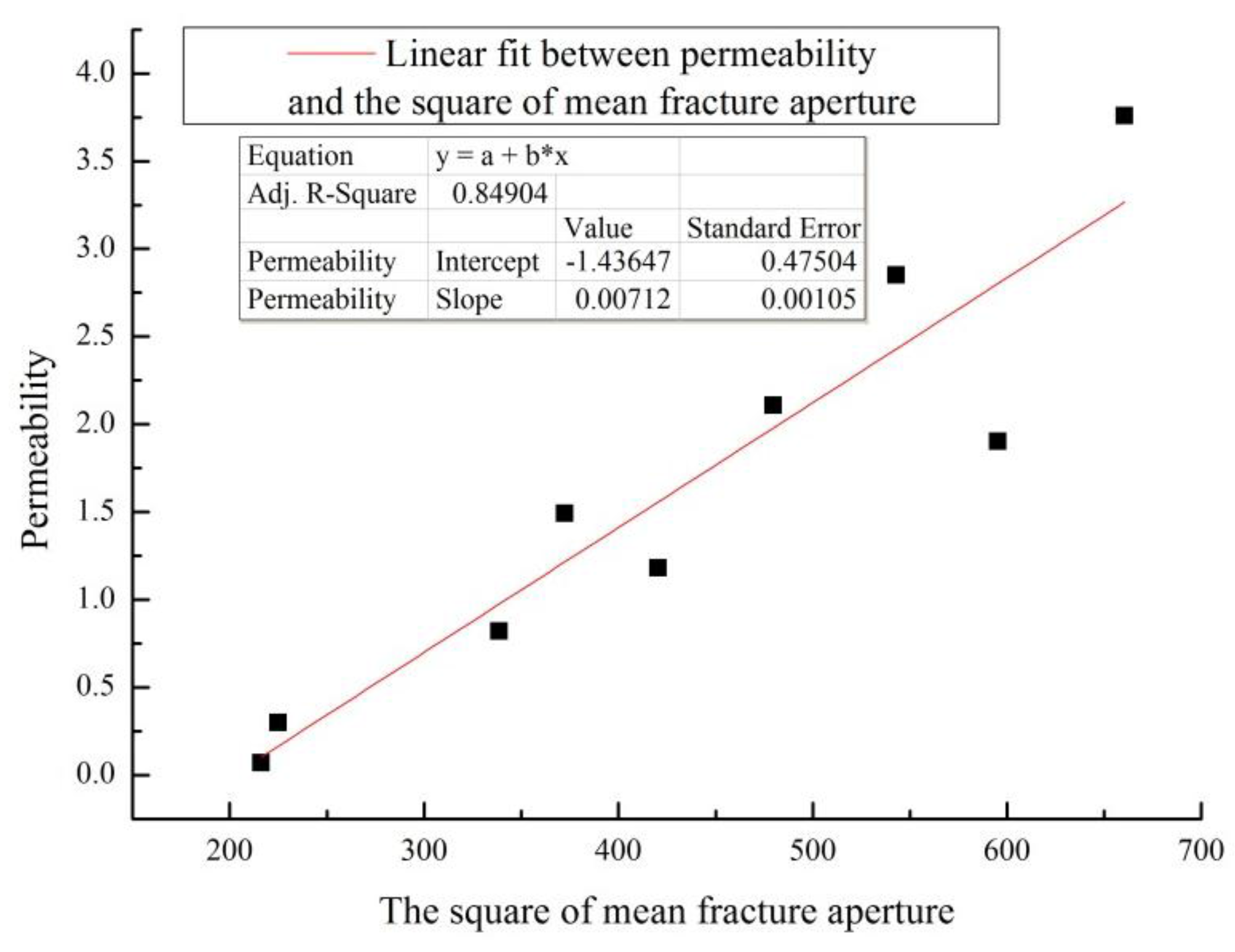
3.4.3. Permeability versus Mean Fracture Aperture
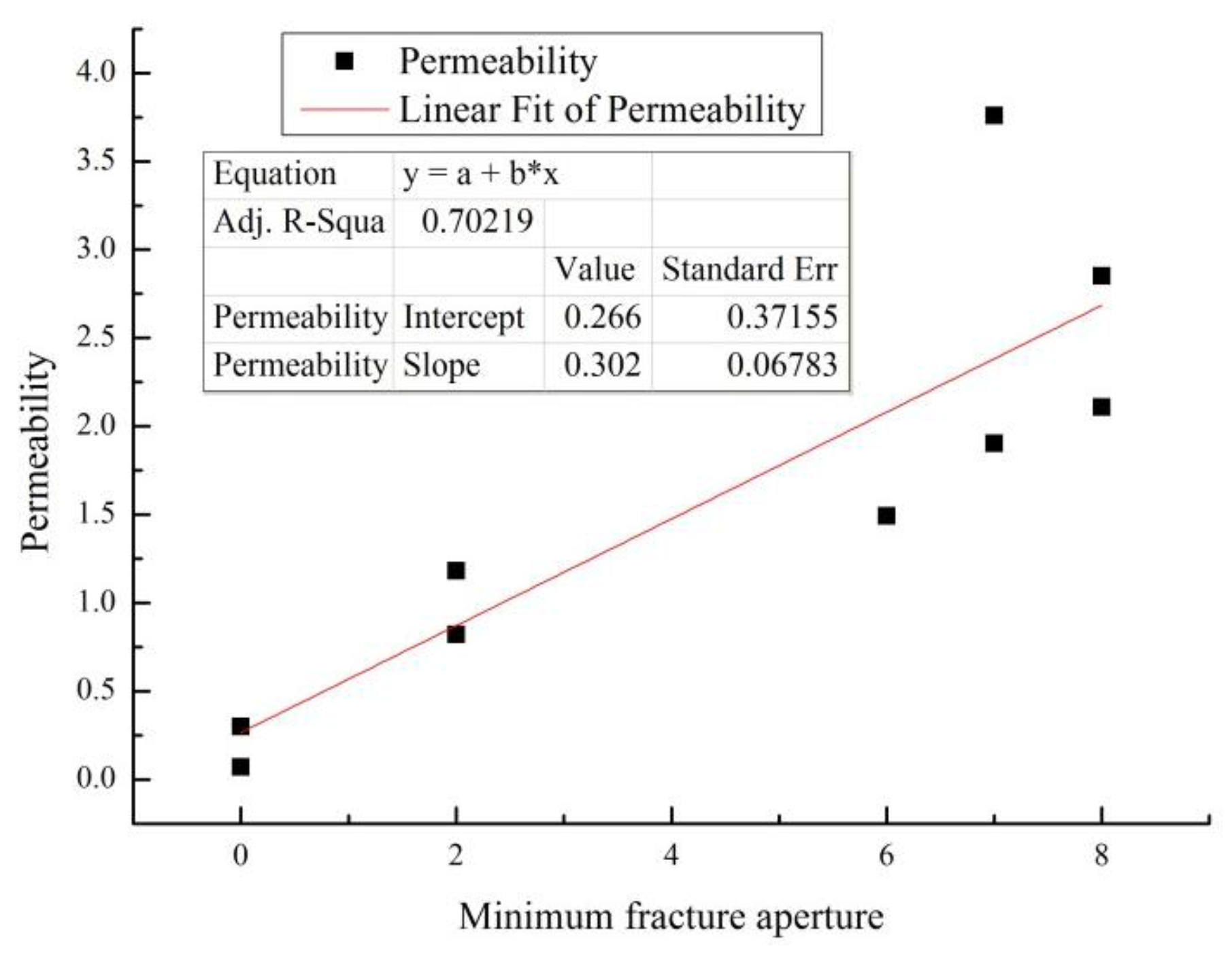
3.4.4. Permeability versus Minimum Fracture Aperture
3.5. The Relationship of 3D Box Fractal Dimension and Other Parameters
3.5.1. 3D Box Fractal Dimension versus Porosity
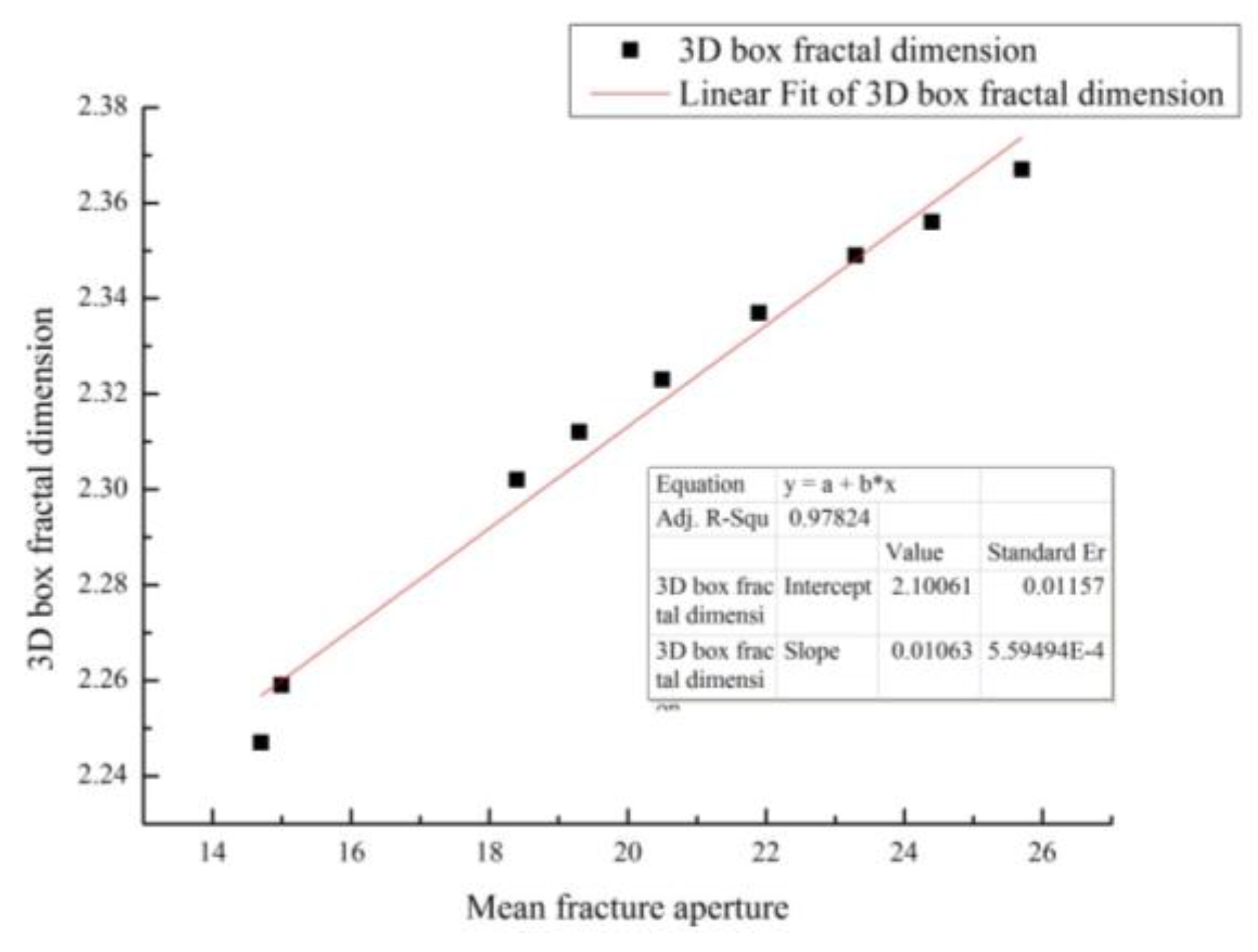
3.5.2. 3D Box Fractal Dimension versus Mean Fracture Aperture
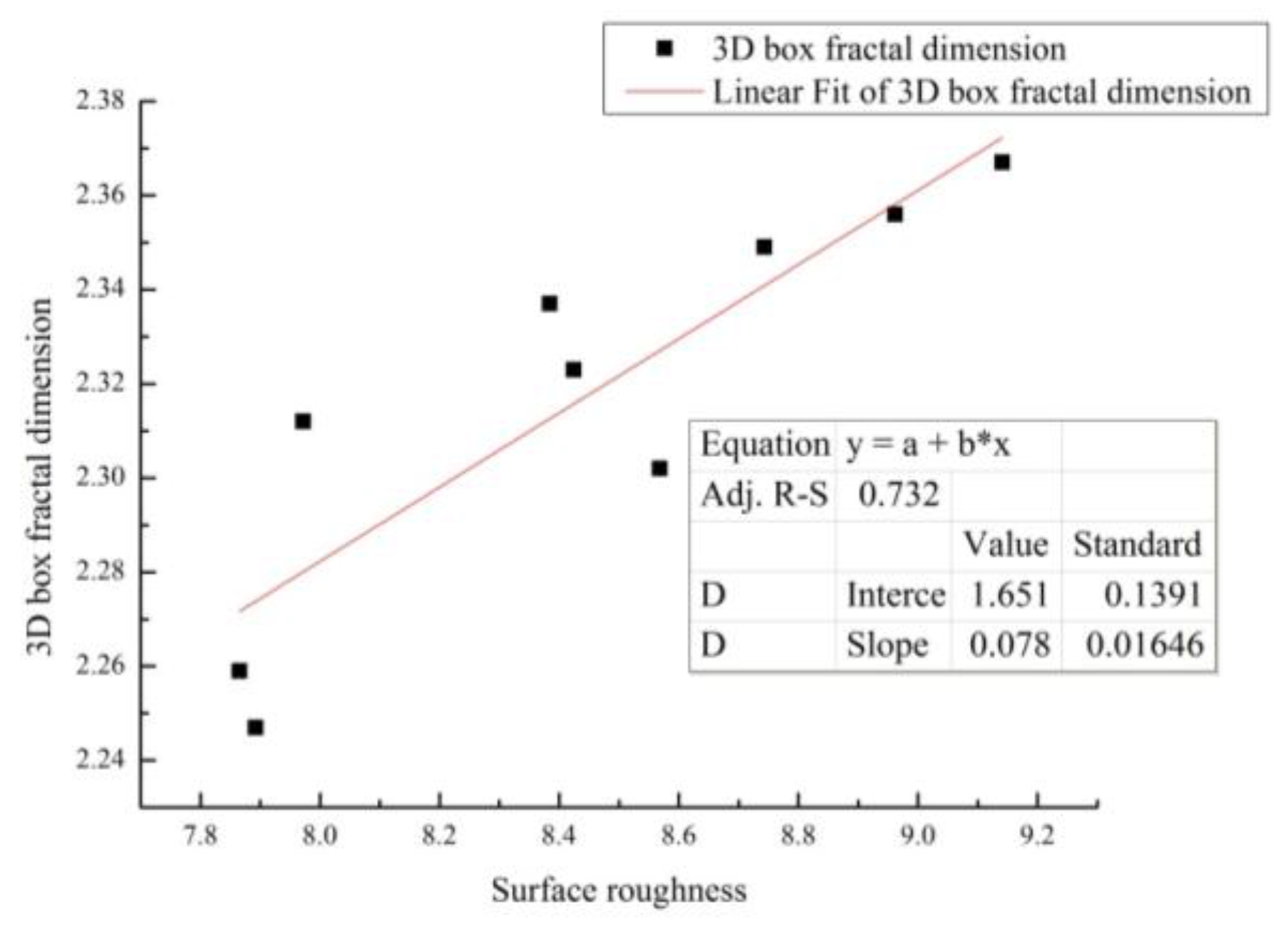
3.5.3. 3D Box Fractal Dimension versus Surface Roughness
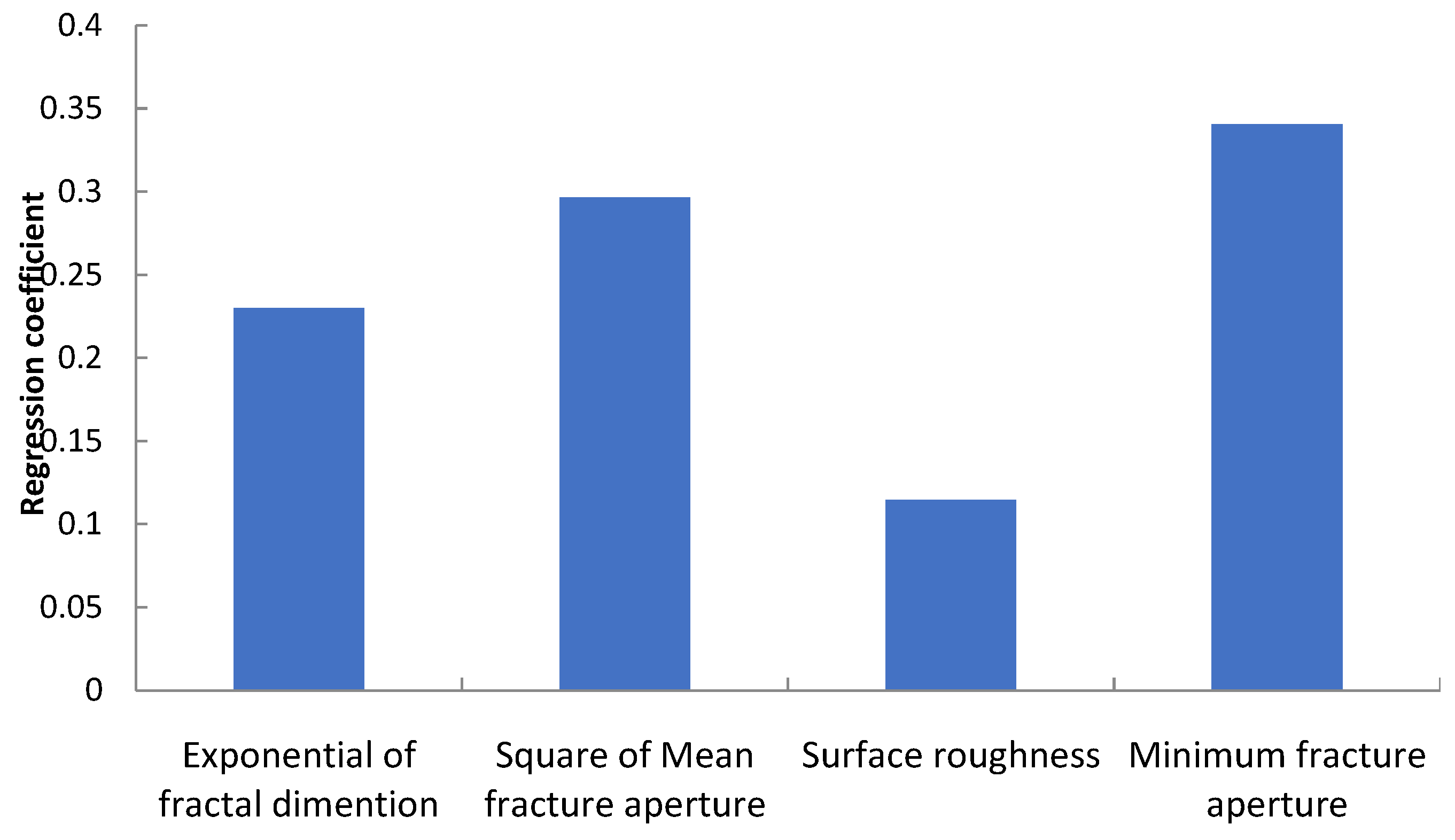
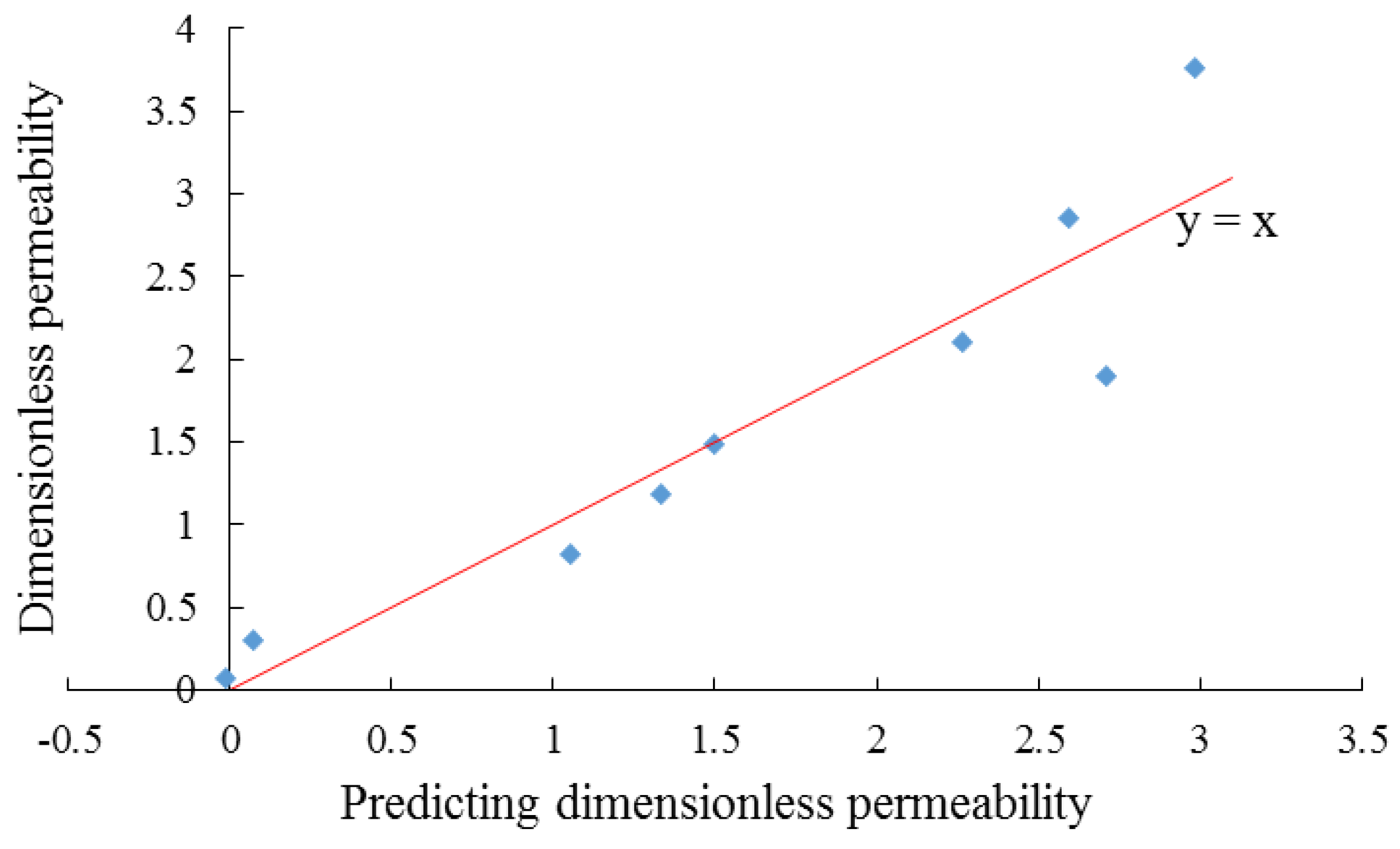
3.6. PLS Regression
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Sagar, B.; Runchal, A. Permeability of fractured rock: Effect of fracture size and data uncertainties. Water Resour. Res. 1982, 18, 266–274. [Google Scholar] [CrossRef]
- Bunger, A.P.; Zhang, X.; Jeffrey, R.G. Parameters Affecting the Interaction Among Closely Spaced Hydraulic Fractures. SPE J. 2012, 17, 292–306. [Google Scholar] [CrossRef]
- Akhavan, A.; Shafaatian, S.M.H.; Rajabipour, F. Quantifying the effects of crack width, tortuosity, and roughness on water permeability of cracked mortars. Cem. Concr. Res. 2012, 42, 313–320. [Google Scholar] [CrossRef]
- Neuman, S.P. Trends, prospects and challenges in quantifying flow and transport through fractured rocks. Hydrogeol. J. 2005, 13, 124–147. [Google Scholar] [CrossRef]
- Or, D.; Tuller, M. Flow in unsaturated fractured porous media: Hydraulic conductivity of rough surfaces. Water Resour. Res. 2000, 36, 1165–1177. [Google Scholar] [CrossRef]
- Samuel, F.; Pejman, T.; Mohammed, P. Interaction Between Fluid and Porous Media with Complex Geometries: A Direct Pore-Scale Study. Water Resour. Res. 2018. [Google Scholar] [CrossRef]
- Snow, D.T. A Parallel Plate Model Of Fractured Permeable Media. Ph.D. Thesis, University of California, Oakland, CA, USA, 1965. [Google Scholar]
- Ge, S. A governing equation for fluid flow in rough fractures. Water Resour. Res. 1997, 33, 53–61. [Google Scholar] [CrossRef]
- Genabeek, O.V.; Rothman, D.H. Critical behavior in flow through a rough-walled channel. Phys. Lett. A 1999, 255, 31–36. [Google Scholar] [CrossRef]
- Konzuk, J.S.; Kueper, B.H. Evaluation of cubic law based models describing single-phase flow through a rough-walled fracture. Water Resour. Res. 2004, 40, 389–391. [Google Scholar] [CrossRef]
- Yang, J.; Zhang, Q.G.; Yang, Y.M.; Xie, H.P.; Gao, F.; Wang, H.J. An experimental investigation on the mechanism of fluid flow through single rough fracture of rock. Sci. China Technol. Sci. 2013, 56, 2070–2080. [Google Scholar]
- Bertels, S.P.; Dicarlo, D.A.; Blunt, M.J. Measurement of aperture distribution, capillary pressure, relative permeability, and in situ saturation in a rock fracture using computed tomography scanning. Water Resour. Res. 2001, 37, 649–662. [Google Scholar] [CrossRef]
- Brown, S.R. Transport of fluid and electric current through a single fracture. J. Geophys. Res. Solid Earth 1989, 94, 9429–9438. [Google Scholar] [CrossRef]
- Renshaw, C.E.; Dadakis, J.S.; Brown, S.R. Measuring fracture apertures: A comparison of methods. Geophys. Res. Lett. 2000, 27, 289–292. [Google Scholar] [CrossRef]
- Wolf-Gladrow, D.A. Lattice Gas Cellular Automata and Lattice Boltzmann Models; Springer: Tokyo, Japan, 2000. [Google Scholar]
- Zhang, L.; Yao, J.; Zhao, J.L.; Li, A.; Sun, H.; Wan, Y.; Su, Y. The influence of wettability and shut-in time on oil recovery through microscale simulation based on an ideal model. J. Nat. Gas Sci. Eng. 2017, 48, 178–185. [Google Scholar] [CrossRef]
- Dou, Z.; Zhou, Z.; Sleep, B.E. Influence of wettability on interfacial area during immiscible liquid invasion into a 3D self-affine rough fracture: Lattice Boltzmann simulations. Adv. Water Resour. 2013, 61, 1–11. [Google Scholar] [CrossRef]
- Chen, Y.F.; Zhou, J.Q.; Hu, S.H.; Hu, R.; Zhou, C.B. Evaluation of Forchheimer equation coefficients for non-Darcy flow in deformable rough-walled fractures. J. Hydrol. 2015, 529, 993–1006. [Google Scholar] [CrossRef]
- Tsang, Y.W. The Effect of Tortuosity on Fluid Flow Through a Single Fracture. Water Resour. Res. 1984, 20, 1209–1215. [Google Scholar] [CrossRef]
- Alyaarubi, A.H.; Pian, C.C.; Grattoni, C.A.; Zimmerman, R.W. Navier-stokes simulations of fluid flow through a rock fracture. Geophys. Monogr. 2013, 162, 55–64. [Google Scholar]
- Hans, J.; Boulon, M. A new device for investigating the hydro-mechanical properties of rock joints. Int. J. Numer. Anal. Meth. Geomech. 2003, 27, 513–548. [Google Scholar] [CrossRef]
- Koyama, T.; Neretnieks, I.; Jing, L. A numerical study on differences in using Navier–Stokes and Reynolds equations for modeling the fluid flow and particle transport in single rock fractures with shear. Int. J. Rock Mech. Min. Sci. 2008, 45, 1082–1101. [Google Scholar] [CrossRef]
- Brown, S.; Caprihan, A.; Hardy, R. Experimental observation of fluid flow channels in a single fracture. J. Geophys. Res. Solid Earth 1998, 103, 5125–5132. [Google Scholar] [CrossRef]
- Berkowitz, B. Characterizing flow and transport in fractured geological media: A review. Adv. Water Resour. 2002, 25, 861–884. [Google Scholar] [CrossRef]
- Liu, Z.; Yang, Y.; Yao, J.; Zhang, Q.; Ma, J.; Qian, Q. Pore-scale remaining oil distribution under different pore volume water injection based on CT technology. Adv. Geo-energ. Res. 2017, 1, 171–181. [Google Scholar] [CrossRef]
- Cai, Y.; Liu, D.; Mathews, J.P.; Pan, Z.; Elsworth, D.; Yao, Y.; Li, J.; Guo, X. Permeability evolution in fractured coal—Combining triaxial confinement with X-ray computed tomography, acoustic emission and ultrasonic techniques. Int. J. Coal. Geol. 2014, 122, 91–104. [Google Scholar] [CrossRef]
- Heriawan, M.N.; Koike, K. Coal quality related to microfractures identified by CT image analysis. Int. J. Coal. Geol. 2015, 140, 97–110. [Google Scholar] [CrossRef]
- Mazumder, S.; Wolf, K.-H.A.A.; Elewaut, K.; Ephraim, R. Application of X-ray computed tomography for analyzing cleat spacing and cleat aperture in coal samples. Int. J. Coal. Geol. 2006, 68, 205–222. [Google Scholar] [CrossRef]
- Montemagno, C.D.; Pyrak-Nolte, L.J. Fracture network versus single fractures: Measurement of fracture geometry with X-ray tomography. Phys. Chem. Earth Part A 1999, 24, 575–579. [Google Scholar] [CrossRef]
- Yang, Y.; Liu, Z.; Sun, Z.; An, S.; Zhang, W.; Liu, P.; Yao, P.; Ma, J. Research on Stress Sensitivity of Fractured Carbonate Reservoirs Based on CT Technology. Energies 2017, 10, 1833. [Google Scholar] [CrossRef]
- Wennberg, O.P.; Rennan, L.; Basquet, R. Computed tomography scan imaging of natural open fractures in a porous rock; geometry and fluid flow. Geophys. Prospect. 2009, 57, 239–249. [Google Scholar] [CrossRef]
- Watanabe, N.; Ishibashi, T.; Hirano, N.; Ohsaki, Y.; Tsuchiya, Y.; Tamagawa, T.; Okabe, H.; Tsuchiya, N. Precise 3D Numerical Modeling of Fracture Flow Coupled With X-Ray Computed Tomography for Reservoir Core Samples. SPE J. 2011, 16, 683–691. [Google Scholar] [CrossRef]
- Jack, D.; Qian, F.; Naum, D. Etudes in computational rock physics: Alterations and benchmarkingEtudes in computational rock physics. Geophysics 2012, 77, D45–D52. [Google Scholar]
- Karpyn, Z.T.; Grader, A.S.; Halleck, P.M. Visualization of fluid occupancy in a rough fracture using micro-tomography. J. Colloid. Interface Sci. 2007, 307, 181–187. [Google Scholar] [CrossRef] [PubMed]
- Mandelbrot, B.B. How long is the coastline of Britain. Science 1967, 156, 3775. [Google Scholar] [CrossRef] [PubMed]
- Cai, J.; Wei, W.; Hu, X.Y.; Liu, R.H.; Wang, J.J. Fractal characterization of dynamic fracture network extension in porous media. Fractals 2017, 25, 1750023. [Google Scholar] [CrossRef]
- Cai, J.; Yu, B.; Zou, M.; Luo, L. Fractal characterization of spontaneous co-current imbibition in porous media. Energy Fuels 2010, 24, 1860–1867. [Google Scholar] [CrossRef]
- King, P.R. The fractal nature of viscous fingering in porous media. J. Phys. Math. Gen. 1987, 20, L529. [Google Scholar] [CrossRef]
- Xie, S.; Cheng, Q.; Ling, Q.; LI, B.; Bao, Z.; Fan, P. Fractal and multifractal analysis of carbonate pore-scale digital images of petroleum reservoirs. Mar. Pet. Geol. 2010, 27, 476–485. [Google Scholar] [CrossRef]
- Zheng, Q.; Yu, B. A fractal permeability model for gas flow through dual-porosity media. J. Appl. Phys. 2012, 111, 024316. [Google Scholar] [CrossRef]
- Mandelbrot, B.B.; Wheeler, J.A. The Fractal Geometry of Nature. Am. J. Phys. 1983, 51, 468. [Google Scholar] [CrossRef]
- Li, J.; Liu, Z.; Li, J.; Lu, S.F. Fractal characteristics of continental shale pores and its significance to the occurrence of shale oil in china: A case study of biyang depression. Fractals 2018, 26, 1840008. [Google Scholar] [CrossRef]
- Yuliang, S.; Sheng, G.; Wang, W.; Zhang, Q.; Lu, M.; Ren, L. A mixed-fractal flow model for stimulated fractured vertical wells in tight oil reservoirs. Fractals 2016, 24, 1650006. [Google Scholar]
- Wang, F.; Liu, Z.; Jiao, L.; Wang, C.; Guo, H. A fractal permeability model coupling boundary-layer effect for tight oil reservoirs. Fractals 2017, 25, 1750042. [Google Scholar] [CrossRef]
- Qian, Y.H.; D'Humières, D.; Lallemand, P. Lattice BGK Models for Navier-Stokes Equation. Europhys. Lett. 1992, 17, 479. [Google Scholar]
- He, X.; Luo, L.S. Lattice Boltzmann Model for the Incompressible Navier–Stokes Equation. J. Stat. Phys. 1997, 88, 927–944. [Google Scholar] [CrossRef]
- Qisu, Z.; He, X. On pressure and velocity boundary conditions for the lattice Boltzmann BGK model. Phys. Fluids 1997, 9, 1591–1598. [Google Scholar]
- Induced Rough Fracture in Berea Sandstone Core Digital Rocks Portal. 2016. Available online: http://www.digitalrocksportal.org/projects/31 (accessed on 10 August 2018).
- Tamura, H.; Mori, S.; Yamawaki, T. Textural Features Corresponding to Visual Perception. IEEE Trans. Syst. Man Cybern. 1978, 8, 460–473. [Google Scholar] [CrossRef]
- Babadagli, T.; Ren, X.; Develi, K. Effects of fractal surface roughness and lithology on single and multiphase flow in a single fracture: An experimental investigation. Int. J. Multiph. Flow 2015, 68, 40–58. [Google Scholar] [CrossRef]
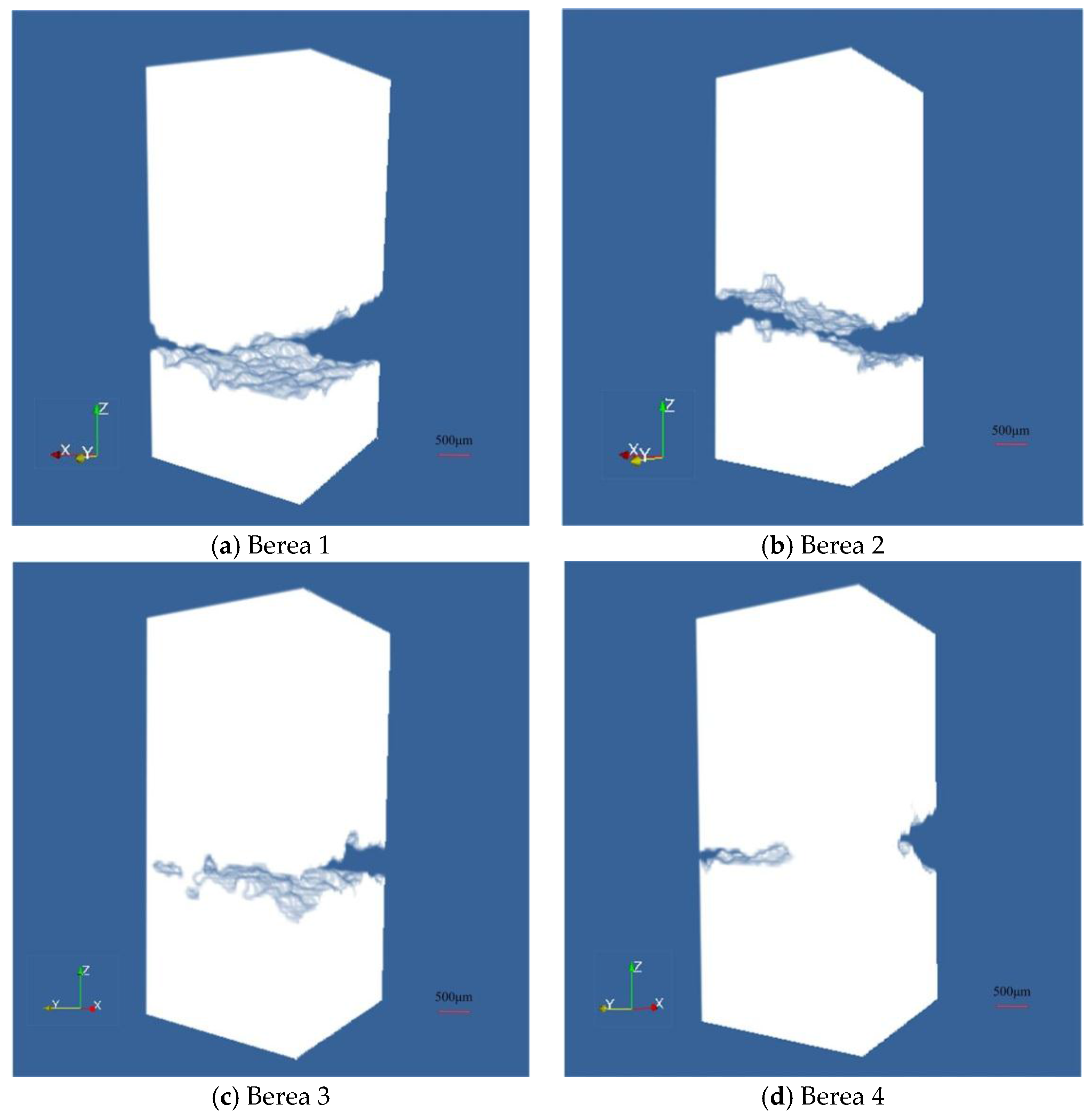
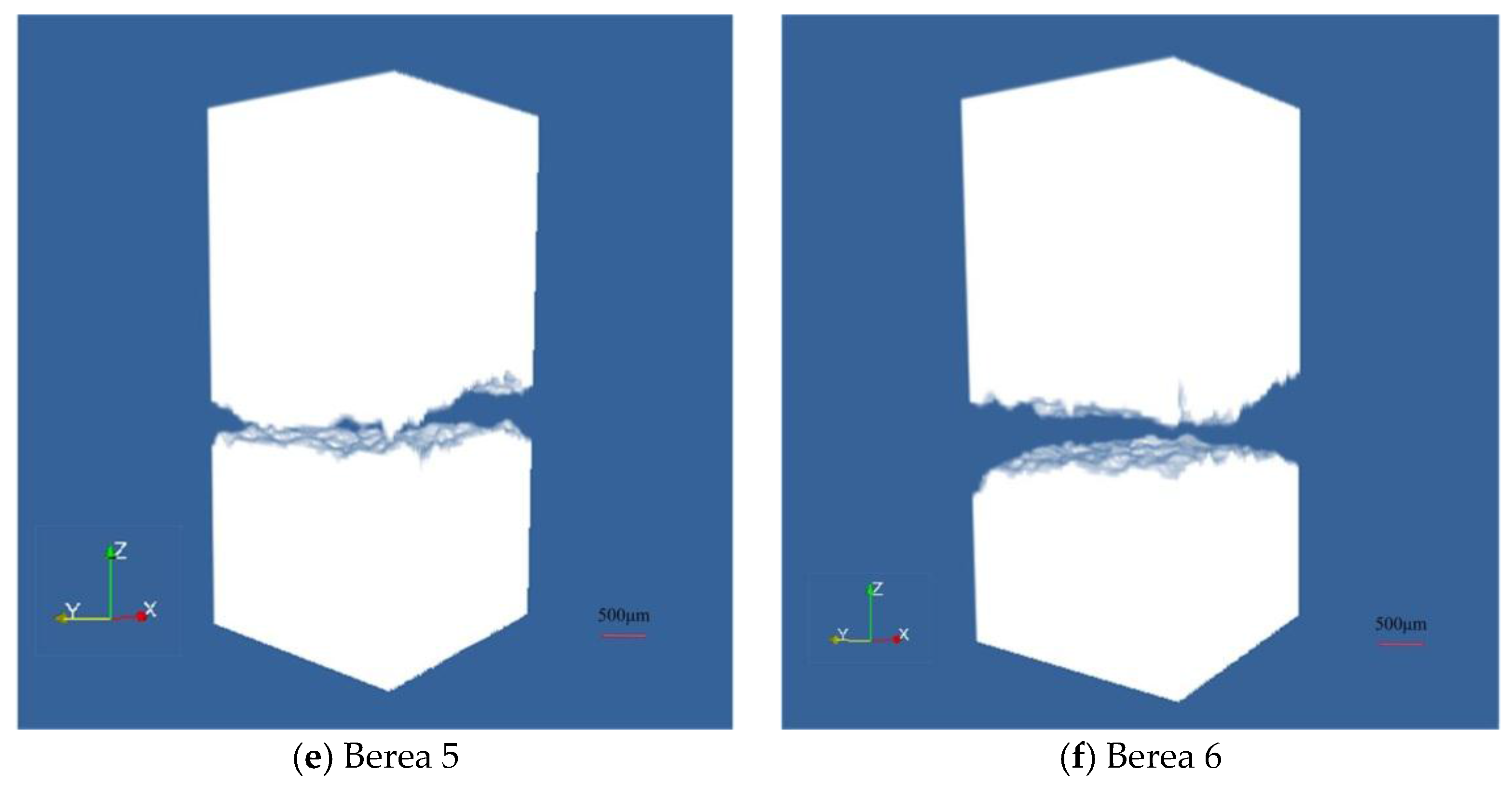

| Core Sample | Porosity | Minimum Fracture Aperture/Pixels | Mean Fracture Aperture/Pixels | Surface Roughness/Pixels |
|---|---|---|---|---|
| Berea 1 | 0.111 | 7 | 24.4 | 8.962 |
| Berea 2 | 0.082 | 2 | 18.4 | 8.568 |
| Berea 3 | 0.068 | 0 | 15.0 | 7.865 |
| Berea 4 | 0.067 | 0 | 14.7 | 7.892 |
| Berea 5 | 0.093 | 2 | 20.5 | 8.424 |
| Berea 6 | 0.100 | 8 | 21.9 | 8.384 |
| Berea 7 | 0.117 | 7 | 25.7 | 9.141 |
| Berea 8 | 0.088 | 6 | 19.3 | 7.972 |
| Berea 9 | 0.106 | 8 | 23.3 | 8.743 |
| r | 1 | 2 | 4 | 8 | 16 | 32 | 64 | 128 | 256 | |
|---|---|---|---|---|---|---|---|---|---|---|
| N(r) | Berea 1 | 243,739 | 64,473 | 14,952 | 3899 | 682 | 112 | 16 | 2 | 1 |
| Berea 2 | 184,084 | 49,754 | 12,946 | 3714 | 679 | 112 | 16 | 2 | 1 | |
| Berea 3 | 149,777 | 40,921 | 10,970 | 3302 | 640 | 104 | 16 | 2 | 1 | |
| Berea 4 | 146,858 | 39,713 | 9936 | 2982 | 637 | 107 | 16 | 2 | 1 | |
| Berea 5 | 205,178 | 54,841 | 13,687 | 3751 | 685 | 112 | 16 | 2 | 1 | |
| Berea 6 | 219,441 | 58,328 | 14,339 | 3866 | 685 | 112 | 16 | 2 | 1 | |
| Berea 7 | 256,973 | 67,771 | 15,537 | 4025 | 686 | 112 | 16 | 2 | 1 | |
| Berea 8 | 193,450 | 51,953 | 13,339 | 3734 | 686 | 112 | 16 | 2 | 1 | |
| Berea 9 | 232,925 | 61,929 | 14,801 | 3926 | 686 | 112 | 16 | 2 | 1 | |
| Core Sample | Berea 1 | Berea 2 | Berea 3 | Berea 4 | Berea 5 | Berea 6 | Berea 7 | Berea 8 | Berea 9 |
|---|---|---|---|---|---|---|---|---|---|
| 3D Box Fractal Dimension | 2.356 | 2.302 | 2.259 | 2.247 | 2.323 | 2.337 | 2.367 | 2.312 | 2.349 |
| Core Sample | Berea 1 | Berea 2 | Berea 3 | Berea 4 | Berea 5 | Berea 6 | Berea 7 | Berea 8 | Berea 9 |
|---|---|---|---|---|---|---|---|---|---|
| Permeability | 1.903 | 0.820 | 0.300 | 0.071 | 1.183 | 2.108 | 3.759 | 1.492 | 2.852 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, Y.; Liu, Z.; Yao, J.; Zhang, L.; Ma, J.; Hejazi, S.H.; Luquot, L.; Ngarta, T.D. Flow Simulation of Artificially Induced Microfractures Using Digital Rock and Lattice Boltzmann Methods. Energies 2018, 11, 2145. https://doi.org/10.3390/en11082145
Yang Y, Liu Z, Yao J, Zhang L, Ma J, Hejazi SH, Luquot L, Ngarta TD. Flow Simulation of Artificially Induced Microfractures Using Digital Rock and Lattice Boltzmann Methods. Energies. 2018; 11(8):2145. https://doi.org/10.3390/en11082145
Chicago/Turabian StyleYang, Yongfei, Zhihui Liu, Jun Yao, Lei Zhang, Jingsheng Ma, S. Hossein Hejazi, Linda Luquot, and Toussaint Dono Ngarta. 2018. "Flow Simulation of Artificially Induced Microfractures Using Digital Rock and Lattice Boltzmann Methods" Energies 11, no. 8: 2145. https://doi.org/10.3390/en11082145
APA StyleYang, Y., Liu, Z., Yao, J., Zhang, L., Ma, J., Hejazi, S. H., Luquot, L., & Ngarta, T. D. (2018). Flow Simulation of Artificially Induced Microfractures Using Digital Rock and Lattice Boltzmann Methods. Energies, 11(8), 2145. https://doi.org/10.3390/en11082145






