Reactive Power Dispatch Optimization with Voltage Profile Improvement Using an Efficient Hybrid Algorithm †
Abstract
:1. Introduction
- Biogeography Based Optimization (BBO) technique: This method has been developed based on the theory of biogeography which is nature’s way of distributing species. It is mainly based on migration and mutation [29].
- Differential Evolution (DE) algorithm: Similar to the genetic algorithm, the DE algorithm is a population-based algorithm that uses crossover, mutation and selection operators [14].
- General passive congregation PSO (GPAC), local passive congregation PSO (LPAC) and coordinated aggregation (CA) are a development of the PSO algorithm using recent advances in swarm intelligence. GPAC and LPAC algorithms are based on the global and local-neighborhood variant PSOs, respectively, and the CA technique is based on the coordinated aggregation observed in swarms [28].
- CLPSO method introduces learning strategy in PSO. In this method, for each particle, besides its own best particle (pbest), other particles’ pbests are used as exemplars. Each particle learns from all potential particles’ pbests in the swarm [9].
- Interior point (IP) method is a conventional technique based on the primal-dual algorithm [11].
2. ORPD Problem Formulation
- J1(x,u) and J2(x,u) are the transmission active power losses and SVD objective functions, respectively.
- g and h are the set of equality and inequality constraints, respectively.
- x is the state or dependent variables vector.
- u is the control or independent variables vector.
2.1. Objective Functions
2.1.1. Power Losses Minimization
- NL is the number of transmission lines.
- Vi and Vj are the voltage magnitude at buses i and j, respectively.
- is the conductance of branch k between buses i and j.
- is the voltage angle difference between bus i and bus j.
- NT is the number of tap regulating transformers.
- NC is the number of shunt VAR compensations.
2.1.2. Minimization of Voltage Deviation
- VLi is the voltage magnitude at load bus i.
- Vref is the voltage reference value which is equal to 1 p.u.
2.2. Problem Constraints
2.2.1. Equality Constrains
- PGi, QGi are the respective active and reactive power of the ith generator.
- PDi, QDi are the respective active and reactive power demand at bus i.
- NB is the total number of buses; Bij, Gij are real and imaginary parts of (i,j)th element of the bus admittance matrix.
2.2.2. Inequality Constraints.
Inequality Constraints on Security Limits
- Active power generated at slack bus
- Load bus voltage
- Generated reactive power
- Thermal limits: the apparent power flowing in line “L” must not exceed the maximum allowable apparent power flow value ()
Inequality Constraints on Control Variable Limits
- Generator voltage limits
- Transformer tap limits
- Shunt capacitor limits
- PG,slack is the real power generation at slack bus.
- VGi is the voltage magnitude at generator bus i.
- Ti is the tap ratio of transformer i.
- Qci is the reactive power compensation source at bus i.
- NPQ is the number of PQ bus.
- (.)max and (.)minare the upper and lower the limits of the considered variables, respectively.
3. Proposed Hybrid Algorithm
3.1. Particle Swarm Optimization
- is the current velocity of particle i at iteration k.
- is the inertia weight.
- rand is a random number between 0 and 1.
- and are the acceleration coefficients.
- is the best position of the current particle achieved so far.
- is the global best position achieved by all informants.
- is the current position of particle i at iteration k.
- itermax is the maximum number of iterations.
- k is the current number of iteration.
- wmax and wmin are the upper and lower limits of the inertia weighting factor, respectively.
- Penalty function approaches, and
- Approaches preserving feasibility throughout evolutionary computation,
3.2. Tabu Search Method
- TS is characterized by its ability to avoid entrapment in a local optimal solution and to prevent the same solution being found by using the flexible memory of the search history.
- TS uses probabilistic transition rules to make decisions, rather than deterministic ones. Hence, TS is a kind of stochastic optimization algorithm that can search a complicated and uncertain area to find the global optimum. This makes TS more flexible and robust than conventional methods.
- TS uses adaptive memory processes for guiding the seeking in the problem search space. Therefore, it can easily deal with non-smooth, non-continuous and non-differentiable objective functions.
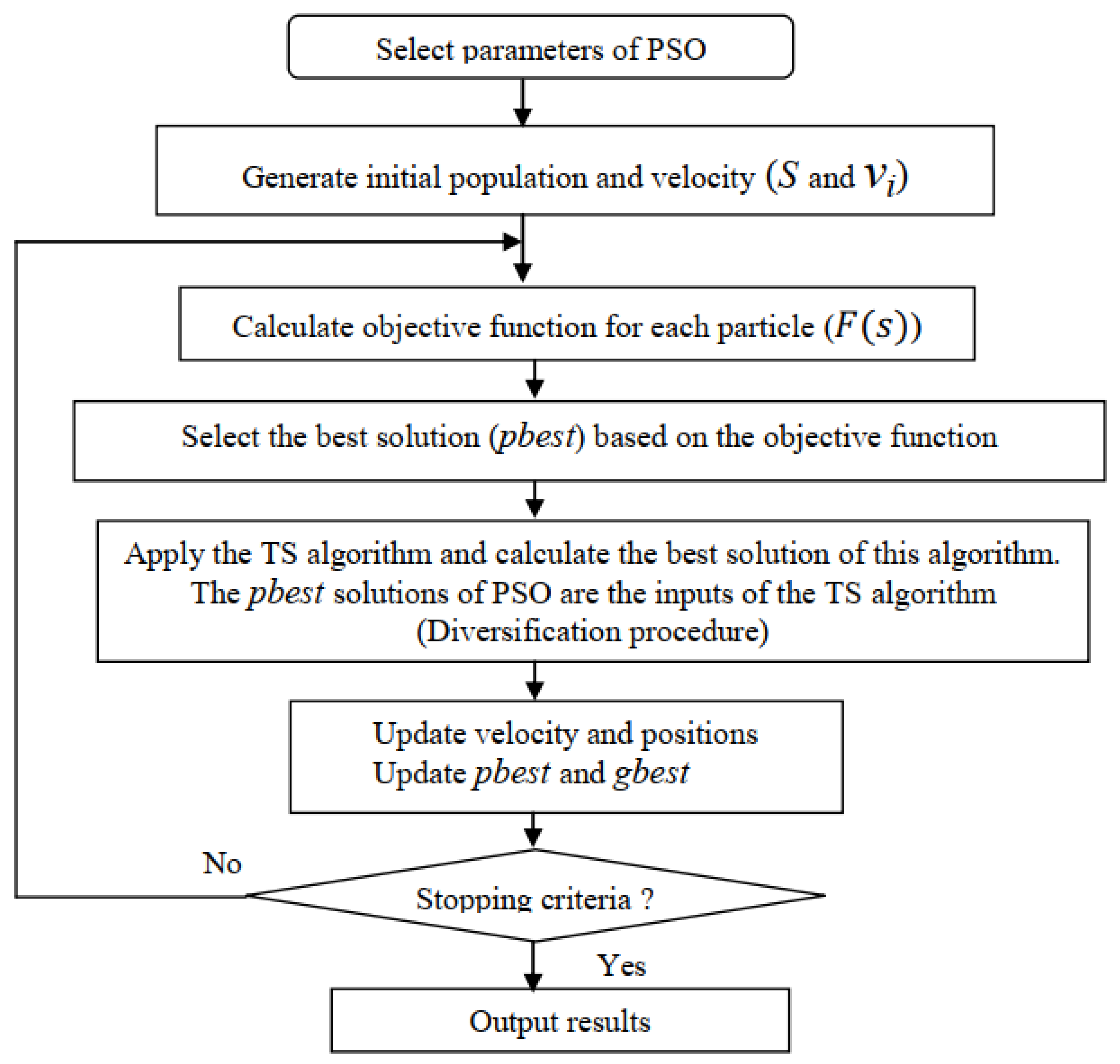
3.3. Hybrid PSO-Tabu Search Approach Applied to ORPD
| Algorithm 1 Tabu search procedure (Diversification) |
| Inputs pbest; // best historical solution of particles pbestval; solutions values m; //neighborhood size r; //radius of hyper-rectangles eps; //threshold for accepting new solution best_list = ( pbest, r); // Initializing the tabu list best_list Repeat For each solution s(VGi ,Ti ,Qci) in pbest //generation of m neighbors i = 1 While i <= m Generate the hyper-rectangle of radius r*i around s, choose randomly a solution NS in the hyper- rectangle If NS ∉ best_list then add the move to best_list; if eval(NS)-pbestval(s) ≤ eps then update pbestval and pbest s = NS, End if i = i + 1; End While Until (stoping criteria) |
4. Application and Results
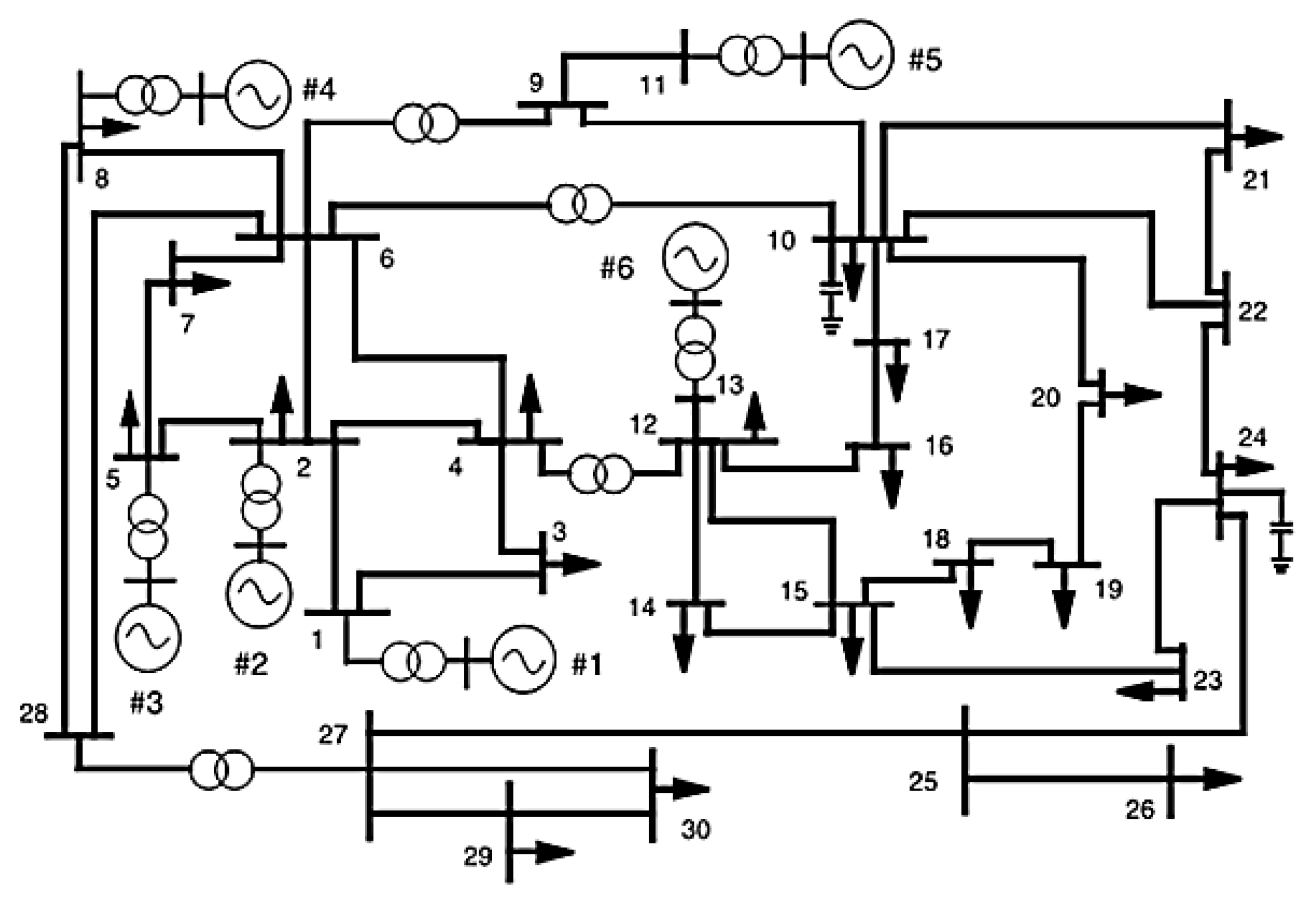
4.1. Case 1: IEEE 30 Bus with 12 Control Variables
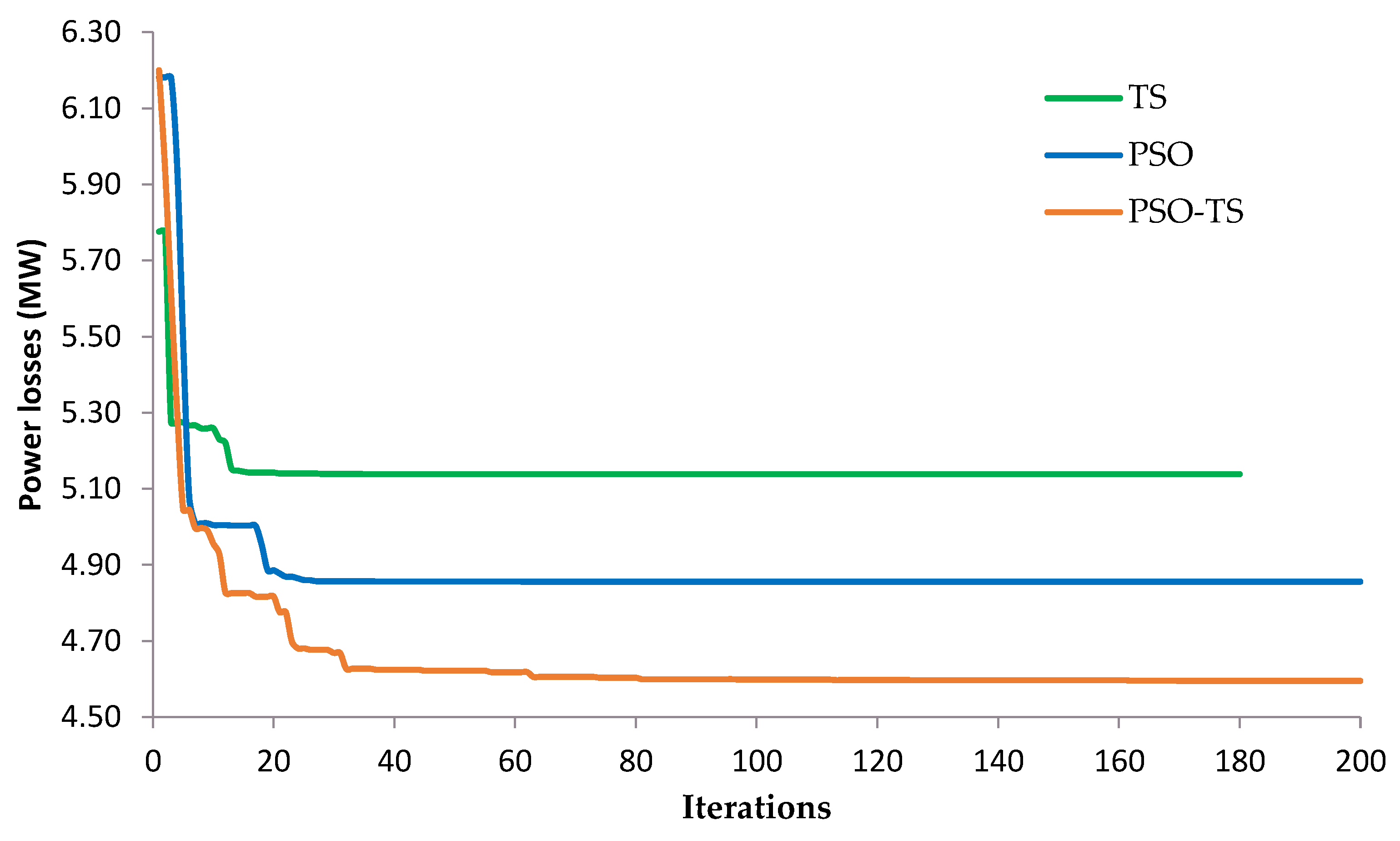
4.1.1. Power Loss Minimization
4.1.2. Voltage Deviation Minimization
4.2. Case 2: IEEE 30 Bus with 19 Control Variables
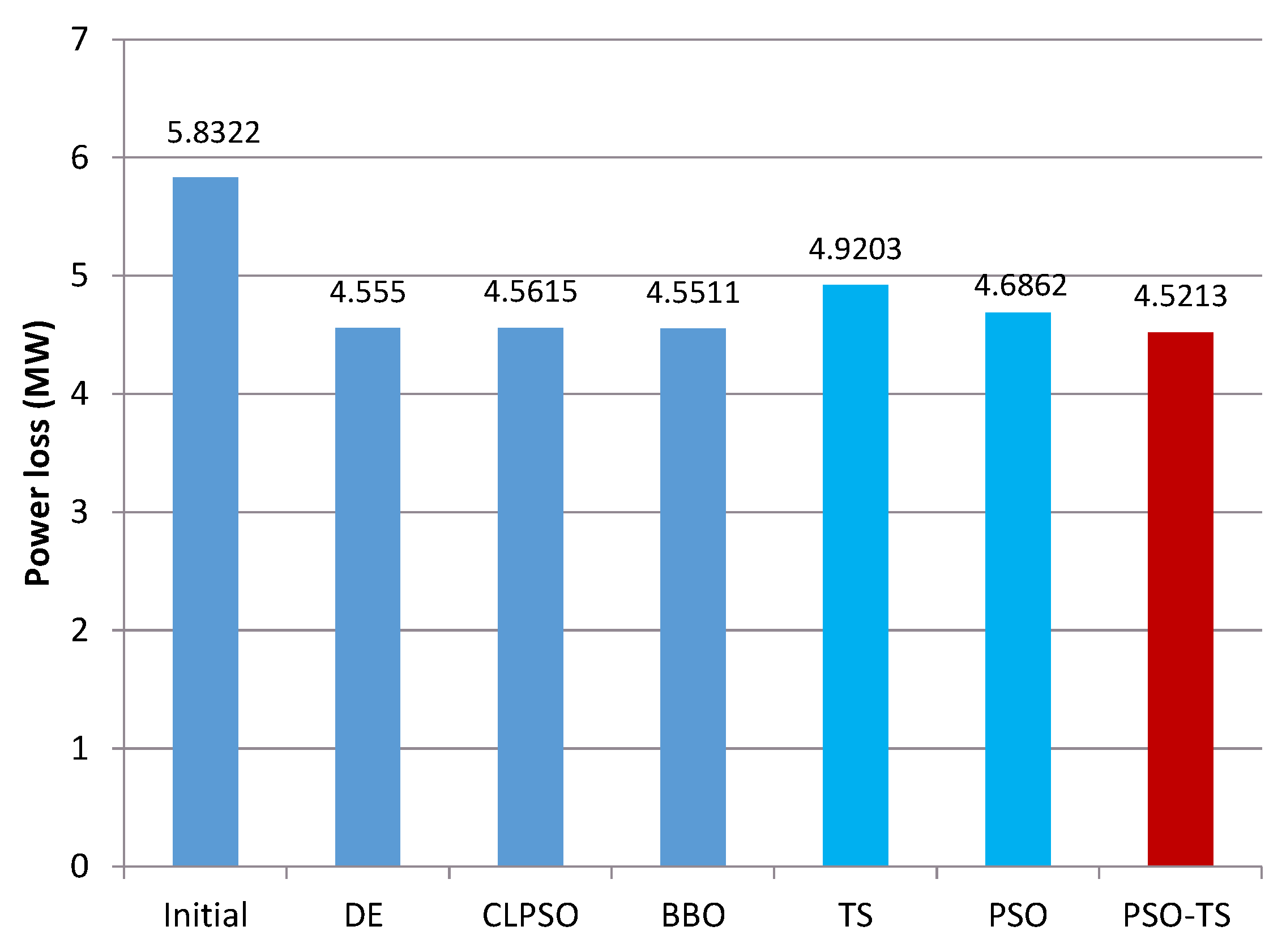
4.2.1. Power Losses Minimization
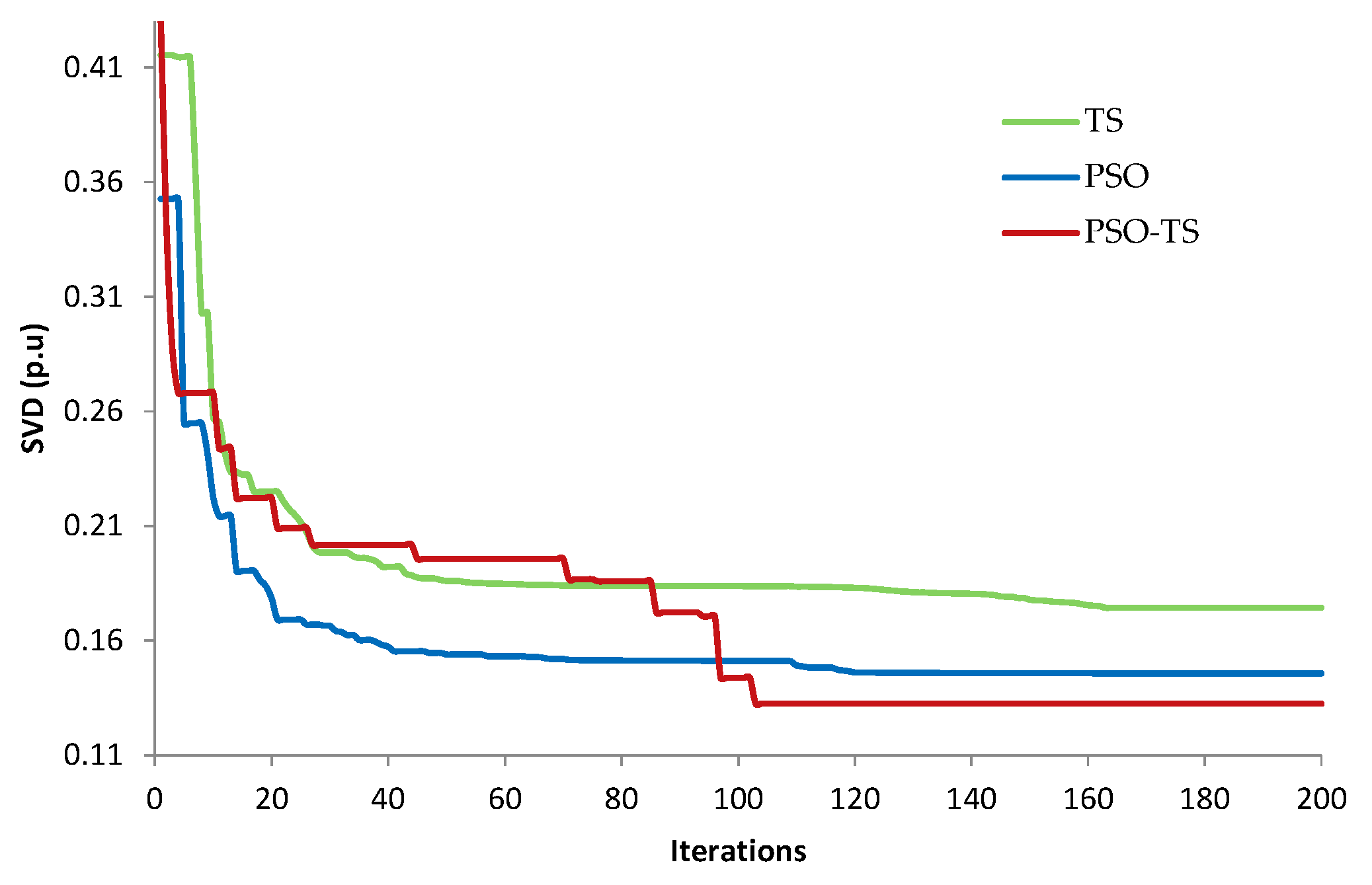
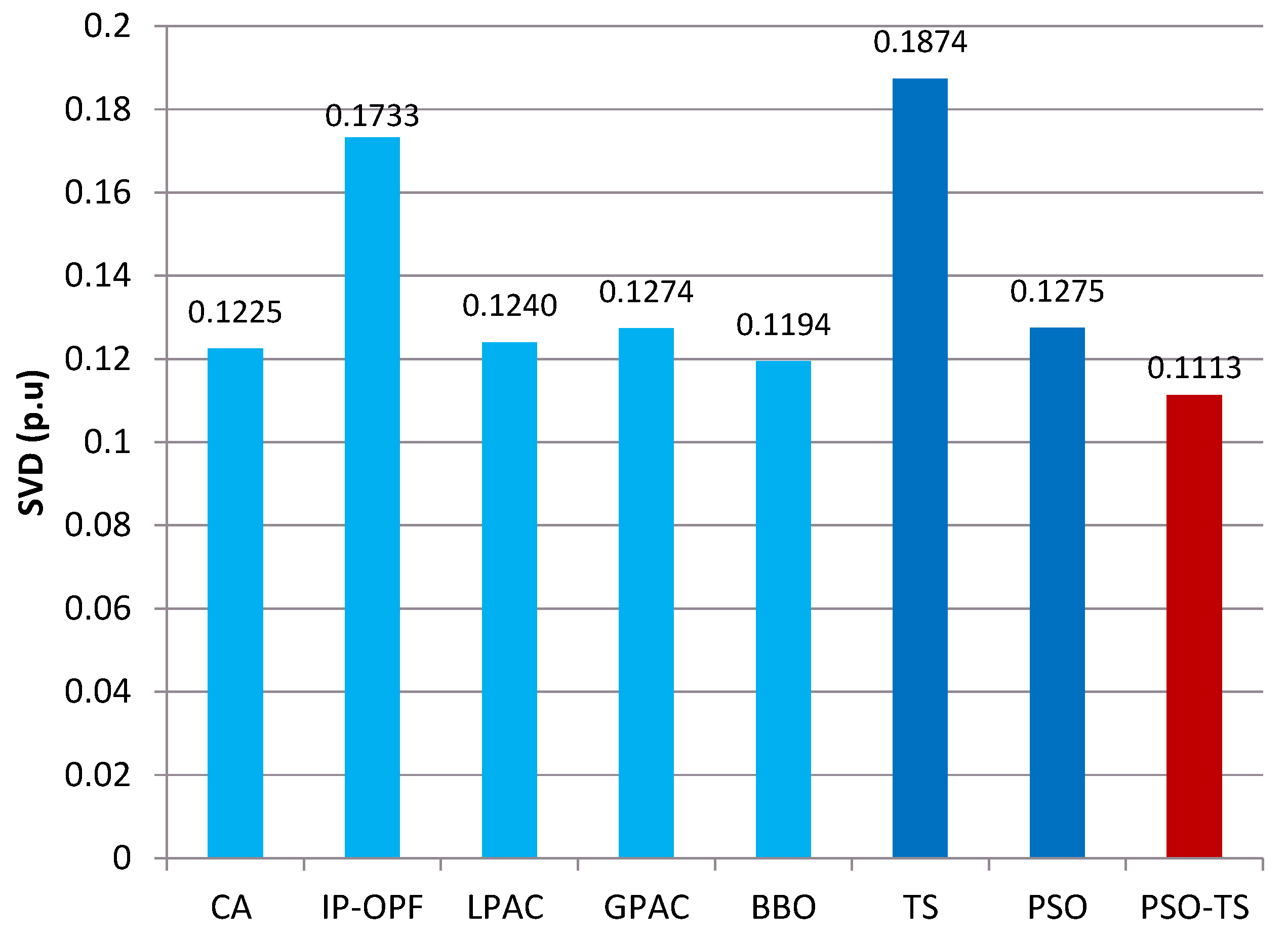
4.2.2. Voltage Deviation Minimization
5. Conclusions
Author Contributions
Funding
Conflicts of Interest
Appendix A
| Bus No. | Bus No. | R (p.u) | X (p.u) | B/2 (p.u) | Bus No. | Bus No. | R (p.u) | X (p.u) | B/2 (p.u) |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 2 | 0.0192 | 0.0575 | 0.0264 | 15 | 18 | 0.1073 | 0.2185 | 0 |
| 1 | 3 | 0.0452 | 0.1852 | 0.0204 | 18 | 19 | 0.0639 | 0.1292 | 0 |
| 2 | 4 | 0.0570 | 0.1737 | 0.0184 | 19 | 20 | 0.0340 | 0.0680 | 0 |
| 3 | 4 | 0.0132 | 0.0379 | 0.0042 | 10 | 20 | 0.0936 | 0.2090 | 0 |
| 2 | 5 | 0.0472 | 0.1983 | 0.0209 | 10 | 17 | 0.0324 | 0.0845 | 0 |
| 2 | 6 | 0.0581 | 0.1763 | 0.0187 | 10 | 21 | 0.0348 | 0.0749 | 0 |
| 4 | 6 | 0.0119 | 0.0414 | 0.0045 | 10 | 22 | 0.0727 | 0.1499 | 0 |
| 5 | 7 | 0.0460 | 0.1160 | 0.0102 | 21 | 22 | 0.0116 | 0.0236 | 0 |
| 6 | 7 | 0.0267 | 0.0820 | 0.0085 | 15 | 23 | 0.1000 | 0.2020 | 0 |
| 6 | 8 | 0.0120 | 0.0420 | 0.0045 | 22 | 24 | 0.1150 | 0.1790 | 0 |
| 6 | 9 | 0 | 0.2080 | 0 | 23 | 24 | 0.1320 | 0.2700 | 0 |
| 6 | 10 | 0 | 0.5560 | 0 | 24 | 25 | 0.1885 | 0.3292 | 0 |
| 9 | 11 | 0 | 0.2080 | 0 | 25 | 26 | 0.2544 | 0.3800 | 0 |
| 9 | 10 | 0 | 0.1100 | 0 | 25 | 27 | 0.1093 | 0.2087 | 0 |
| 4 | 12 | 0 | 0.2560 | 0 | 28 | 27 | 0 | 0.3960 | 0 |
| 12 | 13 | 0 | 0.1400 | 0 | 27 | 29 | 0.2198 | 0.4153 | 0 |
| 12 | 14 | 0.1231 | 0.2559 | 0 | 27 | 30 | 0.3202 | 0.6027 | 0 |
| 12 | 15 | 0.0662 | 0.1304 | 0 | 29 | 30 | 0.2399 | 0.4533 | 0 |
| 12 | 16 | 0.0945 | 0.1987 | 0 | 8 | 28 | 0.0636 | 0.2000 | 0.0214 |
| 14 | 15 | 0.2210 | 0.1997 | 0 | 6 | 28 | 0.0169 | 0.0599 | 0.0650 |
| 16 | 17 | 0.0824 | 0.1923 | 0 |
| Bus No. | Active Load (p.u) | Reactive Load (p.u) | Bus No. | Active Load (p.u) | Reactive Load (p.u) |
|---|---|---|---|---|---|
| 1 | 0.0000 | 0.0000 | 16 | 0.0350 | 0.0180 |
| 2 | 0.2170 | 0.1270 | 17 | 0.0900 | 0.0580 |
| 3 | 0.0240 | 0.0120 | 18 | 0.0320 | 0.0090 |
| 4 | 0.0760 | 0.0160 | 19 | 0.0950 | 0.0340 |
| 5 | 0.9420 | 0.1900 | 20 | 0.0220 | 0.0070 |
| 6 | 0.0000 | 0.0000 | 21 | 0.1750 | 0.1120 |
| 7 | 0.2280 | 0.1090 | 22 | 0.0000 | 0.0000 |
| 8 | 0.3000 | 0.3000 | 23 | 0.0320 | 0.0160 |
| 9 | 0.0000 | 0.0000 | 24 | 0.0870 | 0.0670 |
| 10 | 0.0580 | 0.0200 | 25 | 0.0000 | 0.0000 |
| 11 | 0.0000 | 0.0000 | 26 | 0.0350 | 0.0230 |
| 12 | 0.1120 | 0.0750 | 27 | 0.0000 | 0.0000 |
| 13 | 0.0000 | 0.0000 | 28 | 0.0000 | 0.0000 |
| 14 | 0.0620 | 0.0160 | 29 | 0.0240 | 0.0090 |
| 15 | 0.0820 | 0.0250 | 30 | 0.1060 | 0.0190 |
References
- Zhao, B.; Guo, C.X.; Cao, Y.J. A multiagent-based particle swarm optimization approach for optimal reactive power dispatch. IEEE Trans. Power Syst. 2005, 20, 1070–1078. [Google Scholar] [CrossRef]
- Agamah, S.; Ekonomou, L. A methodology for web-based power systems simulation and analysis using PHP programming. In Electricity Distribution-Intelligent Solutions for Electricity Transmission and Distribution Networks; Karampelas, P., Ekonomou, L., Eds.; Springer: Berlin, Germany, 2016. [Google Scholar]
- Lakshmi, M.; Ramesh, K.A. Optimal reactive power dispatch using crow search algorithm. Int. J. Electr. Comput. Eng. 2018, 8, 1423. [Google Scholar]
- Sulaiman, M.H.; Mustaffa, Z.; Mohamed, M.R.; Aliman, O. Using the gray wolf optimizer for solving optimal reactive power dispatch problem. Appl. Soft Comput. 2015, 32, 286–292. [Google Scholar] [CrossRef]
- Deeb, N.; Shahidehpour, S.M. Linear reactive power optimization in a large power network using the decomposition approach. IEEE Trans. Power Syst. 1990, 5, 428–438. [Google Scholar] [CrossRef]
- Lee, K.Y.; Park, Y.M.; Ortiz, J.L. A united approach to optimal real and reactive power dispatch. Power Eng. Soc. Gen. Meet. 1985, 104, 1147–1153. [Google Scholar]
- Horton, J.S.; Grigsby, L. Voltage optimization using combined linear programming & gradient techniques. IEEE Trans. Power Syst. 1984, 103, 1637–1643. [Google Scholar]
- Saachdeva, S.; Billington, R. Optimum network VAR planning by non linear programming. IEEE Trans. Power Syst. 1973, 92, 1217–1973. [Google Scholar] [CrossRef]
- Mahadevan, K.; Kannan, P.S. Comprehensive learning particle swarm optimization for reactive power dispatch. Appl. Soft Comput. 2010, 10, 641–652. [Google Scholar] [CrossRef]
- Quintana, V.H.; Santos-Nieto, M. Reactive power dispatch by successive quadratic programming. IEEE Trans. Energy Convers. 1989, 4, 425–435. [Google Scholar] [CrossRef]
- Granville, S. Optimal reactive power dispatch through interior point methods. IEEE Trans. Power Syst. 1994, 4, 136–146. [Google Scholar] [CrossRef]
- Polprasert, J.; Ongsakul, W.; Dieu, V.N. Optimal reactive power dispatch using improved pseudo-gradient search particle swarm optimization. Electr. Power Compon. Syst. 2016, 44, 518–532. [Google Scholar] [CrossRef]
- Abdullah, W.N.W.; Saibon, H.; Zain, A.A.M.; Lo, K.L. Genetic algorithm for optimal reactive power dispatch. In Proceedings of the International Conference on Energy Management and Power Delivery (EMPD), Singapore, 5 March 1998. [Google Scholar]
- Abou El Ela, A.A.; Abido, M.A.; Spea, S.R. Differential evolution algorithm for optimal reactive power dispatch. Electr. Power Syst. Res. 2011, 81, 458–464. [Google Scholar] [CrossRef]
- Biswas, P.P.; Suganthan, P.N.; Mallipeddi, R.; Amaratunga, G.A.J. Optimal power flow solutions using differential evolution algorithm integrated with effective constraint handling techniques. Eng. Appl. Artif. Intell. 2018, 68, 81–100. [Google Scholar] [CrossRef]
- Basu, M. Quasi-oppositional differential evolution for optimal reactive power dispatch. Electr. Power Energy Syst. 2016, 78, 29–40. [Google Scholar] [CrossRef]
- Karthikaikannan, D.; Sundarabalan, C.K. Optimal reactive power dispatch with static VAR compensator using harmony search algorithms. Electron. J. 2017. [Google Scholar] [CrossRef]
- Pulluri, H.; Naresh, R.; Sharma, V. Application of stud krill herd algorithm for solution of optimal power flow problems. Int. Trans. Electr. Energy Syst. 2017, 6, 27. [Google Scholar] [CrossRef]
- Medani, K.B.O.; Sayah, S.; Bekrar, A. Whale optimization algorithm based optimal reactive power dispatch: A case study of the Algerian power system. Electr. Power Syst. Res. 2018, 163, 696–705. [Google Scholar] [CrossRef]
- Shaheen, A.M.; El-Sehiemy, R.A.; Farrag, S.M. Optimal reactive power dispatch using backtracking search algorithm. Aust. J. Electr. Electron. Eng. 2016, 13, 200–210. [Google Scholar] [CrossRef]
- Warid, W.; Hizam, H.; Mariun, N.; Abdul-Wahab, N. Optimal power flow using the jaya algorithm. Energies 2016, 678, 9. [Google Scholar] [CrossRef]
- Mei, R.N.S.; Sulaiman, M.H.; Mustaffa, Z.; Daniyal, H. Optimal reactive power dispatch solution by loss minimization using moth-flame optimization technique. Appl. Soft Comput. 2017, 59, 210–222. [Google Scholar]
- Anbarasan, P.; Jayabarathi, T. Optimal reactive power dispatch problem solved by symbiotic organism search algorithm. In Proceedings of the International Conference on Innovations in Power and Advanced Computing Technologies IEEE, Vellore, India, 21–22 April 2017. [Google Scholar]
- Bhattacharyya, B.; Saurav, R. PSO based bio inspired algorithms for reactive power planning. Int. J. Electr. Power Energy Syst. 2016, 74, 396–402. [Google Scholar] [CrossRef]
- Khaled, U.; Eltamaly, A.M.; Beroual, A. Optimal power flow using particle swarm optimization of renewable hybrid distributed generation. Energies 2017, 10, 1013. [Google Scholar] [CrossRef]
- Shaw, B.; Mukherjee, V.; Ghoshal, S.P. Solution of reactive power dispatch of power systems by an opposition-based gravitational search algorithm. Int. J. Electr. Power Energy Syst. 2014, 55, 29–40. [Google Scholar] [CrossRef]
- Thangaraj, R.; Pant, M.; Abraham, A.; Bouvry, P. Particle swarm optimization: Hybridization perspectives and experimental illustrations. Appl. Math. Comput. 2011, 217, 5208–5226. [Google Scholar] [CrossRef]
- Vlachogiannis, J.G.; Lee, K.Y. A Comparative study on particle swarm optimization for optimal steady-state performance of power systems. IEEE Trans. Power Syst. 2006, 21, 1718–1728. [Google Scholar] [CrossRef]
- Roy, P.K.; Ghoshal, S.P.; Thakur, S.S. Optimal VAR control for improvements in voltage profiles and for real power loss minimization using biogeography based optimization. Int. J. Electr. Power Energy Syst. 2012, 43, 830–838. [Google Scholar] [CrossRef]
- Mallipeddi, R.; Jeyadevi, S.; Suganthan, P.N.; Baskar, S. Efficient constraint handling for optimal reactive power dispatch problems. Swarm Evol. Comput. 2012, 5, 28–36. [Google Scholar] [CrossRef]
- Chuanwen, J.; Bompard, E. A hybrid method of chaotic particle swarm optimization and linear interior for reactive power optimization. Math. Comput. Simul. 2005, 68, 57–65. [Google Scholar] [CrossRef]
- Bhattacharyya, B.; Goswami, S.K.; Bansal, R.C. Hybrid fuzzy particle swarm optimization approach for reactive power optimization. J. Electr. Syst. 2009, 5, 1–15. [Google Scholar]
- Naderi, E.; Narimani, H.; Fathi, M.; Narimani, M.R. A novel fuzzy adaptive configuration of particle swarm optimization to solve large-scale optimal reactive power dispatch. Appl. Soft Comput. 2017, 53, 441–456. [Google Scholar] [CrossRef]
- Li, Y.; Jing, P.; Hu, D.; Zhang, B.; Mao, C.; Ruan, X.; Miao, X.; Chang, D. Optimal reactive power dispatch using particle swarms optimization algorithm based Pareto optimal set. In Advances in Neural Networks-ISNN 2009, Proceedings of the International Symposium on Neural Networks, Wuhan, China, 26–29 May 2009; Springer: Berlin/Heidelberg, Germany, 2009. [Google Scholar]
- Subbaraj, P.; Rajnarayanan, P.N. Hybrid particle swarm optimization based optimal reactive power dispatch. Int. J. Comput. Appl. 2010, 1, 65–70. [Google Scholar] [CrossRef]
- Sayah, S.; Hamouda, A. A hybrid differential evolution algorithm based on particle swarm optimization for nonconvex economic dispatch problems. Appl. Soft Comput. 2013, 13, 1608–1619. [Google Scholar] [CrossRef]
- Mehdinejad, M.; Mohammadi-Ivatloo, B.; Dadashzadeh-Bonab, R.; Zare, K. Solution of optimal reactive power dispatch of power systems using hybrid particle swarm optimization and imperialist competitive algorithms. Int. J. Electr. Power Energy Syst. 2016, 83, 104–116. [Google Scholar] [CrossRef]
- Lenin, K.; Reddy, B.R.; Kalavathi, M.S. Hybrid genetic algorithm and particle swarm optimization (HGAPSO) algorithm for solving optimal reactive power dispatch problem. Int. J. Electron. Electr. Eng. 2013, 1, 262–268. [Google Scholar] [CrossRef]
- Yapıcı, H.; Çetinkaya, N. An improved particle swarm optimization algorithm using eagle strategy for power loss minimization. Math. Probl. Eng. 2017, 2017, 1–11. [Google Scholar] [CrossRef]
- Abido, M.A. Optimal power flow using tabu search algorithm. Electr. Power Compon. Syst. 2002, 30, 469–483. [Google Scholar] [CrossRef]
- Zou, Y. Optimal reactive power planning based on improved tabu search algorithm. In Proceedings of the 2010 International Conference on Electrical and Control Engineering (ICECE), Wuhan, China, 25–27 June 2010. [Google Scholar]
- Shen, Q.; Shi, W.M.; Wei, K. Hybrid particle swarm optimization and tabu search approach for selecting genes for tumor classification using gene expression data. Comput. Biol. Chem. 2008, 32, 53–60. [Google Scholar] [CrossRef] [PubMed]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995. [Google Scholar]
- Eberhart, R.C.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science, Nagoya, Japan, 4–6 October 1995. [Google Scholar]
- Hu, X.; Eberhart, R.C. Solving constrained nonlinear optimization problems with particle swarm optimization. In Proceedings of the Sixth World Multi-conference on Systemics, Cybernetics and Informatics, Orlando, FL, USA, 14–18 July 2002. [Google Scholar]
- Özgür, Y. Penalty function methods for constrained optimization with genetic algorithms. Math. Comput. Appl. 2005, 10, 45–56. [Google Scholar]
- Bouchekara, H.R.E.H.; Abido, M.A.; Boucherma, M. Optimal power flow using Teaching-Learning-Based Optimization technique. Electr. Power Syst. Res. 2014, 114, 49–59. [Google Scholar] [CrossRef]
- Bhattacharya, A.; Chattopadhyay, P.K. Solution of optimal reactive power flow using biogeography-based optimization. Electr. Electron. Sci. Eng. 2010, 3, 269–277. [Google Scholar]
- Glover, F.; Laguna, M. Tabu Search; Kluwer Academic Publishers: Norwell, MA, USA, 1997. [Google Scholar]
- Pothiya, S.; Ngamroo, I.; Kongprawechnon, W. Application of multiple tabu search algorithm to solve dynamic economic dispatch considering generator constraints. Energy Convers. Manag. 2008, 49, 506–516. [Google Scholar] [CrossRef]
- Chelouah, R.; Siarry, P. Enhanced continuous tabu search: An algorithm for the global optimization of multiminima functions. In Metaheuristics Advances and Trends in Local Search Paradigms for Optimization; Kluwer Academic Publishers: Norwell, MA, USA, 1999. [Google Scholar]
- Power Systems Test Case Archive. Available online: www.ee.washington.edu/research/pstca/pf30/pg_tca30bus.htm (accessed on 20 September 2017).


| Parameters | Value |
|---|---|
| Initial inertia weight w | 0.9 and decreased to 0.4 |
| Acceleration factor c1 | 2 |
| Acceleration factor c2 | 2 |
| Maximum number of generations (PSO) | 200 |
| Swarm size | 20 |
| Tabu list length | 7 |
| Number of neighborhood | 3 |
| Radius of neighborhood | 0.1 |
| Maximum number of generations (TS) | 1000 |
| Control Variables | CA | IP-OPF | LPAC | GPAC | BBO | TS | PSO | PSO-TS |
|---|---|---|---|---|---|---|---|---|
| V1 | 1.02282 | 1.10000 | 1.02342 | 1.02942 | 1.1000 | 1.0684 | 1.1000 | 1.0992 |
| V2 | 1.09093 | 1.05414 | 0.99893 | 1.00645 | 1.0943 | 1.0933 | 1.0943 | 1.0948 |
| V5 | 1.03008 | 1.10000 | 0.99469 | 1.01692 | 1.0804 | 1.0893 | 1.1000 | 1.0766 |
| V8 | 0.95000 | 1.03348 | 1.01364 | 1.03952 | 1.0939 | 1.0853 | 1.1000 | 1.0977 |
| V11 | 1.04289 | 1.10000 | 1.01647 | 1.03952 | 1.1000 | 1.0017 | 0.9505 | 1.0837 |
| V13 | 1.03921 | 1.01497 | 1.01101 | 1.04870 | 1.1000 | 1.0780 | 1.1000 | 1.0754 |
| T6–9 | 1.07894 | 0.99334 | 1.04247 | 1.04225 | 1.1000 | 0.9979 | 1.0547 | 0.9257 |
| T6–10 | 0.94276 | 1.05938 | 0.99432 | 0.99417 | 0.9058 | 0.9008 | 1.1000 | 1.0291 |
| T4–12 | 1.00064 | 1.00879 | 1.00061 | 1.00218 | 0.9521 | 1.0337 | 0.9000 | 0.9265 |
| T27–28 | 1.00693 | 0.99712 | 1.00694 | 1.00751 | 0.9638 | 0.9441 | 0.9468 | 0.9422 |
| QSh10 | 0.15232 | 0.15253 | 0.17737 | 0.17267 | 0.2891 | 0.1395 | 0.3000 | 0.2864 |
| QSh24 | 0.06249 | 0.08926 | 0.06172 | 0.06539 | 0.1007 | 0.1838 | 0.0000 | 0.1363 |
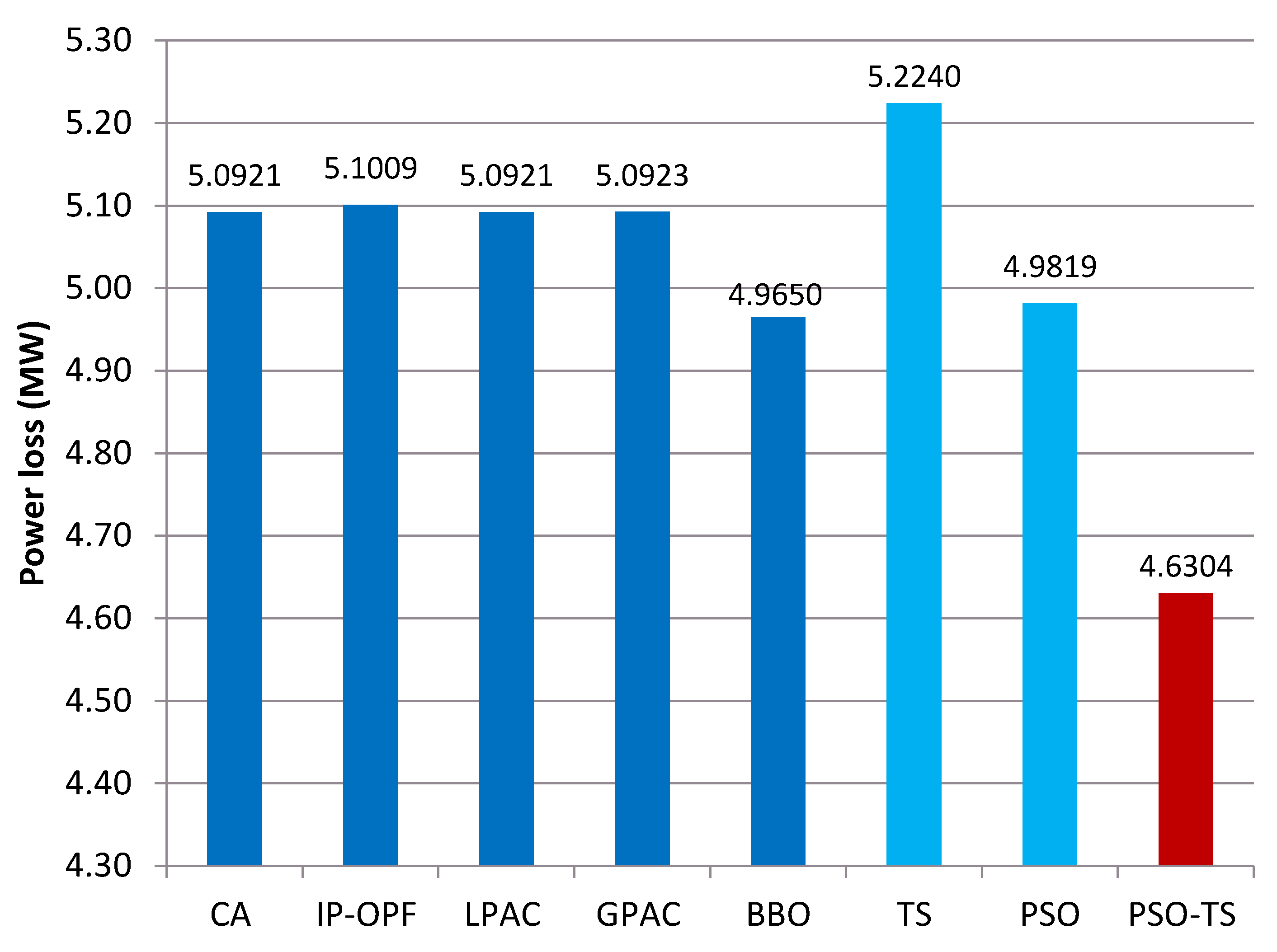
| Ploss (MW) | 5.09209 | 5.10091 | 5.09212 | 5.09226 | 4.9650 | 5.2240 | 4.9819 | 4.6304 |
| Control Variables | CA | IP-OPF | LPAC | GPAC | BBO | TS | PSO | PSO-TS |
|---|---|---|---|---|---|---|---|---|
| V1 | 1.0890 | 1.10000 | 1.03879 | 1.00963 | 1.0033 | 1.0760 | 0.9875 | 1.0014 |
| V2 | 0.9500 | 0.99100 | 1.01776 | 1.00984 | 1.0071 | 1.0494 | 0.9513 | 1.0592 |
| V5 | 1.0860 | 0.96145 | 1.04863 | 1.01000 | 1.0189 | 1.0056 | 1.0641 | 1.0542 |
| V8 | 1.1000 | 0.95986 | 1.04993 | 1.03516 | 1.0148 | 1.0238 | 1.0596 | 1.0133 |
| V11 | 1.0021 | 1.10000 | 0.98373 | 1.03000 | 0.9908 | 1.0085 | 1.0972 | 0.9905 |
| V13 | 1.0279 | 0.95000 | 1.00524 | 1.00274 | 1.0697 | 0.9641 | 1.1000 | 1.0291 |
| T6–9 | 1.0287 | 0.99734 | 1.03054 | 1.02139 | 1.0039 | 0.9486 | 1.0344 | 0.9762 |
| T6–10 | 0.9000 | 1.08595 | 0.91429 | 0.93327 | 0.9000 | 0.9840 | 1.1000 | 1.0163 |
| T4–12 | 0.9929 | 1.00087 | 0.99469 | 0.99338 | 1.0490 | 0.9647 | 0.9000 | 0.9537 |
| T27–28 | 1.0248 | 1.00482 | 1.02078 | 1.02729 | 0.9546 | 1.0287 | 0.9516 | 0.9481 |
| QSh10 | 0.0000 | 0.11072 | 0.00000 | 0.04348 | 0.0924 | 0.0917 | 03000 | 0.2890 |
| QSh24 | 0.0000 | 0.15928 | 0.03586 | 0.00000 | 0.1244 | 0.2278 | 0.0440 | 0.0697 |
| SVD (p.u) | 0.12252 | 0.17328 | 0.12401 | 0.12737 | 0.1194 | 0.1874 | 0.1275 | 0.1113 |
| Control Variables | Initial | DE | CLPSO | BBO | TS | PSO | PSO-TS |
|---|---|---|---|---|---|---|---|
| V1 | 1.0500 | 1.1000 | 1.1000 | 1.1000 | 1.0835 | 1.1000 | 1.1000 |
| V2 | 1.0400 | 1.0931 | 1.1000 | 1.0944 | 1.0567 | 1.1000 | 1.0943 |
| V5 | 1.0100 | 1.0736 | 1.0795 | 1.0749 | 1.0671 | 1.0832 | 1.0749 |
| V8 | 1.0100 | 1.0756 | 1.1000 | 1.0768 | 1.0944 | 1.1000 | 1.0766 |
| V11 | 1.0500 | 1.1000 | 1.1000 | 1.0999 | 0.9873 | 0.9500 | 1.1000 |
| V13 | 1.0500 | 1.1000 | 1.1000 | 1.0999 | 1.0863 | 1.1000 | 1.1000 |
| T6–9 | 1.0780 | 1.0465 | 0.9154 | 1.0435 | 1.0745 | 1.1000 | 0.9744 |
| T6–10 | 1.0690 | 0.9097 | 0.9000 | 0.9011 | 0.9960 | 1.0953 | 1.0510 |
| T4–12 | 1.0320 | 0.9867 | 0.9000 | 0.9824 | 0.9678 | 0.9000 | 0.9000 |
| T27–28 | 1.0680 | 0.9689 | 0.9397 | 0.9691 | 1.0267 | 1.0137 | 0.9635 |
| QSh10 | 0.0000 | 0.0500 | 0.0492 | 0.0499 | 0.0146 | 0.0500 | 0.0500 |
| QSh12 | 0.0000 | 0.0500 | 0.0500 | 0.0498 | 0.0376 | 0.0500 | 0.0500 |
| QSh15 | 0.0000 | 0.0500 | 0.0500 | 0.0499 | 0.0000 | 0.0000 | 0.0500 |
| QSh17 | 0.0000 | 0.0500 | 0.0500 | 0.0499 | 0.0335 | 0.0500 | 0.0500 |
| QSh20 | 0.0000 | 0.0440 | 0.0500 | 0.0499 | 0.0019 | 0.0500 | 0.0386 |
| QSh21 | 0.0000 | 0.0500 | 0.0500 | 0.0499 | 0.0242 | 0.0500 | 0.0500 |
| QSh23 | 0.0000 | 0.0280 | 0.0500 | 0.0387 | 0.0307 | 0.0500 | 0.0500 |
| QSh24 | 0.0000 | 0.0500 | 0.0500 | 0.0498 | 0.0294 | 0.0500 | 0.0500 |
| QSh29 | 0.0000 | 0.0259 | 0.0500 | 0.0290 | 0.0399 | 0.0260 | 0.0213 |
| Ploss (MW) | 5.8322 | 4.5550 | 4.5615 | 4.5511 | 4.9203 | 4.6862 | 4.5213 |
| Control Variables | Initial State | DE | TS | PSO | PSO-TS |
|---|---|---|---|---|---|
| V1 | 1.0500 | 1.0100 | 0.9518 | 0.9898 | 0.9867 |
| V2 | 1.0400 | 0.9918 | 1.0888 | 0.9529 | 0.9910 |
| V5 | 1.0100 | 1.0179 | 1.0502 | 1.0493 | 1.0244 |
| V8 | 1.0100 | 1.0183 | 1.0052 | 0.9988 | 1.0042 |
| V11 | 1.0500 | 1.0114 | 1.0730 | 1.0749 | 1.0106 |
| V13 | 1.0500 | 1.0282 | 1.0637 | 1.0404 | 1.0734 |
| T6–9 | 1.0780 | 1.0265 | 1.0137 | 1.0548 | 1.0725 |
| T6–10 | 1.0690 | 0.9038 | 1.0342 | 1.1000 | 0.9797 |
| T4–12 | 1.0320 | 1.0114 | 0.9993 | 0.9115 | 0.9273 |
| T27–28 | 1.0680 | 0.9635 | 0.9652 | 0.9458 | 0.9607 |
| QSh10 | 0.0000 | 0.0494 | 0.0355 | 0.0500 | 0.0095 |
| QSh12 | 0.0000 | 0.0108 | 0.0419 | 0.0500 | 0.0215 |
| QSh15 | 0.0000 | 0.0499 | 0.0032 | 0.0486 | 0.0226 |
| QSh17 | 0.0000 | 0.0023 | 0.0008 | 0.0500 | 0.0005 |
| QSh20 | 0.0000 | 0.0499 | 0.0491 | 0.0500 | 0.0359 |
| QSh21 | 0.0000 | 0.0490 | 0.0134 | 0.0500 | 0.0401 |
| QSh23 | 0.0000 | 0.0498 | 0.0382 | 0.0500 | 0.0427 |
| QSh24 | 0.0000 | 0.0496 | 0.0426 | 0.0500 | 0.0374 |
| QSh29 | 0.0000 | 0.0223 | 0.0306 | 0.0000 | 0.0210 |
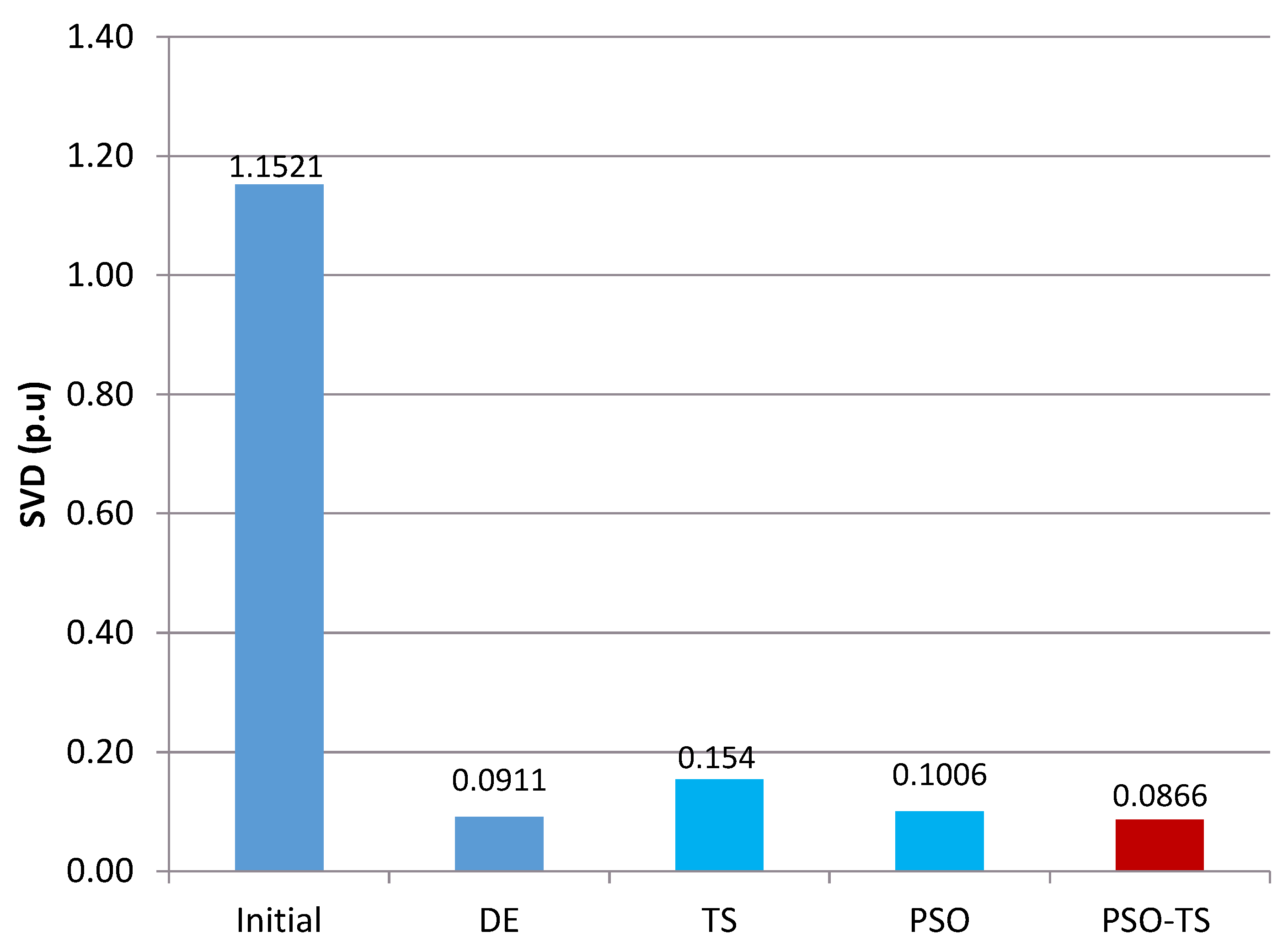
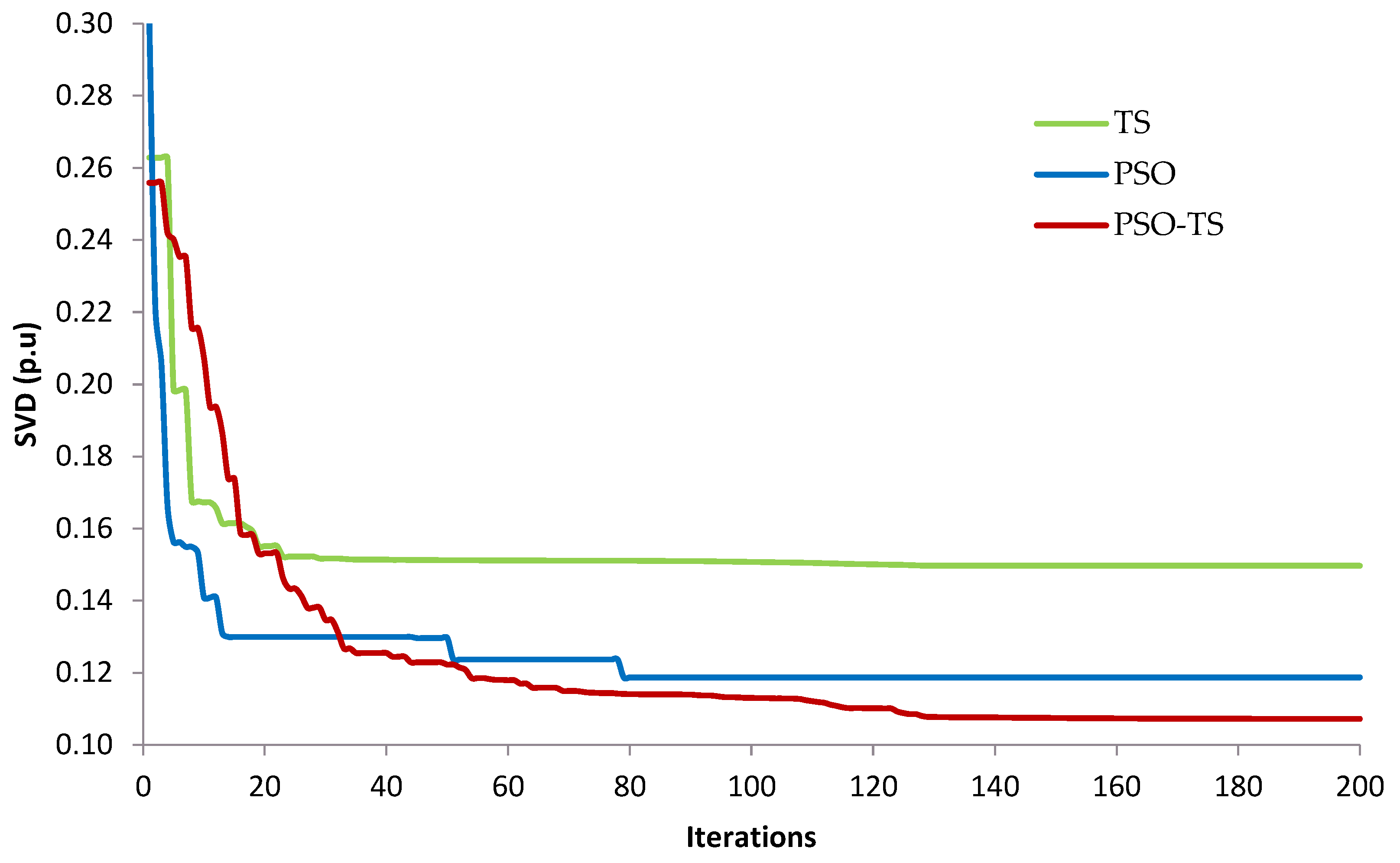
| SVD (p.u) | 1.1521 | 0.0911 | 0.1540 | 0.1006 | 0.0866 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahli, Z.; Hamouda, A.; Bekrar, A.; Trentesaux, D. Reactive Power Dispatch Optimization with Voltage Profile Improvement Using an Efficient Hybrid Algorithm †. Energies 2018, 11, 2134. https://doi.org/10.3390/en11082134
Sahli Z, Hamouda A, Bekrar A, Trentesaux D. Reactive Power Dispatch Optimization with Voltage Profile Improvement Using an Efficient Hybrid Algorithm †. Energies. 2018; 11(8):2134. https://doi.org/10.3390/en11082134
Chicago/Turabian StyleSahli, Zahir, Abdellatif Hamouda, Abdelghani Bekrar, and Damien Trentesaux. 2018. "Reactive Power Dispatch Optimization with Voltage Profile Improvement Using an Efficient Hybrid Algorithm †" Energies 11, no. 8: 2134. https://doi.org/10.3390/en11082134
APA StyleSahli, Z., Hamouda, A., Bekrar, A., & Trentesaux, D. (2018). Reactive Power Dispatch Optimization with Voltage Profile Improvement Using an Efficient Hybrid Algorithm †. Energies, 11(8), 2134. https://doi.org/10.3390/en11082134






