Abstract
By combining together the extended Kalman filter with a newly developed C&I particle swarm optimization algorithm (C&I-PSO), a novel estimation method is proposed for parameter estimation of electromechanical oscillation, in which critical physical constraints on the parameters are taken into account. Based on the extended Kalman filtering algorithm, the constrained parameter estimation problem is formulated via the projection method. Then, by utilizing the penalty function method, the obtained constrained optimization problem could be converted into an equivalent unconstrained optimization problem; finally, the C&I-PSO algorithm is developed to address the unconstrained optimization problem. Therefore, the parameters of electromechanical oscillation with physical constraints can be successfully estimated and better performed. Finally, the effectiveness of the obtained results has been illustrated by several test systems.
1. Introduction
Over the past few decades, there have been a lot of concerns about estimation of electromechanical modes since it can offer a substantial amount of important information about power system stability [1,2,3,4,5]. Therefore, it is necessary to track these parameters in real time to monitor the system stability and prevent blackouts [6,7,8]. In general, electromechanical oscillations are divided into two groups: local and inter-area, which refer to the oscillations between nearby generators and distant generators, respectively [3].
Generally speaking, there are mainly two different methods for the parameters estimation of power system oscillation: one of them is the model-based method, and the other is the measurement-based method. In the model-based method, the governing equations of the studied model are linearized near the present operating point. In contrast, a linear model can be estimated directly from measurement data in the measurement-based method. Therefore, in recent years, for complex modern power systems, the measurement-based method is generally considered easier than the model-based method and is widely used [3,9,10,11,12,13,14,15,16,17]. Normally, two types of measurement data can be obtained by using phasor measurement units (PMUs). One of them is the ambient data, which can be sampled from a power system at a stable operating point [10]; the other one is designed as the ringdown data, which is generated from a power system with a major disturbance. The ringdown data contains key oscillatory information and is the main focus of this paper. In recent years, for ringdown data detection, several methods have been developed. In [11,12], some methods are investigated that are mainly based on frequency estimation and harmonic detection. Furthermore, the matrix pencil method [13], the Kung′s algorithm [14], the rotational invariance technique [15], and the linear prediction methods such as the Prony method [16,17] were proposed and widely utilized for ringdown detection. However, most of the aforementioned approaches cannot be used for real-time application since they are sliding window-based methods, in which the calculations are performed only when a window of data is received [3]. Recently, a novel method for ringdown detection was proposed based on the traditional EKF in [3], where the damping ratio and frequency of ringdown data were modeled in the state vector; then these parameters could be easily estimated by using EKF. However, it should be pointed out that, in the above mentioned results, some critical physical constraints on parameters were ignored; thus, the practical value of the proposed method could be limited.
The Kalman filter is known as an optimal estimator and has been widely used in aerospace, the state estimation of power systems and other fields [18,19,20,21,22,23]. EKF is a famous nonlinear estimator, which is developed by combining the conventional Kalman filter and the linearized technology-based Taylor series expansion. Due to its advantages and convenience, it has been used in many nonlinear state estimation problems. However, in the application of EKF, some known information of the signal is sometimes either ignored or addressed heuristically. For example, the damping ratio and the frequency of oscillation signal are usually meet with the positive constraint condition. In general, for a constrained estimation problem, it is radically difficult within the recursive framework for the traditional EKF to incorporate the constraints into system states. To deal with this problem, many approaches have been developed, such as the projection method, the mean square method [24,25], etc., by which the constrained estimation problem can be successfully converted to the constrained optimization problem after each iteration of EKF [26,27].
The constrained optimization problems are common in many practical applications, such as optimal power flow calculations, allocation problems, and structural optimizations [28]. Until now, various solutions have been developed to address these optimization problems. The most popular method of them is particle swarm optimization (PSO) [29,30,31,32], which has been widely used in many optimization problems. It has the ability to solve difficult optimization problems and converge quickly to a solution [33,34,35,36]. Although the PSO was developed primarily to address unconstrained optimization problems; nevertheless, it performs well when applied to constrained optimization problems. In this case, by adding a penalty term into the objective function, an equivalent unconstrained optimization problem can be obtained; then PSO can be used to address the unconstrained optimization problem. However, in practice, although the traditional PSO algorithm can converge quickly, it is always easy to fall into local optimum [37,38,39,40,41], so the global optimization solutions cannot be obtained easily. Therefore, in this paper, a modified PSO algorithm (namely, C&I-PSO) is developed to address the equivalent unconstrained optimization problem, in which a constrictive factor and a linear decreasing inertia weight (LDIW) are introduced to improve the performance of global searches and local searches [42]. By this method, in the early search stage, a large inertia weight is utilized to extend the search region and avoid the occurrence of premature problems. In the later stage, a small inertia weight is used to obtain a more accurate local search such that a more accurate global optimization solution can be achieved. To the best of the authors’ knowledge, in existing work, there have been little literature that considers parameter estimations of electromechanical oscillation with physical constraints. Based on the above discussion, with the consideration of the physical constraints on parameters, a constrained EKF in combination with C&I-PSO algorithm is proposed in this paper for parameter estimation of the ringdown signal.
The rest of this paper is organized as follows: In Section 2, the state space model for the parameters estimation of ringdown signal is provided. In Section 3, by incorporating the projection method, the traditional EKF with inequality constraints on system states is presented. In Section 4, the C&I-PSO algorithm for the equivalent unconstrained optimization problem is proposed, and the new parameter estimation algorithm is presented. In Section 5, some simulation results are provided to verify the usefulness and effectiveness of the proposed results. Finally, the conclusions are presented in Section 6.
2. State-Space Model of the Ringdown Signal
As stated in [3,7], the ringdown signal can be expressed by the sequence of exponentially damped sinusoids (EDS):
where represents the number of EDSs, is a known constant coefficient, is the damping ratio, represents the frequency, is the initial phase value, the subscript indicates the th component of signal, and is considered a white Gaussian noise sequence with zero mean.
Assume that the signal sampling frequency is . Then the ringdown signal containing multiple EDS signals can be deduced:
Define 4 state variables as [3]:
where the subscript indicates the th component of the signal. Based on Equation (3), the instant state equation of the ringdown signal can be formulated as:
where denotes the system noise and modeling variations, which are usually taken as the zero-mean white noises. The in-phase signal is given by the state variables , is the quadrature signal, represent the frequency to be identified, is the damping factor to be estimated, and the subscript indicates the th component of ringdown signal.
The observation can be obtained by:
where indicates the total number of EDSs, the subscript indicates the th component of the ringdown signal, , and is a white Gaussian noise sequence with zero mean.
Remark 1.
It should be pointed out that most of the monitoring data of electromechanical oscillation in real power systems are stable or positively damped, which means the damping factor is positive, even in some poorly damped cases. Therefore, it is reasonable to assume the damping ratio and frequency are positive under this case. Based on the above discussion, following the idea proposed in [3], the next step of this research is to explore new methods to estimate parameters of electromechanical oscillation by taking into account the physical constraints.
3. Extended Kalman Filter with Inequality Constraints
In this section, the traditional EKF for parameter identification will be introduced in advance. Then, the projection method is utilized to turn the constrained estimation problem into an equivalent constrained optimization problem.
3.1. Traditional Extended Kalman Filter
EKF is usually used for states or the parameters estimation of nonlinear systems, which is developed by combining the conventional Kalman filter and the linearized technology based on Taylor series expansion.
Consider the following nonlinear stochastic system:
where is the system function, is the output function, both of them are nonlinear functions that could be linearized by Taylor series expansion, is the n-dimensional system state, is the input vector, is the state noise process vector denoting disturbances and modeling errors, is the m-dimensional observation vector, and is the measurement noise. Here and are usually considered as the zero-mean Gaussian white noises.
For convenience, the following formulas are defined in advance:
where is the state estimation, is the estimation error covariance matrix, is the state prediction, and is the prediction error covariance matrix, the subscript indicating time instant.
The prediction step:
The filtering step:
where is the Kalman filter gain vector at time instant, and the Jacobian matrices and can be derived by:
and are the covariance matrices of state noise and measurement noise, respectively, and they are usually defined as:
Based on the model of ringdown signal (4) and (5), by using the EKF algorithm, some related equations for estimating parameters of the ringdown signal are obtained:
The function of , and the covariance matrix , can be also obtained:
Remark 2.
In [3], a new method was proposed for ringdown detection, where the traditional EKF method was used to estimate the parameters. However, it should be pointed out that both the frequency and damping ratio of the ringdown signal are usually positive. Thus, the practical value of the method will be inevitably reduced if such state constraints are ignored. In order to obtain a better and more practical estimation algorithm, a new constrained method is proposed to estimate the parameters of the ringdown signal by accounting for the physical constraints.
3.2. The Projection Method
In most cases, it is necessary to specify constraints on parameter values. Therefore, in order to solve the constrained parameter identification problem, the constrained estimation problem can be successfully converted by using the projection method to the equivalent minimum constrained optimization problem at each iteration.
Consider the nonlinear dynamical system (6) with the constraint as follows:
where indicates a known matrix, which has s lines and n columns. s represents the number of constraints, n indicates the number of state variables, usually the rank of is assumed to be s.
By using the projection method, the unconstrained state estimate can be projected onto the constraint surface directly, then the constrained EKF problem is expressed by:
where is a weighting matrix. For simplicity, is chosen as the identify matrix in this paper.
The constrained EKF could be inferred by seeking out an estimation , which satisfies the constraint condition (16) and can be obtained by solving the minimum constrained optimization problem expressed in (17). Therefore, with the projection method, the constrained state estimation problem can be addressed successfully by solving the constrained optimization after each iteration.
4. The C&I Particle Swarm Optimization
In this section, the penalty function method is utilized to change the minimum constrained optimization problem into an equivalent unconstrained optimization problem. Then, the C&I-PSO algorithm is developed to solve the equivalent unconstrained optimization problem.
4.1. The Penalty Function Approach
Due to its simple principle, the penalty function method has been used in many constrained optimization problems; after adding a penalty term, it can be applied to the constrained optimization problem, and an equivalent unconstrained optimization problem can be obtained.
Motivated by the idea proposed in [34], a non-stationary multistage assignment penalty function will be utilized to address the minimum constrained optimization, which can be expressed by:
where represents the minimum constrained objective function expressed in (17). indicates a dynamical modified penalty value, k represents the iteration number of the algorithm, and denotes a penalty factor given by:
where , which is a relative violated function of the constraints, and are the constraints expressed in (17); represents a multi-stage assignment function; is the power of the penalty function.
Based on the above method, the minimum constrained optimization problem expressed in (17) can be turned into an equivalent minimum unconstrained optimization problem, and the unconstrained objective function can be expressed by (18). In order to address this minimum unconstrained optimization problem, the C&I-PSO approach will be introduced in the next part of this paper.
4.2. The C&I-PSO Algorithm
The PSO is one of the most popular swarm intelligence optimization algorithms [29]; its main idea is based simulating simplified social models, such as bird flocking and fish schooling. It begins with an initial population, which is generated in random positions in the search space. Without loss of generality, the -dimensional search space is assumed to be ; the swarm has particles that each having neither weight nor volume and each holding its own position and velocity. These particles update their positions over finite iterations. For the th particle at iteration , the position and velocity vectors are defined as and , respectively. The best historical position visited by particle is taken as a point in , which is denoted as . The best . In the traditional PSO, each particle moves toward the Particle Best and Global Best positions by the specified velocity:
where is a constrictive factor introduced to constrict and control velocities, and is a linear decreasing inertia weight, which can be obtained by:
where represents the inertia weight of initial iteration point, wend indicates the inertia weight of final iteration point, usually chosen as and respectively, is the number of iteration and represents the maximum iteration number.
Remark 3.
It is worth pointing out that, for solving the optimization problem in parameter estimation of electromechanical oscillation, a modified PSO named the C&I-PSO is proposed, in which a constrictive factor and a linearly decreasing inertia weight are introduced to improve the performance of local and global search. By using the proposed C&I-PSO, the premature problem of the traditional PSO can be successfully addressed, and much better solutions to the global optimization problem can be achieved if compared with the traditional PSO. Now we can present the proposed approach for parameter estimation, which is formulated as the following Algorithm 1:
| Algorithm 1: Constrained EKF with C&I-PSO |
| 1: Initialization: Set appropriate values for , , , , , ; |
| 2: for to do |
| 3: Calculate the value of state prediction and prediction error covariance : |
| 4: , ; |
| 5: Compute the Kalman gain matrix at time instant : |
| 6: ; |
| 7: Update the state estimation and estimation error covariance: |
| 8: , ; |
| 9: if then |
| 10: , s.t. ; |
| 11: while do |
| 12: , ; |
| 13: for to do |
| 14: Update , and calculate particle new velocity and position: |
| 15: , |
| 16: , |
| 17: ; |
| 18: end for |
| 19: ; |
| 20: end while |
| 21: ; |
| 22: end if |
| 23: ; |
| 24: end for |
Remark 4.
By using the proposed algorithm, the problem of parameter estimation for the ringdown signal with physical constraints can be solved successfully. It should be noted that not only can the parameters of the ringdown signal be truly identified with physical constraints, but a shorter convergence time can also be expected if compared with the existing results in [3]. Therefore, the proposed algorithm is expected to be much more realistic than the previous work.
5. Simulation Results and Discussions
In this section, three different test systems are provided to demonstrate the performance of the proposed method. The parameters in the penalty function are chosen using the same values as those in [34]. Specifically, the function is set as , other related function values are given by:
In addition, in order to evaluate the whole performance of the proposed approach and conventional EKF method effectively, the root-mean-square deviation (RMSD) used in [43] is adopted:
where is the estimation result of the th corresponding parameter, is the true value of the th corresponding parameter, is the number of parameters, and is the number of time steps.
5.1. Test System 1: Ringdown Signal Composed of One EDS Signal
At first, the ringdown signal in [7] is utilized to evaluate performance of the proposed algorithm. The damping ratio and frequency of this ringdown signal are 0.01 and 1 rad/s, respectively, which is provided by:
The input ringdown signal is shown in Figure 1. By utilizing the Matrix Pencil [13], Prony [17], EKF [3] methods and the proposed algorithm, the damping factor and frequency could be estimated. Figure 2 shows the estimation results, and the RMSD comparison of different approaches is also provided in Figure 3. It can be found that the proposed approach is able to estimate parameters correctly in a short time, while EKF and other methods need a long time to converge to the real values. It follows from these simulation results that, a better convergence and steady state performance could be obtained if compared with those by using EKF, Matrix Pencil and Prony methods.
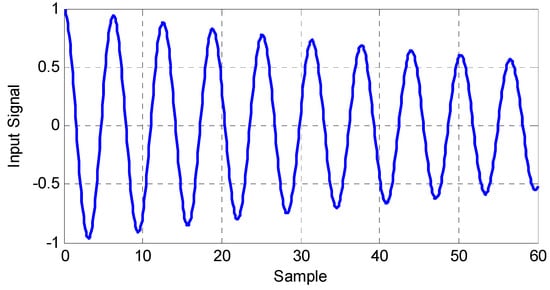
Figure 1.
The input signal of test system 1.
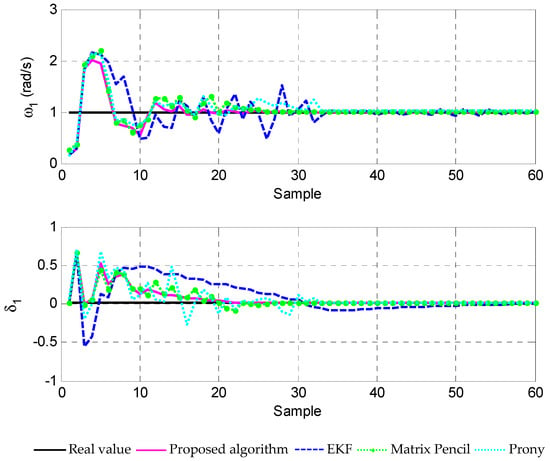
Figure 2.
Estimation of , by using different methods.
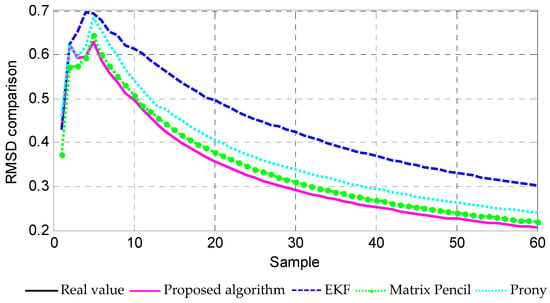
Figure 3.
Comparisons of average estimation errors.
In order further to demonstrate the performance of the proposed algorithm, the final identification results of different methods are also shown in Table 1. It is observed from the results that the proposed method with smallest estimation errors than other approaches in [3,13,17]; which proves that the proposed method can estimate the parameters of ringdown signal accurately.

Table 1.
Identified results of different methods.
5.2. Test System 2: Ringdown Signal Composed of Two EDS Signals
In this case, a ringdown signal consisting of two EDS signals is considered:
where:
and denotes white noise. The input signal is presented in Figure 4. The estimation results of frequency and damping factor by using different methods are shown in Figure 5 and Figure 6. Figure 7 shows the RMSD comparison of the methods. It can be seen from these simulation results that a better convergence and steady state performance could be obtained if compared with those when using other methods in [3,13,17].
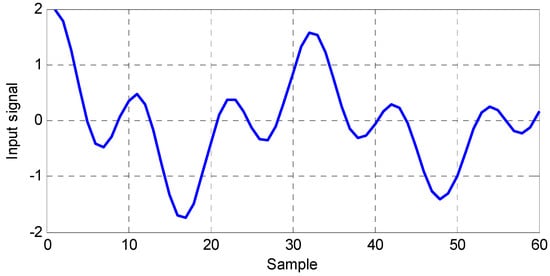
Figure 4.
The input signal of test system 2.
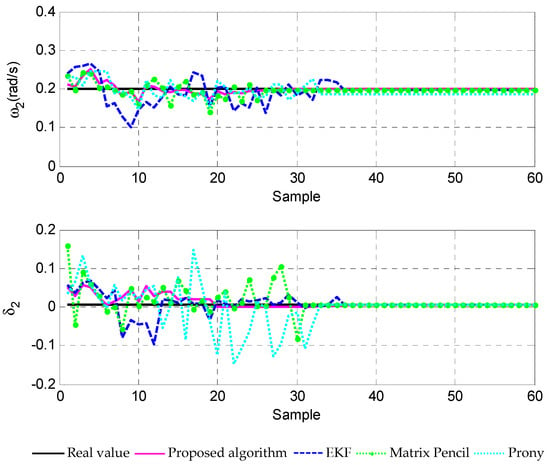
Figure 5.
Estimation of , by using different methods.
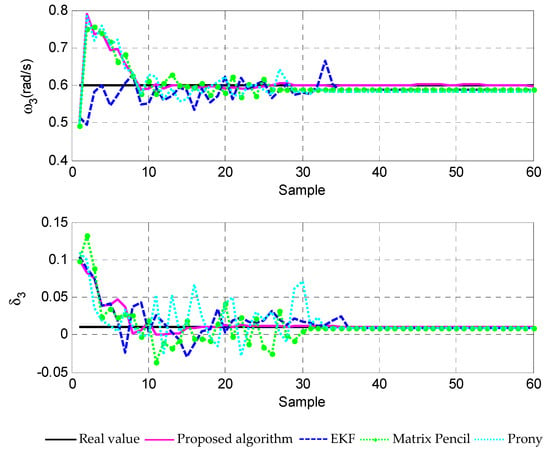
Figure 6.
Estimation of , by using different methods.
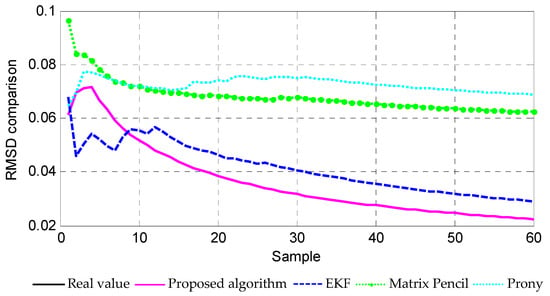
Figure 7.
Comparisons of average estimation errors.
In addition, the final identification results of different methods are also provided in Table 2, which further proves superior performance of the proposed method.

Table 2.
Identified results of different methods.
5.3. Test System 3: WSCC Model
In this case, the WSCC model is taken as the test system [42], which has three generators and nine buses. The network is depicted in Figure 8a. The normal frequency of G2 is 60 HZ, at t = 5.1 s, the load at bus 5 is removed. This disturbance causes an inter-area sustained oscillation in G2 with the frequency of , and the damping factor is . Figure 8b presents the event recorded in the bus frequency signal.
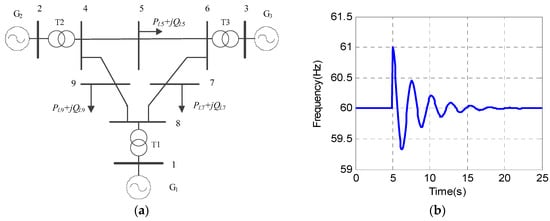
Figure 8.
(a) The model of WSCC power system; (b) The input signal of test system 3.
Figure 9 shows the estimated frequency and damping factor when using the proposed algorithm and other methods. Figure 10 illustrates the RMSD comparison of different methods. It could be found from these simulation results that, in this case, the proposed algorithm can estimate the parameters effectively with better convergence and steady state performance than EKF and other methods. Finally, the final identification results of other methods are also provided in Table 3, which demonstrate the superior performance of the proposed mehthod. Therefore, it can be concluded that the proposed algorithm possesses much more practical value than those shown in previous work.
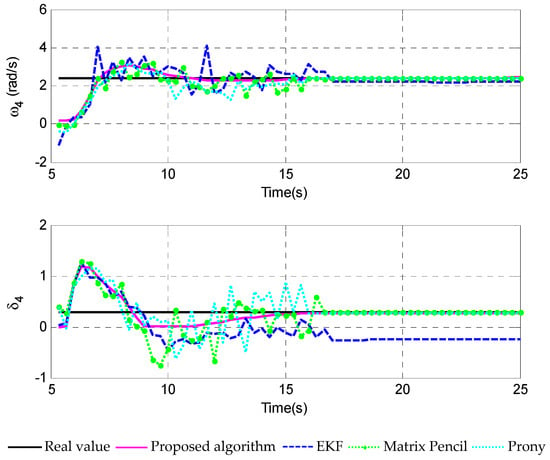
Figure 9.
Estimation of , by using different methods.
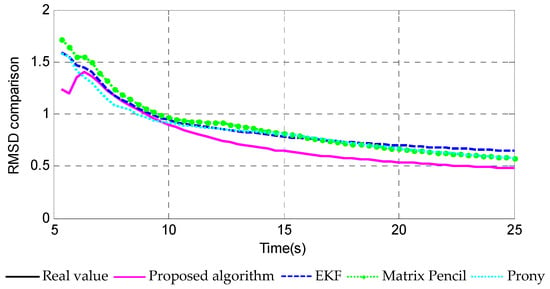
Figure 10.
Comparisons of average estimation errors.

Table 3.
Identified results of different methods.
6. Conclusions
In this paper, with the consideration of the physical constraints on parameters, the constrained parameter estimation problem of ringdown signals has been discussed in detail. Based on the EKF algorithm and the projection method, the constrained estimation problem was converted into a minimum constrained optimization issue. Thus, the constrained optimization issue can be solved successfully by the proposed C&I-PSO with the penalty function method. Finally, the proposed algorithm was successfully applied to estimate the constrained parameters of the ringdown signal. Simulation results have demonstrated in most cases that the proposed algorithm can achieve much better performance and makes more practical sense than using the Matrix Pencil, Prony, and traditional EKF approaches.
Author Contributions
Y.S. performed the experiments and evaluated the data. Y.W. developed the concept, conceived the experiments, and wrote the original manuscript. L.B., Y.H., D.S. and D.P. reviewed and edited the manuscript.
Funding
This work was supported in part by the National Natural Science Foundation of China under Grants 61673161 and 61603122, in part by the Natural Science Foundation of Jiangsu Province of China under GrantBK20161510, in part by the Fundamental Research Funds for the Central Universities of China under Grants 2017B13914 and 2017B655X14, in part by Six Talent Peaks High Level Project of Jiangsu Province under Grant XNY-004, in part by Postgraduate Research & Practice Innovation Program of Jiangsu Province under Grant KYCX17_0484, and in part by the research projects III.17.3.1, III.17.4 of the program of fundamental research of the Siberian Branch of the Russian Academy of Sciences, reg No. AAAA-A17-117030310442-8, No. AAAA-A17-117030310438-1.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Alizadeh, M.; Kojori, S.; Ganjefar, S. A modular neural block to enhance power system stability. IEEE Trans. Power Syst. 2013, 28, 4849–4856. [Google Scholar] [CrossRef]
- Sidorov, D.; Panasetsky, D.; Šmádl, V. Non-Stationary Autoregressive Model for On-Line Detection of Inter-Area Oscillations in Power Systems. In Proceedings of the IEEE PES Innovative Smart Grid Technologies Conference Europe (ISGT Europe), Gothenberg, Sweden, 11–13 October 2010. [Google Scholar]
- Yazdanian, M.; Mehrizi-Sani, A.; Mojiri, M. Estimation of electromechanical oscillation parameters using an extended Kalman filter. IEEE Trans. Power Syst. 2015, 30, 2994–3002. [Google Scholar] [CrossRef]
- Jiang, T.; Yuan, H.; Jia, H.; Zhou, N.; Li, F. Stochastic subspace identification-based approach for tracking inter-area oscillatory modes in bulk power system utilizing synchrophasor measurements. IET Gener. Transm. Distrib. 2015, 9, 2409–2418. [Google Scholar] [CrossRef]
- Wu, F.; Ju, P.; Zhang, X.-P.; Qin, C.; Peng, G.J.; Huang, H.; Fang, J. Modeling, control strategy, and power conditioning for direct-drive wave energy conversion to operate with power grid. Proc. IEEE 2013, 101, 925–941. [Google Scholar] [CrossRef]
- Jiang, T.; Bai, L.; Li, F.; Jia, H.; Hu, Q.; Jin, X. Synchrophasor measurement-based correlation approach for dominant mode identification in bulk power systems. IET Gener. Transm. Distrib. 2016, 10, 2710–2719. [Google Scholar] [CrossRef]
- Yazdanian, M.; Mehrizi-Sani, A.; Mojiri, M. A Novel Approach for Ringdown Detection Using Extended Kalman Filter. In Proceedings of the IECON 2013—39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 10–13 November 2013. [Google Scholar]
- Ju, P.; Handschin, E.; Karlsson, D. Nonlinear dynamic load modelling: Model and parameter estimation. IEEE Trans. Power Syst. 1996, 11, 1689–1697. [Google Scholar] [CrossRef]
- Peng, J.; Nair, N. Enhancing Kalman filter for tracking ringdown electromechanical oscillation. IEEE Trans. Power Syst. 2012, 27, 1042–1050. [Google Scholar] [CrossRef]
- Pierre, J.; Trudnowski, D.; Donnely, M. Initial results in electromechanical mode identification from ambient data. IEEE Trans. Power Syst. 1997, 12, 1245–1251. [Google Scholar] [CrossRef]
- Mojiri, M.; Bakhshai, A. An adaptive notch filter for frequency estimation of a periodic signal. IEEE Trans. Auto. Cont. 2004, 49, 314–318. [Google Scholar] [CrossRef]
- Mojiri, M.; Karimi-Ghartemani, M.; Bakhshai, A. Processing of harmonics and interharmonics using an adaptive notch filter. IEEE Trans. Power Deliv. 2010, 25, 534–542. [Google Scholar] [CrossRef]
- Jain, V. Filter analysis by use of pencil of functions: Part I. IEEE Trans. Circuits Syst. 1974, 21, 574–579. [Google Scholar] [CrossRef]
- Kung, S.Y.; Arun, K.S.; Rao, B. State-space and singular-value decomposition-based approximation methods for the harmonic retrieval problem. J. Opt. Soc. Amer. 1983, 73, 1799–1811. [Google Scholar] [CrossRef]
- Roy, R.; Paulraj, A.; Kailath, T. ESPRIT—A subspace rotation approach to estimation of parameters of cisoids in noise. IEEE Trans. Acoust. Speech Signal Process. 1986, 34, 1340–1342. [Google Scholar] [CrossRef]
- Kumaresan, R.; Tufts, D. Estimating the parameters of exponentially damped sinusoids and pole-zero modeling in noise. IEEE Trans. Acoust. Speech Signal Process. 1982, 30, 833–840. [Google Scholar] [CrossRef]
- Hildebrand, F.B. Introduction to Numerical Analysis, ser. Dover Books on Advanced Mathematics, 2nd ed.; McGraw-Hill: New York, NY, USA, 1956. [Google Scholar]
- Wang, D.; Bao, Y.; Shi, J. Online lithium-ion battery internal resistance measurement application in state-of-charge estimation using the extended Kalman filter. Energies 2017, 10, 1284. [Google Scholar] [CrossRef]
- Xia, B.; Wang, H.; Wang, M.; Sun, W.; Xu, Z.; Lai, Y. A new method for state of charge estimation of lithium-ion battery based on strong tracking cubature Kalman filter. Energies 2015, 8, 13458–13472. [Google Scholar] [CrossRef]
- He, H.; Qin, H.; Sun, X.; Shui, Y. Comparison study on the battery SoC estimation with EKF and UKF algorithms. Energies 2013, 6, 5088–5100. [Google Scholar] [CrossRef]
- Zhang, C.; Jiang, J.; Zhang, W.; Sharkh, S.M. Estimation of state of charge of lithium-ion batteries used in HEV using robust extended Kalman filtering. Energies 2012, 5, 1098–1115. [Google Scholar] [CrossRef]
- Xia, B.; Wang, H.; Tian, Y.; Wang, M.; Sun, W.; Xu, Z. State of charge estimation of lithium-ion batteries using an adaptive cubature Kalman filter. Energies 2015, 8, 5916–5936. [Google Scholar] [CrossRef]
- Li, W.; Wei, G.; Liu, Y. Weighted average consensus-based unscented Kalman filtering. IEEE Trans. Cybern. 2016, 46, 558–567. [Google Scholar] [CrossRef] [PubMed]
- Simon, D.; Chia, T. Kalman filtering with state constraints: A survey of linear and nonlinear algorithms. IET Control Theory Appl. 2010, 4, 1303–1318. [Google Scholar] [CrossRef]
- Simon, D.; Chia, T. Kalman filtering with state equality constraints. IEEE Trans. Aerosp. Electron. Syst. 2002, 38, 128–136. [Google Scholar] [CrossRef]
- Julier, S.; Alveolar, J. On Kalman filtering with nonlinear equality constraints. IEEE Trans. Signal Process. 2007, 55, 2774–2784. [Google Scholar] [CrossRef]
- Massicotte, D.; Morawski, R.; Barwicz, A. Incorporation of a positivity constraint into a Kalman filter based algorithm for correction of spectrometric data. IEEE Trans. Instrum. Meas. 1995, 44, 2–7. [Google Scholar] [CrossRef]
- Li, W.; Jia, Y.; Du, J. Variance-constrained state estimation for nonlinearity coupled complex networks. IEEE Trans. Cybern. 2018, 48, 818–824. [Google Scholar] [CrossRef] [PubMed]
- Mendes, R.; Kennedy, J.; Neves, J. The fully informed particle swarm: Simpler, maybe better. IEEE Trans. Evol. Comput. 2004, 8, 204–210. [Google Scholar] [CrossRef]
- Zhang, Y.; Chiang, H. A novel consensus-based particle swarm optimization-assisted trust-tech methodology for large-scale global optimization. IEEE Trans. Cybern. 2017, 47, 2717–2729. [Google Scholar] [CrossRef] [PubMed]
- Chou, S.; Huang, S. Stochastic set-based particle swarm optimization based on local exploration for solving the carpool service problem. IEEE Trans. Cybern. 2016, 46, 1771–1783. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.; Hsin, W. Weighted fuzzy interpolative reasoning based on the slopes of fuzzy sets and particle swarm optimization techniques. IEEE Trans. Cybern. 2015, 45, 1250–1261. [Google Scholar] [CrossRef] [PubMed]
- Lee, J.; Kim, J.; Song, J.; Kim, Y.; Jung, S. A novel memetic algorithm using modified particle swarm optimization and mesh adaptive direct search for PMSM design. IEEE Trans. Magn. 2016, 52, 1–4. [Google Scholar] [CrossRef]
- Abdelhafiz, A.; Behjat, L.; Ghannouchi, F. Generalized memory polynomial model dimension selection using particle swarm optimization. IEEE Microw. Compon. Lett. 2018, 52, 96–98. [Google Scholar] [CrossRef]
- Ratnaweera, A.; Halgamuge, S.; Watson, H. Self-organizing hierarchical particle swarm optimizer with time-varying acceleration coefficients. IEEE Trans. Evol. Comput. 2004, 8, 240–255. [Google Scholar] [CrossRef]
- Tang, Y.; Wang, Z.; Fang, J. Parameters identification of unknown delayed genetic regulatory networks by a switching particle swarm optimization algorithm. Expert Syst. Appl. 2011, 38, 2523–2535. [Google Scholar] [CrossRef]
- Singh, S.; Singh, B. Optimized passive filter design using modified particle swarm optimization algorithm for a 12-pulse converter-fed LCI synchronous motor drive. IEEE Trans. Ind. Appl. 2014, 50, 2681–2689. [Google Scholar] [CrossRef]
- Ting, T.; Rao, M.; Loo, C. A novel approach for unit commitment problem via an effective hybrid particle swarm optimization. IEEE Trans. Power Syst. 2006, 21, 411–418. [Google Scholar] [CrossRef]
- Pehlivanoglu, Y. A new particle swarm optimization method enhanced with a periodic mutation strategy and neural networks. IEEE Trans. Evol. Comput. 2013, 17, 436–452. [Google Scholar] [CrossRef]
- Selvakumar, A.; Thanushkodi, K. A new particle swarm optimization solution to nonconvex economic dispatch problems. IEEE Trans. Power Syst. 2007, 22, 42–51. [Google Scholar] [CrossRef]
- Park, J.B.; Jeong, Y.W.; Shin, J.R.; Lee, K.Y. An improved particle swarm optimization for nonconvex economic dispatch problems. IEEE Trans. Power Syst. 2010, 25, 156–166. [Google Scholar] [CrossRef]
- Anderson, P.M.; Fouad, A.A. Power System Control and Stability, 2nd ed.; IEEE Press: New York, NY, USA, 2003. [Google Scholar]
- Wang, Y.; Sun, Y.; Wei, Z.; Sun, G. Parameters estimation of electromechanical oscillation with incomplete measurement information. IEEE Trans. Power Syst. 2018. [Google Scholar] [CrossRef]
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).