1. Introduction
Permanent magnet (PM) motors are gaining popularity in electric vehicle (EV) propulsion applications due to features such as high efficiency and high power density [
1]. Of the various topologies of PM motors, stator-PM motors (and their types) have attracted a lot of attention [
2,
3]. The stator-PM doubly salient (SPM-DS) motor, which is a type of stator-PM motor, features special topology with the permanent magnet located in the yoke of the stator. This differs from the PMs that are sandwiched in the stator teeth in stator-PM flux switching (SPM-FS) motors. This feature offers the SPM-DS motor the merit of a simple and robust salient rotor, in addition to effectively realizing heat dissipation and resisting the irreversible risk of demagnetization [
4]. And yet, due to the limited space in the yoke, a relatively small number of permanent magnets are used; torque density is lower than that of the SPM-FS motor, where a large number of permanent magnets are embedded in the stator teeth [
5].
Several hybrid excitation SPM-DS motors have been proposed to improve torque density. By using the additional dc field excitation windings, the enhanced torque can be successfully obtained in a flux-strengthening mode [
6]. However, due to the existence of additional dc excitation winding in the stator, space competition in the limited stator is further intensified. The continuous copper loss in dc field excitation windings also reduces the efficiency of the motor, to some extent. Thus, it usually requires complicated control methods that offer on-line efficiency optimization to improve motor performance [
7].
Researchers have recently switched to alternative double-stator motors in order to further improve the torque density of PM motors. In [
8,
9], several double-stator permanent magnet synchronous motors (PMSMs) are proposed. By adopting serial or parallel magnetic circuits in the internal and external motors, the total PM density can be significantly enhanced, while also improving motor efficiency [
10]. However, since the PMs are located in the middle rotor, the problem of heat dissipation and the corresponding irreversible risk of demagnetization in PMSMs needs to be comprehensively investigated. Besides, in general, current research mainly is biased towards different double-stator PM topologies rather than systematic optimization [
11]. Thus, it is still a challenge to design a reasonable double-stator PM motor through an optimization design method, which will not only enhance the torque density of the motor, but also improve the comprehensive performances of motors (electromagnetic performances, mechanical stress, and temperature rise).
The main purpose of this paper is to design and optimize a new double stator-PM double salient (DS-PMDS) motor, where two stators, two armature windings and a shared middle rotor form the inner and outer motors. For the proposed motor, since there are many flexible modes to control the two separated armature windings, it can operate in a variety of modes to meet the requirements of frequent acceleration, climbing with heavy load and high-speed cruising, which are essential for EVs. Due to the relatively complicated topology of the proposed DS-PMDS motor, the number of design objectives, design variables and constraints will become relatively large. In addition, the corresponding optimization process is often accompanied by a high-dimensional optimization problem. Thus, the conventional single optimization approach can no longer be directly suitable to the proposed multi-objective optimization.
To investigate the proposed motor effectively and comprehensively, a multi-objective optimization strategy is proposed in this paper, where output torque, torque ripple and efficiency are selected according to the potential application field. Meanwhile, a multi-physics analysis is implemented to verify the validity of the motor topology and the proposed optimization method. First, the motor configuration and operating principle of the proposed DS-PMDS motor are introduced in
Section 2. Multi-objective optimization is then performed to improve torque output, reduce torque ripple, increase the PM material utilization ratio, and improve motor efficiency (
Section 3). After the multi-objective comprehensive function is established, the sensitivity of each design parameter is effectively evaluated and optimal structure design parameters are determined. Performances analysis of the DS-PMDS motor is carried out in
Section 4, where multi-physical field analysis is obtained successfully, including the study of mechanical stress, deformation of the middle rotor, and temperature distribution of the proposed motor. Finally, conclusions are drawn in
Section 5.
2. Motor Structure and Operating Principle
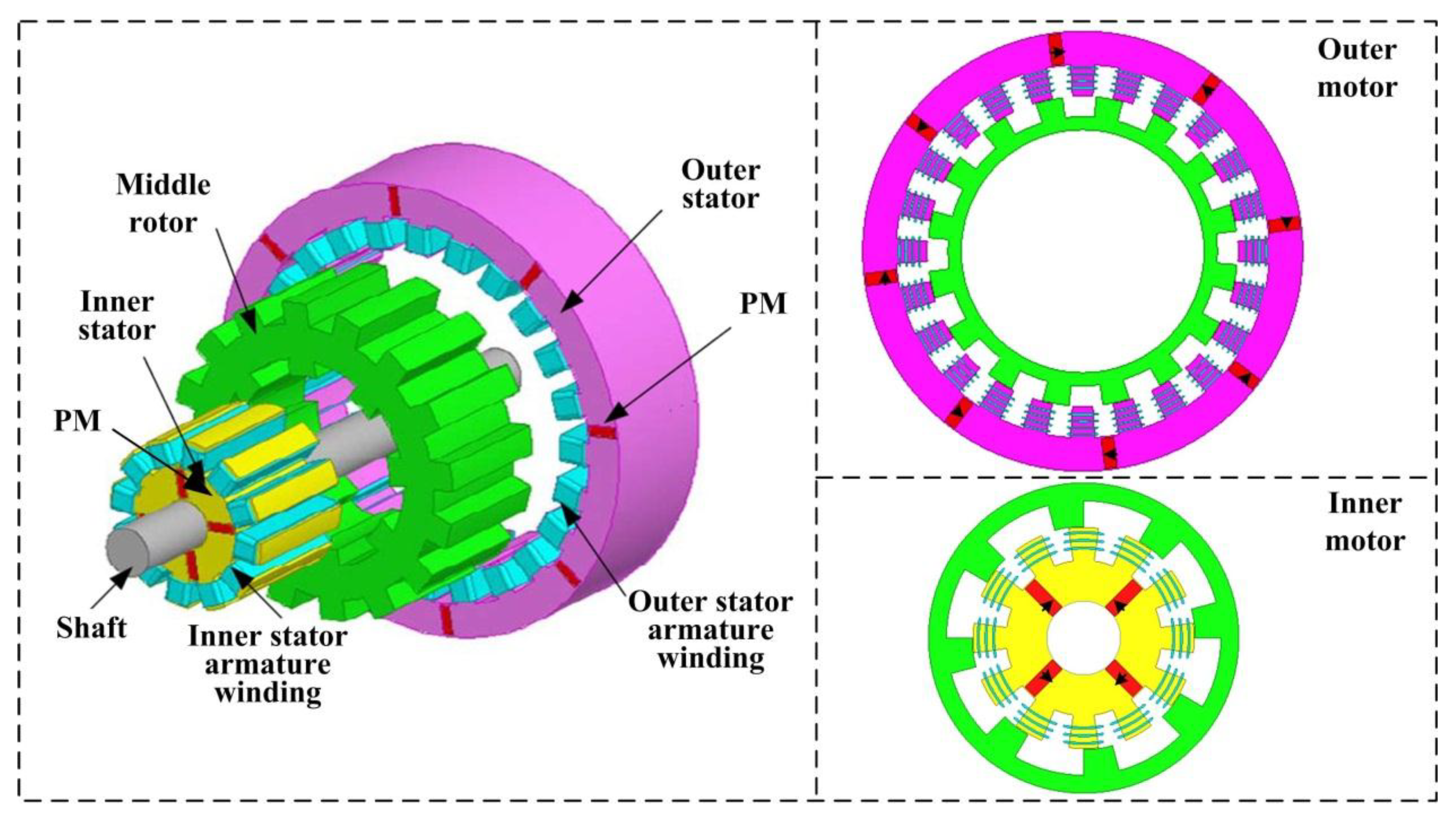
Figure 1 depicts the topology of the DS-PMDS motor, where three parts of the outer stator, middle rotor and inner stator are involved. First, as shown in the figure, the two stators and the middle rotor make up the salient pole structure. The middle rotor is sandwiched by the outer and inner stator. The winding housed in the outer stator couples with the middle rotor, comprising a 24-slot/16-pole outer motor. Meanwhile, a 12-slot/8-pole inner motor is formed through the middle rotor and the inner stator. Since there are neither permanent magnets nor windings in the middle rotor, it results in a simple and reliable rotor structure, which is similar to that of the stator permanent magnet motor. Furthermore, the yoke of both stators contains tangential magnetized permanent magnets. The armature windings in both stators are non-overlapping concentrated windings, which can lead to the reduction of copper loss and a relatively higher efficiency. Finally, it is evident that the internal space of the machine is efficiently used by adding the inner stator, which offers the possibility to improve power and torque levels.
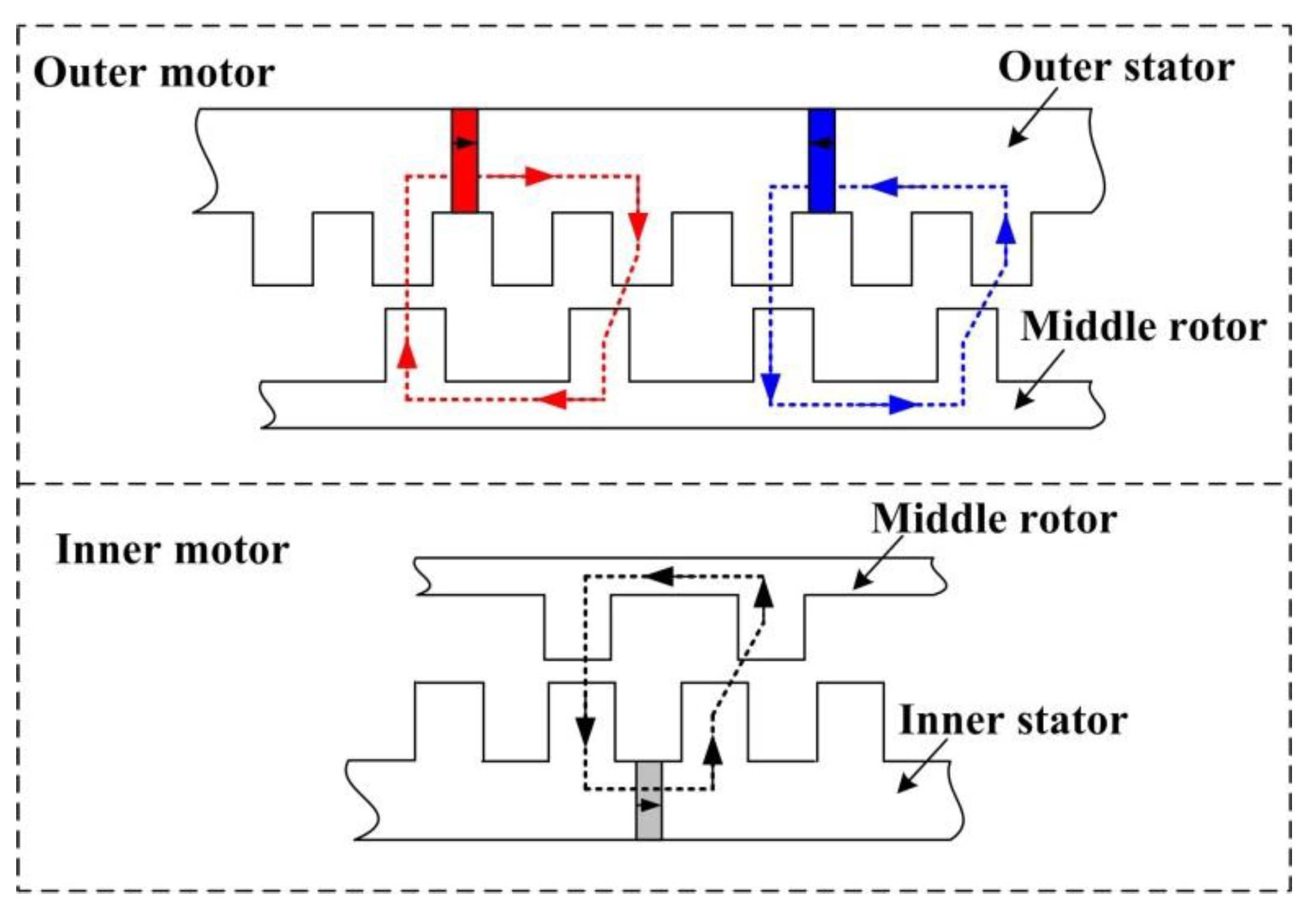
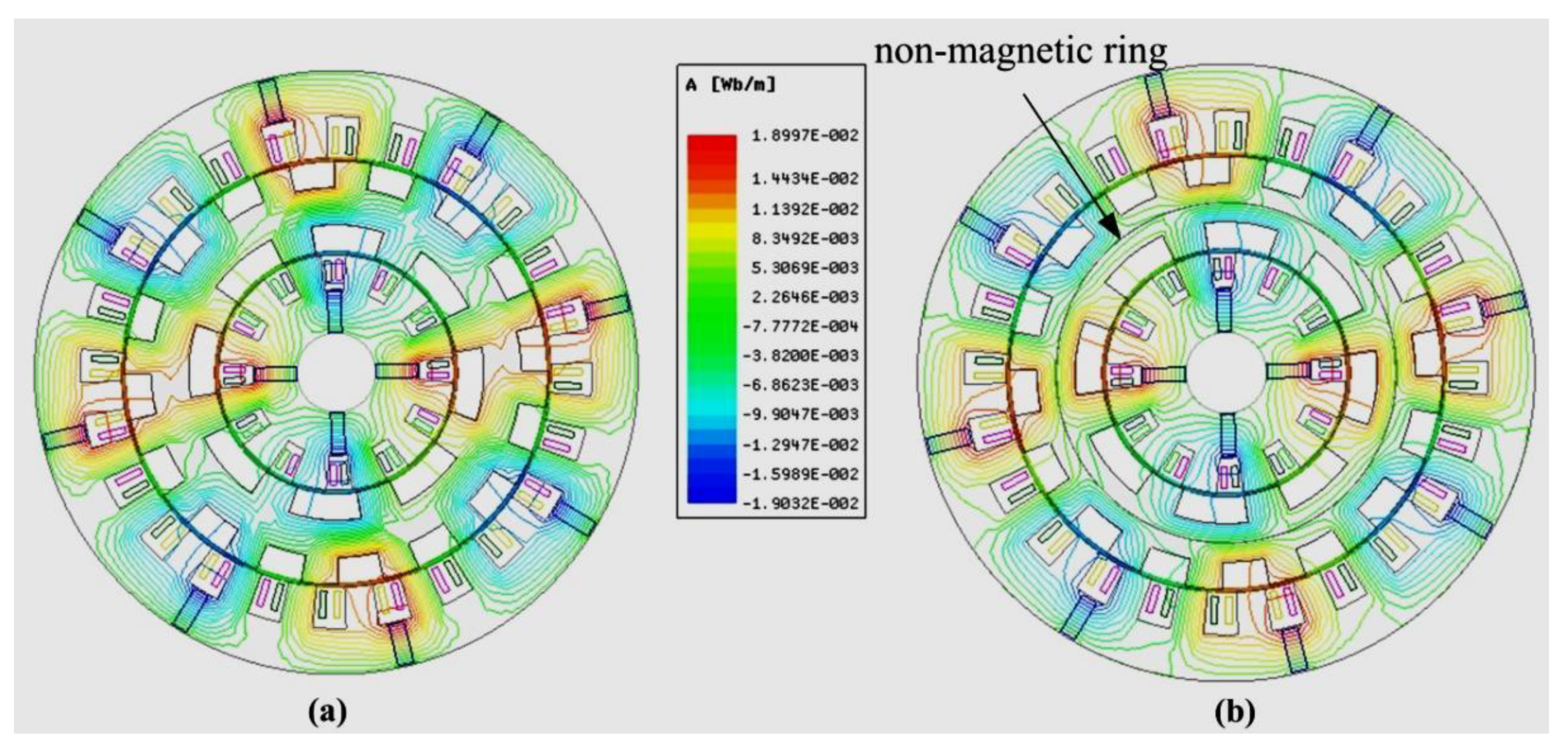
Figure 2 shows the operating principle of the DS-PMDS motor, in which the magnetic field distribution follows the principle of minimum magnetic resistance [
12]. To reduce the electromagnetic coupling degree of the inner and outer motors, a non-magnetic ring is added to the middle rotor. Consequently, the magnetic circuit of the inner motor and the outer motor is parallel with low magnetic coupling degree, which makes control of the inner and outer motors more flexible and offers flexible switching between multiple driving modes of the DS-PMDS motor.
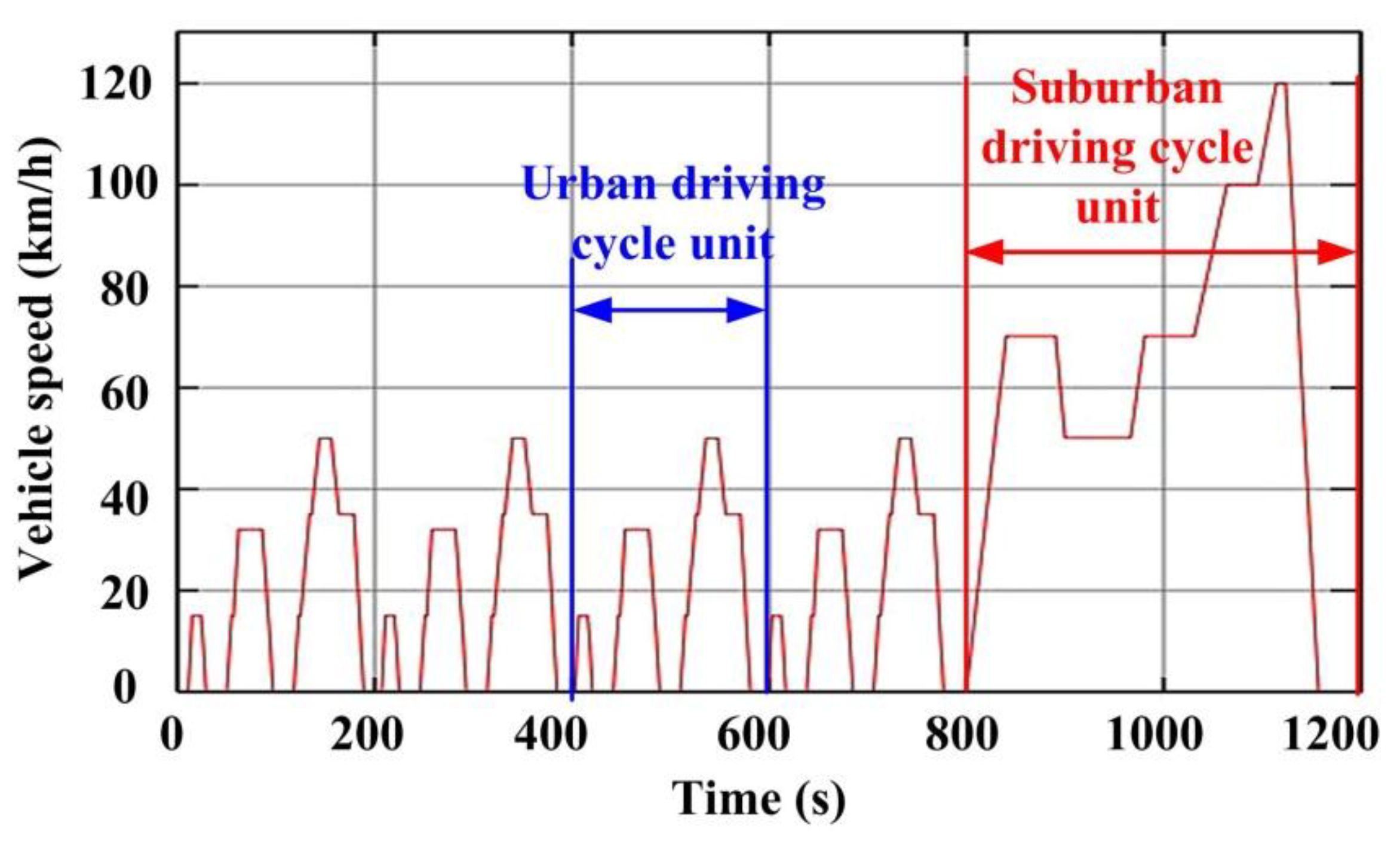
Generally, the driving cycles of vehicles are complex and changeable in actual road conditions. As shown in
Figure 3, the new European driving cycle (NEDC) contains several typical driving cycle units [
13]. These driving conditions includes frequent start and stop, normal and high-speed cruise, acceleration and deceleration, and climbing with heavy load. Hence, multi-operating modes are required for the EV traction motor to meet the various requirements of driving cycle conditions. Owing to the two sets of armature windings, the proposed DS-PMDS motor has a variety of operating modes and can be flexibly switched to suit different working conditions.
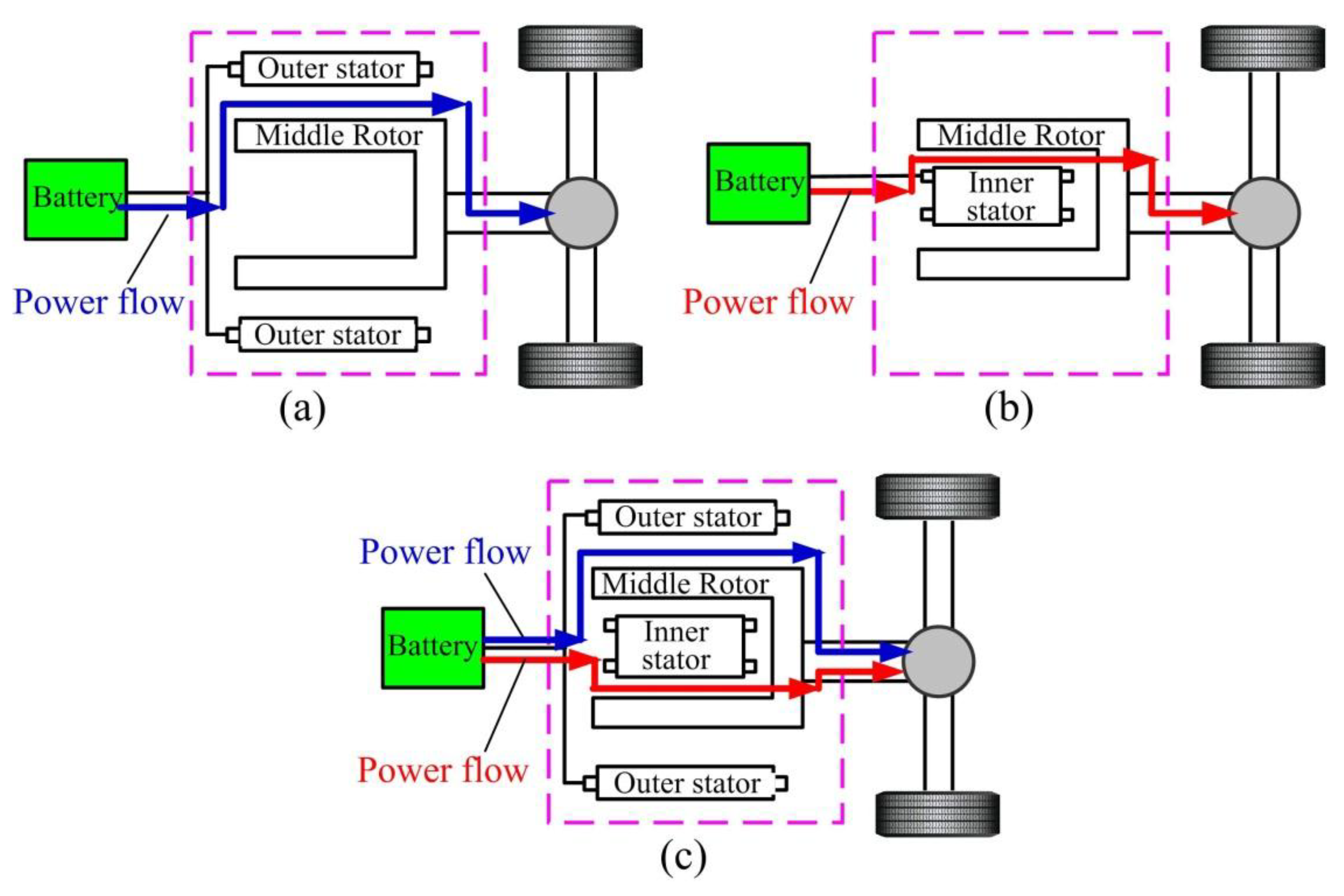
Figure 4 illustrates the corresponding powertrain, based on the DS-PMDS motor in EVs [
14].
Using two sets of windings and converters, power transmission is realized from the battery to the inner and outer motors. Both motors then drive the middle rotor, which is connected to the final driveline. Based on the law of electromechanical energy conversion, the output torque of the DS-PMDS motor can be further expressed as:
where
Toutput is the total output torque of the DS-PMDS motor.
Tload is the vehicle load torque, which varies with driving conditions.
J is the total moment of inertia of the DS-PMDS motor.
ω (rad/s) and
n (
rpm) are rotation angular velocity and speed of the motor, respectively.
G is the weight of the middle rotor.
D is the outer diameter of the intermediate rotor.
Tinner and
Touter are torque of inner motor and outer motor.
iinner and
iouter are phase current of inner and outer motor. The coefficients
k1 and
k2 are functions of the phase current of the inner and outer motors, respectively. Therefore, according to different requirements of load torque, the drive mode of the DS-PMDS motor can be flexibly switched by controlling the current of the two sets of windings.
For the DS-PMDS motor to satisfy different driving cycle conditions, the control coefficients
k1 and
k2 are adjusted accordingly to switch the operating mode of the motor; this is listed in
Table 1 in detail. When the vehicle is in normal cruise or deceleration driving cycle, the power required is relatively low. Consequently, the independent drive mode of the inner motor with 0 ≤
k1 ≤ 1,
k2 = 0 can be adopted to meet the required driving power. When the EV is in high-speed cruise, the low torque output of the inner motor cannot meet driving requirements. Thus, to obtain the desired speed and torque output, the outer motor drive mode is adopted with 0 ≤
k2 ≤ 1,
k1 = 0. For climbing, starting and acceleration, the demand for power and torque is further enhanced. At this point, the dual drive mode is required to obtain higher output power and torque.
3. Multi-Objective Design Optimization
For the proposed DS-PMDS motor, due to its complex configuration with a large number of design variables, the conventional optimal design method that often uses discrete parameter scanning for single objective cannot be effectively applied. Besides, based on the above analysis, the proposed operating modes make the multi-objective optimization design of the motor more complicated. To achieve higher PM material utilization ratio and motor efficiency, higher torque output with lower torque ripple, an effective multi-objective optimization strategy is implemented and introduced in detail in this paper [
15,
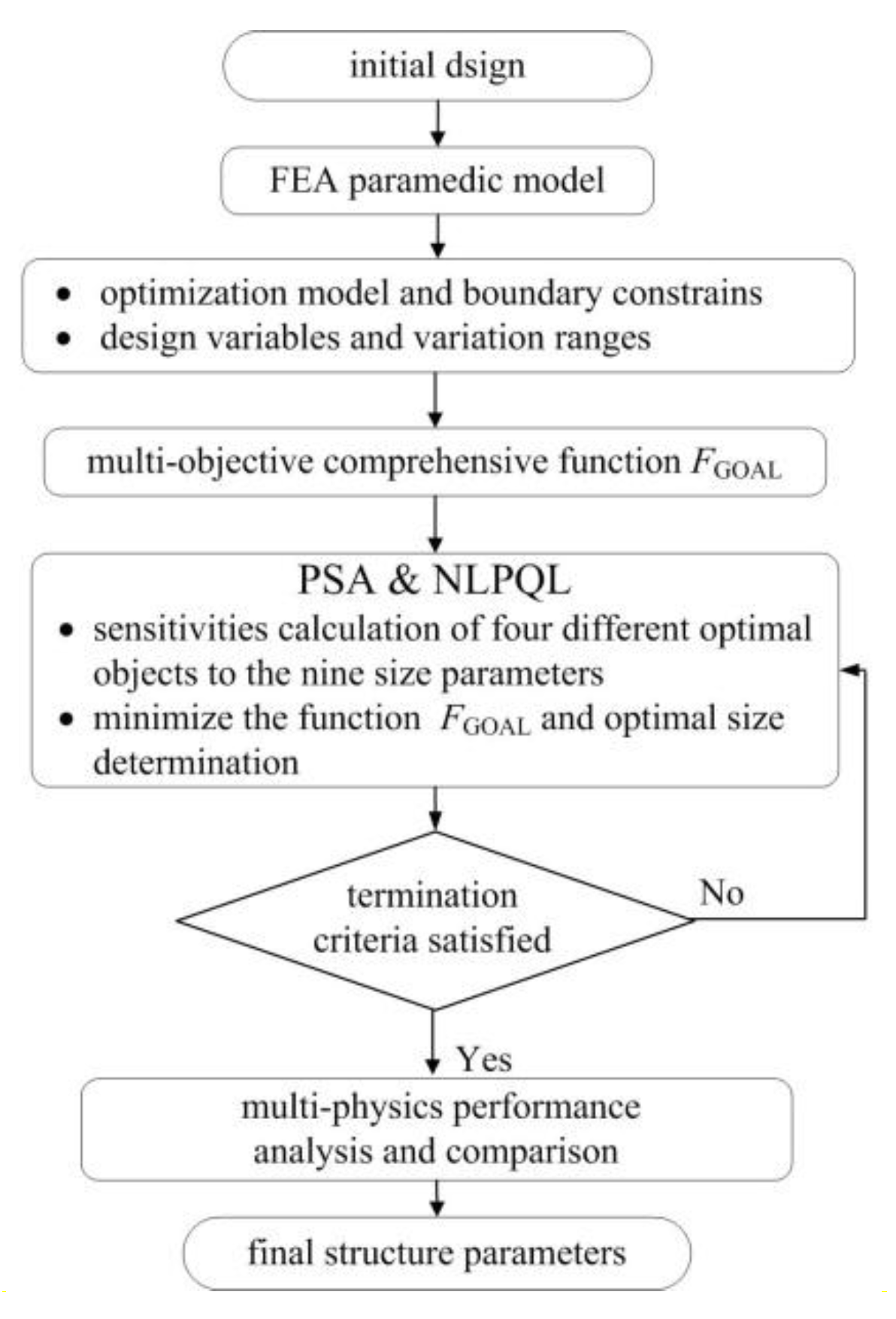
16]. A multi-objective comprehensive function in design strategy is established. Then, by adopting parametric sensitivity analysis (PSA) and the sequential quadratic programming (NLPQL) method, the influence extent of each design parameter for different design objectives is effectively evaluated and the optimal results are determined. The flow diagram of the proposed optimal design is shown in
Figure 5.
3.1. Optimization Model
As the DS-PMDS motor has a double-salient structure, low cogging torque needs to be first considered. In addition, as a traction motor, high torque output is the preferable design requirement to meet the vehicle’s multiple operation conditions of acceleration, deceleration and overload climbing conditions. Moreover, the performances of high PM material utilization ratio and motor efficiency are also required to be satisfied. Consequently, the optimization model of DS-PMDS motor can be presented as:
According to the potential application area in EVs, the added boundary constraints are given as design examples:
where,
Tm is average output torque,
Tri is torque ripple,
δPM is PM material utilization ratio (which is defined as the ratio of output torque to PM volume),
η is motor efficiency,
xi is the vector of the optimization parameters, which can be written as:
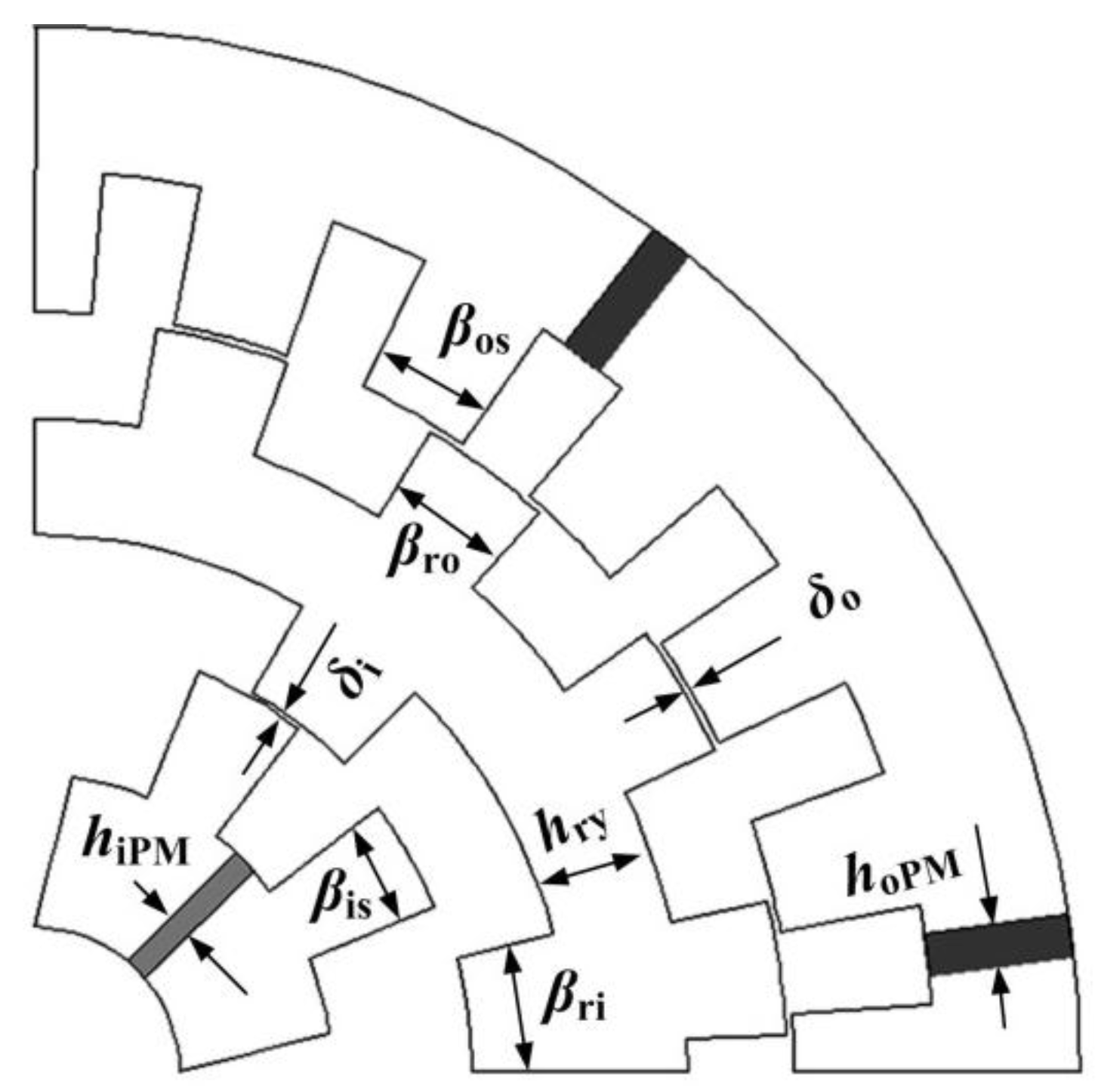
Figure 6 shows the selected nine design variables, which are several in number owing to the structure of a double-stator. The main dimensions are: magnetic thickness of the PM in outer stator
hoPM and magnetic thickness of PM in inner stator
hiPM.
δo and
δi are outer and inner air gaps, respectively.
βis,
βos,
βro and
βri is the tooth width of the inner stator, outer stator and middle rotor.
hry is the middle rotor yoke height. In order to simplify the multi-objective optimization calculation and consider feasibility of manufacturing, the constraint ranges of these parameters are listed in
Table 2.
3.2. Multi-Objective Comprehensive Function
From the above, there are several goals in the optimization model of the DS-PMDS motor. To reduce the conflict of multiple targets, we simplify the complication of trade-off analysis and improve the multi-objective optimization efficiency; the comprehensive objective function of the DS-PMDS motor is built as follows:
where,
T′
ri,
T′
m,
η′ and
δPM′ are the initial values of the torque ripple, output torque, efficiency and PM material utilization ratio, respectively;
Tri(
xi),
Tm(
xi),
η(
xi) and
δPM(
xi) are the functions of the design variables of
xi;
λ1,
λ2,
λ3 and
λ4 are the four weight coefficients that need to meet the relationship of
λ1 +
λ2 +
λ3 +
λ4 = 1 and here the values are 0.3, 0.3, 0.2 and 0.2 separately.
3.3. Parameters Sensitivity Analysis and Multi-Objective Optimization
After the comprehensive objective function is proposed in Equation (6), the multi-objective optimization with tradeoff analysis is implemented, where high-dimension calculation and a time-consuming optimization process is involved. To simplify the multi-objective optimization of the proposed complex motor, the PSA approach is used, integrating multiple optimization targets to obtain a global optimal solution, intuitively and efficiently. Besides, in this way, the sensitivity of each parameter to various optimal goals can also be identified and the key size parameters can be easily selected to improve the efficiency of further optimization and adjustment.
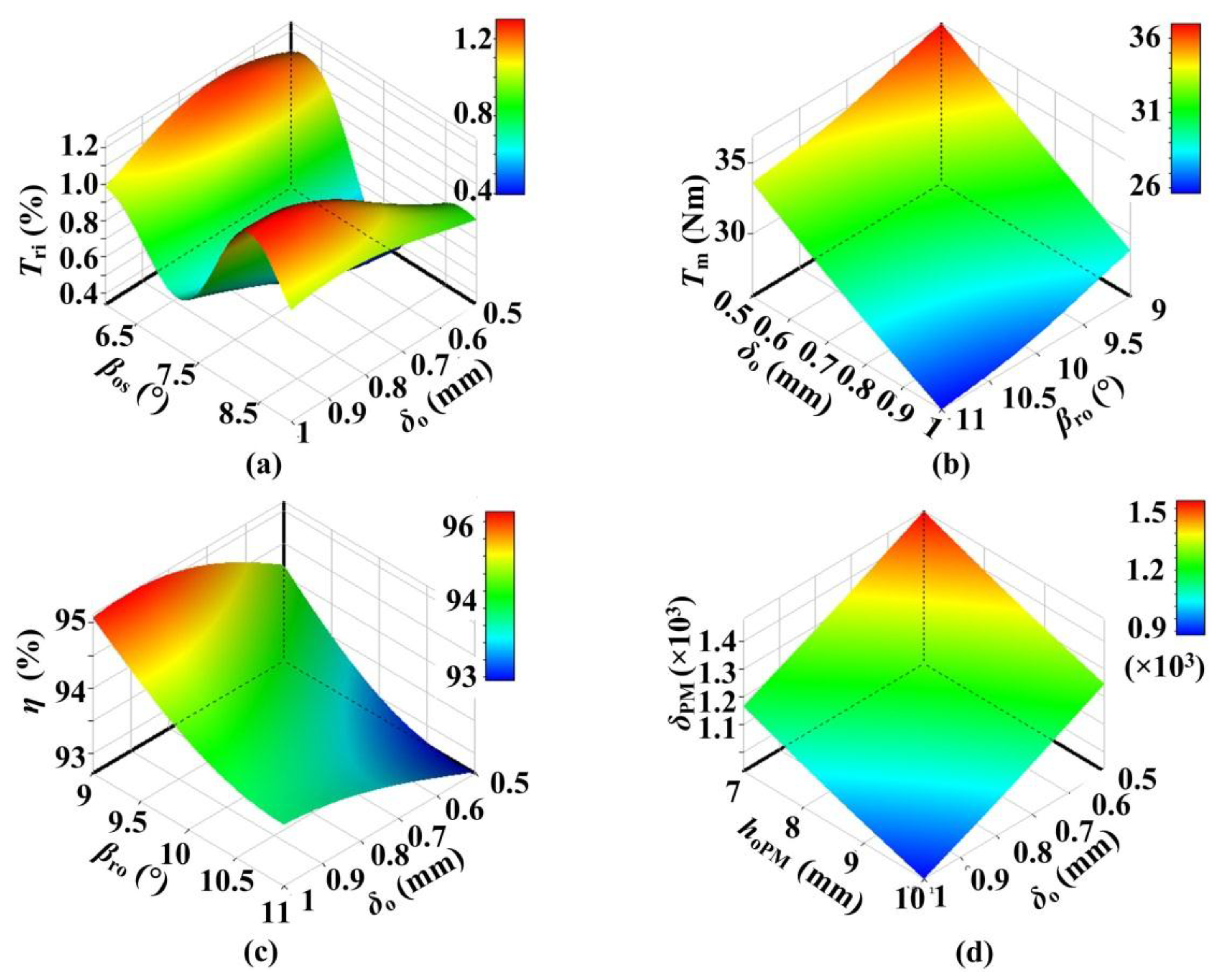
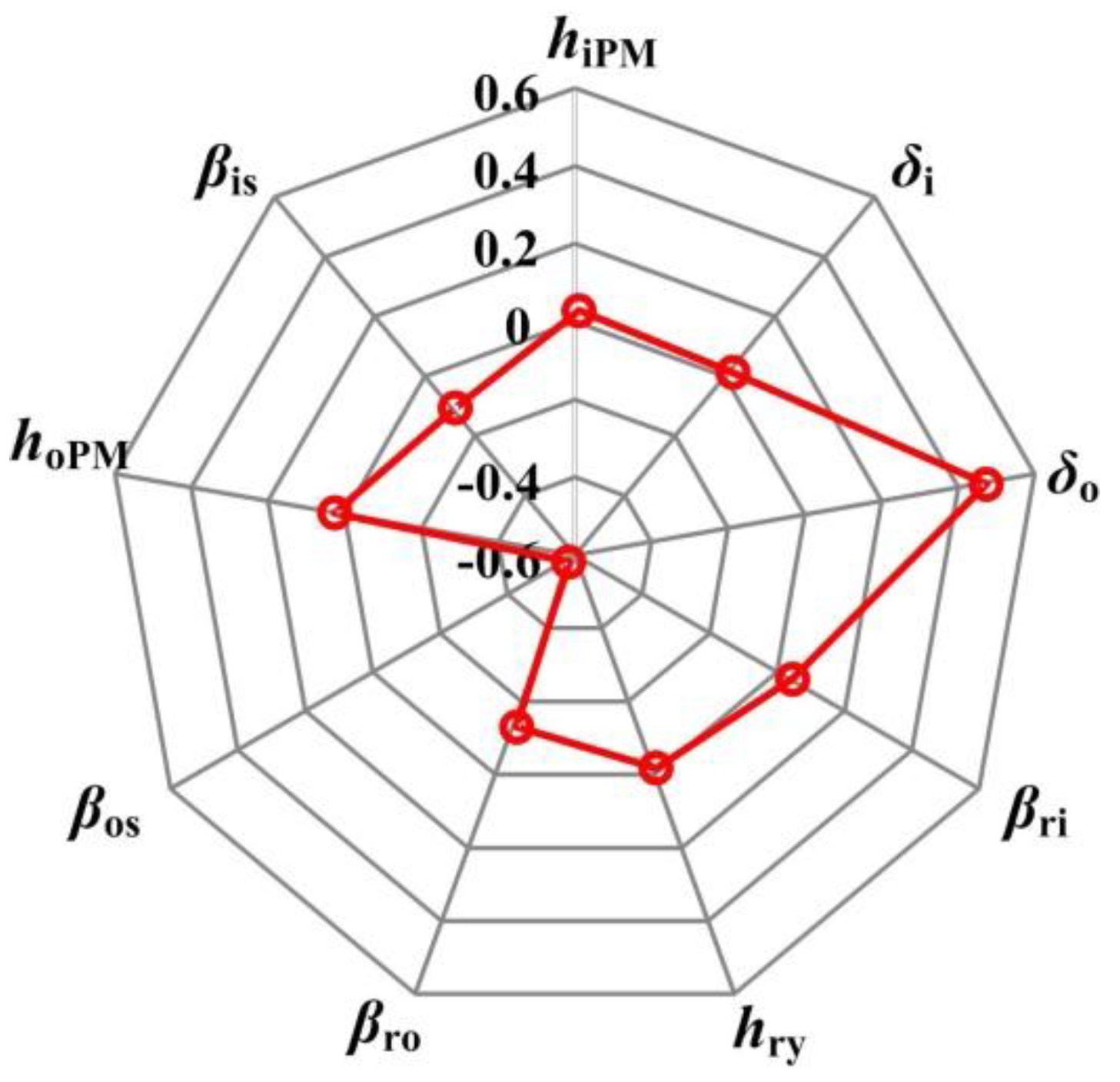
Figure 7 shows the sensitivities of four optimal objects to the nine design variables, taking into consideration the interaction among the different design parameters. Several conflicts exist among the four design objectives. The most critical design parameters affecting
Tri,
Tm,
η and
δPM are the outer stator tooth width
βos, the outer air gap
δo, the outer tooth width of middle rotor
βro, and the magnetized thickness of PM in outer stator
hoPM. The three-dimensional response surface between four targets and nine chosen design parameters can be also obtained; the four typical ones are shown in
Figure 8. The above two figures show that the high sensitivity parameters are different for various application requirements and optimization targets, and different key parameters can be conveniently chosen to further optimization and adjustment.
Based on the defined multi-objective comprehensive function
FGOAL in Equation (6)
, Figure 9 shows the effects of nine design parameters on comprehensive objective function
FGOAL. In addition, as shown in
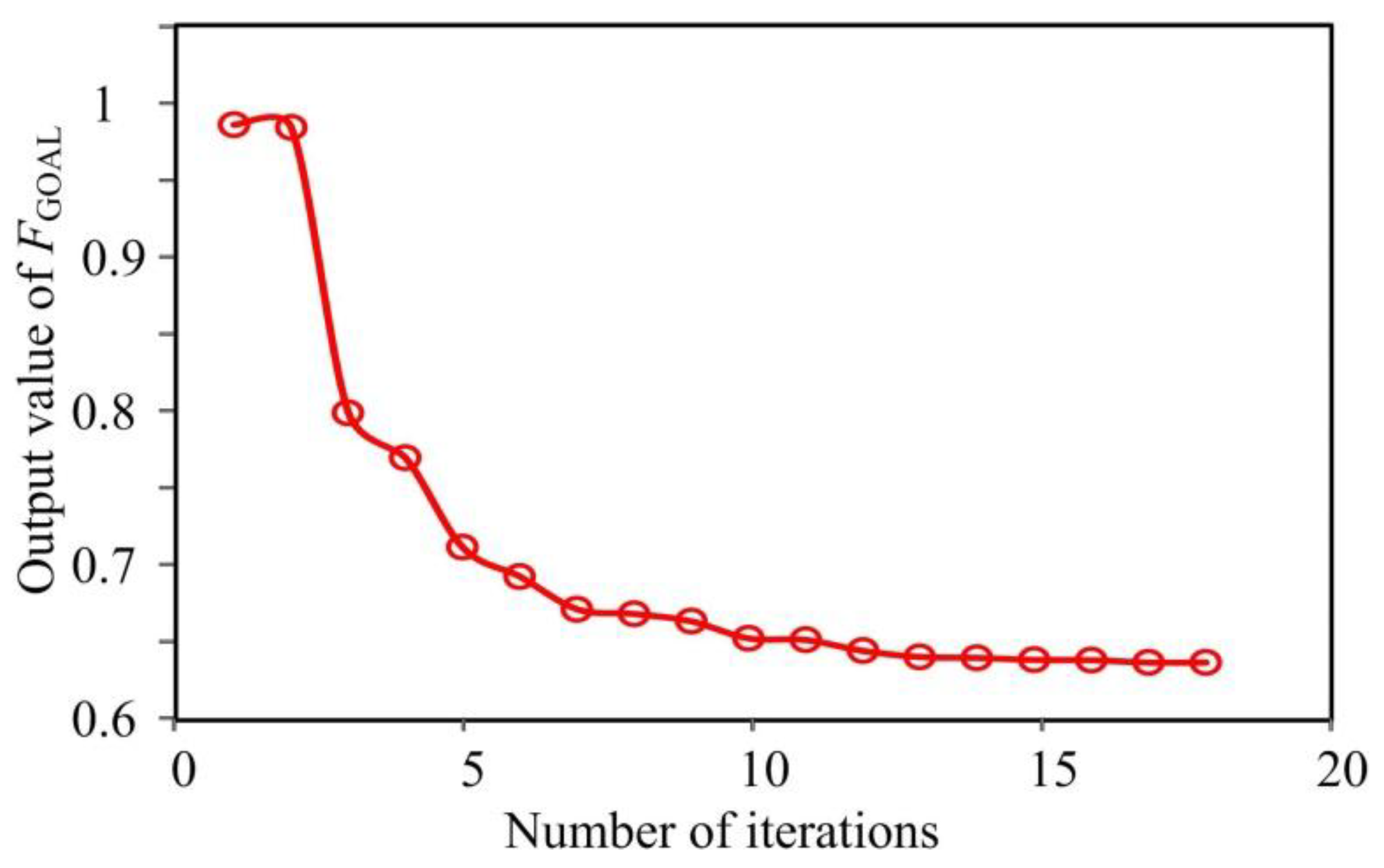
Figure 10, based on the NLPQL approach, after 17 generations of iterative optimization, the optimal solution for the comprehensive objective function
FGOAL can be efficiently achieved. An optimal tradeoff can be obtained for engineering practice, based on comprehensive objective function and special boundary conditions. The corresponding optimal results of
FGOAL, the four optimization targets, and nine design parameters are listed in
Table 3.
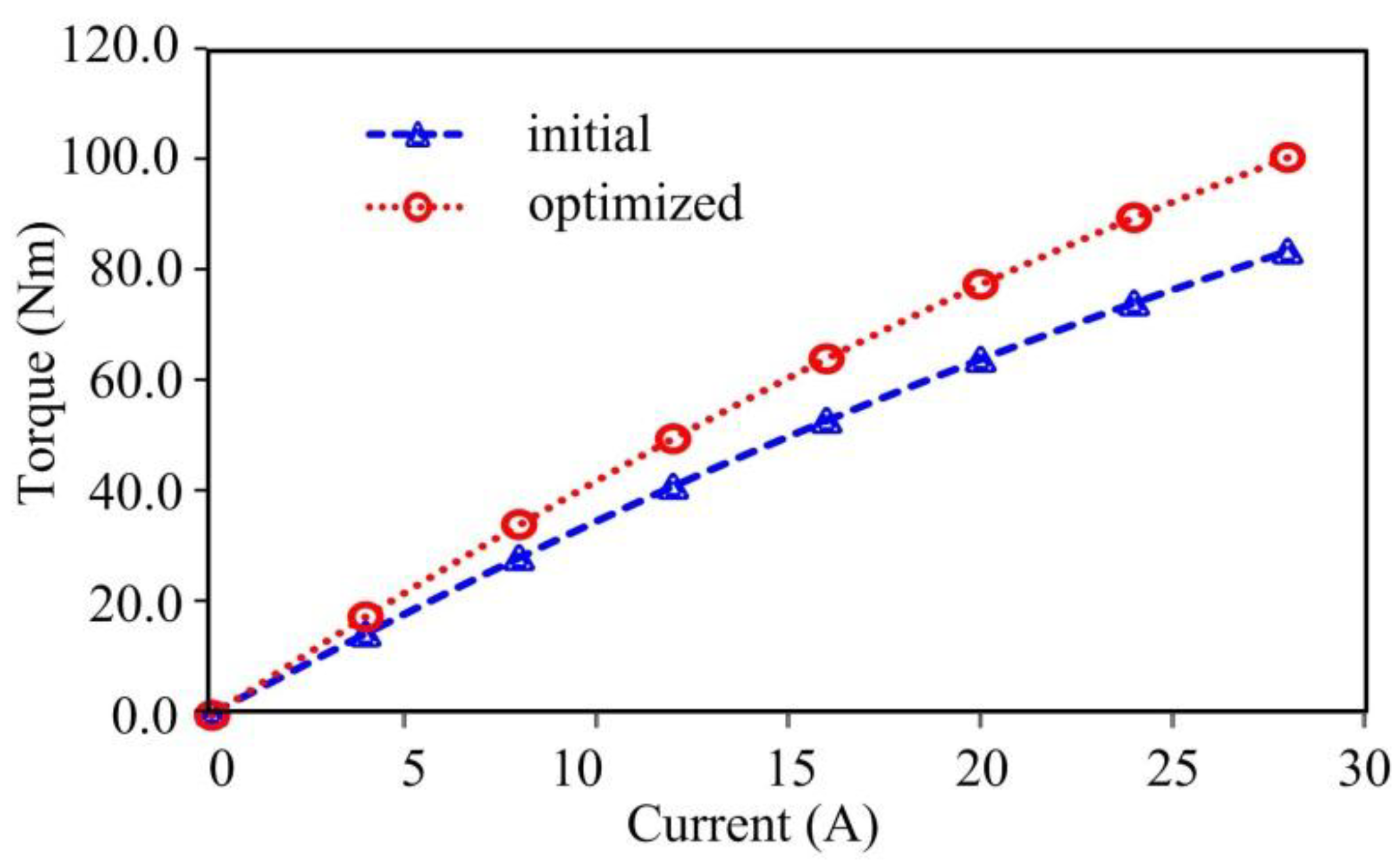
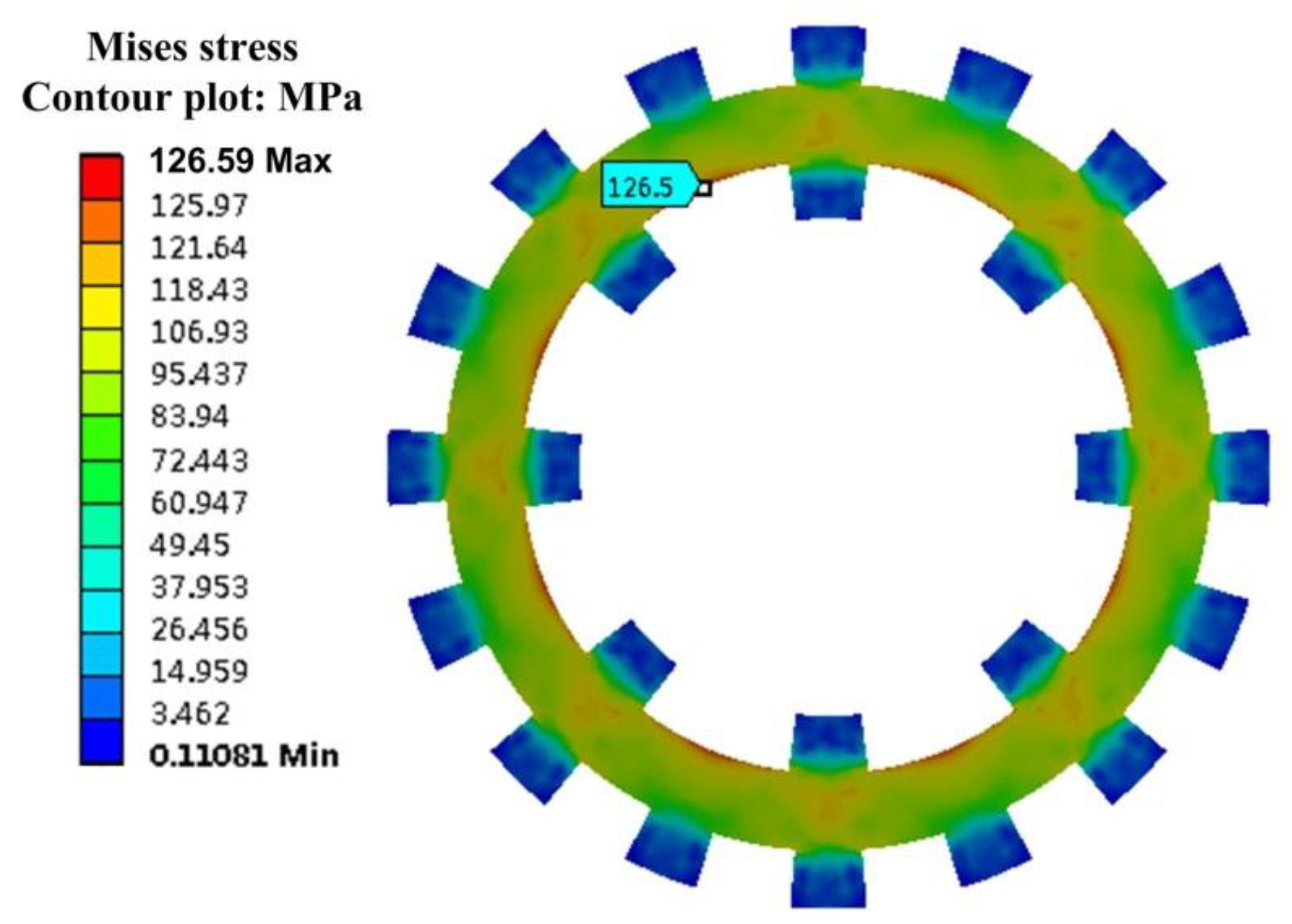
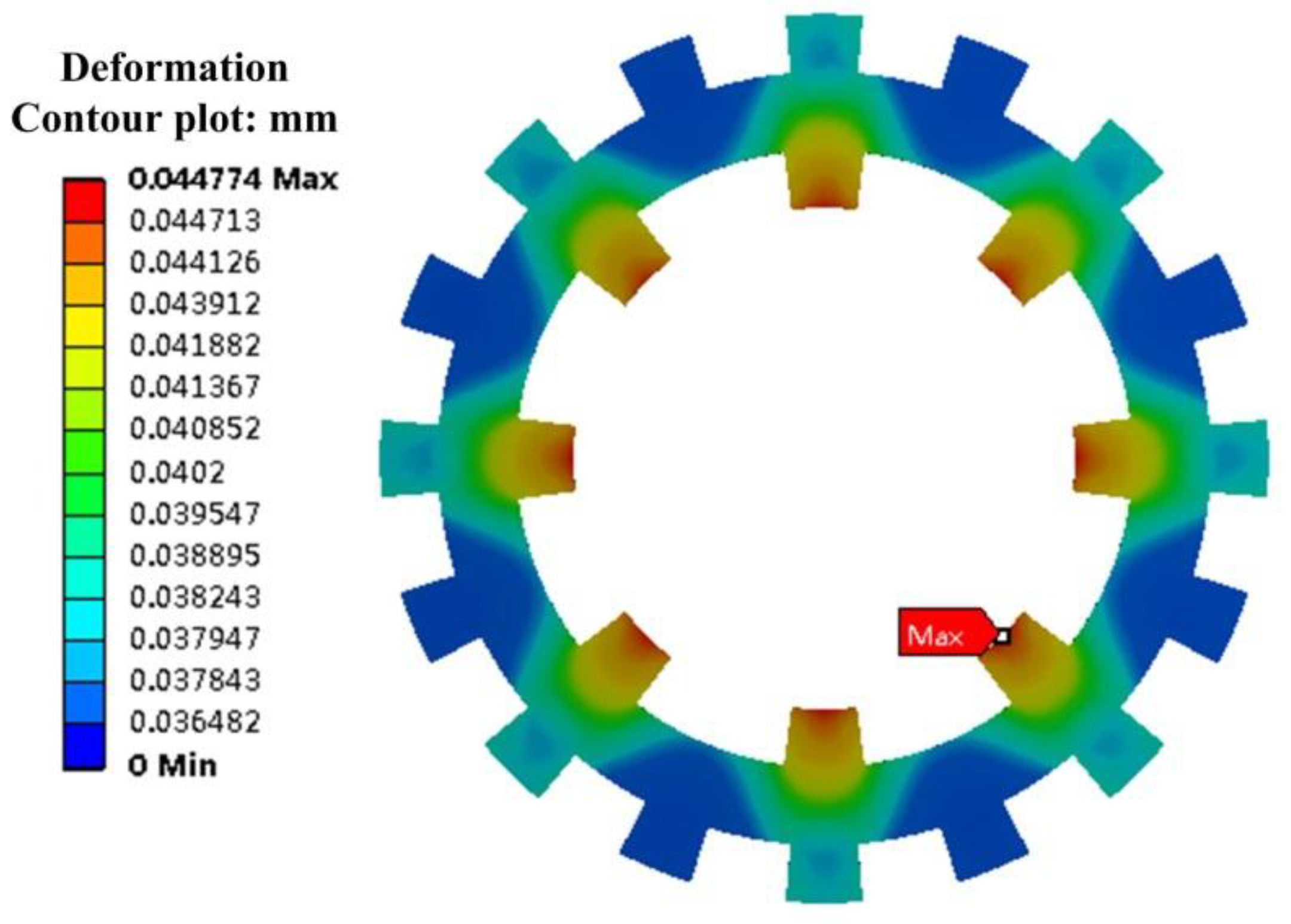
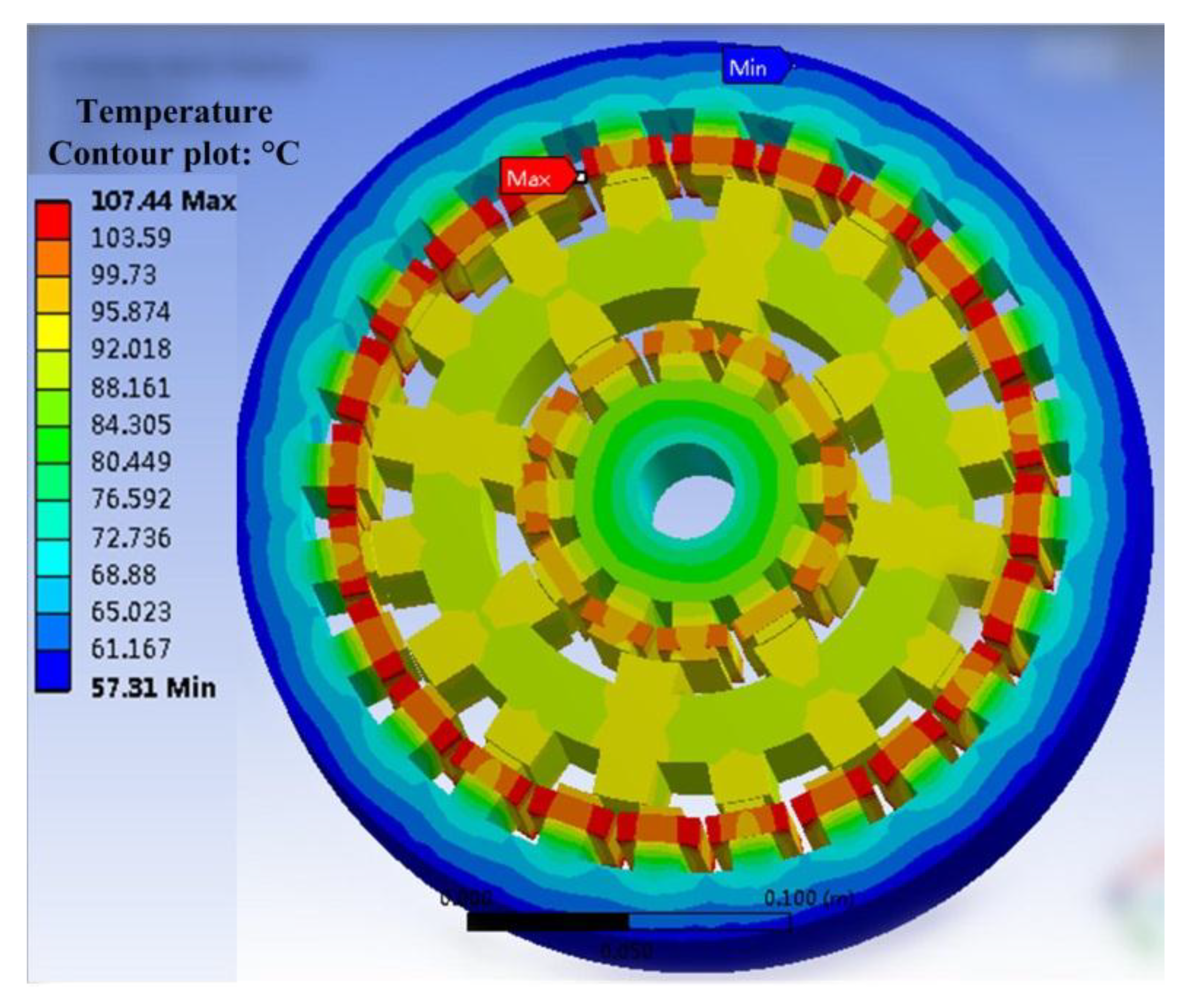
5. Conclusions
In this paper, a multi-objective optimization design procedure with multi-physics field analysis is presented to provide comprehensive optimization of a new type of DS-PMDS motor. Firstly, a multi-objective function is established. Secondly, a design optimization method using parametric sensitivity analysis (PSA) and sequential quadratic programming (NLPQL) is discussed in detail. The significance of the parameters is also effectively evaluated and the optimal structure size parameters are determined. The performance of the proposed DS-PMDS motor, including electromagnetism, structure and heat, is then calculated by multi-physics field analysis. Finally, the proposed machine is shown to offer good electromagnetic performance characteristics of high output torque, low torque ripple and high efficiency. The simulation results of stress and deformation verify the robust rotor structure. The thermal analysis also shows that the proposed DS-PMDS motor can operate at a reasonable temperature. Both the theoretical analysis and multi-physics field simulation verify the validity of the motor design and the effectiveness of the proposed optimization method.