1. Introduction
Carbon capture and storage (CCS) is a technology used to capture CO
2 emissions from power plants or industrial facilities to reduce greenhouse gas emissions; the gas is subsequently injected and stored in depleted oil and gas reservoirs or saline aquifers [
1].
The total value chain of CCS technology comprises capture, transportation, injection, and storage. The CO
2 captured in power plants or industrial facilities is in a subcritical state. However, the CO
2 stored deep underground is maintained in a supercritical state because of the high geothermal heat and pressure in the reservoir. This implies that the operating conditions associated with the critical point and near-critical regions may occur during the transportation and injection processes, which are intermediate steps, because of the phase difference between the captured CO
2 and stored CO
2. In a previous study [
2,
3,
4] by the authors of this paper, a depleted gas field in the East Sea of Korea was studied as a storage reservoir. Near-critical point flow and supercritical state flow of CO
2 were found to occur in the topside pipeline of the offshore platform and the upper part of the injection wellbore at a specific injection point, thereby causing flow instability in the pipeline [
5]. Such flow instability can cause an additional pressure drop in the pipeline or disable flow control. Therefore, the near-critical point and supercritical state flows of CO
2 should be considered in the initial design stage to allow the safe and economic injection and storage of CO
2 in CCS systems. To this end, the properties and flow characteristics of CO
2 at the critical point and in the near-critical region must be studied thoroughly. The purpose of this study is to identify the instability in the CO
2 flow at the critical point and in the near-critical region during the transportation and injection processes for CCS, to analyze the cause and effect of the flow instability, and to propose design specifications that reflect the results of the analysis.
Previous studies on the properties and flow instability of supercritical fluids similar to the case employed in this study can be categorized into four areas. The first area of study pertains to the critical and pseudocritical states of single-component fluids. Pioro and Mokry [
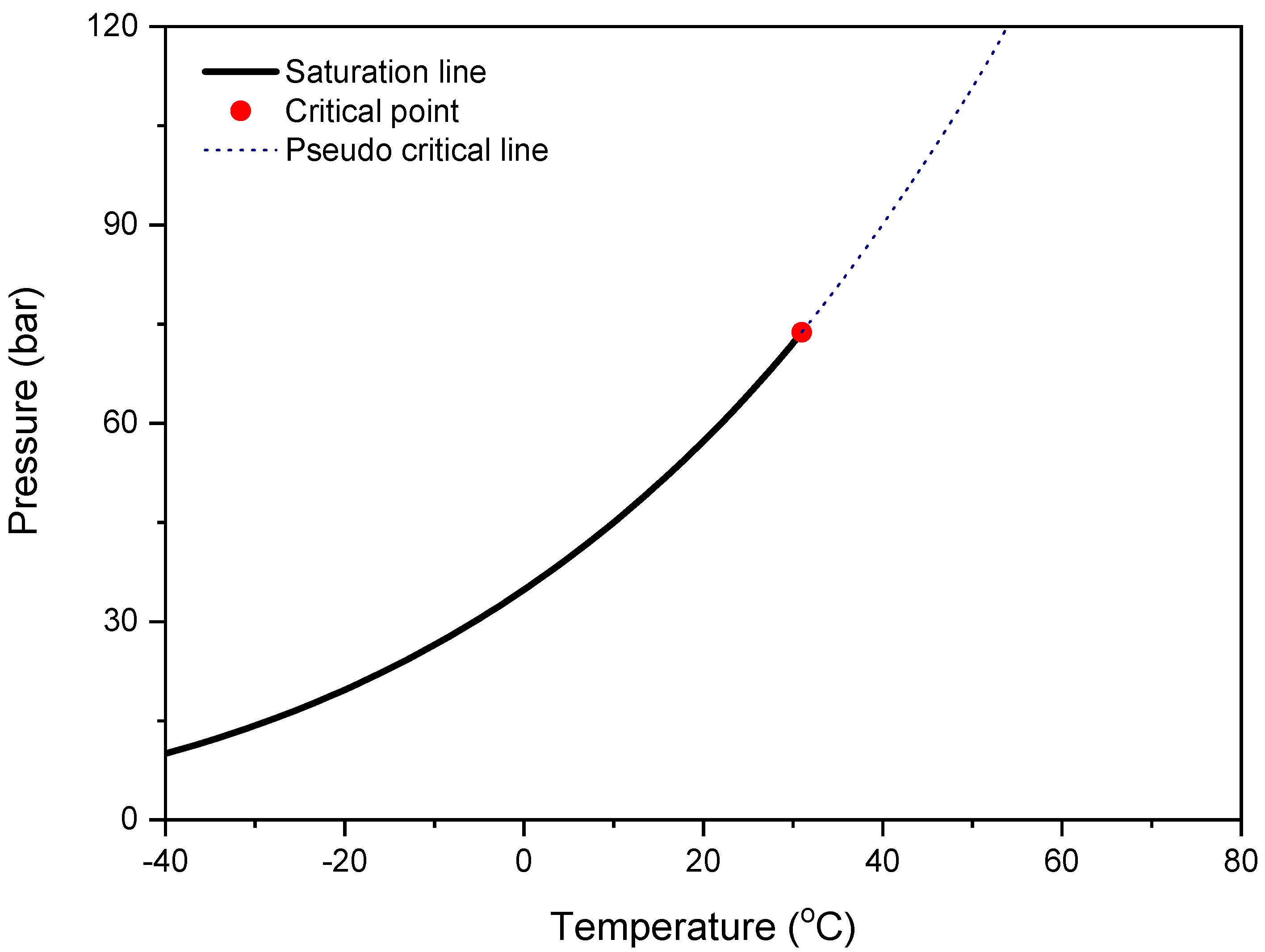
6] presented the terms and definitions for critical and supercritical fluids. The saturation line of fluids such as pure water or CO
2 is a single line, and the pressure and temperature of CO
2 at the critical point are 73.8 bar and 30.9 °C, respectively. In a particular part of the supercritical region above the critical point, the properties of the single-component fluid change abruptly at a particular pressure and temperature, and this is defined as the pseudocritical point. Furthermore, more than one pseudocritical point can exist, and the line connecting these points is called the pseudocritical line [
7]. Every pseudocritical temperature in the pseudocritical line has a corresponding pseudocritical pressure.
Figure 1 shows the phase envelope of CO
2 which was calculated using NIST’s REFPROP [
8]. As shown in
Figure 1, the pseudocritical line tends to extend from the saturation line of CO
2 in the subcritical state to the supercritical state via the critical point. The specific heat, density, and enthalpy of the supercritical CO
2 change drastically near the pseudocritical line [
9]. The abrupt behavior of the properties at the pseudocritical line tends to decrease further from the critical point [
10]. In the case of the phase envelope of natural gas, as shown in
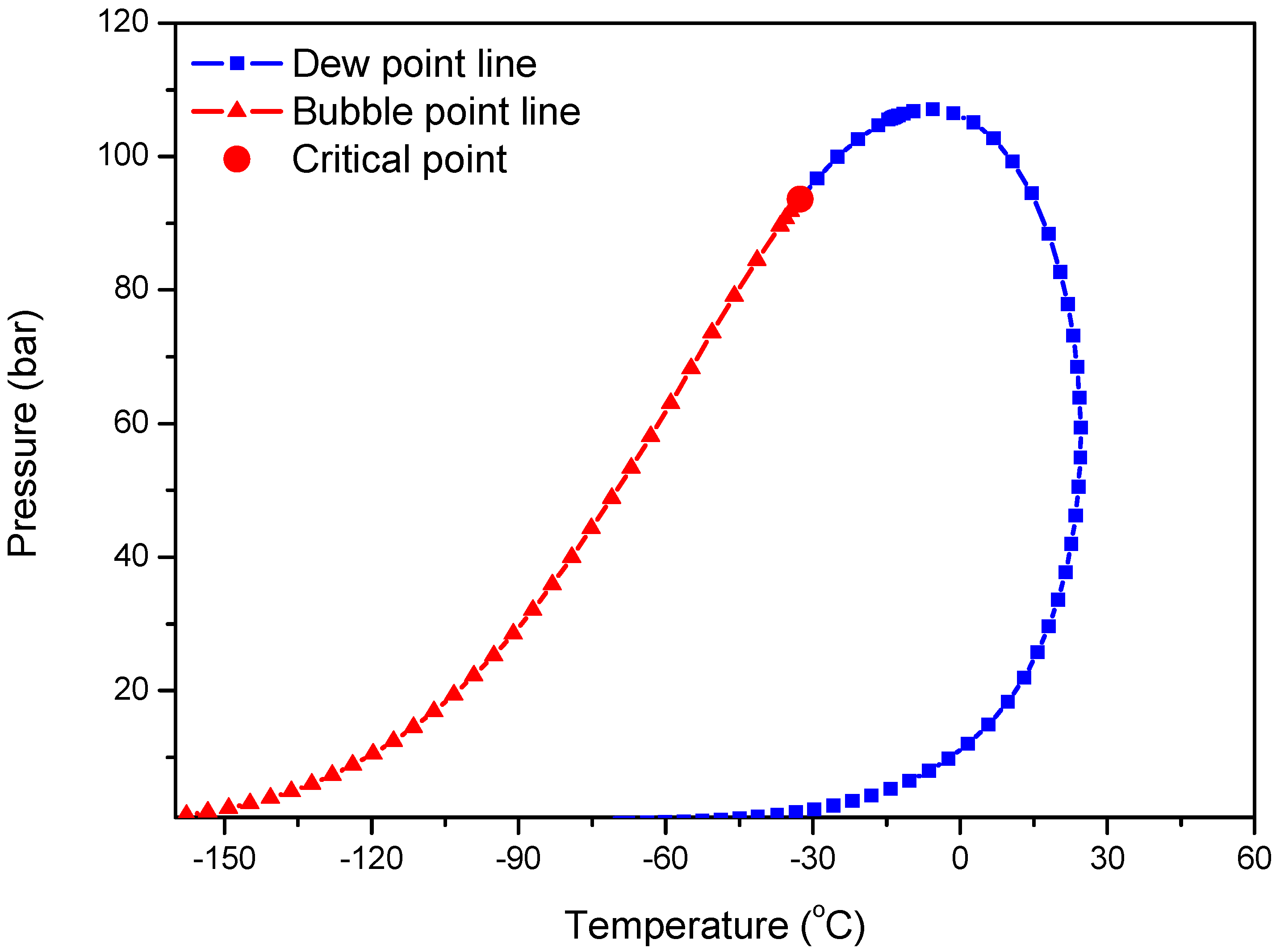
Figure 2 (which was calculated using NIST’s REFPROP [
8]), the saturation line takes the form of a parabola because the gas comprises a hydrocarbon mixture, unlike CO
2.
Although the phase behavior of natural gas has been thoroughly studied, studies of the phase behavior of CO
2 are lacking. Shoaib et al. [
11] investigated the effects of the operating conditions on the dew point and condensation rate of natural gas and developed two quadratic equations to relate them to the operational variables of the dew point control unit (DPCU). Guerrero-Zárate et al. [
12] developed and validated a new algorithm to determine the critical point of a natural gas mixture. Wang et al. [
13] derived implicit curve-fitting equations to increase the speed of calculation of natural gas properties in the supercritical pressure region. In summary, there is an abundance of knowledge and experience regarding the transportation of natural gas through pipelines [
14,
15,
16,
17]. However, it is difficult to analyze the phase transition in the transport of CO
2, which is the objective of this study, because of the single saturation line. Moreover, the behavior of near-critical point flow is significantly more complicated than that of a natural gas flow.
The second area of study relates to the flow of supercritical CO
2 and the application of supercritical and pseudocritical CO
2 to thermodynamic cycles. Ma et al. [
18] conducted a study to improve the performance of the Brayton cycle using the thermodynamic properties of pseudocritical CO
2. Shao and Zhang [
19] considered the saturation temperature of subcritical state CO
2 as the pseudocritical temperature of supercritical state CO
2 and proposed the possibility of using supercritical state CO
2 in the CO
2 cycle by extending the vapor pressure equation. Gupta et al. [
20] established a correlation between the heat transfer characteristics based on the experimental pseudocritical CO
2 data obtained for a supercritical region flow in a vertical tube. They applied the correlation to the Brayton gas turbine cycle. In addition, active studies have been carried out to apply the rapidly increasing specific heat and heat transfer coefficient of pseudocritical CO
2 in the supercritical region to the working fluid of the cycle [
21,
22,
23,
24]. However, most studies have focused solely on the analysis of thermodynamic properties, with relatively few studies considering the flow instability of supercritical state CO
2. Furthermore, because the experimental cycle used for analysis is small compared to a CCS transportation system, wherein the pipelines are on the order of several tens to several hundreds of kilometers, the results are limited in their extension to the CO
2 transportation pipelines employed in CCS technologies.
The third area of study is the flow instability of fluids at supercritical and near-critical points in the natural circulation loops used to cool nuclear power systems. Archana et al. [
25] experimented with and analyzed the transient flow of supercritical CO
2 in a natural circulation loop. Chen et al. [
26] performed a numerical analysis on the flow instability arising from rapid changes in the properties of pseudocritical state CO
2 in a natural circulation loop. Other experiments and numerical analyses have been conducted to analyze the flow instability of supercritical CO
2 in a natural circulation loop [
27,
28,
29]. These studies have investigated the instability of supercritical CO
2 flow, similar to that in this study. However, for the natural circulation loop considered in their studies, the driving force of the flow is the buoyancy arising from the density difference, whereas the driving force of the flow in a long-distance CO
2 pipeline is the pressure difference. Therefore, it is difficult to use the results of their studies for the CO
2 transportation and injection processes in CCS. Moreover, the scale of the system is different.
The fourth area of study regarding the flow instability of supercritical fluids is the flow instability of supercritical water caused by the density wave oscillations that occur near the pseudocritical line. The density and compressibility factor of supercritical water change suddenly along the pseudocritical line, resulting in unstable fluid behavior [
30]. Ambrosini [
31] argued that the flow instability of supercritical water in heated channels is similar to the flow instability caused by the two-phase flow of subcritical water. The similarity in the obtained stability maps validated the results. Xiong et al. [
32] investigated the flow instability of supercritical water flowing in a vertical pipeline and analyzed the main parameters causing flow instability. However, the critical pressure and temperature of water differ from those of CO
2, and the changes in the properties are different in terms of the critical temperature and pressure. Therefore, it is difficult to apply these values to the CO
2 transportation and injection processes of a CCS system.
As mentioned above, to implement CCS technology efficiently, the near-critical state flow and the supercritical state flow of CO2 must be considered. However, existing studies have not thoroughly analyzed the flow instability caused by near-critical or supercritical CO2 flows. Therefore, in this study, a numerical analysis was conducted, focusing on the flow instability caused by the operating conditions associated with near-critical point and supercritical states in a CO2 transportation and injection system.
3. Results
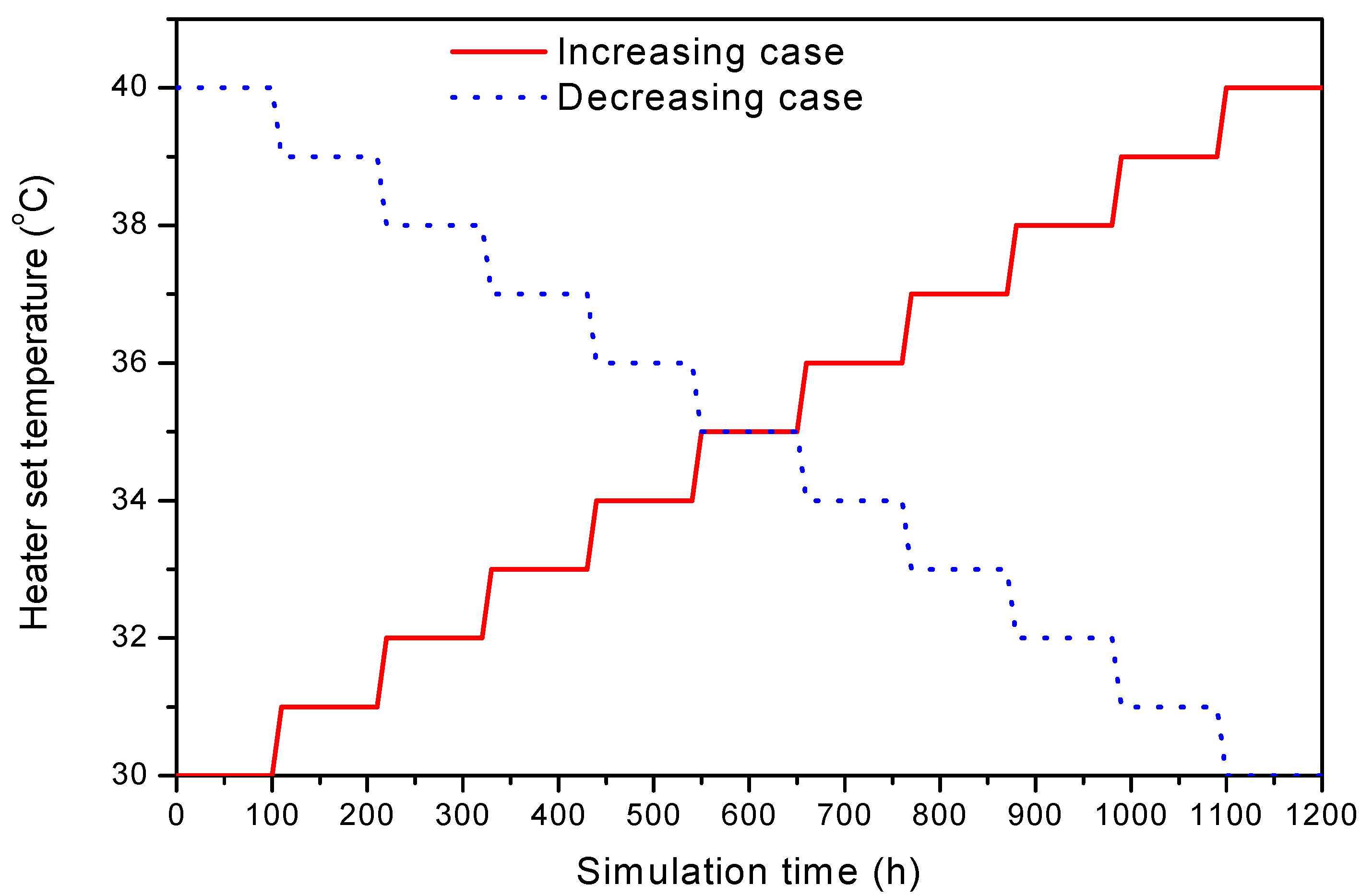
3.1. Identification of the Unstable Region
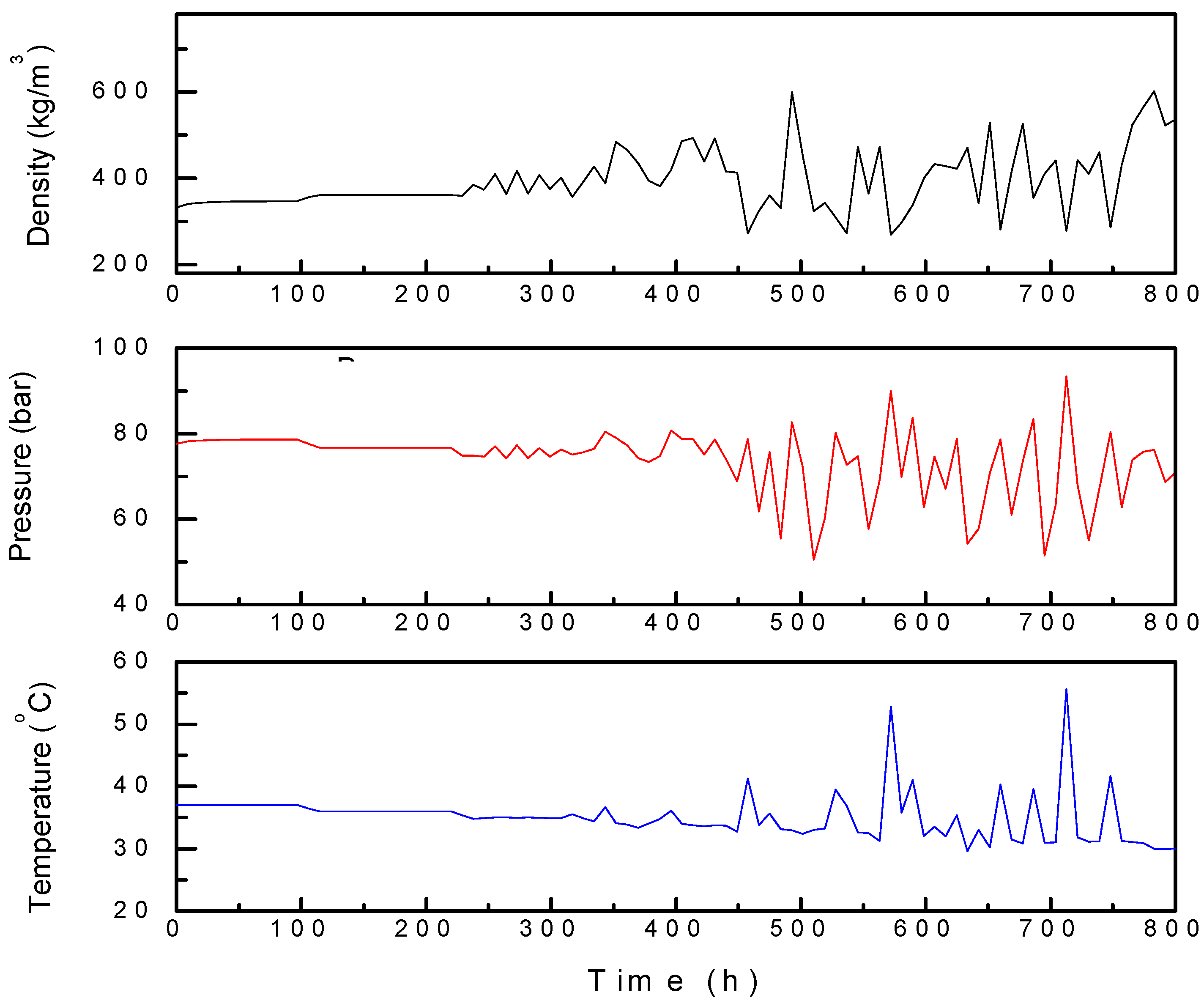
Figure 6 shows the calculation results for case 4 as an example. The density, pressure, and temperature of CO
2 were analyzed at the outlet of the heater. The outlet conditions of the heater include a pressure of 79 bar and a temperature of 37 °C, which are higher than those at the critical point of CO
2 (
Pc = 73.8 bar and
Tc = 30.9 °C). Under these operating conditions, the heater set temperature gradually decreases and approaches the critical point operating condition. When the simulation time is longer than 250 h, the operating pressure and temperature of the heater outlet are approximately 75 bar and 35 °C, respectively. At this point, the density and pressure of the CO
2 at the heater outlet start to vary. In this study, the operating conditions associated with the flow instability at the near-critical point were confirmed for all cases listed in
Table 2. In every case, the flows destabilized because of the fluctuations in the density, pressure, and temperature when the operating conditions were closer to the critical point. In this study, the conditions for the occurrence of flow instability were determined when the density variation was ±50 kg/m
3 or more at a steady state. Furthermore, the pressure and temperature at this time were considered operating conditions, causing flow instability in the pipeline. The temperature and pressure at which the flow started to destabilize were obtained for each case listed in
Table 2. The region of flow instability was determined for the critical point, near-critical region, near the pseudocritical line region, and supercritical region.
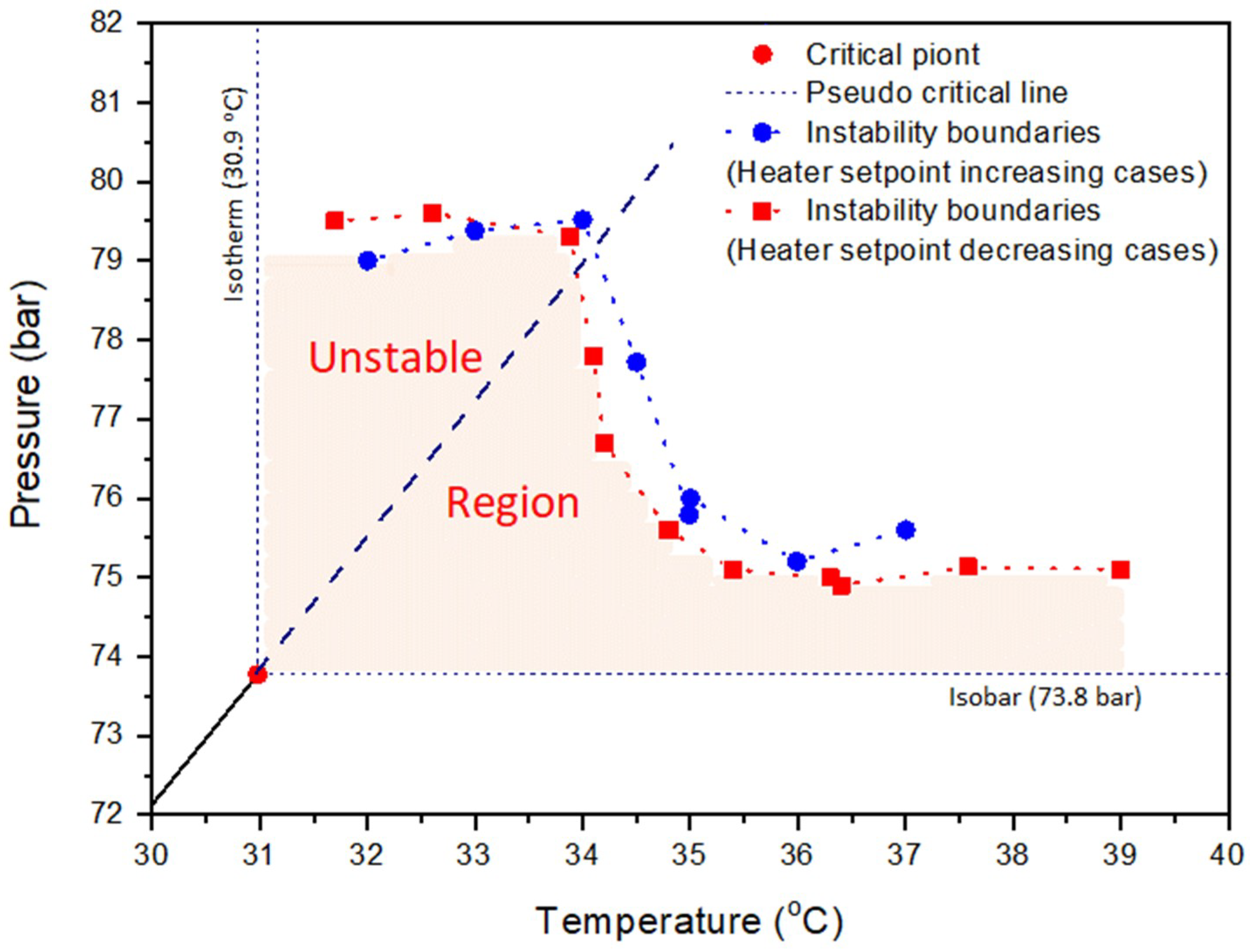
The pressure and temperature at which the flow begins to destabilize can be found using the pressure–temperature diagram of CO
2 by combining the aforementioned simulation results.
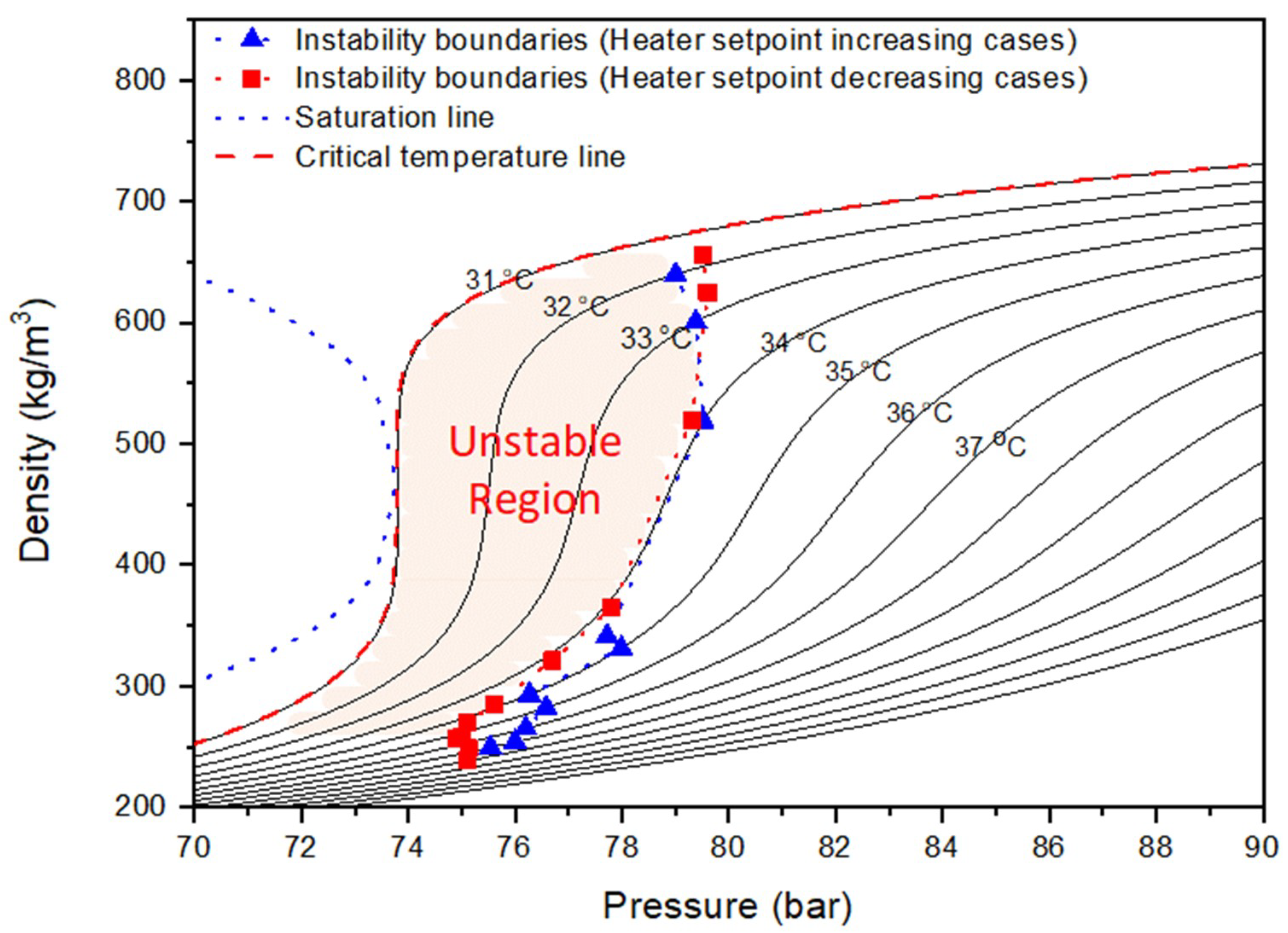
Figure 7 shows the results, wherein the pressure and temperature ranges are indicated. The unstable region is highlighted as the colored region in
Figure 7. Furthermore, the instability boundaries which were obtained through the numerical simulations are also specified.
The unstable region appears to be similar in both heating temperature cases, i.e., increasing and decreasing, and is near the critical point of CO
2. In this study, this region is defined as an unstable region. Among the regions shown in
Figure 7, flow instability was not observed in the topside and injection wellbore when the pressure and temperature are above those at the boundary of the regions.
Such an unstable region exhibits several characteristics. For example, the corresponding pseudocritical pressure is approximately 79.8 bar at a pseudocritical temperature of approximately 34.5 °C. The unstable regions can be distinguished using this value. In other words, the pressure should be higher than 79.8 bar (P > Ppc = 79.8 bar) to prevent instability at a temperature lower than the pseudocritical temperature of approximately 34.5 °C (T < Tpc = 34.5 °C). In addition, the pressure should be higher than 77 bar (P > Ppc = 77 bar) to avoid instability above the pseudocritical temperature of approximately 34.5 °C (T > Tpc = 34.5 °C).
Thus, the existence of an unstable CO2 flow region in the pipeline suggests that the unstable flow must be considered in the design and operation of the entire CCS value chain in which CO2 flows in the supercritical state. Considering the unstable flow, a specific range of operating conditions must be defined for system design and operation. Moreover, analytical results for critical and supercritical CO2 that correspond to the unstable flow are required. The results of this study identify the specific region near the critical point where the CO2 flow is unstable. CO2 near the critical point is known to exhibit sudden changes in its properties even on small pressure and temperature variations based on existing studies and experiments. However, if the CO2 transportation and injection system is operated in an unstable region, the cause of flow instability should be analyzed in detail. Thus, the changes in the properties of CO2 in the unstable region and near the pseudocritical line were analyzed, as explained in detail in the next section.
3.2. Effect of Property Changes Near the Pseudocritical Region
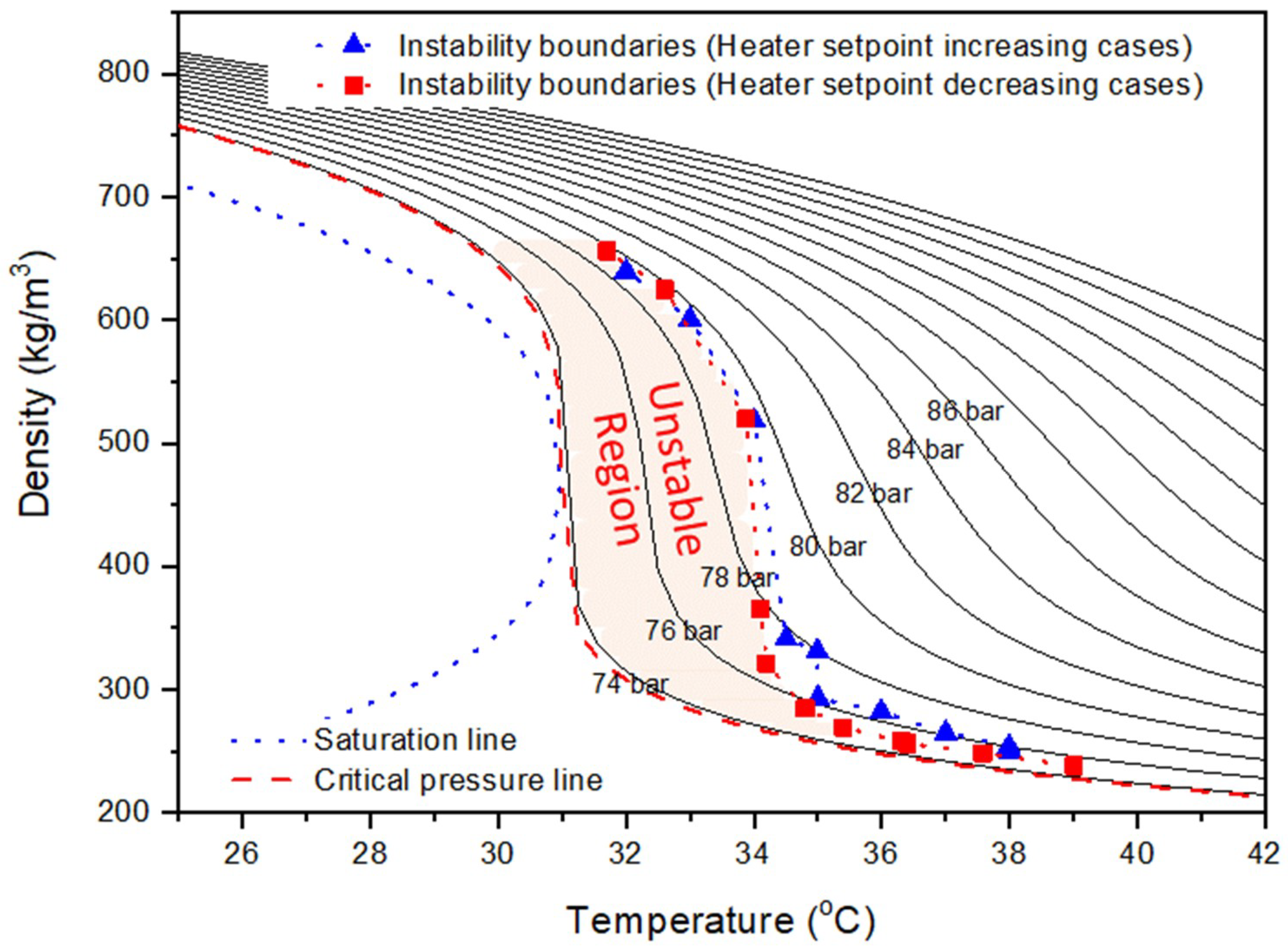
Figure 8 and
Figure 9 show the unstable regions in the temperature–density and the pressure–density diagrams of CO
2, respectively. The unstable region is highlighted as the colored region. Furthermore, the instability boundaries which were obtained through the numerical simulations are also specified. The density of CO
2 changes rapidly even with a slight temperature change at the critical point and in the near-critical region, as shown in
Figure 8.
Similarly, as shown in
Figure 9, a rapid density change was observed, even with a slight pressure change at the critical point and in the near-critical region. However, the density change behavior occurs not only at the critical point and in the near-critical region but also in the supercritical region. For example, as shown in
Figure 8, the density of CO
2 changes rapidly if there is a slight change in the pressure or temperature at supercritical conditions, i.e., a pressure of 78 bar and a temperature of 33.5 °C. Assuming that the temperature changes from 33 to 34 °C at a constant pressure of 78 bar, the change in the density of CO
2 is more than 300 kg/m
3. The unstable region includes an area with significant density variations because of temperature or pressure changes. The sudden changes in the properties are evident along the pseudocritical line, as shown in
Figure 7 and reported in previous studies. In particular, the properties change abruptly near the pseudocritical line in the unstable region. In other words, in the CO
2 transportation and injection system analyzed in this study, if the operating pressure of the topside is in the unstable region and the heater outlet temperature is set to a temperature within the unstable region, the pressure or temperature of the heated CO
2 may change slightly because of the pressure drop or heat transfer in the pipeline, resulting in a significant change in the density.
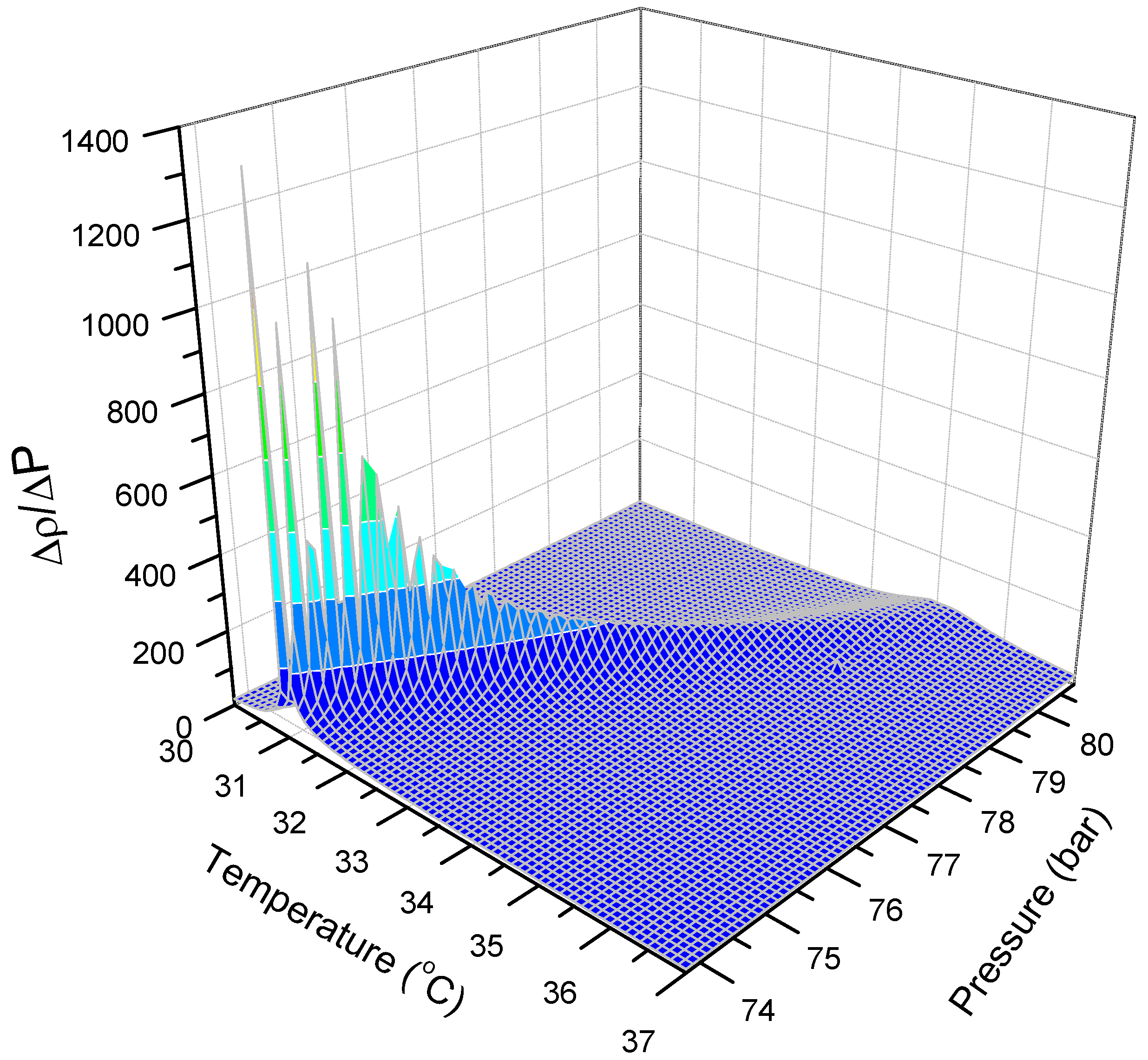
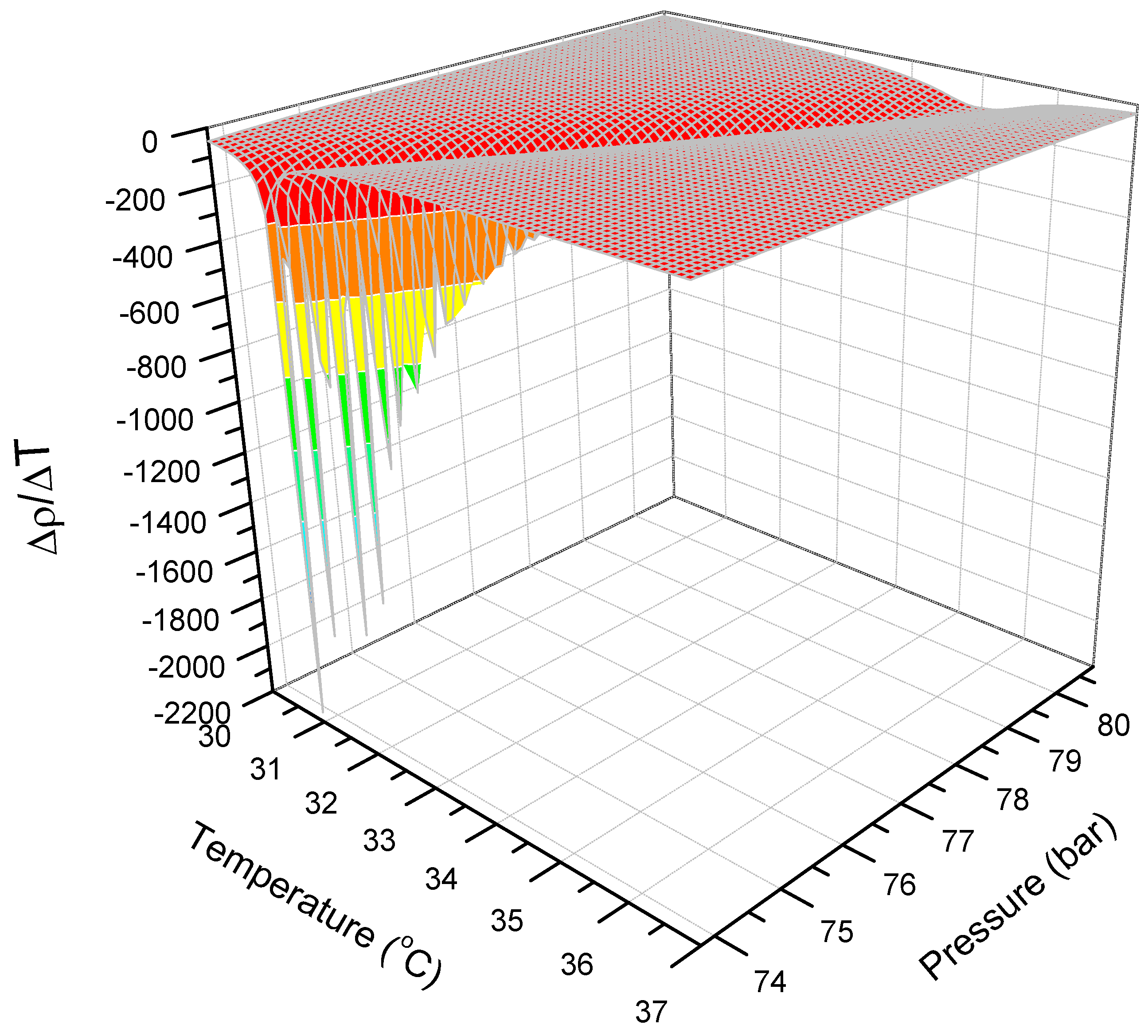
To analyze the density behavior of CO
2 in the unstable region in more detail, the density gradient of CO
2 was plotted with respect to the pressure and temperature, as shown in
Figure 10 and
Figure 11. The pressure and temperature ranges, shown in
Figure 10 and
Figure 11, are within the previously obtained unstable region. Along the pseudocritical line in the unstable region, the density of CO
2 changes significantly depending on the pressure and temperature. The density gradient is considerable at the critical point, whereas it decreases as the temperature and pressure move away from the critical point, i.e., outside the unstable region. In the aforementioned region, shown in
Figure 7, the operating conditions, i.e., a pressure of 80.7 bar and a temperature of 35 °C, are located on the pseudocritical line; however, they are outside the unstable region. If the same logic is applied to the relationship shown in
Figure 10 and
Figure 11, there is no notable density change in the pseudocritical line above 79.8 bar and 34.5 °C.
As shown in the CO
2 density gradient with respect to the pressure in
Figure 10, the pressure and temperature at which the density gradient becomes a maximum lie on the pseudocritical line shown in
Figure 7. At the critical point and in the near-critical region of CO
2, the density gradient arising from the pressure increases sharply up to approximately 1000 kg/m
3·bar. On the other hand, the density gradient of CO
2 with respect to the temperature, as shown in
Figure 11, decreases sharply to approximately 2100 kg/m
3·°C with increasing temperature.
Figure 10 and
Figure 11 show that the density gradient of CO
2 on the pseudocritical line is more susceptible to temperature than to pressure.
The above results show that the density gradient of CO
2 with respect to the changes in the pressure and temperature changes rapidly in the unstable region. If this behavior occurs in the CO
2 transportation and injection system, a phenomenon similar to density wave oscillations arising from the difference in the densities of the liquid and vapor phases in two-phase flow may occur, even though CO
2 is in a single-phase supercritical state. This phenomenon is analyzed in
Section 3.3.
3.3. Analysis of the Instability
Based on the results in the preceding section, CO2 in the supercritical state near the critical point and in the unstable region shows an unstable state with rapid changes in its properties, even when the temperature and pressure change slightly. If these rapid changes in properties occur in the CO2 transportation pipeline and injection wellbore, they can cause severe flow instability, possibly resulting in loss of flow control. In this section, the cause of the above-mentioned flow instability in the unstable region is analyzed.
Generally, in a two-phase flow system, density wave oscillations are due to the difference in the densities between the high-density liquid phase and the low-density vapor phase, and this can cause a sudden pressure drop or perturbation in the flow velocity, resulting in flow instability in the system [
37]. However, the fluid density along the pseudocritical line can change rapidly even in a supercritical fluid, and this can also cause a phenomenon similar to density wave oscillation. Studies have shown that flow instability arising from the density difference occurs even in a supercritical single-phase water flow, which is similar to density wave oscillations in the two-phase flow of subcritical water [
31]. The CO
2 flow instability in the supercritical state and in the near-critical region occurs in the single-phase supercritical region and is, thus, different from the density wave oscillation of the existing two-phase system. However, based on the results reported in the previous chapter, the density change of CO
2 occurring at the pseudocritical line in the unstable region appears to be similar to the density change behavior occurring at the saturation line. This resulted in a behavior similar to the flow instability arising from the phase change in a two-phase flow system.
In the supercritical CO
2 single-phase flow of this study, a phenomenon similar to the flow instability that occurs in two-phase flow because of the phase change of CO
2 was observed. Therefore, the calculation results of this study were applied to a stability map using two non-dimensional numbers: the sub-pseudo-critical number,
NSUBPC, and the trans-pseudo-critical number,
NTPC. The two dimensionless numbers have been used to describe the instability boundaries [
38,
39]. These two dimensionless numbers have been modified such that the phase change number,
NPCH, and the subcooling number,
NSUB, of the existing subcritical fluid stability map could be applied to a supercritical fluid [
38]. A stability map that distinguishes between the stable and unstable flow regions can be obtained by calculating and plotting
NSUBPC (sub-pseudo-critical number) and
NTPC (trans-pseudo-critical number) of the supercritical fluid. The exact formulae are given in Equations (1) and (2), respectively.
Here, βpc is the coefficient of volume expansion at the pseudo-critical point, Cp,pc is the specific heat at the pseudocritical point, hpc is the enthalpy at the pseudocritical point, hin is the enthalpy of CO2 at the topside heater inlet, is the heat flow rate input from the topside heater, and is the mass flow rate of CO2 in the system.
In this study, the same temperature of the heater inlet condition, 5.7 °C, was applied, which is the topside arrival temperature, and
hin was calculated using the operating pressure and inlet temperature of every calculation case. The CO
2 properties were calculated using NIST’s REFPROP [
8]. For the flow rate of CO
2 used, a constant value of 31.5 kg/s was applied to the system. Furthermore, the amount of heat input to the heater was calculated for each simulation case.
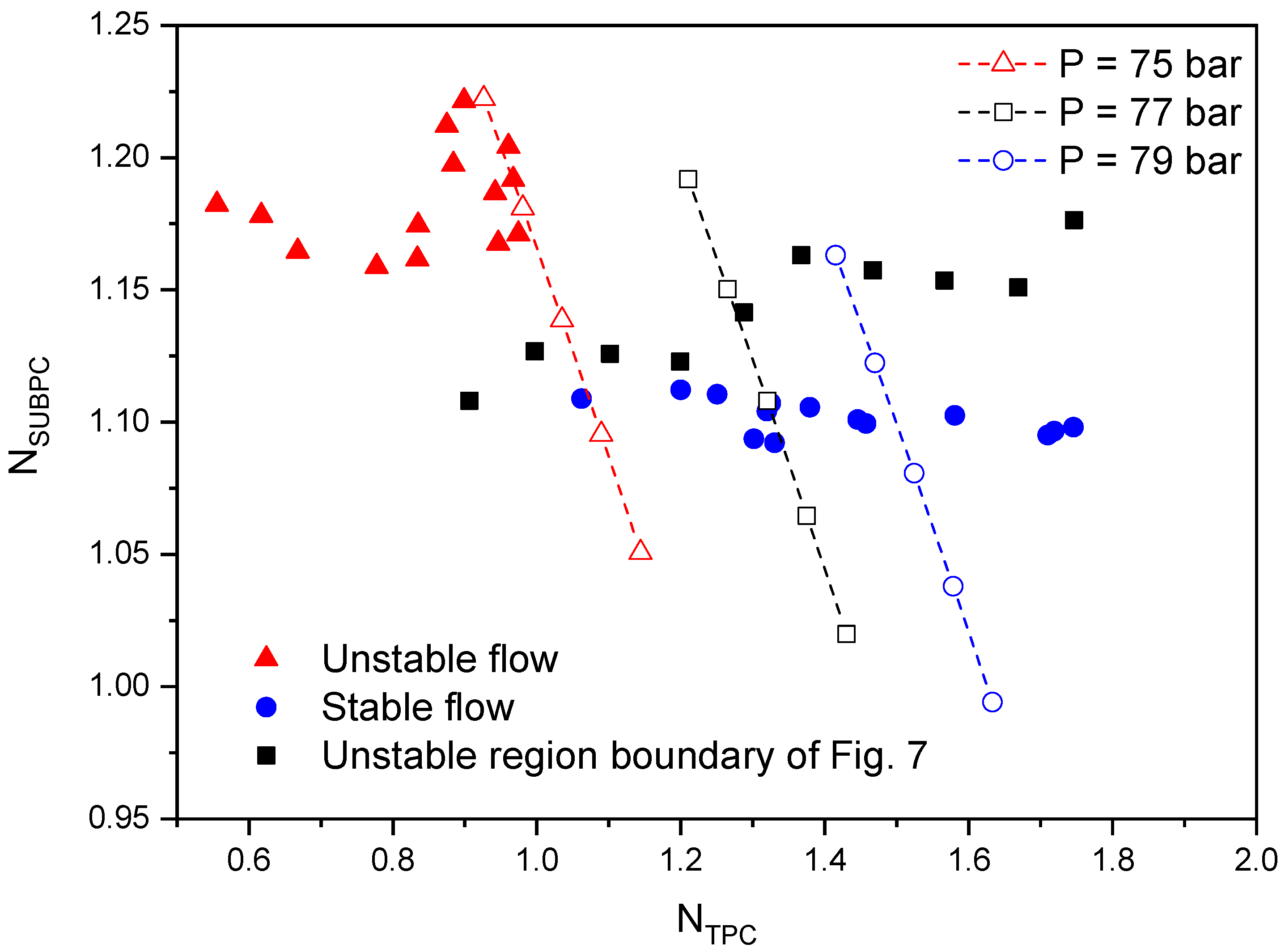
The two non-dimensional numbers applied to this system were calculated separately and categorized into three groups: the operating conditions of the unstable region boundaries obtained above, operating conditions of the unstable region wherein the flow is unstable, and operating conditions outside the unstable region where the flow is stable.
The
NSUBPC value increases with increasing difference between the temperature corresponding to the pseudocritical enthalpy of the heater operating pressure and the temperature at the heater inlet. The
NTPC value tends to increase as the heater increasingly heats the CO
2.
Figure 12 shows that the trend in the flow instability of supercritical CO
2 is clearly different at the boundary of the previously obtained unstable region.
As shown in
Figure 12, the stability map obtained using the two dimensionless numbers indicates that the flow in the system becomes more unstable with increasing subcooling at the heater inlet, and the flow in the system becomes more stable as more heat is input to the heater. The effect of the inlet subcooling and the supplied heat at constant pressure is investigated.
Table 3 shows the calculation conditions. As the subcooling increases (
NSUBPC increase), the flow becomes unstable. Furthermore, as more heat is supplied (
NTPC increase), the flow becomes more stable.
When the results, shown in
Figure 12, are compared to the stability map of supercritical water obtained by Ambrosini and Sharabi [
39], differences in the ranges of
NSUBPC and
NTPC values are observed; however, the flow instability trend was similar. The difference between the ranges of the two dimensionless numbers was caused by the significant differences in the properties of the supercritical water and supercritical CO
2 depending on the pressure and temperature.
3.4. Case Study on CO2 Pipeline Transport
A case study was conducted on a standard CO
2 pipeline to determine whether the results of this study were specific to a system that is heated by a topside heater, as in this study. To this end, a numerical analysis was carried out by modeling a 10 km-long horizontally installed pipeline used to transport CO
2.
Table 4 outlines the calculation conditions for the numerical analysis of the CO
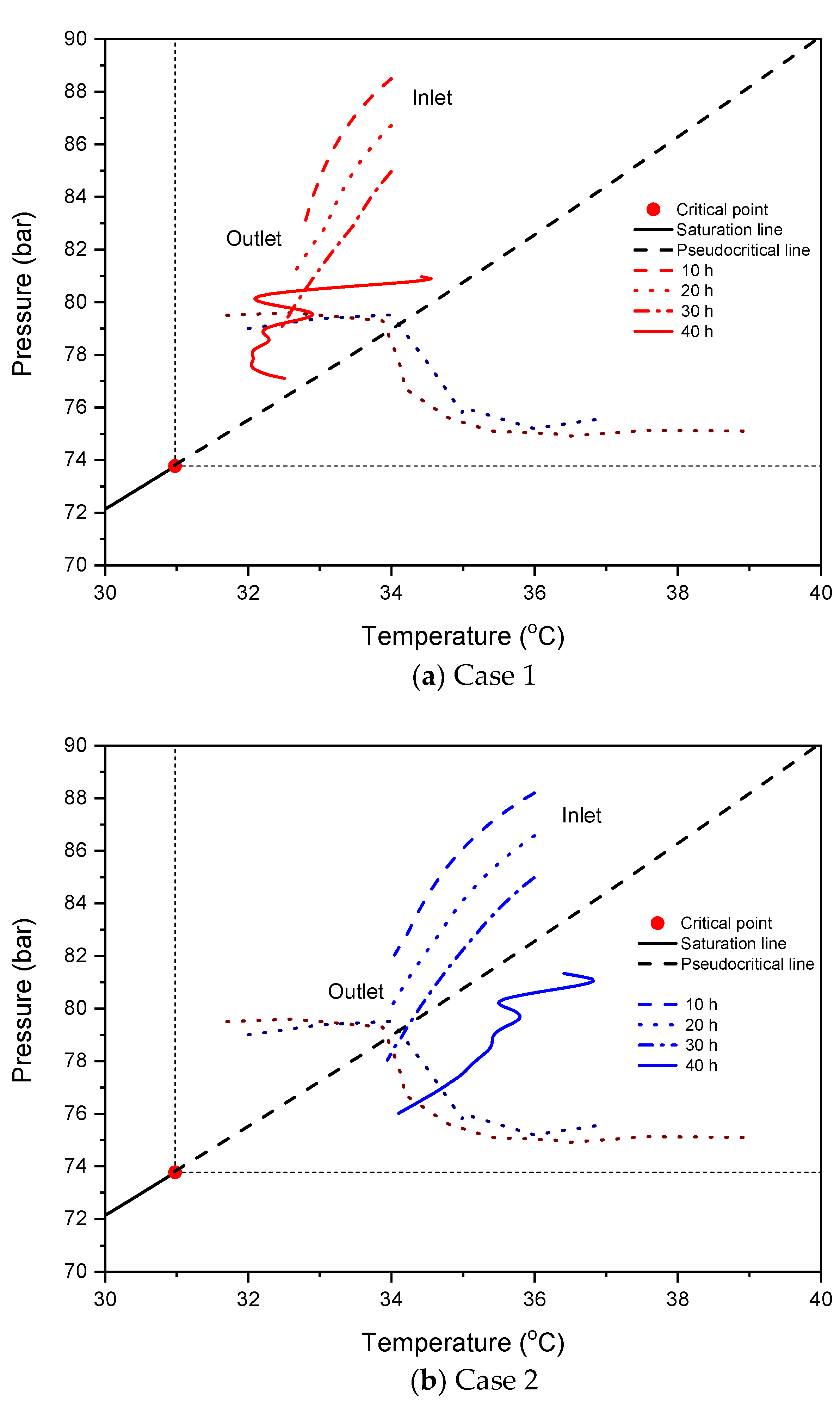
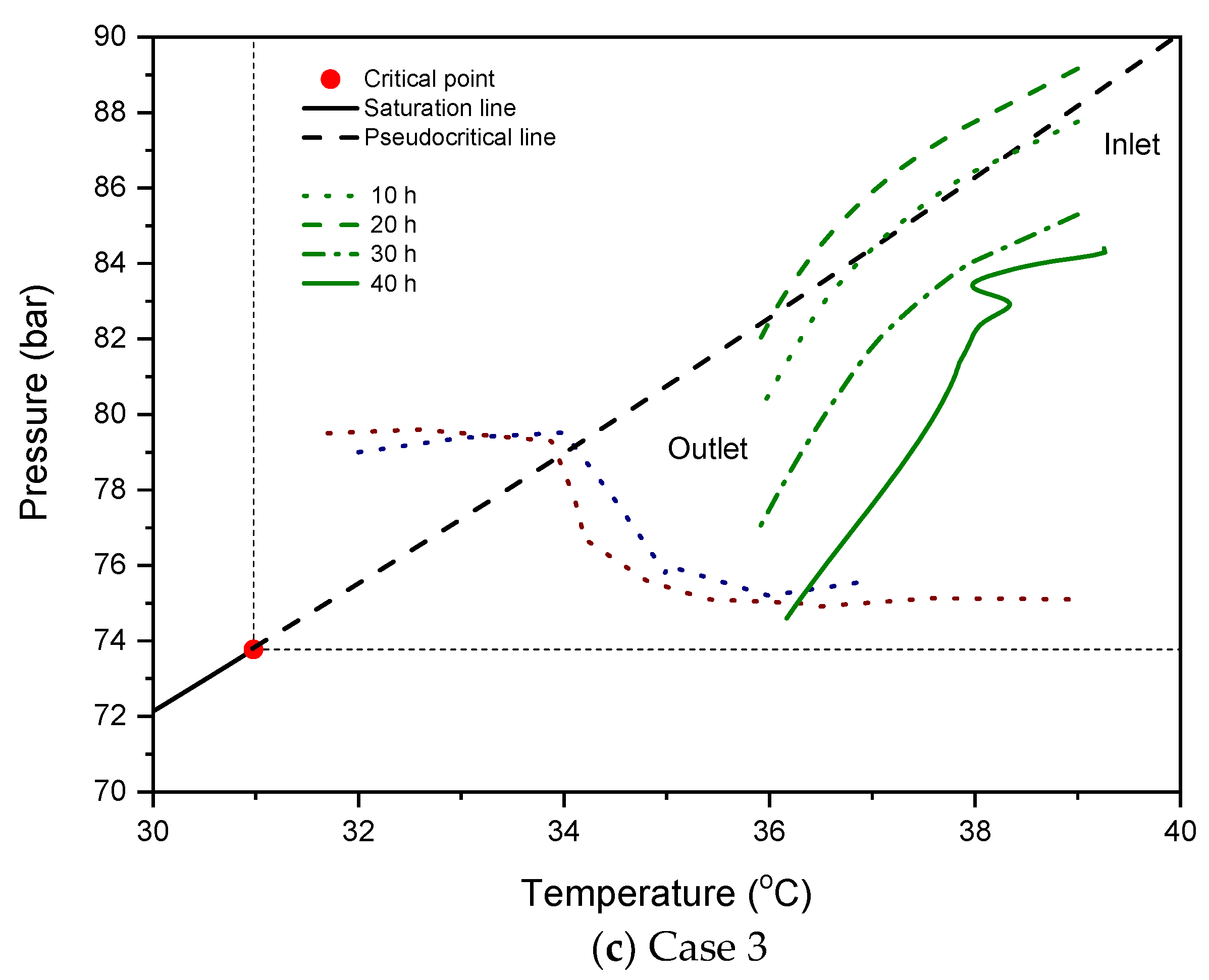
2 pipeline in each case. The same values for the pipeline diameter and flow rate as those of the existing system were used. The initial pressure and temperature in the pipeline were all outside the unstable region of the pipeline. As the simulation time passed from 10 h to 40 h, the outlet pressure of the pipeline decreased, and the operating conditions were within the unstable region. Through this process, we analyzed whether the flow instability occurs in the pipeline when the pipeline inlet with a high pressure operating condition is located outside the unstable region and when the pipeline outlet with a low pressure operating condition is located inside the unstable region.
Figure 13 shows the pressure–temperature diagram of CO
2, showing the pressure and temperature calculated at intervals of 10 h in the pipeline for each case study. In all three cases, the temperature and pressure fluctuated because the operating conditions near the pipeline outlet are located in the unstable region. This fluctuation shows that the flow instability spreads to all pipeline sections. Consequently, the abnormal pressure and temperature profiles were shown in 40 h, see
Figure 13. Concerning the cause of the flow instability mentioned above, the rapid changes in the CO
2 properties at the pipeline outlet affected the entire pipeline. This result suggests that the unstable CO
2 region at the critical point and in the near-critical region obtained from this study affects the flow instability of general pipelines. In other words, the unstable behavior of CO
2 in the unstable region not only occurs when it is heated by a heat exchanger, such as the heater used in this study, but also in more general cases.
If the temperature and pressure of the fluid are within the unstable region in a specific section of the CO2 transportation and injection system, the conditions are sufficient to cause flow instability in the entire system. Therefore, the operating conditions of the CO2 transportation and injection system should be designed in such a manner to avoid the unstable region, as shown in the results of this study.