Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load
Abstract
:1. Introduction
2. Basic Parameters of the Motor and Laboratory Testing Platform
3. Model and Fundamental Equations
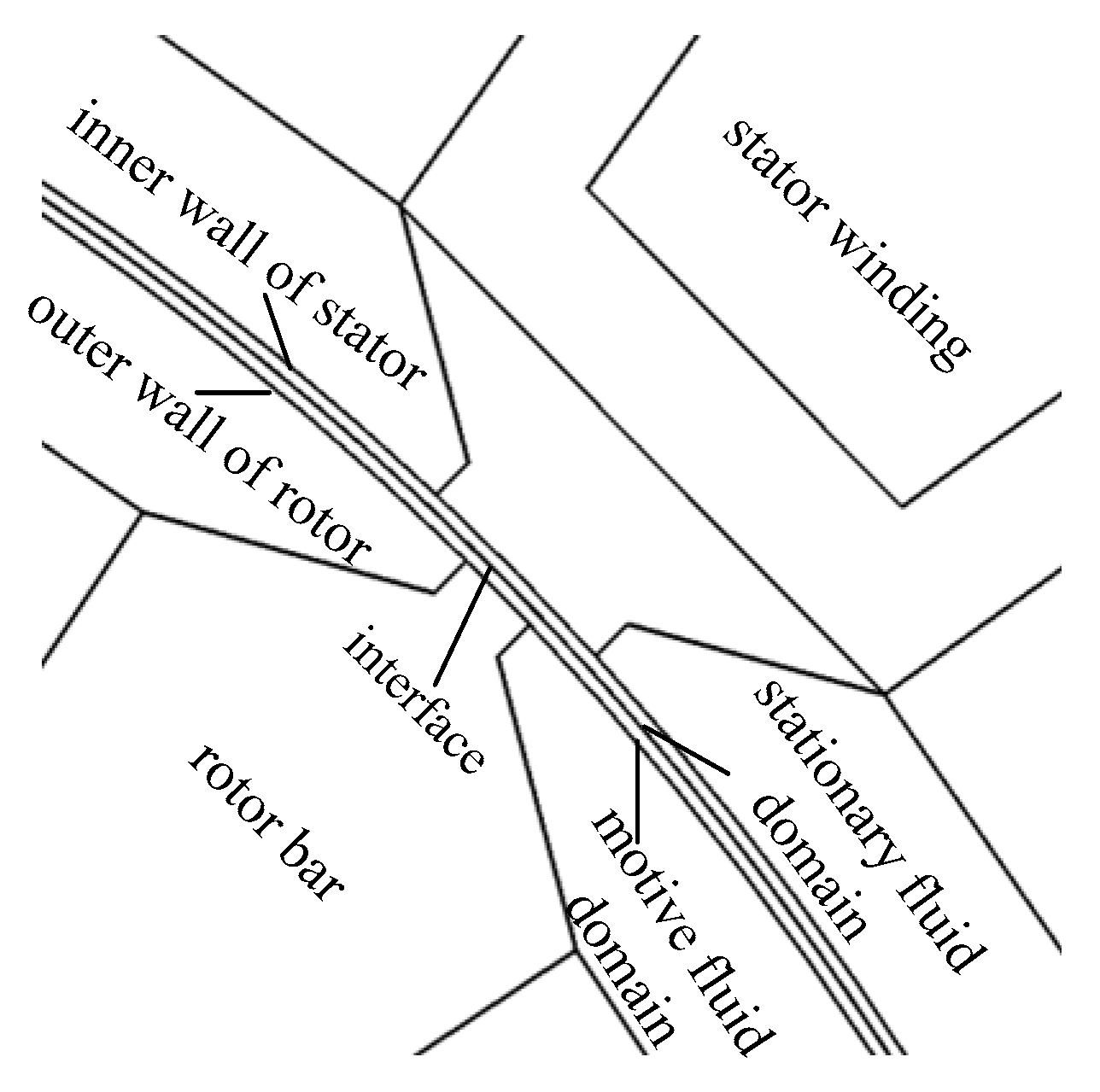
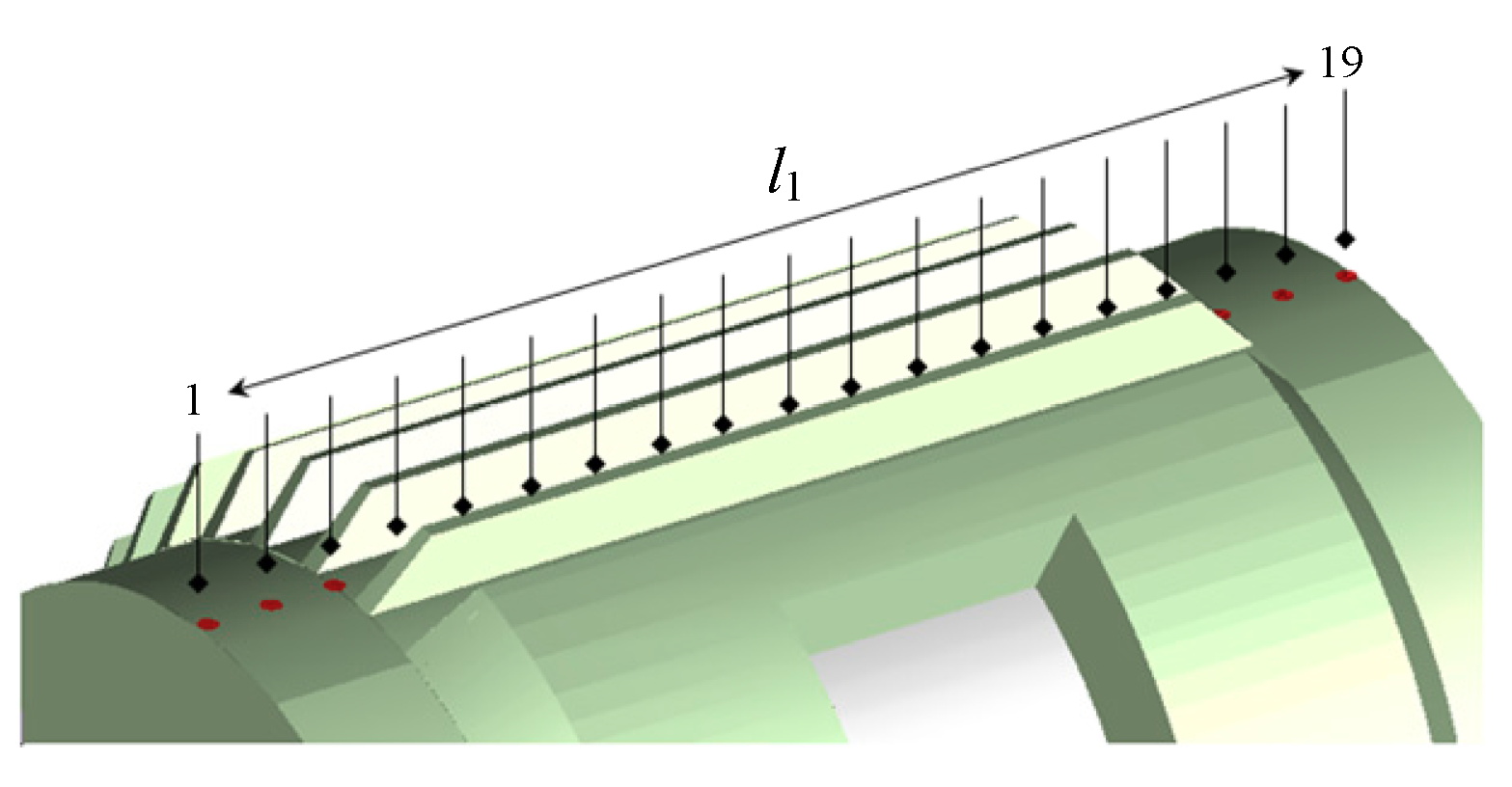
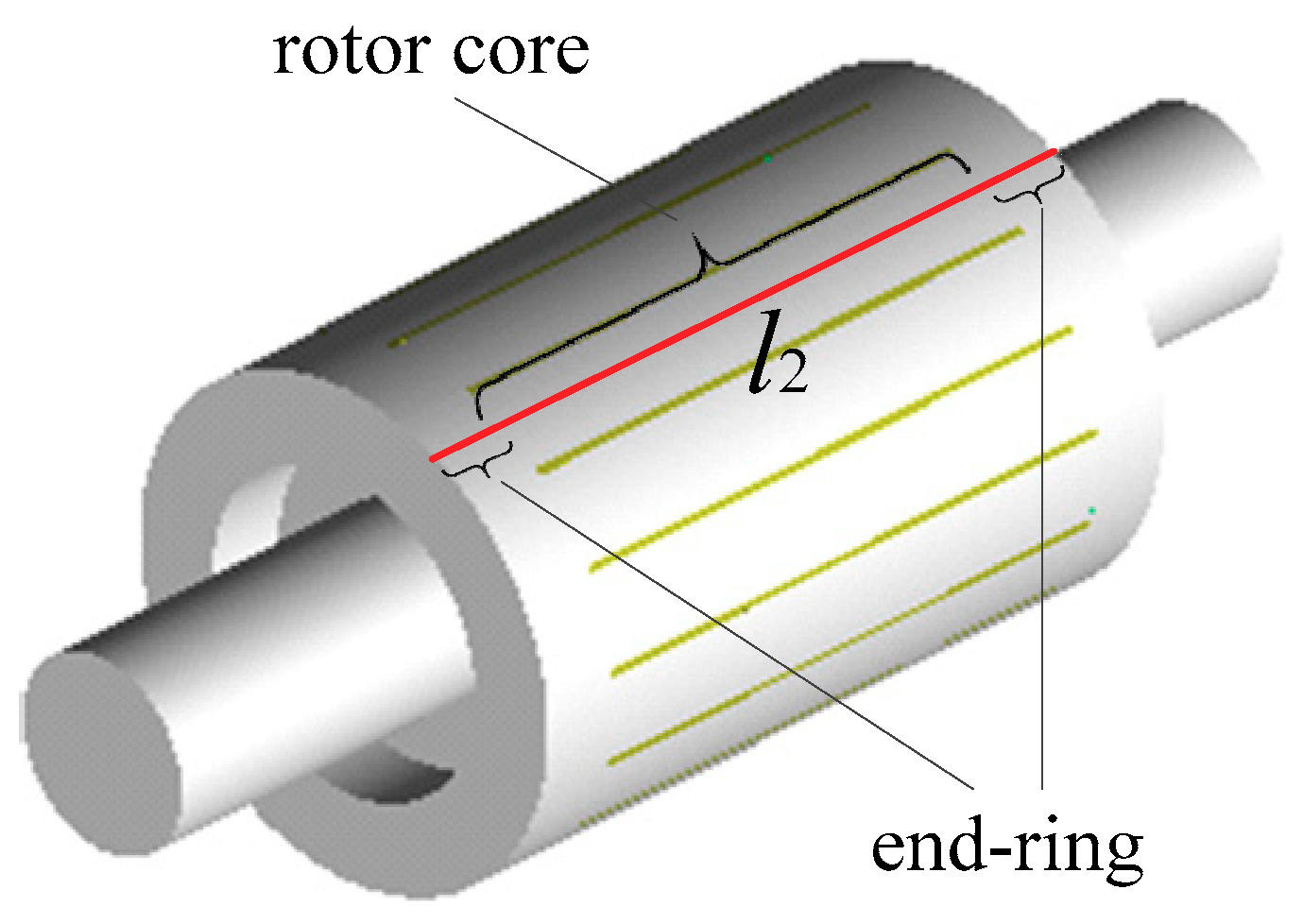
3.1. CFD Model and Temperature Measured Positions
- The stator winding has a good dipping process.
- Insulated lacquer on the stator winding surface is uniformly distributed.
- The equivalent insulation layer in the stator slots is tightly connected with the stator core.
- The thermal difference of all winding in a stator slot can be neglected.
3.2. Fundamental Equations of the Fluid and Thermal Field
3.3. Fundamental Assumptions
- Thermal resistance of windings is neglected because of its good heat conducting properties.
- The thermal contact resistances between the rotor core and rotor bars is negligible.
- Stray loss is focused on the tooth tip of stator and rotor.
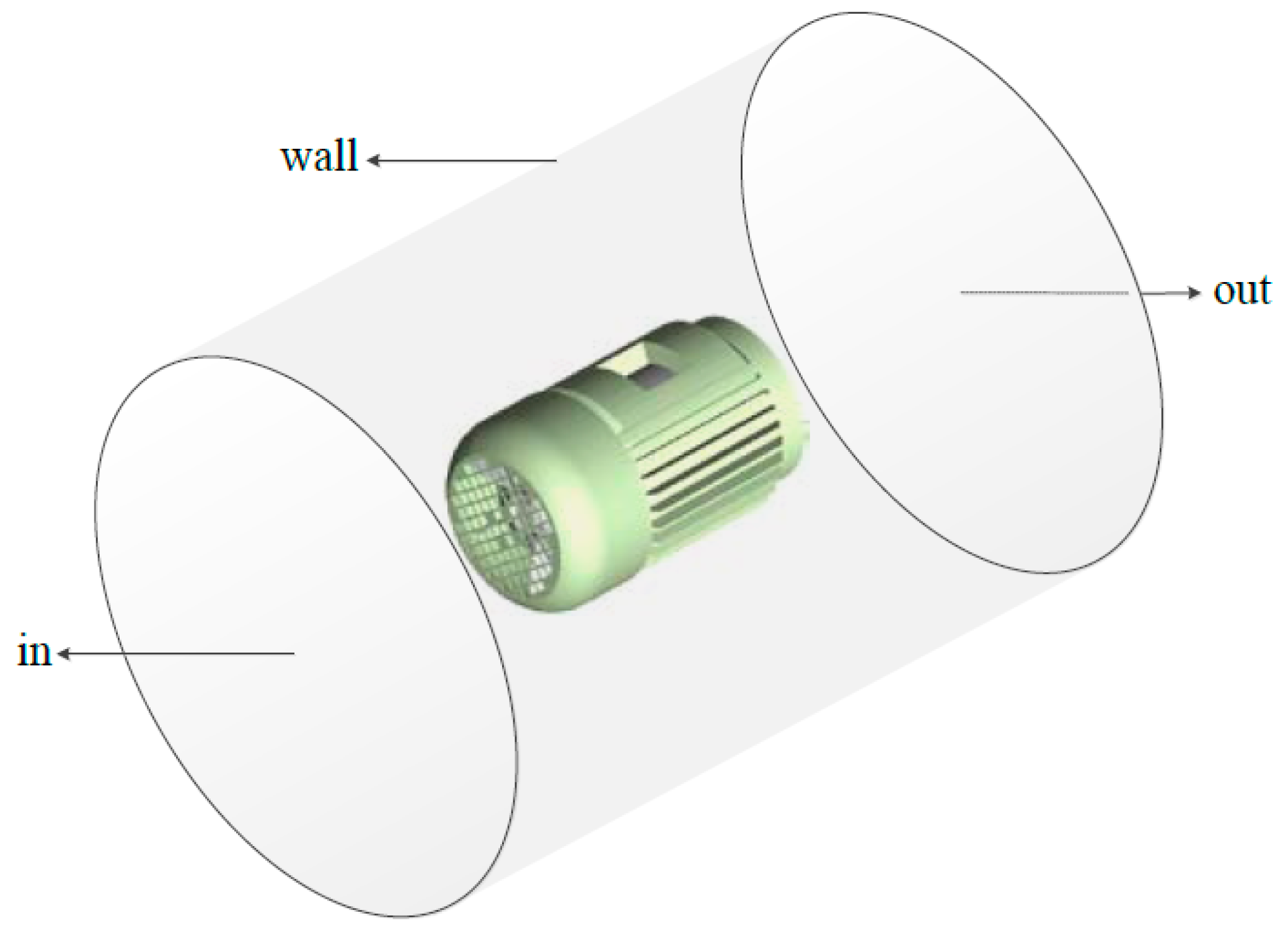
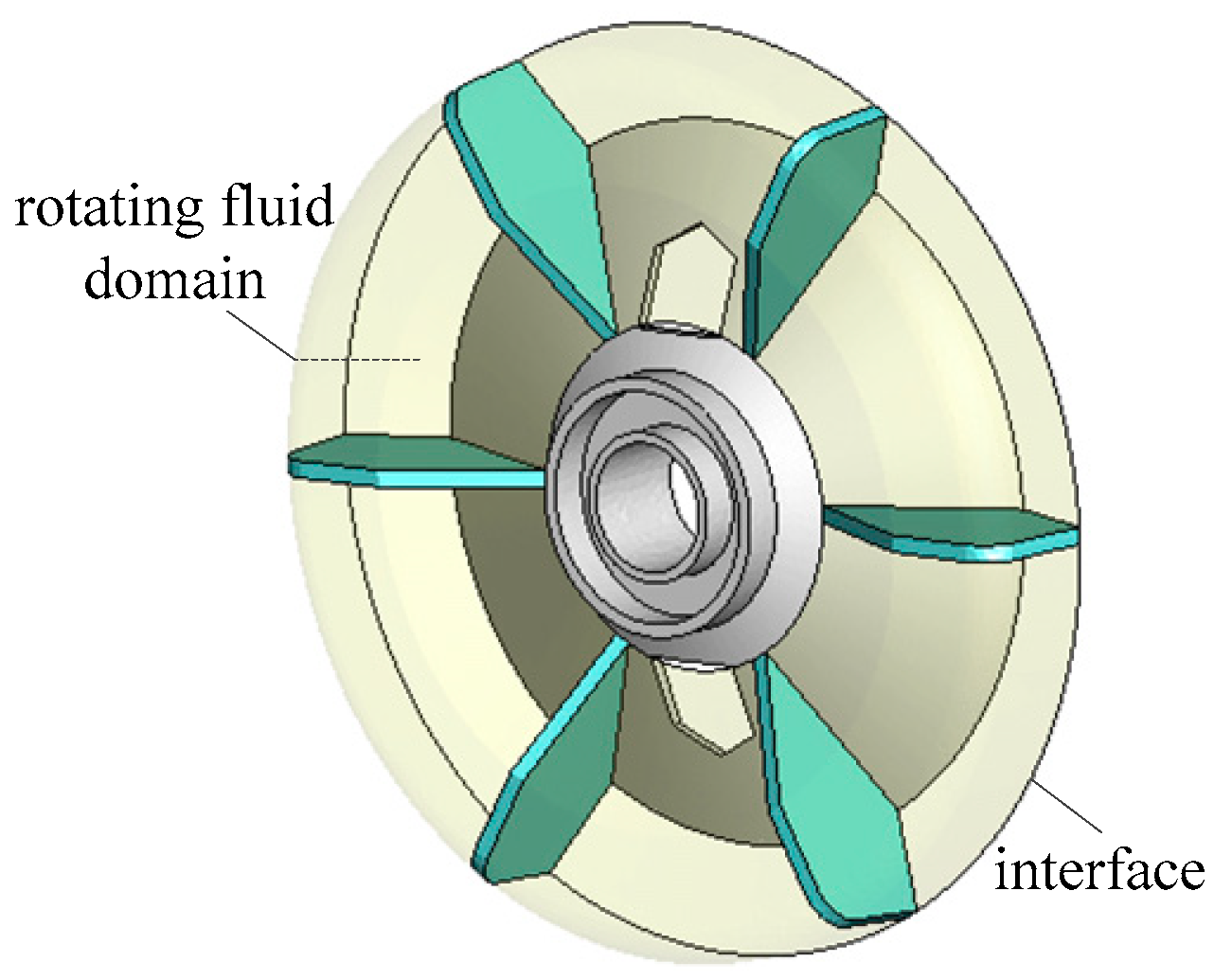
3.4. Boundary Conditions
3.5. Losses
4. Results and Discussion
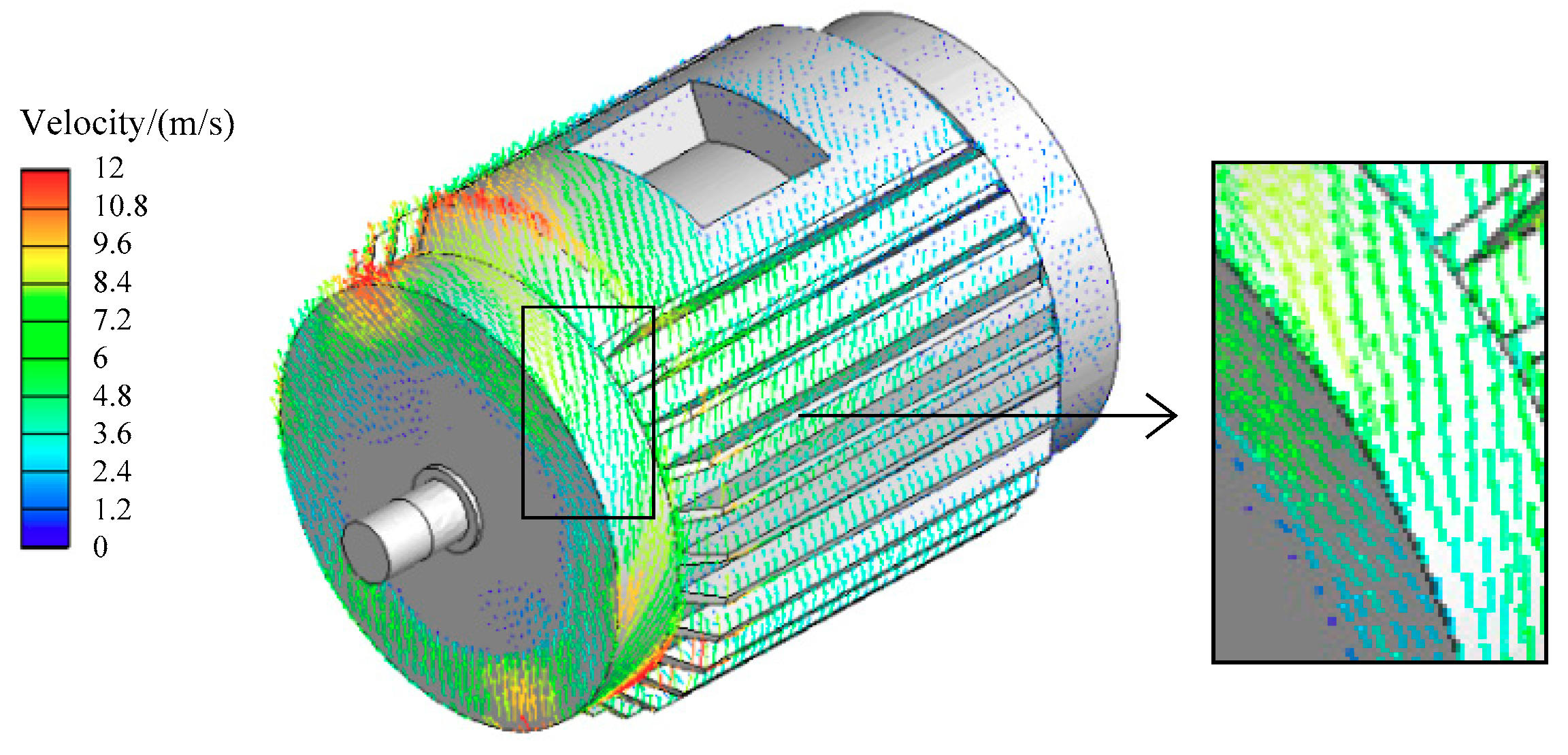
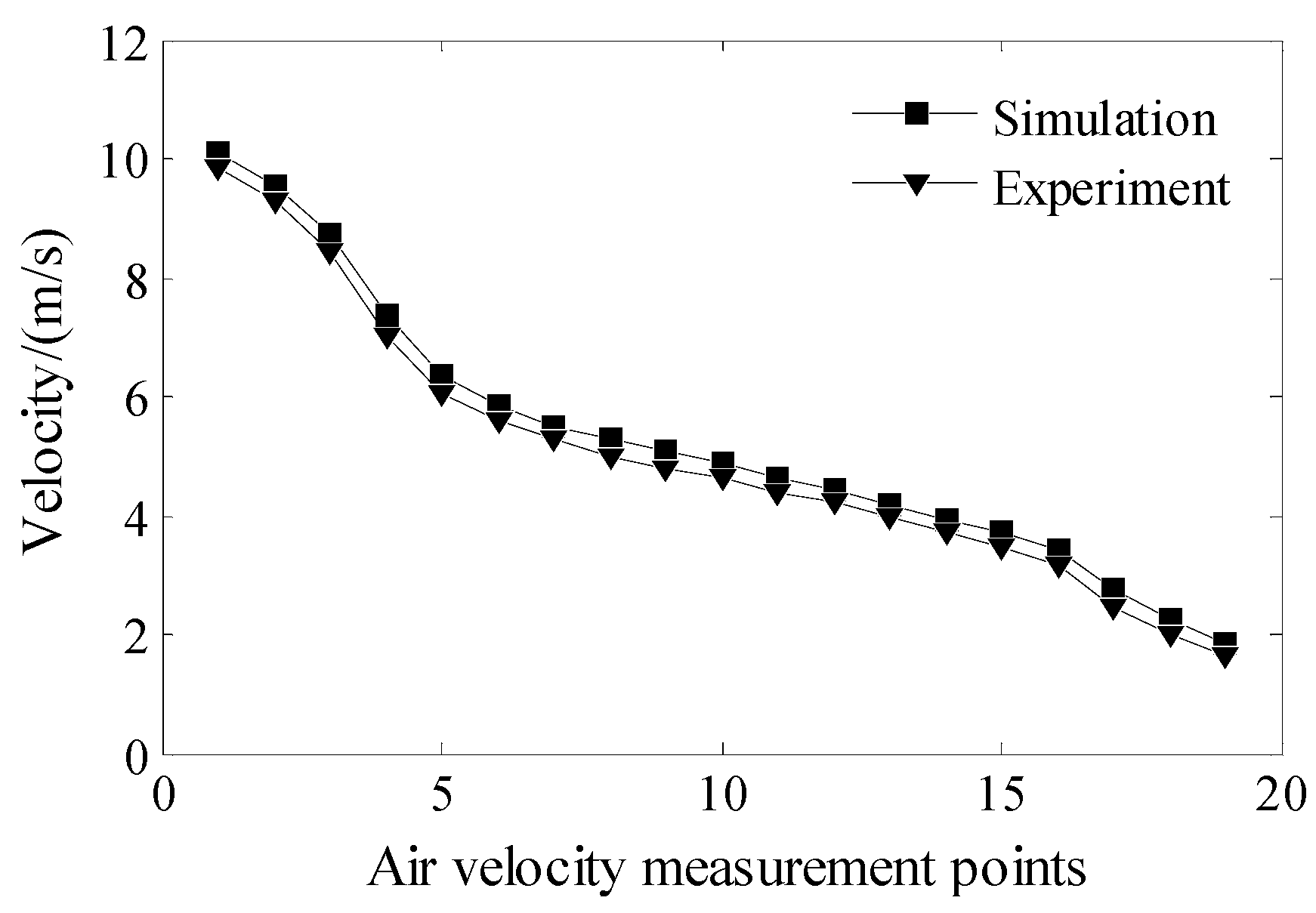
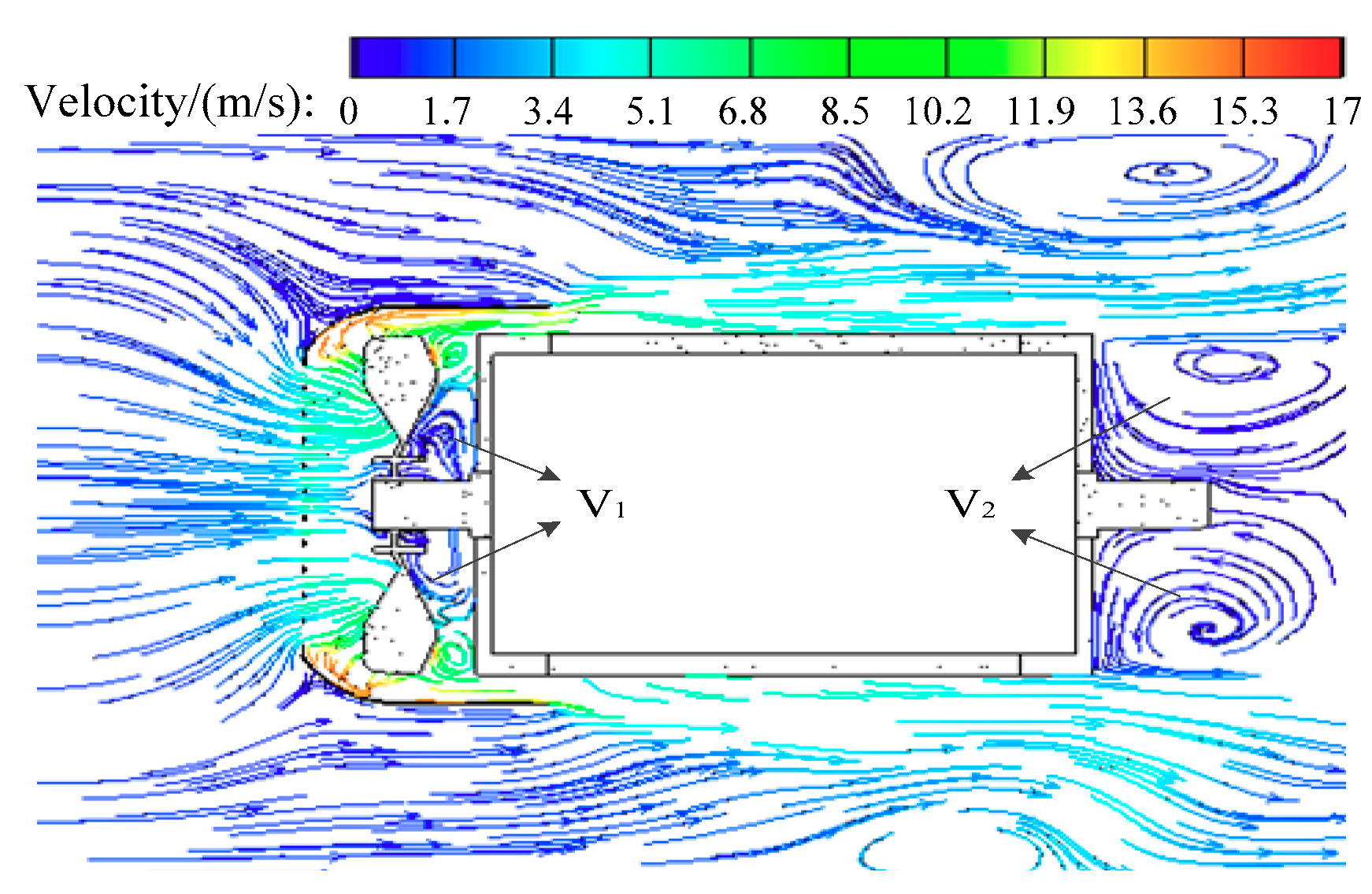
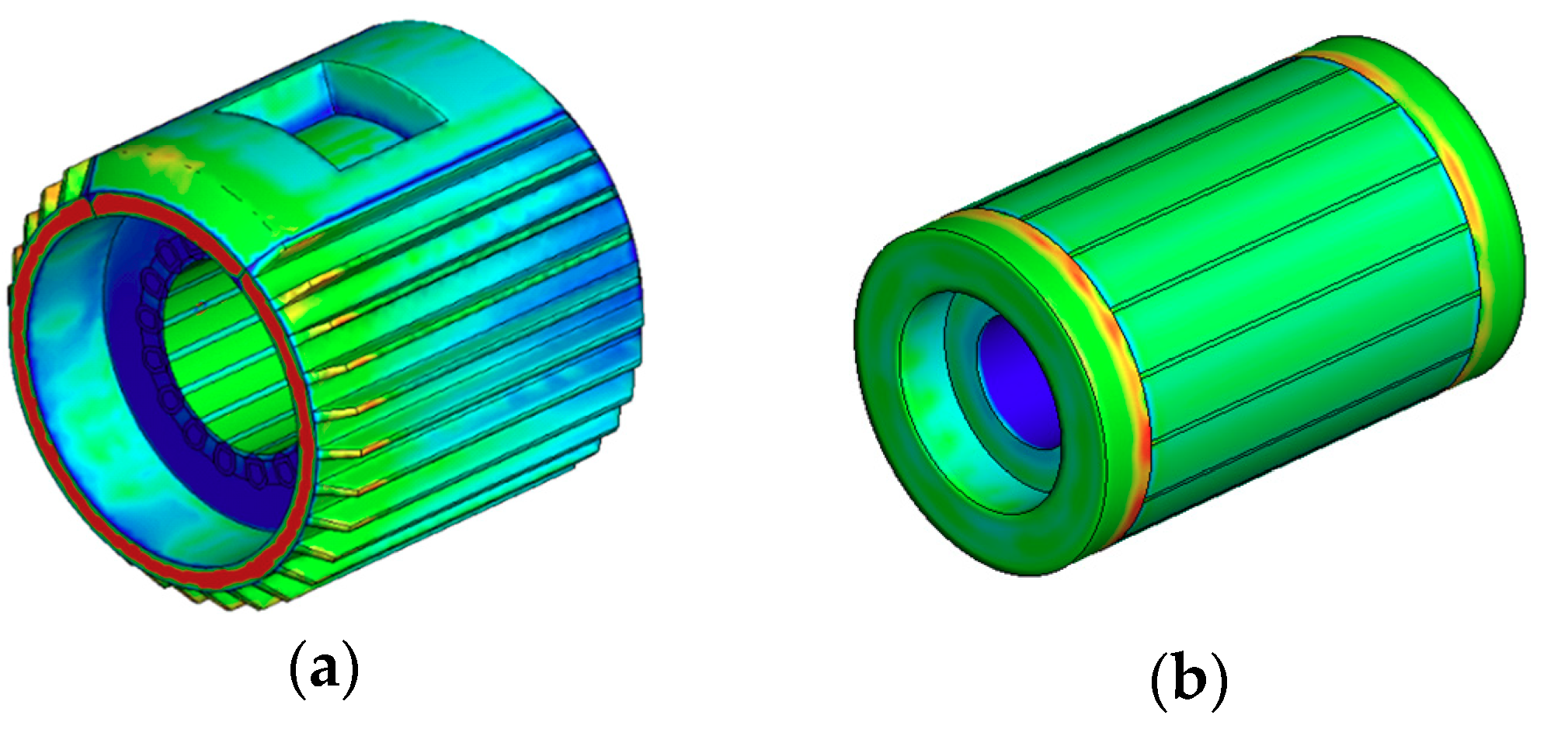
4.1. Fluid Field Results
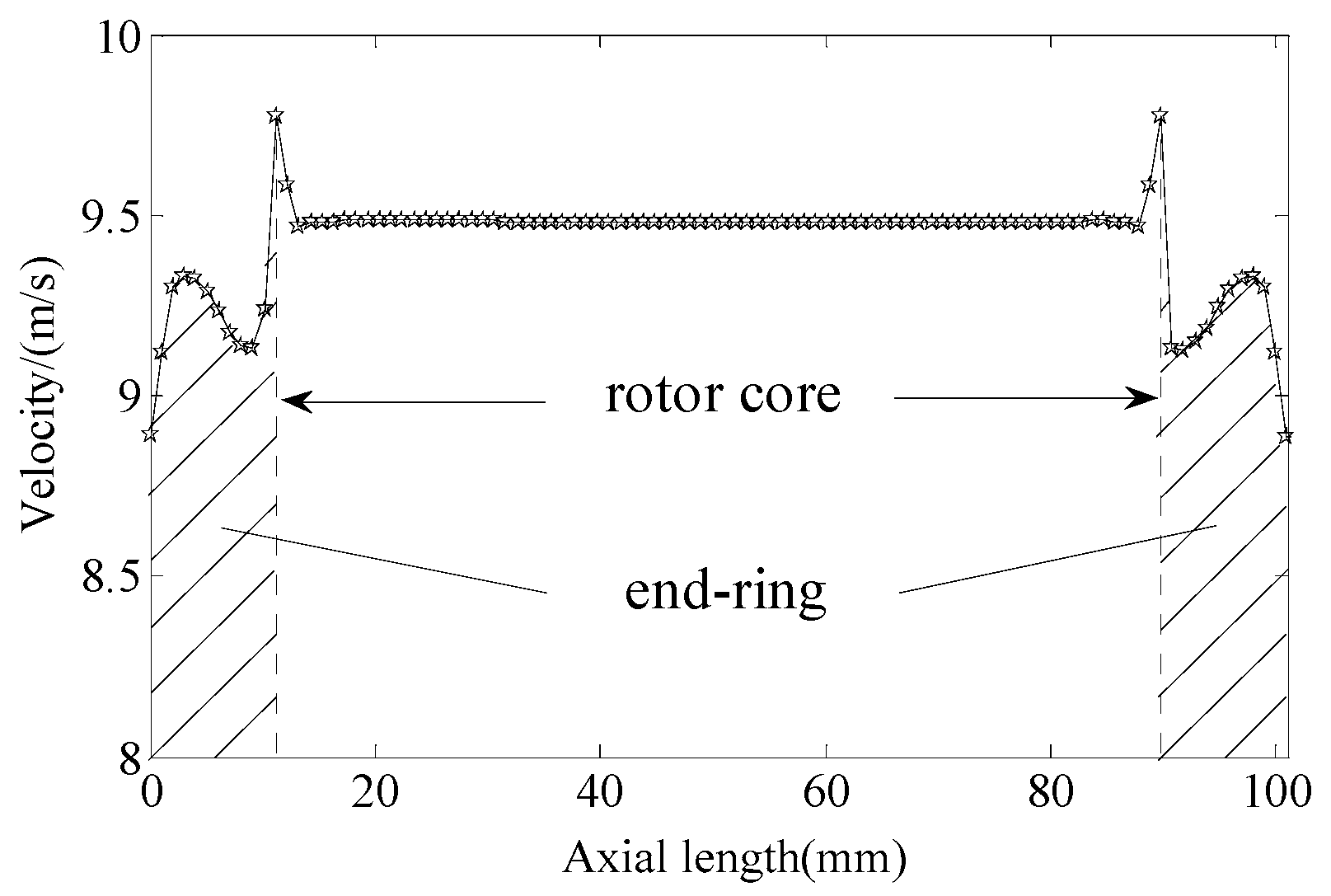
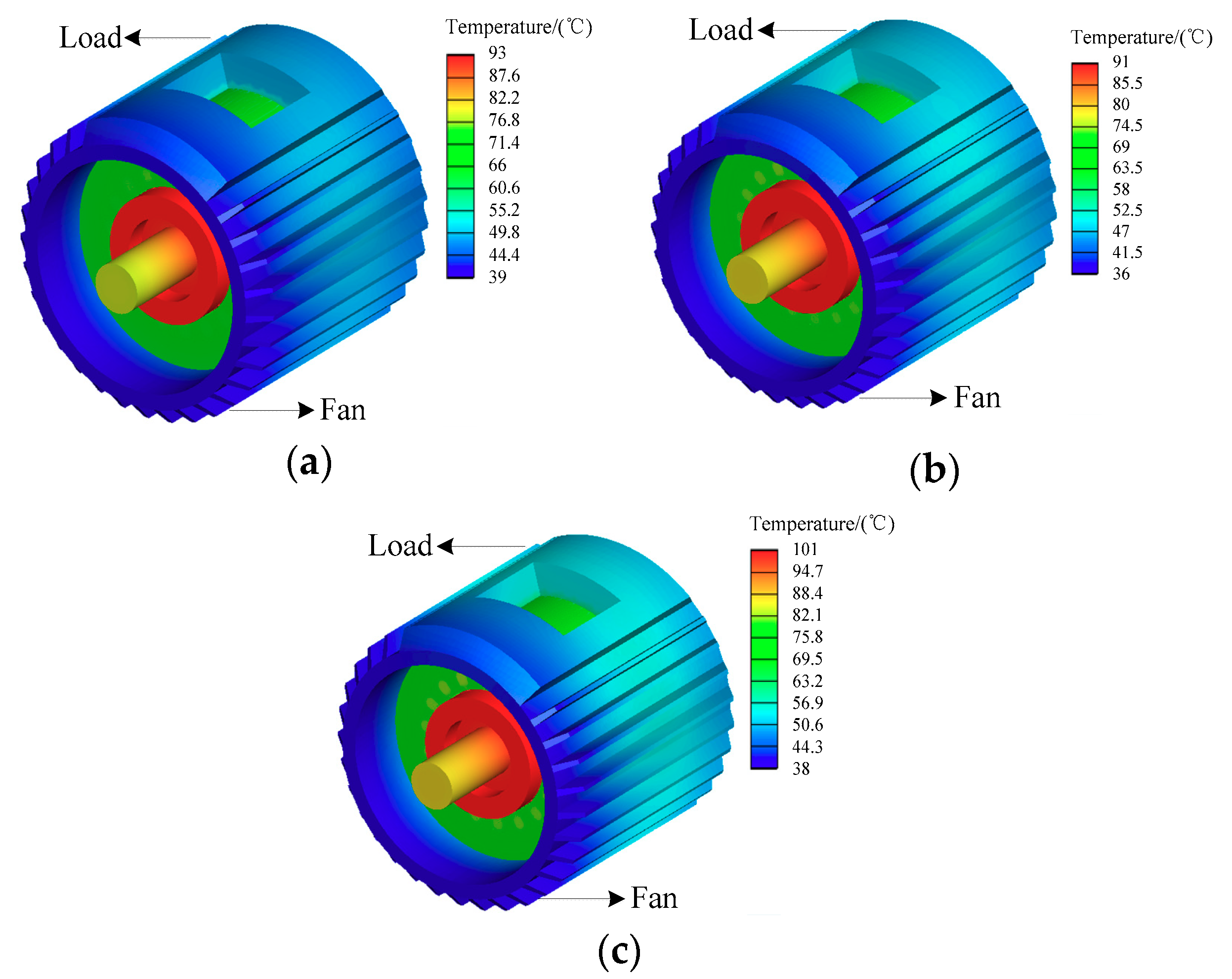
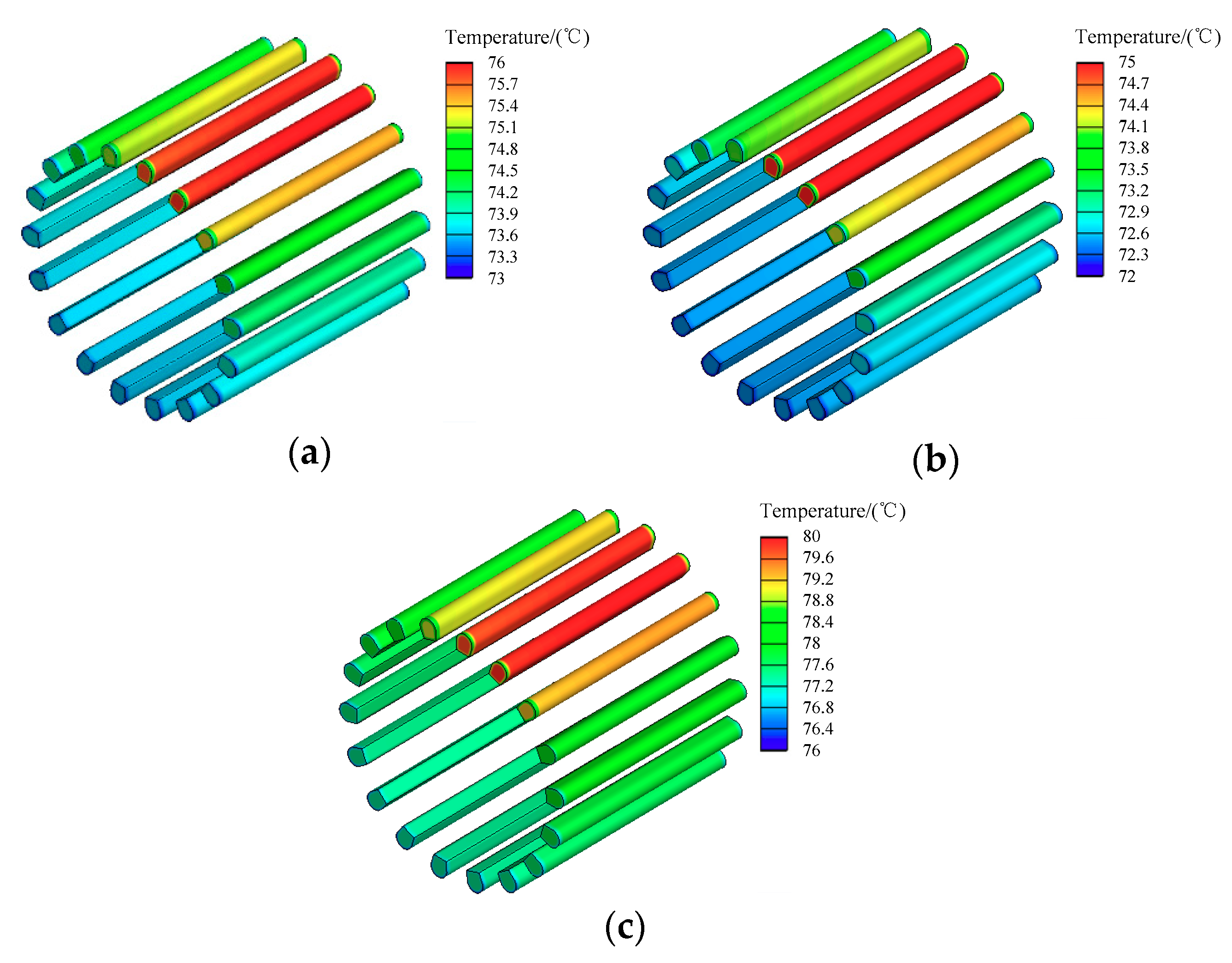
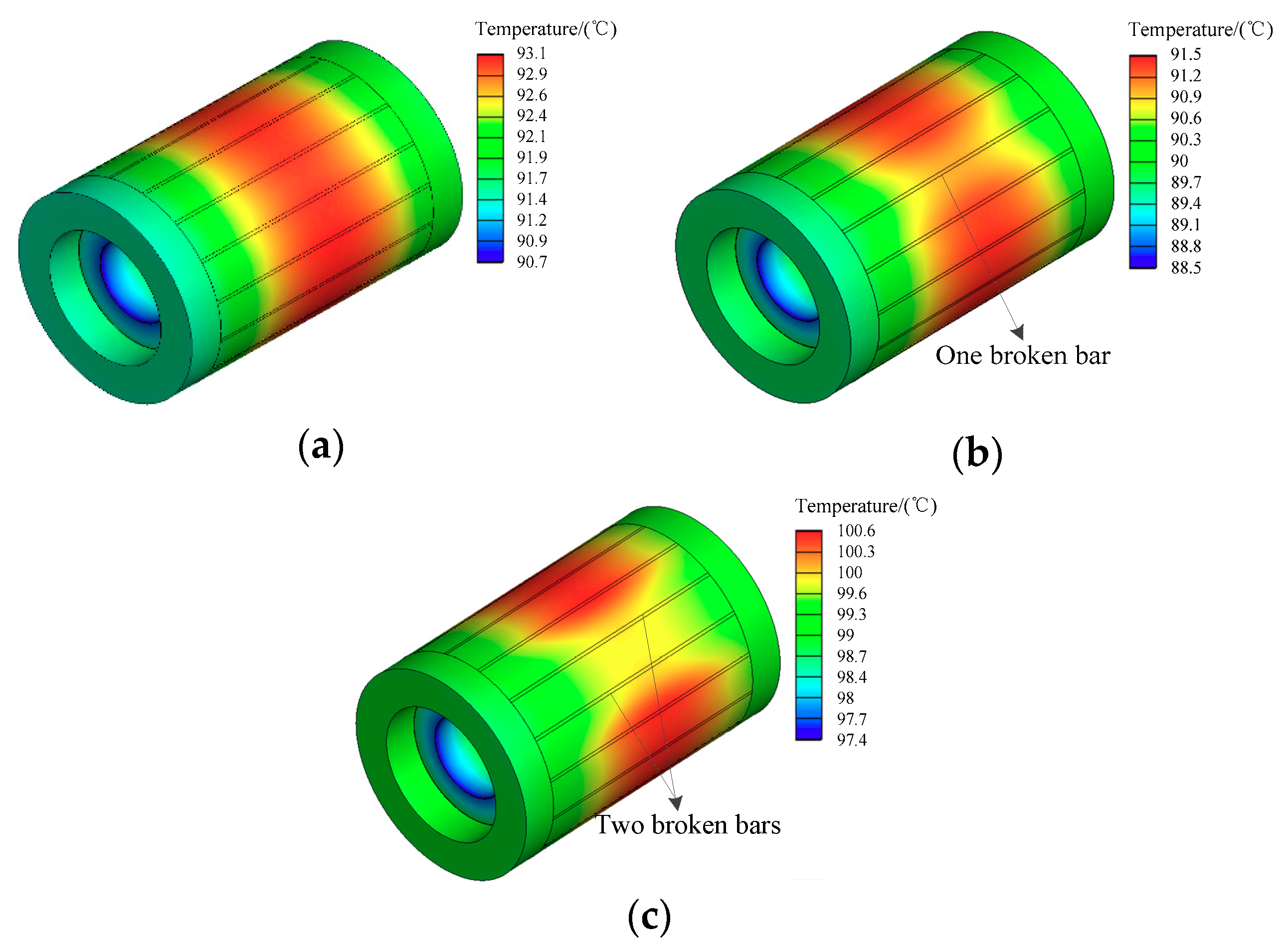
4.2. Thermal Field Results
5. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| λeq | equivalent heat conductivity of the insulation layer in the stator slots, W/m·k |
| δi | equivalent thickness of each insulating material, m |
| λi | average thermal conductivity of each material, W/m·k |
| Rc | thermal contact resistance, Ω |
| δ | gap length between the stator and motor frame, m |
| λ | heat conductivity, W/m·k |
| Aa | contact area between the stator and motor frame, m2 |
| Gk | turbulent generation ratio |
| μt | turbulence viscous coefficient, Pa·s |
| Cμ, C1ε, C2ε | constants |
| σk | turbulence Prandtl number (Pr number) of the k equation |
| σε | turbulence Prandtl number (Pr number) of the ε equation |
| T | temperature, K |
| Tf | fluid temperature, K |
| q | heat generation per unit volume, J/m2·s |
| α | surface heat transfer coefficient, W/m2·k |
| λx, λy, λz | thermal conductivity in x, y, z direction respectively, W/m·k |
| n | unit normal vector of the boundary |
| Sj | adiabatic surface |
| SS | heat transfer surface |
| Pcu | winding loss, W |
| Pal | bar loss, W |
| PFe | core loss, W |
| PΩ | mechanical loss, W |
| P∆ | stray loss, W |
| i | number of iterations |
| αi | coefficient of heat transfer for the th times iteration, W/m2·k |
| TW | surface temperature of solid located on the fluid-solid interface, K |
| ∆X | distance of two elements center, m |
| Tk | temperature obtained at the k times, K |
| ε1, ε2 | residual error |
References
- Nogay, H.S. Prediction of internal temperature in stator winding of three-phase induction motors with ann. Int. Trans. Electr. Energy Syst. 2011, 21, 120–128. [Google Scholar] [CrossRef]
- Arabab, N.; Wang, W. Temperature effect on steady state performance of an induction machine and a switched reluctance machine. In Proceedings of the 2014 IEEE Transportation Electrification Conference and Expo (ITEC), Dearborn, MI, USA, 15–18 June 2014; pp. 1–5. [Google Scholar]
- Arabab, N.; Wang, W.; Lin, C.; Hearron, J.; Fahimi, B. Thermal modelling and analysis of a double-stator switched reluctance motor. IEEE Trans. Energy Convers. 2015, 30, 1209–1217. [Google Scholar] [CrossRef]
- Jang, W.; Jahns, T.M. Coupled electromagnetic-Thermal analysis of electric machine including transient operation based on finite element techniques. IEEE Trans. Ind. Appl. 2015, 51, 1880–1889. [Google Scholar] [CrossRef]
- Li, W.L.; Ding, S.Y.; Jin, H.Y. Numerical calculation of large synchronous generator stator temperature fields based on coupled fields. Proc. CSEE 2005, 25, 129–134. [Google Scholar]
- Mrόz, J. Temperature field of a double squirrel cage motor during startup. IEE Proc.-Electr. Power Appl. 2005, 152, 643–671. [Google Scholar] [CrossRef]
- Staton, D.; Boglietti, A.; Cavagnino, A. Solving the more difficult aspects of electric motor thermal analysis in small and medium size industrial induction motors. IEEE Trans. Energy Convers. 2005, 20, 620–628. [Google Scholar] [CrossRef]
- Li, L.Y.; Sun, Z.Y.; Huang, X.Z.; Cao, J. Thermal analysis of high speed motor based on flow field calculation considering tooth slots effects. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 12 November 2011; pp. 1–4. [Google Scholar]
- Liu, X.; Yu, H.; Shi, Z. Electromagnetic-fluid-thermal field Calculation and analysis of a permane magnet linear motor. In Proceedings of the 2016 IEEE Conference on Electromagnetic Field Computation (CEFC), Miami, FL, USA, 13–16 November 2016. [Google Scholar]
- Kong, X.; Wang, F.; Xing, J. Temperature rise calculation of high speed PM machine based on thermal circuit method and 3D fluid field method. In Proceedings of the 2011 International Conference on Electrical Machines and Systems, Beijing, China, 20–23 August 2011; pp. 1–5. [Google Scholar]
- Howey, D.A.; Holmes, A.S.; Pullen, K.R. Measurement and CFD prediction of heat transfer in air-cooled disc type electrical machines. IEEE Trans. Ind. Appl. 2009, 47, 1716–1723. [Google Scholar] [CrossRef]
- Kral, C.; Haumer, A.; Haigis, M.; Lang, H.; Kapeller, H. Comparison of a CFD analysis and a thermal equivalent circuit model of a TEFC induction machine with measurements. IEEE Trans. Energy Convers. 2009, 24, 809–818. [Google Scholar] [CrossRef]
- Mustafa, M.O.; Nikolakopoulos, G.; Gustafsson, T. Broken bars fault diagnosis based on uncertainty bounds violation for three-phase induction motors. Int. Trans. Electr. Energy Syst. 2015, 25, 304–325. [Google Scholar] [CrossRef]
- Rangel-Magdaleno, J.D.J.; Romero-Troncoso, R.D.J.; Osornio-Rios, R.A. Novel methodology for online half broken bar detection on induction motors. IEEE Trans. Instrum. Meas. 2009, 58, 1690–1698. [Google Scholar] [CrossRef]
- Mohammed, O.A.; Abed, N.Y.; Ganu, S. Modeling and characterization of induction motor internal faults using finite element and discrete wavelet transforms. IEEE Trans. Magn. 2006, 42, 3434–3436. [Google Scholar] [CrossRef]
- Garcia-Perez, A.; Romero-Troncoso, R.J.; Cabal-Yepez, E.; Cabal-Yepez, E.; Contreras-Medina, L.M. Startup current analysis of incipient broken rotor bar in induction motors using high-resolution spectral analysis. In Proceedings of the 8th IEEE Symposium on Diagnostics for Electrical Machines, Power Electronics & Drives (SDEMPED), Bologna, Italy, 5–8 September 2011; pp. 657–663. [Google Scholar]
- Trzynadlowski, A.M.; Ritchie, E. Comparative investigation of diagnostic media for induction motors: A case of rotor cage faults. IEEE Trans. Ind. Electron. 2000, 47, 1092–1099. [Google Scholar] [CrossRef]
- Eltabach, M.; Charara, A.; Zein, I. A comparison of external and internal methods of signal spectral analysis for broken rotor bars detection in induction motors. IEEE Trans. Ind. Electron. 2004, 5, 107–121. [Google Scholar] [CrossRef]
- Rangel-Magdaleno, J.; Peregrina-Barreto, H.; Ramirez-Cortes, J.; Morales-Caporal, R.; Cruz-Vega, I. Vibration analysis of partially damaged rotor bar in induction motor under different load condition using DWT. Shock Vib. 2016, 2016, 3530464. [Google Scholar] [CrossRef]
- Sprooten, J.; Maun, J.C. Influence of saturation level on the effect of broken bars in induction motors using fundamental electromagnetic laws and finite element simulations. IEEE Trans. Energy Convers. 2009, 24, 557–564. [Google Scholar] [CrossRef]
- Борисенко, В.Γ.Д.А.И.; Яковпев, А.И. Air Mechanics and Heat Transfer in Electrical Machine; China Machine Press: Beijing, China, 1974; pp. 62–80. [Google Scholar]
- Huang, G.Z.; Fu, F.L. Small and Medium-Sized Rotating Motor Design Handbook; China Electric Power Publishing: Beijing, China, 2007; pp. 377–390. [Google Scholar]
- Anderson, J.D. Computational Fluid Dynamics, 2nd ed.; Springer: Berlin, Germany, 1995; pp. 32–64. [Google Scholar]
- Rajagopal, M.S.; Seetharamu, K.N. Transent thermal analysis of induction motors. In Proceedings of the International Conference on Power Electronics, Drives and Energy Systems for Industrial Growth, New Delhi, India, 8–11 January 1996; pp. 62–69. [Google Scholar]
- Chauveau, E.; Zaim, E.H.; Trichet, D.; Fouladgar, J. A statistical approach of temperature calculation in electrical machines. IEEE Trans. Magn. 2000, 36, 1826–1829. [Google Scholar] [CrossRef]
- Chen, S.K. Design of Electrical Machines; China Machine Press: Beijing, China, 2000; pp. 237–241. [Google Scholar]
- Xie, Y. Performance evaluation and thermal fields analysis of induction motor with broken rotor bars located at different relative positions. IEEE Trans. Magn. 2010, 46, 1243–1250. [Google Scholar]
- Xie, Y. Characteristic performance analysis of squirrel cage induction motor with broken bars. IEEE Trans. Magn. 2009, 45, 759–766. [Google Scholar]
- Tudorache, T.; Taras, P.; Fireteanu, V. Finite element diagnosis of squirrel cage induction motors with rotor bar faults. In Proceedings of the 10th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 18–19 May 2006; pp. 2–3. [Google Scholar]

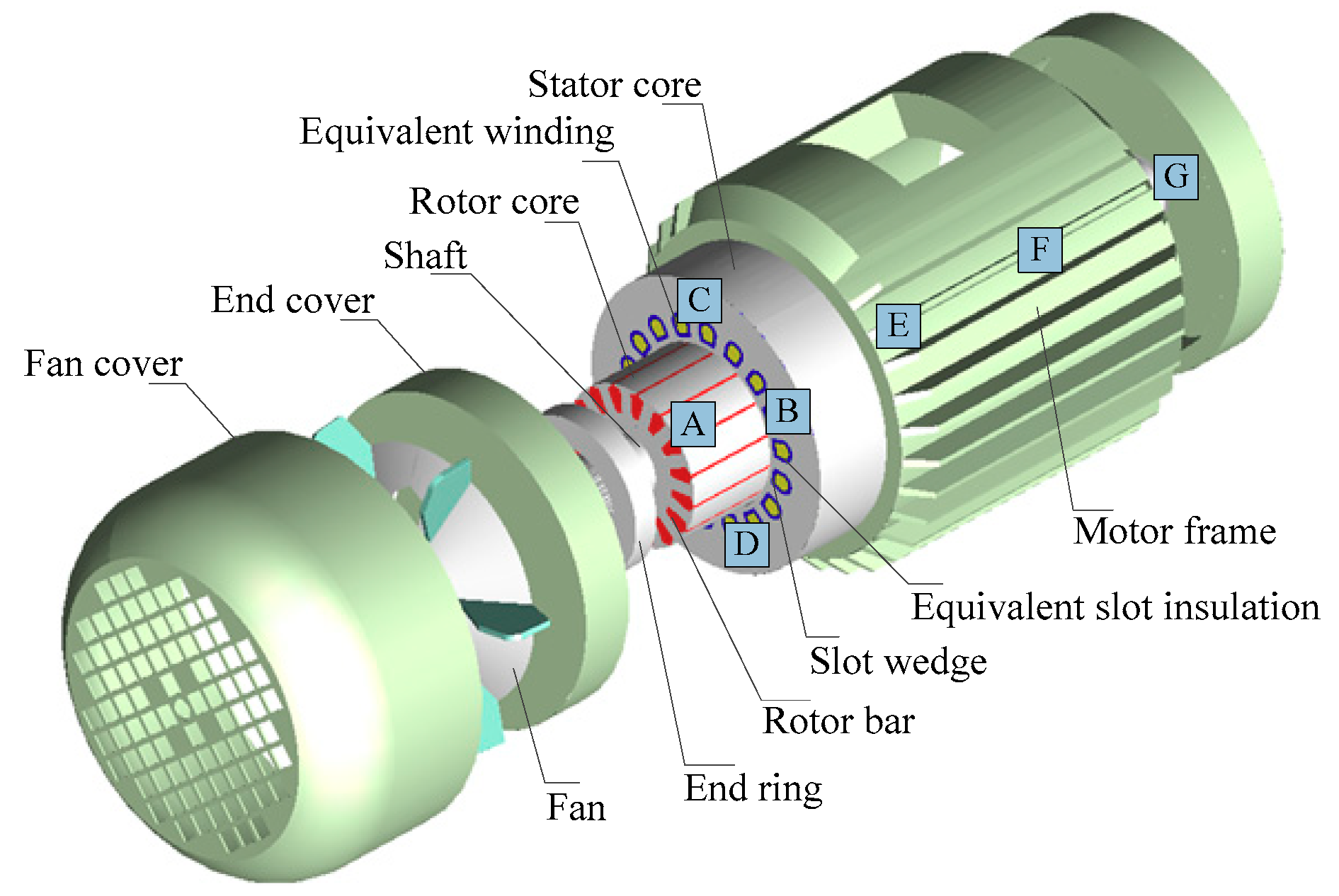
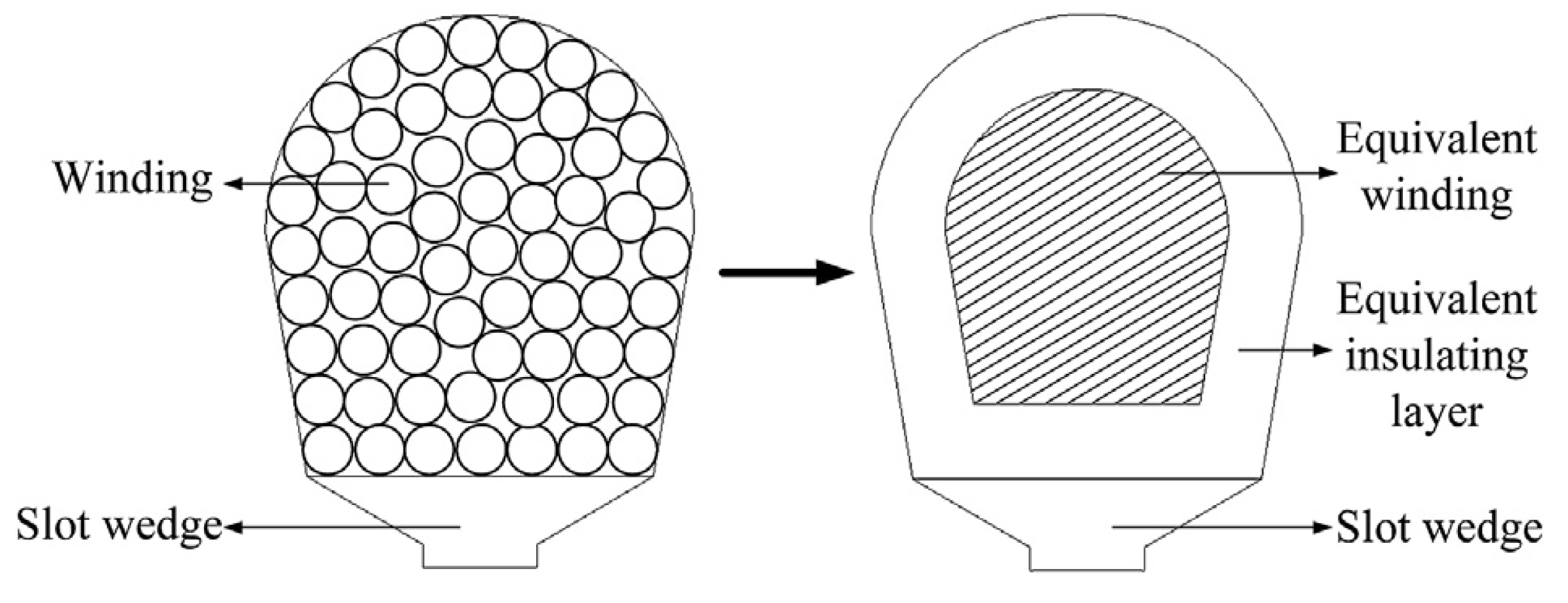


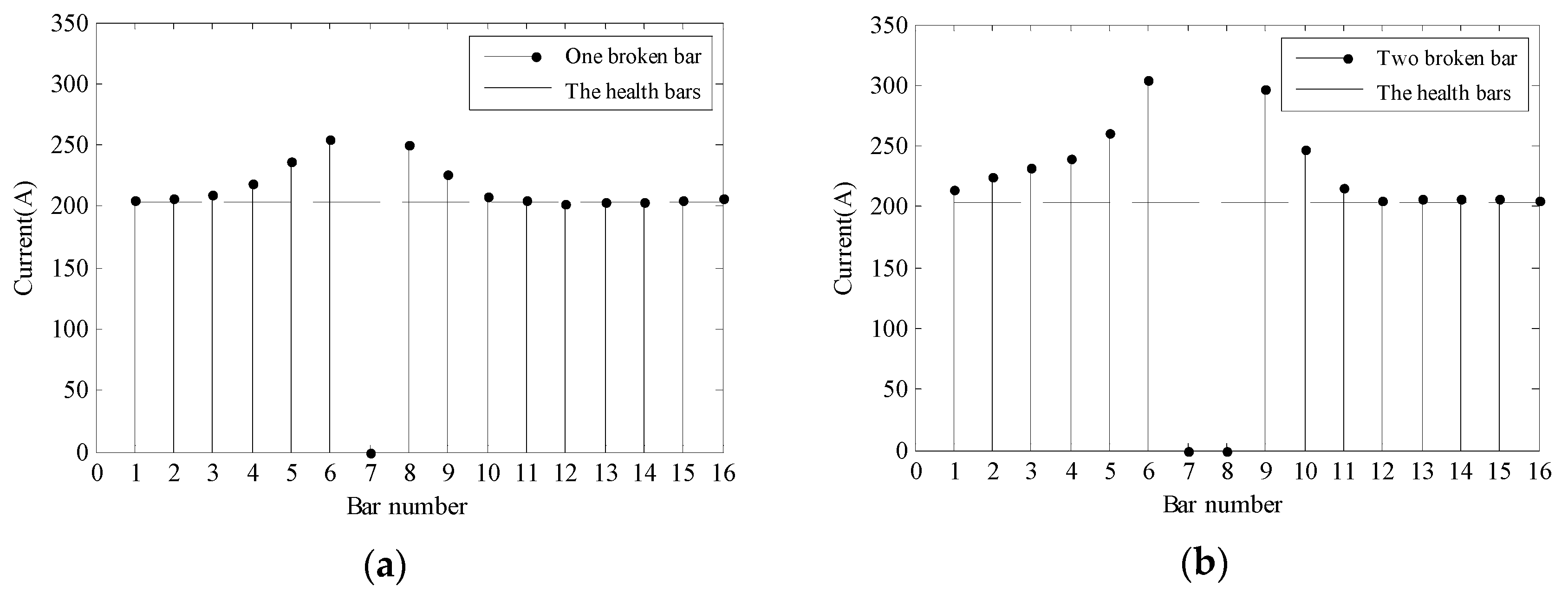
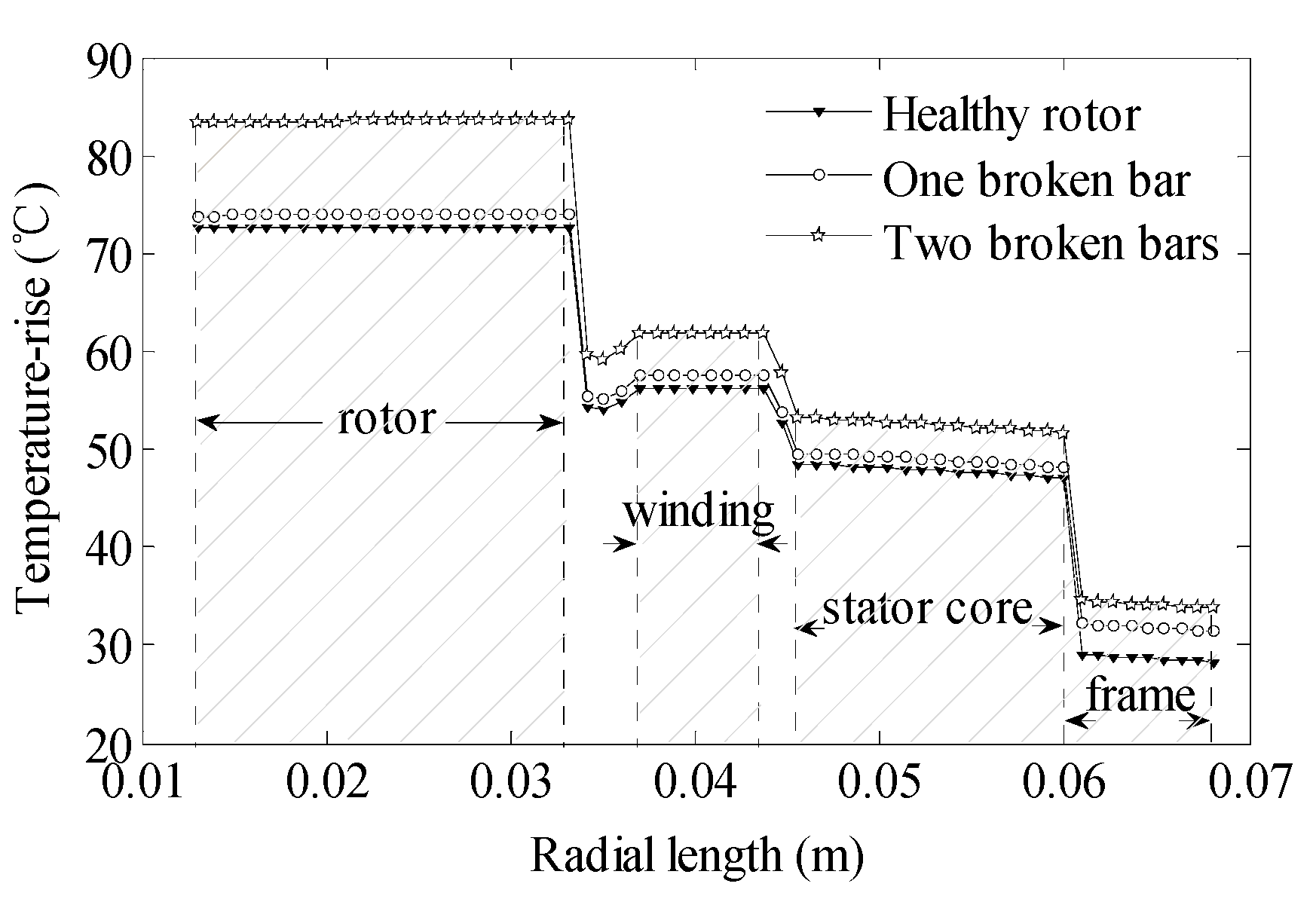
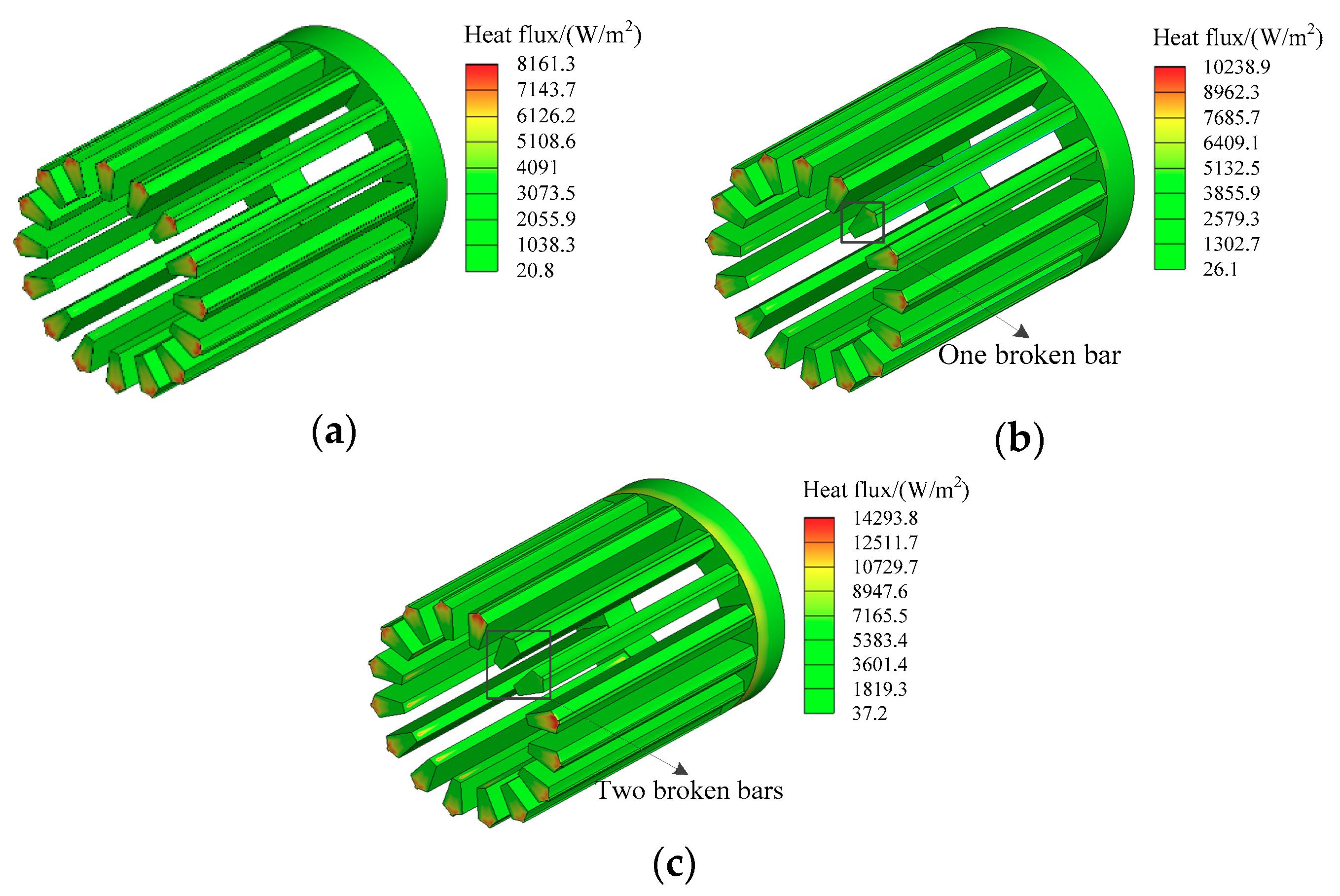
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Rated power | 1.1 KW | Stator outer radius | 120 mm |
| Rated voltage | 380 V | Stator inner radius | 67 mm |
| Number of stator slots | 18 | Rotor outer radius | 66.4 mm |
| Number of rotor slots | 16 | Air-gap length | 0.3 mm |
| Material Type | Name | Density (kg/m3) | Specific Heat (j/kg−k) | Thermal Conductivity (w/m−k) | Viscosity (kg/m−s) |
|---|---|---|---|---|---|
| Fluid | Air | 1.225 | 1006.43 | 0.0242 | 1.7894 × 10−5 |
| Solid | Slot wedge | 2150 | 1200 | 0.5 | |
| Solid | Steel | 7650 | 502.48 | 48 | |
| Solid | Iron core | 7900 | 477.3 | 46 | |
| Solid | Equivalent insulation | 1850 | 1700 | 0.287 | |
| Solid | Copper | 8978 | 381 | 398 | |
| Solid | Aluminum | 2719 | 871 | 202.4 |
| Boundary/Cell Zone | Condition | |
|---|---|---|
| in | Pressure-inlet | Ptotal = 0 Pa |
| out | Pressure-outlet | Ptotal = 0 Pa |
| wall | Stationary wall | No slip |
| inner wall of stator | Stationary wall | No slip |
| outer wall of rotor | Moving wall | No slip |
| interface | Interface | - |
| rotating fluid domain | Angular velocity | 2830 rad/min |
| Motor Condition | Measured Positions | Test Value | Calculated Value | Test Temperature-Rise | Calculated Temperature-Rise |
|---|---|---|---|---|---|
| Healthy rotor (the ambient Temperature 20.5 °C) | A | 91.1 | 93.1 | 70.6 | 72.6 |
| B | 68.1 | 69.4 | 47.6 | 48.9 | |
| C | 76.6 | 76.0 | 56.1 | 55.5 | |
| D | 73.9 | 73.6 | 53.4 | 53.1 | |
| F | 51.2 | 49.2 | 30.7 | 28.7 | |
| One broken bar (the ambient Temperature 16.5 °C) | A | 89.2 | 91.1 | 72.7 | 74.6 |
| B | 68.0 | 70.1 | 51.5 | 53.6 | |
| C | 77.3 | 74.9 | 60.8 | 58.4 | |
| D | 74.3 | 72.5 | 57.8 | 56.0 | |
| F | 50.3 | 48.3 | 33.8 | 31.8 | |
| Two broken bars (the ambient Temperature 17 °C) | A | 99.3 | 100.2 | 82.3 | 83.2 |
| B | 74.4 | 76.7 | 57.4 | 59.7 | |
| C | 83.9 | 79.8 | 66.9 | 62.8 | |
| D | 79.5 | 77.3 | 62.5 | 60.3 | |
| F | 53.4 | 51.1 | 36.4 | 34.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, Y.; Guo, J.; Chen, P.; Li, Z. Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load. Energies 2018, 11, 2024. https://doi.org/10.3390/en11082024
Xie Y, Guo J, Chen P, Li Z. Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load. Energies. 2018; 11(8):2024. https://doi.org/10.3390/en11082024
Chicago/Turabian StyleXie, Ying, Jinpeng Guo, Peng Chen, and Zhiwei Li. 2018. "Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load" Energies 11, no. 8: 2024. https://doi.org/10.3390/en11082024
APA StyleXie, Y., Guo, J., Chen, P., & Li, Z. (2018). Coupled Fluid-Thermal Analysis for Induction Motors with Broken Bars Operating under the Rated Load. Energies, 11(8), 2024. https://doi.org/10.3390/en11082024





