An Improved Algorithm for Optimal Load Shedding in Power Systems
Abstract
1. Introduction
2. Literature Review
- High Accuracy: The proposed algorithm can significantly improve the voltage magnitudes of the power system buses while shedding the least amount of load. The high accuracy comes from utilizing GA in the proposed algorithm.
- Fast Convergence: The proposed algorithm uses PSO to speed up the operation of GA i.e., it replaces the time consuming local search mechanism of GA with the highly efficient global search mechanism of PSO. This results in fast convergence for the proposed algorithm.
3. Preliminary Background
3.1. Fast Voltage Stability Index
3.2. Genetic Algorithms
- Initialization: Generate an initial population of random chromosomes of size N: x1, x2, ...…, xN.
- Fitness: The fitness function creates the basis for choosing chromosomes that will be coupled during reproduction. Calculate the fitness of each individual chromosome: f(x1), f(x2), ……, f(xN).
- Selection: Parent chromosomes are selected with a probability related to their fitness.
- Crossover: Selected parents are crossed with probability Pcross resulting in a new child.
- Mutation: New child modified with probability Pmut.
- Acceptance and Replacement: Accept new children if found better in fitness than the previous generation.
- Termination Criteria: If a maximum number of iterations reached or best solution achieved terminate the algorithm. Otherwise, go to step 2.
3.3. Particle Swarm Optimization
- Initialization: Produce an initial population of random generated particles of size M: y1, y2, ......, yM
- Fitness: The criteria for choosing particles is based on their fitness. Calculate the fitness of each individual particle. f(y1), f(y2), ...... f(yM)
- Selection: Update each particle’s personal best solution Ppbest by comparing the current Ppbest with f(yi).
- Velocity Update: Update the velocity for all particles using the PSO velocity equation
- Position Update: Update the position for all particles using the PSO position equation
- Evaluation: Evaluate the fitness function of all particles (with updated position and velocity) and find and update the global best solution Pgbest.
- Termination Criteria: If a maximum number of iterations reached or best solution achieved terminate the algorithm. Otherwise, go to step 2.
4. Problem Formulation
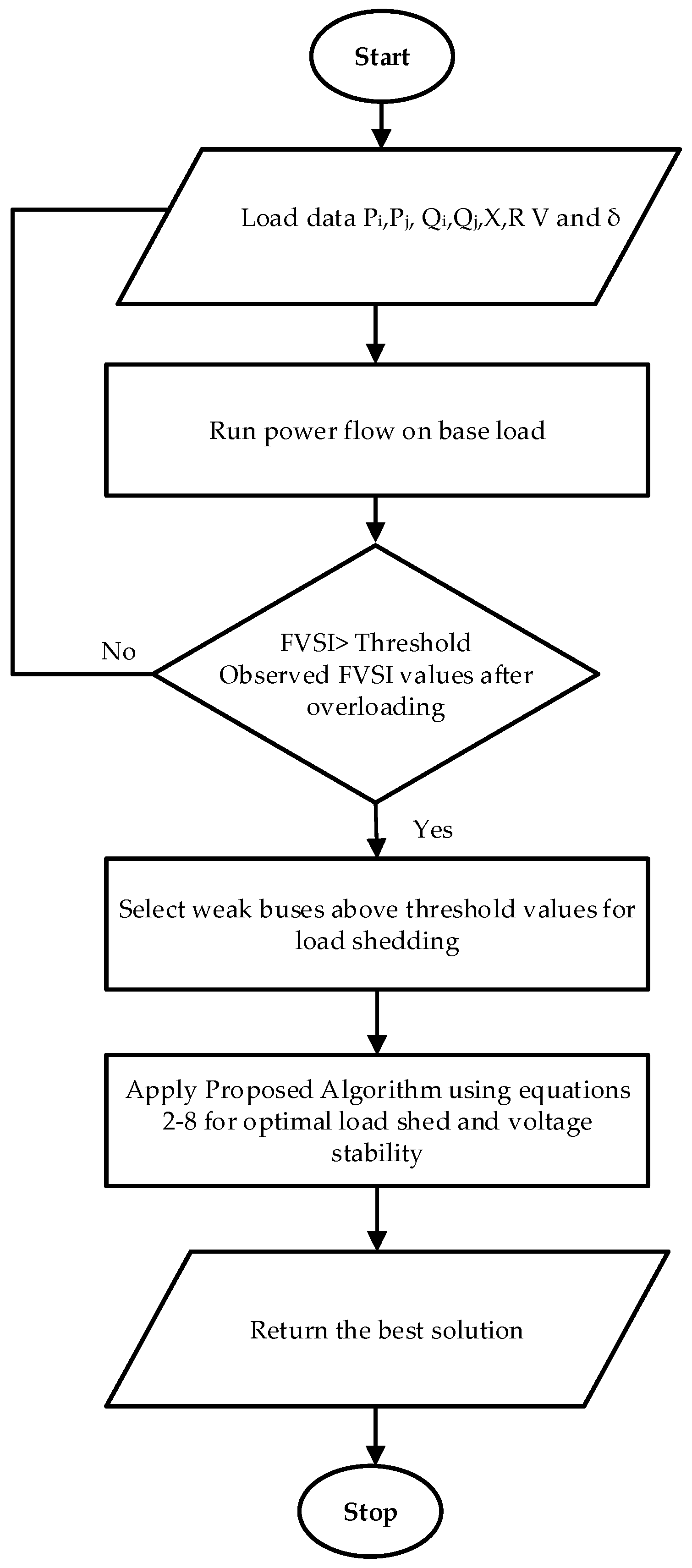
5. Proposed UVLS Algorithm
- (1)
- An initial population of size Psize is initialized with random candidate solutions.
- (2)
- Repeat for NIter number of iterations
- (i)
- Optimize the current population using PSO i.e., move the particles in the population towards the global best solution in PSO.Select weak buses based on above threshold values of FVSI
- (ii)
- Initialize an empty array Parents.
- (iii)
- Sort the population in ascending order of cost function for each candidate solution and select Psize − Ksize candidate solution with the minimum cost and add them to an array named Parents.
- (iv)
- Initialize an empty array Children.
- (v)
- For each pair of parents P1 and P2 in Parents
- (a)
- Produce two off springs Child1 and Child2 using the GA crossover function with probability Pcross.
- (b)
- Apply the GA mutation function on Child1 with probability Pmut.
- (c)
- Apply the GA mutation function on Child2 with probability Pmut.
- (d)
- Add Child1 and Child2 to the array Children.
- (vi)
- Replace the current population with Children keeping Ksize candidate solutions from the current population. This produces the next generation.
- (vii)
- Evaluate the cost function on all the candidate solutions in the new population.
- (viii)
- Find and assign the candidate solution which gives the minimum value of the cost function to Sbest.
- (3)
- Return the best solution Sbest.
- (1)
- Calculate the size of the population Npar.
- (2)
- Initialize the global best solution Pgbest to a maximum value φ.
- (3)
- For each particle P in the population repeat the following steps:
- (i)
- Initialize the particle’s best solution Ppbest to a maximum value φ.
- (ii)
- Calculate the velocity of the current particle using PSO’s velocity function.
- (iii)
- Calculate the position of the current particle using PSO’s position function.
- (iv)
- If the current position evaluates into a lower value of the cost function as compared to Ppbest then assign this value to Ppbest.
- (v)
- If the particle’s current best solution has a lower value as compared to Pgbest then assign this value to Pgbest.
- (vi)
- Update the current particle’s position in the population i.e., replace the current particle (candidate solution) with the optimized solution.
| Algorithm 1. Algorithm for Obtaining Optimal Load Shed | |
| Input: Popsize, Ksize, NIter, Pcross, Pmut | |
| Output: SB | |
| 1 | Pop ← Initialize random population (Psize) |
| 2 | for iter = 1 to NIter do |
| // Update Population using PSO function | |
| 3 | Pop = PSO (Pop) |
| 4 | Parents = [] |
| // Selection | |
| 5 | Parents ← Select Parents Based on Minimum Cost from Population |
| // Crossover | |
| 6 | Children ← [] |
| 7 | for each P1, P2 ∈ Parents do |
| 8 | Child1, Child2 ← Crossover (P1, P2, Pcross) |
| // Mutation | |
| 9 | Child1 ← Mutate (Child1, Pmut) |
| 10 | Child2 ← Mutate (Child2, Pmut) |
| 11 | Add Child1 and Child2 to Children |
| 12 | end |
| // Replace Population with New Generation and keep Ksize Candidates from current Generation | |
| 13 | Pop ← Replace (Pop, Children, Ksize) |
| 14 | θ ← f (population) |
| 15 | Sbest ← Candidate Solution with a minimum value of θ |
| 16 | end |
| 17 | Return Sbest |
| 18 | Function PSO (Pop) |
| // Calculate the Size of the Population | |
| 19 | Npar ← Size(Pop) |
| 20 | Pgbest = φ |
| // Randomly move Particles to the optimal Solution | |
| 21 | for each P ∈ Population do |
| 22 | Ppbest = φ |
| 23 | PVel ← Update Velocity (PVel, Ppbest, Pgbest) |
| 24 | PPos ← Update Position (PPos, PVel) |
| 25 | if f (PPos) ≤ Ppbest then |
| 26 | Ppbest ← f (PPos) |
| 27 | if Ppbest ≤ Pgbest then |
| 28 | Pgbest ← Ppbest |
| // Update the Current Particle’s Position in the Population. | |
| 29 | Pop(P) ← PPos |
| 30 | end |
| 31 | end |
| 32 | end |
| 33 | Return Pop |
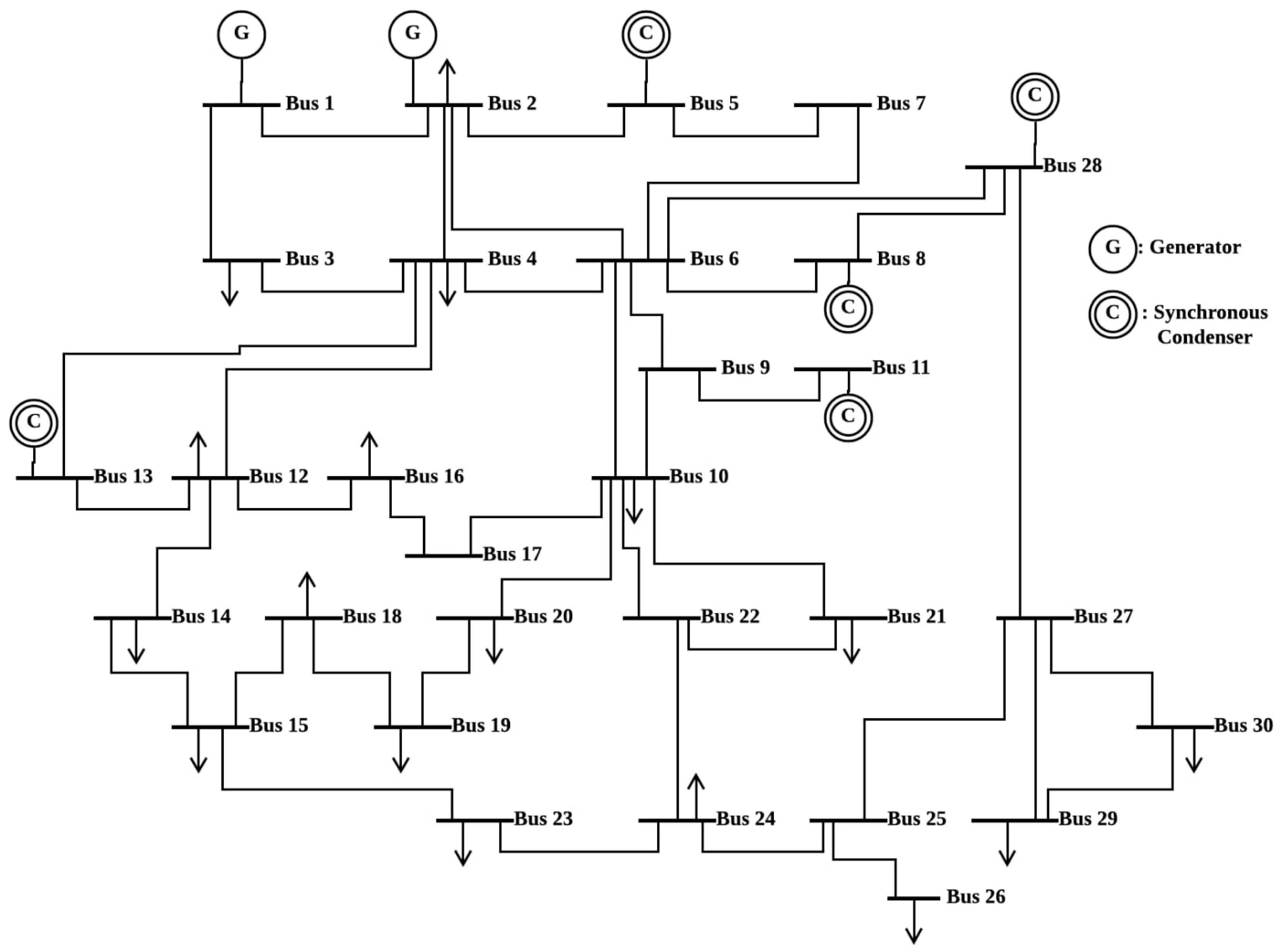
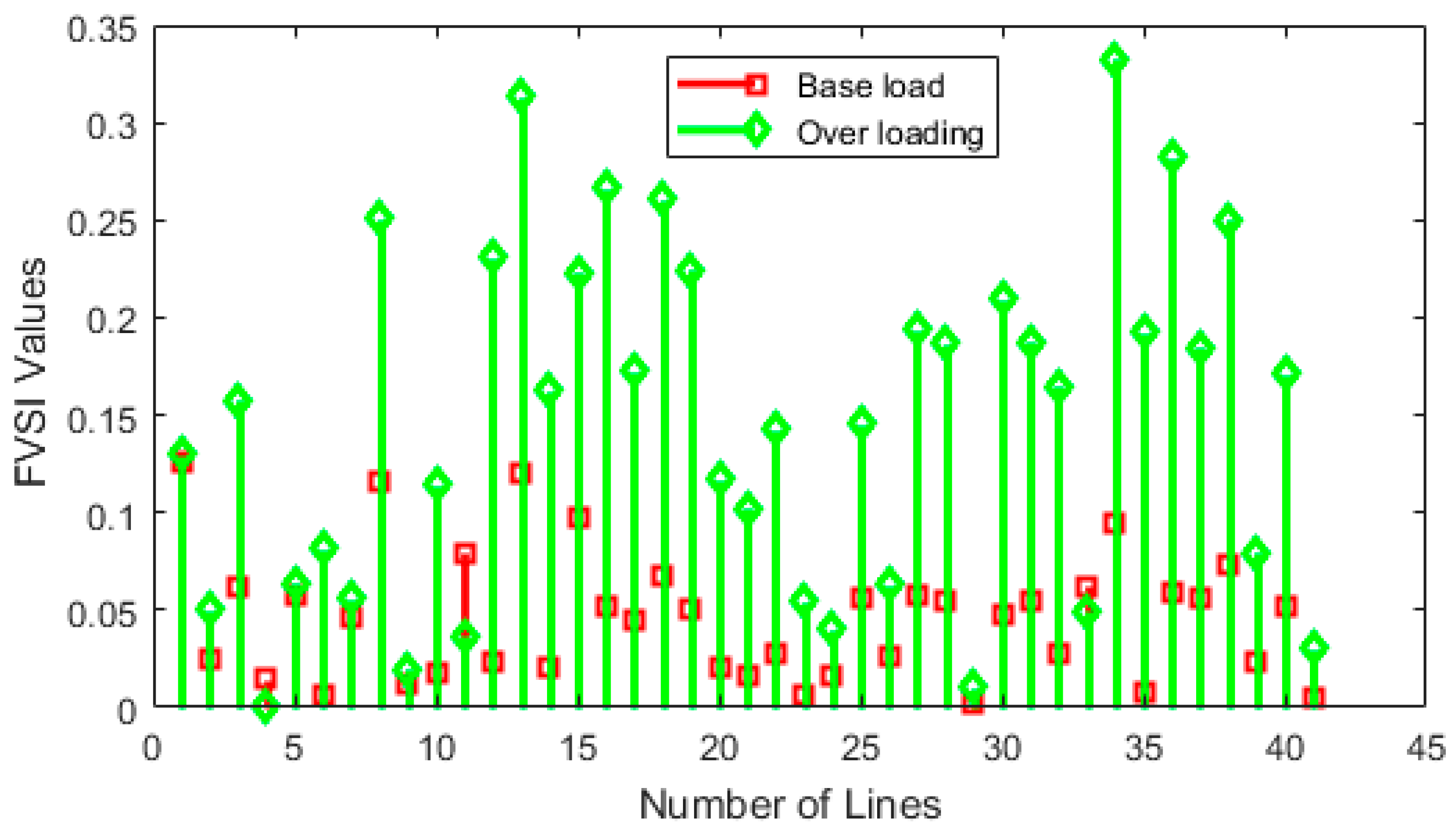
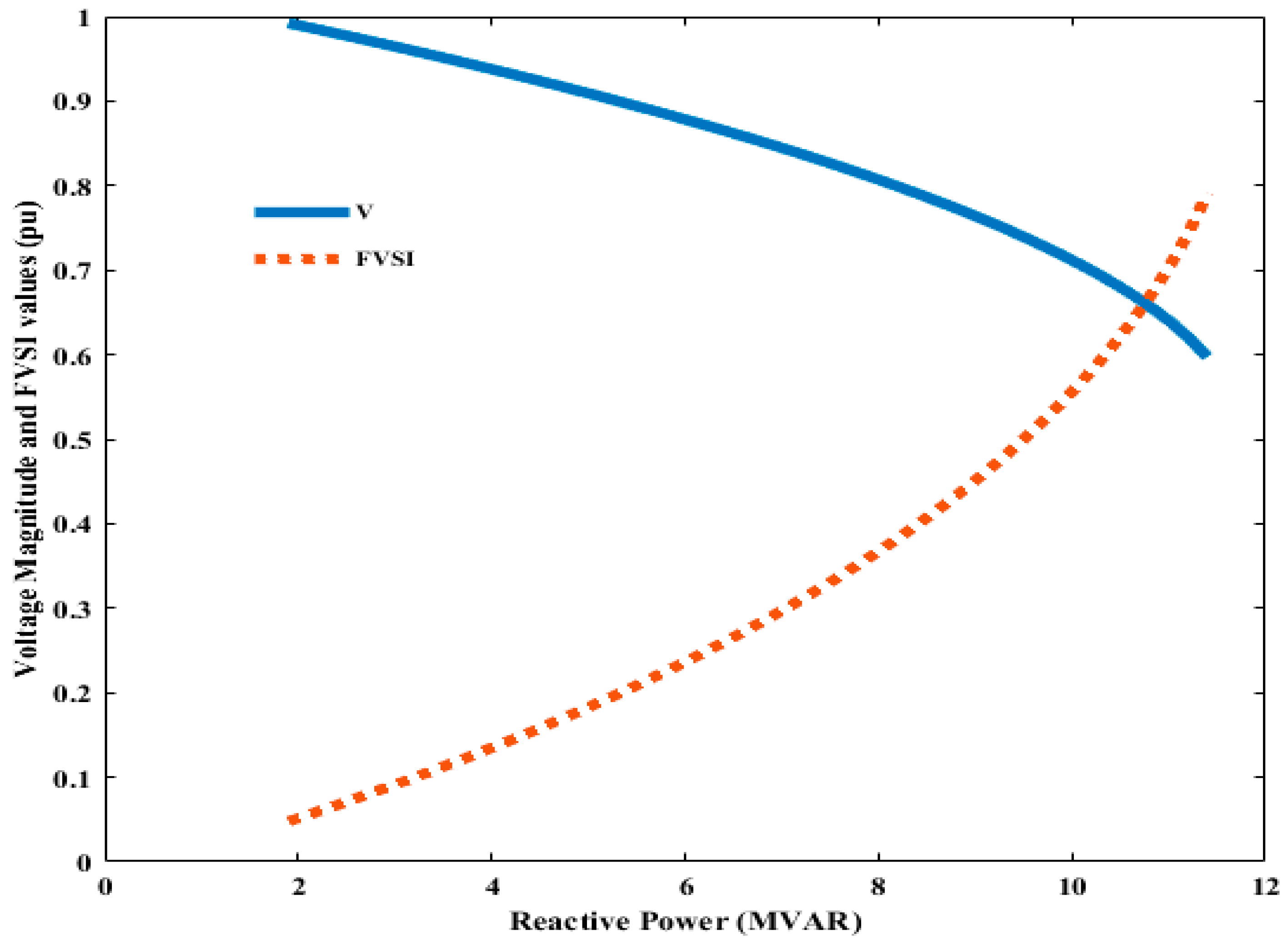
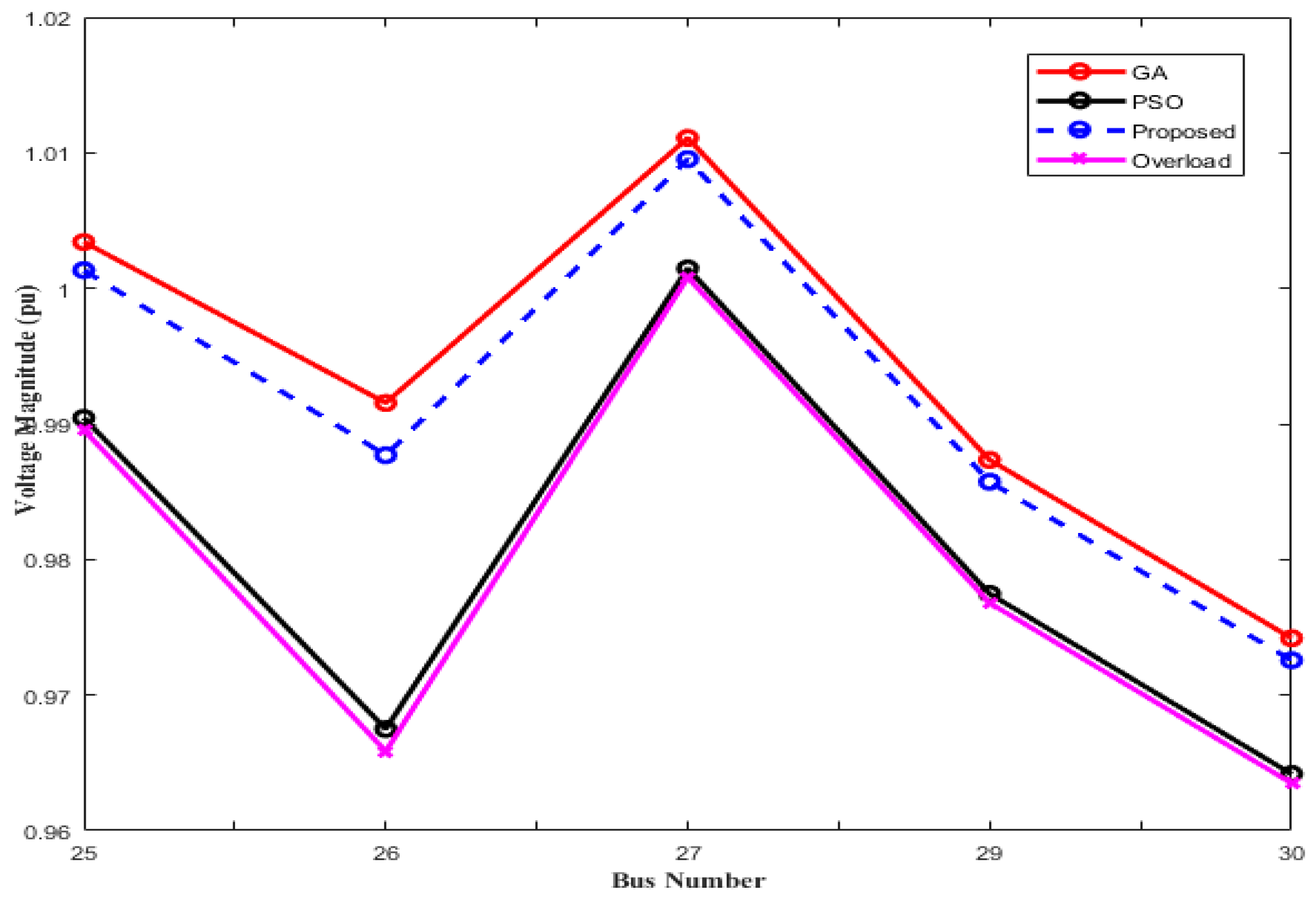
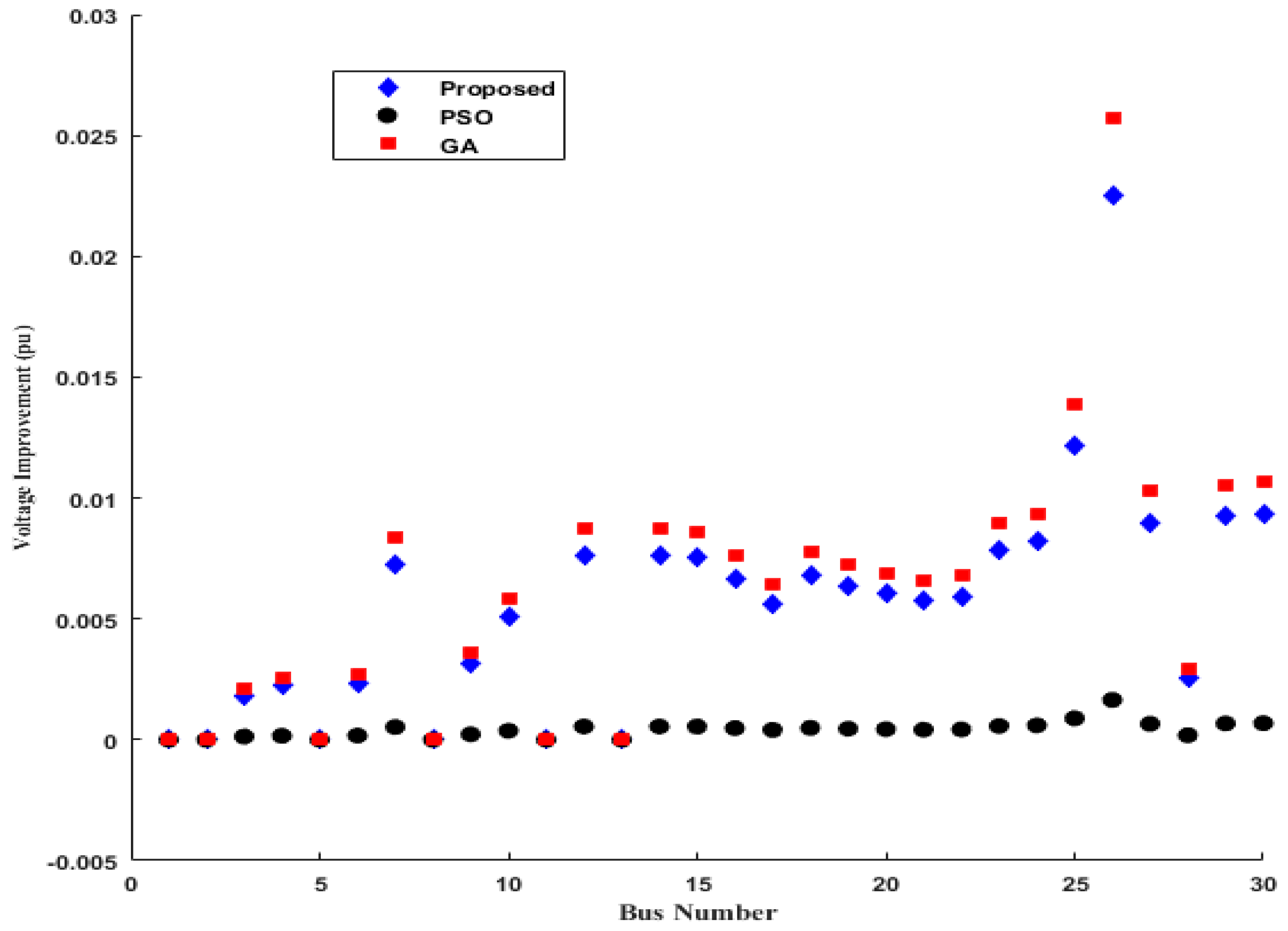
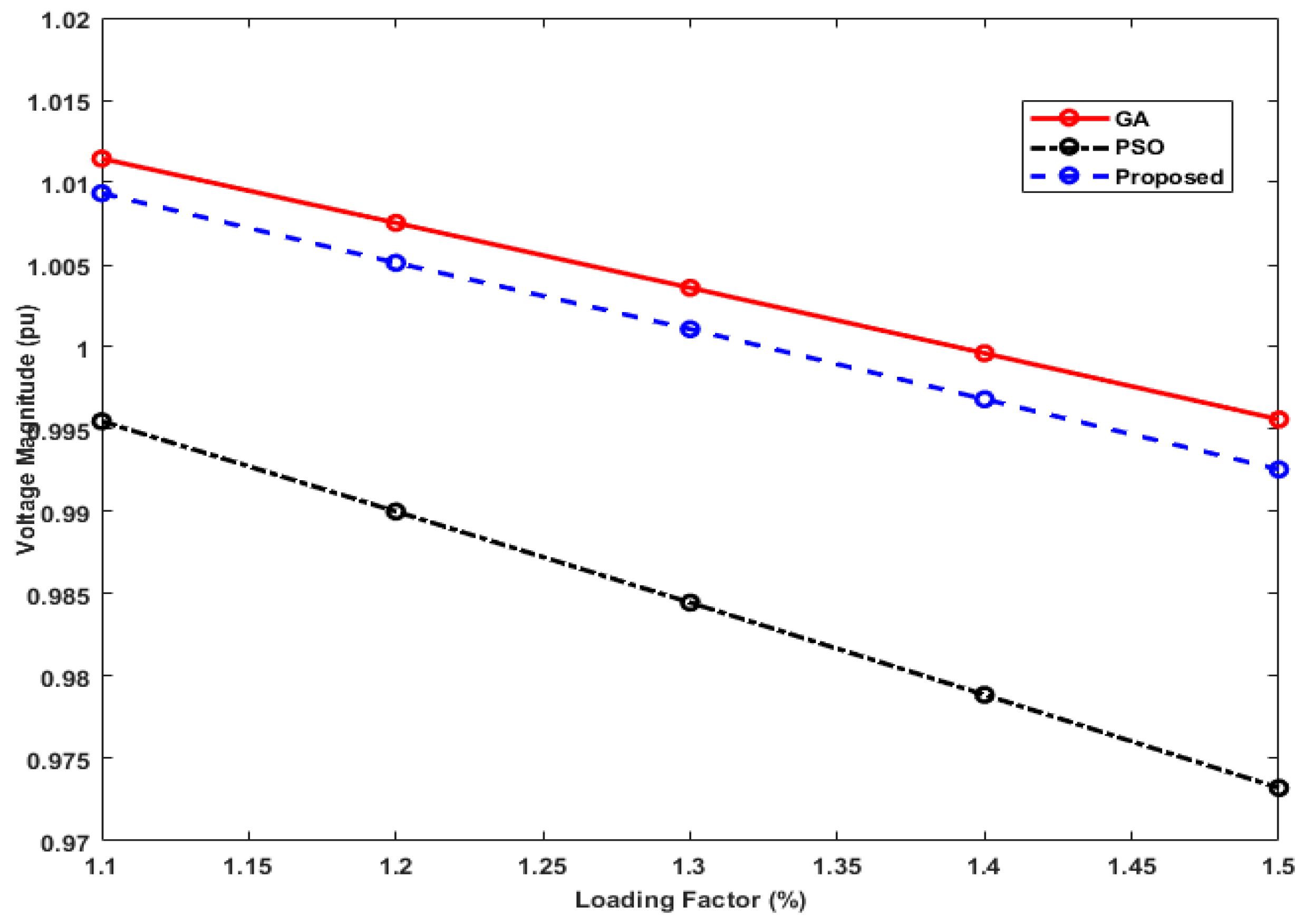
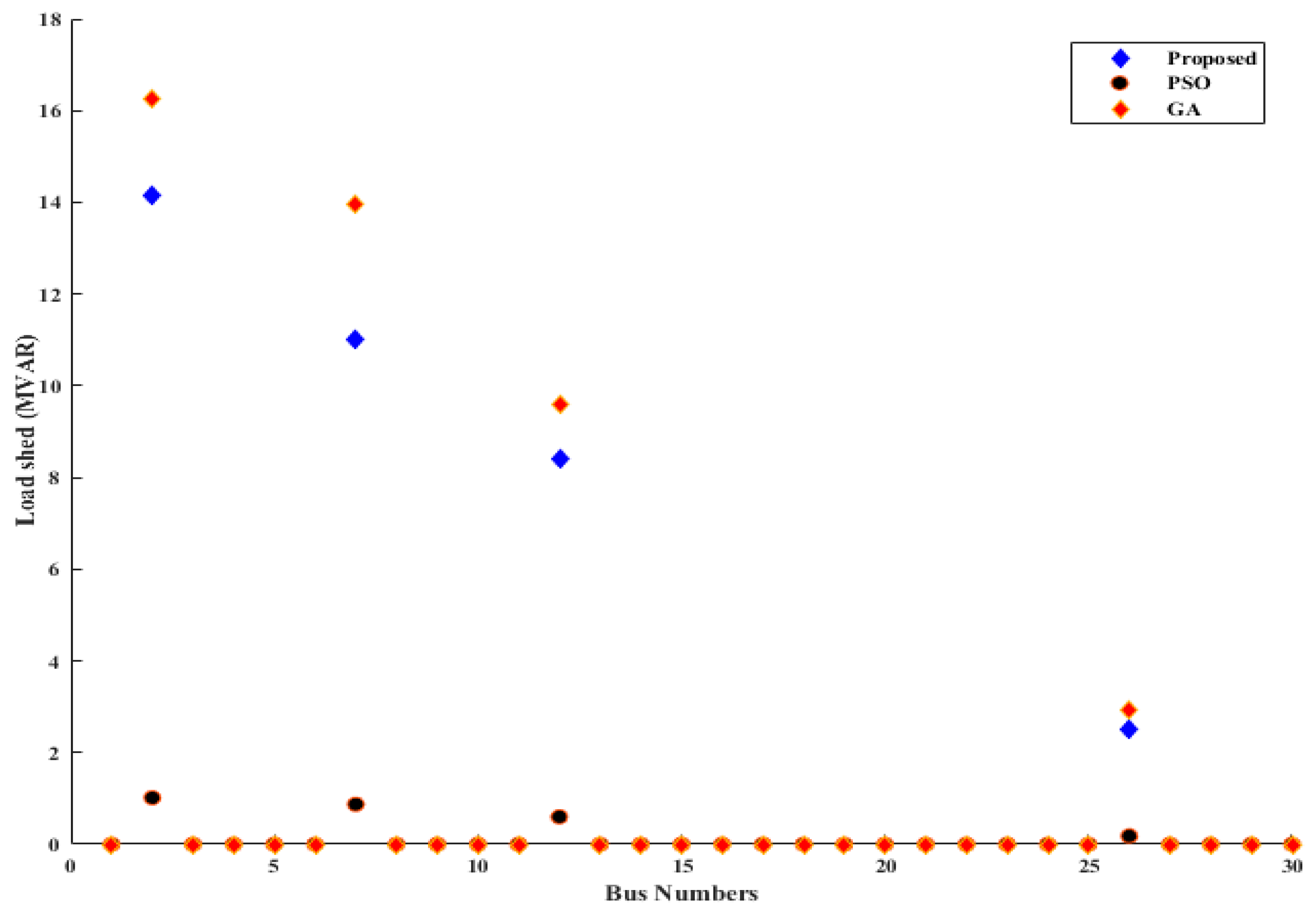
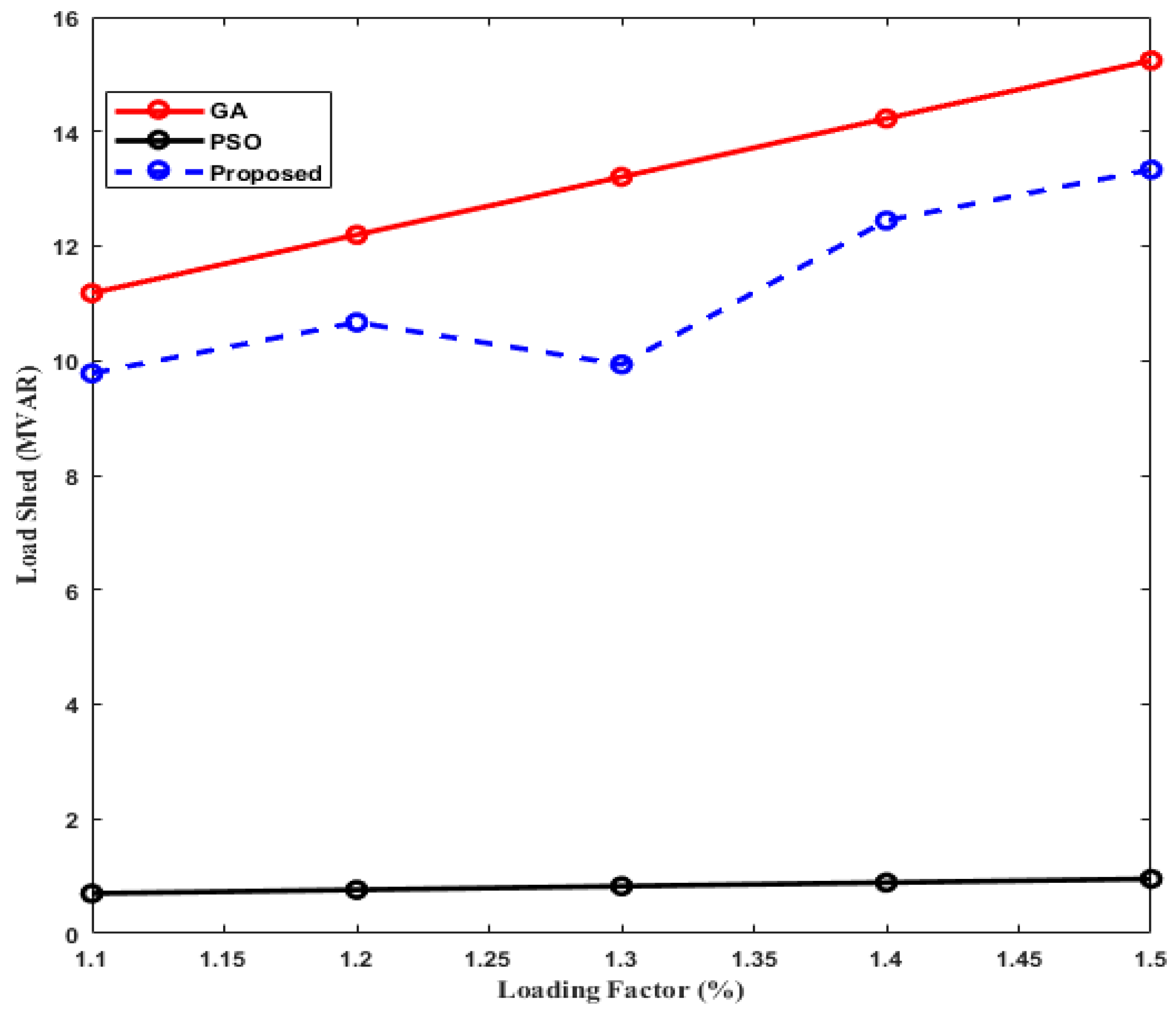
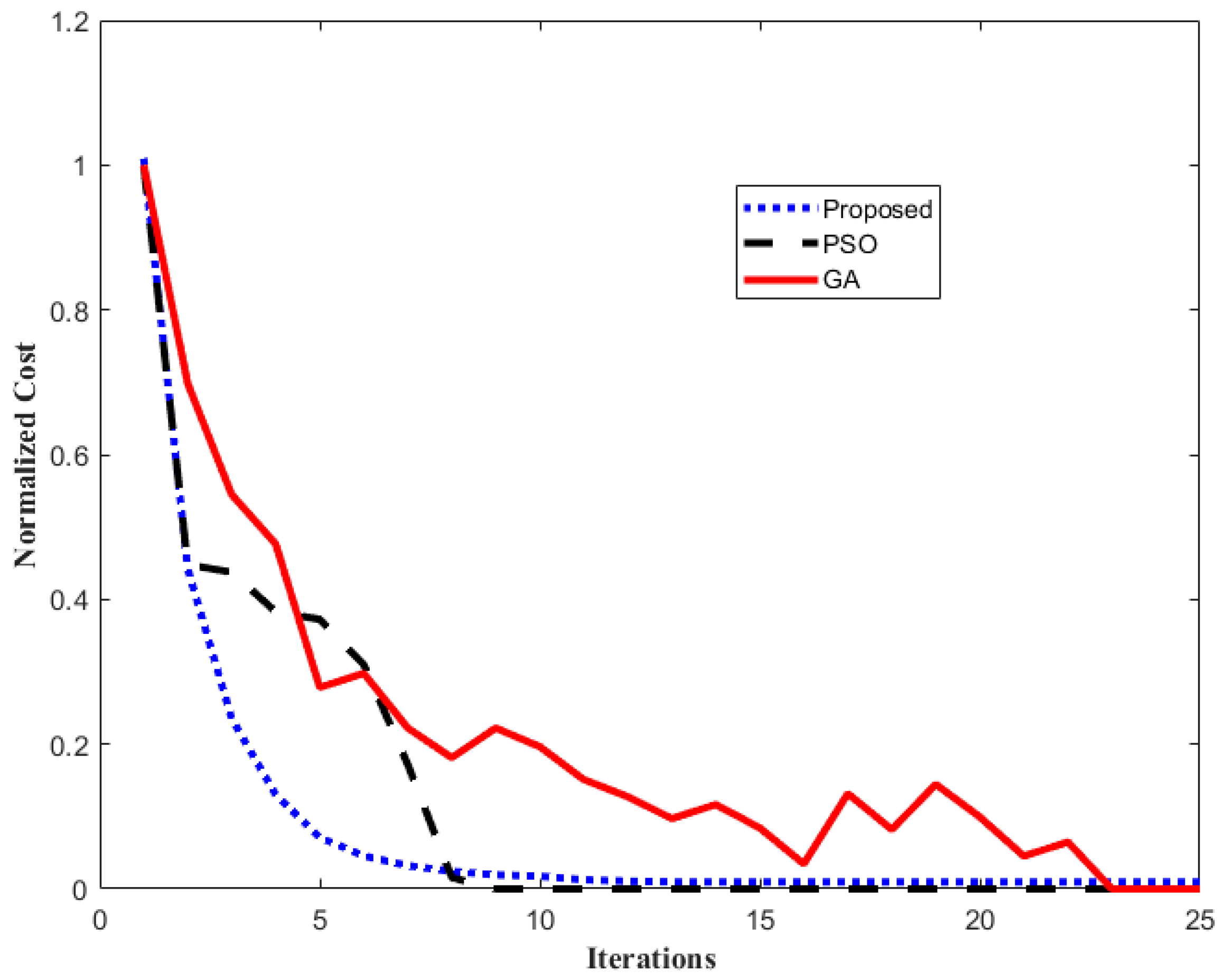
6. Performance Analysis and Results
7. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Andersson, G.; Donalek, P.; Farmer, R.; Hatziargyriou, N.; Kamwa, I.; Kundur, P.; Martins, N.; Paserba, J.; Pourbeik, P.; Sanchez-Gasca, J.; et al. Causes of the 2003 major grid blackouts in North America and Europe, and recommended means to improve system dynamic performance. IEEE Trans. Power Syst. 2005, 20, 1922–1928. [Google Scholar] [CrossRef]
- Charoenphan, B.; Audomvongseree, K. Optimal load shedding scheme under contingency condition considering voltage stability problem. In Proceedings of the 2010 International Conference on Electrical Engineering/Electronics Computer Telecommunications and Information Technology (ECTI-CON), Chiang Mai, Thailand, 19–21 May 2010; pp. 1006–1010. [Google Scholar]
- Taylor, C.W. Concepts of undervoltage load shedding for voltage stability. IEEE Trans. Power Deliv. 1992, 7, 480–488. [Google Scholar] [CrossRef]
- Arnborg, S.; Andersson, G.; Hill, D.J.; Hiskens, I.A. On undervoltage load shedding in power systems. Int. J. Electr. Power Energy Syst. 1997, 19, 141–149. [Google Scholar] [CrossRef]
- Ladhani, S.S.; Rosehart, W. Under voltage load shedding for voltage stability overview of concepts and principles. In Proceedings of the 2004 IEEE Power Engineering Society General Meeting, Denver, CO, USA, 6–10 June 2004; pp. 1597–1602. [Google Scholar]
- Van Cutsem, T.; Moors, C.; Lefebvre, D. Design of load shedding schemes against voltage instability using combinatorial optimization. In Proceedings of the 2002 IEEE Power Engineering Society Winter Meeting, New York, NY, USA, 27–31 January 2002; pp. 848–853. [Google Scholar]
- Moors, C.; Lefebvre, D.; van Cutsem, T. Design of load shedding schemes against voltage instability. In Proceedings of the 2000 IEEE Power Engineering Society Winter Meeting, Singapore, 23–27 January 2000; pp. 1495–1500. [Google Scholar]
- Lefebvre, D.; Moors, C.; van Cutsem, T. Design of an undervoltage load shedding scheme for the Hydro-Québec system. In Proceedings of the 2003 IEEE Power Engineering Society General Meeting, Toronto, ON, Canada, 13–17 July 2003. [Google Scholar]
- Laghari, J.; Mokhlis, H.; Bakar, A.; Mohamad, H. Application of computational intelligence techniques for load shedding in power systems: A review. Energy Convers. Manag. 2013, 75, 130–140. [Google Scholar] [CrossRef]
- Lopes, J.P.; Wa, W.C.; Proença, L. Genetic algorithms in the definition of optimal load shedding strategies. In Proceedings of the International Conference on Electric Power Engineering, PowerTech Budapest 99, Budapest, Hungary, 29 August–2 September 1999; p. 154. [Google Scholar]
- Sauer, P.; Pai, M. Power system steady-state stability and the load-flow Jacobian. IEEE Trans. Power Syst. 1990, 5, 1374–1383. [Google Scholar] [CrossRef]
- Irving, M.; Luan, W.; Daniel, J. Supply restoration in distribution networks using a genetic algorithm. Int. J. Electr. Power Energy Syst. 2002, 24, 447–457. [Google Scholar] [CrossRef]
- Guichon, M.; Melo, M.; Nieto, A.C.; Vignolo, M.; Yedrzejewski, N. Automatic Load Shedding Calculated with genetic algorithms-DAC-CMAG. In Proceedings of the 2012 Sixth IEEE/PES Transmission and Distribution: Latin America Conference and Exposition (T&D-LA), Montevideo, Uruguay, 3–5 September 2012; pp. 1–7. [Google Scholar]
- Al-Hasawi, W.M.; El Naggar, K.M. Optimum steady-state load-shedding scheme using genetic based algorithm. In Proceedings of the 11th IEEE Mediterranean Electrotechnical Conference, (MELECON 2002), Cairo, Egypt, 7–9 May 2002; pp. 605–609. [Google Scholar]
- Sanaye-Pasand, M.; Davarpanah, M. A new adaptive multidimensioanal load shedding scheme using genetic algorithm. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Saskatoon, SA, Canada, 1–4 May 2005; pp. 1974–1977. [Google Scholar]
- Karimi, M.; Mokhlis, H.; Bakar, A.; Laghari, J.; Shahriari, A.; Aman, M. Combination of adaptive and intelligent load shedding techniques for distribution network. In Proceedings of the 2012 IEEE International Power Engineering and Optimization Conference (PEDCO), Melaka, Malaysia, 6–7 June 2012; pp. 57–61. [Google Scholar]
- Dolan, M.J.; Davidson, E.M.; Kockar, I.; Ault, G.W.; McArthur, S.D. Distribution power flow management utilizing an online optimal power flow technique. IEEE Trans. Power Syst. 2012, 27, 790–799. [Google Scholar] [CrossRef]
- Zabaiou, T.; Dessaint, L.-A.; Kamwa, I. Preventive control approach for voltage stability improvement using voltage stability constrained optimal power flow based on static line voltage stability indices. IET Gener. Transm. Distrib. 2014, 8, 924–934. [Google Scholar] [CrossRef]
- He, F.; Wang, Y.; Chan, K.W.; Zhang, Y.; Mei, S. Optimal load shedding strategy based on particle swarm optimization. In Proceedings of the 8th International Conference on Advances in Power System Control, Operation and Management (APSCOM 2009), Hong Kong, China, 8–11 November 2009; pp. 1–6. [Google Scholar]
- Hosseini-Bioki, M.; Rashidinejad, M.; Abdollahi, A. An implementation of particle swarm optimization to evaluate optimal under-voltage load shedding in competitive electricity markets. J. Power Sources 2013, 242, 122–131. [Google Scholar] [CrossRef]
- Amraee, T.; Mozafari, B.; Ranjbar, A. An improved model for optimal under voltage load shedding: particle swarm approach. In Proceedings of the 2006 IEEE Power India Conference, New Delhi, India, 10–12 April 2006; p. 6. [Google Scholar]
- Rad, B.F.; Abedi, M. An optimal load-shedding scheme during contingency situations using meta-heuristics algorithms with application of AHP method. In Proceedings of the 11th International Conference on Optimization of Electrical and Electronic Equipment, Brasov, Romania, 22–24 May 2008; pp. 167–173. [Google Scholar]
- Mozafari, B.; Amraee, T.; Ranjbar, A. An approach for under voltage load shedding using particle swarm optimization. In Proceedings of the 2006 IEEE International Symposium on Industrial Electronics, Montreal, QC, Canada, 9–13 July 2006; pp. 2019–2024. [Google Scholar]
- Tinney, W.; Bright, J.; Demaree, K.; Hughes, B. Some deficiencies in optimal power flow. IEEE Trans. Power Syst. 1988, 3, 676–683. [Google Scholar] [CrossRef]
- Sadati, N.; Zamani, M.; Mahdavian, H.R.F. Hybrid particle swarm-based-simulated annealing optimization techniques. In Proceedings of the IECON 2006—32nd Annual Conference on IEEE Industrial Electronics, Paris, France, 6–10 November 2006; pp. 644–648. [Google Scholar]
- Jalilzadeh, S.; Hosseini, S.H.; Derafshian-Maram, M. Optimal load shedding to prevent voltage instability based on multi-objective optimization using modal analysis and PSO. In Proceedings of the 2010 International Congress on Ultra Modern Telecommunications and Control Systems and Workshops (ICUMT), Moscow, Russia, 18–20 October 2010; pp. 371–376. [Google Scholar]
- Mollah, K.; Bahadornejad, M.; Nair, N.; Ancell, G. Automatic under-voltage load shedding: A systematic review. In Proceedings of the 2012 IEEE Power and Energy Society General Meeting, San Diego, CA, USA, 22–26 July 2012; pp. 1–7. [Google Scholar]
- Ellis, A.; Kosterev, D.; Meklin, A. Dynamic load models: Where are we? In Proceedings of the 2005/2006 IEEE PES Transmission and Distribution Conference and Exhibition, Dallas, TX, USA, 21–24 May 2006; pp. 1320–1324. [Google Scholar]
- Sadati, N.; Amraee, T.; Ranjbar, A. A global particle swarm-based-simulated annealing optimization technique for under-voltage load shedding problem. Appl. Soft Comput. 2009, 9, 652–657. [Google Scholar] [CrossRef]
- Hagh, M.T.; Galvani, S. Minimization of load shedding by sequential use of linear programming and particle swarm optimization. Turk. J. Electr. Eng. Comput. Sci. 2011, 19, 551–563. [Google Scholar]
- Ahmadi, A.; Alinejad-Beromi, Y. A new integer-value modeling of optimal load shedding to prevent voltage instability. Int. J. Electr. Power Energy Syst. 2015, 65, 210–219. [Google Scholar] [CrossRef]
- Ojaghi, M.; Azari, M.; Valujerdi, A.C. Robust UVLS scheme to improve transmission line performance considering interruption cost and voltage stability index. In Proceedings of the 2014 IEEE International Conference on Industrial Technology (ICIT), Busan, South Korea, 26 February–1 March 2014; pp. 541–546. [Google Scholar]
- Musirin, I.; Rahman, T.A. Estimating maximum loadability for weak bus identification using FVSI. IEEE Power Eng. Rev. 2002, 22, 50–52. [Google Scholar] [CrossRef]
- Baker, J.E. Adaptive selection methods for genetic algorithms. In Proceedings of the International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, USA, 24–26 July 1985; pp. 101–111. [Google Scholar]
- Grefenstette, J.; Gopal, R.; Rosmaita, B.; van Gucht, D. Genetic algorithms for the traveling salesman problem. In Proceedings of the First International Conference on Genetic Algorithms and Their Applications, Pittsburgh, PA, USA, 24–26 July 1985; pp. 160–168. [Google Scholar]
- Eberhart, R.; Kennedy, J. A new optimizer using particle swarm theory. In Proceedings of the Sixth International Symposium on Micro Machine and Human Science (MHS’95), Nagoya, Japan, 4–6 October 1995; pp. 39–43. [Google Scholar]
- Shi, Y.; Eberhart, R. A modified particle swarm optimizer. In Proceedings of the 1998 IEEE International Conference on Evolutionary Computation Proceedings and IEEE World Congress on Computational Intelligence, Anchorage, AK, USA, 4–9 May 1998; pp. 69–73. [Google Scholar]
- Zimmerman, R.D.; Murillo-Sanchez, C.E. MATPOWER, A MATLAB Power System Simulation Package. 2007. Available online: http://www.pserc.cornell.edu/matpower/manual.pdf (accessed on 6 May 2018).
- Ritzmann, D.; Wright, P.S.; Holderbaum, W.; Potter, B. A method for accurate transmission line impedance parameter estimation. IEEE Trans. Instrum. Meas. 2016, 65, 2204–2213. [Google Scholar] [CrossRef]
- Wydra, M. Performance and Accuracy Investigation of the Two-Step Algorithm for Power System State and Line Temperature Estimation. Energies 2018, 11, 1005. [Google Scholar] [CrossRef]
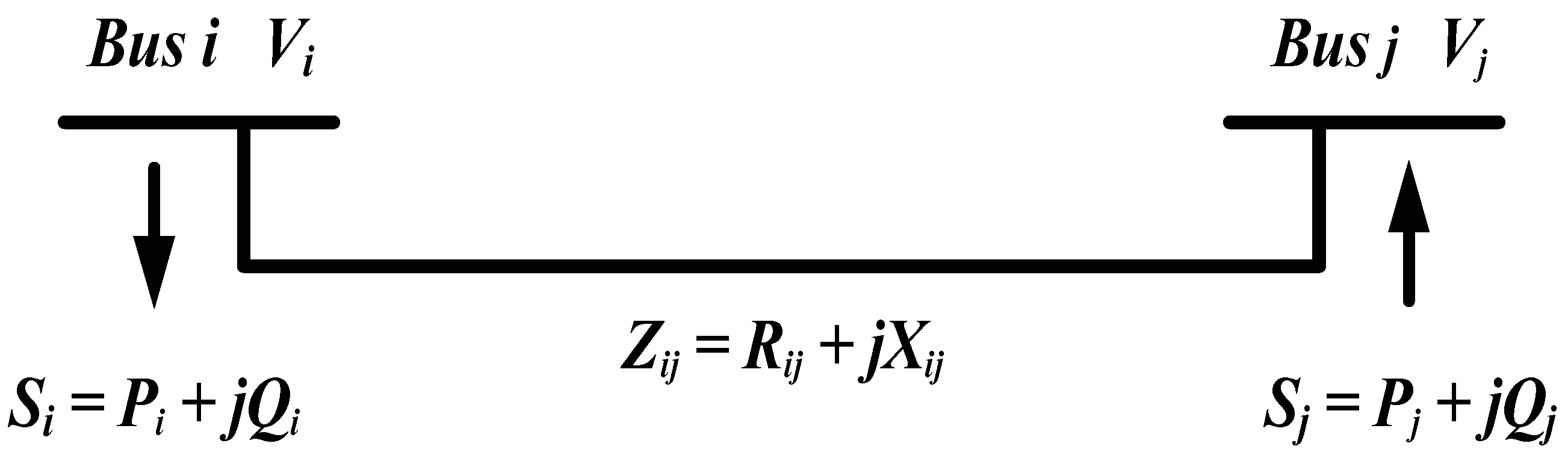
| Notation | Description |
|---|---|
| Pib and Pia | Post-contingency and pre-contingency active power demand at bus i, respectively. |
| Vib and Via | Post-contingency and pre-contingency voltage magnitudes at bus i, respectively. |
| Nbus | Set of all buses. |
| Bsel | Set of buses selected for load shedding. |
| BGen | Set of generation buses. |
| Pi and Qi | Active and reactive power of bus i, respectively. |
| Gij and Bij | Real and imaginary part of the (i; j)th element in the bus admittance matrix, respectively. |
| Pimin and Pimax | Minimum and maximum real power generations at bus i, respectively. |
| Qimin and Qimax | Minimum and maximum reactive power generations at bus i, respectively. |
| Vimin and Vimax | Minimum and maximum allowed voltage at bus i, respectively. |
| Nos. | Line Number | FVSI Value | Bus No. |
|---|---|---|---|
| 1 | 8 | 0.2506 | 26 |
| 2 | 13 | 0.3134 | 27 |
| 3 | 16 | 0.2662 | 29 |
| 4 | 18 | 0.2604 | 30 |
| 5 | 34 | 0.3327 | 30 |
| 6 | 36 | 0.2823 | 26 |
| 7 | 38 | 0.2502 | 25 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Larik, R.M.; Mustafa, M.W.; Aman, M.N.; Jumani, T.A.; Sajid, S.; Panjwani, M.K. An Improved Algorithm for Optimal Load Shedding in Power Systems. Energies 2018, 11, 1808. https://doi.org/10.3390/en11071808
Larik RM, Mustafa MW, Aman MN, Jumani TA, Sajid S, Panjwani MK. An Improved Algorithm for Optimal Load Shedding in Power Systems. Energies. 2018; 11(7):1808. https://doi.org/10.3390/en11071808
Chicago/Turabian StyleLarik, Raja Masood, Mohd Wazir Mustafa, Muhammad Naveed Aman, Touqeer Ahmed Jumani, Suhaib Sajid, and Manoj Kumar Panjwani. 2018. "An Improved Algorithm for Optimal Load Shedding in Power Systems" Energies 11, no. 7: 1808. https://doi.org/10.3390/en11071808
APA StyleLarik, R. M., Mustafa, M. W., Aman, M. N., Jumani, T. A., Sajid, S., & Panjwani, M. K. (2018). An Improved Algorithm for Optimal Load Shedding in Power Systems. Energies, 11(7), 1808. https://doi.org/10.3390/en11071808






