1.1. Literature Review
Environmental deterioration and the increasing shortage of petroleum resources have greatly increased the demand for energy-saving and environmental protective vehicles. The new energy vehicle technology is regarded as an excellent way to simultaneously address the energy crisis and insecurity and reduce environmental impacts [
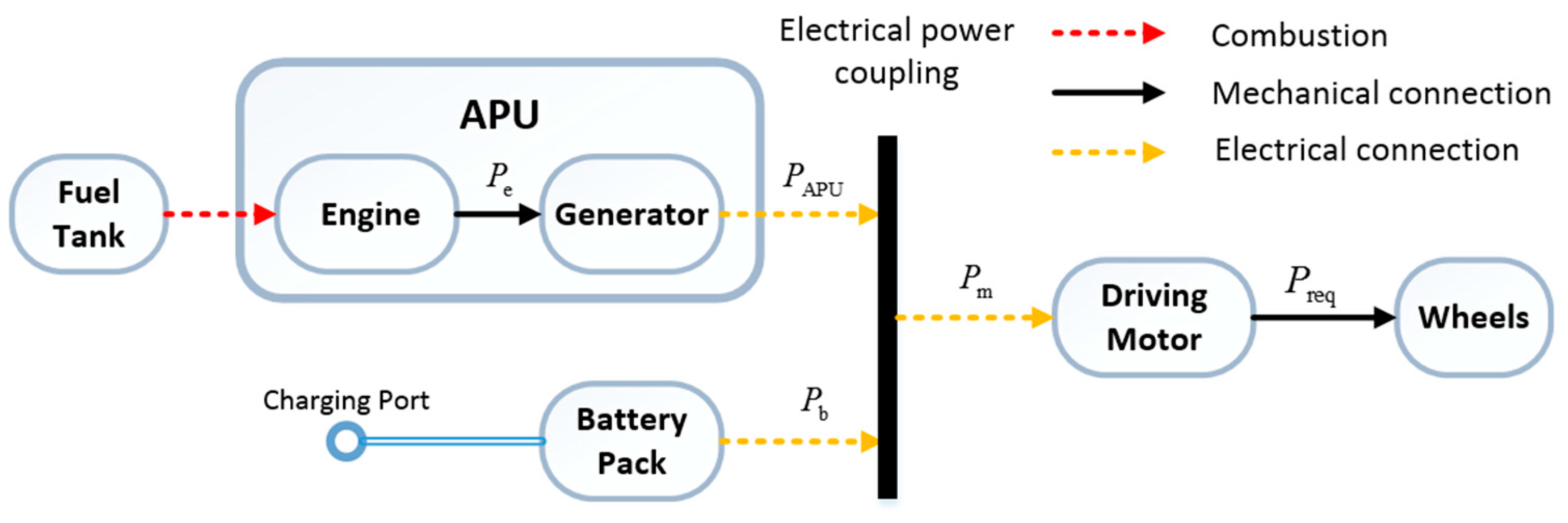
1]. As a type of plug-in hybrid electric vehicle (PHEV), extended-range electric buses (E-REBs) can coordinate the energy allocation between batteries and the auxiliary power unit, and prolong the mileage of pure electric vehicles while improving the fuel economy. Thus, extended-range electric buses have gained growing attention from vehicle manufacturers and customers [
2,
3].
Energy management is still a technical puzzle faced by hybrid electric vehicles because it not only aims at the minimum energy consumption, but also needs to take into consideration the vehicle dynamic performance, emission performance and the characteristic of each component. Due to the presence of multiple power sources, the reasonability of energy allocation directly affects the dynamic performance and fuel economy of vehicles [
4]. However, the conventional energy management strategy only considers a single performance index and cannot achieve an overall optimization. Thus deeper research shows the energy management has gradually transited from the initially single goals of fuel depletion or emission to the currently multi-goal real-time intelligent integrated control. So far, the control strategies can be divided into rule-based and optimization-based energy allocation strategies [
5].
In the first category, the vehicle working states are firstly divided according to pre-set control rules and then controlled separately. The rules are set to make the engine, generator and batteries work within the pre-set high-efficiency zones, but are only slightly dependent on specific working conditions and thereby operate in real-time. The two main directions of this category are the control strategies based on logic thresholds or fuzzy rules [
6]. Firstly, the logic thresholds are usually the state of charge (SOC) of battery power or the speed signals of vehicles, which allow for switching between different operation modes [
7]. Its disadvantage is that the dynamic performance of the vehicle will be greatly reduced when the work mode enters the charging-sustaining phase. The control strategies based on fuzzy rules control energy allocation via the use of fuzzy algorithms. Firstly, the control parameters are fuzzified into a power allocation factor, and thereby the driving system is controlled [
8,
9]. The common problem of rule-based strategies is that energy can only be allocated according to fixed rules without considering optimization, so the fuel consumption is relatively high.
The energy management of extended-range electric vehicles is essentially aimed to solve a multi-objective nonlinear optimization problem. Since the major objective is the minimization of systematic energy consumption, the energy control strategies based on global optimization and instantaneous optimization algorithms have been widely studied. As one global optimization algorithm, PMP constructs a Hamilton function, and when the Hamilton function reaches the minimum value under constraints, the target function is also minimized [
10]. Dynamic programming (DP), another global algorithm, divides the whole working condition into several segments, and starting from the final state, reversely calculates the initial state and finally selects the controlling rule that makes the target function reach the minimum value as the optimal strategy [
11,
12]. However, both PMP and DP can get the optimal solution only when the whole driving cycles are known. Since the road conditions and driving behaviors are all unknown in real driving, global optimization algorithms are unfeasible in reality, but can be used as the benchmark for real-time energy management strategies. With the same hybrid electric vehicle model, Yuan compared DP and PMP and found their control effects were similar, but PMP was faster [
13].
The energy management based on instantaneous optimization does not need any information about driving cycles and can be controlled in real-time according to the real driving conditions. The DP-developed stochastic dynamic programming (SDP) control strategies utilize DP algorithms to solve a number of working conditions, and apply the datasets as-obtained into neural network training [
14]. In real applications, the real-time working conditions are substituted into the classifier to form energy distribution relations. Similarly, the artificial intelligent algorithms for energy management also include neural network control [
15], particle swarm optimization [
16], and genetic algorithm [
17,
18]. These Artificial Intelligence-strategies are faced with the problem of large amount of data training and too much computation in real-time operation. Model prediction control is aimed to model the controlled object, predict the output according to the vehicle state as-collected, optimize the predicted value, and input the resulting optimal energy allocation into the control system [
19,
20]. Borhan built an energy optimization control strategy based on model prediction and the simulations showed in the recycled working conditions of UDDS, the MPC control strategy reduced the oil consumption by 4.7% than the rule-based control strategy [
21]. ECMS originating from PMP finds the minimum value through real-time solving the target function, and obtains the instantaneous energy distribution relation between batteries and APU [
22]. However, the co-state of ECMS is constant and cannot well adapt to different working conditions in real tests. Thus, researchers have proposed adaptive-ECMS (A-ECMS) which is developed on the basis of ECMS. It can adjust the co-state value of Hamilton function in real time according to the operation state of the vehicle. The strategy can well adapt to the actual operation state and make the important vehicle performances reach the ideal value. Gu put forward an adaptive ECMS based on driving pattern recognition, and by identifying the information of working conditions, it adjusted the value of co-state to adapt to different working conditions [
23]. Mahyar proposed to use GPS and ITS to predict the working conditions and built an A-ECMS control strategy based on reference SOC, so that the real SOC could decline along with the reference SOC curve [
24]. According to the optimal co-state values under different driving conditions, Onori et al. plotted a co-state map and used SOC feedback to build a linear co-state function, which performed well in simulations [
25,
26]. Because A-ECMS has the characteristics of strong adaptability, good real-time performance and excellent control effect, it is selected as the energy management strategy of this paper.
1.2. Motivation
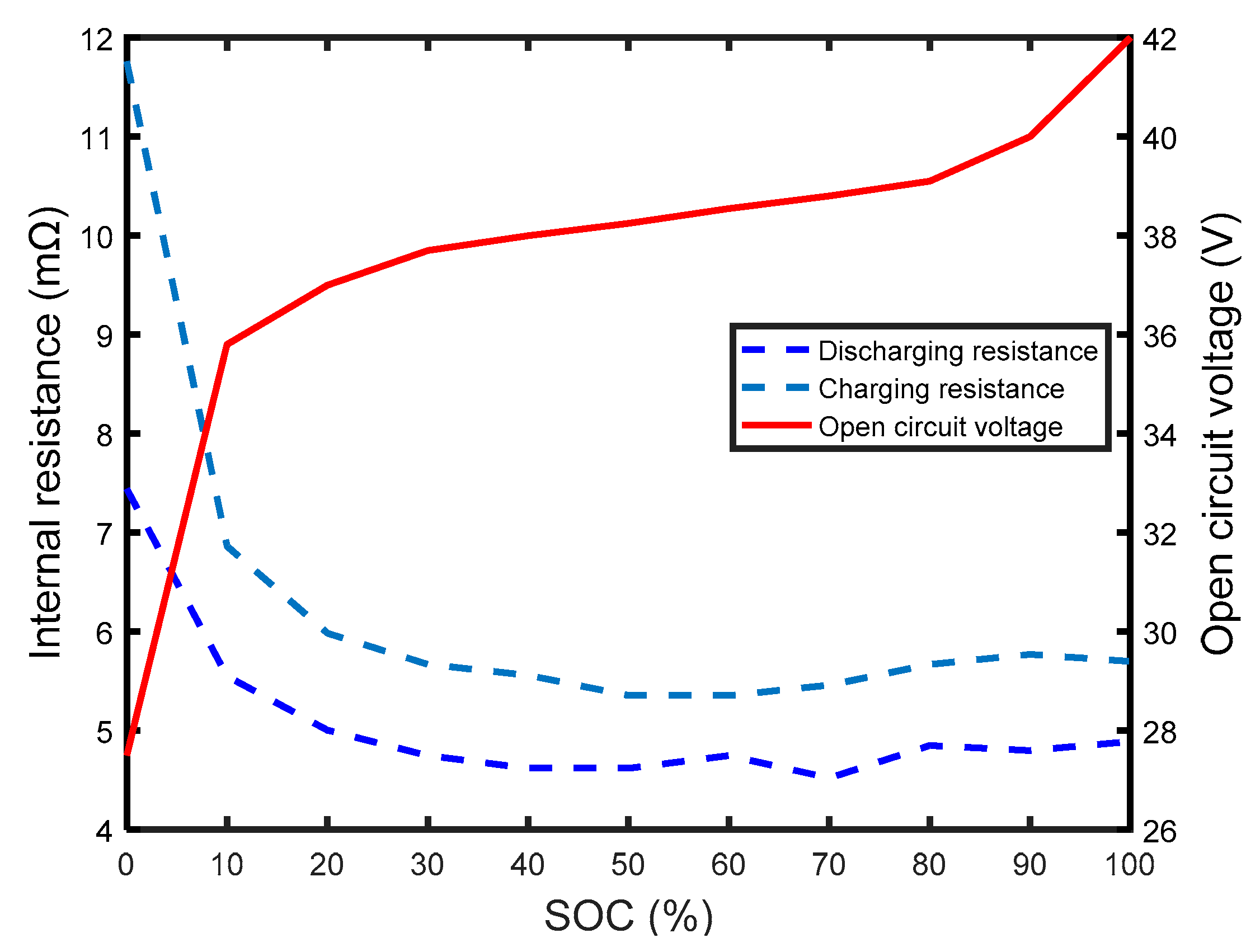
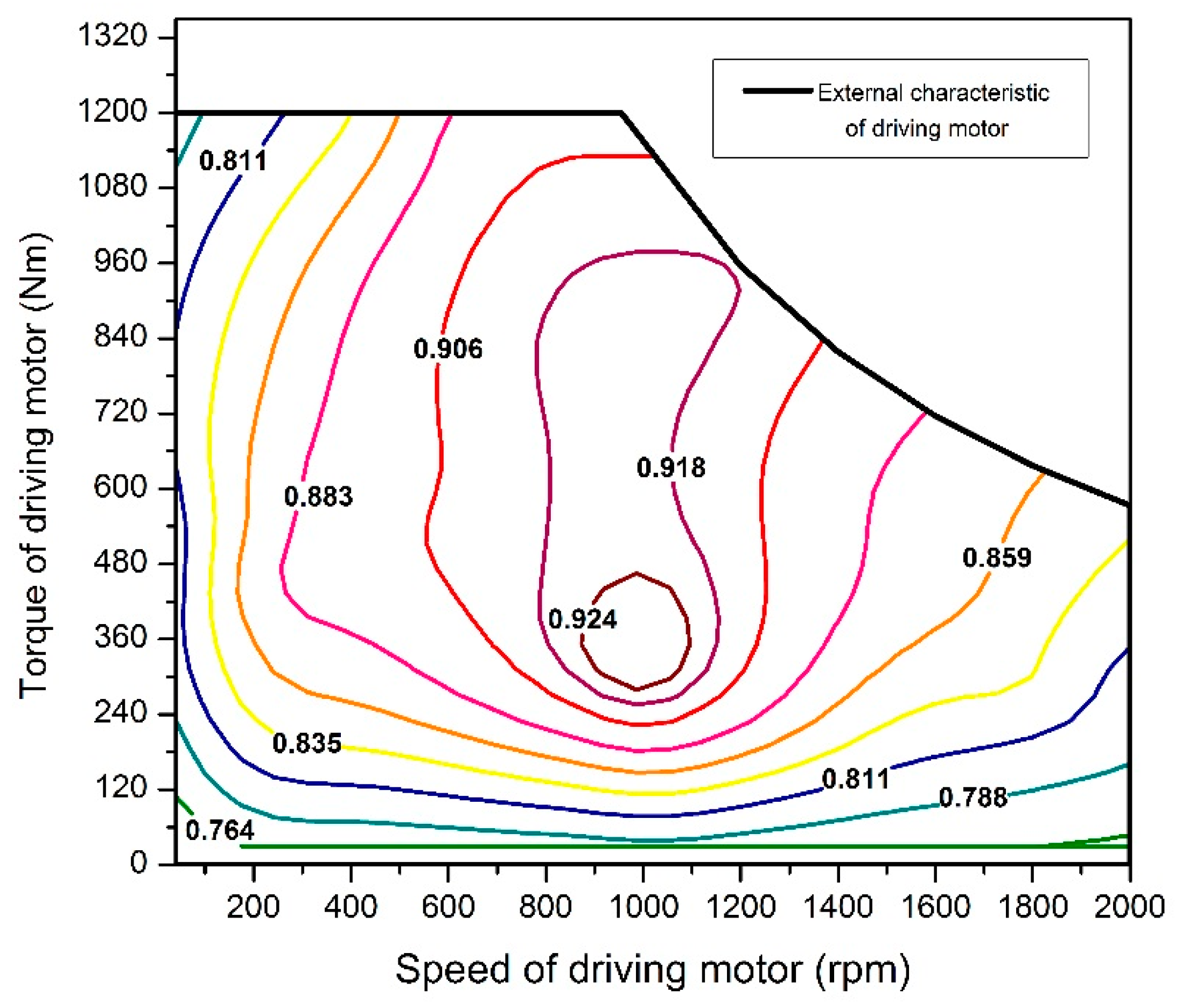
The objective of energy management strategy for an E-REB is to guarantee the dynamic performance of the E-REB during operation. Meanwhile the strategy ensures the SOC is always greater than the pre-set value and makes the final SOC close to the pre-set value, which not only protects the battery pack, but also fully uses the battery pack power.
In order to meet the above performance requirements, the co-state value needs to be adjusted in real time according to the vehicle status. The motivation for this is explained as follows: (1) to solve the optimal co-state value, the Hamilton function and co-state equation for E-REB should be developed based on PMP; (2) the co-state is affected by driving distance and working conditions, so in order to establish the relationship between the co-state and its influencing factors, the target driving cycles are needed, however, there is often a lack of TDCs in practice. In order to solve this problem, the Markov chain based generation technology is proposed; (3) by the way of making the fuel consumption close to the optimal control result, and the final SOC value is similar to the pre-set value, SOC reference curve should be reasonably designed; (4) taking the SOC deviation value as the independent variable, the co-state adaptive function is established by PI control technology; (5) also, the initial value of SOC also has a significant impact on the co-state, thus the change of co-state function should be considered under different initial values.
1.3. Major Contribution
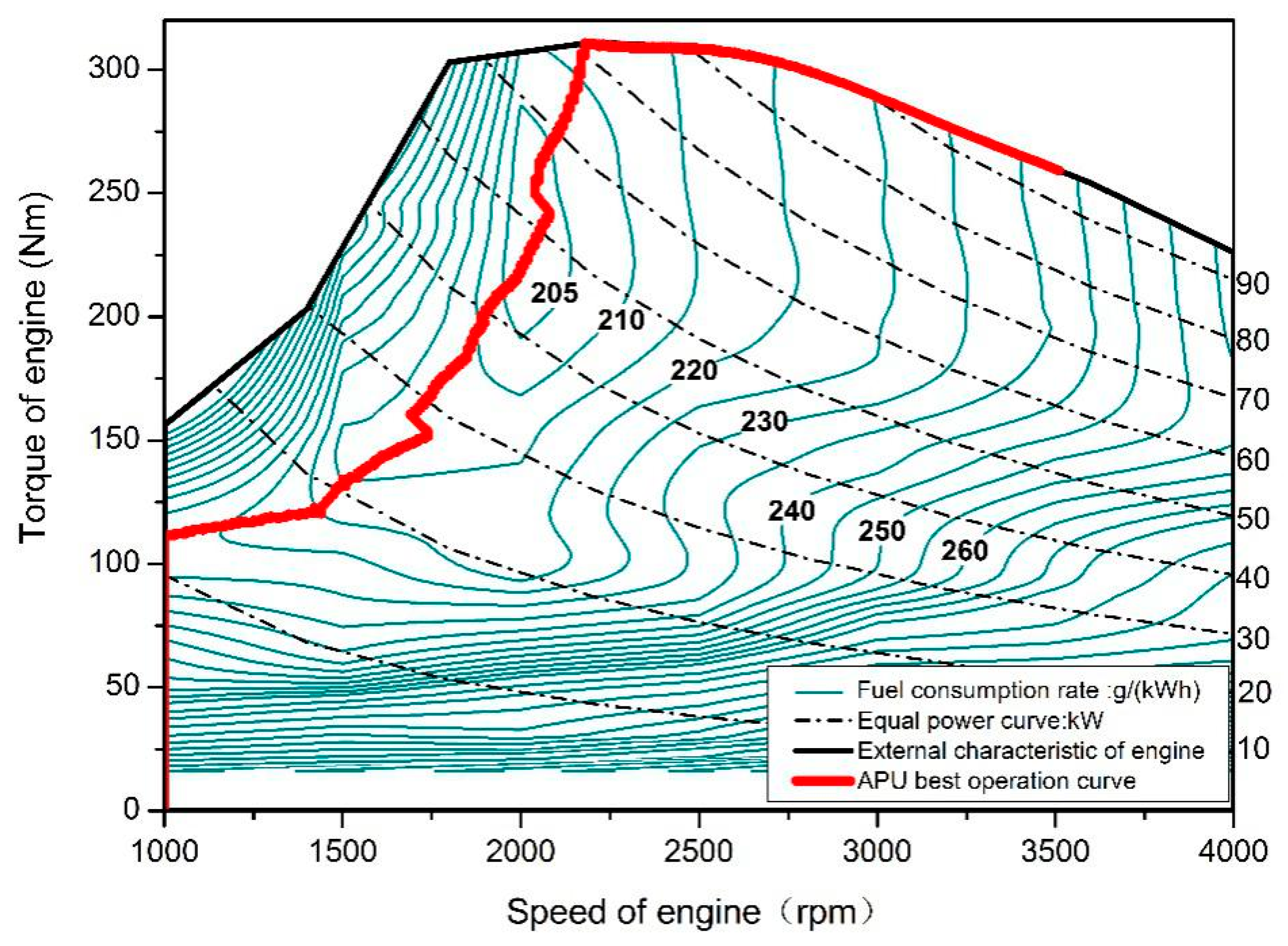
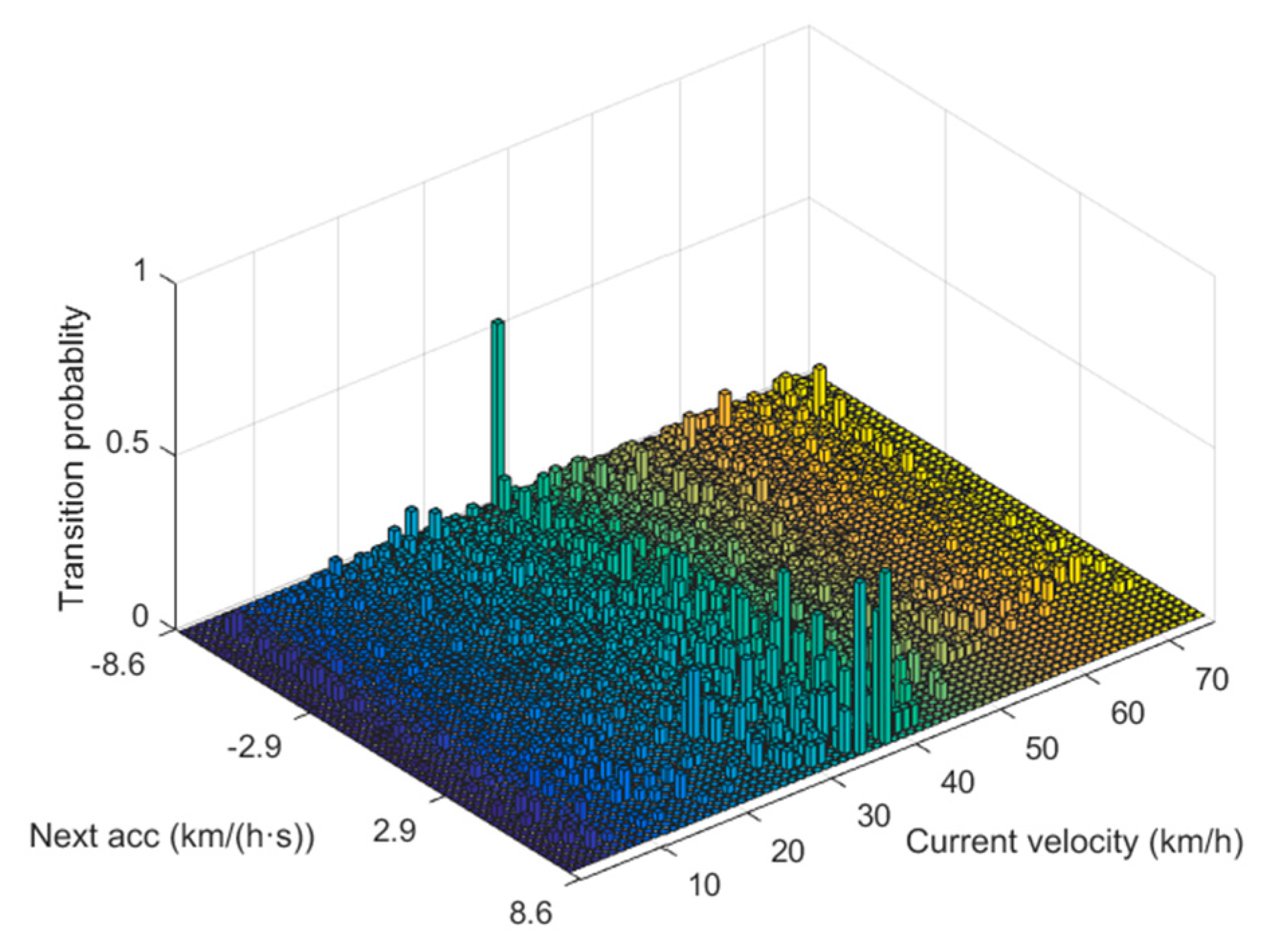
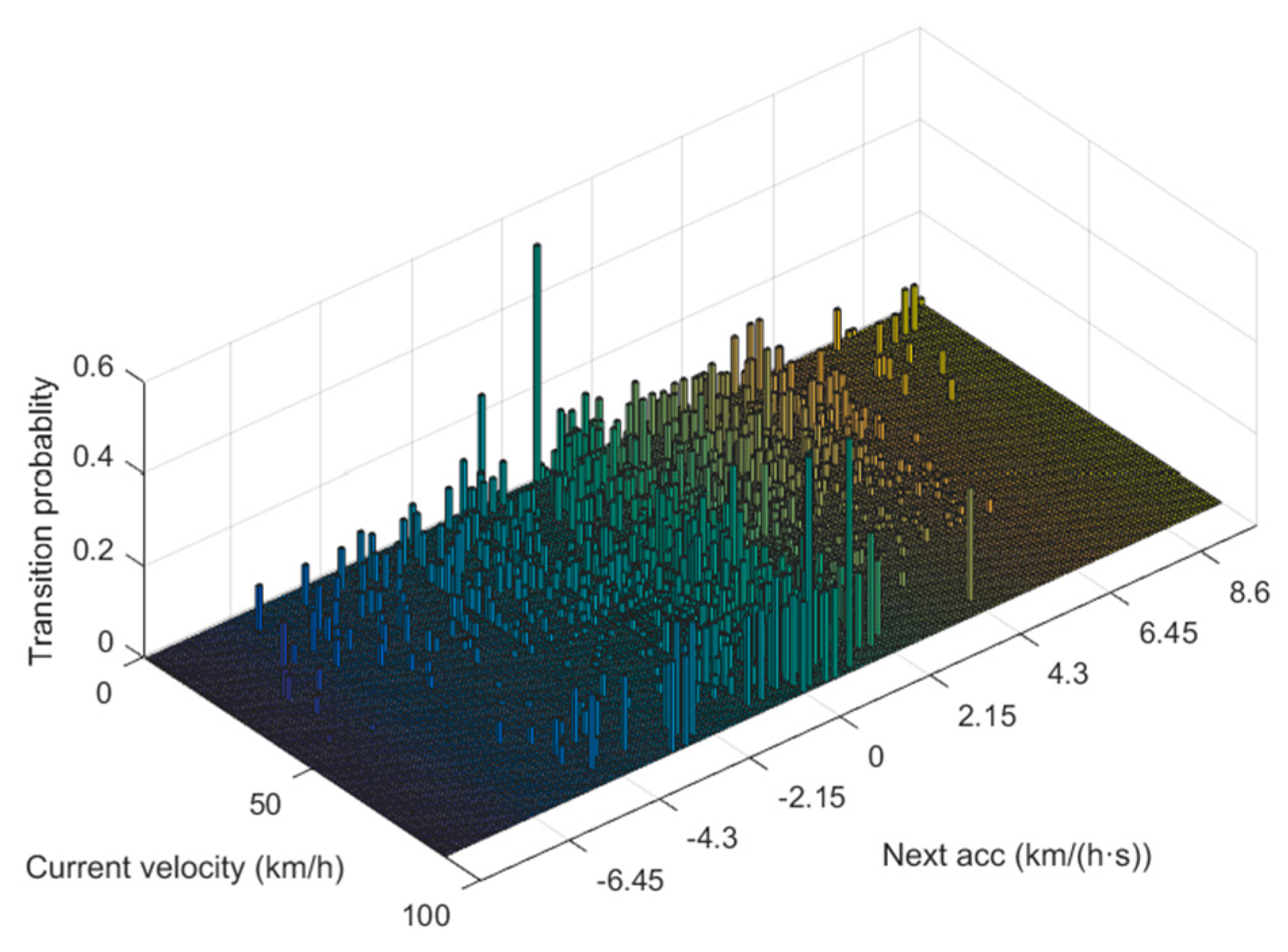
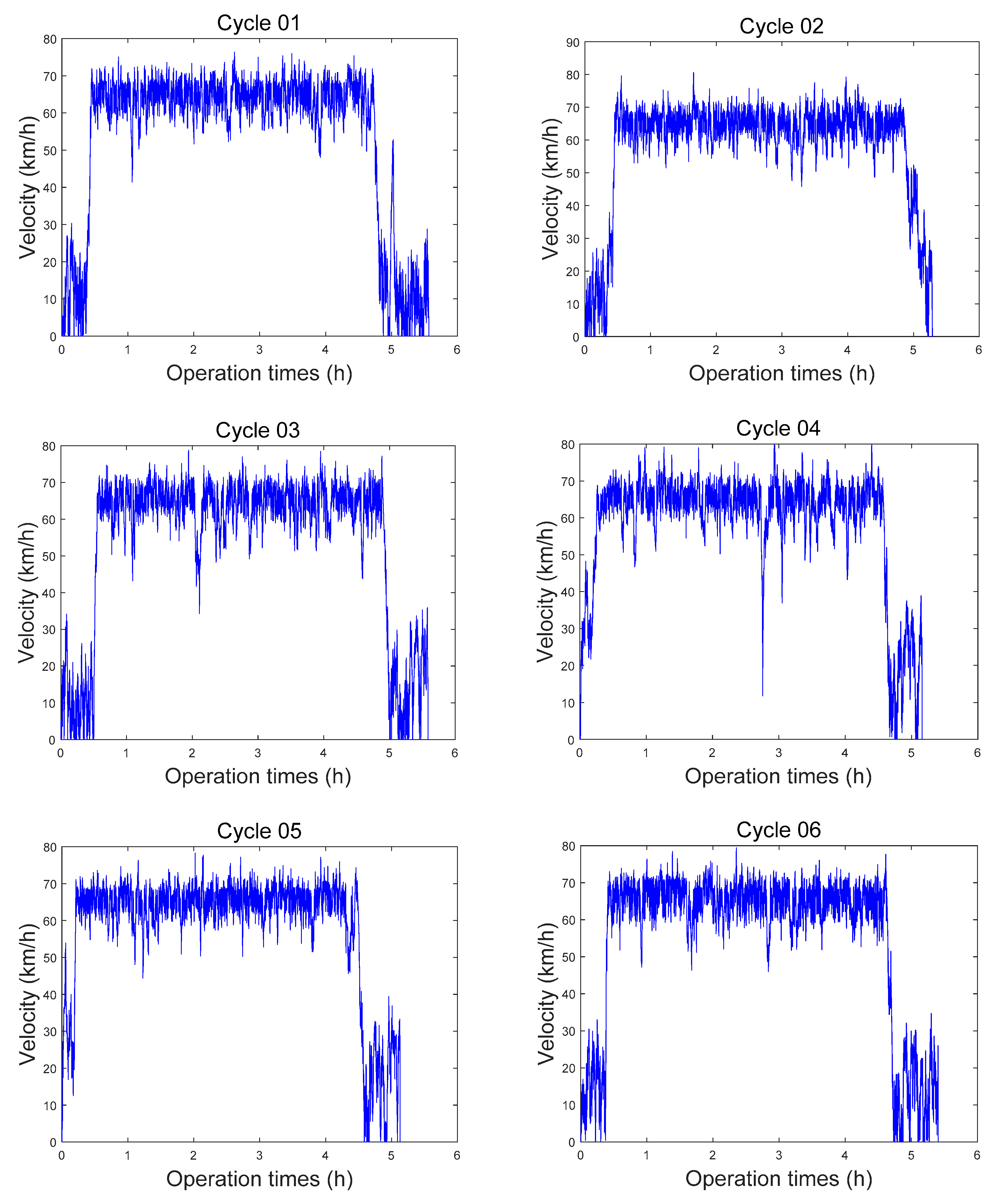
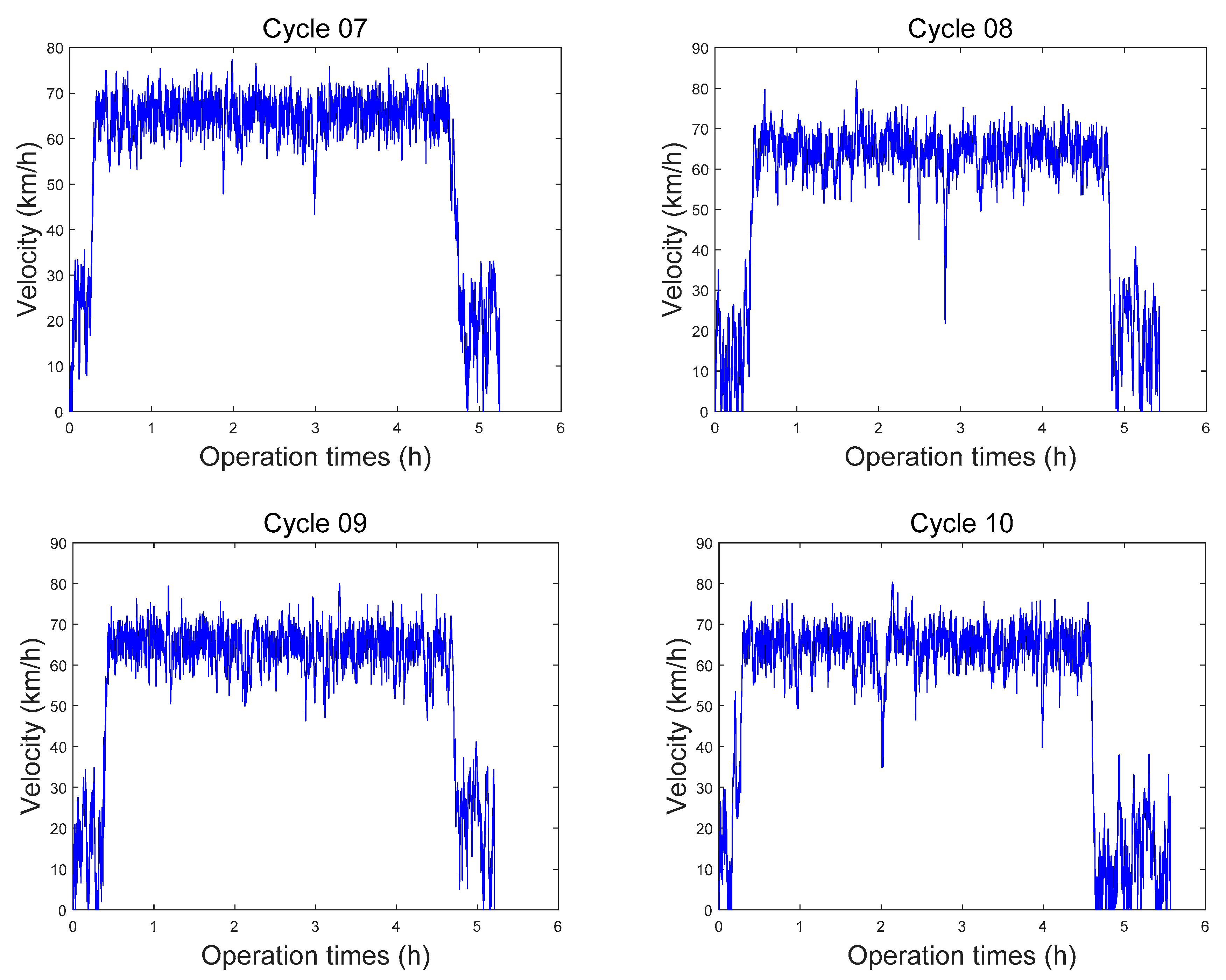
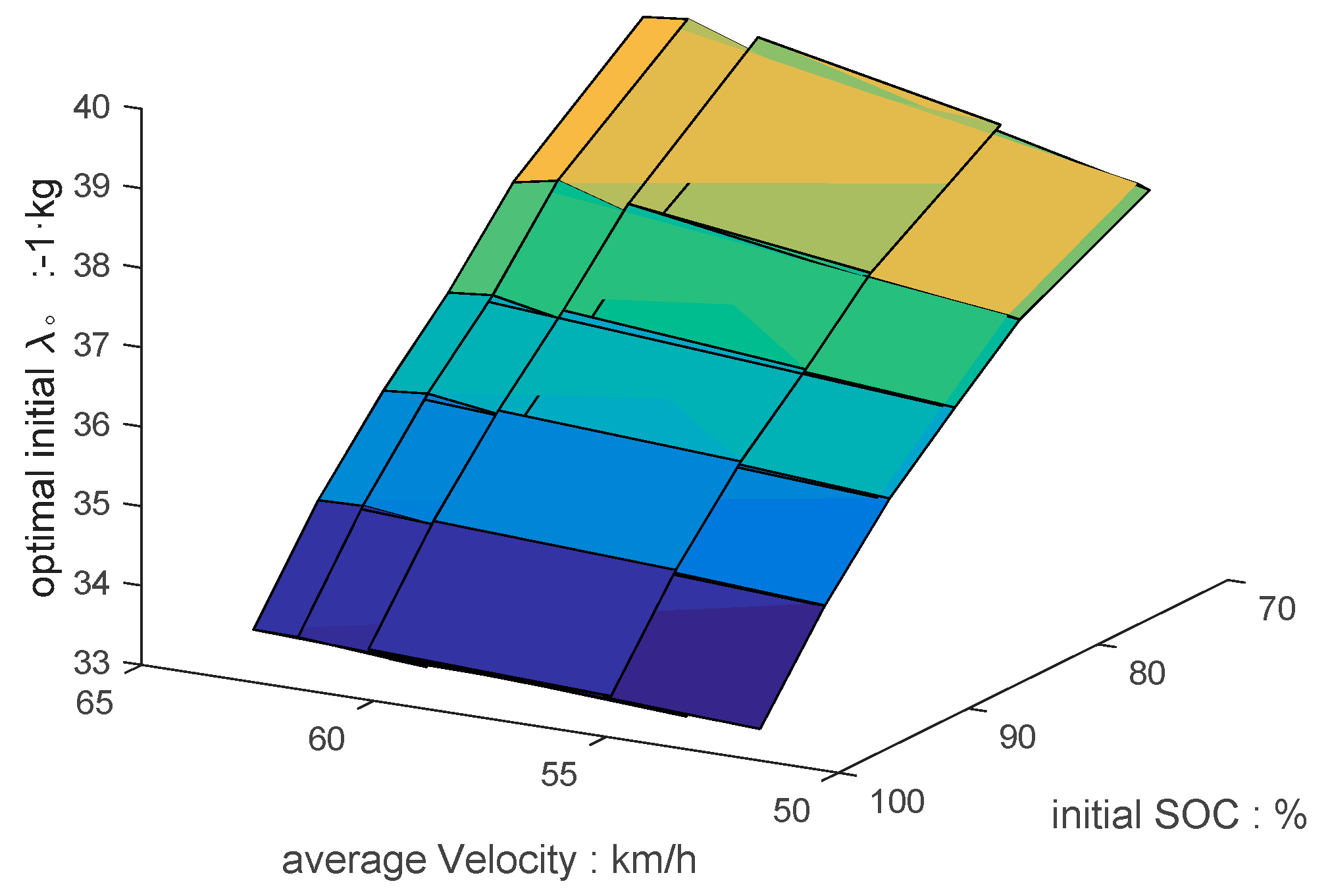
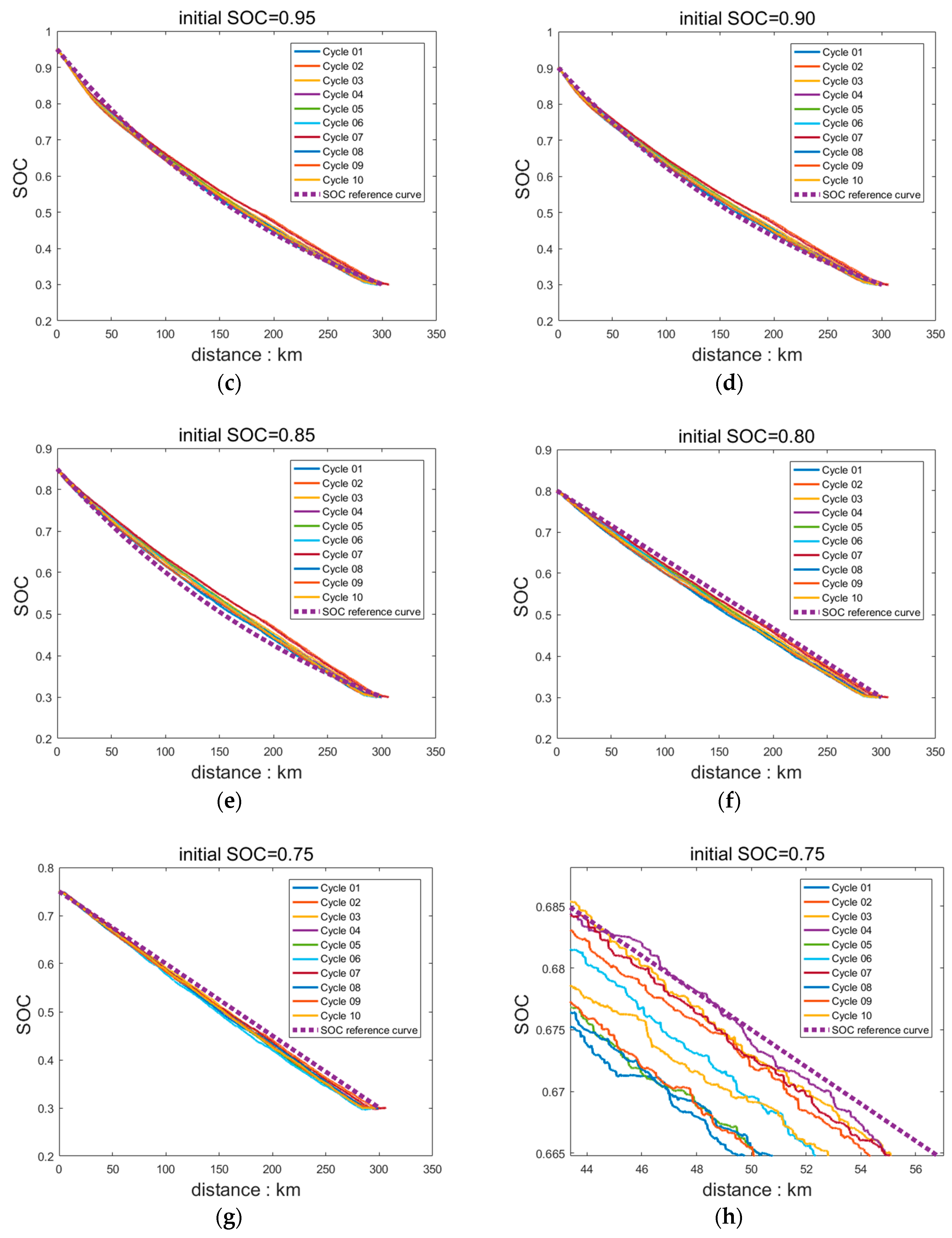
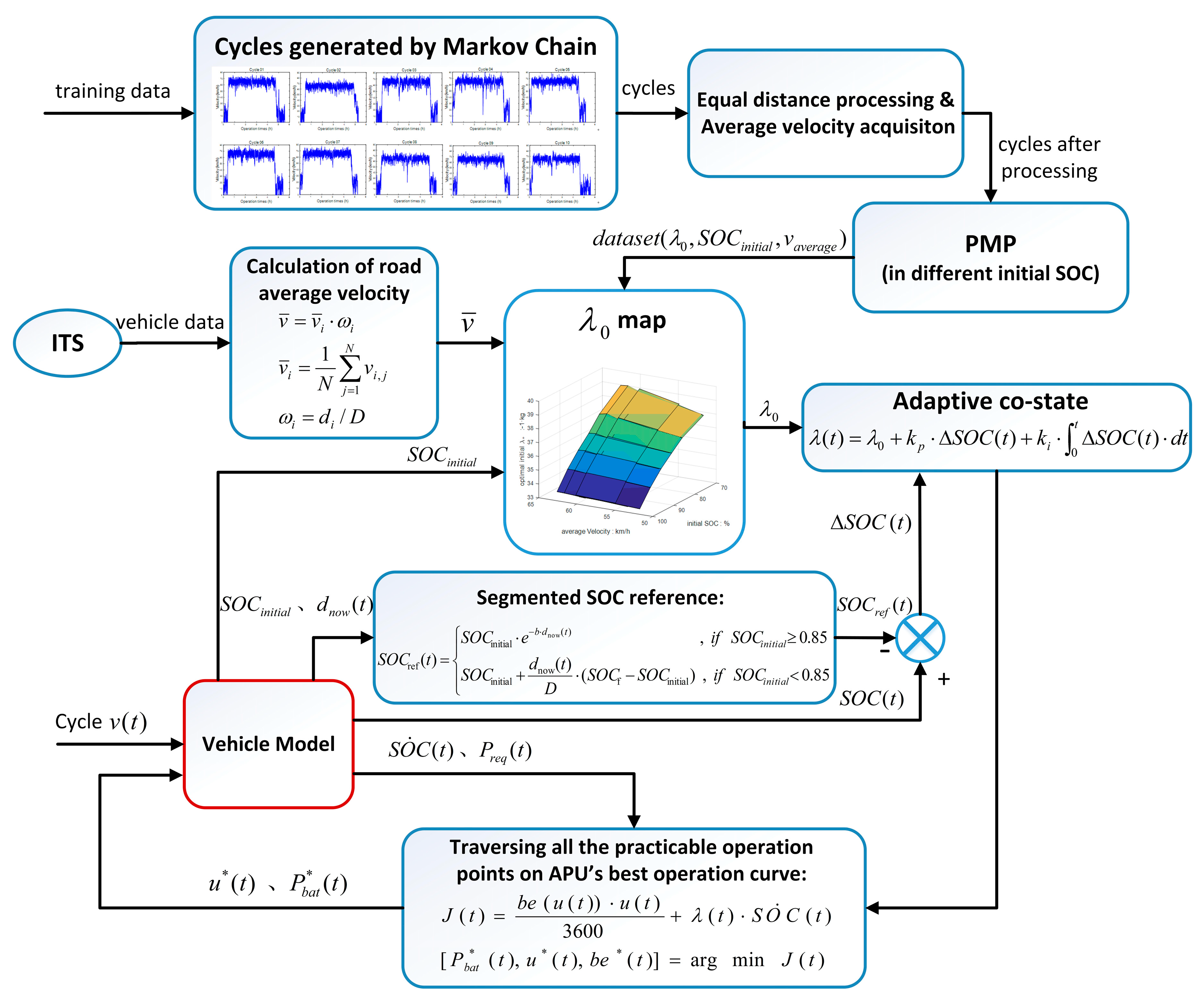
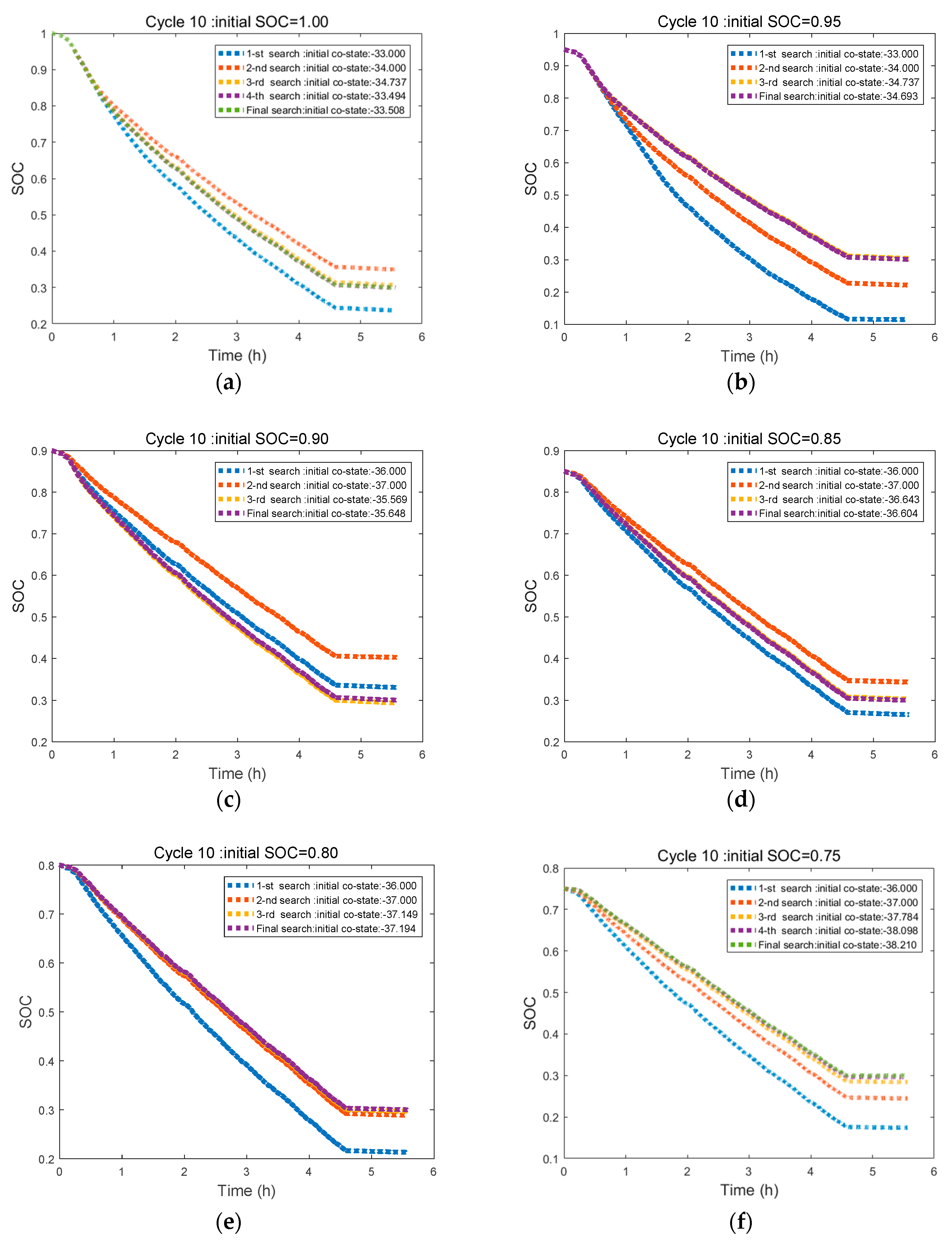
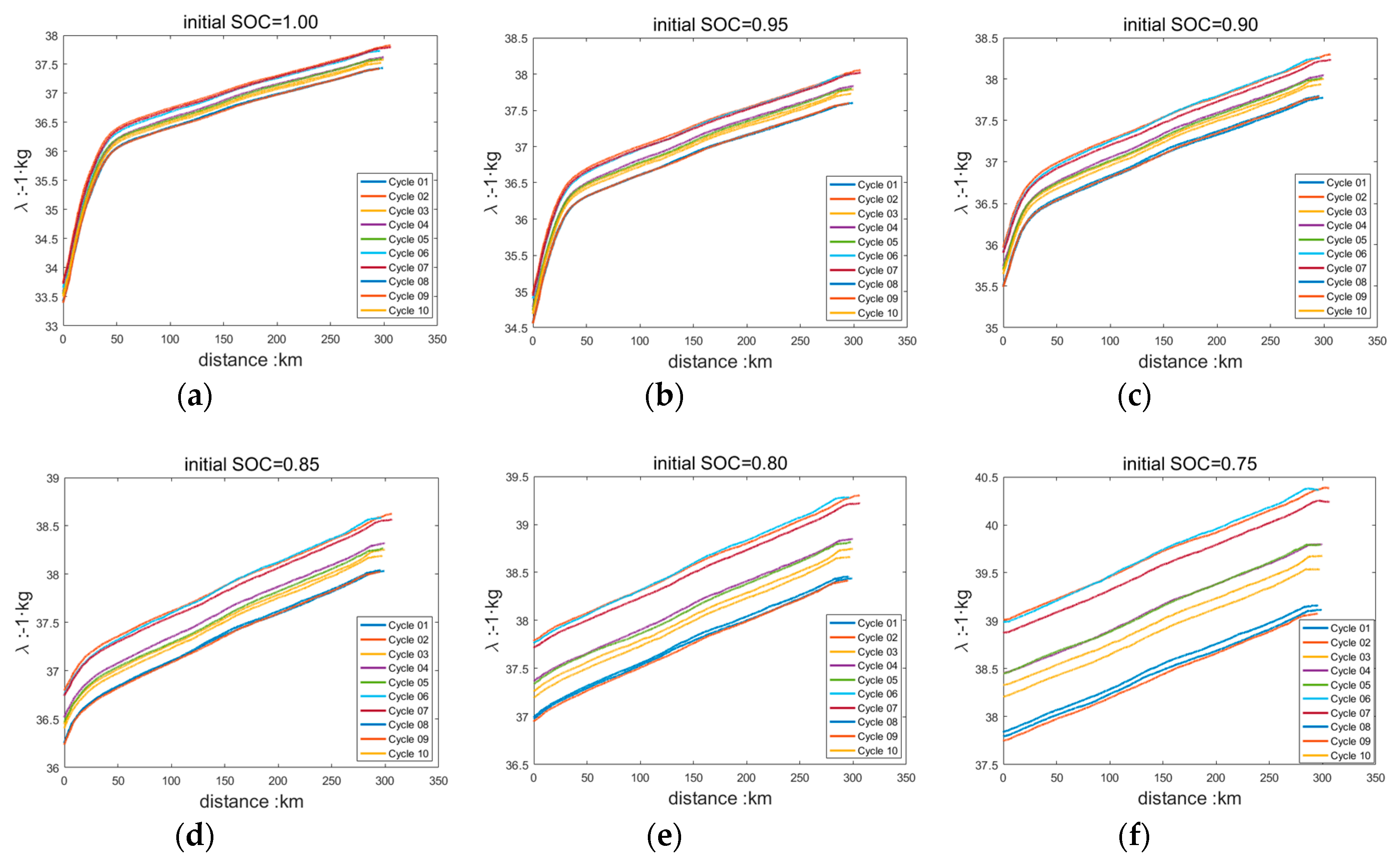
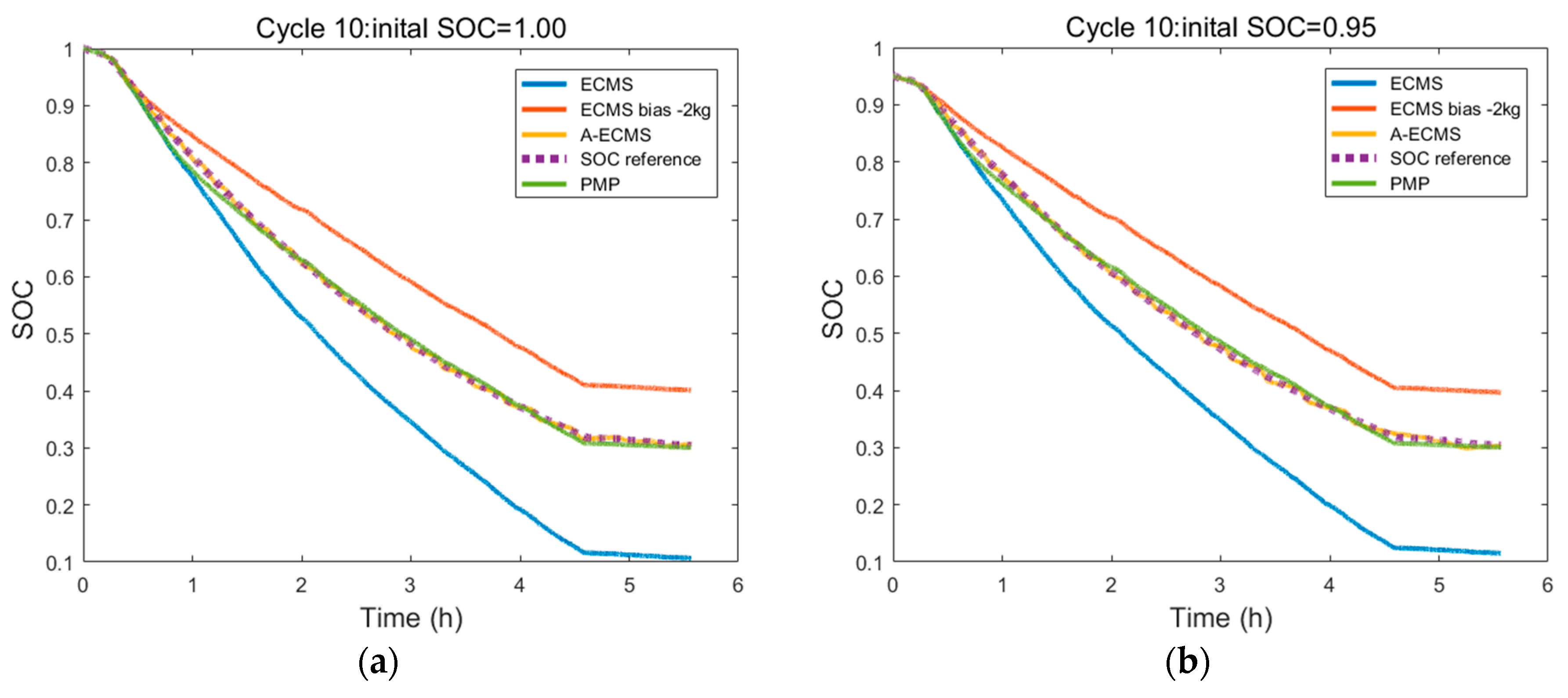
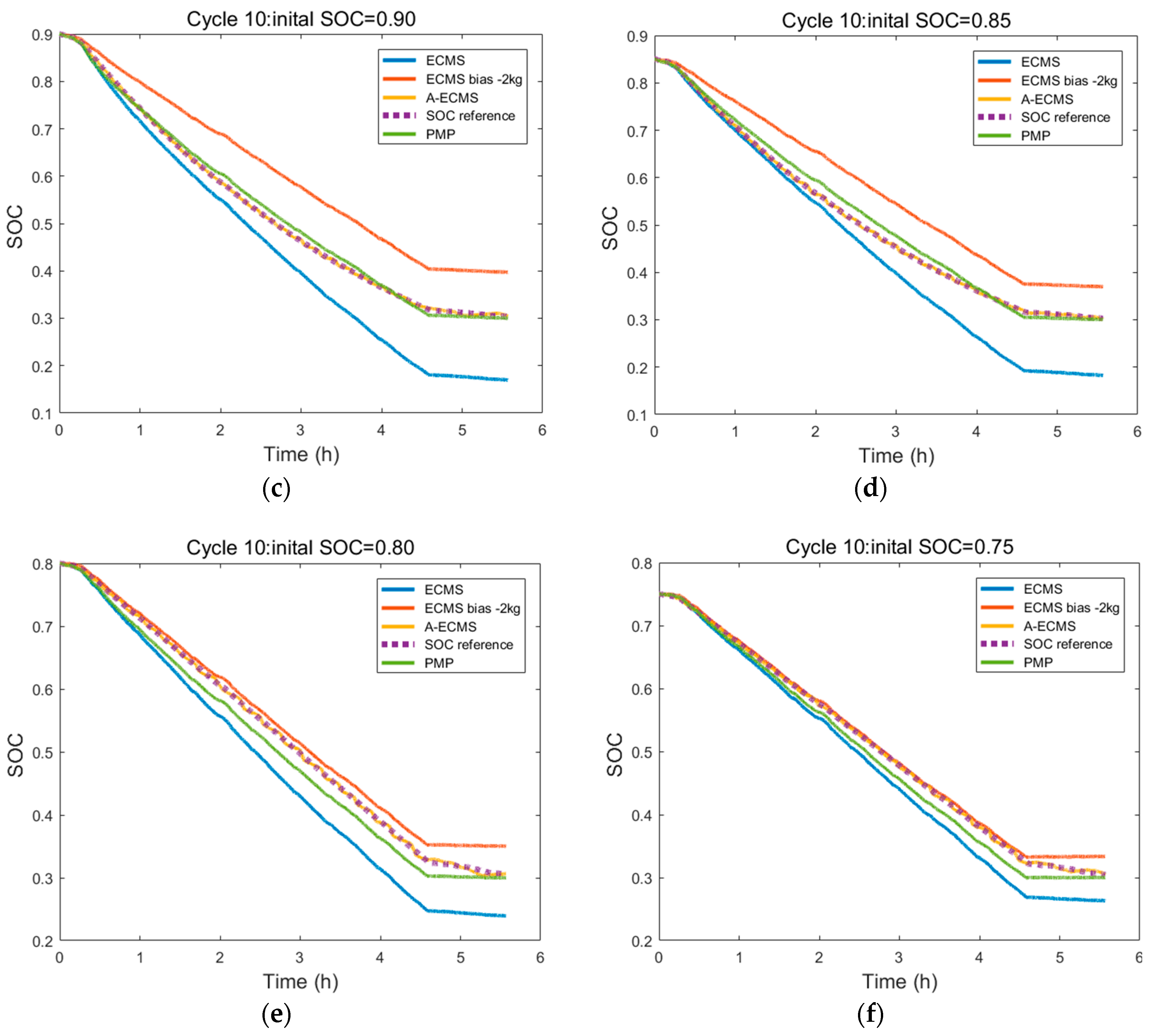
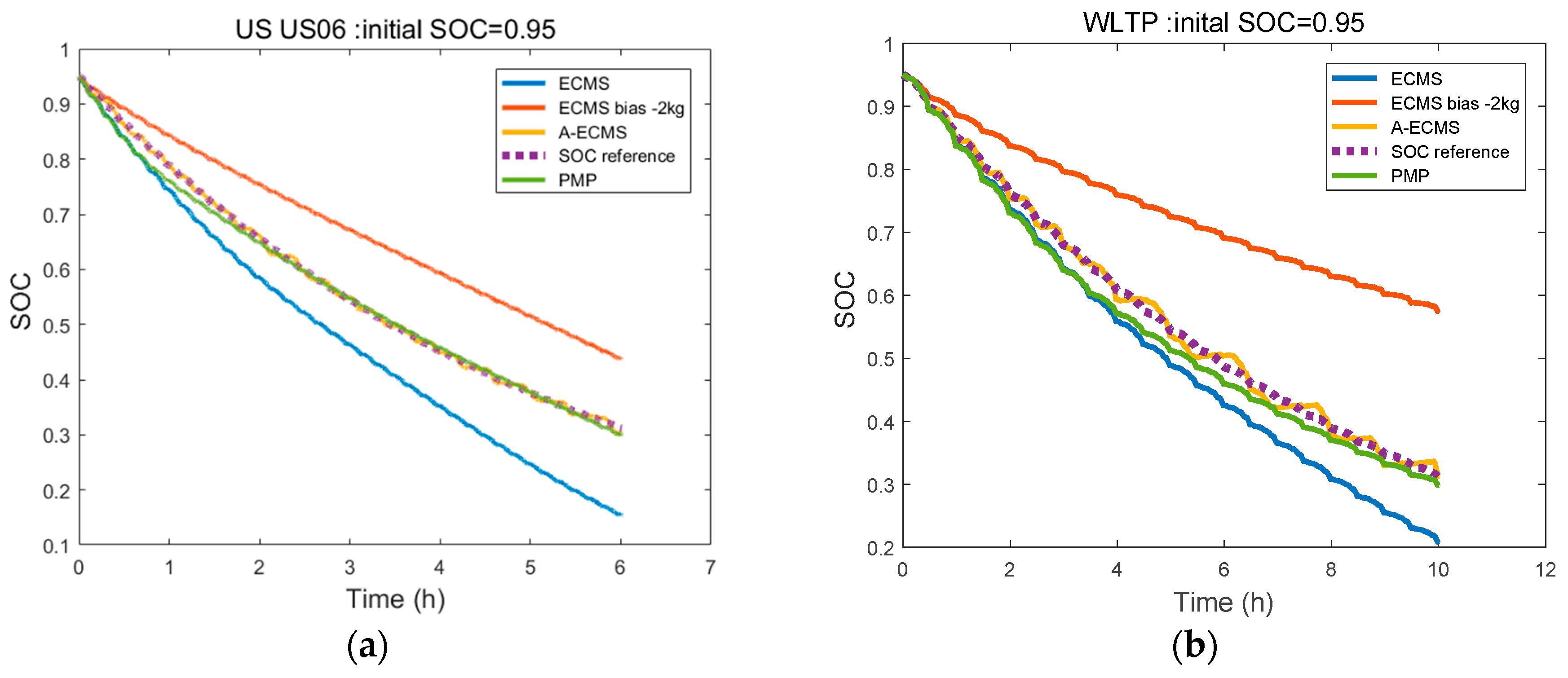
During formulation of A-ECMS, the key is to build a co-state adaptive function, which fully considers the effects of initial SOC, driving distance, and working conditions on the co-state. Since this study was targeted at extended-range electric buses operating on fixed routes, the driving distance could be ignored. The co-state function consisting of fixed term and dynamic term was designed. To determine the fixed term, we first had to get the optimal initial co-state map, which could be determined by solving multiple target driving cycles by using PMP. However, during control strategy research, there are always few working conditions suitable for the exploitation goal, which largely hinders the determination of concrete control strategy parameters and the simulation of control effect. For this problem, a goal condition generation method based on Markov chain was proposed. The working condition was gradually generated through the formation of a highway and city transition probability matrix. Furthermore, with the ITS-acquired vehicle information, the average vehicle speed was determined by weighted averaging. Together with the initial SOCs of vehicles, the fixed terms could be determined by interpolating the co-state map. The role of the dynamic term was to make the SOC at termination be equal to the set value, so as to make full use of the electrical energy. It usually can be realized by following the reference SOC. However, the common SOC reference curve is a linear function of SOC and distance, which totally disobeys the ideal solution. A segmented SOC reference curve was put forward according to the optimal SOC changing curves under different initial SOC conditions solved using PMP. When the initial SOC was large or small, an exponential reference curve and a linear reference curve were selected, respectively, which better fitted the variation of the optimal SOC. With the introduction of PI, the deviation of the real SOC from the reference curve was regarded as the input to real-time adjust the co-state dynamic term, so as to follow the reference curve. During the research, A-ECMS was simulated under different working conditions and different initial SOCs. Results showed A-ECMS could meet the design requirements and was well adaptive.